Neutron relative biological effectiveness in Hiroshima and Nagasaki atomic bomb survivors: a critical review

Abstract

The calculated risk of cancer in humans due to radiation exposure is based primarily on long-term follow-up studies, e.g. the life-span study (LSS) on atomic bomb (A-bomb) survivors in Hiroshima and Nagasaki. Since A-bomb radiation consists of a mixture of γ-rays and neutrons, it is essential that the relative biological effectiveness (RBE) of neutrons is adequately evaluated if a study is to serve as a reference for cancer risk. However, the relatively small neutron component hampered the direct estimation of RBE in LSS data. To circumvent this problem, several strategies have been attempted, including dose-independent constant RBE, dose-dependent variable RBE, and dependence on the degrees of dominance of intermingled γ-rays. By surveying the available literature, we tested the chromosomal RBE of neutrons as the biological endpoint for its equivalence to the microdosimetric quantities obtained using a tissue-equivalent proportional counter (TEPC) in various neutron fields. The radiation weighting factor, or quality factor, Q_n, of neutrons as expressed in terms of the energy dependence of the maximum RBE, RBE_m, was consistent with that predicted by the TEPC data, indicating that the chromosomally measured RBE was independent of the magnitude of coexisting γ-rays. The obtained neutron RBE, which varied with neutron dose, was confirmed to be the most adequate RBE system in terms of agreement with the cancer incidence in A-bomb survivors, using chromosome aberrations as surrogate markers. With this RBE system, the cancer risk in A-bomb survivors as expressed in unit dose of reference radiation is equally compatible with Hiroshima and Nagasaki cities, and may be potentially applicable in other cases of human radiation exposure.

INTRODUCTION

The year 2015 marked the seventieth anniversary since the atomic bomb (A-bomb) explosions over the cities of Hiroshima and Nagasaki in August 1945. As unique cases of human exposure to radiation on a large scale, the health effects of the A-bomb radiation events have attracted worldwide attention. A long-term follow-up of A-bomb survivors in the life-span study (LSS), initiated in 1950 and continued by the US Atomic Bomb Causality Commission (ABCC) and its successor, the USA–Japan binational Radiation Effects Research Foundation (RERF), has provided fundamental information on cancer and non-cancer disease risk in humans following exposure to ionizing radiation [1–3]. The dose–effect relationship obtained from the LSS formed the scientific basis of the radiation protection standard. Despite uncertainties at low-doses (<0.2 Sv) the dose–risk relationship has been pragmatically dealt with in line with an unproven assumption of the ‘linear non-threshold (LNT)’ model [4]. In addition, there is also an upsurge of interest regarding more prospective use of the obtained knowledge as a generalized measure of risk assessment in various scenarios of human radiation exposure, including radiation accidents, medical exposures, and radiation in the environment and workplace. To date, health effects in A-bomb survivors have been correlated with direct radiation exposure, i.e. prompt and delayed γ-rays and neutrons, of which the dosimetry system has been improved by continued revisions up to the present dosimetry system 2002, or ‘DS02’ [5]. For the dose–effect relationships in A-bomb survivors to be applied beyond the quality of radiation as a generalized measure of risk assessment at a Gy or Gy-equivalent basis of reference radiation, the neutron component should be adequately weighted by its relative biological effectiveness (RBE).

To date, neutrons in A-bomb radiation in Hiroshima and Nagasaki have been conventionally weighted by a constant value of RBE = 10. However, this has been repeatedly questioned in light of common radiobiological knowledge. Indeed, an extensive study recently performed on chromosomal effectiveness of fission neutrons with varying energy spectra indicated that the dose-dependent variable RBE was most suitable for explaining the variability of dose–respons for somatic chromosome aberrations and cancer risk in A-bomb survivors [6]. However, this assertion has been criticized by Cullings et al. [7], who claimed that the experimentally derived RBE might be implausible for determining cancer rates in the LSS, and that in the γ–neutron mixed radiation field, the neutron RBE might be highly suppressed at low levels compared with that estimated for neutrons alone in the experimental system. The discrepancy in the neutron weighting system with reference to A-bomb survivors might have a strong impact on the risk evaluation following human exposure to neutrons, since neutron exposure often occurs in association with a mixture of γ-rays of either extrinsic or intrinsic origin. Here, we show that the unique neutron RBE described in Cullings et al. [7] in A-bomb survivors is due largely to an a priori linear setting of dose–response curves for biological endpoints; this can otherwise be better explained by the dose-dependent variable RBE without including biological endpoints in random dosimetry errors. The present weighting system best provides the commonality for Hiroshima and Nagasaki, despite large difference in their γ–neutron ratios, and may provide a common platform for radiobiology, microdosimetry, risk evaluation and setting of radiological protection.

DATA ASSESSMENT AND RESULTS OF ANALYSES

Uncertainties in the ‘survivor dose estimate’ in determining neutron RBE

The cancer incidence (or mortality) in A-bomb survivors has been correlated with organ dose of radiation, in which prompt and delayed source-term γ and neutron data are first converted to the free-in-air (FIA) kerma at the survivor location by considering the transporting factors of the air, then to the shielded kerm by shielding transmission factors, then to the organ dose by considering body transmission factors specific to the particular organ together with neutron-activated γ-rays [5, 7, 8]. In addition, RERF recently introduced further modifications of doses, in the so-called ‘survivor dose estimate’. Modifications include the truncation of unreasonably high doses to 4 Gy, and a dose adjustment made on the basis of random dosimetry errors, which include systematic and random dosimetry errors and imprecise knowledge of survivor location and shielding [9, 10]; these are incorporated as coefficients of variation over an assumed linear dose–response relationship [11–14]. Also considered in the estimation of error magnitude were uncertainties in the various biological endpoints, such as chromosome aberrations and epilation in survivors [15–17].

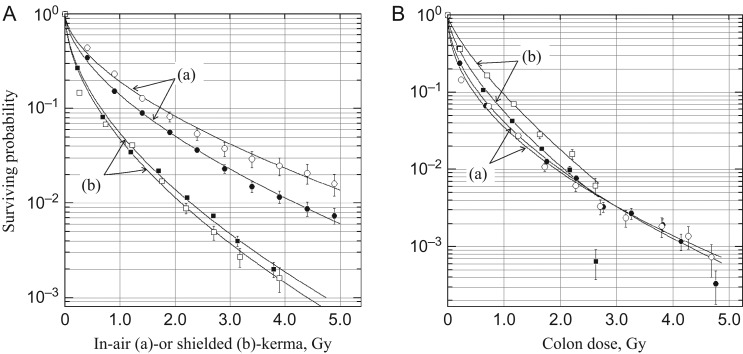
Fig. 1 shows survivor distribution expressed in terms of relative survivor density against dose, S(D), which is fitted to a Weibull hazard function.

$$S(D)=\exp [-{\{(D-\mathrm{\delta })/\mathrm{\eta }\}}^{\mathrm{\kappa }},$$ (1)

where D is dose in Gy, δ is a location parameter, η is a scale parameter and κ is a shape parameter. The mean dose, Ď, and median dose, $\dot{D}$, are given by

$$Ď=\delta +\mathrm{\eta }\mathit{\Gamma }(1/\kappa +1),\dot{D}=\delta +\mathrm{\eta }\mathit{\Gamma }{(ln2)}^{1/\kappa },$$ (2)

in which Γ(…) is a gamma function. Since the location parameters are generally very small, δ ≈ 0, at κ = 1, survival is randomly distributed along with the exponential function of dose, and 37% survival probability is given by R(η) = 1 − S(η). The survivor distribution is not the real probability of surviving, but is a surrogate index in which a relative number of survivors receive at least the indicated doses. Fig. 1A(a) is replotted from Table II of Pierce et al. [11] and shows survivor distribution, where the cumulative number of survivors is plotted against the DS86 ‘In-Air’ tissue kerma. The In-Air tissue kerma is a tissue-equivalent kerma in air at a survivor's location after adjustment for external shielding. The Weibull parameters are η_H = 31.810 ± 12.828 and κ_H = 0.592 ± 0.121 for Hiroshima (H), η_N = 42.778 ± 15.289 and κ_N = 0.592 ± 0.134 for Nagasaki (N), δ = 0.1 Gy for both cities. City-specific differences appear in the scale parameters. The monotonically decreasing densities were the same as those of Pierce et al. [11]. By setting x as the true dose, z as the estimated dose, and ε as the response variable, they determined the adjustment factor, p(z) = [z − E(x|z)]/z, that satisfied the variate response E(ε|x) at several levels of coefficient of variation. The variate E(ε|x) was linear for x and was tested for various biological endpoints. The adjustment factor was thus dose-dependent and differed between the two cities. Currently, a 35% level of error in the coefficient of variation at each dose level has been adopted by RERF, by which shielded kerma and organ doses have been adjusted [1–3, 5]. The dose adjustment factors are dose- and city-dependent, varying from 1.0 at 0.38 Gy to 0.82 at 4 Gy in Hiroshima and from 1.0 at 0.52 Gy to 0.86 at 4 Gy in Nagasaki. The use of these adjustments results in a 10–15% increase in cancer risk [1, 5]. However, it should be noted that when survivor probability is plotted against the DS86 shielded kerma, the Weibull probability densities of the two cities become very similar (η_H = 16.893 ± 2.999, η_N = 13.156 ± 6.036, κ_H = 0.584 ± 0.062, κ_N = 0.550 ± 0.114) and the city difference disappears (Fig. 1A(b)). The shielded kerma is a dose that the survivor could receive after transmission of all shielding structures. Since the LSS cohort was not selected on the basis of dose, the results indicate that the city difference is derived largely from the difference in the external shielding, including city-specific geographical differences, rather than from the difference in systematic dosimetry errors. When the shielding calculation is properly applied, the dose adjustment by city-specific ‘random dosimetry errors’ may not be justified.

Fig. 1.

Relative number of survivors in life-span study (LSS) cohort for unmodified and unweighted dose. (A) DS86 dose system. (a) DS86 ‘In-Air’ tissue kerma. The original data were taken from Table II of Pierce et al. [11]. (b) DS86 shielded kerma. The distribution of survivors was calculated from the RERF ‘DS02can’ database. (B) DS02 colon dose. The distribution of survivors was calculated from the RERF ‘lssinc07’ database. (a) Surviving probability plotted against unmodified colon dose (coluDS02w1). (b) Surviving probability plotted against modified colon dose (colaDS02w1), in which unreasonably high are truncated to 4 Gy and the doses were adjusted by dose- and city-specific adjustment factors. Solid symbols = Hiroshima, open symbols = Nagasaki.

Further to the above, to clarify the problem of dose adjustment, the distribution of survivors was studied for the DS02 dosimetry system using the RERF ‘lssinc07’ database. The survivor distribution was similarly compiled, except for the effects of dose modifications. The survivor distributions are presented in Table 1, and their fit to the Weibull distribution is shown in Fig. 1B. As was the case using DS86 shielded kerma, the city difference was not seen, or commonality between the two cities was greatly improved, when an unadjusted (pre-adjustment) and unweighted (RBE = 1 for neutrons) DS02 colon dose, coluDS02w1, was used (Fig. 1B(a)). In contrast, when the survivor distributions were studied after dose modifications (dose adjustment and truncation) colaDS02w1, the dose–responses clearly dissociated between Hiroshima and Nagasaki (Fig. 1B(b)). The difference was again in their scale parameters (Table 1). As seen at the last dose points (>2.5 Gy) in Fig. 1B(b), the effects of truncation alone are more evident in Hiroshima survivors, reflecting the dominance of truncated doses in this dose category in Hiroshima.

Table 1.

Distribution of survivors according to DS02 colon dose and parameters of the best fit to the Weibull distribution

Dose systema		(a) DS02 colon dose (unmodified)				(b) DS02 colon dose (modified)
City		Hiroshima		Nagasaki		Hiroshima		Nagasaki
Dose category		Mean	Survivor	Mean	Survivor	Mean	Survivor	Mean	Survivor
<0.1		0.017	41 144	0.009	22 190	0.032	21105	0.026	6684
0.1–0.5		0.227	9383	0.246	2079	0.226	9383	0.246	2079
0.5–1.0		0.688	2176	0.738	996	0.661	2200	0.722	996
1.0–1.5		1.256	737	1.260	430	1.180	807	1.195	446
1.5–2.0		1.771	272	1.729	120	1.701	299	1.664	132
2.0–2.5		2.302	241	2.279	74	2.204	316	2.324	101
2.5–3.0b		2.778	31	2.715	24	2.661	22	2.649	65
3.0–3.5		2.273	42	3.173	14
3.5–4.0		3.838	41	3.813	12
4.0–4.5		4.162	46	4.285	17
4.5–5.0		4.784	18	4.694	19
Weibull parameters	μ	10.446 ± 4.424		8.090 ± 4.343		19.314 ± 3.838		32.199 ± 4.571
	κ	0.519 ± 0.199		0.482 ± 0.291		0.643 ± 0.110		0.761 ± 0.077
	Ď	0.212		0.182		0.299		0.404
	$\dot{D}$	0.068		0.046		0.141		0.224

^aDS02 colon doses with neutrons unweighted (RBE = 1): (a) unmodified doses, in which doses are neither truncated nor adjusted. (b) modified doses, in which unreasonably high doses are truncated to 4 Gy and doses are adjusted according to the dose- and city-specific adjustment factors. The number of survivors was compiled from the RERF ‘lssinc07’ database. The surviving probability in Fig. 1 was calculated assuming that the survivors at a given dose category could also tolerate the preceding doses, i.e. S_i = ∑N_i/T, where T is total number of survivors and Ni is the number of survivors at the ith dose category.

^b0.25 ≤ Gy for modified dose system.

The continued efforts of the USA–Japan working group on the assessment of the A-bomb radiation dosimetry for Hiroshima and Nagasaki will have greatly reduced systematic bias and perhaps random errors as well. Therefore, the magnitude of the allowable level of dosimetry error could be based on a flawed assumption concerning neutron RBE and the dose–response model of the biological endpoints considered. The importance of neutron RBE in determining dosimetry errors has been pointed out previously by Jablon [9] and Gilbert [10], and this still needs to be investigated.

Radioactive fallout shadow and its influence on the dose–response model

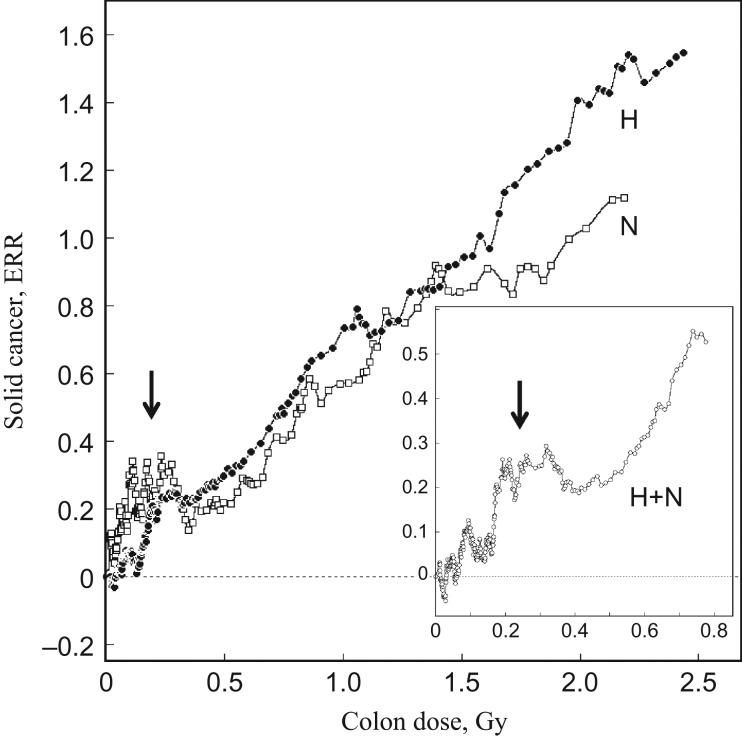
In the mixed radiation field, the a priori setting of the dose–response model for biological endpoints strongly influences the allowance for the kinetics and magnitude of neutron RBE as well. While there is no city-specific difference in the survivor distribution profile as a function of shielded kerma or organ doses (Fig. 1B(a)), differences do exist between the two cities in the dose–response patterns of the biological endpoints, such as chromosome aberrations and cancer risk. This can be seen clearly in Fig. 2, which shows a model-free visualization of excess relative risk (ERR) of solid cancer against the unadjusted colon dose in Gy, in which the neutrons are weighted by RBE = 1, coluDS02w1. ERR was calculated from the RERF ‘lssinc07’ database, as described [6]. The ‘lssinc07’ database contains cancer incidence data for 111 952 persons followed up during the period encompassing 1958–1998, in which information on the occurrence of cancer is cross-tabulated in a total of 26 806 data cells containing information on city, sex, person years at risk, age at the time of bombing, attained age, DS02 dose, etc. Persons exposed to doses <0.05 Gy and those who were not in the city at the time of bombing (NIC) were treated as controls. Instead of following a dose category strategy, the dose–response profiles were visualized by moving window averaging, whereby, to avoid systematic distortion of the distribution of relative risk around the mean, a window of 1500 cells was consecutively moved with a step size of 50, here referred to as MW = w1500s50. The mean dose within the window was expressed as the person-year weighted dose.

Fig. 2.

Model-free visualization of excessive relative risk (ERR) of solid cancer by moving window averaging for unadjusted and unmodified DS02 colon dose, coluDS02w1. Insert shows the ERR at low doses in the two cities combined cohort. Solid circles = Hiroshima (H), open squares = Nagasaki (N), open circles = two cities combined (H + N). The abnormal elevation of ERR at low doses is shown by arrow.

It is evident from Fig. 2 that, in spite of the comparability of dose distribution between the two cities (Fig. 1B(a)), the cancer rate clearly differs between the two cities, implying that the late effects are not simply a function of the shielded kerma or organ dose, or coluDS02w1. It should also be noted that abnormal elevations of the cancer rate are apparent at low doses, below 0.2 or 0.3 Gy, in a manner that is more pronounced in Nagasaki. In order to adjust for the cohort size of the two cities, the calculation was made in a combined cohort. As seen in the insert of Fig. 2, the abnormal elevation at low doses was again evident. The origin of this abnormal elevation will be discussed later. It is highly likely that, in addition to the dose-dependent downward shift of doses by adjustment factors, this abnormal elevation at low doses adds a factor to the global dose–response curve in favor of dose linearity.

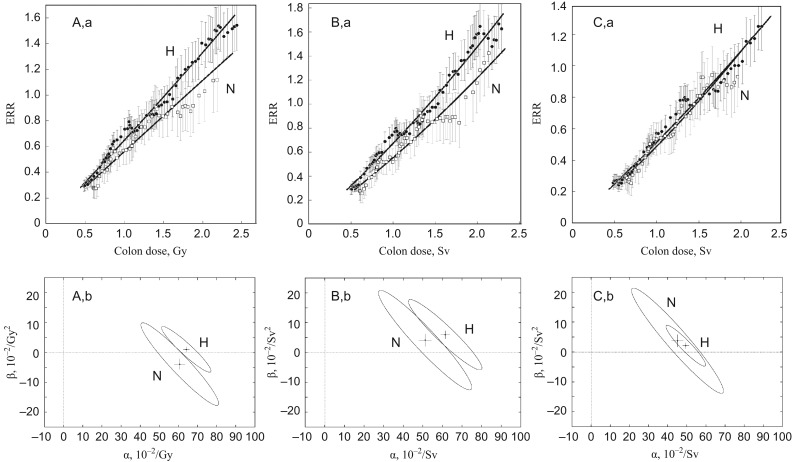
In order to avoid the influence of this abnormality at low doses, ERR dose responses were calculated for doses in which a lower cut-off point of 0.3 Gy (or Sv) and an upper cut-off point of 3 Gy (or Sv) of the doses of individual survivors were used (Fig. 3). The dose-dependent RBE of neutrons used in Fig. 3C is the same as that reported previously [6], i.e.

$$\begin{array}{cc}\mathrm{RBE}\hfill & =D_{\mathrm{\gamma }}/D_{\mathrm{n}}\hfill \\ & =[2({\mathrm{\alpha }}_{\mathrm{n}}+{\mathrm{\beta }}_{\mathrm{n}}{D}_{\mathrm{n}})]/\left[{\mathrm{\alpha }}_{\mathrm{\gamma }}+{\left\{{{\mathrm{\alpha }}_{\mathrm{\gamma }}}^2 + 4{\mathrm{\beta }}_{\mathrm{\gamma }}\left({\mathrm{\alpha }}_{\mathrm{n}}+{\mathrm{\beta }}_{\mathrm{n}}{D}_{\mathrm{n}}\right)D_{\mathrm{n}}\right\}}^{1/2}\right],\hfill \end{array}$$ (3)

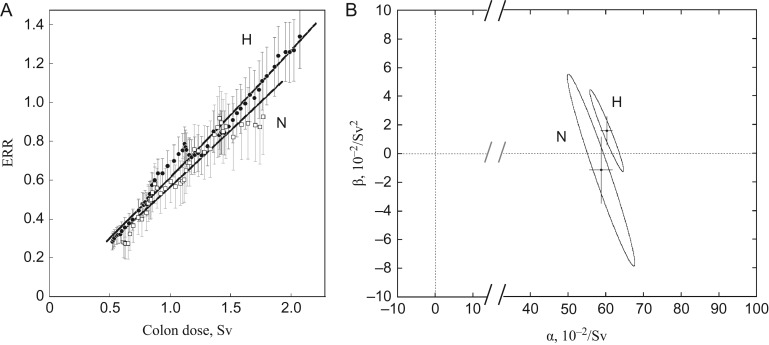
where the ratio of the iso-effective doses of neutrons (D_n) and ⁶⁰Co γ-rays as reference radiation (D_γ) is expressed by the linear–quadratic model, y = C + αD + βD². The parameters used are α_γ = 1.310 × 10⁻²/Gy, α_n = 1.127/Gy, β_γ = β_n = 5.355 × 10⁻²/Gy² and R_m = α_n/α_γ for maximum RBE (RBE_m). The quotient θ = β/α is the curvature parameter, a large value for which implies a strongly curved dose–response relationship. It is θ_γ = 4.08 for γ-rays and θ_n = 0.05 for neutrons. Because of the difference in curvature, the ratio of two doses, D_γ and D_n, yielding the same effect, i.e. RBE, is variable depending on dose. The dose–response relationship of ERR was fitted to a linear–quadratic model, y = αD + βD², by the maximum likelihood method. As seen in Fig. 3, it is apparent that the choice of neutron weighting system is a critical determinant for giving an equivalence of cancer risk between the two cities. In contrast to the survivor distribution presented in Fig. 1B(a), the city difference in cancer risk was already apparent when RBE = 1 was used for neutrons (Fig. 3A), and could not be eliminated by the conventional use of a constant RBE = 10 together with or without the dose adjustment (Fig. 3B). The use of other values for constant RBE did not improve the city equivalence (data not shown). The dose–response relationships of the two cities were highly matched only when neutrons were weighted by a dose-dependent variable RBE (Fig. 3C). The dose–response relationship of ERR for all solid cancers for a combined cohort of the two cities is:

$$\begin{array}{c}y=(4.264\pm 0.129)·{10}^{-1}D+(6.331\pm 0.855)·{10}^{-2}{D}^2,\hfill \\ (0.3\le D<3.0),\hfill \end{array}$$ (4)

where D is the DS02 unadjusted colon dose in Sv in which neutrons are weighted by a dose-dependent variable RBE (Eq. 3). The city difference in the dose–response relatioship was tested by comparing the joint confidence regions of the α- and β-terms as calculated by:

$$S(\mathrm{\alpha },\mathrm{\beta })=S({\mathrm{\alpha }}^{⁎}{,\mathrm{\beta }}^{⁎})[1 + (v_1/v_2)C(v_1;1-q)],$$ (5)

where S(α,β) is the residual sum of squares, S(α^*,β^*) is the variance. C(v₁;1 − q) is the percentile of χ² distribution at the 100 × (1 − q)% level (two-sided test) for the number of degrees of freedom, v₁ = p and v₂ = n − p, where p is the number of parameters and n is the number of data points. As shown in Fig. 3 (lower panel), half-sized 95% confidence ellipses (q = 0.05) of the two cities fully overlap only when neutrons are weighted by a dose-dependent variable RBE (Fig. 3C and b). This indicates that the dose responses of cancer risk in the two cities are comparable and mutually compatible and are potentially applicable to other cases of human radiation exposure as a reference dose–response function. These results thereby reject the use of a constant RBE and dose adjustment by random dosimetry errors. The a priori setting of a linear dose–response relationship could be one reason that renders a large variability in biological endpoints and the neutron RBE inflexible. Indeed, uncertainties in dose–response relationships of chromosome aberrations have been solved by introducing the dose-dependent variable RBE of neutrons [6, 18]. Severe epilation could also be a possible outcome (our unpublished results). In this dose range, the dose–response kinetics of solid cancers and leukemia are also comparable beyond the city difference only when the neutrons are weighted by a dose-dependent RBE [19].

Fig. 3.

Dose–responses of excessive relative risk (ERR) of solid cancers in Hiroshima and Nagasaki (upper panel) and the testing of their statistical significance between two cities by 95% joint confidence regions (lower panel). (A) Unadjusted colon dose with neutrons weighted by RBE = 1 (coluDS02w1). (B) Adjusted colon dose with neutrons weighted by RBE = 10 (colaDS02w10). (C) Unadjusted colon dose with neutrons weighted by dose-dependent variable RBE (coluDS02wgn). Vertical and horizontal lines in the confidence ellipse show the SEs of the mean. For dose-dependent variable RBE, see Eq. (3). H = Hiroshima, N = Nagasaki.

In the context of the abnormal elevation at low doses, here we focused only on solid cancers, because while leukemia/lymphoma did not follow such an abnormal response in Hiroshima, the low-dose response pattern of leukemia/lymphoma in Nagasaki was not clear, possibly due to the inclusion of endemic adult T-cell leukemia/lymphoma, which was assumed to be refractory to the radiation carcinogenesis [19]. The origin of the abnormal elevation of the cancer rate at low doses is not clear. A subset (~20%) of the LSS cohort, called the adult health study (AHS) cohort, was reported to have received more frequent X-ray examinations during biennial medical examinations at ABCC/RERF [20–22]. Cumulative doses to the colon and stomach up to the year 1970 have been estimated to be ~90 mGy and ~500 mGy, respectively. However, the excess medical exposure may not be a factor, since exclusion of the AHS cohort did not eliminate the abnormal elevation of ERR at low doses (data not shown). According to the nuclear explosion scenario, human exposure to ionizing radiations resulting from A-bomb explosion is diverse, and includes prompt and delayed radiation (γ-rays and neutrons), fallout of radioactive fission products and vaporized radioactive fuel materials, and radiation from neutron-activated secondary radionuclides. The pathways are also multiple, consisting of direct acute or chronic external and internal exposure by inhalation or digestion (Ohtaki M, personal communication). However, the evaluation of radiation doses other than direct radiation suffers from the scarcity of systematic information necessary for the calculation of individual survivor doses, while not excluding other possible sources of exposure. Furthermore, uncertainties may also be due to disturbances in predicted levels of radioactive pollution/contamination due to rainfall 20–30 min after the bombing (black rain) and later by the large typhoon on the 17 September. The typhoon was one of the three largest typhoons ever to hit Japan, making landfall first on the island of Kyushu in a region ~160 km south of Nagasaki and then directly hitting Hiroshima. Nevertheless, aided by modern technologies, the radioactive fallout has been estimated from the radiation levels detected in some soil samples taken soon after the bombing: black rain streaks on walls, black rain deposits in roof guttering, and in undisturbed soil samples taken over a wide area [23]. The low-dose abnormality could be a reflection of radioactive fallout in general or of neutron-activated radionuclides. Cancer risk of early entrance into the bombed area is inconclusive; for instance, Kato et al. [24] reported no significant increase in the LSS cohorts of Hiroshima and Nagasaki, whereas in the different setting of the study cohort in Hiroshima, Matsuura et al. [25] suggested an elevation of cancer mortality, particularly in those entering on the day of the bombing. It is noteworthy, however, that the low-dose abnormality is more pronounced in survivors from the Nagasaki bombing, particularly with regards to cancers of the lung, liver and gallbladder [19]. It is thus tempting to correlate such cancer rates with the inhalation and/or ingestion of fuel materials, particularly of ²³⁵U/²³⁸U and ²³⁹Pu (isotope enrichment being 80% for ²³⁵U and 94.5% for ²³⁹Pu), in addition to other transmuted radionuclides. These fuel materials are easily vaporized by fission thermal energy (boiling temperature is 3930°C for ²³⁵U/²³⁸U and 3235°C for ²³⁹Pu). The internally incorporated ²³⁵U/²³⁸U and ²³⁹Pu continue to emit alpha-particles of high biological effectiveness. The air pollution resulting from these radionuclides is suggested by their inclusion in the fallout and/or black rain [26–32]. The biological half-life of ²³⁵U/²³⁸U is 15–100 days and that of ²³⁹Pu is ~200 years [33]. Uncertainties about the origin of the abnormal elevation of the cancer rate at low doses should be rigorously discussed before determining the direct A-bomb radiation as a sole concern in the cancer risk dose response and its modeling.

Assessment of neutron RBE by microdosimetric measurements

Cullings et al. [7] concluded that the RBE of neutrons in a γ–neutron mixed field such as that in A-bomb radiation differed from that of a so-called ‘pure neutron field’ experimental system, or that calculated independently from the intermingled γ-rays. Experimental systems using fission neutrons are usually a mixture of differing levels of γ-rays. Yet, at least at biologically relevant moderate doses, nil or negligible levels of interaction of high– and low–linear energy transfer (LET) radiations have been reported for various biological endpoints in mixed radiation fields [34–41]; however, others have reported synergistic-like effects [42, 43].

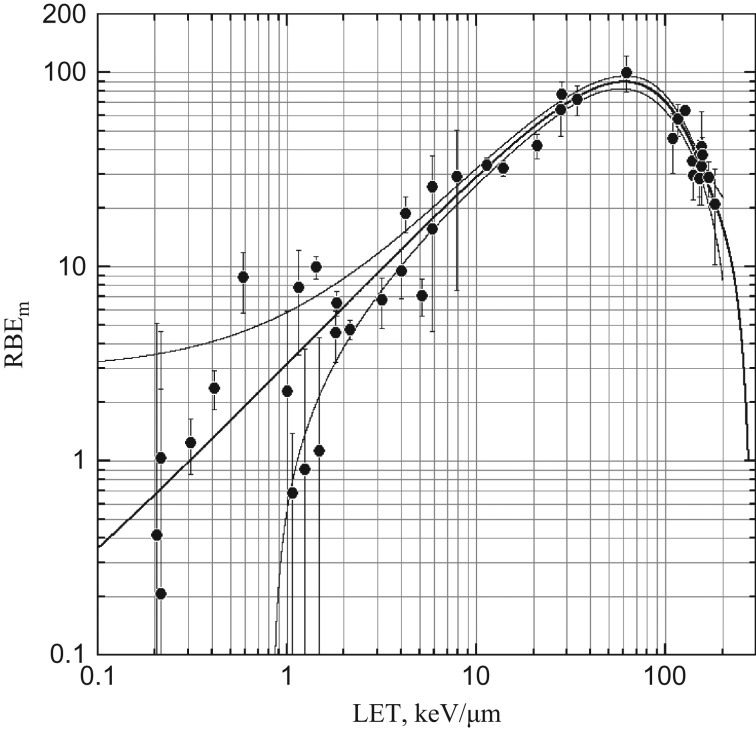
This independency was further confirmed here by comparing the microdosimetric profile of neutrons and neutron-induced chromosome aberrations in human peripheral blood lymphocytes. Fig. 4 shows the LET (L) dependence of RBE_m of dicentric chromosomes induced in human G₀ lymphocytes irradiated in vitro. This quantity, referred to here as r(L), corresponds to the quality factor, Q(L), as defined in ICRP Publication 60 [44], but is restricted here to chromosome aberrations by external beams of monoenergetic light charged particles, i.e. electrons, protons and alpha-particles. The data were taken from literature reports and compiled in Fig. 3 of Sasaki [45], in which the LET dependence of RBE_m was expressed as a function of binary interactions of DNA double-strand breaks (DSB). However, for simplicity it was expressed here as a polynomial function of unrestricted track-average LET, i.e. r(L) = ∑a_iLⁱ, in which i = 0, 1, 2, 3, , , , k, and k was the degree of polynomial as determined by the Akaike information criterion (AIC) maximum likelihood method. Parameters of the best fit are a₀ = (4.053 ± 2.947) × 10⁻², a₁ = 3.194 ± 0.011, a₃ = −(1.682 ± 0.074) × 10⁻⁴, a₄ = (3.247 ± 0.043) × 10⁻⁶, a₅ = −(1.655 ± 0.011) × 10⁻⁸, a₆ = (3.731 ± 0.010) × 10⁻¹¹ and a₇ = −(3.187 ± 0.0003) × 10⁻¹⁷.

Fig. 4.

LET dependence of maximum RBE_m of dicentric chromosomes induced in human lymphocytes irradiated in vitro with various charged particles. The LET dependence was fitted to a polynomial function, r(L) = ∑α_iLⁱ. Curves show regression line (thick line) and 95% confidence intervals (thin lines). Vertical lines show 95% confidence limits.

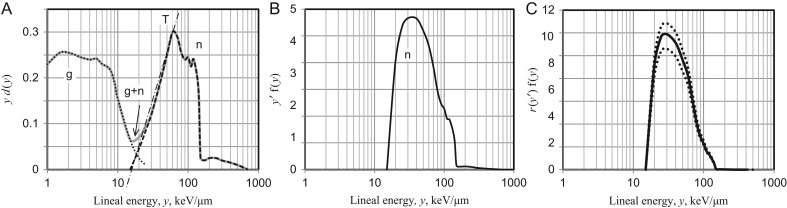
The LET–RBE_m relationship, r(L), was applied to the track-average LET of recoil protons estimated from the microdosimetric spectrum of various neutron fields, and the resulting RBE_m distributions were integrated to estimate the average RBE_m, or C_n(E). The C_n(E) is analogous to the more generalized quantity, mean quality factor of neutrons, Q_n(E), i.e. the mass element-based radiation weighting factor of neutrons. Fig. 5 shows the outline of the estimation of Q_n of the neutron field. The microdosimetry data measured by TEPC with the sensitive cavity of diameter d = 1 or d = 2 μm were selected from the literature, including accelerator-produced monoenergetic and quasimonoenergetic neutrons and fission neutrons [46–66]. The microdosimetric quantities are defined as:

$$y=E_{\mathrm{tr}}/l,E_{\mathrm{tr}}=y·l,l=2d/3,$$ (6)

where E_tr is the initial energy of recoil protons, and l is the mean chord length of the sensitive cavity [67]. The neutron fields are usually contaminated with varying amounts of γ-rays. To subtract the γ component, the γ–neutron boundary was determined by the principle of triangular chord length distribution [68, 69] (Fig. 5A). After subtracting the γ component, the dose distribution, yd(y), was converted to the frequency distribution, yf(y), and then normalized to unity. The lineal energy, y, is analogous to the track-average LET. However, for the low-energy recoil protons, the LET tends to be underestimated, with the track length being shorter than the mean chord length of the sensitive cavity. The correction was made for measured y that produced recoil protons with initial energy insufficient to traverse the cavity diameter. The energy dependence of the continuously slowing down approximation (CSDA) range, R, and track-average LET of recoil protons, y’ = T/R, were calculated according to the Proton Table of ICRU Report 49 for methane-based TE-gas (ρ = 1.0641 × 10⁻³) and ICRU muscle (ρ = 1.04) as a tissue substitute [70]. Accordingly, the adjusted LET, y’, implies y’ > y for R < l and y’ = y for R ≥ l. The break point was y = 70 keV/μm for the sensitive cavity of d = 1 μm and y = 80 keV/μm for d = 2 μm.

Fig. 5.

Microdosimetric estimation of RBE_m of neutrons in mixed γ–neutron field (example). (A) TEPC reading of lineal energy spectrum (solid line) and determination of γ (dotted line) and neutron (dashed line) components. Slashed line (T) shows a tangent to the assumed triangular spectrum. (B) Distribution of lineal energy after adjustment by CSDA range of recoil protons and their LET for ICRU muscle. (C) Distribution of RBE_m. Dotted lines show lower and upper bounds based on 95% confidence intervals of RBE_m-LET curve, r(L), in Fig. 4.

Since the energy dependence of LET of TE-gas was slightly higher than that of ICRU muscle, mainly due to the difference in their electronic collisional stopping power and hence in their CSDA range, the LET values for TE-gas were converted to those for ICRU muscle according to their proportionality (Fig. 5B). Referring to the LET dependence of RBE_m, r(L), the RBE_m distribution against the TEPC reading of y was obtained (Fig. 5C). The average RBE_m of a given neutron field that corresponded to a chromosome version of mean quality factor (Q_n) was calculated by:

$$Q_{\mathrm{n}}=\int r(y’)yf(y)dy/\int yf(y)dy.$$ (7)

The chord length modification, y-to-y’ conversion, mentioned above was not applied in the following instances: (a) high energy spectra (above the proton tail, which is y = 115 keV/μm and y = 225 keV/μm for the sensitive cavity with d = 1 μm and d = 2 μm, respectively) that correspond to alpha recoils by ¹⁷O(n,α)¹⁴C reaction and recoil C-, N- and O-ions; (b) neutron fields with a mean energy of E > 1.5 MeV, in which the low y counts cannot be distinguished from those due to high-energy (fast) protons with low LET. In these neutrons the y’ = y rule may tend to underestimate the RBE; (c) thermal and epithermal neutrons, where the reactions are mostly capture reactions such as ¹H(n,γ)d, ¹⁴N(n,p)¹⁴C and ¹⁷O(n,α)¹⁴C. Their kerma contribution in ICRU muscle is 35.94% for protons (0.59 MeV), 37.24% for γ (2.25 MeV) and 25.94% for ¹⁴C heavy ions (0.40 MeV). The contribution of other components is <1%. High energy γ-rays may not contribute to the RBE. Heavy ions may be disregarded because of their extremely high LET, which is so high that it likely kills cells. Therefore, protons are major species relating to the RBE_m of the thermal and epithermal neutrons. The 0.59 MeV protons have a CSDA range of 11.15 μm and a track-average LET of 52.94 keV/μm. As such, the y’ = y rule will be properly applied for the whole spectrum of the thermal and epithermal neutrons.

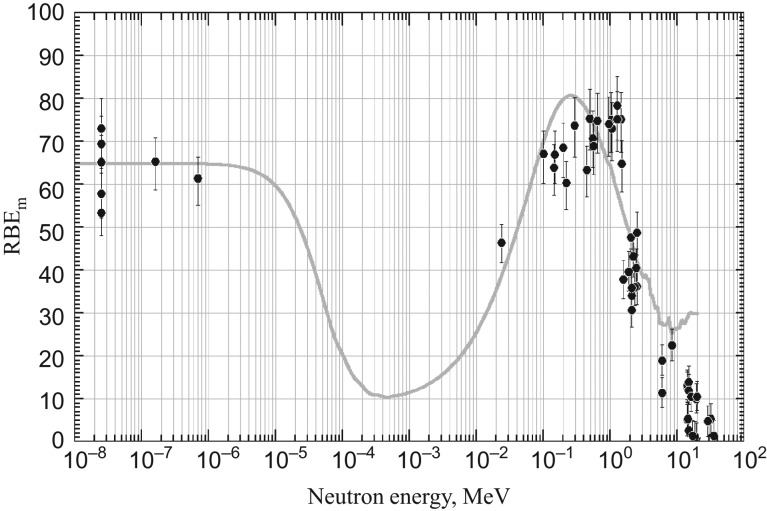
The source-term information for neutron fields and their calculated energy-averaged RBE_m, i.e. Q_n values, are presented in an attached table (supplementary data). The table also includes a simple arithmetic mean of lineal energy, ${\overline{\mathit{y}}}_{\mathrm{F}}$. Although such a rounded quantity may be informative in dealing with cell inactivation, it cannot be applied to such endpoints as mutations, including chromosome aberrations, that could be registered only in living cells. The cells are highly abortive at LET beyond the proton edge. Fig. 6 shows the average RBEm, i.e. chromosomally determined mean quality factor, Q_n, plotted against neutron energy. Except for their magnitude, the energy dependency of Q_n was highly comparable with that of Schuhmacher and Siebert [71] calculated by MCNP Monte Carlo neutron transport code applied to the ICRU tissue substitute. Their calculation was carried out based on the unspecified radiation quality factor, Q(L), of ICRP Publication 60 [44], whereas the r(L) presented here is specific to chromosome aberrations. The values follow similar LET dependence, but differ in their magnitude, each giving a maximum value of Q(L)_max ≈ 30 and r(L)_max ≈ 90 according to their response functions. When the Q_n value was rescaled according to the r(L)_max/Q(L)_max ratio, the energy dependencies were highly comparable with each other (Fig. 6). The Q_n was broadly compatible with the operational radiation protection quantities of ICRP [4], e.g. the effective quality factor, $\overline{Q_{\mathrm{n}}}$, and the radiation weighting factor, w_R, at the high-energy range, giving a maximum at ~1 MeV. However, $\overline{Q_{\mathrm{n}}}$ and w_R dissociate from Q_n, being less sensitive to neutron energy at low energies (<100 MeV). This is because $\overline{Q_{\mathrm{n}}}$ and w_R are specifically defined quantities expressed as the ambient dose equivalent at 10 mm depth in a tissue-equivalent ICRU sphere of 30 cm diameter, where secondary photons from the (n,γ) capture reaction largely contribute to the dose and hence moderate the contribution of the high-LET charged particles from (n,el) elastic recoil and (n,p) and (n,α) capture reactions. In the ICRU tissue substitute, the probability of (n,γ) reaction is highest (σ = 0.037 barn) for thermal neutrons (0.025 eV) and decreases with an increase in neutron energy to σ ≈ 5.3 × 10⁻⁶ barn at 100 MeV.

Fig. 6.

Average RBE_m, i.e. mean quality factor of neutron, Q_n, calculated from microdosimetry spectra of various neutron fields plotted against neutron energy. Vertical lines represent the 95% confidence intervals derived from curve fitting of r(L). The thin curve represents the mean quality factor of neutron, Q_n, of Schuhmacher and Siebert [71] after rescaling by the r(L)_max/Q(L)_max ratio of the radiation quality factor.

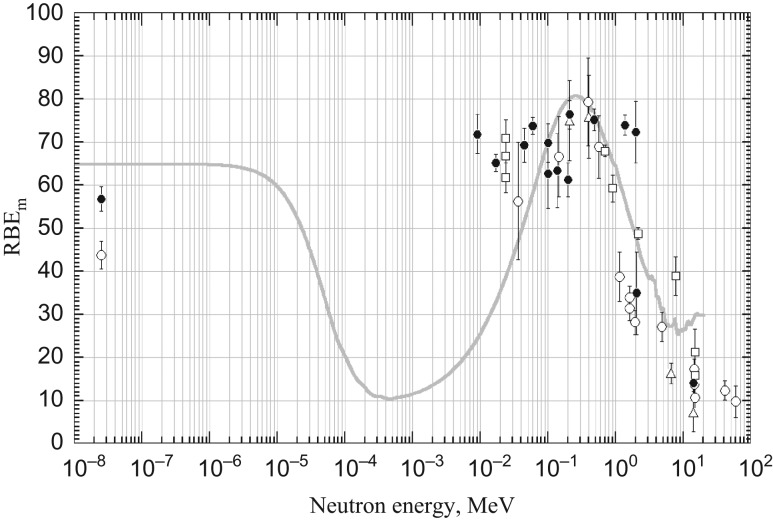
Fig. 7 shows the RBE_m of dicentrics observed in human G₀ lymphocytes irradiated in vitro with neutrons. The dose–response relationships were taken from the literature, and RBE_m was calculated as the ratio of the initial slope of the dose–response relationship to the neutron component and that of ⁶⁰Co γ-rays as the reference radiation, i.e. RBE_m = α_n/α_γ. The initial slope of the γ-ray response was determined from pooled data for laboratories with large-scale experiments, i.e. RBC Kyoto [7, 18, 45, 72–74], GSF Munchen [36, 37, 39, 75–81] and NRPB Harwell [82–87], but was determined individually for solitary head-to-head experiments in other laboratories [88–90]. The relationship between chromosomally determined RBE_m and the neutron energy in the experimental system was highly comparable with those estimated from the microdosimetric spectra of TEPC counting (Fig. 6) and those estimated from the MCNP neutron transport code [71]. The latter two calculations are based purely on neutrons. However, in the chromosomal evaluation, the neutrons are contaminated with varying amounts of γ-rays. The equivalence among the three estimates strongly indicates that, at least at biologically relevant low or moderate doses, the interaction between the γ and neutron components may be negligibly small, if it exists at all.

Fig. 7.

RBE_m of dicentrics observed in human G₀ lymphocytes irradiated with neutrons in vitro. Data are taken from the literature: RBC Kyoto (solid circles), GSF Munchen (open circles), NRPB Harwell (open squares) and other laboratories (open triangles). The vertical lines represent the 95% confidence interval based on the SE of the initial slope for neutrons. For explanation of thin curve, see legend to Fig. 6.

Neutron RBE in the mixed-radiation field

Considerably large RBE values at low doses have been also suggested in A-bomb survivors, but with very large uncertainties due to a small neutron component fraction, particularly in the DS86 and DS02 dosimetry systems [91–98]. Cullings et al. [7] raised the point that neutron RBE values determined independently from the coexisting γ-rays might lead to an erroneous risk evaluation because the neutron RBE could be strongly suppressed in the mixed-radiation field. They assumed that the effects in the mixed field, E(D_γ,D_n), were equivalent to the effects of γ-ray dose, D_γ, plus an increment of γ-equivalent dose, Δ, due to neutrons, E(D_γ + Δ, 0), i.e.:

$$\begin{array}{c}{\mathrm{\alpha }}_{\mathrm{\gamma }}\left[D_{\mathrm{\gamma }}+R_{\mathrm{m}}{D}_{\mathrm{n}}+\mathrm{\theta }\left({D_{\mathrm{\gamma }}}^2+{D_{\mathrm{n}}}^2\right)\right]\hfill \\ ={\mathrm{\alpha }}_{\mathrm{\gamma }}\left[\left(D_{\mathrm{\gamma }}+\Delta \right)+\mathrm{\theta }{\left(D_{\mathrm{\gamma }}+\Delta \right)}^2\right].\hfill \end{array}$$ (8)

The RBE in the mixed field is defined by R(D_γ,D_n) = Δ/D_n. The RBE is dependent both on γ-rays and neutrons (Equation A2 of Cullings et al. [7]). The formula is similar to that previously proposed by Rossi and Zaider [91] for neutron RBE in the mixed field.

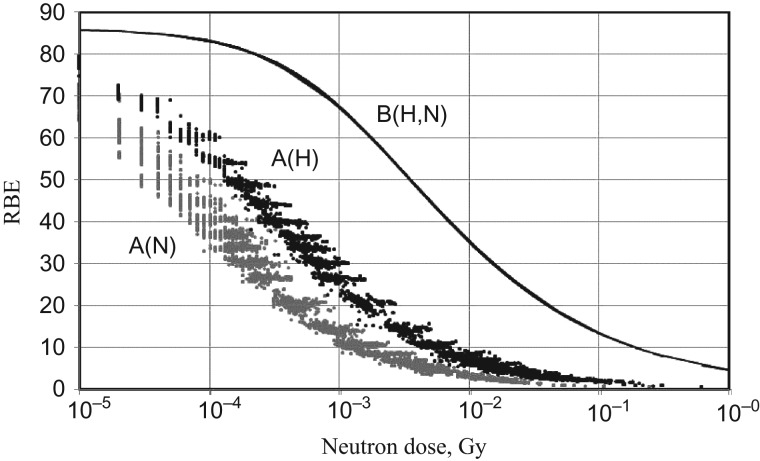
Fig. 8 shows the neutron RBE in the LSS cohorts of Hiroshima and Nagasaki. The neutron RBEs in the mixed field were calculated by the R(D_n,D_γ) formulated by Cullings et al. [7], using the same dose–response parameters presented for Eq. (3) (as was also the case for Cullings et al. [7]). The R(D_n,D_γ) values are scattered and lower in Nagasaki (Fig. 8 A(N)) than in Hiroshima (Fig. 8 A(H)), reflecting varying neutron/γ-ray ratios in individual survivors and their lower ratio in Nagasaki. Fig. 8 also includes the neutron RBEs for individual survivors calculated independently from the γ-rays (Fig. 8 B(H,N)). They are simply dependent on the neutron dose, irrespective of the coexisting γ-rays and were the same for the two cities. In any case, the neutron RBE varies depending on dose, irrespective of whether the calculation is based on the γ-dependence or -independence model, although the magnitude is much smaller for the γ-dependence model.

Fig. 8.

RBE of neutrons in LSS cohorts from Hiroshima (H) and Nagasaki (N) expressed as a function of neutron dose (Gy) for the unadjusted DS02 colon dose, coluDS02w1. (A) RBE of neutrons in terms of γ-dependence model, R(D_γ,D_n) of Cullings et al. [7]. (B) RBE in terms of γ-independence model. Calculations were made using the ‘lssinc07’ database.

The RBE in the γ-dependence model, R(D_γ,D_n), was applied to the dose–response relationship of the ERR of solid cancer in Hiroshima and Nagasaki (Fig. 9). As seen in the figure, equivalence of the two cities was not improved, and even yielded much poorer matching than when a constant RBE = 10 was used. The difference in the dose–response relationship between the two cities was statistically significant, as shown by the non-overlap of the half-sized 95% ellipses (Fig. 9B). Thus, the RBE value for the γ-independence model was more appropriate in eliminating the city difference (Fig. 3C). The reason for the discrepancy remains to be elucidated. It should be noted, however, that in the dependence model, the RBE is defined as an increment of effective dose, ∆, that satisfies RBE = ∆/D_n. This differs from the canonical definition of the equi-effective dose ratio. Since in this case the dimension of ∆ is not dose but ‘effectiveness’, the interactions, D_γ∆ and ∆², are theoretically unrealistic.

Fig. 9.

Dose–responses for ERR of solid cancer in Hiroshima (H) and Nagasaki (N) and test for difference by 95% joint confidence intervals (CIs). Doses are unadjusted colon dose, coluDS02w_mix, in which neutrons were weighted by R(D_γ,D_n) for the γ-dependence model. (A) Dose–response relationships. The vertical lines represent the 80% CIs. (B) The 95% joint CIs are based on the χ² distribution and shown in half size. The vertical and horizontal lines within the ellipse represent the SEs of the mean.

Alternatively, by setting the RBE as an equi-effective dose ratio ω = D_γ/D_n, the yield in the mixed field can be expressed by

$$\begin{array}{cc}\mathrm{\epsilon }\left(D_{\mathrm{\gamma }},D_{\mathrm{n}}\right)\hfill & ={\mathrm{\alpha }}_{\mathrm{\gamma }}\left(D_{\mathrm{\gamma }}+{\mathrm{\theta }}_{\mathrm{\gamma }}{D_{\mathrm{\gamma }}}^2+R_{\mathrm{m}}{D}_{\mathrm{n}}+{\mathrm{\theta }}_{\mathrm{n}}{D_{\mathrm{n}}}^2\right)\hfill \\ & ={\mathrm{\alpha }}_{\mathrm{\gamma }}(D_{\mathrm{\gamma }}+{\mathrm{\theta }}_{\mathrm{\gamma }}{D_{\mathrm{\gamma }}}^2+\mathrm{\omega }{D}_{\mathrm{n}}+{\mathrm{\theta }}_{\mathrm{n}}{\left(\mathrm{\omega }{D}_{\mathrm{n}}\right)}^2,\hfill \end{array}$$ (9)

where the neutron RBE of an individual survivor is given by ω = [−1 + {1 + 4θ_γ(R_m + θ_nD_n)D_n}^1/2]/2θ_γD_n. The RBE thus obtained in the LSS cohort turned out to be independent of the magnitude of the intermingled γ-ray dose, identical to that for the γ-independence model, e.g. RBE given in Eq. (3), and (moreover) identical between the two cities as well (Fig. 8 B(H,N)).

DISCUSSION AND CONCLUSION

On the basis of the microdosimetric analysis presented here, we could not find any evidence for deviation of the neutron RBE in the γ–neutron mixed radiation field. The neutron RBE was independent of the magnitude of the coexisting γ-rays. In the microdosimetric aspect, a possible interaction between the two components could be a function of ζ(D_γD_n), which represents the mutual interaction between the primary DNA damage generated by neutrons and photons. However, its magnitude may be negligibly small at low doses of low-energy neutrons because the energy deposition of recoil protons is highly localized. In contrast, that of γ-associated Compton and photoelectrons is sparsely distributed over the cell nucleus. The difference in cancer risk between Hiroshima and Nagasaki can be readily explained by differences in the neutron component amount, which completely disappear only when the neutrons are weighted by a dose-dependent variable RBE. This indicates that even a small amount of neutrons cannot be disregarded in the risk evaluation.

Interestingly, a chromosome aberration–based RBE provided the most appropriate weighting factor for neutrons for cancer rates in survivors. Obviously, chromosome aberrations themselves may not be the sole and integral events leading to the development of cancer. Yet, the parallelism strongly suggests that they share the same underlying molecular mechanisms, such as pathway choice for the repair of DNA double-strand breaks [19]. The processes leading to cancer are complex and may include a variety of confounding factors. Therefore, the curvature of the dose–response relationship itself does not guarantee the underlying causal mechanisms. The equivalence of cancer rates between the two cities may verify the adequacy of radiation weighting by chromosomally derived RBE and suggests that chromosome structural aberrations (rearrangements) could serve as surrogate biomarkers for radiological cancers. In spite of the proposed modulation of neutron RBE in a mixed-radiation field, chromosomal RBE as assessed by a chromosomal version of quality factor of neutron, Q_n, against neutron energy was confirmed to be independent of the intermingled incident γ-rays; this is consistent with predictions based on microdosimetric measurements and the Monte Carlo simulation of energy transport of neutrons alone. However, it should be noted that the radiation quality factor, r(L), and derived quality factor of neutrons, Q_n, thus chromosomally obtained were much larger than those currently adopted for radiological protection [44, 99]. For radiological protection purposes, ICRP uses a maximum radiation quality factor, Q(L), of the rounded number of ~20, with its possible peak value of ~30 in its recommended response function [4, 44]. This value is a rounded number obtained from experimental data compiled by Sinclair [100], the ICRU Report No. 40 [101] and NCRP Report No. 104 [102]. In conveying a possible variability of biological effects, the Q(L) is not specified for a particular biological endpoint. Endpoints include a range of biological events relevant to radiological protection in general, such as chromosome aberrations, mutations, malignant transformation in cultured mammalian cells, tumor induction and life shortening in experimental animals. It was thus apparent that the current Q(L) and its derived quality factor, Q_n, effective quality factor, ${\overline{Q}}_{\mathrm{n}}$ and radiation weighting factor, w_R, of neutrons are seriously underestimated for the calculation of cancer risk, possibly by a factor of ~3.

All those lines of evidence presented here indicate that the RBE of fission neutrons is variable depending only on neutron dose, not on the magnitude of the intermingled γ-rays in the mixed field. The cancer risk in A-bomb survivors can best be explained by introducing such a dose-dependent variable RBE system, and thus provides a generalized measure for risk assessment in other cases of human radiation exposures.

SUPPLEMENTARY DATA

Supplementary data on the neutron field and its mean quality factor, Q_n, calculated from TEPC-measured microdosimetric spectra are available at the Journal of Radiation Research online.

CONFLICT OF INTEREST

The authors report that there are no conflicts of interest. The authors alone are responsible for the content and writing of this report.