Significance
Sounds produced in the world reflect off surrounding surfaces on their way to our ears. Known as reverberation, these reflections distort sound but provide information about the world around us. We asked whether reverberation exhibits statistical regularities that listeners use to separate its effects from those of a sound’s source. We conducted a large-scale statistical analysis of real-world acoustics, revealing strong regularities of reverberation in natural scenes. We found that human listeners can estimate the contributions of the source and the environment from reverberant sound, but that they depend critically on whether environmental acoustics conform to the observed statistical regularities. The results suggest a separation process constrained by knowledge of environmental acoustics that is internalized over development or evolution.
Keywords: natural scene statistics, auditory scene analysis, environmental acoustics, psychophysics, psychoacoustics
Abstract
In everyday listening, sound reaches our ears directly from a source as well as indirectly via reflections known as reverberation. Reverberation profoundly distorts the sound from a source, yet humans can both identify sound sources and distinguish environments from the resulting sound, via mechanisms that remain unclear. The core computational challenge is that the acoustic signatures of the source and environment are combined in a single signal received by the ear. Here we ask whether our recognition of sound sources and spaces reflects an ability to separate their effects and whether any such separation is enabled by statistical regularities of real-world reverberation. To first determine whether such statistical regularities exist, we measured impulse responses (IRs) of 271 spaces sampled from the distribution encountered by humans during daily life. The sampled spaces were diverse, but their IRs were tightly constrained, exhibiting exponential decay at frequency-dependent rates: Mid frequencies reverberated longest whereas higher and lower frequencies decayed more rapidly, presumably due to absorptive properties of materials and air. To test whether humans leverage these regularities, we manipulated IR decay characteristics in simulated reverberant audio. Listeners could discriminate sound sources and environments from these signals, but their abilities degraded when reverberation characteristics deviated from those of real-world environments. Subjectively, atypical IRs were mistaken for sound sources. The results suggest the brain separates sound into contributions from the source and the environment, constrained by a prior on natural reverberation. This separation process may contribute to robust recognition while providing information about spaces around us.
Perception requires the brain to determine the structure of the world from the energy that impinges upon our sensory receptors. One challenge is that most perceptual problems are ill-posed: The information we seek about the world is underdetermined given the sensory input. Sometimes this is because noise partially obscures the structure of interest. In other cases, it is because the sensory signal is influenced by multiple causal factors in the world. In vision, the light that enters the eye is a function of the surface pigmentation we typically need to estimate, but also of the illumination level. In touch, estimates of surface texture from vibrations are confounded by the speed with which a surface passes over the skin’s receptors. And in hearing, we seek to understand the content of individual sound sources in the world, but the ear often receives a signal that is a mixture of multiple sources. These problems are all examples of scene analysis, in which the brain must infer one or more of the multiple factors that created the signals it receives (1). Inference in such cases is possible only with the aid of prior information about the world.
In real-world settings, audition is further complicated by the interaction of sound with the environment. The sound entering our ears reaches us directly from its source as well as indirectly via reflections off surrounding surfaces, known collectively as reverberation (Fig. 1A). Because reflections follow a longer path to our ears, they arrive later, thus distorting the direct sound from a source (2–5). This distortion can be severe, particularly in closed spaces such as rooms, caves, or dense forests, in which sound reflects multiple times off opposing surfaces (Fig. 1B). On the other hand, reverberation provides information about the environment, because reflection characteristics depend on the geometry of the space around us and the position of a sound source within it. Biological organisms are well adapted to reverberation, using it to infer room size and source distance (6–9) while retaining a robust ability to identify sound sources despite the environmental distortion (10–15). It remains unclear how the auditory system achieves these capabilities.
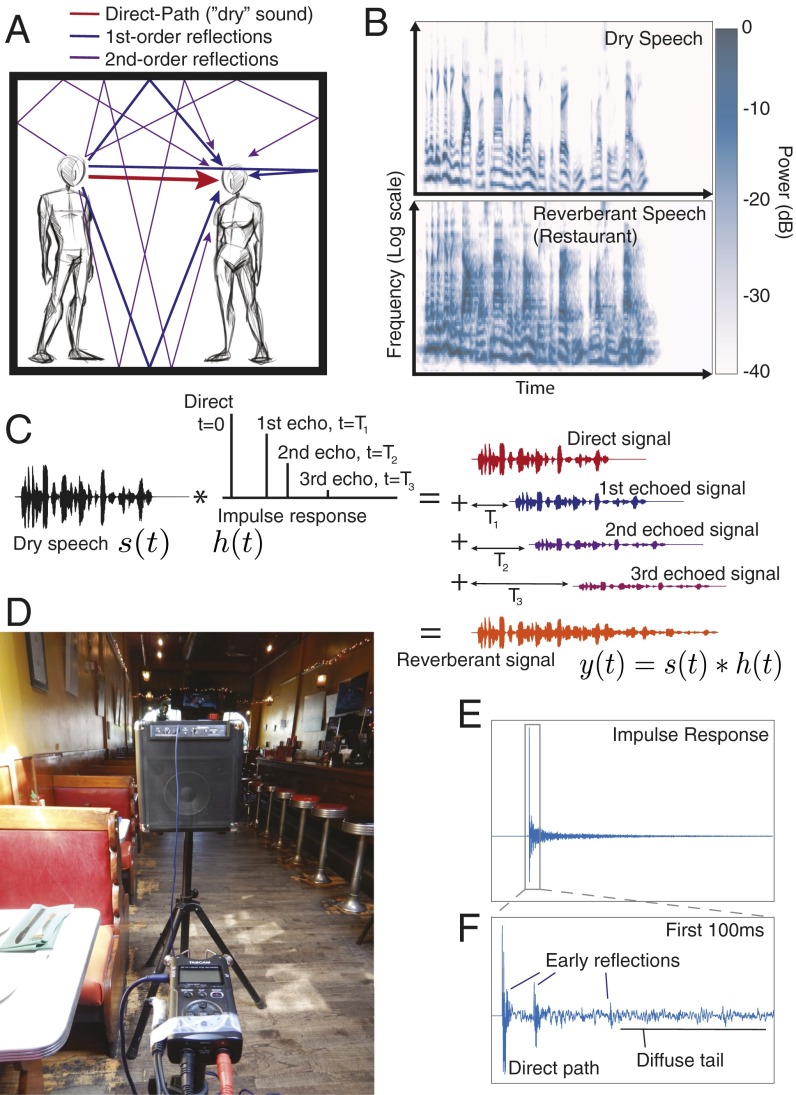
Fig. 1.
The effect of reverberation. (A) Sound reaches a listener directly as well as via reflections off surrounding surfaces. (B) Reverberation distorts the structure of source signals, shown by cochleagrams (representations of the spectrotemporal structure of sound as it is believed to be encoded by the auditory periphery) of speech without (Top) and with (Bottom) reverberation. (C) The effect of reverberation on a sound is described mathematically by the convolution of the sound with the IR of the environment, The original sound is repeated, time-shifted, and scaled for every nonzero point in the IR and the resulting signals are summed. This process is illustrated for a schematic IR with 3 echoes. For clarity these echoes are more widely spaced than in a naturally occurring IR. (D) A photograph of the apparatus we used to measure IRs—a battery-powered speaker and a portable digital recorder in one of the survey sites, a restaurant in Cambridge, MA. (E) An IR measured in the room shown in D. Every peak corresponds to a possible propagation path; the time of the peak indicates how long it takes the reflected sound to arrive at the ear and the amplitude of the peak indicates the amplitude of the reflection, relative to that of the sound that travels directly to the ear. (F) The first 100 ms of the IR in E. Discrete early reflections (likely first- or second-order reflections) are typically evident in the early section of an IR, after which the reflections become densely packed in time, composing the diffuse tail.
The computational challenge of reverberation is that the signal received by the ears results from the combined effects of a sound source and the environment. Specifically, the effect of the reflections arriving at an ear can be described by a single linear filter, and the sound that reaches the ear as the convolution of this filter with the sound of the source: (Fig. 1C) (16). Because the listener lacks direct access to either the source or the filter, their estimation is ill-posed. Although the physics of reverberation are well established (2, 4, 5, 17), as is the fact that human listeners are relatively robust to distortion from reverberation (4, 10–15), the underlying perceptual mechanisms have been little studied and remain poorly understood. One might suppose that robustness simply results from learning how the structure of familiar sounds such as those of speech is altered under reverberation. However, it remains unclear whether this could be viable given the variation in reverberation from space to space. Moreover, such an account does not explain how environmental information could be extracted from reverberation. Here we propose that reverberation should be treated as a scene analysis problem and that, as with other scene analysis problems, the source and filter might in principle be separable given prior knowledge of natural sound sources and environmental filters.
Our approach was to characterize statistical regularities in environmental acoustics that could be exploited to constrain the inference of source and environmental filter. We focused on regularities of the filter, as they had not been documented prior to our investigations. We then tested whether humans can separately estimate the source and filter from reverberant audio and whether these abilities depend on conformity to natural statistical regularities of the filter. Our results suggest that naturally occurring environmental impulse responses are tightly constrained, and that human perception relies critically on these regularities to separate sound into its underlying causes in the world.
Results
Measuring Reverberation.
The acoustic effect of an environment can be summarized by the impulse response (IR), which is the sound that results from an impulse (the sound of a “click”) in the environment. Because the filtering effects of environments are approximately linear (16), the IR can be used to predict the sound that any source would produce in a particular environment and thus provides a means to describe reverberation. The IR for an example room (Fig. 1D) is plotted in Fig. 1 E and F. The first peak corresponds to the sound arriving directly from the source (which thus arrives with the shortest possible delay); subsequent peaks are due to reflections, each corresponding to a particular path sound can take on its way to a listener’s ear. Eventually, the reflections become sufficiently dense that they overlap in time. Because energy is absorbed by environmental surfaces with each reflection (as well as by air), longer paths produce lower amplitudes, and the overlapping echoes produce a “tail” in the IR that decays with time.
The IR is known to contain information about the environment (4, 5, 18). For instance, larger rooms produce fewer reflections per unit time, such that the reverberation decays more slowly. Decay rates are also affected by material (e.g., carpet is more absorbent than stone). The IR also contains information about the distance of a sound source from the listener, via the ratio of direct to reverberant sound (19, 20). But given the vast range of physical environments humans encounter, with materials and geometries that vary in many dimensions, it is not obvious whether IRs could exhibit regularities that would permit their separation from source signals.
Room IRs like that of Fig. 1E are routinely measured (6, 7, 10, 11) and simulated (17, 21). However, studies to date have measured only small numbers of environments (11, 22) and have largely focused on spaces used for music (23–25) (such as cathedrals and concert halls) where reverberation has often been optimized for aesthetic criteria. As a consequence, the distribution of natural environmental IRs remains uncharacterized, and the extent to which they exhibit regularities remains unclear. We thus began by characterizing the distribution of IRs that human listeners encounter in their daily lives. Because it is computationally intractable to simulate the acoustics of complex real-world environments (4, 8, 22), physical measurements of environmental acoustics were required.
Reverberation Statistics in Natural Scenes.
To draw random samples from the distribution of natural acoustic environments, we recruited seven volunteers and sent them randomly timed text messages 24 times a day for 2 weeks. Participants were asked to respond to each message with their location and a photograph of the space. We then attempted to visit each location and measure the IR. We measured IRs using an apparatus that recorded a long-duration, low-volume noise signal produced by a speaker (Fig. 1D). Because the noise signal and the apparatus transfer function were known, the IR could be inferred from the recording (SI Materials and Methods, Real-World IR Measurements, Measurement Apparatus Transfer Function and Fig. S1 E and F). The long duration allowed background noise to be averaged out and, along with the low volume, permitted IR measurements in public places (e.g., restaurants, stores, city streets). Our survey yielded 301 distinct locations, mostly in the Boston metropolitan area (Fig. 2), of which 271 were measured. (The 30 unmeasured locations were private spaces whose owners refused us permission to record.) The surveyed IRs are available at mcdermottlab.mit.edu/Reverb/IR_Survey.html.
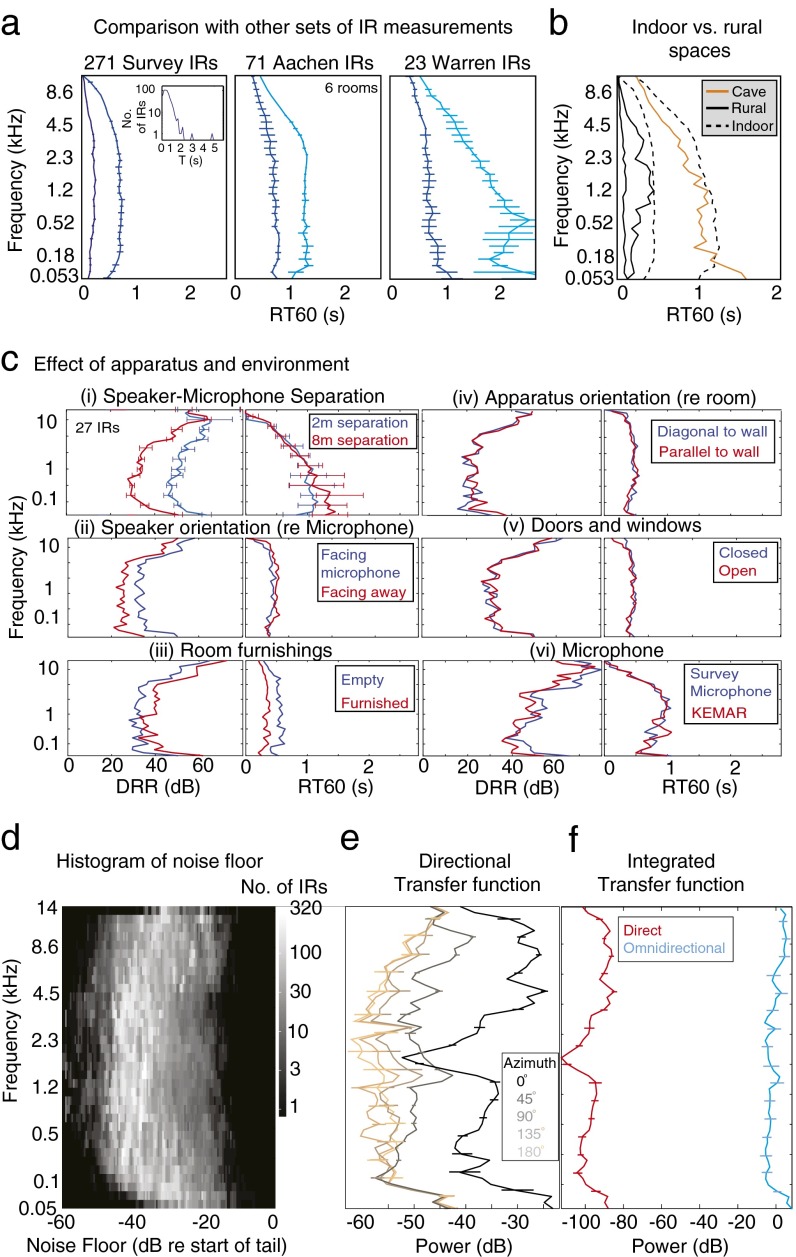
Fig. S1.
IR Measurements. (A) Comparison between our surveyed IRs (Left) and two other sets of IRs: a set measured for the evaluation of dereverberation algorithms (22) (Center) and a set measured for musical use [Right; measured by Chris Warren (www.echothief.com)]. All panels plot the median subband RT60 (median taken across the upper and lower halves of a dataset), as in Fig. 4D. Error bars (here and throughout this figure) show 95% confidence intervals obtained by bootstrap. The other two sets contain longer IRs, but show qualitatively similar frequency dependence of RT60 to that observed in our dataset. A, Left, Inset shows a histogram of the broadband RT60s across the surveyed IRs. (B) Comparison of the decay rates in an example IR from a cave with those from the indoor and rural IRs from Fig. 4D. Indoor and rural IRs are subdivided into more and less reverberant halves, as in A. The cave IR [measured by Chris Warren (www.echothief.com)] shows the same qualitative form as very reverberant indoor spaces. (C) Effect of apparatus and environment on IR properties. The DRR and RT60 are plotted for comparison measurements made in a single room with either the apparatus or the room altered between measurements. Altering the (C, i) speaker–microphone distance or (C, ii) speaker orientation affects the DRR but only very slightly effects the RT60. Furnishing a room (C, iii) reduces both the DRR and RT60 relative to the empty room. Neither (C, iv) rotating the apparatus within the room, nor (C, v) opening doors and windows, nor (C, vi) changing the microphone appreciably affected DRR or RT60. (D) Histogram of the noise floors of our IR measurements, measured in each subband relative to the subband DRR. The variation is due to the variation in background noise at the survey sites. (E) The transfer functions of our speaker and microphone were measured in an anechoic chamber with the microphone located 2 m from the speaker at varying azimuths relative to the speaker face (the microphone always faced the speaker). Each measurement was made by broadcasting the 3-min survey Golay sequence (which has a flat spectrum) and plotting the spectrum of the recorded broadcast. (F) Total speaker transfer function. The directional transfer functions in E were interpolated to approximate a spherical directional spectrum of the speaker and this was integrated over the azimuth to estimate the ominidirectional transfer function (blue), which contains the spectral contribution illuminating the environment. This is compared with the spectrum of the signal emanating directly from the speaker face (red). We assume the energy contributing to the IR tail is filtered by the omnidirectional transfer function whereas the direct arrival is filtered by the direct transfer function and when we compute DRR values from the measured IRs we account for this frequency variation (SI Materials and Methods).
Fig. 2.
Survey of natural reverberation. (A) Maps showing the location of the 271 measured survey sites. (Top) Massachusetts and New Hampshire; (Middle) Greater Boston area with most survey sites in Boston, Cambridge, and Somerville; (Bottom) Cambridge, the location of most survey sites. Red boxes indicate the region shown in higher detail below. (B) Photographs of 14 example locations from the survey (from Top Left: suburban street corner, hallway, restaurant, Boston street, restaurant booth, forest, conference room, bathroom, open-plan office, MIT building 46, car, department store, bathroom, subway station, bar, office, aerobics gym).
Our key findings were typically salient in individual IRs, and we illustrate them in an example IR (Fig. 3) before showing summary statistics from the entire set of surveyed IRs (Fig. 4). As expected, the environmental IRs exhibited sparse early reflections, consisting of a small number of high-amplitude echoes separated by brief periods of relative quiet (4, 16) (Fig. 3A). However, there was also considerable regularity in the way that the dense tail of the IR decayed over time, which, to our knowledge, had not been previously documented. We found that the local statistics of the IR time series typically began to resemble Gaussian noise within ∼50 ms (Fig. 3A), indicating (i) that it was appropriate to describe the IR tail by its amplitude envelope (because Gaussian variables are completely characterized by mean and variance) and (ii) that the tail made up the vast majority of the IR (measured as a fraction of either IR power or duration). This latter finding indicates that the tail induces the majority of the distortion to a source signal, suggesting that it might give rise to important perceptual effects.
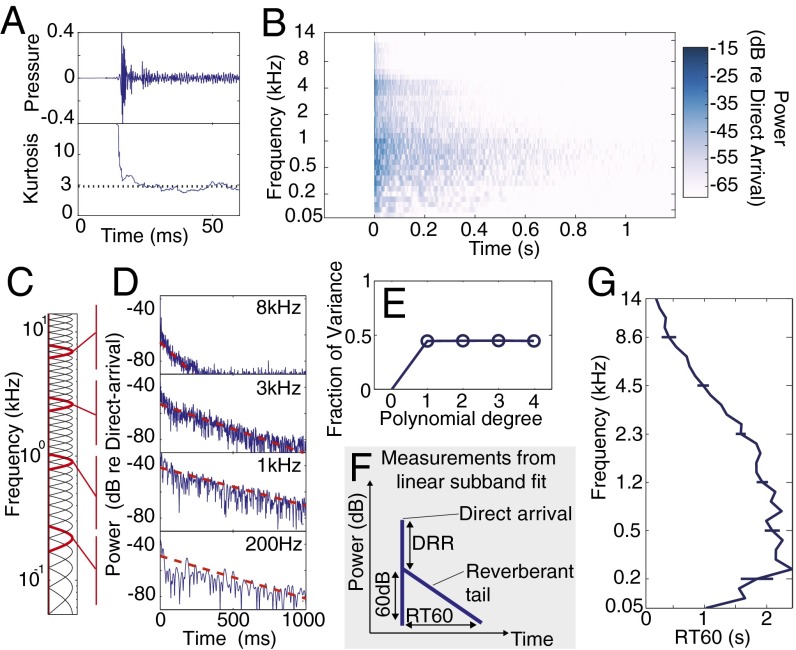
Fig. 3.
Measurement and analysis of reverberation. (A) The first 60 ms of the restaurant IR from Fig. 1 (Top) with the kurtosis (Bottom) computed over a 10-ms sliding window. The dotted line shows the kurtosis of Gaussian noise. Apart from the very earliest section, the IR is well described by Gaussian statistics. (B) Cochleagram of the restaurant IR from Fig. 1 D–F. (C) Transfer functions of simulated cochlear filters used for subband analysis. Filters in red are those corresponding to the subbands shown in D. (D) Amplitude envelopes in frequency subbands of the IR, showing how it redistributes energy in particular frequency bands over time. Dashed lines show best-fitting exponential decay. (E) Fraction of variance of subband log amplitude accounted for by polynomials of varying degree. A degree of 1 corresponds to exponential decay, whereas a degree of 0 corresponds to fitting to the mean. (F) Schematic of reverberation measurements made using linear fits to frequency channel log amplitude: The reverberation time to 60dB (RT60) is the time taken for the reverberation to decay 60 dB; the direct-to-reverberant ratio (DRR) is the difference in power between the direct arriving sound and the initial reverberation. (G) Measured RT60 (i.e., decay rate) from each subband of the example IR in A. Error bars show 95% confidence intervals obtained by bootstrap.
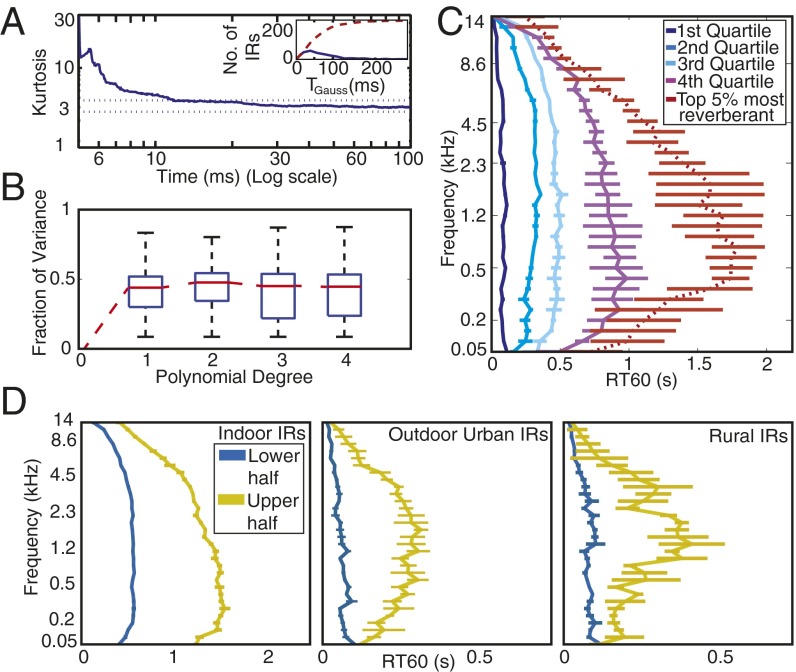
Fig. 4.
Statistics of natural reverberation. (A) IRs have locally Gaussian statistics. Graph plots median kurtosis (sparsity) vs. time for the surveyed IRs. The kurtosis for each IR was calculated in 10-ms windows; the line plots the median across all surveyed IRs for each time point. Here and elsewhere in this figure, error bars show 95% confidence intervals obtained by bootstrap. Horizontal dotted lines show 95% confidence intervals of the kurtosis of 10-ms Gaussian noise excerpts. (A, Inset) Histogram (solid line) of the time at which the IR kurtosis reached the value for Gaussian noise () across the surveyed IRs, along with the corresponding cumulative distribution function (dashed line). (B) Energy decays exponentially. Graph displays box plots of the distribution of the fraction of variance of IR subband envelopes accounted for by polynomial decay models of degree P for P = [1,2,3,4]. The model was fitted to the data recorded by the left channel of the recorder and evaluated on the data recorded by the right channel (i.e., the variance explained was computed from the right channel). The two channels were connected to different microphones that were oriented 90° apart. They thus had a different orientation within the environment being recorded, and the fine structure of the recorded IRs thus differed across channels. Using one channel to fit the model and the other to test the fit helped to avoid overfitting biases in the variance explained by each polynomial. (C) Frequency dependence of reverberation time (RT60) in the surveyed IRs. Lines plot the median RT60 of quartiles of the surveyed IRs, determined by average RT60(T, Eq. S9). Dotted red line plots the median value for the most reverberant IRs (top 5%). (D) Median RT60 profiles (as in C except using halves rather than quartiles because of smaller sample sizes) for indoor environments (n = 269), outdoor urban environments (e.g., street corners, parking lots, etc., n = 62), and outdoor rural environments (forests, fields, etc., n = 29). To increase sample sizes we supplemented the 271 IRs measured here with those of two other studies (ref. 22 and www.echothief.com).
To examine the effect of the decaying tail on information in peripheral auditory representations, we represented IRs as “cochleagrams” intended to capture the representation sent to the brain by the auditory nerve (Fig. 3B). Cochleagrams were generated by processing sound waveforms with a filter bank that mimicked the frequency selectivity of the cochlea (Fig. 3C) and extracting the amplitude envelope from each filter (Fig. 3D). Despite the diversity of spaces (including elevators, forests, bathrooms, subway stations, stairwells, and street corners; Fig. 2), the IRs showed several consistent features when viewed in this way.
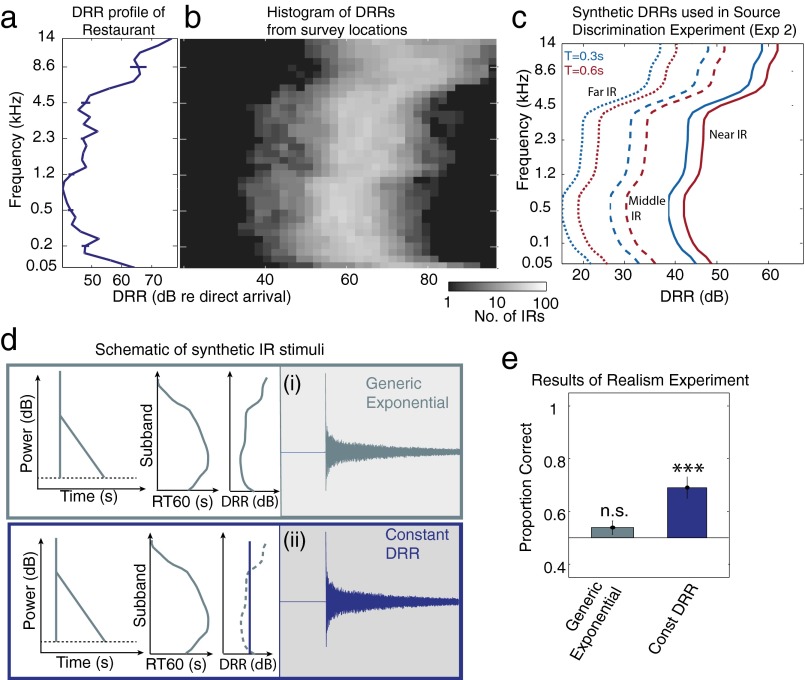
To quantify the nature of reverberant energy decay over time, we fitted polynomials of different degrees to the log power in each frequency band. As shown in Fig. 3D, the decay was well described by a linear function, with negligible additional benefit from higher polynomial terms (Fig. 3E), indicating that the energy in each frequency band decayed exponentially (linear on a log scale). We quantified the rate of this decay by the time taken for the reverberating sound to decay 60 dB [i.e., the 60-dB reverberation time (RT60)] in each subband (Fig. 3F). We observed these decay times to vary with frequency in a regular manner, typically with rapid decay at low and high frequencies but slower decay in the middle of the spectrum (Fig. 3G). A similar dependence was also present in the overall amplitude of reverberation at each frequency, characterized by the direct-to-reverberant ratio (DRR) (Fig. S2).
Fig. S2.
Direct-to-Reverberant Ratio (DRR)—measurements and experiments. (A) The DRR profile of the example IR from Figs. 1 and 3. See Fig. 3F for a schematic of DRR measurement. Error bars show 95% confidence intervals obtained by bootstrapping from the acoustic measurement (by fitting the exponential decay model to multiple random subsets of samples from the time series). (B) Histogram of subband DRRs of all surveyed IR locations. (C) DRR profiles used to create synthetic IRs in the source discrimination experiment (experiment 2). We observed a weak dependence of median DRR on broadband RT60; to mimic this effect in our synthetic IRs the long experimental IRs (T = 0.6 s) had slightly lower DRRs than the short experimental IRs (T = 0.3 s). (D) Conditions from experiment 1 (real vs. synthetic reverberation discrimination) in which DRR was manipulated. Listeners discriminated generic exponential IRs and IRs with constant DRR (in which the DRR was set to the mean value of the generic exponential IR DRR across subbands) from real-world IRs. (E) The proportion of trials in which human subjects correctly identified the synthetic IR for each IR type. The generic exponential data are replotted from Fig. 6. ***P < 0.001 (two-tailed t test) as in Fig. 6.
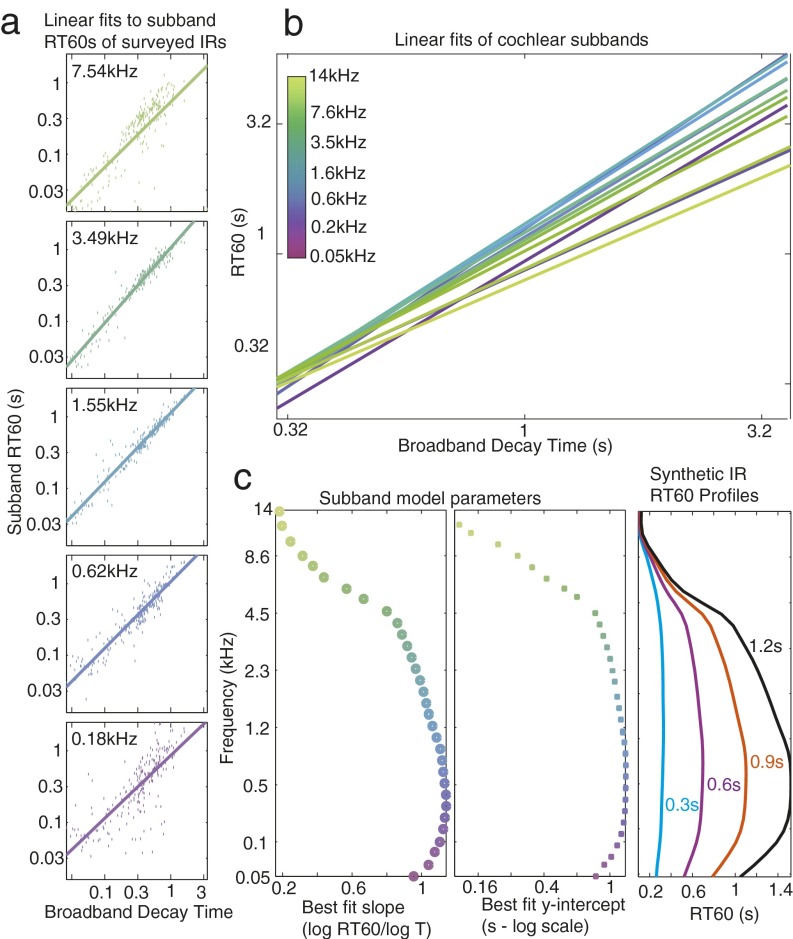
Summary measurements of all of the IRs from our survey (Fig. 4) suggest that the three properties evident in the example IR of Fig. 3 are typical of the environments encountered by humans in daily life. First, reverberation consistently exhibited Gaussian statistics after ∼30 ms (Fig. 4A), indicating the prominence of the decaying tail. Second, the tail invariably decayed exponentially (higher-order polynomials provided a negligible improvement to linear fits to the IR decay profile; Fig. 4B). Although complicated geometries can induce nonexponential decay (26), our analysis suggests that such environments are not typical of daily life. Third, decay rates were consistently frequency dependent [Fig. 4C and Fig. S3; F(1,270) = 9.82, P < 0.001], as were amplitudes [Fig. S2 A and B; F(1,270) = 327, P < 0.001]. In general, decay rates were slowest between 200 Hz and 2,000 Hz and reverberation decayed more rapidly at frequencies above and below this range. The survey also revealed a fourth property apparent in the distribution of natural IRs: The frequency decay profile scales with total reverberation. Spaces with more overall reverberation (corresponding to larger spaces and/or more reflective walls) showed stronger frequency dependence [Fig. 4C; compare red and magenta curves to blue curves; an ANOVA revealed an interaction between frequency and quartile index, F(3,32) = 7.75, P < 0.001]; on a logarithmic time axis, the quartile profiles have similar shapes. These regularities are presumably due to frequency-dependent absorptive properties of typical environmental surfaces and air. We note that although many of the surveyed spaces were manmade, we also measured numerous outdoor spaces in forests or parks, and these did not differ qualitatively from manmade spaces apart from having shorter IRs on average (Fig. 4D).
Fig. S3.
Generation of generic exponential synthetic IR parameters. (A) The measured RT60 of each surveyed IR is plotted (dots) for example subbands as a function of the broadband IR RT60 (Eq. S9) (i.e., the length of the IR). For each subband a line (Eq. S11) was fitted and used to calculate RT60 values for a given frequency and broadband RT60. (B) Linear fits from all cochlear subbands, showing that RT60s in different frequency subbands scale differently with broadband RT60, producing variation in the degree of frequency dependence of decay. (C) The fitted parameters of slope (Left) and y-intercept (Center) for each subband are plotted along with example synthetic IR profiles generated from the fits (Right).
The overall conclusion of our IR measurements is that real-world IRs exhibit considerable regularities. The presence of these regularities raises the possibility that the brain could leverage them for perception.
Experiment 1: Discrimination of Real and Synthetic Reverberation.
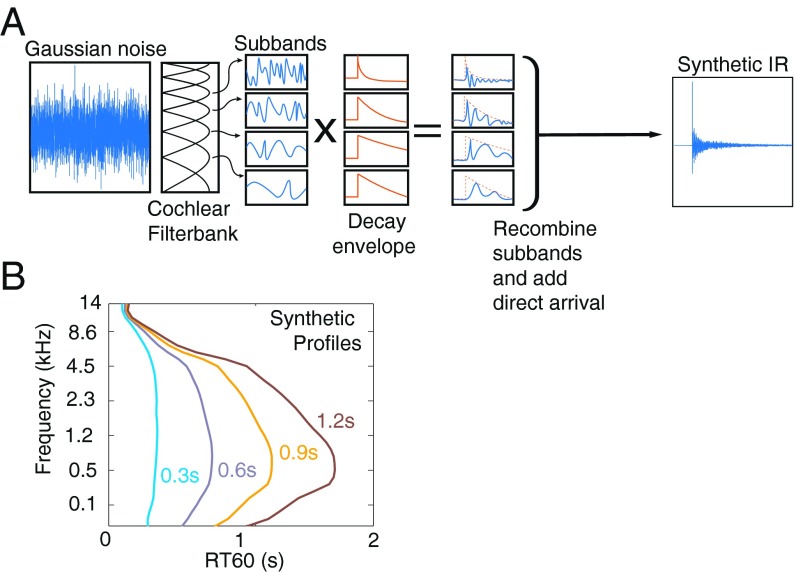
We next tested whether human listeners were sensitive to the four regularities we observed in real-world IRs, by synthesizing IRs that were consistent or inconsistent with these regularities. We synthesized IRs by imposing different types of energy decay on noise filtered into simulated cochlear frequency channels (Fig. 5). To replicate the decay properties observed in the natural IR distribution, we generated frequency-dependent decay rates (Fig. 5B) that mimicked both the frequency dependence and the variation of decay profile with the length of the IR (Fig. 4C and Fig. S3 and SI Materials and Methods, IR Synthesis).
Fig. 5.
Synthetic IR generation. (A) IRs were generated by filtering Gaussian noise into cochlear subbands and multiplying each subband by an amplitude envelope. The modified subbands were then recombined to yield a broadband synthetic IR. The temporal form of the decaying envelopes and the frequency dependence of decay rates were manipulated to produce IRs that either were consistent with the statistics of real-world IRs or deviated from them in some respect. (B) Synthetic decay rate profiles were computed that shared the variation in frequency and the variation of decay-rate profile with average RT60 with the surveyed IR distribution (Fig. 4C).
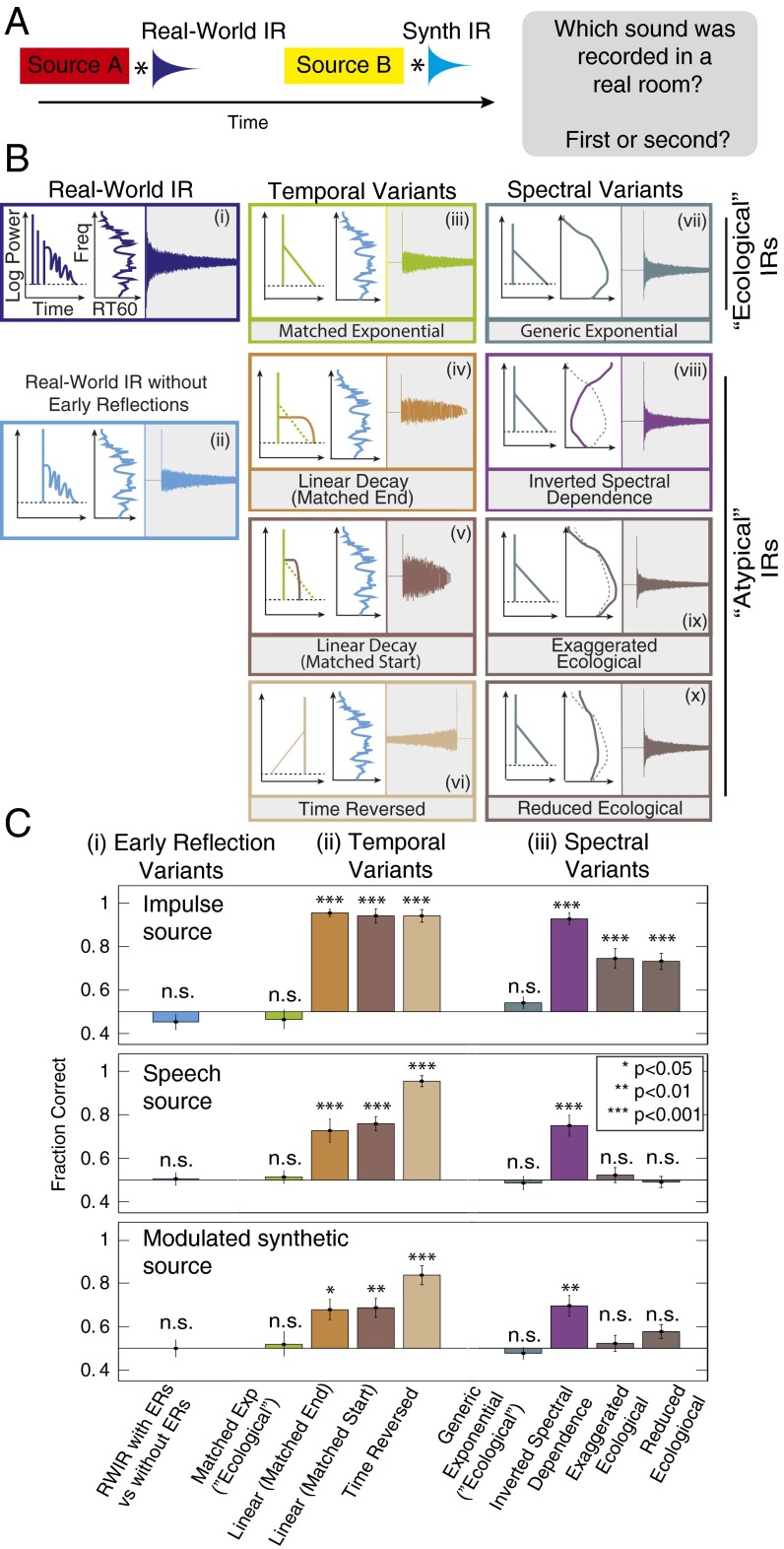
To assess whether the resulting IRs replicated the perceptual qualities of real-world reverberation, we asked listeners to discriminate between real and synthetic reverberation. Listeners were presented with two sounds (Fig. 6A), each of which consisted of a source convolved with an IR. In one case the IR was a real-world IR and in the other it was synthetic. Listeners were asked to identify which of the two sounds was recorded in a real space. If the synthetic IRs replicate the perceptually important effects of reverberation, this task should be difficult. Listeners performed this task for three types of sources: impulses (yielding the IR itself as the stimulus), spoken sentences, and synthetic modulated noise (27). These three types of sources were intended to test the generality of any observed effects across both simple and complex and familiar and unfamiliar sound sources. Because the IR regularities we observed were monaural in nature, sound presentation was always diotic (see Discussion for consideration of binaural effects).
Fig. 6.
Discrimination of synthetic reverberation (experiment 1). (A) Schematic of trial structure. Two sounds were played in succession, separated by a silent interval. Each sound was generated by convolving a source signal (an impulse, a spoken sentence, or a modulated noise) with an IR. The IR was a real-world IR for one sound and one of the synthetic variants for the other one (matched in RT60). Listeners judged which of the two sounds was recorded in a real room. (B) IR variants used in psychophysical experiments, varying in the presence of early reflections (i and ii), temporal dependence of decay (iii–vi), and spectral dependence of decay (vii–x). (B, i) Real-world IR; (B, ii) real-world IR with the early reflections removed; (B, iii) synthetic exponential decay with RT60 and DRR profiles matched to a real-world IR; (B, iv and v) synthetic linear decay matched to a real-world IR in starting amplitude or audible length (B, vi) time-reversed exponential decay; (B, vii) synthetic exponential decay with RT60 and DRR profiles interpolated from the real-world IR distribution; (B, viii–x) inverted, exaggerated, or reduced spectral dependence of RT60. (C) Task performance (proportion correct) as a function of the synthetic IR class for three source types: impulses (Top, yielding the IRs themselves), speech (Middle), and modulated noise (Bottom). Error bars denote SEMs. Asterisks denote significance of difference between each condition and chance performance following correction for multiple comparisons (*P < 0.05, **P < 0.01, and ***P < 0.001, two-sided t test; n.s., not significant).
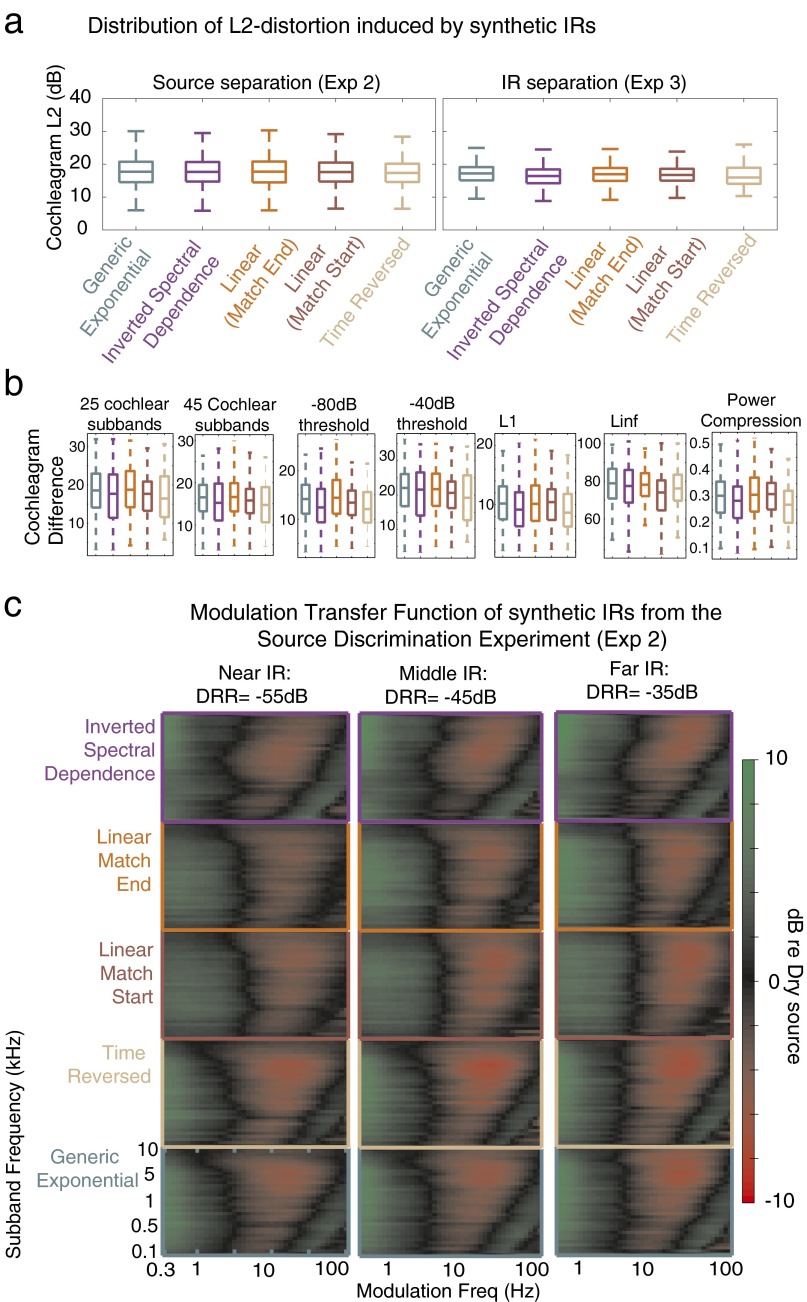
In all experiments, the various types of synthetic IRs were equated for the distortion that they induced to the cochleagram, to minimize the chances that judgments might simply reflect differences in such distortion. Distortion was computed as the mean squared error between the cochleagram of the signal before and after convolution with the IR (Eq. S16; see Fig. S4 for a consideration of other distortion metrics, which produced similar results). Distortion was adjusted by increasing or decreasing the mean decay rate of the synthetic IR; each “atypical” IR was adjusted in this way until it induced a similar distortion to the “ecological” IR (a synthetic IR that incorporated real-world regularities) to which it was compared (details in SI Materials and Methods, Measuring and Equating IR-Induced Distortion). This process was performed separately for each experiment and for each source type.
Fig. S4.
Signal distortion of synthetic IRs. (A) Box plots of the distribution of MSE distortion introduced by synthetic IRs to the stimuli used in the source discrimination (Exp 2, Left) and IR discrimination (Exp 3, Right) experiments. The boxes outline the 25th, 50th, and 75th percentiles. The whiskers delineate the minimum and maximum distortion values. (B) MSE distortion is robust to computational details of the cochleagram. Box plots show the distribution of MSE distortion in the cochleagram across the different IR types (as in A) for a range of changes to the cochleagram, from Left to Right: fewer subbands, more subbands, lower threshold, higher threshold, L1 norm (rather than L2), L-infinity norm, and exponential compression () rather than logarithmic. (C) Modulation transfer functions for the synthetic IRs used in experiment 2. These were obtained by subtracting the modulation spectrum of the dry source signal from that of the corresponding reverberant stimulus presented on an experimental trial and then averaging this difference over all stimuli. The dry and reverberant signals were first normalized to have the same rms level and hence the transfer function is symmetric around 0 dB.
We first sought to test the importance of the decaying tail relative to the sparse early reflections that are also present in real-world IRs (Fig. 1F). The tail forms the bulk of most real-world IRs (Fig. 4A) and its statistics were the focus of our IR analysis, but its perceptual importance was not clear a priori. Listeners discriminated a real-world IR (unaltered, to include early reflections; Fig. 6 B, i) from a real-world IR whose early reflections were excised and replaced with a single delta function (Fig. 6 B, ii). The excised section was the region of the time series whose kurtosis was non-Gaussian (SI Materials and Methods, Analysis of IR Statistics, IR Gaussianity), such that the entirety of the IR after the direct arrival had locally Gaussian statistics. Performance was not significantly different from chance regardless of the source type [IR, t(21) = −1.34, P = 0.2; speech, t(21) = 0.16, P = 0.88; noise, t(21) = 0.00, P = 1.00], suggesting that the early reflections are not critical for realistic reverberation, at least given diotic presentation (Fig. 6 C, i).
We next sought to test the perceptual importance of the temporal pattern of decay in the IR tail, which in real-world IRs is well described by frequency-dependent exponential decay (Fig. 4B). In one case, we replicated the coarse features of particular real-world IRs, imposing exponentially decaying envelopes whose subband RT60 and DRR values matched the values measured in the comparison real-world IR (“matched exponential,” Fig. 6 B, iii). In several other conditions we imposed alternative forms of decay: two types of linear decay or time-reversed exponential decay. The two linear IR types were formed by fixing either the starting amplitude (DRR; “matched start”) or the audible length (time at which the amplitude reached −60 dB; “matched end”) to the real-world IR value and iteratively adjusting the rate of linear decay until the distortion induced by the synthetic IR was equal to that of the real-world IR (the adjustments were modest, never exceeding ±8%; SI Materials and Methods, Measuring and Equating IR-Induced Distortion). Linear decay and time-reversed decay were chosen as alternatives because they are clearly distinct from exponential decay while similarly distorting the source signals as measured by the power spectrum and modulation spectrum (Fig. S4B). In all cases the synthetic IRs lacked early reflections, but were compared with a real-world IR with early reflections intact (similar results were obtained if the comparison was to a real-world IR with excised early reflections).
When asked to discriminate these synthetic IRs from real-world IRs, we found large effects of the temporal decay pattern (Fig. 6 C, ii). Listeners were unable to detect the matched exponential IRs as synthetic, regardless of the source type [IR, t(21) = −0.79, P = 0.44; speech, t(21) = 0.40, P = 0.70; noise, t(21) = 0.44, P = 0.67]. In contrast, all three alternative decay shapes were readily detected as synthetic [linear matched end: IR, t(21) = 26.6, P < 0.001; speech, t(21) = 4.28, P < 0.001; noise, t(21) = 3.78, P = 0.001; linear matched start: IR, t(21) = 13.78, P < 0.001; speech, t(21) = 7.93, P < 0.001; noise, t(21) = 4.26, P < 0.001; time-reversed: IR, t(21) = 15.1, P < 0.001; speech, 18.0, P < 0.001; noise, t(21) = 7.66, P < 0.001].
To test the importance of the frequency dependence of decay (Fig. 4C), we generated exponentially decaying IRs with ecological and nonecological decay-vs.-frequency profiles (spectral variants). The “generic exponential” IRs had RT60 profiles chosen to be consistent with the survey data, such that mid frequencies decayed more slowly than low and high frequencies (Fig. 6 B, vii), but were not explicitly matched to any particular real-world IR. The “inverted spectral dependence” decayed exponentially but had frequency dependence that deviated from that in typical IRs (slow decay at high and low frequencies, but fast decay at intermediate frequencies).
Finally, we tested sensitivity to the fourth regularity from our IR analysis (Fig. 4C) with IRs that had exaggerated or reduced degrees of decay variation with frequency. The reduced and exaggerated profiles test whether humans are sensitive to the dependence of the variation in decay rate with frequency on IR length.
We again found large effects of whether the IR conformed to the regularities of typical real-world IRs (Fig. 6 C, iii). Listeners were unable to detect the ecological synthetic IRs as synthetic [IR, t(21) = 1.52, P = 0.14; speech, t(21) = −0.45, P = 0.66; noise, t(21) = −0.87, P = 0.40], but readily detected inverted frequency dependence as such for all three source types [IR, t(21) = 16.14, P = 0.001; speech, t(21) = 5.23, P < 0.001; noise, t(21) = 4.06, P = 0.001]. The IRs with exaggerated and reduced frequency dependence were detected as synthetic when the source was an impulse [exaggerated: IR, t(21) = 5.457, P < 0.001; reduced: IR, t(21) = 6.289, P < 0.001] but not when the source was more complex [exaggerated: speech, t(21) = 0.654, P = 0.520; noise, t(21) = 0.611, P = 0.548; reduced: speech, t(21) = −0.358, P = 0.724; noise, t(21) = 2.401, P = 0.026]. This latter finding is consistent with our subjective impression that this regularity is the most subtle of the four that we documented.
Collectively, these results suggest that the features revealed by our analysis of real-world IRs—a Gaussian tail exhibiting exponential decay at frequency-dependent rates—are both requisite and sufficient for the perception of reverberation. Consistent with this interpretation, participants reported that IRs with unnatural decay modes sounded artificial (audio demos available at mcdermottlab.mit.edu/Reverb/ReverbDemos.html). In some cases the subjective impression was striking. For instance, IRs with unnatural frequency dependence (i.e., spectrally inverted) often seemed to contain two sounds: a source with moderate reverberation and a high-frequency “hiss.” The auditory system is apparently unwilling to interpret high frequencies that decay more slowly than low frequencies as reverberation, ascribing them to an additional noise-like sound source rather than an impulse interacting with the environment. In contrast, synthetic IRs with ecologically valid decay characteristics typically sounded like a single impulsive source in a reverberant space, despite being generated by merely imposing decay on noise. Similar perceptual effects were observed with DRR variants (Fig. S2 D and E). Example stimuli can be heard at mcdermottlab.mit.edu/Reverb/ReverbDemos.html.
Experiments 2 and 3: Perceptual Separation of Source and Reverberation.
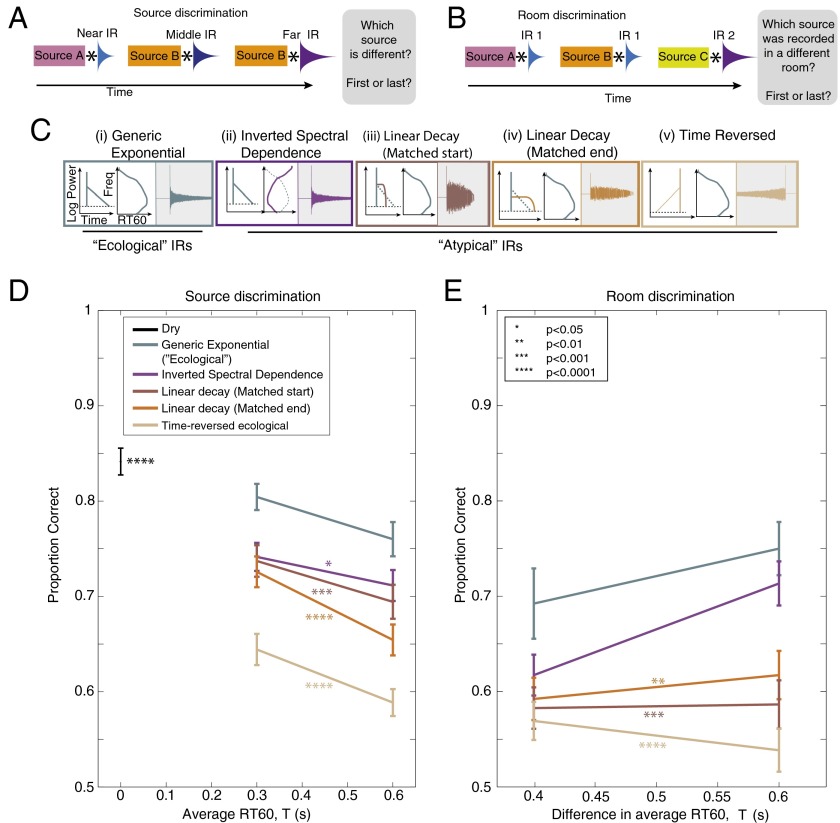
We next tested whether humans can separately estimate source and filter from reverberant sound and whether any such abilities would depend on conformity to the regularities present in real-world reverberation. We designed two tasks in which listeners heard synthetic sources convolved with synthetic IRs. One task measured discrimination of the sources (Fig. 7A), whereas the other one measured discrimination of the IRs (Fig. 7B). In both cases the sources were designed to be structured but unfamiliar, and the IRs were synthesized to be consistent with the natural distribution (Fig. 7C, i) or to deviate from it with either atypical spectral (Fig. 7 C, ii) or temporal structure (Fig. 7 C, iii–v).
Fig. 7.
Perceptual separation of source and IR (experiments 2 and 3). (A) Schematic of trial structure for experiment 2 (discrimination of sources in reverberation). Three sounds were played in succession, separated by silent intervals. Each sound was generated by convolving a source signal (modulated noise) with a different IR. The IRs were all a particular type of synthetic variant and had the same RT60 but differed in DRR (simulating different distances of the source from the listener). Listeners judged which of the three sources was different from the other two. (B) Schematic of trial structure for experiment 3 (discrimination of IRs in reverberant sound). Three sounds were played in succession, separated by silent intervals. Each sound was generated by convolving a source signal (modulated noise) with an IR. The IRs were all a particular type of synthetic variant. Two of them were identical and the third one had a longer RT60 (simulating a larger room). Listeners judged which of the three sources was recorded in a different room. (C) IR variants used to probe the effect of reverberation characteristics on perceptual separation. All IRs of a given RT60 and DRR introduced equivalent distortion in the cochleagram. (D) Source discrimination performance (proportion correct) as a function of IR decay time for different synthetic IR classes. Here, and in E, error bars denote SEMs and asterisks denote significance of difference between average performance in each condition and that of the generic exponential condition. (E) IR discrimination performance (proportion correct) as a function of the IR decay time for different synthetic IR classes.
In the source discrimination task (Fig. 7A), participants were presented with three sounds, two of which were generated from identical sources. The task was to identify the distinct source (either first or last). Because the three sources were convolved with different IRs (corresponding to different source–listener distances in the same room), all three sounds arriving at the ear were different. Participants were thus incentivized to estimate features of the sound sources from their convolutions with the IRs. They were told that sometimes the reverberation would sound natural and in other cases the reverberation would be synthetic and potentially unnatural, but that in either case they should discount its effects as best they could. In all cases, the different types of IRs were adjusted to induce similar distortion (measured by squared error on the cochleagram), such that differences in performance were unlikely to reflect the extent to which the reverberation physically obscured the sources.
As shown in Fig. 7D, listeners performed well above chance, indicating some ability to discriminate source properties in the presence of reverberation. Performance decreased as the IRs became longer (and thus more distortive), as expected, producing a main effect of RT60 [F(1,13) = 43.2, P < 0.0001]. However, performance was consistently higher when the IRs were ecological (generic exponential) than when they violated the regularities of natural environments, producing a main effect of IR type [F(4,52) = 21.6, P < 0.0001; paired comparisons between generic exponential and all other conditions were significant in each case, P < 0.02 or lower; with no interaction between RT60 and IR type, F(4,52) = 0.48, P = 0.75].
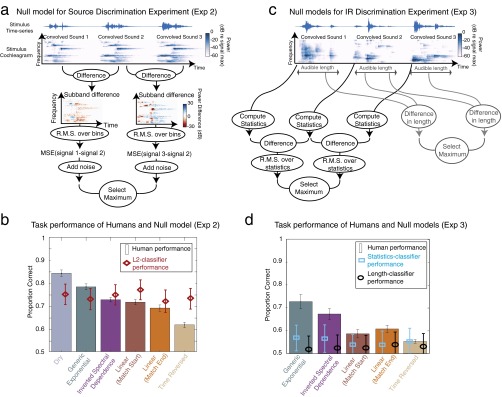
To confirm that this pattern of results could not be explained by the amount of distortion induced by the different IR types, we measured the performance of a null model that chose the stimulus (i.e., source convolved with IR) that was most different from the middle stimulus (i.e., the second of the three sounds presented in a trial) as measured by mean-squared error in the cochleagram. This model performed well above chance on the task, but showed little difference in performance between IR types and did not replicate the pattern of performance variation seen in human listeners (Fig. S5 A and B). This result suggests that if listeners were performing the task by comparing the convolved stimuli, rather than estimating the sources, they would have performed equally well in all conditions. Taken together, the results suggest that listeners could estimate the structure of the underlying sound sources to some extent and that they were better at this when IRs were ecologically valid.
Fig. S5.
Null models of separation task performance. (A) Schematic of the null model for source discrimination using cochleagram differences. (B) Human performance on the source discrimination experiment compared with the null model. Results from IRs of differing length (Fig. 7B) have been averaged. Error bars show 95% confidence intervals obtained by bootstrap. Random noise was added to the decision stage of the null model to equate average performance across all IR classes with that of humans. (C) Schematic of two null models for IR discrimination using either cochleagram statistics or audible signal length. (D) Human performance on the IR discrimination experiment compared with the null models. Results from IRs of differing length (Fig. 7D) have been averaged. Error bars of both human and null model performance show 95% confidence intervals obtained by bootstrap.
In the IR discrimination task (Fig. 7B), subjects were again presented with three sounds, each of which was generated by convolving a synthetic source and IR. All three sources were distinct (different samples of modulated noise), but two of them were convolved with the same IR. The other one was convolved with an IR either longer or shorter than the other two, as would occur under natural conditions if it were recorded in a room of a different size. Subjects were asked to identify which sound was recorded in a different room. The sound sources were randomly varied in length (2–2.4 s) such that the longest (or shortest) stimulus was not necessarily the one with the longest (or shortest) IR. Because the sources were different for all three sounds, we expected task performance to require estimation of IR properties from their convolutions with the sources.
Listeners were able to discriminate IRs from their convolution with sources (Fig. 7E), indicating some ability to estimate IR properties. As expected, performance was better when the difference between the IR lengths was greater, making the task intrinsically easier [F(1,13) = 5.6, P = 0.034, with no interaction with IR type: F(4,52) = 2.1, P = 0.1]. However, performance was again substantially worse when IR properties deviated from those in the real world [F(4,52) = 16.2, P < 0.0001; paired comparisons between ecological (generic exponential) and nonecological IRs were significant in all cases other than the inverted spectral dependence, P < 0.02]. In the inverted spectral dependence condition, several subjects reported noticing a high-frequency hiss from the slowly decaying high frequencies, which may have provided a cue that boosted performance.
To test whether statistical differences induced by the IRs could account for the results, we implemented a model that measured texture statistics (28) from the three stimuli in each trial and chose the stimulus whose statistics were most different from those of the middle stimulus (i.e., the second of the three stimuli presented in a single trial). The performance of this model was only slightly above chance and did not differ substantially across IR types (Fig. S5 C and D). This analysis suggests that listener performance on this task is unlikely to be mediated by basic statistical properties of the convolved stimuli. A second model using stimulus duration to perform the task was similarly unable to explain the results (Fig. S5 C and D). We note also that a cochleagram difference model, like that used in the source discrimination experiment, performs at chance, because the three sources are different. The results indicate that human listeners are better able to infer IR properties from reverberant sounds when the IR is natural, consistent with the idea that separation of source and filter relies on prior knowledge of reverberation statistics.
SI Materials and Methods
Real-World IR Measurements.
IR survey.
The survey was intended to provide samples from the distribution of spaces that participants encountered during their daily lives. IR measurement locations were chosen by tracking volunteer subjects. Each subject was sent 24 text messages a day, at randomized times, and was requested to reply with his or her location at the time the message was sent. If subjects saw the message instantly they were requested to also send a photograph of the space they were occupying. A message was sent once within each hour of the day, with the exact time drawn from a uniform distribution over that hour. Subjects also installed a phone application that allowed us to retrieve their phone’s GPS coordinates every 15 min. The address provided by participants, combined with GPS information, enabled us to locate the spaces from which messages were sent. Subjects were financially compensated for every successful GPS ping (to encourage them to keep their phone batteries charged and GPS enabled) and for every text message that they replied to. Immediate replies were compensated more highly than late ones to encourage timely responses. Each subject was tracked for 14 days.
Seven subjects participated (four female, mean age = 27.3 y, SD = 6.8) with disparate occupations (musician, marketing manager, postdoctoral researcher, part-time nurse, childcare specialist, and two undergraduates). Two subjects lived in dense urban areas (Boston), three lived in moderately dense suburbs (Somerville and Cambridge, MA), one lived in an undergraduate dormitory (MIT), and one lived in a suburban town (Lexington, MA). Subjects replied to an average of 284 of the 336 text messages they received (24 per day 14 days), with an average latency of 23 min between message and response (not including time asleep). Responses were provided from a total of 301 distinct spaces with 156 photographs. We were able to measure IRs for 271 of these sampled spaces.
IR measurement.
IRs were measured by playing a fixed noise signal through a speaker and recording the resulting sound. Because the source signal and speaker transfer function were known, the IR could be derived from the recorded sound. The procedure was designed to be noise robust by presenting the source signal multiple times and averaging the result.
Measurements were made with a portable battery-powered speaker (Ion Block Rocker) and a digital multitrack recorder (Tascam DR-40, using the internal microphones). The speaker and recorder were positioned 1.5 m apart (to simulate conversational distance), with the recorder as close as possible to the position reported by the participant. In the three occasions where the room was too small to accommodate this distance (two showers and one kitchen pantry) the speaker and recorder were placed back to back. The recorder had two microphones spatially separated by 4 cm and 90° orientation. We recorded from both microphones and used the recording from the left channel for IR analysis. The right channel was used to evaluate the goodness of fit of polynomial decay models (SI Materials and Methods, Analysis of IR Statistics, IR Tail Characteristics).
A predetermined signal was broadcast from the speaker via one track of the recorder and was recorded back onto a separate track via the microphone. The broadcast signal was the concatenation of 8, 16, or 32 identical 23.8-s sequences, each of which was subdivided into two 11.9-s Golay complementary sequences (52, 53), here termed and to denote the ith instance of each sequence (each 219 samples at 44.1 kHz). Golay sequences have the property that
| [S1] |
where δ is a Kronecker-delta function, and denotes cross-correlation (i.e., convolution with one of the signals time-reversed). Thus, after broadcasting and rerecording a Golay sequence in a given room, the recorded sequences are the Golay sequences convolved with the IR of the room with the addition of additive background noise,
| [S2] |
where and denote additive noise recorded during the ith broadcast (assumed to be uncorrelated with each other). The recordings are split into their component sequences, and an estimate of the impulse response was obtained as follows (* denotes convolution):
| [S3] |
Because the noise terms and are uncorrelated with the broadcast sounds, the variance of the sum in the last line of Eq. S3 is proportional to Thus, the IR estimate is the sum of the environmental IR h and a noise floor proportional to which approaches zero as N increases. Cross-correlations were performed in the frequency domain. The IR estimate was downsampled to 32 kHz.
The measurement procedure assumes that the reflecting surfaces in the environment are stationary during the recording process. In practice, because we were often recording in public places, there were often minor environmental changes during recording (people moved through the space, and doors opened or closed). In such cases our measured IR reflects the average IR over the recording. Our observations suggest that minor environmental changes such as doors opening or closing have a negligible effect on the parameters we consider in this paper (Fig. S1A, v).
To generate Golay complementary sequences we start with the seed pair and and use the fact that, for any complementary pair, the combinations and are themselves complementary sequences. We thus repeatedly combine and in this way to create sequences of samples at 44.1 kHz with which we made our measurements.
Impulse response noise floor.
The Golay sequences permit background noise to be averaged out of the IR estimate, but due to finite measurement time, a noise floor was always present in practice. In pilot experiments we determined that the eight-repetition sequence (3 min 10 s) produced IR estimates with sufficiently low noise floors to allow accurate measurement of the subband RT60 of typical IRs, provided that the power of the recorded Golay sequence was the same as that of the background noise. However, some spaces necessitated lower levels (e.g., restaurants where management requested it). In such cases we compensated by using longer sequences containing 16 (6 min 20 s) or 32 (12 min 40 s) sets of Golay complementary pairs. This procedure allowed measurements to be made in public places (e.g., restaurants, cafés, parks, city streets, offices, supermarkets, trains, etc.) without using prohibitively loud sound sources. The average noise floor across all recordings was −81 dB relative to the direct arrival and was usually 20–60 dB below the start of the reverberant tail (Fig. S1D).
Measurement apparatus transfer function.
Because the sound recorded during IR measurement was affected both by the environment and by the acoustic characteristics of the measurement apparatus, accurate estimation of the impulse response required inversion of the transfer function of the speaker and microphone. For the purposes of our measurements, the main effect of this transfer function was to alter the DRR. This is because the transfer function of the speaker was slightly different for sound emanating from the front compared with other directions. The direct sound comes from the front of the speaker, but reverberation contains sound emitted from all directions. Thus, the measured ratio of direct to reverberant sound could be colored by nonuniform directional transfer. Notably, all other parameters that we measured (i.e., RT60 and kurtosis) should not have been affected by this. We thus specifically adjusted the DRR, using measurements of the apparatus transfer functions.
Transfer functions were measured in an anechoic chamber by broadcasting the interleaved Golay sequences ( and ) and recording the signal at azimuths of 0°, 45°, 90°, 135°, and 180° relative to the speaker face (Fig. S1E). These were used to estimate the speaker’s transfer function for each direction. These directional transfer functions were integrated over all azimuths to yield the transfer function of all sound broadcast into the environment (i.e., the omnidirectional transfer function; Fig. S1F). Sound broadcast in all directions contributed to the reverberant sound and this omnidirectional transfer function was needed to estimate the coloration of recorded audio. To remove variations in DRR due to the speaker characteristics, the measured subband DRRs were adjusted by
| [S4] |
where and are the direct and omnidirectional transfer functions in the kth subband and and are the mean values of the transfer functions over all subbands.
Analysis of IR Statistics.
IR Gaussianity.
As is evident in Figs. 1 and 3, room impulse responses typically begin with a small number of “early” reflections distributed relatively sparsely in time. Because the density of arriving echoes increases with time, echoes begin to overlap and become difficult to individuate, merging into the IR tail (56). We sought to quantify the time at which this transition occurs [known as the “mixing time” (57)]. To this end we measured the kurtosis of short sections of the IR and identified the time at which the IR kurtosis was consistent with that of Gaussian noise, as proposed by Stewart and Sandler (56).
We split the IR into overlapping 10-ms sections centered on each individual sample and computed the kurtosis of each section. The early sections of the IR had kurtosis values well above 3 (i.e., non-Gaussian) but the kurtosis typically decreased with time, rapidly approaching the value expected for Gaussian noise. We refer to the sparse early section of the IR as the early reflections and to the latter region as the diffuse tail.
To quantify the transition between the early reflections and the diffuse tail we classified each sample as Gaussian or non-Gaussian based on whether the section kurtosis exceeded the confidence interval for the kurtosis of a 10-ms sample of Gaussian noise (with the 32-kHz sampling rate we used, the upper bound of the confidence interval was 3.54). We defined (Fig. 4C, Inset) as the time at which as many Gaussian data points as non-Gaussian data points had occurred. We considered the diffuse tail to be the section of the IR after For most IRs in our survey was ∼50 ms or less (relative to the first-arriving sound) (Fig. 4C).
IR tail characteristics.
We analyzed the IR tail characteristics within 33 frequency subbands. Subbands were obtained from a filter bank mimicking the frequency selectivity of the human ear (28), with center frequencies spanning 20 Hz to 16 kHz, equally spaced on an equivalent-rectangular-bandwidth scale.
Polynomial decay fits.
To examine decay properties, the envelope of each subband was extracted by taking the magnitude of the analytic signal (via the Hilbert transform). We initially observed that when plotted on a decibel scale, most such envelopes decayed linearly down to the noise floor (e.g., Fig. 3D), suggestive of exponential decay. We quantified this observation by fitting polynomials to the envelopes and assessing the goodness of fit for different polynomial degrees. For each subband we jointly estimated the decay profile of the diffuse tail and the recording noise floor by fitting a piecewise model with two sections, the first one a Pth order polynomial (modeling the impulse response) and the second one flat (modeling the measurement noise floor), as
| [S5] |
where k denotes cochlear subband index, denotes time after the direct arrival, is the measurement noise floor, is the time at which the measured IR intersects the noise floor, and is the time after the direct arrival at which the IR has locally Gaussian statistics (SI Materials and Methods, Real-World IR Measurements, Impulse Response Noise Floor). The parameters and polynomial coefficients were chosen to minimize the squared error between the data and the model with error computed in decibels,
| [S6] |
where is the envelope of the kth subband of the IR and denotes root-mean squared. was fully determined from the other function parameters. Because our purpose was to characterize the dense tail of the IR, we fitted only the portion of the IR after
To assess the extent to which exponential decay [well established for simple empty cube models of rooms (5)] would characterize the real-world spaces measured in our survey, we computed the fraction of variance explained by the polynomial fits as a function of the polynomial degree We fitted the polynomial model to IR data derived from the left channel of the recorder and computed the variance explained in IR data derived from the right channel. The variance was computed across sample values from TGauss to Fits and explained variance were obtained from different channels to avoid overfitting.
Decay rates and DRR.
Because the energy decay within IR subbands was well described as exponential, we quantified the IR tail with the two parameters needed to specify exponential decay: the decay rate (or equivalently, the time to decay by a specified amount) and the starting amplitude. We fitted
| [S7] |
to the envelope of each subband, where is the direct-to-reverberant ratio (Fig. S2) and the decay rate in decibels per second. We computed the subband reverberation time (RT60—defined as the time taken for the reverberant energy to drop by 60 dB; Fig. 3) as
| [S8] |
As a summary measure of the reverberation time for an IR, we computed the median RT60 across all 33 subbands between 20 Hz and 16 kHz, which we refer to as the “broadband RT60,”
| [S9] |
We used this parameter to divide the IRs into quartiles (Fig. 4 and Fig. S2).
IR Synthesis.
To test whether the characteristics we observed in real-world IRs were perceptually important, we generated synthetic IRs that either conformed to the real-world characteristics or deviated from them in some way. Synthetic IRs were generated by imposing different types of decay on noise subbands, using the same filter bank used for real-world IR analysis. Gaussian white noise was passed through the filter bank; the resulting subbands were multiplied by a synthetic decay envelope, then filtered again (as is standard in analysis–synthesis subband transforms), and summed to generate a full-bandwidth IR (Fig. 5). For all synthetic IRs a delta function at was used to simulate the direct arrival.
In all experiments, 10 exemplars were generated for each IR condition, each synthesized from a different sample of Gaussian noise. Each stimulus used one of these 10 IRs, drawn randomly.
We next describe how each type of synthetic IR was generated (see Fig. 6B for schematics of each type).
Ecological impulse responses.
To generate synthetic IRs that were consistent with the ecological distribution that we measured in our survey, we imposed exponential decaying envelopes with subband RT60s that varied across frequency in a manner similar to real-world IRs. In one case (matched exponential) the subband RT60s were exactly matched to those of particular comparison real-world IRs. In another (generic exponential) we modeled the real-world IR RT60 vs. frequency dependence and chose subband RT60s that were consistent with this dependence.
Matched exponential.
We imposed the following envelopes on noise subbands,
| [S10] |
where and are the subband DRRs and RT60s measured from a specific real-world IR (Eqs. S7 and S8).
Generic exponential.
The purpose of this condition was to replicate the central tendencies of the surveyed IRs rather than the specific characteristics of any one particular IR. It was apparent from the survey data that the variation in decay rates with frequency depended on the overall RT60 of the IR—longer IRs exhibited stronger frequency dependence (compare the first and fourth quartiles in Fig. 4C). We captured this dependence by fitting lines to the survey data:
| [S11] |
The DRR, in contrast, maintained largely the same shape for short and long IRs, which we captured with a simple scaling factor
| [S12] |
where is the DRR in the kth subband averaged across all IRs in the survey. We determined the constants mk, bk, and empirically via least-mean squares on the survey data for each cochlear subband (Fig. S3).
Before fitting the parameters, we eliminated 30 outliers and all IRs with T < 200 ms. The outlier IRs corresponded to surveyed spaces that were unusual in shape (e.g., long corridors, large atriums in MIT buildings) or construction material (e.g., solid cinderblock walls). We quantified the “typicality” of each IR by computing the L2 distance between its RT60 profile (τk) and the RT60 profile of all other surveyed IRs after normalizing by the broadband RT60 ():
| [S13] |
IR typicality of the ith IR was estimated as the median value of λi,j across all values of j. The 30 IRs that fell outside 1 SD of this measure (across all IRs) were rejected as outliers.
This procedure gave us a method to synthesize RT60 (Fig. S3C) and DRR (Fig. S2C) profiles consistent with our surveyed distribution by substituting a desired broadband RT60 into Eqs. S11 and S12.
Atypical impulse responses.
To test the perceptual importance of individual features of IRs, we generated IRs that violated the regularities we observed in the surveyed data. We manipulated the following IR properties: (i) temporal form of decay (exponential vs. linear or time-reversed), (ii) spectral dependence of decay (ecological vs. inverted), (iii) dependence of decay profile on broadband RT60 (ecological vs. exaggerated or reduced), and (iv) spectral dependence of DRR (ecological vs. constant).
Linear decay.
The envelope of the kth subband decayed linearly to zero,
| [S14] |
where the decay rates were adjusted to match the power in each subband to that of the ecological IR to which they were being compared. In one condition (linear matched start) the IR was additionally constrained to have the same subband DRRs as the ecological IR. In the other (linear matched end) the IR was constrained to have approximately the same audible length (the time at which the linear envelope intersected zero was equal to the time at which the ecological IR envelope intersected −60 dB relative to the direct arrival).
Time-reversed.
The time-reversed IR was generated with the same procedure as the matched exponential and generic exponential IRs except that the IR was reversed in time.
Inverted spectral dependence.
Envelopes decayed exponentially (as with ecological IRs) but with the spectral dependence of subband RT60 reversed. This created an IR that decayed slowly at frequencies where real-world IRs decay quickly and vice versa. Subband RT60s were computed as
| [S15] |
where is the RT60 of the ecological IR in the kth subband.
Exaggerated ecological.
We exaggerated the real-world relationship between shape of the decay profile and overall length of IR by substituting the value of 2T into Eq. S11 and then dividing the resulting RT60 profile by 2. This yielded an IR with frequency-dependent RT60 variation typical of a large IR (2T) but with a broadband RT60 typical of smaller IR (T). In practice this resulted in an IR with an RT60 profile that is more sharply peaked than real-world IRs of comparable size.
Reduced ecological.
We substituted T/2 into Eq. S11 and the resulting values were multiplied by 2. In practice this resulted in an RT60 profile that was less sharply peaked than real-world IRs of comparable size.
Constant DRR.
The RT60 values were generated as for the generic exponential IR, but the DRR values were set to the mean value of those of the generic exponential IR.
Measuring and Equating IR-Induced Distortion.
In experiments 1–3 we generated the synthetic IRs described above that either were consistent with the distribution observed in our real-world IR survey or deviated from it and tested the perception of reverberation. To ensure that differences in perceived reverberation were not merely due to differences in signal distortion induced by different IR types, we sought to normalize the synthetic IRs such that they produced equivalent amounts of audible distortion.
To measure the audible distortion induced by an IR on a given class of signals, the IR was convolved with 100 randomly selected sources used in the relevant experiment. The average MSE between the dry and wet cochleagrams was measured as
| [S16] |
where and indicate indexes of frequency and time bins, and are the numbers of frequency and time bins in the cochleagram, and are the subband envelopes (obtained by Hilbert transforms and downsampled to 100 Hz) of the convolved signal and the dry source, and Θ60 is a truncation operator that sets all values less than −60 dB equal to −60 dB. ρY and ρS are the mean subband rms values of the convolved and dry cochleagrams. Frequencies below 20 Hz (k = 1) and above 16 kHz (k = 33) were neglected. MSE values were then averaged across the 100 sources to yield a measure of the distortion induced by the IR.
Minus 60 dB was chosen as the threshold of audibility based on pilot experiments in which we measured the detectability of pink noise added to the experiment stimuli. Experiment stimuli were normalized to the same levels used in the experiments, and the added noise was presented at a range of levels. Subjects heard a pair of stimuli, one with pink noise and one without, and had to identify which contained the noise. Subjects performed above chance when the noise floor power exceeded −60 dB (relative to ρD), but were at chance when the noise power was less than this value.
When generating the synthetic IRs designed to produce equivalent signal distortion, the average MSE was computed for each IR with the same set of 100 sources. To increase or decrease the distortion for the purposes of equating it across conditions, the RT60 of each of the subbands was increased or decreased by a fixed proportion
| [S17] |
where ε was adjusted until the two IRs produced MSE values within 1%. In all experiments one IR was designed to be ecologically valid (i.e., consistent with the survey) and this IR was held constant while the nonecological IRs were adjusted to match using the above procedure. Values of ε in practice never exceeded ±0.08. Note that this procedure preserves the ratios between the RT60s of different subbands.
The lone exception to the above procedure occurred for the linear-decay–matched-end IR, which was designed to have the same audible length as the ecological IR. To adjust the distortion while preserving the matched length, in this case the DRR was adjusted iteratively to equate distortion:
| [S18] |
Experiment 1: Discrimination of Real and Synthetic Reverberation.
To test whether the variables measured in our IR analysis captured the perceptually important structure of real-world IRs, we measured whether listeners could discriminate synthetic from real IRs. Subjects were presented with a pair of sounds. One was convolved with a real-world IR, and one was convolved with a synthetic IR. Subjects were told that one of the sounds was recorded in a room and that the other had reverberation added synthetically. Listeners were asked to identify which of the two sounds was an actual recording in a room.
Real-world IRs.
Real-world IRs were recorded with the same apparatus as the surveyed IRs. To increase the experiment’s sensitivity we used a 10-m source–receiver separation rather than the 1.5 m of our survey measurements. Pilot experiments showed that increasing the source–receiver distance within a space primarily alters the DRR, without altering the decay characteristics of the IR tail (Fig. S1C). Subjectively, this had the effect of making the reverberation more salient, potentially accentuating differences between the synthetic and real IRs, and making for a stronger test. Ten rooms were chosen from the surveyed locations with a range of T of 0.51—1.19 s and median values of DRR across frequency from 32 dB to 45 dB. These RT60 values were large enough that the reverberation was salient but still well within the distribution of surveyed IRs (Fig. 4). IRs were presented diotically (the left channel of the real-world IR was presented to both ears).
Synthetic IRs.
The stimuli IRs were paired as follows:
Early reflection variants.
Real-world IR with early reflections vs. real-world IR with early reflections excised
Temporal variants (vs. real-world IR).
Matched exponential
Linear decay (matched start)
Linear decay (matched end)
Time-reversed
Spectral variants (vs. real-world IR).
Generic exponential
Inverted spectral dependence
Exaggerated ecological
Reduced ecological
DRR variants (vs. real-world IR).
Generic exponential with constant DRR
To generate real-world IRs without early reflections, the section of the IR before (i.e., the section for which the IR statistics were not Gaussian) was excised and replaced with a delta function directly adjoining the diffuse tail of the real-world IR. Across the real-world IRs in this experiment values ranged from 10 ms to 74 ms and corresponded to 1–20% of the audible IR.
The matched exponential and the generic exponential IRs were generated with parameters measured from the real-world IR (subband RT60 and DRR and broadband RT60, respectively). The other synthetic IRs were adjusted to equate their distortion to that of the ecological IR (SI Materials and Methods, Measuring and Equating IR-Induced Distortion) matched to their comparison real-world IR. Temporal variants were matched to the matched exponential and spectral and DRR variants were matched to the generic exponential.
Source signals.
Three classes of source signals were used and are described in succession below.
Impulses.
IRs were presented in isolation, and subjects were told the sound was an impulsive sound (e.g., a balloon pop) recorded in a real-world room.
Speech.
IRs were convolved with a full sentence, drawn randomly without replacement from the TIMIT database (i.e., the Texas Instruments and Massachusetts Institute of Technology Acoustic-Phonetic Continuous Speech Corpus). No constraints were placed on the sentence length. IRs were downsampled to the TIMIT sampling frequency of 16 kHz before convolution.
Synthetic sources.
IRs were convolved with 2,400-ms modulated noise samples. In this and all subsequent experiments, modulated noise was generated using the method of McDermott et al. (27). Cochleagrams were modeled with a multivariate Gaussian distribution with covariance in time and frequency that resembled that found in natural sounds. Cochleagrams were sampled from this distribution and imposed on noise subbands, which were then summed to produce a waveform. To introduce variability in the source characteristics, covariance parameters were randomly chosen from a distribution (log-uniform) centered around values common to natural sounds (distributions were centered at −0.11 per 20-ms time window and −0.065 per frequency bin and varied from one-fifth to five times these values). The sounds were generated at 32 kHz with the same filter bank as in the IR analysis.
Experiment procedure.
The two stimuli on each trial were presented in a random order separated by 800 ms of silence.
When the source signals were impulses (and the stimuli thus IRs), the levels of the IRs were roved. Pilot experiments showed that the perceived loudness of IRs with equated level varied across conditions, and because we were unsure whether loudness would affect realism judgments, we attempted to discourage listeners from performing the task using loudness cues. The IR pair was presented with a mean sound pressure level (SPL; computed over the first 80 ms of the IR) of 70 dB and a random SPL difference drawn from a uniform distribution between 0 dB and 15 dB. This decibel difference produced substantially larger loudness differences than any due to the IR condition, such that differences between conditions could not be explained by loudness.
When the source signals were speech or modulated noise, stimulus levels were set such that the section of the convolution in which the dry source was nonzero was 70 dB (i.e., the decaying tails at the end of the sentence were not included in the level normalization).
Each of the 10 real-world IRs was paired once with each IR condition for each source type, yielding 300 total trials. Trials for a particular type of source signal were presented in blocks of 30. Trials were randomly ordered within blocks. At the end of each block subjects received feedback on their overall performance.
Twenty-two subjects (9 female, mean age 28.9 y, SD = 8.4) took part. All had self-reported normal hearing.
Audio presentation.
In all experiments, sounds were played via the sound card on a MacMini at a sampling rate of 32 kHz, via a Behringer HA400 amplifier. The Psychtoolbox for Matlab (55) was used to play out sound waveforms. Sounds were then presented to subjects over Sennheiser HD280 headphones (circumaural) in a soundproof booth (Industrial Acoustics).
Experiment 2—Source Discrimination.
Subjects heard three synthetic source signals, two of which were identical and one of which was different. Each of the three sources was convolved with a different synthetic IR. The three IRs used in a trial differed in DRR (mean values of 35 dB, 45 dB, and 55 dB, respectively), simulating different distances from the listener. Subjects were asked to identify the interval that contained the distinct source signal, discounting the effects of the reverberation. The experiment contained 10 conditions in a 5 × 2 design, with five classes of synthetic IRs and two different decay rates (broadband RT60).
Synthetic IRs.
The IRs were generated with two values of broadband RT60 ( = 0.3 and 0.6), simulating two different room sizes (or wall materials). Both of these values fall within the range of values measured in real-world IRs in our survey. For each broadband RT60 we synthesized the following IRs (Fig. 7A): (i) generic exponential, (ii) linear decay (matched start), (iii) linear decay (matched end), (iv) time-reversed, and (v) inverted spectral dependence.
The RT60 and DRR values for the generic exponential IR were derived by substituting the desired broadband RT60s into Eq. S11 and then adjusting the DRR levels to produce the desired mean DRR (Fig. S2C). The spectral and temporal variants were synthesized as described in SI Materials and Methods, IR Synthesis, Atypical impulse responses and for each IR the envelope parameters (DRR and RT60) were adjusted to equate distortion with the generic exponential IR of the same broadband RT60 (Fig. S4A; SI Materials and Methods, Measuring and Equating IR-Induced Distortion). After equating the distortion, all of the IR types exhibited similar modulation transfer functions, indicating that the distortion they introduce is similarly distributed across modulation rates (Fig. S5B).
Source signals.
The source signals were designed to be synthetic and unfamiliar, to rule out the possibility that subjects were recognizing well-known sources and comparing to stored templates. Two 400-ms signals were synthesized, and in the same manner as the synthetic sounds in experiment 1.
These two signals were normalized to have the same SPL level and were then summed both with and without a time offset to create a pair of sources for an experiment trial that have almost identical time-averaged spectra,
| [S19] |
where Δ is a time shift of 100 ms (chosen in pilot experiments to ensure subjects were above chance and below ceiling) and is a window function that is zero for the first 100 ms and the last 50 ms, is −10 dB for the middle 250 ms, and ramps linearly between the middle and end regions over a 25-ms section. The window ensured the two source signals had identical onsets and offsets. Each subject heard 50 random source pairs convolved once with each IR type.
The distinct source was always in the first or the last interval. Intervals were separated by 400 ms relative to the beginning and end of the source signals, sufficient to ensure that the reverberant tail of one interval did not overlap with the onset of the subsequent interval. The IRs were always ordered with decreasing DRR such that the first source was the closest. The three signals in a trial were matched in level after convolution. Because the DRR can sometimes affect perceived loudness (7), equating level while varying the DRR could cause the three sources to appear to vary in loudness (because the perceived distance could vary while the level at the ears remains the same). Our results suggest that listeners can discount any such variation when performing the task.
Experiment procedure.
Subjects were presented with stimuli in blocks of 10 trials. All stimuli within a given block were convolved with the same class of IR. At the end of each block subjects were given feedback on their performance over the block. Blocks were presented in random order, with the exception that every sixth block, beginning with the first one, consisted of 10 trials of dry stimuli. In the blocks of dry stimuli feedback was given after every trial, which served to familiarize subjects with the discrimination task without giving them practice on the convolved stimuli.
Fourteen subjects (5 female, mean age = 42.7 y, SD = 16.4) took part. All had self-reported normal hearing. The same 14 subjects took part in experiment 3 (experiments 2 and 3 were run in a random order in separate sessions). Five of these subjects also participated in experiment 1. Experiment 1 was run last such that the subjects never heard the IRs in isolation until experiments 2 and 3 were completed.
Null model based on cochleagram differences.
To test whether the results could be explained without invoking a separation mechanism, we constructed a model to perform the task simply, using the difference between the cochleagrams of the stimuli. The model computed the MSE between the cochleagrams of the first and second sounds and the MSE between the second and third sounds in a trial. The MSE was computed as in Eq. S16. The model then selected the sound (first or third) that had the largest MSE (Fig. S5A).
The sound formed from the distinct source was on average 6.9 dB different (SD = 1.2 dB) from the second sound, whereas the sound formed from the same source was on average 6.1 dB different (SD = 1.4 dB; Fig. S4). It was thus possible to perform the task to some extent simply by measuring the cochleagram difference. Indeed, the model performed better than humans and we added random noise to the decision process to equate average model performance across all IRs with that of humans. However, in contrast to humans, the model performed equally well in all IR classes (Fig. S5B).
Experiment 3—IR Discrimination.
Subjects were presented with three sounds that were the convolution of an unfamiliar source signal with an IR. All three source signals were distinct. Two of the IRs were the same and one had a different broadband RT60. Listeners were asked to identify the interval containing the distinct IR, analogous to listening to three recordings and judging which one was recorded in a different room from the other two. The three sources were matched in level after convolution to minimize the possibility that the difference in reverberation could be determined by a difference in loudness. The experiment contained 10 conditions in a 5 × 2 design, with five classes of synthetic IRs and two different differences in decay rates (broadband RT60).
Synthetic IRs.
One of the IRs in the pairing had a broadband RT60 of T = 0.6 s and the other one took a value of either 0.9 s or 1.2 s. We expected the task to be easier when the difference in RT60 was greater. On 50% of trials the short IR (T = 0.6 s) occurred twice and the long IR (T = 0.9 s or 1.2 s) once and vice versa on the other 50% of trials. All IRs had a mean DRR of 40 dB across subbands. This experiment used the same five IR classes as experiment 2 (SI Materials and Methods, Experiment 2—Source Discrimination, Synthetic IRs). IR distortion was equated across classes as in experiment 2.
Source signals.
The source signals were excerpts of synthetic sources generated as in experiment 1. All three sources had different values of time correlation, frequency correlation, and modulation depth (selected from the same range as in experiment 1), such that the three sounds had different statistics. For each subject we generated 40 randomly chosen sets of three sounds and used each set once with each condition. The sources were ∼2,200 ms in duration but the exact length varied randomly between 2,000 ms and 2,400 ms such that the longest convolved sound did not necessarily correspond to the longest IR (to discourage subjects from basing their judgments on duration).
Experiment procedure.
Subjects (the same 14 as in experiment 2) were presented with stimuli in blocks of 10 trials. All trials within a block were generated using the same IR class. At the end of each block subjects were given feedback on their performance over the block. Blocks were presented in a random order with the exception that every sixth block, beginning with the first one, consisted of 10 practice trials. On practice trials listeners discriminated dry stimuli with stimuli convolved with a real-world IR (i.e., one of the IRs was simply a delta function). In these practice blocks feedback was given after every trial. The practice blocks helped to ensure that subjects understood the task.
Null models based on stimulus statistics and duration.
Two models were constructed to perform the task from properties of the convolved stimuli (Fig. S5C). A statistics-based model computed the texture statistics [as in the model of McDermott and Simoncelli (28)] of each of the three convolved sounds. To normalize units, these statistics were z-scored across all stimuli used in the experiment. The L2 norm of the difference in z-scored statistics was computed between the first and second sounds and the second and third sounds, and the sound (first or third) with the larger difference from the second sound was chosen as the outlier. This classifier performed barely above chance for all IR classes (Fig. S5D), suggesting that the variation in source statistics overpowered any change in statistics introduced by the different IRs and that human performance was unlikely to be based on statistical properties of the convolved stimuli.
A second model used the audible length of each sound (defined as the time between the first and last samples at which the broadband waveform exceeded 10 dB SPL). This model also performed barely above chance (Fig. S5D), suggesting the random variation in source length exceeded the effects of variation in IR length. The poor performance of this model suggests that subjects were not using stimulus duration to perform the task.
Statistical Tests.
IR analysis.
Repeated-measures ANOVAs were run on the measured RT60s and DRRs, treating the 33 frequency subbands as related measurements. A two-way ANOVA was performed on the RT60 data after grouping the IRs into quartiles by their broadband RT60 (T) and treating quartile and frequency bins as related measurements.
Psychophysical experiments.
In experiment 1, a one-tailed t test was run on the proportion correct for each IR class, testing differences from chance performance (0.5). Uncorrected P values are reported in the text, but modified Bonferroni correction was used to determine statistical significance (due to the large number of conditions). These corrected P values were also used for the statistical significance symbols (asterisks) in Fig. 6.
In experiments 2 and 3, repeated-measures ANOVAs were run on the data to test for main effects and interactions of RT60 and IR class. The results were pooled over RT60 and two-tailed t tests were used to test for significant differences from performance for generic exponential IRs. ANOVAs were used to test for significant differences in the performance of the null models between IR classes (SI Materials and Methods, Experiment 2—Source Discrimination, Null Model Based on Cochleagram Differences and SI Materials and Methods, Experiment 3—IR Discrimination, Null Models Based on Stimulus Statistics and Duration).
Discussion
We have shown that the disparate and varied environments that humans encounter in daily life produce acoustic effects with consistent gross structure and that humans rely on these consistencies to correctly interpret sound. Replicating real-world reverberant energy decay properties was both requisite and sufficient to produce the perception of reverberation (experiment 1). In addition, listeners were able to access properties of the sound source (experiment 2) and IR (experiment 3) from their convolution into reverberant audio, but these abilities were strongly dependent on whether the IR conformed to real-world regularities. Collectively our results suggest that reverberation perception should be viewed as a core problem of auditory scene analysis, in which listeners partially separate reverberant sound into a sound source and an environmental filter, constrained by a prior on environmental acoustics.
Environmental Acoustic Regularities.
Our IR measurements revealed four characteristics common to almost all of the IRs we surveyed: (i) a transition from high kurtosis, produced by sparse early reflections, to Gaussian statistical properties within ∼50 ms of the direct arrival; (ii) exponential decay; (iii) frequency-dependent decay rates, with the slowest decay between 200 Hz and 2,000 Hz and faster decay at higher and lower frequencies; and (iv) decay-vs.-frequency profiles that varied with the overall magnitude of the reverberation (decay rates in more reverberant spaces tended to vary more with frequency). The first two characteristics have been widely noted (2–5), although not extensively evaluated in real-world environments. To our knowledge, the last two characteristics have not been previously documented. Our findings were mostly limited to spaces in the Boston metropolitan area (with a small number from wilderness areas in Massachusetts and New Hampshire), but IRs recorded elsewhere are consistent with our findings (Fig. S1A). Moreover, results were qualitatively similar for manmade and rural environments (Fig. 4D and Fig. S1B), suggesting that the regularities we observed are fairly universal consequences of the interaction between sound and surfaces. Although a detailed discussion of the physical origins of these regularities is beyond the scope of this paper, they are likely due to geometric and physical regularities in environments, such as the absorptive properties of typical materials and of air.
We found that human listeners are sensitive to all four regularities and that they are necessary for the perception of reverberation and the accurate separation of a sound source from reverberation. We also found that realistic reverberation could be synthesized simply by imposing these four regularities on noise (i.e., without constraining the fine structure). Although we did not formally analyze the statistics of the IR fine structure, this psychophysical finding suggests that environmental IRs (excluding early reflections) do not contain statistical structure beyond that present in their temporal envelopes, at least not that is salient to human listeners. This is likely because the fine-grained structure of the IR (i.e., the rapid fluctuations in energy upon which exponential decay is imposed, evident in Fig. 3D) depends sensitively on the particular position of the listener in an environment relative to the surfaces therein and thus may exhibit few statistical regularities.
Early Reflections and Binaural Cues.
Most of the IRs used in our experiments differed from real-world IRs in two respects: They were devoid of early reflections and were identical in the left and right ears. We adopted these two simplifications to isolate the effect of the diffuse tail of IRs. We did so because the tail is the primary source of distortion, and thus poses a core computational challenge, and because we found the tail exhibited strong regularities that had not been documented or examined perceptually. Moreover, we found in experiment 1 that listeners had difficulty distinguishing the realism of IRs with and without early reflections, indicating that their presence or absence is less salient than the tail properties that we manipulated. We note, however, that the early reflections in the first few milliseconds of the IR also contain structure and pose their own computational challenge because they arrive with potentially misleading localization cues. The perceptual effect of such reflections is well documented via the “precedence effect” (29, 30), by which echo location cues are discounted.
Our experiments used diotic sound presentation because we sought to isolate the effect of the IR tail regularities we had observed and because reverberation remains salient under such conditions. We found evidence for source/IR separation under these diotic conditions, suggesting that aspects of reverberation perception are monaural in nature. However, natural listening conditions introduce binaural cues that could complement the effects we have documented. In particular, performance in separation tasks (e.g., experiments 2 and 3) would likely be aided by binaural cues (31–34) and such effects will be important to explore in the future.
Separation of Source and Reverberation.
Participants in our experiments were able to make judgments about sound sources and IRs given only their convolution (i.e., without direct access to the sources or IRs). Both tasks were designed to prevent listeners from performing well simply by comparing the convolutions themselves. Moreover, listeners were better in both cases when the IRs were natural rather than unnatural, despite equivalent levels of acoustic distortion. In contrast, models that performed the tasks by comparing the convolutions (Fig. S5A) or their statistical properties (Fig. S5C) performed similarly across conditions. It is not obvious how to explain the results without supposing that listeners were relying on estimates of source and IR that were more accurate when IRs were natural. The results thus suggest that the human auditory system can at least partially separate reverberant audio into estimates of a source signal and the environmental IR with which it was convolved.
Although there has been little direct evidence for separation of source and filter in reverberation perception, several previous findings are consistent with a separation process. Humans in some cases perceive sound sources as equally loud even when one is farther away and imparts less power to the eardrum (7), suggesting that perceived loudness represents an estimate of the source properties after accounting for effects of the environment. Similarly, humans rate temporally asymmetric sounds as louder and longer when they ramp from quiet to loud than when they are time-reversed (35, 36), possibly because in the latter case some of the sound is attributed to reverberation whereas in the former all of the sound is attributed to the source.
Physiologically, responses to source direction (37), pitch (38, 39), and amplitude modulation (40) are altered in the presence of reverberation, but in some cases there is evidence that reverberation is partially “removed” from the brain’s representation of sound (40, 41). Our results suggest that if these effects reflect the separation process that appears to be at work in human listeners, they should depend on whether the reverberation conforms to real-world IR regularities. Moreover, given that reverberation is accessible to the listener to some extent, it is likely represented explicitly somewhere in the auditory system, although the neural locus remains unclear.
Although reverberation that is unusually pronounced can degrade speech intelligibility (34), humans on the whole are remarkably robust to the profound distortion reverberation imposes (4, 10–15). Comparable robustness remains beyond the capability of automatic speech recognition, the performance of which deteriorates under even moderate reverberation (42). A priori one might suppose that human robustness simply reflects learned templates of reverberant speech. However, such templates are unlikely to account for our source discrimination results (experiment 2) because the source stimuli we used were unfamiliar sounds with relatively unnatural statistics. Our results thus suggest that the robustness evident in human listeners is at least partly due to a separation mechanism that uses a prior on environmental acoustics, raising the possibility that machine hearing algorithms could be aided by a similar prior.
Perceptual Importance of Regularities in Natural Reverberation.
We found perception to depend strongly on whether an IR conformed to the statistical regularities of natural environments, suggesting that the brain has internalized the regularities of natural reverberation. Our results leave open the question of whether knowledge of natural IR regularities is present from birth or learned over development. Our measurements indicate that reverberation in outdoor and indoor environments is qualitatively similar, apart from overall decay rate (slower indoors, because reflected sound is trapped, leading to more reflections). Moreover, we have informally observed that IRs in caves are similar to those in modern rooms (Fig. S1B). These observations indicate that the reverberation encountered by humans in modern industrialized society is probably not qualitatively different from what was typical in preindustrial societies. The demands of real-world hearing long ago could thus, in principle, have shaped priors on reverberation, although the importance of such priors is likely greater in modern life (because we spend more time indoors).
It is possible that a listener’s IR prior could be refined on short time scales based on recent exposure. Indeed, speech comprehension in a room has been reported to improve after a few seconds of exposure to other speech material recorded in the same room (43, 44). These results could reflect updates to a listener’s reverberation prior based on recent experience. It remains to be seen whether short-term exposure could aid listeners when an IR is highly unnatural, as in some of our experimental conditions.
Our results provide an example of environmental statistical constraints on perception. Such effects are relatively common in human vision, where priors have been characterized on orientation (45), speed (46), and contour shape (47). Similar approaches have recently proved fruitful in audition (48–50). The significance of the reverberation regularities we observed, along with their influence on perception, is that they suggest reverberation should be viewed as a scene analysis problem, comparable to the better-known cocktail party problem, rather than simply a source of distortion or noise.
We have focused on the role of prior knowledge of environmental IRs in the perception of reverberation, but prior knowledge of sources could be equally important. We explored IR regularities because they had not been previously examined and because it seemed possible that they might be constrained in their form. To minimize the role of source priors in our separation experiments, we used random synthetic sources with little structure. However, inference could be aided by prior knowledge of the regularities of natural sound sources (51), such that performance on tasks requiring estimates of source and filter might further improve with more naturalistic sources.
Materials and Methods
Real-World IR Statistics.
Survey.
Text messages requesting location information were sent once within each hour of the day, with the delivery time drawn from a uniform distribution over that hour. In addition, participants installed a phone application that sent us their phone’s GPS coordinates every 15 min. Participants were financially compensated for every successful GPS ping (to encourage them to keep their phone batteries charged and GPS enabled) and for every text message that they replied to. Immediate replies were compensated more highly than late replies to encourage timely responses. Each participant was tracked for 14 d. The 7 participants (4 female, mean age = 27.3 y, SD = 6.8) covered a range of occupations (musician, marketing manager, postdoctoral researcher, part-time nurse, childcare specialist, and two undergraduates). Participants replied to an average of 284 of the 336 text messages they received (24/d 14 d), with an average latency of 23 min between message and response (excluding time asleep).
All experiments, including the IR survey, were approved by the Committee on the Use of Humans as Experimental Subjects at Massachusetts Institute of Technology (MIT) and were conducted with the informed consent of the participants.
Measurement.
We measured IRs by recording a noise signal produced by a speaker (Fig. 1D). Because the noise signal and the apparatus transfer function were known, the IR could be inferred from the recording. The noise signal was played from a battery-powered speaker (Ion Block Rocker) and recorded using a digital multitrack recorder (Tascam DR-40, using the two internal microphones; the microphones were oriented at 90° with respect to each other and fed into the left and right recording channels). The speaker and recorder were positioned 1.5 m apart, with the recorder as close as possible to the position reported by the participant. Transfer functions of the apparatus were measured in an anechoic chamber (SI Materials and Methods, Real-World IR Measurements, Measurement Apparatus Transfer Function). The noise signal was a set of interleaved 11.9-s Golay complementary sequences (52, 53) (SI Materials and Methods, Real-World IR Measurements, IR Measurement). Golay sequences have two advantages for measuring IRs in public spaces: (i) They do not need to be played at high volumes, because they are relatively noise robust, and (ii) they are less salient than the sine sweeps commonly used to estimate IRs. They were thus less likely to provoke the curiosity or objections of bystanders or to worry the floor managers of restaurants that we might drive customers away. The average noise floor across all recordings was −81 dB relative to the direct arrival and was usually 20–60 dB below the start of the reverberant tail (Fig. S1D).
Analysis.
We computed the kurtosis of each 10-ms section of the IR (centered on each individual sample more than 5 ms from the beginning or end; SI Materials and Methods, Analysis of IR Statistics, IR Gaussianity). We classified each sample as Gaussian or non-Gaussian based on whether the section kurtosis exceeded the confidence interval for the kurtosis of a 10-ms sample of Gaussian noise (with the 32-kHz sampling rate we used, the upper bound of the confidence interval was 3.54). We defined (Fig. 4C, Inset) as the time at which as many Gaussian data points as non-Gaussian data points had occurred (this metric gives an indication of how long the IR remains non-Gaussian, but is also robust to sparse late-arriving reflections). We considered the diffuse tail to be the section of the IR after Each IR’s diffuse tail was filtered into 33 frequency subbands obtained from a filter bank mimicking the frequency selectivity of the human ear (28, 54), with center frequencies spanning 20 Hz to16 kHz. Polynomials were fitted (SI Materials and Methods, Analysis of IR Statistics, Polynomial Decay Fits) to the envelope of each subband, extracted by taking the magnitude of the analytic signal (via the Hilbert transform).
Statistics.
Repeated-measures ANOVAs were run on the measured RT60s and DRRs, treating the 33 frequency subbands as related measurements. A two-way ANOVA was performed on the RT60 data after grouping the IRs into quartiles by their broadband RT60 () and treating quartile and frequency bins as related measurements.
IR Synthesis.
Synthetic IRs were generated by imposing different types of decay on noise subbands, using the same filter bank used for real-world IR analysis. For all synthetic IRs a delta function at was used to simulate the direct arrival.
To measure the audible distortion induced by an IR on a given class of signals, the IR was convolved with 100 randomly selected sources used in the relevant experiment. Distortion was taken to be the average mean-squared error (MSE) between the cochleagrams of the source before and after filtering by the IR [subband envelopes were downsampled to 100 Hz and all values of < −60 dB were truncated at −60 dB (SI Materials and Methods, Measuring and Equating IR-Induced Distortion); distortion measurements were robust to the specific parameters of the cochleagrams used to compute them; Fig. S4B]. Frequencies below 20 Hz were not included. MSE values were then averaged across the 100 sources to yield a measure of the distortion induced by the IR.
To increase or decrease the distortion of an IR for the purposes of equating it with that of another IR, the RT60 of each of the subbands was increased or decreased by a fixed proportion until the two IRs produced MSE values within 1%. In all experiments one IR was designed to be ecologically valid (i.e., consistent with the survey) and this IR was held constant while the nonecological IRs were adjusted to match it.
Experiment 1: Discrimination of Real and Synthetic Reverberation.
Impulse responses.
Real-world IRs were recorded with a 10-m source–receiver separation. Ten rooms were chosen from the surveyed locations with a range of overall reverberation time (T) of 0.51–1.19 s. These reverberation times were large enough that the reverberation was salient but still well within the distribution of surveyed IRs (Fig. 4). IRs were presented diotically (the left channel of the measured real-world IR was presented to both ears).
To generate real-world IRs without early reflections, the section of the IR before (i.e., the section for which the IR statistics were not Gaussian) was excised and replaced with a delta function directly adjoining the diffuse tail. Across the real-world IRs in this experiment values ranged from 10 ms to 74 ms and corresponded to 1–20% (5.7% on average) of the audible IR duration. In this and all other experiments convolutions were performed in the frequency domain. In all cases the source and IR were zero-padded to have the same length before being Fourier transformed. The length of the padded signals was the smallest even power of 2 that was greater than the sum of their individual lengths, eliminating wraparound artifacts. To eliminate inaudible portions of the resulting waveform, all data points after the last value with magnitude greater than −90 dB (relative to the peak value) were removed before presentation.
Synthetic sources.
In this and all subsequent experiments, modulated noise was generated using the method of McDermott et al. (27). Cochleagrams were modeled with a multivariate Gaussian distribution with covariance in time and frequency that resembled that found in natural sounds. Cochleagrams were sampled from this distribution and imposed on noise subbands, which were then summed to produce a waveform. To introduce variability in the source characteristics, covariance parameters were randomly chosen from a distribution (log uniform) centered around values common to natural sounds (distributions were centered at −0.11 per 20-ms time window and −0.065 per frequency bin and varied from one-fifth of to five times these values). The sounds were 2.4 s long and were generated at 32 kHz with the same filter bank used for the IR analysis.
Participants.
Twenty-two listeners (10 female, mean age 37.4 y, SD = 14.2) took part. All had self-reported normal hearing.
Statistics.
A one-tailed t test was run on the proportion correct for each IR class, testing differences from chance performance (0.5). Uncorrected P values are reported in the text, but modified Bonferroni correction was used to determine statistical significance (due to the large number of conditions). These corrected P values were also used for the statistical significance symbols (asterisks) in Fig. 6.
Audio Presentation.
In all experiments, sounds were played via the sound card on a MacMini at a sampling rate of 32 kHz, via a Behringer HA400 amplifier. The Psychtoolbox for Matlab (55) was used to play out sound waveforms. Sounds were then presented to subjects over Sennheiser HD280 headphones (circumaural) in a soundproof booth (Industrial Acoustics).
Experiment 2: Source Discrimination.
Source signals.
Two 400-ms modulated noise signals were summed both with and without a time offset to create a pair of sources for an experiment trial that had nearly identical time-averaged spectra. A window was applied to ensure that the two source signals had identical onsets and offsets (SI Materials and Methods, Experiment 2—Source Discrimination). Each subject heard 50 random source pairs convolved once with each IR type. The distinct source (i.e., which differed before application of the IRs) was always the first or the last of the three sounds presented in a trial.
Procedure.
Participants were presented with stimuli in blocks of 10 trials. All stimuli within a given block were convolved with the same IR class. At the end of each block participants were given feedback on their performance for that block. Blocks were presented in random order, with the exception that every sixth block (i.e., blocks 1, 7, 13, 19, …) consisted of 10 trials with dry stimuli in which feedback was given after every trial.
Participants.
Fourteen listeners (5 female, mean age = 42.7 y, SD = 16.4) took part. All had self-reported normal hearing.
Statistics.
Repeated-measures ANOVAs were used to test for main effects and interactions of RT60 and IR class. The results were pooled over RT60 and two-tailed t tests were used to test for significant differences from performance for generic exponential IRs. ANOVAs were used to test for significant differences in the performance of the null models (SI Materials and Methods, Statistical Tests), between IR classes.
Experiment 3: IR Discrimination.
Synthetic IRs.
One of the IRs in the pairing had a broadband RT60 of T = 0.6 s and the other took a value of either 0.9 s or 1.2 s. On 50% of trials the short IR (T = 0.6 s) occurred twice and the long IR (T = 0.9 s or 1.2 s) occurred once and vice versa on the other 50% of trials.
Source signals.
The source signals were excerpts of synthetic sources with different values of time correlation, frequency correlation, and modulation depth (selected from the same range as in experiment 1), such that the three sounds all had different statistics from each other. For each participant we generated 40 randomly chosen sets of three sounds and used each set once with each condition. The source length varied randomly between 2,000 ms and 2,400 ms such that the longest convolved sound did not necessarily correspond to the longest IR (to discourage participants from basing their judgments on duration; Fig. S5 C and D).
Procedure.
Participants were presented with stimuli in blocks of 10 trials. All trials within a block were generated using the same IR class. At the end of each block participants were given feedback on their performance over that block. Blocks were presented in a random order.
Participants and statistics.
The participants and statistics were the same as in the source discrimination experiment. The participants were run on the two experiments in a random order.
Methods are described in more detail in SI Materials and Methods.
Acknowledgments
We thank Chris Warren for guidance in implementing the impulse response measurement technique; Bose Corporation for the use of their anechoic chamber; Nicole Schmidt for help testing the IR measurement apparatus and help building the automated system for texting participants; Caitlin Cooper-Courville for help with IR measurements; Erika Trent for helping to develop the computational toolbox for IR analysis and for help with IR measurements; Miranda Gavrin and Sebastian Begg for help conducting perceptual experiments; members of the Laboratory for Computational Audition, Bart Anderson, and Nancy Kanwisher for helpful comments on the manuscript; and the many business owners and managers who permitted IR measurements on their premises.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1612524113/-/DCSupplemental.
References
- 1.Lewicki MS, Olshausen BA, Surlykke A, Moss CF. Scene analysis in the natural environment. Front Psychol. 2014;5:1119. doi: 10.3389/fpsyg.2014.00199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sabine H. 1953. Room acoustics. Trans IRE 1:4–12.
- 3.Schroeder MR. Frequency-correlation functions of frequency responses in rooms. J Acoust Soc Am. 1962;34(12):1819–1823. [Google Scholar]
- 4.Blesser B, Salter L. Spaces Speak, Are You Listening?: Experiencing Aural Architecture. MIT Press; Cambridge, MA: 2009. [Google Scholar]
- 5.Kuttruff H. 2009. Room Acoustics (Spon Press, Oxon, UK), 4th ed, pp 204–251.
- 6.Bronkhorst AW, Houtgast T. Auditory distance perception in rooms. Nature. 1999;397(6719):517–520. doi: 10.1038/17374. [DOI] [PubMed] [Google Scholar]
- 7.Zahorik P, Wightman FL. Loudness constancy with varying sound source distance. Nat Neurosci. 2001;4(1):78–83. doi: 10.1038/82931. [DOI] [PubMed] [Google Scholar]
- 8.Cabrera D, Jeong D, Kwak HJ, Kim J-Y. 2005. Auditory room size perception for modeled and measured rooms. Proceedings of the 2005 Congress and Exposition on Noise Control Engineering (INTERNOISE 2005) (Institute of Noise Control Engineering-USA, Indianapolis), pp 3221–3231.
- 9.Brumm H, Naguib M. Environmental acoustics and the evolution of bird song. Adv Stud Behav. 2009;40:1–33. [Google Scholar]
- 10.Houtgast T, Steeneken HJ. A review of the MTF concept in room acoustics and its use for estimating speech intelligibility in auditoria. J Acoust Soc Am. 1985;77(3):1069–1077. [Google Scholar]
- 11.Bradley JS. Speech intelligibility studies in classrooms. J Acoust Soc Am. 1986;80(3):846–854. doi: 10.1121/1.393908. [DOI] [PubMed] [Google Scholar]
- 12.Bradley JS, Reich RD, Norcross SG. On the combined effects of signal-to-noise ratio and room acoustics on speech intelligibility. J Acoust Soc Am. 1999;106(4 Pt 1):1820–1828. doi: 10.1121/1.427932. [DOI] [PubMed] [Google Scholar]
- 13.Darwin CJ, Hukin RW. Effects of reverberation on spatial, prosodic, and vocal-tract size cues to selective attention. J Acoust Soc Am. 2000;108(1):335–342. doi: 10.1121/1.429468. [DOI] [PubMed] [Google Scholar]
- 14.Culling JF, Hodder KI, Toh CY. Effects of reverberation on perceptual segregation of competing voices. J Acoust Soc Am. 2003;114(5):2871–2876. doi: 10.1121/1.1616922. [DOI] [PubMed] [Google Scholar]
- 15.Nielsen JB, Dau T. Revisiting perceptual compensation for effects of reverberation in speech identification. J Acoust Soc Am. 2010;128(5):3088–3094. doi: 10.1121/1.3494508. [DOI] [PubMed] [Google Scholar]
- 16.Gardner WG. 2002. Reverberation algorithms. Applications of Signal Processing to Audio and Acoustics, eds Kahrs M and Brandenberg K (Springer, New York), pp 85–131.
- 17.Schroeder MR. Natural sounding artificial reverberation. J Audio Eng Soc. 1962;10(3):219–223. [Google Scholar]
- 18.Hameed S, Pakarinen J, Valde K, Pulkki V. 2004. Psychoacoustic cues in room size perception. Proceedings of the 116th Audio Engineering Society Convention (Audio Engineering Society, New York), paper no. 6084.
- 19.Zahorik P. Direct-to-reverberant energy ratio sensitivity. J Acoust Soc Am. 2002;112(5 Pt 1):2110–2117. doi: 10.1121/1.1506692. [DOI] [PubMed] [Google Scholar]
- 20.Shinn-Cunningham BG, Kopco N, Martin TJ. Localizing nearby sound sources in a classroom: Binaural room impulse responses. J Acoust Soc Am. 2005;117(5):3100–3115. doi: 10.1121/1.1872572. [DOI] [PubMed] [Google Scholar]
- 21.Jot J. 1992. An analysis/synthesis approach to real-time artificial reverberation. 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing (IEEE, New York), Vol 2, pp 221–224.
- 22.Jeub M, Schäfer M, Vary P. 2009. A binaural room impulse response database for the evaluation of dereverberation algorithms. Proceedings of 2009 16th International Conference on Digital Signal Processing (IEEE, New York) [DOI]
- 23.Schroeder MR, Gottlob D, Siebrasse K. Comparative study of European concert halls: Correlation of subjective preference with geometric and acoustic parameters. J Acoust Soc Am. 1974;56(4):1195–1201. [Google Scholar]
- 24.Beranek LL. Concert hall acoustics-2008. J Audio Eng Soc. 2008;56(7/8):532–544. [Google Scholar]
- 25.Pätynen J, Tervo S, Robinson PW, Lokki T. Concert halls with strong lateral reflections enhance musical dynamics. Proc Natl Acad Sci USA. 2014;111(12):4409–4414. doi: 10.1073/pnas.1319976111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xiang N, Goggans PM. Evaluation of decay times in coupled spaces: Bayesian parameter estimation. J Acoust Soc Am. 2001;110(3 Pt 1):1415–1424. doi: 10.1121/1.1390334. [DOI] [PubMed] [Google Scholar]
- 27.McDermott JH, Wrobleski D, Oxenham AJ. Recovering sound sources from embedded repetition. Proc Natl Acad Sci USA. 2011;108(3):1188–1193. doi: 10.1073/pnas.1004765108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McDermott JH, Simoncelli EP. Sound texture perception via statistics of the auditory periphery: Evidence from sound synthesis. Neuron. 2011;71(5):926–940. doi: 10.1016/j.neuron.2011.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Litovsky RY, Colburn HS, Yost WA, Guzman SJ. The precedence effect. J Acoust Soc Am. 1999;106(4 Pt 1):1633–1654. doi: 10.1121/1.427914. [DOI] [PubMed] [Google Scholar]
- 30.Brown AD, Stecker GC, Tollin DJ. The precedence effect in sound localization. J Assoc Res Otolaryngol. 2015;16(1):1–28. doi: 10.1007/s10162-014-0496-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Durlach NI, Colburn HS. 1978. Binaural phenomena. Handbook of Perception, eds Carterette EC, Friedman MP (Academic, New York), Vol 4, pp 365–466.
- 32.Lyon RF. A computational model of binaural localization and separation. IEEE. 1983;8:1148–1151. [Google Scholar]
- 33.Kidd G, Mason CR, Brughera A, Hartmann WM. The role of reverberation in release from masking due to spatial separation of sources for speech identification. Acta Acust United Acust. 2005;91(3):526–536. [Google Scholar]
- 34.Ruggles D, Bharadwaj H, Shinn-Cunningham BG. Why middle-aged listeners have trouble hearing in everyday settings. Curr Biol. 2012;22(15):1417–1422. doi: 10.1016/j.cub.2012.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Stecker GC, Hafter ER. An effect of temporal asymmetry on loudness. J Acoust Soc Am. 2000;107(6):3358–3368. doi: 10.1121/1.429407. [DOI] [PubMed] [Google Scholar]
- 36.Grassi M, Darwin CJ. The subjective duration of ramped and damped sounds. Percept Psychophys. 2006;68(8):1382–1392. doi: 10.3758/bf03193737. [DOI] [PubMed] [Google Scholar]
- 37.Devore S, Delgutte B. Effects of reverberation on the directional sensitivity of auditory neurons across the tonotopic axis: Influences of interaural time and level differences. J Neurosci. 2010;30(23):7826–7837. doi: 10.1523/JNEUROSCI.5517-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sayles M, Winter IM. Reverberation challenges the temporal representation of the pitch of complex sounds. Neuron. 2008;58(5):789–801. doi: 10.1016/j.neuron.2008.03.029. [DOI] [PubMed] [Google Scholar]
- 39.Sayles M, Stasiak A, Winter IM. Reverberation impairs brainstem temporal representations of voiced vowel sounds: Challenging “periodicity-tagged” segregation of competing speech in rooms. Front Syst Neurosci. 2015;8:248. doi: 10.3389/fnsys.2014.00248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Slama MC, Delgutte B. Neural coding of sound envelope in reverberant environments. J Neurosci. 2015;35(10):4452–4468. doi: 10.1523/JNEUROSCI.3615-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mesgarani N, David SV, Fritz JB, Shamma SA. Mechanisms of noise robust representation of speech in primary auditory cortex. Proc Natl Acad Sci USA. 2014;111(18):6792–6797. doi: 10.1073/pnas.1318017111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kinoshita K, et al. A summary of the REVERB challenge: State-of-the-art and remaining challenges in reverberant speech processing research. EURASIP J Adv Signal Process. 2016 doi: 10.1186/s13634-016-0306-6. [DOI] [Google Scholar]
- 43.Watkins AJ. Perceptual compensation for effects of reverberation in speech identification. J Acoust Soc Am. 2005;118(1):249–262. doi: 10.1121/1.1923369. [DOI] [PubMed] [Google Scholar]
- 44.Brandewie E, Zahorik P. Prior listening in rooms improves speech intelligibility. J Acoust Soc Am. 2010;128(1):291–299. doi: 10.1121/1.3436565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Girshick AR, Landy MS, Simoncelli EP. Cardinal rules: Visual orientation perception reflects knowledge of environmental statistics. Nat Neurosci. 2011;14(7):926–932. doi: 10.1038/nn.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Stocker AA, Simoncelli EP. Noise characteristics and prior expectations in human visual speed perception. Nat Neurosci. 2006;9(4):578–585. doi: 10.1038/nn1669. [DOI] [PubMed] [Google Scholar]
- 47.Geisler WS, Perry JS. Contour statistics in natural images: Grouping across occlusions. Vis Neurosci. 2009;26(1):109–121. doi: 10.1017/S0952523808080875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Fischer BJ, Peña JL. Owl’s behavior and neural representation predicted by Bayesian inference. Nat Neurosci. 2011;14(8):1061–1066. doi: 10.1038/nn.2872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Monson BB, Han S, Purves D. Are auditory percepts determined by experience? PLoS One. 2013;8(5):e63728. doi: 10.1371/journal.pone.0063728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Parise CV, Knorre K, Ernst MO. Natural auditory scene statistics shapes human spatial hearing. Proc Natl Acad Sci USA. 2014;111(16):6104–6108. doi: 10.1073/pnas.1322705111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Theunissen FE, Elie JE. Neural processing of natural sounds. Nat Rev Neurosci. 2014;15(6):355–366. doi: 10.1038/nrn3731. [DOI] [PubMed] [Google Scholar]
- 52.Foster S. 1986. Impulse response measurement using Golay codes. IEEE International Conference on Acoustics, Speech, and Signal Processing (IEEE, New York), Vol. 11, pp 929–932.
- 53.Parker MG, Paterson KG, Tellambura C. 2003. Golay complementary sequences. Encyclopedia of Telecommunications, ed Proakis JG (Wiley, Hoboken, NJ) [DOI]
- 54.Glasberg BR, Moore BC. Derivation of auditory filter shapes from notched-noise data. Hear Res. 1990;47(1–2):103–138. doi: 10.1016/0378-5955(90)90170-t. [DOI] [PubMed] [Google Scholar]
- 55.Kleiner M, et al. What’s new in Psychtoolbox-3. Perception. 2007;36(14):1–16. [Google Scholar]
- 56.Stewart R, Sandler M. 2007. Statistical measures of early reflections of room impulse responses. Proceedings of the 10th International Conference on Digital Audio Effects (LaBRI, Université Bordeaux, Bordeaux, France), pp 59–62.
- 57.Lindau A, Kosanke L, Weinzierl S. Perceptual evaluation of model-and signal-based predictors of the mixing time in binaural room impulse responses. J Audio Eng Soc. 2012;60(11):887–898. [Google Scholar]