Significance
We have discovered that two proofreading steps amplify the accuracy of genetic code reading, not one step, as hitherto believed. We have characterized the molecular basis of each one of these steps, paving the way for structural analysis in conjunction with structure-based standard free energy computations. Our work highlights the essential role of elongation factor Tu for accurate genetic code translation in both initial codon selection and proofreading. Our results have implications for the evolution of efficient and accurate genetic code reading through multistep proofreading, which attenuates the otherwise harmful effects of the obligatory tradeoff between efficiency and accuracy in substrate selection by enzymes.
Keywords: ribosome, error correction, fidelity, EF-Tu, ternary complex
Abstract
Aminoacyl-tRNAs (aa-tRNAs) are selected by the messenger RNA programmed ribosome in ternary complex with elongation factor Tu (EF-Tu) and GTP and then, again, in a proofreading step after GTP hydrolysis on EF-Tu. We use tRNA mutants with different affinities for EF-Tu to demonstrate that proofreading of aa-tRNAs occurs in two consecutive steps. First, aa-tRNAs in ternary complex with EF-Tu·GDP are selected in a step where the accuracy increases linearly with increasing aa-tRNA affinity to EF-Tu. Then, following dissociation of EF-Tu·GDP from the ribosome, the accuracy is further increased in a second and apparently EF-Tu−independent step. Our findings identify the molecular basis of proofreading in bacteria, highlight the pivotal role of EF-Tu for fast and accurate protein synthesis, and illustrate the importance of multistep substrate selection in intracellular processing of genetic information.
We have found that the bacterial ribosome uses two proofreading steps following initial selection of transfer RNAs (tRNAs) to maintain high accuracy of translation of the genetic code. This means that there are three selection steps for codon recognition by aa-tRNAs. First, there is initial codon selection by aa-tRNA in ternary complex with elongation factor Tu (EF-Tu) and GTP. Second, there is proofreading of aa-tRNA in ternary complex with EF-Tu and GDP. Third, there is proofreading of aa-tRNA in an EF-Tu−independent manner, presumably after dissociation of EF-Tu·GDP from the ribosome (Fig. 1). Seven decades ago, Linus Pauling suggested that the precision by which proteins can choose between cognate and near-cognate substrates of similar structures is greatly limited, and he predicted high amino acid substitution frequency in intracellular protein synthesis (1). However, experiments by Robert Loftfield with rabbit reticulocyte hemoglobin demonstrated an error frequency much lower than Pauling’s prediction (2). One way to resolve this apparent paradox was offered by the principle of proofreading, first formulated by Hopfield (3) and Ninio (4). By this principle, the very same standard free energy difference, , between enzyme-bound noncognate and cognate substrate can be used in both initial selection (I) and subsequent proofreading selection (F) to boost the total accuracy () of selective enzymes above their single-step selection limits. Accuracy amplification by proofreading requires substrate discarding to be driven by a chemical potential decrease from the entering of a substrate to its exit along the proofreading path. One way to implement such a drop in chemical potential is to couple the discarding of substrates by proofreading to hydrolysis of GTP or ATP at high chemical potential to the low chemical potential of their hydrolytic products (5, 6).
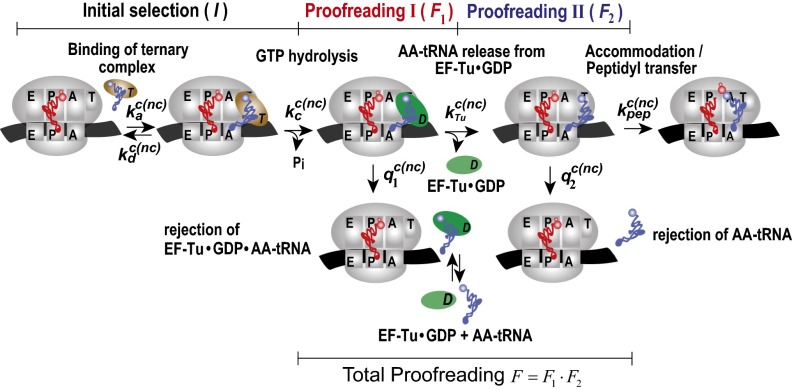
Fig. 1.
Proposed schematic of tRNA selection in bacterial protein synthesis. A ternary complex with aa-tRNA and EF-Tu·GTP binds to A/T state of the pretranslocation ribosome with association rate constant ka. Then, the ternary complex dissociates with rate constant kd or GTP is hydrolyzed with rate constant kc, leading to ribosome-bound ternary complex EF-Tu·GDP·aa-tRNA, which dissociates with rate constant q1, or EF-Tu·GDP dissociates with rate constant kTu, leading to an aa-tRNA−bound preaccommodation state of the ribosome. From this state, aa-tRNA dissociates with rate constant q2 or accommodates into the A site with rate constant kpep. There are three selection steps in this scheme: Near-cognate tRNA can be rejected during initial selection (I), first proofreading step (F1), and second proofreading step (F2). Notations c and nc in rate constants stand for cognate and noncognate reaction, respectively.
Proofreading was first discovered for the IleRS enzyme, which aminoacylates tRNAIle to cognate Ile-tRNAIle and efficiently suppresses near-cognate Val-tRNAIle formation by discarding valine through ATP hydrolysis-driven proofreading (7). Soon thereafter, GTP-driven proofreading of codon reading by aa-tRNAs on the mRNA-translating ribosome was discovered (8, 9) and subsequently subjected to extensive research (10–13). Although it was early recognized that multistep proofreading confers higher accuracy and kinetic efficiency to substrate-selective, enzyme-catalyzed reactions than single-step proofreading (5, 14, 15), it has been taken for granted that there is but a single proofreading step in tRNA selection by the translating ribosome (16). Here, we present data showing that the proofreading factor (F), by which the accuracy (A) is amplified from its initial selection value (I) by aa-tRNA in ternary complex with EF-Tu and GTP, increases linearly with increasing association equilibrium constant, KA, for aa-tRNA binding to EF-Tu. We suggest the cause of this linear increase to be the activity of a first proofreading step, in which aa-tRNA is discarded in complex with EF-Tu and GDP whereas the forward reaction is release of EF-Tu·GDP. In the limit of zero affinity between aa-tRNA and EF-Tu, where the first proofreading step is expected to be completely turned off, we observe a remaining accuracy amplification by proofreading. This amplification, we suggest, comes from the activity of a second proofreading step, involving aa-tRNA only (Fig. 1). We use the present results to discuss the molecular basis for proofreading of aminoacyl-tRNAs, which, until now, has remained obscure (17). We suggest that multistep proofreading in genetic code translation has evolved to neutralize potential error hot spots originating in error-prone initial selection of aa-tRNA in ternary complex with EF-Tu and GTP (18, 19). Recent cryo-EM data of ribosomes from live human cells show two states of ribosome-bound preaccommodated aa-tRNA, one with aa-tRNA in complex with the EF-Tu homolog eEF1α in the GDP form, the other with only aa-tRNA after release of eEF1α⋅GDP (20). With support from these cryo-EM data in conjunction with the present findings, we suggest that two-step proofreading mechanisms are at work not only in bacteria but also in eukaryotes and, perhaps, in all three kingdoms of life.
Results
Mg2+ Concentration Dependence of Proofreading Factors in Genetic Code Translation.
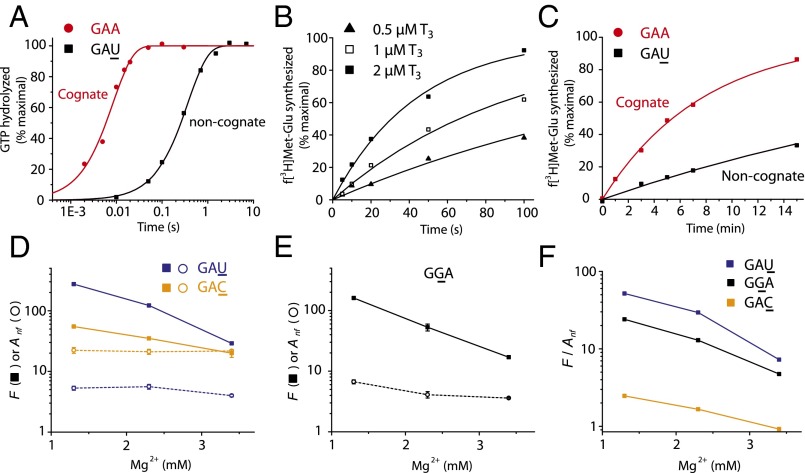
The concentration of free Mg2+ ions affects the accuracy of initial codon selection, I, in mRNA translation by decreasing the rate constant for dissociation of ternary complex from its precodon recognition state (21, 22). Here, we first studied the effect of Mg2+ concentration on the proofreading parameter, F, by which Glu-tRNAGlu favors its cognate GAA codon in relation to its near-cognate GAU, GGA and GAC codons. For this study, we estimated the kcat/Km values for GTP hydrolysis on a Glu-tRNAGlu−containing ternary complex reading GAA, GAU (Fig. 2A), GGA, and GAC in the A site of ribosomes with initiator fMet-tRNAfMet in the P site. In each case, the ratio between cognate and near-cognate kcat/Km values estimated the initial selection accuracy, I (22). We also determined the kcat/Km values for fMet-Glu-tRNAGlu formation in each one of these four cases and thereby obtained the total accuracy,, of peptide bond formation with Glu-tRNAGlu reading its cognate GAA codon versus the near-cognate GAU (Fig. 2B), GGA, and GAC codons. Then, the proofreading parameter F was, in each case, estimated as the A/I ratio at different Mg2+concentrations (Fig. 2 D and E). We also estimated the accuracy, Anf, where nf stands for “no factor,” by which fMet-Glu-tRNAGlu formation was favored by the cognate GAA codon in relation to the near-cognate GAU (Fig. 2C), GGA, and GAC codons in the absence of the translation factor EF-Tu (Scheme S1). For this work, we estimated kcat/Km values for factor-free codon reading by Glu-tRNAGlu under conditions identical to those under which the F values for the EF-Tu−facilitated reactions were obtained.
Fig. 2.
The proofreading factor of ternary complex selection converges to the accuracy of tRNA selection without EF-Tu at high Mg2+ condition. (A) Measurements of GTP hydrolysis for native Glu-tRNAGlu ternary complex (T3; 0.5 µM) binding to 70S initiation complex (IC; 2 µM) programmed with a cognate (GAA, curve in red) or near-cognate (GAU, curve in black) codon in the A site. (B) Kinetics of dipeptide formation from Glu-tRNAGlu reading GAU with varying T3 concentration. (C) Kinetics of EF-Tu−free dipeptide formation from Glu-tRNAGlu reading GAA or GAU with 3 µM tRNA (Scheme S1). (D) [Mg2+] dependence of the proofreading factor, F (filled squares), for codon selection by Glu-tRNAGlu in ternary complex with EF-Tu·GTP and of the accuracy (Anf, opened circles) for EF-Tu−free codon selection by Glu-tRNAGlu. (E) Similar to D, Glu-tRNAGlu reading GGA. (F) [Mg2+] dependence of the F/Anf ratio for Glu-tRNAGlu reading cognate GAA versus near-cognate GAU (blue), GGA (black), and GAC (yellow). Experiments in A−C were performed in buffer containing 2.3 mM free Mg2+. Kinetic data in A−C are representative of at least two independent experiments and are fitted to a single exponential model (see SI Materials and Methods). Data in D and E represent weighted averages from at least two experiments ± propagated SD.
Scheme S1.
Factor-free codon selection by aa-tRNA. In the absence of EF-Tu, aa-tRNA binds to a metastable preaccommodation state of the posttranslocation ribosome with association rate constant knf, from which it proceeds to A-site accommodation with rate constant kpep or dissociates with rate constant qnf. Notations c and nc in rate constants stand for cognate and noncognate reaction, respectively.
The proofreading parameter F decreases sharply with increasing free Mg2+ concentration in the low concentration range (Fig. 2 D and E). At the same time, the factor-free codon selection accuracy varies much more gradually in the low Mg2+ concentration range, bringing the initially higher proofreading factor, F, closer to factor-free accuracy, Anf (Fig. 2F). Inspired by these preliminary observations, we hypothesized that EF-Tu might affect the proofreading factor, F, in a first step and that there is a second, apparently EF-Tu−independent, proofreading step (Fig. 1). The simplistic idea was that, because the accuracy of initial selection of codons by aa-tRNA in ternary complex with EF-Tu·GTP decreases sharply with increasing Mg2+ concentration (22), such a high Mg2+ sensitivity could be typical also of a first proofreading step in which aa-tRNA in ternary complex with EF-Tu·GDP is discarded. Furthermore, because the accuracy of factor-free codon selection has comparatively low sensitivity to Mg2+ concentration (Fig. 2F), such a low Mg2+ sensitivity could be typical of a second proofreading step after dissociation of EF-Tu·GDP from the ribosome. We decided to subject this hypothesis to stringent testing in a series of experiments that were inspired by the observation that the choice of base pairs in the T stem of any tRNA strongly affects its affinity to EF-Tu GTP (23). For these experiments, we first developed a kinetic model for two-step proofreading in ribosomal protein synthesis in bacteria (Fig. 1) as described in Mechanistic Model of a Two-Step Proofreading Mechanism.
Mechanistic Model of a Two-Step Proofreading Mechanism in Bacterial Protein Synthesis.
We designed a kinetic model for codon selection in an initial step, before GTP hydrolysis on EF-Tu, followed by accuracy amplification in two proofreading steps (Fig. 1). Initial codon selection by aa-tRNA in ternary complex with EF-Tu·GTP is followed by a first proofreading step in which aa-tRNA in ternary complex with EF-Tu·GDP is discarded or, alternatively, EF-Tu·GDP dissociates from the ribosome-bound aa-tRNA. In a second proofreading step, aa-tRNA is discarded in an EF-Tu−independent manner or, alternatively, accommodated in the A site. The first proofreading step contributes by the factor F1 and the second contributes by the factor F2 to the overall proofreading factor F, so that . Accordingly, the overall accuracy, A, is given by .
The model predicts that, as long as the current accuracy amplification of the first proofreading step is much smaller than its maximal value, dF1, then F1 is a linear function of the inverse, 1/kTu, of the rate constant for dissociation of EF-Tu·GDP from its ribosome-bound complex with aa-tRNA (Fig. 1) (SI Three-Step Codon Selection). In the limit of small 1/kTu, F1 reaches its smallest value, F1 = 1, and the total proofreading factor F is equal to F2. In the absence of an EF-Tu−dependent first proofreading step, the total proofreading F would always be equal to F2 and would not be expected to vary with varying binding affinity of aa-tRNA to EF-Tu. In the absence of a second proofreading step, F would always be equal to F1 and thus equal to 1 in the limit of small 1/kTu. In the limit of high 1/kTu, F1 would be close to its maximal value, dF1, at the cost of huge excess hydrolysis of GTP per cognate peptide bond (see SI Three-Step Codon Selection). To test the model prediction of a linear relation between the proofreading amplification F and 1/kTu, we took advantage of the findings by Uhlenbeck and colleagues that base pairs in the T stem of tRNAs greatly affect their affinity, KA (per molar), to EF-Tu in the GTP form (24). We note that KA is the ratio between the rate constants for formation and dissolution of the ternary complex between EF-Tu·GTP and aa-tRNA off the ribosome. The experimental determination of KA and the relation between kTu and KA are discussed in Tuning the Affinity Between aa-tRNA and EF-Tu·GTP.
Tuning the Affinity Between aa-tRNA and EF-Tu·GTP by tRNA T-Stem Engineering.
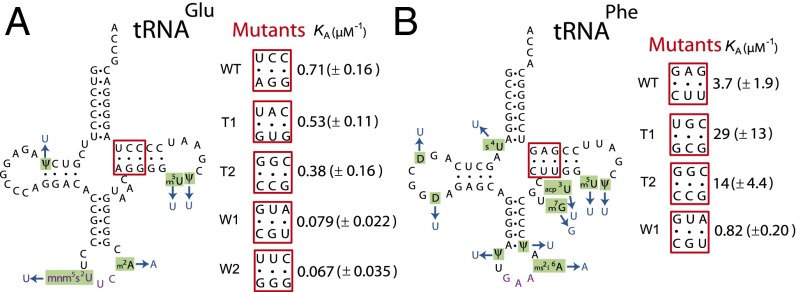
We used T7 RNA polymerase transcription of DNA oligos for in vitro production of five T-stem mutants of tRNAGlu, WT, strong (T1 and T2), and weak (W1 and W2) variants, and four of tRNAPhe, WT, strong (T1 and T2), and weak (W1) variants (Fig. 3), and we estimated association equilibrium constants, KA, for binding of their aminoacylated variants to free EF-Tu·GTP. The KA values were obtained from experiments in which the time dependence of dipeptide formation (fMet-Glu or fMet-Phe) was monitored at constant Glu-tRNAGlu or Phe-tRNAPhe concentration and varying EF-Tu concentration (25). Dipeptide formation from both Glu-tRNAGlu and Phe-tRNAPhe−containing ternary complex is biphasic as illustrated for the wild-type tRNAs in Fig. S1 A and C, respectively. The fast phase reflects peptide bond formation from preformed ternary complex, and the slow phase reflects ternary complex formation from free EF-Tu and aa-tRNA (25). Accordingly, the KA value could, in each case, be estimated from the EF-Tu concentration dependence of the fast-phase fraction (Fig. S1 B and D and SI Materials and Methods). The rate constant for the fast phase, kdip, defined as the inverse of the total reaction times for all steps leading from free ternary complex and ribosome to peptide bond formation (25, 26), is for all tRNA mutants displayed in Table S1. It is seen that the aa-tRNA mutants display a 10-fold and 30-fold KA variation in the tRNAGlu and tRNAPhe cases, respectively (Fig. 3, Fig. S1, and Table S1). There is also some kdip variation among the tRNA mutants (Table S1). In the tRNAPhe case, the similar kdip values in the WT and W1 cases (Table S1) are much smaller than the maximal rate of peptide bond formation (26) and must therefore reflect similar kcat/Km values for the reaction. We suggest that the significantly smaller kdip values for the “strong” T1 and T2 variants in relation to the WT and W1 variants reflect slow release of EF-Tu·GDP from the ribosome, as previously proposed (23). In the tRNAGlu case, the kdip value is similar among the WT, T1, and T2 variants, reflecting similar kcat/Km values for peptide bond formation. For the very weak W1 and W2 variants, the kdip values are significantly smaller than for the WT, T1, and T2 variants (Table S1). This reflects, we suggest, reduced catalytic rate of GTPase activation that, under these conditions, decreases the kcat/Km values. We note that the existence of different kdip values for the mutants of one isoaccepting tRNA does not in any way distort the KA estimates but shows that the mutations may, in some cases, have effects additional to KA-value tuning. We note that, in the tRNAGlu case, KA is larger for WT tRNA than for the nominally strong T1 and T2 variants (Table S1). This apparent anomaly of nomenclature is explained by the observation that WT tRNAGlu has the highest affinity to EF-Tu·GTP among the Escherichia coli tRNAs (27). The implication here is that any mutation is expected to result in lower than WT affinity to the tRNA isoacceptor.
Fig. 3.
Engineered tRNA mutants with altered EF-Tu affinities. (A) The tRNAGlu and (B) tRNAPhe mutants with T-stem mutated sequences (positions 51 to 53 and 61 to 63, shown in red boxes). T-stem sequences of WT and different mutants with their corresponding KA values for EF-Tu binding are shown. (KA values are in per micromolars; see also Fig. S1 and Table S1. Data represent weighted averages from at least two independent experiments ± propagated SD.) All tRNAs (WT and mutants) were unmodified and based on native E. coli (A) tRNAGlu or (B) tRNAPhe (black with purple anticodon; tRNA modifications are in green) with changes in blue.
Fig. S1.
Determination of association constants (KA) for T-stem mutated tRNA transcripts. (A and C) Time evolution of (A) f[3H]Met-Glu synthesized from WT tRNAGlu transcripts or (C) f[3H]Met-Phe synthesized from WT tRNAPhe transcripts at varying EF-Tu concentrations (see SI Materials and Methods). (B and D) Fractions of the fast phase from kinetics of dipeptide synthesis (from A and C) were plotted against EF-Tu concentration. Association constants, KA, for aa-tRNA binding to EF-Tu were estimated as (B) 0.71 ± 0.16 µM (WT tRNAGlu transcripts) and (D) 3.7 ± 1.9 µM (WT tRNAPhe transcripts). Kinetic data in A and C are representative of at least two independent experiments. Data in B and D represent weighted averages from at least two experiments ± propagated SD.
Table S1.
Kinetic and thermodynamic parameters for T-stem mutated tRNAs
| tRNAGlu | tRNAPhe | |||||
| T-stem mutant | kfast,* s−1 | kslow,† s−1 | KA,‡ µM−1 | kfast,* s−1 | kslow,† s−1 | KA,‡ µM−1 |
| WT | 7.5 ± 0.8 | 0.27 ± 0.018 | 0.71 ± 0.16 | 33 ± 5 | 0.26 ± 0.046 | 3.7 ± 1.9 |
| T1 | 8.0 ± 1.5 | 0.45 ± 0.084 | 0.53 ± 0.11 | 4.8 ± 0.3 | 0.18 ± 0.066 | 29 ± 13 |
| T2 | 9.6 ± 1.5 | 0.42 ± 0.060 | 0.38 ± 0.16 | 8.6 ± 1.3 | 0.12 ± 0.029 | 14 ± 4.4 |
| W1 | 1.3 ± 0.1 | 0.12 ± 0.009 | 0.079 ± 0.022 | 17 ± 2 | 0.36 ± 0.064 | 0.82 ± 0.20 |
| W2 | 1.9 ± 0.2 | 0.17 ± 0.023 | 0.067 ± 0.035 | |||
The rates of the fast phase from the kinetics of dipeptide synthesis. Ribosomes (1 µM) were in excess over ternary complex at 37 °C and 2.3 mM free Mg(OAc)2 concentration. Data represent weighted averages from experiments with various EF-Tu concentration ± propagated SD.
The rates of the slow phase from the kinetics of dipeptide synthesis. Data represent weighted averages from experiments with various EF-Tu concentration ± propagated SD.
Association constants for binding of different aa-tRNA mutants to EF-Tu·GTP. Errors represent SD estimates from the fitting procedure.
The KA values determined here (Table S1) refer to the binding of aa-tRNA to EF-Tu·GTP off the ribosome. Relevant for the testing of the model in Fig. 1 is, however, the rate constant for dissociation of EF-Tu·GDP from ribosome-bound aa-tRNA (kTu). We note that the dramatic structural change of EF-Tu from the GTP to GDP form is compatible with preserved interaction between the T stem of aa-tRNA and EF-Tu off the ribosome (Fig. 4A). Furthermore, the shift in ternary complex conformation depicted in Fig. 4A could be modeled on the ribosome without any clashes (Fig. 4B). Thus, in the GDP form, the G domain would lose its interactions with the acceptor stem of tRNA as well as with the sarcin−ricin loop of 23S RNA, domain III of EF-Tu would contact the T stem of tRNA, and domain II would possibly contact the acceptor stem, and, if the tRNA remains in the same position, the h5 and h15 region of 16S rRNA. This finding suggests that ratios between association equilibrium constants for aa-tRNA T-stem mutants binding to free EF-Tu·GTP (KA), ribosome-bound EF-Tu·GTP and ribosome-bound EF-Tu·GDP are similar, although their absolute values are expected to be very different. It is, finally, likely that the major effect of the T-stem variations is on the rate constant for dissociation of EF-Tu from aa-tRNA, so that estimated ratios between KA values predict the inverse ratios of the corresponding rate constants for dissociation of EF-Tu·GDP from ribosome-bound aa-tRNA, kTu (Fig. 1). In Proofreading Factor F Increases Linearly with Association Equilibrium Constant (KA) for aa-tRNA Binding to EF-Tu·GTP, we provide experimental proof that the overall proofreading factor F increases linearly with increasing KA in six cases of near-cognate misreading by WT and mutated variants of Glu-tRNAGlu and Phe-tRNAPhe (Fig. 5).
Fig. 4.
Interaction between EF-Tu and the T-stem base pairs of aa-tRNA in ternary complex before and after GTP hydrolysis on the ribosome. (A) Overlay of EF-Tu·GDP [green, Protein Data Bank (PDB) 1tui (35)] based on domains II and III onto EF-Tu·GDPCP (orange) in complex with Trp-tRNATrp G24A (blue) bound to the 70S ribosome from Thermus thermophilus [PDB 4v5l (36)]. The tRNA base pairs 51 to 63, 52 to 62, and 53 to 61 in the T stem are highlighted in hot pink. Domains II and III of EF-Tu·GDP superpose onto the same domains from EF-Tu·GDPCP with a root-mean-square deviation of 0.79 Å over 189 Cα atoms. (B) The complex of EF-Tu·GDP with aminoacyl-tRNA is sterically compatible with ribosome binding; 30S is shown in light yellow, and 50S is shown in light blue. The conformational change upon GTP hydrolysis is indicated by an arrow. Superpositioning was done using the LSQ commands in O (37). The images were prepared using Pymol version 1.8 (Schrödinger, LLC).
Fig. 5.
Proofreading factors, F, for codon selection by ternary complex increase linearly with increasing aa-tRNA affinity to EF-Tu at unaltered accuracy (Anf) of EF-Tu−free codon selection. F and Anf from different tRNA mutants are plotted against the tRNA affinities to EF-Tu (KA). Measurements are shown for Glu-tRNAGlu mutants misreading (A) GAU, (B) GGA, and (C) GAC and Phe-tRNAPhe mutants misreading (D) CUC, (E) UCC, and (F) UUA by their ternary complexes (F, ▪) or aa-tRNAs only (Anf, ○). In each case, linear regression was used to obtain maximum likelihood estimates of the y axis intercepts F2 and Anf as (A) 8.2 ± 5.0 and 12 ± 0.8, (B) 23 ± 8 and 25 ± 2, (C) 12 ± 5 and 16 ± 1, (D) 34 ± 4 and 39 ± 2, (E) 14 ± 2 and 12 ± 0.3, and (F) 27 ± 6 and 14 ± 0.4. Errors of F2 and Anf estimates represent SD from data fitting procedure (see SI Materials and Methods). Data in the plots represent weighted averages from at least two independent experiments ± propagated SD in both dimensions. Measurements were performed in polymix buffer containing 2.3 mM free Mg2+.
Proofreading Factor F Increases Linearly with Association Equilibrium Constant (KA) for aa-tRNA Binding to EF-Tu·GTP.
We estimated the overall proofreading factor F for the five variants of tRNAGlu misreading GAU, GGA, and GAC and the four variants of tRNAPhe misreading CUC, UCC, and UUA. For this work, we determined the initial codon selection accuracy, I (Fig. S2 A and D as examples for WT tRNAGlu and tRNAPhe, respectively, and Tables S2 and S3), the total accuracy of peptide bond formation, A (Fig. S2 B and E), and the total proofreading factor, F = A/I (Tables S2 and S3). We plotted F versus KA for Glu-tRNAGlu misreading GAU (Fig. 5A), GGA (Fig. 5B), and GAC (Fig. 5C) and for tRNAPhe misreading CUC (Fig. 5D), UCC (Fig. 5E), and UUA (Fig. 5F). For comparison, we also measured corresponding accuracy values of factor-free codon selection (Anf) (Fig. S2 C and F as examples for WT tRNAGlu and tRNAPhe, respectively, and Table S4), and those were plotted versus KA for each one of these tRNAGlu and tRNAPhe variants reading their near-cognate codons. In all cases (Fig. 5), the F parameter increased linearly with increasing KA value, corroborating the hypothesis that there is a first proofreading step with accuracy amplification, F1, in which aa-tRNA can be discarded in ternary complex with EF-Tu·GDP. Furthermore, the linear dependence of F1 on KA and, by hypothesis, 1/kTu, shows that, in these experiments, the proofreading accuracy was far below its maximal value, dF1 (see SI Three-Step Codon Selection). The intercepts with the y axis at zero KA value reveal proofreading factors F2 between 10 and 50. The straightforward interpretation of these results is that the intercepts reflect the accuracy contribution, F2, from a second, EF-Tu−independent proofreading step. Further analysis of the correspondence between association equilibrium constant KA and dissociation time 1/kTu (Fig. 1; see SI More Detailed Model of the First Proofreading Step) shows that sequential dissociation from the ribosome of EF-Tu·GDP followed by aa-tRNA at insignificant mutual affinity leads to a y axis intercept of F in Fig. 5 reflecting the accuracy amplification, F2, of a subsequent proofreading step and not a putative, residual activity of the EF-Tu−dependent, first proofreading step. Inspection of the ribosome structure in Fig. 4 with aa-tRNA and EF-Tu·GDP shows that the two macromolecules must either dissociate together or with EF-Tu·GDP leaving first followed by dissociation of aa-tRNA, even in the case when EF-Tu·GDP has significant affinity to the ribosome itself. This means that F1 can be written as (see SI Relationship Between Proofreading and EF-Tu Affinity to aa-tRNA)
where is a proportionality constant with unit micromolars, KA is the association constant with unit of per micromolar and is the unitless maximal accuracy of the EF-Tu·GDP−dependent step. From these experiments, the analysis of available structures (Fig. 4) and the analysis in SI Relationship Between Proofreading and EF-Tu Affinity to aa-tRNA and SI More Detailed Model of the First Proofreading Step, we suggest that the first, EF-Tu−dependent proofreading step with accuracy amplification, F1, is followed by a second, EF-Tu−independent proofreading step with accuracy F2 that can be estimated from the y axis intercepts in Fig. 5 (Discussion). Accordingly, the total accuracy amplification F is given by , where F1, F2, and F are in the ranges 1 to 8, 10 to 50, and 10 to 250, respectively. We note that the factor-free accuracy of codon selection, Anf, is remarkably similar to the accuracy amplification, F2, in the second proofreading step (compare the proofreading and Anf intercepts in Fig. 5). To assess the significance of this similarity, we estimated the average value of F2/Anf over all intercepts in Fig. 5 as 0.98 ± 0.08 (see SI Materials and Methods). This high-precision value close to 1 suggests strongly correlated values of F2 and Anf (see SI Factor-Free Codon Selection by aa-tRNA and Discussion).
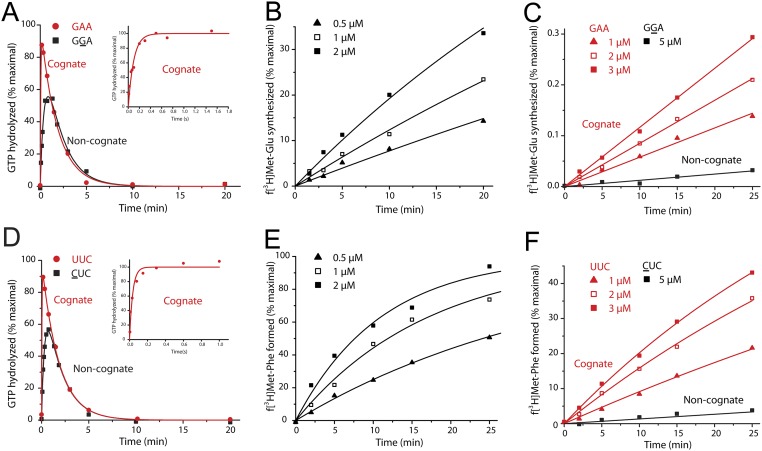
Fig. S2.
Measuring proofreading factor for codon selection by ternary complex, F, and accuracy of factor-free selection by aa-tRNA (Anf) for T-stem mutants of tRNA. (A and D) GTP hydrolysis for (A) tRNAGlu (WT) or (D) tRNAPhe (WT) ternary complexes binding to 70S initiation complex programmed with a cognate (red curves) or near-cognate (black curves) codon in the A site. Time evolutions of [3H]GTP hydrolyzed are shown. (B and E) Measurements of (B) fMet-Glu or (E) fMet-Phe formation, respectively, from tRNAGlu (WT) or tRNAPhe (WT) ternary complex binding to initiation 70S complex programmed with GGA or CUC codon in the A site. The time dependence of the extent of dipeptide formation was measured at varying ternary complex concentrations. (C and F) Measurements of (C) fMet-Glu or (F) fMet-Phe formation, respectively, from Glu-tRNAGlu (WT) or Phe-tRNAPhe (WT) without EF-Tu (Fig. 1B). The figure shows the time dependence of the extent of dipeptide formation from aa-tRNAs at different concentrations on initiation complexes programmed with cognate (red curves) or near-cognate (black curves) codons in the A site. Kinetic data are representative of at least two independent experiments.
Table S2.
Kinetic parameters for GTP hydrolysis and peptidyl transfer from ternary complex with T-stem mutated tRNAGlu
| GAA (Cognate) | GAU | GGA | GAC | ||||||||||
| Mutants | (kcat/Km)GTP | (kcat/Km)GTP | (kcat/Km)dip | I | F | (kcat/Km)GTP | (kcat/Km)dip | I | F | (kcat/Km)GTP | (kcat/Km)dip | I | F |
| (µM-1s-1) | (mM-1s-1) | (mM-1s-1) | (mM-1s-1) | ||||||||||
| WT | 8.1 ± 1.5 | 132 ± 10 | 1.26 ± 0.12 | 61 ± 12 | 105 ± 13 | 39 ± 3 | 0.29 ± 0.03 | 209 ± 42 | 133 ± 17 | 51 ± 3 | 0.38 ± 0.02 | 158 ± 31 | 134 ± 11 |
| T1 | 5.5 ± 0.5 | 95 ± 6 | 1.27 ± 0.07 | 58 ± 6 | 75 ± 6 | 28 ± 2 | 0.27 ± 0.03 | 195 ± 20 | 104 ± 14 | 39 ± 2 | 0.43 ± 0.03 | 142 ± 15 | 89 ± 8 |
| T2 | 10.2 ± 1.9 | 124 ± 25 | 2.26 ± 0.23 | 82 ± 22 | 55 ± 12 | 36 ± 2 | 0.60 ± 0.07 | 284 ± 55 | 60 ± 8 | 52 ± 3 | 0.89 ± 0.14 | 196 ± 38 | 59 ± 10 |
| W1 | 1.2 ± 0.2 | 30 ± 7 | 1.56 ± 0.28 | 40 ± 11 | 19 ± 5 | 12 ± 2 | 0.30 ± 0.03 | 192 ± 24 | 39 ± 7 | 17 ± 2 | 0.62 ± 0.03 | 72 ± 16 | 27 ± 4 |
| W2 | 2.2 ± 0.5 | 18 ± 3 | 1.10 ± 0.08 | 123 ± 32 | 17 ± 3 | 4.4 ± 2.1 | 0.19 ± 0.04 | 502 ± 263 | 23 ± 12 | 6.6 ± 1.6 | 0.34 ± 0.03 | 336 ± 106 | 19 ± 5 |
Kinetic efficiency for cognate and near-cognate GTP hydrolysis, (kcat/Km)GTP, were estimated from experiments with ribosomes at 1 and 2 µM, which are always in excess over ternary complex. The rate of GTP hydrolysis at 2 µM was always twice that at 1 µM with virtually identical kcat/Km estimates. Kinetic efficiencies for near-cognate dipeptide formation, (kcat/Km)dip, were derived from titrations of ternary complex in excess over ribosomes. Initial selection (I) was calculated from the ratio of cognate to near-cognate (kcat/Km)GTP parameters. Proofreading factor (F) was calculated from the ratio between near-cognate kcat/Km-values for GTP hydrolysis and dipeptide formation (see SI Materials and Methods). Data represent weighted averages from at least two independent experiments ± propagated SD.
Table S3.
Kinetic parameters for GTP hydrolysis and peptidyl transfer from ternary complex with T-stem mutated tRNAPhe
| UUC (Cognate) | CUC | UCC | UUA | ||||||||||
| Mutants | (kcat/Km)GTP | (kcat/Km)GTP | (kcat/Km)dip | I x (103) | F | (kcat/Km)GTP | (kcat/Km)dip | I x (103) | F | (kcat/Km)GTP | (kcat/Km)dip | I x (103) | F |
| (µM-1s-1) | (mM-1s-1) | (mM-1s-1) | (mM-1s-1) | ||||||||||
| WT | 47 ± 11 | 65 ± 3 | 1.09 ± 0.18 | 0.72 ± 0.17 | 59 ± 10 | 2.5 ± 0.2 | 0.15 ± 0.03 | 19 ± 5 | 17 ± 4 | 25 ± 2 | 0.54 ± 0.06 | 1.8 ± 0.5 | 47 ± 7 |
| T1 | 44 ± 8 | 90 ± 4 | 0.38 ± 0.02 | 0.48 ± 0.09 | 239 ± 15 | 2.0 ± 0.1 | 0.080 ± 0.016 | 22 ± 4 | 25 ± 5 | 23 ± 2 | 0.18 ± 0.02 | 1.9 ± 0.4 | 127 ± 16 |
| T2 | 46 ± 11 | 94 ± 7 | 0.79 ± 0.11 | 0.49 ± 0.12 | 118 ± 18 | 2.1 ± 0.2 | 0.091 ± 0.010 | 22 ± 6 | 23 ± 3 | 18 ± 1 | 0.23 ± 0.01 | 2.6 ± 0.6 | 78 ± 7 |
| W1 | 41 ± 11 | 67 ± 5 | 1.70 ± 0.09 | 0.61 ± 0.17 | 39 ± 3 | 2.6 ± 0.4 | 0.18 ± 0.01 | 16 ± 5 | 14 ± 2 | 26 ± 4 | 0.94 ± 0.15 | 1.6 ± 0.5 | 28 ± 6 |
Kinetic efficiency for cognate and near-cognate GTP hydrolysis, (kcat/Km)GTP, were estimated from experiments with ribosomes at 1 and 2 µM, which are always in excess over ternary complex. The rate of GTP hydrolysis at 2 µM was always twice that at 1 µM with virtually identical kcat/Km estimates. Kinetic efficiencies for near-cognate dipeptide formation, (kcat/Km)dip, were derived from titrations of ternary complex in excess over ribosomes. Initial selection (I) was calculated from the ratio of cognate to near-cognate (kcat/Km)GTP parameters. Proofreading factor (F) was calculated from the ratio between near-cognate kcat/Km-values for GTP hydrolysis and dipeptide formation (see SI Materials and Methods). Data represent weighted averages from at least two independent experiments ± propagated SD.
Table S4.
EF-Tu−free codon selection by Glu-tRNAGlu and Phe-tRNAPhe
| Glu-tRNAGlu | Phe-tRNAPhe | |||||||||||||
| Mutants | GAA Cognate kcat/Km, M−1⋅s−1 | GAU | GGA | GAC | UUC Cognate kcat/Km, M−1⋅s−1 | CUC | UCC | UUA | ||||||
| kcat/Km, M−1⋅s−1 | AtRNA | kcat/Km, M−1⋅s−1 | AtRNA | kcat/Km, M−1⋅s−1 | AtRNA | kcat/Km, M−1⋅s−1 | AtRNA | kcat/Km, M−1⋅s−1 | AtRNA | kcat/Km, M−1⋅s−1 | AtRNA | |||
| WT | 103 ± 12 | 7.9 ± 1.4 | 13 ± 3 | 4.1 ± 0.7 | 25 ± 5 | 5.0 ± 0.2 | 21 ± 3 | 189 ± 9 | 4.8 ± 0.7 | 39 ± 6 | 18.6 ± 0.3 | 10 ± 0.5 | 15 ± 0.4 | 13 ± 0.7 |
| T1 | 134 ± 13 | 11.9 ± 0.5 | 11 ± 1 | 4.7 ± 0.2 | 29 ± 3 | 5.3 ± 0.4 | 26 ± 3 | 338 ± 10 | 7.1 ± 0.4 | 47 ± 3 | 22.2 ± 0.2 | 15 ± 0.5 | 21 ± 0.2 | 16 ± 0.5 |
| T2 | 111 ± 18 | 7.0 ± 1.0 | 16 ± 3 | 5.6 ± 0.5 | 20 ± 4 | 4.2 ± 0.05 | 26 ± 4 | 346 ± 31 | 12.2 ± 0.4 | 28 ± 3 | 23.2 ± 0.4 | 15 ± 1.4 | 20 ± 0.5 | 17 ± 2 |
| W1 | 82 ± 4 | 8.7 ± 1.3 | 10 ± 1 | 2.9 ± 1.0 | 28 ± 10 | 8.1 ± 1.3 | 10 ± 2 | 239 ± 15 | 5.1 ± 0.2 | 46 ± 3 | 22.9 ± 0.2 | 10 ± 0.7 | 19 ± 0.4 | 12 ± 0.8 |
| W2 | 59 ± 5 | 4.0 ± 0.5 | 15 ± 2 | 2.2 ± 0.2 | 26 ± 3 | 4.1 ± 0.3 | 15 ± 2 | |||||||
The kcat/Km values were determined from titrations with aa-tRNA in excess over 70S ribosomes (Materials and Methods and SI Materials and Methods). Data represent weighted averages from at least two independent experiments ± propagated SD.
SI Materials and Methods
Reagents and Buffer.
Purified E. coli translation components were prepared as described previously (26). Native E. coli tRNAGlu was from Chemical Block. The tRNA mutants were unmodified and prepared by in vitro runoff transcription by T7 polymerase from PCR-amplified DNA templates (24). All experiments were performed at 37 °C in polymix buffer (34) containing 5 mM Mg(OAc)2, 95 mM KCl, 5 mM NH4Cl, 0.5 mM CaCl2, 8 mM putrescine, 1 mM spermidine, 5 mM potassium phosphate, and 1 mM dithioerythritol. The energy supply system of the buffer contained 1 mM ATP and 1 mM GTP (or 2 mM ATP in the ternary complex mixture for GTP hydrolysis measurements) along with 10 mM phosphoenolpyruvate (PEP), 1 µg/mL of pyruvate kinase, and 0.1 µg/mL of myokinase. Extra Mg(OAc)2 was added up to 10 mM to vary free Mg2+. As PEP chelates Mg2+ with a Kd value of 6 mM (38) and one ATP or GTP molecule chelates one Mg2+ ion, the free Mg2+ concentration was estimated to vary from 1.3 mM to 7.5 mM. All kinetic experiments were performed at 37 °C. All reactions of WT and mutant transcripts for tRNAGlu and tRNAPhe were measured polymix buffer containing 2.3 mM free Mg2+.
Cognate and Near-Cognate GTP Hydrolysis Measurement.
Ribosome mixture contained 1 µM 70S ribosomes, 1.5 µM f[3H]Met-tRNAfMet, 1.5 µM mRNA, 1.5 µM IF1, 0.5 µM IF2 and 1.5 µM IF3. Ternary complex mixture contained tRNAs (5 µM for tRNAPhe mutants and native tRNAGlu; 15 µM for tRNAGlu mutants), 0.5 µM EF-Tu, 0.5 µM [3H]GTP, 0.2 mM amino acid, and 1.5 units per microliter of aa-tRNA synthetase. Cognate reactions and fast near-cognate reactions (e.g., misreading by native tRNAGlu) were measured in a quench-flow instrument (RQF-3; KinTek Corp.). Slow near-cognate reactions were measured manually in parallel to cognate reactions to increase precision of the measurement (22, 31).
Dipeptide Formation Measurement.
Ribosome mixtures contained 70S ribosomes (0.2 µM), f[3H]Met-tRNAfMet (0.4 µM), mRNA (0.5 µM), IF1 (0.3 µM), IF2 (0.15 µM), and IF3 (0.3 µM). Ternary complex mixtures contained tRNAs (0.5 µM to 2 µM), EF-Tu (7 µM for native tRNAGlu and tRNAPhe mutants; 15 µM for tRNAGlu mutants), EF-Ts (1.5 µM), amino acid (0.2 mM), and aa-tRNA synethetase (1.5 units per microliter). For factor-free dipeptide formation measurements, EF-Tu and EF-Ts were omitted from ternary complex mixtures, and tRNA concentrations were varied from 1 µM to 6 µM.
Measurement of KA Value for tRNA Mutants.
The EF-Tu binding affinities to the tRNA mutants were estimated from the EF-Tu dependence of the slow-phase fraction in dipeptide formation kinetics experiments. In these experiments, the varying EF-Tu concentration and the constant 70S concentration were always in excess over the aa-tRNA concentration (25). EF-Tu was present in both mixtures at the same concentration to avoid a rapid concentration decrease by dilution during mixing. A ribosome mixture, containing ribosomes programmed with mRNA with cognate A-site codon (GAA for tRNAGlu and UUC for tRNAPhe), were prepared by incubating 70S ribosomes (1 µM), f[3H]Met-tRNAfMet (1.2 µM), mRNA (2 µM), IF1 (1.5 µM), IF2 (0.5 µM), IF3 (1.5 µM), EF-Tu (0.15 µM to 15 µM, always in excess at least 2× over tRNA), and EF-Ts (1.5 µM) in polymix buffer with energy supply and 2 mM extra Mg(OAc)2 at 37 °C for 15 min. A ternary complex mixture was prepared by incubating the tRNA mutants (0.07 µM to 0.5 µM), EF-Tu (0.15 µM to 15 µM), EF-Ts (1.5 µM), amino acid (0.2 mM), and aa-tRNA synethetase (1.5 units per microliter) in polymix with energy supply and 2 mM extra Mg(OAc)2 at 37 °C for 15 min. Kinetics of dipeptide formation was carried out in the quench-flow instrument.
Data Evaluation.
KA values.
Kinetics data of dipeptide synthesis were fitted to , where dip(t) is the normalized amount of dipeptide formed, Afast and Aslow are the fractions of the fast and slow phases, and kfast and kslow are the rates of the fast and slow phases, respectively. The association constant KA was estimated by fitting the fast-phase fraction, Afast, to a hyperbolic function of the EF-Tu concentration: Afast = [EF-Tu] /([EF-Tu] +1/KA) (25).
kcat/Km for GTP hydrolysis.
To measure kcat/Km for GTP hydrolysis, we used ribosomes in excess over ternary complex. For near-cognate reactions with native tRNAGlu, and for all cognate reactions, the rate (kGTP) was estimated by fitting the data to a single exponential model. For the slow near-cognate reaction with tRNA mutants, kGTP was estimated by fitting the data for near-cognate and its cognate reaction together (22). Control experiment with doubled ribosome concentration doubled the kGTP value, suggesting the measurements to be in the kcat/Km range, so that kcat/Km can be estimated as kGTP divided by the ribosome concentration.
kcat/Km for near-cognate dipeptide formation.
The kcat/Km values were estimated from experiments in which ternary complex, T3, was titrated from 0.5 µM to 2 µM, always in excess over the 70S ribosome at 0.2 µM. Accordingly, the rate of dipeptide formation (kdipnc) was determined by [T3]. The kdipnc was estimated by fitting the data into a single exponential model: , where dip(t) is the time evolution of near-cognate dipeptide formed, and the plateau [Rib] is the active ribosome concentration in the reaction. The kcat/Km values were estimated by fitting kdipnc versus [T3] into the Michaelis−Menten expression: .
Total accuracy, A, initial selection, I, and proofreading, F, for dipeptide formation from ternary complex.
Initial selection (I) was calculated as the ratio of kcat/Km values between cognate and near-cognate reaction for GTP hydrolysis: . The total accuracy (A) was calculated as the ratio of kcat/Km values between cognate and near-cognate reactions for dipeptide formation: . Because proofreading in the cognate reaction is insignificant (F 1), we have . Proofreading (F) was calculated as .
Accuracy, Anf, for EF-Tu−free codon selection by aa-tRNAs dipeptide formation.
To estimate the accuracy of codon selection by aa-tRNA in the absence of EF-Tu, we used aa-tRNA in excess over the ribosome, so the rate of dipeptide formation (kdipc/nc) was determined by the aa-tRNA concentration ([tRNA]). The (kcat/Km)c/nc values for cognate and near-cognate reaction were calculated as kdipc/nc divided by [tRNA]. Control experiments with twice [tRNA] resulted in twice faster kdipc/nc, confirming these measurements to be in the kcat/Km range.
Maximum likelihood estimates of F2 and Anf in Fig. 5.
The proofreading factor (F) from different tRNA mutants varied linearly with the KA value for EF-Tu binding (Fig. 5). We obtained maximum likelihood estimates of the slope and y axis intercept, F2, of these lines by accounting for the total SD at each point (). The estimated errors in KAi() and Fi() result in a total SD, , given by . Due to the slope dependence of the total SD, the maximum likelihood estimate was obtained iteratively until the parameter slope converged as explained (supporting information in ref. 22). The accuracy of EF-Tu−free codon selection Anf did not varied with the KA value. We obtained a maximum likelihood estimate for each of the six cases in Fig. 5 by accounting for the estimated errors at each point () through (supporting information in ref. 39)
Averages of F2/Anf ratio for all six cases were calculated as . The SD of the average is given by , where the SD for each F2/Anf ratio, , was calculated as .
Discussion
Major Conclusion: Two Proofreading Steps in Bacterial Protein Synthesis.
We found that proofreading amplification of the accuracy of codon reading by aa-tRNAs, F, increases linearly with the affinity (KA value) of aa-tRNAs to EF-Tu·GTP (Fig. 5) when KA is varied by T-stem mutations (23). From this finding, we propose that EF-Tu plays a fundamental role not only in initial codon selection by ternary complex in the GTP conformation but also in the rechecking of the initial codon choice in a proofreading step following GTP hydrolysis on EF-Tu, Pi release, and conformational change of the factor (Fig. 1). By this mechanism, GTP hydrolysis on ribosome-bound EF-Tu first leads to a ribosome complex with aa-tRNA, EF-Tu·GDP, and inorganic phosphate, Pi, in which aa-tRNA is strongly bound to EF-Tu (16). After rapid release of Pi, EF-Tu changes conformation from the GTP to the GDP form. This leads to a ribosome complex with aa-tRNA·EF-Tu·GDP, in which aa-tRNA is weakly bound to EF-Tu. Our proposal is now that the discard reaction of the KA-dependent proofreading step is dissociation of aa-tRNA·EF-Tu·GDP and that the forward reaction is dissociation of EF-Tu·GDP from ribosome-bound aa-tRNA (Fig. 1). In favor of this proposal, we note that the interaction between the T-stem base pairs and aa-tRNA can be preserved as EF-Tu changes conformation in response to GTP hydrolysis and Pi release (Fig. 4A) and, furthermore, that the transition of ternary complex from its GTP to GDP conformation can occur on the ribosome without sterical clashes (Fig. 4B). From this finding, we suggest, from an elementary thermodynamic consideration, that relative changes in the association constant, KA, in response to T-stem mutations predict the relative changes in the inverse, 1/kTu, of the rate constant for dissociation of EF-Tu·GDP from ribosome-bound aa-tRNA (Fig. 1). This relation between KA and 1/kTu readily explains the experimentally observed linear relation between F and KA in terms of an EF-Tu·GDP−dependent proofreading step by which the accuracy of codon selection of aa-tRNAs is amplified by a factor F1 (Results and SI Relationship Between Proofreading and EF-Tu Affinity to aa-tRNA).
We observe that the straight lines connecting the proofreading factor, F, with KA intercept the y axis at values significantly larger than 1 (Fig. 5) and note that these intercepts are readily explained in terms of a second, KA-independent, proofreading step by which the accuracy of codon selection is amplified by a factor F2. We suggest that the latter step has EF-Tu−independent release of aa-tRNA as its discard reaction and accommodation of aa-tRNA in the A site as its forward reaction. Could, then, an alternative model with dissociation of aa-tRNA in complex with EF-Tu·GDP·Pi as discard reaction account for the present experimental results?
According to this model, aa-tRNA would be discarded in complex with EF-Tu·GDP·Pi after GTP hydrolysis but before Pi release and conformational change of EF-Tu (16). Due to high affinity of aa-tRNA to EF-Tu before the conformational change of the factor, the forward rate constant in such a step would not be dissociation of EF-Tu·GDP·Pi from the ribosome-bound aa-tRNA but Pi release and conformational change of the factor (16). Therefore, such a proofreading step would not be expected to display the linear dependence of the proofreading factor F on the affinity parameter KA as predicted by our model (Fig. 1) and observed by experiment (Fig. 5). Then, could there be two EF-Tu−dependent proofreading steps, where aa-tRNA is discarded with EF-Tu·GDP·Pi in the first step and, after Pi release and conformational change of the factor, with EF-Tu·GDP in the second step? Although we cannot exclude this possibility, the latter model is made less attractive by its failure to account for the very close correspondence between factor-free accuracy, Anf, and the y axis intercepts, F2, in Fig. 5. From these arguments, in conjunction with Occam’s razor, we prefer the simple mechanism in Fig. 1 to other and more complex alternatives.
Outlook: Are There also Two Proofreading Steps in Eukaryote Protein Synthesis?
The present demonstration of two proofreading steps during mRNA translation on the bacterial ribosome resonates with recent cryo-EM data of translating ribosomes directly prepared from live human cells (20). Spahn and coworkers (20) identified a ribosome complex containing aa-tRNA in A/T state with eEF1α in the GDP conformation, where domains II and III were ordered, maintaining the interaction with the tRNA T-stem, while the G domain was disordered. This complex was about equally populated as a preaccommodation complex without eEF1α with aa-tRNA in similar position. These complexes were proposed to constitute two proofreading states from which the near-cognate tRNA can be rejected. This proposition is strongly supported by the present data, and we suggest that, in the living eukaryotic cell, ternary complexes of aa-tRNA·eEF1α·GDP may either dissociate from the ribosome in a first proofreading step or allow the aa-tRNA to move forward by release of eEF1α·GDP to a second proofreading step, only involving aa-tRNA. Together with the present findings, this suggests two-step proofreading mechanisms to be at work in bacteria, in the eukaryotes, and, by speculative inference, in all three kingdoms of life.
Can One GTP Molecule Drive Two Proofreading Steps?
One may ask if the obligatory thermodynamic force that drives the exit reactions of substrates in proofreading (5, 6) is sufficient to drive the two proofreading steps suggested in the present work (Fig. 1). An upper limit of accuracy enhancement of the type of proofreading described here is given by the shift of GTP above equilibrium with its hydrolytic product, estimated as 109 to 1010 (5). This limit demonstrates the feasibility of a multistep accuracy enhancement in the range of 106, far above the here observed modest accuracy amplification in the range of 300. In more concrete terms, the two proofreading steps are separated by dissociation of EF-Tu·GDP, which is virtually irreversible due to rapid, EF-Ts−catalyzed conversion of EF-Tu·GDP to EF-Tu·GTP followed by ternary complex formation (28–30). Furthermore, there is no negative interference in the second proofreading step by a significant influx of free aa-tRNA, because the efficiency of ribosome binding is orders of magnitude smaller for free in relation to EF-Tu−bound aa-tRNA, and the major aa-tRNA fraction off the ribosome is EF-Tu−bound.
Why Did Mother Nature Evolve Two Proofreading Steps in Genetic Code Translation?
The existence of two distinct proofreading steps may appear surprising, because the accuracy of initial codon selection by ternary complex normally is remarkably high (22, 31). Therefore, we suggest that two-step proofreading has evolved to neutralize the deleterious effects of a small number of distinct error hot spots for initial codon selection (31) as observed in vitro (19) and in vivo (18). For instance, initial codon selection values near 100 were seen for reading GGA and reading CGC (31). At high initial selection values (I), logF decreases linearly with logI with a slope close to 2, but as logI decreases further at low I values, logF remains virtually constant (19). This behavior is readily accounted for by the existence of two proofreading steps, where, in the high accuracy range, the amplification factors F1 and F2 decrease in proportion to decreasing maximal possible single-step accuracies dF1 and dF2, respectively (see SI Three-Step Codon Selection). In the low accuracy range, in contrast, F1 and F2 remain approximately constant at further decrease in dF1 and dF2 by compensating increase in the corresponding ratios between discard and forward rate constants (a values) in each step (19); for the first proofreading step, and for the second proofreading step (Fig. 1 and SI Three-Step Codon Selection). Such accuracy compensation by proofreading is only possible at aF1 and aF2 values much smaller than 1, as made feasible by multistep proofreading (5).
Proofreading and the Accuracy of Factor-Free Codon Selection.
We have found, for the data set in Fig. 5, that the accuracy, Anf, of factor-free codon selection is indistinguishable from the accuracy amplification conferred by the second proofreading step, F2, of factor-dependent codon selection. This similarity is highlighted by the average of the F2/Anf ratios over the six cases in Fig. 5 that we estimate as 0.98 ± 0.08. The reason for this similarity is, we suggest, that, when the first proofreading selection ends by dissociation of EF-Tu·GDP from the ribosome, aa-tRNA is in a ribosome-bound high standard free energy complex from which it may be discarded or rapidly accommodated in the A site. In fact, this very scenario may be played out in the previously mentioned cryo-EM snapshot from human cells (see figure 1C in ref. 20). Furthermore, during factor-free aa-tRNA binding to the posttranslocation ribosome (Scheme S1), aa-tRNA-entry into the A site requires passage through the very same complex of high standard free energy as the one rapidly reached with the help of EF-Tu and GTP hydrolysis in factor-dependent A-site binding (A/T state). A scenario, which leads to the virtually identical Anf and F2 values seen in Fig. 5, is described in SI Factor-Free Codon Selection by aa-tRNA. Further study of the strong correlation between Anf and F2 is important for three reasons. The first reason is that, when Anf and F2 are equal, there is no room for two EF-Tu−dependent proofreading steps where one depends on KA and the other one does not. Secondly, in such cases, estimation of Anf provides a shortcut to the determination of F2 with very high precision. The third reason is that the aa-tRNA−ribosome complex in the metastate just after EF-Tu·GDP release can provide valuable information regarding the path by which aa-tRNA accommodates into the A site.
Another View of EF-Tu Function After Initial Selection.
A different view of the role of EF-Tu after initial selection was recently proposed (32). From single-molecule and ensemble kinetics at 21 °C and 25 °C, respectively, in low-accuracy buffer (10), Liu et al. (32) concluded that, after GTP hydrolysis on EF-Tu (Fig. 1), the ribosome forms a complex (Complex B of Liu et al.) with EF-Tu still in the GDP form bound to L11 [scheme 1 of Liu et al.]. After release of Pi and separation of EF-Tu from L11, A-site accommodation of aa-tRNA and peptidyl transfer with EF-Tu in the GTP form take place [Complex C of Liu et al. (32)]. Then, EF-Tu switches to the GDP form and leaves the ribosome. Here, the main role of EF-Tu is to promote rapid A-site accommodation of aa-tRNA. From their buffer and temperature choices, we infer that proofreading (Fig. 5) and initial selection (31) are greatly reduced compared with in vivo rate (26, 33) and accuracy (19) calibrated systems. Comparison of our data sets is therefore nontrivial. At face value, we propose EF-Tu to rapidly change conformation after GTP hydrolysis and provide a second proofreading step, whereas Liu et al. (32) propose EF-Tu in the GTP form to promote rapid aa-tRNA accommodation followed by peptidyl transfer before conformational change and dissociation from the ribosome of the factor. It would, we think, be rewarding to combine their fluorescence-based single-molecule and ensemble kinetics and our quench-flow kinetics in experiments performed under similar conditions in an attempt to integrate our views on the function of EF-Tu after initial selection.
Consequences of the Present Findings.
Apart from the unexpected finding of two proofreading steps, the present study has identified the structural basis of the first, EF-Tu−dependent, step and suggested mechanistic features of both proofreading steps. These findings will facilitate structural analysis of the proofreading steps along with structure-based computations of their codon-discriminating standard free energies for a deeper understanding of the evolution of accurate reading of the genetic code.
SI Three-Step Codon Selection
The accuracy, A, of three-step selection in Fig. 1 is given by
| [S1] |
where
| [S2] |
| [S3] |
and
| [S4] |
with definitions , , , and , , .
SI More Detailed Model of the First Proofreading Step
In Scheme S4, there is no dissociation of from the complex, and the proofreading factor F1 is given by
| [S12] |
where , and and are proportionality constants as 1/kTu is proportional to the association equilibrium constant KA for free ternary complex (see Proofreading Factor F Increases Linearly with Association Equilibrium Constant (KA) for aa-tRNA Binding to EF-Tu·GTP in main text).
Materials and Methods
All experiments were performed at 37 °C in polymix buffer (34) with varying Mg2+ concentration. For cognate and near-cognate GTP hydrolysis measurements, ribosomes (1 µM) were in excess over ternary complexes (0.5 µM); both mixtures were prepared as described in ref. 31. For EF-Tu−dependent dipeptide formation measurements, ternary complexes (0.5 µM to 2 µM) were in excess over ribosomes (0.2 µM). For factor-free dipeptide formation measurements, EF-Tu and EF-Ts were omitted from the reactions, aa-tRNAs (1 µM to 6 µM) were in excess over ribosomes (0.2 µM) (see SI Materials and Methods).
SI Factor-Free Codon Selection by aa-tRNA
The accuracy, Anf, of codon selection by aa-tRNA only in Scheme S1 is given by
| [S5] |
where , , and . In the simple case where , Anf varies from 1 (no discrimination) to dnf (maximal discrimination) as anf varies from zero to infinity.
To see the connection between factor-free codon selection accuracy, Anf, and second proofreading step accuracy amplification, F2, a more detailed kinetic model is required (Scheme S2).
Scheme S2.
EF-Tu−free codon reading by aa-tRNA only. Aminoacyl-tRNA (T) binds to the posttranslocation ribosome (R), leading to ribosome complex C1, in which there is no codon−anticodon contact (40). Entry of T to the ribosomal A site requires formation of a high standard free energy state, , from which establishment of codon−anticodon contact and activation of monitoring bases lead to the high standard free energy complex from which T can accommodate into the A site with the rate constant kpep. The vertical arrow illustrates a particular scenario in which dissociation of EF-Tu·GDP leaves aa-tRNA in complex .
In Scheme S2, the factor-independent kcat/Km values for cognate and near-cognate peptide bond formation are, for this scheme, given by
| [S6] |
where for i = 1, 2, and . By assumption, the transition from C1 to happens before codon−anticodon contact is established so that a1 is the same in cognate and near-cognate reactions, and because, furthermore, this transition is from low to high standard free energy, we will assume that a1 >>1. Factor-free peptide bond formation accuracy is then approximated by
| [S7] |
If we assume that aa-tRNA is delivered to state upon release of EF-Tu·GDP from the ribosome during factor-dependent peptide bond formation, it follows that the probability that aa-tRNA reaches accommodation rather than dissociates in a cognate or a near-cognate case is approximated by
| [S8] |
It follows that the accuracy amplification by the second proofreading step in this scenario can be written as
| [S9] |
The expression Eq. S9 in which F2 = Anf is formally equivalent to Eq. S5 through the definitions and . The approximation involved in the F2 = Anf equality is to neglect the return of the ribosome to from (Scheme S2) as motivated by the assumption that a1>>1; this leads to an error in F2 corresponding to . Other scenarios for the EF-Tu−dependent delivery of aa-tRNA to the ribosome are conceivable, but, in all cases we have inspected, there is a strong correlation between F2 and Anf, this is despite the fact that factor-dependent peptide bond formation is orders of magnitude faster than its factor-independent version.
SI Relationship Between Proofreading and EF-Tu Affinity to aa-tRNA
We constructed T7 transcribed variants of tRNAGlu and tRNAPhe with different sets of base pairs in the T stem and measured their affinity to EF-Tu·GTP: (Scheme S3 and Fig. 3). The structures of T3GTP on (36) and off (35) the ribosome are similar, and the T-stem binding parts of T3GTP and T3GDP appear to be similar (Fig. 4). From this finding, we conjecture that is proportional to as well as to the dissociation rate constants and in Scheme S2. This would mean that the total accuracy of proofreading, F, is given by
| [S10] |
where cp is a proportionality constant with unit micromolars. Experimentally, we find that F always increases linearly with and intercepts the y axis at an accuracy amplification equal to the accuracy, Anf, of tRNA-only codon reading; this suggests that aF1 is always much smaller than 1, so that
| [S11] |
and that, for the current data set, .
Scheme S3.
Aa-tRNA binding to EF-Tu. See also Fig. 4 for structural information.
Scheme S4.
Schematic of the first proofreading step. The ribosome exits the initial selection step with rate constant kc (Fig. 1) and forms the complex, , in which the ribosome is bound to aa-tRNA in ternary complex with . The ternary complex may dissociate from the ribosome with rate constant in cognate and in near-cognate cases. Alternatively, splits with rate constant into a ribosome-bound complex in which and do not interact and where the two molecules are held in place by their respective affinities to the ribosome. Complex may reform ribosome-bound complex with rate constant qF1 or form ribosome complex through dissociation of from the ribosome with rate constant kF1.
Acknowledgments
We thank J. Wang and J. Zhang for technical advice and J. Puglisi and M. Johansson for comments on the manuscript. This work was supported by grants from the Knut and Alice Wallenberg Foundation to the Ribosome Consortium of Research and Education (RiboCORE), the Swedish Research Council, and the Human Frontier Science Program.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1610917113/-/DCSupplemental.
References
- 1.Pauling L. The probability of errors in the process of synthesis of protein molecules. In: Birkhauser A, editor. Festschrift Arthur Stoll. Birkhauser; Basel: 1957. pp. 597–602. [Google Scholar]
- 2.Loftfield RB, Vanderjagt D. The frequency of errors in protein biosynthesis. Biochem J. 1972;128(5):1353–1356. doi: 10.1042/bj1281353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hopfield JJ. Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc Natl Acad Sci USA. 1974;71(10):4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ninio J. Kinetic amplification of enzyme discrimination. Biochimie. 1975;57(5):587–595. doi: 10.1016/s0300-9084(75)80139-8. [DOI] [PubMed] [Google Scholar]
- 5.Ehrenberg M, Blomberg C. Thermodynamic constraints on kinetic proofreading in biosynthetic pathways. Biophys J. 1980;31(3):333–358. doi: 10.1016/S0006-3495(80)85063-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kurland CG. The role of guanine nucleotides in protein biosynthesis. Biophys J. 1978;22(3):373–392. doi: 10.1016/S0006-3495(78)85494-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hopfield JJ, Yamane T, Yue V, Coutts SM. Direct experimental evidence for kinetic proofreading in amino acylation of tRNAIle. Proc Natl Acad Sci USA. 1976;73(4):1164–1168. doi: 10.1073/pnas.73.4.1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ruusala T, Ehrenberg M, Kurland CG. Is there proofreading during polypeptide synthesis? EMBO J. 1982;1(6):741–745. doi: 10.1002/j.1460-2075.1982.tb01240.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thompson RC, Stone PJ. Proofreading of the codon−anticodon interaction on ribosomes. Proc Natl Acad Sci USA. 1977;74(1):198–202. doi: 10.1073/pnas.74.1.198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gromadski KB, Rodnina MV. Kinetic determinants of high-fidelity tRNA discrimination on the ribosome. Mol Cell. 2004;13(2):191–200. doi: 10.1016/s1097-2765(04)00005-x. [DOI] [PubMed] [Google Scholar]
- 11.Zaher HS, Green R. Hyperaccurate and error-prone ribosomes exploit distinct mechanisms during tRNA selection. Mol Cell. 2010;39(1):110–120. doi: 10.1016/j.molcel.2010.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Johansson M, Lovmar M, Ehrenberg M. Rate and accuracy of bacterial protein synthesis revisited. Curr Opin Microbiol. 2008;11(2):141–147. doi: 10.1016/j.mib.2008.02.015. [DOI] [PubMed] [Google Scholar]
- 13.Demeshkina N, Jenner L, Westhof E, Yusupov M, Yusupova G. A new understanding of the decoding principle on the ribosome. Nature. 2012;484(7393):256–259. doi: 10.1038/nature10913. [DOI] [PubMed] [Google Scholar]
- 14.Freter RR, Savageau MA. Proofreading systems of multiple stages for improved accuracy of biological discrimination. J Theor Biol. 1980;85(1):99–123. doi: 10.1016/0022-5193(80)90284-2. [DOI] [PubMed] [Google Scholar]
- 15.Murugan A, Huse DA, Leibler S. Speed, dissipation, and error in kinetic proofreading. Proc Natl Acad Sci USA. 2012;109(30):12034–12039. doi: 10.1073/pnas.1119911109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Maracci C, Rodnina MV. Review: Translational GTPases. Biopolymers. 2016;105(8):463–475. doi: 10.1002/bip.22832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rodnina MV, Wintermeyer W. Protein elongation, co-translational folding and targeting. J Mol Biol. 2016;428(10 Pt B):2165–2185. doi: 10.1016/j.jmb.2016.03.022. [DOI] [PubMed] [Google Scholar]
- 18.Manickam N, Nag N, Abbasi A, Patel K, Farabaugh PJ. Studies of translational misreading in vivo show that the ribosome very efficiently discriminates against most potential errors. RNA. 2014;20(1):9–15. doi: 10.1261/rna.039792.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhang J, Ieong KW, Mellenius H, Ehrenberg M. Proofreading neutralizes potential error hotspots in genetic code translation by transfer RNAs. RNA. 2016;22(6):896–904. doi: 10.1261/rna.055632.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Behrmann E, et al. Structural snapshots of actively translating human ribosomes. Cell. 2015;161(4):845–857. doi: 10.1016/j.cell.2015.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vorstenbosch E, Pape T, Rodnina MV, Kraal B, Wintermeyer W. The G222D mutation in elongation factor Tu inhibits the codon-induced conformational changes leading to GTPase activation on the ribosome. EMBO J. 1996;15(23):6766–6774. [PMC free article] [PubMed] [Google Scholar]
- 22.Johansson M, Zhang J, Ehrenberg M. Genetic code translation displays a linear trade-off between efficiency and accuracy of tRNA selection. Proc Natl Acad Sci USA. 2012;109(1):131–136. doi: 10.1073/pnas.1116480109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schrader JM, Chapman SJ, Uhlenbeck OC. Tuning the affinity of aminoacyl-tRNA to elongation factor Tu for optimal decoding. Proc Natl Acad Sci USA. 2011;108(13):5215–5220. doi: 10.1073/pnas.1102128108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schrader JM, Chapman SJ, Uhlenbeck OC. Understanding the sequence specificity of tRNA binding to elongation factor Tu using tRNA mutagenesis. J Mol Biol. 2009;386(5):1255–1264. doi: 10.1016/j.jmb.2009.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ieong KW, Pavlov MY, Kwiatkowski M, Forster AC, Ehrenberg M. Inefficient delivery but fast peptide bond formation of unnatural L-aminoacyl-tRNAs in translation. J Am Chem Soc. 2012;134(43):17955–17962. doi: 10.1021/ja3063524. [DOI] [PubMed] [Google Scholar]
- 26.Johansson M, Bouakaz E, Lovmar M, Ehrenberg M. The kinetics of ribosomal peptidyl transfer revisited. Mol Cell. 2008;30(5):589–598. doi: 10.1016/j.molcel.2008.04.010. [DOI] [PubMed] [Google Scholar]
- 27.Asahara H, Uhlenbeck OC. The tRNA specificity of Thermus thermophilus EF-Tu. Proc Natl Acad Sci USA. 2002;99(6):3499–3504. doi: 10.1073/pnas.052028599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Burnett BJ, et al. Elongation factor Ts directly facilitates the formation and disassembly of the Escherichia coli elongation factor Tu·GTP·aminoacyl-tRNA ternary complex. J Biol Chem. 2013;288(19):13917–13928. doi: 10.1074/jbc.M113.460014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gromadski KB, Wieden HJ, Rodnina MV. Kinetic mechanism of elongation factor Ts-catalyzed nucleotide exchange in elongation factor Tu. Biochemistry. 2002;41(1):162–169. doi: 10.1021/bi015712w. [DOI] [PubMed] [Google Scholar]
- 30.Ruusala T, Ehrenberg M, Kurland CG. Catalytic effects of elongation factor Ts on polypeptide synthesis. EMBO J. 1982;1(1):75–78. doi: 10.1002/j.1460-2075.1982.tb01127.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang J, Ieong KW, Johansson M, Ehrenberg M. Accuracy of initial codon selection by aminoacyl-tRNAs on the mRNA-programmed bacterial ribosome. Proc Natl Acad Sci USA. 2015;112(31):9602–9607. doi: 10.1073/pnas.1506823112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu W, et al. EF-Tu dynamics during pre-translocation complex formation: EF-Tu·GDP exits the ribosome via two different pathways. Nucleic Acids Res. 2015;43(19):9519–9528. doi: 10.1093/nar/gkv856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Borg A, Ehrenberg M. Determinants of the rate of mRNA translocation in bacterial protein synthesis. J Mol Biol. 2015;427(9):1835–1847. doi: 10.1016/j.jmb.2014.10.027. [DOI] [PubMed] [Google Scholar]
- 34.Jelenc PC, Kurland CG. Nucleoside triphosphate regeneration decreases the frequency of translation errors. Proc Natl Acad Sci USA. 1979;76(7):3174–3178. doi: 10.1073/pnas.76.7.3174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Polekhina G, et al. Helix unwinding in the effector region of elongation factor EF-Tu-GDP. Structure. 1996;4(10):1141–1151. doi: 10.1016/s0969-2126(96)00122-0. [DOI] [PubMed] [Google Scholar]
- 36.Voorhees RM, Schmeing TM, Kelley AC, Ramakrishnan V. The mechanism for activation of GTP hydrolysis on the ribosome. Science. 2010;330(6005):835–838. doi: 10.1126/science.1194460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jones TA, Zou JY, Cowan SW, Kjeldgaard M. Improved methods for building protein models in electron density maps and the location of errors in these models. Acta Crystallogr A. 1991;47(Pt 2):110–119. doi: 10.1107/s0108767390010224. [DOI] [PubMed] [Google Scholar]
- 38.Wold F, Ballou CE. Studies on the enzyme enolase. I. Equilibrium studies. J Biol Chem. 1957;227(1):301–312. [PubMed] [Google Scholar]
- 39.Johansson M, et al. pH-sensitivity of the ribosomal peptidyl transfer reaction dependent on the identity of the A-site aminoacyl-tRNA. Proc Natl Acad Sci USA. 2011;108(1):79–84. doi: 10.1073/pnas.1012612107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gromadski KB, Daviter T, Rodnina MV. A uniform response to mismatches in codon-anticodon complexes ensures ribosomal fidelity. Mol Cell. 2006;21(3):369–377. doi: 10.1016/j.molcel.2005.12.018. [DOI] [PubMed] [Google Scholar]