Effect of balloon-expandable transcatheter aortic valve replacement positioning: a patient-specific numerical model

Abstract

Transcatheter aortic valve replacement (TAVR) has emerged as a life-saving and effective alternative to surgical valve replacement in high-risk, elderly patients with severe calcific aortic stenosis. Despite its early promise, certain limitations and adverse events, such as suboptimal placement and valve migration, have been reported. In the present study, we aim to evaluate the effect of various TAVR deployment locations on the procedural outcome by assessing the risk for valve migration. The deployment of a balloon-expandable Edwards SAPIEN valve was simulated via finite element analysis in a patient-specific calcified aortic root, which was reconstructed from CT scans of a retrospective case of valve migration. The deployment location was parametrized in three configurations and the anchorage was quantitatively assessed based on the contact between the stent and the native valve during the deployment and recoil phases. The proximal deployment led to lower contact area between the native leaflets and the stent which poses higher risk for valve migration. The distal and midway positions resulted in comparable outcomes, with the former providing a slightly better anchorage. The approach presented might be used as a predictive tool for procedural planning in order to prevent prosthesis migration and achieve better clinical outcomes.

INTRODUCTION

Aortic stenosis (AS) is a pathologic cardiovascular condition in which the aortic valve (AV) opening becomes constricted. The leaflets of the AV do not fully open, presenting increased resistance to the flow through the valve. This can lead to wall thickening, pulmonary hypertension and regurgitation. AS is the most frequent valvular heart disease and the third most frequent cardiovascular disease in Europe and North America, especially in the elderly. Once severe symptoms start, the survival rate drops and the annual mortality rate reaches up to about 25% (1). The prevalence in the population older than 65 years is about 6 % (2). Calcific aortic stenosis (CAS) and congenital bicuspid aortic stenosis (3) account for the overwhelming majority of AS cases, followed by less common conditions, such as rheumatic AS, radiation-induced AS, and unicuspid AS. In CAS, formation of calcium deposits thickens and stiffens the valve leaflets, thus causes a significant obstruction to the left ventricle (LV) outflow during systole and limits the closure during diastole.

Currently, replacement of the stenotic valve with a prosthetic valve is the only effective treatment. According to the American College of Cardiology (ACC) and the American Heart Association (AHA) guidelines (4), surgical aortic valve replacement (SAVR) should be performed in all symptomatic patients with severe AS, regardless of LV function, as it has better survival rates than medical treatment. In recent years, a less invasive option of percutaneous transcatheter aortic-valve replacement (TAVR) is available for high-operative-risk patients (5). The prosthesis employed in this procedure is typically comprised of a bovine pericardial valve mounted on a metal stent. In the balloon-expandable versions the valve is crimped on a deflated balloon to fit into a catheter shaft, inserted into the body and threaded to the heart. Once the proper location is reached, the valve is deployed through balloon expansion of the stent that pushes the diseased leaflets against the aortic root (AR) wall to reestablish the lumen passage over the diseased valve. Other available prosthetic solutions include valve mounted on a self-expandable stents made of a shape memory alloy that springs back after deployment and adapts to the anatomy of the diseased AR (6). Clinical studies have demonstrated excellent procedural success rate of approximately 97% (7) and large-patient-cohort-based studies showed how TAVR has good medium-to-long-term durability and mostly preserves hemodynamic function. Specifically, survival at 1, 2, and 3 years was found to be 81%, 74%, and 61%, respectively (8).

However, many clinical studies revealed several adverse effects that may occur as a consequence of a sub-optimal procedure, such as embolic stroke, vascular complications, AR injury and paravalvular leakage (PVL) (9). Unlike SAVR in which the valve is directly sutured to the aortic annulus, in TAVR the valve is ‘anchored’ only by contact and friction forces between the native root and the deployed stent. Because the deployment position is based on angiographic imaging and is performed during heart pacing, a possible suboptimal location can cause longitudinal shift of the prosthesis during the balloon inflation (10), and thus lead to procedural failure. The deployed valve may be susceptible to migration, where the prosthetic valve dislocates toward either the LV cavity (11) or the aorta (12).

The potential benefit of patient-specific modeling lies in enabling clinicians to virtually test different valves sizes and procedural options such as overexpansion and positioning. This led to the development of models of the procedure that can shed light on the biomechanical aspects of intra- and post-intervention complications. Patient-specific modeling of TAVR deployment has recently been developed from computed tomography angiography (CTA) scans in order to assess the TAVR performance in a realistic AR environment (13). Among these, Wang et al. (14) focused on one retrospective AR rupture clinical case in which the reconstructed calcium deposits were connected to the aortic side of the natural leaflets. Other similar studies focused on the implications of the deployment geometry on TAVR valve leaflets deformation inside a non-calcified AR deprived of native leaflets.

Currently, few studies investigated different stent positioning. Moreover, these models either employed a non-calcific AR geometry (15, 16), where it is clear that the calcifications may have a cardinal effect on the deployment outcome, or a self-expandable TAVR valve (17). We hypothesize that the deployed TAVR stent configuration depends on the specific distribution of the calcific deposits within the AR and aim to evaluate the effect of different TAVR deployment positions on the procedural outcome by specifically assessing the risk for valve migration. A finite element analysis of Edwards SAPIEN valve crimping, with and without the prosthetic leaflets, was performed to assess the influence of their inclusion on the stent deformation. This was followed by deploying the crimped TAVR stent via balloon-inflation in a patient-specific calcified AR and repeated in various locations. The resulting configurations were investigated during the inflation and the subsequent recoiling period.

MATERIALS AND METHODS

Procedural information

An 88-year-old male patient with annulus average diameter of 23 mm was referred for TAVR at Stony Brook University Hospital. Echocardiography revealed severe AS with insufficient AV opening area (A_op = 0.62 cm²). A size 26 mm Edward SAPIEN TAV was chosen and deployed via transfemoral approach after positioning the middle of the stent on the AV annulus. Migration of the prosthesis into the LV cavity occurred after retrieval of the delivery system.

Image-Reconstruction

The Computed Tomography Angiography (CTA) scans of this reported case were collected after obtaining approval from IRB (Fig. 1A). The images of the coronaries and the heart, with non-ionic contrast media, were acquired with electrocardiography (ECG)-gated Aquilion ONE 320-channel volume CT scanner (Toshiba, Medical Systems, Ottawara, Japan). The planar resolution was 0.755 mm × 0.755 mm, the slice thickness was 0.5 mm, and the cardiac phase was set to 75% of the inter-beat (R-R) interval. The series of Digital Imaging and Communications in Medicine (DICOM) files were then imported into the open source segmentation tool ITK-SNAP v3.2 (18) and processed to by following three steps. First, a curve-based contrast enhancement by Hounsfield units (HU) filtering was performed (Fig. 1B) and range thresholding through region-competition feature images was applied. Then, automatic segmentation using Region Competition Snakes algorithm was implemented (Fig. 1C). A segmentation window of 150–500 and >500 HU was employed to extract the lumen and the calcifications, respectively. The proximity of the ascending aorta with the pulmonary trunk required a more controlled snake evolution on the sagittal and coronal planes in order to prevent leakage in the surrounding structures. Furthermore, the absence of contrast between AV leaflets and LV required additional manual adjustments to define their separation based on the location of bulky calcium deposits on the AV leaflets. The resulted surface model (Fig. 2, surface model), including the AR, main coronary arteries, and the initial tract of the ascending aorta, was geometrically processed in MATLAB R2014b (MathWorks Inc., Natick, MA). The lumen surface was then extruded to a thickness of 1.56 mm (19) for the aorta by displacing each node along its normal. For the AV leaflets, a variable thickness algorithm was implemented by prescribing extrusion length proportional to the radial location of each node, resulting in thinner leaflets toward the free edge and matching thickness in the connection to the thicker sinus. It was performed in order to better replicate the AV leaflets morphology characterized by a thinner wall than in the aorta. Calcifications deposits were downscaled by a factor of 10% relative to their center of mass to account for the blooming effect in the scans that leads to an overestimation of their volumes. This threshold value was established after consultation with expert radiologists, since measurements for determining the outer boundaries of the calcific deposits are currently not available.

Figure 1.

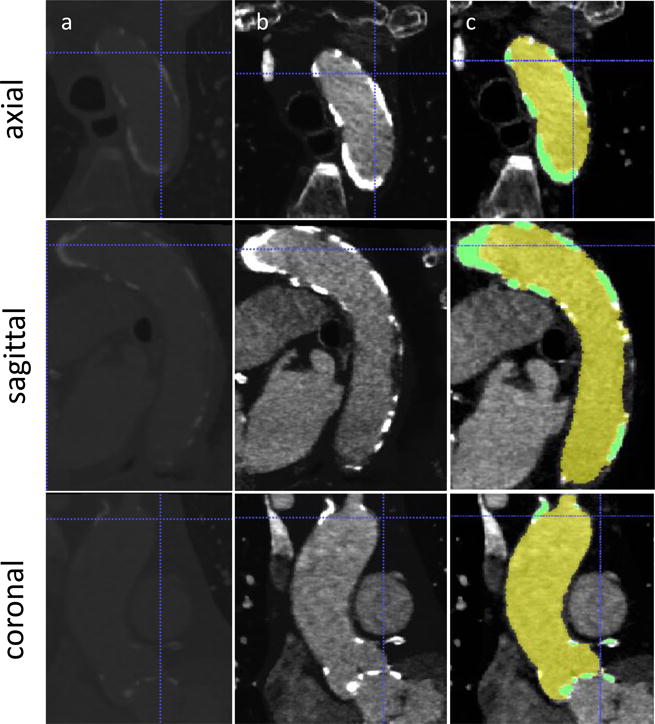
DICOM images from CTA scan employed for the reconstruction. A) Raw DICOM, B) contrast-enhanced images and C) segmentation masks for aortic lumen (yellow) and calcium deposits (green) in the three planes.

Figure 2.

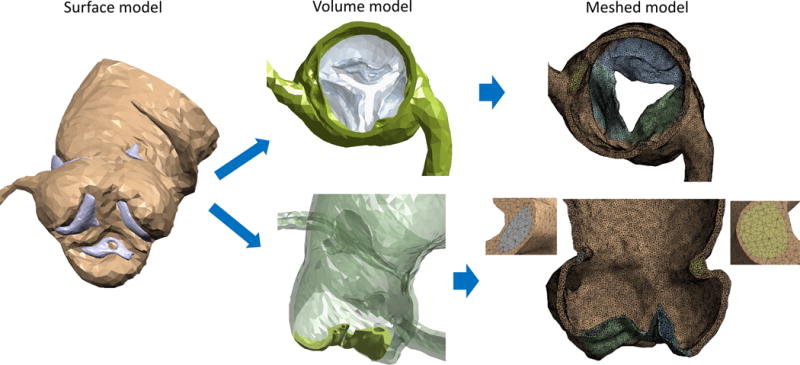
Representation of the AR reconstruction. Left column: Surface model as a result of the segmentation, with lumen (brown) and calcifications (violet). Central column: Volume model sections of the sinus at the sinutubular junction level (top) and of the leaflets (bottom), showing the presence and location of the calcification “pockets”. Right column: Smoothed meshed model from an aortic point of view (top) and longitudinal section with details of the embedded calcification in the sinus. Leaflets were partially opened after the catheterization simulation.

The soft tissue thickness was then modified by an algorithm that assure that the deposits are fully embedded in it. This process resulted in calcification deposits located in confined ‘pockets’ within the soft tissue, as calcific tissue presents itself in such pathologies, rather than ‘stitching’ or ‘gluing’ these deposits to the aortic or lumen sides of the leaflets and vessel walls, respectively (14, 20). For these reasons, the AV leaflets and aortic sinus are characterized by this large degree of variability in their thickness. Boolean operations were subsequently performed to obtain the volume model using ANSYS 15 Design Modeler (Canonsburg, PA). The AV opening was obtained in such a way that the shape and area of the orifice were consistent with the correspondent CTA and echocardiography measurements (Fig. 2, volume model). As visible from the scan, the native leaflets appear to be fused to each other in the commissural regions, as a result of the advanced state of the disease. Since it is difficult to determine whether this fusion is a result of the reconstruction or it is a real characteristic of the stenotic AV (21), it was decided to include this morphological feature in the model, based on the information extracted from the systolic CTA image. Previous numerical studies of TAVR employed models with three separated leaflets (14, 20), probably because no fusion was visible from the scan.

TAV crimping model

The balloon-expandable Edwards SAPIEN with outer stent diameter of 26 mm was chosen following the clinical case under investigation. This stent was recreated in SolidWorks (DS Corp., Waltham, MA) by employing parametric equations that enabled the estimation of the expanded stent configuration.(22) The stent is made of stainless steel (AISI 316 LVM) and its material was modeled as elasto-plastic(23) (ρ = 7760 kg/m³, E = 193 GPa, σ_Y (0.2%) = 340 MPa, σ_U (48%) = 670 MPa, ν = 0.29), whereas the bioprosthetic leaflets are derived from bovine pericardium and were modeled using an hyperplastic material model (Ogden (24), third degree) fitted to experimental biaxial data (25) over the strain range of interest. The crimping process was simulated by applying radial displacement on a cylindrical-surface crimper in Abaqus Explicit 6.14 (SIMULIA, Dassault Systèmes, Providence, RI). A symmetric section of the stent was discretized with a structured and refined mesh, composed of 69,876 brick elements with reduced integration and nodal density proportional to the curvature of the model. In this way, a computationally efficient grid was generated allowing controlled element distortion and reasonable solving time. For the bioprosthetic leaflets, a triangular-shell-elements mesh was built in order to capture their complex folding dynamics (Fig. 3).

Figure 3.

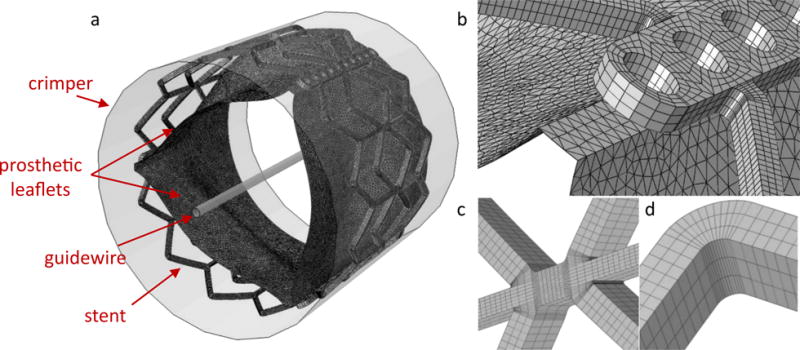
a) Meshed model of the Edwards SAPIEN TAV with stent, leaflets, guidewire and crimper. Details of the commissural region (b) and of the stent mesh in the struts’ link region (c) and in the strut’s corner (d).

A comparative analysis of the TAV crimping with and without the bioprosthetic leaflets (WL and WOL model, respectively) was performed to assess the influence of the inclusion on the stent deformation. The fully crimped position was defined as an outer stent diameter of 8 mm (24 Fr catheter). Contacts and constraints were appropriately defined in order to capture the complex leaflets’ folding and the stent elongation during the crimping process. Particularly, in the model with the leaflets, their nodes located on the commissural and the lower skirt portions were assumed to move with the correspondent inner surface of the stent, in order to model the effect of the sutures. Additionally, a cylindrical and rigid surface body was included to model the presence of the guidewire (D_guide = 0.89 mm), so that less space would be available for the leaflets during their folding. A frictionless contact model was employed and the stent was allowed to move and deform in every direction, as being not directly constrained during the clinical procedure.

Balloon deflation model

The balloon was modeled as axisymmetric thin body with cross sectional profile that was extracted from a photograph of the NovaFlex+ delivery system of known scale (26). The profile was revolved about the balloon axis to create the thin surface (Fig. 4, left) which was then meshed with 216,960 quadrilateral shell elements that can capture the complex balloon folding during its deflation. The thickness of the balloon was defined as 0.06 mm and its material was assumed to be linear elastic (23) (ρ = 1100 kg/m³, E = 600 MPa, ν = 0.45) with a mass-proportional damping coefficient α = 8000 to control the dynamic response of the material. The balloon deflation was simulated through radial displacement of a cylindrical crimper, in the presence of a rigid guidewire, and by constraining all translational degrees of freedom of its distal ends (Fig. 4, mid).

Figure 4.

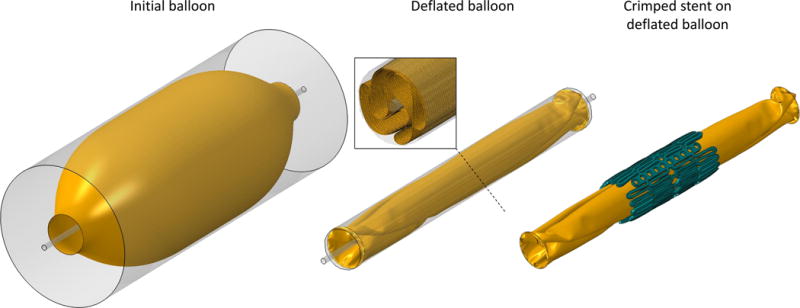
Left column: Initial balloon surface model prior to the deflation. Central column: Deflated balloon with a cross section showing its folding and mesh. Right column: Crimped stent centrally placed on the deflate balloon.

Deployment model

In order to obtain a smoothed AR mesh with limited skewness and appropriate element size, the wrapping method of ANSYS 15 Fluent Meshing was employed. This allowed to obtain a more uniform mesh that can facilitate these large-deformations numerical analyses with controlled element distortion, while not losing the original patient-specific features. These operations were performed for the soft tissue and the calcification regions simultaneously, guaranteeing shared nodes on their interfaces, thus avoiding computationally-expensive contact-related issues during the solution (Fig. 2, meshed model).

This mesh appears to be much finer than in comparable current FE models that recently appeared in the literature, and exceeds mesh independence requirements; balancing accuracy and computational cost it represents the coarsest mesh without losing the finer patient-specific characteristic features. This was achieved by using a tetrahedron-based mesh consisting of 746,263 elements (average size - 300 μm per element) for the whole volume of model, inclusive of the proximal aorta, aortic root, native leaflets and calcifications deposits. Finer meshes were tested, down to reducing the element size by 30% (leading to a mesh of approx. ~1.7M elements) with results showing a variation in the max. von Mises stress within 4% for the same location in the native leaflets, which does not justify the excessive computational cost involved. In all the simulations, a timestep of Δt=10⁻⁷ s was required for the Explicit solver. Additionally, the AR sinus, calcifications and each leaflet were modeled with independent material models. The material of the soft tissue was modeled with dedicated hyperplastic model (Ogden (24), third degree) calibrated with biaxial test measurements (27, 28) whereas the calcification deposits were modeled as homogenous linear elastic material (E = 12.6 MPa, ν = 0.3) (29).

Before adding the TAV stent and the balloon to the overall model, the catheterization process was simulated. As a first step, the displacement (“pushing”) of the almost closed stenotic native leaflets during the insertion of the delivery system was simulated to allow access of the crimped stent in situ. The crimped stent was placed on the deflated balloon (Fig. 4, right) and the assembly was then moved into the AR to model the deployment in Abaqus Explicit 6.14. Three deployment configurations were simulated to replicate different surgical scenarios, by placing the stent centroid in the AV annulus plane (midway), 30% shifted toward the aortic sinus (distal), and 30% of the stent length shifted toward the LV cavity (proximal). In every model, the balloon was gradually inflated with a uniform pressure up to 1.38 atm at full inflation. The balloon was assumed to be in tension and under negligible bending load during the inflation. Therefore, the balloon was meshed with membrane elements requiring reduced computational cost relative to using shell elements. The interaction with the stent and the native AR was modeled as frictionless.

In all the simulations, the translational degrees of freedom of the AR distal end were constrained. A semi-automated mass scaling was initially applied to every model and, in order to control the effect of the inertial forces on the model dynamic response, the ratio between kinetic energy and internal energy was monitored and kept under 5% (30). After the deployment ended, the recoil of the stent was modeled by stopping its interaction with the balloon, while keeping the contact with the native AR. A schematic overview of the various simulations performed is available as a supplementary figure online.

RESULTS

Crimping comparison

The resulting deformation of the stents in the two crimping models, were compared. Similar deformation distributions were found in the three cylindrical directions with larger inward folding of the stent without leaflets at the extremities. For the WOL model the struts in this region were more closely packed, whereas the struts located further from the commissural bars in WL were only partially crimped. The axial and radial displacement normalized with respect to the initial length of the stent and the expected displacement, respectively, are shown in Fig. 5. The stents in both models experience comparable maximum axial elongation, ΔZ = 7.46% vs. 7.84% in WL and WOL, respectively. Axial displacement is more pronounced in the corners regions of the struts, leading to an overall axial elongation of about 2.1 mm in the fully crimped configurations. In the radial and circumferential direction, on the other hand, the largest deformations were observed in the regions where the struts are connected with the commissural bars. Larger radial deformations were observed in WOL (ΔR = 7.31% compared with 4.70%), where the majority of the stent was crimped to a higher extent because of the absence of resistance from the leaflets. The differences in the radial and axial deformations between the two stents were also examined in two sets of typical corner nodes, located on the struts near the commissural bars and on the intermediate struts, both of them on the outer surface of the stent (Fig. 5, left bottom). Calculated radial displacement normalized with respect to the expected radius and difference in elongation are presented in the Table 1 for the various locations. The radial displacements of WOL was larger than WL by less than 8% with an averaged difference of 7.24%, whereas the elongation resulted to be on average 0.13% less in the model with the leaflets. The maximum difference in the circumferential deformation between the two stents was 4.20%. As the inclusion of the prosthetic leaflets would require a considerably higher computational cost and given these relatively small differences, after taking into account the additional volume that the crimped valve leaflets occupy, the leaflets were excluded in the deployment models (31) and the inflation of the stent started at this point.

Figure 5.

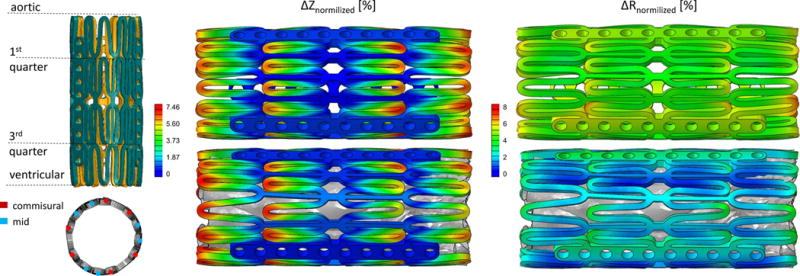
Left panel: superimposition of the two stents in a longitudinal view with highlighted axial levels. Stents from the model with and without prosthetic leaflets are represented in teal and amber, respectively (top). Representation of the location of commissural and mid nodes (bottom). Right panel: Axial displacement contours normalized with respect to the initial stent’s length (left) and radial displacement contours normalized with respect to the expected displacement (right) of the stents from the WOL (top) and WL (bottom) model.

Table 1.

Radial and elongational differences (%) between WO and WOL models for the two nodal sets.

Zlocation	ΔRcommisural [%]	ΔRmid [%]
aortic	7.45	7.79
1st quarter	6.67	7.72
3rd quarter	6.40	7.54
ventricular	7.94	6.37
mean	7.12	7.35
	Δcommisural [%]	Δmid [%]
elongation	0.08	0.17

Stent deployment

The three deployment positions were analyzed and compared during deployment in terms of stress and strain distributions in the native AR, contact pressure and area between the TAV stent and the native AR, and stent deformation. Fig. 6 compares the stent configuration of the three deployment locations in three instances during the balloon inflation. The distribution of von Mises stresses on the native aortic leaflets and on the calcifications are also presented in Fig. 6. A video comparison of the deployment and recoil phases in the three models is available in the supplementary materials online.

Figure 6.

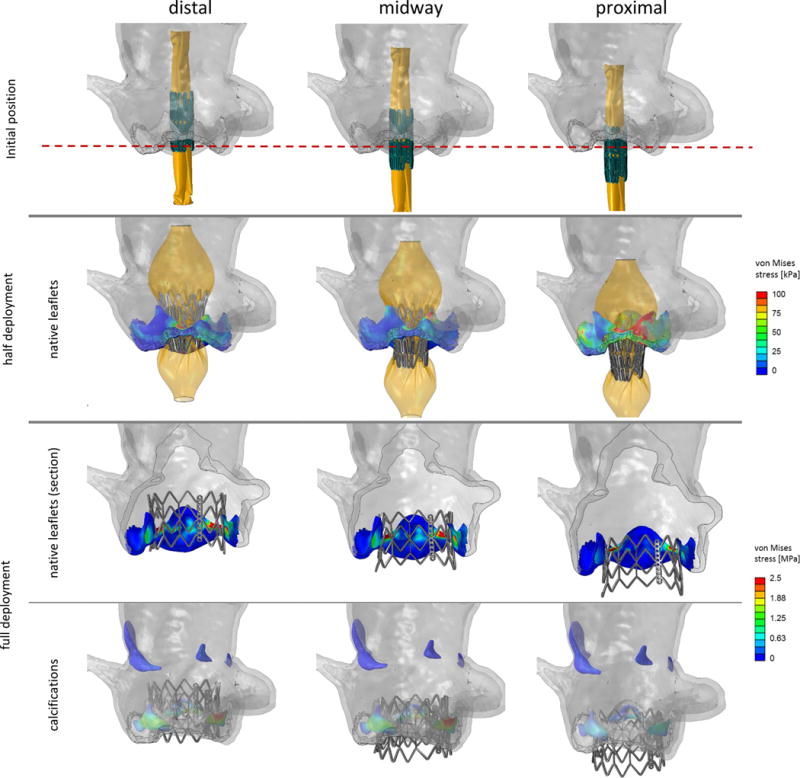
Various stages of the stent deployment in the three deployment locations. Von Mises contours are plotted on the native leaflets (second and third rows) and calcium deposits (fourth row). Sections of the right and left coronary leaflets in the third row show the stress difference between the calcium and the surrounding soft tissue.

Similar stress distribution patterns and magnitudes were observed on the AR for the distal and the midway cases, where maximum values were located in the region in contact with the stent and in each interleaflet region. Sections of the leaflets (Fig. 6, third row) show that the embedded calcifications experience higher stresses than the surrounding soft tissue (for example, 3.4 MPa vs. 0.5 MPa, in the central region of the left coronary leaflet, midway model), a direct result of the stiffer material properties. The proximal deployment resulted in higher stress magnitudes at half deployment, when the native leaflets were in direct contact with the balloon, and in overall lower stresses at the end of the deployment as compared to the other two configurations.

Stent recoil

The anchorage strength and the landing zone of the three configurations were quantitatively assessed based on the contact between the stent and the AR in the final recoiled configuration (Fig. 7). Maximum stresses and true strains at this stage are given in Table 2 for each body in the model and for all the deployment configurations. Nodal contact forces and the correspondent “nodal areas” were extracted from the native leaflets surfaces and used to obtain the contact pressure distribution. The “nodal area” is defined herein as the sum of one third of the area of each triangular external face that shares the node. Spatial maximum contact pressures at the end of the recoil were then calculated, with the distal deployment resulting in the highest magnitude of 10.38 MPa, as compared to the midway and proximal cases (p_{max, mid} = 6.26 MPa, p_{max, proximal} = 3.84 MPa). In addition to contact pressure calculation, this definition of “nodal area” allows area-weighted averaging of the results. Fig. 8 compares the mean contact pressure and the total contact area as a function of time throughout the deployment and the recoil phases. In the first period of the deployment (until 80%), the inflated balloon develops the characteristic “dog-bone” configuration. Then, in the last 20% of the deployment, the balloon expanded rapidly. In this phase, the contact between the AR and the balloon-stent assembly quickly increased with comparable behavior, with the distal configuration reaching higher pressure value at the end of the deployment (468 kPa). At the beginning of the recoil (after 100% deployment in Fig. 8), a sudden drop of the contact area and a moderate increase of the mean contact pressure were observed in all scenarios as the contact between AR and the balloon stopped. The proximal deployment experienced a loss of almost 75% of the contact area at the end of the recoil when the stent was dislocated toward the LV (Fig. 7, right). In this configuration, the recoil of the stent led the native leaflets to partially recover their original position while the mean contact pressure increased as a result of the more localized interaction between the AR and the stent.

Figure 7.

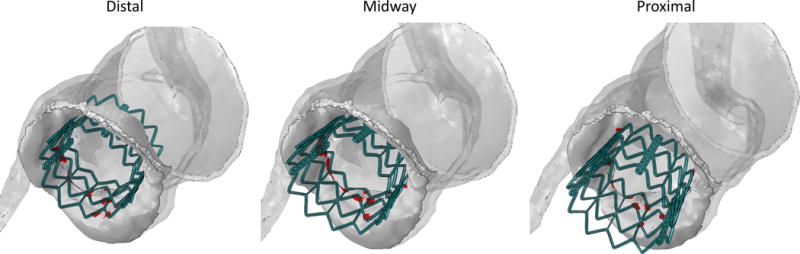
Contact area location in the recoiled position for the distal (left), midway (mid) and proximal (right) configuration.

Table 2.

Spatially maximum values of von Mises stresses, maximum principal stresses and true strains for each body in the model and for each of the three analyzed configurations at the end of the recoil phase.

	Body	σVM [MPa]	σmax, principal [MPa]	ɛmax, principal
Distal	leaflets	21.84	10.35	0.95
	sinus	0.96	0.22	0.44
	calcifications	2.57	2.42	0.19
	stent	455.6	668.1	0.25
Midway	leaflets	10.95	9.52	0.9
	sinus	1.13	0.13	0.34
	calcifications	2.31	2.61	0.19
	stent	471.8	559	0.23
Proximal	leaflets	24.9	14.93	0.74
	sinus	0.47	0.2	0.44
	calcifications	1.78	1.6	0.12
	stent	470	605.9	0.23

Figure 8.

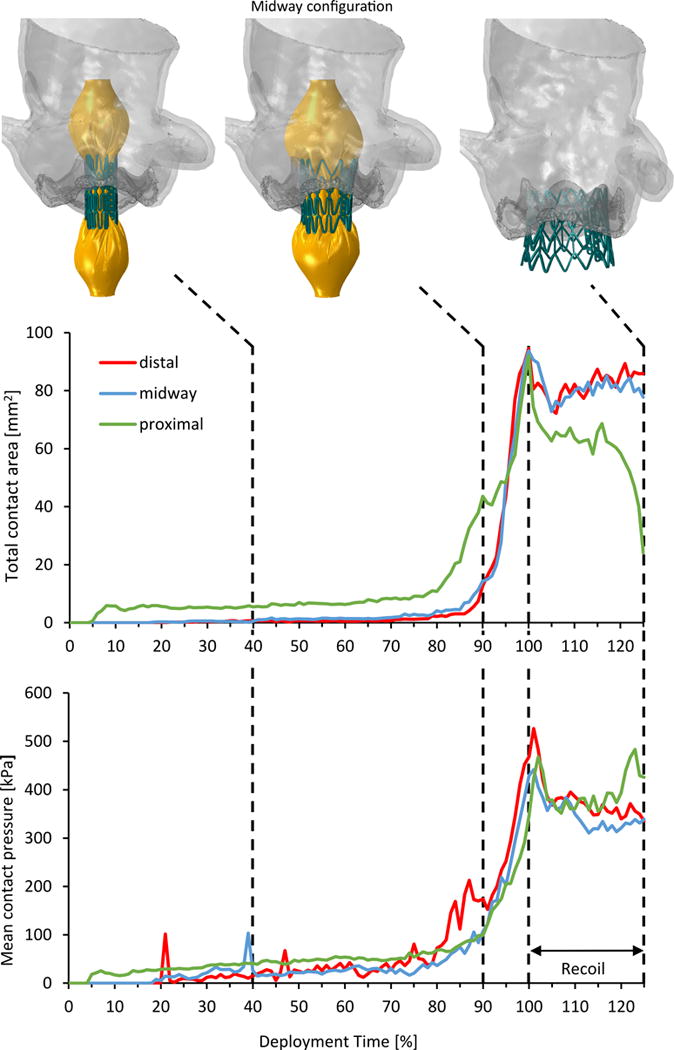
Total contact area (top) and mean contact pressure (bottom) calculated in the deployment and recoil phases for the three configurations. The model in the midway configuration is shown in three instances: 40% and 90% of the deployment time, and at the end of the recoil.

The risk for coronary obstruction was also investigated for each simulated configuration. This was assessed by calculating the shortest distance between the coronaries and the native leaflets or the stent. The right coronary ostia was more proximal than the left one and therefore it was used for this calculation. The distance was computed along the normal of the AV annulus for the most distal point on the stent and the right coronary leaflet. The stent in the distal case was the closest to the right coronary (Δ_distal = 2.28 mm) whereas in the other two cases the leaflet was closer than the stent but further away from the coronary (Δ_midway= 4.42 mm, Δ_proximal = 5.99 mm).

DISCUSSION

This study investigated the impact of TAVR deployment position on the procedural success, as assessed by the risk of device migration, specifically based on the computation of contact area and pressure between the native leaflets and the stent during the recoil phase. Advanced numerical simulations were employed to study several deployment locations in a reconstructed patient-specific anatomy. CTA scans of a patient that suffered from intra-procedural migration were chosen, but the same methodology could be employed for pre-procedural planning cases in which non-repositionable and non-retrievable valves, like the Edwards SAPIEN, are used. It has the potential to prevent malposition and avoid corrective transcatheter implantation (32) or surgical removal of the deployed prosthesis.

As a first step to accurately reproduce the procedure, the crimping of Edwards SAPIEN valve, that is clinically performed prior to the deployment, was modeled. A comparative analysis of the model was carried out to investigate whether the prosthetic leaflets are necessary for accurate modeling of the stent crimping. The stents experienced comparable distribution of the axial deformations, leading to a small difference in elongation between the two models (below 1%). The presence of the bioprosthetic leaflets produced an additional resistance to the crimping, thus resulting in a final configuration which is less crimped radially. The larger diameter in the stent with the leaflets can also be observed from the wider openings between the struts corners that are located further from the commissural bars (Fig. 5). The difference in the radial deformations was larger in the ventricular side for the corners next to the commissures (7.94% vs. 7.45% on the aortic side). Interestingly, in the corners located further from the commissural bars, the largest difference was observed in the aortic side (7.79% vs. 6.37% on the LV side). These two phenomena can be explained by the presence of the leaflets skirt on the LV side. Overall, the difference between the two models was lower than 8% in any direction and the two crimped configurations were generally similar. These results are in agreement with the recent study by Bailey et al. (31) that found comparable kinematics with and without prosthetic leaflets not only during the crimping but also during the deployment. Therefore, in order to significantly reduce the computational cost of the deployment models and similarly to common assumptions used in such complex simulations (15, 16, 33), the bioprosthetic leaflets were not included in the deployment models.

In the three deployment models, the highest stress magnitudes in the calcified native leaflets were found in the regions where two adjacent leaflets are fused together, where the native valve experiences the largest strains. However, additional modeling would be required in the case the fusion portions are characterized by stiffer or more flexible material, which would make the leaflets more durable and more stretchable, respectively. The leaflets of the proximal configuration were exposed to the highest maximum stresses both at the end of the deployment (23.4 MPa) and end of the recoil phase (24.9 MPa). However, these stresses are very localized and in most regions the stress levels in the proximal case are lower than in the other two models. This can be explained by the significantly smaller contact area but slightly higher contact pressure relative to the other models (~30% and ~126%, respectively). Obviously, the highest stresses were found in these small contact regions. The other two configurations experienced similar maximum stresses at the end of the deployment (16.07 MPa in the midway model, 13.89 MPa in the distal model), whereas after the recoil the distal positioning resulted in higher maximum stress then the midway case (21.84 MPa vs. 10.95 MPa). This difference in maximum stress may indicate a higher risk for tissue damage for the distal positioning of the valve, as compared with the midway configuration. In the absence of direct interaction between the stent and the sinus wall, the stresses observed in the sinus were significantly lower in all the configurations studied.

Contact forces and area between the stent to the native AV were calculated throughout the deployment and the recoil phase. During the deployment, the contact parameters (computed from the native leaflets), represent the contact with the balloon in addition to the contact with the stent. On the other hand, during the recoil phase only the stent is coming in contact with the leaflets, thus providing direct information about the prosthesis anchorage. The recoil phase, ignored by most of the previous models of TAVR stent deployment (14, 15, 17, 20, 33), also represents an important phenomenon that is related to valve migration, as observed in the current proximal positioning. In this model the loss of contact area at the beginning of the recoil was more pronounced than in the other two configurations. This area represents the contact area with the balloon, suggesting that in the proximal configuration the balloon had a relatively larger contribution. At the end of the simulated recoil phase, the contact area quickly dropped and the mean contact pressure slightly increased in the proximal model. This is a result of the more localized and scattered contact with the struts of the stent for this case, but it is important to emphasize that the total contact force, is much lower in the proximal case than in the other two cases (F_{tot, proximal =} 10.2 N, F_{tot, mid =} 26.3 N, F_{tot, distal =} 28.8 N, respectively). These results indicate a higher risk of migration for the case in which the prosthesis is deployed in the proximal configuration, suggesting that a more distal positioning would be advisable. Furthermore, a moderate shift of the stent toward the LV was observed in all models, providing additional support for ‘higher’ positioning deployments. The midway and the aortic positioning led to overall similar outcome in terms of stress distribution on the AR and of AV-stent contact parameters. Specifically, larger contact area and mean contact pressure were found in the distal case, but better (lower) stresses were found in the midway case. Based on these data, the preference of one particular configuration is arguable and an intermediate position might show better performance. Future studies might expand the current parametric study to such an intermediate distal position (<30%) and a more distal position (>30%) to facilitate drawing a more definite conclusion.

The risk for coronary obstruction was assessed by calculating the shortest distance between the coronaries and the native leaflets or the stent. The distal deployment led to the shortest distance to the coronary ostia as compared to the other two cases. However, in all the configurations the stent did not block the coronary ostia, suggesting that such a complication is not likely to occur in this clinical case.

The main limitations of the current study are related to the level of accuracy achievable in the reconstruction and to the modeling assumptions. Homogeneous isotropic elastic properties were considered for modeling the calcific deposits, according to published data, even though the calcification deposits are known to have a wide range of stiffness (from E=10 MPa (17, 20) to E=60 GPa (33)). In the current models we used a stiffness value within the lower portion of this range (E = 12.6 MPa (29)), because we were interested in the compliance of the calcium deposits rather than assuming them as almost rigid bodies. Also, the coaptation region of the native leaflets was neglected because the free edges were not visible in the CTA scans and most of the calcific bulk was located in the belly region. The zero pre-stress assumption might have small impact on the solution because the native leaflets are much more compliant than the embedded calcium deposits. Additionally, the balloon inflation was modeled by applying direct pressure, whereas in the clinical practice the interventionalist pumps volume of incompressible fluid into the balloon. The LV outflow tract, which may have provided additional physical constrain, was not included in the model. Although the analysis presented here is based on a patient specific anatomy and its associated pattern of the calcium distribution in this patient’s diseased aortic root, such patterns are common and not unique. At any rate, understanding the migration phenomenon from a biomechanical perspective can serve as a guideline to better inform clinicians on the optimal TAV positioning. Future studies could expand this single patient specific case and employ this model to a larger cohort of patients. This will help to evaluate and calibrate the predictive capabilities of the presented methodology for a possible use as a procedural planning tool. In this way, the impact of such catastrophic events may be minimized. Future development of the model will also aim at quantitatively assessing the PVL and at a more accurate material characterization of the stenotic tissue. This will be achieved by employing Computational Fluid Dynamics (CFD) analyses of the hemodynamics post-deployment migration and by mechanically testing ex vivo calcified valves from SAVR patients. Assuming that high thrombogenicity of TAVR valves could be associated with the presence of paravalvular gaps, this thrombogenic potential will be calculated from the CFD models based on the exposure of platelets to shear stress in the PVL jets. The risk for thrombus formation will be then assessed and compared between the various configurations.

In conclusion, the comparison of the three positions showed that a proximal deployment could lead to valve migration into the LV. This case resulted in lower contact area, which led to higher localized contact pressure and higher stress levels in the native tissue that are likely to dislodge the valve into the LV. The distal and midway configurations had comparable outcomes, possibly leading to similar performance, although a slightly better anchorage was found in the distal model and lower stresses observed in the midway case. After further validation of the current methodology, the proposed approach might be used as a predictive tool for procedural planning in order to ultimately prevent prosthesis migration and achieve better clinical outcomes for the patients.