Analysis of binary responses with outcome-specific misclassification probability in genome-wide association studies

Abstract

Errors in the binary status of some response traits are frequent in human, animal, and plant applications. These error rates tend to differ between cases and controls because diagnostic and screening tests have different sensitivity and specificity. This increases the inaccuracies of classifying individuals into correct groups, giving rise to both false-positive and false-negative cases. The analysis of these noisy binary responses due to misclassification will undoubtedly reduce the statistical power of genome-wide association studies (GWAS). A threshold model that accommodates varying diagnostic errors between cases and controls was investigated. A simulation study was carried out where several binary data sets (case–control) were generated with varying effects for the most influential single nucleotide polymorphisms (SNPs) and different diagnostic error rate for cases and controls. Each simulated data set consisted of 2000 individuals. Ignoring misclassification resulted in biased estimates of true influential SNP effects and inflated estimates for true noninfluential markers. A substantial reduction in bias and increase in accuracy ranging from 12% to 32% was observed when the misclassification procedure was invoked. In fact, the majority of influential SNPs that were not identified using the noisy data were captured using the proposed method. Additionally, truly misclassified binary records were identified with high probability using the proposed method. The superiority of the proposed method was maintained across different simulation parameters (misclassification rates and odds ratios) attesting to its robustness.

Introduction

It is well established that misclassification of the dependent variables adversely affects the detection power of genome-wide association studies (GWAS) and could lead to biased results.1,2 Classifying individuals into different disease classes has proven to be erroneous as binary responses are subjective measurements with no precise or quantifiable guidelines. Consequently, the outcomes from implementing GWAS using case–control studies can be misleading if the observations are inaccurate. Screening and diagnostic tests are used to identify unrecognized diseases or defects and have shown to exhibit potential for bias.3 These testing activities are used to characterize and sort individuals into two groups (eg, high/low risk) or classify them into different subclasses of the same disease or disorder. This screening process typically relies heavily on human perception; therefore, false-positive and false-negative cases are unavoidable.

In disease diagnosis, the quality of a test is often measured by its sensitivity and specificity.4 Thus, a test with low sensitivity/specificity will lead to a high false-negative/positive result. Several reviews have been published in order to assess the variation among studies and to evaluate test performances.5–7 Deeks8 pooled together estimates for sensitivity and specificity and found the average sensitivity to be 0.96. The average specificity was 0.61 exhibiting considerable variation around the mean ranging between 0.21 and 0.88. Such inaccuracy of screening tests will lead to high misdiagnostic rates in disease classification across both clinical practices and perceptual specialties.

In radiology, although false positives are of low frequency (1.5%–2%), false negatives are in excess of 25%.9 False-negative rates in cancer detection have been documented as one of the most difficult limitations.10 Published false-negative rates have ranged between 10% and 25% for breast cancer detection.11,12 Using 282 samples for breast cancer based on the sentinel lymph node biopsy, Goyal et al13 found 19 false-negative cases. Stock et al14 evaluated cervical cancer screening tests and found false-positive estimates ranging between 0.056 and 0.269. Croswell et al15 concluded that using 14 tests for cancer screening, the cumulative risk of a false positive was 60.4% and 48.8% for men and women, respectively.

False-positive and -negative rates are also prevalent in psychological disorders as it is often difficult for clinicians to distinguish between disorders due to overlapping or late development of symptoms. In the case of Alzheimer’s disease (AD), symptoms are more pronounced during later stages; therefore, diagnosis of incipient AD patients is more difficult. Two cognitive tests are generally administered for diagnosis, neurofibrillary tangles (NFTs) and the Mini-Mental State Exam. Reviews of NFT have questioned its validity as an accurate test for AD.16–18

Unfortunately, finding these errors is not simple. Even in the best-case scenario, when misclassification is suspected before analysis, retesting is often not possible and the sample must be removed, thereby reducing power of the study. Extensive research has been carried out to investigate the consequences of misclassification on the well-being of the patient19,20 as well as its effects on the accuracy of the results of studies including GWAS. GWAS aim to statistically associate genetic variants with disease status; therefore, it relies on the accuracy of both the genotypic and phenotypic data. Implementing association studies without proper data quality control measures can lead to the discovery of false associations between markers and disease. This false discovery could lead to different assessment and potentially contradictory conclusion. Using candidate gene approach, Hirschhorn et al21 concluded that out of 600 gene–disease associations reported in the literature, only 1% of these associations are likely to be true. Heterogeneity, population stratification, and noisy dependent variables were often suspected as potential explanation for the lack of replicability of GWAS results.22–25

Studies examining the effects of uncertainty found that it can lead to biased parameter estimates.26,27 A statistical approach capable of eliminating or at least attenuating the negative effects of misclassification represents an attractive solution. The Bayesian approach proposed by Rekaya et al28 made the analysis of noisy binary responses more tractable. They found, using simulated binary data with a 5.6% misclassification rate, that ignoring misclassification resulted in biased parameter estimates, with the true values falling outside the 95% high-density posterior interval. Robbins et al29 concluded that prediction power could be increased by 25% while accounting for misclassification.

Smith et al2 investigated the effects of misclassification in binary responses on GWAS results assuming the same misdiagnostic rate for cases and controls. In this study, such idea has been extended to situations where misclassification occurs with different rates for cases and controls, thus mimicking more realistic disease diagnostic scenarios. For that purpose, case–control data sets were simulated and misclassification was introduced by randomly switching the true binary status to reach the desired error rate in 5% or 7% and 0% or 3% for cases and controls, respectively. True data sets were analyzed with a standard model (M1), and noisy data sets were analyzed with threshold models either ignoring (M2) or contemplating (M3) misclassification.

Materials and methods

The methodology first presented by Rekaya et al28 and later extended and applied by Smith et al2 was adopted in this study to analyze binary data subject to misclassification where the probability of miscoding is different between cases and controls. In the presence of misclassification, the vector of observed binary responses y = (y₁, y_′, …y_n)′ measured on n individuals (eg, clinical diagnosis for a disease) is considered a “contaminated” sample of a real unobserved responses vector r = (r₁, r₂, …, r_n)′. The contamination could be due to several reasons including less than perfect sensitivity and specificity of a test or misdiagnosis by a clinician. Additionally, the n individuals are assumed to be genotyped for a set of single nucleotide polymorphisms (SNPs). Assessing the association between the genotyped SNPs and the trait (eg, disease status) is challenging because only the noisy data are observed. It gets even more complex when misclassification occurs with different rates for cases (false-negative rate) and controls (false-positive rate) as it is likely to be the situation with real data sets. Contrary to a common misclassification rate for both cases and controls assumed by Rekaya et al28 and Smith et al,2 specific misclassification rates for each outcome were adopted in this study, and to the best of our knowledge, this is the first time such distinction was assumed. Assuming misclassification happens with probability π₁ (probability of false negatives) and π₂ (probability of false positives) for cases and controls, respectively, the conditional joint distribution of the observed noisy data is:

$$\begin{array}{l}\mathit{y}|p_i,{\pi }_1,{\pi }_2={\displaystyle \prod _{i=1}^n{\left[(1-{\pi }_1)p_i+{\pi }_2(1-p_i)\right]}^{y_i}}\\ {\left[{\pi }_1{p}_i+(1-{\pi }_2)(1-p_i)\right]}^{(1-y_i)}\\ ={\displaystyle \prod _{i=1}^n{q_i}^{y_i}{\left(1-q_i\right)}^{(1-y_i)}}\end{array}$$

with q_i = [(1−π₁)]p_i + π₂(1−p_i)] and p_i is the probability of the Bernoulli process generating the true unobserved binary response r_i.

Note that when there is no misclassification (π₁ = π₂ = 0), then as expected, q_i is equal to q_i. In our case, the probability p_i was assumed to be a function of the SNP effects (β). Assuming that the true unobserved data, r, is conditionally independent given β:

$$\mathrm{Pr}(\mathit{r}|\mathit{\beta })={\displaystyle \prod _{i=1}^n{p}_i{\left(\mathit{\beta }\right)}^{r_i}}{\left[(1-p_i(\mathit{\beta })\right]}^{(1-r_i)}$$

where p_i (β) indicates that p_i is a function of β (vector of SNP effects).

Let $\mathit{a}={\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{n_1}\right)}^{\prime }$ be a vector of indicator variables for the n₁ case observations, where α_i = 1 if is switched from case (e.g. sick) to control (e.g. healthy) and α_i = 0 otherwise. Similarly, let $\mathbf{\lambda }={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{n_2}\right)}^{\prime }$ be a vector of indicator variables for the n₂ control observations, where λ_i = 1 if r_i is switched from control to case (from zero to one) and λ_i = 0 otherwise. Furthermore, each α_i and λ_i was assumed to be a Bernoulli trial with probability π₁ and π₂, respectively.

$$\begin{array}{l}{\alpha }_i{|{\pi }_1={{\pi }_1}^{{\alpha }_i}\left(1-{\pi }_1\right)}^{(1-{\alpha }_i)}\\ {\lambda }_i{|{\pi }_2={{\pi }_2}^{{\lambda }_i}\left(1-{\pi }_2\right)}^{(1-{\lambda }_i)}\end{array}$$

Given β, π₁, and π₂, the true data (r), α, λ and are jointly distributed as:

$$\begin{array}{l}\mathrm{Pr}\left(\mathit{r},\mathit{a},\mathit{\lambda }|\mathit{\beta },{\pi }_1,{\pi }_2\right)={\displaystyle \prod _{i=1}^n{p}_i{\left(\mathit{\beta }\right)}^{r_i}{\left[(1-p_i(\mathit{\beta })\right]}^{(1-r_i)}}\\ {\displaystyle \prod _{i=1}^{n_1}{{\pi }_1}^{{\alpha }_i}{\left(1-{\pi }_1\right)}^{(1-{\alpha }_i)}}{\displaystyle \prod _{i=1}^{n_2}{{\pi }_2}^{{\lambda }_i}{\left(1-{\pi }_2\right)}^{(1-{\lambda }_i)}}\end{array}$$

where n₁ and n₂ are the number of cases and controls, respectively. A in the previous equation, the first term in the right hand side is the likelihood of the true data. Unfortunately, the true data r is not observed. However, based on the assumed misclassification process, the relationship between y (noisy data) and r (unobserved true data) could be easily established as:

$$\{\begin{array}{c}{r}_i=(1-{\alpha }_i)y_i+{\alpha }_i(1-y_i)\text{if}{r}_i\text{is a case}\\ r_i=(1-{\lambda }_i)y_i+{\lambda }_i(1-y_i)\text{if}{r}_i\text{is a control}\end{array}$$ (1)

Notice that when a_i(λ_i) = 0 (no misclassification), the equations in (1) reduce to r_i = y_i.

Using the equalities in Equation (1), the likelihood of the true data could be expressed as a function of the observed noisy data y, α, and λ. Thus, the joint distribution of the observed data (y), α, and λ is easily obtained as:

$$\begin{array}{l}\mathrm{Pr}\left(\mathit{y},\mathit{\alpha },\mathit{\lambda }|\mathit{\beta },{\pi }_1,{\pi }_2\right)={\displaystyle \prod _{i=1}^{n_1}{{\pi }_1}^{{\alpha }_i}{\left(1-{\pi }_1\right)}^{(1-{\alpha }_i)}{p}_i{\left(\mathit{\beta }\right)}^{(1-{\alpha }_i)y_i+{\alpha }_i(1-y_i)}}\\ {\left[(1-p_i\left(\mathit{\beta }\right)\right]}^{[1-(1-{\alpha }_i)y_i+{\alpha }_i(1-y_i)]}\\ {\displaystyle \prod _{i=1}^{n_2}{{\pi }_2}^{{\lambda }_i}{\left(1-{\pi }_2\right)}^{(1-{\lambda }_i)}{p}_i{\left(\mathit{\beta }\right)}^{(1-{\lambda }_i)y_i+{\lambda }_i(1-y_i)}}\\ {\left[(1-p_i\left(\mathit{\beta }\right)\right]}^{[1-(1-{\lambda }_i)y_i+{\lambda }_i(1-y_i)]}\end{array}$$ (2)

Finally, prior distribution was specified for all unknown parameters

$$\begin{array}{c}\mathit{\beta }~u[{\mathit{\beta }}_{\mathit{min}},{\mathit{\beta }}_{\mathit{max}}];{\pi }_i|a_1,b_1~\mathit{\text{Beta}}(a_1,b_1);\\ {\pi }_2|a_2,b_2~\mathit{\text{Beta}}(a_2,b_2)\end{array}$$ (3)

where β_min, β_max, a₁, b₁, a₂, and b₂ are known hyper-parameters.

The joint posterior distribution of all unknown parameters is easily obtained as the product of Equations 2 and 3.

$$\begin{array}{l}\mathrm{Pr}\left(\mathit{\alpha },\mathit{\lambda }\mathit{\beta },{\pi }_1,{\pi }_2|\mathit{y}\right)={\displaystyle \prod _{i=1}^{n_1}{{\pi }_1}^{{\alpha }_i}{\left(1-{\pi }_1\right)}^{(1-{\alpha }_i)}{p}_i{\left(\mathit{\beta }\right)}^{(1-{\alpha }_i)y_i+{\alpha }_i(1-y_i)}}\\ {\left[(1-p_i\left(\mathit{\beta }\right)\right]}^{[1-(1-{\alpha }_i)y_i+{\alpha }_i(1-y_i)]}\\ {\displaystyle \prod _{i=1}^{n_2}{{\pi }_2}^{{\lambda }_i}{\left(1-{\pi }_2\right)}^{(1-{\lambda }_i)}{p}_i{\left(\mathit{\beta }\right)}^{(1-{\lambda }_i)y_i+{\lambda }_i(1-y_i)}}\\ {\left[(1-p_i\left(\mathit{\beta }\right)\right]}^{[1-(1-{\lambda }_i)y_i+{\lambda }_i(1-y_i)]}\\ p({\pi }_1|a_1,b_1)p({\pi }_1|a_1,b_1)\end{array}$$ (4)

Following Rekaya et al28 and Smith et al,2 a data augmentation algorithm was used to implement the model in (4). A liability threshold model was used with the following relationship between the binary response and a non-observed continuous random variable, l_i:

$$y_i=\{\begin{array}{cc}1& \mathit{\text{if}}{l}_i>T\\ 0& \text{otherwie}\end{array}$$

with T being a subjectively specified threshold value.

At the liability scale, the model can be presented as:

$$l_i=\mu +{\displaystyle {\sum }_{j=1}^p{x}_{ij}{\beta }_j+e_i}$$ (5)

where l_i is the liability for individual i, x_ij is the genotype for marker j, μ is an overall mean, β_j is the effect of marker j and e_i is a white noise. For identifiability reasons, the residual variance, var (e_i), and the threshold, T, were set arbitrarily to 1 and zero, respectively.

Full conditional distributions needed for implementation using Gibbs sampler are normal for μ and β and binomial for each elements of the vectors a and λ

$$\begin{array}{c}p({\alpha }_i|\mathit{\beta },{\pi }_1,{\mathit{\alpha }}_{-\mathit{i}},\mathit{y})\propto {{\pi }_1}^{{\alpha }_i}{\left(1-{\pi }_1\right)}^{(1-{\alpha }_i)}{\left[p_i(\mathit{\beta })\right]}^{(1-{\mathit{\alpha }}_{\mathit{i}}){\mathit{y}}_{\mathit{i}}+{\mathit{\alpha }}_{\mathit{i}}(1-{\mathit{y}}_{\mathit{i}})}\\ {\left[1-p_i(\mathit{\beta })\right]}^{(1-(1-{\mathit{\alpha }}_{\mathit{i}}){\mathit{y}}_{\mathit{i}}+{\mathit{\alpha }}_{\mathit{i}}(1-{\mathit{y}}_{\mathit{i}}))}\\ p({\lambda }_i|\mathit{\beta },{\pi }_2,{\mathit{\lambda }}_{-\mathit{i}},\mathit{y})\propto {{\pi }_2}^{{\lambda }_i}{\left(1-{\pi }_2\right)}^{(1-{\lambda }_i)}{\left[p_i(\mathit{\beta })\right]}^{(1-{\mathit{\lambda }}_{\mathit{i}}){\mathit{y}}_{\mathit{i}}+{\mathit{\lambda }}_{\mathit{i}}(1-{\mathit{y}}_{\mathit{i}})}\\ {\left[1-p_i(\mathit{\beta })\right]}^{(1-(1-{\mathit{\lambda }}_{\mathit{i}}){\mathit{y}}_{\mathit{i}}+{\mathit{\lambda }}_{\mathit{i}}(1-{\mathit{y}}_{\mathit{i}}))}\end{array}$$

where a_−i and λ_−i are the indicator vectors for the cases and controls without the position i.

For the misclassification probabilities, their conditional distributions are proportional to:

$$\begin{array}{l}p({\pi }_1|\mathit{\beta },\mathit{\alpha },\mathit{y})\propto {\pi }_1^{(a_1-1)}{\left(1-{\pi }_1\right)}^{(b_1-1)}{\displaystyle \prod _{\mathit{i}=1}^{{\mathit{n}}_1}{\pi }_1^{{\alpha }_i}{\left(1-{\pi }_1\right)}^{(1-{\alpha }_i)}}\\ p({\pi }_2|\mathit{\beta },\mathit{\alpha },\mathit{y})\propto {\pi }_2^{(a_2-1)}{\left(1-{\pi }_2\right)}^{(b_2-1)}{\displaystyle \prod _{\mathit{i}=1}^{{\mathit{n}}_2}{\pi }_2^{{\lambda }_i}{\left(1-{\pi }_2\right)}^{(1-{\lambda }_i)}}\end{array}$$

Thus, π₁ and π₂ are distributed as Beta (a₁ + Σa_i, n₁ + b₁ − Σa_i) and Beta (a₁ + Σa_i, n₁ + b₁ − Σa_i) with Σa_i and Σλ_i being the total number of misclassified (switched) cases and control observations, respectively. It is worth mentioning that because the number of true cases and controls was unknown, n₁ and n₂ were set equal to the number of observed cases and controls in the first round of the iterative process and then updated to the estimated number of cases and controls thereafter.

Simulation

Typical case–control type data sets were simulated using PLINK software.30 Each data set consisted of 2000 individuals (1000 cases and 1000 controls) genotyped for 1000 common SNPs (minor allele frequency >0.05). Randomly, 15% of the SNPs were assumed to be in association with a binary response trait and the remaining 850 SNPs were considered noninfluential. The odds ratios (ORs) for the influential 150 SNPs were assigned based on the following two scenarios. A moderate scenario where 25, 35, and 90 markers of the 150 influential SNPs were assumed to have ORs of 1:4, 1:2, and 1:1.8, respectively. An extreme scenario where ORs of 1:10, 1:4, and 1:2 were specified for 25, 35, and 90 markers of the 150 influential SNPs, respectively. For each individual, a liability (quantitative phenotype) was generated as the sum of the effect of the disease SNPs and random white noise. Binary status for the simulated disease traits was assigned based on a median split of the continuous phenotype. Misclassification was artificially introduced by switching the true binary status. Randomly 5% or 7% of the cases and 0% or 3% of the controls were miscoded. To some extent, the simulated binary data mimic a clinical data generated by a test with a sensitivity of 0.95 or 0.93 and a specificity of 1 or 0.97. Furthermore, different levels of genetic complexity of the simulated response were assumed through the OR of the influential SNPs.

For two levels of miscoding for cases and controls (5% and 0% or 7% and 3%) and two OR distribution (moderate OR and extreme OR), the following data sets were simulated: 5% and 0% miscoding rates and moderate OR (D1) or extreme OR (D2); 7 and 3% miscoding rates and moderate OR (D3) or extreme OR (D4). Five replicates were simulated for each data set.

Results and discussion

To evaluate the capability of the method to identify miscoded and correctly classified observations, the posterior means (averaged over five replicates) of the true misclassification probabilities for both cases and controls were calculated. Except for scenarios where misclassification was set at 0%, misclassification probabilities were slightly underestimated but still fell within their respective 95% highest posterior density interval (Table 1). For example, when moderate ORs of the influential SNPs were used, posterior means were 0% and 4%, and 5 and 2% for D1 and D3, respectively. However, as the OR was increased for the extreme cases, these means increased to 0% and 5% (D2) and 6% and 2% (D4). Although our algorithm was designed to anticipate and account for potential misclassification, a null data set was run with no coding errors to ensure its ability to indicate no misdiagnostic errors. As expected, this analysis resulted in misclassification probabilities close to zero, with estimates of 0.001 and 0.002.

Table 1.

Summary of the posterior distribution of the misclassification probability (π) for the four simulation scenarios (averaged over five replicates)

True		Moderate*				Extreme
		PM		PSD		PM		PSD
π1	π2	π1	π2	π1	π2	π1	π2	π1	π2
5%	0%	0.04	0.002	0.006	0.0003	0.05	0.002	0.006	0.0003
7%	3%	0.05	0.02	0.008	0.004	0.06	0.02	0.007	0.004

Note:

^*Moderate effects for influential single nucleotide polymorphisms.

Abbreviations: PM, posterior mean; PSD, posterior standard deviation.

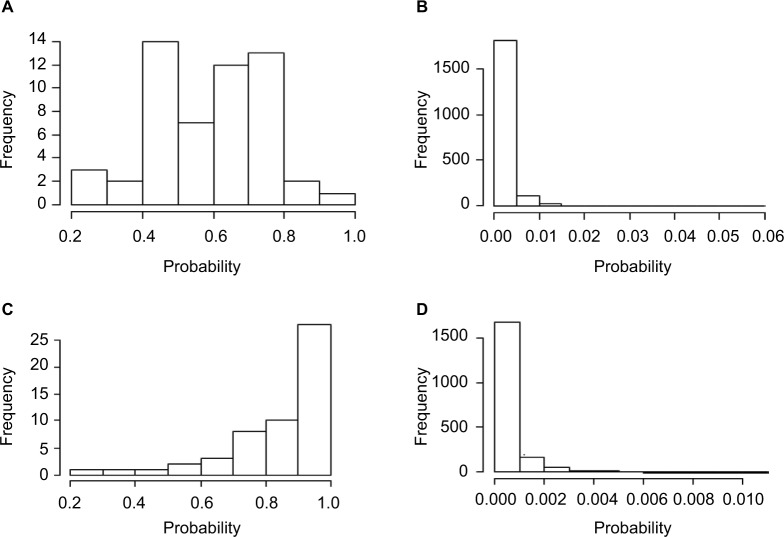
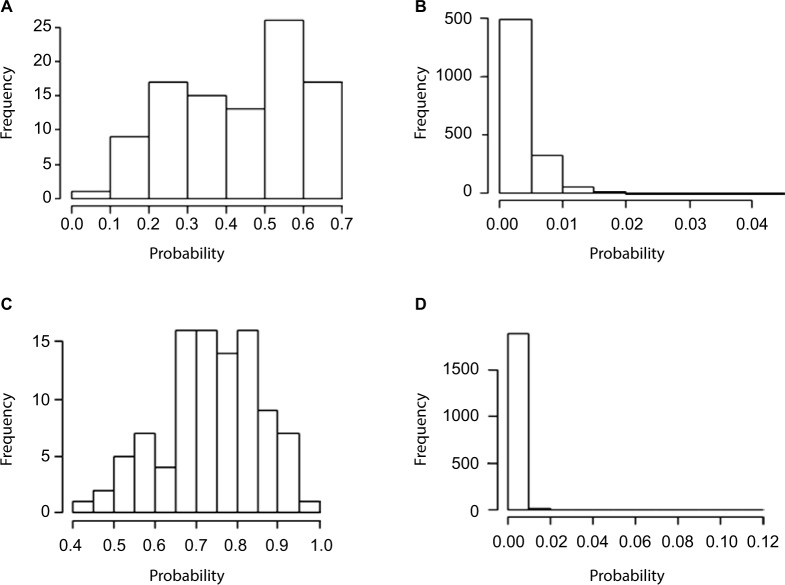
Adequate sample size is one of the major contributing factors to obtain sufficient power of GWAS. Thus, it would be beneficial to identify and correct misclassified samples rather than removing them from the study. Therefore, to continue evaluating the effectiveness of the proposed method to detect miscoded individuals, the posterior probability of an observation being misclassified was calculated (averaged over five replicates) in all four scenarios. With moderate OR and misclassification rates set to 5% for cases and 0% for controls, the 54 miscoded observations exhibited higher misclassification probability with an average of 0.58 (Figure 1A) compared to an average of 0.002 for the 1946 observations of the correctly coded group (Figure 1B). As the odds are increased for the extreme scenario (D2), the distinction became more evident. In fact, the average posterior misclassification probability of the 54 miscoded observations increased to 0.85 (Figure 1C) compared to 0.006 for the correctly coded group (Figure 1D). This is of importance as it shows our method is able to detect miscoded samples with higher probability compared to correctly coded observations. In fact, the smallest misclassification probability of the miscoded observations was 0.28 (Figure 1A) which was substantially higher than 0.06 (Figure 1B), the largest probability observed for the correctly coded group (D1). Similar estimates were obtained when misclassification rates increased to 7% for cases and 3% for controls (Figure 2). For D3 (D4), the average posterior misclassification probability was 0.43 (0.74) and 0.003 (0.002), for the miscoded (Figure 2A and C) and correctly coded (Figure 2B and D) groups, respectively.

Figure 1.

Average posterior misclassification probability for the 54 miscoded observations (A: moderate and C: extreme) and the 1946 correctly coded observations (B: moderate and D: extreme) when the misclassification rates were set to 5% and 0%.

Figure 2.

Average posterior misclassification probability for the 98 miscoded observations (A: moderate and C: extreme) and the 1902 correctly coded observations (B: moderate and D: extreme) when the misclassification rates were set to 7% and 3%.

Outside of a controlled study, there is no indication for which individuals are misdiagnosed. Thus, it is useful to evaluate the performance of the method when a subjective or heuristic criteria are used to declare misclassified samples. The results of using two cutoff values for the probability of misclassification to declare an observation as misclassified are presented in Table 2 (averaged over five replicates). Using our proposed method with a hard cutoff (p=0.5), 65 (D1) and 94% (D2) of the 54 truly miscoded samples were correctly identified. When the rate of misclassification increased to 7% for cases and 3% for controls, of the 98 miscoded observations 44 (D3; moderate OR) and 97% (D4; extreme OR) were correctly detected. Despite the rigidness of the hard cutoff approach (little variability around the designated probability), our procedure was still efficient in identifying considerable amount of misclassified observations. Once the restrictions of the cutoff probability were relaxed (cutoff value was set equal to the average of all samples misclassification probability plus two standard deviations), ~100% of the miscoded samples were identified across all scenarios except for D3 where 86% were detected. Across both cutoff probabilities for the two scenarios where the overall misclassification rate was 10%, there was a higher detection in cases than controls. This is potentially the result of higher misclassification rate in cases compared to controls; 7% versus 3%. Using real clinical data, it will be recommended to use both the classification criteria to assess the misclassification status of a sample. Additionally, other clinical information (eg, medical history) could be helpful in some cases.

Table 2.

Percent of misclassified individuals correctly identified on the basis of two cutoff probabilities across the four simulation scenarios

Cutoff probability	D1		D2		D3		D4
	Misclass	Correct	Misclass	Correct	Misclass	Correct	Misclass	Correct
Hard	0.65	0	0.94	0	0.44	0	0.97	0
Soft	1.00	0	0.98	0	0.86	0	1.00	0

Notes: Hard: cutoff probability was set at 0.5. Soft: cutoff probability was equal to the overall mean of the probabilities of being misclassified over the entire data set plus two standard deviations. Misclass: individuals who were misclassified. Correct: correctly coded individuals. The following data sets were simulated: 5% and 0% miscoding rates and moderate OR (D1) or extreme OR (D2); 7 and 3% miscoding rates and moderate OR (D3) or extreme OR (D4).

Abbreviation: OR, odds ratio.

In GWAS, the association between thousands of genetic variants and a phenotype is evaluated in hope of elucidating the biology of complex traits. In this instance, there is a need for unbiased and accurate identification of relevant polymorphisms. In order to assess the consequences of the presence of misclassified samples on estimating effects, the correlation between estimates of SNP effects obtained using the true (M1) and the miscoded data (M2 and M3) were calculated. For all four scenarios, the proposed approach (M3) was capable of increasing the correlation compared to the “contaminated” data (M2; Table 3). For example, for scenarios when OR of the influential SNPs were moderate, accuracies increased by 8% for D1 and 12% for D3. As the OR increased for the extreme scenarios, the same trend was observed but correlations increased by a more substantial amount. When misclassification rates were 5% and 0%, correlation increased by 0.134 and 0.217 for D2 and D4, respectively (Table 3). This indicates the ability of the method to produce consistent results and to decrease potential misclassification bias on the estimation of SNP effects. This result is important for the dissection of the genetic basis of complex traits using potentially noisy clinical data. This is the case because even without knowing the misclassification rate or the misclassified observations, the proposed method was able to enhance the signal of truly influential SNPs.

Table 3.

Correlation between true^* and estimated SNP effects under four simulation scenarios using noise data analyzed with threshold models either ignoring (M2) or contemplating (M3) misclassification

Model	5% and 0%		7% and 3%
	Moderate**	Extreme	Moderate	Extreme
M2	0.894	0.777	0.807	0.675
M3	0.969	0.911	0.907	0.892

Notes:

^*True effects were calculated based on analysis of the true data (M1).

^**Moderate effects for influential SNPs. M1: true data analyzed with a standard model. M2: noisy data analyzed with threshold model ignoring misclassification. M3: noisy data analyzed with threshold model contemplating misclassification (proposed method).

Abbreviation: SNP, single nucleotide polymorphism.

The effect sizes of SNPs with true association to the phenotype should be larger in magnitude compared to non-causal SNPs. The ranking of the SNPs was observed by monitoring the most influential top 10%, and in the presence of misclassified observations (M2), the noninfluential SNPs tended to have non-zero estimates. Using scenario D4 (ignoring misclassification), eight out of the 15 most influential SNPs were not accounted for. After correction, our method (M3) was able to capture 11 out of the 15 SNPs resulting in an increase of 20% in the power of association. Even in the modest case, when misclassification rates were set at 5% for cases and 0% for controls with moderate OR of the disease associated SNPs, M2 caused a loss of 20% in power but our method reduced it to 7%. The inability to identify large portion of the most influential SNPs in the presence of misclassification will undoubtedly have negative effects on GWAS studies. In fact, it will reduce the efficiency of genomic classifiers used in diagnostics and prediction, and it will hamper the ability to identify causal genes.

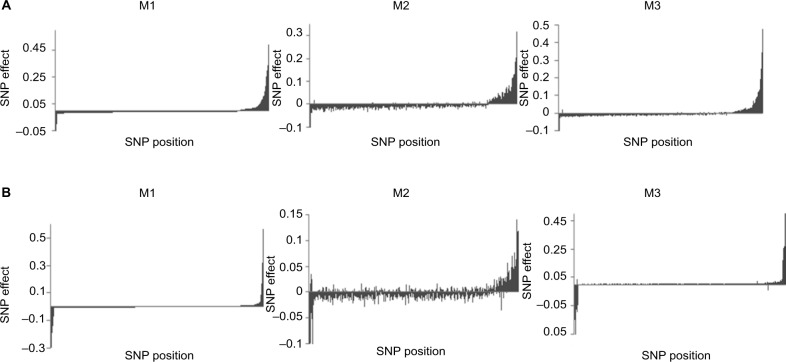
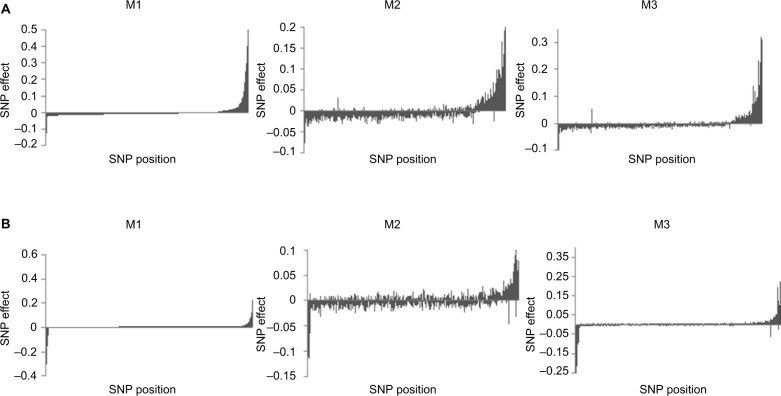
As previously mentioned, a change in rankings of the SNPs was noticed; hence, errors in estimation due to data misclassification were further investigated by examining the magnitude of the SNP effects. Based on their estimates when no misclassification was present (M1), SNP effects were ordered in decreasing order. For scenarios D1 (Figure 3A) and D2 (Figure 3B), it is evident that M2 was not able to capture the true magnitude and direction of the SNP effects when compared to our proposed method (M3). This distinction became more evident when we increased the misclassification rates to 7% for cases and 3% for controls (Figure 4). In fact, imprecise phenotyping leading to reduced estimates of effect sizes is reported as one of the limitations of GWAS.31 Accumulation of erroneous estimates from selection of nonsignificant SNPs leads to biased estimates of genetic parameters, including the variance explained by SNPs, true genetic correlations between disorders, and lower estimates of heritability.32–34 The negative effects of misclassification are expected to increase with the genetic complexity of the trait due to the increase in risk variants.35

Figure 3.

Distribution of SNP effects for 5% and 0% misclassification rates. The effects are sorted in decreasing order based on estimates using M1 when odds ratios of influential SNPs are moderate (A) and extreme (B). M1: true data analyzed with a standard model. M2: noisy data analyzed with threshold model ignoring misclassification. M3: noisy data analyzed with threshold model contemplating misclassification (proposed method).

Abbreviation: SNP, single nucleotide polymorphism.

Figure 4.

Distribution of SNP effects for 7% and 3% misclassification rates. The effects are sorted in decreasing order based on estimates using M1 when odds ratios of influential SNPs are moderate (A) and extreme (B). M1: true data analyzed with a standard model. M2: noisy data analyzed with threshold model ignoring misclassification. M3: noisy data analyzed with threshold model contemplating misclassification (proposed method).

Abbreviation: SNP, single nucleotide polymorphism.

Conclusion

High false-positive and false-negative rates of discrete responses are unavoidable for some disease traits, and correcting misclassified observations is difficult, time-consuming, and often costly to remedy. Ignoring these errors increases the uncertainty of identifying relevant associations, thus decreasing the accuracy in estimating the magnitude and direction of variant effects. This in turn will lead to an increase of false-positive results as noninfluential SNPs will tend to have inflated estimates. The proposed method was able to identify with high probability miscoded samples in both cases and controls. Cases tended to have higher probabilities than controls in part due to having a higher prevalence of being misclassified.

Our proposed method increased the accuracy of estimated SNP effects in the presence of “noisy” data which will aid in decreasing the rate of non-replicative results. Furthermore, it will reduce the false association between genetic variants and the disease of interest. It will lead to an increase in predictive power and a reduction in bias caused by classification errors. Our procedure performed well even when one of the misclassification rates was set to zero which is important when diagnostic procedures have either a high sensitivity or a high specificity. Based on the results of this simulation study, it seems reasonable to conclude that the proposed method will be effective in reducing or eliminating the negative effects of misclassification in association with the analyses of binary responses subject to outcome-specific error rates. Although the results of this studies are based on simulated OR values that are relatively high even in the moderate scenario, preliminary results from an