Pseudo Maximum Likelihood Approach for the Analysis of Multivariate Left-Censored Longitudinal Data

Abstract

The linear mixed effects model based on a full likelihood is one of the few methods available to model longitudinal data subject to left-censoring. However, a full likelihood approach is complicated algebraically due to the large dimension of the numeric computations, and maximum likelihood estimation can be computationally prohibitive when the data are heavily censored. Moreover, for mixed models, the complexity of the computation increases as the dimension of the random effects in the model increases. We propose a method based on pseudo likelihood that simplifies the computational complexities, allows a wide class of multivariate models, and that can be used for many different data structures including settings where the level of censoring is high. The motivation for this work comes from the need for a joint model to assess the joint effect of pro-inflammatory and anti-inflammatory biomarker data on 30-day mortality status while simultaneously accounting for longitudinal left- censoring and correlation between markers in the analysis of Genetic and Inflammatory Markers for Sepsis (GenIMS) study conducted at the University of Pittsburgh. Two markers, interleukin-6 (IL-6) and interleukin-10 (IL-10) which naturally are correlated because of a shared similar biological pathways and are left-censored because of the limited sensitivity of the assays, are considered to determine if higher levels of these markers is associated with an increased risk of death after accounting for the left-censoring and their assumed correlation.

1. INTRODUCTION

Medical studies collect biomarker data to gain insight into the biological mechanisms underlying both acute and chronic diseases. These markers may be obtained at a single point in time to aid in the diagnosis of an illness or may be collected longitudinally to provide information on the relationship between changes in a given biomarker as it relates to the course of the illness. While there are many different biomarkers presented in the medical literature there are not as many studies that examine the relationship between multiple biomarkers, measured longitudinally, and predictors of interest. One example of such studies is the HIV literature where CD4 counts and viral loads are jointly modeled over time (Thiebaut, et al [1]).

Analysis of biomarker data has been important in understanding the relationship between markers of inflammation and the development of sepsis in the Genetic and Inflammatory Markers of Sepsis (GenIMS) study [2] conducted at the University of Pittsburgh. The study enrolled 2320 subjects with community acquired pneumonia through the emergency department of 28 hospitals in southwestern Pennsylvania, Connecticut, Michigan and Tennessee between 2001 and 2003. A battery of inflammatory markers were measured throughout the course of hospitalization in the cohort and subjects were followed for a period of one year to study the relationship between the trajectories of the pro-inflammatory and anti-inflammatory markers and the risk of death and development of sepsis. There was a need for statistical methods that can accommodate multiple longitudinal biomarkers accounting simultaneously for left-censoring and correlation between the markers, rather than relying on a series of separate longitudinal models for each biomarker.

We are interested in studying the association of levels of IL-6 (anti-inflammatory marker) and IL-10 (pro-inflammatory marker) and mortality while accounting for left-censoring and correlation between the markers. A large percentage of both IL-6 and IL-10 are left-censored due to the sensitivity of the assays. The assays used to measure the concentration of the biomarkers were not sensitive enough to detect levels of the molecule at the low end of normal, resulting in moderate to heavy left-censoring of the biomarker. These two markers are also naturally correlated because they share similar biological pathways.

While there are methods available for the analysis of left censored outcome data in the statistical literature, there are limited methods that can handle multivariate truncated longitudinal data when multiple outcomes need to be studied simultaneously. To address the issue of truncation when modeling data, researchers have proposed either the use of imputed values or the development of methods to handle the censoring directly. Imputing the lower quantification limit (Keet et al, [3]) or half of this limit (O’Brien et al,[4]) to substitute for the censored value and use of random imputation procedures (Paxton et al, [5]) are the most frequently used approaches. All of these naive approaches produce estimates with a substantial bias and they do not adjust the standard errors of the estimates for the loss of information due to censoring (Ghebregiorgis and Weissfeld [6]). Hughes [7], Jacqmin-Gadda et al, [8], and Lyles et al [9] proposed methods that handle left-censored measures, however all of these methods are restricted to a longitudinal model with a single outcome and it is difficult to extend them to handle multiple outcomes. In addition, since all of these methods are based on a full likelihood, they involve numeric and algebraic complexities that require the evaluation of a series of multiple integrals and become computationally prohibitive for data with a high rate of censoring. The computations become even more unstable for models with more than two random effects, leading to convergence issues when the current methodology is applied.

We propose a method that addresses the weaknesses of the current methodology for multivariate longitudinal models with left censored outcome data. The two major weaknesses, computational complexity and model instability, are addressed by applying the method of pseudo-likelihood. Using the pseudo-likelihood the estimation problem is broken into two separate steps with estimation of the parameters associated with the covariance taking place in step 1 and then estimating the remaining parameters, based on the modified likelihood, occurring in step 2. The proposed pseudo-likelihood method considerably reduces the computational burden associated with the current methods and is much more stable while preserving the properties of the original estimators.

We present the proposed methodology in section 2, where the multivariate linear mixed model is discussed in section 2.1 and the pseudo-likelihood for left-censored data is developed in section 2.2. Computational details are given in section 2.4 and a simulation study, conducted to assess the performance of the proposed model, is summarized in section 3. The proposed method is applied to analyze the GenIMS data, and results of these methods are compared with results obtained using existing methods in section 4. Finally we give a brief discussion and concluding remarks in section 5.

2. PROPOSED METHODOLOGY

2.1. Multivariate Linear Mixed Effects Model

Let k be the number of outcomes in the model; it will be assumed that each of the k longitudinally measured outcomes can be modeled using the mixed model. Let $Y_i={[Y_i^1,Y_i^2,\dots ,Y_i^K]}^T$ be the response vector for subject i (i = 1, … ,N), where Y_i^k is the n_i^k × 1 vector of measurements for marker k (k = 1, … , K).

For simplicity we present the bivariate case (k=2) in this section.

Let $Y_i=\left[\begin{array}{c}\hfill Y_i^1\hfill \\ \hfill Y_i^2\hfill \end{array}\right]$ be the response vector for subject i, for i=1, … , N and $Y_i^k$ be the $n_i^k$ vector of measurements of marker k (k=1,2), where $n_i=n_i^1+n_i^2$. Let $\beta =\left[\begin{array}{c}\hfill {\beta }^1\hfill \\ \hfill {\beta }^2\hfill \end{array}\right]$ be a p × 1 vector of population parameters, known as fixed effects, and X_i be a known n_i × p design matrix of covariate variables linking β to Y_i. Let ${\gamma }_i=\left[\begin{array}{c}\hfill {\gamma }_i^1\hfill \\ \hfill {\gamma }_i^2\hfill \end{array}\right]$ be a q × 1 vector of subject-specific parameters, known as random effects and Z_i a known n_i × q design matrix of covariates linking γ_i to Y_i.

The fixed effect design matrix is not restricted to assume the use of the same set of predictors for both outcomes. The random effect design matrix can also use different models for the two outcomes.

For multivariate normal data we extend the linear mixed model proposed by Laird and Ware [10]:

$$Y_i=X_i\beta +Z_i{\gamma }_i+{ϵ}_i,$$ (1)

as in Schafer [11] and Bandyopadhyay et.al. [12] with the assumption that the n_i-dimensional vector Y_i satisfies

$$Y_i\mid {\gamma }_i~N(X_i\beta +Z_i{\gamma }_i,{\Sigma }_i),$$

where γ_i and ϵ_i are assumed to be mutually independent with ϵ_i ~ N(0,Σ_i), γ_i ~ N (0,G) and Σ_i is the n_i × n_i covariance matrix of measurement errors, which is a diagonal matrix containing the two elements of the measurement error of each marker, that depends on i only through its dimension n_i, and G is the covariance matrix of the random effects given by:

$$G=\left[\begin{array}{cc}\hfill G^1\hfill & \hfill G^{12}\hfill \\ \hfill {G^{12}}^{\prime }\hfill & \hfill G^2\hfill \end{array}\right],$$

which is partitioned into four sub-matrices: G¹ is the covariance matrix including variance and covariance of random effects for the frst marker, G² the covariance matrix including variance and covariance of random effects of the second marker and G¹²= G^21′ is the matrix of covariances between random effects of each marker. The correlation between the two markers can be studied through the matrix G¹²

Thus the set of unknown parameters in Σ_i will not depend on i. Marginally, the Y_i are independent normals with mean μ = X_iβ and covariance matrix $V_i=\text{Var}\left(Y_i\right)=Z_{i}G{Z}_i^T+{\sum }_i$.

2.2. Standard Likelihood

Let Θ = (β, η) denote the parameter space, where β is the vector of fixed effect parameters and η is the vector of covariance matrix parameters. Then the model in (1) can be rewritten as

$$Y_i=f(X,ϴ)+{ϵ}_i,$$ (2)

where X is the design matrix of the model.

For the i^th, subject each variables value is either observed, censored or missing (missing values are assumed to be missing completely at random and hence doesn’t contribute anything to the likelihood function). Using the notation from section 2.1, and letting $Y_i^o$ denote the $n_i^o$-vector of observed outcomes, $Y_i^c$ the $n_i^c$-vector of censored outcomes and c_i the $n_i^c$-vector of censoring threshold for subject i, the likelihood function is given by

$$L(\beta ,\eta )=L(ϴ)=\prod _{i=1}^N{f}_{Y_i^o\mid ϴ}(Y_i^o\mid ϴ)Pr(Y_i^c<c_i\mid Y_i^o,ϴ).$$

The matrix X_i, vector Y_i, and the covariance matrix V_i in section 2.1 can be partitioned into observed and censored components as

$$X_i=\left[\begin{array}{c}\hfill X_i^o\hfill \\ \hfill X_i^c\hfill \end{array}\right],Y_i=\left[\begin{array}{c}\hfill Y_i^o\hfill \\ \hfill Y_i^c\hfill \end{array}\right],V_i=\left[\begin{array}{cc}\hfill V_i^o\hfill & \hfill V_i^{co}\hfill \\ \hfill V_i^{c{o}^{\prime }}\hfill & \hfill V_i^c\hfill \end{array}\right].$$

From model (1), $Y_i^o$ has a multivariate normal probability density $f{Y}_i^o$, and using properties of the multivariate normal distribution it follows that the conditional distribution of $Y_i^c$ given $Y_i^o$ is normally distributed (Billingsley [26], Casella and Berger [28]) with the following mean and variance expressions respectively:

$${\mu }_i^{c\mid o}=X_i^c\beta +{\eta }_i^{co}{{\eta }_i^o}^{-1}[Y_i^o-{\mu }_i^o].$$

$$V_i^{c\mid o}={\eta }_i^c-{\eta }_i^{co}{{\eta }_i^o}^{-1}{{\eta }_i^{co}}^T.$$

where η_i = V_i(η).

Let the multivariate normal distribution function of the conditional distribution of $Y_i^c$ given $Y_i^o$ be denoted by ${\Phi }_i^{c\mid o}$, then the likelihood function can be rewritten as:

$$\begin{array}{cc}\hfill L(ϴ)& =\prod _{i=1}^N{f}_{Y_i^o\mid ϴ}(Y_i^o\mid ϴ){\Phi }_i^{c\mid o}(c_i\mid ϴ)\hfill \\ \hfill & =\prod _{i=1}^N\frac{1}{2\pi \sqrt{\mid {\eta }_i^o\mid }}{e}^{\left\{\frac{-1}{2{{\eta }_i}^o}{(Y_i^o-X\beta )}^T(Y_i^o-X\beta )\right\}}\hfill \\ \hfill & {\int }_{-\infty }^{c_{i1}}{\int }_{-\infty }^{c_{i2}}\cdots {\int }_{-\infty }^{{c_{in}}_i^c}\frac{1}{2\pi \sqrt{\mid {\eta }_i^{c\mid o}\mid }}{e}^{\left\{\frac{-1}{2{\eta }_i^{c\mid o}}{(u-{\mu }_i^{c\mid o})}^T(u-{\mu }_i^{c\mid o})\right\}}du,\hfill \end{array}$$ (3)

where u is an n^c vector.

Full likelihood based methods involve high dimensional multiple integration and require all parameters in the parameter space to be estimated simultaneously making the methods computationally complex and potentially unstable. To avoid the arduous process of estimating the multivariate normal cumulative distribution function for a large number of variables, we propose an alternate pseudo-likelihood method that improves efficiency with regards to computational time.

2.3. Pseudo Likelihood

The idea behind the pseudo maximum likelihood estimation (PMLE) method is to apply the maximum likelihood estimation (MLE) algorithm to a reduced system of likelihood equations instead of applying the MLE approach to all variables simultaneously. This methodology was used by Fieuws and Verbeke [13] to fit mixed models for multivariate longitudinal profiles by applying the MLE algorithm to pairs of variables and taking averages.

The general concept of the approach is to resolve the computational complexity of high- dimensional joint random-effects models by reducing the dimensionality of the problem. This is achieved by carrying out the estimation in two steps; in the first step instead of maximizing the likelihood of the full joint model, all pairwise bivariate models will be fitted separately, each of these pairwise model yields estimates, with classical optimal asymptotic properties, including consistency and asymptotic normality.

In a second step, the parameters obtained by fitting the pairwise models will be combined and averaged to obtain one single estimate for each parameter in the parameter space of the full joint model. Clearly, these averages are still asymptotically normally distributed with the correct parameter value as mean. Standard errors, however, do not directly follow from the mere combination of the individual results. Therefore, an additional step is needed to correctly calculate the sampling variability of the estimates resulting from the pairwise approach.

In this section we present the pseudo-likelihood approach using the notation in the previous sections and that of Fieuws and Verbeke [13]. Suppose we have data consisting of k variables measured on each of N independent subjects as defined in section 2.1. The number of pairs of variables is then given by $K=\frac{k(k-1)}{2}$. We can denote these K pairs of variables as (Y_·r, Y_·s) for r = 1,… ,k and s = 1,… ,k where r < s. Consider the log-likelihood involving the pair of variables (Y_·r, Y_·s) written as:

$${\mathcal{\ell }}_{rs}\left({\theta }_{rs}\right)=\sum _{i=1}^N{\mathcal{\ell }}_{irs}({\theta }_{irs}\mid Y_{ir},Y_{is})$$ (4)

where θ_rs represents the vector of all parameters in the bivariate joint mixed model corresponding to the specific pair (r, s). To simplify the notation further, let m = r + (s − 1)(s − 2)/2, so that ${\mathcal{\ell }}_{rs}\left({\theta }_{rs}\right)={\mathcal{\ell }}_m\left({\theta }_m\right)$, where m = 1, · · · , K.

Let θ be the stacked vector combining all pair-specific parameter vectors of individual MLEs (i.e. θ = [θ₁, θ₂, · · · , θ_K]^T . Thus maximization in the PMLE case will require maximizing the pseudo-likelihood function of the following form:

$$\mathcal{\ell }\left(\theta \right)=\sum _{m=1}^K{\mathcal{\ell }}_m\left({\theta }_m\right)$$ (5)

Which is the sum of K likelihood functions, so to maximize this likelihood function we simply need to maximize each of the K likelihood functions that are components (summands) of equation 5.

The PMLE, $\widehat{\theta }$ in the vector-valued parameter case is shown to be asymptotically normal (Geys et.al. [14]). However, to obtain consistent estimators and to account for the intra- correlation that may exist between the biomarkers, an appropriate adjustments is carried out by replacing the asymptotic covariance matrix by a robust estimator (the sandwich estimator).

The asymptotic multivariate normal distribution of the estimator for θ is given by

$$\sqrt{N}(\widehat{\theta }-\theta )\stackrel{d}{\to }MVN(0,A{\left(\theta \right)}^{-1}B\left(\theta \right)A{\left(\theta \right)}^{-1}),$$ (6)

where the matrix A(θ)⁻¹B(θ)A(θ)⁻¹ consists of variances and covariances of the estimated parameters. In the PMLE method only block-diagonal portions of this matrix need to be estimated i.e., variances and covariances of MLEs computed within pairs of variables, which are by-products of the full likelihood (MLE) method.The block-diagonal portions of this martix are given by:

$$A_{mm}=E\left\{-\frac{{\partial }^2{\mathcal{\ell }}_m}{\partial {\theta }_m\partial {\theta }_m^{\prime }}\right\},{\mathrm{B}}_{mn}=E\left\{\frac{\partial {\mathcal{\ell }}_m}{\partial {\theta }_m}\frac{\partial {\mathcal{\ell }}_n}{\partial {\theta }_n^{\prime }}\right\},$$

for m, n = 1, · · · , K and estimates are obtained by dropping the expectations and replacing the unknown parameters by their estimates

Our interest in the proposed method is to estimate Θ = (β, η), the vector of fixed effects parameters and covariance matrix parameters which can be calculated by taking averages over all pairs. Θ = Aθ, where A is the matrix that calculates the desired averages. Each row of A selects and averages all elements of θ corresponding to a specific parameter. Then $\widehat{ϴ}=\mathbf{A}\widehat{\theta }$ will produce the unique parameter estimates of interest with

$$\sqrt{N}(\widehat{ϴ}-\theta )~MVN(0,\mathbf{A}\Sigma \left(\widehat{ϴ}\right){\mathbf{A}}^{-1})$$

where $\Sigma \left(\widehat{ϴ}\right)$ is the covariance matrix for $\widehat{ϴ}$ obtained by using equation (6).

While the full multivariate method requires numerical calculation of the multivariate normal distribution function, the pseudo-likelihood method only needs to calculate the bivariate normal distribution function, where many software packages have inherent functions or packages for it.

2.4. Computation

We developed a SAS macro to obtain the pseudo-likelihood estimates of model parameters by maximizing the log pseudo likelihood in (4) or (5) using the dual Quasi-Newton optimization method in SAS Proc NLMIXED. The NLMIXED procedure provides improved ML estimates and unlike other procedures, it allows for the explicit modeling of random effects by allowing the user to write his/her own function. But NLMIXED does not have an option for adjusting standard errors, so we developed a macro that runs NLMIXED and calculates the corrected standard error using the robust(sandwich) estimator given in (6) (SAS macro and other codes developed are available up on request from the the corresponding author). Another limitation of the NLMIXED procedure is that it lacks a REPEATED statement and so has limited capacities for modeling the covariance structure of correlated data, however in modeling longitudinal data in which there is not a high degree of serial correlation this limitation may not be serious.

3. SIMULATION STUDY

A simulation study is conducted to explore the performance of the PMLE and compare it with the full likelihood methods. It is also used to verify that the proposed method produces unbiased estimators, to assess the accuracy of the standard errors obtained and to determine if there is any loss in efficiency compared to the full likelihood methods.

Data were generated as follows; for subject i = 1, … , N a binary variable is randomly generated using Bernoulli(0.5) and is assigned as a covariate value for each subject. For times of measurements, random numbers (similar to the GenIMS data measurement time) uniformly distributed between 1 and 5, were selected. Censored values were selected independent of time and subject after a detection limit is set to achieve a desirable proportion of left-censored data. The parameter values were selected to be close to those obtained from the GenIMS data:

$${\beta }^1=\left(\begin{array}{c}\hfill 0.70\hfill \\ \hfill -0.15\hfill \\ \hfill -0.2\hfill \\ \hfill 0.03\hfill \end{array}\right),and{\beta }^2=\left(\begin{array}{c}\hfill 0.50\hfill \\ \hfill -0.15\hfill \\ \hfill 0.15\hfill \\ \hfill 0.05\hfill \end{array}\right).$$

Using these specifications 1000 measurements of 200 subjects were simulated according two different models. A model with two random effects, one random slope for each response (marker)(model 7), and a model with 4 random effect (model 8)

$$Y_{ij}^k={\beta }_0^k+{\beta }_1^k{t}_{ij}+{\beta }_2^k{X}_i+{\beta }_3^k{t}_{ij}\ast X_i+{\gamma }_{1i}^k{t}_{ij}+{ϵ}_{ij},$$ (7)

$$Y_{ij}^k={\beta }_0^k+{\beta }_1^k{t}_{ij}+{\beta }_2^k{X}_i+{\beta }_3^k{t}_{ij}\ast X_i+{\gamma }_{0i}^k+{\gamma }_{1i}^k{t}_{ij}+{ϵ}_{ij}.$$ (8)

where β and γ are vectors, ε is a matrix as defined in section 2, and X_i is a binary covariate variable.

A binary variable X_i is used as a covariate and its effect over time is studied by including an interaction term in the model.

The proposed method is compared to two different existing full likelihood methods for efficiency and accuracy. The first method used for the comparison is a method proposed by Jacqumin-Gadda et.al [8], in which parameter estimation is carried out by maximizing the full likelihood using a Marquardt algorithm and other multiple iterative process. They used a FORTRAN program called CENSAD (and hence we labeled estimates obtained by this method as ML-CENSAD in the tables of results). The second method used for comparison is that of Thiebaut and Jacqmin-Gadda [23] which is also a full likelihood method, the authors used SAS proc NLMIXED procedure for maximization and hence estimates obtained by this method are labeled as ML-NLMIXED in the tables. Both of these methods are compared with the proposed method for computational time, efficiency and bias.

In Table I we present an efficiency comparison of the methods by reporting a summary of computation time for each method under both models (7) and (8). Estimating using the proposed PMLE takes significantly less time than the other two full likelihood based methods for both models.The two full likelihood methods took comparable time of estimation for the model with two random effects (model 7) with ML-CENSAD converging a little faster than the ML-NLMixed model. But for the model with four random effects (model 8) the ML-NLMIXED did not converge and it was stopped after 3600 cpu seconds.

Table I.

Computational time comparisons according method used. Methods based on the two full Maximum likelihood based approaches(ML-CENSAD and ML-NLMIXED) and the Pseudo likelihood approach (PMLE) proposed in this study. Time given is in cpu seconds^*.

Method	Model with 2 Random Effects	Model with 4 Random Effects
ML-CENSAD	720	1856
ML-NLMIXED	780	Didn’t converge
PMLE	415	715

^*time given is for a single run

Generally speaking, the computation time significantly increased based on the data structure, rate of censoring, and model used for both full likelihood based methods, but the PMLE is not significantly affected by these changes. For instance, the ML-CENSAD is very slow to converge when the number of measures (n_i) for each subject increases (the results reported in table I are for n_i =5 ∀_i) and the ML-NLMIXED has convergence difficulties when the number of random effects in the model increases (for the model with 4 random effects the method fails to converge).

In Table II we present the bias and the the mean of the estimated SEs across all simulations from the full likelihood method (ML-NLMIXED) and the PMLE for the model with two random effects (model 7) for three different levels of censoring (31%, 40%, and 75%). As can be seen from this table, the proposed PMLE method produces estimates comparable to the full likelihood method (no significant difference) in significantly shorter computation time.

Table II.

Simulation results comparing the performance of the PMLE approach with the ML approach at 31%, 40% and 75% censoring rates. Bias and mean SEs for the fixed effect parameters for a model with 2 random effects(model (7)) are reported. Reported Values are the mean of 500 replications.

% Censored	Parameter	True Value	Method
			ML-NLMIXED		PMLE
			Bias	SE	Bias	SE
31	Time1 $\left({\beta }_1^1\right)$	−0.15	−0.006	0.034	0.004	0.033
	Covar1 $\left({\beta }_2^1\right)$	−0.20	0.001	0.043	0.001	0.043
	Inter1 $\left({\beta }_3^1\right)$	0.03	0.009	0.047	−0.009	0.047
	Time2 $\left({\beta }_1^2\right)$	−0.15	−0.024	0.032	0.028	0.035
	Covar2 $\left({\beta }_2^2\right)$	0.15	−0.018	0.043	0.018	0.042
	Inter2 $\left({\beta }_3^2\right)$	0.05	−0.006	0.049	−0.008	0.049
40	Time1 $\left({\beta }_1^1\right)$	−0.15	−0.008	0.064	0.004	0.035
	Covar1 $\left({\beta }_2^1\right)$	−0.20	0.006	0.085	0.007	0.063
	Inter1 $\left({\beta }_3^1\right)$	0.03	0.086	0.065	−0.054	0.077
	Time2 $\left({\beta }_1^2\right)$	−0.15	−0.075	0.072	0.048	0.045
	Covar2 $\left({\beta }_2^2\right)$	0.15	−0.069	0.075	0.038	0.053
	Inter2 $\left({\beta }_3^2\right)$	0.05	−0.057	0.081	−0.018	0.052
75	Time1 $\left({\beta }_1^1\right)$	−0.15	0.009	0.049	−0.020	0.034
	Covar1 $\left({\beta }_2^1\right)$	−0.20	0.091	0.064	0.0033	0.053
	Inter1 $\left({\beta }_3^1\right)$	0.03	0.114	0.056	0.048	0.062
	Time2 $\left({\beta }_1^2\right)$	−0.15	−0.021	0.052	−0.050	0.040
	Covar2 $\left({\beta }_2^2\right)$	0.15	−0.014	0.059	−0.043	0.048
	Inter2 $\left({\beta }_3^2\right)$	0.05	−0.027	0.065	−0.031	0.050

To obtain a better understanding of the strengths and weaknesses of the proposed methodology, a comparison of estimates and mean SEs across all simulations using both univariate and bivariate modeling, is carried out in a simulation study. Table III presents the results of this study by displaying the parameter estimate, and the mean SEs for two different censoring rates (25% and 75%) for the model with four random effects (model 8). The estimated mean SE and the bias based on the bivariate modeling generally tends to be smaller compared to results of the univariate model.

Table III.

Estimates and mean SEs comparison using the fixed effect parameters for the univariate and bivariate models for a model with 4 random effects. PMLE is used for the bivariate model. Values reported are for the mean of 500 replications.

			Univariate			Bivariate:-PMLE
% Censored	Parameter	True Value	Estimate	SE	95% Cov*	Estimate	SE	95% Cov*
25	Time1 $\left({\beta }_1^1\right)$	−0.15	−0.135	0.001	94.5	−0.120	0.045	93.7
	Covariate1 $\left({\beta }_2^1\right)$	−0.20	−0.196	0.040	94.8	−0.207	0.032	94.9
	Interaction1 $\left({\beta }_3^1\right)$	0.03	0.019	0.013	95.1	0.043	0.013	97.2
	Time2 $\left({\beta }_1^2\right)$	−0.15	−0.148	0.176	95.3	−0.157	0.104	95.1
	Covariate2 $\left({\beta }_2^2\right)$	0.15	0.176	0.026	95.3	0.163	0.019	95.8
	Interaction2 $\left({\beta }_3^2\right)$	0.05	0.019	0.108	96.0	0.036	0.102	95.6
75	Time1 $\left({\beta }_1^1\right)$	−0.15	−0.142	0.124	95.2	−0.160	0.115	95.7
	Covariate1 $\left({\beta }_2^1\right)$	−0.20	−0.359	0.241	94.6	−0.293	0.220	95.2
	Interaction1 $\left({\beta }_3^1\right)$	0.03	0.118	0.160	93.9	0.031	0.148	94.7
	Time2 $\left({\beta }_1^2\right)$	−0.15	−0.192	0.121	96.3	−0.184	0.117	96.5
	Covariate2 $\left({\beta }_2^2\right)$	0.15	0.128	0.187	95.3	0.156	0.161	95.8
	Interaction2 $\left({\beta }_3^2\right)$	0.05	0.047	0.128	96.1	0.045	0.118	95.6

^*95% Coverage

4. REAL DATA EXAMPLE

One major aim of the Genetic and Inflammatory Markers for Sepsis study (GenIMS) [2] was to examine the relationship between a set of inflammatory markers and the development of sever sepsis and mortality, that is to determine if changes in these markers over time were related to mortality and/or development of sepsis. Because sepsis can result from multiple illnesses, the study focused on recruiting patients with community-acquired pneumonia (CAP) in order to insure a relatively homogenous group with respect to susceptibility to sepsis. A total of 2320 patients were enrolled into the study through the emergency departments in 28 hospitals (2001–2003). Blood samples for cytokine assays were drawn daily for the first seven days and weekly thereafter while patients remained in the hospital. The biomarkers of greatest interest are IL-6 (interleukin-6) a pro-inflammatory marker and IL-10 (interleukin-10), an anti-inflammatory marker. In both cases, the assay for each of these markers had a lower limit of detection resulting in a censoring of the measurements, IL-6 was censored at either 2 pg/ml or 5 pg/ml depending on the assay used; IL-10 was censored at 5 pg/ml.

Besides left censored values the GenIMS data include missing data as well as right censored values. The data cohort distinguishes missing data according to the reason of missingness (due to limit of detection and other types).

The censoring rate for both IL-6 and IL-10 increases over time. For IL-6 these rates for days 1 through 7 were as follows: 384/1797 or 21.4% for day1, 401/1738 or 23.1% for day 2, 464/1754 or 26.5% for day 3, 474/1463 or 32.4% for day 4, 364/1127 or 32.3% for day 5, 288/869 or 33.1% for day 6 and 229/696 or 32.9% for day 7. The censoring rates for IL-10 were substantially higher with the results for days 1 through 7 as follows: 1086/1797 or 60.4% for day 1, 1138/1738 or 65.5% for day 2, 1281/1754 or 73.0% for day 3, 1128/1463 or 77.1% for day 4, 844/1127 or 74.9% for day 5, 670/869 or 77.1% for day 6 and 532/696 or 76.4% for day 7. Overall 9283 (49.1%) measures of the combined bivariate cases were left-censored.

To examine the relationship between these markers and mortality over time, we fit a linear mixed model with random intercept and random slope for each biomarker. Before applying the methods a normalizing transformation is considered to assure normality, and measurements are transformed using the log transformation function. The models used are:

$$Y_{ij}^1={\beta }_0^1+{\beta }_1^1{t}_{ij}+{\beta }_2^{1}Mortalit{y}_i+{\beta }_3^1(t_{ij}\ast Mortalit{y}_i)+{\gamma }_{0i}^1+{\gamma }_{1i}^1{t}_{ij}+{ϵ}_{ij},and$$

$$Y_{ij}^2={\beta }_0^2+{\beta }_1^2{t}_{ij}+{\beta }_2^{2}Mortalit{y}_i+{\beta }_3^2(t_{ij}\ast Mortalit{y}_i)+{\gamma }_{0i}^2+{\gamma }_{1i}^2{t}_{ij}+{ϵ}_{ij}.$$

where the superscript 1 and 2 represents the two biomarkers IL-6 and IL-10 respectively, and mortality is the day 30 mortality status, whether a patient is dead or alive within 30 days of enrollment, a 0/1 variable. The proposed PMLE and the ML-CENSAD methods are used to estimate the model parameters. The ML-NLMIXED method is not used here as it does not converge for a model with more than two random effects.

Additionally the above models were also fit for each outcome separately providing a univariate analysis and results were compared with those obtained using the multivariate analysis.

The results from these analyses looking at the relationship between 30-day mortality and changes in IL-6 and IL-10 are presented in Table IV. When comparing the estimates obtained using the full likelihood method (ML-CENSAD) and the PMLE, the PMLE produced similar estimates (no significant difference) simplifying the computational complexities of the full likelihood methods. The standard errors of the PMLE estimates are slightly larger, but not significantly different than the values in ML-CENSAD.

Table IV.

Parameter estimates and S.E. of fixed and Random effects according to method (ML-CENSAD and PMLE) and model (Univariate Vs. Bivariate) used. Responses are log(IL-6) and log(IL-10) and time is measured in days

		Bivariate Model according to Method
Parameter	Univariate Models	ML-CENSAD	PMLE
Slope time-IL-6	−0.329(0.160)	−0.234(0.009)	−0.274(0.012)
Slope time-IL-10	−3.279(0.616)	−3.096(0.655)	−3.094(0.665)
Mortality-IL-6	1.277(0.228)	1.194(0.176)	1.194(0.181)
Mortality-IL-10	0.496(0.267)	0.532(0.127)	0.532(0.133)
Mortality*time-IL-6	0.160(0.349)	0.660(0.250)	0.664(0.258)
Mortality*time-IL-10	0.036(0.125)	0.704(0.100)	0.695(0.107)
Random effects Covariance estimates
Parameter	Estimate	SE	P-value
G 11	3.425	0.175	< 0.001
G 21	−0.433	0.035	< 0.001
G 22	0.221	0.014	< 0.001
G 31	0.742	0.063	< 0.001
G 32	−0.148	0.015	< 0.001
G 33	0.693	0.031	0.017
G 41	−0.148	0.012	< 0.001
G 42	0.042	0.004	< 0.001
G 43	−0.124	0.005	0.001
G 44	0.025	0.001	0.021

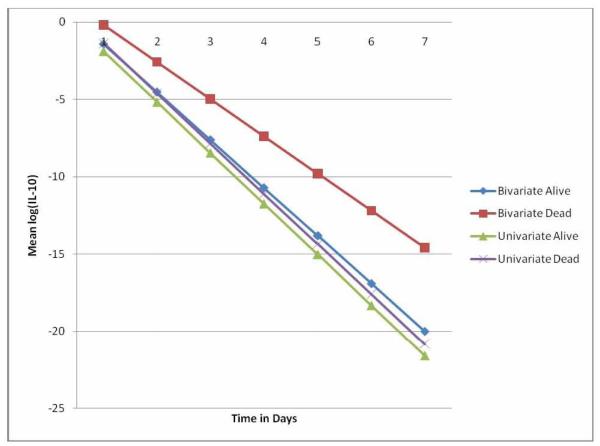
The joint modeling of the two biomarkers using a bivariate model allows us to study the correlation between the markers over time which can be of importance when understanding the role of biomarkers in the development of sepsis. Table IV presents the parameter estimates of the random effects covariance matrix, the elements of the sub-matrix of the covariance between random effects of each marker are all significantly different from zero justifying the use of the bivariate model and showing the gain in efficiency by accounting for the correlation between the markers. Moreover, the use of the bivariate model resulted in a different relationship between mortality and IL-6 values when compared to modeling IL-6 by a univariate model (Fig. 1). In addition, the statistical significance of the interaction term for mortality and time for IL-10 differs depending on the model used, it is non-significant for the univariate model but highly significant for the bivariate model.

Figure 1.

Estimated model means of log(IL-6) for the GenIMS data, using the PMLE parameter estimation by mortality status (dead or alive) and model used (univariate or bivariate).

Similar to the simulation results, estimated coefficients and SEs are generally lower based on the bivariate modeling compared to separate univariate models, this may indicate the contribution of information provided by the second marker data in the bivariate model in the estimation of the first marker. But some of the contrasts between the estimated coefficients and SEs for the univariate and bivarite models in table IV are larger than what is observed in the simulation study. This could be due the big difference in censoring rate of each of the outcome variables (27.4% and 70.5% for IL-6 and IL-10, respectively) when they are analyzed separately. In general the degree and direction of the estimate (or bias) in the fixed effects depend on the relative rate of censoring.

Plots of the estimated means, obtained from the models using PMLE are presented in Fig. 1 and Fig.2. Fig.1 presents the estimated mean IL-6 for both dead and alive patients using a bivariate model (considering IL-6 and IL-10) and a univariate model considering only IL-6 as an outcome. The estimated mean IL-6 increases from day 1 over the subsequent days using bivariate model, while the level decreases using a univariate model. Higher estimated mean levels were observed for patients who died than survived patients using both models.

Figure 2.

Estimated model means of log(IL-10) for the GenIMS data, using the PMLE parameter estimation by mortality status (dead or alive) and model used (univariate or bivariate).

Estimated mean IL-10 level (Fig.2) were high on day 1 using both models, but a rapid decrease was observed on the subsequent days. There is no significant difference in the estimated mean IL-10 levels between patients who died and those who survived for the single outcome analysis, but the multiple outcome analysis (using both IL-10 and IL-6 simultaneously) indicated that the estimated mean IL-10 level is significantly higher for those who died compared with those who survived. In all cases, the computation time for the PMLE method is substantially less than the time needed for ML-CENSAD.

5. DISCUSSION

In this paper, we proposed and evaluated a pseudo maximum likelihood estimator for the analysis of multivariate longitudinal left-censored data that simplifies computational complexities and can be applied to different models and different data structures. The major advantage of the pseudo likelihood estimator is its computational efficiency and simplicity when compared with the full likelihood method currently used for modeling multivariate longitudinal data. The proposed method considerably eases the numerical complexities of the full likelihood approach. Further, it alleviates the need to specify and estimate many nuisance parameters that are required in a full likelihood approach. As is demonstrated by the simulation and the real life data studies, the pseudo likelihood approach yields estimates with small bias and robust standard errors.

For longitudinal data with high rate of censoring, like the GenIMS data, the pseudo likelihood method dramatically decreases the computation time and provides similar results of estimates to those obtained using the full likelihood methods. The full likelihood methods are limited by the rate of censoring as they require numerical evaluation of multiple integrals of a multivariate normal density whose dimension is equal to that of the number of censored measures. Whereas, the pseudo likelihood approach avoids numerical evaluation of multivariate integrals, since filling in censored observations requires computation of the univariate normal distribution function for which efficient numerical algorithms are available.

Unlike the full likelihood, the pseudo-likelihood only requires specification of the correlation structure of the repeated measures on a single individual. Further, compared to maximum likelihood, which requires the full likelihood to be correctly specified in order to obtain consistent estimates, the pseudo- likelihood estimates are consistent as long as the marginal distributions are correctly specified. Note that a Bayesian approach using a Bayesian generalized methods of moments could also be used to deal with the underlying problem.