A Bayesian dose-finding design incorporating toxicity data from multiple treatment cycles

Abstract

Phase I oncology trials are designed to identify a safe dose with an acceptable toxicity profile. The dose is typically determined based on the probability of severe toxicity observed during the first treatment cycle, although patients continue to receive treatment for multiple cycles. In addition, the toxicity data from multiple types and grades are typically summarized into a single binary outcome of dose-limiting toxicity (DLT). A novel endpoint, the total toxicity profile (TTP), was previously developed to account for the multiple toxicity types and grades. In this work, we propose to account for longitudinal repeated measures of TTP over multiple treatment cycles, accounting for cumulative toxicity during dosing-finding. A linear mixed model was utilized in the Bayesian framework, with addition of Bayesian risk functions for decision-making in dose assignment. The performance of this design is evaluated using simulation studies and compared with the previously proposed Quasi-Likelihood CRM (QLCRM) design. Twelve clinical scenarios incorporating four different locations of MTD and three different time trends (decreasing, increasing, and no effect) were investigated. The proposed repeated measures design (RMD) was comparable to the QLCRM when only cycle one data was utilized in dose-finding; however it demonstrated an improvement over the QLCRM when data from multiple cycles were used across all scenarios.

1. Introduction

Phase I oncology clinical trials are typically first in human trials, characterized by a small number of patients with a goal of assessing the safety of the regimen. Nonetheless, extensive data are collected regarding the toxicity endpoints including type, grade, attribution and time of occurrence. In conventional dose-finding designs, only the dose-limiting toxicities (DLT) within the first cycle of treatment impact formal decision-making in the dose finding process. Furthermore, a binary variable indicating the occurrence of DLT is often utilized, which ignores mild or moderate toxicities. Late-onset toxicities occurring in subsequent cycles may be recorded, but generally not utilized in the dose-finding process.

Neglecting toxicity data from late treatment cycles can impact the determination of an appropriate dose for subsequent phase II/III clinical trials. One of the many reasons for a high failure rate in phase II/III clinical trials is an incorrectly determined dose in the prior phase I trials [1]. Specially, the experimental regimen may fail to demonstrate satisfactory efficacy if the recommended dose is too low, or the phase II/III clinical trial may be terminated when the recommended dose is too toxic. Recent research has demonstrated that dose-limiting toxicities are not always observed in the first treatment cycle [2]. However, only limited methods exist for dose-finding designs that take into account toxicities from subsequent cycles of treatment. Cheung and Chappell proposed a sequential dose-finding design using a time-to-event model (TITE-CRM) for late on-set toxicities [3]. A dose-finding design using a mixed-effect proportional odds model for longitudinal graded toxicity in phase I oncology trials was proposed by Doussau et al. [4]. In this design, decision rules on dose escalation were based on evaluation of ordinal toxicity in the mixed-effect proportional odds model after a run-in stage of 15 patients. A third approach was developed by Fernandes et al. to model DLTs in multiple treatment cycles based on Markov chains [5].

Toxicity data are high dimensional in nature, with various types, grades, attribution and times of occurrence. Therefore, dose-finding designs in phase I clinical trials could benefit from a new toxicity endpoint paradigm. To account for the oversimplification of toxicity data in phase I trials, a dose-finding design based on a quasi-continuous toxicity score, the total toxicity profile (TTP), to capture multiple types and grades of toxicities occurring during the first treatment cycle [6], has been previously proposed. While this is certainly an improvement from using the traditional DLT based endpoint, patients participating in phase I clinical trials usually continue to receive more than one cycle of experimental regimen in the absence of DLT or disease progression. This is also true of the subsequent phase II and phase III trials, where treatments are typically repeated for multiple cycles. This work extends the TTP [2] by incorporating toxicity data collected from subsequent cycles of treatment.

An adaptive dose-finding design based on the TTP using a repeated measures design (RMD) for longitudinal toxicity data is proposed. In addition to the novelty on the toxicity endpoint, the RMD methods proposed here are substantially more sophisticated than those used in traditional phase I designs or CRM designs on multiple levels: (1) standard CRM designs consider only binary endpoint data from cycle 1; RMD incorporates adverse event data from all cycles of treatment, to provide for a more robust estimation and dose selection; (2) phase 1 studies normally encounter patient dropouts due to DLT or disease progression; RMD is the first in the Phase I setting to accommodate differing number of cycles across patients and missing toxicity data beyond cycle 1; (3) last but not least, by using data from multiple treatment cycles, RMD provides us with tools to investigate the effect of toxicity across cycles.

In Section 2 of the article, a Bayesian framework coupled with a linear mixed model is introduced for this dose-finding design. Although a linear mixed effect model is simple in its mathematical form, statistical models that are appropriate for dose-finding designs are different from more complex models applied in general statistical analysis. The ability to fit complex models in early phase dose-finding trials is limited by the small sample size and the multiple dose levels investigated. In fact, statistical models in dose-finding designs function as working models to guide dose escalation, rather than precise estimation. This is because the goal of a phase I trial is to identify the maximum tolerated dose (MTD) as accurately as possible and treat as many patients at the doses near the MTD as possible. This differs from a more general goal of estimating or modeling the dose-response or dose-toxicity curve such as in a pharmacokinetic-pharmacodynamic (PK-PD) study. For example, Emax is widely used in PD modeling, and rarely in the dose escalation phase of phase I studies. Legezda and Ibrahim [7] have proposed a simplified PK-PD model for estimation based on a binary endpoint, however, with the assumptions that patients received numerous cycles of treatment without going off study. Simon et al. [8] also developed a Kmax model to retrospectively analyze data from phase I trials, which was shown to be intractable in a prospective dose-finding study. A recent paper by Iasonos et al. [9] points out the many caveats of using PK-PD modeling for phase 1 studies. Therefore, while it is believed that an Emax type model offers potential for future work, it will require extensive validation, especially in terms of its practical use in phase I studies.

In Section 3 and 4, extensive simulations are conducted and evaluated to study the operating characteristics of the proposed RMD under various clinical relevant scenarios. Section 5 concludes with a discussion of the proposed design, as well as some insights into future work.

2. Methods

2.1. Continuous Toxicity Endpoint

Although the DLT definition may vary depending on the type of the cancer and the agent, it often involves a subset of the Grade 3 and 4 toxicities outlined in the NCI Common Terminology Criteria for Adverse Events (CTCAE). The conventional approach defines DLT as the occurrence of an event in the pre-defined categories of toxicities. This process dichotomizes the ordinal grades, which although convenient discards useful information. Specifically, dichotomizing all the toxicities at the same grade assumes that all toxicities are equally important and exchangeable which may not be realistic. For example, this definition of DLT does not distinguish a grade 3 fatigue from a grade 3 hepatic failure, and assumes that they are equally important and exchangeable which might not be realistic. In addition, toxicity data is inherently multivariate in nature, and this definition ignores the multivariate nature, and assuming that different toxicities occur independently.

Bekele and Thall [10] proposed using numerical weights to characterize the clinical importance of each grade of each type of toxicity, and further defined the total toxicity burden (TTB) as the sum of the weights of all toxicities experienced by a patient as the toxicity endpoint. Similar to the TTB, Ezzalfani et al. [6] proposed the total toxicity profile (TTP) as the Euclidean norm of the weights, which is the endpoint used in this design. Following the notation in Ezzalfani et al. [6], let w_lh denote the elicited weight of toxicity type l (l ∈ {1,…, L}) occurring at grade h (h ∈ {0,…, 4}). Hence, the weight vector for toxicity l is w_l = (w_l0,…, w_l4)^T and the weight matrix is denoted as W = (w₁, …, w_L)^T. For patient i, denote the maximum observed grade of toxicity type l as G_il. Then the TTP_i is defined as

$$TT{P}_i=\sqrt{{\displaystyle \sum _{l=1}^L{\displaystyle \sum _{h=0}^4{w}_{jh}^{2}1(G_{il}=h)}}},$$ (1)

where 1(G_il = h) is an indicator function which takes value 1 if the maximum observed grade is h for toxicity type l, and 0 otherwise.

The TTP is further normalized to nTTP, in order to constrain the continuous toxicity endpoint to be within 0 and 1,

$${\mathit{nTTP}}_i=\frac{{\mathit{TTP}}_i}{v},$$ (2)

where v is a normalization constant that is equal to or slightly larger than the maximum TTP that occurs with the most severe toxicity profile. Further details about the specification of the normalization constant v are provided in Section 3.1 and Ezzalfani et al. [6].

2.2. Dose Toxicity Models with Time

Classical parametric models under the continual reassessment method (CRM) [11] specify a generic dose-toxicity model for the linear predictor η for first cycle toxicities:

$${\eta }_i={\beta }_0+{\beta }_1\cdot x_i,{\beta }_1>0,$$ (3)

where, β₁ models the increasing dose and toxicity relationship and is strictly positive. The fixed allocated dose for cycle 1 is x_i, for each patient i (i = 1, 2, …, n), and β’s are the parameters for intercept and slope for dose. In this generalized linear model specification, η = g(μ) where g is the link function and μ is the population mean. Since the TTP is considered as quasi-continuous, g is an identity function with μ = E(nTTP), the expectation of nTTP.

In order to incorporate repeated measures of toxicity data, the classical dose-toxicity model is extended to have a time effect (cycle), in a linear mixed model for longitudinal data [12]. Specifically,

$$\begin{array}{cc}{\eta }_{\mathit{ij}}={\beta }_0+{\beta }_1\cdot x_i+{\beta }_2\cdot t_j,& {\beta }_1>0\end{array}$$ (4)

with allocated dose level x_i and cycle number t_j (j = 1, …, J) as covariates, and the β’s are the parameters for intercept, slopes for dose and cycle, respectively; no intra-patient dose modification or adjustment is considered here. The generalized linear model not only specifies the dose-toxicity curve based on cycle 1, but also incorporates the toxicity trend when multiple cycles of treatments are received.

Furthermore, the parametric linear model can incorporate abating or accumulating dose effect as shown below,

$$\begin{array}{cc}{\eta }_{\mathit{ij}}={\beta }_0+{\beta }_1\cdot x_i+{\beta }_2\cdot t_j+{\beta }_3\cdot x_i\cdot t_j,& {\beta }_1>0\end{array}$$ (5)

with dose x_i, cycle t_j and an interaction term of dose and cycle as covariates. The addition of interaction term for dose and cycle provides further flexibility for allowing abating or accumulating dose effect to vary with the dose level.

2.3. Linear Mixed Effect Model and Bayesian Estimation

Due to the small sample size in phase I trials, parsimonious parametric longitudinal models are preferred as a working model to guide dose escalation. Follow this paradigm, a linear model with a random intercept is used. The random intercept γ_i is introduced to account for the correlation among repeated toxicity measures given a patient treated for several cycles. This leads to the following model:

$$\begin{array}{cc}{y}_{\mathit{ij}}={\beta }_0+{\beta }_1{x}_i+{\beta }_2{t}_j+{\gamma }_i+{\epsilon }_{\mathit{ij}},& {\beta }_1>0\end{array}$$ (6)

where y_ij is the observed value of nTTP for the ith patient at the jth cycle; β₀ is the effect of the intercept, β₁ the effect of dose, and β₂ the effect of time trend; ε_ij is the measurement error ε_ij ~ N(0, σ²); and γ_i is the random intercept for each patient where ${\gamma }_i~\mathrm{N}(0,{\sigma }_{\gamma }^2),{\sigma }_{\gamma }^2$ is the variance of the random intercept.

Using matrix notation, the linear mixed effect model 6 can be rewritten as:

$$\mathit{y}=\mathit{x}{\beta }_1+(\mathbf{1},\mathit{t})\left(\begin{array}{l}{\beta }_0\\ {\beta }_2\end{array}\right)+W\mathit{\gamma }+\epsilon .$$ (7)

where y is a ${\displaystyle {\sum }_{i=1}^n{K}_i\times 1}$ vector of nTTP values. K_i is the observed maximum number of cycles of patient i, which implies that patients can have unequal numbers of repeated measures – this is critical as Phase 1 studies normally suffer from patient dropouts due to DLT or disease progression, and this allows us to accommodate differing number of cycles across patients and missing toxicity data beyond cycle 1. x indicates the dosage assigned to each patient at cycle 1; t is the cycle indicator. W is a ${\displaystyle {\sum }_{i=1}^n{K}_i\times n}$ design matrix where W_ij = 1 if the ith measurement is from the jth patient. γ is an n × 1 vector of random effects with variance ${\sigma }_{\gamma }^2$. ε is a ${\displaystyle {\sum }_{i=1}^n{K}_i\times 1}$ vector of exchangeable error terms with variance ${\sigma }_{\epsilon }^2$.

A MCMC algorithm for Bayesian inference of the model parameters is used here. In Phase I trials, toxicity is assumed to increase with dose, which requires β₁ to be positive. With that constraint, the approach proposed by Gelfand et.al for Bayesian analysis on constrained parameters [13] is adopted here, which is simply to generate from the un-constrained full conditional and retain the value only if it falls into the constraint region.

Conjugate priors are chosen where full conditionals can be derived and posteriors can be sampled directly from the full conditionals. The conjugate priors for β₀, β₁, β₂, ${\sigma }_{\gamma }^2$, and ${\sigma }_{\epsilon }^2$ are available and specified in the Appendix. Sampling from the joint posterior $p({\beta }_0,{\beta }_1,{\beta }_2,\gamma ,{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2|\mathit{y})$ can be performed with a Gibbs sampling algorithm since the full conditionals can be analytically derived and recognized as standard densities. At each iteration of the Gibbs sampling, model parameters can be sequentially drawn from the full conditionals below:

$${\beta }_1|{\beta }_0,{\beta }_2,\mathit{\gamma },{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2~\mathrm{N}({\mu }_{{\beta }_1},{\sigma }_{{\beta }_1}^2),$$ (8)

where ${\mu }_{{\beta }_1}={\sigma }_{{\beta }_1}^2\left\{\frac{1}{{\sigma }_{\epsilon }^2}{\mathit{x}}^T\left(\mathit{y}-W\mathit{\gamma }-\left(\mathbf{1},\mathit{t}\right)\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right)+\frac{u}{v}\right\}$, and ${\sigma }_{{\beta }_1}^2={\left(\frac{1}{{\sigma }_{\epsilon }^2}{\mathit{x}}^T\mathit{x}+\frac{1}{v}\right)}^{-1}$.

$${\beta }_0,{\beta }_2|{\beta }_1,\mathit{\gamma },{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2~{\mathrm{N}}_2({\mathit{\mu }}_{\mathit{\beta }},{\sum }_{\beta }),$$ (9)

where ${\mathit{\mu }}_{\beta }={\sum }_{\beta }\left\{\frac{1}{{\sigma }_{\epsilon }^2}{\left(\mathbf{1},\mathit{t}\right)}^T(\mathit{y}-W\mathit{\gamma }-\mathit{x}{\beta }_1)+B_{\beta }^{-1}{\mathit{a}}_{\beta }\right\}$, and ${\sum }_{\beta }={\left(\frac{1}{{\sigma }_{\epsilon }^2}{\left(\mathbf{1},\mathit{t}\right)}^T\left(\mathbf{1},\mathit{t}\right)+B_{\beta }^{-1}\right)}^{-1}$.

$$\mathit{\gamma }|\mathit{\beta },{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2~{\mathrm{N}}_n({\mathit{\mu }}_{\gamma },{\sum }_{\gamma }),$$ (10)

where ${\mathit{\mu }}_{\gamma }={\sum }_{\gamma }\left\{\frac{1}{{\sigma }_{\epsilon }^2}{W}^T\left(\mathit{y}-\mathit{x}{\beta }_1-(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right)\right\}$, and ${\sum }_{\gamma }={\left(\frac{1}{{\sigma }_{\epsilon }^2}{W}^{T}W+\frac{1}{{\sigma }_{\gamma }^2}{\mathrm{I}}_n\right)}^{-1}$.

$${\sigma }_{\gamma }^2|\mathit{\beta },\mathit{\gamma },{\sigma }_{\epsilon }^2~\mathrm{IG}(u_{\gamma },v_{\gamma }),$$ (11)

where $u_{\gamma }=\frac{1}{2}n+a_{\gamma }$, and $v_{\gamma }=\frac{1}{2}{\mathit{\gamma }}^T\mathit{\gamma }+b_{\gamma }$.

$${\sigma }_{\epsilon }^2|\mathit{\beta },\mathit{\gamma },{\sigma }_{\gamma }^2~\mathrm{IG}(u_{\epsilon },v_{\epsilon }),$$ (12)

where $u_{\epsilon }=\frac{1}{2}n+a_{\epsilon }$, and $v_{\epsilon }=\frac{1}{2}{\left\{\mathit{y}-W\mathit{\gamma }-\mathit{x}{\beta }_1-(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right\}}^T\left\{\mathit{y}-W\mathit{\gamma }-\mathit{x}{\beta }_1-(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right\}+b_{\epsilon }$.

2.4. Dose-finding Design

The basic idea for dose-finding is to sequentially update the knowledge of the dose-toxicity relationship, in order to find the target dose for the next cohort of patients to be enrolled. The Bayesian risk at each dose level is calculated based on the posterior distributions. The dose level that minimizes the Bayesian risk would be selected for the next dose assignment.

Bayesian risk as a decision criteria is well established in decision rule theory [14]. It is defined as the posterior expected value of a loss function. Various loss functions of nTTP(dose, cycle) can be considered depending on the scenarios and the questions of interest. For example, an absolute loss function at the first cycle assesses the difference between the target and the toxicity at cycle 1, and is defined as

$$L_{1a}(\mathit{nTTP}(\mathit{dose},1),{\pi }_1)=|\mathit{nTTP}(\mathit{dose},1)-{\pi }_1|,$$ (13)

where π₁ is the elicited target nTTP at cycle 1. An asymmetric variant of an absolute loss function is to control overdose and would only accept doses that correspond to a toxicity lower than a pre-specified upper bound:

$$L_{1b}(\mathit{nTTP}(\mathit{dose},1),{\pi }_1)=\left\{\begin{array}{ll}|\mathit{nTTP}(\mathit{dose},1)-{\pi }_1|\hfill & \mathit{nTTP}(\mathit{dose},1)\le {\pi }_1+\mathrm{\Delta }\hfill \\ +\infty \hfill & \mathit{nTTP}(\mathit{dose},1)>{\pi }_1+\mathrm{\Delta }\hfill \end{array}\right\}$$ (14)

where Δ is a pre-specified tolerance constant.

When starting a trial for the initial patient cohort, a simpler model or a rule-based design (such as 3+3) could be used in the case of sparse data, and the proposed repeated measures design (RMD) can be switched on once there are sufficient data for estimation. Patients are enrolled in the trial sequentially starting at the lowest dose. A new cohort would be included when the previous cohort has completed one cycle of treatment. For safety, no skipping of dose levels is allowed during dose escalation. Once a dose is assigned to a new cohort, the patients in that cohort will continue the same dose until they stop the treatment – no intra-patient dose modification or adjustment is considered here. The trial will thus be conducted in the following manner:

1. Use 3+3 design for the first 2 cohorts as a run-in, to provide data for initial parameter estimation before switching to the RMD.

2. After the run-in, for every new cohort of patients,

   1. The repeated measure model (Formula 6) is applied to all the available data up to the point of the enrollment of the new cohort.
   2. The decision criteria is evaluated (Formula 13) and the recommended dose that minimizes the Bayesian risk on cycle 1 is identified.
   3. Treat the patients in this cohort with the recommended dose; or if the recommendation skips doses, then treat the patient with the next higher dose instead to prevent dose skipping during dose escalation.

3. Terminate the trial when the maximum number of patients have been treated.

3. Simulations

To evaluate the ability of the proposed RMD to accurately identify the MTD, simulation studies were conducted and performance of RMD was compared to the QLCRM model using nTTP as the toxicity endpoint [6]. The same scenarios and settings as in the QLCRM design were used, where a fixed sample size of 36 patients and cohort size of 3 was included, and 6 dose levels were considered. Each patient is administrated a maximum of 6 treatment cycles, and for each patient treatment is stopped anytime a DLT is observed. A thousand trials were simulated for each scenario.

3.1. Elicitation of Severity Weights and Target Toxicity

The RMD methods require an input from the physicians involved in the trial. Initially, the physicians need to specify toxicities to be monitored and their possible clinical outcomes graded by CTCAE. For example, to simplify, three types of toxicities may be considered: renal, neurological and hematological toxicities as in Ezzalfani et al. [6]. Table 1 lists the possible grades for each toxicity type and whether its occurrence is considered a DLT. Grade 0 corresponds to no toxicity and a null weight, and hence is not listed in the table. The physicians are then asked to assign a severity weight for each grade of each toxicity within some numerical range. As the method is invariant to the range, the range only needs to be positive. Ezzalfani et al.[6] demonstrated one way of specifying the severity weights in their example (Table 1). Based on the severity weights, the most severe toxicity profile (grade 4 for all three toxicity types) corresponds to a maximum TTP score of 2.34. In this case, the normalization constant was chosen as 2.5, just so it is slightly larger than the maximum TTP. By dividing TTP scores by the normalization constant, the nTTP scores are constrained between 0 and 1.

Table 1.

Toxicities and Severity Weights in the Example

Toxicity Type	Grade	Severity Weight	DLT
Renal	1	0.5	No
	2	0.75	No
	3	1	Yes
	4	1.5	Yes
Neurological	1	0.5	No
	2	0.75	No
	3	1	Yes
	4	1.5	Yes
Hematological	3	0.5	No
	4	1	Yes

Given the toxicity types and their severity weights, the target nTTP at cycle 1, denoted as π₁ in the decision criteria, must be specified. Similar to the fixed target toxicity probability where DLT is the toxicity endpoint, the target nTTP may be specific to be agent and the cancer type, and must be elicited from the physician. Details about the elicitation process are available in the appendix.

3.2. Scenarios

Simulations studies were performed to assess the performance of the proposed approach under a range of possible scenarios. Ezzalfani et al. [6] used a fixed set of dose-toxicity probabilities for each scenario to evaluate their QLCRM design. They assumed that the three toxicity types (renal, neurological, and hematological) are independent. For each toxicity type, the probabilities of observing each grade at each dose level were chosen nonparametrically to satisfy: (1) the probability of observing a grade 0 event decreases with dose; (2) the probability of observing a grade 4 event increases with dose; (3) the probability of observing any fixed grade event across dose levels is unimodal.

In order to make comparisons to the QLCRM, the same scenario settings (according to Scenario A, C, F, G in [6]) were adopted, where the target nTTP occurred at dose level 2, 3, 4 and 5, and the target nTTP of 0.28 corresponded to a 33% chance of DLT (Table 2). We mirrored their toxicity probabilities in these scenarios (Figure 1) for generating toxicity data at cycle 1, and then generated toxicity data for subsequent cycles based on the first cycle in the following fashion. Denote the probability of observing a grade h event at cycle 1 for toxicity type l at dose level k as p_l,k,h. Given the toxicity type l and the dose level k, it is assumed that p_l,k,h was generated from a standard normal distribution such that, p_l,k,0 = Φ(c_l,k,0), p_l,k,1 = Φ(c_l,k,1) − Φ(c_l,k,0), p_l,k,2 = Φ(c_l,k,2) − Φ(c_l,k,1), p_l,k,3 = Φ(c_l,k,3) − Φ(c_l,k,2), and p_l,k,4 = 1 − Φ(c_l,k,3), where c_l,k,0, c_l,k,1, c_l,k,2, and c_l,k,3 are a set of fixed real values given l and k. Shifting the mean of the standard normal distribution to the right increases the probability of observing higher grades, which corresponds to a higher nTTP value, and vice versa. Therefore, to generate increasing toxicity over cycles, the mean of the standard normal curve was shifted to the right for each subsequent cycle; to generate decreasing toxicity over cycles, the mean of the standard normal curve was shifted to the left by following this data generation approach. In total, twelve clinical scenarios were generated as shown in Fig 2 with different MTD locations (dose 2, dose 3, dose 4, and dose 5) and different temporal trends (no time trend, decreasing time trend, and increasing time trend). The severe dose-toxicity scenarios were represented when the true MTD = dose 2, intermediate dose-toxicity scenarios when true MTD = dose 3, and mild dose-toxicity when true MTD = dose 4 or 5.

Table 2.

Description of the scenarios: expected nTTP and Probability of DLT at Cycle 1.

	d1	d2	d3	d4	d5	d6
True MTD = d2
nTTP	0.18	0.28	0.36	0.41	0.43	0.44
p(DLT)	0.20	0.33	0.45	0.51	0.56	0.56
True MTD = d3
nTTP	0.11	0.18	0.28	0.36	0.41	0.43
p(DLT)	0.07	0.20	0.33	0.45	0.52	0.56
True MTD = d4
nTTP	0.05	0.11	0.18	0.28	0.36	0.41
p(DLT)	0.01	0.07	0.20	0.33	0.45	0.51
True MTD = d5
nTTP	0.05	0.06	0.11	0.18	0.28	0.36
p(DLT)	0.01	0.01	0.07	0.20	0.33	0.45

Bold entries correspond to values at the true dose.

MTD, maximum tolerated dose; nTTP, normalized total toxicity profile; DLT, dose-limiting toxicity.

Figure 1.

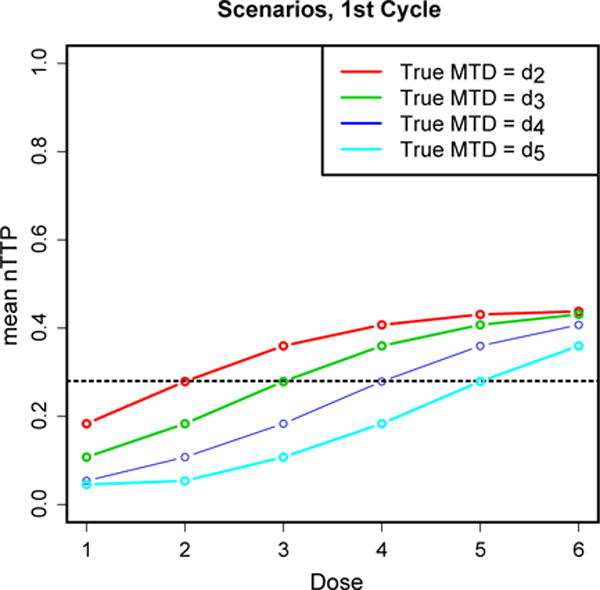
Expected nTTP at each dose level at cycle 1, when the true MTD is dose 2, 3, 4, and 5. The dashed horizontal line represents the target nTTP at 0.28.

Figure 2.

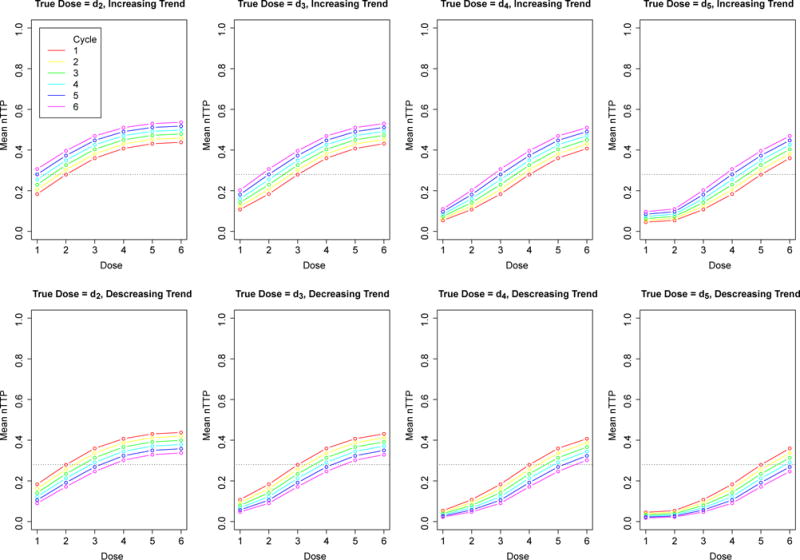
Expected nTTP at each dose level at each cycle when the true MTD is dose 2, 3, 4, and 5. The top panels are dose-toxicity curves with an increasing time trend; the bottom are dose-toxicity curves with a decreasing time trend. The dashed lines represents the targeted nTTP of 0.28.

3.3. Evaluation Criteria

To compare the RMD design with QLCRM, the percentage of correct selection (PCS) which is the proportion of the trials recommending the true target dose was evaluated. In addition, the percentage of patients assigned at each dose level was reported to evaluate the safety and efficiency of this dose-finding design in terms of safe dose allocation. To further indicate the safety profile, the nTTP and DLT distributions at each cycle using box-plots are presented.

4. Results

4.1. Identifying the MTD

The QLCRM was used as a benchmark in the evaluation. For comparison with QLCRM, proposed RMD design was applied to cycle 1 toxicity data only first, and then the RMD design was extended to multiple cycles of data (Table 3).

Table 3.

Dose recommendation percentage and allocation percentage in simulations with drop-outs due to DLT.

	Dose Recommendation %						Dose Allocation %						N. Cycles mean (sd)
	d1	d2	d3	d4	d5	d6	d1	d2	d3	d4	d5	d6
True MTD = d2
QLCRM	3	86	11	0	0	0	17	65	18	0	0	0	NA
RMD, cycle 1	6	84	10	0	0	0	32	65	3	0	0	0	NA
RMD, decreasing trend	3	94	3	0	0	0	22	74	4	0	0	0	2.5(2.2)
RMD, constant trend	6	89	5	0	0	0	24	72	4	0	0	0	2.1(1.8)
RMD, increasing trend	11	88	1	0	0	0	28	69	3	0	0	0	1.8(1.6)
True MTD = d3
QLCRM	0	3	84	13	0	0	9	14	56	20	0	0	NA
RMD, cycle 1	0	7	83	10	0	0	9	42	45	4	0	0	NA
RMD, decreasing trend	0	7	88	5	0	0	12	37	46	5	0	0	2.7(2.1)
RMD, constant trend	0	10	85	5	0	0	11	38	47	4	0	0	2.5(2.0)
RMD, increasing trend	0	11	86	3	0	0	12	35	48	5	0	0	2.3(1.9)
True MTD = d4
QLCRM	0	0	2	80	18	0	8	9	13	51	19	0	NA
RMD, cycle 1	0	0	2	81	17	0	10	14	19	48	9	0	NA
RMD, decreasing trend	0	0	7	87	6	0	9	15	19	48	9	0	3.3(2.1)
RMD, constant trend	0	0	7	86	7	0	10	16	19	37	9	0	2.7(2.0)
RMD, increasing trend	0	0	10	89	1	0	12	14	22	47	7	0	2.4(2.1)
True MTD = d5
QLCRM	0	0	0	4	78	18	6	8	8	12	46	20	NA
RMD, cycle 1	0	0	0	6	79	16	6	9	11	24	38	12	NA
RMD, decreasing trend	0	0	0	5	86	9	7	10	12	16	41	14	3.2(1.9)
RMD, constant trend	0	0	0	6	89	5	8	9	10	15	44	14	2.9(2.1)
RMD, increasing trend	0	0	0	5	90	5	9	9	11	16	45	10	2.8(2.2)

Results at the target dose are in bold. d_i is the dose level i (i = 1 to 6)

QLCRM, quasi-likelihood continual reassessment method; RMD, repeated measures design; MTD, Maximum Tolerated Dose.

The true MTD of dose 2 corresponds to a severe dose-toxicity scenario. The RMD had equivalent performance to the QLCRM when only cycle 1 data was used (PCS = 84%), but better over-dose control than QLCRM. Only 3% of patients in total were assigned doses above the target dose, compared to 18% using QLCRM design. When data from multiple cycles were used, an increase in the percentage of correct dose recommendation was observed with RMD across all the temporal trend assumptions. More than 65% of the patients were allocated at the target dose, with an overdose percentage less than 5%. Because of no subsequent data after the DLT, patients received a mean of 2.1 cycles of treatment out of the maximum of 6 cycles when there was no time trend occurrence of a patient stayed slightly longer in treatment (a mean of 2.5 cycles) in the case of decreasing toxicity over time, and for a smaller duration (a mean of 1.8 cycles) in the case of increasing toxicity over time. On average, when the toxicity profile did not change over time, 30% of the patients experienced a DLT at the first cycle and dropped out at the second cycle, and the cumulative drop-out rate due to DLT increased to 51% at cycle 3, and went all way up to 81% at cycle 6. As expected, the drop-out rate was lower when toxicity decreased over time, and higher when toxicity increased over time (Fig 3). Furthermore, with the RMD method, the percentage of selecting an over toxic dose was reduced compared to the QLCRM method (RMD, less than 5% of selecting a dose above the target dose when data from multiple treatment cycles were used; QLCRM, 11%). This indicates an improved over-dose control with RMD. Or in other words, when the target dose (dose level 2 in this case) is not recommended, RMD is more likely to recommend a safe lower dose level.

Figure 3.

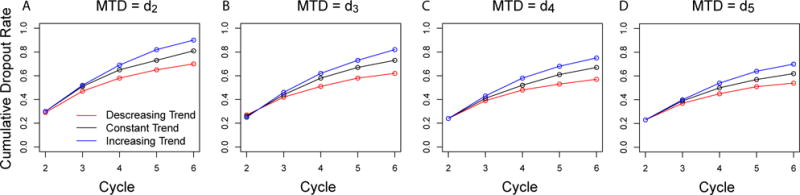
Cumulative percentage of dropouts due to DLT by cycle.

Similar performance was also observed when the true MTD was at dose level 3, where the agent was assumed to have an intermediate level of toxicity. The percentages of correct dose recommendation by the RMD approach were comparable to the QLCRM when only cycle 1 data was used, and higher when data for multiple cycles was used. Over-dose control was improved in all the scenarios. Patients were able to stay on treatment for a longer period, as the agent was considered to have an intermediate dose-toxicity relationship. Similar conclusions were drawn from the mild dose-toxicity scenarios where the true MTD was dose level 4 and 5.

The distributions of the observed nTTP scores and the number of DLTs reflects the safety of the patients included in the trial. The distribution of nTTP and DLT for scenarios when the true MTD = dose 2 (Fig 4) are presented, as this is the most toxic scenario. In case of a decreasing time trend, the median nTTP in the first cycle was around the target 0.28, with a tighter IQR compared to the QLCRM design, which indicates that more patients were treated closer to the target dose. After the first cycle, the median nTTPs decreased over cycles, which indicates a decreasing time trend in the toxicity. Therefore, the distribution of nTTPs over time provide a way to summarize and examine a possible time trend in toxicity. Similar conclusions can be drawn from scenarios where increasing or flat time trends were presented.

Figure 4.

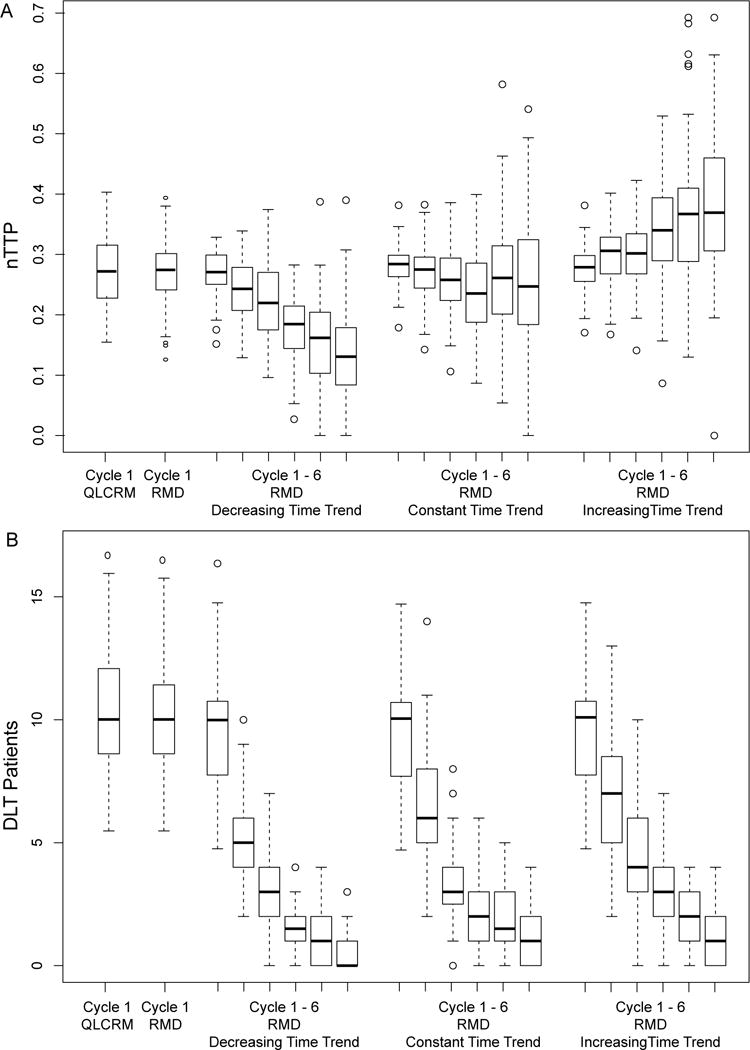
The distributions of observed nTTP score and number of DLTs from the 1000 simulated trials, for QLCRM, RMD using only cycle 1 data, RMD using data from 6 cycles with a decreasing (broken down by cycle), RMD using data from 6 cycles with a constant trend (broken down by cycle), and RMD using data from 6 cycles with an increasing time trend (broken down by cycle). Replication = 1000

The distributions of number of DLTs are similar between the QLCRM and the RMD when only cycle 1 toxicity was used. In cycle 1, the observed median number of DLTs is 10, consistent across all the scenarios (Fig 4). In the subsequent cycles, the occurrence of DLT dropped significantly likely due to the drop-out of patients who developed severe toxicities. However, the median occurrence of DLT in the subsequent cycles was lower in case of a decreasing time trend compared to constant or increasing time trend.

4.2. Sensitivity Analysis

Missing data is a prominent situation in a longitudinal analysis of phase I trials, as patients can drop-out due to either severe toxicity or disease progression. Therefore, additional simulations were conducted to investigate the impact of completely random drop-out on the performance of the RMD design, in addition to the DLT drop-outs. It is assumed that after cycle 1, there is a 10% chance of drop-out at random (simulating disease progression causing removal from treatment) at each of the following cycles. With additional missing data, no significant deterioration of the model performance was observed, with only a small decline in the percentage of the correction dose recommendation (a 6% decrease at most) across all scenarios. The RMD with multiple cycle data continued to out-performed QLCRM and RMD with only cycle 1 data in identifying the MTD.

5. Discussion

In conventional dose-finding designs for phase I clinical trials, toxicity data from late treatment cycles are not used in the dose escalation/deescalation decisions. The current development of molecularly targeted agents (MTAs) makes it necessary to account for the toxicity data from multiple treatment cycles. Unlike cytotoxic agents that are typically administrated for a limited number of treatment cycles, MTA administrations are often prolonged until disease progression [2][15]. A recent study found that more than half of the 445 patients in 36 clinical trials of MTAs developed their worse grade toxicity after the first cycle; 57% of the grade 3 or 4 toxicity events occurred after cycle 1 [2]. Besides the severe toxicity events, repeated and chronic occurrence of lower grade events can also significantly impair patient quality of life [16]. Using multiple-cycle toxicity profiles can potentially improve the evaluation of MTAs and immunotherapies because these agents are likely to induce few DLTs, but do result in multiple mild and moderate adverse events, which are considered unacceptable from a patient perspective, especially in cases of protracted administration [17][18].

This article presented a novel phase I design, RMD, that uses toxicity profiles from multiple treatment cycles during the dose-finding process. The RMD design used a quasi-continuous total toxicity profile (TTP) [6] that includes multiple adverse event types. Unlike traditional designs that simplify the toxicity data into a binary DLT endpoint, the TTP score captures the multidimensional nature of toxicity data and leads to a more comprehensive description of the toxicity data. Simulations were used to demonstrate that the RMD design consistently outperforms the design which only uses single treatment cycle data (QLCRM) in all scenarios considered. A Bayesian framework was adopted because it naturally fits with the adaptive nature of phase I dose-finding trials. Facilitated by an MCMC algorithm, the RMD was able to accurately estimate in all scenarios both the magnitude and direction of toxicity trends in late treatment cycles. Another feature of the Bayesian framework is that decision rules in dose-finding can be easily integrated as loss functions or Bayesian risk functions, and hence it provides the flexibility for clinicians to shape their objectives.

Although the results were simulation based, the scenarios closely mirror real-life situations where patients would stop treatment after experiencing a DLT or disease progression. Disease progression is modeled as a random 10% drop-out at every cycle; more elegant approaches to model drop-out due to progression will be explored as future work. Variation of decision rules can be specified with the RMD design. For example, the MTD can be defined as the dose associated with the nTTP score not only closest to the target, but also less than the target. Furthermore, by adopting a longitudinal model, the RMD has the potential to explore the temporal trend for cumulative toxicity from multiple cycles. This will also be formally investigated as part of the future extensions.

The RMD model assumes the same dose assignment for the same patient across multiple treatment cycles, i.e. no intra-patient dose-escalation or adjustment. However in practice, dose adjustments are common in the late treatment cycles. A study of 54 phase I cancer clinical trials of MTAs from 1999 to 2013 found around 20% of the patients had to be dose reduced after cycle 1 [19]. It is possible to extend RMD to allow dose adjustments/modifications. Finally, MTAs may have different toxicity-efficacy relationships compared to cytotoxic agents. A few studies reported that lower doses of MTAs may offer similar efficacy as higher doses [20][21][22]. As a result, the MTD may not be the optimal treatment strategy for MTAs. We plan to extend the RMD to incorporate both toxicity and efficacy endpoints from multiple cycles. In addition, no stopping rules have been put in place to stop the study earlier before the number maximum of patients has been enrolled. And early stopping will be considered in the future work.

In summary, this article proposes a new dose-finding method that accommodates multiple toxicity types over multiple treatment cycles in the dose-finding process. The simulations demonstrate that the RMD method performs well in terms of identifying the true dose, under realistic assumptions of patient drop-out due to DLT. It is acknowledged that this method requires close collaboration between investigators and statisticians, in terms of specifying toxicity types, severity weights, and target toxicity threshold. It is believed that close interaction is critical in all complex clinical settings, and the effort is clearly worthwhile in this case given its advantages over the conventional designs. In addition, an R package is under development to facilitate the use of the RMD design.

Appendix

Using matrix notation, the linear mixed effect model 6 can be rewritten as:

$$\mathit{y}=\mathit{x}{\beta }_1+(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)+W\mathit{\gamma }+\mathit{\epsilon }.$$ (15)

where y is a ${\displaystyle {\sum }_{i=1}^n{K}_i\times 1}$ vector of nTTP values (K_i is the observed maximum number of cycles of patient i). x indicates the dosage assigned to each patient at cycle 1; t is the cycle indicator. W is a ${\displaystyle {\sum }_{i=1}^n{K}_i\times n}$ design matrix where W_ij = 1 if the ith measurement is from the jth patient. γ is an n × 1 vector of random effects with variance ${\sigma }_{\gamma }^2$. ε is a ${\displaystyle {\sum }_{i=1}^n{K}_i\times 1}$ vector of exchangeable error terms with variance ${\sigma }_{\epsilon }^2$.

A MCMC algorithm for Bayesian inference of the model parameters is used. The conjugate priors for β₀, β₁, β₂, ${\sigma }_{\gamma }^2$, and ${\sigma }_{\epsilon }^2$ are available, and their full conditionals can be derived and recognized as a standard densities. The prior distributions are specified below:

$${\beta }_1~\mathrm{N}(u,v),$$ (16)

$${({\beta }_0,{\beta }_2)}^T~{\mathrm{N}}_2({\mathit{a}}_{\beta },B_{\beta }),$$ (17)

$${\sigma }_{\gamma }^2~\text{IG}(a_{\gamma },b_{\gamma }),$$ (18)

$${\sigma }_{\epsilon }^2~\text{IG}(a_{\epsilon },b_{\epsilon }),$$ (19)

where u, v, a_β, B_β, a_γ, b_γ, a_ε, and b_ε are hyper-parameters whose values are to be specified. To reflect a lack of prior information about the model parameters, the following hyper-parameters are chosen as an example:

$$u=1,v=1000,$$ (20)

$${\mathit{a}}_{\beta }={\left(0,0\right)}^T,B_{\beta }^{-1}=0.001\times {\mathbf{I}}_2,$$ (21)

$$a_{\gamma }=a_{\epsilon }=0.001,$$ (22)

$$b_{\gamma }=b_{\epsilon }=\mathrm{0.001.}$$ (23)

Sampling from the joint posterior $p({\beta }_0,{\beta }_1,{\beta }_2,\gamma ,{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2|\mathit{y})$ can be performed with a Gibbs sampling algorithm since the full conditionals can be analytically derived. At each iteration of the Gibbs sampling, model parameters can be sequentially drawn from the full conditionals below:

$${\beta }_1|{\beta }_0,{\beta }_2,\mathit{\gamma },{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2~\text{N(}{\mu }_{{\beta }_1}\text{,}{\sigma }_{{\beta }_1}^2\text{),}$$ (24)

where ${\mu }_{{\beta }_1}={\sigma }_{{\beta }_1}^2\left\{\frac{1}{{\sigma }_{\epsilon }^2}{\mathit{x}}^T\left(\mathit{y}-W\mathit{\gamma }-(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right)+\frac{u}{v}\right\}$, and ${\sigma }_{{\beta }_1}^2={\left(\frac{1}{{\sigma }_{\epsilon }^2}{\mathit{x}}^T\mathit{x}+\frac{1}{v}\right)}^{-1}$.

$${\beta }_0,{\beta }_2|{\beta }_1,\mathit{\gamma },{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2~{\mathrm{N}}_2({\mathit{\mu }}_{\mathit{\beta }},{\sum }_{\beta }),$$ (25)

where ${\mathit{\mu }}_{\beta }={\displaystyle {\sum }_{\beta }\left\{\frac{1}{{\sigma }_{\epsilon }^2}{\left(\mathbf{1},\mathit{t}\right)}^T(\mathit{y}-W\mathit{\gamma }-\mathit{x}{\beta }_1)+B_{\beta }^{-1}{\mathit{a}}_{\beta }\right\}}$, and ${\displaystyle {\sum }_{\beta }={\left(\frac{1}{{\sigma }_{\epsilon }^2}{(\mathbf{1},\mathit{t})}^T\right(\mathbf{1},\mathit{t})+B_{\beta }^{-1})}^{-1}}$.

$$\mathit{\gamma }|\mathit{\beta },{\sigma }_{\gamma }^2,{\sigma }_{\epsilon }^2~{\mathrm{N}}_n({\mathit{\mu }}_{\gamma },{\sum }_{\gamma }),$$ (26)

where ${\mathit{\mu }}_{\gamma }={\displaystyle {\sum }_{\gamma }\left\{\frac{1}{{\sigma }_{\epsilon }^2}{W}^T\left(\mathit{y}-\mathit{x}{\beta }_1-(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right)\right\}}$, and ${\displaystyle {\sum }_{\gamma }={(\frac{1}{{\sigma }_{\epsilon }^2}{W}^{T}W+\frac{1}{{\sigma }_{\gamma }^2}{\mathrm{I}}_n)}^{-1}}$.

$${\sigma }_{\gamma }^2|\mathit{\beta },\mathit{\gamma },{\sigma }_{\epsilon }^2~\text{IG}(u_{\gamma },v_{\gamma }),$$ (27)

where $u_{\gamma }=\frac{1}{2}n+a_{\gamma }$, and $v_{\gamma }=\frac{1}{2}{\mathit{\gamma }}^T\mathit{\gamma }+b_{\gamma }$.

$${\sigma }_{\epsilon }^2|\mathit{\beta },\mathit{\gamma },{\sigma }_{\gamma }^2~\text{IG}(u_{\epsilon },v_{\epsilon }),$$ (28)

where $u_{\epsilon }=\frac{1}{2}n+a_{\epsilon }$, and $v_{\epsilon }=\frac{1}{2}{\left\{\mathit{y}-W\mathit{\gamma }-\mathit{x}{\beta }_1-(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right\}}^T\left\{\mathit{y}-W\mathit{\gamma }-\mathit{x}{\beta }_1-(\mathbf{1},\mathit{t})\left(\begin{array}{c}{\beta }_0\\ {\beta }_2\end{array}\right)\right\}+b_{\epsilon }$.

During the elicitation process of target nTTP, a set of m hypothetical cohorts with variant toxicity profiles at cycle 1 is specified, to cover a reasonable range of possible toxicities and severities. For each hypothetical cohort, r = 1,…, m, physicians are asked for their decisions: whether the observation of such cohort would cause them to escalate, repeat, or de-escalate the dose for the next cohort. Denote the mean nTTP of the rth hypothetical cohort as $\overline{{\mathit{nTTP}}_r}$. Then the mean nTTP among the m cohorts is ordered according to their magnitudes: $\overline{{\mathit{nTTP}}_{(1)}}\le \dots \le \overline{{\mathit{nTTP}}_{(m)}}$. Denote D_(r) as the decision associated to $\overline{{\mathit{nTTP}}_{(r)}}$. If the associated decisions D₍₁₎,…, D_(m) correspond to a string of escalations, followed by repeats, and further followed by de-escalations, it is considered a consistent classification of the m cohorts, and would define the target nTTP as the average of the mean nTTP of the cohorts for which the physicians have decided to repeat the same dose:

$${\pi }_1=\frac{{\displaystyle {\sum }_{r=1}^m\overline{{\mathit{nTTP}}_r}\cdot 1(D_r=\text{repeat})}}{{\displaystyle {\sum }_{r=1}^{m}1(D_r=\text{repeat})}}$$ (29)

In this case, Ezzalfani et al. [6] elicited an expert with a set of hypothetical cohorts of three patients with various toxicity profiles, given the severity weights in Table 1. They first identified the cohorts associated with the decision to repeat the dose, and then compute the mean nTTP, $\overline{\mathit{nTTP}}$, for each of these cohorts. The $\overline{\mathit{nTTP}}$ values for these cohorts have an average of 0.28, and a range of [0.24, 0.32]. Therefore, the target was set as 0.28 based on the elicitation methods described above (Eqn. 29).