Effects of adaptation on numerosity decoding in the human brain

Abstract

Psychophysical studies have shown that numerosity is a sensory attribute susceptible to adaptation. Neuroimaging studies have reported that, at least for relatively low numbers, numerosity can be accurately discriminated in the intra-parietal sulcus. Here we developed a novel rapid adaptation paradigm where adapting and test stimuli are separated by pauses sufficient to dissociate their BOLD activity. We used multivariate pattern recognition to classify brain activity evoked by non-symbolic numbers over a wide range (20–80), both before and after psychophysical adaptation to the highest numerosity. Adaptation caused underestimation of all lower numerosities, and decreased slightly the average BOLD responses in V1 and IPS. Using support vector machine, we showed that the BOLD response of IPS, but not in V1, classified numerosity well, both when tested before and after adaptation. However, there was no transfer from training pre-adaptation responses to testing post-adaptation, and vice versa, indicating that adaptation changes the neuronal representation of the numerosity. Interestingly, decoding was more accurate after adaptation, and the amount of improvement correlated with the amount of perceptual underestimation of numerosity across subjects. These results suggest that numerosity adaptation acts directly on IPS, rather than indirectly via other low-level stimulus parameters analysis, and that adaptation improves the capacity to discriminate numerosity.

Highlights

• •Numerosity adaptation has long-lasting perceptual effects.
• •We investigated adaptation with fMRI multi-voxel classification techniques.
• •Numerosities were well classified in IPS (but not V1) before and after adaptation.
• •Adaptation changes the patterns of numerosity representation in IPS.
• •Adaptation increases decoding accuracy, both for the MVPA and human psychophysics.

Introduction

Humans share with other animals a non-verbal “approximate numerosity” system that allows reasonably accurate and rapid estimation of the number of elements in a visual scene. Some have suggested that this perceptual system may be the neuronal basis for more complex arithmetical abilities in humans (Dehaene, 1997), and accuracy in number estimation correlates with mathematical achievement (Anobile et al., 2013, Halberda et al., 2008, Mazzocco et al., 2011, Piazza et al., 2010, Pinheiro-Chagas et al., 2014).

There has been extensive research aimed at understanding the neural substrate underlying the number sense (for a review see: Eger, 2016; Piazza and Eger, 2015). Many electrophysiological studies in monkey have reported neurons selective to number, in the intraparietal sulcus and prefrontal cortex (Nieder, 2013, Nieder, 2016, Nieder et al., 2006, Nieder et al., 2002, Nieder and Miller, 2004a, Nieder and Miller, 2004b, Roitman et al., 2007, Viswanathan and Nieder, 2013). Neuroimaging studies have also revealed homologous number systems in humans. Number-specific BOLD activity has been recorded in the intraparietal sulcus (IPS) and in the prefrontal cortex (PFC) in humans performing number comparisons and non-verbal magnitude comparison tasks (Castelli et al., 2006, Fias et al., 2003, Piazza et al., 2004, Piazza et al., 2006, Piazza et al., 2007, Pinel et al., 2001, Pinel et al., 2004, Santens et al., 2010). These number-related parietal activations have been demonstrated to be already present in four-year‐old children (Cantlon et al., 2009, Temple and Posner, 1998), reinforcing the idea that the IPS is the site of the innate non-symbolic number processing system.

fMRI habituation paradigms have also revealed neural selectivity to number (Cohen Kadosh et al., 2011, Demeyere et al., 2014, He et al., 2015, Jacob and Nieder, 2009, Piazza et al., 2004, Piazza et al., 2007, Roggeman et al., 2011). The paradigm involves repeated presentations of a specific numerosity (to habituate populations of neurons tuned to that number), followed by an occasional “deviant” number, which elicits an activation that increases with the numerical distance between adapter and deviant. The strength of the BOLD signal in the right and left IPS is proportional to the ratio of the standard and deviant stimuli. That is to say that tuning increases with number, tending to be constant on a logarithmic axis. Importantly, fMRI adaptation signals in IPS were shown to be unaffected by low-level image properties, such as changes in the shape of the elements, or even in the way that numerosity was presented (non-symbolic or symbolic).

A powerful method extending the capability of functional imaging in humans is multivariate decoding or multi-voxel pattern (MVPA) analysis (Haynes and Rees, 2006, Kriegeskorte et al., 2006, Mahmoudi et al., 2012, Norman et al., 2006). MVPA is becoming increasingly popular in the neuroimaging community because it allows detection of differences between conditions with higher sensitivity than conventional univariate analysis. Various experiments have demonstrated that it is possible to decode numerosity in the intraparietal sulcus, at least over a restricted low range (Bulthe et al., 2014, Damarla and Just, 2013, Eger et al., 2009, Eger et al., 2015).

Using the novel approach of population Receptive Fields (Dumoulin and Wandell, 2008), Harvey et al. (2013) have provided firm evidence for the intuitively appealing notion that numerosity is organized in a “numerotopic” map structure, comparable to those in the primary sensory and motor cortex for more basic sensory attributes. They showed clear tuning of neural populations to numerosities in human parietal cortex, organized within a map structure, with a medio-lateral gradient over the range of 1–7. This topographically organized number-map did not depend on low-level stimulus features (such as area, dot size, circumference, density or feature type) which were carefully controlled individually in repeated experiments. Importantly, Harvey et al. compared the activation of IPS and V1 with respect to the contrast energy of the stimulus, and showed that while the primary visual cortex response was highest for the stimuli with highest energy, contrast energy was not relevant for the pattern of activity in IPS. They concluded that organizational properties described for numerosity extend topographic principles to representation of higher-order abstract features in association cortex.

However, it must be stressed that Harvey et al. deliberately chose to study a low range of numbers (1–7), almost within the subitizing range where discrimination is very high, leaving open the possibility that higher numerosity may use different and more distribute cortical code. Also previous studies using repetitive suppression and decoding have measured numerosity up to maximum 30 items, well above the subitizing range but below the range where other mechanisms, such as analysis of visual texture, may play a role (Anobile et al., 2015a).

One of the most important psychophysical techniques is adaptation. Burr and Ross (2008) showed that numerosity is adaptable: adapting to a patch with large numbers of items causes patches of lower numerosity to appear much less numerous – and vice versa. Several researchers have suggested that the adaptation does not act directly on numerosity, but indirectly through texture-density (Dakin et al., 2011, Durgin, 2008, Durgin and Huk, 1997, Morgan et al., 2014, Tibber et al., 2012), but there is now much evidence to suggest that numerosity and texture are processed by distinct mechanisms (Anobile et al., 2016, Anobile et al., 2015a, Anobile et al., 2014, Anobile et al., 2015b, Fornaciai et al., 2016, Ross and Burr, 2010, Stoianov and Zorzi, 2012). However, it is still not clear whether adaptation acts directly on number mechanisms, or indirectly through more low-level texture mechanisms.

Using multi-voxel pattern analysis, we examined here whether it is possible to decode high numerosities in IPS and/or V1, and how adaptation affects decoding of number. We used a novel adaptation paradigm (Aagten-Murphy and Burr, 2016), where rapid adapting and testing stimuli were separated by more than 20 s, but still producing psychophysical adaptation to number. Unlike classical fMRI habituation paradigms, this procedure allows the activity evoked by the adapter and the test stimuli to be temporally dissociated. We provide clear evidence that high numerosity can be decoded in IPS, but not V1, and that adaptation in IPS improves the accuracy of numerosity decoding.

Methods

Subjects

Ten healthy adults (seven female, three male between 25 and 27 years) with normal or corrected-to-normal acuity were included in the study. All the subjects underwent both a psychophysical and an fMRI experiment. This study was conducted with ethical approval of the Stella Maris Scientific Institute Ethics Committee.

Stimuli and procedures

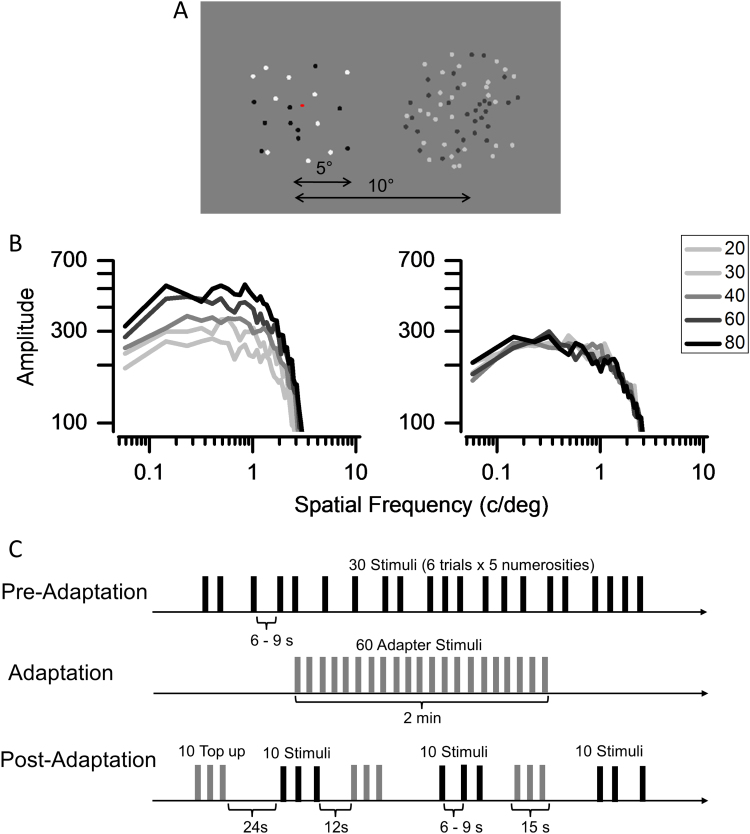
The visual stimuli presented were clouds of non-overlapping dots (of 0.3° diameter), half black half white, of varying numerosity (20, 30, 40, 60 or 80 dots) confined within a 10° diameter patch presented in central vision (Fig. 1A). The contrast of stimuli were scaled with the square-root of the numerosity to balance the overall amplitude spectrum. Fig. 1B shows the amplitude spectra of the random dot fields of various numerosities used in the experiment: after energy balancing all are in overlap, indicating that the contrast-scaling was successful. After the rescaling, the Michelson contrast of each dot varied from a maximum of 90% for numerosity 20–45% for numerosity 80%. The contrast of the adapting stimulus (80 dots) was very low, only 25%, since adapting to low-contrast stimuli avoids local afterimage effects, and is known to produce strong adaptation effects (Burr and Ross, 2008). Subjects were required to maintain gaze on a red fixation dot in the screen center for the entire experiment.

Fig. 1.

Stimuli and procedures. (A): examples of stimuli used in the psychophysical experiment: subjects fixated the red dot and reported which of the two patches (central or peripheral) appeared more numerous. Only the central patch was shown during the fMRI experiment. (B): amplitude spectra of the various numerosity stimuli, before (left) and after (right) scaling the local contrast of the dots with the square root of the numerosity. (C): schematic representation of the three phases of the imaging experiment. In the pre-adaptation condition, the five different numerosities were presented six times each, with the inter stimulus interval randomly varying between 6 and 9 s. During the adaptation sequence (initially 2 min, then 15 s top-up) the highest numerosity (80) was presented in alternating periods of 0.75 s on 0.75 s off. Top-up adaptation (15 s) was presented during the adaptation acquisition every 10 trials, followed by a 24 s pause.

In the psychophysical experiment the stimuli were displayed in a dimly lit room on a DELL monitor with 1920×1080 resolution at 60 Hz refresh rate, mean luminance 60 cd/m², viewed binocularly from 57 cm. During fMRI the stimuli were presented through liquid crystal goggles (VisuaStim XGA Resonance Technology at a resolution of 800×600 voxels, subtending 30°×22.5° at an apparent distance of 1.5 m, with mean luminance of 20 cd/m²) after gamma correction. The stimuli were generated and presented under Matlab 7.10 using PsychToolbox routines (Brainard, 1997).

During both the psychophysical and the rapid event related fMRI experiment subjects were initially presented with the five numerosities tested in pre-adaptation sessions, then they were adapted to the highest numerosity (80 dots), and tested again in post-adaptation sessions (Fig. 1C). The psychophysical testing was performed the day before the scan.

Psychophysical procedure

In the psychophysical experiment the subjects were exposed to two simultaneous patches separated by 10°, one at fixation (test patch), and the other in the periphery at 10° eccentricity (probe patch), both during the pre- and the post-adaptation sessions. Stimuli were shown for 1 s, after which subjects indicated by button-press which of the two seemed more numerous. After a variable delay of 6–9 s the next trial commenced (Fig. 1C). Subjects were randomly presented with 20, 30, 40, 60 or 80 dots in the test (central) patch. The number of dots in the probe was initially equal to the test, then varied from trial to trial depending on subject response, with numerosity determined by the QUEST algorithm (Watson and Pelli, 1983), perturbed with a random Gaussian distribution of 0.15 log-units standard deviation. The local contrast of the probe was scaled by the square-root of the numerosity ratio, so it had the same overall contrast as the test. Five independent quest algorithms were run simultaneously throughout the session.

After the pre-adaptation sessions, a period of rapid adaptation begun for 2 min, where subjects viewed repetitive presentations of the adapting stimulus (80-dot patch). During this period the dots in the adapting patch was flashed intermittently, 0.75 s on, 0.75 s off, as this was found to produce the strongest adaptation (Aagten-Murphy and Burr, 2016). During the adaptation period, only one patch was presented in the central visual field, and subjects were not required to make any response. After adaptation, the five different numerosities were tested again. After every 10 stimuli (again separated by a random period of 6–9 s) we topped adaptation with a 15-s adapter stimulus sequence (alternating as before), followed by a delay of 24 s, then ten new test stimuli.

In the psychophysical experiment each subject performed two pre- and two post-adaptation sessions, for a total of 60 trials per session. Each subject underwent a preliminary training period to familiarize themselves with the task, and only after their judgments were stable and accurate were the data recorded.

fMRI

In the fMRI experiment, only the central stimuli were presented using MR compatible goggles with the same timing and numerosities used in the psychophysical experiment (shown in Fig. 1C). Subjects observed the stimuli passively and no response was required. Stimulus presentation was synchronized with the fMRI sequence at the beginning of each run to analyse the BOLD response as a rapid event-related design, with a random separation between presentations, of 3, 6 or 9 s. Each subject performed four pre-adaptation runs and two post-adaptation runs. Each of the five numerosities were presented six times within each run, hence a total of 120 and 60 trials were recorded for each subject during the pre- and the post-adaptation runs. The initial adaptation to an 80-dot stimulus was like the psychophysics procedure: 2 min presentation, refreshed every 0.75 s. This was presented during the anatomical scan. Like the psychophysical procedure, adaptation was “topped up” with a 15 s exposure after every ten trials. A long temporal gap (24 s) was interspersed between the top-up the test stimuli to disentangle the contribution of top-up presentation to the BOLD response of the test.

MRI data were acquired using a GE 1.5 THD Neuro-optimized System (General Electric Medical Systems) fitted with 40 mT/m high-speed gradients. Each session included a whole brain set of anatomical images with T1-weighted contrast. T1-weighted scans were acquired with TR=8.4 ms, TE=3.9 ms, flip angle=8°, FOV=256×256 mm², slice thickness=1 mm. Echo Planar Imaging (EPI) sequences were used for the fMRI data acquisition (TR=3000 ms, TE=35 ms FOV=192×192 mm, flip angle=90°, matrix size of 64×64 and slice thickness=3 mm). Head movement was minimized by padding and tape.

Data analysis

Psychophysical data were analysed by constructing psychometric functions, plotting the proportion of trials where the probe appeared more numerous than the test against numerosity of the probe, and fitted with cumulative Gaussian functions to yield estimates of the point of perceived equality (PSE: the median of psychometric function) and coefficient of variance (CoV: standard deviation of psychometric function normalized by the physical numerosity), that is an estimate of precision. The adaptation effect was calculated as the difference in PSE between post- and pre-adaptation sessions divided by the pre-adaptation PSE. The PSE and CoV differences between pre-and postadaptation were both tested with a repeated measure ANOVA with numerosity and adaptation condition as factors with 5 and 2 levels respectively.

Imaging data were analyzed with Brain Voyager Qx (version 2.8 Copyright © 2001–2015 Rainer Goebel). Anatomical images were spatially normalized using the Talairach and Tournox (1988) atlas to obtain standardized coordinates for the region of interest. Functional data were pre-processed to compensate for systematic slice-dependent differences in acquisition time (using cubic spline), three-dimensional motion correction (using Trilinear/Sync interpolation realigning data to the first volume of the first scan) and temporal filtered (High-pass filter GLM with Fourier basis set, including linear trend, with 2 cycle). No spatial smoothing was used.

We analyzed the data with a multistudy-multisubjects GLM with one regressor for each numerosity with “top-up” adapters defined as “predictors of no interest”. To create the design matrix we used the BVA–Predictor Tool (1.5.2, J.M. Born, Maastricht, The Netherlands), where data from the pre- and post- adaptation runs were entered together to take into account the acquisition time difference between sessions. Regressors were convolved with the canonical hemodynamic response function (HRF) and beta values calculated and exported to in-house Matlab programs.

The betas estimated by the top-up regressor were never used in the MVPA, but used to retinotopically define the maximum extent covered by the stimuli in the primary visual cortex and in IPS, avoiding statistical circularity. This activation was combined with anatomical criteria to define two regions of interest (ROI) on each individual subject. The first bilateral ROI was defined along the central part of the primary visual cortex and the second of between 1000 and 1600 functional voxels along intraparietal sulcus.

The beta values of each trial extracted from the individual voxels of each ROI were exported to Matlab and used for pattern recognition analysis based on linear support vector machine (SVM). LibSVM was used to train and test classifiers with a multiclass algorithm, with a fixed regularization parameter C=1. For each scan the average beta value for each numerosity across all voxels of the region was subtracted. We also used different normalization procedures, obtaining similar results (not reported here). Given the large extent of the IPS ROI, we used a searchlight analysis (Kriegeskorte et al., 2006), training and testing the classifier to discriminate within spheres of radius three functional voxels, positioned to span all voxels contained in the ROI (sphere centers separated by 1 voxel in each X, Y and Z). To estimate accuracy for the whole area, we averaged the results for all spheres.

Our first analysis was a pairwise classification between the two adaptation states, irrespective of numerosity. We then trained and tested three different multiclass models. In the first model classifiers were trained using 105 pre-adaptation trials (21 for each numerosity) and then tested with the 15 left-out trials (3 per numerosity), and also with 15 trials randomly drawn from the post-adaptation sessions. Similarly, classifiers were trained with 45 (9 for each numerosity) post-adaptation trials and then tested with the 15 left-out trials (3 per numerosity) and with 15 trials randomly drawn from pre-adaptation sessions.

In these two models we evaluated the ability of the model to classify the five numerosity classes, both in the condition in which it was trained, and the other adaptation condition. If the model successfully classified all or some numerosities of the adaptation condition on which it was not trained, it would imply that the adaptation did not change the pattern of BOLD responses to those numerosities. The third model was trained with 45 pre- and 45 post-adaptation trials, and tested all the left-out trials, 15 for pre- and 15 for post-adaptation. For each of these models, the left-out trials (n=3) were selected randomly and kept separated from the training dataset. For all three models, the procedures were repeated 100 times, with different random draws of the 15 left-out trials, to ensure that all the trials were tested, and to give a measure of variability. The average accuracy of the classifier across bootstraps and across numbers was calculated for each sphere of the IPS ROI or for all V1 region. In a subsequent analysis we selected in the IPS ROI the fifty spheres with the highest overall decoding accuracy (averaged across number) to compare the decoding accuracy across numerosities.

Classification accuracy was reported both as proportion correct, and converted to d-prime (probit score after correction for chance classification), allowing comparison of performance between the three different models, with different numbers of classes. D-prime is defined as:

$$p={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi \left(x-d^{\prime }\right){\mathrm{\Phi }}^{m-1}\left(x\right)\mathit{dx}$$ (1)

where p is the proportion correct classification, $\varphi$ the gaussian distribution, Φ the integral of the gaussian distribution, m the number of classification categories (2, 5 or 10). We checked our calculation against published tables (Hacker and Ratcliff, 1979).

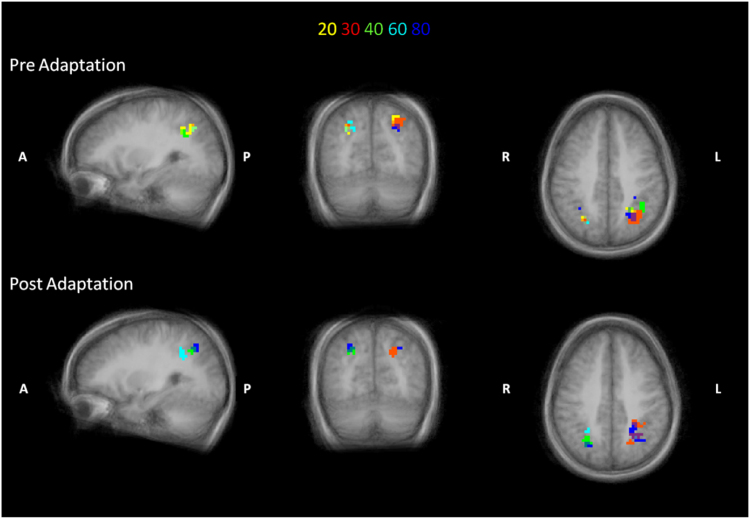
To view on ​the brain the voxel selective for numerosity, the 50 spheres selected for highest accuracy on the ten-class model were plotted back to the brain surface, thresholding the accuracy at the average value for the five numerosities, separately for the pre- and post-adaptation conditions for each subject. The average of the accuracy of the spheres was assigned at each voxel. The resulting spatial selectivity accuracy maps created in all subjects were aligned to the averaged brain. The probabilistic value of each voxel was calculated as the relative number (percentage) of subjects leading to above threshold accuracy in that location and used to create the probabilistic spatial selectivity of Fig. 10, with a minimum threshold of at least five subjects.

Fig. 10.

Distribution of the probability maps across subjects when the voxels of the spheres with the highest decoding accuracy for the ten-class model are plotted on the average brain surface. The color scheme differentiates the number decoded before (first row) and after (second row) adaptation. The threshold corresponds to 5 subjects with above-average accuracy for the specific numerosity. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Results

Psychophysics

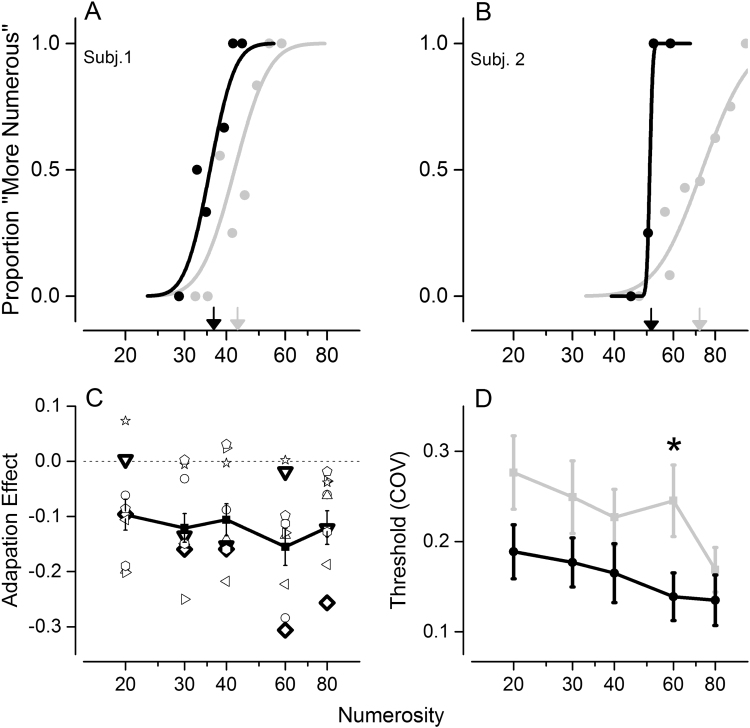
We first measured adaptation to number psychophysically, using the same protocol necessary for the fMRI experiment to disentangle the adapter from the test BOLD response that required very long pauses (24 s). We did this separately, outside the scanner, as the psychophysical technique required the simultaneous presentation of a comparison patch, which would have influenced the BOLD response. In line with previous experiments in the literature (Burr and Ross, 2008), and despite the long pause, adaptation to high numerosity led to an underestimation of the perceived numerosity, consistent with (Aagten-Murphy and Burr, 2016). Fig. 2A and B show examples of psychometric functions for two subjects both before (light gray curve) and after (black curve) adaptation for number 40 and 60 respectively. Adaptation shifted psychometric curves leftward (indicating underestimation), as reported in previous studies (Burr and Ross, 2008, Ross and Burr, 2012), and also made them steeper (indicating increased precision in judgments).

Fig. 2.

Psychophysical effect of adaptation to 80 dots. (A) and (B): sample psychometric functions before (light gray) and after (black) adaptation to 80 dots, for a standard of 40 (A) and 60 dots (B). Arrows on the abscissa indicate the point of subjective equality (PSE). (C): average adaptation effect across subjects. Open symbols refer to individual subjects, while the group average±sem is shown in black (n=10). Subjects 1 and 2 shown in (A) and (B) are marked in bold, and correspond to the triangle and the diamond respectively. (D): coefficient of variation (CoV) before (gray line) and after (black line) adaptation.

Fig. 2C shows the magnitude of the adaptation effect for the various numerosities, expressed as change in PSE relative to the pre-adaptation baseline, normalized by the baseline PSE, both for the individual subjects and for the group average. As expected, given the long pause and the decay of the adaptation effect, the effect was less than observed with longer adaptation, about 10%, statistically significant. The repeated measure ANOVA revealed a main effect of adaptation (F(1,9)=32, p<0.001). The coefficient of variance (CoV) also decreased after adaptation. The repeated measure ANOVA reported a main effect of adaptation (F(1,9)=9.5, p<0.01).

Functional imaging

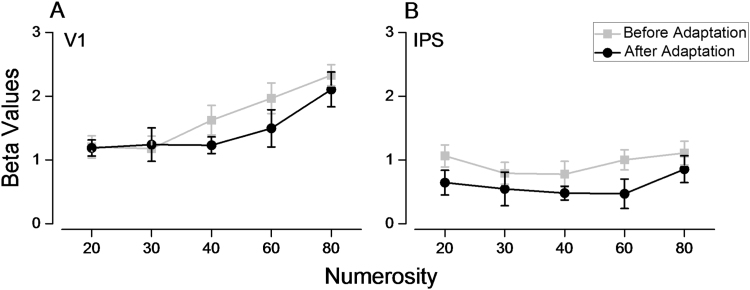
Once we had verified that number adaptation occurs under these conditions, we used this same adaptation paradigm for the fMRI experiment. Subjects were scanned as they viewed dot clouds of varying numerosity in central vision, both before and after adaptation. It is important to note that unlike many BOLD habituation paradigms, the temporal gap, which was longer than the hemodynamic response, allowed for separation of the BOLD signals generated by the two stimuli. A multi-study multi-subject GLM revealed no change in activity for the contrast “pre-adaptation versus post-adaptation” at the whole brain level. Fig. 3 shows average beta values extracted from two anatomically defined ROIs along the calcarine and the intraparietal sulci (see methods). Although the Fourier spectra were well matched in overall power (Fig. 1), we observed a small increase in V1 BOLD response with numerosity (F(4,36)=22.572, p<0.05). This increase is consistent with the known compressive non-linear contrast response functions of neurons and of BOLD responses (Boynton et al., 1999). After adaptation there was a small but non-significant decrease of V1 activity (F(1,9)=2.740, p=0.132). In the IPS ROI there was no difference in overall BOLD response across number (F(4,36)=1.528, p=0.215). Adaptation induced a homogeneous decrease in BOLD at all numerosities, but again, not significant (F(1,9)=3.857, p=0.08).

Fig. 3.

Average BOLD response (beta values) of the mean signal for the V1 (A) and IPS (B) ROIs, before (gray line) and after (black line) adaptation averaged across subjects. There was a small but non-significant decrease of beta value after adaptation in both areas, and a small and significant increase with numerosity in V1.

We used pattern recognition analysis based on linear support vector machine (SVM), first to determine whether adaptation states could be decoded, then whether numerosity could be decoded, both in IPS or V1. We always used the same number of trials in the pre- and post-adaptation conditions for the analysis. Despite the small and non-significant differences in beta values of pre- and post-adaptation, the SVM decoded well the adaptation state (pre- versus post-adaptation, irrespective of numerosity), both in V1 and in the extended IPS, with an average accuracy across subjects of 0.78±0.04 and 0.8±0.02 respectively. This result shows that adaptation does affect the BOLD response. Although the psychophysical effect was only 10%, it changed the response pattern of voxels sufficiently for the model to decode the state reliably.

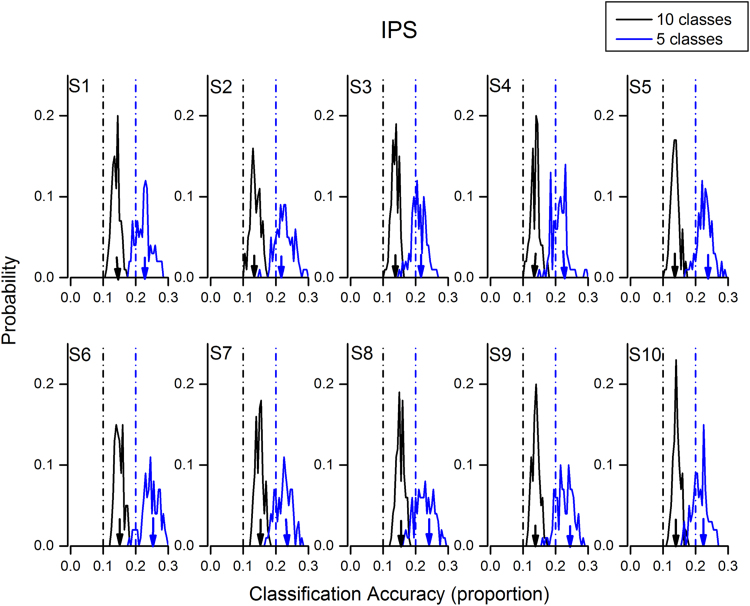
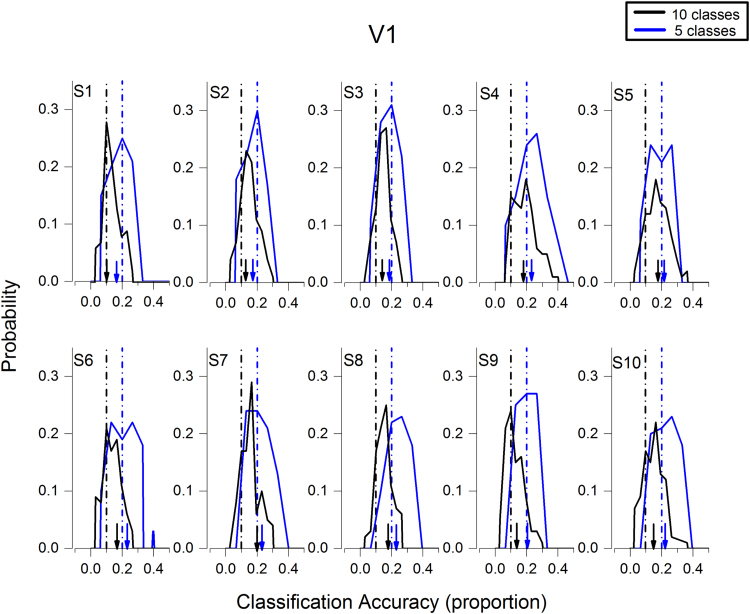
We then tested the ability of the model to classify different numerosities, using the entire regions (V1 and IPS separately) as ROIs, first for the unadapted condition, then on all 10 classes (five numerosities before and five after adaptation). Consistent with previous work on lower numbers (for a review see: Piazza and Eger, 2015), IPS decoded the numerosities reliably for all subjects. The blue curves of Fig. 4 show the distribution of the decoding accuracy, averaged over numerosities, for the 100 bootstrap cross-validation reiterations. Despite the extent of the region under study, and the inevitable noisiness from voxels not participating in numerosity coding, the model decoded number quite well. For all subjects the bulk of the bootstrap distribution classification accuracy was greater than chance (0.2). As the bar graph of Fig. 6A show, the average decoding accuracy was 0.23 (s.e.m=0.003), or d′=0.13 (s.e.m=0.01) for the five classes trained on pre-adaptation, and 0.22 (s.e.m.=0.004), or d′= 0.10 (s.e.m= 0.01). Both were significantly greater than chance (Accuracy: five class trained on pre-adaptation t(9)=9,9, p<10⁻⁵; five class trained on post-adaptation t(9)=5.7, p<10⁻⁵). On the other hand, for V1 (Fig. 5), the cross-validation bootstrap reiterations straddle chance level, showing that V1 failed completely to classify number significantly in any subject. The average decoding did not differ significantly from chance (Fig. 6B: Accuracy: five class trained on pre-adaptation t(9)=0.9, p=0.37; five class trained on post-adaptation p=0.6).

Fig. 4.

Probability distributions of the bootstrap validations of classification accuracy in the IPS ROI, for pre-adaptation trials (5-class model: blue curves) and for all pre- and post-adaptation trials (10-class model: black curves). The black and blue vertical dashed lines show chance performance for the 5- and 10-class models respectively. For all subjects, at least 70% of trials were better than chance. The color-coded arrows show average decoding accuracy for the two conditions, reported in the bar graphs of Fig. 6. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

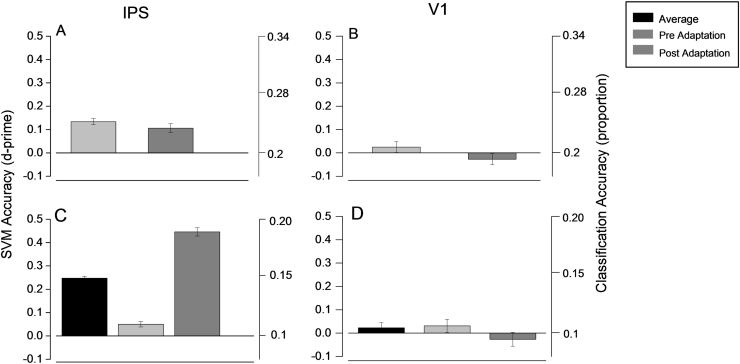
Average decoding accuracy for the IPS and V1 ROIs. The results are taken from Fig. 4, Fig. 5, and expressed as d-prime (Eq. (1)) to allow comparison between the 10- and 5-class models (proportion correct shown on ordinates at right). Error bars show ±1 s.e.m., calculated between subjects. The light bars refer to pre-adaptation trials, the dark bars to post-adaptation trials and the black bars the average. (A) and (B). Five-class model for IPS (A) and V1 (B) ROIs, training on either pre-adaptation trials (light bars) or post-adaptation (dark bars). (C) and (D). Ten-class model for IPS (A) and V1 (B) ROIs, training on both pre- and post-adaptation trials in all cases.

Fig. 5.

Probability distributions of the bootstrap validations of classification accuracy in the V1 ROI. All conventions as for Fig. 4. The distributions are clearly centered around chance. Averages reported in Fig. 6. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

To test the effect of adaptation on numerosity classification, we trained and tested the model on all 10 classes (5 numerosities pre- and post-adaptation). If adaptation had no effect on the activity pattern of voxels, we would expect a two-fold drop in accuracy (after correcting for chance), as the pre- and post-conditions would be confusable. On the other hand, if adaptation changed only specific numbers, rather than the whole network, we would expect better accuracy on the numbers affected. The distributions in Fig. 4 show that in IPS, the model succeeded in classifying all ten classes, for all 10 subjects. The black bars of Fig. 6C show that the model worked well for both pre- and post-numerosity stimuli, when averaging accuracy over numerosities (Accuracy: 10 Classes t(9)=26.2, p<10⁻⁵). The decoding was also significant when considering the two adaptation conditions separately (light and dark gray. Accuracy: 10 Classes PRE t(9)=4.4, p<0.002; Accuracy: 10 Classes POST t(9)=21, p<10⁻⁵). Interestingly, the decoding was much higher for the post-adaptation trials, with d′=0.44, compared with 0.05 for the pre-adaptation trials. This cannot result simply from a stronger BOLD signal, as the average beta in IPS decreased after adaptation. Figs. 5 (and 6D) shows that V1 was not able to classify numerosities in this condition, either pre-or post, as for the five-class model (10 Classes t(9)=0.57, p=0.58; Accuracy: 10 Classes PRE t(9)=0.76, p=0.46; Accuracy: 10 Classes POST t(9)=−0.18, p=0.85).

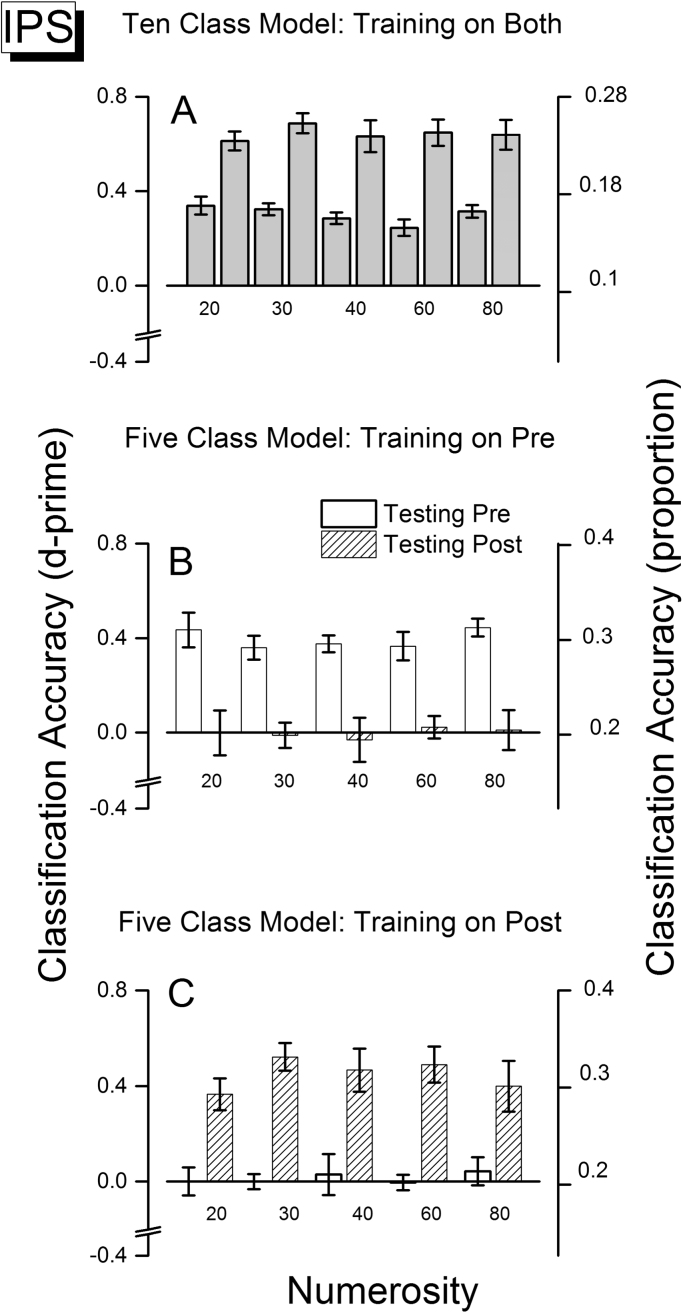
Having established that IPS as a whole does classify number well, we used the searchlight analysis to examine in more detail how adaptation selectively affected decoding of different numbers, and whether there are best-classification foci within the extensive ROI. We selected the 50 spheres with the highest classification accuracy averaged across numbers, first for the ten-class model, and measured classification accuracy as a function of numerosity. The selected spheres with best accuracy spanned the whole region of IPS, with a tendency to cluster around two foci (discussed further later). The results for the three classification models for IPS ROI are shown in Fig. 7. The first row shows results for when the classifier was trained simultaneously on ten classes, comprising both pre-and post-adaptation trials. IPS discriminated numerosity well, both when tested on pre-adaptation and post-adaptation data. Within each adaptation condition, classification accuracy was similarly good for all numerosities, showing that the region represents the entire range of numerosities tested in both conditions. As we found before for the whole region, decoding was more accurate for the post- than the pre-adaptation conditions. The significance of all the effects described above was tested with a two way ANOVA with numerosity and adaptation condition as factors with 5 and 2 levels respectively. There was a main effect of adaptation (F(1,9)=231, p<0.001), no significant effect of numerosity (F(4,36)=0.6, p=0.65) and no interaction between number and adaptation (F(4,36)=0.54; p=0.73).

Fig. 7.

Average classification accuracy (expressed in d-prime) for the fifty spheres with the best classification accuracy for the particular model used within the IPS ROI. The scale at right shows proportion correct classification. Error bars show the s.e.m. calculated over subjects. (A). Classification accuracy for the ten-class model, training with trials from both pre- and post-adaptation sessions. (B). Classification accuracy for the five-class model, training with pre-adaptation trials and testing with the left-out trials from pre-adaptation sessions (white bars) and with the same number of trials from post-adaptation sessions (hatched bars). (C). Classification accuracy for the five-class model, training with post-adaptation trials and testing with the left-out trials from post-adaptation sessions (hatched bars) and with the same number of trials from pre-adaptation sessions (white bars).

We analysed the average confusion matrix for the ten classification classes, but found no significant hotspots, implying no systematic misclassification errors.

The second row of Fig. 7 shows the classification results when the classifier was trained with pre-adaptation trials then tested with the left-out pre-adaptation trials (white bars) or with the same number of post-adaptation trials (hatched bars). Again there was good classification accuracy (Fig. 7B) when tested on pre-adaptation trials (white bars) constant across numerosity. However, the same classifier did not classify post-adaptation trials, shown by the hatched bars straddled the 0 chance level. Adaptation greatly interfered with the way numerosity information is distributed, reinforcing the suggestion that adaptation profoundly changes the entire network. Furthermore, adaptation affected classification equally for all numerosities, implying that no single numerosity was particularly affected by the adaptation, but rather the whole network was altered. The two way 5×2 ANOVA revealed a strong main effect of adaptation (F(1,9)=170, p<0.001), no significant main effect on number (F(4,36)=0.59, p=0.66) and no interaction between number and adaptation(F(4,36)=0.27; p=0.89).

The third row shows the classification results when post-adaptation trials were used to train the classifier. Again, IPS classified all the numerosities well in the same adaptation condition as the training. Indeed, classification over the 50 selected spheres was very similar to that observed for the whole region, consistent with the large spread of the sphere along the ROI. Again, the classifier trained with post-adaptation trials could only classify post-adaptation trials, with no generalization to pre-adaptation trials, indicating that the adaptation interfered with the coding of numerosity. The two way 5×2 ANOVA revealed a strong main effect of adaptation (F(1,9)=152, p<0.001); no main effect of numbers (F(4,36)=0.83, p=0.51), no interaction between number and adaptation (F(4,36)=0.86, p=0.49).

How does the classification compare with human performance? We predicted the classification accuracy of human observers from their psychophysical data (Fig. 2) by assuming that the internal state of numerosity representation can be approximated by a gaussian distribution of standard deviation given by the JND. Specifically, to calculate the predicted classification accuracy, for each subject and numerosity, we centered a gaussian of appropriate standard deviation at the number to be classified, and counted the proportion of responses at that number relative to all other numbers falling within the gaussian. The average results of predicted accuracy are 0.53 for pre-adaptation trials and 0.64 for post-adaptation, corresponding to d-prime values of 1.11 and 1.45 respectively. Clearly they are far higher than the classification of the fifty best spheres, but this is to be expected, as psychophysical thresholds tend to follow best, rather than average, neural response (Parker and Newsome, 1998). Interestingly, however, both the human psychophysics and the SVM show better classification after adaptation than before.

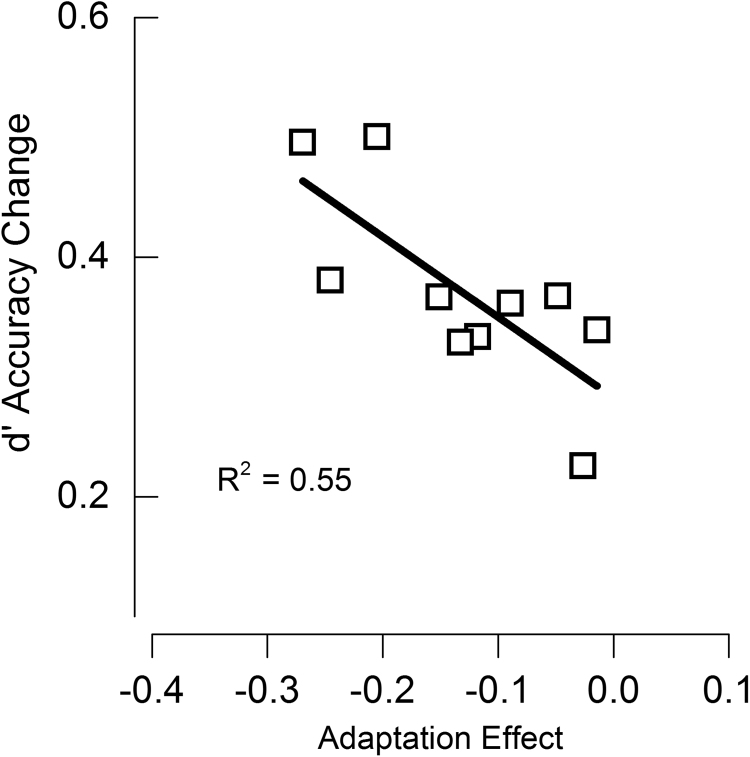
Although ten subjects are a small sample, we examined the correlation between the psychophysical and fMRI measurements, plotting the improvement in accuracy of pre- and post-adaptation (averaged for the three highest numerosities) as a function of the magnitude of psychophysical adaptation for each subject (Fig. 8). Fig. 8 shows that there is a significant negative correlation (ρ=−0.7,R-square=0.55, p<0.01): the stronger the psychophysical effect of number underestimation, the higher is the increase in classification accuracy after adaptation. This is further evidence that psychophysical adaptation effect is linked to the precision of the neuronal coding.

Fig. 8.

Improvement in decoding accuracy after adaptation (difference in d′ for the two conditions of the ten-class model) plotted against the magnitude of psychophysical adaptation (expressed as proportional change in PSE). Data were averaged over the highest 3 adaptation conditions (40, 60 and 80), where the effects were expected to be greater. Each data point refers to a single subject.

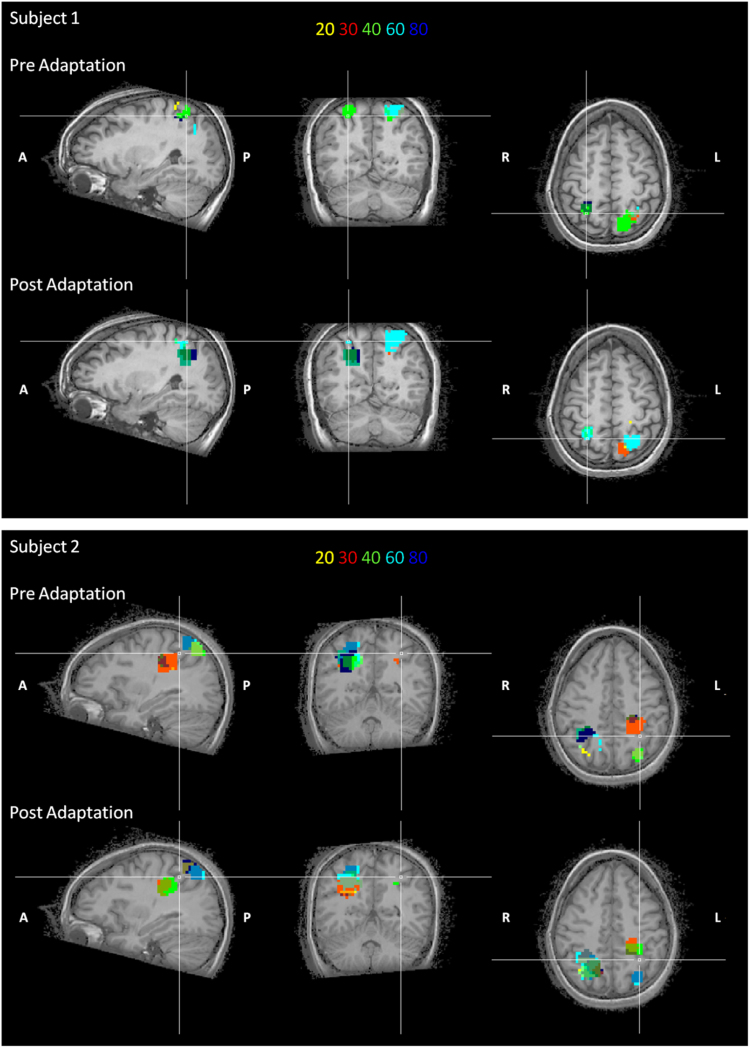
The ROIs of IPS explored by the searchlight procedure are very extended. To highlight the position of possible foci for numerosity processing in these regions, the fifty spheres with the highest average classification accuracy for all three models were plotted back on each subject's brain anatomy. The overlap between the 50 spheres of all three models was quite extensive: 52±10% of spheres were in common between the 10-class and 5-class models, with common spheres scattered over the whole ROI (implying 90% voxel overlap). We therefore report here examples of only the 10-class model (using both pre- and post-adaptation training). For all subjects, the selected 50 spheres cover a very extensive region, indicating that they are well distributed along the sulcus. Along the intraparietal sulcus four subjects out of ten showed only one large continuous region in both hemispheres representing all numerosity selectivities (for example Fig. 9A, Subject 1), while the remaining subjects had two foci, where the different numerosity selectivities overlapped (for example Fig. 9B, Subject 2) at least in one hemisphere. The Talairach coordinates of these two foci are reported in Table 1. Given that the region was selected on the average performance across all numbers, we analysed whether different sub-regions classified with higher than average accuracy particular numerosities. We set as display threshold the average accuracy separately for the pre- and post-adaptation conditions, for each individual subject. In the two example subjects shown in Fig. 9 the voxels with higher-than-average accuracy were clustered into sub-regions for each of the five numerosities, rather than being randomly intermingled. The clustering differed from subject to subject. After adaptation, the spatial layout for numerosity preference changed, with a tendency of similar clusters of voxels to shift decoded category towards higher numerosities.

Fig. 9.

Examples of maps obtained by labeling the voxels of the spheres with the highest decoding accuracy for the ten-class model on two subjects. The colored numerals at the top show the color-coding for the maps before (first row) and after (second row) adaptation. Note that after adaptation there is a change of the preference, for the stimuli. Map thresholds for accuracy are set at the average accuracy for the five numerosities for the different conditions. Subject 2 has two distinct foci along the intraparietal sulcus. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Talairach coordinates of the maps obtained by plotting back the spheres with the highest decoding accuracy on the ten-class model, for all the subjects.

	Left hemisphere			Right hemisphere
	x	y	z	x	y	z
Subj. 1	−24	−48	47	28	−49	57
Subj. 2	−22	−38	42	25	−54	38
	−28	−62	49
Subj. 3	−31	−55	29	40	−49	42
				25	−64	36
Subj. 4	−27	−48	31	23	−60	28
	−22	−64	33
Subj. 5	−35	−33	41	23	−50	33
	−33	−53	43
Subj. 6	−28	−39	46	37	−48	39
	−20	−57	43
Subj. 7	−30	−47	45	28	−53	61
Subj. 8	−33	−48	38	28	−52	39
Subj. 9	−29	−53	39	34	−56	35
Subj. 10	−26	−51	33	32	−49	29
				30	−65	45
Average	−28	−50	40	29	−54	40
Std	5	9	6	5	6	10

To evaluate the spatial consistency of these results across subjects, the spatial selectivity of individual subjects was aligned to calculate “probability maps”, which we define as regions where at least five out of ten subjects showed better-than-average decoding accuracy across the five classes in the two conditions. Before adaptation (Fig. 10A) the organization for numerosity seems to follow a “pinwheel-like” structure, without any clear topographical organization along the sulcus. There is also a large overlap between number preference, consistent with the low psychophysical discriminability between classes. Again the spatial distribution of the different numerosity spatial selectivities changed after adaptation, with a trend of preference shifting towards higher numbers.

Discussion

The present experiment studied how adaptation changes the neural representation of the cortical responses associated with numerosity, and how these changes relate to the behavioral effects. We used a novel adaptation paradigm with a long pause between adapter and test stimuli (Aagten-Murphy and Burr, 2016), allowing us to distinguish the activity generated by the test stimuli from that generated by the adaptation stimuli which, in most habituation paradigms, overlaps over time, and in many cases difficult to de-convolve.

The psychophysical results show that numerosity adaptation does occur with this paradigm, albeit less than with the standard techniques, 10% compared with the 30% usually observed when both stimuli are presented in the periphery without the pauses necessary to dissociate the BOLD responses (Burr and Ross, 2008, Ross and Burr, 2010). Interestingly, the coefficient of variance also decreased after adaptation, as was observed in the study of Burr and Ross (2008) using the classical number adaptation paradigm. The increase in precision after adaptation suggests a mechanism that dynamically adapts to the prevailing statistics to improve discrimination around the adapting point. Interestingly, the increase in psychophysical precision after adaptation was accompanied by an improvement in classification of number from BOLD responses.

The absolute levels of the BOLD modulation were not significantly affected by adaptation, possibly because the long temporal gap between the adapting and testing stimuli allowed the BOLD signal to return to baseline. However, adaptation did have profound effects on the pattern of responses of the brain. Multi-voxel pattern analysis successfully classified the two adaptation states, both in IPS and in V1. Furthermore, the intraparietal sulcus could reliably classify numerosity, both before and after adaptation, even at relatively high numerosities, higher than previously used. On the other hand, under the conditions of our experiment, the classifier could not decode numerosity from activity of the primary visual cortex under any condition, adapted or not. This result may seem to contradict previous experiments in the literature reporting above chance classification accuracy for number discrimination in the primary visual cortex (e.g. Bulthe et al., 2014; Eger et al., 2015). However, in previous studies the spectral content of the stimulus varied with numerosity, and so V1 activity and BOLD responses should also vary. This could allow for classification of the stimuli, not necessarily linked to numerosity. We took special care to ensure that overall contrast energy, to which V1 is very sensitive, did not vary with numerosity. Another difference may be that at low numerosities (such as studies like Bulthè et al. (2014)), the field was not uniformly covered, and the non-homogeneity may also provide information for the classifier. We did observe a small dependence on numerosity in the BOLD signal itself in V1, possibly reflecting the compressive BOLD non-linearity known to occur in V1 (Boynton et al., 1999), but this did not affect the classification performance.

Multi-voxel pattern analysis revealed that in the intraparietal sulcus neural activity patterns represent numerosity. The whole region decoded numerosity well, both when using only the pre-adaptation trials (like previous studies) and when using all pre- and post-trials. With the ten-class model (training on both pre- and post-adaptation data), both pre- and post-adaptation trials were classified well: but the classification was much better for the post-adaptation trials. When we selected the best-classifying 50 spheres, we found that all numerosities within each adaptation state were classified with similar accuracy. This implies that adaptation does not eliminate the spatial irregularities in the fine-scale architecture that allows classification, nor does it affect only a particular numerosity or subset of numerosities, but rather the whole region. The better accuracy for the post-adaptation trials (paralleled by better accuracy predicted from psychophysics) implies that adaptation may act to decrease neural noise in the number network. Interestingly, the increased accuracy is associated with a decrease of the average bold response.

The results of the five-class models reinforce the idea that adaptation affects the entire number network. When trained on pre-adaptation trials, the model failed to classify any post-adaptation condition, and vice versa. Clearly, the classification network was profoundly changed by adaptation, even though the psychophysical effect was only 10%. Importantly, the increase in decoding accuracy after adaptation correlated with the magnitude of the adaptation effect of individual subjects, suggesting that the better decoding performance after adaptation is linked to the strength of the adaptation effect. Although we have only 10 subjects, a rather small sample for a correlation study, the correlation between improvement in classification accuracy and magnitude of adaptation was statistically significant. Unfortunately, our procedures did not permit simultaneous acquisition of psychophysical data (based on two-stimulus comparisons) and fMRI data, but the effect held up nevertheless. The correlation is a clear example of a link between brain activity and visual perception, similar to many others described in the literature (for a review see: Welchman and Kourtzi, 2013).

As mentioned earlier, we also found a qualitative correlation between the psychophysical improvement in thresholds (and hence better predicted decoding) and the overall improvement in classification accuracy. However, we found no significant correlation between individual psychophysical CoV and accuracy classifications. But perhaps this is unsurprising, as psychophysical measures of precision can be quite noisy, and 10 subjects is a small sample. On the other hand, changes in the point of subjective equality are far more robust, and the correlation in Fig. 8, which links the amount of adaptation effect to improvement in classification, is significant. This may be interesting to pursue in future correlations between decoding accuracy of humans and SVM classifiers more directly, with a larger sample and modified techniques.

Our results also show some evidence for a spatial organization for numerosity up to quite large numbers, eighty items, within a large region of IPS. Plotting classification accuracy of the most accurate spheres back on the brains of individual subjects showed a hint of spatial organization for the various numerosities tested in this experiment. These spheres spanned the entire IPS ROI, but selectivity to individual numbers revealed a spatial organization. While there was some variability across subjects, in five out of ten subjects we noticed a common pattern of clustering of voxels that best classified specific numbers, in both hemispheres. Unfortunately we did not have the spatial resolution to quantify precisely the morphological structure for numerosity, so the observation of separate columns remains qualitative at this stage. Nevertheless, it does corroborate Harvey et al.'s (2013) clear demonstration of spatial segregation of numerosity for low ranges of numbers (using high-field imaging), and extends this principle it to a higher numerosity range. While Harvey et al. (2013) observed a lateral-medial organization for small numbers, the clustering observed here appears to be less orderly. This could represent a different coding strategy for larger, less discriminable numerosity sets, or simply a limitation of our low-field imaging. The spatial selectivity for numerosity of Fig. 9, Fig. 10 clearly show that adaptation changes not only the coding of numerosity, but also the spatial organization. However, to understand the exact nature of this change further studies using a different fMRI design or technique are necessary.

Our results are consistent with a broad neuronal tuning for numerosity within our selected areas, similar to the tuning evaluated psychophysically. The psychophysical effect of adaptation is an underestimation of numerosity and this effect is successfully simulated by a decrease of activity that it is larger for the detector with peak selectivity at the adapter (Blakemore and Campbell, 1969). However, to be able to simulate the improvement in the threshold (CoV) that we observed here, the most probable model is a sharpening of the selectivity of the numerosity channels that respond to the adapter and a decoding mechanism that is unaware of the adaptation state (for a review see: Series et al., 2009). A shift of bias in the psychometric function of 10% would not be sufficient to be revealed within a confusion matrix of the discrete categories used here, so our data cannot really test this possibility. However, a small improvement of the neuronal tuning is consistent with the simultaneous classification of all pre-and post-adaptation, and the better classification of the post-adaptation responses that we observed here. On the other hand, our results are not consistent with a broad gradient model, where each neuron responds with increasing amplitude to the various numerosities, and adaptation changes the steepness of the increase. These models inevitably would produce more classification errors for specific sets of numerosities between adaptation conditions, which we never observed here. Whatever the detailed changes in the neuronal numerosity tuning by adaptation, our results indicate that all neurons are modified by the adaptation trace, possibly by a decorrelation-like process affecting the whole network, along the lines suggested by Barlow and Foldiak (1989).

To conclude, in line with previous neuroimaging and neuro-physiological findings, this experiment supports the idea of the existence of number-selective neurons in the human IPS, and extends these findings to higher numerosities not tested previously. Number adaptation affects the pattern representation of numbers specifically in the intraparietal sulcus, suggesting that it is altering higher-order representations of magnitude, possibly sharpening its coding and altering coding networks. The change in coding strategies in IPS suggests that this structure plays a fundamental role in mediating the number adaptation effect with little or no effect on primary visual cortex.