Abstract
The development of new protein-ligand scoring functions using machine learning algorithms, such as random forest, has been of significant interest. By efficiently utilizing expanded feature sets and a large set of experimental data, random forest based scoring functions (RFbScore) can achieve better correlations to experimental protein-ligand binding data with known crystal structures; however, more extensive tests indicate that such enhancement in scoring power comes with significant under-performance in docking and screening power tests compared to traditional scoring functions. In this work, in order to improve scoring-docking-screening powers of protein-ligand docking functions simultaneously, we have introduced a ΔvinaRF parameterization and feature selection framework based on random forest. Our developed scoring function ΔvinaRF20, which employs twenty descriptors in addition to the AutoDock Vina score, can achieve superior performance in all power tests of both CASF-2013 and CASF-2007 benchmarks compared to classical scoring functions. The ΔvinaRF20 scoring function and its code are freely available on the web at: https://www.nyu.edu/projects/yzhang/DeltaVina.
Graphical Abstract
A new machine-learning protein-ligand scoring function ΔvinaRF20 has been developed to achieve better performance for a variety of protein-ligand docking tasks compared to classical scoring functions.
1. Introduction
Protein ligand docking is a computational approach that attempts to predict the binding mode between a protein receptor and a small molecule ligand as well as their binding affinity. It plays an increasingly important role in structure-based drug design as well as in functional studies of proteins. The most critical component of docking is the scoring function, which is needed to determine binding site and binding mode of a ligand on a protein,[1] to screen virtual small-molecule libraries to identify potential leads for further inhibitor development,[2–8] and to explicitly estimate the binding affinity between a protein and a ligand given their complex structure. Correspondingly, in order to assess performance of scoring functions for these different important tasks, several key metrics have been developed and adopted, including: (i) a docking power test, which evaluates the ability of the scoring function to identify the native binding site and binding mode among a set of computer generated decoys; (ii) a screening power test to evaluate the ability of the scoring function to identify a true binder for a given target from a pool of random molecules; and (iii) a scoring power test, which assesses the linear correlation between predicted and experimental binding affinities.[9–13] Extensive retrospective and comparative studies[10,11,14–18] indicate that some widely used scoring functions, such as GlideScore[19–21], can perform relatively well in docking and screening power tests, but most perform less satisfactorily in the scoring power test. Thus, the accuracy of scoring functions remains a central limitation of protein-ligand docking.
In the last few years, machine learning approaches have proven useful for many technologies in modern society, such as computer vision and natural language processing.[22–25] In the field of biomolecular modeling, there has been significant interest to develop new protein-ligand scoring functions using state-of-the-art machine learning methods,[26–40] such as the random forest (RF) algorithm. By efficiently utilizing expanded feature sets and a large set of experimental data, random forest based scoring functions (RFbScore)[26–32] have achieved significantly better correlations with experimental protein-ligand binding data for known crystal structures; however, more extensive testing indicates that this enhancement in scoring power comes with significant under-performance in docking and screening power tests compared to traditional scoring functions.[41,42]
Random forest is an ensemble learning method based on the aggregation of numerous decision trees.[43,44] In RFbScore, every regression tree is a non-parametric predictive model to relate structural features to binding affinities, the predicted values of which are bounded by the learning set. Thus random forest can do interpolation but not extrapolation.[45] Without a predetermined function form, random forest has the ability to learn complicated interactions directly from a large set of experimental data based on numerous input features. Up to now, almost all published RFbScores that predict binding affinity have used experimental protein-ligand binding data with known crystal structures as the training set alone. Thus, in retrospect, it is not surprising that RFbScores can achieve success in scoring power tests, which mostly rely on interpolation—i.e. to estimate binding affinities given experimentally determined structures.[29] On the other hand, numerous tasks in docking and screening tests depend on extrapolation—i.e. to estimate binding affinities for computationally generated structures which should have weaker binding affinities. Thus, it is understandable that RFbScores would falter when applied to such decoy structures, leading to significant underperformance of RFbScores in docking and screening power tests.[41,42]
From the above discussion, we can see that the inferior performance of RFbScores in docking tests may reflect two problems: 1. Random forest is restricted to do interpolation; 2. Use of experimental protein-ligand binding data with known crystal structures as the training set alone limits the applicability of RFbScores. In this work, in order to improve scoring-docking-screening powers of scoring functions simultaneously, we employ a two-pronged strategy:
One is to expand the training set. Besides enlarging the experimental data set to include crystal structures with weak binding affinities, we have added a similar amount of computationally generated structures (decoy data) into the training set. The idea of including decoy data in the training set has been previously employed in the development of several other scoring functions.[34,37]
The other is to employ a ΔvinaRF approach, in which random forest is employed to parameterize corrections to the AutoDock Vina scoring function. This is partly inspired by the recent development of the Δ-machine learning approach to predict enthalpies of organic molecules.[46] AutoDock Vina is one of most widely used open-source docking programs, which has been successfully employed in numerous docking and screening tasks.[47] Our ΔvinaRF parameterization framework aims to combine the excellent docking power of the Vina docking function with the strength of random forest for improving scoring accuracy.
Furthermore, by employing random forest for feature selection and introducing a pharmacophore-based solvent-accessible surface area (SASA) feature set, our developed ΔvinaRF20, which employs twenty descriptors in addition to the AutoDock Vina score, can achieve superior performance compared to traditional scoring functions in all tests of both CASF-2013 and CASF-2007 benchmarks, including scoring, ranking, docking and screening power tests. It should be noted that our new scoring function ΔvinaRF20 has not been incorporated into AutoDock Vina for ligand sampling, and currently it can only be used for post-scoring.
2. Methods
2.1 Training Set of Protein-ligand Complexes
The training set of protein-ligand complexes for this work consists of two subsets: one is an experimental subset, which includes 3336 crystal complex structures with experimentally measured binding affinities; the other is a decoy subset, which includes 3322 computer generated decoy structures with computationally estimated binding affinities (Table S1). These are obtained, respectively, from the PDBbind database,[12,48–50] which is a collection of protein-ligand complex PDBs with experimental binding affinities, and the CSAR decoy set, which is a collection of computer generated binding poses as well as native poses for structures in the CSAR-NRC HiQ benchmark release.[51,52] Any structure in the CASF-2007 or CASF-2013 benchmark sets,[12,13] which will be used for the test set, is excluded from the training set.
The experimental subset consists of data from three sources: the PDBbind refined set (v2014), native poses in the CSAR decoy data set, and weak-binding protein-ligand crystal structures (pKd between 0.4 to 3) in PDBbind v2014 general set. Any entry in the CASF-2007 or CASF-2013 benchmark set is excluded.
The decoy subset contains decoy data for 302 protein-ligand complexes in the CSAR decoy set, excluding 41 complexes that are also in the CASF-2007 or CASF-2013 benchmark set. For each native pose, 11 decoys are selected from up to 500 decoys in the original CSAR decoy set based on the rank of AutoDock Vina score at 0%, 10%, 20%, …, 90%, 100%, respectively. Thus the decoy subset has a similar number of data entries as in the experimental subset.
The binding affinity for each complex in the training set is denoted as pKd(train). For each entry in the experimental subset, pKd(train) is the experimental binding affinity pKd(exp). The binding affinity for each entry in the decoy subset should not be larger than the experimental binding affinity for the corresponding native pose. For each decoy, first we calculate pKd(Vina) based on the AutoDock Vina score: if the calculated pKd(Vina) of a decoy structure is less than pKd(exp) of the corresponding native pose, we assign pKd(Vina) as pKd(train) for this decoy structure; otherwise pKd(train) of the decoy structure is assumed to be at the upper limit, which is the pKd(exp) of the corresponding native pose.
2.2 The ΔvinaRF Parameterization Approach
Our main idea is to employ random forest to parameterize corrections to the AutoDock Vina scoring function, and thus to take advantage of both the excellent docking power of the Vina docking function and the strength of random forest in improving scoring accuracy. The Vina scoring function consists of six components: two Gaussian steric terms, one repulsion term, one hydrogen bonding (HB) term, and one torsion count factor, and has been parameterized to improve both binding pose and affinity prediction.[47] The original score calculated by the AutoDock Vina program is in the unit of kcal/mol, and can be converted into pKd unit with the following formula: pKd(Vina) = −0.73349 E(Vina). Thus, our overall ΔvinaRF scoring function can be cast into the following form:
where ΔpKd(RF) is the correction term trained by the random forest (RF) algorithm using ΔpKd(train), i.e., pKd(train) − pKd(Vina).
Given a learning set L= {(X(1), y(1)), …, (X(N), y(N))}, which contains N pairs of input feature vectors X= (x1, x2, …, xp) and output values y, each regression tree in a random forest model can be grown as follows: (1). Sample the learning set. Prior to growing a decision tree k, a bootstrap learning subset Lk* is drawn at random from L with replacement, and the left-out data (L − Lk*) constitutes the (OOB) out-of-bag subset OOBk; (2). Grow a single decision tree Tk. Based on the bootstrap learning subset Lk*, Tk is constructed by recursively splitting each terminal node of the tree into two child nodes until the minimum node size is reached. For each splitting, it picks the best feature from a pool of mtry features. The mtry features are randomly selected from all p features. (3). The prediction error of the Tk is estimated using the out-of-bag subset OOBk. After repeating steps 1–3 to grow M regression trees, the collection of all regression trees (Tk, k = 1, …, M) is considered as a predictive RF model. To make a prediction with a new input feature vector X(new), its predicted value is the average of predictions from all trees: [44]
In our development of ΔvinaRF20 parameterization, the learning set L is derived from our training set that has been described above: N is 6658; the output value y is ΔpKd(train), i.e., pKd(train) − pKd(Vina); the input feature vector has p = 20 features, which are calculated based on the corresponding protein-ligand structure in the training set. The randomForest package in R is used to build random forest models.[53] The final ΔvinaRF20 model is built by using M = 500 regression trees with mtry = 4, selected based on the OOB performance of the learning set.
The twenty features in ΔvinaRF20 are listed in Table 1. There are 10 terms from the AutoDock Vina source code and 10 terms related to buried solvent-accessible surface area (bSASA). In the AutoDock Vina source code[47], there are a total of 58 terms implemented as listed in Table S2, among which 6 terms have been selected for the AutoDock Vina scoring function, including: two Gaussian steric terms, one repulsion term, one hydrogen bonding (HB) term, and one torsion count factor. These 58 Vina-implemented terms have been explored in the development of smina and user-specified custom scoring functions with linear regression.[54] During our development of ΔvinaRF20, we first ranked 58 Vina-implemented terms based on the permutation variable importance indices %IncMSE, which is OOB mean square error (MSE) increase as a result of feature i being permuted (values are randomly shuffled). For a given feature i, it is calculated by
Table 1.
20 Features in ΔvinaRF20
| No. | Feature Description | |
|---|---|---|
| AutoDock Vina Interaction Termsa | ||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4–5 |
|
|
| AutoDock Vina Ligand Dependent Terms | ||
| 6 | number of heavy atoms | |
| 7 | number of hydrophobic atoms | |
| 8 | number of torsion | |
| 9 | number of rotors | |
| 10 | ligand length | |
| bSASA Featuresb | ||
| 11 | positive | |
| 12 | negative | |
| 13 | donor-acceptor | |
| 14 | donor | |
| 15 | acceptor | |
| 16 | aromatic | |
| 17 | hydrophobic | |
| 18 | polar | |
| 19 | halogen | |
| 20 | total bSASA | |
Interaction terms are from the AutoDock Vina source code.[54] d is the distance between two atoms, a1 and a2. ddiff is the surface distance calculated by ddiff = d − R(a1) − R(a2), where R(a1) and R(a2) are the van der Waals radius of atom a1 and a2.[47] q is the atomic charge and V is the atomic volume. ASP and QASP refer to atomic solvation parameter and charge-based solvation parameter respectively.[59]
The pharmacophore type definitions are presented in Table S3.
where MSEOOB is the OOB MSE and MSEiOOB is the OOB MSE when feature i is permuted. More important features have higher %IncMSE values. Then we have employed a backward feature selection approach, in which the least important features are removed one by one to build random forest models, to choose the least number of features with a comparable top performance. The selected 10 Vina-implemented terms in Table 1 include 5 polar interaction terms and 5 ligand-dependent terms.
The bSASA terms are calculated using atomic SASA changes between the unbound and bound structures: for an atom i, bSASAi = SASAi, unbound − SASAi, complex, where atomic SASAs are calculated by the MSMS program using a probe radius of 1.0 Å.[55] As shown in Table S3, nine pharmacophore types are defined for the atoms in the protein and ligand based on SYBYL atom types and neighboring atoms as in DOCK.[56] The SYBYL atom types[57] are converted by Pybel from the structures with hydrogen atoms added.[58] Thus in Table 1, there are 9 pharmacophore-based bSASA terms and 1 total bSASA term.
2.3 Testing Set and Evaluation Methods
Both CASF-2013 and CASF-2007 benchmark sets[12,13] are used as testing sets so that the results can be directly compared with other docking functions. Both datasets consist of 195 protein-ligand complexes selected from a refined dataset in their respective year’s PDBbind database.[12,48] Scoring, ranking and docking powers have been evaluated for 16 scoring functions (in Table S4) for the CASF-2007 benchmark set[12], while scoring, ranking, docking and screening power tests have been carried out for 20 scoring functions (in Table S5) for the CASF-2013 benchmark set.[13] In our current work, all power tests for AutoDock Vina and ΔvinaRF20 are carried out in the same way as those described in comparative assessment articles for CASF-2007 and CASF-2013,[13] which are summarized below.
Scoring Power
The scoring power test evaluates the linear correlation between predicted binding affinity and experimental binding affinity. It is evaluated by the Pearson’s correlation coefficient (R) between predicted binding affinity and experimental binding affinity and the standard deviation (SD) in regression:
where xi is the predicted binding affinity for ith complex; yi is the experimental binding affinity for ith complex; a and b are the intercept and the slope of linear regression between experimental binding affinity and predicted binding affinity.
Ranking Power
The ranking power test assesses the ability of a scoring function to correctly rank the known ligands of the same target protein based on their predicted binding affinity given the poses from the crystal structures. For each benchmark, there are 65 target proteins and 3 known ligands for each protein. Two levels of success, namely high-level and low-level, are evaluated in CASF-2013. For the high-level, the three ligands for target protein should be ranked by predicted score as the best > the median > the poorest, while the low-level only needs to pick the best one out of three. The success rate is calculated by the number of the correctly ranked targets among all 65 targets. In CASF-2007, only the high-level success rate is evaluated.[12]
Docking Power
The docking power test evaluates the ability of a scoring function to identify native binding poses among computer generated decoys. In CASF-2007, 100 decoy binding poses are selected from the poses generated by LigandFit,[60] GOLD,[61,62] Surflex[63,64] and FlexX[65] for each ligand. Success is defined as one pose from the top one, the top two, or the top three poses ranked by predicted scores is within 2 Å RMSD from the native pose. The RMSDs of decoys relative to the native are provided in CASF-2007 benchmark and used directly. In CASF-2013, up to 100 decoy binding poses are selected from the poses generated by GOLD, Surflex and MOE. The property-matched RMSDs (RMSDPM) of decoys, are calculated by considering the symmetry of the molecule in CASF-2013, however, RMSDPM is not provided in CASF-2013. The symmetry-corrected RMSDs used here are calculated by Pybel.[58] The native poses are included in the decoy set for success rate calculation.
Screening Power
The screening power test assesses the ability of a scoring function to identify a true binder from a pool of random molecules for a given target. The test set for screening in CASF-2013 is designed by cross docking 195 ligands on 65 target proteins. For each protein, there are at least 3 true binders, as defined in Ref. 13. The remaining 192 ligands are searched through the ChEMBL database for possible cross-binders and 12 target proteins have more than 3 true binders in the dataset from the search. There are 12,675 (65 × 195) protein-ligand pairs from docking 195 ligands to 65 target proteins and up to 50 poses are selected for each protein-ligand pair. For a given target protein, 195 ligands are ranked based on the best-scored pose for a given protein-ligand pair. Screening power is measured by two metrics-enhancement factors and success rates—both based on the counts of the total number of true binders among the 1%, 5% and 10% top-ranked molecules. Enhancement factors are computed for each target by
NTB1%, NTB5% and NTB10% are the number of true binders among the 1%, 5% and 10% top-ranked molecules. NTBtotal is the total number of true binders for a given target protein. The average EFs over 65 targets are calculated for each scoring function. Success rates are calculated as the number of targets that have true binders in 1%, 5% and 10% of the top-ranked molecules among the total 65 targets.
3. Results
Based on a learning set which consists of 3336 experimental crystal structures and 3322 computer generated decoy structures, we have developed a new scoring function ΔvinaRF20 by employing random forest to parameterize a correction term to the original AutoDock Vina score.[47] The overall scoring function ΔvinaRF20 has the following form: pKd(ΔvinaRF20) = pKd(Vina) + ΔpKd(RF20), where pKd(Vina) is the pKd value calculated by multiplying the original Vina score by a factor of −0.73349. ΔpKd(RF20) is the correction term parameterized with random forest using 20 features as listed in Table 1. The ΔvinaRF20 model and code are available at: https://www.nyu.edu/projects/yzhang/DeltaVina. We have carried out all power tests on both CASF-2013 and CASF-2007 benchmark sets[12,13] for ΔvinaRF20 as well as the AutoDock Vina scoring function,[47] and compared with, respectively, 20 other and 16 other docking functions that were tested in the original 2013 and 2007 comparative assessment articles. The results are presented in Figures 1–3 and Tables S6–S13. The new scoring function ΔvinaRF20, which employs twenty descriptors in addition to the AutoDock Vina score, has achieved superior performance compared to classical scoring functions in all tests of both CASF-2013 and CASF-2007 benchmarks, including scoring, ranking, docking and screening power tests.
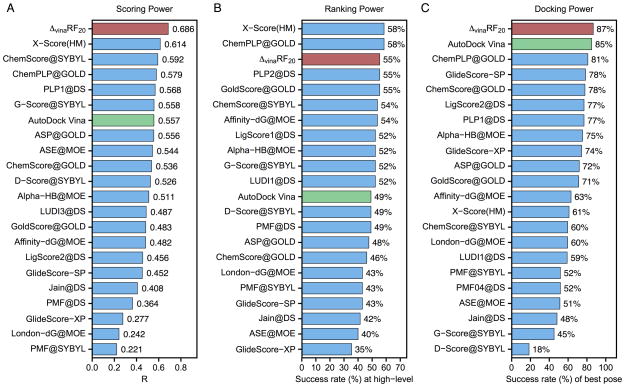
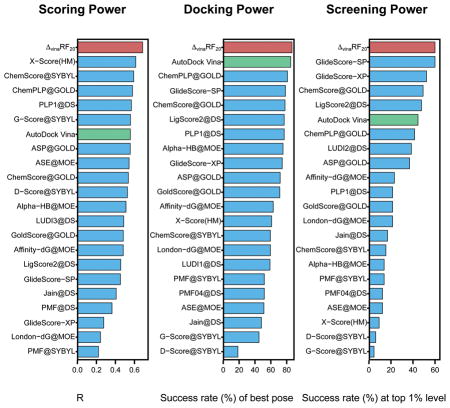
Figure 1.
Performance of 22 scoring functions in (A) scoring power measured by Pearson’s R, (B) ranking power in terms of high-level success rate and (C) docking power measured by the success rate when the best-scored pose is considered to match the native pose in CASF-2013 benchmark. ΔvinaRF20 is colored in red and AutoDock Vina is colored in green. All results colored in blue are obtained from reference[13].
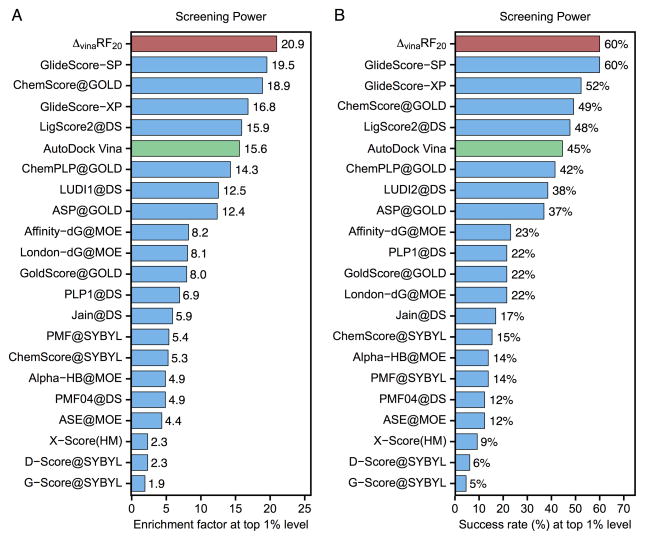
Figure 3.
Performance of 22 scoring functions in screening power measured by (A) enrichment factor and (B) success rate at top 1% level in CASF-2013 benchmark. ΔvinaRF20 is colored in red and AutoDock Vina is colored in green. All results colored in blue are obtained from reference[13].
Scoring Power
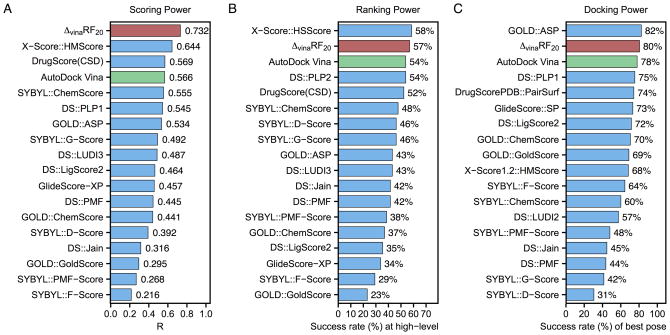
The scoring power of ΔvinaRF20 significantly outperforms AutoDock Vina as well as all scoring functions that have been tested in the original 2013 and 2007 comparative assessment articles, as shown in Figure 1 and 2. It achieves the best Pearson’s correlation coefficients of 0.686 and 0.732 for the CASF-2013 and CASF-2007 benchmarks respectively, and significantly improves upon AutoDock Vina, which has corresponding Pearson’s correlation coefficients of 0.557 and 0.566 respectively.
Figure 2.
Performance of 18 scoring functions in (A) scoring power measured by Pearson’s R, (B) ranking power in terms of high-level success rate and (C) docking power measured by the success rate when the best-scored pose is considered to match the native pose in CASF-2007 benchmark. ΔvinaRF20 is colored in red and AutoDock Vina is colored in green. All results colored in blue are obtained from reference[12].
Ranking Power
The ranking power of ΔvinaRF20 is improved over AutoDock Vina, and is among the top 3 for both benchmarks. In CASF-2013, ΔvinaRF20 has a ranking power of 55% for high-level (in Figure 1) and 74% for low-level (in Table S10), which places it third for high-level successes and second for low-level successes. In CASF-2007, the ranking power of ΔvinaRF20 is 57%, following the best X-Score::HSScore’s success rate of 58%.[66]
Docking Power
The docking power of ΔvinaRF20 is among the top rank for both benchmarks. Its success rate to identify the top pose as the native pose is 87% in CASF-2013 (see Figure 1), which outperforms all other scoring functions. In CASF-2007 (in Figure 2), the success rate of ΔvinaRF20 is 80%, which ranks second following the best one GOLD::ASP (82%).[67] We can see that the docking power of ΔvinaRF20 has improved upon AutoDock Vina by about 2% in both benchmarks. Recently, a new SPA-SE score function was developed by combining knowledge-based atom-pair potential with the atomic solvation energy of a charge-independent implicit solvent model.[68] It shows excellent performance in scoring (with a Pearson’s correlation coefficient of 0.662), ranking (60.0% for high level and 75.4% for low level) and docking power (83.1% success rate for the best pose) for the CASF-2013 benchmark, while the screening power of SPA-SE was not reported. We can see that ΔvinaRF20 is still slightly better than SPA-SE in both scoring and docking power tests for the CASF-2013 benchmark.
Screening Power
The screening power of ΔvinaRF20 is the best as shown in Figure 3 for both metrics: enrichment factor and success rate at top 1% level. The average enrichment factor of ΔvinaRF20 is 21 at top 1% level, which is slightly better than GlideScore-SP’s 20, and the success rate is 60% (39 out of 65), which is the same as GlideScore-SP at top 1% level.[19,20] It should be noted that ΔvinaRF20 has significantly improved upon AutoDock Vina, which has an enrichment factor of 15.6 and success rate of 45% at top 1% level respectively.
4. Discussion
Scoring functions play a central role in protein-ligand docking. An ideal, robust scoring function should perform well across different important tasks, including scoring, docking, and screening power tests. Extensive retrospective and comparative studies[10,11,14–18] indicate that although some widely used scoring functions can do relatively well in docking and screening power tests, most of them are weaker in performance in the scoring power test. Furthermore, it is very challenging for a docking function to achieve superior performance on all three power tests simultaneously.[41,42] For example, X-Score(HM)[66] is the top performer in the scoring power test in the original CASF-2013 comparative study, with a Pearson’s correlation coefficient of 0.614, but its performance in the docking power test only ranks in the middle among about 20 tested scoring functions. Its success rate is 61% in predicting the best pose, which is significant lower than the value of 81% for ChemPLP@GOLD.[69] These disparities in performance for different power tests become significantly worse for recently developed machine learning-based scoring functions (MLbScores).[41,42] For example, in a recent comparative assessment of a dozen MLbScores[42] for the CASF-2013 benchmark, RF@ML, which is parameterized with random forest using more than one hundred features, achieved the best scoring power of 0.704 in Pearson’s correlation coefficient among all 12 scoring functions developed using different machine learning algorithms. However, the docking and screening powers of these 12 MLbScores are all significantly worse. The docking power of RF@ML is only 12.2% for success in predicting the best pose, while the screening power of RF@ML is just 6.45% for the success rate in finding the best ligand molecule. These values are significantly lower than those of classical scoring functions, whose top performances are 81% (ChemPLP@GOLD)[69] and 60% (GlideScore-SP)[19,20] for docking and screening power respectively. On the other hand, as presented in the above results section, our newly developed ΔvinaRF20 scoring function, using 20 features, achieved superior performance compared to traditional scoring functions in all power tests for both CASF-2013 and CASF-2007 benchmarks.
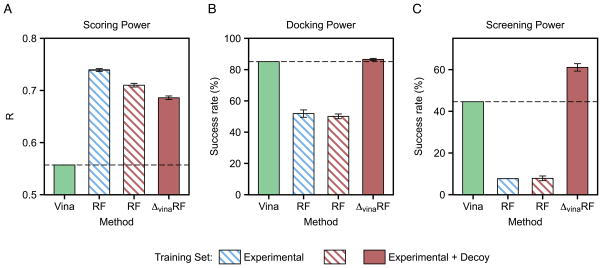
The main idea of our ΔvinaRF approach is to use random forest to parameterize a correction term to the AutoDock Vina score so that it can combine Vina’s excellent docking power with RF’s ability to significantly improve scoring accuracy. We tested both RF and ΔvinaRF approaches using the same twenty features and training set for the development of the ΔvinaRF20 scoring function, and compared them with Vina in Figure 4 for the scoring, docking and screening power tests in CASF-2013. In addition, we have also trained a RF model using experimental data alone and the same twenty features. The results clearly demonstrate that the RF approach can only improve the scoring power by significantly sacrificing docking and screening powers, while the ΔvinaRF approach, with a combined experimental and decoy training set, can achieve the improvement over AutoDock Vina in all three tests simultaneously.
Figure 4.
CASF-2013 benchmark test performance of AutoDock Vina (colored in green), scoring function developed with RF approach (colored in blue) using experimental data alone and the same twenty features in ΔvinaRF20 scoring function, and scoring functions developed with RF approach and ΔvinaRF approach (colored in red) using the same twenty features and the same training set for the development of the ΔvinaRF20 scoring function. (A) Scoring power; (B) Docking power; (C) Screening power. Each set is run 10 times with different random seed for random forest and calculated by averaging over 10 performances except AutoDock Vina. The AutoDock Vina performance is also indicated by dashed line.
One attractive capability of the random forest algorithm is that it can efficiently utilize a large set of training data. It has been previously demonstrated that the larger the training data, the better the resulting RFbScore’s performance in the scoring power test[28,29,70], even when low-quality structures are included[30]. For the ΔvinaRF approach, as shown in Figure S1, we also find that a larger experimental learning set can significantly improve the scoring power, but it does not necessarily improve the docking power. By expanding the learning set to include decoy structures, both docking and screening power of the scoring function can be improved over AutoDock Vina with the ΔvinaRF approach.
Besides the training set, another critical component of a random forest based scoring function (RFbScore) is the feature set. For a random forest model, both the number of features and feature relevance will affect its performance. Numerical experiments show that increasing the fraction of relevant features can improve the performance of the random forest model by increasing the chance that important features will be selected at each tree splitting.[44] In this work, by taking advantage of random forest in ranking features, we employ a strategy that includes both feature selection and aggregation, to yield the twenty features in ΔvinaRF20. As listed in Table 1, the feature set of ΔvinaRF20 consists of 5 interaction terms and 5 ligand-dependent terms, which are selected from 58 terms implemented in the AutoDock Vina source code and 10 terms related to buried solvent-accessible surface area (bSASA). Interestingly, all 5 interaction terms in the ΔvinaRF20 are related to polar interactions, and there is only one overlap term between ΔvinaRF20 and the original Vina score, which is the number of torsions in the ligand. In comparison with using only 6 terms in the original Vina score and all 58 terms implemented in the AutoDock Vina source code, the ΔvinaRF model, developed using 10 selected features, performs better in all scoring, docking and screening power tests for the CASF-2013 benchmark test as shown in Figure S2.
Among 5 ligand-dependent terms, rotors and torsions have been previously used to approximate the entropic change in several empirical scoring functions.[19,66,71,72] Number of heavy atoms and ligand length could also be viewed as entropy-related features since both of them are highly correlated with rotors (Pearson’s correlation coefficients are 0.802 and 0.906, respectively) in the crystal structure training set. Number of hydrophobic atoms is related to the hydrophobic interaction and the Pearson’s correlation coefficient between number of hydrophobic atoms and the hydrophobic term defined in AutoDock Vina source code is around 0.85 for the crystal structure training set.
Surface area and related features are widely used in protein-ligand scoring function development due to their relation to solvation.[66,68,71–74] The buried solvent-accessible surface area of a ligand (bSASA) has also been tested as a naive scoring function in CASF-2013 scoring comparison list[13] and outperforms most of other scoring functions in the scoring power test but ranks the worst in both docking and screening power tests. Since no bSASA term has been implemented in the AutoDock Vina source code, we have explored 9 pharmacophore-based bSASA terms and 1 total bSASA term as the feature set. As shown in Figure S3, the ΔvinaRF model developed using 10 bSASA terms alone would also perform quite well in all three power tests, but not as good as when combined with 10 selected AutoDock Vina terms. By combining two feature sets, the resulting Vina10-bSASA, the feature set used in ΔvinaRF20, performs better than either Vina10 or bSASA in all three power tests for the CASF-2013 benchmark. We have tested the importance of features measured by percentage of increased mean squared error (%IncMSE) for the 20 features in ΔvinaRF20 as shown in Figure S4. Except for the halogen bSASA, which may be limited by the rarity of halogens in the training set, each of the other 19 features has a %IncMSE value significantly larger than 20%, indicating their general importance and justifying their inclusion in the feature set of ΔvinaRF20. Meanwhile, the additional test results in Figures S1–S4 further indicate the robustness of the ΔvinaRF approach.
5. Conclusion
A major challenge in developing a robust protein-ligand scoring function is to improve scoring, docking and screening performances simultaneously. In this work, we have made advances in overcoming this challenge by introducing a new ΔvinaRF parameterization and feature selection framework based on random forest. Our new scoring function ΔvinaRF20 employs twenty features in addition to the AutoDock Vina score, and can achieve superior performance compared to classical scoring functions in all tests of both CASF-2013 and CASF-2007 benchmarks, including scoring, ranking, docking and screening power tests. This work suggests that Δ-machine learning is a promising approach to systemically improve the performance and robustness of docking functions by employing larger diverse experimental/decoy data sets of high quality, developing and selecting physically meaningful features, as well as adapting advanced machine learning algorithms.
Supplementary Material
Figure S1: Performance comparison between scoring functions developed with different training sets using the ΔvinaRF approach.
Figure S2: Performance comparison between scoring functions developed with different Vina feature sets using the ΔvinaRF approach.
Figure S3: Performance comparison between scoring functions developed with Vina10, bSASA and Vina10 + bSASA features using the ΔvinaRF approach.
Figure S4 Importance of features measured by percentage of increased mean squared error (%IncMSE) for 20 features in ΔvinaRF20.
Table S1: Training Set Description.
Table S2: AutoDock Vina Features in Source Code.
Table S3: Pharmacophore Type Definition.
Table S4: Summary of the Scoring Functions Evaluated in CASF-2007 Benchmark.
Table S5: Summary of the Scoring Functions Evaluated in CASF-2013 Benchmark.
Table S6: Performance of 18 Scoring Functions in the Scoring Power Test in CASF-2007.
Table S7: Performance of 18 Scoring Functions in Ranking Power Test in CASF-2007.
Table S8: Success rates of 18 Scoring Functions in the Docking Power Test in CASF-2007.
Table S9: Performance of 22 Scoring Functions in the Scoring Power Test in CASF-2013.
Table S10: Performance of 22 Scoring Functions in Ranking Power Test in CASF-2013.
Table S11: Success rates of 22 Scoring Functions in the Docking Power Test in CASF-2013.
Table S12: Enrichment Factors of 22 Scoring Functions in the Screening Power Test in CASF-2013.
Table S13: Success Rates of Finding the Best Ligand Molecule of 22 Scoring Functions in the Screening Power Test in CASF-2013.
Acknowledgments
We would like to acknowledge the support by NIH (R01-GM079223). We thank NYU-ITS and NYUAD for providing computational resources.
References
- 1.Huang SY, Grinter SZ, Zou XQ. Phys Chem Chem Phys. 2010;12:12899. doi: 10.1039/c0cp00151a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lyne PD. Drug Discovery Today. 2002;7:1047. doi: 10.1016/s1359-6446(02)02483-2. [DOI] [PubMed] [Google Scholar]
- 3.Shoichet BK. Nature. 2004;432:862. doi: 10.1038/nature03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.McInnes C. Curr Opin Chem Biol. 2007;11:494. doi: 10.1016/j.cbpa.2007.08.033. [DOI] [PubMed] [Google Scholar]
- 5.Guido RVC, Oliva G, Andricopulo AD. Curr Med Chem. 2008;15:37. doi: 10.2174/092986708783330683. [DOI] [PubMed] [Google Scholar]
- 6.Cheng TJ, Li QL, Zhou ZG, Wang YL, Bryant SH. AAPS J. 2012;14:133. doi: 10.1208/s12248-012-9322-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lavecchia A, Di Giovanni C. Curr Med Chem. 2013;20:2839. doi: 10.2174/09298673113209990001. [DOI] [PubMed] [Google Scholar]
- 8.Ma DL, Chan DSH, Leung CH. Chem Soc Rev. 2013;42:2130. doi: 10.1039/c2cs35357a. [DOI] [PubMed] [Google Scholar]
- 9.Wang RX, Lu YP, Wang SM. J Med Chem. 2003;46:2287. doi: 10.1021/jm0203783. [DOI] [PubMed] [Google Scholar]
- 10.Ferrara P, Gohlke H, Price DJ, Klebe G, Brooks CL. J Med Chem. 2004;47:3032. doi: 10.1021/jm030489h. [DOI] [PubMed] [Google Scholar]
- 11.Marsden PM, Puvanendrampillai D, Mitchell JBO, Glen RC. Org Biomol Chem. 2004;2:3267. doi: 10.1039/B409570G. [DOI] [PubMed] [Google Scholar]
- 12.Cheng TJ, Li X, Li Y, Liu ZH, Wang RX. J Chem Inf Model. 2009;49:1079. doi: 10.1021/ci9000053. [DOI] [PubMed] [Google Scholar]
- 13.Li Y, Han L, Liu ZH, Wang RX. J Chem Inf Model. 2014;54:1717. doi: 10.1021/ci500081m. [DOI] [PubMed] [Google Scholar]
- 14.Halperin I, Ma BY, Wolfson H, Nussinov R. Proteins: Struct, Funct, Genet. 2002;47:409. doi: 10.1002/prot.10115. [DOI] [PubMed] [Google Scholar]
- 15.Perola E, Walters WP, Charifson PS. Proteins: Struct, Funct, Bioinf. 2004;56:235. doi: 10.1002/prot.20088. [DOI] [PubMed] [Google Scholar]
- 16.Warren GL, Andrews CW, Capelli AM, Clarke B, LaLonde J, Lambert MH, Lindvall M, Nevins N, Semus SF, Senger S, Tedesco G, Wall ID, Woolven JM, Peishoff CE, Head MS. J Med Chem. 2006;49:5912. doi: 10.1021/jm050362n. [DOI] [PubMed] [Google Scholar]
- 17.Kim R, Skolnick J. J Comput Chem. 2008;29:1316. doi: 10.1002/jcc.20893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Plewczynski D, Lazniewski M, Augustyniak R, Ginalski K. J Comput Chem. 2011;32:742. doi: 10.1002/jcc.21643. [DOI] [PubMed] [Google Scholar]
- 19.Friesner RA, Banks JL, Murphy RB, Halgren TA, Klicic JJ, Mainz DT, Repasky MP, Knoll EH, Shelley M, Perry JK, Shaw DE, Francis P, Shenkin PS. J Med Chem. 2004;47:1739. doi: 10.1021/jm0306430. [DOI] [PubMed] [Google Scholar]
- 20.Halgren TA, Murphy RB, Friesner RA, Beard HS, Frye LL, Pollard WT, Banks JL. J Med Chem. 2004;47:1750. doi: 10.1021/jm030644s. [DOI] [PubMed] [Google Scholar]
- 21.Friesner RA, Murphy RB, Repasky MP, Frye LL, Greenwood JR, Halgren TA, Sanschagrin PC, Mainz DT. J Med Chem. 2006;49:6177. doi: 10.1021/jm051256o. [DOI] [PubMed] [Google Scholar]
- 22.Jordan MI, Mitchell TM. Science. 2015;349:255. doi: 10.1126/science.aaa8415. [DOI] [PubMed] [Google Scholar]
- 23.LeCun Y, Bengio Y, Hinton G. Nature. 2015;521:436. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 24.Lavecchia A. Drug Discovery Today. 2015;20:318. doi: 10.1016/j.drudis.2014.10.012. [DOI] [PubMed] [Google Scholar]
- 25.Libbrecht MW, Noble WS. Nat Rev Genet. 2015;16:321. doi: 10.1038/nrg3920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ballester PJ, Mitchell JBO. Bioinformatics. 2010;26:1169. doi: 10.1093/bioinformatics/btq112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ballester PJ, Schreyer A, Blundell TL. J Chem Inf Model. 2014;54:944. doi: 10.1021/ci500091r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li HJ, Leung KS, Wong MH, Ballester PJ. BMC Bioinf. 2014;15:291. doi: 10.1186/1471-2105-15-291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li HJ, Leung KS, Wong MH, Ballester PJ. Mol Inf. 2015;34:115. doi: 10.1002/minf.201400132. [DOI] [PubMed] [Google Scholar]
- 30.Li HJ, Leung KS, Wong MH, Ballester PJ. Molecules. 2015;20:10947. doi: 10.3390/molecules200610947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zilian D, Sotriffer CA. J Chem Inf Model. 2013;53:1923. doi: 10.1021/ci400120b. [DOI] [PubMed] [Google Scholar]
- 32.Liu Q, Kwoh CK, Li JY. J Chem Inf Model. 2013;53:3076. doi: 10.1021/ci400450h. [DOI] [PubMed] [Google Scholar]
- 33.Ashtawy HM, Mahapatra NR. BMC Bioinf. 2015;16(Suppl 4):S8. doi: 10.1186/1471-2105-16-S4-S8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Durrant JD, McCammon JA. J Chem Inf Model. 2010;50:1865. doi: 10.1021/ci100244v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Durrant JD, McCammon JA. J Chem Inf Model. 2011;51:2897. doi: 10.1021/ci2003889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wallach I, Dzamba M, Heifets A. [accessed Apr 20, 2016]; http://arXiv.org/abs/1510.02855.
- 37.Li L, Wang B, Meroueh SO. J Chem Inf Model. 2011;51:2132. doi: 10.1021/ci200078f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ding B, Wang J, Li N, Wang W. J Chem Inf Model. 2013;53:114. doi: 10.1021/ci300508m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Li GB, Yang LL, Wang WJ, Li LL, Yang SY. J Chem Inf Model. 2013;53:592. doi: 10.1021/ci300493w. [DOI] [PubMed] [Google Scholar]
- 40.Wang W, He WL, Zhou X, Chen X. Proteins: Struct, Funct, Bioinf. 2013;81:1386. doi: 10.1002/prot.24282. [DOI] [PubMed] [Google Scholar]
- 41.Gabel J, Desaphy J, Rognan D. J Chem Inf Model. 2014;54:2807. doi: 10.1021/ci500406k. [DOI] [PubMed] [Google Scholar]
- 42.Khamis MA, Gomaa W. Eng Appl Artif Intel. 2015;45:136. [Google Scholar]
- 43.Breiman L. Mach Learn. 2001;45:5. [Google Scholar]
- 44.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer-Verlag; New York: 2009. [Google Scholar]
- 45.Wyner AJ, Olson M, Bleich J, Mease D. [accessed Apr 20, 2016]; http://arXiv.org/abs/1504.07676.
- 46.Ramakrishnan R, Dral PO, Rupp M, von Lilienfeld OA. J Chem Theory Comput. 2015;11:2087. doi: 10.1021/acs.jctc.5b00099. [DOI] [PubMed] [Google Scholar]
- 47.Trott O, Olson AJ. J Comput Chem. 2010;31:455. doi: 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li Y, Liu ZH, Li J, Han L, Liu J, Zhao ZX, Wang RX. J Chem Inf Model. 2014;54:1700. doi: 10.1021/ci500080q. [DOI] [PubMed] [Google Scholar]
- 49.Wang RX, Fang XL, Lu YP, Wang SM. J Med Chem. 2004;47:2977. doi: 10.1021/jm030580l. [DOI] [PubMed] [Google Scholar]
- 50.Wang RX, Fang XL, Lu YP, Yang CY, Wang SM. J Med Chem. 2005;48:4111. doi: 10.1021/jm048957q. [DOI] [PubMed] [Google Scholar]
- 51.Dunbar JB, Smith RD, Yang CY, Ung PMU, Lexa KW, Khazanov NA, Stuckey JA, Wang SM, Carlson HA. J Chem Inf Model. 2011;51:2036. doi: 10.1021/ci200082t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Huang SY, Zou XQ. J Chem Inf Model. 2011;51:2107. doi: 10.1021/ci200080g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liaw A, Wiener M. R News. 2002;2:18. [Google Scholar]
- 54.Koes DR, Baumgartner MP, Camacho CJ. J Chem Inf Model. 2013;53:1893. doi: 10.1021/ci300604z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sanner MF, Olson AJ, Spehner JC. Biopolymers. 1996;38:305. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 56.Jiang LL, Rizzo RC. J Phys Chem B. 2015;119:1083. doi: 10.1021/jp506555w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Clark M, Cramer RD, Vanopdenbosch N. J Comput Chem. 1989;10:982. [Google Scholar]
- 58.O’Boyle NM, Morley C, Hutchison GR. Chem Cent J. 2008;2:5. doi: 10.1186/1752-153X-2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Huey R, Morris GM, Olson AJ, Goodsell DS. J Comput Chem. 2007;28:1145. doi: 10.1002/jcc.20634. [DOI] [PubMed] [Google Scholar]
- 60.Venkatachalam CM, Jiang X, Oldfield T, Waldman M. J Mol Graphics Modell. 2003;21:289. doi: 10.1016/s1093-3263(02)00164-x. [DOI] [PubMed] [Google Scholar]
- 61.Jones G, Willett P, Glen RC. J Mol Biol. 1995;245:43. doi: 10.1016/s0022-2836(95)80037-9. [DOI] [PubMed] [Google Scholar]
- 62.Jones G, Willett P, Glen RC, Leach AR, Taylor R. J Mol Biol. 1997;267:727. doi: 10.1006/jmbi.1996.0897. [DOI] [PubMed] [Google Scholar]
- 63.Jain AN. J Med Chem. 2003;46:499. doi: 10.1021/jm020406h. [DOI] [PubMed] [Google Scholar]
- 64.Jain AN. J Comput-Aided Mol Des. 2007;21:281. doi: 10.1007/s10822-007-9114-2. [DOI] [PubMed] [Google Scholar]
- 65.Rarey M, Kramer B, Lengauer T, Klebe G. J Mol Biol. 1996;261:470. doi: 10.1006/jmbi.1996.0477. [DOI] [PubMed] [Google Scholar]
- 66.Wang RX, Lai LH, Wang SM. J Comput-Aided Mol Des. 2002;16:11. [Google Scholar]
- 67.Mooij WTM, Verdonk ML. Proteins: Struct, Funct, Bioinf. 2005;61:272. [Google Scholar]
- 68.Yan ZQ, Wang J. Proteins: Struct, Funct, Bioinf. 2015;83:1632. [Google Scholar]
- 69.Korb O, Stutzle T, Exner TE. J Chem Inf Model. 2009;49:84. doi: 10.1021/ci800298z. [DOI] [PubMed] [Google Scholar]
- 70.Ashtawy HM, Mahapatra NR. IEEE/ACM Trans Comput Biol Bioinf. 2015;12:335. doi: 10.1109/TCBB.2014.2351824. [DOI] [PubMed] [Google Scholar]
- 71.Bohm HJ. J Comput-Aided Mol Des. 1994;8:243. doi: 10.1007/BF00126743. [DOI] [PubMed] [Google Scholar]
- 72.Cao Y, Li L. Bioinformatics. 2014;30:1674. doi: 10.1093/bioinformatics/btu104. [DOI] [PubMed] [Google Scholar]
- 73.Krammer A, Kirchhoff PD, Jiang X, Venkatachalam CM, Waldman M. J Mol Graphics Modell. 2005;23:395. doi: 10.1016/j.jmgm.2004.11.007. [DOI] [PubMed] [Google Scholar]
- 74.Bohm HJ. J Comput-Aided Mol Des. 1998;12:309. doi: 10.1023/a:1007999920146. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: Performance comparison between scoring functions developed with different training sets using the ΔvinaRF approach.
Figure S2: Performance comparison between scoring functions developed with different Vina feature sets using the ΔvinaRF approach.
Figure S3: Performance comparison between scoring functions developed with Vina10, bSASA and Vina10 + bSASA features using the ΔvinaRF approach.
Figure S4 Importance of features measured by percentage of increased mean squared error (%IncMSE) for 20 features in ΔvinaRF20.
Table S1: Training Set Description.
Table S2: AutoDock Vina Features in Source Code.
Table S3: Pharmacophore Type Definition.
Table S4: Summary of the Scoring Functions Evaluated in CASF-2007 Benchmark.
Table S5: Summary of the Scoring Functions Evaluated in CASF-2013 Benchmark.
Table S6: Performance of 18 Scoring Functions in the Scoring Power Test in CASF-2007.
Table S7: Performance of 18 Scoring Functions in Ranking Power Test in CASF-2007.
Table S8: Success rates of 18 Scoring Functions in the Docking Power Test in CASF-2007.
Table S9: Performance of 22 Scoring Functions in the Scoring Power Test in CASF-2013.
Table S10: Performance of 22 Scoring Functions in Ranking Power Test in CASF-2013.
Table S11: Success rates of 22 Scoring Functions in the Docking Power Test in CASF-2013.
Table S12: Enrichment Factors of 22 Scoring Functions in the Screening Power Test in CASF-2013.
Table S13: Success Rates of Finding the Best Ligand Molecule of 22 Scoring Functions in the Screening Power Test in CASF-2013.