Abstract
The evaluation of measurement invariance is an important step in establishing the validity and comparability of measurements across individuals. Most commonly, measurement invariance has been examined using one of two primary latent variable modeling approaches: the multiple groups model or the multiple-indicator multiple-cause (MIMIC) model. Both approaches offer opportunities to detect differential item functioning within multi-item scales, and thereby to test measurement invariance, but both approaches also have significant limitations. The multiple groups model allows one to examine the invariance of all model parameters but only across levels of a single categorical individual difference variable (e.g., ethnicity). In contrast, the MIMIC model permits both categorical and continuous individual difference variables (e.g., sex and age) but permits only a subset of the model parameters to vary as a function of these characteristics. The current paper argues that Moderated Nonlinear Factor Analysis (MNLFA) constitutes an alternative, more flexible model for evaluating measurement invariance and differential item functioning. We show that the MNLFA subsumes and combines the strengths of the multiple group and MIMIC models, allowing for a full and simultaneous assessment of measurement invariance and differential item functioning across multiple categorical and/or continuous individual difference variables. The relationships between the MNLFA model and the multiple groups and MIMIC models are shown mathematically and via an empirical demonstration.
The progress of any science depends in large part upon the availability of reliable, valid measures for the quantities and qualities of theoretical interest. More colloquially, we require that our measures produce precise measurements of the things they are supposed to be measuring. One important aspect of validity concerns the comparability of measurements across observations. In particular, we can only meaningfully compare between scores that are scaled equivalently. If a measure produces scores that are, say, systematically too high under some circumstances and systematically too low under others then the observed score differences will not accurately reflect true differences in the quantity being measured. In the educational testing literature, for instance, such differential measurement would be referred to as test bias. When a test is biased, examinees with certain characteristics are advantaged over others, scoring higher even at equal levels of underlying ability. Due to this differential measurement, differences in the test scores fail to accurately represent differences in ability. More broadly, when measurements are not scaled equivalently, analyses of individual differences may not only reflect the phenomena of interest (e.g., construct-level relationships or change) but also systematic variation in measurement. It is thus essential to determine whether our measures produce comparable measurements for all individuals within the population under study.
A great deal of theoretical and empirical research has been conducted on this topic within the contexts of factor analysis and item response theory (IRT), particularly as the issue pertains to psychological and educational assessment. Given the increasing convergence of the factor analysis and IRT literatures, here we shall provide a brief, unified overview of the key concepts, including measurement invariance (MI) and differential item functioning (DIF). MI refers to “the situation in which a scale or construct provides the same results across several different samples or populations” (APA, 2014, p. 211). If MI holds, one may validly compare scores and other results between individuals from the different populations. Typically, MI is evaluated for a multi-item scale by evaluating whether the items relate to the construct(s) in the same way for all individuals. If instead these relationships vary then there is DIF, defined as “the circumstance in which two individuals of similar ability do not have the same probability of answering a question in a particular way” (APA, 2014, p. 93). A well-known example is that girls endorse the item “cries easily” more often than boys who share the same level of depression (Steinberg and Thissen, 2006). If this DIF was ignored when generating scale scores it might lead to a sex bias, with girls who endorse the item receiving higher scores than boys even if their underlying depression is equal. Scale developers often attempt to remove or replace items with DIF to enhance MI, but this is not always possible to do without sacrificing coverage of the construct domain (AERA, APA, NCME, 2014, p. 82). To continue the example, it would be difficult to justify removing the item “cries easily” from a depression inventory, since this is a core behavioral manifestation of depression. Thus, when developing, evaluating, and applying measures, key interrelated tasks are to evaluate MI, identify specific items with DIF, and account for DIF when generating scale scores so as to mitigate bias.
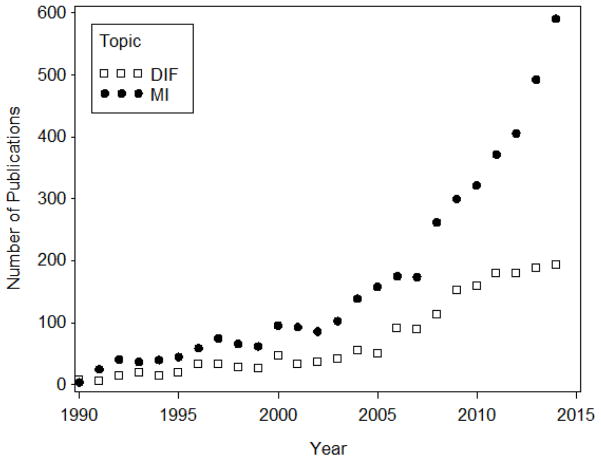
Recognition of the importance of assessing MI/DIF has grown rapidly since approximately 1990, as can be seen in Figure 1, which reports the number of articles, proceedings papers, reviews, and book chapters on the topics of MI and DIF published between 1990 and 2014 and cataloged in the Web of Science database. Given the increasing prominence of these topics in the field, it is a timely moment at which to re-examine the procedures used to evaluate MI/DIF. A variety of approaches exists, with many techniques developed in the context of large-scale high-stakes educational testing programs (Holland and Wainer, 1993). Here, however, we restrict our focus specifically to latent variable modeling approaches, as we believe these to be both most frequently used and best suited to a wide array of research contexts. The overarching goal of our paper is to therefore to present and contrast latent variable modeling approaches for the assessment of MI/DIF, including a relatively new approach that we argue offers important advantages over current practice.
Figure 1.
Number of publications by year that include the topics of measurement invariance (MI) and differential item functioning (DIF).
We begin by defining measurement invariance and reviewing the two latent variable modeling approaches that are most frequently used to evaluate MI/DIF, namely the multiple groups (MG) modeling approach and the multiple-indicator multiple-cause (MIMIC) modeling approach. In comparing these traditional approaches for assessing MI/DIF, we highlight that MG and MIMIC approaches offer contrasting strengths and weaknesses. We then present and advocate a third, more general approach which employs a moderated nonlinear factor analysis (MNLFA) model. MNLFA was recently developed by Bauer and Hussong (2009) for the purpose of facilitating integrative data analysis but has not previously been described as a general tool for evaluating MI/DIF, nor has its relationship to MG and MIMIC models been fully explicated, two of the primary aims of this paper. We will show that MNLFA incorporates the strengths of both the MG and MIMIC modeling approaches while avoiding their limitations. Next, we present an empirical analysis illustrating how the MNLFA can be used to evaluate MI/DIF. Finally, we conclude with general recommendations for the use of MNLFA in studies of MI/DIF and future directions for research.
A General Definition of Measurement Invariance
Here we establish formal definitions of MI and DIF that will prove useful as we proceed to compare modeling approaches. To begin, MI is said to exist if the distribution of the item responses we might obtain for an individual depends only on the person’s values for the latent variables and not also on other characteristics of the individual (Mellenbergh, 1989). Drawing upon Millsap (2011, p. 46), we can express this definition mathematically as
| (1) |
where f designates a probability distribution, yi is a p × 1 vector containing the observed item responses for person i, ηi is a r × 1 vector of unobserved latent factors, and xi is a q × 1 vector of observed person-level characteristics (e.g., gender, ethnicity, or age). In words, Equation (1) states that MI exists if the distribution of the observed items depends only on the values of the latent variables. This condition does not preclude that xi may be related to ηi, but it does imply that xi has no direct influence on the distribution of yi other than through its influence on ηi.
Measurement invariance would hold, for instance, if the values for a set of depression items depend only on a person’s underlying level of depression. But if the response distributions for some items (e.g., frequency of crying) differ as a function of sex, even after controlling for the level of depression, then this would indicate a lack of MI and the presence of DIF for those items. A general definition of DIF is then that, for a given item j,
| (2) |
That is, an item that shows DIF is one for which Equation 1 is not satisfied; the distribution of the item responses depends not only on the latent variable the item is intended to measure but on other individual characteristics as well. The term partial invariance is often used to describe measures for which Equation (1) is satisfied for a subset of items, but where a small proportion of items evince DIF (Byrne, Shavelson and Muthén, 1989). Although full invariance is not satisfied, valid individual difference analyses can still be conducted under partial invariance as long as DIF is appropriately identified and modeled.
Although we have defined MI/DIF here with respect to the conditional response distributions of the items, many comparisons are valid under the less stringent condition of first-order invariance (Millsap, 2011, p. 49–51). First-order invariance is defined in terms of the expected (average) values of the item responses as opposed to their full distributions, and is satisfied if
| (3) |
For instance, first-order invariance would be met if the expected values for a set of depression items depended only on a person’s underlying level of depression, and would be violated if the expected value differed depending on, say, sex. If, holding constant depression, there was greater variability in the item responses of girls than boys then this would violate Equation (1), since the response distribution for girls would differ from boys, but would not necessarily violate Equation (3), since the expected values of these distributions might still be equivalent.
Assessing MI/DIF with Multiple Groups Models
Historically, a common way to assess measurement invariance was to fit a factor analysis model separately to the data obtained from each of two or more groups, with the goal of identifying similarities and differences in the obtained factor pattern matrices (e.g., Holzinger and Swineford, 1939). Apparent differences in factor structure or in the magnitude of factor loadings might then lead to a rejection of MI. More rigorous assessments of such differences became possible through the development of the multiple groups confirmatory factor analysis model (and structural equation model) by Jöreskog (1971) and Sörbom (1974). With the MG model, one can simultaneously fit a confirmatory factor analysis in each of two or more groups, with the option to impose equality constraints on subsets of the model parameters. Comparing the fit of models with more versus fewer equality constraints (e.g., via likelihood ratio tests) thereby offers a formal means to assess across-groups invariance in measurement.
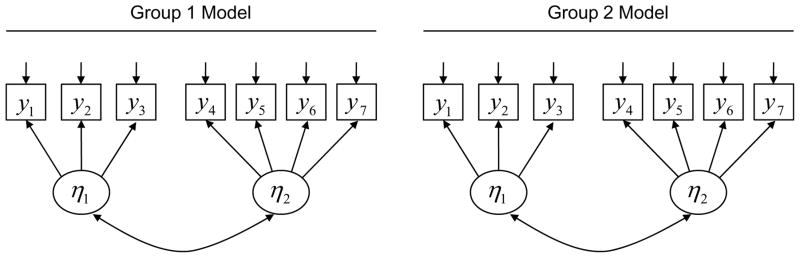
The basic principle behind the MG approach is that the data is subdivided by group. A confirmatory factor model is also stipulated for each group, with the potential to impose across-group equality constraints on specific parameter values. For example, Figure 2 depicts the situation where seven continuous items, y1-y7, are used to measure two factors, η1 and η2, in each of two groups (e.g., a seven item measure that divides into two subscales). In this case, the same basic factor structure holds in each group, a condition that is sometimes referred to as configural invariance (Horn and McArdle, 1992) and is necessary but not sufficient to ensure MI. What the diagram does not indicate, but is critical for the establishment of MI, is whether the parameter values governing the relationships between the items and the factors are identical across groups.
Figure 2.
Example conceptual diagram for a multiple groups linear confirmatory factor analysis with two groups and the same underlying factor structure in each group. Any of the non-zero model parameters could differ in value across groups (subject to identification restrictions).
To formalize this point, we can write the multiple groups factor analysis model in terms of two sets of equations. The first set of equations expresses the expected values and (co)variances of the observed variables conditional on the latent variables and group membership, and the second set of equations expresses the expected values and (co)variances of the latent variables in each group. Indexing group by g = 1, 2, … G and assuming continuous items, these equations may be written
| (4) |
| (5) |
and
| (6) |
| (7) |
The intercepts and slopes (or factor loadings) from the regression of the items on the factors within group g are contained in the p × 1 vector νg and p × r matrix Λg, respectively, whereas the group-specific residual variances and covariances of the indicators are contained in the p × p matrix Σg. Usually, Σg is assumed to be diagonal, consisting only of the residual variance parameters , a condition referred to as local independence. Finally, the r × 1 vector αg contains the group means for the factors whereas the r × r matrix Ψg contains the group-specific factor variances and covariances.
This conditional representation of the model is somewhat non-standard but has several advantages. First, as we will see, we can straightforwardly define measurement invariance in terms of the conditional distributions of the items. Second, this way of writing the model will facilitate subsequent comparisons to the MIMIC and MNLFA models. Finally, although written as a linear model for continuous items, this expression can easily be generalized for discrete outcomes. One way to accomplish this generalization is to posit that for a vector of binary or ordinal items yi there exists a corresponding vector of underlying continuous latent response variables, , which are related to yi through a threshold model (see Bollen, 1989, pp. 433–447; Muthén, 1984). Then Equations (4) and (5) would express the expected value and variance of . Alternatively, we can invoke a generalized linear modeling perspective and replace E(yi | ηi, g) in Equation (4) with a vector of linear predictor values (e.g., logits for binary outcomes) which pass through a nonlinear link function (e.g., the logistic link) to produce the expected values of the discrete responses (e.g., endorsement probabilities; see Skrondal & Rabe-Hesketh, 2004). In this alternative formulation, Equation (5) might or might not include scale parameters, as for many discrete distributions the variance is a function of the expected value. Our empirical example will illustrate this generalization of the MG model (as well as the MIMIC and MNLFA models) to discrete outcomes, but until then we shall retain the simplifying assumption that the items are continuous and linearly related to the factors.
For the linear factor analysis model, Meredith (1993) defined a hierarchy of levels of invariance that validate different types of between-group comparisons on the latent variables. The highest level of invariance is strict invariance, which requires that all of the item parameters are equal over groups, i.e., νg = ν, Λg = Λ, Σg = Σ. In this case Equations (4) and (5) simplify to
| (8) |
| (9) |
Thus the moments of the response distributions are independent of group membership after conditioning on the values of the latent factors. If, as is common, we additionally assume that the item responses are normally distributed in each group then Equations (8) and (9) imply that full measurement invariance is met. That is, the model conforms to Equation (1), where g takes the place of the vector x.
The next lower level of invariance is strong invariance, which requires only equality of the intercepts and factor loadings, i.e., νg = ν, Λg = Λ. In contrast to strict invariance, in this case the residual variances of the items are free to differ. Thus, the simplification in Equation (9) is no longer possible, but Equation (8) continues to hold. Equation (8) conforms to Equation (3), establishing first-order invariance. That is, group membership has no impact on the expected values of the items given the values of the latent variables. Under this condition, between-group comparisons of the factor means, variances, and covariances all remain valid. Since these are the usual comparisons of interest, strong invariance is often considered sufficient for most practical purposes.
Finally, the lowest level of invariance is weak invariance, in which only the factor loadings are equal over groups, i.e., Λg = Λ, and both the intercepts and residual variances are free to differ. Weak invariance satisfies neither Equation 1 nor 3, but continues to permit valid comparisons of factor variances and covariances.
Within the IRT literature there has been less emphasis on levels of invariance and more emphasis on the types of DIF that may be present. This difference in emphasis naturally follows the context within which IRT models are typically applied. Most IRT models were developed for categorical items, and the distributions of these items (e.g., binomial or multinomial) ordinarily do not include scale parameters (e.g., Σg) that would differentiate strict versus strong invariance. Equality of the intercepts and loadings (or, in an IRT parameterization, the related difficulty and discrimination parameters) is then sufficient to satisfy either Equation (1) or (3). Additionally, weak invariance does not permit the comparison of individual scores, which is the primary emphasis of many IRT applications, and is thus not a desirable property of a measure. Thus, within the IRT literature, Meredith’s (1993) levels of invariance are less relevant, and a different distinction has arisen, between uniform and non-uniform DIF. Uniform DIF exists if only the intercept for an item differs over groups, whereas non-uniform DIF exists if there is a between-group difference in the factor loading (whether or not the intercept differs as well).
Regardless of whether one approaches the problem from a factor analytic or IRT perspective, however, the principal concern is the same: determining whether the item parameters (e.g., intercepts, loadings, residual variances) are equal across groups. Customarily, the factor means, variances, and covariances are permitted to freely differ across groups, as improperly restricting their values could bias estimates of the item parameters and compromise tests of their equality. Moreover, the goal of establishing MI is often to unambiguously examine precisely these sorts of between-group differences in the latent factors while ruling out superficial differences in measurement. Thus the evaluation of MI/DIF ultimately hinges on whether there is empirical evidence that the item parameters differ over groups. A variety of model comparison strategies and inferential tests (e.g., likelihood ratio tests, modification indices, and Wald tests) have been proposed for the evaluation of MI/DIF. We will discuss some of these procedures in the context of the empirical demonstration but a thorough review is beyond the scope of the present manuscript (for a more complete treatment, see Millsap, 2011).
To get a better sense of MI/DIF evaluation with the MG approach, consider again the model in Figure 2. Suppose that strong invariance holds for this model with the exception that the intercept and factor loading for item y5 differs over groups. That is, y5 is characterized by non-uniform DIF. The goal of MI/DIF evaluation would then be to empirically determine that y5 is the sole indicator that fails to conform to strong invariance. Accommodating this partial invariance within the model by allowing the item parameters for y5 to differ over groups may in turn mitigate potential biases that could otherwise emerge at the level of the latent variables (i.e., in their means, variances, or covariance). In this scenario, only one item exhibits DIF, lending credibility to the notion that the factors retain comparability across groups so long as this DIF is incorporated in the model. When a higher proportion of items evince DIF, however, it becomes less clear whether the factors retain the same meaning and scale across groups and the comparison of results becomes less defensible (Widaman and Reise, 1997).
There are several key features of the MG approach for evaluating MI/DIF. First, because parallel models are fit in unison to the data from each group, any and all parameters of these models can be constrained to equality or permitted to differ between groups. As noted above, usually the factor means and (co)variances are allowed to differ between groups and interest centers on the equality of the item parameters, critically the intercepts and factor loadings but sometimes also the residual variances. Second, the architecture of the MG approach is designed to evaluate MI/DIF across discrete groups. It does not, therefore, accommodate possible DIF as a function of continuously distributed individual characteristics, such as age or socioeconomic status. This limitation follows from the original development of the fitting functions for MG models which relied on sufficient statistics, namely the within-group observed means, variances, and covariances of the items. The calculation of these sufficient statistics within each level of a grouping variable (e.g., males and females) is straightforward, but this is not the case for a continuously measured characteristic such as age or socioeconomic status, for which there may be only one set of item responses per observed value. These features of the MG approach, summarized in Table 1, contrast directly with those of the approach we describe next, the MIMIC model.
Table 1.
Comparison of types of predictors for which parameter values may differ over individuals in multiple groups (MG), multiple-indicator multiple-cause (MIMIC), MIMIC-interaction, and moderated nonlinear factor analysis (MNFLA) models.
| Parameters | Model |
|||
|---|---|---|---|---|
| MG* | MIMIC | MIMIC-Interaction | MNLFA | |
| α | Categorical | Categorical and Continuous | Categorical and Continuous | Categorical and Continuous |
| Ψ | Categorical | - | - | Categorical and Continuous |
| ν | Categorical | Categorical and Continuous | Categorical and Continuous | Categorical and Continuous |
| Λ | Categorical | - | Categorical and Continuous | Categorical and Continuous |
| Σ | Categorical | - | - | Categorical and Continuous |
Note: α = factor means; Ψ = variance-covariance matrix of latent factors; ν = item intercepts; Λ = factor loadings; Σ = variance-covariance matrix of item residuals.
MG model also allows for the possibility of distinct factor structures in each group, permitting tests of configural invariance.
Assessing MI/DIF with MIMIC Models
Currently, the primary alternative to the MG model for evaluating MI/DIF is the MIMIC model. At its inception, the MIMIC model was defined by the presence of a single latent variable that was both measured by multiple items (i.e., the multiple indicators) and also predicted by multiple exogenous observed variables (i.e., the multiple causes; Hauser and Goldberger, 1971; Jöreskog and Goldberger, 1975). Only later was the MIMIC model repurposed for assessing MI/DIF. Specifically, Muthén (1989) showed that with a modest modification, namely the addition of a direct effect from a predictor to an item, the MIMIC model could capture uniform DIF (a difference in the item intercepts). At about the same time, Oort (1992, 1998) proposed restricted factor analysis, which differs from the MIMIC model only in having the exogenous variables correlate with rather than predict the factors. Here, we focus on the more commonly implemented MIMIC model formulation.
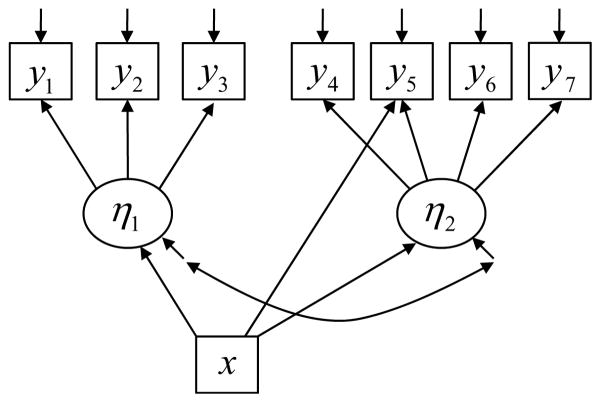
Figure 3 provides an example of a MIMIC model for MI/DIF in path diagram form, again in the situation where seven continuous items, y1-y7, are used to measure two factors, η1 and η2, in two groups. Notice that the MIMIC model is a unitary model for the entire population and that, here, the groups are differentiated explicitly by the exogenous predictor, x, which might be dummy coded as x = 0 for individuals in Group 1 and x = 1 for individuals in Group 2. Note also the regression of both the factors and the item y5 on the predictor x. The regression of the factor on x allows for differences in the conditional mean of the factor as a function of x (i.e., the expected values of η1 and η2 differ between the two groups). Beyond this, the regression of the item y5 on x implies that the expected value of y5 differs as a function of x even when holding η2 constant (i.e., individuals from one group score more highly on y5 than individuals from the other group even when their true scores on η2 are equal). This direct, main effect of x on y5 thus captures uniform DIF.
Figure 3.
Example conceptual diagram showing a multiple-indicators, multiple causes (MIMIC) model in which item y5 shows differential item functioning by characteristic x.
The general form of the MIMIC model may be written via the equations
| (10) |
| (11) |
and
| (12) |
| (13) |
where K is a p × q matrix of regression coefficients for the direct effects of the predictors on the items, and Γ is a r × q matrix of regression coefficients for the effects of the predictors on the latent factors. All other notation and parameters remain defined as before, with the exception that intercepts, νi, and factor means, αi, are now covariate dependent and thus ν0 and α0 represent baseline values when xi = 0. Again, generalizations of Equations (10) and (11) for discrete items are straightforward based on these expressions.
A defining feature of the MIMIC model is that the expected values of both the observed and latent variables are linear functions of xi and are therefore individual-specific. That is, the factor mean may vary as a function of individual characteristics (e.g., girls may have a higher mean level of depression than boys), as may the intercept of an item (e.g., even after controlling for mean-level differences in depression, girls tend to provide higher ratings on a “crying” item than boys). For this reason, αi and νi are subscripted by i, as their values depend on the values of xi observed for the person (αi and νi are not, however, random effects, nor do they have probability distributions; they are deterministic functions of xi).
When the intercept of an item depends directly on xi, this represents uniform DIF. Thus, MI is obtained only if K is a null matrix, for then νi = ν0 and Equation (10) simplifies to
| (14) |
This equation conforms to Equation (3), establishing first-order invariance. That is, differences in the expected values of the items are explicable entirely by differences in the latent variables ηi, and do not otherwise vary as a function of the individual characteristics xi. Moreover, if the item responses are normally distributed, Equations (11) and (14) together are sufficient to satisfy Equation (1), implying that the response distributions differ only as a function of the latent variables.
At this juncture it is useful to compare the MIMIC approach to the MG approach for evaluating MI/DIF. This comparison is facilitated by initially assuming that one is concerned only with assessing MI/DIF across groups of individuals. In this case, if there were G groups, the xi vector in the MIMIC model would consist of G – 1 coding variables (e.g., dummy codes). The factors would be regressed upon these coding variables, as would any indicators manifesting DIF.
In contrast, in the MG approach, a factor model would be specified for each of the G groups, and subsets of the model parameters would be restricted to be equal across groups, depending on the level of MI and the location of DIF.
In this scenario, the MIMIC model imposes a number of restrictions relative to the MG model. First, because the MIMIC model is specified for the total population, configural invariance is implicitly assumed to hold across groups, whereas this not required when using the MG approach. Although this is an advantage of the MG approach, it may not always be of much consequence. In our experience, many investigations of MI/DIF presume configural invariance to hold (sometimes on the basis of prior empirical evidence) and have the principal goal of identifying higher levels of invariance that will permit objective comparisons of results and scores between groups.
Second, both the MIMIC and MG model allow the factor means to differ between groups, but only the MG model also allows the factor variances and covariances to differ. That is, when xi consists solely of coding variables differentiating nominal groups, αi in Equation (12) will represent group-specific factor means, paralleling αg from Equation (6). For example, the MIMIC model in Figure 3 implies that the factor means are
| (15) |
If x has been dummy coded 0 for individuals in the first group and 1 for individuals in the second group, then the implied factor means for the first group are simply α10 and α20 and for the second group they are α10 +γ11 and α20+γ21. Thus, in this MIMIC model, the values of the factor means α1i and α2i differ only by group, just as α1g and α2g differ by group in the corresponding MG model. In contrast, in the MIMIC model, the within-group variance-covariance matrix for the latent variables, given by Equation (13) as Ψ, bears no subscript and is assumed to be constant (i.e., at any given level of xi or for any given group). This assumption differs from the MG model, for which Equation (7) allows for a different variance-covariance matrix for each group, designated Ψg.
The third difference between the MIMIC and MG models concerns DIF evaluation. Both models offer the ability to capture uniform DIF, but they differ in their ability to capture non-uniform DIF. Consider again the model depicted in Figures 2 and 3. The MIMIC model implies an expected value for y5 of
| (16) |
The intercept of this equation is ν50 for individuals in the first group and ν50 +κ51 for individuals in the second group. Thus ν5i varies by group when the predictor is a coding variable, capturing uniform DIF. Likewise, ν5g varies by group in the MG model. Specifically, per Equation (4), the MG model implies an expected value for y5 of
| (17) |
Notice, however, that the MG model also allows for between group differences in the factor loading or non-uniform DIF, whereas the factor loading in the MIMIC model is assumed to be constant over groups. Additionally, comparing the conditional variance expressions in Equation (11) versus Equation (5) shows that the MIMIC model assumes the within-group residual variance for the item to be equal across groups whereas the MG model allows the residual variance to differ in value over groups.
Recently, Woods and Grimm (2011) proposed incorporating non-uniform DIF into the MIMIC model through the specification of latent by observed variable interactions, referred to as the MIMIC-interaction model (see also Barendse, Oort and Garst, 2010). For instance, using the symbol ω to designate the interaction, the equation for y5 would be specified as
| (18) |
Here, the top line shows the inclusion of the product interaction η2ixi in the model; the middle line regroups terms to show how the intercept and slope of the y5 on η2 regression line depend linearly on the value of x; finally, the last line shows that the intercept and slope are individual specific (depending on x). Again, if x is a dummy coded predictor, then we simply obtain group-specific intercepts and slopes, thus matching the MG model and allowing for non-uniform DIF across groups.
In sum, the MIMIC model requires configural invariance, implicitly assumes homogeneity of (co)variance for both the latent variables and items, and assumes equal factor loadings, precluding the assessment of non-uniform DIF (unless one extends to the MIMIC-interaction model). Notwithstanding these limitations, however, the MIMIC model offers two principal advantages. First, the MIMIC model may have greater power to detect uniform DIF, particularly when some group sample sizes are small, provided its restrictions on the nature of between-group differences are not entirely unreasonable (Muthén, 1989; Woods, 2009b). It is worth noting, however, that imposing parallel restrictions in a MG model would be expected to result in comparable power (Kim & Cao, 2015). Second, the MIMIC model easily accommodates multiple predictors and these may include continuous covariates. We can thus evaluate DIF for multiple characteristics simultaneously, including main effects and possibly also interactions (e.g., ethnicity, gender, age, and gender × age). In contrast, even given sufficient within-group sample sizes it would be cumbersome to separate main effects and interactions for multiple grouping variables within the MG model. Additionally, any continuous characteristics would have to be discretized (e.g., by a median split), a practice that can reduce power and bias estimates (MacCallum et al., 2002). Thus, as summarized in Table 1, the MG and MIMIC approaches for assessing MI/DIF offer contrasting strengths and weaknesses.
Assessing MI/DIF via Moderated Nonlinear Factor Analysis
The MNLFA approach to MI/DIF evaluation is inspired by the desire to combine the strengths of the MG model with those of the MIMIC model. In particular, the MNLFA model retains the principal strength of the MG model, namely that all parameters, including variances, covariances, and factor loadings, can be allowed to differ as a function of known individual characteristics. At the same time, the MNLFA incorporates the principal strength of the MIMIC model, namely that there may be multiple individual characteristics of interest for MI/DIF and that these may be either discrete or continuous in nature.
Bauer and Hussong (2009) originally presented the MNLFA as a modeling approach to facilitate integrative data analysis (IDA), or the pooled analysis of raw data from multiple studies, for which a primary challenge is to establish common, equivalent measures. More recently, Curran et al. (2014) provided a review and practical guidance on the use of MNLFA for integrative data analysis. Here, we depart from those earlier works in presenting the MNLFA as a general purpose tool that offers significant advantages relative to MG or MIMIC approaches for assessing MI/DIF even in single-study investigations. For instance, one could use the MNLFA to evaluate MI/DIF for a quality of life measure as a function of age, intelligence, and/or socioeconomic status, without the need to discretize these naturally continuous variables.
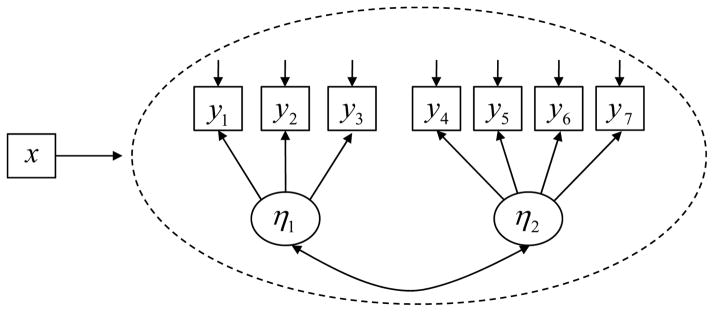
In the MNLFA model, MI/DIF is viewed as a form of parameter moderation. Figure 4 conveys this idea conceptually via the arrow pointing from x to the measurement model for the indicators y1-y7. The exogenous variable x (e.g., age) may alter the values of any subset of the model parameters in this measurement model, including the means, variances, and covariance of η1 and η2 as well as the item intercepts, factor loadings, and residual variances of y1-y7. The presence or absence of MI/DIF then becomes a question of which parameters are moderated by x. If moderation is restricted to the parameters characterizing the factors – their means, variances, and covariance – then this is consistent with MI. If, however, the item parameters are also moderated by x then this represents DIF. Moderation of the intercepts would indicate uniform DIF, whereas moderation of the factor loadings would indicate nonuniform DIF. Moderation of the residual variances is also possible.
Figure 4.
Example conceptual diagram showing a moderated nonlinear factor analysis (MNLFA) model. The arrow pointing to the dashed ellipse is meant to convey that the values any of the model parameters can be specified to be a function of x (subject to identification restrictions).
More formally, the MNLFA for continuous items may be written as
| (19) |
| (20) |
and
| (21) |
| (22) |
with similar potential for generalization to models for discrete outcomes (see Bauer and Hussong, 2009). The notation used in these equations, defined as before, differs somewhat from prior presentations of the MNLFA but facilitates comparison to the MG and MIMIC models. Of particular importance for the current discussion is the presence of the i subscript on each parameter vector/matrix. This subscript indicates that the values of these parameters may vary deterministically (not randomly) over individuals as a function of xi. To complete the model specification, the moderation function must be defined for each parameter. In the event that a parameter is invariant, we will simply remove the i subscript.
For parameters that depend on xi various moderation functions might be considered. For intercepts, factor means, and factor loadings, Bauer and Hussong (2009) suggested the use of linear functions. Following this suggestion, we can write the functions for the intercepts and factor means as
| (23) |
| (24) |
where vectors subscripted by zero contain the baseline values of the parameters when xi = 0 and the coefficient matrices K and Γ (defined as before) capture the linear dependence of the intercepts and factor means on xi, respectively. Similarly, to express linear moderation for any given column of factor loadings, say for factor a, we may write
| (25) |
where λa0 is a p × 1 vector of baseline factor loadings for factor a when xi = 0 and Ωa is a p × q matrix of coefficients that produce linear changes in the loadings associated with factor a given changes in the values of xi.
In contrast to means, intercepts, and loadings, a linear moderation function is plainly not suitable for elements of the variance-covariance matrices, Σi and Ψi. Linear moderation could, for instance, imply negative variances or correlations exceeding one in their absolute values. This issue of how best to specify moderation of variance-covariance parameters is complex and greater detail is provided in the Appendix for the interested reader. In the interest of brevity, here we will present one set of moderation functions that we find appealing. First, we employ log-linear moderation functions for variances to avoid obtaining negative values. For instance, the variance of factor a may be expressed as
| (26) |
where ψ(aa)0 is the baseline variance when xi = 0, and β(aa) is a q × 1 vector of moderation effects, capturing differences in the factor variance (i.e., heteroscedasticity) as a function of xi. The log-linear form of this equation ensures that the implied factor variance is positive for any value of xi so long as the baseline variance is positive. Log-linear moderation equations can likewise be used to model residual variances within Σi.
Second, we model covariance parameters indirectly through Fisher’s z-transformation of the corresponding correlations to ensure that the correlations remain bounded between −1 and 1. Designating the Fisher-transformed correlation between factors a and b as ζ(ab)i, we can specify the linear moderation function
| (27) |
Here, ζ(ab)0 is the baseline value when xi = 0 and moderation effects are contained within the q × 1 vector υ(ab) . The model-implied conditional correlation between the two factors at any given value of xi can be obtained by inverting Fisher’s z-transformation. In turn, the covariance ψ(ab)i can be computed as a function of this correlation and the constituent factor variances (see Appendix for details). If present, covariances among the residuals could be modeled using the same approach.
Having now established the MNLFA model we can explicate its relationships to the MG and MIMIC models. We describe these relationships mathematically here, and demonstrate them empirically in the example analysis to follow. Most straightforward is the relationship between the MIMIC model and the MNLFA model. Simply put, the MNLFA model generalizes and subsumes the MIMIC model. The MNLFA model reduces to the standard MIMIC model if the following restrictions are imposed: only the factor means and intercepts are moderated by the exogenous variables and the functional form of moderation is in each case linear. Equations (19) – (22) for the MNLFA model then simplify to have the same form as Equations (10) – (13) for the standard MIMIC model. If we relax the constraint that the factor loadings are equivalent, and instead permit linear moderation of the factor loadings per Equation (25) then the MLFA is equivalent to the MIMIC-interaction model. The MNLFA, however, also permits the variance-covariance parameters of the model to vary as a function of the predictors. In this sense, another way to conceptualize the MNLFA is as an extended MIMIC model in which not only the factor loadings but also the variance-covariance parameters depend on the predictors. Indeed, one way to implement a MNLFA is to specify the model as a MIMIC-type model with nonlinear constraints on the loadings and variance-covariance parameters (see Supplemental Materials on the journal website).1
The relationship between MNLFA and MG models is slightly more complicated. The MNLFA model (like the MIMIC model) presumes configural invariance, whereas the MG model allows for potentially distinct factor structures in each group. Notwithstanding this difference, however, a large and important class of MG models is nested within the MNLFA. Specifically, any configurally invariant MG model can be expressed equivalently as an MNLFA where xi consists solely of coding variables to differentiate the levels of a grouping variable. The MNLFA allows for between-group differences in the intercepts and factor means in precisely the same way as the MIMIC model, reproducing the corresponding parameter differences in the MG model as shown in our earlier comparison of the MIMIC and MG models. Similarly, the MNLFA allows for between-group differences in the factor loadings in the same way as the MIMIC-interaction model. Unlike these MIMIC models, however, the MNLFA also allows for between-group differences in the variance-covariance parameters of the model, enabling the MNLFA to fully reproduce the range of potential between-group parameter differences provided by the MG model.
To better see how the MNLFA reproduces between-group differences in the variance-covariance parameters, we shall compare the MNLFA in Figure 4 to the parallel MG model in Figure 2. For this example we have two groups, represented in Figure 4 via the dummy-coded predictor x. The MNLFA model, using the log-linear moderation function given in Equation (26), implies the following factor variances:
| (28) |
When x = 0 (i.e., for the first group) the terms within the exponential functions equal zero, and since exp(0) = 1 we obtain implied factor variances of ψ(11)0 and ψ(22)0. These correspond directly to the factor variances that would be obtained from the MG model for the first group. In contrast, if x = 1 (i.e., for the second group) then the implied factor variances are ψ(11)0 exp(β(11)) and ψ(22)0 exp(β)(22)). The exponentiated regression coefficients in these equations therefore indicate the ratios by which the factor variances differ between groups (e.g., if β(11) = .69, then exp (β(11)) = 2, and the variance of the factor is twice as large in the second group relative to the first). Thus, in this MNLFA model, the values of the factor variances differ only by group, just as ψ(11)g and ψ(22)g differ by group in the corresponding MG model. The principal difference is that these variances are estimated directly in each group in the MG model whereas they are estimated directly only in the reference group in the MNLFA model and are captured by multiplicative contrasts in the other group.
Similarly, the MNLFA model equally captures between-group differences in covariance parameters, albeit through an alternative parameterization. The MNLFA models heterogeneity in the factor covariance in Figure 4 through the Fisher-transformed correlation via the equation
| (29) |
When x = 0 we obtain ζ(21)0 and when x = 1 we obtain ζ(21)0 + υ(21) and these values would result in correspondingly different covariance values ψ(21)i for each group, matching the ψ(21)g covariance values obtained from the MG model. Likewise, the MNLFA and MG models are equivalent but differ in their parameterization when expressing residual variance or covariance differences. In short, because the MNLFA can reproduce group differences in any parameter of the model, an equivalent MNLFA can be specified for any configurally invariant MG model. Unlike the MG model, however, the MNLFA can also allow for heterogeneity in these parameters as a function of continuous predictors.
To summarize, the MNLFA model offers a number of important advantages relative to the MG and MIMIC models. Unlike the MG model, MNLFA permits the assessment of MI/DIF as a function of individual characteristics which may include continuous variables. Unlike the MIMIC model, MNLFA allows for the moderation of variance and covariance parameters in addition to means and intercepts, as well as allowing for non-uniform DIF through moderation of the factor loadings. These differences are summarized in Table 1.
We now turn to an empirical application to demonstrate the flexibility of the MNLFA model for modeling MI/DIF relative to the MG and MIMIC models.
Empirical Application
Our empirical application focuses on the evaluation of measurement invariance for measures of violent and non-violent delinquent behaviors, with particular attention to age and sex differences during adolescence. We use this example to demonstrate the application of the MNLFA as well as its relations to the MG and MIMIC modeling approaches. Specifically, we show that different restrictions on the MNLFA model produce the MG and MIMIC models but that these restrictions are not empirically supported by the data.
Sample and Measures
We analyze a subsample drawn from the National Longitudinal Study of Adolescent to Adult Health (Add Health), and we include items drawn from the Delinquency and Fighting and Violence scales administered during the Wave I in-home interview. The Add Health sample is representative of adolescents in the United States who were in grades 7–12 during the 1994–1995 school year. To be selected for inclusion in the current analyses, an adolescent needed to be part of the public-use, self-weighting core sample, have at least partial item-level data, have no missing data on age or sex, and be between 12 and 18 years of age. In total, our sample consisted of N = 4,243 adolescents from 124 schools (47% male; MAge = 14.9; SDAge = 1.7).
All analyses reported here were conducted with maximum likelihood estimation (with adaptive quadrature and 15 quadrature points per dimension) using Mplus 7.3 (Muthén & Muthén, 2012). Detailed information on fitting MNLFAs using the Mplus software program is provided in online Supplemental Materials at the journal website. For the current analyses, standard errors and test statistics were adjusted to account for the complex sampling design (Muthén & Satorra, 1995). Note that this approach to analyzing clustered data provides aggregated (total) effect estimates and does not differentiate within- versus between-school factor structures, which were not of specific interest in this investigation (see, however, Wu & Kwok, 2012, for concerns about the interpretation of total effect estimates, and Ryu, 2014, 2015 on MI/DIF evaluation with multilevel data). Due to sparseness within the upper categories of the ordinal response scales, for the present purposes all items were dichotomized to reflect yes/no responses, and models were fit using a logistic specification. We also centered age at 15 years to enhance the interpretability of the model parameters.
Steps for Fitting the MNLFA
Testing MI/DIF typically involves a specification search in which multiple models are compared to identify an optimal model for the data. This is true for MG and MIMIC models as much as it is for the MNLFA, but the greater complexity of the MNLFA requires additional decisions on the part of the analyst. We draw upon the steps described by Curran et al (2014) for unidimensional MNLFA applications in integrative data analysis, modified here in Table 2 for greater generality and in view of possible multidimensional applications.
Table 2.
Suggested steps for MI/DIF evaluation using MNLFA models
| Step | Description |
|---|---|
| 1. Determination of the Factor Structure | Using prior research, content analysis and/or preliminary data analysis, identify the basic factor structure for the item set. Preliminary subsample analyses may be useful for providing an indication of whether configural invariance is tenable. |
| 2. Fit MNLFA models separately to each factor | In the absence of a complex factor structure (i.e., many cross-loading items), divide the items into unidimensional sets and fit single-factor MNLFAs within each set to identify the optimal specification for each factor |
| a. Mean and variance specification | Based on theory, prior research and/or graphical data analysis (e.g., inspection of trends in total scores or factor scores), identify the moderation functions to be used with respect to the factor mean and variance |
| b. DIF detection | Identify items with and without DIF. Several DIF-detection strategies might be considered, depending on the number of items under consideration. For short scales, consider an iterative DIF detection procedure. For longer scales alternative approaches may be more practical. |
| 3. Fit multidimensional MNLFA model | Combine optimal unidimensional models and analyze the full item set simultaneously. It is in this step that the factor covariance specification is introduced. |
Step 1: Determination of the factor structure
This step consists of preliminary research to determine the basic structure of the item set prior to fitting MNLFA models. Such a determination may be made based on theoretical considerations, the factor structure reported in prior literature, and/or through preliminary analyses conducted in the full sample as well as specific subsamples (see Curran et al., 2014, for more elaboration). In the current case our theoretical expectation was that the items would divide into non-violent and violent sub-dimensions of delinquent behavior (Barnes, Beaver & Miller, 2010; Molinengo & Testa, 2010; Willoughby, Chalmers & Busseri, 2004). Content analysis of the available items and preliminary factor analyses (not shown) supported this view. Several items were, however, excluded due to low content validity (e.g., “Run away from home”), high local dependence (e.g., “Get into a serious physical fight” with “Got into a physical fight”), or substantial cross-loadings (e.g., “Use a weapon to get something from someone” includes both a property crime and threat of violence). The remaining items (shown in Table 3) nicely mapped onto the theoretical sub-dimensions of interest.
Table 3.
Description of items included in analyses
| Item Label and Stem (Abbreviated) | Marginal % Endorsement |
|---|---|
| Involvement in Non-Violent Delinquent Behavior | |
| DS1. Paint graffiti/signs on someone else’s property or in a public space | 8.2 |
| DS2. Deliberately damage property that did not belong to you | 17.9 |
| DS3. Lie to parents/guardians about where you had been or whom with | 53.2 |
| DS8. Drive a car without it’s owner’s permission | 8.8 |
| DS9. Steal something worth more than $50 | 4.3 |
| DS10. Go into a house or building to steal something | 4.7 |
| DS13. Steal something worth less than $50 | 18.6 |
| DS15. Were loud, rowdy, or unruly in a public place | 48.2 |
| Involvement in Violent Behavior | |
| FV1. Saw someone shoot or stab another person | 10.2 |
| FV2. Someone pulled a knife or gun on you | 11.2 |
| FV3. Someone shot you | 1.1 |
| FV4. Someone cut or stabbed you | 3.7 |
| FV5. You got into a physical fight | 29.7 |
| FV6. You were jumped | 9.6 |
| FV7. You pulled a knife or gun on someone | 4.0 |
| FV8. You shot or stabbed someone | 1.5 |
| DS6. Hurt someone badly enough to need bandages or care from doctor/nurse | 16.2 |
| DS14. Take part in a fight where a group of your friends was against another group | 17.8 |
Note: DS = Delinquency Scale; FV = Fighting and Violence scale
Step 2: Fit MNLFA models separately to each factor
Given the complexity of the MNLFA and the additional computing time required to fit multidimensional versus unidimensional models2, it may often prove useful to pursue a “divide and conquer” strategy in conducting the analysis. In particular, in applications that involve a simple factor structure (no cross-loadings) we suggest first identifying the optimal model for each factor in isolation of the other factors before fitting a model that includes all factors simultaneously. For each factor, model specification is determined in two steps.
Step 2a is to identify the moderation functions for the factor mean and variance. This may be based on theory and/or empirical information. In the present case, it is well known that delinquent, criminal, and aggressive behaviors tend to be higher among boys and exhibit a curvilinear trend across adolescence and young adulthood in which there is an initial increase followed by a later decrease (Farrington, 1986; Loeber & Dale, 1997; Moffit, 1993). For the current data, such trends were apparent in scatterplots of total scores by age and gender (as well as with factor score estimates computed from a model excluding covariates). These plots also suggested potential differences in the factor variances with age. We thus included male, age, age2, male × age and male × age2 effects on the factor mean and variance via the functions given in Equations (24) and (26) (regardless of significance level).
Step 2b is to identify items exhibiting DIF. As noted previously, many DIF detection procedures have been proposed and investigated within the context of fitting factor analysis or IRT models. Generalizing one of these approaches to the MNLFA, Curran et al. (2014) suggested using likelihood ratio tests to evaluate DIF for each item while holding all other items invariant. Because this general approach has been shown to produce higher than nominal Type I error rates (Finch, 2005, Woods, 2009; Millsap, 2011, p. 199–200), Curran et al. (2014) subsequently fit a simultaneous model in which DIF is permitted for each flagged item followed by trimming of non-significant effects (on the basis of Wald tests). Another option, which we pursue here, is to use an iterative strategy in which we initially assumed all items to be invariant and then tested DIF associated with the set of covariates (i.e., male, age, age2, male × age and male × age2) in a sequential process. Using the scaled likelihood ratio test of Satorra and Bentler (2001) to account for the cluster-correlated nature of the data3, we first identified the item for which DIF would result in the largest improvement in fit. We retained DIF for this item and then determined whether allowing for DIF in a second item would significantly improve model fit. Allowing for DIF in the second item that would most improve model fit, we then considered a third item, and so on, until no further significant improvement in model fit could be obtained. Finally, we removed non-significant DIF terms, other than lower-order terms involved in higher-order effects (based on scaled LRTs). Similar iterative approaches have been shown to perform reasonably well for related models (Oort, 1998; Navas-Ara & Gomez-Benito, 2002), but the number of model comparisons increases rapidly with the number of items in the analysis. Woods (2009) suggested an alternative approach that is more practical with large item sets and which could also be generalized to the MNLFA. In addition, it may be useful to consider adjusting significance tests to maintain a specific family-wise Type I error rate (e.g., the Benjamini-Hochberg procedure; Thissen, Steinberg & Kuang, 2002; Thissen, Steinberg, & Wainer, 1993). We did not use any such adjustment in the present case in an effort to be overly inclusive in the initial iterative identification of DIF prior to subsequent model trimming.
Step 3: Fit multidimensional MNLFA model
Finally, we recombine the items and fit the full MNLFA, incorporating the specifications obtained in Step 2 for each factor (i.e., for the factor means, factor variances, and DIF) and adding moderation of the factor covariances (using the Fisher’s z specification in Equation (29)). Our covariate set for the covariance between the non-violent and violent factors again included male, age, age2, male × age and male × age2. Non-significant effects were trimmed (based on the scaled LRT), with the exception that we retained all main effects on the factor means, variances, and covariance/correlation (regardless of significance).
MNLFA Results
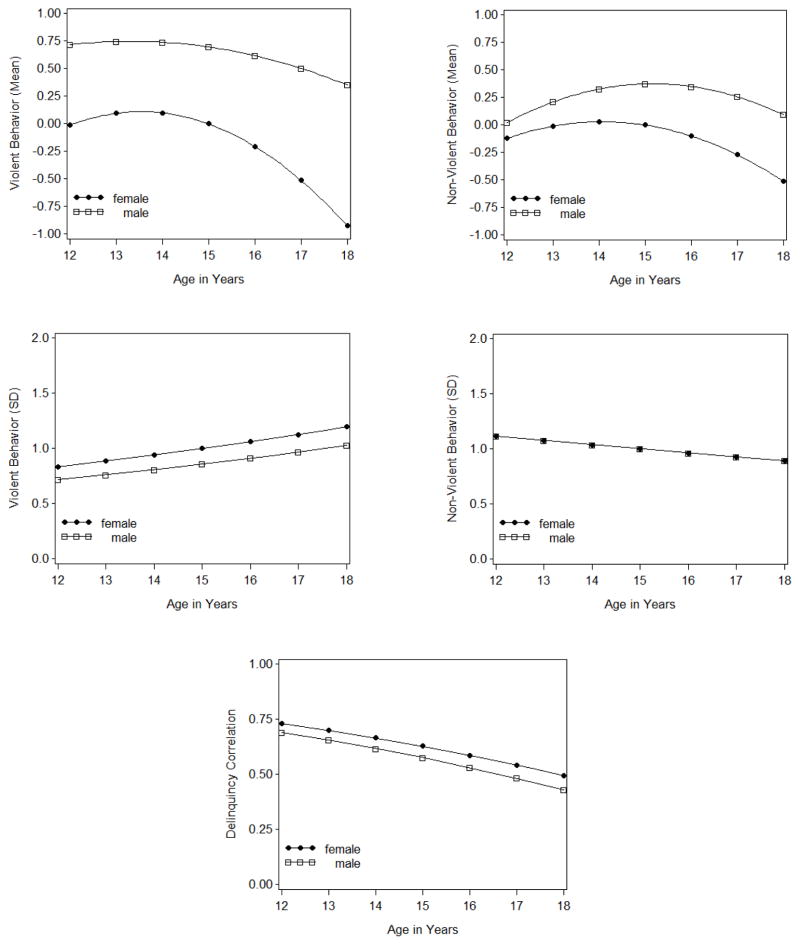
The results obtained from the final MNLFA model are presented in Table 4, which reports the factor mean, variance, and covariance parameter estimates followed by the item parameter estimates. We shall focus first at the level of the latent factors. In interpreting these parameters we must be mindful that we have specified linear models for the means, log-linear models for the variances, and a linear model for Fisher’s z to capture differences in the factor covariance. To enhance interpretation, we can convert the implied factor variances to standard deviations and the implied Fisher’s z values to factor correlations, as shown in Figure 5. As seen in the upper row of plots, for the factor means, we observed quadratic age trends as well as sex differences, with girls displaying lower levels and more rapid desistance in late adolescence. The sex differences are more marked for violent behavior (upper left panel) than non-violent delinquency (upper right panel). As shown in the middle row of Figure 5, the standard deviation for violent behavior increased with age, whereas individual differences in non-violent delinquency decreased with age. Slightly more variability in violent behavior was observed among female than male adolescents. Finally, as shown in the bottom panel, the correlation between violent and non-violent delinquent behavior decreased significantly with age. Notably, the variance and covariance trends depicted in middle and lower panels of Figure 5 are unique to the MNLFA; neither the MG nor MIMIC model could produce these substantively interesting findings.
Table 4.
Parameter estimates from final moderated nonlinear factor analysis model
| Reference Parameter | Baseline | Covariate Effect |
||||
|---|---|---|---|---|---|---|
| Age | Age2 | Male | Male × Age | Male × Age2 | ||
| Non-Violent Factor | ||||||
| Mean | 0.00a | −0.07 (.02) | −0.04 (.01) | 0.37 (.06) | 0.08 (.02) | – |
| Variance | 1.00a | −0.07 (.03) | – | 0.00 (.07) | – | – |
| Violent Factor | ||||||
| Mean | 0.00a | −0.15 (.03) | −0.05 (.01) | 0.70 (.06) | 0.09 (.03) | 0.03 (.01) |
| Variance | 1.00a | 0.12 (.04) | – | −0.30 (.10) | – | – |
| Factor Covariance | ||||||
| Fisher’s z | 0.74 (.05) | −0.07 (.02) | – | −0.08 (.07) | – | – |
|
| ||||||
| DS1. Graffiti | ||||||
| Intercept | −3.91 (.19) | – | – | – | – | – |
| Loading | 1.98 (.14) | – | – | – | – | – |
| DS2. Property Damage | ||||||
| Intercept | −2.94 (.17) | −0.10 (.04) | – | −0.40 (.31) | – | – |
| Loading | 2.03 (.15) | – | – | 0.95 (.27) | – | – |
| DS3. Lie Parents | ||||||
| Intercept | 0.62 (.08) | 0.31 (.04) | −0.05 (.02) | −0.83 (.10) | −0.25 (.05) | – |
| Loading | 1.42 (.09) | – | – | – | – | – |
| DS8. Car w/o Permission | ||||||
| Intercept | −3.02 (.13) | 0.11 (.04) | −0.06 (.02) | – | – | – |
| Loading | 1.39 (.09) | – | – | – | – | – |
| DS9. Steal > $50 | ||||||
| Intercept | −5.07 (.30) | – | – | – | – | – |
| Loading | 2.15 (.19) | – | – | – | – | – |
| DS10. Steal from House | ||||||
| Intercept | −5.27 (.29) | – | – | – | – | – |
| Loading | 2.37 (.19) | – | – | – | – | – |
| DS13. Steal < $50 | ||||||
| Intercept | −2.50 (.15) | – | – | – | – | – |
| Loading | 1.91 (.11) | – | – | – | – | – |
| DS15. Rowdy in Public | ||||||
| Intercept | 0.01 (.07) | – | – | −0.48 (.11) | – | – |
| Loading | 1.41 (.08) | – | – | – | – | – |
|
| ||||||
| FV1. Saw Shoot/Stab | ||||||
| Intercept | −3.66 (.26) | 0.26 (.08) | 0.09 (.04) | −0.87 (.13) | – | – |
| Loading | 2.27 (.16) | −0.09 (.06) | −0.08 (.03) | – | – | – |
| FV2. Pulled Weapon on You | ||||||
| Intercept | −4.60 (.29) | 0.39 (.10) | 0.12 (.05) | – | – | – |
| Loading | 2.70 (.19) | −0.09 (.08) | −0.09 (.04) | – | – | – |
| FV3. Shot You | ||||||
| Intercept | −6.66 (.40) | 0.56 (.18) | 0.12 (.05) | – | – | – |
| Loading | 1.73 (.17) | −0.35 (.11) | – | – | – | – |
| FV4. Cut/Stabbed You | ||||||
| Intercept | −5.78 (.35) | – | – | – | – | – |
| Loading | 2.32 (.20) | – | – | – | – | – |
| FV5. Physical Fight | ||||||
| Intercept | −2.27 (.17) | – | – | – | – | – |
| Loading | 2.44 (.16) | – | – | – | – | – |
| FV6. Were Jumped | ||||||
| Intercept | −4.16 (.22) | – | – | – | – | – |
| Loading | 2.14 (.14) | – | – | – | – | – |
| FV7. You Pulled Weapon | ||||||
| Intercept | −6.97 (.49) | – | – | – | – | – |
| Loading | 3.12 (.29) | – | – | – | – | – |
| FV8. You Shot/Stabbed | ||||||
| Intercept | −10.55 (1.35) | – | – | – | – | – |
| Loading | 4.11 (.63) | – | – | – | – | – |
| DS6. Hurt Other Badly | ||||||
| Intercept | −3.56 (.18) | 0.03 (.08) | – | 0.23 (.12) | 0.15 (.06) | – |
| Loading | 2.25 (.16) | −0.15 (.07) | – | – | – | – |
| DS14. Group Fight | ||||||
| Intercept | −2.60 (.15) | −0.02 (.08) | – | −1.47 (.35) | 0.57 (.15) | – |
| Loading | 1.84 (.15) | −0.16 (.08) | – | 0.90 (.32) | −0.30 (.14) | – |
Note: See Table 1 for full descriptions of items. Age = 0 corresponds to 15 years of age; units are years. Male = 0 corresponds to females; Male = 1 corresponds to males.
Indicates that the value of the parameter was fixed (not estimated) to identify the model and set the scale of the latent variables.
Figure 5.
Model-implied age and sex differences in the factor means, standard deviations, and correlation.
The validity of these findings hinges on our ability to measure the factors equivalently at all ages and across male and female adolescents. We thus now turn to the interpretation of the item parameters, in particular, those that capture DIF. For the non-violent factor, we detected some form of DIF for four of eight items, including age DIF for three items and sex DIF for three items. For the most part, this DIF was restricted to the item intercepts. Only DS2, which refers to the deliberate damaging of property, displayed non-uniform DIF (a significantly higher factor loading for boys versus girls). In contrast, for the violent factor, DIF was more extensive – five of the eight items displayed age DIF and three of these items also displayed sex DIF. In each case non-uniform DIF was detected. Thus, for both factors, a relatively high proportion of items were detected with DIF. To some extent, this reflects the high power of the current analysis, as well as the fact that our DIF-detection strategy may have been somewhat overly inclusive. Our interpretations of age and sex differences in the factors remain valid to the extent that we did not fail to detect and model any DIF present in the population.
Relation to the Multiple Groups Model
As noted above, the MNLFA is equivalent to an MG model that minimally assumes configural invariance, provided that the only covariate included in the MNLFA is a nominal, grouping variable. To show this correspondence we re-fit the MNLFA with only sex included as a covariate (excluding all age effects) and compared the results to a standard MG model in which sex was the grouping variable. We permitted the intercepts and loadings of those items showing any form of sex DIF in the prior MNLFA model to also differ in the current models.
Table 5 presents the subset of estimates that differs across groups, permitting a side-by-side comparison of the MG and MNLFA results. As can be seen, the MG and MNLFA results are equivalent, with estimates differing only due to alternative model parameterizations. Separate estimates are obtained for each group in the MG model, whereas baseline estimates are obtained for the reference group (girls) and differences are estimated for the contrast group (boys) in the MNLFA. Accordingly, the baseline estimates from the MNLFA directly reproduce the corresponding estimates for girls from the MG model. For means, intercepts, and loadings, one can add the male covariate effect to the baseline value from the MNLFA to match the corresponding values for boys from the MG model (within rounding error). The computations for variances and covariance are slightly more complicated but again yield converging values. For boys, the MNLFA implies that the variance of the non-violent factor is 1*exp(-.01) = .99, and the variance of the violent factor is 1*exp(-.30) = .74, matching the MG model results. Standardizing the covariance values from the MG model and inverting Fisher’s z transformation for the MNLFA model, both analyses yield inter-factor correlations of .65 for girls and .58 for boys.
Table 5.
Multiple Groups (MG) model estimates versus corresponding Moderated Nonlinear Factor Analysis (MNLFA) estimates for parameters that differ in value across groups
| Reference Parameter | MG Model |
MNLFA Model |
||
|---|---|---|---|---|
| Girls | Boys | Baseline | Male Effect | |
| Non-Violent Factor | ||||
| Mean | 0.00a | 0.35 (.06) | 0.00a | 0.35 (.06) |
| Variance | 1.00a | 1.00 (.07) | 1.00a | −0.01 (.07) |
| Violent Factor | ||||
| Mean | 0.00a | 0.77 (.05) | 0.00a | 0.77 (.05) |
| Variance | 1.00a | 0.74 (.07) | 1.00a | −0.30 (.10) |
| Factor Covariance | ||||
| Covariance | 0.65 (.03) | 0.50 (.04) | – | – |
| Fisher’s z | – | – | 0.77 (.05) | −0.11 (.07) |
|
| ||||
| DS2. Property Damage | ||||
| Intercept | −3.12 (.18) | −3.54 (.30) | −3.12 (.18) | −0.42 (.33) |
| Loading | 2.11 (.17) | 2.98 (.25) | 2.11 (.17) | 0.87 (.28) |
| DS3. Lie Parents | ||||
| Intercept | 0.29 (.08) | −0.44 (.10) | 0.29 (.08) | −0.73 (.10) |
| FV1. Saw Shoot/Stab | ||||
| Intercept | −3.62 (.20) | −4.48 (.24) | −3.62 (.20) | −0.85 (.12) |
| DS6. Hurt Other Badly | ||||
| Intercept | −3.75 (.17) | −3.58 (.20) | −3.75 (.17) | 0.16 (.12) |
| DS14. Group Fight | ||||
| Intercept | −2.75 (.15) | −4.18 (.32) | −2.75 (.15) | −1.44 (.35) |
| Loading | 1.86 (.15) | 2.60 (.25) | 1.86 (.15) | 0.74 (.29) |
Note: See Table 1 for full descriptions of items.
Indicates that the value of the parameter was fixed (not estimated) to identify the model and set the scale of the latent variables.
Of course, what is missing in Table 3 is any information about measurement invariance with respect to age. Since the current MNLFA model (excluding age effects) is nested within the prior MNLFA model (including age effects), we can conduct a scaled likelihood ratio test to evaluate the relative fit of the two models. The result, χ2(df=34) = 363.99, p < .0001, indicates that the MNLFA with both age and sex differences fits significantly better than the MNLFA with only sex differences. Since the latter model is equivalent to the MG model, we conclude that the fitted MG model neglected an important source of individual differences in the measurement of violent and non-violent delinquent behavior. This result is not surprising, given the large number of significant age differences detected in the prior MNLFA. Neglecting age may even occlude important sex differences. For instance, in the current models no significant sex DIF was detected for item DS6, whereas the prior MNLFA analysis indicated male × age DIF for this item. Within the MG modeling approach, capturing such effects would require that we first discretize age into two or more categories, then cross these categories with gender to create a single nominal grouping variable. With this approach, however, it would quickly become cumbersome to specify the model, evaluate invariance constraints, parse age and sex main effects from interactions, and interpret results. The MNLFA much more easily accommodates this second, continuous dimension of individual differences.
Relation to the MIMIC Model
An alternative approach for simultaneously evaluating measurement differences due to age and gender is the MIMIC model. In the traditional formulation of the MIMIC model, however, the factor loadings, variances, and covariance are all held constant across individuals; only the factor means and item intercepts depend upon the covariates. The standard MIMIC model thus represents a constrained MNLFA in which moderation is restricted to the means and intercepts. For comparison purposes, we fit a MIMIC model of the same form as the full MNLFA model with the exception that the covariate effects reported in Table 4 for the factor loadings, variances, and covariance (Fisher’s z) were all omitted. Table 6 presents the subset of estimates from the MIMIC model that varies as a function of sex and/or age (no corresponding estimates are presented for a restricted MNLFA as the models are in this case not just equivalent but also identically parameterized).
Table 6.
Parameter estimates from multiple-indicator multiple-cause (MIMIC) model for which covariate effects are present
| Reference Parameter | Baseline | Covariate Effect |
||||
|---|---|---|---|---|---|---|
| Age | Age2 | Male | Male × Age | Male × Age2 | ||
| Non-Violent Factor | ||||||
| Mean | 0.00a | −0.08 (.02) | −0.03 (.01) | 0.37 (.05) | 0.08 (.02) | – |
| Violent Factor | ||||||
| Mean | 0.00a | −0.09 (.03) | −0.04 (.01) | 0.67 (.07) | 0.06 (.03) | 0.03 (.01) |
|
| ||||||
| DS2. Property Damage | ||||||
| Intercept | −3.34 (.18) | −0.10 (.04) | – | 0.45 (.14) | – | – |
| DS3. Lie Parents | ||||||
| Intercept | 0.62 (.08) | 0.33 (.04) | −0.05 (.02) | −0.81 (.09) | −0.25 (.05) | – |
| DS8. Car w/o Permission | ||||||
| Intercept | −3.03 (.13) | 0.11 (.04) | −0.06 (.02) | – | – | – |
| DS15. Rowdy in Public | ||||||
| Intercept | −0.00 (.07) | – | – | −0.46 (.10) | – | – |
| FV1. Saw Shoot/Stab | ||||||
| Intercept | −3.29 (.21) | 0.17 (.05) | 0.00 (.03) | −0.90 (.13) | – | – |
| FV2. Pulled Weapon on You | ||||||
| Intercept | −4.13 (.21) | 0.31 (.04) | 0.01 (.02) | – | – | – |
| FV3. Shot You | ||||||
| Intercept | −6.46 (.38) | 0.09 (.08) | 0.14 (.04) | – | – | – |
| DS6. Hurt Other Badly | ||||||
| Intercept | −3.41 (.16) | −0.09 (.05) | – | 0.24 (.12) | 0.10 (.06) | – |
| DS14. Group Fight | ||||||
| Intercept | −2.78 (.15) | −0.13 (.06) | – | −0.55 (.14) | 0.15 (.07) | – |
Note: See Table 1 for full descriptions of items.
Indicates that the value of the parameter was fixed (not estimated) to identify the model and set the scale of the latent variables.
Since the traditional MIMIC model is nested within the full MNLFA, we can again conduct scaled likelihood ratio tests to compare their fit. Relative to the full MNLFA (Table 4), the restrictions imposed within the traditional MIMIC model (Table 6) resulted in a significant reduction in model fit, χ2(df=16) = 101.47, p < .0001. Again, this result is not surprising. In our prior MNLFA analyses we detected both non-uniform DIF (i.e., moderation of the factor loadings) as well as differences in the factor variances and covariance, particularly with respect to age. These effects are all omitted from the MIMIC model. Failure to attend to these other covariate effects could lead to a distorted pattern of results. In particular, comparison of the parameter estimates between Tables 4 and 6 shows that DIF estimates provided by the MIMIC model were similar to the MNLFA for items with only uniform DIF (DS3, DS8, and DS15) but differed meaningfully for items with non-uniform DIF (DS2, FV1, FV2, FV3, DS6, and DS14). For the latter set of items, covariate effects on the intercepts were often smaller in absolute magnitude and in some instances reversed sign (e.g., the intercept difference associated with male for the item DS2). Additionally, covariate effects on the violent factor mean were diminished relative to the corresponding MNLFA estimates. Not coincidentally, it was this factor for which the greatest nonuniform DIF was detected in the MNLFA.
As an additional point of comparison, we fit the MIMIC-interaction model to the data, adding non-uniform DIF effects (thus excluding only moderation of the factor variances and covariance). Table 7 presents the subset of estimates from the MIMIC-intereaction model that vary as a function of sex and/or age. Like the standard MIMIC model, the MIMIC-interaction model (Table 7) produced inferior fit relative to the full MNLFA (Table 4), χ2(df=6) = 48.20, p < .0001, indicating the need to model differences in the factor variances and covariances in addition to non-uniform DIF. Comparing the estimates between Tables 4 and 7 reveals a generally similar pattern of results. Particularly for parameters related to the violent factor, however, the estimates tend to be somewhat smaller in magnitude in the MIMIC-interaction model relative to the MNLFA.4
Table 7.
Parameter estimates from multiple-indicator multiple-cause interaction model for non-uniform differential item functioning (MIMIC-Interaction model) for which covariate effects are present
| Reference Parameter | Baseline | Covariate Effect |
||||
|---|---|---|---|---|---|---|
| Age | Age2 | Male | Male × Age | Male × Age2 | ||
| Non-Violent Factor | ||||||
| Mean | 0.00a | −0.08 (.02) | −0.03 (.01) | 0.38 (.05) | 0.08 (.02) | – |
| Violent Factor | ||||||
| Mean | 0.00a | −0.09 (.03) | −0.05 (.01) | 0.67 (.06) | 0.06 (.03) | 0.03 (.01) |
|
| ||||||
| DS2. Property Damage | ||||||
| Intercept | −2.98 (.17) | −0.10 (.04) | – | −0.38 (.29) | – | – |
| Loading | 2.07 (.16) | – | – | 0.93 (.25) | – | – |
| DS3. Lie Parents | ||||||
| Intercept | 0.62 (.08) | 0.33 (.04) | −0.05 (.02) | −0.84 (.09) | −0.25 (.05) | – |
| Loading | 1.41 (.08) | – | – | – | – | – |
| DS8. Car w/o Permission | ||||||
| Intercept | −3.04 (.13) | 0.11 (.04) | −0.06 (.02) | – | – | – |
| Loading | 1.40 (.09) | – | – | – | – | – |
| DS15. Rowdy in Public | ||||||
| Intercept | 0.00 (.07) | – | – | −0.49 (.10) | – | – |
| Loading | 1.41 (.08) | – | – | – | – | – |
| FV1. Saw Shoot/Stab | ||||||
| Intercept | −3.54 (.25) | 0.19 (.07) | 0.09 (.04) | −0.89 (.13) | – | – |
| Loading | 2.09 (.13) | −0.03 (.05) | −0.08 (.03) | – | – | – |
| FV2. Pulled Weapon on You | ||||||
| Intercept | −4.42 (.27) | 0.29 (.09) | 0.12 (.05) | – | – | – |
| Loading | 2.45 (.17) | 0.01 (.07) | −0.09 (.04) | – | – | – |
| FV3. Shot You | ||||||
| Intercept | −6.51 (.39) | 0.49 (.18) | 0.12 (.05) | – | – | – |
| Loading | 1.55 (.16) | −0.27 (.10) | – | – | – | – |
| DS6. Hurt Other Badly | ||||||
| Intercept | −3.40 (.16) | −0.06 (.07) | – | 0.23 (.12) | 0.12 (.06) | – |
| Loading | 2.04 (.12) | −0.04 (.07) | – | – | – | – |
| DS14. Group Fight | ||||||
| Intercept | −2.56 (.15) | −0.10 (.07) | – | −1.20 (.28) | 0.49 (.14) | – |
| Loading | 1.77 (.14) | −0.06 (.08) | – | 0.61 (.25) | −0.25 (.12) | – |
Note: See Table 1 for full descriptions of items. Age = 0 corresponds to 15 years of age; units are years. Male = 0 corresponds to females; Male = 1 corresponds to males.
Indicates that the value of the parameter was fixed (not estimated) to identify the model and set the scale of the latent variables.
Aside from these differences in fit and parameter estimates, a notable limitation of both MIMIC modeling approaches is the inability to evaluate potential individual differences in variance and covariance parameters. Such changes may be of key interest. For instance, theory may posit that initially highly correlated characteristics differentiate with age (e.g., distress in infancy differentiating into anger, sadness, and disgust; Lewis, 2007), or that previously distinct characteristics become more correlated with time (e.g., crystallized and fluid intelligence may become more integrated in senescence; Baltes, et al., 1980). For the present application, the MNLFA showed that, with age, violent behavior becomes more variable across individuals whereas non-violent behavior becomes less variable and that the correlation between the two forms of delinquency is high in early adolescence but becomes fairly modest by late adolescence. These important results (shown in Figure 5) could only be obtained from the MNLFA.
Conclusions
There is growing awareness within the field regarding the need to determine whether our measures provide equally valid and comparable scores for all individuals. As we have discussed, the evaluation of measurement invariance has traditionally drawn on two alternative latent variable modeling approaches with opposing advantages and disadvantages, the MG model and the MIMIC model. The MG model provides full flexibility in evaluating the invariance of measurement model parameters but is limited with respect to the kinds of individual characteristics that may be considered, namely those that may be represented via a single grouping variable. The MIMIC model permits the assessment of MI/DIF with respect to both categorical and continuous individual difference variables, but permits only the factor means and item intercepts to depend upon these variables, thus limiting the kinds of MI/DIF that may be evaluated. In this paper we have endeavored to show that a more recent modeling approach, the MNLFA, offers the advantages of both approaches while overcoming their respective limitations. Specifically, with the MNLFA, one may assess MI/DIF across levels of both categorical and continuous variables, and can allow any parameter within the measurement model to differ as a function of these variables (see Table 1). Further, we demonstrated analytically and via demonstration that both the MIMIC model and a broad class of MG models represent restricted versions of the MNLFA. The MNLFA thus offers a more flexible approach for evaluating MI/DIF for multiple-item scales and thereby for establishing the validity and comparability of our measurements across individuals.
Increased flexibility comes with increased complexity, and the chief challenge in conducting an MNLFA analysis is that one must contend with this complexity both in model specification and in the interpretation of results. Regarding specification, one set of choices concerns the moderation functions implemented for the model parameters. Here we have suggested the use of linear functions for item intercepts, factor loadings, and factor means, log-linear functions for residual and factor variances, and Fisher’s z for modeling factor covariances. So parameterized, the MNLFA can be viewed as a MIMIC-type model in which the factor loadings and variance-covariance parameters are subject to nonlinear constraints as a function of the predictors. Further, depending on the software program, this way to specify the model may be both convenient and computationally most efficient. Using Mplus, for instance, we used the MIMIC-type specification when fitting MNLFAs to the delinquent behavior data (see online Supplemental Material associated with this article). In contrast, in earlier implementations of the MNLFA within the NLMIXED procedure of SAS we explicitly specified each moderation function (see Bauer & Hussong, 2009, Supplemental Materials5). The latter specification approach could also be taken in Mplus to implement nonlinear moderation functions for the item intercepts and factor means, if desired, but with a potential increase in the computational time needed to fit the model.
How best to triangulate on an optimal MNLFA specification for a given set of data is another question without a clear, uniform answer. Curran et al. (2014) demonstrated one sensible approach to model building, with a particular focus on unidimensional models fit within an integrative data analysis context. Here, grappling with a two-factor model, we adopted a somewhat different model building approach (outlined in Table 2). Useful model building approaches may well vary from application to application to accommodate the varied demands of different analyses.
Interpretation of MNLFA results can also be somewhat daunting. One way to enhance interpretation is to suitably scale the predictor variables so that the baseline estimates are sensible. For instance, in our demonstration, male and age were scored zero for females and 15-year-olds, respectively. As such, the baseline estimates reported in Table 4 reference 15-year-old girls, and all other estimates reflect differences relative to this reference point. Additionally, the interpretation of the model results is greatly aided by transforming and plotting the model-implied parameter values into more easily understood metrics. For instance, rather than interpret age-related changes in Fisher’s z values, we chose to transform these to the model-implied correlations displayed in Figure 5. Transformations and plots can also be valuable for interpreting and visualizing DIF (see Curran et al., 2014, for examples).
Given its relative novelty, much additional research is needed on the MNLFA model. Although we can draw on the broader literature on MI, the MNLFA prompts many new questions. Some such questions are fairly amenable to empirical analysis. For instance, it will be important to determine the best way to model covariance parameters. We chose to model the covariance between the two factors in our empirical demonstration indirectly, though a linear moderation function for the Fisher z-transformed correlation. Although this approach has some appealing features and is (relatively) intuitive, it also has limitations, particularly for models involving multiple covariance parameters, as discussed in the Appendix. It will be important to consider other options for modeling covariances in multidimensional models and to compare the finite-sample performance of these options via simulation studies. Another issue worthy of further investigation is the best way to conduct a specification search to identify DIF in a MNLFA so as to minimize Type I errors while maintaining adequate power. Many procedures have been developed in the MG context but their applicability to the MNLFA is made unclear by the need to assess DIF across multiple predictors simultaneously. Other questions are more conceptual in nature. For instance, in a standard MG analysis, partial invariance is often tolerated to the degree that the majority of items display no DIF. When evaluating DIF in a multidimensional context, however, it is unclear whether the majority of items should display no DIF with respect to any given predictor or with respect to all predictors. For instance, in our empirical application, non-violent delinquent behavior was measured by eight items. Half of these items displayed DIF of one kind or another, but less than half displayed DIF by age and less than half displayed DIF by sex. Which is the more important consideration?
Further, it will be important to consider the features of the MNLFA relative to other possible approaches for modeling parameter moderation. For instance, Merkle and Zeileis (2013) proposed a technique for identifying subgroups with different model parameters by dividing continuous covariates at empirically determined thresholds. An advantage of their approach is that it obviates the need to implement specific moderation functions for the measurement parameters. The corresponding disadvantage, however, is that inductively discretizing the continuous variables precludes modeling their effects as smooth functions as is done in the MNLFA. Also conceptually related to the MNLFA is the heteroscedastic latent trait model (Molenaar et al., 2012; Molenaar, 2015), which permits moderation of the residual variances of the items by the values of a continuous latent factor. In contrast, the MNLFA permits moderation only by observed variables.
Overall, we believe the MNLFA offers new opportunities to investigate the validity of our measures and their comparability across individuals. Additionally, the MNLFA prompts us to look anew at the task of evaluating MI/DIF, opening up many avenues of potential methodological research.
Supplementary Material
Acknowledgments
The author thanks Patrick Curran and James McGinley for discussions leading up to and shaping this manuscript. This work was supported by National Institutes of Health grant R01 DA034636 (PI: Daniel Bauer). The content is solely the responsibility of the author and does not represent the official views of the National Institute on Drug Abuse or the National Institutes of Health. This research uses data from Add Health, a program project designed by J. Richard Udry, Peter S. Bearman, and Kathleen Mullan Harris, and funded by a grant P01-HD31921 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development, with cooperative funding from 17 other agencies. Special acknowledgment is due Ronald R. Rindfuss and Barbara Entwisle for assistance in the original design. Persons interested in obtaining data files from Add Health should contact Add Health, Carolina Population Center, 123 W. Franklin Street, Chapel Hill, NC 27516-2524 (addhealth@unc.edu). No direct support was received from grant P01-HD31921 for this analysis.
Appendix: Details on the Moderation of Variance and Covariance Parameters
For variance and covariance parameters, the specification of moderation functions in MNLFA models requires care to minimize the possibility of obtaining improper estimates. Improper estimates include negative variances or correlations exceeding one in absolute magnitude. Additionally, even if no one element of a correlation or covariance matrix is out of bounds, the matrix as a whole may nevertheless be non-positive definite. Improper estimates can also arise in MG or MIMIC models, or even in a standard factor analysis (e.g., “Heywood cases”). In these contexts, improper estimates are often taken to indicate a misspecified model; however, they can also arise due to sampling variability (Chen et al., 2001). For the MNLFA, it is also possible that improper estimates could arise due to selection of a poor moderation function. Here, we focus on how to optimally specify moderation of Ψi, the covariance matrix for the latent factors, while also noting any unique considerations that arise when specifying moderation of Σi.
To begin, we can rewrite the covariance matrix for the latent factors as follows
| (30) |
where Pi is a correlation matrix and Δi is a diagonal matrix consisting of standard deviations, i.e., . Rewriting the covariance matrix in this way permits us to specify different moderation functions for variance parameters versus correlations.
Moderation of Variance Parameters
For modeling variance parameters, such as those within Δi, we followed earlier literature in specifiying a long-linear function (Aitkin, 1987; Bauer & Hussong, 2009; Harvey, 1976; Hedeker, Mermelstein & Demirtas, 2008; Hessen & Dolan, 2009; although see Molenaar et al., 2012, Equation 9, and Molenaar, 2015). For a given factor a, one way to write this function is as
| (31) |
A virtue of this specification is that, as long as ψ(aa)0 is positive, the conditional variance ψ(aa)i will also be positive at all values of xi. While with Equation (31) it is theoretically possible that one could obtain a negative estimate for the baseline variance, this would in turn imply negative conditional variances at all levels of xi and it seems unlikely that such a solution would yield the maximum likelihood for the data. To exclude the possibility of negative baseline variance estimates one could use the alternative parameterization
| (32) |
in which the baseline variance, ψ00i = exp(β(aa)0), must be positive.
Moderation of Correlations/Covariances
When predicting correlations, such as those within Pi, it is often recommended to implement Fisher’s z-transformation (see Cohen, Cohen, West and Aiken, 2003, p. 240). This transformation serves both to linearize relationships with predictors and to impose bounds of −1 and 1 on the implied correlations. For example, suppose we wish to model the correlation between factors a and b, designated ρ(ab)i. We would specify that the corresponding Fisher-transformed value, ζ(ab)i, is a linear function of xi:
| (33) |
Equation (33), in turn, implies a nonlinear moderation function for the correlation (obtained by inverting Fisher’s z-transformation), with asymptotes of −1 and 1:
| (34) |
Per Equation (30), the corresponding covariance is then
| (35) |
An expanded moderation equation for ψ(ab)i can be obtained by substitution.
This elementwise approach has both advantages and disadvantages. A key advantage is that distinct moderation processes can be specified and tested for each correlation within Pi. The corresponding disadvantage, however, is that although no single estimated correlation will be improper, no restrictions ensure that the estimated matrix , as a whole, remains positive definite at all values of xi. There are at least two special cases in which will always be positive definite. The first case is when is a 2 × 2 matrix (e.g., our empirical demonstration), since there is only one correlation that is moderated and the value is restricted to be within bounds. The second case follows from the first. A matrix composed of blocks that are all positive definite is itself positive definite, therefore will be positive definite if it can be arranged as a block diagonal matrix in which no block is larger than 2 × 2. In the more general case, however, elementwise moderation of Pi runs the risk that could be non-positive definite for some values of xi. Empirically, one could check for this possibility by seeing whether the determinant associated with is negative for any of the observed data vectors xi.
In some cases one may wish to consider alternative model specifications that enforce positive definiteness of . For instance, one could move from a factor analysis model to a structural equation model, replacing covariances between factors with directional paths (regression slopes) and then specifying linear moderation functions for these paths. Another possibility would be to specify a higher-order factor model. For instance, the covariances between three factors could be re-expressed in terms of the factor loadings of a single higher-order factor. One could then specify a linear moderation function for the factor loadings. Still another possibility would be to retain the original model structure but perform a decomposition of the covariance or correlation matrix (e.g., an eigenvalue decomposition or Cholesky decomposition) through which it might be easier to enforce positive definiteness of .
Although all of these approaches have potential merits, we chose to present and implement the elementwise Fisher-transformed correlation approach in our analysis of the delinquency data both because this approach provides relatively straightforward interpretations and because it is sufficient to ensure positive definiteness when considering a model with only two correlated factors.
Footnotes
This way of thinking about and specifying the MNLFA presumes, however, that a linear moderation function is specified for the item intercepts and the factor means. The MNLFA no longer conforms to a MIMIC-like specification if the moderation functions for these parameters are nonlinear.
On the author’s standard-issue personal computer, single-factor models typically converged within a minute or two, whereas two-factor models often required 15–30 minutes to converge.
See http://statmodel.com/chidiff.shtml for implementation details.
To some extent, the reduction in magnitude of item parameter estimates in Tables 6 and 7 relative to Table 4 may reflect differences in the scaling of the latent factors. In the MIMIC models each marginal factor variance is set to one, whereas in MNLFA models it is the conditional variance that is set to one when all covariates are zero (in this case, representing 15-year old girls).
References
- Aitkin M. Modelling variance heterogeneity in the normal regression using GLIM. Applied Statistics. 1987;36:332–339. [Google Scholar]
- American Educational Research Association, American Psychological Association, National Council on Measurement in Education, & Joint Committee on Standards for Educational and Psychological Testing (U.S.) Standards for educational and psychological testing. Washington, DC: American Educational Research Association; 2014. [Google Scholar]
- American Psychological Association. APA Dictionary of Statistics and Research Methods. Washington DC: American Psychological Association; 2014. [Google Scholar]
- Baltes PB, Cornelius SW, Spiro A, Nesselroade JR, Willis SL. Integration versus differentiation of fluid/crytallized intelligence in old age. Developmental Psychology. 1980;16:625. [Google Scholar]
- Barendse MT, Oort FJ, Garst GJA. Using restricted factor analysis with latent moderated structures to detect uniform and nonuniform measurement bias: a simulation study. ASta Advances in Statistical Analysis. 2010;94:117–127. [Google Scholar]
- Barnes JC, Beaver KM, Miller JM. Estimating the effect of gang membership on nonviolent and violent delinquency: a counterfactual analysis. Aggressive Behavior. 2010;36:437–451. doi: 10.1002/ab.20359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer DJ, Hussong AM. Psychometric approaches for developing commensurate measures across independent studies: traditional and new models. Psychological Methods. 2009;14:101–125. doi: 10.1037/a0015583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrne BM, Shavelson RJ, Muthén B. Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychological Bulletin. 1989;105:456–466. [Google Scholar]
- Chen F, Bollen KA, Paxton P, Curran PJ, Kirby J. Improper solutions in structural equation models: Causes, consequences, and strategies. Sociological Methods and Research. 2001;29:468–508. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analyses for the behavioral sciences. 3. Mahwah, NJ: Lawrence Erlbaum Associates, Inc; 2003. [Google Scholar]
- Curran PJ, McGinley JS, Bauer DJ, Hussong AM, Burns A, Chassin L, Sher K, Zucker R. A moderated nonlinear factor model for the development of commensurate measures in integrative data analysis. Multivariate Behavioral Research. 2014;49:214–23. doi: 10.1080/00273171.2014.889594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farrington DP. Age and crime. In: Tonry M, Morris N, editors. Crime and justice: An annual review of research. Vol. 7. Chicago: University of Chicago Press; 1986. pp. 189–250. [Google Scholar]
- Harvey AC. Estimating regression models with multiplicative heteroscedasticity. Econometrica. 1976;44:461–465. [Google Scholar]
- Hauser RM, Goldberger AS. The treatment of unobserved variables in path analysis. In: Costner HL, editor. Sociological Methodology 1971. San Francisco: Jossey-Bass; 1971. pp. 81–177. [Google Scholar]
- Hedeker D, Mermelstein RJ, Demirtas H. An application of a mixed-effects location scale model for analysis of ecological momentary assessment (EMA) data. Biometrics. 2008;64:627–634. doi: 10.1111/j.1541-0420.2007.00924.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hessen DJ, Dolan CV. Heteroscedastic one-factor models and marginal maximum likelihood estimation. British Journal of Mathematical and Statistical Psychology. 2009;62:57–77. doi: 10.1348/000711007X248884. [DOI] [PubMed] [Google Scholar]
- Holland PW, Wainer H. Differential item functioning. Mahwah, NJ: Erlbaum; 1993. [Google Scholar]
- Holzinger KJ, Swineford F. A study in factor analysis: the stability of a bi-factor solution. University of Chicago; 1939. Supplementary Educational Monographs. [Google Scholar]
- Horn JL, McArdle JJ. A practical and theoretical guide to measurement invariance in aging research. Experimental Aging Research. 1992;18:117–144. doi: 10.1080/03610739208253916. [DOI] [PubMed] [Google Scholar]
- Jöreskog KG. Simultaneous factor analysis in several populations. Psychometrika. 1971;36:409–426. [Google Scholar]
- Jöreskog KG, Goldberger AS. Estimation of a model with multiple indicators and multiple causes of a single latent variable. Journal of the American Statistical Association. 1975;70:631–639. [Google Scholar]
- Kim ES, Cao C. Testing group mean differences of latent variables in multilevel data using multiple-group multilevel CFA and multilevel MIMIC modeling. Multivariate Behavioral Research. 2015;50:436–456. doi: 10.1080/00273171.2015.1021447. [DOI] [PubMed] [Google Scholar]
- Lewis M. Early Emotional Development. In: Slater A, Lewis M, editors. Introduction to Infant Development. 2. England: Oxford University Press; 2007. pp. 216–232. [Google Scholar]
- Loeber R, Dale H. Key issues in the development of aggression and violence from childhood to early adulthood. Annual Review of Psychology. 1997;48:371–410. doi: 10.1146/annurev.psych.48.1.371. [DOI] [PubMed] [Google Scholar]
- MacCallum RC, Zhang S, Preacher KJ, Rucker DD. On the practice of dichotomization of quantitative variables. Psychological Methods. 2002;7:19–40. doi: 10.1037/1082-989x.7.1.19. [DOI] [PubMed] [Google Scholar]
- Mellenbergh GJ. Item bias and item response theory. International Journal of Educational Research. 1989;13:127–143. [Google Scholar]
- Meredith W. Measurement invariance, factor analysis and factorial invariance. Psychometrika. 1993;58:525–543. [Google Scholar]
- Merkle EC, Zeileis A. Tests of measurement invariance without subgroups: a generalization of classical methods. Psychometrika. 2013;78:59–82. doi: 10.1007/s11336-012-9302-4. [DOI] [PubMed] [Google Scholar]
- Millsap RE. Statistical approaches to measurement invariance. New York, NY: Routledge; 2011. [Google Scholar]
- Moffitt TE. Adolescent-limited and life-course persistent antisocial behavior: a developmental taxonomy. Psychological Review. 1993;100:674–701. [PubMed] [Google Scholar]
- Molenaar D. Heteroscedastic latent trait models for dichotomous data. Psychometrika. 2015;80:625–644. doi: 10.1007/s11336-014-9406-0. [DOI] [PubMed] [Google Scholar]
- Molenaar D, Dolan CV, de Boeck P. The heteroscedastic graded response model with a skewed latent trait: testing statistical and substantive hypotheses related to skewed item category functions. Psychometrika. 2012;77:455–478. doi: 10.1007/s11336-012-9273-5. [DOI] [PubMed] [Google Scholar]
- Molinengo G, Testa S. Analysis of the psychometric properties of an assessment tool for deviant behavior in adolescence. European Journal of Psychological Assessment. 2010;26:108–115. [Google Scholar]
- Muthén B. A general structural equation model with dichotomous, ordered categorical and continuous latent variable indicators. Psychometrika. 1984;49:115–132. [Google Scholar]
- Muthén BO. Latent variable modeling in heterogeneous populations. Psychometrika. 1989;54:557–585. [Google Scholar]
- Muthén BO, Satorra A. Complex sample data in structural equation modeling. Sociological Methodology. 1995;25:267–316. [Google Scholar]
- Muthén LK, Muthén BO. Mplus user’s guide. 7. Los Angeles, CA: Muthén & Muthén; 2012. [Google Scholar]
- Oort FJ. Using restricted factor analysis to detect item bias. Methodika. 1992;6:150–166. [Google Scholar]
- Oort FJ. Simulation study of item bias detection with restricted factor analysis. Structural Equation Modeling. 1998;5:107–124. [Google Scholar]
- Ruy E. Factorial invariance in multilevel confirmatory factor analysis. British Journal of Mathematical and Statistical Psychology. 2014;67:172–194. doi: 10.1111/bmsp.12014. [DOI] [PubMed] [Google Scholar]
- Ryu E. Multiple group analysis in multilevel structural equation model across Level 1 groups. Multivariate Behavioral Research. 2015;50:300–315. doi: 10.1080/00273171.2014.1003769. [DOI] [PubMed] [Google Scholar]
- Satorra A, Bentler PM. A scaled difference chi-square test statistic for moment structure analysis. Psychometrika. 2001;66:507–514. doi: 10.1007/s11336-009-9135-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skrondal A, Rabe-Hesketh S. Generalized latent variable modeling: Multilevel, longitudinal, and structural equation models. Boca Raton, FL: Chapman & Hall; 2004. [Google Scholar]
- Sörbom D. A general method for studying differences in factor means and factor structure between groups. British Journal of Mathematical and Statistical Psychology. 1974;27:229–239. [Google Scholar]
- Steinberg L, Thissen D. Using effect sizes for research reporting: examples using item response theory to analyze differential item functioning. Psychological Methods. 2006;11:402–415. doi: 10.1037/1082-989X.11.4.402. [DOI] [PubMed] [Google Scholar]
- Thissen D, Steinberg L, Gerrard M. Beyond group-mean differences: The concept of item bias. Psychological Bulletin. 1986;99:118–128. [Google Scholar]
- Thissen D, Steinberg L, Kuang D. Quick and easy implementation of the Benjamini-Hochberg procedure for controlling the false positive rate in multiple comparisons. Journal of Educational and Behavioral Statistics. 2002;27:77–83. [Google Scholar]
- Thissen D, Steinberg L, Wainer H. Use of item response theory in the study of group difference in trace lines. In: Wainer H, Braun H, editors. Test validity. Hillsdale, NJ: Erlbaum; 1988. pp. 147–169. [Google Scholar]
- Thissen D, Steinberg L, Wainer H. Detection of differential item functioning using the parameters of item response models. In: Holland PW, Wainer H, editors. Differential item functioning. Hillsdale, NJ: Erlbaum; 1993. pp. 67–111. [Google Scholar]
- Woods CM. Empirical selection of anchors for tests of differential item functioning. Applied Psychological Measurement. 2009a;33:42–57. [Google Scholar]
- Woods CM. Evaluation of MIMIC-model methods for DIF testing with comparison to two-group analysis. Multivariate Behavioral Research. 2009b;44:1–27. doi: 10.1080/00273170802620121. [DOI] [PubMed] [Google Scholar]
- Woods CM, Grimm KJ. Testing for nonuniform differential item functioning with multiple indicator multiple cause models. Applied Psychological Measurement. 2011;35:339–361. [Google Scholar]
- Widaman KF, Reise SP. Exploring the measurement invariance of psychological instruments: applications in the substance use domain. In: Bryant KJ, Windle M, West SG, editors. The science of prevention: Methodological advances from alcohol and substance abuse research. Washington, DC: American Psychological Association; 1997. pp. 281–324. [Google Scholar]
- Willoughby T, Chalmers H, Busseri MA. Where is the syndrome? Examining co-occurrence among multiple problem behaviors in adolescence. Journal of Consulting and Clinical Psychology. 2004;72:1022–1037. doi: 10.1037/0022-006X.72.6.1022. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.