Abstract
Recent advances in mass spectrometry have enabled system-wide analyses of protein turnover. By globally quantifying the kinetics of protein clearance and synthesis, these methodologies can provide important insights into the regulation of the proteome under varying cellular and environmental conditions. To facilitate such analyses, we have employed a methodology that combines metabolic isotopic labeling (Stable Isotope Labeling in Cell Culture - SILAC) with isobaric tagging (Tandem Mass Tags - TMT) for analysis of multiplexed samples. The fractional labeling of multiple time-points can be measured in a single mass spectrometry run, providing temporally resolved measurements of protein turnover kinetics. To demonstrate the feasibility of the approach, we simultaneously measured the kinetics of protein clearance and accumulation for more than 3000 proteins in dividing and quiescent human fibroblasts and verified the accuracy of the measurements by comparison to established non-multiplexed approaches. The results indicate that upon reaching quiescence, fibroblasts compensate for lack of cellular growth by globally downregulating protein synthesis and upregulating protein degradation. The described methodology significantly reduces the cost and complexity of temporally-resolved dynamic proteomic experiments and improves the precision of proteome-wide turnover data.
Analysis of protein expression is central to our understanding of cellular physiology and regulation. Recent advances in the field of proteomics have provided powerful experimental tools for global analyses of protein expression. Tandem mass spectrometry (LC-MS/MS)1 can now readily capture information on composition, expression levels and modifications of very complex protein mixtures (1). Though immensely powerful, these techniques typically provide temporally static snapshots of the proteome. Within a cell, proteins are in a state of continual flux, and kinetics of synthesis and degradation (turnover) are intimately linked to the function and regulation of proteins (2, 3). As such, there is great interest in the development of proteomic methodologies capable of analyzing protein turnover dynamics on a global scale (4).
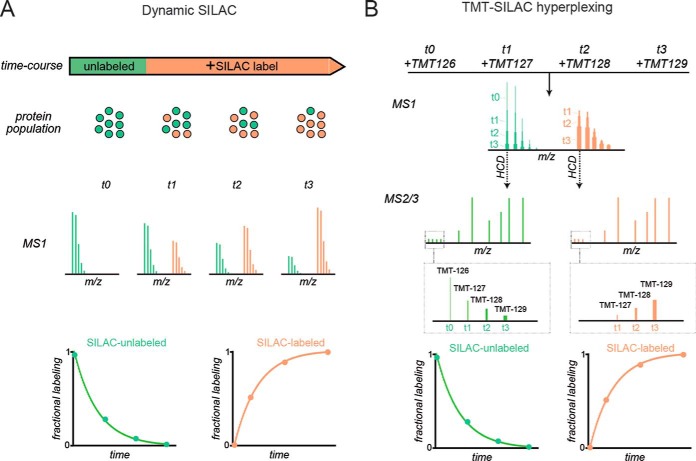
Proteome-wide analyses of turnover have been greatly propelled by the development of stable isotope labeling in cell culture (SILAC)—a set of standardized protocols, reagents and analysis tools for quantifying the incorporation of 15N/13C labeled amino acids into proteins by tandem mass spectrometry (LC-MS/MS) (5, 6). Dynamic (i.e. time-resolved or pulsed) SILAC experiments (Fig. 1) can effectively measure the labeling kinetics of proteins and provide rates of protein degradation and synthesis on a global scale. Such analyses have successfully obtained proteome-wide surveys of protein dynamics for a number of in vitro and in vivo model systems and have provided important insights into the regulation of the proteome under varying environmental and cellular conditions (2, 7–10).
Fig. 1.
Comparison of dynamic SILAC and TMT-SILAC hyperplexing for measurement of protein turnover. A, In dynamic SILAC experiments, the fractional labeling of proteins is monitored at the MS1 level. During the course of isotopic labeling, unlabeled proteins (green) are cleared and replaced by labeled proteins (orange). Fractional labeling is measured by analyzing the spectra of intact peptide ions over time in distinct LC-MS/MS runs. Resulting curves for either the decay of unlabeled peptides or appearance of labeled peptides are fitted to exponential equations to obtain the turnover rate constants or half-lives of proteins. B, In TMT-SILAC hyperplexing, experimental samples from different SILAC labeling time-points are reacted with different TMT tags and combined in a single multiplexed sample prior to LC-MS/MS. At different time-points, a peptide generated from the same protein will have identical (overlapped) masses in MS1 spectra but will generate reporter ions with distinct masses in MS2 spectra. Thus, fragmentation of SILAC-unlabeled peaks will provide the kinetics of decay for unlabeled peptides and fragmentation of SILAC-labeled peaks will provide the kinetics of appearance for labeled peptides.
A practical limitation of SILAC-based dynamic proteomic analyses is that each labeling time point produces an experimental sample that must be analyzed in a distinct LC-MS/MS run. Thus, conducting kinetic analyses composed of large numbers of time-points is expensive and time consuming. Furthermore, SILAC-based dynamic proteomic analyses often suffer from the problem of “missing values”: proteins that can be identified and quantified in some time-points but not others. To circumvent these limitations, we sought to develop a more efficient procedure for obtaining multi-time-point kinetic data for proteome-wide analyses of protein turnover. The methodology combines and builds upon three previously reported techniques: integration of SILAC and tandem mass tags (TMT) to produce highly multiplexed samples (“hyperplexing” (11, 12)), synchronous precursor selection (SPS) to minimize co-isolation of interfering ions and enhance accuracy of MSn quantitation of TMT reporters (13, 14) and incorporation of isobaric and metabolic labeling for analysis of protein dynamics (15, 16). Using this combined approach, we analyzed the global impact of cellular quiescence on the kinetics of protein degradation and synthesis in human dermal fibroblasts.
EXPERIMENTAL PROCEDURES
Experimental Design and Statistical Rationale
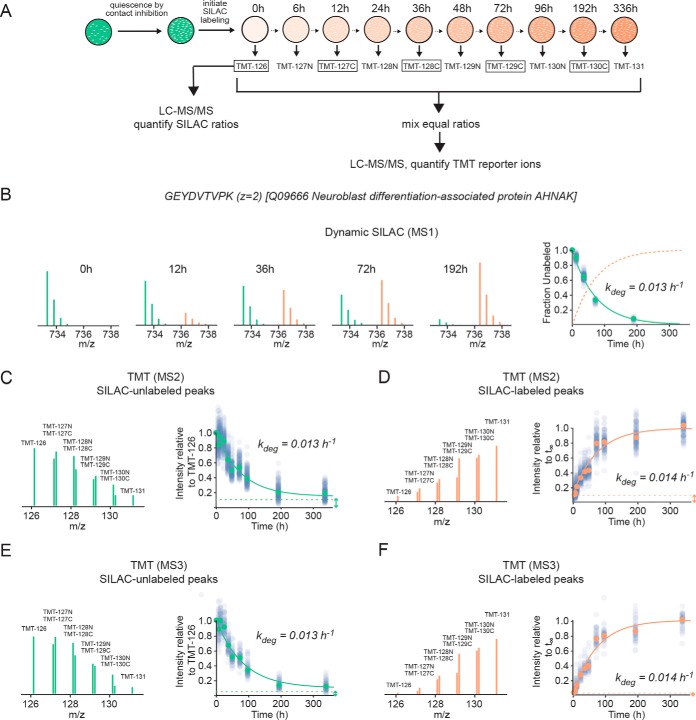
The theoretical rationale for the assay workflow (Fig. 2A) is discussed in the Results section. Briefly, two replicate experiments were conducted. In the first experiment, 10 cultures of human dermal fibroblasts were grown to confluency and labeled for varying times in SILAC media. The time-points were then labeled with different TMT tags, multiplexed and the fractional labeling of the peptides were analyzed at the MS1, MS2 and MS3 levels using the procedures described below. In a second biologically replicate experiment, the quiescence experiment was repeated with four time-points and the samples were multiplexed with similarly labeled dividing cells for comparison. The determination of the rate constants for fractional labeling was conducted by least squares regression analysis of the time-resolved data fitted to equations derived from the kinetic model described below and the goodness of fit was assessed by R2 values. The spread of rate constants for peptides encompassing the same protein was assessed by measuring the coefficient of variation, as the mean rates for peptides for different proteins had variable magnitudes. The correlation of measured rates at the protein level using different procedures was assessed by conducting pairwise comparisons. For this analysis, Spearman rank correlation was used, as the measured degradation rates were not normally distributed.
Fig. 2.
TMT-SILAC hyperplexing experimental design and sample data. A, Experimental design. HCA2-hTert cells were grown to confluency and SILAC labeling was conducted over the course of 336 h as cells were in a contact-inhibited quiescent state. Extracts were collected from 10 time-points and, following trypsinization, each was labeled with a different TMT tag. The TMT-tagged peptides were combined in a single multiplexed sample and analyzed by LC-MS/MS as described under Experimental Procedures. Additionally, a number of TMT-tagged time-points (boxed) were individually analyzed by LC-MS/MS without multiplexing using a standard dynamic SILAC approach. B, The fractional labeling of a tryptic peptide ion (GEYDVTVPK, z = 2) belonging to neuroblast differentiation-associated protein analyzed at the MS1 level by dynamic SILAC. The green and orange peaks indicate the relative intensities of unlabeled and labeled peptides, respectively. The plot indicates the decay curve for the fractional labeling of the unlabeled peaks for GEYDVTVPK (green circles) and all other peptides mapped to the protein (transparent blue circles). The green line indicates a fit to a single exponential equation. The fractional labeling of labeled peaks (calculated as one minus the fractional labeling of unlabeled peaks) is indicted by a dotted orange line. C, The kinetics for clearance of GEYDVTVPK analyzed at the MS2 level by TMT-SILAC hyperplexing. The MS2 spectrum indicates the relative intensities of TMT reporter ions for the SILAC-unlabeled peptide ion. The plot indicates intensities of peaks relative to the t0 sample (TMT-126) for GEYDVTVPK (green circles) and all other peptides mapped to the protein (transparent blue circles). The green line indicates a fit to a single exponential equation with a non-zero baseline indicated by a dashed line and double-headed arrow. D, The kinetics for appearance of GEYDVTVPK analyzed at the MS2 level by TMT-SILAC hyperplexing. The MS2 spectrum indicates the relative intensities of TMT reporter ions for the SILAC-labeled peptide ion. The plot indicates intensities of peaks relative to the fitted intensity of the exponential curve (orange line) at infinite time (t∞). The dashed line indicates the intensity of the t0 sample (TMT-126) and represents the initial baseline of the curve. E and F, Data analyzed as in C and D, respectively, except at the MS3 level using SPS-MS3.
Cell Culture and Stable Isotope Labeling
Human dermal fibroblasts (HCA2-hTert) (17, 18) were maintained in Eagle's Minimum Essential Medium (ATCC) supplemented with 15% fetal bovine serum (Invitrogen, Carlsbad, CA), 100 U/ml penicillin, 100 U/ml streptomycin at 37 °C with 5% CO2. The media utilized for isotopic labeling was Eagle's minimum essential medium (ATCC) supplemented with 15% dialyzed fetal bovine serum (Thermo Scientific, Boston, MA), 100 U/ml penicillin, and 100 U/ml streptomycin. Cells were gradually adapted to the labeling media and were then plated at a density of 500,000 cells per 10 cm plate. For dividing cells, 1 day after plating, the cultures were switched to MEM labeling media for SILAC (Thermo Scientific) supplemented with l-arginine:HCl (13C6, 99%) and l-lysine:2HCl (13C6, 99%; Cambridge Isotope Laboratories, Tewksbury, MA) at concentrations of 0.1264 g/l and 0.087 g/l and 15% dialyzed fetal bovine serum (Thermo Scientific) and were subsequently collected after 0, 24, 48, 72 h of labeling. Cell numbers were determined by a hemocytometer. The number of cells increased in an approximate exponential fashion during this period. Least-square fitting of a plot of cell numbers versus time to an exponential equation was used to determine the growth rate (kdiv) of the cells. For quiescent cells, the cultures were grown for 8 days to achieve a state of quiescence by contact inhibition (see (19) for additional details). The confluent quiescent cultures were switched to the labeling media and cells were collected after 0, 6, 12, 24, 36, 48, 72, 96, 144, 192, 336 h of labeling. All cells were washed with PBS and frozen as cell pellets prior to further analysis.
Mass Spectrometry Sample Preparation
Cell Lysis
Lysis buffer was composed of 8 m urea, 75 mm NaCl, 50 mm Tris, pH 8.5. 50 μl of lysis buffer was used for one million cells. Cell lysis was conducted by adding lysis buffer to pelleted cells, followed by vortexing and sonication using a QSonica sonicator. Sonication cycles consisted of 5 × 10 s sonications with 1 min incubations on ice between each cycle. Samples were then centrifuged for 10 min at 15,000 × g, and the supernatant was collected. Protein concentration was determined by BCA assays.
Trypsinization and TMT Labeling
One hundred micrograms of each extract was removed, and brought up to 100 μl in 100 mm ammonium bicarbonate. This dilution lowered the urea concentration to less than 1.5 m such that trypsinization efficiency was not inhibited. 2 μg of trypsin (Thermo Scientific) was added to each extract and the samples were allowed to incubate overnight at 37 °C. Disulfide bonds were reduced with the addition of Bond-Breaker TCEP Solution (Thermo Scientific) to a final concentration of 5 mm with incubation at 55 °C for 1 h. Reduced cysteines were alkylated by the addition of iodoacetamide at a final concentration of 10 mm by incubating in the dark at room temperature for 30 min. Subsequently, an additional 2 μg of trypsin was added to the samples and incubated for 3 h at 37 °C. Formic acid was added to a final concentration of 1% to stop trypsin activity. Samples were then desalted with 100 μl C18 Tips (Thermo Scientific) to remove primary amines that would interfere with TMT labeling. After drying down, the samples were re-suspended in 100 μl of 100 mm triethylammonium bicarbonate (TEAB). TMT ten-plex reagents (0.8 mg) (Thermo Scientific) were removed from −20 °C and allowed to reach room temperature before being re-suspended in 40 μl of acetonitrile. Ten microliters of each reagent was added to the corresponding sample. For analysis of degradation kinetics in quiescent cells, the ten samples derived from different SILAC labeling time-points were tagged with TMT-126, TMT-127N, TMT-127C, TMT-128N, TMT-128C, TMT-129N, TMT-129C, TMT-130N, TMT-130C, and TMT-131 in order of increasing time. For comparison of degradation and synthesis kinetics between dividing and quiescent cells, the dividing cells SILAC labeled for 0, 24, 48 and 72 h were tagged with TMT-126, TMT-127N, TMT-127C, and TMT-128N, respectively, and the quiescent cells were labeled SILAC labeled for 0, 48, 96 and 144 h were tagged by TMT-129C, TMT-130N, TMT-130C, and TMT-131, respectively. After the addition of TMT tags, the samples were vortexed and incubated at room temperature for 1 h before being quenched with 8 μl of 5% hydroxylamine for 15 min. 10 μg of each TMT-labeled samples were combined according to the experimental design described in Results and dried down by SpeedVac (Labconco, Kansas City, MO). The remaining labeled peptides were left un-mixed for quantitation using the precursor MS1 SILAC peaks. Un-mixed labeled peptides were desalted with 100 μl C18 tips, and dried down by SpeedVac.
High pH Fractionation
Digested samples were reconstituted in 300 μl of 0.1% TFA and were fractionated using the Pierce High pH Reversed-Phase Peptide Fractionation Kit (Thermo Scientific). Briefly, the columns were prepared by adding 300 μl of acetonitrile and centrifuging at 5000 × g for 2 min (twice), then washed with 300 μl 0.1% TFA (twice). Samples were then loaded onto the column and centrifuged at 3000 × g for 2 min, then washed once with HPLC grade water (JT Baker). Peptides were eluted in 8 fractions, with 10%, 12.5%, 15%, 17.5%, 20%, 22.5%, 25%, 50% acetonitrile in 0.1% triethylamine. Fractions were dried down by SpeedVac, resuspended in 50 μl of 0.1% TFA, and analyzed as described below.
LC-MS/MS Analysis
LC-MS/MS for MS2 TMT and SILAC Analysis Using Q Exactive Plus Mass Spectrometer
Six microliters of each high pH fraction was analyzed on a Q Exactive Plus mass spectrometer (Thermo Scientific) coupled with an Easy nLC-1000 pump (Thermo Scientific). Columns were hand-pulled using 100 μm fused silica, which was packed with 30 cm of 1.8 μm, 120 Angstrom C18 beads (Sepax). Mobile phase A was 0.1% formic acid in water, and mobile phase B was 0.1% formic acid in acetonitrile. Peptides were separated using a gradient of 8–30% B over 145 min, 30–50% B over 10 min, and 50–70% B over 4 min, holding at 70% B for 5 min. The gradient returned to 0% B over 4 min, and held there for 10 min to prepare for the next injection. The flow rate throughout the run was held at 300 nL/minute. A data-dependent top 10 MS2 method was used for peptide detection and fragmentation. For each cycle, one full scan from m/z 400–1700 was acquired in the Orbitrap at a resolution of 70,000 at m/z = 200, with an AGC target of 3e6, and a maximum injection time of 50 ms. After each full scan, the top 10 most intense ions were selected for fragmentation in the HCD cell, followed by detection in the Orbitrap at a resolution of 35,000 at m/z = 200. The AGC target was set to 1e5, with a maximum injection time of 150 ms, an isolation width of 0.5 Da, and a normalized collision energy of 35. A dynamic exclusion window of 25 s was used, while excluding unassigned, +1, and greater than +5 charge states. The polysiloxane 445.12003 m/z was used for lockmass. For SILAC LC-MS/MS analysis on the TMT-labeled, un-mixed samples, all settings remained the same except for the isolation width, which was adjusted up to 1.0 Da, with an offset of 0.3 Da.
LC-MS/MS for SPS-MS3 Analysis Using Orbitrap Fusion Tribrid Mass Spectrometer
Six microliters of each fraction was analyzed on a Fusion mass spectrometer (Thermo Scientific). Chromatographic separation of derived peptides were accomplished on a SCIEX ekspertTM nanoLC 425 system (SCIEX, Redwood City, CA). Mobile phase A and B were 0.1% formic acid in 2% acetonitrile and 0.1% formic acid in 88% acetonitrile, respectively. Peptides were loaded onto a reversed-phase trap (300 μm ID ×1 cm, packed with Zorbax 3 μm C18 material), with 1% mobile phase B at a flow rate of 10 μl/min, and the trap was washed for 3 min. A series of nanoflow gradients (flow rate at 250 nL/min) was used to back-flush the trapped samples onto the nano-LC column (75-μm ID × 100 cm, packed with Pepmap 3 μm C18 material) for separation. The nano-LC column was heated at 52 °C to improve both chromatographic resolution and reproducibility. A 3 h gradient was used to achieve sufficient peptide separation. The optimized gradient profile was as follows: 4–10% B over 3–8 min; 10–32% B over 8–125 min; 32–44% B over 125–130 min; 44–60% B over 130–135 min; 60–97% B in 135–136 min, and isocratic at 97% B over 136–153 min. A data-dependent multi-notch synchronous precursor selection (SPS) method was employed (13). For each cycle, one MS1 scan was done in the Orbitrap with a mass range of 400–1500 m/z at a resolution of 120,000 at 200 m/z. The AGC was set to 2e5 with a maximum ion injection time of 50 ms. Dynamic exclusion was used with a 10-ppm tolerance, and a 40 s exclusion duration. MS2 scans were done in the ion trap with CID, fragmenting the most intense precursors in the Top Speed mode, with an isolation width of 0.5 Da. The “Ion Trap Scan Rate” was set to Rapid, with an AGC target of 1e4, and a maximum injection time of 35 ms. Only ions with a charge state between 2 and 5 were selected for fragmentation. MS3 scans were done by isolating the 10 most intense fragment ions from CID fragmentation over a 400–2000 m/z range, excluding 40 Da below and 15 Da above the precursor ion. These fragment ions were sent to the HCD cell using the SPS waveform with an isolation width of 2.0 Da and an AGC of 1e5, and subsequently fragmented with an HDC collision energy of 65%, then detected in the Orbitrap at a resolution of 60,000 at 200 m/z. The maximum injection time was set to 120 ms.
Data Analysis
Peptide Identification
All LC-MS/MS runs were analyzed using Mascot version 2.3.2 (Matrix Science) within Proteome Discoverer 2.1 (Thermo Scientific) against the SwissProt human database (2015/12/29, 42,085 entries). The eight fractions that were run on each instrument were searched together to create one report. A 10 ppm MS1 error tolerance was used, with a 25 mmu error used for MS2 product ions on the Q Exactive Plus, and 0.8 Da on the Fusion, because the MS2s were done in the ion trap. Trypsin was set as the enzyme, allowing for 1 missed cleavage. Methionine oxidation (15.994915 Da) was set as a variable modification, and carbamidomethyl (57.021464 Da) on cysteines was set as a static modification for all searches. Because we could not search the heavy lysine as a dynamic modification with the TMT6 plex on lysine as a static modification, we had to conduct separate searches to get data for both the unlabeled and labeled SILAC peptides. When searching for the unlabeled SILAC peak, TMT6 plex modifications (229.162932 Da) on both lysine and peptide N termini were used. When searching for the labeled SILAC peak, a new modification was created that added the heavy lysine mass with the TMT6 plex mass, for a total mass of 235.183061 Da. This was set as a static modification, along with heavy labeled arginine (6.020129 Da), TMT6 plex on peptide N termini, and carbamidomethyl on cysteine. Percolator was used as the false discovery rate calculator, and all peptides were filtered at the “Strict” Target FDR level of 0.01.
SILAC Quantitation
SILAC peptides and protein quantification was performed with Proteome Discoverer 1.4 using the Precursor Ions Quantifier node. For each peptide, the H/L ratio was determined by a regression model fitted to all isotopic peaks within all scans that the peptide eluted in. H/L ratio for each protein was determined as the median of all the peptides assigned to the protein. Analysis of the isotopic distribution of incompletely cleaved peptides that contained two lysines or arginines indicated that >98% of the internal amino acid pool was labeled at all time-points (8). For a given protein, fractional labeling was calculated as the H/(H+L) ratio based on the H/L ratio from Proteome Discoverer outputs. Peptide fractional labeling measurements at all time-points were combined to obtain an aggregated plot for the kinetics of labeling. The aggregated plots were fitted to a single exponential function by least-square fitting to obtain first order degradation rate constant (kdeg) for each protein.
TMT Quantitation
For peak integration of the TMT product ions, an error tolerance of 15 ppm with the integration method set to “Centroid with the Smallest Delta Mass” within the “Reporter Ions Quantifier” node was used. The MS Order was set to MS2 for the Q Exactive Plus data, and MS3 when searching the Fusion data. Reporter abundances were based on Signal/Noise ratio (S/N) if all spectrum files had a S/N value. Otherwise, reporter abundances were based on signal intensities. Peptides with an isolation interference of greater than 30% were not used for quantitation. Fractional labeling of PSMs at all time-points were combined to obtain an aggregated plot for the kinetics of labeling. The aggregated plots were fitted to a single exponential function by least-square fitting to obtain first order degradation rate constant (kdeg) for each protein. When aggregating PSM data, the kinetics of labeling for individual PSMs were initially fit to a single exponential function by least-square fitting. The data were then filtered to exclude PSMs that had R2<0.8 prior to aggregation and protein-level determination of kdeg. When fitting exponential curves for decay of signal from TMT reporters derived from SILAC-unlabeled peptides, TMT measurements were normalized with respect to the t0 reporter (TMT-126) and a constant fractional baseline at infinite time was incorporated in the fitting equation. The equation used for fitting the curves was therefore: intensity = baseline + (1 − baseline) × e−kdeg×time. When fitting exponential curves for increase of signal from TMT reporters derived from SILAC-labeled peptides, TMT measurements were normalized with respect to the t0 reporter (TMT-126) and the amplitude of the curve was treated as a fitted parameter in the regression analysis. The equation used for fitting the curves was therefore: intensity = 1 + amplitude × (1 − e−kdeg×time). For measurement of kdeg in proliferating cells, the rate constant for cell division (0.40 d−1) was subtracted from the measured rate constants (see below). This subtraction should theoretically yield a positive rate constant. However, for a fraction of proteins, a negative calculated kdeg value was measured, likely because of experimental error. These proteins were not considered in subsequent analyses.
Kinetic Model
The kinetic model applied in this study is based on the following assumptions:
Protein synthesis is a zero-order process with respect to protein concentration.
Protein degradation occurs at a constant fractional rate that is uniform for the entire protein pool. Thus, protein degradation can be modeled as a first order process with respect to protein concentration.
The total protein concentration of each cell does not change during the experimental time-course and the system is at steady-state.
Based on these assumptions, we can devise the following rate equations for clearance of unlabeled proteins and accumulation of labeled proteins:
| (Eq. 1) |
| (Eq. 2) |
Where ksyn is the zero-order rate constant for protein synthesis, kdeg is the first order rate constant for protein degradation and kdiv is the first order rate constant for cell division.
We solve for [unlabeled protein](t) using the constraint [unlabeled protein](0) = [protein]steady-state and for [labeled protein](t) using the constraint [labeled protein](0) = 0.
| (Eq. 3) |
| (Eq. 4) |
Where
| (Eq. 5) |
Because our protein labeling measurements are fractional (i.e. internally normalized with respect to total steady-state protein levels), the observed fractional labeling is derived as:
| (Eq. 6) |
| (Eq. 7) |
In quiescent cells, where the rate of cell division is zero, equations 5, 6, and 7 simplify to
| (Eq. 8) |
| (Eq. 9) |
| (Eq. 10) |
The ratio of synthesis rates of quiescent cells to synthesis rates of proliferating cells as a function of ratios of steady-state protein levels and degradation rate constants can be derived by dividing equation 8 by equation 5:
| (Eq. 11) |
RESULTS
Assay Workflow
Our approach takes advantage of the multiplexing capabilities of isobaric tandem mass tags (TMT) (20–22) to measure fractional SILAC labeling of multiple time-points in a single LC-MS/MS run (Fig. 1B). In this procedure, isotopically labeled amino acids are introduced to cultured cells. Over time, as cellular proteins are degraded and replaced by newly synthesized proteins, the fractional labeling of the protein pool increases. At each time point, protein extracts are collected, digested with trypsin and labeled with distinct TMT tags. Tagged peptides from different time-points are subsequently combined into a single multiplexed sample and analyzed by LC-MS/MS with higher-energy collisional dissociation (HCD). Isobaric TMT tags have identical intact masses but produce reporter ions of varying masses following HCD. Hence, tryptic peptides of a given sequence obtained from different time-points will have identical masses in MS1 spectra but will produce reporter ions of varying masses in MS2 spectra. As protein turnover leads to the gradual disappearance of SILAC-unlabeled and appearance of SILAC-labeled MS1 peaks, the kinetics of this process are revealed by the relative intensities of the TMT reporter ions in the MS2 spectra. Specifically, the relative intensities of TMT reporter ions generated by SILAC-unlabeled precursor peptides monitors their clearance and the relative intensities of TMT reporter ions generated by SILAC-labeled precursor peptides monitors their accumulation.
As a proof of principle, we used the above approach to globally measure the kinetics of protein turnover in primary human dermal fibroblasts (HCA2-hTert) (17, 18) (Fig. 2A). Cells were grown to confluency, resulting in the arrest of cell division by contact inhibition. After reaching quiescence, the cultures were switched to a media containing 13C labeled lysines and arginines. The fact that cells were labeled in a non-dividing state ensured that dilution of cellular proteins by cell division did not contribute to the kinetics of fractional labeling, and protein turnover was the sole determinant of labeling kinetics (2, 23). Cells were collected at 10 different time-points ranging from 0 to 336 h. For each time point, cell extracts were digested with trypsin, covalently tagged with ten different TMT tags before being combined in a single multiplexed sample. Following offline fractionation, the multiplexed sample was analyzed by LC-MS/MS as described under Experimental Procedures. Additionally, in order to compare the results with a standard dynamic SILAC approach, TMT-tagged peptides at five selected time-points were individually analyzed at the MS1 level without multiplexing.
Representative TMT-SILAC Hyperplexed Data
To illustrate a typical datapoint, Figs. 2B–2F show the labeling kinetics of a peptide belonging to neuroblast differentiation-associated protein (AHNAK) (24). Protein turnover was quantified by five different parameters:
Fractional labeling of intact precursor peptides in MS1 spectra obtained from individual non-multiplexed time-points (Dynamic SILAC; Fig. 2B).
Relative intensities of TMT reporter ions obtained from MS2 spectra of SILAC-unlabeled precursor peptides (Fig. 2C).
Relative intensities of TMT reporter ions obtained from MS2 spectra of SILAC-labeled precursor peptides (Fig. 2D).
Relative intensities of TMT reporter ions obtained in MS3 spectra of SILAC-unlabeled precursor peptides by isolation of multiple fragment ions in the MS2 spectra using isolation waveform with multiple notches (synchronous precursor selection; SPS-MS3 (13, 14)) (Fig. 2E). The SPS-MS3 method has been reported to diminish TMT ratio distortion by partially alleviating the co-isolation and fragmentation of interfering ions (13, 14).
Relative intensities of TMT reporter ions obtained by SPS-MS3 spectra of SILAC-labeled precursor peptides. (Fig. 2F).
The kinetic model used to interpret labeling kinetics is presented under Experimental Procedures. The salient assumptions of the model are as follows: (1) the system is at steady-state and population-averaged cellular protein concentrations are not changing during the course of the experiment, (2) protein degradation is a first order process with respect to protein concentration, (3) protein synthesis is a zero order process with respect to protein concentration, and (4) given that the cells are in a quiescent state, protein dilution by cell division is not impacting the fractional labeling of proteins. Based on this model, both protein clearance and accumulation should follow single exponential kinetics with the apparent rate constant equaling the rate constant for protein degradation (kdeg). In support of this model, Fig. 2 indicates that peptide labeling measured by all five methods fit well to single exponential equations and have similar apparent first order rate constants (0.013–0.014 h−1).
It is interesting to note that the kinetic curves measured by TMT-SILAC hyperplexing methods have non-zero baseline intensities (Fig. 2C–2F, dashed lines). In MS2/MS3 analyses of SILAC-unlabeled peptides, the kinetic curve would ordinarily be expected to level off at zero intensity as the protein population becomes fully labeled at progressively longer time-points. Conversely, SILAC-labeled peptides would be expected to have zero intensities at time zero. However, at the MS2 level, both curves have non-zero baselines that have a magnitude of ∼10–15% of the total amplitude of the curve. This suggests that at the MS2 level, a fraction of TMT reporter ions are not generated by the targeted peptide precursors but are instead produced by co-isolation of interfering ions. This interference phenomenon has been described by a number of previous publications (13, 14, 25–30). We observed that for most peptides, the relative contribution of interfering precursor ions to total TMT signal is roughly constant at varying time-points. For example, for MS2 TMT analyses of SILAC-labeled precursors peptides mapped to neuroblast differentiation-associated protein (Fig. 2C), ∼12% of the total intensity of the reporter ions remained at long time-points where >99% of the protein was expected to have turned over (Fig. 2B). Nonetheless, the fractional labeling curve was well fit by a single exponential equation with a baseline of 0.12. Thus, although co-isolation of interfering precursors are likely distorting the measurements of fractional labeling, their influence on the measured rate constant is minimized by the fact that our regression analysis accounts for the presence of a constant baseline intensity that is independently determined as a fitted parameter.
To further mitigate the contribution of interfering species, we used synchronous precursor selection (SPS) to co-isolate and fragment multiple MS2 fragment ions generated by the targeted precursor as described by McAlister et al. (13). The reporter ions generated in the MS3 spectra were quantified as described above for MS2 spectra (Fig. 2E, 2F). The reduction in co-isolation of interfering ions was evident by decreases in baseline intensities (compare dotted baselines between Figs. 2C, 2D and Figs. 2E, 2F).
Global Validation of Precision and Accuracy of TMT-SILAC Hyperplexing
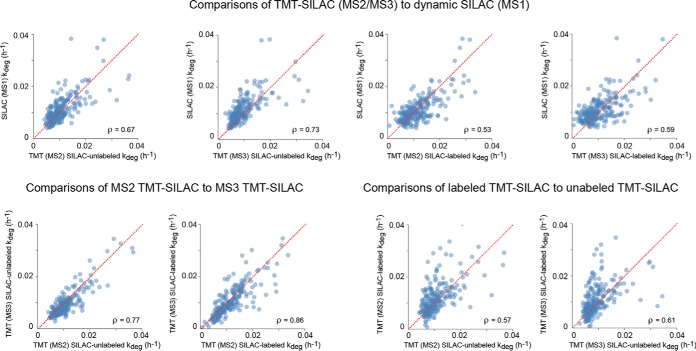
Coverage statistics for all proteome-wide analyses are summarized in supplemental Table S1. By combining the four TMT-SILAC hyperplexing analyses, we were able to measure the degradation kinetics of peptides belonging to 3009 unique protein groups in one or more analysis (supplemental Table S2). To obtain a protein-level data set, we aggregated PSMs whose labeling kinetics were able to be fit with a first order rate equation having R2 values greater than 0.8, and then limited our analysis to 1307 protein groups with 2 or more unique quantified peptides that passed this criterion in at least one of the analyses (supplemental Table S3). We next compared the TMT-hyperplexing data to dynamic SILAC experiments based on quantitation of the MS1 spectra (supplemental Tables S4, S5). For these comparisons, we limited our analyses to 229 proteins that were quantified by all five approaches. First, we analyzed the correspondence of degradation rates of different peptides mapped to the same protein (Fig. 3). For most proteins, it would be expected that all peptide ions matched to a given protein should have the same apparent kdeg. Indeed, we observe that the range of values for coefficients of variation (CV) for filtered peptide kdegs within a protein is very low in comparison to the CV for all analyzed peptide kdegs within the proteome. The range of CVs for intra-protein peptides measured by all approaches had similar magnitudes. However, the mean CV for dynamic SILAC analyses were somewhat lower than the TMT-SILAC approaches, suggesting that it has somewhat better experimental precision. The comparison also indicates that SPS-MS3 improves the precision of the TMT-hyperplexing approach.
Fig. 3.
Labeling of different peptides mapped to the same protein have similar kinetics. As examples, the traces in the plot (A) indicate exponential fits to peptide data for two different proteins with varying degradation rates, ACTB and AHNAK. The data was collected from MS2 TMT reporter tags of SILAC labeled precursors. The boxplots (B) provide a global analysis of variance in rate measurements between peptides belonging to the same protein. The box shows the median and interquartile range (IQR) of the coefficient of variations (CV) of degradation rates for peptides encompassing a single protein for all methods. The error bar represents the entire range of CVs excluding outliers (>1.5 IQR). The white lines and numbers represent mean values. The red circles indicate the CV among all measured peptide degradation rates for each method. The analysis was limited to proteins shared between all analyses.
Next, we analyzed the correlation between protein kdeg measurements obtained from the different analyses in pairwise comparisons. (Fig. 4). The data indicate that there is significant correlation between the measurements obtained from the five methods, validating the general accuracy of kdeg measurements. However, there is considerable experimental noise in the pairwise comparisons. The hyperplexing data obtained at the MS2 level appeared to have a weaker correlation with the MS1 data in comparison to the SPS-MS3 experiments. This is likely because of the higher presence of interfering co-isolated ions that distort the fractional labeling measurements. In general, there also appeared to be more experimental noise in the TMT-hyperplexing data obtained from SILAC-labeled precursor peptides in comparison to SILAC-unlabeled data. This is likely because of increased error in the regression analysis. Unlike unlabeled precursors that have a uniform final baseline signal near zero that can be assigned as a constant in the regression analysis, the signal of labeled peaks at infinite time is undetermined and must be treated as a variable fitted parameter. Our extended labeling time-course allowed many proteins to reach near complete labeling during the experiment and thus the intensity of fully labeled peptides could be determined with high confidence. However, for proteins whose labeling had not reached near completion after 14 days of labeling, a considerable error could have potentially been introduced in determination of their labeling rate constants.
Fig. 4.
Pairwise comparison of kdeg measurements obtained by TMT-SILAC hyperplexing and dynamic SILAC. The analysis was limited to proteins shared between all analyses. Spearman rank correlation coefficients are indicated. The identity line is shown in red.
Global Impact of Cellular Quiescence on Protein Synthesis and Degradation Rates
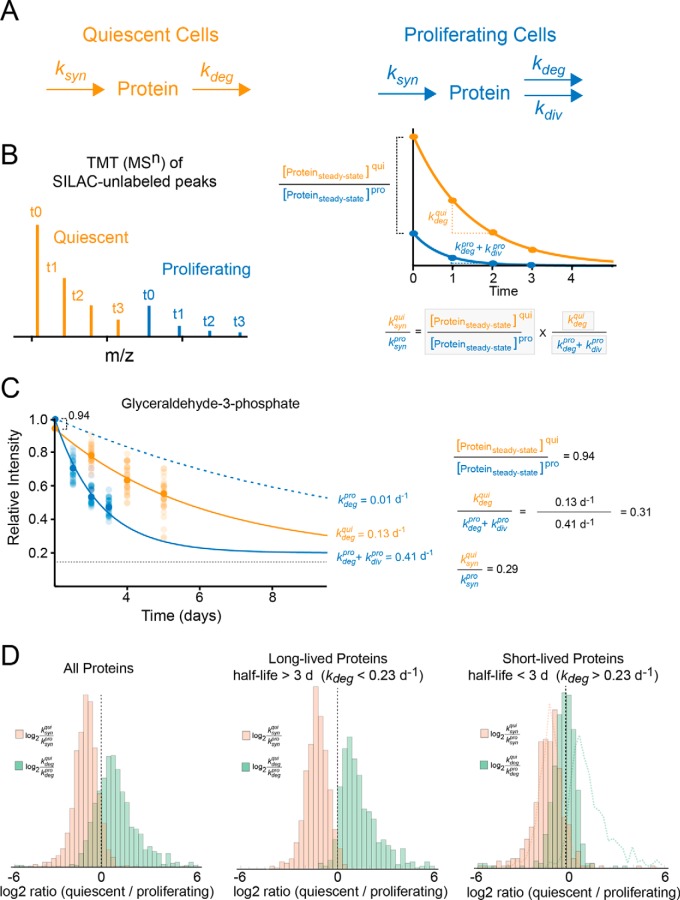
In the above experiments, the apparent rate constants for clearance and accumulation are measured by analysis of fractional labeling. In other words, the intensities of unlabeled and labeled reporters were internally normalized with respect to fully unlabeled or labeled time-points, respectively. Because the kinetics of protein degradation typically follows first order kinetics whereas protein synthesis is a zero-order process with respect to protein concentrations, the apparent rate constants for fractional labeling for both the disappearance of unlabeled reporters and appearance of labeled reporters correspond to the first-order rate constant for degradation (kdeg). However, the TMT-SILAC hyperplexing methodology can be readily modified to additionally measure relative changes in synthesis rates (ksyn) between two experimental conditions under steady-state conditions. By conducting TMT-SILAC hyperplexing analyses of labeling time-points obtained from two conditions, ratios of steady-state protein levels, as well as protein degradation rates can be measured in a single experiment. In turn, these two parameters can be used to calculate the ratio of ksyn values in the two experimental conditions (Fig. 5, Experimental Procedures). We employed this approach to compare global changes in both protein degradation and synthesis as cells transition from a proliferating to a quiescent state.
Fig. 5.
The use of TMT-SILAC hyperplexing to measure relative differences in steady-state protein levels, degradation rates (kdeg) and synthesis rates (ksyn) between proliferating and quiescent cells. A, The schematic illustrates the kinetic model for synthesis and clearance of proteins in quiescent and proliferating cells. B, A theoretical TMT-SILAC hyperplexing analysis of a hypothetical protein with varying ksyn and kdeg values in quiescent and proliferating cells. The analysis of the decay of SILAC-unlabeled peaks allows the measurement of kdeg for both conditions as well as the ratio of steady-state protein levels. These parameters (boxed in the equation at the bottom of the figure) enable the measurement of the ratio of ksyn between the two conditions. The equation is derived based on the model presented under Experimental Procedures. C, Experimental analysis of an example protein (Glyceraldehude-3-Phosphate) showing the measured values for ratios of ksyn, kdeg and steady-state protein levels. The plot indicates the decay curve for the fractional labeling of SILAC-unlabeled peaks for all peptides mapped to the protein (transparent circles) as well as the median value for all peptides (solid circles). The solid line indicates a fit to a single exponential equation for measurement of clearance rate constants. For quiescent cells, the clearance rate constant equals the degradation rate constant. For proliferating cells, the rate of cell division (0.40 d−1) is subtracted from the clearance rate in order to determine the degradation rate (dashed blue line). D, The distribution of log2 ratios of synthesis and degradation rate constants between quiescent and dividing cells. The histograms are shown for all proteins, long-lived proteins (half-lives greater than 3 days in proliferating cells) and short-lived proteins (half-lives less than 3 days in proliferating cells). The dotted lines on the rightmost plot indicate the distribution of long-lived proteins for comparison.
Proliferating and quiescent cells have widely different metabolic demands. Much of the energy expenditure in dividing cells is devoted to accumulation of biomolecules necessary for formation of new daughter cells (31). Exempt from this anabolic requirement, quiescent cells typically downregulate the synthesis of proteins at the level of transcription and translation (32–34). This homeostatic adjustment ensures that the overall rate of protein production does not exceed the rate of clearance and protein concentrations are maintained at steady-state levels in quiescent cells.
Moreover, a newly quiescent cell can potentially counteract the reduced requirement for protein accumulation not only by reducing rates of protein synthesis, but also by increasing rates of protein degradation. The relationship between cellular growth and protein degradation has previously been investigated by a number of classic radioactive tracer studies. By analyzing the degradation of the bulk cellular protein population, some of these studies have reported significant changes in degradations kinetics in quiescent cells (35–39), whereas others have failed to observe such an effect (40–45). Here, we addressed this question by simultaneously measuring proteome-wide changes in synthesis and degradation rates between dividing and quiescent cells using TMT-SILAC hyperplexing.
We combined four SILAC-labeled time-points for both proliferating and quiescent cells in a single hyperplexed analysis (Fig. 5). The experiment allowed us to simultaneously measure relative ratios of steady-state protein levels and degradation rates between quiescent and proliferating cells. The relative ratios of steady-state protein levels were obtained by comparing reporter tag intensities for SILAC-unlabeled (t0) peptides between dividing and quiescent cells. Protein degradation rate constants were determined by measuring the first order rate constant for clearance of SILAC-unlabeled peptides and correcting for the contribution of protein dilution by cell division in dividing cells. In turn, the experimentally measured relative ratios of steady-state protein levels and degradation ratios were used to calculate the relative ratio of synthesis rates according to the model presented under Experimental Procedures. The relative log2 ratios of steady-state protein levels (), degradation rates () and synthesis rates () were measured for 1277 protein and are tabulated in supplemental Table S5.
As expected, our data indicates that the synthesis rate of proteins are globally decreased in quiescent cells. However, somewhat unexpectedly, our data also provides clear evidence that for a large cross-section of the proteome, protein degradation rates are enhanced in quiescent cells (Fig. 5D). Interestingly, the enhancement of degradation rates, but not reduction of synthesis rates, is particularly pronounced in long-lived proteins (Fig. 5D, see Discussion). Together, our data indicate that quiescent fibroblasts compensate for the reduced requirement for protein accumulation by both decreasing global rates of synthesis and enhancing rates of protein of degradation. The results reported here provide the first quantitative global census of these two effects in quiescent cells.
DISCUSSION
The proof-of-principle experiments described above validate a potentially powerful approach for global analyses of proteome dynamics. By combining dynamic SILAC and TMT technologies, multi-time-point kinetics of protein turnover can be analyzed in a single LC-MS/MS run, significantly reducing the cost and complexity of dynamic proteomic experiments. For example, here, we were able to analyze the kinetics of protein clearance at ten distinct time-points in a single 3-hour LC-MS/MS run with nearly no missing time-points for each analyzed protein. If each time point were to be analyzed independently in equivalent dynamic SILAC experiments, more than 24 h of instrument time would be needed and most proteins would not have been quantifiable at all time-points. However, our analyses also indicate that in comparison to conventional dynamic SILAC experiments, this improvement in time-resolution and instrument time comes at the cost of quantitative precision and proteome coverage. These limitations are caused by a number of factors. First, the co-isolation and fragmentation of interfering ions introduce error into the quantitation of TMT reporter ions. Although this effect can be somewhat mitigated by accounting for a constant baseline signal in the kinetic analysis and utilization of the SPS-MS3 protocol, in general we found more experimental noise in the labeling kinetics of reporter MSn ions in comparison to MS1 ions. Second, TMT labeling leads to a reduction in observed peptides because of a general increase in charge state on the labeled peptides. Finally, because of the small mass differences between some TMT 10plex labels, a relatively high resolution is needed to ensure peak separation, increasing the scan time and reducing the number of MS2 scans in the run. Future improvements to the TMT-SILAC hyperplexing methodology will require the development of further strategies for maintaining proteome coverage while minimizing the co-isolation of interfering ions with targeted precursor ions. Until then, the decision to employ conventional dynamic SILAC or TMT-SILAC hyperplexing for analysis of proteome dynamics will likely hinge on the relative importance of temporal resolution and experimental cost versus quantitative precision and maximal proteome coverage.
When conducted under steady-state conditions, apparent rate constants of fractional isotopic labeling typically provide information on protein degradation kinetics (e.g. half-lives). However, by co-analyzing samples collected under two or more environmental conditions, TMT-SILAC hyperplexing has the potential ability to provide proteome-wide measurements of relative ratios of steady-state protein levels in addition to degradation kinetics. Together, these two measured parameters can be used to measure relative changes in protein synthesis rates under steady-state conditions. To demonstrate this capability, we measured differences in protein synthesis and degradation rates between proliferating and dividing cells. Our data indicate that quiescent cells globally decrease rates of protein synthesis and increase rates of protein degradation.
Decreased rates of protein synthesis are a well-described feature of the quiescent state and reductions in overall rates of transcription and translation have been described in bacteria, yeast and higher eukaryotes (31–33, 46). In stationary-phase S. cerevisiae, where this phenomenon has been best described, the inhibition of the mTOR pathway appears to be a key player in inhibiting protein synthesis, although other contributing pathways, such as protein kinase A and C are also known to play a role (47). The inhibition of the mTOR pathway results in a number of downstream effects that promotes the quiescent state, including the shutdown of ribosomal biogenesis required for protein synthesis (48).
Our data also demonstrate that rates of protein degradation are enhanced in quiescent cells and that this effect is most pronounced for long-lived proteins. In dividing cells, two general processes contribute to protein clearance: cytoplasmic dilution by cell division and hydrolysis by cellular degradation pathways (23, 49). Indeed, if we consider a simplified kinetic model of protein expression (see Experimental Procedures), the rate constant of protein clearance is the mathematical sum of the rate constants for these two flux pathways. As has been previously noted (23), degradation is the predominant route of clearance for short-lived proteins, whereas long-lived proteins are predominantly cleared from a cell through the process of proliferation. Thus, as cells transition from a dividing to a non-dividing state, it is the clearance kinetics of long-lived proteins that are particularly impacted. If no compensatory response is initiated, this phenomenon would result in a global increase in cellular concentrations of long-lived proteins relative to short-lived proteins in quiescent cells. By selectively increasing rates of degradation for long-lived proteins, quiescent cells can counter this potential proteostatic disruption and ensure that their production does not exceed cellular demand.
It has previously been shown that basal macroautophagy is up-regulated in quiescent fibroblasts (50). Given that macroautophagy is known to preferentially degrade long-lived proteins (19, 51), its activation may form the molecular basis of the proteome-wide trends observed in our study. Further studies are required to assess this hypothesis and investigate the role of other potential pathways in quiescence-induced protein degradation. It is also important to note that the proteostatic response to quiescence may vary in different cell types. Indeed, the quiescent state of dermal fibroblasts is somewhat unique in that fibroblasts maintain a rather active metabolic state in order to synthesize and secrete extracellular matrix proteins such as collagen fibers that form the basement membrane of connective tissues (31). Conversely, many other cell types enter a quiescent state primarily as a response to nutritional deprivation. Whether different cell types differ in their global proteostatic response to quiescence remains to be determined. More generally, the methodology described in this study may provide a useful proteomic approach for globally investigating biological processes in which the kinetics of protein synthesis and degradation are jointly modulated.
Associated Content
Spectral search results, SILAC and TMT quantitations, and rate measurements at peptide and protein levels are provided in tabular format in the supplementary information.
Accession Numbers
All raw and processed data are available at ProteomeXchange Consortium via the PRIDE database (accession number: PXD004725).
Supplementary Material
Footnotes
Author contributions: K.A.W., T.Z., and S.G. designed research; K.A.W., T.Z., J.R.H., S.S., J.Q., and S.G. performed research; K.A.W., T.Z., and S.G. analyzed data; K.A.W., T.Z., and S.G. wrote the paper.
* This work was supported by a grant from the National Science Foundation (MCB-1350165 CAREER).
 This article contains supplemental material.
This article contains supplemental material.
1 The abbreviations used are:
- LC-MS/MS
- tandem MS
- AGC
- automatic gain control
- CID
- collision induced dissociation
- CV
- coefficient of variation
- FDR
- false discovery rate
- HCD
- higher-energy collisional dissociation
- H/L
- heavy to light isotope ratio
- IQR
- interquartile range
- MEM
- minimal essential medium
- PSM
- peptide-spectrum match
- SILAC
- stable isotope labeling in cell culture
- SPS
- synchronous precursor selection
- TCEP
- tris(2-carboxyethyl)phosphine
- TEAB
- triethylammonium bicarbonate
- TFA
- trifluoroacetic acid
- TMT
- tandem mass tags.
REFERENCES
- 1. Bantscheff M., and Kuster B. (2012) Quantitative mass spectrometry in proteomics. Anal. Bioanal. Chem. 404, 937–938 [DOI] [PubMed] [Google Scholar]
- 2. Claydon A. J., and Beynon R. (2012) Proteome dynamics: revisiting turnover with a global perspective. Mol. Cell. Proteomics 11, 1551–1565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Schoenheimer R. (1942) The Dynamic State of Body Constituents, Harvard University Press, Boston [Google Scholar]
- 4. Hinkson I. V., and Elias J. E. (2011) The dynamic state of protein turnover: It's about time. Trends Cell Biol. 21, 293–303 [DOI] [PubMed] [Google Scholar]
- 5. Mann M. (2006) Functional and quantitative proteomics using SILAC. Nat. Rev. Mol. Cell Biol. 7, 952–958 [DOI] [PubMed] [Google Scholar]
- 6. Ong S. E., Blagoev B., Kratchmarova I., Kristensen D. B., Steen H., Pandey A., and Mann M. (2002) Stable isotope labeling by amino acids in cell culture, SILAC, as a simple and accurate approach to expression proteomics. Mol. Cell. Proteomics : MCP 1, 376–386 [DOI] [PubMed] [Google Scholar]
- 7. Cambridge S. B., Gnad F., Nguyen C., Bermejo J. L., Kruger M., and Mann M. (2011) Systems-wide proteomic analysis in mammalian cells reveals conserved, functional protein turnover. J. Proteome Res. 10, 5275–5284 [DOI] [PubMed] [Google Scholar]
- 8. Schwanhausser B., Busse D., Li N., Dittmar G., Schuchhardt J., Wolf J., Chen W., and Selbach M. (2011) Global quantification of mammalian gene expression control. Nature 473, 337–342 [DOI] [PubMed] [Google Scholar]
- 9. Price J. C., Guan S., Burlingame A., Prusiner S. B., and Ghaemmaghami S. (2010) Analysis of proteome dynamics in the mouse brain. Proc. Natl. Acad. Sci. U.S.A. 107, 14508–14513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Toyama B. H., Savas J. N., Park S. K., Harris M. S., Ingolia N. T., Yates J. R. 3rd, and Hetzer M. W. (2013) Identification of long-lived proteins reveals exceptional stability of essential cellular structures. Cell 154, 971–982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Dephoure N., and Gygi S. P. (2012) Hyperplexing: a method for higher-order multiplexed quantitative proteomics provides a map of the dynamic response to rapamycin in yeast. Sci. Signal. 5, rs2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Everley R. A., Kunz R. C., McAllister F. E., and Gygi S. P. (2013) Increasing throughput in targeted proteomics assays: 54-plex quantitation in a single mass spectrometry run. Anal. Chem. 85, 5340–5346 [DOI] [PubMed] [Google Scholar]
- 13. McAlister G. C., Nusinow D. P., Jedrychowski M. P., Wuhr M., Huttlin E. L., Erickson B. K., Rad R., Haas W., and Gygi S. P. (2014) MultiNotch MS3 enables accurate, sensitive, and multiplexed detection of differential expression across cancer cell line proteomes. Anal. Chem. 86, 7150–7158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Ting L., Rad R., Gygi S. P., and Haas W. (2011) MS3 eliminates ratio distortion in isobaric multiplexed quantitative proteomics. Nat. Methods 8, 937–940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Jayapal K. P., Sui S., Philp R. J., Kok Y. J., Yap M. G., Griffin T. J., and Hu W. S. (2010) Multitagging proteomic strategy to estimate protein turnover rates in dynamic systems. J. Proteome Res. 9, 2087–2097 [DOI] [PubMed] [Google Scholar]
- 16. Wang F., Cheng K., Wei X., Qin H., Chen R., Liu J., and Zou H. (2013) A six-plex proteome quantification strategy reveals the dynamics of protein turnover. Sci. Rep. 3, 1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Bodnar A. G., Ouellette M., Frolkis M., Holt S. E., Chiu C. P., Morin G. B., Harley C. B., Shay J. W., Lichtsteiner S., and Wright W. E. (1998) Extension of life-span by introduction of telomerase into normal human cells. Science 279, 349–352 [DOI] [PubMed] [Google Scholar]
- 18. Voskarides K., and Deltas C. (2009) Screening for mutations in kidney-related genes using SURVEYOR nuclease for cleavage at heteroduplex mismatches. J. Mol. Diagnostics 11, 311–318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Zhang T., Shen S., Qu J., and Ghaemmaghami S. (2016) Global analysis of cellular protein flux quantifies the selectivity of basal autophagy. Cell Rep. 14, 2426–2439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Thompson A., Schafer J., Kuhn K., Kienle S., Schwarz J., Schmidt G., Neumann T., Johnstone R., Mohammed A. K., and Hamon C. (2003) Tandem mass tags: a novel quantification strategy for comparative analysis of complex protein mixtures by MS/MS. Anal. Chem. 75, 1895–1904 [DOI] [PubMed] [Google Scholar]
- 21. Ross P. L., Huang Y. N., Marchese J. N., Williamson B., Parker K., Hattan S., Khainovski N., Pillai S., Dey S., Daniels S., Purkayastha S., Juhasz P., Martin S., Bartlet-Jones M., He F., Jacobson A., and Pappin D. J. (2004) Multiplexed protein quantitation in Saccharomyces cerevisiae using amine-reactive isobaric tagging reagents. Mol. Cell. Proteomics 3, 1154–1169 [DOI] [PubMed] [Google Scholar]
- 22. Dayon L., Hainard A., Licker V., Turck N., Kuhn K., Hochstrasser D. F., Burkhard P. R., and Sanchez J. C. (2008) Relative quantification of proteins in human cerebrospinal fluids by MS/MS using 6-plex isobaric tags. Anal. Chem. 80, 2921–2931 [DOI] [PubMed] [Google Scholar]
- 23. Eden E., Geva-Zatorsky N., Issaeva I., Cohen A., Dekel E., Danon T., Cohen L., Mayo A., and Alon U. (2011) Proteome half-life dynamics in living human cells. Science 331, 764–768 [DOI] [PubMed] [Google Scholar]
- 24. Shtivelman E., Cohen F. E., and Bishop J. M. (1992) A human gene (AHNAK) encoding an unusually large protein with a 1.2-microns polyionic rod structure. Proc. Natl. Acad. Sci. U.S.A. 89, 5472–5476 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Bantscheff M., Boesche M., Eberhard D., Matthieson T., Sweetman G., and Kuster B. (2008) Robust and sensitive iTRAQ quantification on an LTQ Orbitrap mass spectrometer. Mol. Cell. Proteomics 7, 1702–1713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Karp N. A., Huber W., Sadowski P. G., Charles P. D., Hester S. V., and Lilley K. S. (2010) Addressing accuracy and precision issues in iTRAQ quantitation. Mol. Cell. Proteomics 9, 1885–1897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Lu R., Markowetz F., Unwin R. D., Leek J. T., Airoldi E. M., MacArthur B. D., Lachmann A., Rozov R., Ma'ayan A., Boyer L. A., Troyanskaya O. G., Whetton A. D., and Lemischka I. R. (2009) Systems-level dynamic analyses of fate change in murine embryonic stem cells. Nature 462, 358–362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Ow S. Y., Salim M., Noirel J., Evans C., Rehman I., and Wright P. C. (2009) iTRAQ underestimation in simple and complex mixtures: “the good, the bad and the ugly”. J. Proteome Res. 8, 5347–5355 [DOI] [PubMed] [Google Scholar]
- 29. Shirran S. L., and Botting C. H. (2010) A comparison of the accuracy of iTRAQ quantification by nLC-ESI MSMS and nLC-MALDI MSMS methods. J. Proteomics 73, 1391–1403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Wenger C. D., Lee M. V., Hebert A. S., McAlister G. C., Phanstiel D. H., Westphall M. S., and Coon J. J. (2011) Gas-phase purification enables accurate, multiplexed proteome quantification with isobaric tagging. Nat. Methods 8, 933–935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Valcourt J. R., Lemons J. M., Haley E. M., Kojima M., Demuren O. O., and Coller H. A. (2012) Staying alive: metabolic adaptations to quiescence. Cell Cycle 11, 1680–1696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Braun E. L., Fuge E. K., Padilla P. A., and Werner-Washburne M. (1996) A stationary-phase gene in Saccharomyces cerevisiae is a member of a novel, highly conserved gene family. J. Bacteriol. 178, 6865–6872 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Fuge E. K., Braun E. L., and Werner-Washburne M. (1994) Protein synthesis in long-term stationary-phase cultures of Saccharomyces cerevisiae. J. Bacteriol. 176, 5802–5813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Levine E. M., Becker Y., Boone C. W., and Eagle H. (1965) Contact Inhibition, Macromolecular Synthesis, and Polyribosomes in Cultured Human Diploid Fibroblasts. Proc. Natl. Acad. Sci. U.S.A. 53, 350–356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Fuertes G., Martin De Llano J. J., Villarroya A., Rivett A. J., and Knecht E. (2003) Changes in the proteolytic activities of proteasomes and lysosomes in human fibroblasts produced by serum withdrawal, amino-acid deprivation and confluent conditions. Biochem. J. 375, 75–86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Pfeifer U., Tessitore L., Bonelli G., and Baccino F. M. (1988) Regulation of protein turnover versus growth state. III. Growth cessation is associated with activation of autophagy in Yoshida ascites hepatoma AH-340. Virchows Arch. B Cell Pathol. Incl. Mol. Pathol. 55, 363–369 [PubMed] [Google Scholar]
- 37. Hendil K. B. (1977) Intracellular protein degradation in growing, in density-inhibited, and in serum-restricted fibroblast cultures. J. Cell. Physiol. 92, 353–364 [DOI] [PubMed] [Google Scholar]
- 38. Gronostajski R. M., Goldberg A. L., and Pardee A. B. (1984) The role of increased proteolysis in the atrophy and arrest of proliferation in serum-deprived fibroblasts. J. Cell. Physiol. 121, 189–198 [DOI] [PubMed] [Google Scholar]
- 39. Lockwood T. D., and Minassian I. A. (1982) Protein turnover and proliferation. Failure of SV-3T3 cells to increase lysosomal proteinases, increase protein degradation and cease net protein accumulation. Biochem. J. 206, 251–258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Bradley M. O. (1977) Regulation of protein degradation in normal and transformed human cells. Effects of growth state, medium composition, and viral transformation. J. Biol. Chem. 252, 5310–5315 [PubMed] [Google Scholar]
- 41. Kaplan J., and Moskowitz M. (1975) Studies on the turnover of plasma membranes in cultured mammalian cells. II. Demonstration of heterogeneous rates of turnover for plasma membrane proteins and glycoproteins. Biochim. Biophys. Acta 389, 306–313 [DOI] [PubMed] [Google Scholar]
- 42. Kaplan J., and Moskowitz M. (1975) Studies on the turnover of plasma membranes in cultured mammalina cells. I. Rates of synthesis and degradation of plasma membrane proteins and carbohydrates. Biochim. Biophys. Acta 389, 290–305 [DOI] [PubMed] [Google Scholar]
- 43. Eagle H., Piez K. A., Fleischman R., and Oyama V. I. (1959) Protein turnover in mammaliar cell cultures. J. Biol. Chem. 234, 592–597 [PubMed] [Google Scholar]
- 44. Libby P., and O'Brien K. V. (1984) The role of protein breakdown in growth, quiescence, and starvation of vascular smooth muscle cells. J. Cell. Physiol. 118, 317–323 [DOI] [PubMed] [Google Scholar]
- 45. Baccino F. M., Tessitore L., and Bonelli G. (1984) Control of protein degradation and growth phase in normal and neoplastic cells. Toxicol. Pathol. 12, 281–287 [DOI] [PubMed] [Google Scholar]
- 46. Navarro Llorens J. M., Tormo A., and Martinez-Garcia E. (2010) Stationary phase in gram-negative bacteria. FEMS Microbiol. Rev. 34, 476–495 [DOI] [PubMed] [Google Scholar]
- 47. Gray J. V., Petsko G. A., Johnston G. C., Ringe D., Singer R. A., and Werner-Washburne M. (2004) “Sleeping beauty”: quiescence in Saccharomyces cerevisiae. Microbiol. Mol. Biol. Rev. 68, 187–206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Dickson L. M., and Brown A. J. (1998) mRNA translation in yeast during entry into stationary phase. Mol. Gen. Genet. 259, 282–293 [DOI] [PubMed] [Google Scholar]
- 49. Claydon A. J., Thom M. D., Hurst J. L., and Beynon R. J. (2012) Protein turnover: measurement of proteome dynamics by whole animal metabolic labelling with stable isotope labelled amino acids. Proteomics 12, 1194–1206 [DOI] [PubMed] [Google Scholar]
- 50. Valentin M., and Yang E. (2008) Autophagy is activated, but is not required for the G0 function of BCL-2 or BCL-xL. Cell Cycle 7, 2762–2768 [DOI] [PubMed] [Google Scholar]
- 51. Klionsky D. J. (2007) Autophagy: from phenomenology to molecular understanding in less than a decade. Nat. Rev. Mol. Cell Biol. 8, 931–937 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.