Colocalization of GWAS and eQTL Signals Detects Target Genes

Abstract

The vast majority of genome-wide association study (GWAS) risk loci fall in non-coding regions of the genome. One possible hypothesis is that these GWAS risk loci alter the individual’s disease risk through their effect on gene expression in different tissues. In order to understand the mechanisms driving a GWAS risk locus, it is helpful to determine which gene is affected in specific tissue types. For example, the relevant gene and tissue could play a role in the disease mechanism if the same variant responsible for a GWAS locus also affects gene expression. Identifying whether or not the same variant is causal in both GWASs and expression quantitative trail locus (eQTL) studies is challenging because of the uncertainty induced by linkage disequilibrium and the fact that some loci harbor multiple causal variants. However, current methods that address this problem assume that each locus contains a single causal variant. In this paper, we present eCAVIAR, a probabilistic method that has several key advantages over existing methods. First, our method can account for more than one causal variant in any given locus. Second, it can leverage summary statistics without accessing the individual genotype data. We use both simulated and real datasets to demonstrate the utility of our method. Using publicly available eQTL data on 45 different tissues, we demonstrate that eCAVIAR can prioritize likely relevant tissues and target genes for a set of glucose- and insulin-related trait loci.

Introduction

Genome-wide association studies (GWASs) have successfully detected thousands of genetic variants associated with various traits and diseases.^{1, 2, 3, 4} The vast majority of genetic variants detected by GWASs fall in non-coding regions of the genome, and it is unclear how these non-coding variants affect traits and diseases.⁵ One potential approach to identifying the mechanism of these non-coding variants in disease is through integration of expression quantitative loci (eQTL) studies and GWASs.⁵ This approach is based on the concept that a GWAS variant, in some tissues, affects expression at a nearby gene and that both the gene and the tissue might play a role in the disease mechanism.^{6, 7}

Unfortunately, integrating GWASs and eQTL studies is challenging for two reasons. First, the correlation structure of the genome, known as linkage disequilibrium (LD),⁸ produces an inherent ambiguity in interpreting results of genetic studies. Second, some loci harbor more than one causal variant for any given disease. We know that marginal statistics of a variant can be affected by other variants in LD.^{8, 9, 10, 11} For example, the marginal statistics of two variants in LD can capture a fraction of the effect of each other. Although GWASs have benefited from LD in the human genome by tagging only a subset of common variants to capture a majority of common variants, a fine-mapping process, which attempts to detect true causal variants that are responsible for an association signal at the locus, becomes more challenging. Colocalization determines whether a single variant is responsible for both GWAS and eQTL signals in a locus. Thus, colocalization requires correctly identifying the causal variant in both studies.

Recently, researchers proposed a series of methods^{6, 12, 13, 14, 15, 16, 17} to integrate GWASs and eQTL studies. PrediXscan⁷ and TWAS,¹⁷ which impute gene expression and then associate the imputed expression with the trait, are examples of such methods. However, these methods do not provide a basis for determining colocalization of GWAS causal variants and eQTL causal variants. Another class of methods integrates GWASs and eQTL studies to provide insight about the colocalization of causal variants. For example, regulatory trait concordance (RTC)¹³ detects variants that are causal in both studies while accounting for LD. RTC is based on the assumption that removing the effect of causal variants from eQTL studies will reduce or eliminate any significant association signal at that locus. Thus, when the GWAS causal variant is colocalized with the eQTL causal variant, re-computing the marginal statistics for the eQTL variant by conditioning on the GWAS causal variant will remove any significant association signal observed in the locus. Sherlock,¹² another method, is based on a Bayesian statistical framework that matches GWAS association signals with eQTL signals for a specific gene in order to detect whether the same variant is causal in both studies. Similar to RTC, Sherlock accounts for the uncertainty of LD. QTLMatch¹⁶ is another proposed method of detecting cases where the most significant GWAS and eQTL variants are colocalized as a result of a causal relationship or coincidence. COLOC,^{14, 15} a method expanded from QTLMatch, is the state-of-the-art method that colocalizes GWAS and eQTL signals. COLOC utilizes an approximate Bayes factor to estimate the posterior probabilities that a variant is causal in both GWASs and eQTL studies. Unfortunately, most existing colocalization methods that utilize summary statistics assume the presence of only one causal variant in any given locus for both GWASs and eQTL studies. As we show below, this assumption reduces the accuracy of results when the locus contains multiple causal variants.

In this paper, we present a probabilistic model for integrating GWAS and eQTL data. For each study, we use only the reported summary statistics and simultaneously perform statistical fine-mapping to optimize integration. Our approach, eCAVIAR (eQTL and GWAS Causal Variant Identification in Associated Regions), extends the CAVIAR¹⁸ framework to explicitly estimate the posterior probability that the same variant is causal in both a GWAS and eQTL study while accounting for the uncertainty of LD. We apply eCAVIAR to colocalize variants that pass the genome-wide significance threshold in a GWAS. For any given peak variant identified in a GWAS, eCAVIAR considers a collection of variants around that peak variant as one single locus. This collection includes the peak variant itself, M variants upstream of this peak variant, and M variants downstream of this peak variant (e.g., M can be set to 50). Then, for all variants in a locus, we consider their marginal statistics obtained from the eQTL study in all tissues and all genes. We consider only genes and tissues in which at least one of the genes is an eGene.^{19, 20} eGenes are genes that have at least one significant variant (p value ≤ 10⁻⁵ when corrected for multiple hypothesis) associated with the expression of that gene. We assume that the posterior probability that the same variant is causal in both a GWAS and eQTL study is independent. Thus, this posterior probability is equal to the product of posterior probabilities that a given variant is causal in a GWAS and eQTL study. We refer to the amount of support for a variant responsible for the associated signals in both studies as the colocalization posterior probability (CLPP).

Our framework allows for multiple variants to be causal in a single locus, a phenomenon that is widespread in eQTL data and referred to as allelic heterogeneity (AH). Our approach can accurately quantify the amount of support for a variant responsible for the associated signals in both studies and identify scenarios where there is support for an eQTL-mediated mechanism. Moreover, we can identify scenarios where the variants underlying both studies are clearly different. Utilizing simulated datasets, we show that eCAVIAR has high accuracy in detecting target genes and relevant tissues. Furthermore, the amount of CLPP depends on the complexity of the LD.

We applied our method to colocalize the MAGIC (Meta-analyses of Glucose and Insulin-Related Trait Consortium)^{21, 22, 23, 24} GWAS dataset and publicly available eQTL data on 45 different tissues. We obtained 44 tissues from the Genotype-Tissue Expression (GTEx) eQTL dataset (release v.6, dbGaP: phs000424.v6.p1)¹⁹ and one pancreatic islet tissue from the van de Bunt et al. study.²⁵ Our results provide insight into disease mechanisms by identifying specific GWAS loci that share a causal variant with eQTL studies in a tissue. In addition, we have identified several loci where GWAS and eQTL causal variants appear to be different, suggesting that the genetic factors underlying disease mechanisms are more complex than previously thought.

Material and Methods

CAVIAR Model for Fine-Mapping

Standard GWAS and Indirect Association

We collect quantitative traits for N individuals and genotypes for all individuals at M SNPs (variants). In this case, we collect data for one phenotype and the expression of multiple genes. We assume that both the phenotype and gene expression have at least one significant variant. To simplify the description of our method, we assume that the number of individuals and the pairwise Pearson’s correlations of genotype (LD) in both the GWAS and eQTL study are the same. (In Appendix A, we describe a more general model where the number of individuals and LD in both the GWAS and eQTL study are not the same.) Let Y^(p) indicate an N × 1 vector of the phenotypic values where $y_j^{\left(\text{p}\right)}$ denotes the phenotypic value for the j^th individual. We use Y^(e) to indicate an N × 1 vector of gene expression collected for one gene of interest, for which there exists one significant variant associated with the expression of that gene. Let G indicate an N × M matrix of genotype information where G_i is an N × 1 vector of minor allele counts for all N individuals at the i^th variant. In this setting, g_ji indicates the j^th element from vector G_i, or the minor allele count for the j^th individual. In diploid genomes, such as those of humans, we can have three possible minor allele counts: g_ji = {0, 1, 2}. We standardize both the phenotypes and the genotypes to mean 0 and variance 1, where X is the standardized matrix of G. Let X_i denote an N × 1 vector of standardized minor allele counts for the i^th variant. We assume an “additive” Fisher’s polygenic model, which is widely used by the GWAS community. In Fisher’s polygenic model, the phenotypes follow a normal distribution. The additive assumption implies that each variant contributes linearly to the phenotype. Thus, we consider the following linear model:

$$Y^{\left(\text{p}\right)}={\text{μ}}^{\left(\text{p}\right)}1+\sum _{i=1}^M{\text{β}}_i^{\left(\text{p}\right)}{X}_i+{\mathit{e}}^{\left(\text{p}\right)},$$

$$Y^{\left(\text{e}\right)}={\text{μ}}^{\left(\text{e}\right)}1+\sum _{i=1}^M{\text{β}}_i^{\left(\text{e}\right)}{X}_i+{\mathit{e}}^{\left(\text{e}\right)},$$

where μ^(p) is the phenotypic mean and μ^(e) is the gene-expression mean. Let ${\text{β}}_i^{\left(\text{p}\right)}$ and ${\text{β}}_i^{\left(\text{e}\right)}$ be the effect size of the i^th variant toward the phenotypes and gene expression, respectively. In addition, e^(p) is the environment and measurement error toward the collected phenotype, and e^(e) is the environment and measurement error toward the gene expression. In this model, we assume that e^(p) is a vector of independent and identically distributed and normally distributed random variables. Let ${\mathit{e}}^{\left(\text{p}\right)}\sim N\left(0,{\text{σ}}_{\text{e}}^{\left(\text{p}\right)2}\mathit{I}\right)$, where ${\text{σ}}_{\text{e}}^{\left(\text{p}\right)}$ is a covariance scalar and I is an N × N identity matrix. In our setting, we have the marginal statistics of M variants for the phenotype of interest and gene expression. Let $S^{\left(\text{p}\right)}=\left\{s_1^{\left(\text{p}\right)},s_2^{\left(\text{p}\right)},\cdots s_M^{\left(\text{p}\right)}\right\}$ indicate the marginal statistics for the phenotype of interest, and let $S^{\left(\text{e}\right)}=\left\{s_1^{\left(\text{e}\right)},s_2^{\left(\text{e}\right)},\cdots s_M^{\left(\text{e}\right)}\right\}$ indicate the marginal statistics for gene expression. The joint distribution of the marginal statistics, given the true effect sizes, follows a multivariate normal (MVN) distribution and is similar to that found in our previous works.^{18, 26, 27, 28} Thus, we have

$$\begin{array}{c}\left(S^{\left(\text{p}\right)}|{\text{Λ}}^{\left(\text{p}\right)}\right)\sim \mathcal{N}\left({\text{ΣΛ}}^{\left(\text{p}\right)},\text{Σ}\right),\\ \left(S^{\left(\text{e}\right)}|{\text{Λ}}^{\left(\text{e}\right)}\right)\sim \mathcal{N}\left({\text{ΣΛ}}^{\left(\text{e}\right)},\text{Σ}\right),\end{array}$$ (Equation 1)

where Σ is the pairwise Pearson’s correlations of genotypes. Let ${\text{Λ}}^{\left(\text{p}\right)}=\left\{{\text{λ}}_1^{\left(\text{p}\right)},{\text{λ}}_2^{\left(\text{p}\right)},\cdots {\text{λ}}_M^{\left(\text{p}\right)}\right\}$ and ${\text{Λ}}^{\left(\text{e}\right)}=\left\{{\text{λ}}_1^{\left(\text{e}\right)},{\text{λ}}_2^{\left(\text{e}\right)},\cdots {\text{λ}}_M^{\left(\text{e}\right)}\right\}$ be the true standardized effect size for all the variants of the desired phenotype and gene expression, respectively. The true effect size is zero for a non-causal variant and non-zero for a causal variant. Let ΣΛ^(p) and ΣΛ^(e) be the LD-induced non-centrality parameter (NCP) for the desired phenotype and gene expression, respectively.

CAVIAR Generative Model for a Single Phenotype

We introduce a new variable, C^(p), which is an M × 1 binary vector. We refer to this binary vector as the causal status. The causal status indicates which variants are causal and which are not. We set $c_i^{\left(\text{p}\right)}$ to 1 if the i^th variant is causal; otherwise, we set it to 0. In CAVIAR,^{18, 27} we introduce a prior on the vector of effect sizes by utilizing the MVN distribution. Given the vector of causal status, we define this prior on the vector of effect sizes as

$$\begin{array}{c}\left({\text{Λ}}^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}\right)\sim \mathcal{N}\left(0,{\text{σ}}^{\left(\text{p}\right)2}{\text{Σ}}_c^{\left(\text{p}\right)}\right),\end{array}$$ (Equation 2)

where ${\text{Σ}}_c^{\left(\text{p}\right)}$ is a diagonal matrix and ${\text{σ}}^{\left(\text{p}\right)2}$ is a constant that indicates the variance of our prior over the GWAS NCPs. We set ${\text{σ}}^{\left(\text{p}\right)2}$ to 5.2.^{18, 27} The diagonal elements of ${\text{Σ}}_c^{\left(\text{p}\right)}$ are set to 1 or 0 such that for variants selected as causal in C^(p), their corresponding diagonal elements in ${\text{Σ}}_c^{\left(\text{p}\right)}$ are set to 1; otherwise, we set them to 0. CAVIAR uses this prior as a conjugate prior to compute the likelihood of each possible causal status. The joint distribution of the marginal statistics given the causal status is as follows:

$$\begin{array}{c}\left(S^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}\right)\sim \mathcal{N}\left(0,\text{Σ}+{\text{σ}}^{\left(\text{p}\right)2}{\text{ΣΣ}}_c^{\left(\text{p}\right)}\text{Σ}\right).\end{array}$$ (Equation 3)

In a similar way, for the gene of interest for which we perform eQTL mapping, we have

$$\begin{array}{c}\left({\text{Λ}}^{\left(\text{e}\right)}|C^{\left(\text{e}\right)}\right)\sim \mathcal{N}\left(0,{\text{σ}}^{\left(\text{e}\right)2}{\text{Σ}}_c^{\left(\text{e}\right)}\right),\end{array}$$ (Equation 4)

where ${\text{Σ}}_c^{\left(\text{e}\right)}$ is a diagonal matrix and ${\text{σ}}^{\left(\text{e}\right)2}$ is set to 5.2.^{18, 27} The diagonal elements of ${\text{Σ}}_c^{\left(\text{e}\right)}$ are set to 1 or 0. For variants selected as causal in C^(e), their corresponding diagonal elements in ${\text{Σ}}_c^{\left(\text{e}\right)}$ are set to 1; otherwise, we set them to 0.

eCAVIAR Computes the Colocalization Posterior Probability for a GWAS and eQTL Study

Given the marginal statistics for a GWAS and eQTL study, which are denoted by S^(p) and S^(e), respectively, we want to compute the CLPP. CLPP is the probability that the same variant is causal in both studies. For simplicity, we compute the CLPP for the i^th variant. We define the CLPP for the i^th variant as $\text{P}\left(c_i^{\left(\text{p}\right)}=1,c_i^{\left(\text{e}\right)}=1|S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}\right)$, and we use ${\varphi }_i$ to indicate the CLPP for the i^th variant. We utilize the law of total probability to compute the summation probability of all causal statuses where the i^th variant is causal in both the GWAS and eQTL study and other variants can be causal or non-causal. Thus, the above equation can be extended as follows:

$$\begin{array}{c}{\varphi }_i=\text{P}\left(c_i^{\left(\text{p}\right)}=1,c_i^{\left(\text{e}\right)}=1|S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}\right)\\ =\sum _{C_{/i}^{\ast \left(\text{p}\right)}\in {\left\{\mathrm{0,1}\right\}}^{M-1}}\sum _{C_{/i}^{\ast \left(\text{e}\right)}\in {\left\{\mathrm{0,1}\right\}}^{M-1}}\text{P}\left(C_{/i}^{\left(\text{p}\right)}=C_{/i}^{\ast \left(\text{p}\right)},C_{/i}^{\left(\text{e}\right)}=C_{/i}^{\ast \left(\text{e}\right)},c_i^{\left(\text{p}\right)}=1,c_i^{\left(\text{e}\right)}=1|S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}\right)\\ =\sum _{C^{\ast \left(\text{p}\right)}\in {\left\{\mathrm{0,1}\right\}}^M}\sum _{C^{\ast \left(\text{e}\right)}\in {\left\{\mathrm{0,1}\right\}}^M}\text{P}\left(C^{\left(\text{p}\right)}=C^{\ast \left(\text{p}\right)},C^{\left(\text{e}\right)}=C^{\ast \left(\text{e}\right)}|S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}\right)\mathbb{I}\left(c_i^{\ast \left(\text{p}\right)}=1,c_i^{\ast \left(\text{e}\right)}=1\right),\end{array}$$ (Equation 5)

where $C_{/i}^{\left(\text{p}\right)}$ and $C_{/i}^{\left(\text{e}\right)}$ are vectors of causal status for all variants, excluding the i^th variant for the phenotype of interest and gene expression. Let $\mathbb{I}\left(\right)$ be an indicator function defined as follows:

$$\mathbb{I}\left(c_i^{\ast \left(\text{p}\right)}=1,c_i^{\ast \left(\text{e}\right)}=1\right)=\{\begin{array}{cc}1& c_i^{\ast \left(\text{p}\right)}\text{and}{c}_i^{\ast \left(\text{e}\right)}\text{are}\text{causal}\\ 0& o/w\end{array}.$$ (Equation 6)

Utilizing the Bayes’ rule, we compute the CLPP as follows:

$${\varphi }_i=\frac{{\sum }_{C^{\ast \left(\text{p}\right)}}{\sum }_{C^{\ast \left(\text{e}\right)}}\text{P}\left(S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}|C^{\left(\text{p}\right)}=C^{\ast \left(\text{p}\right)},C^{\left(\text{e}\right)}=C^{\ast \left(\text{e}\right)}\right)\text{P}\left(C^{\ast \left(\text{p}\right)},C^{\ast \left(\text{e}\right)}\right)\mathbb{I}\left(c_i^{\ast \left(\text{p}\right)}=1,c_i^{\ast \left(\text{e}\right)}=1\right)}{{\sum }_{C^{\ast \left(\text{p}\right)}}{\sum }_{C^{\ast \left(\text{e}\right)}}\text{P}\left(S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}|C^{\left(\text{p}\right)}=C^{\ast \left(\text{p}\right)},C^{\left(\text{e}\right)}=C^{\ast \left(\text{e}\right)}\right)\text{P}\left(C^{\ast \left(p\right)},C^{\ast \left(\text{e}\right)}\right)},$$ (Equation 7)

where $\text{P}\left(C^{\ast \left(\text{p}\right)},C^{\ast \left(\text{e}\right)}\right)$ is the prior probability of the causal status of $C^{\ast \left(\text{p}\right)}$ and $C^{\ast \left(\text{e}\right)}$ for the GWAS and eQTL study, respectively. We assume that the prior probability over the causal status for the GWAS and eQTL study is independent: $\text{P}\left(C^{\ast \left(\text{p}\right)},C^{\ast \left(\text{e}\right)}\right)=\text{P}\left(C^{\ast \left(\text{p}\right)}\right)\text{P}\left(C^{\ast \left(\text{e}\right)}\right)$. To compute the prior of causal status, we use the same assumptions that are widely used in fine-mapping methods,^{18, 27, 29} whereby the probability of causal status follows a binomial distribution where the probability that a variant is causal is equal to γ. Thus, this prior is equal to $\text{P}\left(C^{\ast \left(\text{p}\right)}\right)={\prod }_{i=1}^M{\text{γ}}^{c_i^{\ast \left(\text{p}\right)}}{\left(1-\text{γ}\right)}^{1-c_i^{\ast \left(\text{p}\right)}}$, and γ is set to 0.01.^{18, 30, 31, 32}

GWASs and eQTL studies are usually performed on independent sets of individuals. Furthermore, given the causal status in both studies, the marginal statistics for these two studies are independent. We have $\text{P}\left(S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}|C^{\ast \left(\text{p}\right)},C^{\ast \left(\text{e}\right)}\right)=\text{P}\left(S^{\left(\text{p}\right)}|C^{\ast \left(\text{p}\right)}\right)\text{P}\left(S^{\left(\text{e}\right)}|C^{\ast \left(\text{e}\right)}\right)$. Thus, we simplify Equation 7 and compute the CLPP as follows:

$${\varphi }_i=\frac{{\sum }_{C^{\ast \left(\text{p}\right)}}\text{P}\left(S^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}=C^{\ast \left(\text{p}\right)}\right)\text{P}\left(C^{\ast \left(\text{p}\right)}\right)\mathbb{I}\left(c_i^{\ast \left(\text{p}\right)}=1\right)}{{\sum }_{C^{\ast \left(\text{p}\right)}}\text{P}\left(S^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}=C^{\ast \left(\text{p}\right)}\right)\text{P}\left(C^{\ast \left(\text{p}\right)}\right)}\times \frac{{\sum }_{C^{\ast \left(\text{e}\right)}}\text{P}\left(S^{\left(\text{e}\right)}|C^{\left(\text{e}\right)}=C^{\ast \left(\text{e}\right)}\right)\text{P}\left(C^{\ast \left(\text{e}\right)}\right)\mathbb{I}\left(c_i^{\ast \left(\text{e}\right)}=1\right)}{{\sum }_{C^{\ast \left(\text{e}\right)}}\text{P}\left(S^{\left(\text{e}\right)}|C^{\left(\text{e}\right)}=C^{\ast \left(\text{e}\right)}\right)\text{P}\left(C^{\ast \left(\text{e}\right)}\right)}.$$ (Equation 8)

According to the above equation, the probability that the same variant is causal in both the GWAS and eQTL study is independent. This probability is equal to the multiplication of two probabilities: (1) the probability that the variant is causal in the GWAS and (2) the probability that the same variant is causal in the eQTL study. Thus, we compute the CLPP as $\text{P}\left(c_i^{\left(\text{p}\right)}=1,c_i^{\left(\text{e}\right)}=1|S^{\left(\text{p}\right)},S^{\left(\text{e}\right)}\right)=\text{P}\left(c_i^{\left(\text{p}\right)}=1|S^{\left(\text{p}\right)}\right)\times \text{P}\left(c_i^{\left(\text{e}\right)}=1|S^{\left(\text{e}\right)}\right)$, where $\text{P}\left(c_i^{\left(\text{p}\right)}=1|S^{\left(\text{p}\right)}\right)$ and $\text{P}\left(c_i^{\left(\text{e}\right)}=1|S^{\left(\text{e}\right)}\right)$ are computed from the first and second parts of Equation 8, respectively.

Detecting Target Genes and Relevant Tissues

In the previous sections, we described the process of computing the CLPP score for each variant in a locus for a given eGene in a tissue. In this section, we describe a systematic way to detect the target genes and relevant tissues.

We compute the CLPP score for every GWAS significant variant. Thus, for a given GWAS variant, an eGene that has a CLPP score above the colocalization cutoff is considered a target gene. In addition, we consider tissues from which the target genes are obtained as the relevant tissues. Moreover, we can rank the relevant tissues and target genes for a given GWAS significant variant according to their CLPP scores. Thus, we utilize the magnitude of CLPP to rank the tissues and genes on the basis of their importance for a given GWAS risk locus.

Generating Simulated Datasets

Simulating Genotypes

We first simulate genotype data starting from the real genotypes obtained from the European population in the 1000 Genomes data.^{33, 34} In order to simulate the genotypes, we utilize HAPGEN2³⁵ software, which is widely used to generate genotypes. We focus on chromosome 1 and the GWAS variants obtained from the NHGRI catalog.³⁶ We consider 200-kb windows around the lead SNP to generate a locus. Then, we filter out monomorphic SNPs and SNPs with a low minor allele frequency (MAF ≤ 0.01) inside a locus.

Simulating Summary Statistics Directly from LD Structure

We generate an LD matrix for a locus by computing the Pearson’s correlations of each pair of variants from the genotypes. Then, we generate marginal summary statistics for each locus by assuming that the marginal summary statistics follow the MVN distribution utilized in our previous studies.^{18, 26, 27, 28, 37, 38} We measure the strength of a causal variant on the basis of NCPs. We set the NCP of the causal variant to obtain a certain statistical power. The NCPs of the non-causal variants are set to 0. The statistical power is the probability of detecting a causal variant under the assumption that the causal variant is present. The statistical power is computed as follows:

$$\text{power}=1-\frac{1}{\sqrt{2\text{π}}}{\int }_{{\text{Φ}}^{-1}\left(\text{α}/2\right)+\text{λ}}^{{\text{Φ}}^{-1}\left(1-\text{α}/2\right)+\text{λ}}{e}^{-\frac{1}{2}{x}^2}dx=\text{Φ}\left({\text{Φ}}^{-1}\left(\text{α}/2\right)+\text{λ}\right)+1-\text{Φ}\left({\text{Φ}}^{-1}\left(1-\text{α}/2\right)+\text{λ}\right),$$

where α is the significant threshold. Moreover, Φ and Φ⁻¹ denote the cumulative density function (CDF) and the inverse of CDF, respectively, for the standard normal distribution. In our experiment, the NCP is computed for the genome-wide significance level (α = 10⁻⁸). We use a binary search to compute the NCP for a desired statistical power.

Simulating Summary Statistics with a Linear Additive Model

We utilize 100 variants in a locus to generate the simulated phenotypes from the simulated genotypes. We simulate the phenotypes by assuming the following linear additive model:

$$\begin{array}{c}Y=\sum _{i=1}^M{\text{β}}_i{X}_i+\mathit{e}\end{array}\text{,}$$ (Equation 9)

where $\mathit{e}\sim N\left(0,{\sigma }_{\text{e}}^2\right)$. We generate the effect size of the causal variant from a normal distribution with mean 0 and variance ${\text{σ}}_g^2/M_{\text{c}}$, where M_c indicates the number of causal variants in a locus. Furthermore, we set the effect size to 0 for variants that are not causal. Thus, the effect size for each variant is simulated as follows:

$$\{\begin{array}{cc}{\text{β}}_i=0& \text{if}\text{the}{i}^{\text{th}}\text{variant}\text{is}\text{non-causal}\\ {\text{β}}_i\sim N\left(0,{\text{σ}}_g^2/M_{\text{c}}\right)& \text{if}\text{the}{i}^{\text{th}}\text{variant}\text{is}\text{causal}\end{array}.$$

After simulating the phenotype for all the individuals, we utilize linear regression to estimate the effect sizes and the marginal statistics for all M variants in a locus. In our simulations, M is equal to 100.

Results

Overview of eCAVIAR

The goal of our method is to identify target genes and the most relevant tissues for a given GWAS risk locus while accounting for the uncertainty of LD. Target genes are genes with expression levels that affect the phenotype (e.g., disease status) of interest. Our method detects the target gene and the most relevant tissue by utilizing our proposed quantity of CLPP. eCAVIAR estimates the CLPP, which is the probability that the same variant is causal in both a GWAS and eQTL study. eCAVIAR computes the CLPP by utilizing the marginal statistics (e.g., Z score) obtained from GWAS and eQTL analyses, as well as the LD structure of genetic variants in each locus. LD can be computed from genotype data or approximated from existing datasets, such as the 1000 Genomes data^{33, 34} or HapMap.³⁹ We show in the Material and Methods that the marginal statistics of both the GWAS and eQTL study follow a MVN distribution given the causal variants and effect sizes for both studies. We use the MVN distribution to estimate the CLPP. We show that the CLPP is equal to the product of the posterior probability that the variant is causal in the GWAS and the posterior probability that the variant is causal in the eQTL study. Calculating the posterior probability of a causal variant is computationally intractable. Therefore, we assume the presence of at most six causal variants in a locus.

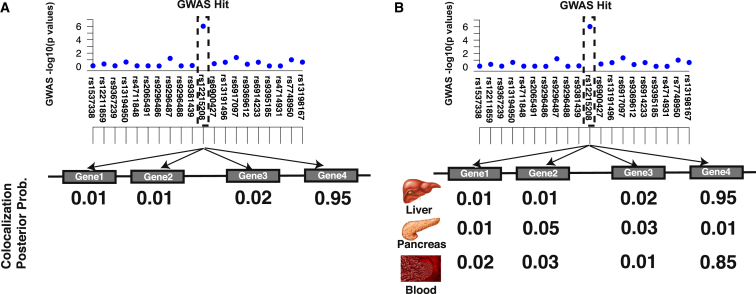
The estimated CLPP for a GWAS risk locus and a gene, which is obtained from eQTL studies, can be used for inferring specific disease mechanisms. First, we identify genes that have expression levels affected by a GWAS variant. These genes are referred to as target genes. Second, we identify in which tissues the eQTL variant has an effect. To identify target genes, we compute the CLPP for all genes in the GWAS risk locus. Genes that have a significantly higher CLPP are selected as target genes (Figure 1A). Similarly, we compute the CLPP for all tissues and identify relevant tissues as those with comparatively high CLPP values (Figure 1B). Figure 1B shows that the GWAS risk locus affects gene 4, and the relevant tissues are liver and blood. However, Figure 1B indicates that the pancreas is not a relevant tissue for this GWAS risk locus. Another application of CLPP is to identify loci where the causal variants between a GWAS and eQTL study are different. We can identify these loci if the CLPP is low for all variants in the loci and if there are statistically significant variants in both the GWAS and eQTL study.

Figure 1.

Overview of Our Method for Detecting the Target Gene and Most Relevant Tissue

We compute the CLPP for all genes and all tissues.

(A) A simple case where we have only one tissue and want to find the target gene. We consider all genes for this GWAS risk locus and observe that gene 4 has the highest CLPP. Thus, the target gene is gene 4.

(B) We have three tissues and utilize the quantity of CLPP. Thus, the target gene is gene 4 again. Moreover, in this example, liver and blood are considered the relevant tissues for this GWAS risk locus, whereas the pancreas is not relevant.

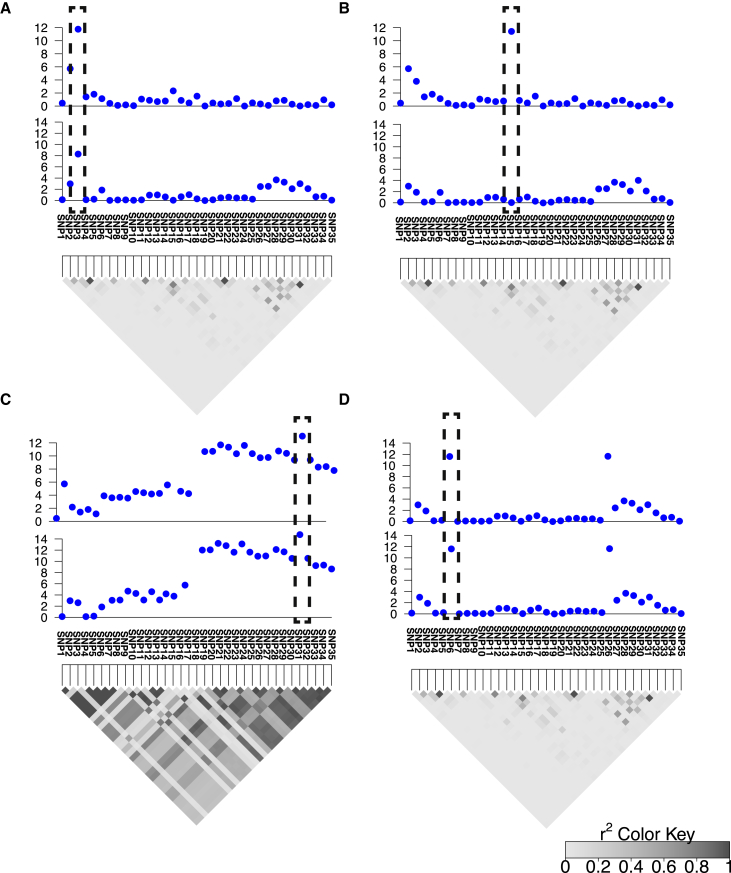
To better motivate the behavior of CLPP, we consider the following four scenarios in Figure 2. In the first scenario, the same variant has effects in both the GWAS and eQTL study. Thus, its CLPP is high (Figure 2A). In the second scenario, we consider that the variant is associated with a phenotype in the GWAS and not associated with gene expression. In this case, the quantity of CLPP is low (Figure 2B). In the third scenario, we consider that the variant is not associated with a phenotype in the GWAS. However, it is associated with expression of a gene. In this case, the CLPP is not computed for this variant. Rather, we compute the CLPP for GWAS risk loci that are considered significant. In the fourth scenario, we have a variant that appears significant in both the GWAS and eQTL study. However, other variants in both studies are also significant because of high LD with the causal variant. The complex LD (see Figure 2C) of these variants results in a low CLPP. Here, we remain uncertain about which variants are actual causal variants. Finally, Figure 2D illustrates an example in which there is more than one causal variant. This demonstrates that assuming the presence of a single causal variant can result in underestimation of CLPP. In this example, we have a locus with 35 variants (SNPs), and we have two causal variants (SNP6 and SNP26) that are not in high LD with each other. If we assume that we have only one causal variant, there are 35 possible causal variants for this locus, and most of the causal variants have a very low likelihood. The likelihoods of selecting either SNP6 or SNP26 as causal are similar, and they are higher than the likelihoods of selecting any other variant as causal. In this example, the estimated posterior probability that SNP6 or SNP26 is causal is 50%. Thus, the estimated CLPP for SNP6 or SNP26 is 25%. However, if we allow more than one causal variant in the locus, all sets of causal variants have very low likelihood values, except the set in which both SNP6 and SNP26 are selected as causal. In this case, the posterior probability that SNP6 or SNP26 is causal is close to 1. In this case, we assume that we have more than one causal variant in this locus given that the CLPP values of SNP6 and SNP26 are close to 1.

Figure 2.

Overview of eCAVIAR

Broadly, eCAVIAR aligns the causal variants in an eQTL study and GWAS. The x axis is the variant (SNP) location, and the y axis is the significance score (−log of p value) for each variant. The gray triangle indicates the LD structure, and every diamond in this triangle indicates the Pearson’s correlation. The darker the diamond, the higher the correlation; and the lighter the diamond, the lower the correlation between the variants.

(A) In the case where the causal variants are aligned, the colocalization posterior probability (CLPP) is high for the variant that is embedded in the dashed black rectangle.

(B) However, in the case where the causal variants are not aligned (the causal variants are not the same variants), the quantity of CLPP is low for the variant that is embedded in the dashed black rectangle.

(C) In this case, the LD is high, which implies that the uncertainty is high as a result of LD, and the CLPP value is low for the variant that is embedded in the dashed black rectangle.

(D) A case where a locus has two independent causal variants. If we consider that we have only one causal variant in a locus, then the CLPP of the causal variants is estimated to be 0.25. However, if we allow more than one causal variant in the locus, eCAVIAR estimates the CLPP to be 1.

eCAVIAR Accurately Computes the CLPP

In this section, we use simulated datasets to assess the accuracy of our method. We simulated summary statistics by utilizing the MVN distribution used in our previous studies.^{18, 26, 27, 28, 38} More details on simulated data are provided in the Material and Methods. In one set of simulations, we fixed the effect size of a genetic variant so that the statistical power for the causal variant was 50%. In another set, we fixed the effect size so that the power was 80%. We considered two cases. The first case included only one causal variant in both studies. The second case included more than one causal variant in these studies. For both scenarios, we simulated two datasets. In the first dataset, we implanted a shared causal variant. We generated 1,000 simulated studies, which we used to compute the true-positive rate (TP). In the second dataset, we implanted a different causal variant in the eQTL study and GWAS. We filtered out cases where the most significant variant was different between the two studies. As in the previous case, we generated 1000 simulated studies.

eCAVIAR Is Accurate in the Case of One Causal Variant

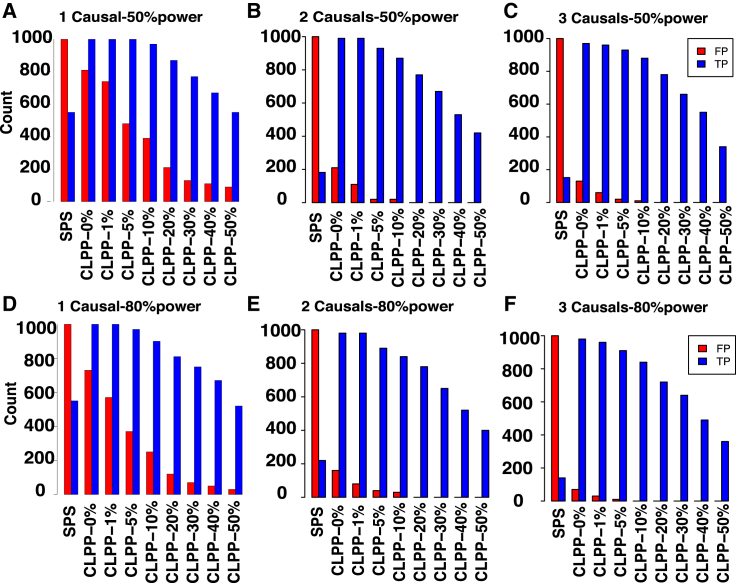
We applied eCAVIAR to the simulated datasets and computed the CLPP for each case. We used different cutoffs to determine whether or not a variant was shared between the two studies. For each cutoff, we computed the false-positive rate (FP) and TP. The baseline method detects the most significant variant in a study as the causal variant. Thus, in the baseline method, we have colocalization when the eQTL study and GWAS share the same most significant variant. We refer to this method as the shared peak SNP (SPS) method. The results are shown in Figures 3A and 3D. Moreover, the same results are plotted in a receiver operating characteristic (ROC) curve (Figure S1). Our method has a higher TP and lower FP than SPS. However, eCAVIAR has a low TP when the cutoff for CLPP is high. Furthermore, eCAVIAR has an extremely low FP. Our results imply that eCAVIAR has high confidence for selecting loci to be colocalized between a GWAS and eQTL study. eCAVIAR is conservative in selecting a locus to be colocalized. Given the high cutoff of CLPP, eCAVIAR can miss some true colocalized loci. However, loci that are selected by eCAVIAR to be colocalized are likely to be predicted correctly.

Figure 3.

eCAVIAR Is Robust to the Presence of AH

We simulated marginal statistics directly from the LD structure for an eQTL study and GWAS. In both studies, we implanted one, two, or three causal variants on which the statistical power was 50% (A–C, respectively) or 80% (D–F, respectively). eCAVIAR had a low TP for a high cutoff and a low FP. This indicates that eCAVIAR has high confidence in detecting a colocalized locus in both the GWAS and eQTL study, even in the presence of AH.

The computed CLPP depends on the complexity of the LD at the locus. We applied eCAVIAR to the simulated datasets and computed the CLPP (Figure S2). Here, the average quantity of CLPP decreased as we increased the Pearson’s correlation (r) between paired variants. This effect increased the complexity of LD between the two variants. Furthermore, the 95% confidence interval for the computed quantity increased as we increased the Pearson’s correlation. This result implies that the computed CLPP can be small for a locus with complex LD, even when a variant is colocalized in both a GWAS and eQTL study.

eCAVIAR Is Robust to the Presence of AH

The presence of more than one causal variant in a locus is a phenomenon referred to as AH. AH can confound the association statistics in a locus, and colocalization for a locus harboring AH is challenging. In order to investigate the effect of AH, we performed the following simulations. We implanted two or three causal variants in both the GWAS and eQTL study, and we then generated the marginal statistics by using the MVN distribution mentioned in the previous section. Next, we computed the TP and FP for eCAVIAR and SPS (see Figure 3). In the case of eCAVIAR, colocalization is considered true when all colocalized variants are detected. However, for SPS, colocalization is considered true when at least one of the colocalized variants is detected. Figures 3A, 3B, and 3C illustrate the results of one, two, and three causal variants, respectively, when the statistical power was 50%. Similarly, Figures 3D, 3E, and 3F illustrate the results of one, two, and three causal variants, respectively, when the statistical power was 80%. Interestingly, SPS had a very low TP when there were two or three causal variants (see Figure 3). This implies that SPS is not accurate when AH is present. Similar to cases with one single casual variant (see Figures 3A and 3D), eCAVIAR had a very low FP when there were two or three causal variants (see Figures 3B, 3C, 3E, and 3F). This implies that eCAVIAR has high confidence in detecting a locus to be colocalized between a GWAS and eQTL study.

We generated simulated datasets where the causal variants were different between the two studies. We computed the CLPP for all variants in a region. Our experiment indicated that eCAVIAR has a high TN and an extremely low FN. eCAVIAR has a high negative predictive value (NPV): NPV = TN/(TN + FN). These results are shown in Figures S3 and S4. Thus, eCAVIAR can detect with high accuracy loci where the causal variants are different between the two studies.

eCAVIAR Is More Accurate Than Existing Methods

Here, we compare the results of eCAVIAR with those of RTC¹³ and COLOC,¹⁴ two common methods for eQTL and GWAS colocalization. The procedure in the previous section can be used to simulate datasets; however, RTC is not designed to work with summary statistics. In order to provide a dataset compatible with RTC, we simulated eQTL and GWAS phenotypes under a linear additive model in which we used simulated genotypes obtained from HAPGEN2.³⁵ More details on the simulated datasets are provided in the Material and Methods.

We compare the accuracy, precision, and recall rate of all three methods. Each method computes a probability that a variant is causal in both a eQTL study and GWAS. In order to determine this probability for our comparison, we need to select two cutoff thresholds. We devised one threshold for detecting variants that are colocalized in both studies and another threshold for detecting variants that are not colocalized. Here, we consider a variant to be causal in both studies if the probability of colocalization is greater than the colocalization cutoff threshold. The second cutoff threshold is used for detecting variants that are not causal in both studies. We consider a variant to be non-causal in both studies if the probability of colocalization is less than the non-colocalization cutoff threshold. In our experiment, we set the non-colocalization cutoff threshold at 0.1% and the colocalization cutoff threshold at a value ranging from 0.1% to 90%.

eCAVIAR outperformed the existing methods when the locus contained one causal variant. We observed that all three methods had a similarly high recall rate (see Figure S5). eCAVIAR had much higher accuracy and precision than RTC (see Figure 4). Next, we considered the performance of the three methods when the locus had AH. We used the same simulation described in this section, but instead we implanted two causal variants instead of one. In this setting, eCAVIAR had higher accuracy and precision than COLOC and RTC. However, RTC had a slightly higher recall rate than eCAVIAR. Moreover, RTC tended to perform better than COLOC in the presence of AH (see Figure 5). This result indicates that eCAVIAR is more accurate than existing methods—even in the presence of AH. However, if a locus contains only one causal variant, COLOC performs better than RTC. In cases with more than one causal variant, RTC performs better. These results were obtained when we set the non-colocalization cutoff threshold to 0.1%. We changed this value to 0.01% to check the robustness of eCAVIAR and observed that even when we used different values of non-colocalization, eCAVIAR outperformed existing methods (see Figures S6 and S7). In all of the above experiments, we implanted the causal variants uniformly in the locus. Next, we simulated causal variants in genomic variants enriched with functional annotations. In order to simulate the genomic enrichment, we used the same process utilized in PAINTOR.⁴⁰ We observed that eCAVIAR outperformed existing methods in these experiments (Figures S8 and S9).

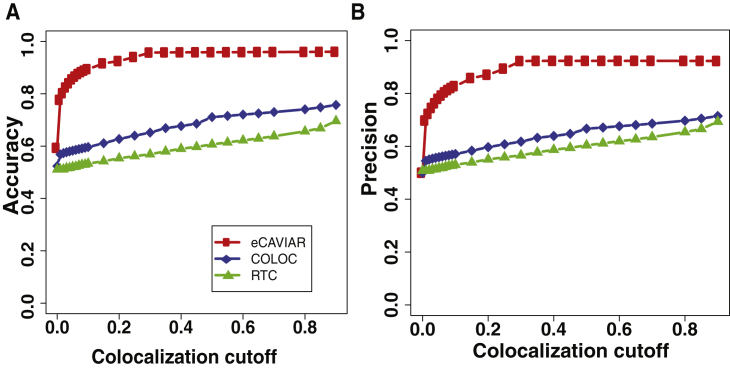
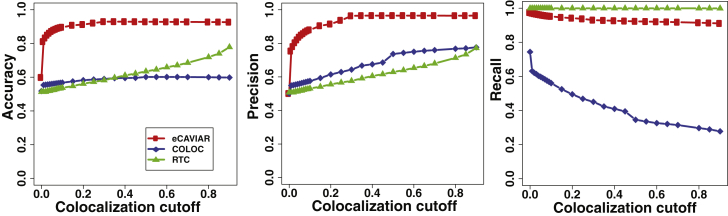
Figure 4.

eCAVIAR Is More Accurate Than Existing Methods for Regions with One Causal Variant

We compare the accuracy and precision of eCAVIAR with those of the two existing methods (RTC and COLOC). The x axis is the colocalization cutoff threshold. In these datasets, we implanted one causal variant, and we utilized simulated genotypes. We simulated the genotypes by using HAPGEN2³⁵ software. We used the European population from 1000 Genomes data³³, ³⁴ as the starting point to simulate the genotypes. The accuracy and precision of all three methods are shown in (A) and (B), respectively. We computed the TP (true-positive rate), TN (true-negative rate), FN (false-negative rate), and FP (false-positive rate) for the set of simulated datasets for which we generated the marginal statistics in a linear model. Accuracy = (TP + TN)/(TP + FP + FN + TN), and precision = TP/(TP + FP). We set the non-colocalization cutoff threshold to 0.001. We observed that eCAVIAR and COLOC had higher accuracy and precision than RTC.

Figure 5.

eCAVIAR Is More Accurate Than Existing Methods in the Presence of AH

To generate the datasets, we used a process similar to that shown in Figure 4. However, in this case, we implanted two causal variants. We simulated the genotypes by using HAPGEN2³⁵ software. We used the European population from 1000 Genomes data³³, ³⁴ as the starting point to simulate the genotypes. We compared the accuracy, precision, and recall rate. In these results, eCAVIAR tended to have higher accuracy and precision than RTC and COLOC. However, RTC had a slightly higher recall rate.

Thus, eCAVIAR performs better than COLOC and RTC, the pioneering methods for eQTL and GWAS colocalization. COLOC and RTC require different input data to perform the colocalization. COLOC requires only the marginal statistics from a GWAS and eQTL study. Unlike eCAVIAR, COLOC and RTC do not require the LD structure of genetic variants in a locus. However, RTC requires individual-level data (genotypes and phenotypes) and is not applicable to datasets for which we have access to only the summary statistics.

Effect of eQTL Sample Size on CLPP

We know that the statistical power to detect a true casual variant increases as we increase the number of samples in a GWAS. Because most GWAS sample sizes are in the order of thousands of samples, we aimed to investigate the effect of eQTL sample size on colocalization.

We simulated datasets in which we set the number of GWAS samples to 5,000. Then, we varied the number of eQTL samples from 500 to 3,500. We simulated the effect size for the causal variant in the eQTL study such that it accounted for 1%, 4%, and 10% of heritability. We computed the CLPP for different cases; the distribution of CLPP is shown in a boxplot in Figure S10. The red horizontal line indicates the 1% colocalization cutoff used for eCAVIAR. We observed that when the causal variant accounted for 1% of heritability, we required at least 2,000 eQTL samples. Conversely, when the causal variant accounted for a larger portion of heritability, eCAVIAR required fewer samples.

Using eCAVIAR to Integrate Available eQTLs for 45 Tissues and MAGIC Datasets

We utilized the MAGIC dataset and GTEx dataset¹⁹ to detect the target gene and most relevant tissue for each GWAS risk locus. MAGIC datasets consist of eight phenotypes.²¹ These phenotypes are as follows: fasting glucose (FG), fasting insulin, fasting proinsulin (FP), HOMA-B (β cell function), HOMA-IR (insulin resistance), Hb1Ac (hemoglobin A1c test for diabetes), 2 hr glucose, and 2 hr insulin after an oral glucose-tolerance test. In our analysis, we used FG and FP phenotypes containing the most significant loci. FG phenotypes had 15 variants, and FP phenotypes had ten variants reported to be significantly associated with these phenotypes by previous studies.^{21, 22} We considered 44 tissues included in the GTEx Portal (release v.6, dbGaP: phs000424.v6.p1).¹⁹ In addition, we used previously published data on human pancreatic islets,²⁵ a key tissue in glucose metabolism that is not captured in the GTEx data. Table S1 lists tissues and the number of individuals for each tissue.

We wanted to detect the most relevant tissue and a target gene for each of the previously reported significant GWAS variants. eCAVIAR utilizes the marginal statistics of all variants in a locus obtained from a GWAS and eQTL study. We obtained each locus by considering 50 variants upstream and downstream of the reported variant. Then, we considered genes in which at least one variant is significantly associated with expression of that gene. Thus, for one GWAS variant, multiple genes in one tissue could satisfy these requirements, and we considered these pairs of variants and genes as potential colocalization loci. Tables S2 and S3 list the potential colocalization loci for FG and FP phenotypes, respectively. For any given variant, we used the CLPP to detect the most relevant tissue and a target gene. We selected the target gene and most relevant tissue as the gene and tissue, respectively, demonstrating the highest CLPP value.

Tables 1 and 2 indicate the results of eCAVIAR for FG and FP, respectively. These results show genetic variants that are causal in both the eQTL study and GWAS. We considered only variants reported to be significant with FG²¹ and FP²² phenotypes. We used a cutoff threshold of 0.01 (1%) to conclude that two causal variants are shared.

Table 1.

eCAVIAR Joint Analysis of FG and the GTEx Dataset

Chr	Position	rsID	Relevant Tissuea	Target Gene (MIM)
3	123,082,398	rs11717195	islet (N = 118)	ADCY5 (600293)
7	15,064,309	rs2191349	islet (N = 118)	DGKB (604070)
7	44,235,668	rs4607517	colon sigmoid (N = 124)	GCK (138079)
			thyroid (N = 278)
11	45,873,091	rs11605924	whole blood(N = 338)	MAPK8IP1 (604641)
11	47,336,320	rs7944584	nerve tibial (N = 256)	CELF1 (601074)
			artery tibial (N = 285)	MADD (603584)
			islet (N = 118)
			pituitary (N = 87)
			artery tibial (N = 285)	MDK (162096)
			nerve tibial (N = 256)	NR1H3 (602423)
			nerve tibial (N = 256)	RAPSN (601592)

The following abbreviation is used: Chr, chromosome.

^aFor each tissue, N indicates the number of individuals for whom we had access to summary statistics from GTEx¹⁹ and van de Bunt et al.²⁵

Table 2.

eCAVIAR Joint Analysis of FP and the GTEx Dataset

Chr	Position	rsID	Relevant Tissuea	Target Gene (MIM)
11	47,293,799	rs10501320	pituitary (N = 87)	ARHGAP1 (602732)
			esophagus muscularis (N = 218)	C1QTNF4 (614911)
			artery tibial (N = 285)	MADD (603584)
			esophagus mucosa (N = 241)
			islet (N = 118)
			artery tibial (N = 285)	MDK (162096)
11	72,432,985	rs11603334	skin of sun-exposed lower leg (N = 302)	ARAP1 (606646)
			pituitary (N = 87)	PDE2A (602658)
			islet (N = 118)	STARD10
15	71,109,147	rs1549318	adipose visceral omentum (N = 185)	LARP6 (611300)
			cultured primary fibroblasts (N = 272)
			ovary (N = 85)

The following abbreviation is used: Chr, chromosome.

^aFor each tissue, N indicates the number of individuals for whom we had access to summary statistics from GTEx¹⁹ and van de Bunt et al.²⁵

Many of the significant variants had CLPP values in a range where it is difficult to conclude whether the causal variants are shared. However, we detected a large number of loci for which the GWAS causal variants were clearly distinct from the causal variants in the eQTL data (Table 3). This included several genes that could be excluded in all tissues tested (e.g., SEC22A [MIM: 612442] at the rs11717195 FG locus, where there was non-colocalization).

Table 3.

Loci where the Causal Variants between eQTL Studies and GWASs Are Different

Phenotype	Chr	Position	rsID	GWAS p Value	eQTL p Value	No. of Genes	No. of Tissues
FG	2	27,741,237	rs780094	2.49 × 10−12	2.95 × 10−55	17	30
	2	169,763,148	rs560887	4.61 × 10−75	1.36 × 10−14	5	20
	3	123,065,778	rs11708067	8.72 × 10−9	4.28 × 10−42	5	34
	9	4,289,050	rs7034200	0.0001204	9.95 × 10−12	8	7
	10	113,042,093	rs10885122	8.41 × 10−11	7.73 × 10−11	2	3
	11	61,571,478	rs174550	1.48 × 10−8	1.03 × 10−125	24	29
	11	92,708,710	rs10830963	1.26 × 10−68	7.49 × 10−6	7	6
FP	1	99,177,253	rs9727115	5.285 × 10−6	7.04 × 10−16	3	12
	10	114,758,349	rs7903146	3.48 × 10−18	7.92 × 10−33	7	26
	15	62,383,155	rs4502156	3.80 × 10−11	8.48 × 10−14	7	15
	17	2,262,703	rs4790333	2.15 × 10−8	5.39 × 10−75	21	33

The numbers of genes and tissues indicate the genes and tissues, respectively, that we applied to eCAVIAR for a GWAS risk variant. The complete lists of genes and tissues are provided in Tables S2 (FG) and S3 (FP). eCAVIAR utilizes the marginal statistics of all variants in a locus obtained from a GWAS and eQTL study. We obtain each locus by considering 50 variants upstream and downstream of the reported variant. Then, we consider genes where at least one of the variants in the locus is significantly associated with the expression of that gene. Thus, for one GWAS variant, multiple genes in one tissue can satisfy our condition. The eQTL p value indicates the most significant variant in eQTLs among all genes and all tissues. Abbreviations are as follows: Chr, chromosome; FG, fasting glucose; and FP, fasting proinsulin.

More interesting examples could be found among genes that colocalized in one tissue yet could be excluded in many others. For example, ADCY5 (MIM: 600293) was also at the rs11717195 FG locus. In pancreatic islet data, the GWAS variant itself colocalized with ADCY5 eQTLs, whereas eQTLs for the same gene did not overlap the GWAS association signal in several GTEx tissues. This suggests that the phenotype influences the disease mechanism through a tissue-specific regulatory element that is active in islets yet inactive in other tissues.

For a majority of loci in which we identified a single causal variant in both the GWAS and eQTL study, our results implicate more than one target gene across the 45 tissues. eCAVIAR detected that three of five colocalized variants in the FG phenotype and all three variants in the FP phenotype had multiple target genes. Other eQTL studies support causal roles for MADD (MIM: 603584) at rs7944584 (FG) and rs10501320 (FP) in human pancreatic islets of Langerhans²⁵ and for LARP6 (MIM: 611300) at rs1549318 (FP) in adipose tissue.²² Assessing the potential candidacy of these different implicated genes will require additional sources of information, such as chromosome conformation capture (3C) experiments,⁴¹ to demonstrate chromatin interactions between causal variants and gene promotors and/or in vitro function validation in relevant model systems. Even so, the current analysis points to many loci where no colocalizing variant can be identified. The main reason for this is probably found in the limited power of eCAVIAR at the current sample sizes for the majority of tissues, especially for those as pertinent to the phenotype as human islets (see Figure S10). Overcoming this hurdle and uncovering further mechanistic insights will require additional collection of samples.

Discussion

Integrating GWASs and eQTL studies provides insights into the underlying mechanism for genetic variants detected in GWASs. In this paper, we propose a quantity that can measure CLPP, the probability that the same variant is causal in both a GWAS and eQTL study, while accounting for the LD. Utilizing CLPP, we can identify target genes and relevant tissues. It is worth mentioning that we can use epigenomic data (e.g., NIH Roadmap Epigenomics⁴²) to detect relevant tissues as an orthogonal analysis instead of using eCAVIAR. Moreover, eCAVIAR can detect loci where the causal variants are different between the two studies with high confidence. In our analysis, GWAS risk loci and eQTLs were different in most cases.

Because most GWAS loci are discovered to lie outside of coding regions, it is implicitly assumed that these implicated loci affect gene regulation. However, our results show a lower than expected number of variants colocalized between the GWAS and eQTL study. This points to a more complicated relationship between gene regulation and disease. It is likely that future studies will shed some light to explain this observation.

One conjecture is that the GWAS loci in fact do affect expression but are secondary signals in comparison to the stronger associations found in current eQTL studies. Because eQTL studies are including an increasing number of individuals, we will be able to prove or disprove this conjecture. Furthermore, the heterogeneity of tissues could render it hard to detect eQTLs specific to a disease-relevant cell type that composes only a fraction of the tissue. A second possibility is that GWAS variants affect other aspects of gene regulation, such as splicing or regulation at a level other than transcription regulation. Several studies have shown that alternative splicing could explain the causal mechanism of complex disease associations (e.g., a multiple-sclerosis-associated variant that leads to exon skipping in SP140 [MIM: 608602]⁴³). Methods that identify variants associated with differences in relative expression of alternative transcript isoforms or exon-junction abundances are being applied to the latest version of GTEx data.^{44, 45} As we obtain more functional genomic information and are able to measure quantities such as protein abundance, we will be able to systematically catalog variants that affect regulation at levels other than transcription. A third possibility is that GWAS loci are eQTL loci only in certain conditions, such as development, where expression levels are not typically measured. Regardless, our study demonstrates strong evidence in support of the idea that most GWAS loci are not strong eQTL loci and that the mechanism by which GWAS loci affect gene regulation is more complicated than we expected.

Broadly, we have identified an analogy between colocalization and fine-mapping methods. Fine-mapping methods can be categorized into three main classes. One class relies only on the computed marginal statistics that are obtained from a GWAS or eQTL study. In this class of methods, the probability that a variant is causal depends on a variant’s rank, which is obtained from the marginal statistics. Recently, Maller et. al⁴⁶ proposed a fine-mapping method that utilizes the Bayes factor. This method provides results similar to those of approaches that rank variants solely on the basis of their marginal statistics. The Maller et. al⁴⁶ method for fine-mapping is similar in nature to COLOC,¹⁴ which is used for colocalization. The second class of methods is based on a conditional model that re-computes the marginal statistics of all variants by conditioning on variants selected as causal. The conditional method for fine-mapping and RTC¹³ have some similarities in nature. The third class of methods includes CAVIAR,^{18, 27} CAVIARBF,⁴⁷ and FINEMAP,²⁹ which assume a presence of more than one causal variant in a region. These probabilistic-based methods use the MVN distribution and detect a set of variants that can capture all causal variants with a predefined probability. eCAVIAR is analogous in process to CAVIAR, CAVIARBF, and FINEMAP. However, eCAVIAR and CAVIAR-like methods try to solve different problems. CAVIAR-like methods (CAVIARBF and FINEMAP) are designed to perform fine-mapping. CAVIARBF is based on the CAVIAR statistical model that utilizes the Bayes factor to detect the causal set. FINEMAP is based on the CAVIAR statistical model that utilizes sampling techniques to speed up the computational process of detecting the causal set.

eCAVIAR is a probabilistic method that integrates GWAS and eQTL signals to detect biological mechanisms. eCAVIAR has several advantages over prior approaches. First, it can account for multiple causal variants in any given locus. Second, it leverages summary statistics without accessing the raw individual data. In addition, eCAVIAR can provide confidence levels for the colocalization of a GWAS risk variant. Utilizing the confidence level, we can categorize a variant into three categories: colocalizing variants, non-colocalizing variants, and variants whose ambiguity prevents detection of their colocalization status for the current data. eCAVIAR can be extended to utilize functional annotations to improve our results. The functional annotation can be used as a prior for a given causal status. Alternatively, we can adopt more sophisticated techniques similar to PAINTOR⁴⁰ and RiVIERA-beta,⁴⁸ which incorporate functional annotations to improve fine-mapping results. High-throughput technologies have made it possible to obtain multi-tissue eQTL studies. Leveraging multi-tissue eQTL studies such as GTEx and methods such as eCAVIAR will potentially advance discovery of new biological mechanisms for GWAS risk loci.

Published: November 17, 2016

Appendix A: CAVIAR and eCAVIAR General Models where the GWAS and eQTL Study Have Different Numbers of Individuals

Standard GWAS Association Test

We assume that there are N^(p) individuals in the GWAS for the phenotype of interest, and we collect the phenotypic values of a quantitative trait for all individuals. Moreover, we collect the genotypes of all individuals for M variants. Let Y^(p) be an N^(p) × 1 vector of phenotypic values obtained from a GWAS. Let G^(p) be an N^(p) × M matrix of genotypes where $G_i^{\left(\text{p}\right)}$ is an N^(p) × 1 vector of the minor allele count for the i^th variant. We use $X_i^{\left(\text{p}\right)}$ to indicate the standardized vector of the minor allele count for the i^th variant, $G_i^{\left(\text{p}\right)}$, where $x_{ji}^{\left(\text{p}\right)}$ is the standardized genotype of the i^th variant for the j^th individual. We assume that both phenotypes and genotypes are standardized. We standardize a vector to make the mean and variance equal to 0 and 1, respectively. Thus, we have $1^T{X}_i^{\left(\text{p}\right)}=0$ and $X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}=N^{\left(\text{p}\right)}$, which we can show as follows:

$$E\left(X_i^{\left(\text{p}\right)}\right)=0\to \frac{{\sum }_{j=1}^N{x}_{ji}^{\left(\text{p}\right)}}{N}=0\to \frac{1}{N}{1}^T{X}_i^{\left(\text{p}\right)}=0\to 1^T{X}_i^{\left(\text{p}\right)}=0,$$

$$\text{Var}\left(X_i^{\left(\text{p}\right)}\right)=1\to E\left(X_i^{\left(\text{p}\right)2}\right)-E{\left(X_i^{\left(\text{p}\right)}\right)}^2=1\to E\left(X_i^{\left(\text{p}\right)2}\right)=1\to \frac{1}{N}{X}_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}=1\to X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}=N^{\left(\text{p}\right)}.$$ (Equation A1)

We assume the “additive” Fisher’s polygenic model. In this model, each variant has a small effect toward the phenotype, where these effects are linear and additive. Thus, we have

$$Y^{\left(\text{p}\right)}={\text{μ}}^{\left(\text{p}\right)}1+\sum _{i=1}^M{\text{β}}_i^{\left(\text{p}\right)}{X}_i^{\left(\text{p}\right)}+{\mathit{e}}^{\left(\text{p}\right)},$$ (Equation A2)

where μ^(p) is the population mean for the phenotype, ${\text{β}}_i^{\left(\text{p}\right)}$ is the effect of the i^th variant toward the phenotype, and ${\mathit{e}}^{\left(\text{p}\right)}$ is the environmental and measurement noise that we assume follows a normal distribution, ${\mathit{e}}^{\left(\text{p}\right)}\sim \mathcal{N}\left(0,{\text{σ}}_e^{\left(\text{p}\right)2}\mathit{I}\right)$, where ${\text{σ}}_e^{\left(\text{p}\right)2}$ is a covariance scalar. As mentioned in the Material and Methods, we test the significance of each variant one at a time. Moreover, we assume that the c^th variant is causal. Thus, we have the following model:

$$Y^{\left(\text{p}\right)}={\text{μ}}^{\left(\text{p}\right)}1+{\text{β}}_c^{\left(\text{p}\right)}{X}_c^{\left(\text{p}\right)}+{\mathit{e}}^{\left(\text{p}\right)}.$$ (Equation A3)

To ease our notations, we utilize the fact that both phenotypes and genotypes are standardized. Thus, the phenotypes follow a normal distribution with mean ${\text{β}}_c^{\left(\text{p}\right)}{X}_c^{\left(\text{p}\right)}$ and variance ${\text{σ}}_e^{\left(\text{p}\right)2}\mathit{I}$, $Y^{\left(\text{p}\right)}\sim \mathcal{N}\left({\text{β}}_c^{\left(\text{p}\right)}{X}_c^{\left(\text{p}\right)},{\text{σ}}_e^{\left(\text{p}\right)2}\mathit{I}\right)$. To estimate the effect size, we utilize the maximum likelihood. The likelihood is computed as follows:

$$\mathit{L}\left(Y^{\left(\text{p}\right)}|{\text{μ}}^{\left(\text{p}\right)},{\text{β}}_c,{\text{σ}}_e^{\left(\text{p}\right)}\right)=\frac{1}{\sqrt{2\text{π}}{\text{σ}}_e^{\left(\text{p}\right)}}\text{exp}\left(-\frac{1}{2{\text{σ}}_e^{\left(\text{p}\right)2}}{\left(Y^{\left(\text{p}\right)}-{\text{μ}}^{\left(\text{p}\right)}-{\text{β}}_c^{\left(\text{p}\right)}{X}_c^{\left(\text{p}\right)}\right)}^T\left(Y^{\left(\text{p}\right)}-{\text{μ}}^{\left(\text{p}\right)}-{\text{β}}_c^{\left(\text{p}\right)}{X}_c^{\left(\text{p}\right)}\right)\right).$$ (Equation A4)

We compute the optimal effect size that maximizes the above likelihood by computing the likelihood derivative and setting it to 0. As a result, the optimal effect size is computed as follows:

$$\frac{\partial \mathit{L}\left(Y^{\left(\text{p}\right)}|{\text{μ}}^{\left(\text{p}\right)},{\text{β}}_c,{\text{σ}}_e^{\left(\text{p}\right)}\right)}{\partial {\text{β}}_c}=0\to \widehat{{\text{β}}_c}={\left(X_c^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}\right)}^{-1}{X}_c^{\left(\text{p}\right)}\left(Y^{\left(\text{p}\right)}-{\text{μ}}^{\left(\text{p}\right)}\right)\to {\widehat{\text{β}}}_c\sim \mathcal{N}\left({\text{β}}_c,\frac{{\text{σ}}_e^{\left(\text{p}\right)2}}{X_c^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}}\right).$$ (Equation A5)

We calculate the marginal statistics by dividing the estimated effect size by the SD of the estimated effect size. Thus, we have

$$S_c=\frac{{\widehat{\text{β}}}_c}{{\widehat{\text{σ}}}_e^{\left(\text{p}\right)}}\sqrt{X_c^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}}\sim \mathcal{N}\left(\frac{{\text{β}}_c}{{\text{σ}}_e^{\left(\text{p}\right)}}\sqrt{N^{\left(\text{p}\right)}},1\right),$$ (Equation A6)

where ${\text{λ}}_c=\left({\text{β}}_c/{\text{σ}}_e^{\left(\text{p}\right)}\right)\sqrt{N^{\left(\text{p}\right)}}$ is the true effect size of the c^th variant, which is the causal variant. The normal distribution for the marginal statistics holds under asymptotic assumptions.

Indirect GWAS Association Test

We assume that there are two variants where the c^th variant is causal and the i^th variant is not causal. To estimate the effect size, we use the same testing model as in the previous section. Thus, we have

$$Y^{\left(\text{p}\right)}={\text{μ}}^{\left(\text{p}\right)}1+{\text{β}}_i^{\left(\text{p}\right)}{X}_i^{\left(\text{p}\right)}+{\mathit{e}}^{\left(\text{p}\right)},$$ (Equation A7)

where we maximize the likelihood function to obtain the optimal effect sizes. The optimal effect size for the i^th variant is as follows:

$$\widehat{{\text{β}}_i}={\left(X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}\right)}^{-1}{X}_i^{\left(\text{p}\right)}\left(Y^{\left(\text{p}\right)}-{\text{μ}}^{\left(\text{p}\right)}\right)\to {\widehat{\text{β}}}_i\sim \mathcal{N}\left({\text{β}}_i,\frac{{\text{σ}}_e^{\left(\text{p}\right)2}}{X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}}\right).$$ (Equation A8)

We compute the marginal statistics similarly to in the previous section:

$$S_i=\frac{{\widehat{\text{β}}}_i}{{\widehat{\text{σ}}}_e^{\left(\text{p}\right)}}\sqrt{X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}}\sim \mathcal{N}\left(\frac{{\text{β}}_i}{{\text{σ}}_e^{\left(\text{p}\right)}}\sqrt{N^{\left(\text{p}\right)}},1\right).$$ (Equation A9)

The variance of the marginal statistics is 1. Thus, the correlation and covariance of marginal statistics are equal. We compute the covariance of the marginal statistics between the causal variant and the non-causal variant. We compute this correlation as follows:

$$\text{Cov}\left(S_c,S_i\right)=\text{Cov}\left(\frac{{\widehat{\text{β}}}_c}{{\widehat{\text{σ}}}_{\text{e}}^{\left(\text{p}\right)}}\sqrt{X_c^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}},\frac{{\widehat{\text{β}}}_i}{{\widehat{\text{σ}}}_{\text{e}}^{\left(\text{p}\right)}}\sqrt{X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}}\right)$$

$$=\text{Cov}\left(\frac{X_c^{\left(\text{p}\right)T}{Y}^{\left(\text{p}\right)}}{{\widehat{\text{σ}}}_{\text{e}}^{\left(\text{p}\right)}}\frac{1}{\sqrt{X_c^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}}},\frac{X_i^{\left(\text{p}\right)T}{Y}^{\left(\text{p}\right)}}{{\widehat{\text{σ}}}_{\text{e}}^{\left(\text{p}\right)}}\frac{1}{\sqrt{X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}}}\right)$$

$$=\frac{1}{{\widehat{\text{σ}}}_{\text{e}}^{\left(\text{p}\right)2}}\frac{X_i^{\left(\text{p}\right)}}{\sqrt{X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}}}\text{Cov}\left(Y^{\left(\text{p}\right)},Y^{\left(\text{p}\right)}\right)\frac{X_c^{\left(\text{p}\right)}}{\sqrt{X_c^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}}}.$$ (Equation A10)

Using the Slutsky’s theorem and the fact that the number of individuals in a study is large enough, we assume that ${\widehat{\text{σ}}}_{\text{e}}^{\left(\text{p}\right)2}$ approaches Var(Y^(p)). Thus, asymptotically we have

$$\text{Cov}\left(S_c,S_i\right)=\frac{X_i^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}}{\sqrt{X_i^{\left(\text{p}\right)T}{X}_i^{\left(\text{p}\right)}}\sqrt{X_c^{\left(\text{p}\right)T}{X}_c^{\left(\text{p}\right)}}}=r_{ci}.$$ (Equation A11)

This indicates that the correlation between the marginal statistics of two variants is equal to their genotype correlation. This result is known from our previous studies.¹⁸, ²⁷, ⁴⁹

Standard eQTL Association Test

We assume that in the eQTL study, we collect the expression of multiple genes for N^(e) individuals. Let superscript (p) and (e) indicate variables related to the GWAS and eQTL study, respectively. Let Y^(e) indicate the expression level of all N^(e) individuals for one gene. We consider one gene to ease the presentation of the method. As illustrated in the previous GWAS section, we use the “additive” Fisher’s polygenic model:

$$Y^{\left(\text{e}\right)}={\text{μ}}^{\left(\text{e}\right)}1+\sum _{i=1}^M{\text{β}}_i^{\left(\text{e}\right)}{X}_i^{\left(\text{e}\right)}+{\mathit{e}}^{\left(\text{e}\right)},$$ (Equation A12)

where μ^(e) is the population mean for the expression of the gene of interest, ${\text{β}}_i^{\left(\text{e}\right)}$ is the effect of the i^th variant toward the gene expression, and ${\mathit{e}}^{\left(\text{e}\right)}$ is the environmental and measurement noise that follows a normal distribution, ${\mathit{e}}^{\left(\text{e}\right)}\sim \mathcal{N}\left(0,{\text{σ}}_{\text{e}}^{\left(\text{e}\right)2}\mathit{I}\right)$, where ${\text{σ}}_e^{\left(e\right)2}$ is a covariance scalar. As mentioned in the Material and Methods, we test the significant of each variant one at a time. Similarly, we assume that the c^th variant is causal. Thus, we have the following model:

$$Y^{\left(\text{e}\right)}={\text{μ}}^{\left(\text{e}\right)}1+{\text{β}}_c^{\left(\text{e}\right)}{X}_c^{\left(\text{e}\right)}+{\mathit{e}}^{\left(\text{e}\right)}.$$ (Equation A13)

The optimal estimated effect size is similar between the eQTL study and GWAS.

CAVIAR Model for GWASs and eQTL Studies

We know that the covariance between the estimated effect size of two variants is equal to their genotype correlation. Furthermore, the mean of the marginal statistics of the non-causal variants is equal to the mean of the marginal statistics of the causal variants scaled by the genotype correlation. Thus, we have

$$\left(S^{\left(\text{p}\right)}|{\text{Λ}}^{\left(\text{p}\right)}\right)\sim \mathcal{N}\left({\text{Λ}}^{\left(\text{p}\right)}{\text{Σ}}^{\left(\text{p}\right)},{\text{Σ}}^{\left(\text{p}\right)}\right),$$ (Equation A14)

where the ${\text{Σ}}^{\left(\text{p}\right)}$ matrix is the pairwise genotype correlations obtained from a GWAS. For the eQTL study, we obtain a similar equation for the joint marginal statistics:

$$\left(S^{\left(\text{e}\right)}|{\text{Λ}}^{\left(\text{e}\right)}\right)\sim \mathcal{N}\left({\text{Λ}}^{\left(\text{e}\right)}{\text{Σ}}^{\left(\text{e}\right)}{\text{,Σ}}^{\left(\text{e}\right)}\right),$$ (Equation A15)

where the ${\text{Σ}}^{\left(\text{e}\right)}$ matrix is the pairwise genotype correlations obtained from the eQTL study. We consider ${\text{Λ}}^{\left(\text{p}\right)}$ and ${\text{Λ}}^{\left(\text{e}\right)}$ to be the true effect-size vectors for the GWAS and eQTL study, respectively. True effect sizes are non-zero for causal variants and zero for the non-causal variants. Moreover, we consider ${\text{Λ}}^{\left(\text{p}\right)}{\text{Σ}}^{\left(\text{p}\right)}$ and ${\text{Λ}}^{\left(\text{e}\right)}{\text{Σ}}^{\left(\text{e}\right)}$ to be the LD-induced effect sizes for the GWAS and eQTL study, respectively.

We introduce a MVN prior over the true effect-size vectors. The true effect sizes for variants are independent and, for causal variants, non-zero. Thus, we have the following prior:

$$\left({\text{Λ}}^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}\right)\sim \mathcal{N}\left(0,{\text{σ}}^{\left(\text{p}\right)2}{\text{Σ}}_c^{\left(\text{p}\right)}\right),$$

$$\left({\text{Λ}}^{\left(\text{e}\right)}|C^{\left(\text{e}\right)}\right)\sim \mathcal{N}\left(0,{\text{σ}}^{\left(\text{e}\right)2}{\text{Σ}}_c^{\left(\text{e}\right)}\right),$$ (Equation A16)

where ${\text{Σ}}_c^{\left(p\right)}$ is a diagonal matrix and ${\text{σ}}^{\left(p\right)2}$ is set to 5.2,¹⁸, ²⁷ which indicates the variance of our prior over the GWAS effect sizes. The diagonal elements are set to 1 or 0. For variants that are selected as causal, we set the corresponding diagonal elements to 1; otherwise, we set them to 0.

Utilizing the conjugate prior, we can combine Equations A14 and A16 to obtain the joint distribution of the marginal statistics given the vector of causal status. These distributions are

$$\left(S^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}\right)\sim \mathcal{N}\left(0,{\text{Σ}}^{\left(\text{p}\right)}+{\text{σ}}^{\left(\text{p}\right)2}{\text{Σ}}^{\left(\text{p}\right)}{\text{Σ}}_c^{\left(\text{p}\right)}{\text{Σ}}^{\left(\text{p}\right)}\right),$$

$$\left(S^{\left(\text{e}\right)}|C^{\left(\text{e}\right)}\right)\sim \mathcal{N}\left(0,{\text{Σ}}^{\left(\text{e}\right)}+{\text{σ}}^{\left(\text{e}\right)2}{\text{Σ}}^{\left(\text{e}\right)}{\text{Σ}}_c^{\left(\text{e}\right)}{\text{Σ}}^{\left(\text{e}\right)}\right).$$ (Equation A17)

To show the correctness of the above equations, we utilize the law of total expectation and law of total variance. Given two random variables A and B, the law of total expectation is as follows:

$$\text{E}\left[A\right]={\text{E}}_B\left[{\text{E}}_{A|B}\left[A|B\right]\right].$$ (Equation A18)

If we let $A=\left(S^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}\right)$ and $B={\text{Λ}}^{\left(\text{p}\right)}$, we can compute the mean of the marginal statistics given the causal status as follows:

$$\text{E}\left[S^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}\right]={\text{E}}_{{\text{Λ}}^{\left(\text{p}\right)}}\left[E_{\left(S^{\left(\text{p}\right)}|{\text{Λ}}^{\left(\text{p}\right)}\right)}\left(S^{\left(\text{p}\right)}|{\text{Λ}}^{\left(\text{p}\right)}\right)\right]={\text{E}}_{{\text{Λ}}^{\left(\text{p}\right)}}\left[{\text{Σ}}^{\left(\text{p}\right)}{\text{Λ}}^{\left(\text{p}\right)}\right]={\text{Σ}}^{\left(\text{p}\right)}{\text{E}}_{{\text{Λ}}^{\left(\text{p}\right)}}\left[{\text{Λ}}^{\left(\text{p}\right)}\right]=0.$$ (Equation A19)

To compute the variance of the joint distribution of the marginal statistics given the causal status, we use the law of total variance:

$$\text{Var}\left[A\right]={\text{E}}_B\left[\text{Var}\left[A|B\right]\right]+{\text{Var}}_B\left[{\text{E}}_B\left[A|B\right]\right].$$ (Equation A20)

Thus, we compute the variance of joint distribution as follows:

$$\begin{array}{l}\begin{array}{c}\text{Var}\left[S^{\left(\text{p}\right)}|C^{\left(\text{p}\right)}\right]={\text{E}}_{{\text{Λ}}^{\left(\text{p}\right)}}\left[{\text{Var}}_{S^{\left(\text{p}\right)}|{\text{Λ}}^{\left(\text{p}\right)}}\right]+{\text{Var}}_{{\text{Λ}}^{\left(\text{p}\right)}}\left[\text{E}\left[S^{\left(\text{p}\right)}|{\text{Λ}}^{\left(\text{p}\right)}\right]\right]\\ ={\text{E}}_{{\text{Λ}}^{\left(\text{p}\right)}}\left[{\text{Σ}}^{\left(\text{p}\right)}\right]+{\text{Var}}_{{\text{Λ}}^{\left(\text{p}\right)}}\left[{\text{Σ}}^{\left(\text{p}\right)}{\text{Λ}}^{\left(\text{p}\right)}\right]\\ ={\text{Σ}}^{\left(\text{p}\right)}+{\text{σ}}^{\left(\text{p}\right)2}{\text{Σ}}^{\left(\text{p}\right)}{\text{Σ}}_c^{\left(\text{p}\right)}{\text{Σ}}^{\left(\text{p}\right)}.\end{array}\\ \end{array}$$ (Equation A21)

Web Resources

• eCAVIAR, http://genetics.cs.ucla.edu/caviar/

• GTEx Portal (release v.6), http://www.gtexportal.org