Zipf’s Law and Criticality in Multivariate Data without Fine-Tuning

Abstract

The joint probability distribution of states of many degrees of freedom in biological systems, such as firing patterns in neural networks or antibody sequence compositions, often follows Zipf’s law, where a power law is observed on a rank-frequency plot. This behavior has been shown to imply that these systems reside near a unique critical point where the extensive parts of the entropy and energy are exactly equal. Here, we show analytically, and via numerical simulations, that Zipf-like probability distributions arise naturally if there is a fluctuating unobserved variable (or variables) that affects the system, such as a common input stimulus that causes individual neurons to fire at time-varying rates. In statistics and machine learning, these are called latent-variable or mixture models. We show that Zipf’s law arises generically for large systems, without fine-tuning parameters to a point. Our work gives insight into the ubiquity of Zipf’s law in a wide range of systems.

Advances in high throughput experimental biology now allow the joint measurement of activities of many basic components underlying collective behaviors in biological systems. These include firing patterns of many neurons responding to a movie [1–4], sequences of proteins from individual immune cells in zebrafish [5,6], protein sequences more generally [7,8], and even the simultaneous motion of flocking birds [9]. A remarkable result of these data and their models has been the observation that these large biological systems often reside close to a critical point [1,10]. This is most clearly seen directly from the data by the following striking behavior. If we order the states σ of a system by decreasing probability, then the frequency of the states decays as the inverse of their rank r(σ) to some power:

$$P(\mathit{\sigma })\propto \frac{1}{r{(\mathit{\sigma })}^{\alpha }}.$$ (1)

Many systems, in fact, exhibit α ≃ 1, which is termed Zipf’s law, and on which we will focus.

It has been argued that Zipf’s law is a model-free signature of criticality in the underlying system, using the language of statistical mechanics [10]. Without loss of generality, we can define the “energy” of a state σ to be

$$E(\mathit{\sigma })=-\text{log }P(\mathit{\sigma })+\text{const}.$$ (2)

The additive constant is arbitrary, and the temperature is k_BT = 1. We can also define the “entropy” S(E), using the density of states ρ(E) = ∑_σδ(E − E(σ)), as

$$S(E)=\text{log }\rho (E).$$ (3)

Both the energy E and the entropy S(E) contain extensive terms that scale with the system size N. An elegant argument [10] converts Eq. (1) with α = 1 into the statement that, for a large system N → ∞, the energy and entropy are exactly equal (up to a constant) to leading order in N. Thus, in the thermodynamic limit, the probability distribution is indeed poised near a critical point where all derivatives beyond the first of the entropy with respect to energy vanish to leading order in N.

The observation of Zipf’s law in myriad distributions of biological data has contributed to a revival of the idea that biological systems may be poised near a phase transition [10–15]. Yet, most existing mechanisms to generate Zipf’s law can produce a variety of power-law exponents α (reviewed in Refs. [16,17]), have semistringent conditions [18], are domain specific, or require fine-tuning to a critical point, highlighting the crucial need to understand how Zipf’s law can arise in data-driven models.

Here, we present a generic mechanism that produces Zipf’s law and does not require fine-tuning. The observation motivating this new mechanism is that the correlations measured in biological data sets have multiple origins. Some of these are intrinsic to the system, while others reflect extrinsic, unobserved sources of variation [19,20]. For example, the distribution of activities recorded from a population of neurons in the retina reflects both the intrinsic structure of the network as well as the stimuli the neurons receive [21], such as a movie of natural scenes or activity of nonrecorded neurons. Likewise, in the immune system, the variable external pathogen environment influences the observed antibody combinations. We will show that the presence of such unobserved, hidden random variables naturally leads to Zipf’s law. Unlike other mechanisms [16,18], our approach requires a large parameter (i.e., the system size, or the number of observables), with power-law behavior emerging in the thermodynamic limit. On the other hand, our mechanism does not require fine-tuning of parameters to a point or any special statistics of the hidden variables [22]. In other words, Zipf’s law emerges universally when marginalizing over relevant hidden variables.

A simple model

In order to understand how a hidden variable can give rise to Zipf’s law and concomitant criticality, we start by examining a simple case of N conditionally independent binary spins σ_i = ±1. The spins are influenced by a hidden variable h drawn from a probability distribution q(h), which is smooth and independent of N. In particular, we consider the case

$$P(\mathit{\sigma }|h)=\prod _{i=1}^{N}P({\sigma }_i|h)=\prod _{i=1}^N\frac{e^{h{\sigma }_i}}{2\text{ cos}\mathrm{h}h}.$$ (4)

Note that our chosen form of P(σ_i|h) imposes no loss of generality for noninteracting binary variables. We let the parameter h change rapidly compared to the duration of the experiment, so that the probability distribution of the measured data σ is averaged over h:

$$P(\mathit{\sigma })=\frac{1}{2^N}\int dhq(h)e^{N[hm(\mathit{\sigma })-\text{log cos}\mathrm{h}h]}$$ (5)

$$\equiv \frac{1}{2^N}\int dhq(h)e^{-N\mathscr{H}(m,h)},$$ (6)

where we have defined the average magnetization m = ∑_iσ_i/N, and the last equation defines ℋ(m, h). Note that the distribution P(σ) does not factorize, unlike P(σ|h). That is, the conditionally independent spins are not marginally independent. Indeed, as in Ref. [23], a sequence of spins carries information about the underlying h and hence about other spins (e.g., a prevalence of positive spins suggests h > 0, and thus subsequent spins will also likely be positive). We note that the simple model in Eq. (6) is intimately related to the MaxEnt model constructed in Ref. [4] to match the distribution of the number of simultaneously firing retinal ganglion cells.

In the limit N ≫ 1, we can calculate the integral within Eq. (6) by the saddle point approximation:

$$P(\mathit{\sigma })\approx 2^{-N}q(h^{*})e^{N(h^{*}m-\text{log cos}\mathrm{h}{h}^{*})},\hspace{1em}\text{tan}\mathrm{h}{h}^{*}=m.$$ (7)

Here, h* is the maximum-likelihood estimate of h given the data σ. In Eq. (7), we assumed that the distribution q(h) has support at h* and is sufficiently smooth, e.g., does not depend on N, so that the saddle point over h is determined by ℋ, and not by the prior. In other words, we require the Fisher information ℱ(h*) ≡ −N(∂²ℋ/∂h²)|_h* = N(1 − m²) ≫ 1, and for the location and curvature of the saddle point to not be significantly modulated by q(h). These conditions are violated at m = ±1, and there is a semi-infinite range of h that could have contributed to such states. For all nonzero values of ℱ, the saddle point will eventually dominate over q(h) as N → ∞. However, the convergence is not uniform.

Substituting Eq. (7) into Eq. (2) and using the identities $\text{tan}{\mathrm{h}}^{-1}m=\frac{1}{2}\text{log }(1+m/1-m)$ and cosh [tanh⁻¹m] = (1 − m²)^−1/2, we obtain the energy to leading order in N:

$$E(m)\approx -N\left[\right(\frac{1+m}{2}\left)\text{ log }\right(\frac{1+m}{2})+(\frac{1-m}{2}\left)\text{ log }\right(\frac{1-m}{2}\left)\right]\equiv NH(m).$$ (8)

Here, we neglected subdominant terms that come from both the prior q(h*) and the fluctuations about the saddle point. It is worth noting that this energy considered as a function of the σ_i, rather than m, includes interactions of all orders, not just pairwise spin couplings.

We can also calculate the entropy S(m) associated with the magnetization m. For a system of N binary spins, each state with magnetization m has K = N(1 + m/2) up spins, and there are $\left(\begin{array}{l}N\hfill \\ K\hfill \end{array}\right)$ such states. Using Stirling’s approximation, one finds that the entropy takes the familiar form $S(m)=\text{log}\left(\begin{array}{l}N\hfill \\ K\hfill \end{array}\right)\approx NH(m)$. Of course, this is the same as the energy [Eq. (8)] for the system with a hidden variable h, to leading order in N.

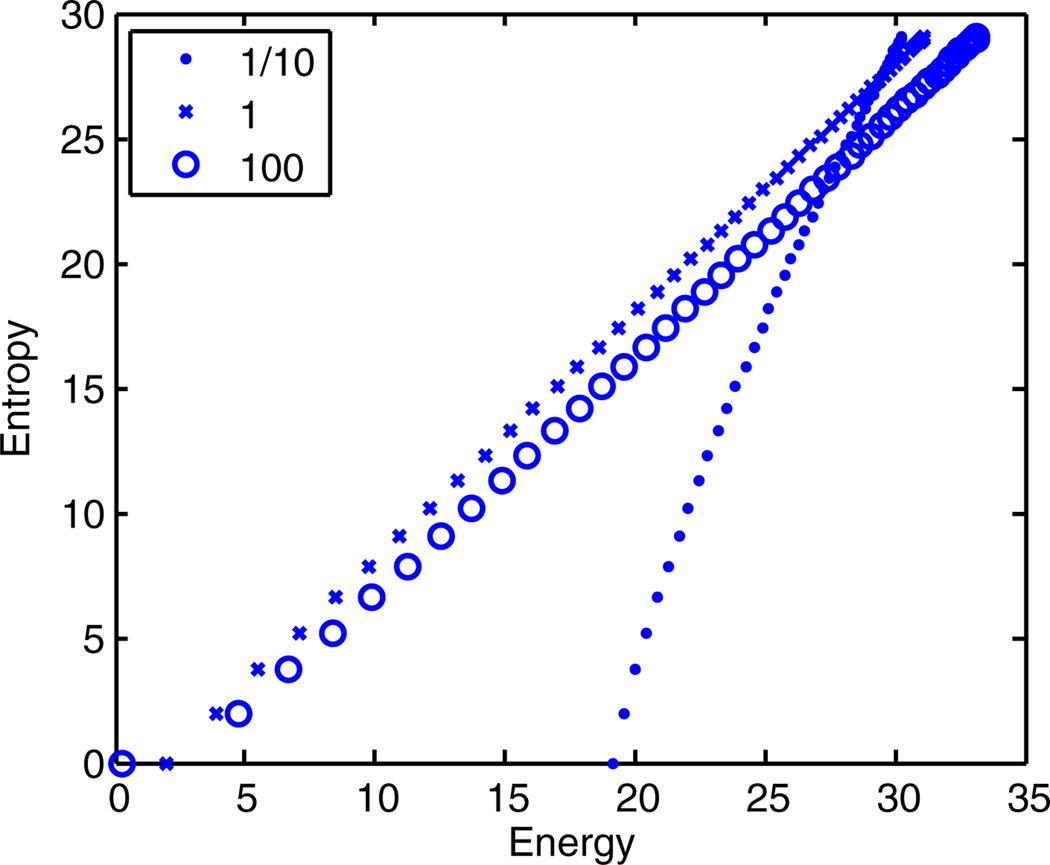
The analytic equivalence between energy and entropy only applies when N → ∞. To verify our result for finite N, we numerically calculate E(m) from Eq. (6) with q(h) chosen from a variety of distribution families (e.g., Gaussian, exponential, uniform). For brevity, we only show plots for Gaussian distributions, but the others gave similar results. Figure 1 plots the entropy $S(m)=\text{log}\left(\begin{array}{l}N\hfill \\ K\hfill \end{array}\right)$ vs the energy E(m) for N = 100 conditionally independent spins, where q(h) has mean 0 and varying standard deviation s ∈ {0.1, 1, 100}. For small s, the hidden variable h is always close to 0, there is no averaging, and all states are nearly equally (im)probable. As s increases, entropy becomes equal to energy over many decades, modulo an arbitrary additive constant. This holds true for 2 orders of magnitude of the standard deviation s, confirming that our mechanism does not require fine-tuning.

FIG. 1.

(color online). Entropy S(m) vs energy E(m) for N = 100 identical and conditionally independent spins. Zipf’s law (E = S) emerges as the standard deviation s ∈ {0.1, 1, 100} of the Gaussian distribution characterizing the hidden variable h is increased. Notice that there is a nearly perfect Zipf’s law for 2 orders of magnitude in s. The mean of q(h) is set to 0, and thus there is a twofold degeneracy between states with magnetization m and −m.

The stable emergence in the thermodynamic limit N → ∞, with no fine-tuning, distinguishes our setup from a classic mechanism explaining 1/f noise in solids [18] and certain other biological systems [24]. We could have anticipated this result: if the extensive parts of the energy and entropy do not cancel, in the thermodynamic limit, the magnetization will be sharply peaked around the m that minimizes the free energy Nf(m) = E(m) − S(m). Thus, in order for there to be a broad distribution of magnetizations within P(σ), the extensive part of f(m) must be a constant. In other words, the observation of a broad distribution of an order-parameter-like quantity in data is indicative of a Zipfian distribution. One straightforward mechanism to produce a broad order-parameter distribution for large N is to couple it to a hidden fluctuating variable.

A generic model

We now show that Zipf criticality is a rather generic property of distributions with hidden variables and is not a consequence of the specific model in Eq. (4). In particular, it does not require the observed variables to be identical or conditionally independent, or the fluctuating parameter(s) to be temperature-like.

Consider a probabilistic model of discrete data x = (x₁, x₂, …, x_N) on a finite alphabet. Assume we can write the conditional probability distribution in the log-linear form:

$$P(x_1,x_2,\dots ,x_N|\mathbf{g})=\frac{1}{Z(\mathbf{g})}\text{exp }[-N\sum _{\mu =1}^M{g}_{\mu }{𝒪}_{\mu }(\mathbf{x})],$$ (9)

where each N𝒪_μ contains ≫ 1 terms each of O(1), and the parameters g = (g₁, …g_M) may be tied together (that is, are functions of each other). Here, we have defined the partition function

$$Z(\mathbf{g})=\sum _{x\prime }\text{exp }[-N\sum _{\mu =1}^M{g}_{\mu }{𝒪}_{\mu }(\mathbf{x}\prime )].$$ (10)

As an example, the fully connected Ising model would have g = (h, J), with 𝒪₁ = −(1/N)∑_ix_i and 𝒪₂ = −(1/2N²)∑_i,jx_ix_j, with each x_i ∈ {−1, 1}.

The parameters g are drawn from some probability distribution Q(g). A subset of the parameters may be nonvarying, so Q(g) may contain terms such as $\delta (g_{\mu }-g_{\mu }^{*})$. Additionally, if some parameters are tied together, then Q will contain terms such as δ[g_μ − f(g_ν)]. The marginal distribution of the data x is given by

$$P(\mathbf{x})=\int d\mathbf{g}Q(\mathbf{g})e^{-NF(\mathbf{g};\mathbf{x})},$$ (11)

where $F(\mathbf{g};\mathbf{x})={\sum }_{\mu =1}^M{g}_{\mu }{𝒪}_{\mu }(\mathbf{x})+(1/N)\text{ ln }Z(\mathbf{g})$.

We first write down the microcanonical entropy S({𝒪_μ(x)}), which depends on the observed data. The multidimensional form of the Gärtner-Ellis theorem [25,26] states that the entropy is the Legendre-Fenchel transform of the cumulant generating function c(g). For our problem, this can be written as

$$S(\{{𝒪}_{\mu }(\mathbf{x})\})=\underset{\mathbf{g}}{\text{inf}}[\sum _{\mu }{g}_{\mu }{𝒪}_{\mu }(\mathbf{x})+c(\mathbf{g})],$$ (12)

where c(g) is just minus the free energy

$$c(\mathbf{g})=\underset{N\to \infty }{\text{lim}}{N}^{-1}\text{ ln }Z(\mathbf{g})-C,$$ (13)

save for an unimportant constant C = (1/N) ln ∑_x′. Note that the infimum in Eq. (12) is over all g_μ independently.

We next compute the energy of a state x. If the distribution of the K fluctuating variables Q(g) is not too narrow, as discussed after Eq. (7), we can evaluate Eq. (11) using a saddle point approximation. Importantly, the extremum is performed subject to any constraints, such as nonvarying or tied parameters in Q(g). Denoting the solution to the saddle point equations by g* and neglecting subleading terms, we have

$$E(\mathbf{x})≔-\frac{1}{N}\text{ln }P(\mathbf{x})=\sum _{\mu }{g}_{\mu }^{*}{𝒪}_{\mu }(\mathbf{x})+\frac{1}{N}\text{ln }Z({\mathbf{g}}^{*}).$$ (14)

Notice that $g_{\mu }^{*}$ are functions of the data through 𝒪_μ(x).

If all parameters vary independently, Eqs. (12) and (14) are identical, and we have proven Zipf’s law, i.e., S({𝒪_μ(x)}) = E(x). Even if parameters are tied together or only a subset varies, if the unconstrained [Eq. (12)] and the constrained [Eq. (14)] minimizations yield the same result, Zipf’s law still holds. For example, in the fully connected Ising model with varying h and static J, the entropy at fixed 𝒪₁ is the same as the entropy at fixed (𝒪₁, 𝒪₂) since ${𝒪}_2={𝒪}_1^2/2$. Thus, minimizing Eq. (12) over h is the same as over (h, J), and Zipf’s law holds even if J is static [27].

Numerical tests

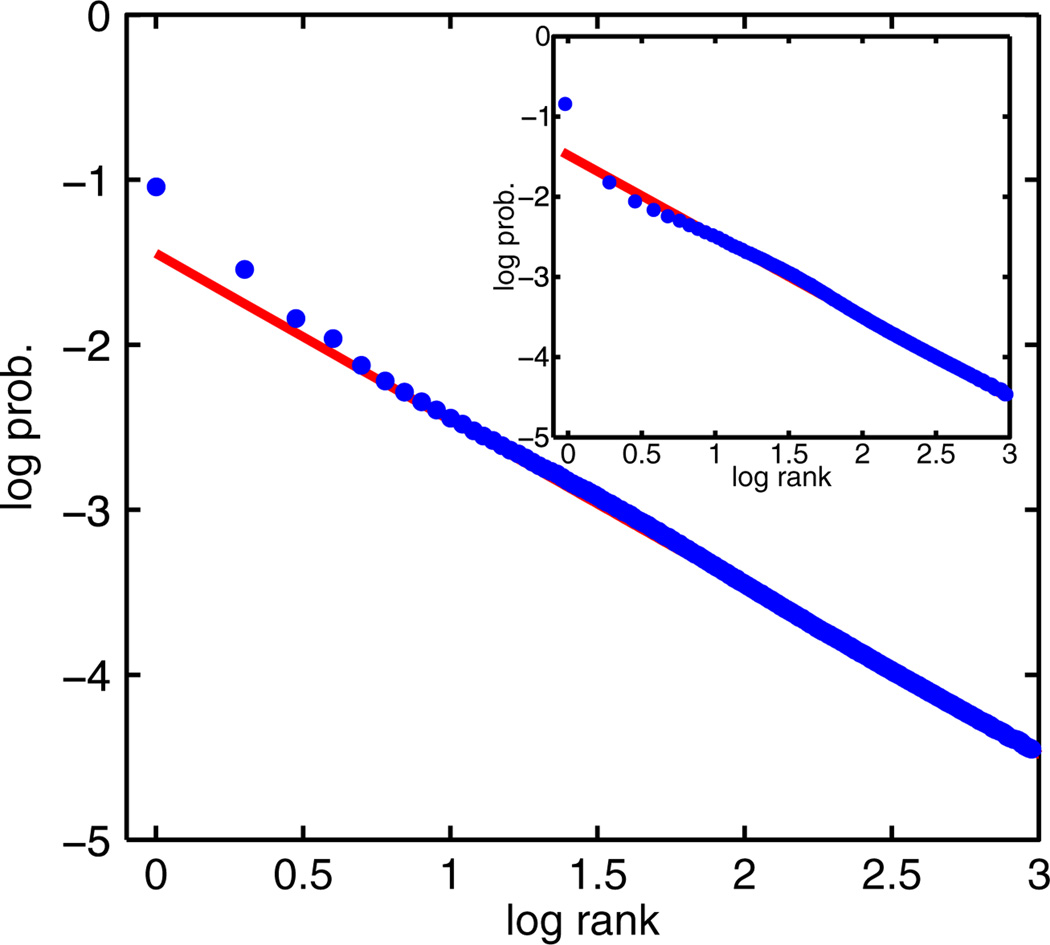
We numerically test the validity of our analytic results for finite N in two systems more complex than Eq. (4): (a) a collection of nonidentical but conditionally independent spins and (b) an Ising model with random interactions and fields. The main graph of Fig. 2 shows a Zipf plot for system (a), so that

$$P(\mathit{\sigma }|\beta )=\prod _{i=1}^{N}P({\sigma }_i|\beta )=\prod _{i=1}^N\frac{e^{-\beta h_i{\sigma }_i}}{2\text{ cos}\mathrm{h}\beta h_i},$$ (15)

where h_i are quenched, Gaussian random variables unique for each spin. In the figure, the hidden variable β was drawn from a Gaussian distribution, but similar results were found for other distributions. The quenched fields h_i break the symmetry between spins. In agreement with our derivation, on a log-log plot, the states generated from simulations fall on a line with slope very close to −1 (Fig. 2), the signature of Zipf’s law.

FIG. 2.

(color online). Main plot: Plot of log₁₀ probability vs log₁₀ rank of the most frequent 10³ states for a system of N = 200 nonidentical, conditionally independent spins [model (a)]. Plots are an average over 200 realizations of the quenched variables h_i that break the symmetry between spins, with 5 × 10⁵ samples taken for each realization. Parameters: h_i ~ 𝒩(μ = 1, s = 0.3) and β ~ 𝒩(μ = 0, s = 2). The red line represents the least-squares fit to patterns 100–1000, slope of −1.012. Inset: Same as above, except for a model of N = 200 spins with quenched random interactions J_ij and biases h_i [model (b)]. An average over ten realizations of J_ij and h_i is chosen from J_ij ~ 𝒩(μ = 1, s = 0.5), h_i ~ 𝒩(μ = 1, s = 0.85), and β ~ 𝒩(μ = 0.5, s = 0.5), with 3 × 10⁵ samples taken for each realization. The red line represents the least-squares fit to patterns 100–1000, slope of −1.011.

To verify that conditional independence is not required for this mechanism, we studied system (b) that generalizes the model in Eq. (15) to include random exchange interactions between spins:

$$P(\mathit{\sigma }|\beta )\propto e^{-\beta [(1/N){\sum }_{i\ne j}{J}_{ij}{\sigma }_i{\sigma }_j+{\sum }_i{h}_i{\sigma }_i]},$$ (16)

where the J_ij and h_i are quenched Gaussian distributed interactions and fields, and β is as above. As shown in the inset of Fig. 2, the data again fall on a line with slope nearly equal to −1.

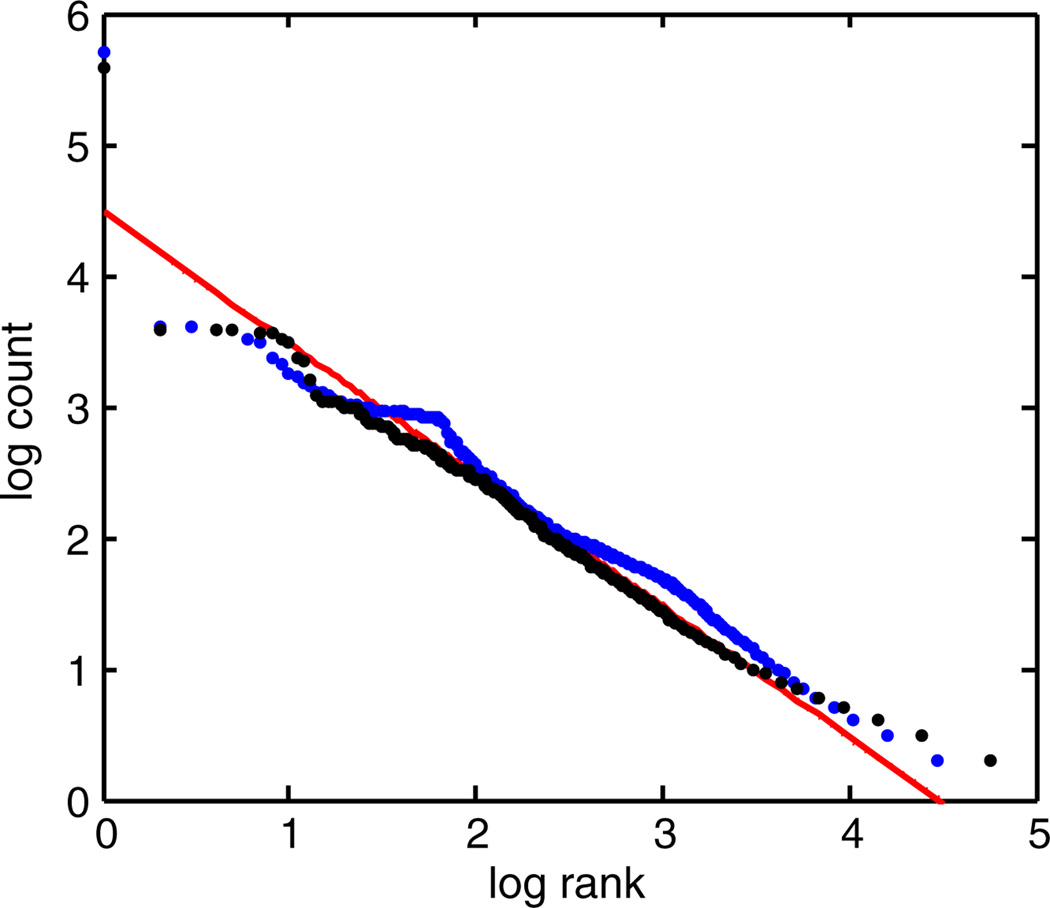
To see our mechanism at work in empirical data, consider a neural spike train from a single blowfly motion-sensitive neuron H1 stimulated by a time-varying motion stimulus υ(t) (see Refs. [28,29] for experimental details). We can discretize time with a resolution of τ and interpret the spike train as an ordered sequence of N spins, such that σ_i = ±1 corresponds to the absence or presence of a spike in a time window t ∈ [τ(i − 1), τi). The probability of a spike in a time window depends on υ. However, neural refractoriness prevents two spikes from being close to each other, irrespective of the stimulus, resulting in a repulsion that does not couple to υ. The rank-ordered plot of spike patterns produced by the neuron is remarkably close to the Zipf behavior (Fig. 3). We also simulated a refractory Poisson spike train using the same values of υ(t). We chose the probability of spiking (spin up) as in Eq. (4) with h(t) = aυ(t), a = const, and with a hard repulsive constraint between positive spins extending over a refractory period of duration τ_r.We then choose τ_r as the shortest empirical interspike interval (≈2 ms) and set a such that the magnetization (the mean firing rate) matches the data. The rank-ordered plot for this model that manifestly includes interactions uncoupled from the hidden stimulus υ(t) still exhibits Zipf’s law (Fig. 3).

FIG. 3.

(color online). Rank-count plot from a motion-sensitive blowfly neuron, logs base 10; discretization is τ = 1 ms, and N = 40. The black dots represent empirical rank-ordered counts. The blue dots represent rank-ordered counts from a simulated refractory Poisson spike train with the input stimulus the same as in the experiment, and with mean firing rate and refractory period matched to the experimental data. The red line represents a slope of −1 as a guide to the eye.

Discussion

It is possible that evolution has tuned biological systems or exploited natural mechanisms of self-organization [11] to arrive at Zipf’s law. Alternatively, informative data-driven models may lie close to a critical point due to the high density of distinguishable models there [19,30]. Our work suggests another possibility: Zipf’s law can robustly emerge due to the effects of unobserved hidden variables. While our approach is biologically motivated, it is likely to be relevant to other systems where Zipf’s law has been observed, and it will be interesting to unearth the dominant mechanisms in particular systems. For this, if a candidate extrinsic variable can be identified, such as the input stimulus to a network of neurons, its variance could be modulated experimentally, as in Fig. 1. Our mechanism would expect Zipf’s law to appear only for a broad distribution of the extrinsic variable and for N ≫ 1 observed variables.

While our mechanism does not require fine-tuning, it nonetheless suggests that biological systems operate in a special regime. Indeed, the system size N required to exhibit Zipf’s law depends on the sensitivity of the observed σ to the variations of the hidden variable. If the system is poorly adapted to the distribution of h, e.g., the mean of q(h) is very large or its width is too small to cause substantial variability in σ (as in Fig. 1, s = 0.1), a very large N will be required. In other words, a biological system must be sufficiently adapted to the statistics of h for Zipf’s law to be observed at modest system sizes. Indeed, this type of adaptation is well established in both neural and molecular systems [31–34].