DNA and its counterions: a molecular dynamics study

Abstract

The behaviour of mobile counterions, Na⁺ and K⁺, was analysed around a B-DNA double helix with the sequence CCATGCGCTGAC in aqueous solution during two 50 ns long molecular dynamics trajectories. The movement of both monovalent ions remains diffusive in the presence of DNA. Ions sample the complete space available during the simulation time, although individual ions sample only about one-third of the simulation box. Ions preferentially sample electronegative sites around DNA, but direct binding to DNA bases remains a rather rare event, with highest site occupancy values of <13%. The location of direct binding sites depends greatly on the nature of the counterion. While Na⁺ binding in both grooves is strongly sequence-dependent with the preferred binding site in the minor groove, K⁺ mainly visits the major groove and binds close to the centre of the oligomer. The electrostatic potential of an average DNA structure therefore cannot account for the ability of a site to bind a given cation; other factors must also play a role. An extensive analysis of the influence of counterions on DNA conformation showed no evidence of minor groove narrowing upon ion binding. A significant difference between the conformations of the double helix in the different simulations can be attributed to extensive α/γ transitions in the phosphate backbone during the simulation with Na⁺. These transitions, with lifetimes over tens of nanoseconds, however, appear to be correlated with ion binding to phosphates. The ion-specific conformational properties of DNA, hitherto largely overlooked, may play an important role in DNA recognition and binding.

INTRODUCTION

It has been known since the first experimental studies on DNA structure that both solvent and counterions play a major role in stabilizing the double helix and in determining its overall conformation (1). Solvent and counterion effects have also been evoked at a finer level in explaining the base-sequence-dependent structure of DNA oligomers, as observed in the single crystal structure of the so-called Drew–Dickerson dodecamer (2). This oligomer, containing the underlined EcoRI binding site (CGCGAATTCGCG), attracted particular attention because of the narrow minor groove formed by the central AATT sequence which constitutes a short A-tract, a feature associated both with conformational rigidity and with DNA bending. Several factors have been proposed to explain the unusual properties of A-tracts, subsequently observed in a number of different crystal structures. These include bifurcated hydrogen bonds, linking the adenine and thymine bases of adjacent base pairs (3), and the so-called ‘hydration spine’, a layer of water molecules forming a set of hydrogen bonds between the minor groove edges of the adenine–thymine bases, observed in the central part of the Drew–Dickerson dodecamer (4,5).

The structuring role of ordered water molecules in the first and higher solvation shells has been discussed at length, yet relatively little attention has been accorded to counterions. These ions are clearly necessary for DNA stability but are more difficult to study. Nevertheless, recent data obtained both by experimental and theoretical methods have described the association of monovalent cations with the double helix and their impact on DNA conformation. In crystal structures of the Drew–Dickerson dodecamer, it has been found that partially dehydrated monovalent cations (Na⁺ and K⁺) bind in the minor groove (6,7). Such sequence-specific cation binding has been interpreted as contributing to DNA conformational heterogeneity and linked notably to axial bending and to minor groove narrowing (6). A subsequent study of an atomic-resolution crystal structure of the same sequence grown under a higher Mg²⁺/Na⁺ ratio did not show such bound ions (8), and the results of the earlier works were challenged (9). However, Rb⁺ has been shown to bind at the central ApT step of the dodecamer with 50% occupancy (10), and Tl⁺ has been localized within the G-tract major groove (20–35%) and the A-tract minor groove (10%) in these crystals (11,12). Solution NMR studies of A-tract sequences show that monovalent ions penetrate into the minor groove (13), but the low occupancy binding argues against a strong structural influence on DNA (14).

Another way to approach the problem of counterion effects is by means of all-atom molecular dynamics simulations. Such simulations give us the possibility of following in detail the trajectories of individual counterions over multi-nanosecond timescales, and at the same time giving access to detailed information on DNA conformational dynamics. Although early simulations were severely limited due to both computer power and problems of instability, fast processors and the introduction of the particle–mesh Ewald (PME) approach to treat long-range electrostatic interactions have enabled simulations to be carried well beyond the nanosecond timescale. A number of specific questions concerning counterions in simulations, however, remain to be answered including the accuracy of ion–DNA interactions in solution and the sampling of the available conformational space around the DNA double helix (15).

Previous studies have addressed the question of direct, sequence-specific ion binding to DNA with contradictory results. Early molecular dynamics simulations described the movements of ions in the minor groove of the Drew–Dickerson dodecamer (16). In an extended 15 ns trajectory, it was found that the Na⁺ fractional occupancy in the AATT segment of the minor groove was 5–10%, while >10% occupancy was found at the CpG step in the major groove (17). The presence of sodium ions in the AATT region was found to exert a negligible influence on the width of the minor groove (with an apparent change of <1 Å, which is well below the thermal fluctuations of groove width), but was, however, found to be linked to major groove narrowing.

The same oligomer has been analysed in a 15 ns simulation in another study (18) with surprisingly different conclusions, although the only notable change in conditions involved a slightly different salt concentration. This analysis consisted of studying variations in groove width as a function of percentage site occupancies. The authors considered the effects of direct binding in the minor groove, especially at the central ApT step, and of binding at the entrance to the minor groove bridging the anionic oxygens of the two interstrand phosphates. It was concluded that the minor groove width was coupled to ion binding with a difference of up to 2 Å separating the cases of 0 and 100% occupancy (no error bounds were given).

Simulations of two 25mers containing A-tracts ATAGGCA₆TAGGCA₅TGG and G₅(GA₄T₄C)₂C₅ indicated a correlation between axial bending and the presence of a counterion close to the bending locus (17). Other AT-rich oligomers, C(AT)₄G, CA₄T₄G and CT₄A₄G, have also been simulated for 8 ns each (19), leading to the conclusion that Na⁺ intrusions into the first hydration shell of the minor groove of A-tracts occurred but were not coupled to axial bending.

Studies of a decamer C₅T₅ (20) described Na⁺ binding to guanines within the major groove and along the hydration spine in the minor groove of the AT base pair sequence, and reported a small (≤0.7 Å) reduction in groove width linked to ion binding within the AT segment. No such coupling was found for either monovalent ions or spermine in simulations of three non-A-tract B-DNA decamers in periodic conditions chosen to model a crystalline environment (21). Simulations of alternating (CG)₁₂ and (AT)₁₂ sequences with K⁺ were reported to result in direct major groove binding at purine/pyrimidine (RpY) steps, but no binding was seen in the minor groove (22,23). Finally, dependence of ion distribution on the force field used was noted for the CGATTAATCG decamer, but these simulations were too short (1.2 ns) to achieve ion convergence (24).

Although this summary is not exhaustive, it shows clearly that the influence of counterions on DNA conformation remains an open question. All the sequences studied previously had special features including either A-tracts, homopolymeric runs or alternating sequences. Therefore, it is important to gain insight into the behaviour of counterions around a sequence, which does not show any of these properties. In an attempt to answer this question, we have carried out two 50-ns simulations of a double-stranded B-DNA dodecamer, CCATGCGCTGAC, containing the underlined target sequence for HhaI cytosine methyltransferase, which we have previously used to study base pair opening (25). We note that our simulation is far longer than current standards. This is particularly important as it has been observed that ions can get trapped in particular binding sites for nanoseconds (18). The two simulations (using equivalent initial conditions and simulation protocols) were carried out with different monovalent cations, Na⁺ and K⁺, both of which are important for DNA stability and are commonly used in experimental studies. Ions can also serve as sensitive electrostatic probes to map the dynamic surface of DNA for macromolecular recognition. In this study, we analyse how well ions sample the space around DNA, their direct site binding and diffusion properties, and concurrent changes in DNA structure.

MATERIALS AND METHODS

Simulation protocol

Model building and simulations were performed using the AMBER 6 suite of programs (26) and the parm99 parameter set (27). Simulations were carried out on a dodecamer with the sequence d(CCATGCGCTGAC) which was constructed in a standard B-DNA conformation. This oligomer was neutralized with 22 Na⁺ or K⁺ ions (placed following electrostatic potential values) and solvated with more than 5000 TIP3P water molecules in a truncated octahedral box, which allowed for at least a 10 Å shell of water around the solute. The minimal salt conditions were chosen because the proper description of ions in simulations represents highly controversial parts of current force fields (28–30). Molecular dynamics simulations were then carried out at constant temperature (300 K) and pressure (1 bar) using the Berendsen algorithm (31) and periodic boundary conditions. An integration time step of 2 fs was used and all bond lengths involving hydrogens were constrained using SHAKE (32). Long-range interactions were treated using the PME approach (33) with a 9 Å direct space cut-off. The non-bonded pair list was updated heuristically, whenever any atom has moved more than half of a ‘skin’ distance of 2 Å, and the centre of mass motion was removed every 10 ps during the simulation. Initially, the water molecules and ions were relaxed by energy minimization and allowed to equilibrate at 300 K around the fixed DNA oligomer for 100 ps at constant volume. The entire system was then heated from 100 to 300 K during 10 ps and equilibrated for 40 ps with harmonic restraints of 5.0 kcal/mol/Ų on the solute atoms at constant volume. Subsequently, the simulation was continued at constant pressure. The restraints were gradually removed over a period of 250 ps and the system was equilibrated for 1 ns. The following 50 ns of unrestrained simulation was used for analysis.

Counterion analysis

In order to analyse ion movements around the solute in a periodic boundary simulation, the ions that move far away need to be first translated back to the primary simulation cell. These ‘imaging’ calculations were performed with the ptraj utility of the AMBER package. We next analysed what percentage of the available space in the simulation box was effectively sampled by counterions during the course of the simulation. The volume occupied by the solute was calculated numerically using a grid with a 0.2 Å spacing and taking into account the van der Waals radii of the DNA atoms (H, 1.0 Å; C, 1.7 Å; N, 1.5 Å; O, 1.4 Å; P, 1.9 Å) incremented by the radius of the ion (Na⁺, 1.0 Å; K⁺, 1.4 Å).

The volume sampled by the counterions was calculated using the same grid spacing and ionic radius. An analysis of the ion displacement with 1 ps time intervals, corresponding to the saving frequency of coordinates, showed that the mean displacement was ∼1 Å, although displacements of up to 5 Å were also observed (excluding any effects caused by the imaging procedure mentioned above). Ion positions not sampled due to the use of 1 ps steps were taken into account by generating intermediate points. One such point was created by linear interpolation when the distance between two consecutively sampled points was between 2.5 and 3 Å and two equally spaced points were created for distances between 3 and 5 Å.

Diffusion coefficients

Motions of the counterions in the presence of DNA were characterized by their diffusion coefficients (D) according to Einstein's formula:

This requires calculation of the mean square displacements of each ion for a series of time intervals. The diffusion coefficient is then simply given by the slope of the plot of the average square displacements versus time. The time intervals used in this calculation were varied from 10 to 1000 ps in steps of 10 ps. For each calculation, the displacement was averaged over all time intervals along the trajectory.

Binding site analysis

An ion was considered bound to the solute if its distance from an electronegative solute atom was <3.0 and 3.5 Å for Na⁺ and K⁺, respectively. This value corresponds to a minimum in the radial distribution function of the ions around the electronegative solute atoms, which separates a sharp maximum corresponding to a direct binding and a secondary maximum corresponding to water-mediated interactions (20,22).

Site occupancy was calculated for both base- and backbone-binding sites on DNA. There are two potential binding sites in the minor groove, Y(O2) and R(N3) (where Y = pyrimidine and R = purine), and three in the major groove, R(N7), G(O6) and T(O4). For the backbone, we considered all five oxygen atoms: the phosphate anionic oxygens, O1P and O2P, the phosphate esteric oxygens, O5′ and O3′ and the sugar-ring oxygen, O4′. For each of these sites, we calculated the occupancy, defined as a percentage of the simulation time during which a counterion was directly bound. We also recorded the average and the maximum durations of binding. For the sites with the highest occupancies we calculated the ion residence times using a standard time correlation function (34), with residence time distribution (rtd) for a given binding site defined as

where p_i(t) is 1 if the ion i is present at time t and otherwise 0. Events when an ion fluctuates across the boundary within 1 ps are ignored. Calculations were carried out with time intervals ranging from 10 to 1000 ps. The effective residence time (R) is then calculated from the decay coefficient of an exponential function fitted to rtd:

Counterion influence on DNA conformation

In order to investigate the possible impact of ion binding on DNA conformation we calculated both helicoidal parameters and axial-bending angles throughout the simulation using the Curves program (35). Minor groove widths were measured using two different approaches. First, we calculated the interstrand distance between the phosphorous atoms P_i and P′_i+3 across the minor groove (d_PP). This distance was reduced by 5.8 Å (sum of the van der Waals radii of the two phosphate groups) in order to be comparable with the convention adopted by other authors. Second, we used the minor groove width calculated by the Curves program, which corresponds to the shortest distance between splines passing through the backbone phosphorus atoms and lying in a plane passing through the pseudodyad vector of the chosen base pair (36). DNA structures were sorted into groups depending on the presence or absence of counterions at particular locations around the DNA, and the average groove width and standard deviation were calculated for each group. The following groups were considered: (i) counterions bound in the minor groove associated with a given base pair; (ii) counterions bound in the major groove associated with a given base pair; (iii) counterions between two phosphate groups across the minor groove; and (iv) no bound counterions. Note that structures satisfying more than one criterion were rare and were subsequently excluded from our analysis.

To find structures belonging to the third group, we considered ions falling at less than (2 + d_PP/2) Å from the phosphorous atoms, P_i and P′_i+3, which defines the local minor groove width. This approach defines a convex-lens-shaped volume equidistant from the phosphate groups at the entrance to the minor groove. An alternative approach, where the volume of the lens is constant, was also tested and gave very similar results. We also calculated the relationship between the minor groove width and ion site occupancy in order to compare our results with those of Hamelberg and co-workers (18). This involved calculating the average groove width and the corresponding groove and phosphate ion occupancies for all 10 ps segments during the total simulation time.

Molecular electrostatic potential

Calculation of the electrostatic potential around the DNA oligomer was carried out with the program Delphi (37). The program was adapted to calculate an average value of the electrostatic potential over the solvent accessible area assigned to a given atom. A grid of 145 points was used and calculations were performed with radii of 1.2 or 1.4 Å. The internal and external dielectric constants were set to 2 and 80, respectively, and the ionic force was zero.

RESULTS AND DISCUSSION

Counterion convergence

Let us consider first the problem of how efficiently ions sample the simulation box during the available simulation time. The total volume of the simulation box fluctuated around 1.79 × 10⁵ ų (±1500 ų) as a consequence of the constant pressure adjustments, and the volume excluded by the DNA was 10920 ų (±60 ų). Figure 1A presents the volume visited by the total number of counterions as a function of simulation time. The curves shown correspond to the imaging of ions with the solute molecule centred in the box. The molecule can tumble during the simulation and this movement changes the apparent volume occupied by the solute to some extent, however, this change is small in comparison with the volume of the box (see below). The figure shows that the volume sampled by K⁺ increases faster than that for Na⁺. The main increase takes place during the first 10 ns of the simulation time and a large fraction of the total volume is already sampled (practically 100% for K⁺ and 80% for Na⁺). This increase then reaches a plateau value at 1.73 × 10⁵ ų, ∼98% of the total box volume. The difference of 6000 ų between the total volume of the simulation box and the volume visited by counterions is slightly lower than the excluded volume of the solute because the tumbling of the DNA opens some new space for the ions.

Figure 1.

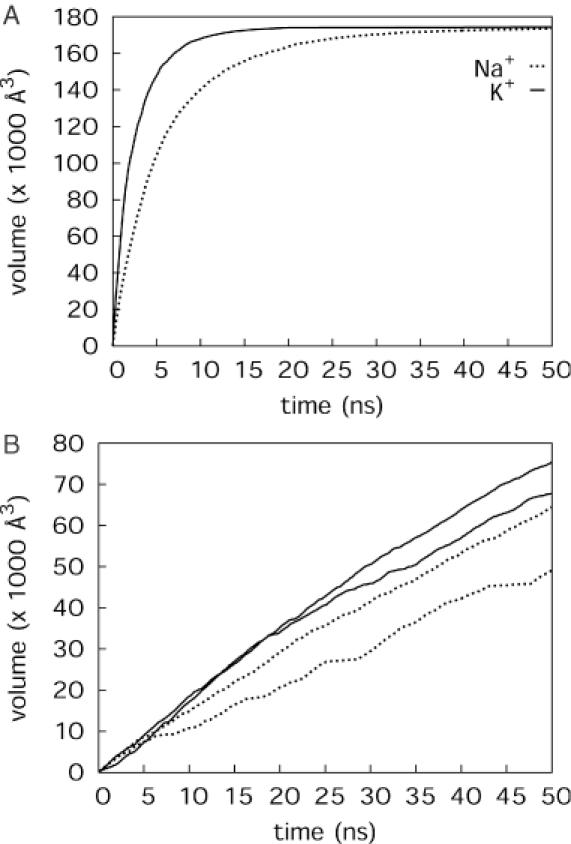
Volume sampled by Na⁺ (dotted line) and K⁺ (solid line) counterions during 50 ns simulation time calculated for all the ions (A) and for the slowest and fastest ions (B).

Although virtually the whole simulation box is visited by at least one ion, individual ions sample only ∼30–40% of the available space. Figure 1B illustrates this for the ‘slowest’ and ‘fastest’ moving ions. While the fast ion moves through the box rather uniformly, the trajectory of the slower ones is characterized by long pauses. For example, the slowest Na⁺ contacts many points on the DNA molecule; starting from a location close to T₉ it moves to the opposite end of the helix, and 6 ns later, it is back at phosphate 10. It then contacts the terminal base G₁₃, before moving back to the centre of the oligomer. Owing to such pauses, the total volumes sampled by individual ions can vary by >10⁴ ų. In the simulation with K⁺, individual ions sample a higher fraction of the total volume and the curves show many short pauses with more uniform sampling of space.

An analysis of sampling of separate volume elements around DNA was also performed. This calculation shows how cylindrical shells with increasing radial distances from a linear DNA axis are visited along the simulation time (Supplementary Figure S1). A maximum in visited volume is observed at a distance of ∼14 Å from the DNA axis, which corresponds to a hydrated ion close to the surface of the DNA.

Ion diffusion coefficient

Movements of the ions during the simulation can be characterized by their diffusion coefficient (D), although this must be considered an approximate measure due to the existence of binding events. Nevertheless, the mean-square displacement averaged for all the ions over time intervals gives a perfect line. The slope corresponds to D = 1.7 × 10⁻⁹ m² s⁻¹ for Na⁺ and 2.8 × 10⁻⁹ m² s⁻¹ for K⁺. Values for individual Na⁺ ions vary between 1.3 and 2.1 × 10⁻⁹ m² s⁻¹, whereas those for K⁺ are between 2.5 and 3.3 × 10⁻⁹ m² s⁻¹.

Our average value for Na⁺ is identical to that reported in earlier DNA simulations under similar conditions (38), although lower values (1.3 × 10⁻⁹ m² s⁻¹) have been calculated from simulations under different conditions, and, notably, using a flexible, simple point-charge water model and the CHARMM 22 force field for DNA (21). In comparison, the experimental value for Na⁺ in pure water is 1.33 × 10⁻⁹ m² s⁻¹ (39), which has been well reproduced by simulation (1.28 × 10⁻⁹ m² s⁻¹) (40). Diffusion properties of K⁺ in the presence of DNA have not, to our knowledge, been published. The experimental diffusion constant of K⁺ in pure water is 1.96 × 10⁻⁹ m² s⁻¹ (39), and a value of 1.86 × 10⁻⁹ m² s⁻¹ was calculated from simulations (40). Our calculated diffusion coefficients in the presence of DNA show a similar Na⁺/K⁺ ratio as those found in aqueous solution.

Ion mobility was calculated as a function of the mean distance of ions from the DNA axis (Supplementary Figure S2). This shows that K⁺ has a mobility of 1.2 Å/ps on average that is roughly independent of its distance from DNA. In contrast, Na⁺ mobility is low in the vicinity of DNA (0.75 Å/ps), characteristic of direct binding, and then increases to 1.1 Å/ps beyond 15 Å from the DNA axis.

Ions in the grooves

To get a clear picture of where the ions were most frequently located during the simulation, each snapshot was re-oriented by superposing the solute and the ion occupation of each volume element was counted using a 1 ų grid. Locations in the simulation box that correspond to >20% of the maximum occupancy along with the average DNA structure are shown in Figure 2.

Figure 2.

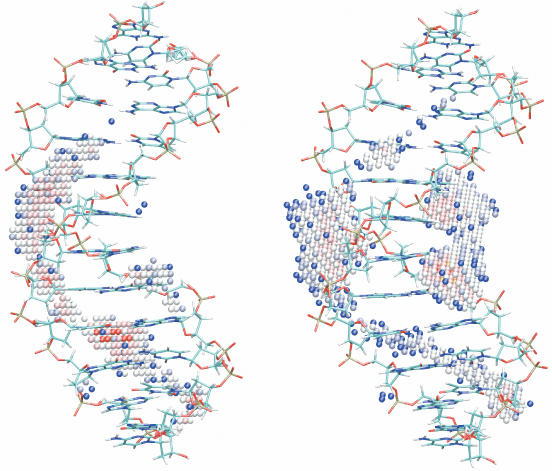
Counterion distribution around an average DNA structure for Na⁺ (left) and K⁺ (right). The positions shown correspond to roughly 700 to 3500 visits per 1 ų over 50 ns simulation (top 80% of ion density) with red for the highest, white for the medium and blue for the lowest densities.

Both monovalent ions, as would be expected, preferentially visit volume elements in the vicinity of (but not necessarily directly bound to) the double helix. This does not imply that individual ions spend most of their time around the DNA and this is indeed not the case. The figure shows that, in the case of Na⁺, the minor groove has higher ion density than the major groove, even for this GC-rich sequence, although there is a favoured site in the central region of the major groove of the oligomer. The highest occupancies are located in the minor groove, mainly around T₉(O2), shown in red at the lower half of the oligomer (Figure 2). A different picture emerges from simulations with K⁺ where ions preferentially visit the central part of the oligomer. The highest ion density locations for K⁺, however, correspond to the major groove, specifically to the GpC steps in the central GCGC recognition sequence of the oligomer.

Calculated percentage ion occupancies for direct binding to bases in the grooves and to phosphates are summarized in Table 1. Note that occupancy values for various sites are not strictly additive since an ion can simultaneously interact with more than one site. The most important feature is the significantly different binding pattern for the two monovalent ions. Sodium binding to DNA is highly non-uniform along the sequence. High occupancies were found in both the minor and major grooves of the G₇–A₁₁ segment as well as around certain phosphate groups. The most occupied sites are located away from the centre of the oligomer, in contrast to what might be expected from an oligomeric electrostatic potential distribution or from sequence-dependent electrostatic properties. While direct binding to T₉(O2) dominates with a 12% occupancy, many base sites have occupancy values <1%. Interestingly, much lower occupancies were found at the ApT step at the opposite end of the oligomer, in contrast to results seen in previous studies for central ApT step in the Drew–Dickerson dodecamer (7,16). The different sequence contexts of AT pairs explain the different ion-binding patterns. Ions that are shared between different sites are not very frequent, mainly at G(O6) in the major groove and at C/T(O2) in the minor groove. All phosphate groups, and specifically the O1P site, which lies on the minor groove side of the duplex, have direct ion binding for at least 2% of the simulation time, and these values increase to ∼10% for phosphates close to bases with high ion occupancies. The single exception is P₂₁ with 17% direct binding, which is mainly due to the unusually high occupancy in the final 15 ns of simulation time. An analysis of the structure of bound counterions at this site revealed a rare coordination of two Na⁺ around O1P, a configuration also seen in the crystal structure of the disodium salt of adenosine triphosphate (41).

Table 1. Binding site occupancy (%) of counterions.

The inner rows correspond to base sites in the grooves; values in the minor groove are given in brackets; the outer lines correspond to phosphate sites.

In the case of K⁺, the distribution of the ion-binding sites appears to reflect the electrostatic potential distribution of an oligomeric DNA fragment. The most occupied sites are located in the centre of the sequence with a strong preference for the major groove. The highest occupancy is 13% at G₇(O6), a similar value to that observed for Na⁺ at T₉(O2). High K⁺ occupancy between interstrand G(O6) in GpC steps has been observed in other studies (22,23). Direct binding in the minor groove also takes place, although with low occupancy values. Binding to phosphates is uniform with occupancies varying between 1 and 6%.

It should be noted that overall the major groove is better than the minor groove for direct binding of either counterion. In relative terms, however, there is more Na⁺ binding in the minor groove compared with K⁺. The accumulated sodium occupancy (calculated from analysis where an ion is assigned to the closest groove atom) is 23% in the minor groove and 36% in the major groove. For potassium, these values are 14 and 45%, respectively. The preferential Na⁺ binding site at T₉(O2) in the minor groove provide an explanation for this fact. Interestingly, despite the different binding patterns of the two counterions, the average number of cations directly bound to base sites of the oligomer is roughly equal (∼1.2 cations per nanosecond) in the two simulations.

It is important to remark that every ion spends some time directly bound to DNA sites during the 50 ns of simulation. The reliability of our results, even for the ‘stickier’ Na⁺, is supported by the fact that many independent binding events occur at a given site along the trajectory. For example, sites on base pair T₉–A₁₆ are visited by 9 different Na⁺ ions in the minor groove and 16 different ions in the major groove. Interestingly, simultaneous occupancy of both grooves at this base pair level, as well as simultaneous binding to base sites in the same groove, were observed several times. Nevertheless, such binding events represent only a small fraction (∼1–3%) of the total simulation time and hence they do not influence the normal behaviour of B-DNA. On the other hand, Na⁺ can have an important structural role in other nucleic acid structures, such as RNA loops (42,43) or the G-DNA quadruplex (44,45), with correlated binding and high occupancies (>50%).

To characterize the dynamics of binding of Na⁺ and K⁺ to DNA, we calculated ion residence times, the number of binding events, the average direct-binding time and the longest duration of binding for sites with high occupancies (Table 2). As noted above, the site T₉(O2) is exceptionally attractive for Na⁺ with relatively few binding events, but with long residence times (381 ps) and a maximum binding duration of 988 ps. Other base sites show more frequent Na⁺ binding–unbinding events (between 65 and 149) associated with considerably shorter residence times (from 73 to 143 ps). Interestingly, the most occupied phosphate sites have residence times comparable with those of the groove sites, ranging from 147 to 372 ps. Overall, these values are of the same order as those obtained in other studies for Na⁺ (20,21). Importantly, however, the binding properties of K⁺ are very different from those of Na⁺. For similar total site occupancies, there were several hundred binding events with much shorter average binding times, of the order of 10 ps. This corresponds well with the picture of a fast-moving K⁺ around DNA that was also indicated by its higher diffusion coefficient.

Table 2. Ion residence time τ, number of binding events (nb), the average direct binding time and the longest duration of binding (ps) for selected binding sites.

Site	τ	nb	<t>	tmax
Sodium
T9(O2)	381	35	169	988
A16(N7)	132	65	64	559
G17(N7)	73	149	22	220
G17(O6)	143	128	32	243
P7(O1P)	372	124	35	880
P10(O1P)	190	132	48	247
P16(O1P)	147	83	46	284
P18(O1P)	192	167	37	373
P21(O1P)	319	190	44	967
Potassium
G5(N7)	43	414	7	136
G7(O6)	66	552	11	156
G17(N7)	6	441	7	84
G17(O6)	59	608	9	104
G19(O6)	69	334	11	245

It is informative to look in detail at the evolution of the occupancy values along the 50 ns simulation time. This is especially important in judging previous, shorter molecular dynamics simulation studies of counterion behaviour around DNA. Binding occupancies are shown for consecutive 5 ns segments of the trajectories in Table 3. Cumulative occupancy values can be calculated from these data for various simulation lengths. It is remarkable that Na⁺ binding to DNA, which is restricted to a few sites, shows very irregular results based on the 5 ns occupancy sampling. For example, G₅(O6) is occupied only during the first and the last 5 ns, and C₁₂(O2) is occupied significantly only after 35 ns. The highest occupancy calculated for a single 5 ns segment is 33% at T₉(O2). In contrast, K⁺ binds to more base sites on DNA and the time distribution is more uniform. High occupancies are observed in the central part of the oligomer, specifically around G₇ and G₁₇. The highest value of 21% was calculated for G₁₇(O6). It is important to note that no bias was visible in the site occupancy values in the production phase of the simulation attributable to the initial (electrostatic potential based) placement of counterions.

Table 3. Binding site occupancy (%) of counterions for selected groove atoms averaged over 5 ns intervals.

Atom	Time
	1–5	6–10	11–15	16–20	21–25	26–30	31–35	36–40	41–45	46–50
Sodium
G5(O6)	14	2	0	0	2	0	0	1	0	12
G7(O6)	8	13	16	2	7	3	3	6	1	7
T9(O2)	15	21	0	7	13	9	11	33	16	9
G10(O6)	2	2	0	7	4	0	0	0	0	0
G10(N7)	0	2	2	9	2	0	0	0	0	0
C12(O2)	0	0	0	0	0	0	2	29	16	11
G13(O6)	0	3	3	6	3	0	7	0	0	0
A16(N7)	9	5	23	14	2	15	5	1	5	0
G17(O6)	9	7	16	4	11	8	8	6	2	10
G17(N7)	1	8	10	15	3	18	5	1	0	2
G19(O6)	17	2	0	0	3	4	0	1	1	8
G19(N7)	1	2	2	1	0	0	0	0	4	5
C20(O2)	0	0	0	1	6	0	2	2	0	1
T22(O2)	0	0	0	0	7	11	0	0	0	0
G24(O6)	0	4	1	4	0	0	2	0	0	10
G24(N7)	0	5	1	2	0	0	3	1	1	8
Potassium
T4(O2)	0	3	0	1	1	0	1	2	2	9
G5(O6)	3	5	13	4	1	8	5	7	3	19
G5(N7)	1	3	2	3	2	1	1	1	2	4
C6(O2)	1	4	2	3	1	8	15	1	4	1
G7(N3)	0	5	0	1	0	9	12	0	3	0
G7(O6)	17	15	18	11	11	9	11	20	3	14
G7(N7)	11	4	12	3	6	5	6	7	1	10
G13(O6)	2	2	3	1	1	0	2	2	1	2
G13(N7)	2	1	4	2	1	0	3	2	3	2
T14 (O2)	0	0	3	4	2	2	0	1	0	0
A16(N7)	7	10	9	6	3	4	1	12	0	3
G17(O6)	13	15	15	11	10	7	8	21	2	12
G17(N7)	8	8	9	9	7	2	4	14	1	6
C18(O2)	2	6	0	2	13	6	0	0	0	0
G19(N3)	1	7	0	3	12	6	0	1	1	0
G19(O6)	4	4	17	5	0	9	6	11	2	19
G19(N7)	3	4	11	3	0	5	4	6	3	6
A21(N3)	1	2	0	0	1	0	0	0	0	0
T22(O2)	0	3	0	2	1	0	3	0	2	11
G24(O6)	0	3	2	0	2	6	2	2	1	0
G24(N7)	0	4	2	0	2	7	3	3	0	0

Binding occupancies of Na⁺ around phosphates again show large fluctuations along the trajectory (Table 4). Several phosphates, such as P₇, P₁₀, P₁₈ and P₂₁, have occupancy values well above 30% for a given 5 ns segment. The rare coordination of two Na⁺ around O1P mentioned above is responsible for an occupancy of 66% between 41 and 45 ns of simulation time. For K⁺, the phosphate occupancy values are again more uniform, rarely >10%, with the single exception of 18% for P₁₆ between 36 and 40 ns.

Table 4. Binding site occupancy (%) of counterions for selected phosphates averaged over 5 ns intervals.

Atom	Time
	1–5	6–10	11–15	16–20	21–25	26–30	31–35	36–40	41–45	46–50
Sodium
P3	0	3	0	2	10	4	2	1	7	1
P4	3	5	3	2	4	2	4	3	3	2
P5	0	4	2	7	3	3	0	3	0	3
P6	3	2	0	3	3	1	5	4	0	7
P7	3	8	3	5	7	5	6	11	40	24
P8	0	0	3	1	3	2	6	12	1	9
P9	8	3	4	3	0	3	15	1	11	3
P10	14	6	6	12	8	6	33	15	28	19
P11	9	5	3	5	2	1	3	3	1	1
P15	5	0	4	2	0	1	4	8	9	1
P16	0	7	6	3	5	13	8	26	6	9
P17	1	1	0	3	5	3	10	6	2	0
P18	4	5	1	9	11	28	34	12	16	11
P19	2	1	4	3	15	6	0	6	7	4
P20	4	0	6	5	0	0	1	2	2	2
P21	4	4	3	6	8	1	12	35	66	34
P22	13	6	7	2	4	1	1	4	3	5
P23	10	5	5	7	2	3	13	3	7	4
Potassium
P3	4	1	2	1	2	4	2	1	4	1
P4	2	2	4	1	2	2	3	2	2	1
P5	3	2	2	3	3	4	3	3	2	4
P6	4	2	3	2	2	2	1	1	2	2
P7	3	3	5	5	3	2	3	2	1	2
P8	2	3	1	2	2	2	3	2	3	3
P9	6	4	3	3	2	1	1	3	4	9
P10	3	4	4	2	7	6	2	1	2	3
P11	1	0	3	3	2	5	4	4	2	3
P15	2	2	1	2	1	2	2	1	3	3
P16	1	1	3	3	6	7	9	18	3	9
P17	4	4	5	2	6	2	2	8	2	2
P18	3	4	3	4	6	5	2	4	2	2
P19	3	2	5	6	6	1	2	3	2	5
P20	2	2	4	5	1	1	4	1	2	6
P21	7	2	2	3	4	1	4	4	2	3
P22	3	2	3	2	2	2	2	3	1	3
P23	2	4	3	2	3	3	2	3	4	2

Influence of ion binding on DNA groove widths and bending

In order to analyse the effect of ions on the conformation of the double helix, we calculated the minor groove width and bending properties, both considered to be sensitive measures of DNA conformation, along the trajectories. Structures were sorted into groups depending on the presence of ions in the minor or major groove, between the phosphates at the entrance to the minor groove, or the absence of ions around the given base pair level. The minor groove width was measured either as an interstrand distance between the two phosphorous atoms, P_i and P_i+3, or by using the Curves algorithm. Both methods gave similar results and hence we present only the average P–P distances along the oligomer for the different structural groups obtained from simulations with either Na⁺ or K⁺ (Figure 3).

Figure 3.

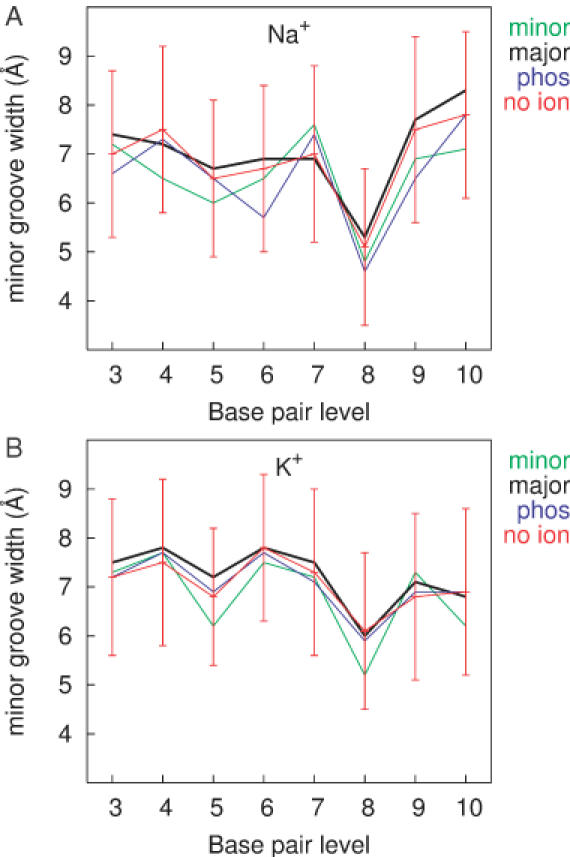
Minor groove width along the sequence calculated for structures sorted according to their counterion positions from simulation with Na⁺ (A) and K⁺ (B). In green is the average width for structures with ions located in the minor groove of the corresponding base pair, black for ions in the major grove, in blue for ions located between phosphates and average values with standard deviations in red correspond to structures without ions in the given zone. The groove width was measured as a P–P distance reduced by 5.8 Å, the sum of the van der Waals radii of two phosphates.

The average groove width along the sequence is rather constant with the narrowest part located at the C₈–G₁₇ base pair level for both counterions. An interesting observation is that the narrowest site of the oligomer does not correspond to the highest occupancy site for either ion. Instead, counterions bind to the neighbouring base pairs, at the T₉ and G₇ levels in the case of Na⁺ and K⁺, respectively. Binding of ions in the minor groove appears to slightly narrow the groove width, an effect varying from 0 to 1.5 Å along the sequence for both Na⁺ and K⁺. Ions in the major groove seem to have a small opening effect on the minor groove, while the presence of counterions between phosphates at the minor groove entrance does not seem to have any consistent influence on the minor groove width. A comparison of the influence of the different counterions shows that the minor groove width is somewhat narrower for Na⁺, along the entire oligomer. However, variations between the structural groups with a given ion at any base pair level or between the different ions are well within the large fluctuations of the minor groove width in the absence of bound counterions. This implies that the flexibility of the minor groove alone could explain the narrow structures seen, without evoking the presence of a bound counterion.

Hamelberg and co-workers (18) have calculated the dependence of the minor groove width on the site occupancy, and obtained a linear dependence with a difference of 2 Å between 0 and 100% occupancy. We repeated this calculation at the narrowest part of our oligomer, around the C₈–G₁₇ base pair level, where recurring Na⁺ binding resulted in long residence times and high occupancy. Our analysis, however, did not lead to any statistically significant correlation for either the base or the phosphate sites. It is important to note in this respect that even during the longest Na⁺ binding event of almost 1 ns at T₉(O2), no clear minor groove narrowing was seen. This might be attributable to the fact that during the same period, several binding events took place in the major groove, which indicates a dynamic equilibrium of monovalent ions in the DNA grooves rather than the exclusive minor or major groove binding in this sequence.

Asymmetric charge neutralization is expected to result in DNA axis bending (46), and DNA bending was found to be influenced by groove-bound counterions in long oligomers containing A-tracts (17). We also analysed the DNA curvature in our sequence using the local helical axis bending angles calculated by the Curves algorithm for each base pair level along the simulation. Bending angles were sorted into groups depending on the presence or absence of ions at the base pair. Our analysis finds only very small effects with differences of 1–2°, compared to standard deviations in bending of ∼3°. This reinforces the finding that the sequence studied here behaves differently from A-tract and G-tract sequences, for which the predominance of ion binding in only one of the grooves was suggested (47).

Finally, using an alternative approach to the question, we selected two groups of 1000 structures having either a very narrow or a very wide minor groove at the level of the C₈–G₁₇ base pair. The DNA structures were superposed using P₁₀ and P₁₉ atoms and the midpoint of the C1′–C1′ vector of the C₈–G₁₇ base pair, and ion positions were recorded if they fell within the direct-binding distance from this plane. We then analysed the ion distributions for these two groups (Figure 4). For Na⁺, the two groups correspond to structures with d_PP < 7.9 Å and d_PP > 14.0 Å, for the narrow and wide structures, respectively. Roughly half of the narrowest structures have counterion in the minor groove, while 330 ions were located in the minor groove of the widest structures. For K⁺, the limiting d_pp for the narrowest and widest minor groove corresponds to 8.6 and 15.0 Å, respectively. There were only 160 and 120 counterions in the minor groove of the narrowest and widest structures, respectively. These results show that although fewer counterions are located in the widest minor grooves, the narrowest minor grooves appear without the presence of any counterion in more than half of the cases.

Figure 4.

Counterion distribution in the minor groove of an average DNA using the 1000 narrowest (left) and widest (right) minor groove structures at site C₈–G₁₇ from simulations with Na⁺ (top) and K⁺ (bottom). Phosphates that were used to measure the minor groove width, P₁₀ and P₁₉, are indicated with black spheres.

An important factor in determining the counterion distribution is the electrostatic potential of DNA. We therefore calculated the surface electrostatic potential using average DNA structures corresponding to either the narrowest or the widest minor grooves discussed above. The results indicate that the potential of electronegative atoms in the minor groove gets more negative with the narrowing of the groove. A patch of low electrostatic potentials was seen at the level of C₆–T₉ in the minor groove of the narrow structure obtained with Na⁺. This area is significantly more negative (−23 kT/e) than the potential in the major groove (−17 kT/e). A similar patch, but with a potential value reduced to −19 kT/e, was observed for the narrow minor groove with K⁺. Finally, the potential in the minor and major grooves become comparable for the wide minor groove structures. Therefore, the preference of K⁺ to enter the major groove cannot be explained by the electrostatic potential of these structures, other factors, such as the size of the hydrated ion and the desolvation free energy must also play a role.

Influence of ion binding on DNA backbone conformations

We have shown that the different types of monovalent counterions exhibit different binding patterns around DNA and that the minor groove widths are somewhat narrower in the case of Na⁺. Nevertheless, no direct coupling of bound ions and groove narrowing could be deduced from our simulations. The narrowest minor groove was located at C₈ in simulations with either counterions and hence this appears to be a feature of this particular sequence rather than an effect of direct ion binding. The analysis of helicoidal parameters and backbone torsions, however, revealed an interesting difference between the two simulations.

Minor groove width variations at level C₈ along the simulation time showed that while the groove width is constant in the simulation with K⁺, it narrows significantly in the second half of the simulation with Na⁺ (Figure 5). Similarly, the twist between the levels C₈/T₉ is roughly constant at 34° in the simulation with K⁺; however, it drops to 20° after a ∼15 ns simulation with Na⁺ (Supplementary Figure S3). We compare variations in backbone torsions α and γ for the two simulations in Figure 6. The most striking observation is that roughly half of the canonical α and γ backbone torsions (gauche⁻ and gauche⁺, respectively, in canonical B-DNA) transit to alternative conformations during the simulation with Na⁺. These mainly include coupled transitions to α/γ:g⁺/t, but α/γ:g⁻/t conformations are also seen as a result of γ flipping to trans. Incidentally, most backbone torsions occur in the G₇–A₁₁ part of the oligomer where increased ion binding was also found. Most transitions occurred after a simulation time of 20 ns, which would explain why this conformational heterogeneity was not discussed in earlier theoretical studies based on shorter molecular dynamics trajectories. Some of the alternative α/γ states flipped back to the canonical form after 10–15 ns, but the rest remained stable until the end of the simulation time. Such α/γ transitions appear to be coupled to reduced twist and minor groove width in the neighbouring base pair steps. A comparison of Table 4 and Figure 6 suggests that the counterion binding to phosphates and the presence of non-canonical backbone are correlated. Curiously, these alternative backbone conformations appeared only in very few instances during the simulation with K⁺.

Figure 5.

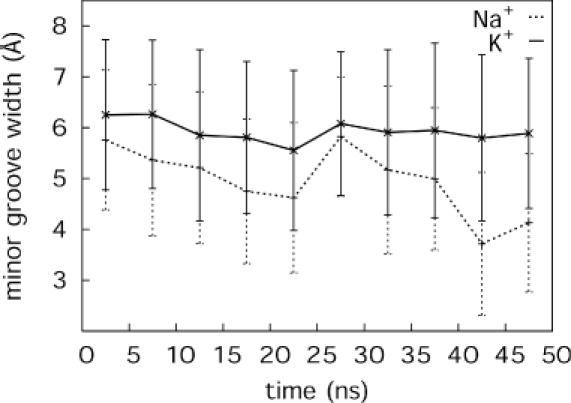
Minor groove width at level C₈ as a function of simulation time. Average values over 5 ns with standard deviation are given for simulation with Na⁺ (dotted line) and K⁺ counterions (solid line).

Figure 6.

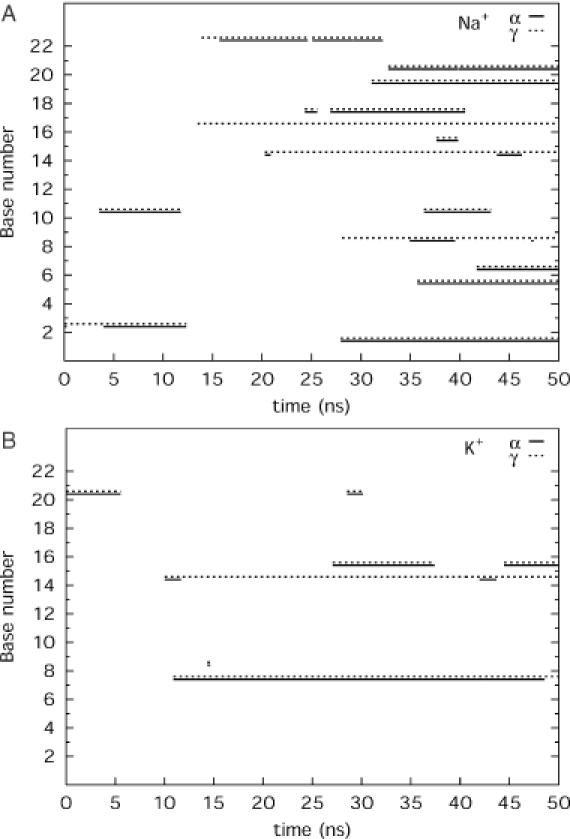
Non-canonical α/γ backbone torsions (gauche⁺/trans) as a function of time for simulation with Na⁺ (A) and K⁺ (B); α in solid line and γ in dotted line.

Non-canonical α/γ states have been observed in crystal structures of many protein–DNA complexes, but only in some particular cases in data of B-DNA oligomers. The spontaneous appearance of alternative α/γ conformations has been reported in early molecular dynamics simulations of B-DNA, with Nuclear Overhauser Effect distance restraints (48,49). A more recent NMR study found γ in trans conformation (50). The sequence studied in the present work has been the subject of an earlier study in our laboratory where the structural and energetic properties of α/γ transitions in the central GpC step were analysed (25). It was found that the lowest free-energy barrier is >7 kcal/mol, and hence the spontaneous occurrence of alternative forms is unlikely. However, the present study clearly shows that backbone transitions are strongly counterion dependent and this raises the question of how the barrier heights are affected by the presence of direct cation binding. Another important problem is the evaluation of this backbone flexibility in different sequence contexts. Undoubtedly, more stringent evaluation of force-field parameters as well as more solution-phase experimental data are needed to clarify this point.

CONCLUSIONS

The behaviour of two commonly studied monovalent counterions, Na⁺ and K⁺, has been analysed around a B-DNA dodecamer containing the target sequence for HhaI cytosine methyltransferase using 50 ns long molecular dynamics trajectories. Our results show that the averaged movement of counterions in the presence of DNA remains diffusive, the movement of K⁺ being much faster than that of Na⁺. Ions sample the complete space available around the solute during the simulation time, but individual ions sample only about one-third of the space.

Ions preferentially visit electronegative sites around DNA, although direct binding to DNA bases is still a rather rare event, with highest site occupancy values not >13%. All ions spend some time in the DNA grooves and the most occupied sites are visited by many different ions during the simulation. The preferred binding sites depend greatly on the nature of the ion: Na⁺ binds mostly in the minor groove around T₉(O2), while K⁺ binds in the centre of the major groove. Interestingly, the A₃pT₄ step, considered as a likely binding pocket in the minor groove, does not show strong ion binding. This indicates that the ion-binding sites may be sensitive to their sequence contexts. Phosphate site occupancy is more uniform along the sequence, but phosphates proximate to bases with high ion occupancy generally exhibit higher fractional occupancy. The Na⁺ and K⁺ exhibit very different binding dynamics. Residence times for Na⁺ range from 100 to 400 ps for highly occupied sites with the longest binding duration reaching 1 ns. In contrast, K⁺ binds and dissociates more frequently, resulting in residence times of <70 ps. These features, along with its dominance in the intracellular environment, make K⁺ particularly well adapted for simulations of DNA.

Using various analysis techniques, we have found no evidence for coupling of monovalent ion binding and changes in local helix geometry. Important structural features of the oligomer (such as the narrow minor groove at C₈–G₁₇) were present in simulations with either counterion and between different groups of structures. Therefore, the structural properties of DNA seem to be coded in its base sequence. Nevertheless, we found differences in the DNA structure depending on the type of monovalent ion used in the simulations. Specifically, non-canonical α/γ backbone conformations appeared mainly in the simulation with Na⁺ and were responsible for reduced twist and narrower minor groove. These α/γ transitions produce long-lived conformational substates on the nanosecond time-scale, which require particular attention in future studies. It cannot be excluded that these conformational substates arise as an artefact of the force field. However, they might have been simply overlooked in experimental studies. The final answer to this question can only come from specially designed experimental studies of nucleic acid backbones.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.