Efficient system-wide coordination in noisy environments

Abstract

Many natural and social systems display global organization and coordination without centralized control. The origin of this global coordination is a topic of great current interest. Here we investigate a density-classification task as a model system for coordination and information processing in decentralized systems. We show that sophisticated strategies, selected under idealized conditions, are not robust to environmental changes. We also demonstrate that a simple heuristic is able to successfully complete the classification task under a broad range of environmental conditions. Our findings hint at the possibility that complex networks and ecologically efficient rules coevolve over time.

Many systems in nature and society display globally organized collective behavior without the need for centralized control. Examples include conventions and norms (1, 2) and social learning in animals and humans (2, 3) as well as fads, rumors, and revolts (4). Examples are also abundant in biology and medicine: the saltation model of human growth (5) speaks of decentralized cellular coordination, as does the transition of Dictyostelium to a multicellular developmental program (6, 7). In each of these examples, a unit changes its state by observing the states of other units relayed by communication pathways. The emergence of a globally ordered condition in these self-organizing systems depends on the units developing strategies based on local information. These strategies are not necessarily, or even typically, “rational” or “error-free.” Rather, units may make mistakes, may be prone to processing errors, and may need to rely on incomplete, possibly corrupted information. Surprisingly, simple strategies perform remarkably well in many experimental environments (8).

A source of complexity in real-world systems is the structure of the communication pathways. The typical idealized picture consisting of agents that are located on a regular matrix and interact with their neighbors is clearly inadequate. Recent studies have demonstrated the intricate structure of the network of interactions of the units comprising complex biological, social, and technological systems (9–11). This complex topology is known to affect the process dynamics and can cast a strong influence on global organization (12).

In this article we demonstrate how complex topology and noise can alter the efficiency with which a system of decentralized units performs a global task. We show that a strategy that is optimal under idealized conditions is susceptible to failure when a complex topology and noise are present. Surprisingly, our analysis reveals that a remarkable degree of coordination can be achieved for more realistic environments through simple heuristic methods. Specifically, we find that a majority rule, for which each unit typically adopts the state of the majority of its neighbors, can efficiently lead to global coordination. We investigate this rule because experimental work in social learning has demonstrated that humans and other animals use this rule in various environments. For example, in food-choice experiments, an individual rat will continue to eat a given food item if most other rats also consume the item, even if the rat experiences induced nausea when eating the food item (3).

Methods

We model system-wide coordination as a computational task. Specifically, we use density classification as a measure of coordination and global information processing (13). For a system comprised of units with a state that is a binary variable, the density-classification task is completed successfully if all units converge to the same state and the coordinated state is identical to the majority state in the initial configuration. Additionally, it is usually required that the time to reach the correct classification scales at most linearly with the number of units in the system. For example, for a system comprising 99 units, initially in a configuration in which 50 units are in state “1” and 49 are in state “-1,” the density-classification task is completed successfully if all units converge to state “1” within 2 × 99 = 198 time steps. Density classification is a trivial task for systems with centralized control; one span of the system immediately yields the correct result. In contrast, a decentralized system performing density classification has to overcome two challenges: (i) information aggregation (the ability to extract global information from local interactions, because each unit accesses only a small fraction of the units in the system) and (ii) system coordination (all units have to converge to the same state).

The Units. Cellular automata (CA) (14) are a widely used class of models of interacting agents evolving according to local rules. The prototypical CA comprises discrete units placed at the nodes of a one-dimensional lattice. The state of each unit is a binary variable: it can assume only one of two values, for example “1” and “-1.” The system evolves in discrete time steps, with the state of all the units being updated simultaneously in accordance with a defined rule. The rule according to which a unit updates its state takes as inputs the state of the unit itself and the states of a finite number k of other units: the neighbors. Each unit knows only its state at each step and can only access information about the units to which it is connected, having no memory about the previous steps. Hence, there is no mechanism for central coordination in CA models. This fact and the versatility in the selection of the updating rule make CA suitable model systems for investigating coordination and global information processing.

Noisy Environments. Noise is an unavoidable component of real-world systems. The noise acting on a system may originate from external factors such as fluctuations in the environmental conditions and from intrinsic properties of the units comprising the system or the way in which they communicate. Naively, one might surmise that the presence of noise must increase the difficulty in completing the classification task. However, it now is clear that, under certain conditions, noise may in fact drive a system toward coordination (15).

We generalize the CA dynamics to incorporate noise in the communication between the units. To update its state, each unit takes into consideration the states of its neighbors. We surmise here that the presence of noise may corrupt the information obtained from the neighbors. Formally,

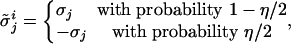[1]

where 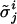is the value unit i reads for the state of unit j, σ_j is the true state of j, and η, which parametrizes the intensity of the noise, ranges from η = 0 (noiseless dynamics) to η = 1 (random dynamics). Note that the noise does not change σ_j, just the value read by unit i.

System Topology. Recent work has demonstrated that the structure of the network of interactions in real-world systems is quite complex. Among the properties of these networks is the small-world phenomenon (12), which implies that pairs of units in the network are typically separated by just a few intermediaries. A small-world topology permits the fast spread of information and can change the efficiency of a system dramatically when performing global tasks.

To build a system with complex topology, we use here the small-world network model of ref. 12, but the results we obtain are robust to changes in topology as long as the small-word property is present. In the model of ref. 12, the network is built in two steps. First, an ordered network is created by placing the units on the nodes of a one-dimensional lattice with periodic boundary conditions. Each unit is then linked to its k nearest neighbors in the lattice. Next, one rewires, with probability p, each of the links in the network.§ The rewired links are redirected to a randomly selected unit in the lattice.

By varying the value of p, the system spans topologies from the ordered one-dimensional lattice (p = 0) to a random graph (p = 1). Despite its simplicity, this model has been shown to capture two important properties of real-world networks: local cliquishness and the small-world property (12). Another property observed in many real-world networks is a scale-free topology (11). To test the generality of our results, we also address the effect this property has on systems performing the density-classification task.

Classification Efficiency. The efficiency E_φ(p, η, N) of an updating rule φ is a function of noise intensity η, rewiring probability p, and system size N. As stated above, the density-classification task is completed successfully if all units converge to the same state and the coordinated state is identical to the majority state in the initial configuration. We perform 1,000 realizations of the system for each set of parameter values and estimate E_φ(p, η, N) as the fraction of times the system reaches the correct classification within 2N time steps.¶ For each realization of the parameter values, we choose the initial configuration at random with each of the units having equal probability of being in each of the two states. Additionally, when p ≠ 0, we generate a different rewiring pattern for each realization.

Density Classification with the Gacs–Kurdyumov–Levin (GKL) Rule

Noiseless One-Dimensional Environments. Crutchfield and coworkers (13, 16) studied the case η = 0 and p = 0. They considered a system in which each unit receives inputs from three neighbors on each side, i.e., k = 6. This value of k implies that there are in excess of 10³⁸ distinct rules, making it virtually impossible to search for the one that performs the task with optimal efficiency. To solve this difficulty, Crutchfield and coworkers used genetic algorithms. They found that the population of rules evolved toward a small number of efficient rules. Interestingly, none of them showed higher efficiency than the GKL rule (17),

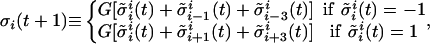[2]

where G(x) is a step function

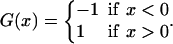[3]

The mechanism by which the GKL rule leads to a consensus can be understood by noticing that a unit i assumes the state of the majority of a set of units comprising itself and its first and third neighbors, making the decision based only on its left or right neighbors depending on its state. The GKL rule thus gives rise to dynamics in which the units evolve toward a configuration of domains with boundaries that move through the system in opposite directions. Quite rapidly, the domains merge and all units attain a consensus state (Fig. 1A).

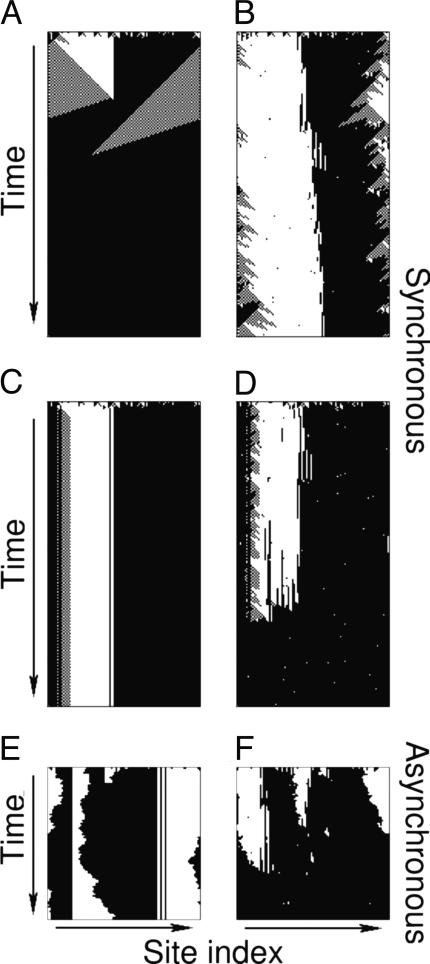
Fig. 1.

Effect of noise intensity η and rewiring probability p on the time evolution of a system of CA operating according to the GKL rule (17). We consider systems starting from random configurations that are allowed to evolve for 2N time steps, where N = 99 is the number of units in the system. (A) p = 0 and η = 0. In this case, which corresponds to the classic GKL rule, the system shows the sophisticated dynamics studied in ref. 13 with the boundaries of the domains traveling in opposite directions. The domains quickly merge, and the units find a consensus state. (B) p = 0 and η = 0.05. In this case, the noise destabilizes the dynamics of the domains, and the system does not converge to a consensus within 2N time steps. (C) p = 0.05 and η = 0. Without the regularity of the one-dimensional lattice, the GKL rule is unable to process local information properly. As a result, the system typically reaches a stable configuration but does not converge to a consensus. (D) p = 0.05 and η = 0.05. It is surprising that when both noise and rewiring are present, the system is able again to converge to consensus. (E) With asynchronous updating, the GKL rule is not capable of coordinating the domain dynamics, and the system does not reach the consensus when p = 0 and η = 0. (F) p = 0.05 and η = 0.05. For asynchronous update, a system with both noise and rewiring still converges to a consensus. As we will see later, in the presence of noise and rewiring, the GKL rule operates analogously to the majority rule.

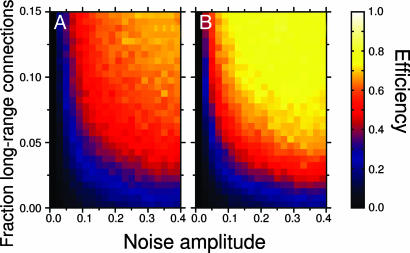
Noisy Environments with Complex Topology. To investigate the efficiency of the GKL rule in more realistic environments, we studied the rule for different values of noise intensity η and rewiring probability p (Fig. 1). Fig. 2 displays the efficiency E_GKL(p, η, N) of the GKL rule in the phase-space (η, p). The high efficiency observed by Crutchfield and coworkers for η = 0 and p = 0 is lost if only noise or only rewiring is introduced. If both noise and rewiring are present, however, the system still reaches an efficient regime.

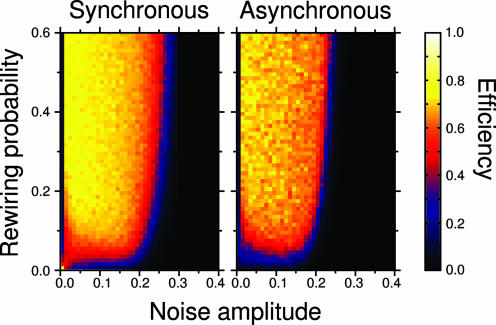
Fig. 2.

Efficiency of the GKL rule in performing the density-classification task for different updating schemes. We systematically investigate the efficiency of systems under different intensities of noise and rewiring probability. When all units update their states synchronously, we find the highest efficiency when p = 0 and η = 0. If η = 0 and p ≠ 0 or η ≠ 0 and p = 0, then the efficiency of the GKL rule decreases dramatically. An efficiency of ≈0.75 is achieved for a large range of parameter values when both noise and rewiring are present. In this regime, the GKL rule performs as a sort of majority rule. It is significant that when using asynchronous update the system is not in the efficient regime when p = 0 and η = 0. These results confirm that the GKL is not a robust rule, i.e., is a rule optimized for very restrictive conditions.

Asynchronous Updating. In traditional CA models, units update their states simultaneously at every time step. This synchronous evolution is computationally efficient but artificial. Fig. 2 demonstrates that the efficiency of the updating rules changes when the system evolves asynchronously.∥ Surprisingly, we find that a noiseless one-dimensional system with units that conform to the GKL rule cannot reach a consensus with an asynchronous update (Fig. 1E). Thus, the success of the GKL rule in the condition p = 0 and η = 0 truly depends on it being implemented in a very restrictive and unrealistic environment.

Density Classification Through Heuristic Methods

In the density-classification problem, each unit has to evolve toward the correct final state with only local information about the current configuration of the whole system. As discussed above, the sophisticated strategies devised to solve this problem rely on an organized structure of interactions, in which the units need to have a precise notion of the state of their neighbors, as well as the position of the neighbors in the network. Although these strategies perform well in idealized environments (17–19), in real-world decentralized systems the environment is rather more complex. It thus is reasonable to hypothesize that in real-world systems the units make their decisions by using simple heuristics that are robust against errors and do not depend on the precise structure of interactions.

A plausible heuristic to reaching a consensus is to adopt the majority state of one's neighbors (2, 3). In the CA class of models, this strategy is described by the rule

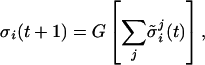[4]

where G is the step function defined in Eq. 3. We display in Fig. 3 the time evolution of a system of units obeying the majority rule. Unlike the GKL rule, the majority rule is inefficient in the limits η → 0 and p → 0. Under these conditions, a system of units obeying the majority rule evolves toward a stationary configuration of alternating domains, never reaching a consensus. This result is not changed when p << 1 (Fig. 3A) (20), but a different picture emerges when both noise and rewiring are present (Fig. 3B).

Fig. 3.

Effect of noise intensity η and rewiring probability p on the time evolution of a system of CA operating according to the majority rule. We consider three systems comprising N = 99 and starting from the same initial configuration. As for the GKL rule, k = 6. (A) p = 0.05 and η = 0. The small-world topology alone has little effect on the evolution of the system, which rapidly converges to a configuration of stable domains of alternating states, similar to what is expected for a one-dimensional lattice. (B) p = 0.05 and η = 0.1. In this case, the noise destabilizes the boundaries of the domains. However, with only a few long-range connections, the system evolves slowly and some of the domains persist until the end of the simulation. (C) p = 0.1 and η = 0.1. In this case, the larger value of p enables local information to spread quickly, and all units rapidly evolve to a consensus.

Noiseless Environments. Watts (20) studied the efficiency of the majority rule in performing the density-classification task in noiseless environments. Watts surmised that in noiseless environments, the system reaches an efficient regime only for a rewiring probability for which each unit typically has one rewired connection, which implies that the critical rewiring probability p_c for which a transition to the efficient regime occurs is independent of system size, depending only on the average connectivity as p_c ≈ 1/k (20). We tested this hypothesis and found that the conditions to reach the efficient regime in a noiseless environment are considerably more strict: p_c increases with the system size, approaching 1 as N ≈ ∞ (Fig 4A).

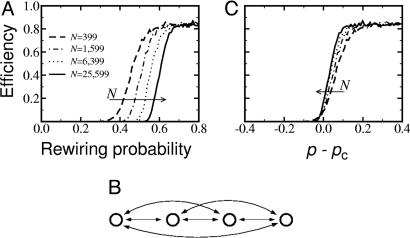
Fig. 4.

Efficiency of the majority rule in noiseless environments. (A) E_maj for k = 6, η = 0, and different system sizes as a function of p. When noise is not present, a system evolving according to the majority rule can perform the density classification only for large values of p. Note that the critical value p_c at which the system reaches the efficient regime increases with increasing system size. (B) A block of four locally connected units. Each unit has three connections to the other units in the block. Without noise, whenever all the units in the block attain the same state, they will not switch states even if all the rest of the system converges to the opposite state. (C) Onset of the transition to the efficient regime. The efficient regime is achieved when p is large enough so that there can be no blocks of locally connected units. From Eq. 5, one has p_c ≈ 1 - N ^{-[4/(k2 + 2k)]}. As the figure shows, when one subtracts the expected value of p_c, the onset of the transition of all curves collapse to a value close to zero.

As Watts (20) notes, the amount of rewiring needed to reach the efficient regime is larger than that needed to reach the small-world regime. We hypothesize that the reason a system may not reach consensus, even when in the small-world regime, is the presence of blocks of consecutive units that do not rewire the connections internal to the block (Fig. 4B). For a noiseless system, the probability that a sequence of (k/2) + 1 neighboring units will be connected in such a way that they can maintain a minority state even if all the other units in the system are in the opposite state is simply (1 - p)^k/2[(k/2)+1]. One thus expects a system of N units to reach the efficient regime when the probability with which such sequences occur becomes very small:

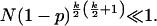[5]

Fig. 4C gives support to this hypothesis as it shows that Eq. 5 provides a good approximation to the onset of the transition to the efficient regime.

These blocks of units are remnants of the local structure of the network. Thus, the necessary condition to reach the efficient regime in a noiseless environment is that p is large enough that no local structures remain. In this regime, the network is no longer a small world; instead, it is a random graph. It should be noted that in a random graph the neighborhood of every unit is a random sample of the whole network. Thus, more units switch to the state of the majority in the first step, which continues in the following steps in a bootstrap process. After a few time steps, all units converge to the same state. In this regime, the density classification is a rather trivial task; because all units have access to global information.

Noisy Environments. Fig. 5 displays the values of E_maj(p, η, N) in the phase-space (η, p) for different values of k. The efficiency of the majority rule increases with the number of connections. For k = 6, the case for which the GKL rule was optimized, the efficiency of the majority rule reaches a value of 0.85, which is greater than what is obtained with the GKL rule under the idealized conditions η = 0 and p = 0. Strikingly, unlike the GKL rule, the majority rule yields efficient coordination even for asynchronous updating.

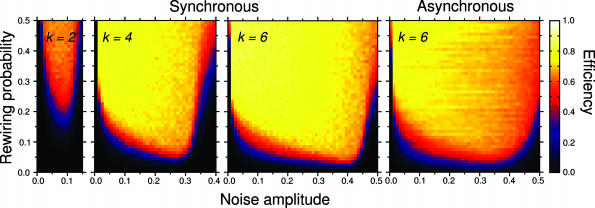
Fig. 5.

Phase-space (η, p) for systems evolving in accordance with the majority rule. We systematically investigate systems of size N = 399 with number of connections k = 2, 4, and 6. As could be expected from the results shown in Fig. 3B, the majority rule performs poorly when p = 0. However, when long-range connections are included, the system displays a very high value of efficiency for a wide range of noise intensities. The efficiency increases with the number of connections, reaching a maximum value of ≈0.85 for k = 6. With asynchronous updating, the majority rule still displays efficient behavior in a large region of the (η, p) phase space. Thus, the majority rule is a highly robust and efficient strategy for performing a global computation from local information.

Thus, one can understand the role of each of the components in this condition. The noise enables the system to escape conformations with multiple domains. When p = 0, the boundaries move as random walks. For small values of η, a unit with all its neighbors inside a domain is very unlikely to be affected by the noise. In contrast, a single corrupted signal is enough to change the state of a unit at the boundary of two domains. Eventually some domains collapse, and the system converges to consensus in a time of order N² (21–24, **). Thus, the role of noise is to allow the boundaries of the domains to move and assure that the system will not get trapped in a metastable configuration with multiple domains.

The rewiring of the connections allows fast access to information from across the system, i.e., the long-range connections make the system a small world. When p ≠ 0, the units in the boundary of the domains may get an input signal from a rewired connection. Given the current distribution of states, a rewired connection is more likely to send a signal consistent with the majority. Importantly, the small-world phenomena is not enough to ensure the convergence to the correct classification. Even after rewiring there is always a large probability that the system will evolve toward conformation with multiple stable domains. Only with the combined effect of the noise (enabling the system to escape the metastable states) and the small-world topology (giving a bias to the movements of the domain boundaries) can the system reach a consensus within the permitted evolution time.

Systems with Scale-Free Topology. Many real-world networks display a scale-free distribution of number of connections (11). To test the effect that degree heterogeneity casts on the ability of a system to perform the density-classification task, we perform simulations in which the degree associated with the number k_r of rewired connections follows a power-law distribution (Fig. 6). We obtain a power-law distribution by selecting the long-range connections not at random but by using a preferential attachment rule (11). We find that if the nodes with more outgoing connections (which have a global influence on the system) are also the ones with more incoming connections (which access information from the entire system), then there is a global spread of information, allowing the system to reach the efficient regime.

Fig. 6.

Density classification for a scale-free network topology. (A) If only the distribution of outgoing links decays as a power law, some of the units, the ones with more outgoing connections, cast a global influence on the system while accessing only local information. These units act as “blind” leaders, determining the evolution of the system without querying the state of the majority of the units. In this case, the scale-free topology decreases the efficiency of the majority rule. (B) A different picture emerges if the longrange connections are bidirectional. Then, the units that influence a large number of other units also access a large amount of information. In this case, the system is able to reach consensus and attains an efficiency of 0.8.

In contrast, if only the distribution of outgoing connections is scale-free, the efficiency is reduced. The inefficiency in this case is not caused by a difficulty in reaching a consensus but by the fact that, with this topology, the consensus is determined not by the majority but by only the most connected units. This may explain why in some communication systems, such as the network of social acquaintances and the neuronal network of Caenorhabditis elegans (in which the evolution of network topologies depends on the efficiency of information aggregation), one does not find scale-free topologies (25).

Transition to the Efficient Regime

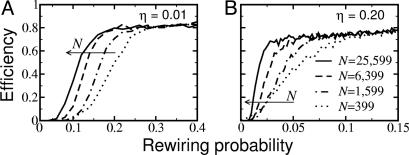
The majority rule undergoes a transition from an inefficient to an efficient regime as p increases. To characterize this transition quantitatively, we plot in Fig. 7 the efficiency as a function of the rewiring probability for k = 6 and different system sizes. It is known that the small-world regime emerges for probabilities that scale with system size as 1/N (26, 27). Our data demonstrate that the transition becomes more abrupt as N increases, which suggests that the only condition to perform the density classification in a large system is the presence of noise and the small-world regime.

Fig. 7.

Transition to the efficient regime in noisy environments. We plot the efficiency of the majority rule for systems with k = 6 and η = 0.01 (A) and η = 0.20 (B). Note that, when noise is present, the transition becomes sharper, and p_c → 0 as N → ∞.

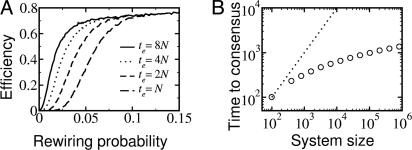
To test this hypothesis, we determine the limiting value of p_c as N → ∞. Specifically, we study the efficiency of the majority rule as a function of the rewiring probability when varying the evolution time t_e, i.e., the number of time steps the system is allowed to evolve to reach the classification. Fig. 8A shows that the onset of the transition moves toward smaller values of p as t_e grows. Note that the efficiency of the systems with larger p does not increase when one lets the system evolve for longer times. In this regime, all realizations converge to a stationary configuration with all units in the same state, the consensus. The asymptotic value of E in this efficient regime indicates the probability that the system will reach a consensus with the correct classification. In the inefficient region of the phase-space (η, p), the system does not reach a consensus within the allotted evolution time.

Fig. 8.

The time needed to reach a consensus. (A)Efficiency as a function of the rewiring probability for systems with η = 0.2, N = 1599, and different values of total evolution time t_e. When the system is allowed to evolve for longer times, the transition moves toward smaller values of p. The shape of the curve after the transition is independent of the evolution time, indicating that the system always reaches a stationary configuration with all the units in consensus. The efficiency in this region depends on the number of times the system evolves to the correct classification. (B) Mean time 〈t_c〉 to reach consensus as a function of the system size, for systems with p = 0.1 and η = 0.25. The dotted line corresponds to the linear behavior. It is visually apparent that 〈t_c〉 displays a sublinear growth with system size.

The dependence of p_c on N can be determined indirectly by studying how the time t_c to reach a consensus increases with system size. An increase of t_c faster than linear means that there cannot be an efficient regime in the N → ∞ limit, whereas an increase of t_c slower than linear means that the efficient regime is reached for p > 1/N. The data in Fig. 8B demonstrate that 〈t_c〉 grows slower than the system size, implying that 〈t_c〉/N → 0 in the limit of large systems. As a consequence, the onset of the transition to the efficient regime will move to smaller values of p as N increases, i.e., p_c → 0 when N → ∞.

Discussion

Our results demonstrate that noise and topology critically affect the performance of strategies for achieving global coordination and information aggregation. Rules such as GKL, which perform well in noiseless, regular environments, are inefficient if complex topologies and noisy information transmission are present. In contrast, simple heuristics such as the majority rule investigated here are efficient in exactly such environments. Because real social and natural networks are characterized by noisy transmission and complex, small-world topologies, our findings provide an explanation for the observed use of such social-learning heuristics by animals and humans (2, 3).

Furthermore, our results suggest that decision rules cannot be evaluated in isolation from the environment of their system. That is, their success in coordinating behavior and aggregating information depends on both the rule and the typical environment in which it is used. In this sense, the majority rule is “ecologically efficient”; it is well suited to interaction systems that resemble the real world. Put together, our findings hint at the possibility that networks and ecologically efficient rules coevolve over time.