Abstract
The chemical kinetic description of time evolution where the phase is random but the states are discrete is discussed as a basis for a computational approach. This proposed scheme uses numbers in the entire range of 0 to 1 to represent Boolean propositions. In the implementation by chemical kinetics these numbers are the mole fractions of different species. Vibrational relaxation in a mixture of HCl and DCI is the physical system that is used to illustrate the approach. Energy exchange in such a mixture corresponds to two strongly coupled two-level systems. A search problem, previously discussed in the quantum computing literature, is solved as an example. The solution requires the same number of function evaluations as in the quantal case. The action of the oracle is described in detail.
The basic element of current logic devices is a switch. It is either on or off. This corresponds to the two possible values, say 0 and 1 or true and false, of a Boolean variable. The values of physical observables are not usually either 0 or 1. A molecule is not easily made to act as a switch. On the other hand, molecules exhibit a rich dynamical behavior that we would like to take advantage of so as to perform logic operations.
In this article we focus on what is, to us, a rather common characteristic of molecules. It is that molecules can be classified into discrete alternatives. The simplest such distinction is the very idea of a chemical species. The operational definition of a molecule is made possible by the (relative) stability of the entities we know as atoms and by the atoms combining into molecules in simple and definite proportions. Thereby a molecule can be identified to be, say, HCl and not HBr or any other diatomic one. A finer but still operationally fully viable resolution is that molecules of a given chemical species can be identified to occupy definite quantum states (or groups of states). Except for special circumstances it is typical of molecules that the quantum mechanical phase of its states is random. So the different states of molecules act as discrete and mutually exclusive classical alternatives. This state of affairs is what we mean by quasiclassical. We want to perform logic operations by taking advantage of the probabilities of occupancy of the different quantum states that are resolvable in an experiment. By the end of this article we intend to show, by an explicit example, that this is possible.
To implement our program we need input from several directions. In this introduction we review the different ideas that we intend to invoke. Then we describe a solution of a particular problem with special reference to what is the logic problem that we claim to solve, what is the physical system that is used, and how we set up the interface between them.
We do not use the phase of the quantum mechanical state because we propose to operate under conditions where this phase is random. Starting with the work of Deutsch (1, 2), there is an extensive current literature emphasizing the critical computational advantages that can accrue when the elementary logic operation is a unitary transformation on a quantum mechanical state vector (3–8). As discussed in many papers there are two very essential new features brought in by quantum mechanics. One is the linearity of quantum mechanics that allows the creation of superposition of states and hence parallels the computation. The other is the entanglement-enhanced processing (9, 10). Both of these important advantages make essential use of both the phase and the amplitude of the state, and so any application is sensitive to dephasing processes. There is much progress in quantum error correcting algorithms (4, 6). On the other hand, starting with the work of Ehrenfest in the old quantum theory, we know that action variables are much more robust to perturbations than angle variables (11). It is the quantum numbers, which correspond to action variables, that we use. We take it that both intermolecular and intramolecular perturbations have had sufficient time to act to randomize the phase.
Chemists have traditionally taken it for granted that the phase is random. For the chemists it is the possibility of a coherent superposition that is in need of demonstration. The systematics of chemistry is based on our ability to categorically say that a molecule is HCl and not, say, DCl, (D is the heavier isotope of H). The Gibbs paradox is a paradox when we phrase it so as to imply that molecules are either identical or completely different. Chemists on empirical grounds and Einstein and von Neumann on thermodynamic grounds went further to argue that we can say that the HCl molecule is either in the ground vibrational state, ν = 0 or in the first excited vibrational state, ν = 1. It is the case that one could, although not so easily for a molecule with a high vibrational frequency as HCl, prepare a coherent superposition of the ν = 0 and ν = 1 states of a molecule. One certainly can prepare a coherent superposition of different rotational states and such rovibrational coherent superpositions have been proposed for molecule-based quantum computing (12, 13). But on a longer time scale molecular states decohere quite rapidly. Quite often the initial fast dephasing is not necessarily caused by external perturbations but is intramolecular in origin, being caused by the anharmonicity of the motion that means that the period is energy dependent (14). Perturbations then prevent the dephased system from ever recurring. Our approach in this article is that at the time of probing the system we take the phase to be random.
Our long-term interest is in computing on the molecular scale (15–17). In this article we want to stress that we do not in any way use phase information in our computational scheme. The science that describes the evolution of macroscopic chemical systems in time is chemical kinetics. Chemical kinetics (implicitly) makes the random phase approximation and this is what we mean by quasiclassical. We take from quantum mechanics the notion of discrete quantum states, and we describe a molecule in a definite quantum state (or disjoint group of states) as a particular species. Notwithstanding the possibility of interference, in this article we take the observed occupancies of such species to be mutually exclusive. A molecule can be found to be either this species or another species but not both. There have been suggestions on how to use chemical kinetic networks as combinational logic circuits (18). These schemes require that the concentrations of species be switched essentially completely on or off. It is an aspect of our proposal that variable concentrations of the different species are allowed. It is the fractional concentrations, what chemists call mole fractions, that provide the probabilities that we use in our scheme. In chemical kinetics it is the collisions between molecules that lead to changes in these probabilities.
To demonstrate our approach we will discuss a particular problem. Since we want to compare with quantum computation we discuss what is arguably the canonical problem, due to Deutsch, whose solution is usually known as the Deutsch–Josza algorithm. We will use a variant of the Deutsch problem that can also be viewed as a search problem. We want to pick one among four alternatives, and we want to do it in two (linear) operations.
There are three ingredients in our approach. First is the use of not necessarily 0 or 1 valued numbers to represent Boolean propositions. Cox (19, 20) has shown that the probability of a proposition is such a function. The work of Cox is discussed by Tribus (21) and Jaynes (22). The final result is that starting with a Boolean algebra of propositions we have a consistent and unique scheme for relating numerical values of probabilities. By choosing the value of the probability of a proposition to be in the range zero to unity the resulting rules for compounding the values of probabilities are the very same ones given in every textbook on probability and all the needed rules can be derived from
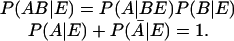 |
The bar denotes the negation of a proposition and the notation AB means the logical AND.
What the work of Cox provides for us is the calculus of probabilities for propositions that can be either true or false. These propositions are to be compounded as in a Boolean algebra. The use of Boolean algebra is not possible when one seeks to generalize to quantum mechanical propositions because of the possibility of interference. In the quasiclassical limit we deal with propositions that can be compounded by using the distributive law.¶
The second ingredient is the definition of the problem we aim to solve. A function of one Boolean variable can be evaluated at the two different values for its argument, x = 0 or 1. There are therefore four Boolean functions of one variable. They fall into two classes depending on their values at the two points. If the two values of the function are the same then we call the function a constant and there are two such functions [f(x) = 1 and f(x) = 0]. A balanced function is when one value equals zero and the other equals unity. There are two such functions [f(x) = x and f(x) = x̄ where the bar denotes the negation]. The original Deutsch problem is to determine whether a Boolean function of one variable is constant or balanced by using just one function evaluation (2). An extension is to identify an unknown Boolean function of n variables that is given to be either constant or balanced. The problem is to determine which, using n function evaluations (23). Another generalization (24–26) is to distinguish between Boolean functions of n variables that are of the type 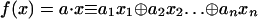 , where a is an n dimensional Boolean variable and
, where a is an n dimensional Boolean variable and 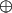 is addition modulo two. For the 2D case the Boolean variable a can assume four different values and the four functions of the form a · x are listed in Table 1. The problem we solve in this article is to identify which one of the four functions, using just two function evaluations. The extension to higher values of n is to use just n function evaluations to distinguish between the 2n possible functions of the form a · x.
is addition modulo two. For the 2D case the Boolean variable a can assume four different values and the four functions of the form a · x are listed in Table 1. The problem we solve in this article is to identify which one of the four functions, using just two function evaluations. The extension to higher values of n is to use just n function evaluations to distinguish between the 2n possible functions of the form a · x.
Table 1. Values of the four functions a · x for the four possible values of a, at the four possible arguments x.
| x/a | 0,0 | 0,1 | 1,0 | 1,1 |
|---|---|---|---|---|
| 0,0 | 0 | 0 | 0 | 0 |
| 0,1 | 0 | 1 | 0 | 1 |
| 1,0 | 0 | 0 | 1 | 1 |
| 1,1 | 0 | 1 | 1 | 0 |
The other notion we need from the discussions of quantum algorithms is that of an oracle. The oracle is a device that is able to recognize the solution to the problem (3). It is sometimes also called a black box. In this article we describe the inner workings of our oracle.
The third ingredient is the physical system whose time evolution specifies which one of the four different Boolean functions of the type a · x (and listed explicitly in Table 1) is the answer. It is two two-level systems coupled to one another. One system is a gaseous mixture of HCl in the ground and the first excited vibrational states. Left on its own this system will relax exponentially back to thermal equilibrium (14). The other system is a mixture of DCl in its ground and first excited vibrational states. It, too, will relax on its own. But following Chen and Moore (27, 28) we use a mixture of HCl and DCl. The two systems are then strongly coupled by the one quantum exchange process
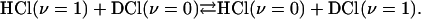 |
All other relaxation processes in an HCl/DCl mixture do not conserve the number of vibrational quanta and are less efficient. The four propositions that we use for computing are the chemical identity of the molecule (HCl or DCl) and the vibrational state (ν = 0 or 1). The probabilities are the concentrations of these different four species normalized to a given total.
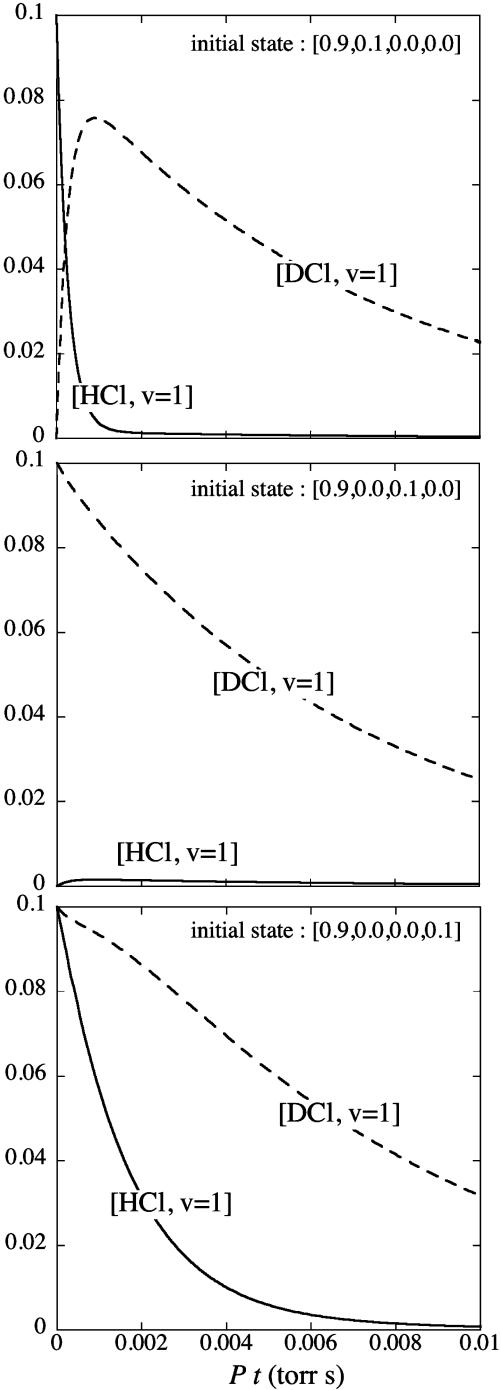
The kinetics of the HCl/DCl mixture were thoroughly studied (27, 28) by using an HCl laser to pump the HCl molecules in the gaseous mixture to the ν = 1 state. In the numerical example shown in Fig. 1 we use the rate constants that were measured. One can also use a DCl laser to pump the DCl component. It is also possible by pumping to distinguish between HCl molecules with the lighter or heavier isotope of chlorine (29, 30).
Fig. 1.
Fractional concentration of HCl in ν = 1 and of DCl in ν = 1 vs. time for three different initial states as determined by integration of the kinetic scheme. The initial state is given as pT (0). For the do nothing initial state (data not shown), the system remains in thermal equilibrium. The rate constants are given in the text and satisfy detailed balance. Time is scaled by the pressure in Torr.
The Oracle
The oracle we use specifies an initial state for the dynamics. Explicitly, it specifies whether to laser excite HCl or DCl or neither or both.
The Boolean functions that we want to distinguish are the four functions of the form a · x of the 2D Boolean variable x, x ≡ {x1, x2}. The scalar product is defined as 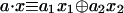 and a can assume one of the four values 0,0; 0,1; 1,0; and 1,1. Table 1 lists the values of the four functions at the four possible values of their argument x. The possible values of each function are given as a column identified by the value of a.
and a can assume one of the four values 0,0; 0,1; 1,0; and 1,1. Table 1 lists the values of the four functions at the four possible values of their argument x. The possible values of each function are given as a column identified by the value of a.
The two function evaluations that we use are the values of f(0,1) and f(1,0). The oracle performs them. For the four possible values of a the two evaluations yield four distinct pairs 0,0; 1,0; 0,1; and 1,1. In the kinetic scheme 1,0 is the condition HCl excited to ν = 1 whereas 0,1 is the condition DCl excited to ν = 1. Inspection of the rows corresponding to x = 0,1 or 1,0 shows that the two function evaluations specify different outputs for the four possible values of a. The four different outputs are then used as initial conditions for the kinetic scheme. Fig. 1 shows that, using realistic values for the rates of energy transfer processes, one can easily discern between them.
There are other oracles that could be constructed for identifying one among four possibilities. For example, we may want to distinguish four possibilities defined as follows: A function of two Boolean variables can be evaluated at four different values for its arguments. We label these four points as 0,1,2,3. There are 16 Boolean functions of two variables. They fall into four classes depending on their values at the four points. If all four values of the function are the same then we call the function a constant. A balanced function is when two values equal zero and two equal unity. Or the function can be true at just one point or the function can be true at three points. The oracle is to recognize which of the four classes the function belongs to, using just two function evaluations.
The first evaluation computes the parity of the function:
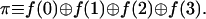 |
The parity is 0 if the function values at the four points have an even number of unities and the parity equals 1 otherwise. The parity will distinguish between the constant and balanced functions (eight functions all together) on the one hand and the other eight possibilities.
The second evaluation computes σ, the sum (modulo two) of all possible binary products
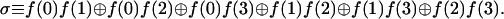 |
This sum is a parity check on the binary products meaning that the value of σ distinguishes between those classes of functions where the number of nonzero binary products is even or odd. For the functions for which π = 1, σ resolves the constant (σ = 0) and the balanced (σ = 1) functions and for the two classes with an odd number of 1s, it will distinguish between those that have one value that equals 1 (σ = 0) and those that have three values of 1 (σ = 1). It should be noted, however, that the evaluation of σ is not linear in the unknown function.
With two evaluations giving the values of σ and of π the oracle knows the class that the unknown function belongs to. Specifically, the four classes are encoded by the four values 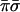 ,
, 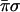 ,
, 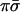 and πσ. Any one of the possible 16 functions will produce only one output that is not zero. The output that is unity identifies the class. A yet alternative oracle with the same purpose works to base 4. Then just one function evaluation of the parity to base 4, which is equivalent to two evaluations to base 2, will suffice to recognize the class.
and πσ. Any one of the possible 16 functions will produce only one output that is not zero. The output that is unity identifies the class. A yet alternative oracle with the same purpose works to base 4. Then just one function evaluation of the parity to base 4, which is equivalent to two evaluations to base 2, will suffice to recognize the class.
Kinetics
The aim of the kinetic scheme is to demonstrate four distinct temporal outputs that can be used to distinguish the four functions listed in Table 1.
The probabilities that we operate with are the mole fractions of the different species.
We consider a mixture of HCl and DCl plus possibly some inert buffer gas such as Ar at a low total pressure (say in the range 1 to 50 torr). Our description follows Moore (28) and Chen and Moore (27). At thermal equilibrium at ordinary temperatures both the HCl and DCl molecules are very predominately in their ground, ν = 0, vibrational state but we take it as given that the system can be pumped away from equilibrium by rapidly raising the concentration in the ν = 1 state of HCl or of DCl molecules or of both.
When the mixture is displaced from equilibrium very fast near resonant vibration–vibration transfer collisions
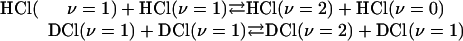 |
[1] |
are possible. These are so efficient that on the μs time scale of interest to us here they can be taken to have equilibrated the ν ≥ 1 states. The fastest process that we probe is the not quite resonant transfer
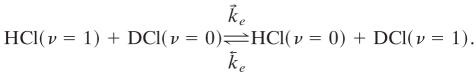 |
[2] |
This takes many thousands of collisions to reach equilibrium (cf. tables 1 and 2 of ref. 27). The vibration to translation and rotation cross relaxation processes
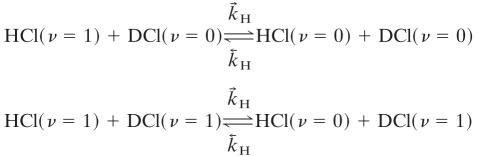 |
[3] |
are less efficient by an order of magnitude or so because of the high value of the HCl vibrational frequency (2,886 cm-1). The other cross relaxation processes are
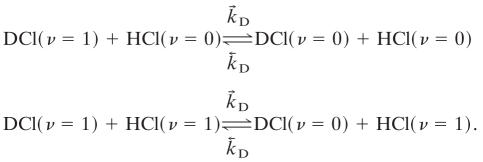 |
[4] |
The three processes (2–4) give rise to three distinct eigenvalues and eigenvectors of the relaxation kinetics. Process 2 drains excited HCl molecules via excited DCl molecules as intermediates. Process 3 drains excited HCl molecules directly to the ground state, whereas process 4 drains excited DCl molecules without significantly exciting HCl along the way because process 2 favors the left to right direction as written. Actual simulations are shown in Fig. 1. There are other processes that are possible but we do not include in the kinetic scheme. One is the vibration to translation/rotation relaxation of HCl (ν = 1) by collision with HCl (ν = 0). Others include vibration to translation/rotation relaxation by collisions with Ar, processes that are far too inefficient to effectively compete.
There are four events, and we denote their probabilities as [νHCl, νDCl], where the νs are vibrational quantum numbers and the meaning is that of AND. So, for example, the concentration of DCl in ν = 1 is ([1,1] + [0,1]) PDCl, where PDCl is the partial pressure of DCl. To keep it simple we take the partial pressures of HCl and of DCl to be the same. The kinetic scheme is then
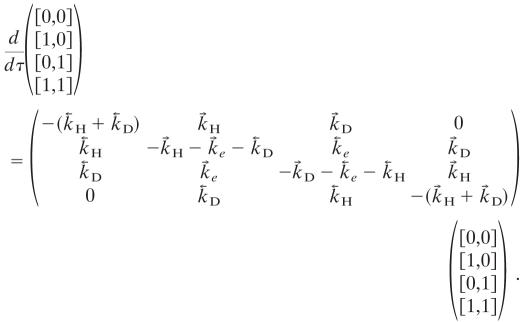 |
Here τ is time measured in the units torr · sec, where torr is the unit for the value of the partial pressure P.
The relaxation matrix, A, can be diagonalized by a similarity transformation, A = U-1 λU, where λ is a diagonal matrix so every initial probability vector p(0) propagates as p(τ) = U-1 exp(λτ)Up(0). The eigenvalues of A are negative except for one zero eigenvalue that corresponds to the distribution at thermal equilibrium. That the relaxation reaches equilibrium is insured by defining the rate constants for the reversed reactions in terms of the rate constants for the forward reactions and detailed balance, for example
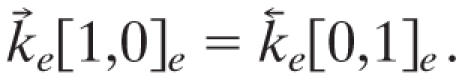 |
By multiplying both sides by PHClPDCl and using the conventional chemical notation for concentrations and that, at equilibrium, the concentrations of different species are independent, this relation reads
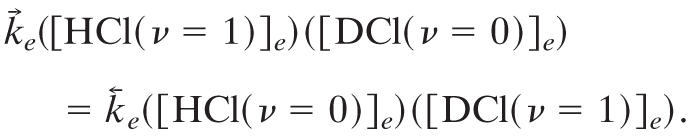 |
At room temperature (1°K ≡ 0.695 cm-1) and using the vibrational frequencies of HCl (2,886 cm-1) and of DCl, (2,091 cm-1), 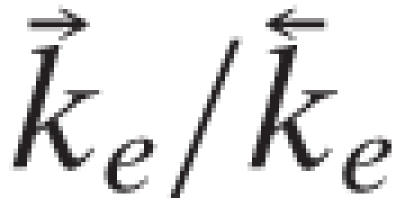
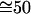 . Similarly
. Similarly
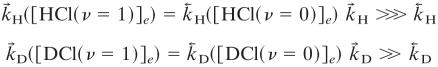 |
and 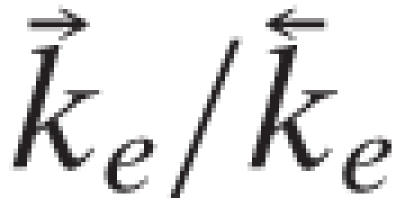 =(
=(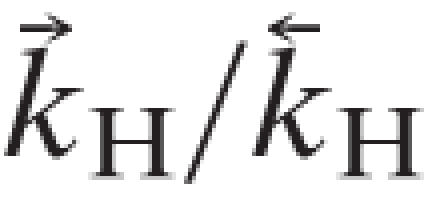 )/(
)/(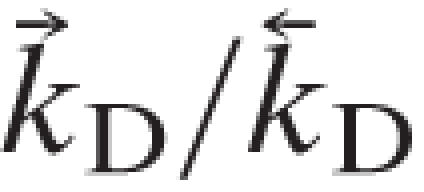 ). The values used in the simulations are
). The values used in the simulations are 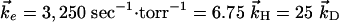 and the partial pressures are taken to be equal. The results are shown in Fig. 1, where the concentrations [HCl(ν = 1)] and [DCl(ν = 1)] are plotted vs. Pt, where P is the pressure in torr and time is in sec. As discussed by Chen and Moore (27), the concentration of HCl and of DCl in the ν = 1 state is monitored through their slow emission in the IR, an emission that is too slow to significantly deplete the concentration but is sufficient for detection.
and the partial pressures are taken to be equal. The results are shown in Fig. 1, where the concentrations [HCl(ν = 1)] and [DCl(ν = 1)] are plotted vs. Pt, where P is the pressure in torr and time is in sec. As discussed by Chen and Moore (27), the concentration of HCl and of DCl in the ν = 1 state is monitored through their slow emission in the IR, an emission that is too slow to significantly deplete the concentration but is sufficient for detection.
Discussion
Consider a search for one among N mutually exclusive possibilities. Quasiclassical information theory (meaning discrete propositions that satisfy the distributive law) shows that by using binary questions it should in principle be possible to reach an answer by using log2 N queries (31). The information theoretic proof does not provide a construction on how to actually do so. What our kinetic scheme provides is a coding that allows the answer to be determined. In fact, the first theorem of information theory provides a stronger result. If the N alternatives are equally likely, then log2 N is indeed the best that one can aim for. But if the alternatives differ in their likelihood then it is possible to do better.
The particular search problem that we solve was chosen such that the operation of the oracle is linear in the unknown function. If this condition is relaxed then the repertoire of problems that can be solved is far wider.
Another generalization that is possible is to write the quasiclassical time evolution in a manner that more closely mimics the unitary evolution of quantum computing. This is made possible by the underlying geometry of the quasiclassical description (32). Instead of unitary matrices quasiclassical transformations are described by orthogonal matrices, but if one can allow improper rotations then such quantum gates (3, 33) as the Hadamard or the quantum XOR, also known as controlled-NOT,
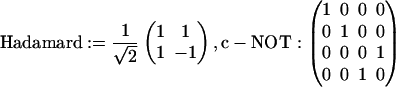 |
are possible also for the quasiclassical transformations.
The quasiclassical time evolution that we used as a concrete example describes a macroscopic system. We chose it intentionally so as to emphasize that we do not use phase information. But apart from a short induction period the random phase approximation is equally useful to describe intermolecular dynamics (14). It should therefore be possible to devise gates down to single-molecule spectroscopies (34).
Acknowledgments
We thank Michael Ben-Or and Steve Leone for their critical comments. This work was supported by the U.S.–Israel Binational Science Foundation, Jerusalem. F.R. is a Maitre de Recherche of Fonds National de la Recherche Scientifique, Brussels.
Footnotes
The distributive law  and
and  is a necessary condition on the algebra being Boolean. The logical OR operation is here denoted by
is a necessary condition on the algebra being Boolean. The logical OR operation is here denoted by  and the logical AND operation is denoted by
and the logical AND operation is denoted by  . The distributive law is not satisfied when one seeks to generalize to quantum mechanical propositions because of the possibility of interference.
. The distributive law is not satisfied when one seeks to generalize to quantum mechanical propositions because of the possibility of interference.
References
- 1.Deutsch, D. (1985) Proc. R. Soc. London Ser. A 400, 97-117. [Google Scholar]
- 2.Deutsch, D. (1989) Proc. R. Soc. London Ser. A 425, 73-90. [Google Scholar]
- 3.Nielsen, M. A. & Chuang, I. L. (2000) Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, U.K.).
- 4.Preskill, J. (1998) Proc. R. Soc. London Ser. A 454, 385-410. [Google Scholar]
- 5.Preskill, J. (1998) Proc. R. Soc. London Ser. A 454, 469-486. [Google Scholar]
- 6.Preskill, J. (1999) Physics Today 52, 24-30. [Google Scholar]
- 7.Ekert, A., Ericsson, M., Hayden, P., Inamori, H., Jones, J. A., Oi, D. K. L. & Vedral, V. (2000) J. Mod. Opt. 47, 2501-2513. [Google Scholar]
- 8.Ekert, A., Hayden, P., Inamori, H. & Oi, D. K. L. (2001) Int. J. Mod. Phys. A 16, 3335-3363. [Google Scholar]
- 9.Ekert, A. & Jozsa, R. (1998) Proc. R. Soc. London Ser. A 356, 1769-1782. [Google Scholar]
- 10.Jozsa, R. & Linden, N. (2004) Proc. R. Soc. London Ser. A 459, 2011-2032. [Google Scholar]
- 11.Landau, L. D. & Lifschitz, E. M. (1976) Mechanics (Pergamon, Oxford).
- 12.Amitay, Z., Kosloff, R. & Leone, S. R. (2002) Chem. Phys. Lett. 359, 8-14. [Google Scholar]
- 13.Vala, J., Amitay, Z., Zhang, B., Leone, S. R. & Kosloff, R. (2002) Phys. Rev. A 66, 062316-6. [Google Scholar]
- 14.Levine, R. D. (2004) Molecular Reaction Dynamics (Cambridge Univ. Press, Cambridge, U.K.).
- 15.Remacle, F. & Levine, R. D. (2001) J. Chem. Phys. 114, 10239-10246. [Google Scholar]
- 16.Remacle, F., Schlag, E. W., Selzle, H., Kompa, K. L., Even, U. & Levine, R. D. (2001) Proc. Natl. Acad. Sci. USA 98, 2973-2978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Remacle, F., Speiser, S. & Levine, R. D. (2001) J. Phys. Chem. A 105, 5589-5591. [Google Scholar]
- 18.Hjelmfelt, A., Weinberger, E. D. & Ross, J. (1992) Proc. Natl. Acad. Sci. USA 89, 383-387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cox, R. T. (1946) Am. J. Phys. 14, 1-13. [Google Scholar]
- 20.Cox, R. T. (1961) The Algebra of Probable Inference (Johns Hopkins Univ. Press, Baltimore).
- 21.Tribus, M. (1969) Rational Descriptions, Decisions, and Designs (Pergamon, New York).
- 22.Jaynes, E. T. (2003) Probability Theory (Cambridge Univ. Press, Cambridge, U.K.).
- 23.Deutsch, D. & Jozsa, R. (1992) Proc. R. Soc. London Ser. A 439, 553-558. [Google Scholar]
- 24.Bernstein, E. & Vazirani, U. (1993) in Proceedings of the 25th Annual ACM Symposium on the Theory of Computing (ACM Press, New York), pp. 11-20.
- 25.Jozsa, R. (1998) Proc. R. Soc. London Ser. A 454, 323-337. [Google Scholar]
- 26.Cleve, R., Ekert, A., Macchiavello, C. & Mosca, M. (1998) Proc. R. Soc. London Ser. A 454, 339-354. [Google Scholar]
- 27.Chen, H.-L. & Moore, C. B. (1971) J. Chem. Phys. 54, 4072-4080. [Google Scholar]
- 28.Moore, C. B. (1967) in Fluorescence, ed. Guilbault, G. G. (Dekker, New York), pp. 133-199.
- 29.Kneba, M. & Wolfrum, J. (1979) J. Phys. Chem. 83, 69-73. [Google Scholar]
- 30.Leone, S. R., McDonald, R. J. & Moore, C. B. (1975) J. Chem. Phys. 63, 4735-4741. [Google Scholar]
- 31.Abramson, N. (1963) Information Theory and Coding (Wiley, New York).
- 32.Levine, R. D. (1986) J. Chem. Phys. 84, 910-916. [Google Scholar]
- 33.DiVincenzo, D. P. (1998) Proc. R. Soc. London Ser. A 454, 261-276. [Google Scholar]
- 34.Brunel, C., Lounis, B., Tamarat, P. & Orrit, M. (1998) Phys. Rev. Lett. 81, 2679-2682. [Google Scholar]