Initial information prior to movement onset influences kinematics of upward arm pointing movements

We show that information coming from the initial state of the sensorimotor system is determinant to planning movements in the gravity field. When the muscular command necessary to counteract the gravitational shoulder torque was replaced with a support, we observed that the central nervous system changed motor planning in a way suggesting that the forthcoming dynamics was not reliably estimated. We suggest that the brain then adopts a more general strategy in the context of uncertainty.

Abstract

To elaborate a motor plan and perform online control in the gravity field, the brain relies on priors and multisensory integration of information. In particular, afferent and efferent inputs related to the initial state are thought to convey sensorimotor information to plan the upcoming action. Yet it is still unclear to what extent these cues impact motor planning. Here we examined the role of initial information on the planning and execution of arm movements. Participants performed upward arm movements around the shoulder at three speeds and in two arm conditions. In the first condition, the arm was outstretched horizontally and required a significant muscular command to compensate for the gravitational shoulder torque before movement onset. In contrast, in the second condition the arm was passively maintained in the same position with a cushioned support and did not require any muscle contraction before movement execution. We quantified differences in motor performance by comparing shoulder velocity profiles. Previous studies showed that asymmetric velocity profiles reflect an optimal integration of the effects of gravity on upward movements. Consistent with this, we found decreased acceleration durations in both arm conditions. However, early differences in kinematic asymmetries and EMG patterns between the two conditions signaled a change of the motor plan. This different behavior carried on through trials when the arm was at rest before movement onset and may reveal a distinct motor strategy chosen in the context of uncertainty. Altogether, we suggest that the information available online must be complemented by accurate initial information.

NEW & NOTEWORTHY

We show that information coming from the initial state of the sensorimotor system is determinant to planning movements in the gravity field. When the muscular command necessary to counteract the gravitational shoulder torque was replaced with a support, we observed that the central nervous system changed motor planning in a way suggesting that the forthcoming dynamics was not reliably estimated. We suggest that the brain then adopts a more general strategy in the context of uncertainty.

motor control relies on a mixture of predictive and feedback mechanisms that allow us to perform successful actions in a changing environment. The theoretical framework of internal models and optimal control nicely explains why the central nervous system (CNS) selects stereotyped movements among an infinite set of solutions and for a wide class of actions. Before an action takes place, the controller calculates the required motor commands necessary to achieve a desired trajectory (Wolpert and Kawato 1998) and an internal forward model estimates their sensory consequences (Flanagan and Wing 1997; Izawa et al. 2012; Wolpert and Ghahramani 2000). If a mismatch between predicted and actual sensory information is detected, the CNS launches appropriate task-protective corrective actions and updates the internal representation of the motor task. In this process, information conveyed by all sensory modalities during the initial state, i.e., before the action, is as critical as information available during the movement.

Gravity is immutable on Earth. The CNS has learned to estimate its mechanical effects in myriad actions. In the context of vertical arm pointing movements, several studies have shown directional kinematic asymmetries early in the movement (Gaveau and Papaxanthis 2011; Gentili et al. 2007; Papaxanthis et al. 1998a, 1998b, 2003). Specifically, these authors observed that the limb spent proportionally less of the total movement time to accelerate upward compared with downward and horizontal movements. It has been proposed that the mechanical consequences of gravity are centrally integrated into the motor plan. For example, it has been suggested that the brain integrates the assistive role of gravity in slowing down an upward movement; hence deceleration phases are longer to save muscular effort (Papaxanthis et al. 2003). Computational approaches reproduced the asymmetries in the velocity profiles of vertical movements (Berret et al. 2008a; Crevecoeur et al. 2009a; Gaveau et al. 2014), elegantly showing that the CNS accounts for the action of the gravitational torque on the limb to optimize the motor command.

To elaborate a motor plan that incorporates the effects of gravity, the brain relies on priors and multisensory integration of visual, proprioceptive, and vestibular signals (Angelaki and Cullen 2008; Berniker et al. 2010; Berthoz and Viaud-Delmon 1999; Blouin et al. 2014; Körding et al. 2006). Experiments using visuomotor rotation paradigms (Sciutti et al. 2012) and involving catching free-falling virtual balls (McIntyre et al. 2001) established a clear influence of the visual vertical on the motor plan. For instance, a recent study that induced changes in visual and somatosensory/vestibular information by tilting the body and the visual scene confirmed that vertical visual gravity is used as a reference to process visual and nonvisual cues in action planning (Scotto Di Cesare et al. 2014). In particular, forward body tilt revealed systematic undershooting and more asymmetric velocity profiles.

Proprioceptive signals also provide critical information in judgment of limb position before movement execution. Conditions that alter proprioceptive signals such as water immersion (Macaluso et al. 2016), loaded (Bock 1994) or paralyzed (Gandevia et al. 2006) limb experiments, and examination of the transmission of the sensory afferent signals (Saradjian et al. 2014) revealed that position sense plays an important role in motor planning. In addition to afferent proprioceptive signals, the efferent “outflow,” giving rise to the sense of effort (Winter et al. 2005), may also be used by the CNS to integrate the effects of gravity so as to adjust future movements (Allen and Proske 2006; Gandevia et al. 2006).

The above studies, in which the dynamical and/or visual contexts remained constant within the trial, suggest that the initial state of the sensorimotor system may provide crucial information for action planning (Crevecoeur et al. 2014). In particular, initial information necessary to implement the motor command that holds the arm motionless against gravity may provide valuable sensorimotor information for planning the upcoming movement. The aim of this study was to examine the role of the initial information on the planning and execution of vertical arm movements. We asked 12 participants to perform upward arm single-joint movements around the shoulder at three speeds and in two different arm conditions. In the first condition, the arm was outstretched horizontally and required a significant muscular command to compensate for the gravitational shoulder torque. In contrast, in the second condition the arm was passively maintained in the same position with a cushioned support and did not require any muscle contraction. We hypothesized that if initial information influences the elaboration of motor commands, we should observe differences in kinematic features between the two arm conditions.

MATERIALS AND METHODS

Subjects

Twelve adults (7 women, 5 men; 24–57 yr old, mean age = 32.6 yr, SD = 10.9 yr) voluntarily participated in the main experiment. Seven adults (3 women, 4 men; 20–47 yr old, mean age = 28.7 yr, SD = 8.5 yr) voluntarily took part in control experiment 1 and the same 15 adults (3 women, 12 men; from 21–38 yr old, mean age = 27.3 yr, SD = 4.8 yr) in control experiments 2 and 3. Three participants were excluded in control experiment 2 because they were not able to contract their muscles sufficiently in the “Vertical Rest Cocontract” condition to meet the instructions. All participants were right-handed, healthy, without neuromuscular disease, and with normal or corrected to normal vision and gave informed consent. The experimental protocol was carried out in accordance with the Declaration of Helsinki (1964), and the regional ethics committee of Burgundy (C.E.R) approved the experimental protocol.

Experimental Procedure

Main experiment.

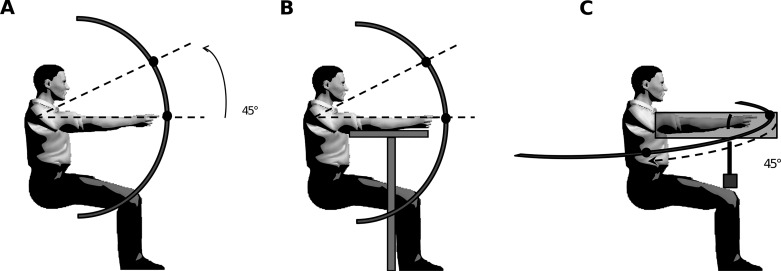
Participants were comfortably seated on a chair with their trunk vertical. A steel semicircular bar was centered on their right shoulder (parasagittal plane) in a polar frame of reference and at a distance equal to the length of their fully extended arm (similar to Gaveau and Papaxanthis 2011). For each participant, a starting target was placed on the bar such that the virtual line crossing the shoulder center and the starting target was horizontally aligned. An ending target was then placed upward so as to require a 45° shoulder flexion (Fig. 1, A and B). Participants performed visually guided single-degree of freedom upward arm movements between the two targets in two arm conditions. In the “Vertical Active” condition, participants actively maintained the initial position against gravity by contracting the shoulder flexor muscles (Fig. 1A). In the “Vertical Rest” condition, participants started with their arm lying on a horizontal support (Fig. 1B), which almost canceled the initial gravity torque and muscular activity. Note that we do not consider that this condition eliminates all sensory information about gravity force. Indeed, mechanical pressure between the arm and the support still exists and may provide information about gravity effects on the arm. The horizontal support was adjusted to each participant's morphology. Participants performed reaching movements at three different speeds. A metronome continuously paced at 60, 90, and 115 beats/min for the “Slow,” “Medium,” and “Fast” speeds, respectively. Participants practiced some trials prior to the experiment in order to become familiar with the required movement speeds. Each participant performed a total of 120 trials in a block design fashion (2 arm conditions × 3 speeds × 20 trials). Blocks were presented in a counterbalanced random order. A 5-s rest period separated the trials, and a 1-min pause was provided between blocks in order to prevent muscular fatigue. Each trial was carried out as follows: The experimenter asked participants to adopt one of the two arm conditions (Vertical Active or Vertical Rest), arm orientated toward the horizontal mark without touching it. After a variable period (2–3 s), a GO signal instructed participants to perform the 45° rotation movement. Because the metronome emitted tones continuously, participants had to synchronize movement onset and offset with two consecutive tones. We did not provide any instruction regarding reaction time but insisted on matching pace instead. Furthermore, we asked participants to produce uncorrected arm movement, i.e., without drawing excessive attention to final position accuracy. Finally, participants were also requested to maintain the final position for 2 s. A last verbal signal marked the end of the trial, and participants adopted a relaxed position for a few seconds before the next trial. In complement to the main experiment, three control experiments were realized.

Fig. 1.

A and B: experimental protocol illustrating the Vertical Active (A) and Vertical Rest (B) conditions of the main experiment. Arrow indicates a 45° upward arm movement. Gray T (B) represents the support for the outstretched arm. Black disks indicate the initial and final positions of the target. C: experimental protocol illustrating control experiment 3. Arrow indicates a 45° rightward arm movement. Gray cube represents the masses used to generate vertical shoulder torques. Black disks indicate the initial and final positions of the target.

Control experiment 1: Do visual cues influence kinematics?

Control experiment 1 was carried out to check that visual cues did not influence temporal kinematics. Because we observed that the acceleration phase was shortened in the Vertical Rest condition (see results), we verified that participants did not increase deceleration phases in order to reach the target accurately, with visual tracking. Participants were asked to perform the same movements as in the main experiment but with eyes closed. We focused on the slowest speed only in order to maximize a hypothetical effect of visual feedback. Similarly to the main protocol, participants initiated movements in two arm conditions (Vertical Active and Vertical Rest) and performed a total of 80 trials in a block design fashion (2 arm conditions × 20 trials, repeated twice) at the slow speed condition. The four blocks were presented in a counterbalanced random order. In the Vertical Rest condition, the instruction words played back every second were “LOOK!”, “CLOSE!”, and “GO!”. The injunctions “LOOK!”, “CLOSE!”, and “GO!” instructed the participant to look at the 45° target, close his/her eyes, and start the trial, respectively. In the Vertical Active condition, the additional command “READY!” was provided before the sequence in order to instruct the participant to get ready with the arm outstretched. The experimenter visually verified that subject's eyes were closed.

Control experiment 2: Does initial muscle contraction influence kinematics?

In control experiment 2, we tested whether the difference in kinematics between the two arm conditions might be specifically attributable to the muscle state itself. Indeed, muscles have shown state-dependent properties typically characterized by scaling of force production with background activity, such as here the initial muscular state required to maintain the arm outstretched. The participants performed visually guided upward 45° rotation arm movements in three arm conditions (Vertical Active, Vertical Rest, and Vertical Rest Cocontract) and at natural speed (900 ms). The Vertical Active and Vertical Rest conditions were exactly the same as in the main experiment. The Vertical Rest Cocontract condition was similar to the Vertical Rest condition with the important difference that participants were asked to cocontract pairs of antagonist arm muscles, preferentially the deltoids, without losing contact with the support. This design allowed us to dissociate the potential effects of muscle state and initial information about the weight of the arm on motor planning. Since this is not a natural situation, we trained participants to reach appropriate levels of muscle contraction while leaving the arm weight unchanged on the horizontal support.

Force transducers mounted under the support recorded the weight of the arm. We therefore controlled that the participant complied with the condition. Before each trial, online feedback of the force exerted on the support allowed the participant to tune her/his muscular contraction so as to match the arm weight obtained in the Vertical Rest condition.

In the Vertical Active condition, the instruction words were “READY!” to instruct the participant to actively maintain the initial position against gravity and “GO!” to start the trial. In the Vertical Rest condition, the arm already laid on the horizontal support and the instruction word was “GO!”, indicating the start of a trial. In the Vertical Rest Cocontract condition, while the arm rested relaxed on the horizontal support the word “CONTRACT!” instructed the participant to contract the muscles of the arm, then “GO!”. Participants performed 60 trials in a block design fashion (3 arm conditions × 20 trials). The three blocks were presented in a counterbalanced random order.

Control experiment 3: Does initial shoulder torque influence kinematics?

A final control experiment was carried out to investigate the extent to which differences in magnitude of initial shoulder torque between arm conditions affected velocity profiles. In the Vertical Active condition of the main experiment, an initial shoulder torque was required to maintain the arm horizontally outstretched against gravity. In contrast, in the Vertical Rest condition, the torque jumped from zero, when the arm weight was canceled out by the support, to some value close to that in the Vertical Active condition, when the subject lifted his arm from the horizontal support. We now ask the question as to whether this difference in initial shoulder torque (Vertical Rest) may alter the asymmetry of velocity profiles.

Participants performed visually guided horizontal 45° rotation arm movements at natural speed (900 ms) from the left to the right side and in two arm conditions (“Horizontal Active” and “Horizontal Rest”). Participants actively maintained their right arm horizontally in the sagittal plane. Their right wrist was tied with a string linked to a weight through a pulley system (Fig. 1C). This weight generated a leftward horizontal force. Masses of 1 kg and 1.5 kg were used to generate horizontal forces of 10 N and 15 N, respectively. In the Horizontal Active condition, before movement execution, participants had to counteract the horizontal pulling force and the gravitational force applied on the arm. In the Horizontal Rest condition, a rigid support was placed vertically against the left side of the participant's arm, hence mechanically canceling the leftward pulling force but still providing contact information. The only torque that had to be actively canceled was caused by gravity. As soon as the arm moved to the right and lost contact with the mechanical support, the participant had to generate a vertical delta shoulder torque component.

The word “READY!” instructed the participant to actively maintain the initial position, and the word “GO!” marked the start of the trial. Participants performed 40 trials in a block design fashion (2 arm conditions × 20 trials). The two blocks were presented in a counterbalanced random order.

Data Processing

Kinematic analysis.

Arm movements were recorded with seven TV cameras (sampling frequency 200 Hz) of a motion analysis optoelectronic system (Vicon). Five reflective markers (plastic spheres of 1.5-mm diameter) were placed on the shoulder (acromion), elbow (lateral epicondyle), wrist (radius styloid process), middle of the wrist joint (between the cubitus and radius styloid processes), and nail of the index fingertip. After calibration, the spatial resolution was <1 mm. Data processing was performed with custom software written in MATLAB (MathWorks, Natick, MA). Raw 3D kinematic signals were low-pass filtered with a digital zero-phase lag fifth-order Butterworth filter at a cutoff frequency of 20 Hz. The 3D kinematic data of all markers were differentiated twice to obtain velocity and acceleration signals. Trial onsets and offsets were defined as the time at which the finger velocity went above or dropped below 5% of maximum velocity (as in Gaveau and Papaxanthis 2011). The difference between offset time and onset time defined movement duration (MD). All kinematic parameters were normalized in time to ensure that velocity and acceleration profiles were independent of MD. For each trial, we measured peak velocity (PV) and peak acceleration (PA) and their times of occurrence (tPV and tPA, respectively). We also assessed the ratio of peak to mean velocity (C ratio). The symmetry of the velocity profile was therefore quantified by the ratio of acceleration duration (AD) to total MD. A AD/MD of 0.5 indicates symmetric velocity profiles.

In a second step we analyzed acceleration profiles more thoroughly in order to highlight temporal differences across arm conditions. For each participant, in a given speed condition, we evaluated normalized acceleration profiles and calculated the mean trace for each speed. Then we calculated the time shift between the mean trace of the Vertical Rest and Vertical Active conditions to obtain the temporal difference between acceleration profiles according to a fixed amplitude. From the beginning of the movement, and every 5 ms, we detected the amplitude value of the Vertical Rest Condition (A_Rest) and then the time t′ at which the corresponding acceleration profile of the Vertical Active condition reached the same amplitude (A_Active = A_Rest). Thus, for each participant and each speed, the time shift Δt was defined as Δt = [t′ − t], such that A_Active(t′) = A_Rest(t). A paired t-test (between subjects) was conducted (every 5 ms) to identify the moments at which this shift became significantly different.

EMG analysis.

We used a differential EMG device (Aurion wireless EMG system) to synchronically record muscle activity (1,000 Hz) with arm kinematics. Electrodes were placed along the fiber of the right anterior deltoid, which is the main agonist muscle for an upward motion. This allowed us to verify that muscular activity was only residual (significantly decreased) in the Vertical Rest compared with the Vertical Active condition. EMG signals were band-pass filtered with a fifth-order digital Butterworth filter (20–30 Hz) and rectified. For each trial, the root mean square (RMS) was then computed, from 450 ms to 150 ms before movement onset, with the following formula:

$$\text{RMS}=\sqrt{\frac{1}{N}{\displaystyle \sum _n^{n+N}{\left(\text{emg}\right)}^2}}$$

where N is the duration of the integration window (300 ms), n is the onset timing of the integration window, and emg denotes the numerical EMG signal of a given trial. Since the electromechanical delay for human upper limb movements is generally <100 ms (Cavanagh and Komi 1979; Howatson et al. 2009), this measurement provided us with a reliable estimate of motor commands before the movement started.

In addition, to identify when significant differences in temporal latencies occurred between arm conditions, we performed further data processing to investigate EMG profiles before and during movement execution. For each subject and each speed condition, we proceeded as follows: for each trial, we subtracted out for each RMS-EMG signal of the Vertical Active condition the initial muscular activity (offset of the Vertical Active condition). This value corresponds to the mean of RMS-EMG signal from 350 ms to 300 ms before movement onset. Then we averaged the offset of the Vertical Active condition across trials for each speed condition and divided the mean trace of RMS-EMG signals, in the Vertical Rest and Vertical Active conditions, by this mean “Active offset.”

Force transducer analysis.

In control experiment 2, we used two single-axis transducers (Celtron; STC 250 kg) to record the force exerted by the participants' arm on the horizontal support. Transducers were mounted between a table and the rigid horizontal support. These signals, sampled at 1,000 Hz, were synchronized with kinematics and EMG. The average signal between the transducers was presented online on a computer screen. For each trial, we computed the RMS with the same equation as for the EMG signal, from 500 ms to 0 ms before movement onset. This variable allowed us to verify that participants' arm was indeed at rest in both the Vertical Rest Cocontract and Vertical Rest conditions.

Statistical analysis.

After verification that data followed a normal distribution (P < 0.050; Kolmogorov-Smirnov test), we conducted two-way repeated-measures analysis of variance (RM-ANOVA) on variables of interest. The factors examined were arm condition (Vertical Rest or Vertical Active) and speed (Slow, Medium, or Fast). We set significance level at P < 0.010 for all statistical analyses. We conducted the same analysis for the control experiments. In control experiment 1, we used visual condition (“Eyes open” or “Eyes closed”) as the second factor. In control experiments 2 and 3, one-way RM-ANOVAs were conducted with arm condition (Vertical Rest, Vertical Rest Cocontract, or Vertical Active and Horizontal Rest or Horizontal Active, respectively). In control experiment 3, we initially analyzed data for each weight separately (unrepeated factor weight, 1 kg or 1.5 kg) and pooled the data, since no test reached significance regarding that factor. Post hoc differences were assessed with Scheffé tests (level of significance, P < 0.010).

RESULTS

Participants performed upward outstretched arm reaching movements in two different arm conditions and at three speeds (Fig. 1, A and B). We did not mechanically prevent rotations about the elbow joint to avoid nonecological motor commands, but we measured that no elbow rotation occurred (Table 1; mean = 3.8°, SD = 2.3°).

Table 1.

Average values of the main parameters for the main experiment in all conditions

	Vertical Rest			Vertical Active
	Slow	Medium	Fast	Slow	Medium	Fast
Elbow rotation, °	3.19 (1.67)	3.58 (2.09)	4.35 (2.42)	3.46 (2.26)	4.17 (2.36)	4.14 (2.42)
Shoulder elevation angle, °	46.65 (4.07)	48.16 (6.09)	47.27 (5.47)	42.47 (5.81)	43.77 (5.36)	45.77 (8.19)
MD, s	0.90 (0.17)	0.72 (0.13)	0.63 (0.11)	0.89 (0.14)	0.66 (0.09)	0.60 (0.09)
RMS, AU	0.02 (0.01)	0.02 (0.01)	0.01 (0.01)	0.08 (0.02)	0.08 (0.03)	0.08 (0.03)
PV, m/s	1.20 (0.20)	1.53 (0.28)	1.74 (0.24)	1.05 (0.26)	1.47 (0.27)	1.70 (0.32)
PA, m/s2	0.03 (0.008)	0.04 (0.01)	0.05 (0.01)	0.02 (0.01)	0.04 (0.02)	0.05 (0.02)
AD/MD	0.40 (0.04)	0.42 (0.04)	0.41 (0.03)	0.44 (0.04)	0.45 (0.03)	0.44 (0.02)
SD of angular displacement, °	1.80 (0.76)	2.08 (1.09)	1.95 (0.92)	2.18 (1.20)	2.23 (0.73)	2.36 (0.87)
C ratio	1.85 (0.11)	1.85 (0.09)	1.87 (0.08)	1.75 (0.07)	1.80 (0.04)	1.83 (0.07)

Data are average (SD) values of the main parameters for the main experiment in all conditions. Elbow rotation and shoulder elevation angle represent the angle between arm and forearm and the angular amplitude of the arm during movement, respectively. MD, PV, PA, and AD/MD correspond to movement duration, peak velocity, peak acceleration, and normalized time of the acceleration phase, respectively. RMS is the root mean square of the EMG signal between 450 ms and 150 ms before movement onset. The SD of angular displacement corresponds to the SD of shoulder elevation angle. C ratio is the ratio of peak to mean velocity evaluated between movement onset and offset.

AU, arbitrary units.

Movement end point was on target (Table 1; mean shoulder elevation angle = 45.7°, SD = 3.6°) and was influenced neither by arm condition (F_1,11 = 7.28, P = 0.020) nor by speed condition (F_2,22 = 1.44, P = 0.258). There was no effect of interaction (F_2,22 = 2.43, P = 0.111). As expected, MD (Table 1) was affected by speed; on average, MDs were 890 ± 111 ms, 690 ± 75 ms, and 610 ± 50 ms for Slow, Medium, and Fast movements, respectively. This was confirmed by a two-way RM-ANOVA that showed a significant effect of speed condition (F_2,22 = 54.8, P < 0.010) but not of arm condition (F_1,11 = 4.51, P = 0.057) and no interaction (F_2,22 = 1.09, P = 0.353).

We verified that muscular activity was residual prior to movement onset in the Vertical Rest condition. Indeed, muscle activity (Table 1) was significantly higher in the Vertical Active condition compared with the Vertical Rest condition (F_1,11 = 94.87, P < 0.010). RMS prior to movement onset was not influenced by speed condition (F_2,22 = 3.92, P = 0.035).

Arm Condition Influences Kinematic Profiles

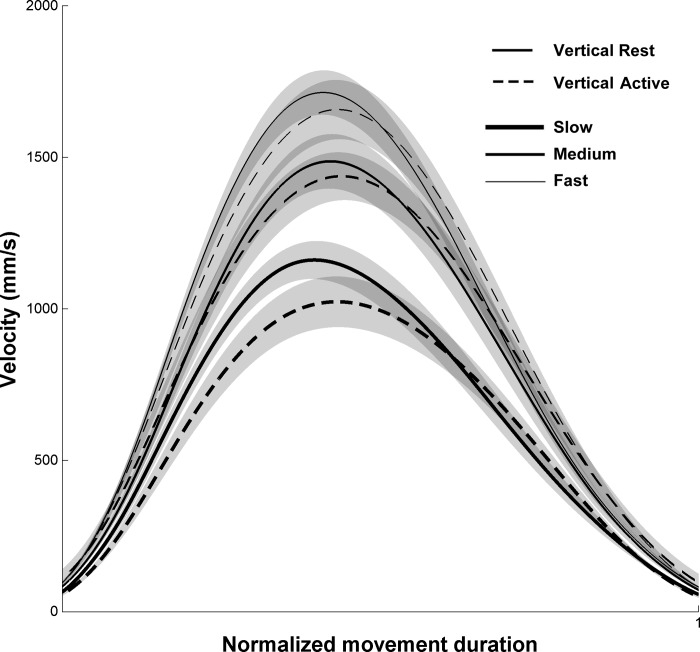
Figure 2 depicts normalized velocity profiles in all conditions. Velocity profiles were single peaked, and acceleration profiles (data not shown) were double peaked, with one peak during the acceleration phase and one peak during the deceleration phase. PVs and PAs (Table 1) significantly decreased when speed decreased (PV: F_2,22 = 46.71, P < 0.010; PA: F_2,22 = 39.05, P < 0.010). In contrast to speed, arm condition had no significant effect on these parameters (PV: F_1,11 = 3.38, P = 0.090; PA: F_1,11 = 2.09, P = 0.176) and the interaction was not significant either for PV (F_2,22 = 1.03, P = 0.374) or for PA (F_2,22 = 0.40, P = 0.674). C ratio was, however, influenced by arm condition (F_1,11 = 15.72, P < 0.010); it was significantly higher in the Vertical Rest condition compared with the Vertical Active condition. In contrast, speed condition had no significant effect on C ratio (F_2,22 = 2.94, P = 0.076), and there was no effect of interaction (F_2,22 = 2.93, P = 0.076).

Fig. 2.

Velocity profiles normalized in time in the Vertical Rest and Vertical Active conditions. Slow, Medium, and Fast speeds are depicted by thick, normal, and thin lines, respectively. Shaded areas correspond to SE between participants.

To assess the symmetry of velocity profiles, we computed the relative proportion of AD (Table 1, ratio AD/MD). A ratio of 0.50 would correspond to a movement during which the participant would have spent the same time to accelerate and to decelerate. Overall, participants spent significantly less time to accelerate than to decelerate (mean normalized AD = 0.43, SD = 0.04); t-tests were conducted between the ratio AD/MD in all conditions and the symmetric reference value of 0.5 (t₁₁ = 13.25, P < 0.010).

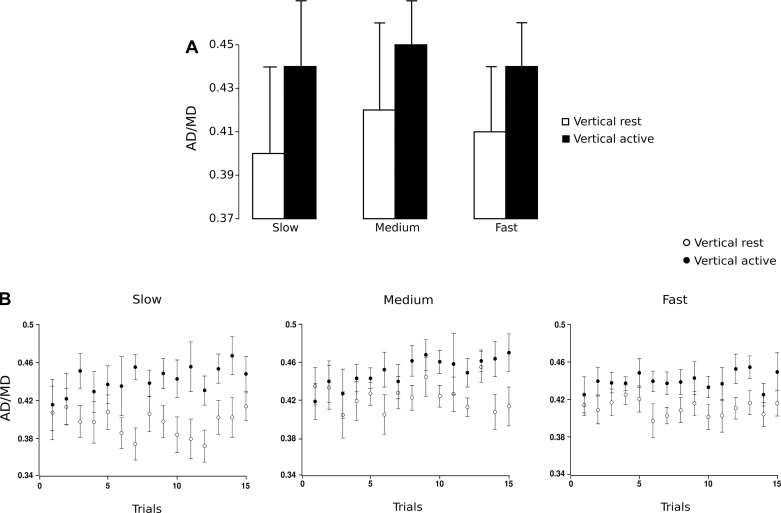
To test the effect of repetition, we conducted a three-way ANOVA with trial (1–15) as the third factor. Speed had no significant effect on AD/MD (F_2,14 = 1.26, P = 0.314); nor did trial (F_14,98 = 1.17, P = 0.313). Therefore, no adaptation occurred with movement repetition (Fig. 3B). In contrast, there was a main effect of arm condition (F_1,7 = 9.61, P < 0.010). Post hoc analysis revealed that AD/MD decreased (P < 0.010) in the Vertical Rest condition compared with the Vertical Active condition (Fig. 3A). In other words, participants spent more time accelerating the arm in the Vertical Active condition. Three-way interactions between speed, trial, and arm condition did not reach significance (all F < 1.33, P > 0.200). It is noteworthy that AD/MD of the very first trial was similar between arm conditions. One-way RM-ANOVA showed that there was a significant effect on AD/MD of the mean of the last 14 trials between arm conditions (F_1,11 = 20.69, P < 0.010) but not for the first trial (F_1,11 = 0.004, P = 0.950). In focusing on each arm condition and in using trial as the factor examined, we highlighted a significant increase between the first trial and the mean of the last 14 trials only in the Vertical Active condition (F_1,11 = 6.52, P = 0.015). The question naturally arises as to when acceleration profiles diverged between the two arm conditions. For Slow, Medium, and Fast speeds, positive time shift calculated on acceleration profiles between Vertical Rest and Vertical Active conditions became significant at 110 ms, 150 ms, and 125 ms, respectively, after movement onset.

Fig. 3.

A: acceleration duration normalized in time in the Vertical Rest and Vertical Active conditions for Slow, Medium, and Fast speeds. Error bars represent SD across participants. B: acceleration duration normalized in time in the Vertical Rest and Vertical Active conditions averaged between subjects and represented for the first 15 trials in Slow (left), Medium (center), and Fast (right) speeds. Error bars represent SE across participants.

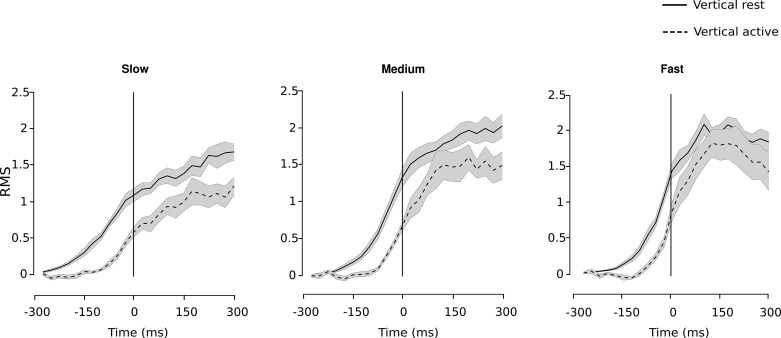
Claiming that no feedback at all could already have influenced the movement between 100 ms and 150 ms after movement onset (time 0 ms) is speculative. Therefore, we also analyzed EMG data to identify when significant differences in temporal latencies occurred between arm conditions (see materials and methods). We found that the latencies between the Vertical Rest and Vertical Active conditions became significant from −275 ms to −50 ms in Slow, from −200 ms to 0 ms in Medium, and from −200 ms to −25 ms in Fast speed conditions (Fig. 4). In other words, we found significant differences between arm conditions before movement onset.

Fig. 4.

RMS signal of EMG for the Vertical Rest and Vertical Active conditions for Slow (left), Medium (center), and Fast (right) speeds. RMS signal profiles are averaged between subjects, and shaded areas correspond to SE between participants. Vertical line corresponds to movement onset.

Vision Does Not Influence Kinematic Profiles

In the main experiment, we found an effect of the initial state of the arm on the shape of velocity profiles. However, both visual and proprioceptive information before movement onset can update the state estimate of the arm and the estimation of the mechanical effects of gravity. Control experiment 1 was designed to test whether visual information could influence this effect.

Participants completed movements within 930 ± 70 ms in the Vertical Active condition and 940 ± 60 ms in the Vertical Rest condition (Table 2). Movement durations were not different from the Slow speed condition of the main experiment, therefore serving as the basis of comparison for kinematic effects. Thus we compared movement kinematics in this control experiment with kinematics of the main experiment in the Slow speed condition (see Tables 1 and 2). We did not find any effect of visual condition (F_1,6 = 0.020, P = 0.891), arm condition (F_1,6 = 0.478, P = 0.515), or interaction (F_1,6 = 0.003, P = 0.959) on MD. Furthermore, movement amplitude (mean shoulder elevation; Table 2) was not influenced by arm condition (F_1,6 = 0.980, P = 0.423). We also verified that vision did not influence movement precision by assessing variability of angular displacements. A comparison between the main experiment and control experiment 1 revealed that the SD of angular displacement (Tables 1 and 2) was not significantly influenced by visual (F_1,6 = 2.33, P = 0.187) or arm (F_1,6 = 1.97, P = 0.219) condition.

Table 2.

Average values of the main parameters for all control experiments in all conditions

	Control Experiment 1		Control Experiment 2			Control Experiment 3
	Vertical Rest	Vertical Active	Vertical Rest Cocontract	Vertical Rest	Vertical Active	Horizontal Rest	Horizontal Active
Shoulder elevation angle, °	41.70 (3.04)	40.55 (2.80)	48.30 (4.84)	49.10 (5.08)	48.51 (6.70)	38.90 (6.03)	38.70 (5.31)
MD, s	0.94 (0.09)	0.93 (0.10)	0.91 (0.12)	0.94 (0.11)	0.93 (0.11)	1.02 (0.11)	0.99 (0.08)
RMS, AU	0.01 (0.01)	0.06 (0.03)	0.02 (0.01)	0.01 (0.01)	0.09 (0.04)	0.09 (0.03)	0.09 (0.03)
FT, AU	NA	NA	151 (24.7)	145 (22.9)	NA	NA	NA
PV, m/s	0.72 (0.06)	0.70 (0.09)	0.95 (0.16)	0.91 (0.14)	0.86 (0.11)	0.68 (0.08)	0.65 (0.06)
PA, m/s2	0.02 (0.01)	0.01 (0.01)	0.02 (0.01)	0.02 (0.01)	0.02 (0.01)	0.01 (0.01)	0.01 (0.01)
AD/MD	0.42 (0.03)	0.46 (0.02)	0.42 (0.03)	0.42 (0.03)	0.45 (0.04)	0.53 (0.04)	0.51 (0.03)
SD of angular displacement, °	2.65 (1.11)	3.08 (0.72)	NA	NA	NA	NA	NA

Data are average (SD) values of the main parameters for all control experiments in all conditions. Shoulder elevation angle represents the angular amplitude of the arm during the movement. MD, PV, PA, and AD/MD correspond to movement duration, peak velocity, peak acceleration, and normalized time of the acceleration phase, respectively. RMS is the root mean square of the EMG signal from 450 ms until 150 ms before the onset. FT corresponds to the RMS of the force transducer signal from 500 ms until 0 ms before movement onset.

NA, not applicable.

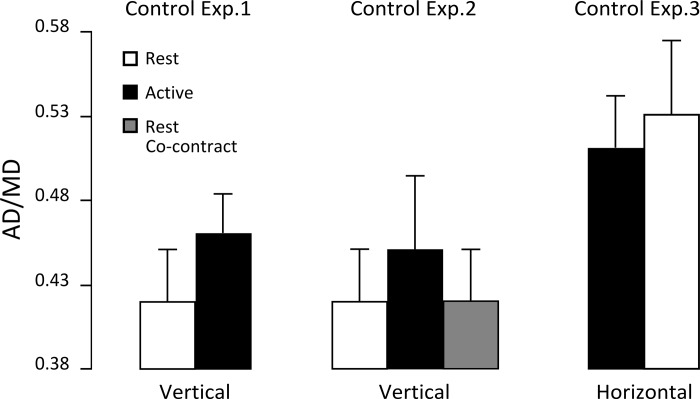
Importantly, as in the main experiment, we still observed a main effect of arm condition on AD/MD, which decreased in the Vertical Rest condition (F_1,6 = 13.81, P < 0.010) (Fig. 5). However, we failed to report an effect of visual condition (F_1,6 = 2.98, P = 0.135) on this asymmetry index (Table 2). The interaction between visual and arm conditions was not significant for the SD of the angular displacement (F_1,6 = 0.010, P = 0.997) and AD/MD (F_1,6 = 0.052, P = 0.828). t-Tests conducted on PV and PA (Table 2) showed that these parameters were not significantly affected by arm condition, either (PV: t₅ = 0.800, P = 0.405; PA: t₅ = 5.25, P = 0.062). Altogether, control experiment 1 demonstrated that arm condition preserved its influence on AD/MD independently of vision.

Fig. 5.

Acceleration duration normalized in time in the Vertical Rest, Vertical Active, and Vertical Rest Cocontract conditions for control experiments 1 (left) and 2 (center) and acceleration duration normalized in time in the Horizontal Active and Horizontal Rest conditions for control experiment 3 (right). Error bars represent SD across participants.

Muscle Contraction Does Not Influence Kinematic Profiles

In control experiment 2, we tested whether the difference in kinematics between the two arm conditions might be specifically attributable to the initial muscular state required to maintain the arm outstretched. We introduced a third arm condition for which participants had to cocontract pairs of antagonist arm muscles used for an upward movement when their arm was at rest before movement execution. There was no effect of arm condition (F_2,22 = 0.240, P = 0.788) on MD (Table 2). Movement amplitude (mean shoulder elevation; Table 2) was not influenced by arm condition (F_2,22 = 0.100, P = 0.905). PVs and PAs (Table 2) were significantly influenced by arm condition (PV: F_2,22 = 3.45, P < 0.010; PA: F_2,22 = 6.35, P < 0.010). Post hoc analysis revealed that PV and PA increased (P < 0.010) in the Vertical Rest Cocontract condition compared with the Vertical Active condition.

We verified that initial muscular activity was significantly larger (t_1,11 = 15.40, P < 0.010) in the Vertical Rest Cocontract condition compared with the Vertical Rest condition. Besides, there was no difference between RMS of force transducers measured before onset between the Vertical Rest Cocontract and Vertical Rest conditions (average 4.5% ± 4%). Therefore, participants were able to successfully perform significant muscle cocontractions while laying their arm on the support. We found that normalized AD was significantly affected by arm condition (F_2,22 = 13.42, P < 0.010) (Fig. 5). As expected, post hoc analysis showed that AD/MD decreased in the Vertical Rest Cocontract condition compared with the Vertical Active condition (P < 0.010), whereas there was no difference between Vertical Rest and Vertical Rest Cocontract conditions (P = 0.999).

To ensure that the acceleration phase did not change as a function of muscle state, we pushed the analysis one step further. Since there is variability both in the asymmetry index and in the RMS signal of EMG data in particular in the Vertical Rest and Vertical Rest Cocontract conditions, we expected to find no correlation between these two variables. For this additional analysis, we normalized AD/MD and the RMS signal of the EMG data of the Vertical Rest Cocontract condition by AD/MD and the RMS signal of the EMG data, respectively, of the Vertical Rest condition, while each participant had her/his own EMG impedance. In line with our expectations, no correlations were found in particular in Vertical Rest and Vertical Rest Cocontract conditions (r = 0.27, P = 0.394 and r = 0.39, P = 0.213, respectively).

Initial Shoulder Torque Influences Kinematic Profiles

Finally, to investigate the extent to which differences in normalized ADs observed on velocity profiles were affected by differences in initial shoulder torque between arm conditions, we performed control experiment 3, during which participants conducted horizontal movements. First, we did not find differences of mass (1 kg or 1.5 kg) on AD/MD (F_2,11 = 0.433, P = 0.659); hence we pooled all data together for subsequent analyses (Table 2).

The RM-ANOVA failed to report an effect of arm condition on MD (F_1,14 = 4.09, P = 0.063). Movement amplitude (mean shoulder elevation; Table 2) was not influenced by arm condition (F_1,14 = 0.172, P = 0.685). Similarly, PVs and PAs (Table 2) were not significantly influenced by arm condition, either (PV: F_1,14 = 2.11, P = 0.168; PA: F_1,14 = 3.59, P = 0.079). In contrast, asymmetry of the velocity profiles was significantly influenced by arm condition: AD/MD (Table 2) increased in the Horizontal Rest condition (F_1,14 = 19.36, P < 0.010). It is important and interesting to note that the delta torque effect observed in the horizontal plane was reversed compared with that observed in the vertical plane (Fig. 5). We combined data from the main experiment and control experiment 3 and ran another ANOVA with arm condition (Active vs. Rest) as first factor and plane of motion (Horizontal vs. Vertical) as second factor. This new analysis revealed a main effect of plane of motion (F_1,25 = 73.27, P < 0.010) but not of arm condition (F_1,25 = 1.19, P = 0.286). Interestingly, we found a significant interaction between these factors (F_1,25 = 18.01, P < 0.001), which showed that both contribute differently to movement execution.

To sum up, our results showed that the initial state of the arm influenced the shape of upward movement velocity profiles, irrespective of speed and visual conditions. Participants spent less time to accelerate when the initial level of muscular contraction was reduced in the Vertical Rest condition. Furthermore, initial muscular activity or magnitude of shoulder torque at the beginning of the movement did not explain a decrease of normalized AD. However, initial shoulder torque affected kinematics.

DISCUSSION

This study investigates how information related to the initial state of the arm prior to movement onset influences the planning and execution processes of arm movements. Two different initial states, corresponding to two different muscular commands, were generated by starting vertical movements either with the arm outstretched (large shoulder torque) or laid on a support (reduced shoulder torque). We observed differences in velocity profiles early after movement onset and in EMG before movement onset between the two arm conditions. Namely, a lack of information coming from shoulder torque before movement onset further amplified the asymmetry between acceleration and deceleration phases in the velocity profile. These early modifications indicated a change of the motor plan.

Humans can perform and adjust actions under various contexts, because the brain maintains internal representations of the dynamical interactions with the environment. In that process, the initial state provides critical information to elaborate the upcoming action. For instance, previous studies have shown that foveation of the starting position improves some characteristics of the movement in speeded tasks (Flanagan et al. 2006; Starkes et al. 2002; White et al. 2012). Another study demonstrated that pressure cues under the feet activate the internal model of gravity in naive participants exposed to microgravity and thus improve the accuracy of their perception of vertical (Carriot et al. 2004).

Here we posit that the initial state may also influence how a motor strategy is established prior to movement execution. In the framework of optimal control, arm motor commands are optimized with respect to the action of gravity on the limb, whose consequences are integrated in motor planning and anticipated in terms of expected sensory states (Berret et al. 2008a, 2008b; Crevecoeur et al. 2009a; Gaveau et al. 2014; Gaveau and Papaxanthis 2011). A signature of this optimization is reflected by the shift of PV either backward or forward in time depending on whether a vertical reaching movement is performed against or with gravity, respectively (Gaveau and Papaxanthis 2011; Gentili et al. 2007). In agreement with these studies, our data highlighted shorter normalized acceleration durations in all conditions compared with symmetric bell-shaped velocity profiles observed in horizontal movements of the previous studies. The earlier occurrences of PVs in upward movements compared with downward movements are the consequences of a genuine optimization process by the CNS.

In some contexts, this index can be modulated. For instance, the asymmetry vanishes when participants perform very fast vertical movements (Pinter et al. 2012) or decreases when accuracy constraints require a great deal of online control (Chua and Elliott 1993; Sarlegna et al. 2003; Terrier et al. 2011). Other investigations found a significant longer acceleration phase in microgravity and, conversely, a shorter acceleration phase in hypergravity compared with normal gravity, respectively (Crevecoeur et al. 2009b; Papaxanthis et al. 2005). Even the simulation of gravity-like shoulder torques in weightlessness by means of elastic bands attached to the forearm provides sufficient online information to allow participants to generate the same movement kinematics as in normal gravity (Bringoux et al. 2012). In our experiment, this asymmetry was even further marked (4%) when the initial muscular activity was severely reduced. Furthermore, this difference appeared early after movement onset, as measured on kinematics. Early changes on EMG profiles between arm conditions ensured that differences of AD/MD happened in the feedforward phase of the movement, before sensory feedback is available. We show here that initial information influences the upcoming movement and is therefore integrated into the motor plan. Interestingly, in a human centrifuge experiment Fisk and colleagues found that proprioceptive information from supporting structures, such as the shoulder joint and muscles, influenced the way motor commands are generated (Fisk et al. 1993).

Optimization Hypothesis

The question remains open as to why participants spent less time to accelerate the limb to the target when the arm was at rest on a support. Motor planning needs task-relevant information to produce an optimal movement. In particular, it may require the estimation of the mass of the moving limb. To this end, one can use gravitational forces (m × g, when the object is static) and/or inertial signals (m × a, when the object moves). Within this context, previous investigations have suggested that the brain differentiates these two components to calibrate motor commands (Atkeson and Hollerbach 1985; Berret et al. 2008b; Crevecoeur et al. 2009a, 2009b; Gaveau et al. 2011; Papaxanthis et al. 2005; Pozzo et al. 1998; White 2015). In the framework of optimal control, several hypotheses can explain the reduction of the normalized AD when the arm was at rest before movement onset, implying or not mass estimation of the arm. A first hypothesis could be that altered patterns of velocity profiles may only reflect changes in the peripheral apparatus such as the initial muscle state. However, when we imposed initial muscular arm cocontractions while keeping the arm at rest (in control experiment 2), the acceleration phase was still reduced. Furthermore, no correlation between the asymmetry of the velocity profiles and initial muscular activity was found. A second hypothesis could be that differences in initial shoulder torques between arm conditions could explain the differences in velocity profiles. Surprisingly, when participants generated an initial delta shoulder torque in a situation in which the effects of gravity vary less than in vertical movements (during horizontal movements), we found that normalized AD increased in the Horizontal Rest condition. The interaction observed between arm condition (Active vs. Rest) and plane of motion (Vertical vs. Horizontal) shows that, depending on movement direction, the CNS integrates and/or processes the initial information differently to elaborate the forthcoming action. Thus the main reason why participants spent less time to accelerate the limb to the target in the Vertical Rest condition does not seem to be due to muscular background activity or initial shoulder torque. It is noteworthy that initial shoulder torque had a significant effect on asymmetry of the velocity profiles, which implies that prior kinesthetic information about the load is treated by the CNS during motor planning.

Alternatively, Crevecoeur and colleagues suggested that the processing of weight and inertial signals into motor commands uses sensory information available just prior to each individual movement (Crevecoeur et al. 2014). In light of our data, one could speculate that the brain is suboptimal to estimate the mass of the limb when the gravitational torque is compensated by a support. In the Vertical Rest condition, the brain could overestimate the mass of the arm and predict larger inertial force in the initial phase of the movement. In that case, we should observe initial overshoots, corrected by feedback. This view is also supported by kinematics observed in hypergravity environments and also with additional loads placed on the arm (Gaveau et al. 2011), which show a longer deceleration phase providing a longer time to brake the movement. However, in our experiments, reach errors were small (<10° and SD <3°) and no systematic overshoots were observed. In addition, EMG signals did not capture online correction during movement execution, which rules out the presence of feedback. While underestimation of mass limb would have generated longer AD, these verifications suggest that the brain does not overestimate gravity torque. Recently, Pinter and colleagues asked participants to perform very fast vertical and horizontal arm movements supported by a robot (Pinter et al. 2012). For each participant and each movement, five switches were made from moving in the vertical plane to moving in the horizontal plane. The authors found that the very first movement in the other direction was never adapted to the new condition and adaptation occurred rapidly after, an observation compatible with task switching in another context (White and Diedrichsen 2013). This imperfect switching ability is also observed in our experiment, since asymmetry of the velocity profiles in the first trial was similar when initial information allowing accurate estimation of the mass of the moving limb was limited (Vertical Rest condition) or not (Vertical Active condition). Finally, because we did not observe any sign of adaptation across trials and the asymmetry persisted over time in the Vertical Rest condition (Fig. 3B), this suggests that the mass of the arm was not erroneously estimated and the lack of information prior to movement onset strongly affects the motor plan.

Decreased Acceleration Duration in Context of Uncertainty

Thus, when the arm was at rest before movement execution, the CNS may lack a critical error or teaching signal that prevents it from correctly estimating the arm dynamics. A recent investigation that compared control participants with a deafferented patient concluded that static and dynamic proprioception play different roles in motor learning (Yousif et al. 2015). It is therefore possible that different combinations of proprioceptive modes (such as muscles, tendons, and skin afferents) were differently involved in the Vertical Rest and Vertical Active conditions. More precisely, static proprioceptive information (Vertical Rest condition) may not be sufficient to precisely integrate the effects of gravity on the subsequent movement and to feed the internal model. We therefore suggest that the CNS voluntarily uses another strategy to circumvent the critical lack of information in the Vertical Rest condition. Elliott and colleagues observed that participants decreased movement speed when information was limited (Elliott et al. 2004; Hansen et al. 2006). However, in our experiment, speed was imposed and the emphasis was not on movement end-point accuracy. Therefore, participants' only flexibility was to alter the shape of the kinematic profile. We speculate that the CNS deliberately decreases the normalized AD to save time for rapid online control and optimal utilization of feedback. This is in agreement with previous studies that reported systematic lengthening of the deceleration phase with increased task difficulties (MacKenzie et al. 1987; Soechting 1984) and also the “play it safe” strategy introduced by Elliot and colleagues to optimize not only speed-accuracy performance but also energy expenditure (Elliott et al. 2009). A higher C ratio found when the arm was at rest before movement execution supports this view. Finally, although a “play it safe” strategy seems plausible, kinematic differences observed in our results are specifically attributable to proprioception, as we did not highlight any effect of removing vision. Normalized AD only decreased when proprioceptive information was severely reduced, independently of vision. This shows that impeding vision is less detrimental than reducing proprioceptive signals to planning an optimal kinematic profile.

In conclusion, the present results suggest that the planning of vertical arm movements critically relies on a monitoring of the initial proprioceptive information in order to reliably estimate the forthcoming dynamics. Indeed, even if that information is later available during the movement, it is not sufficient to program an optimal strategy. In that case, the CNS uses a general strategy when uncertainty strongly affects the elaboration of the motor plan.

GRANTS

This research was supported by the Institut National de la Santé et de la Recherche Médicale (INSERM), the Conseil Régional de Bourgogne (France), the Agence Nationale de Recherche (ANR, projet MOTION, 14-CE30-007-01), and the Fonds européen de développement régional (FEDER).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

C.R., C.P., and O.W. conception and design of research; C.R. performed experiments; C.R. and O.W. analyzed data; C.R., C.P., J.G., and O.W. interpreted results of experiments; C.R. prepared figures; C.R. and O.W. drafted manuscript; C.R., C.P., J.G., T.P., and O.W. edited and revised manuscript; C.R., C.P., J.G., T.P., and O.W. approved final version of manuscript.