Dynamics of excitatory and inhibitory networks are differentially altered by selective attention

Excitation and inhibition interact to imbue neuronal networks with the computational power that enables cognitive processes, such as attention, yet the details of this interaction remain unknown. We developed a means to identify neuronal subtypes in population recordings and leveraged this to study their functional interactions during attention. We found evidence that selective modulation of inhibitory subnetworks, resulting in a reduction of functional interactions, was a key feature of the attentional state.

Abstract

Inhibition and excitation form two fundamental modes of neuronal interaction, yet we understand relatively little about their distinct roles in service of perceptual and cognitive processes. We developed a multidimensional waveform analysis to identify fast-spiking (putative inhibitory) and regular-spiking (putative excitatory) neurons in vivo and used this method to analyze how attention affects these two cell classes in visual area V4 of the extrastriate cortex of rhesus macaques. We found that putative inhibitory neurons had both greater increases in firing rate and decreases in correlated variability with attention compared with putative excitatory neurons. Moreover, the time course of attention effects for putative inhibitory neurons more closely tracked the temporal statistics of target probability in our task. Finally, the session-to-session variability in a behavioral measure of attention covaried with the magnitude of this effect. Together, these results suggest that selective targeting of inhibitory neurons and networks is a critical mechanism for attentional modulation.

NEW & NOTEWORTHY

Excitation and inhibition interact to imbue neuronal networks with the computational power that enables cognitive processes, such as attention, yet the details of this interaction remain unknown. We developed a means to identify neuronal subtypes in population recordings and leveraged this to study their functional interactions during attention. We found evidence that selective modulation of inhibitory subnetworks, resulting in a reduction of functional interactions, was a key feature of the attentional state.

attending to a region of visual space improves the speed and reliability of our perception at that location. Rigorous quantification of these behavioral improvements due to attention has been documented for nearly 150 years (Helmholtz 1867; Posner et al. 1980; Treisman 1969). In the last 30 years, the mechanisms of attention at the neural level have begun to emerge: neurons at the attended location increase their firing rate (Moran and Desimone 1985), whereas at the same time, decrease their trial-to-trial fluctuations in response strength or correlated variability (Cohen and Maunsell 2009; Mitchell et al. 2009). Whereas both of these changes can improve the ability of downstream neurons to decode signals from the population of attended neurons (Averbeck et al. 2006; Cohen and Maunsell 2009), the means by which a neural network instantiates these changes remain poorly understood. The simplest mechanism for selective attention—an excitatory feedback signal from brain areas implicated in executive control processes—fits well with observed firing-rate increases at the attended location. However, such an elevation in common input is seemingly inconsistent with a decrease in correlated variability.

Correlated variability in pairs of cortical neurons has been used both to infer functional connectivity in neural networks (Alonso and Martinez 1998; Moore et al. 1970; Nauhaus et al. 2009; Smith et al. 2013; Smith and Kohn 2008; Smith and Sommer 2013; Snyder et al. 2014) and also to constrain models of cortical coding (Doiron et al. 2016). The structure of correlated variability has a direct impact on information encoding by a neuronal population, although this impact depends intimately on the structure of the correlations: their spatial extent, dependence on tuning similarity, and most importantly, the way in which neuronal activity is decoded (Kohn et al. 2016). However, whereas the balanced network models that are often used to simulate neuronal populations do so by using excitatory and inhibitory neurons (Litwin-Kumar and Doiron 2012; Renart et al. 2010; van Vreeswijk and Sompolinsky 1996), the physiological data with which they are compared are typically agnostic to cell type. In the context of attention, the study of correlated variability provides an opportunity to illuminate both the computational principles of a cognitive process and the circuit-level mechanisms by which it is instantiated. This, in turn, is key evidence that constrains future models of attentive processes in neural networks.

Targeted pharmacological and optogenetic investigations have elucidated some of the likely mechanisms of attention and highlighted the role of different cell classes and neurotransmitter systems. Excitatory N-methyl-d-aspartate receptors appear to be necessary participants in attention-induced changes in variability and covariability but not mean firing rate (Herrero et al. 2013), whereas acetylcholine administration potentiates firing-rate modulation, and acetylcholine antagonism (via scopolamine) reduces it (Herrero et al. 2008). Moreover, this effect of acetylcholine may be mediated primarily by GABAergic neurons, which express acetylcholine receptors more than excitatory neurons (Disney et al. 2006) and are suppressed by acetylcholine receptor agonists (Disney et al. 2012). The role of GABAergic neurotransmission in correlated variability on a fast time scale (synchrony) has been studied extensively (Buzsaki and Wang 2012; Diba et al. 2014; Ledoux and Brunel 2011), including in the context of attention (Tiesinga et al. 2004). Glutamatergic long-range connections between cortical areas can also recruit local inhibition, which appears to play a role in modulatory effects related to attention (Zhang et al. 2014). Taken together, these studies point to the importance of understanding attention via the interplay between excitatory and inhibitory forces.

Whereas it has recently become clear that many of the computational properties of the brain emerge through the delicate organization of excitatory and inhibitory cell classes (Isaacson and Scanziani 2011), a network-level understanding of how attention can simultaneously produce increases in responsiveness and decreases in covariability remains elusive. A potential path to resolve this discrepancy lies in recent accounts of model networks in which balanced, recurrent excitation and inhibition act to cancel correlations (Renart et al. 2010; van Vreeswijk and Sompolinsky 1996) and in the physiological findings in which the effect of attention on response gain is stronger for putative inhibitory neurons than for other cell classes (Mitchell et al. 2007), and attention differentially affects the synchronization of putative inhibitory and excitatory neurons with ongoing network oscillations (Vinck et al. 2013). We reasoned that if attention signals target inhibitory neurons more strongly, as suggested by the anatomical and functional observations to date, then the decorrelating effect of attention might also be strongest in populations of inhibitory neurons. The testing of this hypothesis led us to develop a novel maximum likelihood estimation method using multiple measures of waveform shape to classify neurons as inhibitory or excitatory—an improvement on previous attempts largely focused on a single waveform shape measure [Anderson et al. (2013); Mitchell et al. (2007), but see Peyrache et al. (2012); Qi and Constantinidis (2012); and Shin and Sommer (2012)]. With the use of a spatial-selective attention task, we report that the magnitude and time course of decorrelation were strongest among inhibitory neurons and matched to behavioral measures of attention. These findings are bolstered by a recent theoretical study reporting that selective modulation of inhibitory networks is the key to producing the concomitant increases in responsiveness and decreases in variability observed with attention (Wiese et al. 2014). It thus appears that a single mechanism—selective top-down targeting of inhibitory networks—may mediate two effects of attention that at first blush, appear irreconcilable.

MATERIALS AND METHODS

Experimental procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh. A separate analysis of a portion of these data was previously reported (Snyder et al. 2015).

Subjects.

We implanted a 100-electrode “Utah” Array (Blackrock Microsystems, Salt Lake City, UT) in extrastriate cortex visual area V4 in each of two adult, male rhesus macaques (Macaca mulatta). We implanted in right V4 for Monkey B and in left V4 for Monkey R. Surgeries were performed in aseptic conditions under isoflurane anesthesia. In a separate procedure before the array implants, a titanium headpost was attached to the skull with titanium screws to immobilize the head during experiments. After each subject was trained to perform the spatial attention task, we implanted an electrode array in V4 using the same procedures that we have described previously (Smith and Sommer 2013). The main physiological findings were individually apparent and qualitatively similar in the results from each monkey, so we collapsed across the data from the two monkeys except where shown.

Microelectrode array recordings.

Signals from the arrays were band-pass filtered (0.3–7,500 Hz), digitized at 30 kHz, and amplified by a Grapevine system (Ripple, Salt Lake City, UT). Signals crossing a threshold (periodically adjusted using a multiple of the root-mean-squared noise) were stored for offline analysis. Each waveform segment consisted of 52 samples (1.73 ms). We first performed a semisupervised sorting procedure to separate putative action-potential waveforms from noise, using principle components analysis and an automatic Fuzzy c-Means clustering algorithm (Shoham et al. 2003), followed by manual refinement using custom MATLAB software (MathWorks, Natick, MA) (Kelly et al. 2007), taking into account waveform shapes and interspike interval distributions. These initial sorting steps yielded 103.8 ± 2.5 (means ± SE) candidate units per session for Monkey B and 80.6 ± 1.7 candidate units per session for Monkey R. To focus our analysis better on well-isolated individual neurons (as opposed to multiunit activity), we calculated the signal-to-noise (SNR) ratio of each candidate unit as the ratio of the average waveform amplitude to the SD of the waveform noise (Kelly et al. 2007) and excluded units with SNR values <2.5 (9.9%). We also excluded units with waveform shapes that were, on average, <40% correlated with the waveforms of the rest of the population (0.4%). This yielded a total of 6,962 units for the analysis. The arrays were chronically implanted and likely recorded some individual neurons over more than one recording session, but we treated each recording session as an independent sample for the analysis. Following spike sorting, we used a separate automated classification procedure (described below) to identify fast-spiking (putative inhibitory) and regular-spiking (putative excitatory) cells.

Receptive-field mapping and tuning curves.

Before beginning the experiments, we mapped the receptive fields (RFs) of the units recorded on our arrays by presenting small (∼1°) sinusoidal gratings at four orientations, positioned one at a time on the vertices of a lattice covering the likely RF area per the anatomical location of the implant. We subsequently used a grating size and position to cover roughly the aggregate RF area. For Monkey B, this was 5.87° diameter centered 4.00° below and 4.00° to the left of fixation, and for Monkey R, this was 5.87° diameter centered 8.94° below and 4.99° to the right of fixation. We next measured tuning curves by presenting gratings to the RF area in four orientations and at a variety of spatial and temporal frequencies. For each subject, we chose a temporal and spatial frequency that evoked a robust response from the population overall (i.e., our stimulus was not optimized for any single neuron).

Attention experiment.

We trained the subjects to maintain fixation on a 0.6° yellow dot at the center of a flat-screen cathode ray tube monitor, positioned 36 cm from their eyes (Fig. 1). The background of the display was 50% gray. We measured monitor luminance gamma functions by photometer and linearized the relationship between input voltage and output luminance using lookup tables. We tracked the gaze of the subjects using an infrared eye-tracking system (EyeLink 1000; SR Research, Ottawa, Ontario, Canada). Gaze was monitored online by the experimental control software to ensure fixation within 1.17° of the central fixation point throughout each trial.

Fig. 1.

Behavioral task. A: task schematic. While the subject maintained central fixation, a peripheral visual cue indicated the spatial location that was more likely to contain the target (80% validity). Subsequently, 2 drifting gratings appeared. The task was to detect a change in the drift speed in 1 of the 2 gratings and to make an eye movement to this stimulus. On 40% of trials, neither stimulus changed speed, and the subject was rewarded for maintaining fixation. The dashed circle and “spotlight” symbol represent the receptive-field (RF) area and focus of attention, respectively, and were not actually present in the stimulus display. For 1 subject, the cue was an isoluminant yellow annulus that encircled the aggregate RF area, whereas for the other subject (shown), the cue was a low-contrast dot at the center of the RF area. B: hit-rate performance. Error bars represent ± 1 SE. For both subjects, target-detection performance was improved when the cue validly indicated the target location compared with when no cue was given, and performance was diminished when the cue was invalid [2-way ANOVA, interaction between factors of “cue direction” and target location; Monkey R: F_{(2, 264)} = 10.28, P = 3.5 × 10⁻⁵; Monkey B: F_{(2, 222)} = 211.77, P = 5.0 × 10⁻⁵²]. This pattern of results is the hallmark for spatial-selective attention. C: the hazard function for target (speed change) onset time (left) combines with the gradual nature of the target speed change (middle) to define an anticipation function (right). The anticipation function describes the expected amount of task-relevant information in the stimulus over the course of a trial. The anticipation function shown here corresponds to the timing of targets from a representative session for Monkey B.

After fixating for a randomly chosen duration of 300 or 700 ms (50% probability of each), a peripheral visual cue was presented for 120 ms on 89% of trials (no-cue trials were identical in all other respects). For Monkey B, the cue was a 0.6° dim gray dot (87 cd/m²; 9% contrast) centered on one of the two potential imperative stimulus locations. For Monkey R, the cue was a yellow annulus (isoluminant with the display background, 6.45° inner diameter, 7.03° outer diameter, masked to prevent crossing the vertical meridian) that encircled one of the two stimulus locations.

Following another randomly chosen duration of 300 or 700 ms (50% probability of each), two full-contrast, drifting sinusoidal gratings were presented, one at 0° orientation and the other at 90° orientation. Orientation was counterbalanced between stimulus locations across trials. One grating was presented in the RF area of the neurons recorded on the array, and the other grating was presented in the mirror-symmetric location in the opposite hemifield.

The task was to detect a speed change (acceleration or deceleration) of one of the two gratings and to saccade to the stimulus that changed (i.e., the “target”) within 800 ms of the change onset. Correct responses were reinforced with juice or water. The speed change was governed by a triangular ramp function (i.e., a gradual increase or decrease followed by a return to baseline; Fig. 1C) that lasted 500 ms (except for 3 early sessions with Monkey B, where it was 650 ms). We titrated the maximum magnitude of the acceleration and deceleration before the experiment using a staircasing procedure to set an overall correct detection rate for each type of speed change between 70% and 80% correct. Forty percent of trials had no target (catch trials), and the animals were rewarded for maintaining fixation for the full stimulus duration—1.2 s for Monkey B or 1.5 s for Monkey R. If a cue and target both occurred, then the cue validly indicated the correct location of the target with 80% probability. The range of target-onset times was 250–700 ms after grating onset for Monkey B or 250-1,000 ms for Monkey R. In this report, we show the data from time periods that were common to both subjects (i.e., up to 1.2 s poststimulus onset, truncating the last 300 ms of Monkey R's data). In total, Monkey B completed 40 sessions, and Monkey R completed 42 sessions of the attention task.

Quantification of waveform shapes.

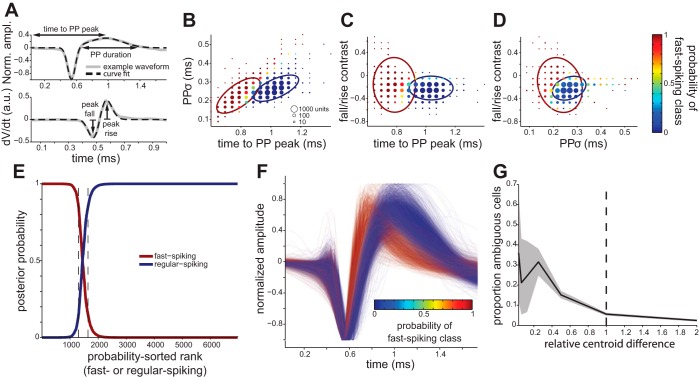
Previous in vitro work has shown that excitatory and inhibitory neurons have different action-potential dynamics (Bartho et al. 2004; Kawaguchi 1993; McCormick et al. 1985). Thus to classify our units as putative excitatory and inhibitory neurons, we used measures of action-potential waveform shape. We used the following three measures that have each been demonstrated to differ between excitatory and inhibitory neurons (see Fig. 3A): 1) time to the peak of the positive phase (PP) of the extracellular action potential (Bartho et al. 2004; Kawaguchi 1993; McCormick et al. 1985), 2) duration of PP (Kawaguchi 1993; McCormick et al. 1985), and 3) relative rate of depolarizing and repolarizing phases of the spike (McCormick et al. 1985). We found that no single measure clearly dichotomized our sample (see results), so we classified using the three measures in parallel. We also tried classification with greater numbers of waveform measures beyond these three, such as the time between successive zero crossings of the waveforms (Bruno and Simons 2002) and principal component scores, but found no appreciable improvement in classification performance. For ease of visual comparison of waveform shapes in Fig. 2F, we normalized waveforms to have a maximum deviation of ±1 unit by dividing by the most extreme value. Note that because our measures are time based (measures 1 and 2) or a ratio of two within-waveform measurements (measure 3), this amplitude normalization was only aesthetic and had no effect on classification outcome.

Fig. 3.

Classification performance with single measures of waveform shape. A–C: neurons are sorted by the probability of being fast spiking (red) or regular spiking (blue). The dashed lines denote the zones where neurons have <85% probability of belonging to either class. A: with the use of only the time to the peak of the positive phase (PP) of the extracellular action potential, 19.3% of neurons were ambiguous. B: with the use of only the width of the PP, 81.4% were ambiguous. C: with the use of only the fall/rise contrast, 18.9% were ambiguous. For comparison, when all 3 measures were used together to classify neurons, only 4.8% were ambiguous (see description of Fig. 2E in main text). D–F: normalized histograms of waveform shape measures for the neurons in our sample overlaid with the fitted Gaussian mixture distribution (dashed black lines). The 2 components comprising each mixture are plotted in red (putative fast-spiking class) and blue (putative regular-spiking class).

Fig. 2.

Multidimensional waveform analysis. A: illustration of waveform shape measures. Top: we fit a sum of Gaussians to each neuron's waveform to extract estimates of the relative amplitude, time, and duration of each phase of the spike; Norm. ampl., normalized amplitude; bottom: the derivative of the voltage waveform (dV/dt) above, similarly fitted with a sum of Gaussians. To quantify waveform shape, we used the peak time of the positive phase (PP) of the extracellular action potential (Kawaguchi 1993; McCormick et al. 1985), duration of PP (Kawaguchi 1993; McCormick et al. 1985), and difference between peak depolarization and repolarization rates (McCormick et al. 1985). We used the SD of a Gaussian fit to the PP (“PPσ”) to quantify PP duration (see materials and methods). B–D: 2-dimensional, marginal distributions for our 3-dimensional waveform shape data. Each plot point aggregates observations from several individual neurons; the size of each plot point is proportional to the number of observations in its neighborhood, whereas the color of each plot point reflects the average observed probability of belonging to the fast-spiking cell class (putative inhibitory). The ellipses circumscribe 95% of the fitted probability densities for the fast-spiking (red) and regular-spiking (blue; putative excitatory) component distributions. E: classification performance. Neurons are sorted by the probability of being fast spiking (red) or regular spiking (blue). The dashed lines denote the zone where neurons have <85% probability of belonging to either class (336 of 6,962 total). Classification performance was similar when performed separately for individual subjects. F: each waveform, colored according to the probability that the neuron is fast spiking. G: classification performance for synthetic data. We generated surrogate data by modeling a Gaussian mixture distribution identical to our fitted result but with the means of the 2 component distributions moved toward (relative centroid difference < 1) or away from each other (relative centroid difference > 1). We next iteratively generated random observations from these surrogate distributions and classified them to test the sensitivity and reliability of our method. When component distributions were closer together, more ambiguous classification resulted, indicating that the Gaussian mixture method does not spuriously dichotomize the data. Conversely, the doubling of the distance between the component distributions does not lead to an appreciable improvement in classification, suggesting that the classification of the observed data was near-ceiling levels. Shading represents 90% bootstrap confidence intervals (1,000 iterations). The dashed line represents the centroid separation that was actually observed for the dataset.

To improve our precision in estimating the time courses of action-potential waveforms, we modeled each waveform using parametric functions. The model parameters reflect the timing information of interest and can be estimated with arbitrary precision. Since each waveform is essentially two “peaks” of voltage—one negative and one positive—we first fit (in the least-squares sense) a sum of two Gaussian curves—one negative and one positive—to each unit's average waveform. We imposed the constraint that the negative (depolarizing) component must precede the positive (repolarizing) component. Through curve fitting, we reduced the waveform description to a set of six parameters: the amplitude, time shift, and width of the first Gaussian component and the amplitude, time shift, and width of the second Gaussian component. We took the value of the time-shift parameter for the second Gaussian component as the time to peak of the PP of the extracellular action potential (measure 1) and the value of the width parameter for the second Gaussian component as proportional to the duration of the PP (measure 2). We found that the time of the PP peak relative to the initial threshold crossing was highly correlated to the time of the PP peak relative to the action-potential trough (i.e., trough-to-peak time)—a measure that had been used by previous researchers to classify neuron types (Anderson et al. 2013; Mitchell et al. 2007; Peyrache et al. 2012; Qi and Constantinidis 2012; Shin and Sommer 2012)—but provided more reliable classification performance (the poorer classification performance for trough-to-peak time may be due to combining two noisy timing measurements—one for the trough and one for the peak—compared with just one noisy measurement when using threshold-to-peak time). Thus we used the time to the PP peak rather than trough-to-peak time to classify our sample. To compare the relative rate of depolarization and repolarization, we calculated the derivative of each normalized action-potential waveform and approximated the derivative waveform using two Gaussian components, as we did for the voltage waveforms described above. We took the difference of the absolute amplitudes of the two Gaussian components fit to the derivative wave as the contrast in rate between depolarizing and repolarizing phases (measure 3). Figure 2A illustrates the three measures of waveform shape, as well as how the Gaussian components were fit to the waveforms. We also found qualitatively similar results using other measures of waveform shape—namely, the time between successive zero crossings (Bruno and Simons 2002) or principal component coefficients—but ultimately, used the particular measures reported here because they have been validated in vitro.

Classification of cell types.

We used maximum likelihood estimation to classify neurons as putative excitatory or inhibitory on the basis of our three waveform shape measures. Specifically, we assumed that each class of neurons forms a roughly Gaussian distribution in the three-dimensional space describing waveform shapes (Fig. 2, B–D). In the raw data, these two clouds overlap, and our goal is to estimate best the separate parameters of the two component distributions. To achieve this, we used an expectation maximization algorithm (using the MATLAB “gmdistribution” class). For the expectation maximization, we used only our best-isolated units: neurons with SNR values of at least 4.0 (n = 1,434 units; see Microelectrode array recordings above). Because expectation maximization can be sensitive to locally optimized solutions, we repeated the analysis 10 times with random initial conditions and used the globally optimal solution. Note that the use of maximum likelihood estimation for classification confers the benefit (compared with other methods, such as linear discriminants or k-means clustering) of using higher moments of waveform shape distributions (in particular, the variances) to improve identification of the two cell classes. Once we determined the maximally likely parameters for the two distributions based on our best-isolated units, we used the fitted probability distributions to calculate the posterior probability of belonging to either class for all of the units (Fig. 2, B–F). This ability to quantify probability of class membership is another advantage of using maximum likelihood estimation to classify neurons compared with linear discriminants or k-means clustering. We considered units with <85% probability of belonging to either class ambiguous, and we excluded them from subsequent analyses (336 of 6,962 units excluded, or 4.8%, resulting in a total of 6,626 units classified as either fast spiking or regular spiking). The qualitative pattern of our results was robust to changes in the specific values of these thresholds.

Our expectation maximization approach assumes that the data come from two separate underlying distributions, and we wished to ensure that this assumption would not lead to a spurious dichotomization of the sample. To test this, we generated surrogate data that were similar to our observed data in every way except with respect to the degree of bimodality in the mixture distribution, which we varied parametrically by moving the centroids of the component distributions toward or away from each other when generating the surrogate data. At each centroid separation, we drew a number of observations from the modified mixture distribution equal to our sample size (n = 6,962), submitted these surrogate data to the same expectation maximization and classification procedure, and noted the proportion of neurons classified as ambiguous (Fig. 2G). Finally, we iterated this entire procedure 1,000 times to derive a distribution of classification performances at each centroid separation. We reasoned that if our procedure does not spuriously dichotomize unimodal samples, then we would observe the number of resultant ambiguous classifications rapidly increase as the centroids of the component distributions were moved closer to each other, which was precisely what we found (see results).

Spike count correlation.

To assay functional connectivity between pairs of neurons, we measured spike count correlation (r_sc), which describes the tendency for the responses of a pair of neurons to co-vary over repeated trials of an identical stimulus (Kohn and Smith 2005; Smith and Kohn 2008). Since the stimulus is unchanging in this case, such covariation is not due to demands of stimulus processing, but rather reflects correlated trial-to-trial variability in the neurons comprising the pair, perhaps due to the presence of common endogenous input. Since we were interested in how excitatory and inhibitory neurons were targeted by endogenous attention signals, we examined r_sc as a function of cell class.

We analyzed trials for which the subjects correctly identified validly cued targets, as attention was likely to be consistently deployed to the cued location for those trials. Since r_sc assumes repeated identical trials, we calculated r_sc at each time point using the data only from trials in which the grating had not yet started to change speed (at which point, trials were no longer identical). For each unit, we summed the spike count in bins 150 ms wide, sliding by 5 ms steps, following grating onset on each trial. In the data figures, we plot r_sc at the right edge of the corresponding time bin so that each point in the time series is influenced only by past events. Since two orientations of grating were used, we first z-scored each unit's spike counts separately for each orientation so that orientation-tuning preferences would not confound our measurements of r_sc. Then, we calculated r_sc as the Pearson product-moment correlation of spike counts across trials for each pair of units (excluding pairs recorded on the same channel, which could be affected by the spike-sorting process). We calculated r_sc separately for trials following a cue near the RF area of the array (“attended” trials) and for trials following a cue contralateral to the RF area of the array (“unattended” trials). We treated each recording session as a separate sample of neurons and calculated r_sc only between neurons that were recorded simultaneously within a single session.

To measure the dynamic change in r_sc over the course of an entire trial, we also analyzed data from trials in which neither stimulus changed (“catch” trials), and the subjects correctly withheld responses. Because catch trials occurred unpredictably, the subjects would have deployed attention identically as on target trials, and since the gratings drifted at a fixed rate on these trials, we could calculate r_sc for the entire duration of the stimulus, using sliding, 150 ms windows, as described above.

Statistical analysis.

We calculated the effect of attention as the difference between conditions (attended minus unattended) in firing rate or r_sc for each individual neuron or neuron pair, respectively. Neurons with an average firing rate across conditions of <1 spike (sp)/s were excluded (327/6,626 units, or 4.9%); this resulted in 4,958 regular-spiking neurons (79% of the remaining sample) and 1,341 fast-spiking neurons (21%) in the analyses. This sample yielded 48,347 (60%) simultaneously recorded, regular-spiking pairs; 4,431 (6%) simultaneously recorded, fast-spiking pairs; and 27,651 (34%) “mixed” pairs, comprised of one neuron from each class. Statistical hypothesis testing for significantly nonzero attention effects was performed using two-tailed, one-sample t-tests at each time point, corrected for multiple comparisons. Testing for differences in attention effects between cell classes was performed using two-tailed, independent-samples t-tests. For each test, we used a significance criterion of α = 0.05. We corrected for multiple comparisons by requiring a minimum run length of consecutive, significant time points. This correction relies on the fact that increasing numbers of consecutive significant t-scores become increasingly unlikely under the null hypothesis. The run-length threshold was determined by using the autocorrelation of the signals (since adjacent samples are not entirely independent) to determine the minimum run length, such that the false discovery rate for finding a single effect over all time points under the null hypothesis is the desired 5% (Altschuler et al. 2012; Guthrie and Buchwald 1991), which in our case, we found to be nine samples. For the purposes of hypothesis testing, Fisher's r-to-z transformation was first applied to r_sc values to normalize the sampling distributions. Furthermore, spike trains of individual neurons were convolved with Gaussian functions (20 ms full width at half maximum) before hypothesis testing and determination of minimum run length for significance of firing-rate effects.

RESULTS

Behavioral task performance.

We trained two rhesus macaque monkeys (Monkey B and Monkey R) to detect gradual changes in the drift speed of sinusoidal gratings in a cued spatial attention paradigm (Fig. 1A). Most of the task trials were preceded by visual cues that indicated the location of the grating that would change with 80% validity. Cues that validly indicated the location of a subsequent target led to a performance improvement, whereas invalid cues led to a performance detriment (Fig. 1B), verifying that the animals selectively attended during this task [two-way ANOVA, interaction between factors of “cue direction” and “target location”; Monkey R: F_{(2, 264)} = 10.28, P = 3.5 × 10⁻⁵; Monkey B: F_{(2, 222)} = 211.77, P = 5.0 × 10⁻⁵²; Fig. 1B]. We observed this effect not only for hit rate, but also for the discriminability index [Monkey R: F_{(2, 264)} = 87.76, P = 6.0 × 10⁻³⁰; Monkey B: F_{(2, 209)} = 58.22, P = 7.97 × 10⁻²¹]. For Monkey B, 4 of 40 sessions were excluded from the discriminability index analysis, because information on the target chosen in false alarms was not saved. This pattern of benefits for valid information and costs for invalid information is the hallmark of selective attention.

Cell-type classification.

While the animals performed the task, we recorded their neuronal population activity using 100-electrode Utah arrays implanted in visual area V4. Our goal was to identify subclasses of neurons on the basis of waveform shape and to test for evidence that one of these two neuronal populations is preferentially targeted by top-down attention signals. A number of in vitro studies of neurons identified various action-potential features that are characteristic of inhibitory neurons, such as relatively short latencies to peak depolarization (Bartho et al. 2004; Kawaguchi 1993; McCormick et al. 1985), brief hyperpolarization durations (Kawaguchi 1993; McCormick et al. 1985), and rapid peak rates of repolarization (McCormick et al. 1985). A neuron with one or more of these action-potential features is said to exhibit “fast spiking” (or “narrow spiking”) compared with “regular spiking” (or “broad spiking”), and it is this distinction between fast spiking and regular spiking that we used to classify neurons as putatively inhibitory or excitatory, respectively (Fig. 2). Although this heuristic is not perfect—a minority of inhibitory neurons has relatively slow spikes (Kvitsiani et al. 2013; Nowak et al. 2003)—cell-type classification based on waveform shapes has become a popular approach for tapping into the roles of excitation and inhibition in the cortex (Anderson et al. 2013; Mitchell et al. 2007; Peyrache et al. 2012; Qi and Constantinidis 2012; Shin and Sommer 2012). However, unlike previous researchers that used single electrodes (Anderson et al. 2013; Mitchell et al. 2007; Qi and Constantinidis 2012; Shin and Sommer 2012), we did not find that our sample was clearly dichotomized into separate classes by any single waveform shape measure (Fig. 3). In fact, for our data, we did not find the distribution of the most commonly used measure (trough-to-peak time) to be at all bimodal, according to Hartigan's Dip statistic (dip = 0.0028; P = 0.997; bootstrap test with 2,000 iterations) (Hartigan and Hartigan 1985). We did find, however, that combining three waveform shape measures (Fig. 2A) led to distinct clusters in the higher-dimensional space (Fig. 2, B–D) corresponding to two classes of waveform shape. Because we were interested in firing rate as a dependent variable of attention and wished to avoid introducing artificial effects, we intentionally did not use firing rate to aid in classification, despite that fast-spiking neurons are known to have faster firing rates than regular-spiking neurons (Connors and Gutnick 1990; Nowak et al. 2003) (see also Fig. 6A below).

Fig. 6.

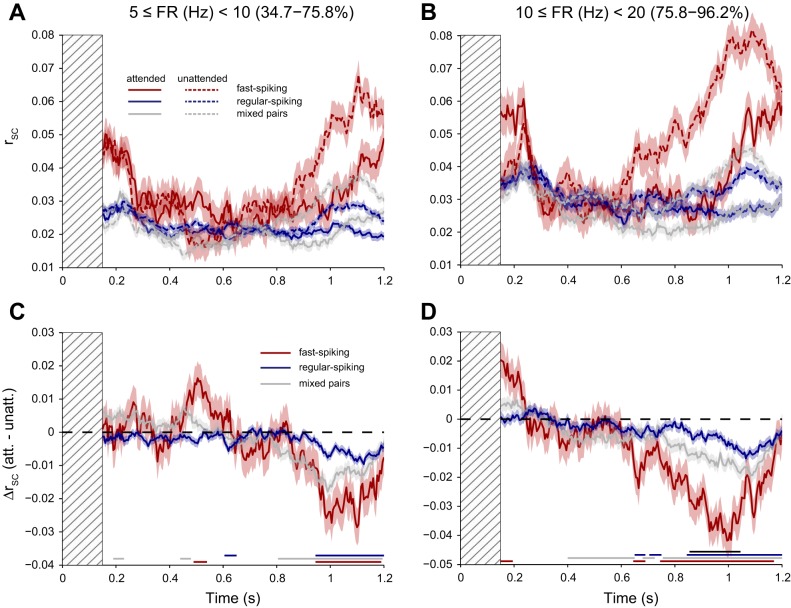
Attention results from target-present trials. Shading represents ± 1 SE. A and B: firing rate (Hz; A) and spike count correlation (r_sc; B) for fast-spiking (red; n = 1,341 neurons; 4,431 pairs) and regular-spiking (blue; n = 4,958 neurons; 48,347 pairs) cells when the stimulus in the receptive field was attended (solid lines) and when the stimulus in the receptive field was unattended (dashed lines). Mixed-class pairs are plotted in gray, and pairs of cells recorded on the same electrode were excluded. r_sc was calculated in 150 ms sliding time bins; note that the magnitude of r_sc can be small when measured in short time windows (Cohen and Kohn 2011). The r_sc value for each bin is plotted at the right-most edge (i.e., the first plot point reflects r_sc, calculated using spike counts in the gray-hatched time window). C and D: attention effect on firing rate (C) and r_sc (D), calculated for each neuron or pair by subtracting the unattended response from the attended response (Δ). Firing rates were greater, and r_sc was lesser for attended (att.) than unattended (unatt.) stimuli. Effect sizes of attention were greater for fast-spiking than for regular-spiking cells. Lines along the bottom of the plots reflect time points with significant nonzero attention effects for fast-spiking cells (red), regular-spiking cells (blue), and pairs of cells with mixed-class membership (gray), as well as significant differences between classes (black); P < 0.05, corrected for multiple comparisons. Only data up to the time of target onset on each trial were used for analysis (n = 246.7 ± 9.5 trials/session for each condition until the start of the target-onset window at 0.25 s, decreasing roughly linearly thereafter to n = 51.0 ± 5.7 trials/session by 0.7 s).

The estimation of the probability that each neuron belonged to each class enabled us to quantify classification performance (Fig. 2E) and to exclude neurons with ambiguous waveforms (Fig. 2F). Moreover, we are confident that our approach did not spuriously dichotomize the sample: when we repeated our procedure using simulated data drawn from component distributions that were highly overlapping, many ambiguous classifications resulted (Fig. 2G). Since very few ambiguous classifications were observed from the real sample (4.8%; Fig. 2E), this suggests the dichotomization was valid.

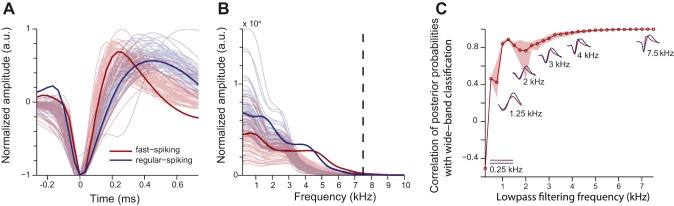
One potential concern is that the preamplifier filter settings on our recording equipment (7.5 kHz high cutoff) might have “smeared” the waveforms in time, making the fast-spiking neurons appear to have slower waveform time courses, thereby making it more difficult to discriminate them from regular-spiking neurons. We checked for this possibility in two ways and determined that filter settings did not limit our ability to quantify waveform shape accurately (Fig. 4). First, we obtained recordings of action potentials recorded using equipment with a higher-frequency filter cutoff (10 kHz) in the primary visual cortex area (V1; see Fig. 4 legend for details). We found that those action potentials were representative of the waveforms that we recorded for our experiment (Fig. 4A) and that the 10-kHz-filtered waveforms did not have meaningful spectral content above our 7.5 kHz cutoff (Fig. 4B). Second, we filtered the data that we recorded from the experiment at successively lower cutoff frequencies to determine the range in which filter settings might impact our classification (Fig. 4C). We found that classification remained >95% correlated with our original analysis when the data were low-pass filtered as low as 4 kHz, indicating that a 7.5-kHz cutoff is more than adequate to measure the waveform shapes accurately.

Fig. 4.

Effects of low-pass filtering on waveform classification. A: two units recorded with a 10-kHz, low-pass preamplifier filter from macaque visual area V1 (in contrast to the 7.5-kHz filter that was used for our study) are shown in bold (data courtesy of Dr. Adam Kohn, Albert Einstein College of Medicine, Bronx, NY). Plotted in lighter shades are 50 example waveforms chosen at random from each class from our manuscript (light red: fast spiking; light blue: regular spiking). Note that the spikes recorded with the 10-kHz filter are representative of the spikes that we recorded with the 7.5-kHz filter. B: frequency-domain representation of the waveforms in A. The dashed line shows the 7.5-kHz cutoff. Note that there is little power above this range regardless of which preamp filter was used, showing that there was virtually no power in the signal at these frequencies. The 2 conditions do not have different spectral content from each other at frequencies above ∼4 kHz. C: we filtered our original waveforms at various frequencies and repeated our classification analysis. Then we measured how correlated the classifications on the filtered waveforms were with our original reported classification at 7.5 kHz. Again, the classification was unaffected by filtering down to ∼4 kHz, suggesting that information above this frequency range is not useful for distinguishing the 2 waveform classes. Insets: average waveforms for each class at the different cutoff frequencies. SEs are smaller than the line thickness.

Spatial structure of r_sc.

In previous work in both V1 (Smith and Kohn 2008) and V4 (Smith and Sommer 2013), we found that the magnitude of correlated variability decreased with increasing distance. To compare our results with these previous studies and to investigate any differences based on cell class using our classification method, we performed the same analysis on pairs of neurons that were fast spiking and regular spiking and of mixed-class membership (Fig. 5). We analyzed only catch trials with correctly withheld responses, averaging over all time bins and conditions. We found that each of these three neuron-pair types showed a trend of decreasing r_sc with increasing distance (Pearson product-moment correlation, fast spiking: r = −0.080, P = 2.4 × 10⁻⁷; regular spiking: r = −0.065, P = 2.4 × 10⁻⁴⁵; mixed pairs: r = −0.047, P = 1.2 × 10⁻¹⁴). These trends were qualitatively similar to previous findings in V4 (Smith and Sommer 2013), although a more direct, quantitative comparison is difficult because of task differences and the period over which spike counts were measured. We tested for main effects and interactions of distance and cell class on r_sc using a two-way ANOVA with factors of cell class (2 levels: fast spiking and regular spiking) and distance (10 levels of distance bins; Fig. 5). We found a significant main effect of cell class, with greater correlation among fast-spiking neurons than regular-spiking neurons [F_{(4, 52789)} = 136.35, P < < 0.001], and a main effect of distance [F_{(9, 52789)} = 20.21, P < < 0.001], but the interaction of cell class and distance was not significant [F_{(9, 52789)} = 1.71, P = 0.08].

Fig. 5.

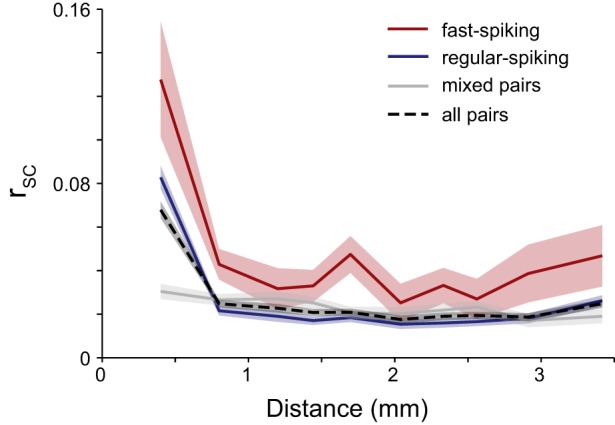
Spike count correlation diminishes over distance. Pairs were binned based on the distance between recording sites. There was a significant main effect of cell class, with greater correlation among fast-spiking neurons than regular-spiking neurons [F_{(4, 52789)} = 136.35, P < < 0.001] and a main effect of distance [F_{(9, 52789)} = 20.21, P < < 0.001], but the interaction of cell class and distance was not significant [F_{(9, 52789)} = 1.71, P = 0.08]. Shading represents ± 1 SE.

Effect of attention on firing rates.

We next considered classical effects of attention on firing rates for the two cell classes that we identified. When we examined the firing-rate responses of the neurons to grating stimuli as a function of which stimulus was cued, we found several effects of attention. In this and the following section, we discuss together the results of trials in which targets were correctly detected (Fig. 6) and catch trials in which a cue was presented but a target never shown (Fig. 7). Both fast-spiking and regular-spiking neurons exhibited a higher firing rate in trials in which the cue was directed toward their RFs (attended) compared with trials in which the cue was directed away (unattended). We found this to be true in analyses of trials in which targets were correctly detected (Fig. 6A) and also during catch trials in which a cue was presented, but the animal correctly remained fixating because the target was never shown (Fig. 7A). A pairwise comparison in which we computed the differential response for each neuron between the attended and unattended trials made this effect more apparent [Fig. 7C; regular-spiking firing-rate difference (ΔFR) = 0.26 sp/s, t₄₉₅₇ = 16.29, P = 3.5 × 10⁻⁵⁸; fast-spiking ΔFR = 0.53 sp/s, t₁₃₄₀ = 11.92, P = 3.2 × 10⁻³¹; analyzed in the window from 700 to 1,000 ms after grating onset on catch trials]. There were three notable trends in our analysis of firing rate. First, the magnitude of the effect of attention on firing rates was significantly greater for the fast-spiking class of cells than for the regular-spiking class of cells (Figs. 6C and 7C), consistent with a prior report (Mitchell et al. 2007). This pattern of greater attention effects for fast-spiking cells was true when we considered absolute differences in firing rate (t₆₂₉₇ = 7.00, P = 2.8 × 10⁻¹², analyzed in the same epoch as above) and also when we considered differences in firing rate relative to each neuron's average firing rate across conditions (t₆₂₉₇ = 2.60, P = 0.01). Second, the effects of attention on firing rate seemed to match qualitatively the temporal structure of our task, with larger firing-rate effects noted at the time when speed change was most likely to be detectable. Third, although our waveform categorization algorithm did not use this as a variable, we found significantly higher firing rates in fast-spiking neurons (9.01 sp/s) than in regular-spiking neurons (6.65 sp/s; t₆₂₉₇ = 7.71, P = 1.4 × 10⁻¹⁴), consistent with previous reports (Connors and Gutnick 1990; Nowak et al. 2003). Taken together, our findings—that fast-spiking neurons show a greater effect of attention than their regular-spiking counterparts—suggest that the inhibitory subpopulation is more strongly driven by endogenous attention signals.

Fig. 7.

Attention results from catch trials. Shading represents ± 1 SE. A and B: firing rate (A) and spike count correlation (r_sc; B) for fast-spiking (red) and regular-spiking (blue) cells when the stimulus in the receptive field was attended (solid lines) and when the stimulus in the receptive field was unattended (dashed lines). Pairs of cells recorded on the same electrode were excluded. r_sc was calculated in 150 ms sliding time bins. The r_sc value for each bin is plotted at the right-most edge (i.e., the first plot point reflects r_sc, calculated using spike counts in the gray-hatched time window). C and D: attention effect on firing rate (C) and r_sc (D), calculated for each neuron by subtracting the unattended response from the attended response. Particularly toward the end of the trial, firing rates were greater, and r_sc was lesser for attended than unattended stimuli. Effect sizes of attention were greater for fast-spiking than for regular-spiking cells. This pattern of r_sc results was similar when controlling for differences in overall firing rate between cell classes (see Fig. 8). Lines along the bottom of the plots reflect time points with significant nonzero attention effects for fast-spiking (red) and regular-spiking (blue) cells, as well as significant differences between classes (black); P < 0.05, corrected for multiple comparisons.

Effect of attention on r_sc.

Next, we examined functional connectivity by measuring the shared trial-to-trial fluctuations in response strength among neuron pairs over repeated identical trials (“noise correlation” or r_sc), isolating attention effects on different neuron classes (Figs. 6, B and D, and 7, B and D). One proposed mechanism for attention is a normalization signal introduced by modulation of inhibitory neurons (Mitchell et al. 2007; Reynolds and Heeger 2009). We hypothesized that if inhibitory neurons are preferentially targeted by attention signals, then we might see larger effect sizes of attention in that population. Moreover, we predicted that the dynamics of those attention signals would follow the time course of the expected target strength throughout the trial.

We found a robust reduction in r_sc in the attended compared with the unattended state across our entire population of neurons (Figs. 6B and 7B). Once again, this effect was made particularly salient by analyzing the differential signal [the difference in r_sc (Δr_sc) between attended and unattended trials] for each pair of neurons (Fig. 7D; regular-spiking Δr_sc = −0.004, t₄₈₃₄₇ = −4.51, P = 6.4 × 10⁻⁶; fast-spiking Δr_sc = −0.023, t₄₄₃₀ = −6.93, P = 5.0 × 10⁻¹²; analyzed in the window 700–1,000 ms after grating onset on catch trials, as for firing-rate effects above). The magnitude of the drop in correlation was greater for the fast-spiking neurons than for the regular-spiking neurons (t₅₂₇₇₆ = −6.65, P = 3.0 × 10⁻¹¹), much as the effect of attention on firing rates was greater for fast-spiking than for regular-spiking neurons. We also analyzed the effects of attention in pairs of neurons comprised of one fast-spiking and one regular-spiking cell. These mixed-class pairs showed attention-related decorrelation that was intermediate in magnitude but similar in time-course to that of the class-matched pairs (Δr_sc = −0.010, t₂₇₆₅₀ = −8.60, P = 8.2 × 10⁻¹⁸). However, since our study aimed to contrast functional connectivity profiles across cell classes, we focused our analyses on pairs with matching cell types.

Our task involved the detection of a gradual, rather than abrupt, change in speed with some jitter in the onset latency (see materials and methods and Fig. 1C). Thus the strength of the information about the target waxed and then waned over the course of the trial. Because it is difficult to sustain selective attention to a single location for more than a few hundred milliseconds at a time (James 1890; VanRullen et al. 2007; Wilschut et al. 2011), we reasoned that our subjects would concentrate their attentive efforts during the periods later in the trial, during which the drift speed of the target was likely to be most clearly different from the baseline speed, and this temporal expectation would be reflected in our measurements of the neurophysiological correlates of attention. In support of this prediction, the attention effects on firing rates of neurons recorded in lateral intraparietal sulcus (Janssen and Shadlen 2005), V1 (Sharma et al. 2014), and V4 (Ghose and Maunsell 2002) have been shown to track the expected value of task-relevant information (i.e., a time-dependent “anticipation function”). We observed that the effect of attention on r_sc appeared aligned with the temporal structure of our task, most notably, for the fast-spiking neuronal pairs. Taken together, the stronger effect of attention on the fast-spiking cells and the alignment of this effect to the time course of the task could indicate that the fast-spiking subpopulation receives stronger attention-related feedback signals than does the regular-spiking subpopulation.

As we mentioned above, fast-spiking neurons tend to have a greater firing rate than regular-spiking neurons (Connors and Gutnick 1990; Nowak et al. 2003) (Figs. 6A and 7A). This is an important consideration, because firing rate has been shown to impact the measurement of correlation directly (Cohen and Kohn 2011; de la Rocha et al. 2007), raising the possibility that any correlation effects that we found might be epiphenomenal. However, since attention inversely affected these two variables in our study—increasing firing rate but decreasing correlation—the decorrelation effect of attention that we observed cannot be explained merely by an effect of firing rates. A control analysis using firing-rate-matched subsamples of neurons confirmed that all of the differences between cell classes that we observed were robust when firing rate was matched across classes (Fig. 8).

Fig. 8.

r_sc attention effects matched for firing rate. Shading represents ± 1 SE. We partitioned pairs of neurons into bins based on their geometric mean firing rates and repeated our analysis of the effects of attention on r_sc. A and B: r_sc for both cell classes and attention conditions during stimulus presentation in medium (A)- and high (B)-rate bins. The measurement of r_sc for especially low-rate pairs (geometric mean rate < 5 sp/s) was subject to high noise levels, and those pairs were excluded from this analysis. The firing-rate range for each bin (and the corresponding percentiles) are at the top. C and D: effect of attention (attended minus unattended) from the data in A and B. As with our full sample, the rate-binned analysis revealed late, decorrelating effects of attention that were of greater magnitude for fast-spiking than for regular-spiking cells. This pattern of results was consistent across rate bins but particularly evident in the highest-rate bin, for which measurement of r_sc was least noisy. The high-rate bin also showed an increase in correlation with attention during the earliest portion of the stimulus but only for fast-spiking cells, which was also found for the full sample (see Fig. 7D). The r_sc value for each bin is plotted at the right-most edge (i.e., the first plot point reflects r_sc, calculated using spike counts in the gray-hatched time window).

Dynamic allocation of attention.

We described how the attention effects on firing rate and on spike r_sc appeared to co-vary with the evolution of the expected value of target strength over the course of the trial (the anticipation function). To quantify the strength of this covariation, and reasoning that the neural effects of attentional deployment might lead or lag a bit from the task's temporal statistics, we calculated cross-correlations (Fig. 9) between the attention-effect time series from catch trials (Fig. 7, C and D) and the anticipation function calculated from the actual target-onset times and duration in each recording session (Fig. 1C). We found a significant zero-lag correlation between the anticipation function and the effects of attention on firing rate (Fig. 9A; fast spiking: r = 0.09, t₁₃₄₀ = 14.22, P = 7.7 × 10⁻⁴³; regular spiking: r = 0.05, t₄₉₅₇ = 17.29, P = 4.6 × 10⁻⁶⁵), as well as between the anticipation function and the effects of attention on r_sc (Fig. 9B; fast spiking: r = −0.05, t₄₃₃₅ = −11.72, P = 2.8 × 10⁻³¹; regular spiking: r = −0.01, t₄₆₅₃₉ = −11.94, P = 7.8 × 10⁻³³; mixed pairs: r = −0.03, t₂₆₈₈₃ = −15.53, P = 3.7 × 10⁻⁵⁴). These effects were significant at the single-subject level, with the exception of that for the decorrelating effect of attention on the fast-spiking population in Monkey R, which trended in the same direction (see Fig. 9 legend).

Fig. 9.

Cross-correlation between the time course of attention effects and the time course of the anticipation function. Shading represents ± 1 SE. A: the effect of attention on firing rate had a significant positive cross-correlation with the anticipation function, peaking ∼0 lag. That is, firing-rate modulations manifested in proportion to the expected value of target strength. The strength of this cross-correlation was significantly greater for fast-spiking units than for regular-spiking units. The lines along the bottom of the plot show the lags at which the cross-correlation is significantly nonzero for fast-spiking cells (red) and regular-spiking cells (blue) or at which the cross-correlation differs significantly between classes (black; point-wise t-test; P < 0.05, Bonferroni-corrected for multiple comparisons). B: the effect of attention on spike count correlation was significantly negatively cross-correlated with the anticipation function. That is, the strength of attention-related decorrelation was proportional to the evolution of the expected target information. The extremum of cross-correlation was near-zero lag, and the strength of cross-correlation was significantly greater for fast-spiking units than for regular-spiking units. The lines along the bottom of the plot show the lags at which the cross-correlation is significantly nonzero for fast-spiking pairs (red), regular-spiking pairs (blue), or mixed pairs (gray) or at which the cross-correlation differs significantly between fast- and regular-spiking classes (black; point-wise t-test; P < 0.05, Bonferroni-corrected for multiple comparisons). All of the effects from each animal's individual data were consistent with the population results shown (Monkey B firing rate: fast spiking: r = 0.12, t₈₂₁ = 14.71, P = 1.3 × 10⁻⁴³, and regular spiking: r = 0.07, t₂₅₀₂ = 16.43, P = 1.2 × 10⁻⁵⁷; spike count correlation, fast spiking: r = −0.07, t₃₄₁₂ = −11.80, P = 1.6 × 10⁻³¹, regular spiking: r = −0.02, t₂₂₁₈₃ = −11.5, P = 9.4 × 10⁻³¹, and mixed pairs: r = −0.03, t₁₇₅₀₈ = −15.63, P = 2.5 × 10⁻⁵⁴; Monkey R firing rate, fast spiking: r = 0.03, t₅₁₈ = 3.83, P = 1.5 × 10⁻⁴, and regular spiking: r = 0.03, t₂₄₅₄ = 7.48, P = 1.0 × 10⁻¹³; spike count correlation, fast spiking: r = −0.01, t₉₂₂ = −1.15, P = 0.25, regular spiking: r = −0.003, t₂₄₃₅₅ = −3.52, P = 4.3 × 10⁻⁴, and mixed pairs: r = −0.003, t₉₃₇₄ = −2.20, P = 0.028).

The dynamics of the attention effects on both firing rate and correlation of fast-spiking neurons followed the anticipation function more closely than the attention effects of regular-spiking neurons did (Fig. 9; firing rate, two-sample t-test: t₆₂₉₇ = 5.58, P = 2.6 × 10⁻⁸; r_sc: t₅₀₈₇₄ = −10.47, P = 1.2 × 10⁻²⁵). This is not simply a consequence of the larger attention-effect size for the fast-spiking cells as the cross-correlation is a normalized measure.

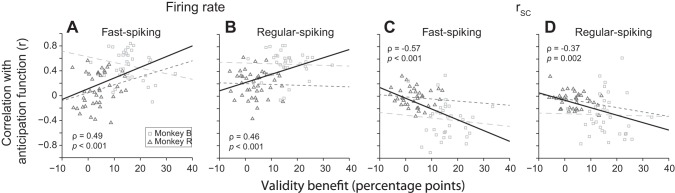
With the use of this normalized measure, we were able to exploit the behavioral variability of our subjects across sessions to test the behavioral significance of the neural effects that we observed. Specifically, we measured the zero-lag correlation between the attention effects on firing rate and r_sc and the anticipation function for each session. We found that this value had the greatest magnitude in sessions in which the subjects showed stronger behavioral effects of attention (Fig. 10). In other words, the subjects' behavioral performance was best when the neural effects of attention were most in alignment with the timing of the task. This correlation between the behavioral and neural effect sizes was significant for both fast-spiking and regular-spiking neurons when measured over all sessions from both animals [Fig. 10; firing-rate effects, fast spiking: Spearman's rank correlation (ρ) = 0.49, P < 0.001, and regular spiking: ρ = 0.46, P < 0.001; r_sc effects, fast spiking: ρ = −0.57, P < 0.001, and regular spiking: ρ = −0.37, P = 0.002]. In general, we did not find these relationships to be statistically significant at the level of single subjects, although Monkey R did show a significant correlation between firing-rate attention-effect size and behavioral effect size for the fast-spiking subpopulation (ρ = 0.32, P = 0.04; for all other comparisons, P > 0.29). These data are consistent with previous studies demonstrating the behavioral impact of trial-to-trial changes in population variability (Cohen and Maunsell 2010; Mayo et al. 2015).

Fig. 10.

Relationship between neural and behavioral effect sizes. The zero-lag correlation between the effect of attention on firing rate (A and B) or spike count correlation (C and D) and the anticipation function (Fig. 9A) is plotted against the improvement in hit rate in percentage points for trials with valid cues compared with trials without cues (i.e., the “validity benefit”). Lines depict the best-fitting trends for Monkey R (dark gray, short dashes) and Monkey B (light gray, long dashes) and for all sessions of both subjects (black, solid). Sessions with stronger behavioral effects of attention had neural effects that more closely tracked the anticipation function. Spearman's rank correlation coefficient and the corresponding P value are shown (inset). The relationships were significant at the group level but not within individual subjects (ρ = 0.32, −0.04, −0.14, −0.16; P = 0.04, 0.81, 0.83, and 0.35 for Monkey R in A–D, respectively; ρ = −0.18, −0.10, −0.04, −0.05; P = 0.30, 0.57, 0.83, and 0.78 for Monkey B in A–D, respectively).

DISCUSSION

Our goal was to test for differential effects of attention between excitatory and inhibitory neurons to understand better the roles of excitation and inhibition for cognition. We trained monkeys to attend selectively to one of two grating stimuli. The animals endogenously enhanced their processing of the attended stimulus at the expense of the unattended stimulus, revealing the behavioral effects of attention (Fig. 1B). This endogenous attentional deployment was accompanied by increases in firing rate (Figs. 6C and 7C) and decreases in r_sc (Fig. 6D and 7D) that tracked the time course of anticipation during the task (Fig. 9). The magnitude of all of these attention effects was greater for the fast-spiking (putative inhibitory) subpopulation of neurons than for the regular-spiking (putative excitatory) subpopulation (Fig. 7, C and D), suggesting that inhibitory cells might be targeted more directly by attention feedback signals than excitatory cells.

Although many have speculated about distinct roles for inhibition and excitation in cognition (Isaacson and Scanziani 2011; Reynolds and Heeger 2009), testing these hypotheses has proved elusive. Selective modulation of inhibitory interneurons is central to several attention models (Reynolds and Heeger 2009), but finding in vivo experimental support for such models has proved challenging. Two recent studies showed that putative inhibitory neurons (identified by waveform shape) have stronger attentional modulation in firing rate and variability than excitatory neurons (Mitchell et al. 2007) but less adaptation in spike height during bursting (Anderson et al. 2013), supporting the notion that inhibitory neurons mediate attentional gain in sensory cortex. Our study provides three key innovations over previous work. First, we measured functional connectivity (in the form of r_sc) between neurons classified by type in the context of an attention task. We found that putative inhibitory neuron pairs had higher correlation overall, and attention had a stronger decorrelating effect on their activity when compared with putative excitatory neurons, suggesting a key role for inhibitory networks in attention mechanisms. Second, we measured the time course of two electrophysiological correlates of attention and found that the magnitude of the attention signals that we identified tracked the anticipation function and that this relationship was also stronger for the subpopulation of putative inhibitory neurons. The third innovation was the use of multidimensional waveform analysis to identify neuronal subpopulations, instead of a single metric, as in previous work. This method provides access to analysis of putative inhibitory and excitatory neurons in massive multielectrode data in which the individual neurons are not targeted, opening up numerous possibilities for future research on the roles of inhibition and excitation in alert, behaving animals performing complex cognitive tasks.

Previous researchers have been interested in the question of how correlated variability might differ between excitatory and inhibitory cell classes, although the lower incidence of inhibitory neurons in cortex has made the study of interactions among them particularly challenging. To date, these efforts have examined interactions between pairs of excitatory neurons and between pairs comprised of one neuron from each class, but the details of correlated variability between pairs of putative inhibitory neurons have not yet been reported. For example, Qi and Constantinidis (2012) examined how correlated variability between excitatory and inhibitory neurons in the prefrontal cortex changed due to training on a working memory task. They found a reduction in correlations between pairs of neurons with similar tuning properties, consistent with improved information capacity in the neuronal population after training. They also found that this effect was driven primarily by pairs of putative excitatory neurons compared with pairs with mixed-class membership. They did not report effects for pairs of inhibitory neurons, most likely because with eight recording electrodes, they did not encounter a sufficient number of pairs of inhibitory neurons to perform an adequately powered analysis of their correlated variability. In another example, Middleton et al. (2012) studied correlated variability of spiking activity of neurons in rat barrel cortex during whisker deflections. They reported that excitatory neurons maintain relatively low levels of correlation throughout spontaneous and stimulus-driven activity. In contrast, pairs with mixed-class membership had fairly high levels of correlation during spontaneous activity, with a marked reduction in correlation during whisker stimulation. These two studies, together with our results, point strongly to differences in functional interactions between excitatory and inhibitory subpopulations. Our 96-channel recordings, combined with the use of multiple measures of waveform shape and a Gaussian mixture model, enabled us to access sufficient numbers of inhibitory neurons to isolate and study this subpopulation in the context of an attention task, a feat not previously possible with smaller-scale recordings or simpler waveform classification techniques. Whereas our focus here was on the distinction between putative excitatory and inhibitory neurons, there is interest in further subclassifications of neurons within these broad groups based on functional properties, such as temporal spike-train statistics (Ardid et al. 2015; Nowak et al. 2003). A particular advantage of our methodology is the ease of incorporating such additional neuronal characteristics.

A critical difficulty in understanding the neural circuits that give rise to attention has been the conceptual difficulty in reconciling various neural attention effects, such as increases in firing rate and decreases in correlated variability. This has led to the rise of network modeling as a means to understand input-output relationships at a network level and to explain how synaptic and other neuronal properties are transmitted into correlation (Ostojic et al. 2009; Shea-Brown et al. 2008). A number of influential network models rely on a precise balance of inhibition and excitation to model neural activity (Middleton et al. 2012; Renart et al. 2010; van Vreeswijk and Sompolinsky 1996), and a recent study used such a model to show that selective modulation of inhibitory networks may be a key to explaining the neural effects of attention (Wiese et al. 2014). Our findings are compatible with the intuitions gleaned from such a network-level model and strongly support a specialized role for inhibitory networks in spatial-selective attention.

GRANTS

Support for A. C. Snyder was provided by the National Eye Institute (Grants F32EY023456 and K99EY025768). Support for M. J. Morais was provided by a National Institute on Drug Abuse undergraduate research training fellowship through the University of Pittsburgh's Program in Neural Computation (R90DA023428). Support for M. A. Smith was provided by the National Eye Institute (Grants R00EY018894, R01EY022928, and P30EY008098); Research to Prevent Blindness (a Career Development Grant and an Unrestricted Award); and the Eye and Ear Foundation of Pittsburgh.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.C.S. and M.A.S. conception and design of research; A.C.S. performed experiments; A.C.S. and M.J.M. analyzed data; A.C.S. and M.A.S. interpreted results of experiments; A.C.S. prepared figures; A.C.S. and M.A.S. drafted manuscript; A.C.S. and M.A.S. edited and revised manuscript; A.C.S. and M.A.S. approved final version of manuscript.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript be found at the institutional website of one of the authors, which at the time of publication, they indicate is: http://www.smithlab.net. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.