Savings for visuomotor adaptation require prior history of error, not prior repetition of successful actions

Learning to adapt movements to compensate for unexpected perturbations shows savings, or faster readaptation to a previously encountered perturbation. Using a factorial design, we examined how savings is affected by prior experience of similar errors and prior repetition of the action required to eliminate errors. The data show that prior experience of errors is both necessary and sufficient for savings, whereas prior repetition of a successful action is neither necessary nor sufficient for savings.

Abstract

When we move, perturbations to our body or the environment can elicit discrepancies between predicted and actual outcomes. We readily adapt movements to compensate for such discrepancies, and the retention of this learning is evident as savings, or faster readaptation to a previously encountered perturbation. The mechanistic processes contributing to savings, or even the necessary conditions for savings, are not fully understood. One theory suggests that savings requires increased sensitivity to previously experienced errors: when perturbations evoke a sequence of correlated errors, we increase our sensitivity to the errors experienced, which subsequently improves error correction (Herzfeld et al. 2014). An alternative theory suggests that a memory of actions is necessary for savings: when an action becomes associated with successful target acquisition through repetition, that action is more rapidly retrieved at subsequent learning (Huang et al. 2011). In the present study, to better understand the necessary conditions for savings, we tested how savings is affected by prior experience of similar errors and prior repetition of the action required to eliminate errors using a factorial design. Prior experience of errors induced by a visuomotor rotation in the savings block was either prevented at initial learning by gradually removing an oppositely signed perturbation or enforced by abruptly removing the perturbation. Prior repetition of the action required to eliminate errors in the savings block was either deprived or enforced by manipulating target location in preceding trials. The data suggest that prior experience of errors is both necessary and sufficient for savings, whereas prior repetition of a successful action is neither necessary nor sufficient for savings.

NEW & NOTEWORTHY

Learning to adapt movements to compensate for unexpected perturbations shows savings, or faster readaptation to a previously encountered perturbation. Using a factorial design, we examined how savings is affected by prior experience of similar errors and prior repetition of the action required to eliminate errors. The data show that prior experience of errors is both necessary and sufficient for savings, whereas prior repetition of a successful action is neither necessary nor sufficient for savings.

the remarkable flexibility of our motor system is evident in our ability to quickly adapt movements to unexpected perturbations, which are ubiquitous to everyday life. A key feature of such motor adaptation is rapid responsiveness to errors. Humans readily alter behavior to compensate for error, adjusting motor commands to achieve accurate movements despite ever-changing body and environment states. Although behavior rapidly reverts to the unadapted state upon perturbation removal, reexposure to a previously experienced perturbation elicits faster readaptation, even months later (Landi et al. 2011) or after many no-perturbation trials (Berniker and Kording 2011; Zarahn et al. 2008). This phenomenon, known as “savings” (Ebbinghaus 1913), shows that some aspects of motor adaptation are retained over long timescales, although the memory is latent because behavior continuously accommodates the current sensorimotor state.

Motor adaptation was traditionally thought to occur by updating internal forward models that predict the sensory consequences of motor commands. Perturbations evoke sensory prediction errors, or discrepancies between predicted and actual sensory consequences of movements, which appear to be reduced by incrementally updating the internal model (Miall and Wolpert 1996; Wolpert et al. 1995). It is clear, however, that additional processes other than model-based adaptation influence behavior, including reward-based reinforcement of successful actions (e.g., Galea et al. 2015; Huang et al. 2011; Izawa and Shadmehr 2011; Nikooyan and Ahmed 2015; Shmuelof et al. 2012), use-dependent bias toward repeated movements (Diedrichsen et al. 2010; Huang et al. 2011; Verstynen and Sabes 2011), and strategic reaiming to compensate for systematic errors (e.g., Mazzoni and Krakauer 2006; Taylor et al. 2014). The debate continues as to which of these mechanistic processes contribute to savings and even as to the empirical preconditions required for savings to be expressed (Herzfeld et al. 2014; Huang et al. 2011; Morehead et al. 2015; Orban de Xivry and Lefevre 2015; Turnham et al. 2012).

One theory suggests that savings results from the retrieval of remembered actions (Huang et al. 2011). The theory that savings relies not on (internal) model-based mechanisms but on a memory of successful actions was prompted by the surprising finding of savings in adaptation to rotated visual feedback after prior exposure to a rotation in the opposite direction (Huang et al. 2011). Because savings occurred only when a common action eliminated errors from the two opposing rotations, savings was argued to result from faster retrieval and reselection of actions that became associated with success (i.e., target acquisition) via repetition at asymptote. This model-free account of savings is attractive because traditional state-space models of adaptation predict a similar rate of error correction for a given perturbation and model state and thus cannot fully account for savings (Smith et al. 2006; Zarahn et al. 2008). An alternative theory suggests that savings requires prior experience of similar errors. According to this theory, savings can be accounted for by an error-based model of adaptation that allows for experience-dependent adjustment of error sensitivity. Here, a systematic sequence of errors evoked by a perturbation is argued to increase sensitivity for those errors, increasing the gain of error correction upon reencountering similar errors (Herzfeld et al. 2014). According to this account, savings after an opposite direction rotation (e.g., Huang et al. 2011) results from experiencing similarly signed errors upon abrupt removal of that rotation. This proposal was supported by findings of diminished savings when prior experience of similarly signed and similarly sized errors was reduced by gradually removing the original rotation or by allowing time to elapse postrotation, such that time-dependent decay reduced the size of the errors experienced. Prior experience of similarly signed errors therefore appears crucial to faster readaptation under the conditions studied by Herzfeld et al. (2014).

A third account for savings holds that faster error correction after prior experience to a visuomotor rotation occurs because subjects more rapidly, or more effectively, apply a strategy to explicitly aim in the direction necessary to counter the perturbation (Morehead et al. 2015). This idea builds on evidence that both explicit and implicit processes typically contribute to error reduction upon exposure to visuomotor distortion but that explicit processes dominate the fast rate of initial error reduction (e.g., Haith et al. 2015; Taylor et al. 2014). Morehead et al. (2015) provided evidence that strategic reaiming was largely responsible for savings under the conditions of their experiments, although some aspects of those results were somewhat atypical (no savings for 30° rotation and poor asymptotic performance levels). Other lines of evidence similarly suggest that strategic reaiming can contribute to savings, as restricting movement preparation time to suppress strategic reaiming suppressed the expression of savings (Haith et al. 2015). Given that people can fully compensate for a visuomotor rotation in a single trial with appropriate instructions and cues (Mazzoni and Krakauer 2006), savings should occur whenever previous exposure to a perturbation provides a cue to prompt reaiming (e.g., retrieval of a reaiming strategy or retrieval of a learned aiming direction). However, it is unclear whether alternative, implicit processes, such as increased error sensitivity or implicit retrieval of a previously successful action, also contribute to savings. Furthermore, the question of whether explicit reaiming is necessary for savings is difficult to answer, as it depends on how one distinguishes between explicit and implicit learning. One definition suggests that explicit learning is marked by awareness of what is being learned (Reber 1967). Others define explicit learning as processes that can be deliberately engaged and disengaged; implicit learning is therefore automatic and difficult to deliberately disengage (Huberdeau et al. 2015b). According to this definition, extended training might render previously explicit reaiming automatic, such that people begin to implicitly use a previously explicit strategy and deliberate use of a strategy is no longer necessary for savings. Alternatively, one might argue that explicit reaiming, by definition, implies intention to use a strategy and thus can never become implicit. Whether or not savings requires strategic reaiming thus depends on the chosen distinction between implicit and explicit learning. A full resolution of this issue is beyond the scope of this report.

In the present study, we sought to contribute to the debate on the mechanisms of savings by examining whether prior experience of errors and/or prior repetition of successful actions constitute necessary conditions for savings. The error sensitivity hypothesis of Herzfeld et al. (2014) predicts that savings requires prior experience of errors similar to those encountered at relearning. The alternative hypothesis that savings results from retrieval of a previously successful action (Huang et al. 2011) predicts that prior execution of the action is required for task success at relearning. In a factorial design, we manipulated prior repetition of the action that would eliminate errors at relearning and prior experience of errors encountered at relearning. The data indicate that prior history of similar errors is necessary and sufficient for savings, whereas prior repetition of the action required to eliminate errors is neither necessary nor sufficient for savings.

MATERIALS AND METHODS

Participants

A total of 46 right-handed adults with no self-reported neurological or psychiatric problems (age: 17–47 yr, mean: 20.84 yr, SD: 4.11 yr, 38 women and 8 men) participated in this study. This encompassed a total of 36 participants for the main experiment (Err⁻Rep⁻: 9 subjects, Err⁺Rep⁻: 9 subjects, Err⁻Rep⁺: 9 subjects, and Err⁺Rep⁺: 10 subjects) and 10 participants for the control experiment (Err⁺Rep⁻Far). All participants were naïve to visuomotor rotation tasks and naïve to the aims of the experiment. This study was approved by the Human Research Ethics Committee of The University of Queensland. All participants provided written informed consent.

Apparatus

Participants sat on a height-adjustable chair in front of a digitizing tablet (WACOM Intuos4 PTK 1240, size: 19.2 × 12 in., resolution ± 0.25 mm) mounted horizontally such that a planar movement on the tablet translated to a planar on-screen movement. The monitor was placed ∼10 cm away from the participant. Participants moved a digitizing pen (15.95 cm long, 1.4 cm wide, 17 g) on the tablet. The pen's position on the tablet (xy coordinates) was sampled at 100 Hz and displayed on the computer monitor as a circular cursor with a 5-pixel radius (1.32 mm). The monitor frequency was set at 60 Hz. Direct vision of the hand was prevented by placing the tablet and the hand directly beneath a stand, with the monitor placed horizontally on top of the stand.

General Procedure

The experimental task required participants to move the on-screen cursor from a start location to a target by moving the pen on the digitizing tablet. Participants were first instructed to move a cursor representing the pen's position into the start circle (8 pixels, i.e., 2 mm). After the cursor came within the start circle for 500 ms, a single target circle (radius: 15 pixels, i.e., 4 mm) appeared 75 mm from the target. A tone sounded immediately after target appearance, signaling participants to move the cursor to the target. Participants were instructed to move the cursor from the start circle to the target circle as accurately and as quickly as possible, in a single, uncorrected movement. Online visual feedback of the cursor position was shown on screen.

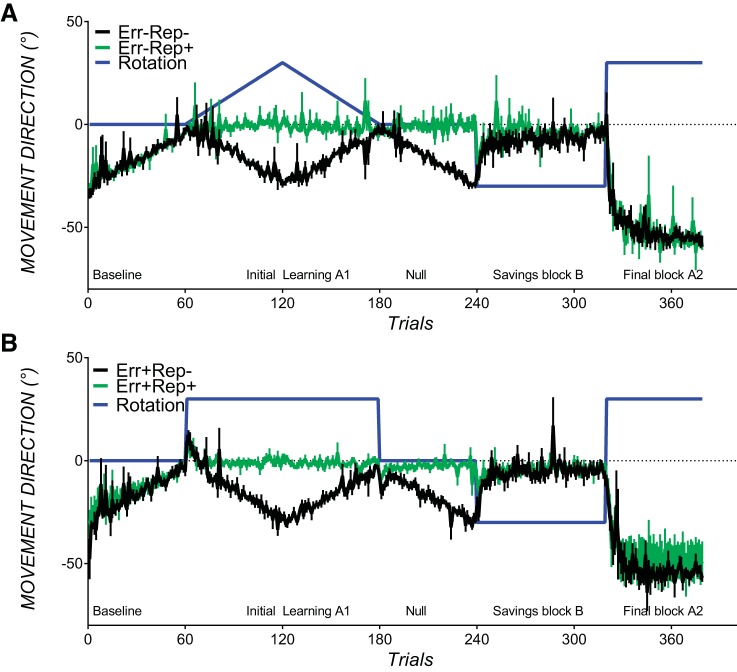
Across all experimental conditions, the trial structure proceeded as follows. First, all participants completed 60 baseline trials with veridical cursor feedback of the hand position to ensure similar reaching performance before adaptation. To reduce the potential for use-dependent effects in this baseline block, the target location started at 15° relative to the 12 o'clock position and rotated 1° clockwise every two trials. The test phase consisted of blocks A1-null-B-A2, as described below. The first (naïve) adaptation block A1 consisted of 119 trials with a 30° clockwise rotation of visual feedback of the movement relative to the center of the start circle (see Fig. 1, black lines). The rotation was either abruptly imposed and abruptly removed or was gradually imposed and gradually removed. A1 was followed by a null (no-rotation) block of 60 trials. Subsequently, in savings block B (80 trials), a 30° counterclockwise rotation of visual feedback was abruptly imposed. This was followed by the final block A2 (60 trials), which contained an abruptly imposed 30° clockwise rotation and was used to measure the combined effects of savings and anterograde interference from the preceding block B. The target direction and rotation schedules were the same across conditions for savings block B and final block A2. There were no rest breaks in between adaptation blocks. The entire test session took between 35 and 45 min.

Fig. 1.

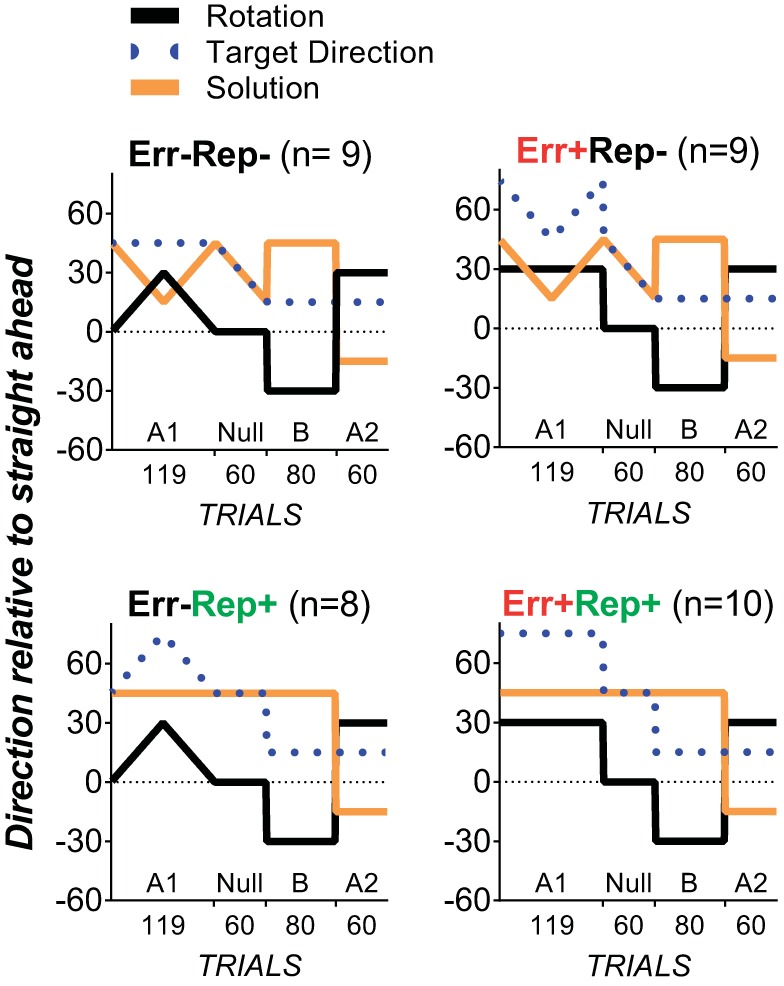
Experimental design. The black lines indicate the extent of angular rotation of visual feedback of the movement trajectory relative to the center of the start circle. Positive values indicate clockwise rotation; negative values indicate counterclockwise rotation. In the no prior error conditions (Err⁻Rep⁻ and Err⁻Rep⁺; left), the 30° clockwise rotation in first adaptation block A1 was gradually removed to prevent experience of the 30° counterclockwise error in that would be later encountered in savings block B. In the prior error conditions (Err⁺Rep⁻ and Err⁺Rep⁺; right), the abruptly imposed 30° clockwise rotation at block A1 was abruptly removed to allow experience of large counterclockwise errors that would be later encountered in savings block B. The blue dotted lines indicate the target direction (0° = 12 o'clock, 90° = 3 o'clock, −90°= 9 o'clock, and 180° = 6 o'clock), which was manipulated to encourage repetition of the savings block B movement solution in the prior repetition conditions (Err⁻Rep⁺ and Err⁺Rep⁺), such that the movement solution in all blocks before savings block B (indicated by the orange lines) was the same as in savings block B.

Design

Prior experience of errors and prior repetition of the adapted movement was manipulated in a 2 × 2 design, as follows.

Prior experience of errors.

Abrupt removal of a clockwise rotation evokes counterclockwise errors (Herzfeld et al. 2014). In conditions ensuring prior experience of similar counterclockwise errors as in the savings block (i.e., the prior-error conditions, Err⁺Rep⁻ and Err⁺Rep⁺), the abruptly imposed 30° clockwise rotation of visual feedback in A1 was abruptly removed to allow experience of counterclockwise errors (see black lines in Fig. 1, right). To prevent prior experience of error in the no-prior error conditions, Err⁻Rep⁻ and Err⁻Rep⁺(see black lines in Fig. 1, left), the 30° clockwise rotation of visual feedback in A1 was gradually imposed by 0.5° per trial, reaching 30° on trial 60, and then gradually removed by 0.5° per trial to reach 0° by trial 120.

Prior repetition of the movement solution.

We manipulated repetition of the action that would successfully eliminate the savings block errors (hereafter termed the “movement solution”). In conditions with repetition of the movement solution (Err⁻Rep⁺ and Err⁺Rep⁺), a single direction of movement was encouraged in all test phase blocks (i.e., A1 and washout) before savings block B (see orange lines in Fig. 1, bottom). This was achieved by rotating the target relative to the movement solution in the same direction and magnitude as the visual feedback rotation. The different perturbation schedules for the two conditions with limited repetition of the solution (Err⁻Rep⁻ and Err⁺Rep⁻) necessitated different target manipulations. In Err⁻Rep⁻, the target stayed in the same position throughout A1 as the clockwise rotation was gradually imposed by 0.5° per trial and gradually removed by 0.5° per trial. Repetition of the solution was limited as participants adapted incrementally to the rotation. In Err⁺Rep⁻, repetition was limited by rotating the target direction (see blue lines in Fig. 1B) in the same direction and magnitude as the visuomotor rotation, such that the movement solution profile in A1 (see orange lines in Fig. 1B) was matched to that of Err⁻Rep⁻ (see orange lines in Fig. 1A).

For savings block B, all conditions contained the same 30° counterclockwise rotation and the same target direction. The savings block was followed by final block A2 of 60 trials with a 30° clockwise rotation, which allowed us to assess the combined effects of savings and anterograde interference, detailed as follows. Anterograde interference is the phenomenon of slowed subsequent learning as a result of previously learning a task with opposite demands, such as adapting to a counterclockwise rotation and subsequently adapting to clockwise rotation (e.g., Miall et al. 2004; Sing and Smith 2010). Error reduction during adaptation to the 30° counterclockwise rotation in final block A2 is susceptible to savings from prior adaptation to the clockwise rotation in block A1 and to anterograde interference from the counterclockwise rotation from block B. Importantly, block A2 might also be sensitive to error and repetition manipulations. Reduction of errors from the 30° clockwise rotation at block A2 could be influenced by the presence of similar errors from the abruptly imposed 30° clockwise errors in block A1 (Err⁺Rep⁻ and Err⁺Rep⁺) or the absence of similar clockwise errors from the gradually imposed 30° clockwise rotation in block A1 (Err⁻Rep⁻ and Err⁻Rep⁺). The repetition manipulation ensured extended repetition of the block B movement solution (i.e., in blocks A1, null, and B) (Err⁻Rep⁺ and Err⁺Rep⁺) or limited repetition of the movement solution only after attaining asymptote in block B (Err⁻Rep⁻ and Err⁺Rep⁻). Note that the solution for savings block B was at least 60° away from the block A2 solution. Hence, the repetition manipulation generated limited or extended repetition of a movement that differed from that required for task success in block A2. In short, the final block A2 allowed the rare opportunity to study the influence of prior history of error and prior repetition of a different movement solution on both savings and anterograde interference, which, to the best of our knowledge, has yet to be systematically examined.

Data Analysis

Cartesian xy coordinates were recorded and used to plot movement trajectory. Movement direction was scored 15 mm into the movement, which occurred <150 ms after the movement onset. Directional error was calculated as the angular difference between this movement direction and an idealized movement direction from the start circle to the target circle. A negative value in directional error indicates that the cursor movement trajectory was counterclockwise to an ideal movement trajectory plotted from the start to a target.

One data set from Err⁻Rep⁺ was excluded due to programming error. A second data set from Err⁺Rep⁻ was excluded because the subject failed to aim accurately to the target even in the baseline trials in the absence of a rotation; averaged directional error in the last 10 trials of the baseline block was mean: 19.46, SD: 22.69. A third data set from the control condition, Err⁺Rep⁻Far, was excluded because the subject failed to comply with instructions to move quickly; averaged movement times were in excess of 1 s. The final numbers of participants in each condition were as follows: Err⁻Rep⁻, n = 9; Err⁺Rep⁻, n = 9; Err⁻Rep⁺, n = 8; Err⁺Rep⁺, n = 10; and Err⁺Rep⁻Far, n = 9.

We examined savings and anterograde interference using both rate constants and directional errors averaged across bins, described as follows.

Rate constants.

Directional errors in learning a visuomotor rotation can be characterized with a single-rate exponential function (Zarahn et al. 2008), as follows: y = y₀ × e^−kx + a, where y is the directional error, x is the trial number, k is the rate constant that indicates the rate with which directional error changes, a is the directional error at which performance reaches asymptote, and y₀ + a is the hypothetical y value when x is zero. We fit single subject data to the single exponential function using GraphPad 6.0 least-squares nonlinear regression. We did not analyze rate constants for individual subject data when the nonlinear regression procedure failed to converge on the best fit and when the model deviated significantly from the data, as shown with the Wald-Wolfowitz (or Runs) test for randomness (Wald and Wolfowitz 1940). A significant P value (P < 0.05) for the Runs test suggests that the fitted curve deviated from the data. For savings block B, this procedure excluded one data set from Err⁻Rep⁺ and two data sets each from Err⁻Rep⁻ and Err⁺Rep⁻ (postexclusion: Err⁻Rep⁻, n = 7; Err⁺Rep⁻, n = 7; Err⁻Rep⁺, n = 7; and Err⁺Rep⁺: n = 10). For final block A2, this excluded one data set each from Err⁻Rep⁻ and Err⁻Rep⁺ and two data sets from Err⁻Rep⁺ and Err⁺Rep⁺ (postexclusion: Err⁻Rep⁻, n = 8; Err⁺Rep⁻, n = 9; Err⁻Rep⁺, n = 7; and Err⁺Rep⁺, n = 8). These sample sizes are sufficient to quantify savings based on rate constants (Huang et al. 2011). Rate constants were subjected to error (no prior error or prior error) × repetition (no repetition or repetition) ANOVAs. Partial η² values were used to report ANOVA effect sizes, with values in excess of 0.14 considered large. Post hoc paired t-tests and independent-sample t-tests (two-tailed) were used to evaluate within- and between-group differences in rate constants. For t-tests, Hedges' g instead of Cohen's d was used to estimate effect size, as Hedge's g is a variation of Cohens' d that corrects for biases due to small sample sizes (Hedges 1981). Hedges' g values exceeding 0.8 were considered large.

Directional errors.

As shown above, single-exponential functions often do not fit well to individual adaptation data sets (e.g., Villalta et al. 2015). To ensure that our results were not dependent on the exclusion of data sets that did not fit well to the function, we additionally quantified error reduction with directional errors averaged in bins of five trials. Directional errors in the error reduction phase (bins 1–4, i.e., trials 1–20, where all participants reduced at least 60% of directional errors) were subjected to error (no prior error or prior error) by repetition (no prior repetition or prior repetition) × bin ANOVAs. To evaluate whether the asymptotic phase differed between conditions, error × repetition ANOVAs were also run for all bins after bin 4 of that block. Partial η² values were used to report ANOVA effect sizes, with values in excess of 0.14 considered large. Where applicable, Greenhouse-Geisser corrections were used to correct for violations of sphericity.

Similar to previous studies (Orban de Xivry and Lefevre 2015), we did not quantify savings by comparing naive learning block A1 mean directional errors to savings block B mean directional errors (e.g., Krakauer et al. 2005). This is because in the no prior error conditions, the block A1 rotation was imposed gradually and removed gradually, eliciting only small directional errors throughout block A1, thus making it inappropriate to compare these small errors to large errors evoked by an abruptly imposed rotation. Furthermore, while the savings block B target location was the same across all experimental conditions, the block A1 target location changed from trial to trial in Err⁺Rep⁻ and Err⁻Rep⁺ but not in Err⁻Rep⁻ or Err⁺Rep⁺.

RESULTS

Error Reduction at Initial Adaptation Block A1

Gradually imposed rotations in Err⁻Rep⁻ and Err⁻Rep⁺ (Fig. 2A) elicited smaller errors than abruptly imposed rotations in Err⁺Rep⁻ and Err⁺Rep⁺ (Fig. 2B). Thus, error reduction was compared between groups with similar rotation profiles in initial adaptation block A1 (Err⁺Rep⁻ and Err⁺Rep⁺ as well as Err⁻Rep⁻ with Err⁻Rep⁺). Error reduction in initial learning block A1 did not differ reliably between Err⁺Rep⁻ and Err⁺Rep⁺ (see Fig. 2A), as condition × bin ANOVAs yielded a nonsignificant main effect of condition [F(1,17) = 0.63, P = 0.43, partial η² = 0.03] and a nonsignificant bin × condition interaction [F(7.4,127.1) = 0.95, P = 0.47, partial η² = 0.05]. Directional errors also did not differ reliably between Err⁻Rep⁻ and Err⁻Rep⁺ (see Fig. 2B), as the main effect of condition [F(1,15) = 3.32, P = 0.08, partial η² = 0.18] and the bin × condition interaction [F(6.3, 94.5) = 1.74, P = 0.11, partial η² = 0.10] were not significant.

Fig. 2.

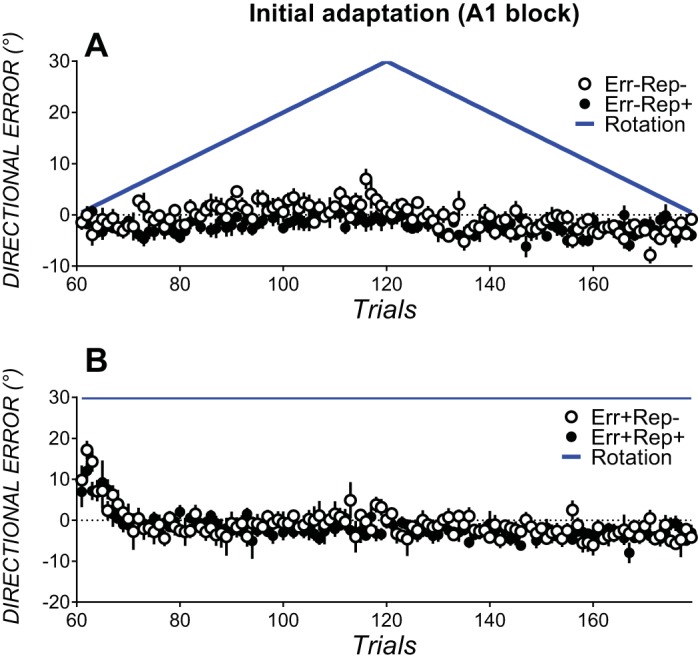
Initial adaptation block A1 trial-by-trial directional errors in conditions without (A) and with (B) prior experience of counterclockwise errors. Open circles indicate conditions with no repetition of the movement solution (i.e., the action that would eliminate errors in savings block B); solid circles indicate conditions with prior repetition of the movement solution required for savings block B. Data are group means ± SE.

Prior Experience of Counterclockwise Error From Abrupt Offset of the Clockwise Rotation

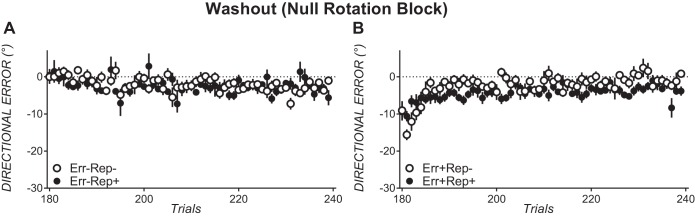
According to the Herzfeld et al. (2014) interpretation, savings when adapting to a 30° counterclockwise rotation requires a history of systematic counterclockwise errors, provided here by abrupt offset of the clockwise rotation in Err⁺Rep⁻ and Err⁺Rep⁺. We attempted to prevent systematic counterclockwise errors by gradually removing the clockwise rotation in Err⁻Rep⁻ and Err⁻Rep⁺. To ensure that these manipulations succeeded, we ran bin × error ANOVAs on binned directional errors upon rotation offset (null block trials 1–60 for the prior error conditions and trials 61–120 of block A1 in the no prior error conditions, as shown in Fig. 3). Large, systematic counterclockwise errors were evident upon rotation offset in the prior error conditions but not in the no prior error conditions (see Fig. 3), as these errors differed between the no prior error conditions and the prior error conditions, shown in a significant main effect of error [F(1,34) = 4.78, P = 0.036, partial η² = 0.12] and a significant bin × error interaction [F(6.5,219.8) = 13.62, P < 0.001].

Fig. 3.

Trial-by-trial directional errors upon rotation offset for conditions that do not evoke a systematic sequence of counterclockwise errors (A) and for conditions that do evoke a sequence of counterclockwise errors (B). All data are means ± SE.

Prior Repetition of the Savings Block Movement Solution

Figure 4 shows movement directions for conditions that did not allow extended repetition of the savings block B movement solution (green lines) and conditions that did allow extended repetition of the savings block B movement solution (black lines). To quantify the extent of repetition of the savings block movement solution, we calculated the proportion of trials from all test phase trials before the savings block (i.e., block A1 and washout) that fell within 5° of the savings block movement solution. Conditions with limited repetition of the solution had fewer trials within 5° of the savings block movement solution (11.24 ± 2.73%, Err⁻Rep⁻: 10.8 ± 3.8% and Err⁺Rep⁻: 11.6 ± 3.8%) than the conditions with extended repetition of the solution (62.78 ± 2.5%, Err⁻Rep⁺: 58.6 ± 3.4% and Err⁺Rep⁺: 66.9 ± 3.6%), as a repetition × error ANOVA revealed a significant main effect of repetition [F(1,32) = 193.12, P < 0.001, partial η² = 0.86]. The main effect of error was not reliable [F(1,32) = 1.5, P = 0.23, partial η² = 0.04], and there were no reliable interactions.

Fig. 4.

Trial-by-trial movement direction for conditions that did not allow extended repetition of the savings block B movement solution (black lines, Err⁻Rep⁻, Err⁺Rep⁻) and conditions that did allow extended repetition of the savings block B movement solution (green lines, Err⁻Rep⁺, Err⁺Rep⁺). A: conditions that did not evoke a systematic sequence of counterclockwise errors (Err⁻Rep⁻, Err⁻Rep⁺). B: conditions that did evoke a sequence of counterclockwise errors (Err⁺Rep⁻, Err⁺Rep⁺). All data are means ± SE.

Savings Requires Prior Experience of Errors But Not Repetition of the Rotation Solution

Rate constants.

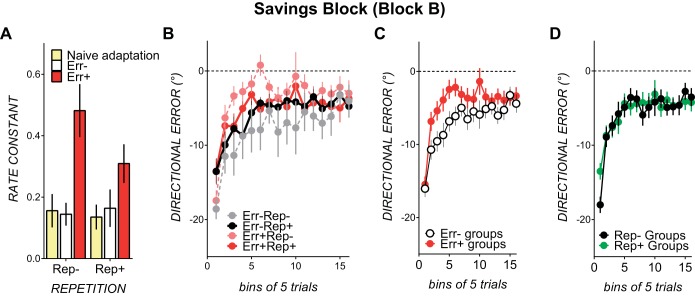
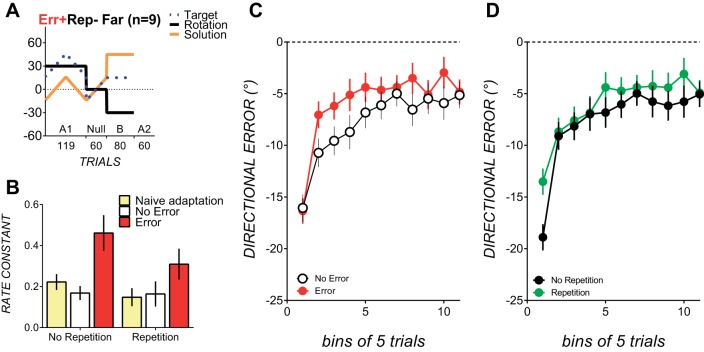
Savings is typically evaluated by comparing rate constants from naïve learning to rate constants from subsequent learning. However, in the no prior error groups (Err⁻Rep⁻ and Err⁻Rep⁺), we could not fit an exponential function to block A1 as the counterclockwise rotation was gradually imposed and gradually removed. Hence, similar to previous studies in which perturbation was applied gradually (Orban de Xivry and Lefevre 2015; Roemmich and Bastian 2015), savings block rate constants were compared between experimental conditions. Mean rate constants for each condition were as follows: Err⁻Rep⁻, 0.14 ± 0.09; Err⁺Rep⁻, 0.48 ± 0.22; Err⁻Rep⁺, 0.16 ± 0.16; and Err⁺Rep⁺, 0.30 ± 0.19. The error × repetition ANOVA on savings block B rate constants showed a significant main effect of error [F(1,27) = 13.48, P < 0.001, partial η² = 0.33]. Errors decreased in the savings block at a significantly faster rate in conditions with prior experience of similar counterclockwise errors, as shown by the larger mean rate constants (0.29 ± 0.04) than in conditions without prior experience of error (0.15 ± 0.04). The effect size of this difference was large (Hedges' g = 1.18). Neither the main effect of repetition [F(1,27) = 1.35, P = 0.25, partial η² = 0.047] nor the repetition × error interaction [F(1,27) = 2.13, P = 0.15, partial η² = 0.07] was significant, as rate constants did not differ reliably with prior repetition (0.23 ± 0.04) or without prior repetition (0.32 ± 0.05) of the movement solution: the effect size was small (Hedges' g = 0.28). If anything, rate constants appeared larger in the no repetition conditions than in the repetition conditions, but this tendency was likely to be driven by the large rate constant in Err⁺Rep⁻ (0.48 ± 0.22).

For conditions with an abrupt onset of the rotation in block A1 (Err⁺Rep⁻ and Err⁺Rep⁺), we could compare rate constants from naive adaptation block A1 with savings block B for data sets that adequately fit the exponential function in both blocks (n = 14). Rate constants were larger in savings block B (0.40 ± 0.06) than in naive block A1 [0.21 ± 0.05, t(13) = 3.49, P = 0.004, Hedges' g = 0.82].

Binned directional errors.

error reduction phase (bins 1–4).

Corroborating our rate constant analyses, directional errors in the first four blocks of savings were smaller in conditions with prior experience of error [significant main effect of error, F(1,32) = 5.00, P = 0.03, partial η² = 0.13; see Fig. 5C]. Repetition did not result in smaller errors in the savings block (see Fig. 5D), as the main effect of repetition was not significant [F(1,32) = 0.32, P = 0.57, partial η² = 0.009]. The repetition × error interaction was also not significant [F(1,32) = 1.3, P = 0.26, partial η² = 0.03]. There was, however, a significant bin × repetition interaction [F(2.2,70.4) = 3.11, P = 0.04, partial η² = 0.08]. This appeared to result from smaller directional errors at bin 1 (bin 1: Rep⁻ conditions, −17.82 ± 1.16; and Rep⁺ conditions, −13.39 ± 1.17) but not in subsequent bins (see Fig. 4C). Followup ANOVAs run separately for bin 1 and bins 2–4 showed a significant main effect of repetition for bin 1 [F(1,32) = 7.21, P = 0.01, η_p² = 0.18] but not for bins 2–4. Smaller first bin directional errors in the savings block (i.e., smaller directional errors in the first five trials) might indicate a use-dependent bias from repetition (Huang et al. 2011) and do not necessarily indicate savings. Indeed, because there were no reliable differences in directional error in subsequent bins, it appears that repetition of the solution did not cause faster error reduction, as required to constitute savings. There were no other reliable interactions.

Fig. 5.

A: rate constants in savings block B in conditions with prior experience of counterclockwise error (red bars) and with no prior experience of counterclockwise error (open bars) compared with naïve adaptation block A1 rate constants (yellow bars). Conditions with no prior repetition of the savings block movement solution are shown on the left; conditions with prior repetition are shown on the right. B: binned directional error in savings block B in each of the experimental conditions. Conditions with no repetition are shown as dotted lines; conditions with repetition of the savings block movement solution are shown as solid lines. Conditions with prior experience of clockwise errors are shown in red and pink; conditions with no prior experience of clockwise errors are shown in black and gray. Binned directional errors in savings block B for each condition are shown. C: binned directional errors collapsed across conditions with prior experience of error (red circles) and without prior experience of error (open circles). D: binned directional errors collapsed across conditions with prior repetition of the movement solution (green circles) and without prior repetition of the movement solution (black circles). All data are means ± SE.

asymptotic phase (bins 5–16).

Prior experience of errors and prior repetition of the movement solution did not alter the extent of error reduction at asymptote, as main effects of error [F(1,32) = 1.96, P = 0.17, partial η² = 0.05] and repetition [F(1,32) = 0.0, P = 0.99, partial η² = 0.05] were both not significant, and there were no reliable interactions.

Savings From Prior Experience of Errors Reduced Anterograde Interference

We next examined adaptation performance in final block A2 (30° clockwise rotation), which is susceptible to both anterograde interference from the preceding block B (30° counterclockwise rotation) and savings from block A1 (30° clockwise rotation). Block A2 rate constants are shown in Fig. 5A, and block A2 binned directional errors are shown in Fig. 5, B and C.

Rate constants.

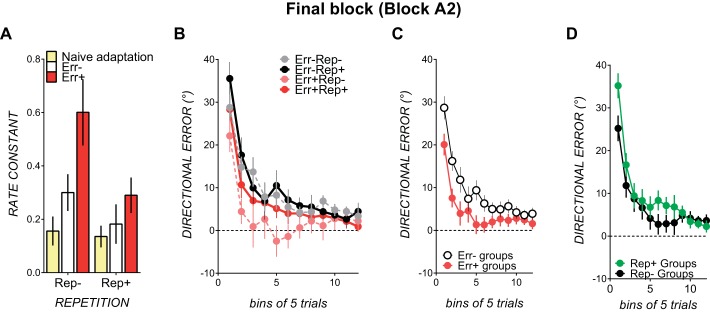
As all conditions contained the same abruptly imposed 30° counterclockwise rotation in savings block B and the same 30° clockwise rotation in final block A2, we could assess anterograde interference from blocks B to A2 in the conventional way by comparing rate constants between these two blocks. To evaluate how reduction of clockwise errors in block A2 was affected by prior experience of clockwise errors in block A1 and the amount of repetition of the block B movement solution (which was 60° away from the block A2 movement solution), we ran a block (B, A2) by error (no prior error or error) by repetition (less repetition or more repetition) ANOVA. For this analysis, rate constants for both blocks B and A2 had to fit adequately to the single-rate exponential function (nonsignificant Runs test). This criterion excluded three data sets from Err⁻Rep⁻ and two participants each from Err⁺Rep⁻, Err⁻Rep⁺, and Err⁺Rep⁺. Prior experience of similar clockwise errors in block A1 resulted in faster error reduction in block A2 (error: 0.41 ± 0.04 and no prior error: 0.26 ± 0.05), as shown by a significant main effect of error [F(1,22) = 7.44, P = 0.01, partial η² = 0.25].

Our prior repetition conditions were designed to enforce extended repetition of the block B movement solution, which was 60° away from the block A2 movement solution. Repeating this movement elicited slower error reduction in block A2, as rate constants were smaller with repetition (0.25 ± 0.05) than without repetition (0.42 ± 0.05; see Fig. 5A, bars on the right vs. bars on the left), as shown by a reliable main effect of repetition [F(1,22) = 4.99, P = 0.03, partial η² = 0.18] and a near-significant block × repetition interaction [F(1,22) = 4.01, P = 0.057, partial η² = 0.15]. There were no other reliable interactions. In conditions with less repetition of the solution (Rep⁻ conditions), rate constants tended to increase from savings block B (0.32 ± 0.21) to final block A2 (0.52 ± 0.35) but not in conditions with more repetition of the solution (Rep⁺ conditions) (savings block B: 0.27 ± 0.17 and final block A2: 0.24 ± 0.08). Hence, consistent with previous work (Leow et al. 2014; Sing and Smith 2010), more repetition of a movement that was inappropriate for the current perturbation increased anterograde interference.

For the prior error conditions with abrupt onset of clockwise rotation in block A1 (Err⁺Rep⁻ and Err⁺Rep⁺), we could also evaluate savings from blocks A1 to A2 using paired t-tests to compare rate constants from naïve adaptation in block A1 to final rotation block A2 in 15 data sets where the data fit adequately to the function. Rate constants were larger in block A2 (0.41 ± 0.31) than in block A1 [0.21 ± 0.13, t(14) = 2.16, P = 0.048, Hedges' g = 0.74]. Hence, despite anterograde interference from blocks B to A2, savings from blocks A1 to A2 remained evident our prior error conditions.

In summary, despite initially larger counterclockwise directional errors at the beginning of the counterclockwise block A2, observed as a result of anterograde interference from the preceding clockwise rotation block B, savings from blocks A1 to A2 was evident in conditions with prior experience of similar errors. Conversely, anterograde interference resulting from extended repetition of a movement that was inappropriate for the current rotation reduced the amount of savings shown.

Binned directional errors.

error reduction phase (bins 1–4).

To compare error reduction between block B (counterclockwise rotation) and block A2 (clockwise rotation), final block A2 errors were first sign adjusted. Block (B, A2) × bin (bins 1–4) × repetition × error ANOVAs were then run on binned directional errors for blocks B and A2. Similar to the rate constant analyses, prior experience of the 30° clockwise error in block A1 elicited greater error reduction when adapting to the 30° clockwise error in block A2 (see Fig. 6C), shown by a significant main effect of error [F(1,61) = 6.38, P = 0.01, partial η² = 0.09]. Corroborating our rate constant analyses, repetition of a movement that was 60° away from the block A2 solution elicited poorer error reduction in block A2, as mean errors across bins 1–4 in the final block A2 were larger with more repetition (less repetition: −8.70 ± 11.46 and repetition: −15.32 ± 18.76), as shown by a significant block × repetition interaction [F(1,61) = 11.63, P = 0.001, partial η² = 0.16].

Fig. 6.

A: final block A2 mean rate constants in conditions with prior experience of clockwise errors (red bars) and with no prior experience of clockwise error (open bars) compared with naïve block A1 rate constants (yellow bars). Block A2 was susceptible to savings from adapting to a clockwise rotation in block A1 and anterograde interference from adapting to a counterclockwise rotation in block B. B: binned directional error in block B in each of the experimental conditions. Conditions with no repetition are shown as dotted lines; conditions with repetition of movement solution are shown as solid lines. Conditions with prior experience of clockwise errors are shown in red and pink; conditions with no prior experience of clockwise errors are shown in black and gray. Binned directional errors in savings block B for each condition are shown. C: binned directional errors in final block A2 (30° clockwise rotation). 1 bin = 5 trials. Binned directional errors collapsed across conditions with prior experience of error (red circles) and without prior experience of error (open circles) are shown. D: binned directional errors collapsed across conditions with prior repetition of the movement solution (green circles) and without prior repetition of the movement solution (black circles). All data are means ± SE.

asymptotic phase (bins 5–12).

At asymptote, the effect of prior error was no longer significant. The block × repetition ANOVA was significant, as repetition did not alter the savings block B errors (mean across bins 5–12: less repetition, −4.08 ± 5.56; and repetition, −4.06 ± 5.9) but did elicit poorer error reduction in subsequent block A2 (mean across bins 5–12: repetition, −4.32 ± 6.42; and less repetition, −1.44 ± 3.12). Hence, repeating a movement that was 60° away from the solution elicited larger errors in block A2, even at asymptote.

Prior Experience of Errors Elicits Savings Despite Zero Prior Repetition of the Solution

Although the naïve adaptation block A1 of Err⁺Rep⁻ contained no repetition of the exact 45° movement solution required for savings block B, the block A1 movement solution did come into the vicinity (i.e., within 5°) of the savings block B movement solution in an average of 9.5 ± 1.4 trials in the first 10 and last 10 trials of block A1. One might argue that relatively rare executions of these movements in the presence of sensory prediction errors could associate similar movements with task success, because in the presence of sensory prediction errors, even few executions of movements that approximate the movement solution can elicit savings (Huberdeau et al. 2015a). To evaluate whether savings occurred without a history of movements that approximated the savings block movement solution, we ran a control condition, Err⁺Rep⁻Far (see Fig. 7) (originally n = 10; however, 1 subject was excluded due failure to follow instructions to maintain movement times of <1,000 ms). Err⁺Rep⁻Far replicated the design of Err⁺Rep⁻ but moved the movement solution at least 30° away from the movement solution ultimately required in the savings block (see Fig. 7). This manipulation was effective in ensuring zero prior repetition of the savings block solution (0% of trials were within 5° of the savings block movement solution). Rate constants for the savings block (0.46 ± 0.08) were significantly larger than rate constants for naïve adaptation block A1 (0.22 ± 0.03), demonstrating savings [t(9) = 2.56, P = 0.03, Hedges' g = 1.07]. Rate constants for final block A2 (0.55 ± 0.14) were also significantly larger than rate constants for the naïve adaptation block [0.19 ± 0.03, t(8) = 2.31, P = 0.049, Hedges' g = 1.07; 1 data set was excluded from this comparison because the single-exponential function failed to fit to errors from final block A2]. An error by repetition ANOVA on savings block rate constants using rate constants from this control group in place of those from Err⁺Rep⁻ resulted in qualitatively similar results from the original analysis. There was a significant main effect of error [F(1,29) = 8.95, P = 0.006, partial η² = 0.24], no significant main effect of repetition, and no other significant interactions.

Fig. 7.

Design and results for the control Err⁺Rep⁻Far condition. A: design of the Err⁺Rep⁻Far condition. B: rate constants for savings block B mean rate constants in conditions with prior experience of counterclockwise errors (red bars) and with no prior experience of counterclockwise error (open bars) compared with naïve adaptation block A1 rate constants (yellow bars) in conditions where the rotation was abruptly imposed. C: binned directional errors collapsed across conditions with prior experience of error (red circles) and without prior experience of error (open circles). D: binned directional errors collapsed across conditions with prior repetition of the movement solution (green circles) and without prior repetition of the movement solution (black circles). All data are means ± SE.

DISCUSSION

This study was designed to examine what are the necessary conditions for savings to test the predictions of two influential theories about savings. The first account predicts that savings requires prior repetition of the action required to eliminate errors (i.e., the movement solution) (Huang et al. 2011). The second account predicts that savings requires prior experience of errors similar to those evoked upon second exposure to the perturbation (Herzfeld et al. 2014). Prior repetition of the movement solution failed to elicit faster error reduction and thus failed to elicit savings. Conversely, prior experience of similar errors led to savings, even when the movement solution was never previously executed. Hence, our results suggest that prior experience of similar errors is both necessary and sufficient for savings, whereas prior repetition of the movement solution is neither necessary nor sufficient for savings.

What Are the Necessary Conditions for Savings?

We found savings during adaptation to a 30° counterclockwise rotation after previous experience of counterclockwise errors evoked by abrupt removal of a 30° clockwise rotation. Furthermore, savings persisted despite limited (Err⁺Rep⁻) or zero (Err⁺Rep⁻Far) repetition of the action that would ultimately be required to compensate for the rotation in the savings block. Hence, savings does not require prior execution of actions that would ultimately eliminate errors. These results appear to contradict Huang et al.'s (2011) findings of no savings in a condition without prior repetition of the solution. However, this particular condition (cf. experiment 2 Adp⁺Rep⁻ in Huang et al. 2011) involved a random series of counterclockwise rotations between 0° and 40°. Such a protocol might not provide sufficient perturbation stability for the development of a memory for errors (Herzfeld et al. 2014) or encoding of a single action or strategy that could be later recalled (Huberdeau et al. 2015a; Morehead et al. 2015), thus preventing the occurrence of savings.

In conditions allowing prior repetition of the movement solution but not prior experience of errors, the target direction was manipulated to ensure a single movement solution throughout the initial learning A1, null, and savings blocks. To show savings in block B, participants merely had to repeat the same action executed in all preceding blocks. Note that this finding extends the previous report that mere repetition of an action in the absence of any perturbation does not lead to savings (Huang et al. 2011). Remarkably, savings was absent when prior experience of error was prevented in Err⁻Rep⁺. Prior repetition of the movement solution resulted in smaller errors in the first bin of five trials but did not increase the overall rate of error reduction throughout the entire block. The effect on the first bin seems likely to be due to a use-dependent effect (see also Huang et al. 2011), as the movement solution had been repeated in the previous 119 trials. Our results therefore demonstrate that savings does not require repetition of the movement solution. These results extend recent findings of savings despite limited trials at initial learning (Huberdeau et al. 2015a).

Possible Mechanisms for Savings: Error Sensitivity Versus Retrieval

Although the present experiments were designed to identify the necessary conditions for savings, they also prompt speculation as to the underlying computational mechanisms. The present data are clearly consistent with Herzfeld's et al. (2014) hypothesis that savings occurs because prior experience of similar sensory prediction errors increases the sensitivity to errors encountered during relearning, but this is not the only possible explanation for the results. Alternatively, experience of errors at initial learning might be required to encode an action (Huang et al. 2011), identify an aiming strategy (Morehead et al. 2015), or learn the structure (rather than the parameters) of the perturbation (Braun et al. 2009; Turnham et al. 2012) that can be subsequently retrieved at relearning. If savings is due to recall of an “action,” then it is important to consider what form this memory could take. Krakauer et al. (2006) demonstrated savings with initial adaptation to a 30° rotation with arm movements followed by subsequent adaptation to the same 30° rotation with wrist movements. During initial adaptation with the arm, wrist movements were prevented by a splint. Thus, we already knew that savings cannot be a recall of muscle activities or joint torques. Our present finding of savings despite no previous execution of the action needed at relearning further shows that the effect cannot be due either to recall of an end-point movement trajectory. Thus, any memory that is recalled to increase performance at relearning would have to be more abstract in nature: a strategy to reaim (Morehead et al. 2015), a remapping between target direction and end-point trajectory planning, or meta-learning of the perturbation structure (Braun et al. 2009; Turnham et al. 2012).

Whereas the present data are compatible with mechanisms for savings based either on error sensitivity or retrieval of previously developed aiming strategies or visuomotor remappings, some previous results are difficult to reconcile with the error sensitivity hypothesis. Krakauer et al. (2005) found no savings during adaptation to a counterclockwise rotation even though participants had initially adapted to the same counterclockwise rotation, when initial adaptation to the counterclockwise rotation was followed by a second clockwise rotation 24 h afterward (Krakauer et al. 2005). To account for such findings, Herzfeld et al.'s (2014) hypothesis would have to be extended to include a limit to aggregate error sensitivity (i.e., any increase in sensitivity to one type of error must come at the expense of reduced sensitivity to other error types). Huberdeau et al. (2015a) showed savings for a 30° rotation despite only being previously exposed to errors induced by a 15° rotation, and Haith et al. (2015) found no savings under conditions in which strategic reaiming was suppressed. Thus, as noted above, it seems clear that savings can occur via mechanisms that do not involve increased sensitivity to error. The question remains whether error sensitivity contributes to (or even wholly accounts for) savings under some circumstances.

Yet another recent model suggests that savings results from reweighted recruitment of motor primitives (i.e., that represent the direction of action) due to predicted prospective errors (Takiyama et al. 2015). In this model, initial adaptation to a perturbation (e.g., a 30° rotation of visual feedback) activates motor primitives with prospective errors that are close to 30°, and the weighting parameters of these primitives are modified to decrease those errors. Reencountering a 30° rotation reactivates the modified primitives, resulting in faster relearning. This model cannot explain our findings of savings in conditions with little prior repetition of the savings block movement solution (Err⁺Rep⁻ and Err⁺Rep⁻Far), because the continual change in target location in these conditions ensured that initial learning engaged motor primitives that were always distinct from motor primitives engaged at subsequent learning. Our results are therefore more consistent with an account for savings based on a memory of errors or on retrieval of a previous strategy or visuomotor remapping that is cued by errors (Huberdeau et al. 2015a; Morehead et al. 2015).

Do Reward Prediction Errors Contribute to Savings?

Although the present results demonstrate that prior experience of errors is crucial for savings, they do not distinguish the type of error required. Sensory prediction errors have been proposed to drive savings (Herzfeld et al. 2014); however, it is also possible that savings requires reward prediction errors, which are the discrepancy between a desired outcome and actual outcome of an action (Schultz 1997; Schultz et al. 1998). It is difficult to dissociate the contribution of sensory prediction errors and reward prediction errors to savings, because both typically occur together in goal-directed movement. When moving to a target, participants expect that the movement proceeds straight toward the target and also expect to be rewarded by hitting the target. An unexpected perturbation therefore typically evokes both sensory prediction errors and reward prediction errors. Since savings apparently does not occur when gradual introduction and removal of visuomotor rotation prevents experience of sizeable errors (Herzfeld et al. 2014; Orban de Xivry and Lefevre 2015; Turnham et al. 2012), it is conceivable that savings requires reward prediction errors to encode a memory for sensory prediction errors. Alternatively, the presence of reward prediction errors at relearning might prompt retrieval of control policies or actions that previously restored task success at initial learning (Huberdeau et al. 2015a), which could manifest in the use of reaiming strategies to eliminate errors (e.g., Haith et al. 2015; Mazzoni and Krakauer 2006; Morehead et al. 2015).

The potential role for reward prediction errors in savings is supported by findings of impaired savings in Parkinson's disease patients (Bedard and Sanes 2011; Leow et al. 2012, 2013; Marinelli et al. 2009). The primary neuropathology in Parkinson's disease is degeneration of the dopamine-producing neurons in the basal ganglia (Hornykiewicz and Kish 1987), which are known to be crucial to process reward prediction errors (Schultz 1998). A blunted response to reward prediction errors as a result of basal ganglia degeneration is thought to underlie this impairment in savings, despite no observable impairment in error compensation at initial learning. Poor processing of reward prediction errors might also underlie the observed impairments in error correction in patients in response to large perturbations that typically evoke strategic reaiming but intact error reduction to small perturbations that typically evoke no strategic reaiming (Gutierrez-Garralda et al. 2013; Mongeon et al. 2013). Moreover, some suggest that savings can occur without similarly signed sensory prediction errors, provided that reward prediction errors occur at initial learning (Orban de Xivry and Lefevre 2015). In that study, the action that eliminated reward prediction errors at initial learning could also eliminate reward prediction errors at subsequent learning. As originally proposed by Huang et al. (2011), a possible interpretation is that reinforced actions represent attractors, which are more likely to be reselected when reward prediction errors subsequently drive a (possibly explicit) search for alternative actions that lead to task success. Hence, although our present data show that repetition of a previously successful action is not required for savings and that prior history of similar errors is sufficient for savings, there remain multiple potential error-driven mechanisms that could plausibly account for savings.

Repetition Increases Anterograde Interference

We assessed error reduction in the clockwise rotation block A2, which was sensitive to savings from the clockwise initial adaptation block A1 and to interference from the preceding counterclockwise adaptation block B. Corroborating our results from savings block B, error reduction was faster in conditions with prior experience of clockwise errors (Err⁺Rep⁻ and Err⁺Rep⁺). Errors at block A2 were reduced at a faster rate than in initial learning block A1 in these conditions, even though errors in the first few trials were large because of interference from the preceding block B, as reported by Zarahn et al. (2008). We also found that more prior repetition of a movement that was at least 60° away from that required to hit the target in block A2 elicited larger errors in block A2. These results are consistent with previous work showing that more repetition of the solution at initial learning can result in greater anterograde interference at subsequent learning of an oppositely signed perturbation, when the solution at initial learning differed from the solution at subsequent learning (Leow et al. 2014; Sing and Smith 2010). An amplified anterograde interference, as a result of more repetition of a different movement solution, was reported even when the size of the first perturbation was halved, effectively reducing the difference in perturbation between the first and second perturbation (Sing and Smith 2010) and even when the first rotation was learned in the presence of a gradually imposed rotation (Leow et al. 2014). Hence, unlike savings, anterograde interference appears sensitive to prior repetition of the solution at initial learning.

An alternative possibility that could account for the better performance at block A2 in the absence of prior repetition of the incorrect solution (i.e., Err⁺Rep⁻) is that changing target location in the presence of a constant perturbation size might have prompted subjects to engage with the task more strategically. This could have led to more effective reaiming at block A2 and thereby superior performance. We note also the apparently similar, but nonsignificant, trend for superior performance of Err⁺Rep⁻ in the savings block, to which similar arguments regarding reaiming strategy could apply.

Conclusions

Our finding that prior execution of the movement required to counteract the savings block perturbation was neither necessary nor sufficient for savings shows that savings does not result from repeating movements to associate them with task success. Our results rather emphasize the importance of prior experience of errors as a necessary condition for savings, but it remains to be resolved by what mechanism(s) this condition operates. Future work will need to resolve the extent to which a history of error leads to savings by increasing sensitivity to experienced errors (Herzfeld et al. 2014) or by acting as a cue to encode and later recall a re-aiming strategy or sensorimotor remapping.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

L.-A.L., A.d.R., W.M., S.R., and T.J.C. conception and design of research; L.-A.L. performed experiments; L.-A.L. analyzed data; L.-A.L., A.d.R., W.M., S.R., and T.J.C. interpreted results of experiments; L.-A.L. prepared figures; L.-A.L. and T.J.C. drafted manuscript; L.-A.L., A.d.R., W.M., S.R., and T.J.C. edited and revised manuscript; L.-A.L., A.d.R., W.M., S.R., and T.J.C. approved final version of manuscript.