Abstract
Cell protrusion through polymerization of actin filaments at the leading edge of motile cells may be influenced by spatial gradients of diffuse actin and regulators. Here we study the distribution of two of the most important regulators, capping protein and Arp2/3 complex, which regulate actin polymerization in the lamellipodium through capping and nucleation of free barbed ends. We modeled their kinetics using data from prior single molecule microscopy experiments on XTC cells. These experiments have provided evidence for a broad distribution of diffusion coefficients of both capping protein and Arp2/3 complex. The slowly-diffusing proteins appear as extended “clouds” while proteins bound to the actin filament network appear as speckles that undergo retrograde flow. Speckle appearance and disappearance events correspond to assembly and dissociation from the actin filament network and speckle lifetimes correspond to the dissociation rate. The slowly-diffusing capping protein could represent severed capped actin filament fragments or membrane-bound capping protein. Prior evidence suggests that slowly-diffusing Apr2/3 complex associates with the membrane. We use the measured rates and estimates of diffusion coefficients of capping protein and Arp2/3 complex in a Monte Carlo simulation that includes particles in association with a filament network and diffuse in the cytoplasm. We consider two separate pools of diffuse proteins, representing fast and slowly-diffusing species. We find a steady state with concentration gradients involving a balance of diffusive flow of fast and slow species with retrograde flow. We show that simulations of FRAP are consistent with prior experiments performed on different cell types. We provide estimates for the ratio of bound to diffuse complexes and calculate conditions where Arp2/3 complex recycling by diffusion may become limiting. We discuss the implications of slowly diffusing populations and suggest experiments to distinguish among mechanisms that influence long range transport.
1. Introduction
The lamellipodial protrusions at the leading edge of motile cells have been studied extensively, both due to their importance in cell motility and as model systems of cytoskeletal dynamics [1–5]. In the lamellipodium, actin filaments form a dynamic network that polymerizes primarily close to the leading edge of the cell, with the filament barbed ends pointing toward the cell membrane. In the dendritic nucleation model, many of these filaments are created as branches off pre-existing filaments [6]. Filament capping by capping protein regulates the concentration of free ends. As filaments polymerize, the whole actin network undergoes retrograde flow towards the cell center. The difference between the rates of polymerization and retrograde flow results in net lamellipodial protrusion or retraction. The actin subunits in the filament that move towards the back of the network break off from the network due to cofilin-induced severing into oligomers.. The disassembled pieces further depolymerize and are recycled close to the leading edge by diffusion.
Since lamellipodial components are recycled, the transport of disassembled proteins through the cytoplasm back towards the leading edge is an important component of the kinetics in lamellipodia. Some studies suggested that diffusion is fast enough to deliver actin subunits to the leading edge [7, 8] while others have proposed a role for active transport mechanisms [9, 10]. Theoretical work has shown how diffusion may become limiting depending on both the value of the diffusion coefficient in the cytoplasm as well as the spatial distribution of sources and sinks of actin subunits in the cytoplasm [11, 12]. One of the difficulties in directly measuring the existence of gradients of diffuse actin experimentally is that the diffuse population is a small fraction of the actin in filaments. Further, the dynamics in photoactivation or photobleaching experiments reflect a combination of reaction and diffusion that can be hard to disentangle [12, 13].
Recent studies have shown how mathematical models based on data obtained by single molecule speckle (SiMS) microscopy can be combined with fluorescence recovery after photobleaching (FRAP) or photoactivation (PA) studies to model the dynamics of the diffuse actin pool [8, 12]. In SiMS, cells contain fluorescently labeled proteins at a concentration sufficiently low to resolve single molecules [14]. If a fluorescent protein is diffusing freely in the lamellipodium, it will appear as a diffuse background or localized cloud, depending on its diffusion coefficient and the exposure time of the camera. When the tagged protein binds to the actin network it appears as a speckle undergoing retrograde flow while it remains bound to the network. Speckle disappearance reflects dissociation of the tagged protein to the diffuse pool. By contrast, cells in FRAP or PA experiments typically contain a large fraction of labeled protein that leads to spatially extended intensity fields, the redistribution of which around an area of interest reflects the dynamics of reaction, retrograde flow, and diffusion [12]. The model of Smith et al. [12] used SiMS data as input to suggest that accounting for a population of slowly diffusing actin oligomers, the result of actin filament severing, allows for a better fit of the model to the FRAP data due to local release and rebinding to the actin filament network. Comparison of an extension of the Smith at el. model to PA experiments further supported the existence of a recycling pool at the back of the lamellipodium together with a fast-diffusing pool that delivers subunits close to the leading edge at nearly the diffusion-controlled rate [8].
Capping protein and the Arp2/3 complex are two of the most important regulators of actin dynamics in cells. Slowly-diffusing capping proteins have been observed by SiMS microscopy [15], which may reflect capping protein bound to slowly-diffusing actin oligomers or to the membrane. The Arp2/3 complex has also been observed to form a slowly-diffusing complex with its activators prior to attachment to the actin network [16]. However the implications of slowly-diffusing capping protein and Arp2/3 complex on the spatial distribution and turnover kinetics in the lamellipodium has not been modeled.
This paper extends the approach of Smith et al. to the study of the diffusive dynamics of capping protein and Arp2/3 complex for which extensive SiMS experiments have been performed on the same cell type, XTC cells. A simplifying assumption in this model is that two distinct diffusion coefficients describe the fast and slow pools, which is the limit of a possibly broad range of diffusion coefficients in cells. The model incorporates parameters describing (i) the relative fraction of fast/slow species that incorporate into the actin network as function of distance from the leading edge, and (ii) the diffusive state upon dissociation from the network, as function of distance from the leading edge. By varying these parameters and considering prior experimental constraints, the model is used to estimate the magnitude of cytoplasmic concentration gradients and associated diffusion limitations. We also compare the results of this model to prior FRAP experiments of capping protein and Arp2/3 complex in lamellipodia. Even though these experiments were performed by different groups on different cell systems, such a comparison is useful since these FRAP experiments have been interpreted in the past with models that do not account for separate slow and fast cytoplasmic pools.
In the following sections we first introduce the general framework of our mathematical model with one bound species and two diffuse populations. We then proceed to apply it to capping protein and Arp2/3 complex dynamics to derive concentration profiles across the lamellipodium at steady state. The focus throughout is on lamellipodia of stationary cells at steady state with steady retrograde flow and no net protrusion and retraction. We discuss the implications of the calculated concentration gradients in the control of cell motility.
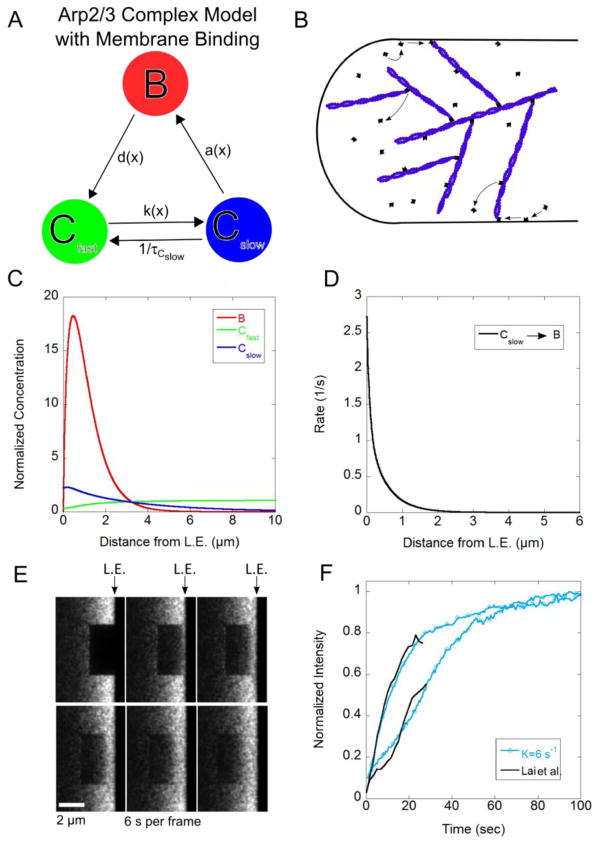
2. Methods
2.1 Calculating Steady State Profiles
Since proteins in the lamellipodium are frequently associating to larger complexes or binding to the membrane, we consider the simplest model to account for this behavior that has two distinct cytoplasmic populations. A fast diffusing cytoplasmic population, Cfast, and a slow diffusing cytoplasmic population, Cslow, are shown in the cartoon of the model in Figure 1, which is an extension of the model used in Smith et al [12]. Bound cytoplasmic protein, B, can depolymerize into either Cfast with probability s1 or Cslow with probability s2, where s2 = 1− s1. The diffuse protein Cfast can become bound protein with spatially dependent rate rCfast(x), and Cslow can become bound with spatially dependent rate rCslow (x), where x is the distance from the leading edge. The diffuse component Cfast can become Cslow with a lifetime of τCfast, and the component Cslow can become Cfast with a lifetime of τCslow.
Figure 1.
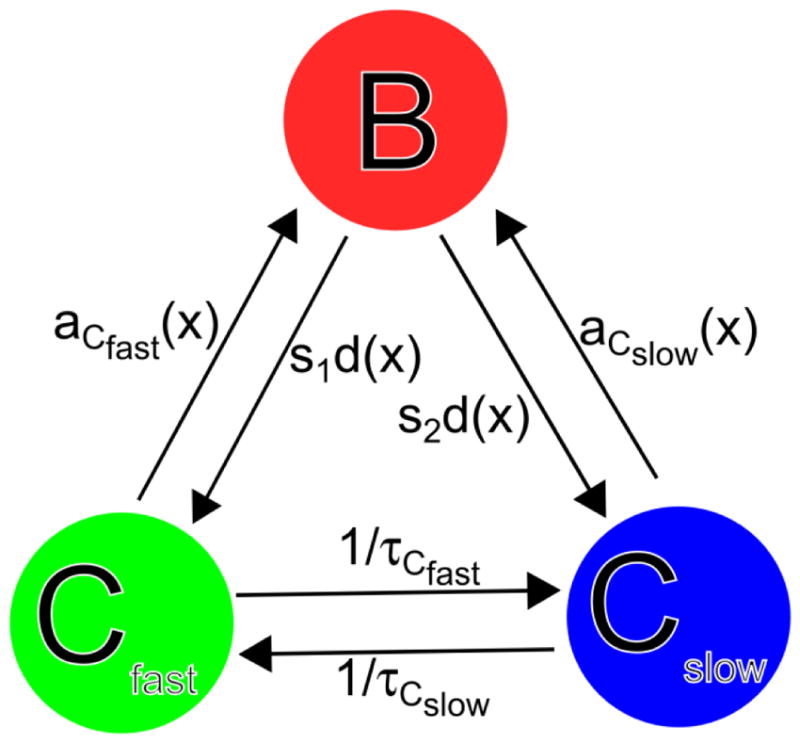
Diffusion reaction model for actin binding protein and protein complexes in lamellipodia. The three species are bound (B), fast diffusing in the cytoplasm (Cfast), and slow diffusing in the cytoplasm (Cslow). The lifetimes of Cfast and Cslow respectively are τCfast and τCslow. The appearance rates aCfast (x) and aCslow (x) that depend on the distance to the leading edge x are defined in Equations (2) and (3) and the detachment rate d(x) is defined in Equation (8). The parameter s1 is the probability for the bound protein to dissociate into Cfast and s2 = 1−s1.
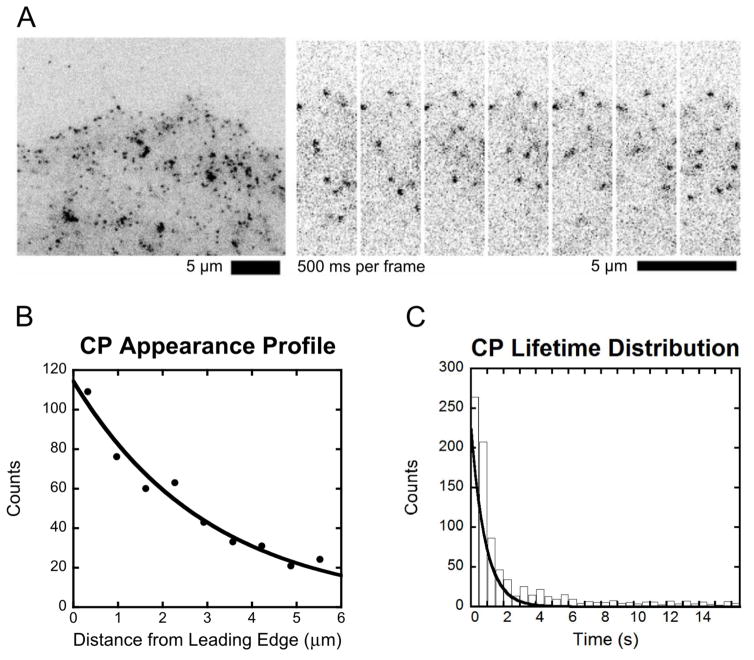
In SiMS microscopy (Figure 2A), each speckle that appears is a fluorescently tagged protein that becomes bound from the cytoplasmic pool. Where the speckle appears with respect to distance from the leading edge is recorded and the appearances are then binned in a histogram. This appearance profile, an example of which is shown in Figure 2B, is the sum of two separate appearance profiles, aCfast (x) and aCslow (x), due to the fast and slow cytoplasmic pools as follows:
| (1) |
Figure 2.
Capping protein single molecule speckle microscopy data. (A) Example image of SiMS microscopy in an XTC cell expressing EGFP-CPβ1 (left) and time lapse images (right) [17]. (B) Appearance profile for capping protein fit with a single exponential with decay length λ = 3.0. Data from [17]. (C) Lifetime distribution of capping protein speckles fit with a single exponential with decay time τ = 2.0 s. Data reproduced from [17].
The units of a(x) are μM/s. Generally, a(x) can be fitted by either a single or a double exponential with two length-scales λshort and λlong. This is an empirical fit and the two length-scales do not necessarily correspond to Cfast and Cslow. While in some cases it is possible to use SiMS to monitor the diffusive state of the protein prior to becoming bound, how the a(x) profile is split into two components in Equation (1) is an assumption of the model. We define Cfast,∞ and Cslow,∞ to be the concentrations of Cfast and Cslow respectively at distances far from the leading edge of the cell. Using C∞= Cfast,∞ + Cslow,∞ to normalize concentrations, the constant K defines the magnitude of the association reactions:
| (2) |
| (3) |
The dimensionless coefficients in Equations (2) and (3) satisfy and define the fraction of Cfast and Cslow that contribute to each of λshort and λlong. Since three independent parameters can be used to describe the main features on scales λshort and λlong, we will assume that the coefficients are constants, independent of x.
SiMS microscopy also measures the lifetime distribution for protein speckles p(t) that typically shows weak dependence upon distance from the leading edge, within a range of a few μm [14, 15, 17]. In the examples we consider in this paper, it is fitted with a single exponential:
| (4) |
An example of a lifetime distribution is shown in Figure 2C for capping protein speckles.
The bound protein profile, B(x), can be calculated analytically using the function Y(x,x′), which gives the amount of bound protein at x that came from x′ due to retrograde flow, taking into account the lifetime distribution:
| (5) |
The parameter vr is the retrograde flow in the lamellipodium, and Θ is the step function. Using Y(x,x′) one can find the profile of bound protein B1(x) and B2(x) due to each of the diffuse species, Cfast and Cslow, respectively, such that B(x) = B1(x) + B2(x), where:
| (6) |
| (7) |
The steady state reaction diffusion equations that describe the system in Figure 1 are as follows:
| (8) |
| (9) |
| (10) |
Parameters DCfast and DCslow are the diffusion coefficients for Cfast and Cslow respectively and d(x) is the detachment rate of bound proteins to the cytoplasm, which is found by solving Equation (8), given a(x) and B(x) from Equations (1), (6), and (7). Equation (8) is a transport equation that shows how retrograde flow of B is balanced by the association and detachment. Equation (9) balances diffusion of Cfast with association and detachment of the fast species and conversion between fast and slow diffusing states. The parameter s1 is the probability for the bound protein to dissociate into Cfast. Equation (10) is the same as Equation (9) for the slowly diffusing species Cslow. The concentrations far from the leading edge obey: Cslow,∞/Cfast,∞ = τCslow/τCfast.
Equations (1)–(10) can be solved numerically to find Cfast (x)/ Cfast,∞ and Cslow(x)/Cslow,∞ given vr, τCfast, τCslow, DCfast, DCslow, s1, and the parameters that define aCfast (x), aCslow (x), and p(t). The method used involves adding time dependence to Equations (9) and (10) and allowing them to relax for a sufficiently long time:
| (11) |
| (12) |
We impose a no-flux boundary condition at the leading edge: diffusion to the leading edge is balanced by the retrograde flow taking the bound protein away from the leading edge. The equations are solved on a 1D lattice with a width much larger than the lamellipodium width and fix the concentrations to Cfast,∞ and Cslow,∞ at the boundary far from the leading edge.
2.2 Calculation of Rate Constants Based on Steady State Profile and Monte Carlo Simulation
The local rates with which the cytoplasmic protein binds to the network from the fast and slow diffusing states can be found using the appearance profiles and the cytoplasmic protein profiles calculated in the preceding subsection:
| (13) |
| (14) |
These are the reaction rates for Cfast to convert into B1 and for Cslow into B2.
The equations above described the steady state profiles, assuming the lamellipodium is uniform along the axis parallel to the leading edge. This is a good approximation since lamellipodia can extend laterally along the membrane over larger distances compared to their width normally to the membrane. FRAP or PA experiments however involve dynamics along the 2D plane of the lamellipodium. We used the model in Figure 1 to create a 2D Monte Carlo simulation of independent particles in the lamellipodium by extending the method of Smith et al. [12]. The simulation was initialized using the steady state concentrations evaluated by Equations (11) and (12). At each simulation step that corresponds to time dt, the following processes occur:
Each diffusing particle is displaced by a distance chosen from the 2D free diffusion propagator with the corresponding diffusion coefficient.
Particles in the bound state undergo movement by distance vrdt that corresponds to retrograde flow.
The rates in Equations (13) and (14) are used to choose whether or not a diffusing particle converts to the bound state.
The lifetime of each particle that converts to the bound state is chosen from the SiMS distribution p(t).
Bound particles convert to the diffusing state when their lifetime has been reached. Parameter s1 is used to determine the fraction of these particles that become fast or slowly diffusing.
The fast and slow diffusing species convert between each other with probabilities chosen from exponential distributions with average lifetimes τCfast and τCslow, respectively.
The value of dt was chosen such that the probability of any transition occurring per time step is sufficiently smaller than 1, typically dt = 1 ms. The corresponding diffusion distance over dt is also small compared to the lamellipodium width, 0.13 μm for D = 4 μm2/s. The side boundary conditions in our simulation are reflective. Any bound protein that exists at the back of the simulation box is converted into a diffusing protein and subsequently recycled. We used boxes large enough such that a very small fraction reaches the rear as bound protein and the diffuse pools reach a plateau. To model FRAP experiments, particles in a defined region are deleted. Particles outside of the region are then able to move into the bleached region. Recovery curves can be thus measured and compared to experimental data. To model PA experiments, particles outside of the photoactivated region are deleted and the particles are then able to diffuse and react in the manner described above.
3. Results
3.1 Application to Capping Protein Dynamics
We first apply the general model of Section 2 to capping protein, the lamellipodial dynamics of which have been studied in prior studies with SiMS of XTC cells [15, 17] (Figure 2A). In these studies capping protein was found to associate over an extended area of the lamellipodium (Figure 2B), to have a large slowly-diffusing cytoplasmic pool with D ≈ 0.5μm2/s and a surprisingly short bound lifetime, τ ≈ 2 s (Figure 2C) [15, 17]. Our main goal in this section is to study the implications of these observations for the concentration profile of capping protein across the lamellipodia.
Kapustina et al. [18] analyzed FRAP data of fibroblast cells expressing EGFP-CapZ in a circular region of diameter 5 μm centered at 5 μm from the leading edge of the cell [19]. They fitted the recovery to a model that used Virtual Cell with various components. This study also showed a short lifetime of bound capping protein compared to the lifetime of polymerized actin that is 24–30 s in lamellipodia [14, 15]. However the fitted lifetime when bound to the actin network, τ = 10 s, was larger than the values in [15, 17] and the diffusion coefficient of capping protein in the cytoplasm, D= 5–10μm2/s, was much larger than in [15, 17]. A second goal in this Section is finding out if these studies are contradictory (which could be due to the use of different cell types) or else if a mechanism that includes slowly diffusing capping protein and shorter capping protein lifetimes can also fit the FRAP data from [18].
We consider two previously-proposed possibilities for the reasons behind slow capping protein diffusion: one being that capping protein is bound to severed actin oligomers, the other being that capping protein binds to the membrane. We use the SiMS data of Figure 2 (Miyoshi et al.) to predict the concentrations profiles at steady state and to calculate rate constants for our Monte Carlo simulation. We then simulate bleaching of a 5 μm by 5 μm square region centered 5 μm from the leading edge to compare to the data of Kapustina et al. using a circular bleach region (this difference in shape has only a small effect on the recovery curve). In the simulations for capping protein below we used a typical value for retrograde flow, vr= 0.03μm/s [20].
3.1.1 Model including Oligomers
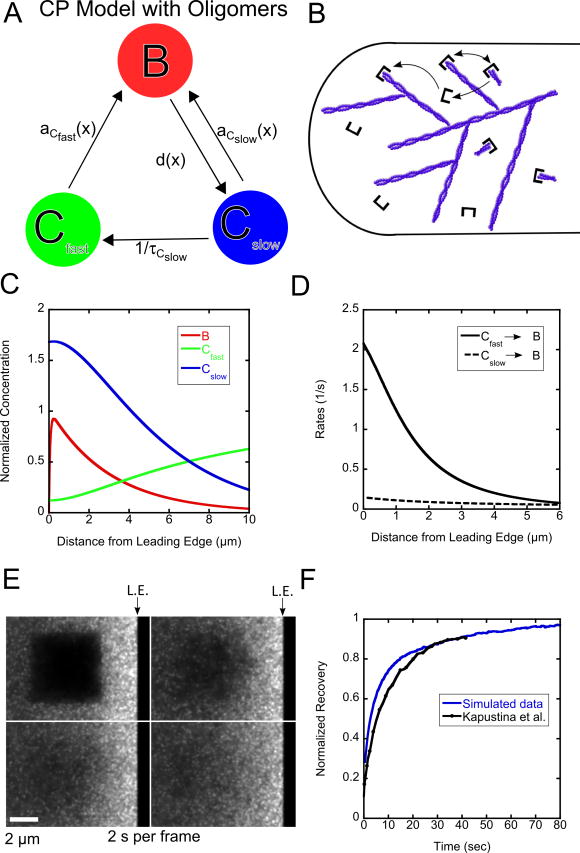
We first consider the model with oligomers shown in Figure 3A, B, a specific case of the general model (Figure 1). The motivation for this model is the suggested existence of short actin filaments (actin oligomers) in the lamellipodium, a result of cofilin-mediated severing [12]. If severed actin filaments are capped by capping protein, this could explain why 50% of capping protein has been observed in a slowly diffusing state with diffusion coefficient ≈ 0.5 μm2/s [15]. In this model Cfast represents capping protein heterodimers diffusing in the cytoplasm and Cslow represents capping protein heterodimers attached to the barbed end of an actin oligomer diffusing in the cytoplasm. The bound protein can only dissociate into capped oligomers, Cslow, that can either rebind to the network or become uncapped and convert to Cfast.
Figure 3.
Results of model with oligomers for capping protein. (A, B) Schematic and cartoon of model with oligomers for capping protein. (C) Steady state concentration profiles for capping protein. (D) Binding rates as function of distance. (E) Snapshot images of simulated FRAP. (F). FRAP curves compared to experimental data from Kapustina et al. [18]. The ending time of the experimental measurement (40 s) is normalized to the value of the simulation at 40 s. The simulated recovery is normalized to one at long times. Simulations in panels C–F use K = 0.5 s−1, DCfast = 2.0 μm2/s, DCslow = 0.5 μm2/s, vr = 0.03 μm/s, τ = 2.0 s and τCfast = 13.0 s.
We assume that both fast and slow diffusing species can bind to the network, representing capping of free barbed ends and re-binding of oligomers to the lamellipodial network, respectively. Since SiMS microscopy only measures the total appearance profile a(x) (Figure 2B), an additional assumption in our model is how a(x) is split into aCfast (x) and aCslow (x). Since the total appearance profile can be fit by a single exponential with λ = 3.0 μm (Figure 2B), we assume that the appearance rates are broken up such that a fraction ACfast is due to Cfast and ACslow to Cslow:
| (15) |
| (16) |
Several parameters in the model can be calculated from prior experiments or their range can be estimated. The lifetime distribution of capping protein bound to the network, p(t) (Figure 2C) can be fit with a single exponential where τ = 2.0 s [17]. The lifetime of the capping protein bound to the actin oligomer (τCslow) is likely in the range of the lifetime of an actin oligomer, 5–30 seconds [12]. The diffusion coefficients of the slow component is DCslow = 0.5 μm2/s [15], and DCfast =2–5 μm2/s is expected, comparable to the diffusion coefficient of actin monomers [8, 13]. The important parameter K controls the ratio of the concentration of bound protein to cytoplasmic protein. We estimated this from experimental data from the Watanabe lab from [15] and using SpeckleTrackerJ to count the number of speckles that correspond to bound protein and the number of diffusing proteins that appear as broadened speckle “clouds” [15]. The measured ratio of cytoplasmic protein to bound protein was estimated to be 2.3 to 1.
Scanning the model parameters within the range described in the preceding paragraph allows us to run the simulation to obtain concentration profiles and fits to FRAP data. Figure 3C shows a representative steady state concentration profile using K = 0.5 s−1, DCfast = 2 μm2/s, DCslow = 0.5 μm2/s, vr = 0.03 μm/s, τ = 2.0 s, τCslow = 13.0 s, and ACfast=ACslow=0.5. With these values of K, ACfastACslow, the resulting profile has a big fraction of slowly-diffusing capping proteins, consistent with our measured ratio of bound to diffuse species (see Supplementary Figure 1 for the effect of varying ACfast, ACslow). Interestingly, the production of slowly diffusive capping protein near the leading edge causes a decreasing concentration of slow protein along the direction away from the leading edge. Combined with retrograde flow of the bound pool, this gradient induces an opposite gradient in the fast pool due to mass balance (Figure 3C). This concentration profile persists even when making different assumptions regarding the spatial contribution of fast and slow pools to speckle appearances (see Supplementary Figure 2). The reaction rates for the simulation, as function of distance from the leading edge, found using the concentration profile in Equations (13) and (14), are shown in Figure 3D. The rate for Cslow to bind to the network is very small compared to the rate for Cfast to bind to the network (even though appearances due to Cslow account for a large fraction of appearances at the back of the lamellipodium, see Fig. 2B).
Relatively good fits to the experimental FRAP data for capping protein can be obtained when the lifetime τCslow is maximized, and the diffusion coefficient DCfast minimized, within the range of values described above and the range that gives non-negative concentration profiles in the model equations (if the sink described by the appearance profile is too strong for diffusion to replenish it, integration of Equations (9) and (10) over space would generate negative concentrations). The simulated FRAP was applied to a steady state initialized with the concentrations found after relaxing Equations (11) and (12) in time. An example of simulated FRAP is shown in Figure 3E while Figure 3F (Movie 1) shows the recovery of the intensity in the bleached region along with the recovery in Kapustina et al. The recovery curve for DCslow = 0.5 μm2/s that uses the same parameters as Figure 3C is an overall good fit to the experimental curve, however the initial recovery is more rapid compared to experiment.
The above results show that parameters measured with SiMS can be used to model the FRAP data in [18], using a smaller diffusion coefficient DCslow and faster dissociation time τ compared to the parameters used in the fit in [18]. The diffusion of long-lived oligomers out of the bleached region contributes to making the recovery slower initially and a value τCslow ≈ 13 s is needed for a good fit. This is in agreement with the fact that slowly-diffusing speckles can be tracked for a few seconds and thus the lifetime of the slowly-diffusing capping protein is likely in the range of 5–30 s [15] (note: τCslow cannot become much longer than a threshold above which the calculated Cfast in Equations (9) and (10) becomes negative). Even though the dissociation time τ = 2 s is small compared to the measured FRAP half-time, the bound species is a small fraction of the total amount.
3.1.2 Model with Membrane Binding
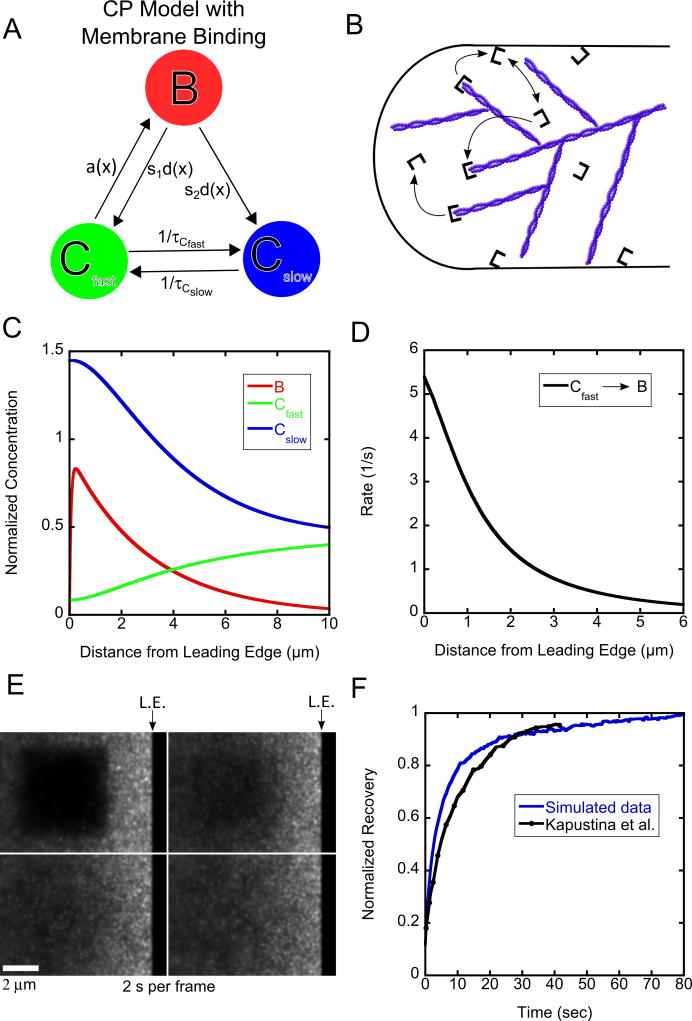
Another way of accounting for slowly diffusing capping protein is considering that capping protein binds and diffuses along the membrane [15]. Membrane binding can occur through a fast-diffusing state in the cytoplasm or by membrane-induced uncapping of capped barbed ends. The model shown in Figure 4A, B is another possible mechanism of why capping protein dissociates so frequently from the actin network and diffuses slowly. CARMIL is a membrane bound protein complex that also binds capping protein and may account for the very short lifetime of capping protein bound to the actin filament [21–23]. In this model only fast diffusing cytoplasmic protein is able to become bound (representing capping of barbed ends) so that the appearance rate is:
| (17) |
with λ = 3.0 μm. The bound protein can dissociate into either Cfast or Cslow and the parameter s1 is the probability of dissociating into Cfast. The fast diffusing capping protein can convert to slow with lifetime τCfast and slow can become fast with lifetime τCslow. The model in Figure 4A, B is another specific case of the general model (Figure 1).
Figure 4.
Results of model with membrane binding for capping protein. (A, B). Schematic and cartoon of model with membrane binding. (C). Steady state concentration profiles for capping protein (D) Binding rates as function of distance. (E) Snapshot images of simulated FRAP. (F). FRAP curves compared to experimental data from Kapustina et al. [18]. The ending time of the experimental measurement (40 s) is normalized to the value of the simulation at 40 s. The simulated recovery is normalized to one at long times. Simulations in panels C–F use K = 0.45 s−1, DCfast = 2.0 μm2/s, DCslow = 0.5 μm2/s, vr = 0.03 μm/s, τ= 2.0 s, τCfast = 5.0 s, τCslow = 5.0 s, s1 = 0.1.
The model with membrane binding (Figure 4) has more parameters compared to the model with oligomers (Figure 3). Similar constraints to Figure 3 exist for DCfast, DCslow, τ, vr, and K. The new parameters are the lifetime τCfast, and the dissociation probability s1. As mentioned in 3.1.1, the lifetime of the slowly-diffusing capping is likely in the range of 5–30 s. We start by assuming that τCfast= τCslow so that Cfast and Cslow each correspond to 50% of the concentration far from the leading edge [15]. A concentration profile similar to Figure 3C can be generated with K = 0.45 s−1, DCfast = 2 μm2/s, DCslow = 0.5 μm2/s, vr = 0.03 μm/s, τ= 2.0 s, τCfast = 5.0 s, τCslow =5.0 s, s1=0.1. These parameters give the reaction rate as a function of distance from the leading edge shown in Figure 4D for binding to the network from Cfast, which is the only reaction rate to the bound state.
We find that we are able to fit the experimental FRAP data using parameters consistent with SiMS data. The simulated recovery for the parameters of Figure 4C is shown in a montage in Figure 4E and the corresponding recovery curve shown in Figure 4F (Movie 1), along with the experimental data. Similar to the model with oligomers, DCfast needs to be on the lower range of the physically plausible values 2–5 μm2/s (in Figure 4C, further lowering of DCfast also makes the calculated steady state concentration profile of Cfast in Equation (9) negative). Parameter s1 needs to be small compared to unity, otherwise the bleached region recovers too quickly and none of the other parameters are able to slow the recovery down enough to capture what occurs in the experiment (see Supplementary Figure 1). Keeping τCfast = τCslow, we varied these two parameters together and find that they also need to be in the range of a few seconds (see Supplementary Figure 3). In conclusion, obtaining a good fit drives this model to a similar kinetic scheme as the model with oligomers, with the majority of the bound protein dissociating into slowly diffusing protein. However the lifetime of the slowly-diffusing species can be smaller than in the model with oligomers as slow diffusing capping protein can be generated by both uncapping and conversion from the fast species.
3.1.3 Comparison of Two Models for Capping Protein Turnover
Interestingly, both models demonstrate significant concentration gradients of the two diffuse species across the lamellipodium (Figures 3C and 4C). The origin of this gradient is mainly the local production of slowly diffusing capping protein close to the leading edge. The inward flux of the slowly-diffusing population plus the retrograde flow of the bound species must be balanced by the diffusive flux of the fast species at steady state. The free energy source to maintain this non-equilibrium gradient must be sought in ATP hydrolysis, the free energy of which drives actin polymerization: in both models the actin network “pumps” fast-diffusing capping protein into the slowly-diffusing pool.
Both models of Fig. 3 and 4 work to fit the FRAP results from Kapustina et al. [18] using parameters from the SiMS microscopy data of Miyoshi et al. [17]. The pool of slowly diffusing protein is important to fit FRAP recovery with a half-time on the order of 10 s, using a bound lifetime of 2 s. Retrograde flow contributes little to FRAP since the distance traveled by retrograde flow during recovery is small compared to the size of the bleached region. We showed that when both models are driven to similar kinetic transition rates, it is hard to distinguish between them using FRAP. A clearer difference between the two models can be seen in lamellipodium photoactivation simulations with the same parameters as for the FRAP data. This is shown in Movie 2 where it is possible to see that, directly after photoactivation, there is more rebinding throughout the lamellipodium from the model with oligomers as compared to the model with membrane binding. This reflects the assumption of oligomer re-association with the actin network at the back of the lamellipodium.
3.2 Application to Arp2/3 Complex Dynamics
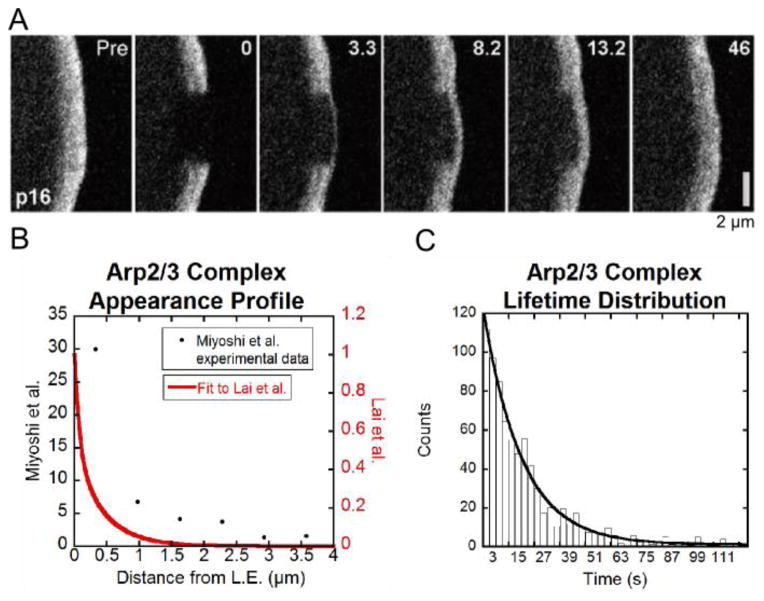
Both FRAP and SiMS microscopy experiments have been performed to study the kinetics of Arp2/3 complex in the lamellipodium. Figure 5A shows FRAP of the p16 subunit of the Arp2/3 complex by Lai et al. [24]. The bleached region is a 2 μm by 4 μm box positioned at the leading edge of a B16-F1 melanoma cell. Recovery is faster at the leading edge of the cell than it is away from the leading edge. While this has been interpreted to suggest that Arp2/3 complex forms branches within a very narrow region close to the leading edge, SiMS experiments using XTC cells (tagging the p40 and p21 subunits) by Miyoshi et al. [17] show distributed speckle appearances 1 μm away from the leading edge and further (Figure 5B) and an exponential distribution of speckle lifetimes with τ =18 s (Figure 5C). Our aim is to (i) use modeling to check if the FRAP recovery observed in Figure 5A is consistent with the distributed appearances in Figure 5B, and (ii) explore the implications for the concentration profiles of the diffuse species. Smith et al. [12] showed that distributed turnover of EGFP-actin can give faster FRAP at the cell front as compared to the cell back, however this has not been addressed for the Arp2/3 complex. We will be comparing data from different systems but we note that FRAP of actin in lamellipodia of B16-F1 melanoma cells [24] has similar qualitative features to FRAP of XTC cells [12] as well as PA of neuronal cells [8].
Figure 5.
Summary of Arp2/3 complex FRAP and SiMS data. (A) FRAP snapshots of leading edge of cell expressing EGFP-ArpC5B (p16 subunit) reproduced from Lai et al. [24]. (B) Speckle appearance rates for Arp2/3 complex from Miyoshi et al. [17] (black dots) and calculated to match the steady state Arp2/3 complex concentration profile in [24] (double exponential with A1 = 0.49, A2 = 0.51, λshort = 0.08 μm, λlong= 0.43 μm, see Equation (18)). (C). Arp2/3 complex speckle lifetime distribution from [17].
In the simulations below we used a profile with distributed appearances that is narrower compared to the profile measured in XTC cells, which have wider lamellipodia compared to the B16-F1 melanoma cells. This appearance profile, shown in Figure 5B, was calculated to give an Arp2/3 complex concentration profile that matches the concentration profile of the B16-F1 melanoma cells. This was done by measuring the intensity in excess of the cytoplasmic background as a function of distance from the leading edge in Figure 5A, and averaging over a strip of a few micron μm laterally across the lamellipodium. It was then assumed that this profile is approximately proportional to the bound profile B(x) and thus a(x) = B(x)/τ + vrdB(x)/dx that can be derived from Equations (2–7). We use the speckle lifetime τ of Miyoshi et al. [17]. The calculated a(x) profile was fit to a double exponential and the resulting curve is shown in Figure 5B. The difference between the calculated appearance profile in Figure 5B and the data by Miyoshi et al. is evident further than 1 μm away from the leading edge where the calculated appearance distribution approaches zero.
Using SiMS microscopy, Millius et al. [16] suggested that some Arp2/3 complexes bind to the WAVE complex on the cell membrane of XTC cells and perform a slow diffusion prior to incorporation of the actin network while other Arp2/3 complexes are recruited directly from the cytosol. Millius et al. observed slowly diffusing speckles of Arp2/3 complex components within a few μm from the leading edge. We thus considered a model with membrane binding of the Arp2/3 complex (Figure 6A,B). The two diffuse species in this model represent Arp2/3 complex in the cytoplasm, Cfast, and bound to the membrane, Cslow. The bound Arp2/3 complex dissociates into Cfast only, representing debranching and dissociation of the Arp2/3 complex from the pointed end. This occurs with the detachment rate d(x) corresponding to bound lifetime τ. This lifetime may include Arp2/3 complex attachment without branch formation, as observed in single molecule in vitro experiments where bound Arp2/3 complex has bound lifetimes in the range 2–200 s [25]. We assume that binding to the membrane occurs close to the leading edge with a spatially dependent rate k(x) = kme−x/λm defined by parameters λm and km. This was achieved in the simulations by using a spatially-dependent τCfast in equations (9) and (10) and in the Monte Carlo model accordingly. Spontaneous unbinding occurs with lifetime τCslow. The appearance profile describing association of membrane-bound Arp2/3 complex to the actin network is given by
Figure 6.
Results of model with membrane binding for Arp2/3 complex. (A, B) Schematic and cartoon of model with Arp2/3 complex membrane binding. (C) Steady state concentration profile for Arp2/3 complex. (D) Binding rates as function of distance. (E) Snapshot images of simulated FRAP. (F) FRAP curves compared to experimental data from Lai et al. [24]. The simulated recovery is normalized to one at long times. Simulations in panels C–F use DCfast = 3 μm2/s, K = 6.0 s−1, τCslow = 20 s, vr = 0.04 μm/s, λm = 0.2 μm and km = 40 s−1.
| (18) |
with A1 = 0.49, A2 = 0.51, λshort = 0.08 μm, and λlong = 0.43 μm (Figure 5).
Using an estimated retrograde flow rate vr = 0.04 μm/s in Figure 5A, DCslow = 0.6 μm2/s (the estimate in Millius et al. [30]) and assuming membrane binding occurs close to the leading edge, λm = 0.2 μm, leaves DCfast, K, τCslow and km as undetermined parameters. Knowing the larger size of the Arp2/3 complex as compared to actin monomers and capping protein, we anticipate a diffusion coefficient of 2–6 μm2/s. In the steady state profile in Figure 6C we use DCfast = 3 μm2/s, K = 6 s−1, τCslow = 20 s, and km = 40 s−1. This profile matches the experimental profile taken by a line scan in Figure 5A, as expected since the appearance profile was calculated using the experimental intensity profile. With these parameters, the bound protein is sharply peaked close to the leading edge while the fast diffusing protein is small compared to the bound species and slightly depleted at the leading edge. The depletion reflects the diffusive flow towards the leading edge that balances both the retrograde flow and diffusive flow of the slow species away from the lamellipodium. The slowly diffusing protein concentration is also much smaller than the bound concentration close to the leading edge. The parameters used in Figure 6C lead to the binding rate of the slowly diffusing to bound species as function of distance shown in Figure 6D
We used the model to fit the experimental FRAP data by Lai et al. [24], which shows faster recovery at the lamellipodium front as compared to the back (Figure 5A). The simulated FRAP snapshots using the same parameters as in the concentration profile of Figure 6C are shown in Figure 6E. The recovery is quantified in Figure 6F where the front recovery curve is taken 0–1 μm from the leading edge, and the back recovery curve is taken 1–2 μm from the leading edge as in Lai et al. [24]. For these parameters, the recovery curves compare well to experiment (Figure 6F, Movie 3). The recovery at the back has a small initial increase due to the diffusion of the cytoplasmic component, followed by a slower recovery. This slower recovery is driven by binding at the back of the lamellipodium and retrograde flow that brings labelled subunits from the cell front. We found that in order to fit the experimental FRAP data the value of K has to be sufficiently high to keep the bound to cytoplasmic ratio sufficiently smaller than unity; otherwise the back of the lamellipodium recovers faster than in experiments (see Supplementary Figure 4 A–C). Similarly, decreasing coefficient km to a value where the concentration of slowly-diffusing species becomes a small fraction of the bound concentration gives a better fit to the FRAP curve at the back (Supplementary Figure 4 D–G). The recovery is also affected by the diffusion coefficient of the fast diffusing species. Values above DCfast = 2 μm2/s give a good fit to the experimental FRAP data. A high bound to cytoplasmic ratio is also required in a model without slowly-diffusing Arp2/3 (Supplementary Figure 5).
The results of Figure 6 suggest that the diffusing population is a small fraction of the bound. The fact that the concentration of Arp2/3 complex increases by about 8-fold after stimulation in XTC cells [26] is consistent with the existence of a small fraction of fast-diffusing Arp2/3 complex (presumably the only species present prior to lamellipodia stimulation). Inspection of the movies in Millius et al. [16] indicates however that the number of slowly-diffusing speckles is comparable to the bound population. While the slowly-diffusing Arp2/3 complex speckles may also represent Arp2/3 complex bound to debranched actin oligomers (not considered here as a separate species, for simplicity), such a pool would also need to be as small for the model to reproduce the FRAP data. Thus our work motivates further studies to investigate if the fraction of diffusible Arp2/3 complex varies by a large factor among cell systems and/or during different stages of stimulation of the same cell.
4. Discussion
In this paper we used modeling to calculate concentration profiles of capping protein (Figures 3C and 4C) and Arp2/3 complex (Figure 6C) based on prior SiMS data on XTC cells. In these profiles the cytoplasmic pool is modeled with two diffuse populations (“fast” and “slow”). This limit of two pools is a simplifying approximation that is helpful to examine transport limitations across the lamellipodium. Our model can be extended to cover additional diffuse pools to account for protein complexes with a distribution of diffusion coefficients. We showed that the simulated capping protein FRAP is consistent with prior experiments in different cell types and provided a reinterpretation of these data in which the slowly diffusing pool plays a role in the recovery. For the case of Arp2/3 complex, the simulated FRAP is slower at the back of the lamellipodium. This is similar to experiments in different cell types though precise agreement depends on the ratio of diffuse to bound Arp2/3 complex, which we suggested deserves further experimental investigation.
While transport by diffusion was adequate as a mechanism to establish a steady state consistent with experiments, we found that significant concentration gradients can develop in the cytoplasm. The gradients in the diffuse pool will have implications on the behavior of the lamellipodium when perturbed from steady state, for example during the stimulation of a protrusion by increase of free barbed end concentration close to the leading edge [26, 27]. Thus the slowly diffusing species could be part of a mechanism to regulate lamellipodial response.
In the model with capping proteins bound to oligomers (Figure 3C), a sudden increase of free barbed ends close to the leading edge will not be accompanied by a proportional increase in the capping rate as the system is close to the diffusion rate of “fast” capping protein towards the leading edge. Since the slowly-diffusing capping proteins, assumed to be capped oligomers, are produced by the bound species, a local increase in barbed end concentration would lead to an increase in the concentration of the “slow” diffuse pool. In this model, the slow capping protein will bind to the back of the lamellipodium with an increased overall rate, which could be part of a mechanism of structural remodeling in the lamellipodium during protrusion [17]. In the corresponding case in the model with membrane binding (Figure 4C), the response would be similar but in that model the slow membrane-bound pool does not associate with the network and it would just accumulate and dissociate to the cytoplasm. Further, the diffuse pool gradients of both models rely on the continuous production of slow capping protein; tuning of this rate by cells (through severing or uncapping [22]) may remove or enhance the diffusion limitations and thus act as part of a control mechanism. The slow population of the capping protein near the leading edge may also act as a buffer of capping protein close to the leading edge but we note that we did not consider capping protein association to barbed ends through the slowly-diffusing membrane-bound capping protein pool.
Diffusion limitations of the Arp2/3 complex towards the leading edge could become important upon protrusion initiation (see concentration gradients of Cfast in Figure 6C). In addition to enhancing the rate of Arp2/3 complex association to the actin filaments through a 2D diffusive search [16], the slowly-diffusing pool could also act as a buffer of Arp2/3 complex for the faster response of active lamellipodia. The smallness of the diffusion coefficient of Arp2/3 complex (0.6 μm2/s) is important for keeping it close to the leading edge. Further SiMS and FRAP or PA studies of capping protein and Arp2/3 complex under non-steady state conditions should help resolve some of these mechanisms.
Photoactivation experiments can give a clear picture of where binding and unbinding occurs, complimentary to FRAP. Modeling and PA experiments using labeled actin provided support for two separate pools of actin [8]: (i) a pool coming from the center of the cell and bound to thymosin β4 that targets polymerization at the leading edge of the cell, and (ii) a second pool that is recycling actin at the back of the lamellipodium. The model in [8] included two diffuse actin cytoplasmic pools and one membrane bound in complex with thymosin β4 in order to account for the enhanced diffuse actin concentration close to the leading edge of neuroblastoma cells, similar to the models with membrane binding in the current work. We provide examples of anticipated results of PA experiments for capping protein and Arp2/3 complex in Movies 2 and 4.
Evidence for incorporation of diffuse actin to the lamellipodia network throughout the lamellipodium has also been provided by the FRAP and PA experiments of labeled actin by Lewalle et al. [28]. These authors also performed FRAP of Arp2/3 complex in lamellipodia and found recovery throughout the lamellipodia pronounced close to the leading edge, consistent with the assumptions in our work. This study describes the distributed turnover of actin, Arp2/3 complex, and capping protein as a system with a unique length-scale [28]. Other studies using fluorescence speckle microscopy however suggest different length scales for each component with capping protein, Arp2/3 complex, and F-actin having increasingly broader concentration profiles [29]. In the results of our work the capping protein distribution is broader than that of Arp2/3 complex but both are narrower than F-actin. Future work should examine if these differences are cell-type specific. Here we focused on the FRAP experiments by Lai et al. [24] because the width of the Arp2/3 complex distribution in [28] was narrower. We also used SiMS data rather than data for capping protein and Arp2/3 complex from fluorescent speckle microscopy on Drosophila S2 cells [29] where each speckle is a group of molecules rather than single molecules.
Some prior mathematical models have studied aspects that relate to the kinetics of capping protein and Arp2/3 complex across the lamellipodium. The model by Ditlev et al. [30] that includes many known reactions that occur within the lamellipodium was used by Kapustina et al. [18] to model FRAP experiments, as described in Section 3.1. However its predictions on Arp2/3 complex turnover have not been explored. Huber et al. [31] and Stuhrmann et al. [32] developed computational and mathematical models that account for actin monomer diffusion and actin filament severing and annealing throughout the lamellipodium but not accounting for diffusion of filaments after severing. Branch nucleation was assumed to only occur close to the leading edge and the barbed end capping rate was assumed uniform. They assumed that any severed filament that has an Arp2/3 complex bound to it does not anneal to another filament since it is treated as a minus-end capper. Slowly diffusing Arp2/3 complex bound to actin oligomers may represent a third cytoplasmic pool, in addition to the other two pools of Figure 6A. We did not include such a third pool in order to focus on the mechanism for slowly diffusing Arp2/3 complex proposed by Millius et al. [16]. Hu and Papoian [33, 34] use a stochastic simulation model that includes physical and chemical interactions for actin, Arp2/3 complex, and capping protein in the lamellipodium to model protrusions. They only allow Arp2/3 complex-mediated branching very close to the membrane, similar to Huber et al. and Stuhrmann et al. but in addition account for cytoplasmic diffusion with diffusion coefficient 20 μm2/s for all species. This reference value is larger than what we used here for the fast and slow diffusing pools. One of the findings in Hu and Papoian is a significant dependence of protrusion dynamics on the concentrations of capping protein and Arp2/3 complex. Since cytoplasmic concentration gradients result for slower values of the diffusion coefficients, this effect would provide an additional influence on protrusion dynamics.
We conclude with a discussion of the diffusive dynamics of some other lamellipodia regulators that have been studied with SiMS, for which our analysis may be applicable in the future. Tsuji et al. [35] studied cofilin and AIP1, which collaborate in actin filament severing [36, 37]. These SiMS studies, as well as FRAP studies of cofilin [24], indicate short bound lifetimes on the order of seconds and a broad appearance profile across the lamellipodium. Cofilin and AIP1 may be bound to the piece of severed filament after detachment for the network, which can be included in the model as a slowly diffusing cytoplasmic pool. Depending on the fraction of bound to diffuse protein, the FRAP curve for both proteins may be similar to that of capping protein. VASP is another important regulator that typically localizes close to the leading edge of the cell as well as in focal adhesions [17, 38]. SiMS data show very transient associations with the actin network [17] and FRAP of VASP at the leading edge of lamellipodia has a half time of 8.4 s [39]. VASP can form tetramers so future work could explore the role of the anticipated slowing down of cytoplasmic diffusion on these kinetics. The WAVE complex is another interesting protein to study as it is involved in the activation of the Arp2/3 complex. The FRAP recovery of WAVE2 close to the leading edge has a half-time of 8.6 s [24]. SiMS shows a broad distribution of WAVE2 appearance events and lifetimes [16]. Only a small fraction of WAVE complex speckles undergo retrograde flow compared to the Arp2/3 complex (20% compared to 90%) [16]. Extensions of our model can be used to study the implications of slow WAVE2 diffusion with 0.41 μm2/s [16].
Supplementary Material
Acknowledgments
This work was supported by NIH grant R01GM098430. We are grateful to Matt Smith for his help modifying the code developed in [8] and Naoki Watanabe for extended discussions and for providing us with SiMS data of XTC cells.
References
- 1.Pollard TD, Cooper JA. Actin, a central player in cell shape and movement. Science. 2009;326(5957):1208–1212. doi: 10.1126/science.1175862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mogilner A, Keren K. The Shape of Motile Cells. Curr Biol. 2009;19(17):R762–R771. doi: 10.1016/j.cub.2009.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Watanabe N. Inside view of cell locomotion through single-molecule: fast F-/G-actin cycle and G-actin regulation of polymer restoration. Proceedings of the Japan Academy, Series B. 2010;86:62–83. doi: 10.2183/pjab.86.62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Danuser G, Allard J, Mogilner A. Mathematical modeling of eukaryotic cell migration: insights beyond experiments. Annual review of cell and developmental biology. 2013;29:501–28. doi: 10.1146/annurev-cellbio-101512-122308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Blanchoin L, Boujemaa-Paterski R, Sykes C, Plastino J. Actin dynamics, architecture, and mechanics in cell motility. Physiological reviews. 2014;94(1):235–63. doi: 10.1152/physrev.00018.2013. [DOI] [PubMed] [Google Scholar]
- 6.Pollard TD, Borisy GG. Cellular Motility Driven by Assembly and Disassembly of Actin Filaments. Cell. 2003;112(4):453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 7.Kiuchi T, Nagai T, Ohashi K, Mizuno K. Measurements of spatiotemporal changes in G-actin concentration reveal its effect on stimulus-induced actin assembly and lamellipodium extension. The Journal of cell biology. 2011;193(2):365–80. doi: 10.1083/jcb.201101035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vitriol EA, McMillen LM, Kapustina M, Gomez SM, Vavylonis D, Zheng JQ. Two functionally distinct sources of actin monomers supply the leading edge of lamellipodia. Cell Rep. 2015;11(3):433–45. doi: 10.1016/j.celrep.2015.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zicha D, I, Dobbie M, Holt MR, Monypenny J, Soong DY, Gray C, Dunn GA. Rapid actin transport during cell protrusion. Science. 2003;300(5616):142–5. doi: 10.1126/science.1082026. [DOI] [PubMed] [Google Scholar]
- 10.Fan Y, Eswarappa SM, Hitomi M, Fox PL. Myo1c facilitates G-actin transport to the leading edge of migrating endothelial cells. The Journal of cell biology. 2012;198(1):47–55. doi: 10.1083/jcb.201111088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Novak IL, Slepchenko BM, Mogilner A. Quantitative analysis of G-actin transport in motile cells. Biophysical journal. 2008;95(4):1627–38. doi: 10.1529/biophysj.108.130096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Smith MB, Kiuchi T, Watanabe N, Vavylonis D. Distributed actin turnover in the lamellipodium and FRAP kinetics. Biophysical journal. 2013;104(1):247–57. doi: 10.1016/j.bpj.2012.11.3819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.McGrath JL, Tardy Y, Dewey CF, Jr, Meister JJ, Hartwig JH. Simultaneous measurements of actin filament turnover, filament fraction, and monomer diffusion in endothelial cells. Biophys J. 1998;75(4):2070–8. doi: 10.1016/S0006-3495(98)77649-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Watanabe N, Mitchison TJ. Single-Molecule Speckle Analysis of Actin Filament Turnover in Lamellipodia. Science. 2002;295(5557):1083–1086. doi: 10.1126/science.1067470. [DOI] [PubMed] [Google Scholar]
- 15.Smith MB, Karatekin E, Gohlke A, Mizuno H, Watanabe N, Vavylonis D. Interactive, Computer-Assisted Tracking of Speckle Trajectories in Fluorescence Microscopy: Application to Actin Polymerization and Membrane Fusion. Biophys J. 2011;101(7):1794–1804. doi: 10.1016/j.bpj.2011.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Millius A, Watanabe N, Weiner OD. Diffusion, capture and recycling of SCAR/WAVE and Arp2/3 complexes observed in cells by single-molecule imaging. Journal of cell science. 2012;125:1165–76. doi: 10.1242/jcs.091157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Miyoshi T, Tsuji T, Higashida C, Hertzog M, Fujita A, Narumiya S, Scita G, Watanabe N. Actin-turnover dependent fast dissociation of capping protein in the dendritic nucleation actin network: evidence of frequent filament severing. J Cell Biol. 2006;175(6):947–955. doi: 10.1083/jcb.200604176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kapustina M, Vitriol E, Elston TC, Loew LM, Jacobson K. Modeling capping protein FRAP and CALI experiments reveals in vivo regulation of actin dynamics. Cytoskeleton. 2010;67(8):519–34. doi: 10.1002/cm.20463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vitriol EA, Uetrecht AC, Shen F, Jacobson K, Bear JE. Enhanced EGFP-chromophore-assisted laser inactivation using deficient cells rescued with functional EGFP-fusion proteins. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(16):6702–7. doi: 10.1073/pnas.0701801104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yamashiro S, Mizuno H, Smith MB, Ryan GL, Kiuchi T, Vavylonis D, Watanabe N. New single-molecule speckle microscopy reveals modification of the retrograde actin flow by focal adhesions at nanometer scales. Molecular biology of the cell. 2014;25(7):1010–24. doi: 10.1091/mbc.E13-03-0162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fujiwara I, Remmert K, Hammer JA., 3rd Direct observation of the uncapping of capping protein-capped actin filaments by CARMIL homology domain 3. The Journal of biological chemistry. 2010;285(4):2707–20. doi: 10.1074/jbc.M109.031203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fujiwara I, Remmert K, Piszczek G, Hammer JA. Capping protein regulatory cycle driven by CARMIL and V-1 may promote actin network assembly at protruding edges. Proc Natl Acad Sci U S A. 2014;111(19):E1970–9. doi: 10.1073/pnas.1313738111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Edwards M, Liang Y, Kim T, Cooper JA. Physiological role of the interaction between CARMIL1 and capping protein. Molecular Biology of the Cell. 2013;24(19):3047–3055. doi: 10.1091/mbc.E13-05-0270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lai FP, Szczodrak M, Block J, Faix J, Breitsprecher D, Mannherz HG, Stradal TE, Dunn GA, Small JV, Rottner K. Arp2/3 complex interactions and actin network turnover in lamellipodia. The EMBO journal. 2008;27(7):982–92. doi: 10.1038/emboj.2008.34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Smith BA, Daugherty-Clarke K, Goode BL, Gelles J. Pathway of actin filament branch formation by Arp2/3 complex revealed by single-molecule imaging. Proc Natl Acad Sci U S A. 2013;110(4):1285–90. doi: 10.1073/pnas.1211164110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ryan GL, Petroccia HM, Watanabe N, Vavylonis D. Excitable actin dynamics in lamellipodial protrusion and retraction. Biophysical journal. 2012;102(7):1493–502. doi: 10.1016/j.bpj.2012.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Koestler SA, Steffen A, Nemethova M, Winterhoff M, Luo N, Holleboom JM, Krupp J, Jacob S, Vinzenz M, Schur F, Schluter K, Gunning PW, Winkler C, Schmeiser C, Faix J, Stradal TE, Small JV, Rottner K. Arp2/3 complex is essential for actin network treadmilling as well as for targeting of capping protein and cofilin. Molecular biology of the cell. 2013;24(18):2861–75. doi: 10.1091/mbc.E12-12-0857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lewalle A, Fritzsche M, Wilson K, Thorogate R, Duke T, Charras G. A phenomenological density-scaling approach to lamellipodial actin dynamics(dagger) Interface Focus. 2014;4(6):20140006. doi: 10.1098/rsfs.2014.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Iwasa JH, Mullins RD. Spatial and temporal relationships between actin-filament nucleation, capping, and disassembly. Curr Biol. 2007;17(5):395–406. doi: 10.1016/j.cub.2007.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ditlev JA, Vacanti NM, Novak IL, Loew LM. An Open Model of Actin Dendritic Nucleation. Biophys J. 2009;96(9):3529–3542. doi: 10.1016/j.bpj.2009.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huber F, Käs J, Stuhrmann B. Growing Actin Networks Form Lamellipodium and Lamellum by Self-Assembly. Biophys J. 2008;95(12):5508–5523. doi: 10.1529/biophysj.108.134817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stuhrmann B, Huber F, Kas J. Robust organizational principles of protrusive biopolymer networks in migrating living cells. PloS one. 2011;6(1):e14471. doi: 10.1371/journal.pone.0014471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hu L, Papoian GA. Mechano-chemical feedbacks regulate actin mesh growth in lamellipodial protrusions. Biophys J. 2010;98(8):1375–84. doi: 10.1016/j.bpj.2009.11.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hu L, Papoian GA. How does the antagonism between capping and anti-capping proteins affect actin network dynamics? Journal of physics Condensed matter: an Institute of Physics journal. 2011;23(37):374101. doi: 10.1088/0953-8984/23/37/374101. [DOI] [PubMed] [Google Scholar]
- 35.Tsuji T, Miyoshi T, Higashida C, Narumiya S, Watanabe N. An order of magnitude faster AIP1-associated actin disruption than nucleation by the Arp2/3 complex in lamellipodia. PLoS One. 2009;4(3):e4921. doi: 10.1371/journal.pone.0004921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lin MC, Galletta BJ, Sept D, Cooper JA. Overlapping and distinct functions for cofilin, coronin and Aip1 in actin dynamics in vivo. J Cell Sci. 2010;123(Pt 8):1329–42. doi: 10.1242/jcs.065698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jansen S, Collins A, Chin SM, Ydenberg CA, Gelles J, Goode BL. Single-molecule imaging of a three-component ordered actin disassembly mechanism. Nature communications. 2015;6:7202. doi: 10.1038/ncomms8202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rottner K, Behrendt B, Small JV, Wehland J. VASP dynamics during lamellipodia protrusion. Nature cell biology. 1999;1(5):321–2. doi: 10.1038/13040. [DOI] [PubMed] [Google Scholar]
- 39.Applewhite DA, Barzik M, Kojima S, Svitkina TM, Gertler FB, Borisy GG. Ena/VASP proteins have an anti-capping independent function in filopodia formation. Molecular biology of the cell. 2007;18(7):2579–91. doi: 10.1091/mbc.E06-11-0990. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.