Reassessing random-coil statistics in unfolded proteins

Abstract

The Gaussian-distributed random coil has been the dominant model for denatured proteins since the 1950s, and it has long been interpreted to mean that proteins are featureless, statistical coils in 6 M guanidinium chloride. Here, we demonstrate that random-coil statistics are not a unique signature of featureless polymers. The random-coil model does predict the experimentally determined coil dimensions of denatured proteins successfully. Yet, other equally convincing experiments have shown that denatured proteins are biased toward specific conformations, in apparent conflict with the random-coil model. We seek to resolve this paradox by introducing a contrived counterexample in which largely native protein ensembles nevertheless exhibit random-coil characteristics. Specifically, proteins of known structure were used to generate disordered conformers by varying backbone torsion angles at random for ≈8% of the residues; the remaining ≈92% of the residues remained fixed in their native conformation. Ensembles of these disordered structures were generated for 33 proteins by using a torsion-angle Monte Carlo algorithm with hard-sphere sterics; bulk statistics were then calculated for each ensemble. Despite this extreme degree of imposed internal structure, these ensembles have end-to-end distances and mean radii of gyration that agree well with random-coil expectations in all but two cases.

The protein folding reaction, unfolded (U) ⇄ native (N), is a reversible disorder ⇄ order transition. Typically, proteins are disordered (U) at high temperature, high pressure, extremes of pH, or in the presence of denaturing solvents, but they fold to uniquely ordered, biologically relevant conformers (N) under physiological conditions. With some exceptions (1), the folded state is the biologically relevant form, and it can be characterized to atomic detail by using x-ray crystallography and NMR spectroscopy. In contrast, our understanding of the unfolded state is based primarily on a statistical model, the random-coil model, which was developed largely by Flory (2) and corroborated by Tanford (3) in the 1950s and 1960s.

In a random coil, the energy differences among sterically accessible backbone conformers are of order ≈kT (where k is Boltzmann's constant, and T is the absolute temperature). Consequently, there are no strongly preferred conformations, the energy landscape is essentially featureless, and a Boltzmann-weighted ensemble of such polymers would populate this landscape uniformly.

Our motivation here is to dispel the belief, which is widespread among protein chemists, that the presence of random-coil statistics for denatured proteins confirms the absence of residual structure in these molecules. Indeed, it is well known to polymer chemists that rods of any stiffness (e.g., steel I-beams) behave as Gaussian-distributed, temperature-dependent random coils if they are long enough. Chains in which the persistence length exceeds one physical link can be treated effectively by rewriting them as polymers of Kuhn segments (ref. 2, page 12). Consequently, a protein chain can behave as a random coil even if it is comprised of nonrandom segments.

A denatured protein is a heteropolymer in which different amino acid residues will have differing average conformations but in which an average backbone conformation is attained within a window of ≈10 residues. For such a heteropolymer, coil dimensions can be assessed by using the following two related measures: the radius of gyration and the end-to-end distance. Flory showed (ref. 4, page 43) that the radius of gyration, R_G, follows a simple scaling law:

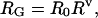[1]

where N is the number of residues, R₀ is a constant related to persistence length, and ν is the scaling factor of interest that depends on solvent quality. Values of ν range from 0.33 for a collapsed, spherical molecule in poor solvent, through 0.5 for an ideal solvent, to 0.6 in good solvent. The mean-squared end-to-end distance, 〈L²〉, for unfolded proteins is also expected to scale linearly with chain length:

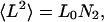[2]

with the L₀ prefactor obtained from experiment.

Tanford et al. (5) corroborated these random-coil expectations for unfolded proteins by using intrinsic viscosity measurements, which scale with chain length in a conformation-dependent way. From this relationship, they obtained values of ν = 0.67 and L₀ = 70 ± 15 Ų. To a good approximation, end-to-end distances for random coils of sufficient length are Gaussian distributed (6), and in fact, this behavior has been observed in recent simulations (7).

Tanford and coworkers (8) emphasized that such measurements are meaningful only after eliminating all residual structure, requiring denaturation in 6 M guanidinium chloride. This issue is crucial. Structure induced by peptide hydrogen bonds is abolished only under strongly denaturing conditions. As pointed out by Millett et al.,

Additional evidence that chemically or thermally denaturing conditions are typically good solvents for the unfolded state stems from the observation that R_G is generally fixed over a broad range of temperatures or denaturant conditions. (ref. 9, page 255)

Today, the most reliable experimental values of R₀ and ν in Eq. 1 are obtained from small-angle x-ray scattering (SAXS) (9). By using this approach for a series of 28 unfolded proteins, values of R₀ = 2.08 ± 0.19 Å and ν = 0.598 ± 0.029 were obtained (10). These results are a strong indicator of random-coil behavior. Additionally, SAXS data can be used to construct a Kratky plot, s versus s²I(s), where s is the small-angle scattering vector and I(s) is the corresponding scattering intensity (11, 12). For random coils, the plot increases monotonically and approaches linearity in s (13). This behavior is observed for unfolded proteins, whereas folded proteins plotted in this way exhibit a notable maximum (figure 1 in ref. 9). Such plots have become the present-day standard for assessing random-coil behavior in unfolded proteins (11, 12).

The success of the random-coil model in fitting experimentally determined coil dimensions of unfolded proteins is undisputed. Accordingly, researchers in this field have grown accustomed to believing that unfolded proteins are featureless random coils. Here, we demonstrate that nonrandom coils can also exhibit random-coil statistics.

Tanford knew that denatured proteins need not be entirely random simply because they satisfy random-coil statistics, and he warned:

A cautionary word is in order regarding the use of the measurement of the radius of gyration of a particular protein as the sole criterion for random-coil behavior. Other conformations can have similar radii of gyration. For example, an α-helical rod has a length of 1.50 Å per residue. There is a narrow range of N where essentially identical values of R_G are predicted for α-helices and random coils. (3)

In this article, we introduce the “rigid-segment model,” a highly contrived, limiting model in which known protein structures are partitioned alternately into rigid segments linked by individual flexible residues. The x-ray elucidated coordinates are retained for the rigid segments, but backbone torsion angles were allowed to vary freely for the flexible residues. The fraction of the chain allowed to vary (≈8%) was chosen to approximate one residue per peptide chain turn (14). If this physically unrealistic, extreme model still exhibits random-coil statistics, it follows that a lesser degree of preorganization in the unfolded state need not violate random-coil expectations. In fact, we find that our limiting model still reproduces random-coil statistics when ≈92% of the structure is held rigidly in its native conformation.

The Rigid-Segment Model. Our strategy is to devise an algorithm that operates on native protein structures and generates ensembles of highly structured, sterically allowed conformers. We then test these ensembles and determine the extent to which they exhibit randomcoil statistics. A largely native ensemble that nevertheless appears to be random serves as a counterexample to the random-coil model.

The algorithm consists of several steps. First, each residue is examined in turn, and those with the maximum possible flexibility are identified. Flexibility is measured by evaluating the range of sterically allowed backbone torsion angles for each residue; the broader the range, the greater the flexibility. Next, by using a biochemically motivated rationale, a subset of these flexible residues is selected as links, transforming the polypeptide chain into rigid segments interconnected by flexible links. The links are then varied at random in concerted fashion to generate clash-free ensembles that are suitable for statistical analysis (Table 1). These steps are described in detail below.

Table 1. Proteins used in rigid segment simulations.

Protein	PDB ID	Chain	Resolution, Å	Refinement factor	Chain length
Angiotensin II	1N9V	A	(NMR)	(NMR)	8
Chicken villin headpice	1VII	—	(NMR)	(NMR)	36
PKC Δ Cys2 domain	1PTQ	—	1.95	0.196	50
Protein G	2GB1	—	(NMR)	(NMR)	56
Fyn SH3	1SHF	A	1.90	0.180	59
CspB	1CSP	—	2.50	0.195	67
Ubiquitin	1UBQ	—	1.80	0.176	76
λ Repressor	1LMB	3	1.80	0.189	87
Barstar	1A19	A	2.76	0.203	89
ctAcP	2ACY	—	1.80	0.170	98
Plastocyanin	2PCY	—	1.80	0.160	99
Horse cytochrome c	1HRC	—	1.90	0.179	104
pI3K SH2 (rat)	1FU6	A	(NMR)	(NMR)	111
Myohemerythrin	2HMQ	A	1.66	0.189	113
Bovine ?-lactalbumin	1F6S	A	2.20	0.216	122
Bovine ribonuclease A	1XPT	A	1.90	0.162	124
CheY	1EHC	—	2.26	0.143	128
Lysozyme	1HEL	—	1.70	0.152	129
Intestinal FA binding protein	1IFB	—	1.96	0.188	131
Staphylococcal nuclease	2SNS	—	1.50	N/A	141
Calmodulin	1CM1	A	2.00	0.234	143
Myoglobin	1MBO	—	1.50	0.159	153
Ribonuclease H	2RN2	—	1.48	0.196	155
ASV integrase core	1ASU	—	1.70	0.152	162
T4 phage lysozyme	2LZM	—	1.70	0.193	164
DHFR	1AI9	A	2.76	0.203	192
MutY catalyic domain	1MUN	—	1.20	N/A	225
Triosephosphate, isomerase	5TIM	A	1.83	0.183	249
Human glyoxase II	1QH3	A	1.90	0.185	260
EcoRI endonuclease	1ERI	A	2.70	0.170	261
UDP-galactose 4-epimerase	1NAH	—	1.80	0.165	338
Creatine kinase	1QK1	A	2.70	0.195	379
Yeast PGK	3PGK	—	2.50	N/A	415

ctAcP, common-type acylphosphatase; ASV, avian sarcoma virus; DHFR, dihydrofolate reductase.

Identifying Individual Flexible Residues. The first step quantifies the backbone flexibility of individual residues. For each residue, sterically allowed φ, ψ-space (15) was explored by using torsion-angle Monte Carlo sampling with hard-sphere sterics, with the acceptance ratio taken as the measure of flexibility. Steric clashes were evaluated in a window of 15 residues flanking the residue in question (but with diminishing window size nearing chain termini). A half-window of 15 residues was chosen to approximate the average size of a protein secondary structure element together with its adjoining turn (14).

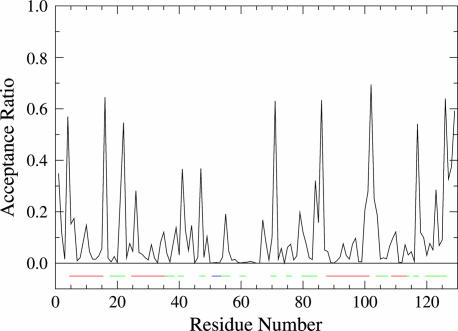
To construct a flexibility profile of acceptance ratio versus residue number, 10,000 backbone φ, ψ-pairs were sampled for each residue, as shown for lysozyme in Fig. 1. Generally, although not invariably, the most flexible residues correspond to turns; glycines also promote chain flexibility.

Fig. 1.

Flexibility profile for lysozyme (PDB ID code 1HEL). Secondary structure is indicated by bars beneath the plot, which are color-coded as follows: red, α-helices; blue, β-strands; and green, turns. Secondary structure determinations are based on backbone torsions, as described in ref. 23.

Selecting Sets of Flexible Residues. Individual acceptance ratios were ranked by flexibility, and a set of suitable size was chosen based on the average length of a protein α-helix, which is 12 residues (16). Accordingly, a flexible residue set, 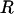, of size m = N/12 residues was chosen, having one flexible linker for every 12 residues in the protein. The value of m was rounded to the nearest integer, with a minimum value of 1.

The most flexible residues were chosen for inclusion in 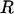, with the following two minor qualifications: sites were chosen to be at least five residues apart, and those within five residues of chain termini were not included. These qualifications promote a uniform distribution of flexible links along the polypeptide chain and ensure that the chosen backbone torsion angles are independent of one another (17).

An ensemble of structures was generated for each protein by concerted sampling of backbone torsions, chosen at random from all sterically allowed regions of φ, ψ-space. Random-coil statistical measures were then used to characterize this ensemble. Details are described in Methods.

Methods

We selected 33 proteins of 8–415 residues in size from the Protein Data Bank (18) based on structure quality, scientific interest, and size distribution (Table 2). Where possible, proteins studied previously by SAXS were included. All crystallographic waters, heteroatoms, and nonbiological chain terminators (acetyl groups, N-methylamide, etc.) were removed, and any disulfide bonds were broken.

Table 2. Flexibility set selection in lysozyme.

Residue no.	SS type*	Residue type	Flexibility†	Included in set
102	C	GLY	0.694	Yes
16	C	GLY	0.645	Yes
126	T	GLY	0.640	No‡
86	C	SER	0.635	Yes
71	T	GLY	0.630	Yes
129	C	LEU	0.592	No‡
4	P	GLY	0.570	No‡
22	T	GLY	0.546	Yes
117	T	GLY	0.542	Yes
128	P	ARG	0.375	No§
47	T	THR	0.368	Yes
41	T	GLN	0.366	Yes
1	C	LYS	0.349	No‡
127	P	CYS	0.327	No‡
84	T	LEU	0.321	No§
123	T	TRP	0.285	Yes
26	H	GLY	0.282	No§
101	H	ASP	0.277	No§
21	T	ARG	0.264	No§
103	C	ASN	0.250	No§
100	H	SER	0.207	No§
79	P	PRO	0.196	Yes
55	T	ILE	0.191	Yes

C, coil; T, turn; P, polyproline II helix; and H, α-helix.

^*Secondary structure types were determined as in ref. 23.

^†Flexibility values, in rank order, correspond to those plotted in Fig. 2.

^‡Not included because of its proximity to the N or C terminus.

^§Not included because of its proximity to a previously selected residue.

Hard-sphere, torsion-angle Monte Carlo simulations (19) were performed by using a suite of freely available programs (http://roselab.jhu.edu/dist/index.html). Default van der Waals radii (20) were used unless the experimentally reported distance between two atoms was smaller than the sum of their hard sphere radii, in which case the minimum interatomic distance was taken from Protein Data Bank coordinates. At each Monte Carlo step, random values of backbone torsions, chosen from allowed regions on the dipeptide map, were assigned in concert to residues in 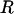. In the event of a steric clash, the step was rejected.

Statistics of interest for each ensemble include the average radius of gyration and end-to-end distance. The geometric radius of gyration for a chain is given by the following equation:

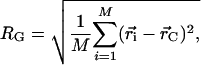[3]

where M is the number of atoms in the protein structure, 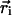is the position of atom i in three-dimensional space, and 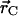is the geometric center of the molecule. Weighting by mass or atomic scattering factor does not change the radius of gyration significantly, and therefore, the ensemble-averaged radius of gyration was computed simply by averaging R_G over all chains in the ensemble.

The mean squared end-to-end distance, 〈L²〉, is given by the following equation:

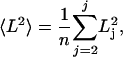[4]

where n is the number of conformers in the ensemble, and L_j is the end-to-end distance of conformer j, taken from the N-terminal nitrogen to the C-terminal oxygen. End-to-end distance histograms were generated by using the R statistics package (21).

For each protein in the data set, an ensemble of at least 1,000 clash-free conformers was generated as described above, with flexible residues selected from the corresponding flexibility profile (e.g., Fig. 1). This process was repeated five times. To assure convergence, SDs for both R_G and 〈L²〉 were calculated. As a further test, ensembles of 10,000 and 500 structures were examined; all have similar statistics.

The program crysol (22) was used to generate simulated SAXS scattering profiles for every conformer in each ensemble. In crysol, the scattering vector s is defined as follows:

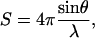[5]

where θ is the scattering angle and λ is the x-ray wavelength (in angstroms). Default options were used for all values. Scattering profiles of all conformers were averaged at every point, and errors were reckoned as the SD of I(s) for that point over the entire ensemble. Simulated Kratky plots were produced by plotting s against s²I(s) for every point.

Results

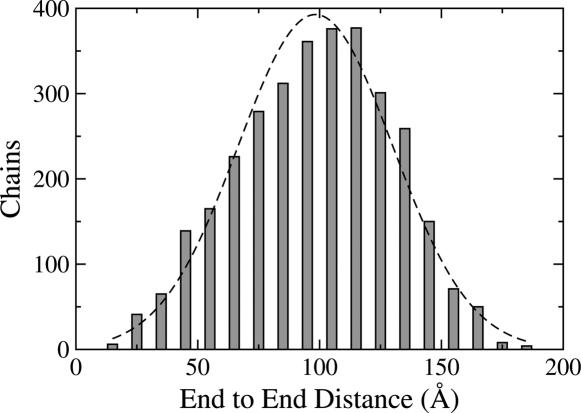
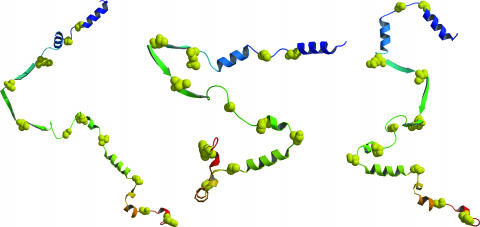
Detailed results for lysozyme (1HEL) using the rigid-segment model are described as an illustrative example. Almost all flexible residues are situated in turn and coil regions (Fig. 1), as identified from backbone torsion angles (23). The set of flexible linker residues, 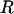, selected by our algorithm is {16, 22, 41, 47, 55, 71, 79, 86, 102, 117, 123}, and the resultant ensemble of segmentally rigid chains was found to be consistent with random-coil expectations (see Table 2). In particular, the value of R_G for denatured lysozyme predicted by Eq. 1 is 35.0 ± 4.3 Å, and the average R_G from five rigid-segment simulations is 37.93 ± 0.14 Å (in good agreement). The experimentally determined R_G for trifluoroethanol (TFE)-denatured lysozyme is 35.8 ± 0.5 Å (24); this value may be especially relevant for comparison with the rigid-segmental model because TFE stabilizes helical segments (25). Similarly, the value 〈L²〉 for denatured lysozyme predicted by Eq. 2 lies between 7,095 Ų and 10,965 Ų, and 〈L²〉 from rigid-segment ensembles is 10,690 ± 160 Ų, which is near the high end of the predicted Gaussian distribution (Fig. 2). Thus, highly structured lysozyme chains (Fig. 3), generated by using the rigid-segment model, exhibit random-coil statistics.

Fig. 2.

End-to-end distance histogram for lysozyme using 5,000 chains generated from the rigid-segment model. Chains were grouped into 10-Å bins based on the distance from the N-terminal nitrogen to the C-terminal oxygen. For comparison, a Gaussian curve having the same mean and SD as the actual distribution is also shown (dashed line).

Fig. 3.

Representative lysozyme structures from rigid-segment simulations. The entire chain was held fixed in its x-ray-determined conformation, except for 11 flexible hinge residues (shown as yellow space-filling spheres). Ribbon diagram depicts elements of secondary structure, defined here from the Protein Data Bank header records and generated by using molscript (49) and raster3d (50). Termini are color-coded as follows: blue, N termini; red, C termini.

The rigid-segment model was applied to 33 proteins, as summarized in Table 3. In general, values of both R_G and 〈L²〉 are consistent with random-coil expectations, and histograms of the end-to-end distances fit well to a Gaussian curve with two exceptions: angiotensin II (1N9V, eight residues) and PKC δ-Cys-2 domain (1PTQ, 50 residues). Both outliers are small and deviate from the normal distribution that is expected for longer chains (more than ≈100 residues), consistent with the systematic deviations from Eqs. 1 and 2 that Tanford noted for short chains (figure 2 in ref. 3, and ref. 26, page 994). However, two other small proteins in our data set (e.g., 1VII, 36 residues; 2GB1, 56 residues) behave as expected for longer chains. The rigid-segment model, which tends to localize chain flexibility at peptide chain turns, is expected to be sensitive to differences in the average segment length between consecutive turns. This expectation is borne out in the following way: in comparison with the values predicted by Eq. 1, the rigid-segment model underestimates R_G for α-helical proteins (1VII, 1LMB, 1HRC, 2HMQ, 1CM1, 1MBO, and 1MUN) but overestimates R_G for β-sheet proteins (1SHF, 1CSP, 2PCY, and 1IFB), as shown in Table 1.

Table 3. Summary of simulations and comparison with the random-coil model and SAXS.

			Radius of gyration, Å			Mean-squared end-to-end distance, Å2
PDB ID	Chain length	Flexible residues	SAXS*	Random-coil model†	Segment simulations‡	Random-coil model§	Segment simulations
1N9V	8	1	9.1 ± 0.3	6.96 ± 0.68	6.8790 ± 0.0086	560 ± 120	346.3 ± 3.5
1VII	36	3	—	16.7 ± 1.8	16.044 ± 0.019	2,520 ± 540	2,015 ± 13
1PTQ	50	4	—	20.2 ± 2.3	16.988 ± 0.012	3,500 ± 750	2,313 ± 13
2GB1	56	5	23 ± 1	21.6 ± 2.5	25.396 ± 0.039	3,920 ± 840	5,407 ± 57
1SHF	59	5	—	22.2 ± 2.5	23.269 ± 0.037	4,130 ± 890	3,580 ± 71
1CSP	67	6	—	23.9 ± 2.8	29.047 ± 0.066	4,700 ± 1,000	4,261 ± 77
1UBQ	76	6	25.2 ± 0.2	25.8 ± 3.0	25.176 ± 0.048	5,300 ± 1,100	4,290 ± 120
1LMB	87	7	—	27.9 ± 3.3	24.244 ± 0.048	6,100 ± 1,300	4,420 ± 140
1A19	89	7	—	28.2 ± 3.4	28.628 ± 0.060	6,200 ± 1,300	6,372 ± 74
2ACY	98	8	30.5 ± 0.4	29.9 ± 3.6	34.945 ± 0.095	6,900 ± 1,500	7,430 ± 270
2PCY	99	8	—	30.0 ± 3.6	40.439 ± 0.075	6,900 ± 1,500	11,690 ± 110
1HRC	104	9	—	30.9 ± 3.7	28.06 ± 0.10	7,300 ± 1,600	5,200 ± 180
1FU6	111	9	30.3 ± 0.3	32.1 ± 3.9	29.87 ± 0.10	7,800 ± 1,700	5,990 ± 180
2HMQ	113	9	—	32.4 ± 3.9	30.07 ± 0.10	7,900 ± 1,700	6,200 ± 120
1F6S	122	10	—	33.9 ± 4.2	36.04 ± 0.17	8,500 ± 1,800	8,650 ± 240
1XPT	124	10	33.2 ± 1.0	34.2 ± 4.2	36.777 ± 0.077	8,700 ± 1,900	8,420 ± 130
1EHC	128	11	38.0 ± 1.0	34.9 ± 4.3	36.613 ± 0.049	9,000 ± 1,900	8,270 ± 200
1HEL	129	11	35.8 ± 0.5	35.0 ± 4.3	37.93 ± 0.14	9,000 ± 1,900	10,690 ± 160
1IFB	131	11	—	35.3 ± 4.4	47.61 ± 0.15	9,200 ± 2,000	15,260 ± 370
2SNS	141	12	37.2 ± 1.2	36.9 ± 4.6	41.10 ± 0.14	9,900 ± 2,100	10,660 ± 240
1CM1	143	12	—	37.2 ± 4.6	33.76 ± 0.25	10,000 ± 2,100	7,920 ± 320
1MBO	153	13	40 ± 2	38.7 ± 4.8	40.084 ± 0.083	10,700 ± 2,300	13,140 ± 270
2RN2	155	13	—	39.0 ± 4.9	39.50 ± 0.21	10,900 ± 2,300	11,850 ± 200
1ASU	162	14	—	40.0 ± 5.0	42.94 ± 0.19	11,300 ± 2,400	11,160 ± 320
2LZM	164	14	—	40.3 ± 5.1	36.83 ± 0.19	11,500 ± 2,500	9,730 ± 300
1AI9	192	16	44 ± 2	44.1 ± 5.6	51.71 ± 0.13	13,400 ± 2,900	21,370 ± 330
1MUN	225	19	—	48.4 ± 6.3	47.12 ± 0.21	15,800 ± 3,400	16,200 ± 710
5TIM	249	21	—	51.3 ± 6.7	49.88 ± 0.24	17,400 ± 3,700	15,910 ± 340
1QH3	260	22	—	52.6 ± 6.9	61.34 ± 0.54	18,200 ± 3,900	21,240 ± 810
1ERI	261	22	—	52.7 ± 6.9	62.78 ± 0.10	18,300 ± 3,900	24,900 ± 1,100
1NAH	338	28	—	61.3 ± 8.3	62.67 ± 0.61	23,700 ± 5,100	23,700 ± 680
1QK1	379	32	46.1 ± 1.5	65.5 ± 8.9	79.812 ± 0.078	26,500 ± 5,700	43,500 ± 2,400
3PGK	415	35	71 ± 1	69.0 ± 9.5	67.58 ± 0.41	29,100 ± 6,200	32,200 ± 1,100

^*SAXS data from Millett et al. (9) and Kohn et al. (10).

^†Random-coil radii of gyration calculated from Eq. 1 by using constants from refs. 9 and 10. Error is calculated by using standard propagation of error formulae.

^‡Segment simulation error was calculated as the error on the mean from five simulations.

^§Random-coil mean-squared end-to-end distance values calculated from Eq. 2 (5). Error is propagated from the initial constant.

Among the R_Gs, one outlier warrants particular comment. The value of R_G for creatine kinase (1QK1) from rigid-segment calculations is 79.812 ± 0.078 Å, but the corresponding value predicted by Eq. 1 is only 66.5 ± 8.9 Å. It is noteworthy that both values substantially exceed the actual, experimentally determined value of 46.0 ± 1.5 Å, which was observed by using SAXS. We find no explanation for this anomalous behavior.

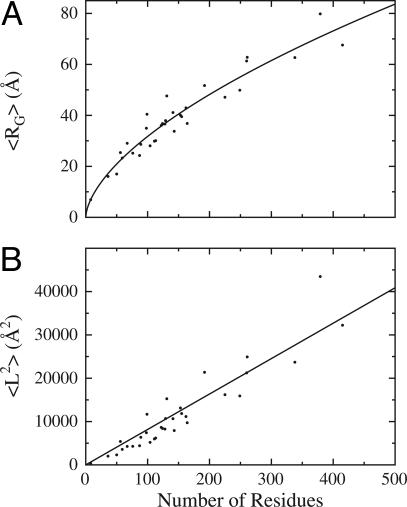
Data from all 33 proteins were fit to Eqs. 1 and 2 and are displayed in Fig. 4. A nonlinear least-squares best fit (21) to Eq. 1 gives R₀ = 1.98 ± 0.37 Å and ν = 0.602 ± 0.035, which are indistinguishable from recent experimentally determined values (10). The corresponding fit to Eq. 2 gives L₀ = 81.8 ± 3.4 Ų, similar to Tanford's value of L₀ = 70 ± 15 Ų (5). The SDs reported here for R_G and 〈L²〉 represent a convergence criterion and not the actual uncertainties of those values, and weights were not used during the fits.

Fig. 4.

Coil dimensions for 33 proteins using the rigid-segment model. (A) Radius of gyration (〈R_G〉) versus chain length in residues for 33 ensembles from rigid-segment simulations. The curve is well fitbyEq. 2, with R₀ = 1.98 ± 0.37 Å and ν = 0.602 ± 0.035. (B) Mean-squared end-to-end distance (〈L²〉) versus chain length in residues for the same 33 ensembles. The best-fit value of L₀, the slope of the line, is 81.8 ± 3.4 Ų. These fitted parameters are in close agreement with accepted random-coil values.

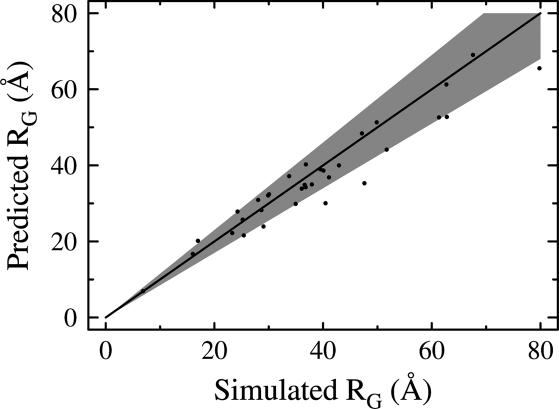
Values of R_G derived from the rigid-segment and random-coil models are strongly correlated (r² = 0.916, Fig. 5). In all, characteristic statistics for the random-coil model resemble those for the rigid-segment model, despite the fact that in the latter, 92% of each chain is fixed in its native conformation.

Fig. 5.

Comparison between our values of R_G from the rigid-segment model and corresponding values of R_G from random-coil expectations by using Eq. 1. All data points fall near the diagonal line. To aid in visualization, a shaded region marks the ±15% boundary, ranging between y = 1.15x and y = 0.85x.

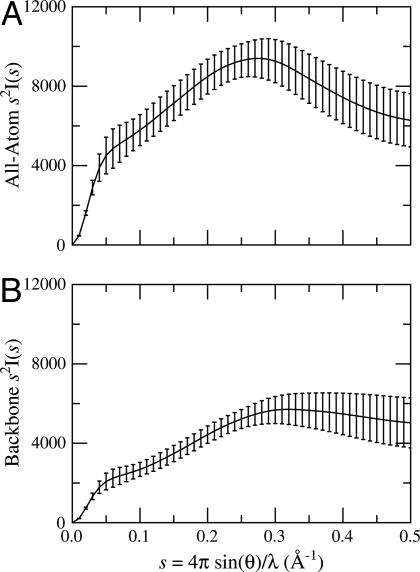
SAXS and Kratky Plots. SAXS profiles monitor the correlation among interatomic distances. In our simulations, interatomic distances do not vary within each rigid segment, so it is conceivable that a segmentally rigid ensemble could have random-coil values of R_G and 〈L²〉 but yet appear to be structured in a Kratky plot. To test this possibility, a Kratky plot was calculated for random chains from the lysozyme ensemble (Fig. 6A). Although the simulated plot has a maximum at 0.275 Å^–1, it lacks the pronounced hump typical of Kratky plots for native proteins. A second test shows that side chain rigidity is a major factor contributing to this maximum. After removal of side-chain atoms beyond Cβ, the corresponding plot resembles that of a denatured protein (Fig. 6B).

Fig. 6.

Kratky plots of rigid-segment simulations. (A) Calculated Kratky plot for 1,296 structures chosen at random from the lysozyme ensemble. (B) Calculated Kratky plot for the same structures after removal of side-chain atoms beyond Cβ. The maximum in A suggests a native protein, whereas B resembles a denatured protein, suggesting the fact that the hump in A is caused by sidechain rigidity and not by lack of backbone flexibility.

Discussion

The random-coil model has a long and impressive record of successfully predicting the chain dimensions of denatured proteins (3, 9, 10). However, two recent lines of evidence suggest that denatured protein chains may be far from random. First, experiments have identified native-like organization in unfolded proteins. By using residual dipolar couplings (RDCs) from NMR, Shortle and Ackerman (27) showed that native-like topology persists under strongly denaturing conditions in a truncated staphylococcal nuclease. Contention about the origin of RDCs in unfolded proteins notwithstanding (28), other NMR methods also detect structure in the unfolded state. By using triple-resonance NMR, native-like topology has been observed in protein L (29). A second line of evidence suggests that unfolded proteins are conformationally biased toward polyproline II (P_II) helical conformations. Both theory (30–37) and experiment (38–42) have investigated the preference for P_II in unfolded peptide ensembles. If the experimental results are correct and the ensemble is not random, then why is the random-coil model so successful? This paradox has been dubbed “the reconciliation problem” by Plaxco and coworkers (9).

Our contrived counterexample was designed to address the reconciliation problem directly. Indeed, we find that the randomcoil model is insensitive to a preponderance of stiff segments in an otherwise flexible chain.

In our simulations, chains of interest are comprised of rigid segments of native protein structure interconnected by flexible hinge residues. This approach is deliberately extreme in its neglect of physical reality, and we emphasize that it is not intended as a model of the unfolded state. With the exception of steric repulsion, all interatomic forces and temperature-dependent effects are ignored, together with resultant structural fluctuations. Yet, this physically absurd model (in which 92% of the native structure is retained) successfully reproduces random-coil statistics for R_G and 〈L²〉 in good solvent (e.g., 6 M guanidinium chloride). Therefore, it is not too surprising that transient organization in denatured proteins could also give rise to the random-coil statistics observed in experiment (10).

The presence of preorganization in denatured proteins changes our perspective about the disorder ⇄ order transition that occurs during protein folding. Despite much evidence to the contrary, a persisting view holds that denatured proteins are random coils, lacking in correlations beyond nearest-chain neighbors. If so, there is a puzzling, time-dependent search problem as unfolded polypeptide chains negotiate self-avoiding Brownian excursions through this featureless landscape en route to their native conformation (43). Concepts like folding funnels, kinetic traps, and frustration arose as attempts to rationalize this process (44). However, such conundrums are eliminated by the presence of sufficient conformational bias in the unfolded state (45, 46). In fact, significant conformational bias is inescapable, and it originates from sterically imposed chain organization that extends beyond nearest sequential neighbors (47, 48), at least in part.

The random-coil model has been construed to imply that denatured proteins lack organization, which is an interpretation that has become a mainstay in protein-folding studies. Against this backdrop, there was no motivation to seek out organizing steric interactions beyond the linked alanyl dipeptide (15). Nonetheless, such interactions do exist (48) and are easy to detect. Our rigid-segment counterexample was developed to challenge this conventional interpretation of the random-coil model and to remove a conceptual obstacle that has impeded alternative explanations.