Abstract
Performance-based building requirements have become more prevalent because it gives freedom in building design while still maintaining or exceeding the energy performance required by prescriptive-based requirements. In order to determine if building designs reach target energy efficiency improvements, it is necessary to estimate the energy performance of a building using predictive models and different weather conditions. Physics-based whole building energy simulation modeling is the most common approach. However, these physics-based models include underlying assumptions and require significant amounts of information in order to specify the input parameter values. An alternative approach to test the performance of a building is to develop a statistically derived predictive regression model using post-occupancy data that can accurately predict energy consumption and production based on a few common weather-based factors, thus requiring less information than simulation models. A regression model based on measured data should be able to predict energy performance of a building for a given day as long as the weather conditions are similar to those during the data collection time frame. This article uses data from the National Institute of Standards and Technology (NIST) Net-Zero Energy Residential Test Facility (NZERTF) to develop and validate a regression model to predict the energy performance of the NZERTF using two weather variables aggregated to the daily level, applies the model to estimate the energy performance of hypothetical NZERTFs located in different cities in the Mixed-Humid climate zone, and compares these estimates to the results from already existing EnergyPlus whole building energy simulations. This regression model exhibits agreement with EnergyPlus predictive trends in energy production and net consumption, but differs greatly in energy consumption. The model can be used as a framework for alternative and more complex models based on the experimental data collected from the NZERTF.
Keywords: net-zero, residential buildings, statistical modeling, whole building energy simulation, regression analysis
1. Introduction
In 2014, roughly 41 % of total U.S. energy consumption came from commercial and residential buildings [1]. The growing concerns about energy consumption in buildings – in particular, residential buildings – have driven an interest in low- and net-zero energy buildings and legislation to increase building energy efficiency. States’ building energy codes continue to increase the energy efficiency requirements across the US, with greater emphasis on performance-based over prescriptive-based requirements. Performance-based building requirements give more freedom to builders while still maintaining energy performance that meets or exceeds the resulting energy performance from prescriptive-based requirements.
In order to determine if building designs reach the target level of energy-efficiency, it is necessary to estimate the energy performance of a building using predictive models and regional weather conditions. Physics-based whole building energy simulation models (e.g., DOE-2, EnergyPlus, or TRNSYS) using one or more years’ worth of weather data are the most common approach to estimate this energy performance.1 However, these models include underlying assumptions and require significant amounts of information in order to specify the input parameter values, including equipment performance specifications across a variety of conditions. The performance specifications supplied by manufacturers are based on standard test procedures (specific temperatures, loads, etc.) that rarely represent the conditions under which the equipment operates once installed. The combination of varying weather conditions and integrated design considerations may be difficult to model using simulation models. Even when detailed information is available to a simulation modeler to define these inputs using post-occupancy equipment performance and occupant activity, the modeling software may not be able to accurately predict energy performance as a result of capabilities, or lack thereof, built into the software. Issues due to capability limits in these simulation models are more prominent when modeling low- and net-zero energy building designs, which often incorporate emerging technologies, new processes and techniques, and renewable-based energy production systems.
An alternative approach to test the performance of a building is to develop a predictive regression model using post-occupancy data that can accurately predict energy consumption and production based on a few common weather-based factors. A specific building design should perform similarly for two days that have the same weather conditions and similar occupant activity. Assuming that occupant activity is relatively stable, a regression model based on measured data should be able to predict energy performance of this building design for a given day as long as the weather conditions are similar to those during the data collection timeframe (i.e., locations within the same climate zone). The statistics-based model estimates can be compared to validated energy models of the same building to determine similarities in the results. If the regression estimates match the simulation model results, then the regression model could be used in lieu of the simulation software to estimate performance for different weather conditions, either due to seasonal variations at the building’s location or for different locations across the same climate zone while potentially requiring less information.
Completing such a model and comparing its performance to that of a simulation both require detailed specifications for a building’s design combined with post-occupancy energy performance data and simulation models developed to predict that building’s design. The National Institute of Standards and Technology (NIST) constructed a Net-Zero Energy Residential Test Facility (NZERTF) in order to demonstrate that a net-zero (NZ) energy residential design can “look and feel” like a typical home in the Gaithersburg area while creating a test facility for building technology research. This facility includes extensive collection of data on the building’s energy use and on-site renewable energy production. The NZERTF design includes a 10.2 kW solar photovoltaic array mounted on the roof, a solar water heating system, energy efficient wall and roof designs, energy efficient appliances, as well as a heat recovery ventilation system [2]. Data collection and simulation of occupants is automated and includes a weekly schedule of routines based on a family of four [3]. Table 1 provides the full specifications for the NZERTF design.
Table 1.
Specifications of NZERTF
| Building Category | Specifications | Details |
|---|---|---|
| Windows | U-Factor | 1.14 W/(m2K) (0.20 (Btu/h)/(ft2F)) |
| SHGC | 0.25 | |
| VT | 0.40 | |
|
| ||
| Framing and Insulation | Framing | 5.1 cm × 10.2 cm − 40.6 cm OC (2 in × 6 in − 24 in OC) |
| Exterior Wall | RSI−3.5 + 4.2 (R-20+24*)† | |
| Basement Wall | RSI−3.9 (R-22*)† | |
| Basement Floor | RSI−1.76 (R-10)† | |
| Roof | RSI−7.9 + 5.3 (R-45+30*)† | |
|
| ||
| Infiltration | Air Change Rate | 0.61 ACH50 |
| Effective | 1st Floor = 98.8 cm2 (15.3 in2) | |
| Leakage Area | 2nd Floor = 90.2 cm2 (14.0 in2) | |
|
| ||
| Lighting | % of Efficient Lighting | 100 % efficient built-in fixtures |
|
| ||
| HVAC | Heating/Cooling | Air-to-air heat pump (SEER 15.8/HSPF 9.05) |
| Outdoor Air** | Separate HRV system (0.04 m3/s) | |
|
| ||
| Domestic Hot Water | Water Heater | 189 L (50 gallon) heat pump water heater (COP 2.33) |
| Solar Thermal | 2 panel, 303 L (80 gallon) solar thermal storage tank | |
|
| ||
| Solar PV System | System size | 10.2 kW |
|
| ||
| Thermostat Set Points | Temperature | 21.11°C (70°F) for heating |
| Range | 23.89°C (75°F) for cooling | |
Interior + Exterior R-Value
Minimum outdoor air requirements are based on ASHRAE 62.2-2010
Units: m2K/W (ft2F/(Btu/h)
The initial year of demonstration for the NZERTF (referred to moving forward as “Round 1”) has been completed and successfully met its net-zero goal of producing as much or more energy as it consumed over the entire year (July 1, 2013 through June 30, 2014). The data collected during Round 1 was used to adjust and validate both an EnergyPlus (E+) and TRNSYS whole building energy simulation developed for the NZERTF [4, 5]. The plethora of information on the NZERTF makes it an ideal case for generating a predictive regression model that can then be compared to an existing simulation model. A brief overview of E+ can be found in Crawly et al. [6].
This article uses the NZERTF database for Round 1 to develop and validate a parsimonious regression model that can accurately predict the energy performance of the NZERTF using only the most important daily weather conditions, applies the model to estimate the energy performance of the NZERTF as though it were located in different locations throughout the Mixed-Humid climate zone2, and compares these estimates to the results from comparable E+ whole building energy simulations. The regression model will serve as a framework for alternative and more complex models based on the experimental data collected from the NZERTF. As more data are collected from the operation of the NZERTF with varying building systems (e.g., heating and cooling system configurations) and operation approaches (e.g., set points and occupancy) or from similar test facilities, the model can be generalized and expanded to account for these additional parameters.
2. Literature Review
The validated E+ model has been used in sensitivity analysis related to a number of parameters, including weather conditions. Kneifel, et al. [8] noted that changing the location of the NZERTF over a relatively small geographic space resulted in large differences in energy predictions. Larger heating and cooling loads due to a more northern or southern latitudinal positioning quickly drove up consumption, while areas with similar weather bands had different net productions due to variations in solar radiation [8]. The impact of weather on simulation results is further illustrated through an analysis of the use of Typical Meteorological Year 3 (TMY3) data [9]. A typical meteorological year is determined using a statistical approach to create the most representative weather year from a collection of actual weather data. For TMY3, the most recent TMY data, 34 years of weather were used. Their research, focused on TMY3 data and actual meteorological year (AMY) data from Gaithersburg Maryland, found that the use of TMY3 data can lead to misleading results in estimating building energy performance when comparing long-run average estimates of the 34 years of AMY data with TMY3 data. The consumption determined through the use of TMY3 data in simulations underestimated consumption 76 % when compared to the use of AMY data. On the solar PV production side, the model consistently overestimated energy production. The combined effect can possibly lead to overly optimistic net consumption predictions [9].
The use of statistical models in predicting building energy use is common. Several methods were developed as part of the first and second “Energy Predictor Shootout” through ASHRAE [10]. In both cases the goal was to make hour by hour energy use predictions for large buildings using historical data. A common theme among those who placed highest in the contests was the use of artificial neural networks (ANN). Artificial neural networks are a form of machine learning meant to mimic how the human brain perceives patterns and makes predictions from them. They can be extremely complex in nature, involving large numbers of nodes and multiple layers. A sufficiently defined ANN can approximate any continuous function provided it is defined on a closed and bounded set. Both MacKay [11] and Dodier and Henze [12] implemented ANNs in winning the second and first Energy Predictor Shootouts respectively. In general, most attempts at energy modeling using ANN have been at the hourly level [11–13]. Kalogirou and Bojic [14] applied an ANN to a solar passive building, achieving a coefficient of determination of 0.9991 when completely unknown data were fed into the network. The use of ANN in modeling solar photovoltaic (PV) applications is also common [14–20].
Yang, et al. [16] notes that standard regression techniques are beneficial for predicting energy uses for longer periods of time, e.g., days or months, but fail when applied to hourly measurements. For example [21] applied a multivariate regression model to building energy consumption at the daily level. Problems with multicollinearity and autocorrelation complicate regression at the hourly level where more explanatory variables warrant consideration. Time series forecasts, such as autoregressive (AR) models or autoregressive integrated moving average (ARIMA) models are commonly employed to handle autocorrelation and, in the case of ARIMA, seasonality [16].
Others have used regression models in the realms of energy consumption as well as solar PV generation and energy demand modeling [16, 21–31]. The most recent research in residential applications is the work of Fumo and Biswas [32], which reviewed the use of regression analysis for building energy consumption in current literature. While regression analysis on datasets is by no means a new concept, Fumo and Biswas [32] provides a comprehensive overview of the general theory and practical application of it in residential energy consumption. Their work does not consider the production side of residential energy use, however, assuming no on-site generation. Of particular interest is the assertion that future residential energy modeling could be done on an individual building basis as a result of the proliferation of smart meters [32].
Most energy consumption models, statistical or otherwise, focus on weather variables. Amiri, et al. [33] however utilized a regression approach to predict energy consumption indicators for commercial buildings based on construction materials, design features, and occupant schedule. The use of “dummy” variables to facilitate the use of non-numeric inputs into the regression model indicates that regression is flexible enough to handle level based inputs. This finding is further illustrated through the level of accuracy achieved by their model [33]. Various other papers have shown that regression-based approaches provide an accurate modeling technique for building energy related applications [29, 34, 35].
An example of how a simplified model can prove to be extremely powerful is the “Simple” model developed by Blasnik [36]. Blasnik’s model reduces the number of inputs for its energy consumption model to 32 and relies on less operator knowledge than simulation models like E+ that require an extensive number of inputs and an in depth knowledge of home construction. In general, the simple model outperformed the Home Energy Saver model, both full and mid versions, and the REM/rate model in predicting energy for an existing home. Blasnik cites the use of too many inputs, focus on the wrong building aspects, and poor assumptions as some of the deficiencies in the more complex models. When the more complex models were applied to newer homes they exhibited an improvement in predictive accuracy, mainly due to higher R-values and lower rates of air leakage [36].
3. Methodology
The model developed for the NZERTF was chosen to be the simplest possible model that had some accuracy in predicting its net energy consumption. A model of the daily net consumption was the primary goal, ideally with one variable modelling the energy produced and one variable modeling the energy consumption.
It must be stated that the developed model was intended to be predictive, not explanatory, in nature. While some explanatory results were identified the model is not meant to describe the underlying physics of the NZERTF, nor could it be expected to, given the explicit effort to reduce the model’s complexity based solely on computational convenience. Development and verification of such a predictive model produces two primary benefits: 1) It establishes that a regression model could serve as a viable alternative to a physics-based model provided the necessary weather and performance data are collected and 2) It establishes a baseline for comparing the NZERTF performance under different conditions, such as year-to-year weather variability, different operational profiles, or alternative heating and cooling equipment.
Daily averages or sums, whichever was more appropriate for the variable in question, were used for modeling purposes. Daily values negated most of the autocorrelation that exists at the hourly level, removing the need for auto-regressive modeling techniques. As noted in the literature review, artificial neural networks (ANN) are commonplace in building energy prediction, however the goal herein is to use the simplest justifiable model. If an ANN model can be avoided while still achieving accuracy there is no reason to add the associated complexity.
3.1. Data Collection from the NZERTF
Operation of the NZERTF is controlled and monitored by a team of researchers at NIST through a data acquisition and control system. Based on the narrative of occupant activity, devices are remotely energized each day of the week at specific times to emulate occupant heat and moisture loads as well as appliance, water, lighting, and plug load use. The instrumentation installed in and around the NZERTF measures weather conditions and the building’s energy and thermal comfort performance. Data are collected at intervals of 3 seconds or 60 seconds depending on the specific measurement. The authors manipulated data on hourly weather conditions (solar insolation, outdoor dry bulb (ODB) temperature, and relative humidity), electricity consumption (building-wide as well as system-specific values), and electricity production into daily average values (or total values when appropriate) for use in this analysis.
Only one year of data was available for the analysis. The NZERTF operates and collects measurements in real time, meaning a full year of data requires a full year of measurements under identical operation. In order to make the most efficient use of the facility, operating conditions were changed from year one to year two, making year two’s data representative of a fundamentally different process. In future analysis, systems are going to be tested in smaller time frames to obtain more system specific data. The nature of the operation of the facility meant that the year one data was the only set that existed for the specified operating conditions. Thus, using only one year of data was a requirement imposed by the NZERTF operation. This did present issues in the analysis. First, having full data from more years would provide a better validation set than the partitioning that was done to create the validation set described later in the analysis. Second, it was unlikely that the single year used provided a full development of the extreme weather conditions for the area.
3.2. Initial Data Analysis
Prior to model development, the NZERTF Round 1 data were analyzed to identify any apparent trends that could determine explanatory variables and correlations that need to be addressed. Part of this procedure involved identifying any data points within the set that needed to be censored. The censoring of data points was based on three conditions; (1) missing hourly data, (2) instrumentation or equipment errors, or (3) snow cover on the solar PV array. The first two points are self-explanatory however the snow cover requires clarification. The solar insolation measurements related to the solar PV system are collected by a reference cell located on the roof next to the PV array. After snowfall, the reference cell has a tendency to clear before the solar PV array, causing measurements of solar irradiance to be higher than the amount of sunlight actually reaching the PV array. By removing days with snow cover the model is implicitly conditioned on snow cover as a variable. In total 313 days out of the 365-day test period were available for modeling after censoring, which will be referred to moving forward as the “dataset.” The NZERTF Round 1 data contain a large number of variables related to power and energy use, weather conditions, solar PV output, and thermal energy loads for the NZERTF. Pruning the data required first identifying the most important variables in modeling energy performance of the structure. Based on knowledge of the building’s operation, it was determined that the weather variables would have the greatest impact on the overall energy use, and would be the most commonly available data for other years and locations. Specifically, the temperature and plane of array (POA) solar irradiance were selected as they drive the HVAC system and solar PV production, respectively. Another identified factor was the “Day of Week.” Each day of the week has a unique schedule that is followed by the simulated occupants and, therefore, impacts energy consumption.
Table 2 lists all potential explanatory variables considered for initial modeling purposes: outdoor dry bulb temperature (ODB), relative humidity (RH), POA solar insolation (INS) calculated from POA solar irradiance, and day of the week (DoW). All NZERTF database variables are reported at the hourly level.
Table 2.
Potential explanatory variables aggregated to daily values
| Variable | Daily value representation | Abbreviation | Units |
|---|---|---|---|
| Outdoor Dry Bulb Temperature | Average | ODB | °C |
| Relative Humidity | Average | RH | % |
| (POA) Insolation* | Sum | INS | Wh/m2*** |
| Day of Week** | N/A | DoW | unitless |
POA insolation is calculated using the POA irradiance from the NZERTF database
Day of week treated as an index variable, not included in initial model
Units: Watt-hours per meter squared
However, detailed information on daily occupant activity variation is rarely readily available in practice, and is thus excluded from the model in this paper. Proxy data for this factor may become available as smart meters proliferate and databases of energy usage for specific houses can be built up. Future work will determine whether occupant behavior variation during the week has a meaningful impact on the predictive power of the model.
The formula for net energy consumption in Watt-hours (Wh) is given in Eq. 1.
| (1) |
Total energy consumption is not explicitly measured in the NZERTF, though it can be calculated using Eq. 2 and its specified inputs. As before all variables are converted Wh.
| (2) |
A visual inspection of the variables served as an initial analysis. All plotting was done at the daily level for the dataset. Figure 1 contains plots from the visual analysis including Production versus INS, Consumption versus ODB, and Net Consumption versus both INS and ODB. Due to the large number of plots in the analysis those exhibiting weak or no trends are omitted.
Figure 1.
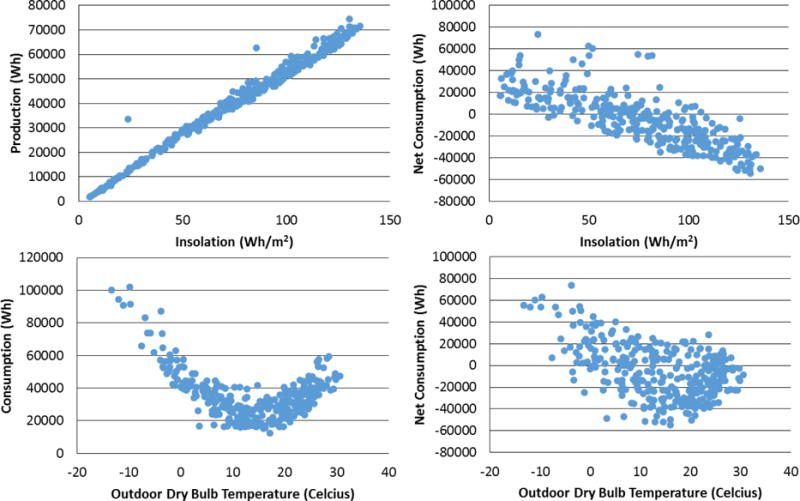
Scatter plots of key NZERTF database explanatory variables with predictor variables
The plots in Figure 1 provided insight on which variables are worth considering in developing the model. Insolation has a strong linear correlation with production and a noticeable linear trend with net consumption. Outdoor dry bulb temperature exhibits a non-linear trend with consumption. ODB’s relationship with net consumption is less clear, however, there appears to be a central band within the data that follows a nonlinear trend. Relative humidity (not pictured) had the weakest relationship with net consumption. There is positive dependence between RH and net consumption but the form is difficult to discern.
Figure 2 plots insolation versus ODB as a check for correlation. There is a very weak trend in the plot and the linear correlation is only 0.163. The clear non-linear trend in the Consumption versus ODB plot implied a polynomial fit would be more appropriate, requiring higher orders of the ODB variable be used. Based on its weak correlation, RH was excluded from the analysis. The omission of relative humidity from initial consideration does not imply it has no impact on net consumption. Higher RH will lead to additional operation of the dehumidifier in the NZERTF, which will contribute to total energy consumption. The applicability is limited though, as the dehumidifier only operates when the RH level on the 1st floor of the NZERTF exceeds the maximum allowed relative humidity level of 50 % at the same time the heat pump is not operating in cooling mode. A cursory analysis of how inclusion of relative humidity affects the regression model was performed, and it was found to have little impact in the parsimonious context of the current model. A more in depth investigation of the effects of relative humidity and whether or not the addition of relative humidity to the model is statistically significant (s-significant) or warrants any increased complexity is left to future research.
Figure 2.
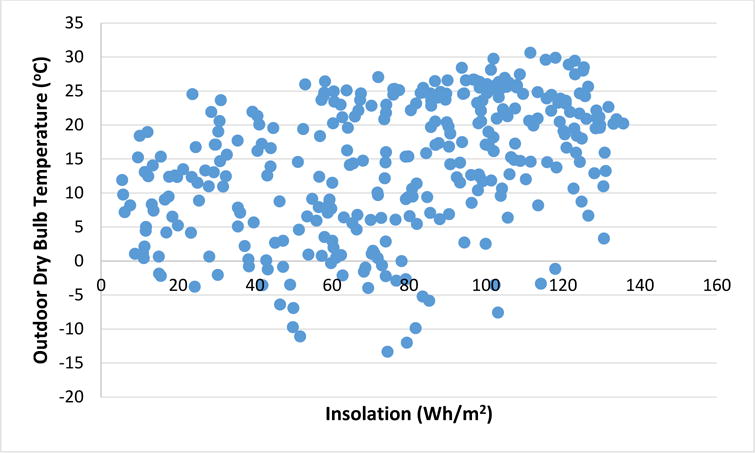
Scatterplot of insolation versus outdoor dry bulb temperature
Thermal mass can impact both the magnitude and timing of heating and cooling energy consumption. The thermal mass of a structure leads to autocorrelation between certain environmental variables and building energy consumption. The autocorrelations related to thermal mass tend to be most prevalent over a time frame of hours rather than days. As such, autocorrelation at the daily level should be less prominent.
Therefore, the parsimonious model herein will exclude autocorrelation effects – however, future models will examine if lagged variables improve the model.
3.3. Model Development and Diagnosis
Before fitting a model of any type, the dataset is partitioned into a training set and test set. Overfitting was not an immediate concern, but the lack of an available test data set posed a challenge. There is only a single year’s worth of data under the given operating conditions used in the dataset so fitting to all Round 1 data would leave no means to determine predictive power. The training set was chosen to be the first two weeks of each month, leaving the test set as all remaining days. By using data for the first two weeks of each month for the training set, conditions from every month, and therefore every season, were represented in the model. Any censored data in the training set was not replaced with another data point from the month. In total the training set consisted of 140 data points out of the 313 available.
Using the plots in Figure 1, the relationships of insolation and ODB temperature with net consumption could be estimated. Insolation has a strong linear relationship with production that should dictate its relationship with net consumption. Likewise, a polynomial relationship can be inferred from ODB temperature’s relationship with consumption.
Models were regressed to the training set using multivariate linear regression and the least-squared error principle and the standard assumption of a normally distributed error term with a mean of zero. Although powerful, regression does have limitations. Most notable is the regression model can only be used with confidence in the range of the data to which it is fit. It is possible to apply the model beyond the training set, however the confidence and prediction intervals inflate rapidly beyond that point. Worse, while the model fit to the data may be accurate in the data range there is the possibility it changes outside of the range, be it a change in model form, or a limiting value being reached. Thus once beyond the data range to which the model is fit, there is no statistical basis for asserting that the regression is valid or that the predictions from it are significant [37]. For brevity not all of the results from statistical tests performed on the net consumption model are reported. Any instance where a test indicated a possible violation of the assumptions of multivariate linear regression are noted herein.
Regression models were initially fit to the production and consumption data. Fitting to the production and consumption components separately helped guide the form of the regression model for net consumption and identified areas where the model may be lacking in explanatory power. The resulting models, their root mean-squared error (RMSE) and their corresponding correlation coefficient (R2) values are reported in Table 3. The equations in Table 3 represent the final form of the model chosen. This form was arrived at by adding variables incrementally to determine whether or not a variable, and any additional explained variation a variable produced, were s-significant. Multiple combinations ODB powers were analyzed using sum of squares techniques before deciding on the final model.
Table 3.
Summary of models for net consumption components
| Variable | Model | R2 (adjusted R2) | RMSE (Wh) |
|---|---|---|---|
| PROD | PROD = 520.68 * INS | 0.997 (0.997) | 2462.8 |
| CONS | CONS = 46666 − 3250.8 * ODB + 116.97 * ODB2 | 0.753 (0.749) | 6726.7 |
The production model has an extremely strong linear correlation, while the consumption model has considerably more unexplained variation. Considering the larger scatter in the consumption data it was expected to have higher uncertainty. An analysis of variance (ANOVA) was performed on both regressions and found them to be s-significant (p<0.001). All regression coefficients were found to be s-significant as well (p<0.001).
It is possible to infer a physical reasoning for the forms of the models. For instance, the solar PV system of the NZERTF operates at a roughly constant conversion rate of insolation to electricity even under different conditions. This constant conversion rate can be viewed as the slope of the line, meaning one additional Wh/m2 in the average insolation for a day produces and additional 520.68 Watts of electrical power. The consumption model is primarily driven by the HVAC system. As the temperature deviates from the balance point, the HVAC equipment will operate more often and at a higher capacity, which also correlates with lower performance efficiency. However, the complex physics associated with a system of integrated systems, such as a house, cannot be easily articulated in a condensed explanation. A full investigation of the physical factors driving the form of the regressed equations, while interesting, was beyond the scope of the analysis. Instead the focus was on whether the simplified empirically derived model had predictive power comparable to commercially available software. It is therefore acknowledged that it the model is not intended to be, nor likely to be, a true model of the physical relationships governing the NZERTF. Instead it is a statistically defined predictive relationship between the net consumption data from the NZERTF to the weather data from the NZERTF.
Care needed to be taken in use of the production model. The solar PV system does have a maximum output it can produce based on a multitude of factors including the inverter, solar module type, system size, and how the system is wired. Although that maximum is not reached for the NZERTF, or any of the applications of the model later in this paper, it is vital that the production model be applied, and corrected when necessary, with knowledge of its maximum output. There is also a theoretical maximum consumption based on how much power the NZERTF can draw before the circuit breaker trips. The controlled operation of the NZERTF and energy efficiency measures it uses ensured that limit was never reached for the dataset.
A rigorous analysis on the production and consumption models was foregone, as their development was meant to guide the variables to include in the net consumption model, and identify where major sources of uncertainty exist.
The basic form of the net consumption model is given in Eq. 3. Performing a least squares regression yielded the fitted model in Eq. 4. The R2 value for the regression is 0.895 (adjusted R2 = 0.893) and the root mean square error is 7284.1 Wh.
| (3) |
| (4) |
It must be noted that the standard limitations of regression apply to Eq. 4, most notably that the model is only valid for the specific process it was fit to, and only in the range of the data that was used to calibrate it. As a result, Eq. 4 can only be considered valid for a structure operating identically to the NZERTF in the range of ODB and INS found in its associated weather data.
ANOVA results, see Table 4 and Table 5, indicates the regression and all coefficients were s-significant at a 5 % level of significance. Examining the confidence bounds in Table 5 reveals that the coefficients for the separate production and consumption models are all within the confidence interval of the coefficients of Eq. 4. This suggests that the difference between Eq. 4 and the models in Table 3 is not s-significant. Thus simply adding the individual production and consumption models could produce a model that would be statistically indistinguishable from the net consumption model. An F-test indicates the hypothesis that the coefficients of Eq. 4 are not equal, simultaneously, to the coefficients of the models in Table 3 is statistically insignificant (p = 0.146). Such a finding illustrates the independence of the production and consumption sides of the model. This independence is beneficial in that, when determining the range of data over which the regression model is valid, the ODB and INS ranges can be established independent of each other, instead of being based on their combination.
Table 4.
ANOVA table and regression statistics for net consumption regression model
| Degrees of Freedom | Sum of Squares | Mean Square | Estimated F-statistic | p-value | |
|---|---|---|---|---|---|
| Regression | 3 | 6.14 × 1010 | 2.05 × 1010 | 385.59 | 2.78 × 1010 |
| Residual | 136 | 7.22 × 109 | 53058011 | ||
| Total | 139 | 6.86 × 1010 |
Table 5.
Regression statistics for net consumption least squares regression
| Variable | Coefficient Values | Standard Error | t-statistic | p-value | 95 % Lower Confidence Interval | 95 % Upper Confidence Interval |
|---|---|---|---|---|---|---|
| INS | −547.48 | 20.27 | −27.02 | <0.001 | −587.55 | −507.40 |
| ODB | −3085.09 | 172.55 | −17.88 | <0.001 | −3426.31 | −2743.86 |
| ODB2 | 116.22 | 6.66 | 17.44 | <0.001 | 103.04 | 129.4 |
| Constant | 45 486 | 1652.41 | 27.53 | <0.001 | 42 218.27 | 48753.73 |
Residuals plots are given in Figure 3. These plots are generated by first determining the errors between the individual model-predicted net consumption versus the actual net consumption for the training set, referred to as the residuals. Residuals are plotted against the predictor variables used to generate them one at a time. A proper least-squares model should show no trend in the residuals and a constant variance over the range of the predictor variables.
Figure 3.
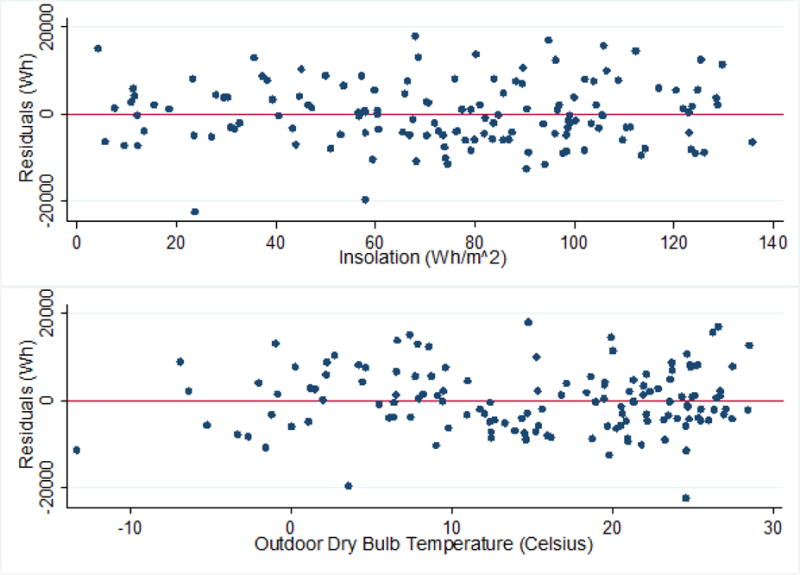
Residual plots for net consumption model
All assumptions required for least-squares regression are met, however the current training set corresponds to only one possible partition of the dataset. Changing the training set has the potential to alter the regression results, as well as the results of any hypothesis tests. These concerns are addressed later in the analysis.
3.4. Model Validation
Testing of the net consumption model was completed by predicting the test data set using the fitted model and comparing the results to the actual net consumption. Figure 4 plots the reported daily net consumption against the model predicted net consumption for the test set. The black line represents perfect agreement between the model-predicted net consumption and the actual net consumption. In examining the plot, the key observations are: (1) the data tends to follow the line of perfect agreement; (2) the scatter around the line of perfect agreement tends to be within a well-defined range; (3) there are clusters of data indicating the model may be consistently under-predicting net consumption in some ranges; and (4) there may be a tendency to over-predict net consumption at larger values, though there are less data in that region to substantiate the claim. It was decided to continue the validation of the model, acknowledging observations 3 and 4 suggest a potential issue with the model. As the model was meant to be parsimonious in nature, some loss of predictive power was to be expected.
Figure 4.
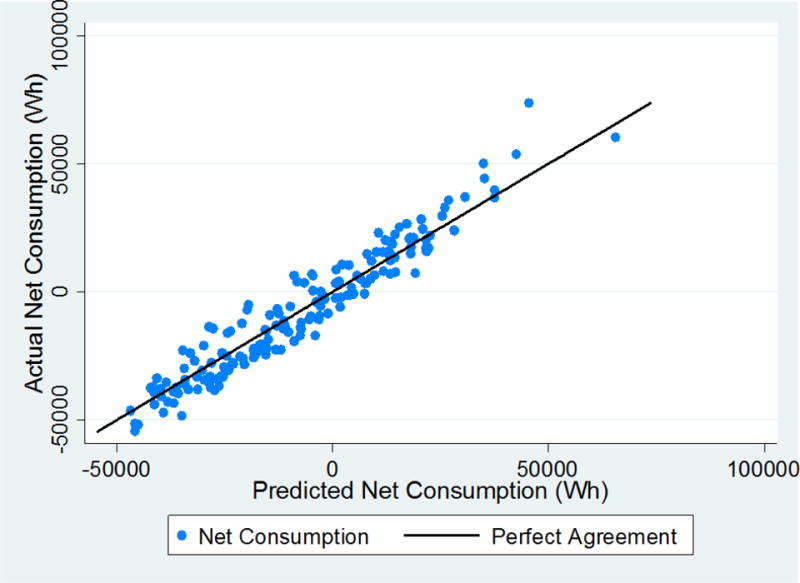
Plot of predicted net consumption versus actual net consumption
Another check of the model was to determine how accurately it predicts a net-zero day. Probit or logistic regression is generally used for binary outcomes. However, if the net consumption model is accurate it should be able to predict the sign of daily net consumption correctly for the test set on a consistent basis. Out of the 173 days used in the test set the model accurately predicts whether or not the day will be net-zero (negative net consumption) 159 times. This result corresponds to a 92 % accuracy in predicting the test set. The accuracy on the training data is 125 correct net-zero predictions out of 140 days (89 %). Figure 5 plots the net-zero boundary along with the actual data points from the NZERTF test set, which shows that a greater level of solar insolation is required for more extreme ODB conditions (hot or cold). The boundary was created by selecting a value of ODB and determining the minimum insolation required to achieve net-zero according to the model.
Figure 5.
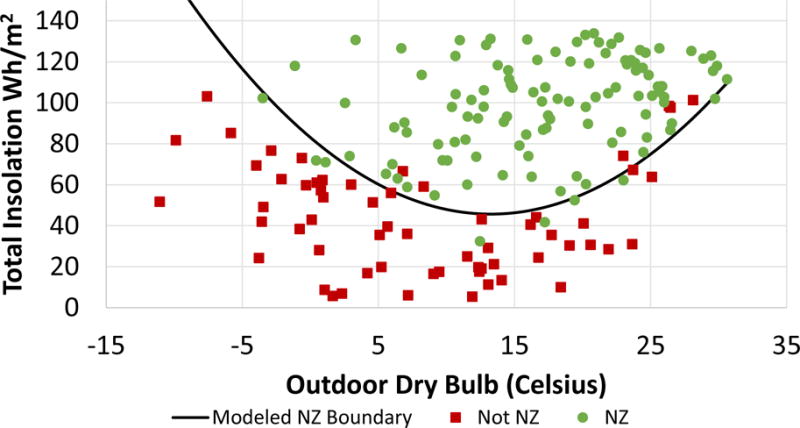
Plot of net-zero (NZ) boundary as predicted by the model
Figure 5 indicates that the model does a fairly good job at defining the net-zero envelope for the house. The non-net-zero days above the envelope in the higher ODB range may be due to relative humidity effects not accounted for in the model. In the lower ODB range it appears that the envelope is too “steep” to account for colder temperatures. Issues with limited data at the extremes of the temperature ranges makes predicting behavior in said regions difficult. The heating and cooling cycles also do not operate at the same rated efficiencies. Therefore, a segmented regression model may be better suited to account for the apparent deviation in lower temperature ranges.
A measure of uncertainty in the model is achieved through calculation of the prediction and confidence intervals on the regression. The confidence interval for a regression line is the likely range of the mean response given specific predictor variables. The prediction interval on the other hand is the likely range of a new observation given specific predictor variables. Prediction intervals include uncertainty from estimating the population mean and uncertainty due to scatter in the data, whereas confidence intervals are only concerned with the former. As such prediction intervals are always wider than confidence intervals for the same set of predictor variables.
Due to the three dimensional nature of the model, confidence intervals become hard to visualize for all scenarios. As net-zero performance is the primary goal, the confidence interval on the net consumption regression when the net consumption is zero is more meaningful. Figure 6 plots the confidence and prediction intervals for daily net-zero conditions, where the daily average insolation is set to whatever value is required to achieve net-zero for the ODB on the x-axis, in the same way the envelope in Figure 5 was determined.
Figure 6.
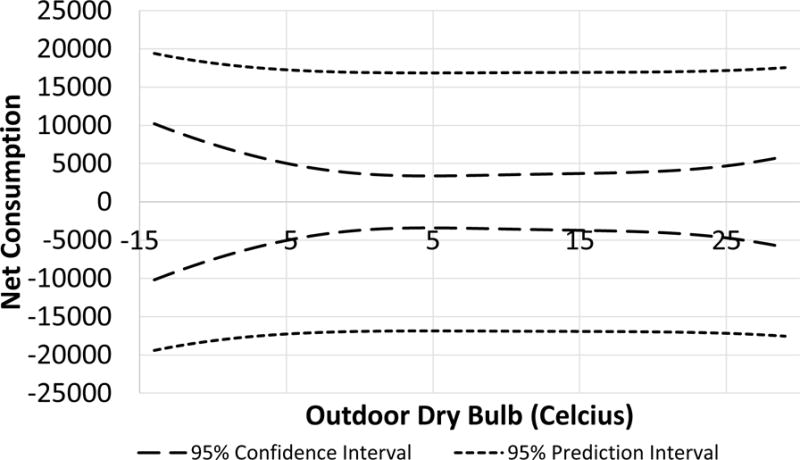
Confidence and prediction intervals on net-zero conditions
The prediction interval is wide due to the large amount of uncertainty on the consumption side of the model. The confidence interval however is relatively tight, indicating a large difference in the uncertainty of the mean response compared to that of a forecasted value.
It is important to note the model up to this point is based only on 140 points out of the data set. Changing the training set could potentially produce different results, especially considering that the initial training set was chosen arbitrarily. To get an understanding of how changing the training set affects model parameters, a bootstrap method was implemented. The bootstrap used here was designed to help alleviate the issue of the arbitrary definition of the training set. To do so 5000 random training sets were generated from the dataset by pulling 40 % of the usable days from each month. A regression model was fit to each random training set with the form in Eq. 3. The 95 % parameter confidence intervals were obtained as shown in Table 6. Note that confidence bounds are sensitive to the size of the training set as well as the individual data points it contains.
Table 6.
Bootstrapped 95 % confidence bounds for model parameters, based on percentile rank, from pulling 5000 random training sets of 40 % of the usable data points in the dataset
| Variable | 95 % Lower | 95 % Upper |
|---|---|---|
| INS | −608.17 | −546.59 |
| ODB | −3506.1 | −2840.9 |
| ODB2 | 107.23 | 131.89 |
| Constant | 44 863 | 50 572 |
The parameters for the initial model all fall within the bootstrapped confidence intervals, though the INS coefficient is at the very edge of the upper bound. Equation 5 provides the model fit to the entire dataset using multivariate least-squares regression. Equation 5 has little utility by itself, since it is impossible to validate it against a test set. It is useful in understanding how the 40 % validation set bootstrapped regressions compare with a model that uses all available data in determining the regression.
| (5) |
It should be noted that the Shapiro-Wilks test for most of the bootstrapped samples and the full fit to the dataset violate the assumption of normality of residuals. Linear regression is somewhat robust against such violations; however, it still calls into question the validity of any ANOVA tests on regressed models.
Since the original training set did not violate the normality assumption its results are still valid. The bootstrapped confidence intervals in Table 6 are based on percentile rank, and therefore are valid regardless of the underlying distribution. The bootstrapped regression parameters do not differ from those of a robust least-squares regression, indicating the violation of non-normality is likely not a major issue.
The coefficients of Eq. 5 are all within the 95 % confidence bounds of the bootstrap intervals, indicating that partitioning the data set did not have a significant impact on the nature of the predicted trend. Therefore, the partitioned data models can be used to predict daily net consumption with confidence, enabling the use of bootstrapping with the 5000 regression models that generated Table 6. After considering all of the evidence acquired through the validation process it was decided to continue with the model while remaining aware of its potential faults.
An investigation of the model’s predictive capabilities outside the training data set to which it was fitted and the validation set it was tested against was also vital. In order to have any use as a comparison tool, the model needs to exhibit some forecasting utility to be compared with more complex models. Otherwise it becomes difficult to examine the tradeoffs between model complexity and predictive accuracy.
Ideally it would have been possible to prove the form of Eq. 4 using a physics-based approach. Unfortunately, the complex interactions of systems, interfaces, and occupancy behavior meant simplifying the physical equations down to a single equation with the same limitations on variables was unrealistic. Utilizing physics-based models from available software to prove the model form was also infeasible, as they are either given as a “black-box” where the underlying equations and assumptions are unknown, or do not simplify down to a single simple equation. Instead, in order to show compatibility with physics-based predictions, the regression model was compared to the results of a well calibrated physics-based model. As previously noted there is only one year of data under the operation conditions that generated the data used in the regression, so comparing prediction from the model to a second year of output from the NZERTF was also impossible.
4. Model Based Predictions
Using the fitted model to predict net consumption for varying weather conditions and comparing them to simulation results for those conditions helps identify the level of predictive power in the model. At issue is the model is fitted to data specific to the NZERTF and its location in Gaithersburg, Maryland. In order to achieve a basic estimate, the model was used to predict net consumption using TMY3 data from Gaithersburg, MD and other locations with a similar climate and comparing those results to simulated values from E+. EnergyPlus is chosen over other energy models in order to leverage previous work on the NZERTF.
The analysis consisted of: (1) comparing the net consumption regression model, defined by the 5000 bootstrapped regressions previously developed for Table 6, applied to the NZERTF using actual weather data for the year that the Round 1 consumption data were collected; and (2) using TMY3 data for 42 locations in the Mixed-Humid climate zone to obtain the E+ and regression model estimates of net consumption, total consumption, and total production for each location and develop Kriging maps for comparison. Kriging is a method of interpolation where values are interpolated via a Gaussian process directed by prior covariance values. The purpose of each analysis is to apply the regression model to some reference to understand the predictive power of the parsimonious model.
4.1. Assumptions
Table 7 lists all assumptions for the model based predictions.
Table 7.
Summary of assumptions for using the model to predict net consumption for a year
| Assumption | Notes |
|---|---|
| 1. The fitted model sufficiently predicts mean response. | The potential biases noted in Figure 4 and loss of normality in the residuals could weaken this assumption. If there are a large number of days in regions where the potential prediction biases exists the results could be skewed. |
| 2. A calendar year contains a sufficient number of days for mean response to overcome prediction variability. | Aggregating a daily model over a year’s worth of predictions inherently increases uncertainty in the summed value. Confidence intervals on the sum can easily inflate to absurd widths. If assumption 1 and 2 hold, the resulting sum should be somewhat representative of the mean yearly total. |
| 3. The E+ results are sufficiently accurate to serve as a basis for comparison. | EnergyPlus is a simulation model with its own implicit uncertainty and assumptions. Its results cannot be considered a perfect predictor, however its overall acceptance in practice and vetted physics-based models provide some confidence in its accuracy. |
| 4. TMY3 data is used for all locations. | Issues with TMY3 data are noted in the literature review. However, they are currently the best source of estimated weather data. |
| 5. The Perez model was used in converting TMY3 irradiance data to plane of array insolation data. | Albedo was not used in determining insolation, as some weather files did not contain albedo measurements. |
| 6. The NZERTF house operates identically regardless of location. | Occupant behavior, appliance usage, and thermostat set points are unchanged. |
| 7. The NZERTF construction is identical regardless of location | Building orientation, envelope, materials, and plane of array for the solar PV system are unchanged. |
| 8. All locations are within the Mixed-Humid climate zone, the region the NZERTF is located in and designed for. | This assumption reduces the chance of applying the regression model to conditions outside those it was fit to. It is still possible certain the chosen locations may produce ODB or INS values outside the range of the validation set, increasing uncertainty in their reported net consumptions. |
| 9. Reported values are the result of a bootstrap procedure. The 5000 regressions performed to produce Table 6 were used to predict the yearly net consumption, producing 5000 yearly net consumption values. | This assumption simplified the calculation of confidence bounds on the yearly total of net consumption. As noted the partitioned data sets showed strong agreement with the trend in the full data, lending credence to the reduced data set having roughly equivalent predictive power. |
| 10. Snow cover in the TMY3 files is properly accounted for in determining the irradiance values used in calculations. | Irradiance was calculated through NREL’s System Advisory Model with the option of including effects due to snow cover selected [38]. Doing so should provide appropriate irradiances for the calculation of solar PV generation. |
4.2. Model Comparison for Round 1
The ability of the regression model to predict the actual performance of the NZERTF can be compared to the simulation models (E+ and TRNSYS) developed for the NZERTF by analyzing the estimated and measured production and consumption using the weather data for Round 1. For this comparison, the “un-tuned” TRNSYS model is based solely on equipment rated specifications and data derived performance measurements while the “tuned” model reverse engineers some system specifications to lead to the measured consumption [39].
The E+ model was calibrated using the collected data from the NZERTF where available. This is different from the reverse engineering in the TRANSYS model, in that the E+ calibration was not done to achieve a specific net-consumption result. Instead it used the measured data of each subsystem to determine the actual operating conditions of the equipment and implemented those values as inputs into the E+ model without foreknowledge of what the resulting net-consumption. Thus the “tuned” TRANSYS model explicitly altered performance inputs without concern for the actual performance or rating to achieve a desired result, while the E+ and “un-tuned” TRANSYS models used data-derived performance inputs to determine the result, meaning their results could be compared to the actual NZERTF results as a verification of their physical models. A full discussion on how the E+ model was built and validated can be found in Kneifel [4] and Kneifel et al. [40].
In the case of a hypothetical building, a simulation modeler will not have the measured data available for such adjustments to equipment performance. In such cases the only option would be to use the rated capacities of the equipment. While that was a possible comparison to include for the regression model, it would have been an equal one. The regression model is implicitly based on the actual performance of the equipment and systems, as they define the energy output. For a meaningful comparison between the regression model and the physics-based model it is required they be evaluated on equal terms. As such, the E+ model with performance inputs adjusted based on measured performance data serves as the primary comparison.
The simulation models use the AMY weather file for Round 1 (July 2013 through June 2014) from the KGAI weather station, the closest weather station to the NZERTF (within 4 miles), because simulations require data for many weather variables to complete the estimation [41]. The regression model uses both the KGAI weather data and weather data collected at the NZERTF (referred to as “Site weather data” in Table 8). The KGAI weather data were used to supplement any missing weather data in the site weather data. The close proximity of the KGAI weather station means its weather data should be roughly similar to that measured at the NZERTF.
Table 8.
Measured and predicted performance for Round 1
| Actual net consumption | Regression Model* | E+ Model | TRNSYS Model** | ||
|---|---|---|---|---|---|
| Site weather data | KGAI AMY data | KGAI AMY data | KGAI AMY data | ||
| Total Consumption (kWh) | 12 927 | 13 216 | 13 317 | 12 383 | 12 246 |
| Total Production (kWh) | 13 523 | 13 735 | 13 548 | 13 889 | 13 937 |
| Net Consumption (kWh) | −596 | −565*** | −353**** | −1506 | −1691 |
Mean of bootstrapped net consumption results
“Un-tuned” Model from Balke [39]
95 % bootstrapped confidence bound for 40 % of usable days training set – [−935 kWh, −193 kWh] (based on percentile rank).
95 % bootstrapped confidence bound for 40 % of usable days training set – [−734 kWh, 30 kWh] (based on percentile rank).
For missing actual consumption values of the NZERTF in the NZERTF data base, a five nearest-neighbor search was implemented to populate missing days. The impact on production resulting from snow cover is also accounted for in the model. To achieve the best accuracy, the log on snow cover kept for the NZERTF was examined. The irradiance used in calculations for each day was determined by the percentage of hours the PV system was clear of snow, with linear interpolation over the hours capable of generating electricity used to determine the percentage output in the event the system was gaining or losing snow over time. Light snow or “dustings” of snow had little to no impact on the output, thus the PV system was assumed to have full output on such days. If snow started in the evening or the panels were cleared of snow by morning it was assumed that the time the solar panels were covered was prior to times when they were capable of generating electricity and therefore produced full output. The value used was dependent on what information was available in the log. Any snow cover days where no percentage value was given were treated as having the solar array covered for the full day.
Table 8 summarizes the various Round 1 results. The results for the regression model in the table are the result of a bootstrap procedure. Using the 5000 regression models that determined the values in Table 6, 5000 predictions of annual net consumption were determined. The mean of all of these predictions was taken as the predicted value for each variable of interest. Using all 5000 regressions reduced the reliance of the prediction on a single, arbitrarily chosen training set which may not be the most representative model. Doing so also allowed for the calculation of the annual net consumption confidence intervals without making any assumptions on the underlying distribution of residuals.
Based on Round 1 AMY conditions from the KGAI weather station, including system failures and snow cover, the E+ and TRNSYS simulation models under-predict total annual consumption and over-predict production, leading to greater net production (additional 910 kWh and 323 kWh, respectively) than was measured during Round 1. The regression model leads to estimated consumption and production that is closer (underestimate in net consumption of 31 kWh) to the measured annual performance than the simulation models. These results suggest that the regression model is more accurate at predicting the energy performance of the NZERTF for Gaithersburg, MD when using the KGAI AMY data.
The results in Table 8 are not surprising nor are they a significant indicator of model accuracy or superiority in a global sense. When using least-squares regression, the model biases the mean of the residuals in the training set towards zero, thus the repeated application of the model on the training set should produce a result with a residual value close to zero, with any extreme variation coming only from the test set. While only 40 % of the data were used in the training set, if it is fairly representative of the entire data set then the same bias should exist in the test set as well. The KGAI data is not used to fit the model, however it is also not independent of the data used to fit the model due to their geographic proximity and their variable collection occurred over the same time span. This dependence means that, while the KGAI data is better than the AMY data taken at the NZERTF in terms of comparing for accuracy, the conclusions regarding accuracy that can be drawn from it are limited.
The true takeaway from Table 8 is that the regression model behaves as it should regarding the first two assumptions of Table 7, namely the model appears to be capturing the mean response well, and mean response appears to dominate over the prediction variability for the year. Ideally a second year of data or more statistical output from E+ would have been available to facilitate a more meaningful comparison; lacking them, such an effort was infeasible. Still, given that the E+ model was physically verified using the actual NZERTF in-situ performance data, any similarities between the regression model and the E+ model give reason to believe the regression model is representing the physical realities of the structure well [40]. More evidence would have been beneficial but the noted limitations on the NZERTF output data and the E+ output made that impossible.
While Table 8 does not prove that the regression model is any more accurate than the other models, it should be remembered that the goal was to show that the model had predicative capability similar to that of a physics-based model and was sufficient to serve as a comparison baseline for future NZERTF data. If so, then it would serve as a viable alternative to a physics-based approach while using significantly less input information. While some divergence between the two models exists, Table 8 lends credence to the idea that the regression model may be a viable alternative to a physics-based model when data are available. It must be acknowledged however that the analysis herein shows at most proof of concept, falling short of absolute proof.
4.3. Comparison for Mixed-Humid Climate Zone
This section will analyze the predicted performance of the NZERTF using the regression model across the Mixed-Humid Climate Zone and compare those results to those using the E+ simulation model. As noted in Table 7, Assumption 8 is made to keep the ODB and INS ranges of locations used in the comparison within a relatively similar range. So long as the temperature and insolation values are within the range of the validation set there will be more confidence, however the extremes of the climate zone could potentially see conditions that exceed the validation data, increasing their uncertainty. Results for the climate zone comparison therefore only focus on mean response over a full year, which has less associated uncertainty, per Assumptions 1 and 2. Still it is acknowledged that the climate zone comparison is less certain than the Gaithersburg only comparison, however there is little other alternative to get a broad view for how the regression model results compare to the E+ results. Considering most of the locations within that geographical range have similar ODB and INS ranges to the Gaithersburg analysis most of the interior locations produce results with similar uncertainty to those in Gaithersburg.
There are several results that would be expected when expanding the use of the regression model to predict the performance of the NZERTF in different locations. First, given the results for Gaithersburg, MD, it would be expected that the estimated performance of the NZERTF by the regression model will consistently be higher for total consumption and lower for total production than the simulation model results. Second, the results will vary across the climate zone because, even though the locations are in the same “zone,” the weather conditions will vary significantly from south to north (e.g., Georgia to Ohio) and west to east (e.g., Oklahoma to New Jersey). Third, given that the regression model is based on performance in Gaithersburg, MD, the accuracy of the model to predict performance in other locations would be expected to decrease as the location is geographically and climactically different from Gaithersburg, MD.
The regression model values that were used in the kriging process were the average of the predicted yearly results from the 5000 bootstrapped regressions. Any results from them will have associated confidence bounds on the sum. EnergyPlus does not produce a confidence bound on its results though, so a comparison of model uncertainties was not possible.
The kriging analysis for the consumption, generation, and net consumption results was done in two phases. The first phase involved kriging to the results of the regression model and E+ model separately and comparing the two maps. When comparing the two maps the closeness of their agreement was not considered, instead what was of interest was whether or not any patterns, referred to as “trends” from here on, existed over geographic space. While trends do not indicate the numerical accuracy of prediction or whether or not the models agree in magnitude, they do display whether or not the models agree in how predicted values change over geographic space. In light of this limitation, the kriging bands were determined based on percentile, resulting in intervals with unequal widths and differing bounds between the two maps. Doing so allowed for a comparison of how the largest and smallest values were distributed without losing resolution in the maps due to forcing identical band widths and limits.
Phase two of the analysis is where the agreement of the models was examined. In this phase, and all cases involving the difference between the E+ results and the regression model, the value from the former is subtracted from the value of the latter. By analyzing the maps of the differences the closeness of the estimation can be examined as well as how those differences vary across geographic space.
Figures 7 and 8 show that the regression model and E+ model lead to nearly identical trends. Predicted energy production ranges from 14 023 kWh to 17 644 kWh for the regression model and 14 587 kWh to 18 339 kWh for the E+ model with the lowest production occurring in the northern portion of the climate zone, particularly Indiana, Ohio, and northern Kentucky and the most northeastern states. The greatest production occurs in the western portion of the climate zone (Texas, Oklahoma, and Kansas) followed by the southern ring in the Deep South.
Figure 7.
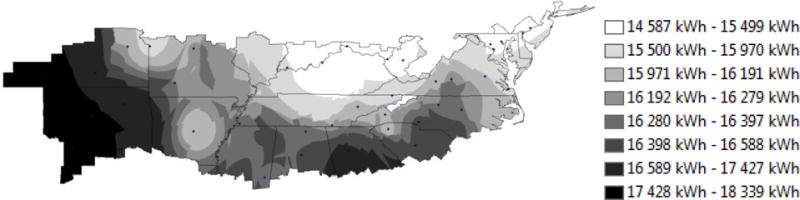
EnergyPlus predicted energy production over the mixed-humid climate zone
Figure 8.
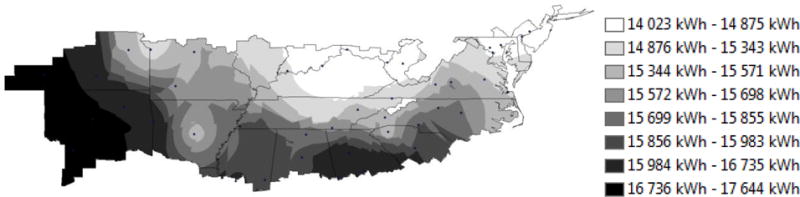
Regression model predicted energy production over the mixed-humid climate region
Figure 9 plots the difference between the two predictions, with an under-prediction by the regression model resulting in a negative difference and an over-prediction by the regression model resulting in a positive difference. The regression model consistently predicts lower production values than the E+ model, which is in line with the expected result. Differences are greatest in the northern portions of the climate region, becoming smallest in the southern states. The consistency of the difference exhibited in Figure 9, and the similarity of the general pattern in Figures 7 and 8 indicate that the disagreement between models is due to a systemic difference in the calculation, and not the general form of the model used for prediction of energy production from the solar PV system. In this case the regression model does not produce the best agreement around the Gaithersburg, MD region. This result is likely caused by the TMY3 data in the Gaithersburg region being different than the AMY data to which the model was fit.
Figure 9.
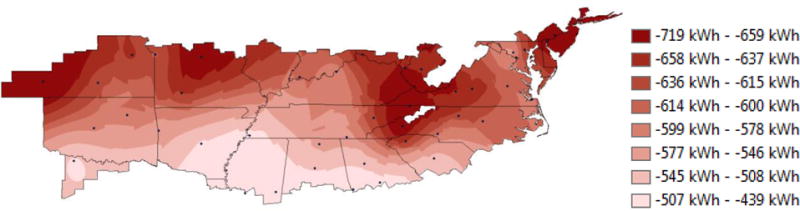
Difference between E+ and regression model energy production over the mixed-humid climate region
Figure 10 and Figure 11 show that the regression model predicts that energy consumption ranges from 11 638 kWh to 14 160 kWh for the regression model and 11 457 kWh to 13 011 kWh for the E+ model. The regression model predicts that consumption tends to increase the further north and west the NZERTF is located. The lowest consumption is in the Southeastern states. The trends in the E+ model predictions differ significantly. The lowest consumption is predicted for the southern Appalachians, western North Carolina and Virginia and adjacent portions of the surrounding states. Consumption generally increases the further west the NZERTF is located until it peaks in Arkansas and Missouri, and then decreases for locations further west. Here the differences in the models are evident. The driving force is likely to be the E+ model considering more variables and utilizing more complex physics-based models. Given the trend in Figure 10; wind velocity, relative humidity, or precipitation effects could possibly be the cause of the deviations.
Figure 10.
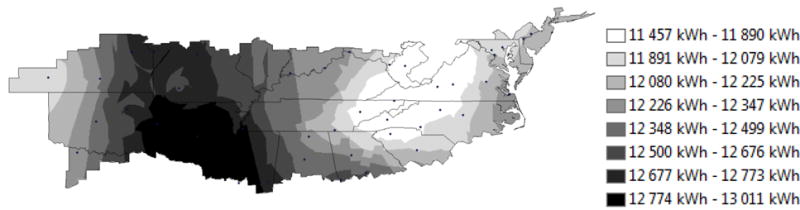
EnergyPlus predicted energy consumption over the mixed-humid climate region
Figure 11.
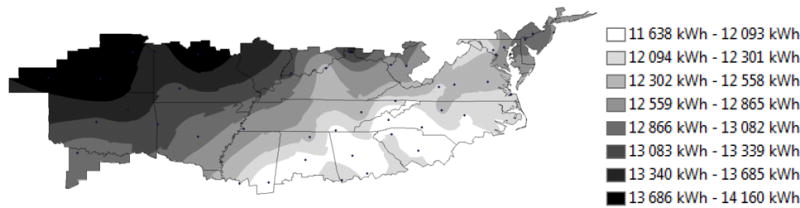
Regression model predicted energy consumption over the mixed-humid climate region
The difference between the predicted consumption based on the regression model and E+ model, see Figure 12, is lowest throughout the white band through the southern states. Relative to this range, the most southern locations result in the regression model predicting lower consumption than the E+ model (up to 856 kWh in the Deep South). Locations in the north and west result in predictions of consumption that are greater than the E+ model (up to 2090 kWh). As expected the regression model consistently over-predicts consumption when compared to the E+ model except for two bands in the Deep South.
Figure 12.
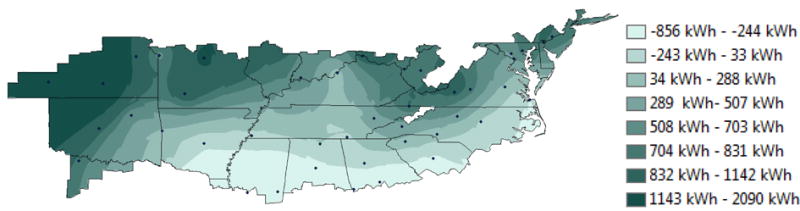
Difference between E+ and regression model energy consumption over the mixed-humid climate region
Figure 13 and Figure 14 display the predicted net consumptions for both models. The net consumption predictions for both the regression model and E+ model are negative for all locations, which means the NZERTF would produce excess electricity and reach net-zero throughout the Mixed-Humid Climate Zone. Similar to total production, the regression model consistently under-predicts the magnitude of net consumption across locations in the climate zone when compared to the E+ results. The regression model net consumption ranges from −740 kWh to −4816 kWh while the E+ model ranges from −2699 kWh to −5831 kWh. Additionally, the trends across the climate zone differ between the two modeling approaches. For the regression model, net consumption is smallest in the southwest and southeast portions of the climate zone while the largest net consumption occurs throughout the northern portions in the central and Midwestern U.S. There appears to be a geographical impact along the Appalachian Mountains. For the E+ model, the smaller net production also occurs in the western portion of the climate zone, but the impact of the Appalachian Mountains is not as apparent. The largest net consumption occurs in northern locations, particularly in the Midwestern and Northeastern States.
Figure 13.
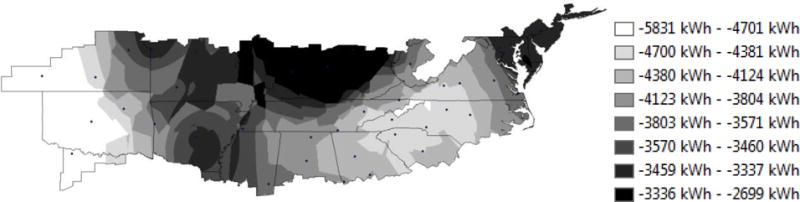
EnergyPlus predicted net energy consumption over the mixed-humid climate region
Figure 14.
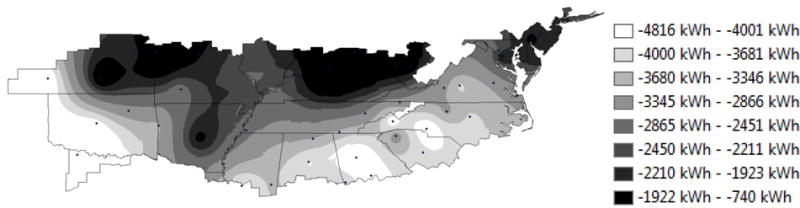
Regression model predicted net energy consumption over the mixed-humid climate region
While the trends do not match as well as production, a few key features of the net consumption trend are displayed by both models. The bulge of higher net consumption in the Midwest, as well as a band of higher net consumption along the Mississippi river are found in both models. A bulge of higher net consumption in the Eastern Great Plains is also picked up, though is more pronounced in the regression model. The Mid-Atlantic States appear to have a similar trend between models as well. The greatest difference occurs in the Southern States. Here an inconsistent distribution of net consumption is identifiable in the regression model, while the E+ model shows a consistent increase in net consumption radiating out from the Carolinas.
Figure 15 presents the difference between the two models. It is evident that the difference in the net consumption follows the same general band pattern as the difference in consumption plot in Figure 12. This result is not surprising given that production follows the same general trend for both models, leaving any differences in trend to be driven by the consumption side. Differences are most pronounced in the north, with little to no difference in predicted net consumption evident in the Deep South.
Figure 15.
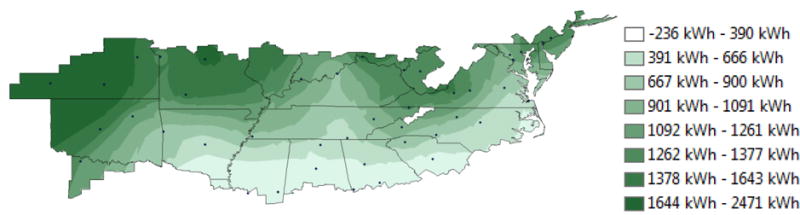
Difference between E+ and regression model net energy consumption over the mixed-humid climate region
In general, the Kriging maps show that the regression model does extremely well at predicting production trends when compared with E+, reasonably well at predicting trends in net consumption, and produces large disagreement in prediction of consumption. Differences are most likely driven by variables considered in the E+ model being omitted in the regression model, as well as differences in the structures of the models themselves. It is impossible to say which method is objectively correct in terms of value or trend however, since no field data exists for the NZERTF design in any other locations.
4.4. Results Summary
The regression model performs well considering its parsimonious nature. Using the data from the KGAI AMY weather file, the regression model predicts consumption and production within 3.0 % and 0.2 % respectively, and net consumption within 243 kWh of net consumption. In comparison, the E+ simulation model deviates from the measured consumption and production by greater than 4.0 % and 2.7 % respectively, and over 900 kWh in net consumption.
Considering the regression model is directly fit to the NZERTF data, the accuracy of the net consumption prediction in Table 8 is unsurprising. What is of more interest are the kriging map results. Although consistently under-predicting as compared to the E+ model, the production kriging maps are near identical in terms of trend. This suggests that the production model is a good representation of the actual relationship between production and plane of array insolation for the conditions under which the NZERTF data were collected. The consumption side is where future modeling efforts need to improve. There is a pattern in the difference between the two results, indicating that the difference is driven by one or more missing factors. If that is the case, the inclusion of more explanatory variables in the model may improve the model’s predictive performance. Overall the net consumption model developed here offers a good baseline for evaluating future statistics based models of the NZERTF data.
5. Conclusion and Future Work
In conclusion, the regression model herein, based solely on daily total consumption and production and daily average solar insolation and ODB temperature values, can predict the energy performance of the NZERTF with accuracy relative to the E+ model. The regression model is more accurate at estimating actual yearly performance in Gaithersburg, MD than the E+ and TRNSYS models while requiring less system performance information, although basic post-occupancy data are necessary to develop the regression model. The regression model is within 243 kWh of measured net consumption while the simulation models are off by 1095 kWh (TRNSYS) and 910 kWh (E+) using the KGAI AMY data. This increased accuracy is due in large part to the regression model being calibrated with in-situ energy outputs from the NZERTF, while the physics-based models were calibrated using in-situ performance of individual subsystems of the NZERTF. A regression model that considers individual NZERTF subsystems, though more complicated, may improve agreement of the models and would be the next step in using regression modeling on the NZERTF data.
Similar to the E+ model, the regression model predicts that the NZERTF design would reach or exceed net-zero energy performance throughout the Mixed-Humid Climate Zone, which includes areas of the country from southern New Jersey to western Kansas to central Georgia. Similar trends in energy production performance are seen between the regression model and the E+ model across the climate zone, with the greatest production in the west followed by the southeast. However, the regression model consistently predicts lower production of approximately 500 kWh to 700 kWh. Trends in energy consumption predictions across the climate zone vary significantly between the regression model and E+ model. The regression model predicts the greatest consumption in the northwestern portion and the smallest in the southeastern portion of the climate zone. The E+ model predicts the greatest consumption in Missouri, Arkansas, and Mississippi; with consumption decreasing with distance from those states. Two factors could be driving these results. First, the differences in the E+ model results for the NZERTF in Gaithersburg, MD may carry through to other locations. Second, the regression model will become less accurate as the weather conditions (e.g., cloud cover, heating degree days, and cooling degree days) under which the prediction occurs become significantly different than those in the underlying data used to develop the model. The combination of these production and consumption prediction differences leads to net consumption predictions to be lower for nearly the entire mixed-humid climate zone, with the variation growing from the Southeast and the most western locations in the climate zone and up into the Appalachian Mountains in West Virginia.
The results for Gaithersburg, MD indicate that even when given detailed performance data, physics based simulation models still may have issues accurately predicting energy usage. Since physics models are often based on assumptions and simplifications for calculation purposes the simulations themselves introduce model uncertainty. Data-based models, like the one presented here, may offer more accuracy for a specific building because the model derives relationships based on actual output that are not affected by simplifications and assumptions at lower levels. However, post-occupancy data are often not available, and when they are available, models derived from it are limited in scope to the specific building and variable range from which the data was collected.
What the regression model illustrates most of all is the importance of collecting post-occupancy data. Without collecting and analyzing data after occupancy, the validity of the assumptions and energy usage predictions from simulations are left unchecked. A regression model fit to actual energy use data after “move in” is a viable way to confirm that the building exhibits the energy characteristics it was predicted to display, and can be implemented in predicting how the performance would change under similar but different annual weather conditions, such as historical weather data or projected weather conditions based on current weather trends.
The current model predicts performance using daily average weather data. Future work should determine if more aggregated weather conditions (i.e., weekly, monthly, and annual) can be used to accurately predict annual performance, which would further decrease the level of detailed information required to predict performance. Alternative training data (random) and statistical approaches (e.g., jackknife, neural network) should be considered in order to try to improve the accuracy of the predictions.
The use of statistical analysis and modeling also serve as a framework to analyze the impact of different energy efficiency features and operating conditions while accounting for variations in weather. NIST plans to continue operating the NZERTF while running trials of different energy systems (e.g., HVAC and DHW system configurations) while keeping other systems and building operations (e.g., set point and occupancy) constant. The resulting database will have an identical form to the one used to generate the model herein. Having a baseline relationship means the energy impacts of each new system can be compared to a like value. Differences can then be quantitatively examined for significance even if the weather conditions of the baseline and trial are not necessarily identical. Without knowing the baseline statistics or model, differences become harder to justify as meaningful. The second phase of the demonstration phase for the NZERTF (“Round 2”) included changes to the configuration and operation of the HVAC system (changes in thermostat and humidity controls), a similar model should be developed to compare the performance of Round 1 and Round 2 data, which will assist in identifying under which weather conditions the operational changes have the most significant energy performance impacts. The same regression models should be used to predict performance across historical annual data (AMY) for Gaithersburg, MD and compare to the results from the E+ energy simulations using the same AMY data. A similar model can be developed to estimate the weather conditions under which the NZERTF will reach net-zero for a given day.
The model also sets up possibilities of generalization as well as increased complexity. The parsimonious model herein is meant to serve as the baseline for comparison to additional models derived from the NZERTF data. By comparing the results of the model outlined in this paper to more complicated models, it will be possible to determine what benefit any alternative models may have over the simplified model, and if those benefits warrant any additional complexity required by the alternative models. The current model does not consider occupancy and additional weather factors that would be expected to impact energy performance, such as occupant activity variations across days of the week, differences in HVAC efficiency between heating and cooling, and relative humidity during the cooling season. A future study should develop a more complex regression model that controls for factors currently excluded to increase the model accuracy and determine if the improved accuracy is worth the additional complexity and data requirements. If occupancy-based energy activities can be effectively isolated, then the model can be separated into occupancy-based energy and building systems-based energy usage. Such a decoupling would allow the non-occupied house model to serve as a template, allowing predictions to be made on how changes in occupancy behavior impact overall energy usage. A deeper statistical analysis on the NZERTF database is required for such a relationship to be established but, given the depth of information in the database, is not unrealistic.
List of Abbreviations
- AMY
Actual Meteorological Year
- ANN
Artificial Neural Network
- ANOVA
Analysis of Variance
- AR
Autoregressive
- ARIMA
Autoregressive Integrated Moving Average
- CONS
Electricity Consumption
- DOE-2
Department of Energy building energy analysis program
- DoW
Day of Week
- E+
EnergyPlus
- EPT
Electricity Export
- HVAC
Heating, Ventilation, and Air Conditioning
- IMP
Electricity Import
- INS
Plane of Array Solar Insolation
- KGAI
Call Letters of Weather Station Nearest to the Net-Zero Energy Residential Test Facility
- NC
Net Consumption
- NIST
National Institute of Standards and Technology
- NZ
Net-Zero
- NZERTF
Net-Zero Energy Residential Test Facility
- ODB
Outdoor Dry Bulb Temperature
- POA
Plane of Array
- PROD
Electricity Production
- PV
Photovoltaic
- R2
Correlation Coefficient
- RH
Relative Humidity
- RMSE
Root Mean-Squared Error
- s-significant
Statistically Significant
- TMY3
Typical Meteorological Year 3
Footnotes
Certain trade names and company products are mentioned in the text in order to adequately specify the technical procedures and equipment used. In no case does such identification imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products are necessarily the best available for the purpose.
The Mixed-humid zone is defined according to the U.S. Department of Energy’s Building America Program Classification. These climate zones are meant to guide builders in identifying best practices for construction to improve energy performance, and various other aspects of residential buildings [7].
References
- 1.Energy Information Agency (EIA) Consumption and Efficiency. 2015 Jun; Available: http://www.eia.gov/consumption/
- 2.Fanney AH, Payne V, Ullah T, Ng L, Boyd M, Omar F, et al. Net-zero and beyond! Design and performance of NIST’s net-zero energy residential test facility. Energy and Buildings. 2015;101:95–109. [Google Scholar]
- 3.Omar F, Bushby ST. Simulating Occupancy in the NIST Net-Zero Energy Residential Test Facility. National Institute of Standards and Technology; Gaithersburg, MD: 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kneifel J. Annual Whole Building Energy Simulation of the NIST Net Zero Energy Residential Test Facility Design: US Department of Commerce. National Institute of Standards and Technology; 2012. [Google Scholar]
- 5.Kneifel J, Payne V, Ng L. In: Simulated versus Measured Energy Performance of the NIST Net Zero Energy Residential Test Facility Design. U. S. D. o. Commerce, editor. National Institute of Standards and Technology; 2015. [Google Scholar]
- 6.Crawley DB, Lawrie LK, Winkelmann FC, Buhl WF, Huang YJ, Pedersen CO, et al. EnergyPlus: creating a new-generation building energy simulation program. Energy and buildings. 2001;33:319–331. [Google Scholar]
- 7.Baechler MC, Williamson JL, Gilbride TL, Cole PC, Hefty MG, Love PM. High-performance home technologies: guide to determining climate regions by county. Pacific Northwest National Laboratory; 2010. [Google Scholar]
- 8.Kneifel J, Healy W, Filliben J, Boyd M. Energy performance sensitivity of a net-zero energy home to design and use specifications. Journal of Building Performance Simulation. 2015:1–14. [Google Scholar]
- 9.Kenifel J, O’Rear E. Comparing the Energy and Economic Performance of the NIST Net-Zero Energy Residential Building Design across the Mixed-Humid Climate Zone. NIST Special Publication. 2015:1603. [Google Scholar]
- 10.Haberl JS, Thamilseran S. Great energy predictor shootout II: Measuring retrofit savings–overview and discussion of results. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc; Atlanta, GA (United States): 1996. [Google Scholar]
- 11.MacKay DJ. Bayesian nonlinear modeling for the prediction competition. ASHRAE transactions. 1994;100:1053–1062. [Google Scholar]
- 12.Dodier RH, Henze GP. Statistical analysis of neural networks as applied to building energy prediction. Journal of solar energy engineering. 2004;126:592–600. [Google Scholar]
- 13.Karatasou S, Santamouris M, Geros V. Modeling and predicting building’s energy use with artificial neural networks: Methods and results. Energy and Buildings. 2006;38:949–958. [Google Scholar]
- 14.Kalogirou SA, Bojic M. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy. 2000;25:479–491. [Google Scholar]
- 15.Hiyama T, Kitabayashi K. Neural network based estimation of maximum power generation from PV module using environmental information. Energy Conversion, IEEE Transactions on. 1997;12:241–247. [Google Scholar]
- 16.Yang J, Rivard H, Zmeureanu R. On-line building energy prediction using adaptive artificial neural networks. Energy and buildings. 2005;37:1250–1259. [Google Scholar]
- 17.Yona A, Senjyu T, Saber AY, Funabashi T, Sekine H, Kim C-H. Application of neural network to one-day-ahead 24 hours generating power forecasting for photovoltaic system. Intelligent Systems Applications to Power Systems. 2007. ISAP 2007. International Conference on; 2007. pp. 1–6. [Google Scholar]
- 18.Izgi E, Öztopal A, Yerli B, Kaymak MK, Şahin AD. Short–mid-term solar power prediction by using artificial neural networks. Solar Energy. 2012;86:725–733. [Google Scholar]
- 19.Kalogirou SA. Applications of artificial neural-networks for energy systems. Applied Energy. 2000;67:17–35. [Google Scholar]
- 20.Dean SR. Quantifying the variability of solar PV production forecasts. American Solar Energy Society SOLAR National Conference; Phoenix, AZ. 2010. [Google Scholar]
- 21.Katipamula S, Reddy TA, Claridge DE. Multivariate regression modeling. Journal of Solar Energy Engineering. 1998;120:177–184. [Google Scholar]
- 22.Bruckman LS, Wheeler NR, Ma J, Wang E, Wang C, Chou I, et al. Statistical and domain analytics applied to PV module lifetime and degradation science. Access, IEEE. 2013;1:384–403. [Google Scholar]
- 23.Kalogirou SA. Artificial neural networks in renewable energy systems applications: a review. Renewable and sustainable energy reviews. 2001;5:373–401. [Google Scholar]
- 24.Sauer KJ. Real-world challenges and opportunities in degradation rate analysis for commercial PV systems. 37th IEEE Photovoltaic Specialists Conference (PVSC); Seattle, WA. 2011. [Google Scholar]
- 25.TamizhMani G, Kuitche J. Accelerated lifetime testing of photovoltaic modules. Arizona State University; 2013. [Google Scholar]
- 26.Ruch D, Claridge DE. A four-parameter change-point model for predicting energy consumption in commercial buildings. Journal of Solar Energy Engineering. 1992;114:77–83. [Google Scholar]
- 27.Reddy T, Claridge D. Using synthetic data to evaluate multiple regression and principal component analyses for statistical modeling of daily building energy consumption. Energy and buildings. 1994;21:35–44. [Google Scholar]
- 28.Braun M, Altan H, Beck S. Using regression analysis to predict the future energy consumption of a supermarket in the UK. Applied Energy. 2014;130:305–313. [Google Scholar]
- 29.Lü X, Lu T, Kibert CJ, Viljanen M. Modeling and forecasting energy consumption for heterogeneous buildings using a physical–statistical approach. Applied Energy. 2015;144:261–275. [Google Scholar]
- 30.Coughlin K, Piette MA, Goldman C, Kiliccote S. Statistical analysis of baseline load models for non-residential buildings. Energy and Buildings. 2009;41:374–381. [Google Scholar]
- 31.Kialashaki A, Reisel JR. Modeling of the energy demand of the residential sector in the United States using regression models and artificial neural networks. Applied Energy. 2013;108:271–280. [Google Scholar]
- 32.Fumo N, Biswas MR. Regression analysis for prediction of residential energy consumption. Renewable and Sustainable Energy Reviews. 2015;47:332–343. [Google Scholar]
- 33.Amiri SS, Mottahedi M, Asadi S. Using multiple regression analysis to develop energy consumption indicators for commercial buildings in the US. Energy and Buildings. 2015;109:209–216. [Google Scholar]
- 34.Asadi S, Amiri SS, Mottahedi M. On the development of multi-linear regression analysis to assess energy consumption in the early stages of building design. Energy and Buildings. 2014;85:246–255. [Google Scholar]
- 35.Catalina T, Virgone J, Blanco E. Development and validation of regression models to predict monthly heating demand for residential buildings. Energy and buildings. 2008;40:1825–1832. [Google Scholar]
- 36.Holladay M. Energy Modeling Isn’t Very Accurate. 2012 Dec 29; Available: http://www.greenbuildingadvisor.com/blogs/dept/musings/energy-modeling-isn-t-very-accurate.
- 37.Ayyub BM, McCuen RH. Probability, statistics, and reliability for engineers and scientists. CRC press; 2011. [Google Scholar]
- 38.System Advisor Model Version 2015.6.30 (SAM 2015.6.30) Sep 2; Available: https://sam.nrel.gov/download.
- 39.Balke E. M.S. Thesis. Mechanical Engineering, University of Wisconsin; 2016. Modeling, Validation, and Evaluation of the NIST Net Zero Energy Residential Test Facility. [Google Scholar]
- 40.Kneifel J, Payne WV, Ullah T, Ng L. In: Simulated versus Measured Energy Performance of the NIST Net Zero Energy Residential Test Facility. U. S. D. o. Commerce, editor. National Institute of Standards and Technology; 2015. [Google Scholar]
- 41.Weather Analytics. Actual Meteorological Year (AMY) Formatted Weather Data for July 1, 2013 through June 30, 2014. 2014 ed. [Google Scholar]


