Abstract
The comparison study of high pressure superconducting state of recently synthesized H3S and PH3 compounds are conducted within the framework of the strong-coupling theory. By generalization of the standard Eliashberg equations to include the lowest-order vertex correction, we have investigated the influence of the nonadiabatic effects on the Coulomb pseudopotential, electron effective mass, energy gap function and on the 2Δ(0)/TC ratio. We found that, for a fixed value of critical temperature (178 K for H3S and 81 K for PH3), the nonadiabatic corrections reduce the Coulomb pseudopotential for H3S from 0.204 to 0.185 and for PH3 from 0.088 to 0.083, however, the electron effective mass and ratio 2Δ(0)/TC remain unaffected. Independently of the assumed method of analysis, the thermodynamic parameters of superconducting H3S and PH3 strongly deviate from the prediction of BCS theory due to the strong-coupling and retardation effects.
The first-principles theoretical studies of the metallization and high-temperature superconductivity of dense hydrogen sulfide were reported for the first time by Li et al.1. This directly initiated the experimental work of Drozdov et al. who found that H2S compressed in a diamond anvil cell exhibits the superconductivity ranging from 30 to 150 K measured in the low-temperature runs2,3, which is consistent with calculations mentioned1. Furthermore, the results achieved in samples prepared at high-temperature showed that the record critical temperature of 164 K for cooper-oxide system HgBa2Ca2Cu3O8+δ under quasihydrostatic pressure4 has been trumped. Based on a sharp drop of the resistivity to zero and an expulsion of the magnetic field, Drozdov et al. observed a transition from metal to superconducting state at 203 K in H2S sample compressed up to 155 GPa2,5. Subsequent theoretical6,7,8 and experimental9,10 studies suggested that at high pressure, the phase diagram favors decomposition of H2S into H3S and elemental sulfur. This result means that the superconducting state observed at 203 K comes from a decomposition product H3S. More recently, referring to the theoretical crystal structure searches performed by Duan et al.11, the stability of high-pressure cubic 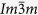 structure of H3S was confirmed by Li et al. in first-principles DFT structure searches joined with high-pressure X-ray diffraction experiments9, and then by Einaga et al. in synchrotron X-ray diffraction measurements combined with the electrical resistance measurements10. In contrast to cuprates where the nature of superconductivity is still not fully understood12,13,14, the presence of a strong isotope effect in H3S clearly suggests the electron–phonon origin of the superconducting state2,15,16,17. In addition, Jarlborg and Bianconi predict that the Fermi surface of H3S consists of multiple sheets similar to those in MgB218. However, the existence of multi-gap superconductivity in H3S has not been so far confirmed.
structure of H3S was confirmed by Li et al. in first-principles DFT structure searches joined with high-pressure X-ray diffraction experiments9, and then by Einaga et al. in synchrotron X-ray diffraction measurements combined with the electrical resistance measurements10. In contrast to cuprates where the nature of superconductivity is still not fully understood12,13,14, the presence of a strong isotope effect in H3S clearly suggests the electron–phonon origin of the superconducting state2,15,16,17. In addition, Jarlborg and Bianconi predict that the Fermi surface of H3S consists of multiple sheets similar to those in MgB218. However, the existence of multi-gap superconductivity in H3S has not been so far confirmed.
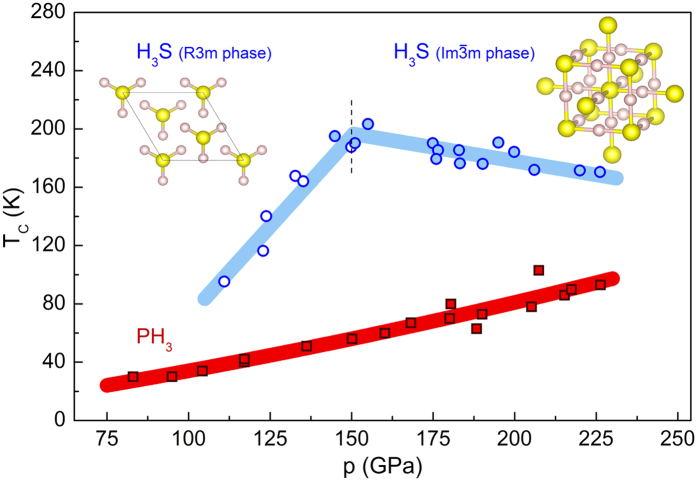
The above theoretical and experimental discovery have stimulated significant interest in finding new hydrogen-containing superconductors19,20,21. Very recently, Drozdov et al. reported superconductivity in compressed PH3 with a TC above 100 K22. The pressure dependence of the experimental critical temperature for H3S and PH3 compounds together with the relevant crystal structures is presented in Fig. 1. For H3S the second-order structural phase transition from trigonal R3m to cubic 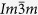 is experimentally observed at pressure close to 150 GPa10,23. However, according to the static lattice calculations the phase transition from R3m to
is experimentally observed at pressure close to 150 GPa10,23. However, according to the static lattice calculations the phase transition from R3m to 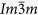 occurs at ~180 GPa11. A recent theoretical study found that quantum nuclear motion lowers the transition pressure to 103 GPa24. In the case of PH3, a theoretical search of crystal structure reveals two phases with lowest energy: orthorhombic P212121 and monoclinic C2/m. The DFT studies realized by Liu et al. indicate that both structures are dynamically stable and superconducting but C2/m phase are in a better agreement with an experimental results25. Unfortunately, the lack of structural informations on the superconducting phases from suitable measurements do not allow at this moment for the unambiguous verification of these assumptions.
occurs at ~180 GPa11. A recent theoretical study found that quantum nuclear motion lowers the transition pressure to 103 GPa24. In the case of PH3, a theoretical search of crystal structure reveals two phases with lowest energy: orthorhombic P212121 and monoclinic C2/m. The DFT studies realized by Liu et al. indicate that both structures are dynamically stable and superconducting but C2/m phase are in a better agreement with an experimental results25. Unfortunately, the lack of structural informations on the superconducting phases from suitable measurements do not allow at this moment for the unambiguous verification of these assumptions.
Figure 1. The experimental data of critical temperature as a function of pressure for H3S2,10 and PH322.
In addition the stable structures of H3S11 are presented.
Motivated by a recent significant experimental and theoretical progress in chemistry and physics of hydrogen-dense materials, we have carried out calculations to explore in detail the thermodynamic properties of superconducting hydrogen sulfide H3S and hydrogen phosphide PH3 at extremely high pressure (p = 200 GPa). The very large values of electron-phonon coupling interaction observed in these systems, caused that our investigations were performed within the framework of the Migdal-Eliashberg (ME) theory of superconductivity26, which goes beyond the BCS model27 by taking into account the retardation and strong-coupling effects.
This paper is organized as follows. In Section II, we introduce the theoretical model used to determine the quantities characterizing the superconducting state. Moreover, we present details of the first-principles calculations carried out to study the phonon properties and electron-phonon interactions. Then, in Section III, we report and compare the thermodynamic properties of superconducting H3S and PH3 systems at 200 GPa. We discuss the validity of the conventional Migdal-Eliashberg theory by introduce the lowest-order vertex correction and we examine its effect on Coulomb pseudopotential, energy gap, 2Δ(0)/TC ratio and electron effective mass. Finally, we give a summary of this study in Section IV.
Theoretical model and computational methods
Besides the experimental works, most of the theoretical studies concluded that compressed H3S and PH3 are phonon-mediated strong-coupling superconductors8,11,25,28,29. Thus, the superconducting state of these compounds can be accurately described by the Migdal-Eliashberg theory30,31. The Eliashberg equations for the superconducting order parameter function φn ≡ φ(iωn) and the electron mass renormalization function Zn ≡ Z(iωn) written in the imaginary-axis formulation are given by26,32:
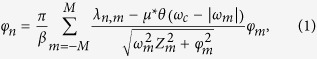 |
and
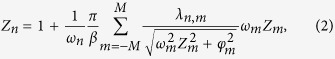 |
where the pairing kernel for the electron-phonon interaction is given by:
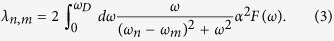 |
Moreover, β = 1/kBT and kB = 0.0862 meV/K states the Boltzmann constant. Symbols μ* and θ denote the screened Coulomb repulsion and the Heaviside function with cut-off frequency ωc equal to ten times the maximum phonon frequency: ωc = 10ωD.
The application of the above Eliashberg equations to describe the electron-phonon superconductivity is justified for systems in which the value of the phonon energy scale (Debye frequency, ωD) to the electron energy scale (Fermi energy, εF) ratio is negligible. Otherwise the Eliashberg equations should be generalized by taking into account the lowest-order vertex correction33,34,35,36,37:
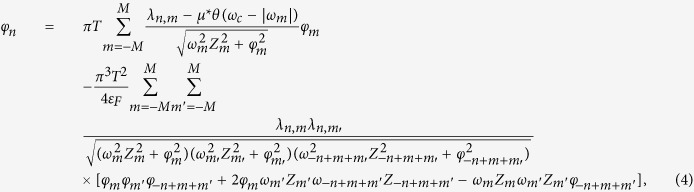 |
and
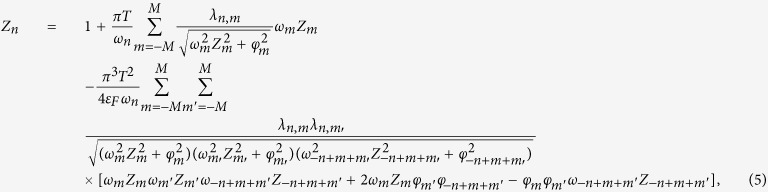 |
where, the modified electron-phonon pairing kernel takes the following form:
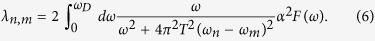 |
The Eliashberg spectral function, one of the main input element to the Eliashberg equations, is defined as:
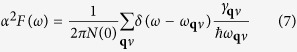 |
with
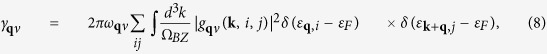 |
where N(0), γqν and gqν(k, i, j) denote the density of states at the Fermi energy, the phonon linewidth and the electron-phonon coefficients, respectively. The α2F(ω) functions for H3S and PH3 were calculated in this paper using density functional perturbation theory and the plane-wave pseudopotential method, as implemented in the Quantum-Espresso package38. We assume that H3S has cubic crystal  structure with lattice parameter a = 2.984 Å11, whereas PH3 crystallize in monoclinic C2/m structure with lattice parameter a = 5.152 Å, b = 2.961 Å, c = 2.960 Å, α = γ = 90° and β = 90.23° 39. The Vanderbilt-type ultrasoft pseudopotentials for S, P and H atoms were employed with a kinetic energy cutoff equal to 80 Ry. The phonon calculations were performed for 32 × 32 × 32 Monkhorst-Pack k-mesh with gaussian smearing of 0.03 Ry. The electron-phonon coupling matrices were computed using 8 × 8 × 8 q-grid for H3S and 4 × 4 × 4 q-grid for PH3. The calculated phonon band structures together with the Eliashberg spectral functions and electron-phonon integrals
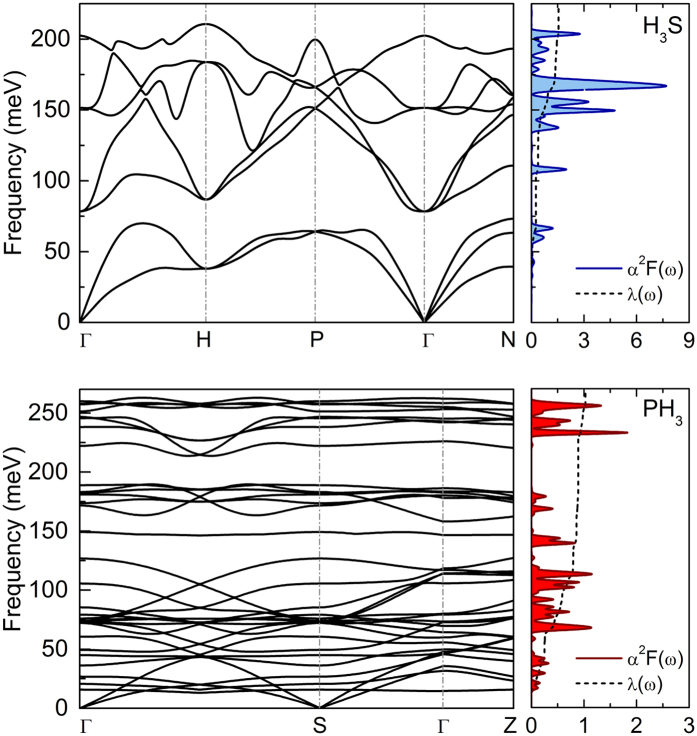
structure with lattice parameter a = 2.984 Å11, whereas PH3 crystallize in monoclinic C2/m structure with lattice parameter a = 5.152 Å, b = 2.961 Å, c = 2.960 Å, α = γ = 90° and β = 90.23° 39. The Vanderbilt-type ultrasoft pseudopotentials for S, P and H atoms were employed with a kinetic energy cutoff equal to 80 Ry. The phonon calculations were performed for 32 × 32 × 32 Monkhorst-Pack k-mesh with gaussian smearing of 0.03 Ry. The electron-phonon coupling matrices were computed using 8 × 8 × 8 q-grid for H3S and 4 × 4 × 4 q-grid for PH3. The calculated phonon band structures together with the Eliashberg spectral functions and electron-phonon integrals  for both investigated hydrides are presented in Fig. 2. The absence of imaginary frequencies in the full phonon spectra indicates that both systems are dynamically stable.
for both investigated hydrides are presented in Fig. 2. The absence of imaginary frequencies in the full phonon spectra indicates that both systems are dynamically stable.
Figure 2. Phonon dispersion and the Eliashberg spectral function α2F(ω) with electron-phonon integral λ(ω) for H3S and PH3 superconductors at 200 GPa.
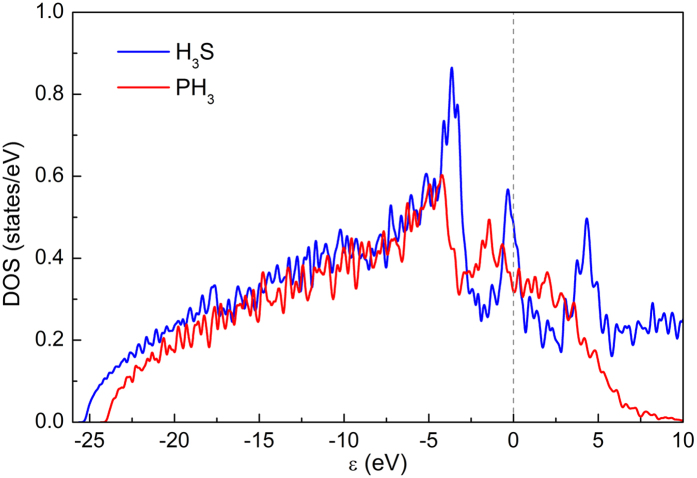
The electronic band structures of H3S and PH3 at 200 GPa were also explored. The investigated compounds are good metals with a large density of states (DOS) at the Fermi level. To clarify the difference of the electronic structures between  H3S and C2/m PH3, the DOS calculated for these two crystal structures are shown in Fig. 3. A strong peak around the Fermi level (the Van Hove singularities) is favorable for a strong electron-phonon coupling and thus really high superconducting temperature in the case of H3S40.
H3S and C2/m PH3, the DOS calculated for these two crystal structures are shown in Fig. 3. A strong peak around the Fermi level (the Van Hove singularities) is favorable for a strong electron-phonon coupling and thus really high superconducting temperature in the case of H3S40.
Figure 3. Density of states (DOS) for H3S (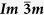 ) and PH3 (C2/m) at 200 GPa.
) and PH3 (C2/m) at 200 GPa.
The dotted line at zero indicates the Fermi level.
Our ab-initio studies showed that ratio λωD/εF is equal to 0.020 for H3S and 0.014 for PH3. These values are rather small in comparison to fullerene compounds or high-Tc cuprates, however, are not zero. Due to the above, we decided to conduct our calculations simultaneously using the conventional Eliashberg equations and equations with the lowest-order vertex correction, which allows us to examine the influence of nonadiabatic effects on the thermodynamic properties in studied compounds. The numerical analysis was performed using a self-consistent iteration methods41, which were implemented successfully in our previous papers31,42,43,44. The convergence and precision of our results are controlled by assuming the sufficiently high number (M = 1100) of Matsubara frequencies ωn ≡ (π/β)(2n − 1), where n = 0, ±1, ±2, …, ±M.
Results and Discussion
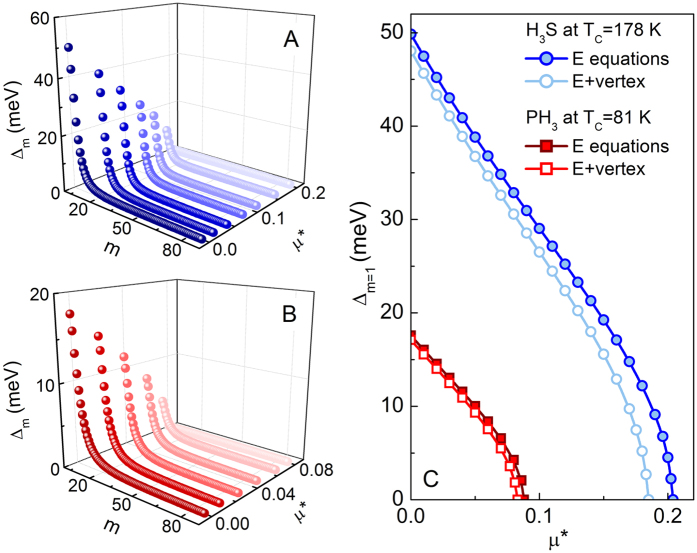
To study the thermodynamic properties of phonon-mediated superconductors on the quantitatively level in the first step we determine the critical value of the Coulomb pseudopotential 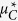 . For this purpose, in the Eliashberg equations we replace T by the experimental value of critical temperature: TC = 178 K for H3S2 and TC = 81 K for PH322. Then, starting from zero, we increase the value of μ* until we reach the equality
. For this purpose, in the Eliashberg equations we replace T by the experimental value of critical temperature: TC = 178 K for H3S2 and TC = 81 K for PH322. Then, starting from zero, we increase the value of μ* until we reach the equality 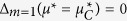 , where the order parameter is defined as: Δm = φm/Zm45. The obtained results are presented in Fig. 4. In particular, on the basis of the full dependence of Δm=1(μ*) we can conclude that if we take into account the conventional Eliashberg equations, the Coulomb pseudopotential takes a relatively high critical value for H3S (
, where the order parameter is defined as: Δm = φm/Zm45. The obtained results are presented in Fig. 4. In particular, on the basis of the full dependence of Δm=1(μ*) we can conclude that if we take into account the conventional Eliashberg equations, the Coulomb pseudopotential takes a relatively high critical value for H3S (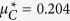 ) and low value for PH3 (
) and low value for PH3 (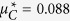 ) at 200 GPa. Moreover, at this point we can found that, for a fixed value of critical temperature, the lowest-order vertex correction changes
) at 200 GPa. Moreover, at this point we can found that, for a fixed value of critical temperature, the lowest-order vertex correction changes 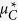 by −9.3% for H3S and −5.7% for PH3.
by −9.3% for H3S and −5.7% for PH3.
Figure 4.
The order parameter on the imaginary axis as a function of m and μ* for (A) H3S and (B) PH3 at 200 GPa - the results was obtained using conventional Eliashberg (E) equations. (C) The full dependence of the first value of the order parameter as a function of Coulomb pseudopotential.
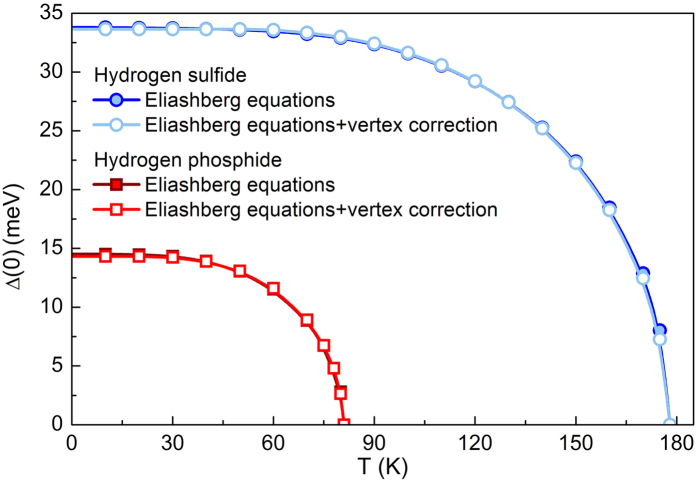
In the next step, by using the analytical continuation of the imaginary-axis solutions to the real frequency axis46, we calculate the temperature dependence of superconducting energy gap Δ(T) = Re[Δ(ω = Δ(T), T)]45. The obtained results are presented in Fig. 5. Knowledge of the energy gap value at zero temperature allowed us to calculate the dimensionless ratio RΔ ≡ 2Δ(0)/TC for which the BCS theory predicts universal value [RΔ]BCS = 3.53. In the case of studied hydrides, RΔ exceed the value of 4, in particular by using the conventional Eliashberg equations we received 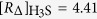 and
and 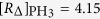 . This behavior is connected with the strong-coupling and retardation effects, which in the framework of the Eliashberg formalism can be characterized by the ratio TC/ωln, where ωln is the logarithmic phonon frequency, correspondingly 131 meV for H3S and 79 meV for PH3. Thus, the considered ratio equals 0.12 and 0.09, respectively, while in the weak-coupling BCS limit we have: TC/ωln → 0. Moreover, we find that although the vertex corrections seriously reduce
. This behavior is connected with the strong-coupling and retardation effects, which in the framework of the Eliashberg formalism can be characterized by the ratio TC/ωln, where ωln is the logarithmic phonon frequency, correspondingly 131 meV for H3S and 79 meV for PH3. Thus, the considered ratio equals 0.12 and 0.09, respectively, while in the weak-coupling BCS limit we have: TC/ωln → 0. Moreover, we find that although the vertex corrections seriously reduce 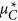 for H3S and PH3, the ratio 2Δ(0)/TC remains practically unaffected. Similar situation is observed in the case of electron effective mass at TC calculated from
for H3S and PH3, the ratio 2Δ(0)/TC remains practically unaffected. Similar situation is observed in the case of electron effective mass at TC calculated from 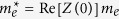 , where me denotes the electron band mass. In our case
, where me denotes the electron band mass. In our case 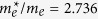 for H3S and
for H3S and 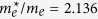 for PH3, regardless of the equations applied. This means that the thermodynamic properties of phonon-mediated superconductors can be successfully obtained in the framework of the conventional Migdal-Eliashberg formalism with the proviso that
for PH3, regardless of the equations applied. This means that the thermodynamic properties of phonon-mediated superconductors can be successfully obtained in the framework of the conventional Migdal-Eliashberg formalism with the proviso that 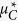 has to be accurately determined.
has to be accurately determined.
Figure 5. The temperature dependence of the superconducting energy gap.
The numerical results can be reproduced using the analytical formula 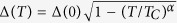 , where α = 3.36.
, where α = 3.36.
In the last step, to investigate the specific heat and thermodynamic critical field behavior, the condensation energy was numerically calculated:
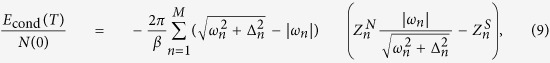 |
where 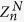 and
and 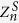 denote the mass renormalization functions for the normal and superconducting states, respectively. The specific heat difference between superconducting and normal state was then obtained from the second derivative of Econd(T):
denote the mass renormalization functions for the normal and superconducting states, respectively. The specific heat difference between superconducting and normal state was then obtained from the second derivative of Econd(T):
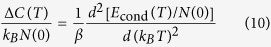 |
and thermodynamic critical field is defined as:
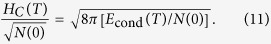 |
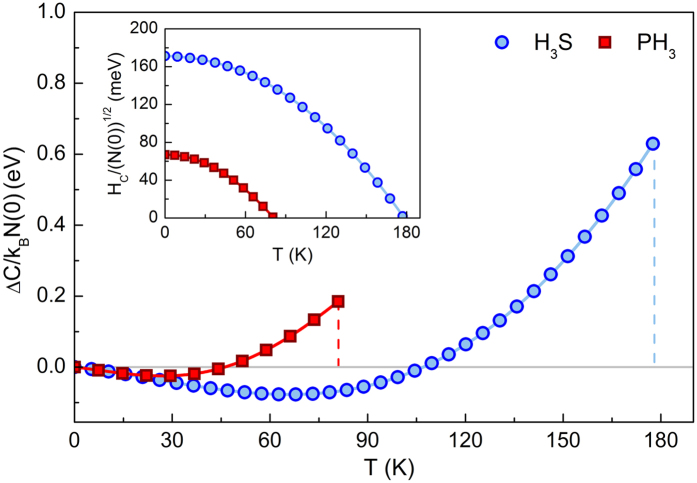
The temperature dependence of ΔC, with characteristic specific heat jump at TC marked by vertical line, is presented in Fig. 6. The inset shows the thermodynamic critical field for investigated hydrides. These results allow us to determine the other two fundamental dimensionless ratios: 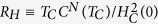 and RC ≡ ΔC(TC)/CN(TC), where the specific heat for the normal state is defined as CN = γT, and γ denotes the Sommerfeld constant:
and RC ≡ ΔC(TC)/CN(TC), where the specific heat for the normal state is defined as CN = γT, and γ denotes the Sommerfeld constant: 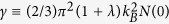 . It is noteworthy that, in the framework of the BCS theory, these ratios adopt universal values of 0.168 and 1.43, respectively45. We emphasize that these dimensionless ratios, similar to that of energy gap, take non-BCS values, in particular: RH = 0.136, RC = 2.47 for H3S and RH = 0.150, RC = 1.99 for PH3. We can see that with increasing values of TC/ωln ratio the thermodynamic properties take increasingly non-BCS behavior.
. It is noteworthy that, in the framework of the BCS theory, these ratios adopt universal values of 0.168 and 1.43, respectively45. We emphasize that these dimensionless ratios, similar to that of energy gap, take non-BCS values, in particular: RH = 0.136, RC = 2.47 for H3S and RH = 0.150, RC = 1.99 for PH3. We can see that with increasing values of TC/ωln ratio the thermodynamic properties take increasingly non-BCS behavior.
Figure 6. The specific heat difference between the superconducting and the normal state as a function of temperature.
Inset presents the temperature dependence of the thermodynamic critical field.
Conclusions
In this work, using the first-principles calculations and Eliashberg theory with and without vertex corrections, we systematically study the nonadiabatic effects on the superconductivity of compressed H3S and PH3 compounds. We find that for a fixed experimental value of critical temperature the lowest-order vertex correction reduces the Coulomb pseudopotential (from 0.204 to 0.185 in the case of H3S and from 0.088 to 0.083 for PH3), however, the energy gap, electron effective mass and ratio 2Δ(0)/TC remain unaffected. It means that the superconducting behavior can be properly determined even in the framework of the classical Migdal-Eliashberg formalism, as long as the value of the Coulomb pseudopotential is correctly determined. Moreover, we calculated the specific heat and thermodynamic critical field and we proved that strong-coupling and retardation effects caused that thermodynamic properties of H3S and PH3 at high pressures cannot be correctly estimated in the framework of the BCS theory.
Additional Information
How to cite this article: Durajski, A. P. Quantitative analysis of nonadiabatic effects in dense H3S and PH3 superconductors. Sci. Rep. 6, 38570; doi: 10.1038/srep38570 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Acknowledgments
Author would like to express his gratitude to Krzysztof Durajski, for his assistance in the numerical calculations. Research reported in this paper was financially supported by the Czestochowa University of Technology under Grant No. BS/MN-203-301/2016.
Footnotes
Author Contributions A.P. Durajski designed and carried out the numerical calculations, collected data and drafted the final version of the manuscript.
References
- Li Y., Hao J., Liu H., Li Y. & Ma Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 140, 174712 (2014). [DOI] [PubMed] [Google Scholar]
- Drozdov A. P., Eremets M. I., Troyan I. A., Ksenofontov V. & Shylin S. I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73 (2015). [DOI] [PubMed] [Google Scholar]
- Ma Y. Near-room-temperature superconductivity in hydrogen sulfide. NPG Asia Materials 8, e236 (2016). [Google Scholar]
- Gao L. et al. Superconductivity up to 164 K in HgBa2Cam−1CumO2m+2+δ (m = 1, 2, and 3) under quasihydrostatic pressures. Phys. Rev. B 50, 4260–4263 (1994). [DOI] [PubMed] [Google Scholar]
- Troyan I. et al. Observation of superconductivity in hydrogen sulfide from nuclear resonant scattering. Science 351, 1303–1306 (2016). [DOI] [PubMed] [Google Scholar]
- Bernstein N., Hellberg C. S., Johannes M. D., Mazin I. I. & Mehl M. J. What superconducts in sulfur hydrides under pressure and why. Phys. Rev. B 91, 060511 (2015). [Google Scholar]
- Duan D. et al. Pressure-induced decomposition of solid hydrogen sulfide. Phys. Rev. B 91, 180502 (2015). [Google Scholar]
- Errea I. et al. High-pressure hydrogen sulfide from first principles: A strongly anharmonic phonon-mediated superconductor. Phys. Rev. Lett. 114, 157004 (2015). [DOI] [PubMed] [Google Scholar]
- Li Y. et al. Dissociation products and structures of solid H2S at strong compression. Phys. Rev. B 93, 020103 (2016). [Google Scholar]
- Einaga M. et al. Crystal structure of the superconducting phase of sulfur hydride. Nat. Phys. 12, 835–838 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan D. et al. Pressure-induced metallization of dense (H2S)2H2 with high-TC superconductivity. Sci. Rep. 4, 6968 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao G. The pairing mechanism of high-temperature superconductivity: experimental constraints. Phys. Scripta 83, 038302 (2011). [Google Scholar]
- Szczęśniak R. Pairing mechanism for the high-TC superconductivity: Symmetries and thermodynamic properties. PLoS ONE 7, e31873 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Q. & Wang J. Pseudogap phenomena in ultracold atomic fermi gases. Front. Phys. 9, 539–570 (2014). [Google Scholar]
- Mazin I. I. Superconductivity: Extraordinarily conventional. Nature 525, 40–41 (2016). [DOI] [PubMed] [Google Scholar]
- Nicol E. J. & Carbotte J. P. Comparison of pressurized sulfur hydride with conventional superconductors. Phys. Rev. B 91, 220507 (2015). [Google Scholar]
- Ortenzi L., Cappelluti E. & Pietronero L. Band structure and electron-phonon coupling in H3S: A tight-binding model. Phys. Rev. B 94, 064507 (2016). [Google Scholar]
- Jarlborg T. & Bianconi A. Breakdown of the migdal approximation at Lifshitz transitions with giant zero-point motion in H3S superconductor. Sci. Rep. 6, 24816 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge Y., Zhang F. & Yao Y. First-principles demonstration of superconductivity at 280 K in hydrogen sulfide with low phosphorus substitution. Phys. Rev. B 93, 224513 (2016). [Google Scholar]
- Zhong X. et al. Tellurium hydrides at high pressures: High-temperature superconductors. Phys. Rev. Lett. 116, 057002 (2016). [DOI] [PubMed] [Google Scholar]
- Zhang S. et al. Phase Diagram and High-Temperature Superconductivity of Compressed Selenium Hydrides. Sci. Rep. 5, 15433 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drozdov A. P., Eremets M. I. & Troyan I. A. Superconductivity above 100 K in PH3 at high pressures. preprint at arxiv.org/abs/1508.06224 (2015).
- Gor’kov L. P. & Kresin V. Z. Pressure and high-TC superconductivity in sulfur hydrides. Sci. Rep. 6, 25608 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Errea I. et al. Quantum hydrogen-bond symmetrization in the superconducting hydrogen sulfide system. Nature 532, 81 (2016). [DOI] [PubMed] [Google Scholar]
- Liu H., Li Y., Gao G., Tse J. S. & Naumov I. I. Crystal structure and superconductivity of PH3 at high pressures. J. Phys. Chem. C 120, 3458–3461 (2016). [Google Scholar]
- Eliashberg G. M. Interactions between electrons and lattice vibrations in a superconductor. J. Exp. Theor. Phys. 11, 696 (1960). [Google Scholar]
- Bardeen J., Cooper L. N. & Schrieffer J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957). [Google Scholar]
- Akashi R., Kawamura M., Tsuneyuki S., Nomura Y. & Arita R. First-principles study of the pressure and crystal-structure dependences of the superconducting transition temperature in compressed sulfur hydrides. Phys. Rev. B 91, 224513 (2015). [Google Scholar]
- Flores-Livas J. A. et al. Superconductivity in metastable phases of phosphorus-hydride compounds under high pressure. Phys. Rev. B 93, 020508 (2016). [Google Scholar]
- Durajski A. P., Szczęśniak R. & Li Y. Non-BCS thermodynamic properties of H2S superconductor. Physica C 515, 1 (2015). [Google Scholar]
- Durajski A. P., Szczęśniak R. & Pietronero L. High-temperature study of superconducting hydrogen and deuterium sulfide. Ann. Phys. (Berlin) 528, 358–364 (2016). [Google Scholar]
- Marsiglio F., Schossmann M. & Carbotte J. P. Iterative analytic continuation of the electron self-energy to the real axis. Physical Review B 37, 4965 (1988). [DOI] [PubMed] [Google Scholar]
- Miller P., Freericks J. K. & Nicol E. J. Possible experimentally observable effects of vertex corrections in superconductors. Physical Review B 58, 14498 (1998). [Google Scholar]
- Pietronero L., Strässler S. & Grimaldi C. Nonadiabatic superconductivity. I. vertex corrections for the electron-phonon interactions. Phys. Rev. B 52, 10516–10529 (1995). [DOI] [PubMed] [Google Scholar]
- Grimaldi C., Pietronero L. & Scattoni M. The physical origin of the electron-phonon vertex correction. Eur. Phys. J. B 10, 247–255 (1999). [Google Scholar]
- Grimaldi C., Pietronero L. & Strässler S. Nonadiabatic superconductivity. II. generalized Eliashberg equations beyond Migdal’s theorem. Phys. Rev. B 52, 10530–10546 (1995). [DOI] [PubMed] [Google Scholar]
- Pietronero L. & Strässler S. Theory of nonadiabatic superconductivity. Europhys. Lett. 18, 627 (1992). [Google Scholar]
- Giannozzi P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]
- Shamp A. et al. Decomposition products of phosphine under pressure: PH2 stable and superconducting? J. Am. Chem. Soc. 138, 1884–1892 (2016). [DOI] [PubMed] [Google Scholar]
- Sano W., Koretsune T., Tadano T., Akashi R. & Arita R. Effect of Van Hove singularities on high-TC superconductivity in H3S. Phys. Rev. B 93, 094525 (2016). [Google Scholar]
- Szczęśniak R. The numerical solution of the imaginary-axis Eliashberg equations. Acta Phys. Pol. A 109, 179 (2006). [Google Scholar]
- Szczęśniak R., Drzazga E. A. & Szczęśniak D. Isotropic and anisotropic description of superconducting state in CaC6 compound. Eur. Phys. J. B 88, 52 (2015). [Google Scholar]
- Szczęśniak D. & Szczęśniak R. Thermodynamics of the hydrogen dominant potassium hydride superconductor at high pressure. Solid State Commun. 212, 1–4 (2015). [Google Scholar]
- Szczęśniak R., Zemła T. & Szczęśniak D. Superconducting state in bromium halide at high pressure. Physica B 495, 106–116 (2016). [Google Scholar]
- Carbotte J. P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 62, 1027 (1990). [Google Scholar]
- Marsiglio F., Schossmann M. & Carbotte J. P. Iterative analytic continuation of the electron self-energy to the real axis. Phys. Rev. B 37, 4965–4969 (1988). [DOI] [PubMed] [Google Scholar]