Synchronization and Random Triggering of Lymphatic Vessel Contractions

Abstract

The lymphatic system is responsible for transporting interstitial fluid back to the bloodstream, but unlike the cardiovascular system, lacks a centralized pump-the heart–to drive flow. Instead, each collecting lymphatic vessel can individually contract and dilate producing unidirectional flow enforced by intraluminal check valves. Due to the large number and spatial distribution of such pumps, high-level coordination would be unwieldy. This leads to the question of how each segment of lymphatic vessel responds to local signals that can contribute to the coordination of pumping on a network basis. Beginning with elementary fluid mechanics and known cellular behaviors, we show that two complementary oscillators emerge from i) mechanical stretch with calcium ion transport and ii) fluid shear stress induced nitric oxide production (NO). Using numerical simulation and linear stability analysis we show that the newly identified shear-NO oscillator shares similarities with the well-known Van der Pol oscillator, but has unique characteristics. Depending on the operating conditions, the shear-NO process may i) be inherently stable, ii) oscillate spontaneously in response to random disturbances or iii) synchronize with weak periodic stimuli. When the complementary shear-driven and stretch-driven oscillators interact, either may dominate, producing a rich family of behaviors similar to those observed in vivo.

Author Summary

For decades, cardiovascular physiology has been an area of intense research, and we have a fundamental understanding of the mechanisms the heart uses to drive blood flow through the distributed network of vessels in the body. The lymphatic system is now receiving similar attention as more is learned about its functional role in disease processes. The importance of the lymphatic system in collecting excess fluid from tissues and returning it to the blood is well known, but how the lymph flow is regulated without a central pump is poorly understood. Each segment of collecting lymphatic vessel can independently contract yielding a network of distributed pump/conduits. This paper shows how the lymphatic muscle cells that squeeze fluid along the lymphatic vessels can be effectively regulated using only chemical and mechanical signals that they receive from their immediate microenvironment. Using stability theory and the tools of nonlinear dynamics we identify two complementary oscillators that respond to stretch of the vessel wall and shear of fluid flowing over the vessel wall. Numerical simulations of the combined oscillators show that they have characteristics well suited to the regulation of distributed systems in general and may have application in other biological and physical contexts.

Introduction

To maintain fluid homeostasis, interstitial fluid drains into the lymphatic system through initial lymphatic vessels that carry it to the collecting lymphatic vessels. The collecting lymphatic vessels transport the fluid (known as lymph) both passively and actively to lymph nodes and back to the systemic blood circulation. Collecting lymphatic vessels are surrounded by specialized lymphatic muscle cells (LMCs) [1] and sub-divided by valve structures that define individual segments called lymphangions (Fig 1) [2]. Lymphangions serve as both pumps and conduits. In contrast to the blood circulation, where a single pump drives flow through relatively passive conduits, each lymphangion has the ability to pump lymph through the converging network to lymph nodes and eventually to the thoracic duct. Pumping occurs when expansions in radius draw fluid into the upstream end of the lymphangion and then expel it downstream during a contraction. Directional flow is enforced by intraluminal valves, which favor flow toward the thoracic duct. Lymphatic vessel contractions are triggered when cytosolic Ca²⁺ entering from intravascular stores and outside the cell surpasses a threshold concentration in the cytoplasm of the LMC, resulting in actin and myosin cross-bridging within the LMCs [3]. The contraction phase ends as transmembrane pumps restore cytoplasmic Ca²⁺ concentration to equilibrium allowing actin-myosin binding to relax, and the trans-wall pressure and the passive elastic properties of the wall to reopen the vessel. The effects of Ca²⁺ on LMC contraction are moderated by endothelial-derived relaxation factors (EDRFs) that act as potent dilators of lymphatic and blood vessels when produced by the vessel-lining lymphatic endothelial cells (LECs) in response to dynamic fluid shear stresses. The best known EDRF is nitric oxide although others such as histamine have been shown to be important [4, 5]. For notational simplicity we represent the entire class of EDRFs herein as NO. The NO and Ca²⁺ levels are both subject to mechanical regulation; Ca²⁺ can enter the cell through stretch-activated ion channels [6, 7], and NO is produced by LECs when they are exposed to increased fluid shear stress [8]. Although rhythmic contractions can be produced by purely chemical oscillations in Ca²⁺ within the LMCs [9, 10], it is likely that feedback regulation is necessary for robust homeostasis. Indeed, we previously used a relatively complex numerical simulation of lymphatic pumping to demonstrate that a wide spectrum of oscillatory behaviors is possible, and that the behavior is very sensitive to local levels of stretch and stress [11].

Fig 1. A single lymphangion while opening and closing with valves at the inlet and outlet.

Our present aim is to reduce the complexity of our previous model to examine how the observed oscillations arise from the integration of simple mechanical and chemical processes within a physiological system. Once simplified, we employ tools such as linear stability analysis to identify key parameter groups that determine the qualitative dynamic behaviors of such systems. Linear stability analysis seeks to determine which parameter values cause a small disturbance to grow rapidly from an initial state, or alternatively decay back to equilibrium. In addition, our approach allows us to show how oscillations can arise from the interactions between mechanical and chemical processes that lack intrinsic oscillators when considered separately. Here we develop generic formulations of the mechano-chemical processes in the muscular lymphatic vessel wall based on Ca²⁺ and NO signaling, then explore the dynamics of each chemical species while holding the effects of the other constant. Finally we examine the behavior of the fully coupled system. Linear stability analysis reveals a new class of oscillator arising from the dynamics of shear and NO that can act alone or in concert with the better recognized Ca²⁺ dynamics. The most remarkable feature of the shear-NO mechanism is its ability to offer distributed control of the pumping process, which is essential for managing a decentralized network of pumps and conduits.

Methods

Model Formulation

Our model is based on a single lymphangion (Fig 1) bounded at each end by one-way valves. The radius of the lymphangion is governed by the radial forces which are determined by the contractile (Ca²⁺) and dilatory (NO) signaling molecules. Neglecting inertial effects, the radial forces on the vessel wall balance as

$$D\frac{dR}{dt}=-\mathcal{E}(R)-\mathcal{F}(R,C_{Ca},C_{NO})+{\mathcal{A}}_R(t)$$ (1)

where the left hand side represents rate dependent effects with D incorporating the visco-elastic material properties of the vessel wall as well as viscous losses in the flow and lags in the transduction of concentrations into force, $\mathcal{E}$ is a restoring force-including elastic forces and vessel “tone” -imparted by the material properties of the vessel wall and $\mathcal{F}$ is a dynamic inward acting contractile force produced by muscle cells that surround the vessel. To a first approximation, we assume that the concentration of Ca²⁺ is transduced into a contractile force as $\mathcal{F}=F_{Ca}{C}_{Ca}/(1+\alpha C_{NO})$ where α scales the possible desensitizing effect of NO [12]. The activation term ${\mathcal{A}}_R$ can include a steady component from the mean transmural pressure difference p_m that influences the baseline radius as well as extrinsic disturbances to the radius from the surrounding tissue and adjacent lymphangions.

The restoring force is typically highly nonlinear[13–15]. Here we adopt the form $\mathcal{E}(R)=A{e}^{aR}-p_{offset}$ with stiffening coefficient a, scaling coefficient A, and offset pressure p_offset selected to give a good fit of Shirasawa and Benoit (see the third figure of reference [15]) at typical operating pressures. In our numerical simulations we retain the full nonlinear form of $\mathcal{E}(R)$, but for the stability analysis that follows we linearize the elastic force near an equilibrium radius R₁ in the absence of dynamic increments to Ca or NO as $\mathcal{E}(R)\approx E_0+E_1(R-R_1)$ where E₀ is the elastic force at equilibrium and a Taylor series expansion near equilibrium yields $E_1=Aa{e}^{a{R}_1}$. We find the equilibrium radius by solving $0=D\frac{dR}{dt}=-(A{e}^{a{R}_1}-p_{offset})-F_{Ca}{S}_{C{a}_0}/K_{Ca}+p_m$ for R₁ where p_m is the mean transmural pressure. Given the stiffening behavior of the wall ($E_1\propto e^{a{R}_1}$), we expect that appropriate values of E₁ will be larger at higher mean transmural pressures where the equilibrium radius will be somewhat larger.

The concentrations of the signaling molecules (i ∈ {Ca, NO}) are governed by the generic conservation law

$$\frac{d{C}_i}{dt}=-{\mathcal{K}}_i(C_{Ca},C_{NO})+{\mathcal{S}}_i(R,\dot{R},C_{Ca},C_{NO})+{\mathcal{A}}_i(t)$$ (2)

where all concentrations are taken to be dimensionless ratios relative to a suitable reference, ${\mathcal{K}}_i$ is clearance of the signaling species through chemical reaction, transmembrane ion pumps and advective-diffusive transport, ${\mathcal{S}}_i$ is a dynamic source term for the signaling molecule and ${\mathcal{A}}_i$ is an additional source term that can include the effects of imposed flow from upstream fluid pressure, inflammation, pace-making signals from adjacent cells, neural signaling, random disturbances, etc.

Stretch-Ca Dynamics

Since our focus is on the interactions between Ca²⁺ and NO, we introduce a minimal representation of the Ca²⁺ dynamics rather than a fully detailed model of Ca²⁺ oscillations as may be found in the literature [10, 16]. We retain the following features: i) at rest, Ca²⁺ is at a low concentration in the cytoplasm of LMCs; ii) a contraction is initiated when Ca²⁺ is rapidly admitted to the cytoplasm through ion-selective channels thereby triggering cross bridge formation between actin and myosin chains creating a contractile force [17]; iii) relaxation of LMCs coincides with a drop in cytoplasmic Ca²⁺ concentration due to a drop in the rate of influx and the restoration of baseline conditions by ion pumps in the cell membrane and sarcoplasmic reticulum; and iv) the LMC is refractory to a new contraction cycle until Ca²⁺ levels have returned to near equilibrium. As the Ca²⁺ levels approach their threshold level, we hypothesize that the membrane acquires sensitivity to small perturbations. Furthermore, the sensitivity is enhanced when the membrane is stretched to a larger radius. This models stretch-sensitive ion channels found in LMCs [6, 18]. Each step in the process has the potential for modulation by NO. Alternatively, each form of modulation by NO can be disabled to demonstrate behaviors that have been observed in experimental preparations, for example after removal of LECs (which produce NO) or the genetic or pharmacological suppressions of NO [19–21].

We mathematically express the release of Ca²⁺ into the cytoplasm from intracellular stores and the extracellular fluid as the sum of a steady source S_ca0 needed to maintain the baseline Ca²⁺ concentration and a transient component that is sufficiently rapid to be modeled as an impulse function δ(t) where t is the time since the Ca²⁺ concentration most recently passed the threshold necessary to trigger another contraction C_CaThresh. This is expressed as,

$${\mathcal{S}}_{Ca}=S_{Ca0}+\frac{S_{Ca1}\delta (t)}{(1+\gamma C_{NO})}$$ (3)

where S_Ca1/(1 + γC_NO) is the magnitude of a bolus of Ca²⁺ with a possible reduction due to NO that is scaled by γ. We model the clearance of Ca²⁺ from the cytoplasm with

$${\mathcal{K}}_{Ca}=K_{Ca}(1+\beta C_{NO})(C_{Ca}-C_{\text{CaThresh}})$$ (4)

where K_Ca is a rate constant and β scales the possible enhancement of Ca²⁺ clearance attributed to NO [12, 16]. At high concentrations of Ca²⁺ the clearance rate may be limited by the membrane pump capacity, but near the threshold required to trigger a contraction we assume clearance rates proportional to the concentration increment. The threshold itself may include a random component that we incorporate into the activation term.

The linearized form of the model for a constant level of NO can now be written as

$$D\frac{dR}{dt}=-E_{1}R-F_{Ca}{C}_{Ca}+{\mathcal{A}}_R(t)$$ (5)

and

$$\frac{d{C}_{Ca}}{dt}=-K_{Ca}{C}_{Ca}+S_{Ca1}\delta (t)+{\mathcal{A}}_{Ca}(t)$$ (6)

where the constants have been absorbed into the activation terms so that the radius and concentration now represent the increments from baseline values. The parameters S_Ca1 and K_Ca now include the adjustments due to NO introduced in Eqs 3 and 4.

Shear-NO Dynamics

In the previous section we developed the model so that it reproduces Ca²⁺ induced contractions. We next considered how NO, created when LECs experience increased shear stress, can modulate contractions when it diffuses rapidly into adjacent LMCs. A suitable form for the NO source term can be obtained by considering steady laminar flow in a circular tube with negligible inertia [22]. Conservation of mass in a tube of time-varying radius requires that $\frac{\partial Q}{\partial z}=-2\pi R\frac{dR}{dt}$ which when integrated with respect to z along a vessel yields $Q(z)=-2\pi R\frac{dR}{dt}z+C_1$ where the constant of integration depends on the end conditions for the lymphangion. When the segment is contracting $\frac{dR}{dt}<0$ and the upstream valve is closed [Q(0) = 0] we have $Q(z)=-2\pi R\frac{dR}{dt}z$. Alternatively, if the segment is expanding $\frac{dR}{dt}>0$ and the downstream valve is closed (Q(L) = 0), we obtain $Q(z)=2\pi R\frac{dR}{dt}(L-z)$. We can express the mean flow along the length more compactly as $\overline{Q}=\pi R\left|\frac{dR}{dt}\right|L$. When additional flow Q₀ is imposed on the segment by an axial pressure gradient we have $\overline{Q}=\pi R\left|\frac{dR}{dt}\right|L+Q_0$. Approximating the velocity profile with that of steady laminar flow with negligible inertia [22] we relate the mean shear stress τ to the flow rate by $\tau =\frac{4\mu \overline{Q}}{\pi R^3}$. The mean shear stress along the segment due to dynamic changes during contraction or expansion is therefore approximately $\tau =\frac{4\mu L}{R^2}\left|\frac{dR}{dt}\right|+\frac{4\mu Q_0}{\pi R^3}$. Recent studies show that valves in collecting lymphatic vessels are biased toward the open condition [23], but the simplification employed here allows us to study the basic stability of the system, at the possible expense of some accuracy in the predictions of pumping efficiency. There may be levels of shear stress below which NO production is negligible and above which NO production saturates at a maximum, but here we linearize the transduction of shear stress into the production of NO in an intermediate range to yield

$${\mathcal{S}}_{NO}=\frac{S_{NO}}{R^2}\left|\frac{dR}{dt}\right|+S_{N{O}_0}$$ (7)

where S_NO has absorbed the remaining constants in the shear stress expression and $S_{N{O}_0}$ represents NO released due to the through-flow term Q₀ or chronic sources of NO such as might arise during inflammation. The source term $S_{N{O}_0}$ can be time varying, but arises from the local environment of the lymphangion and mathematically acts as an input to our model of a single lymphangion rather than as an interaction within the system itself. $S_{N{O}_0}$ therefore can serve as an external trigger to the system or as a steady offset, but does not directly impact the dynamics of an individual lymphangion, except by parametrically (rather than dynamically) changing the equilibrium radius.

We can examine the effects of fluid viscosity on the pressure by using the same set of assumptions. The pressure will vary due to viscous flow effects according to $\frac{\partial p}{\partial z}=\frac{-8\mu Q}{\pi R^4}$. When contracting we have $\frac{\partial p}{\partial z}=\frac{16\mu }{R^3}\frac{dR}{dt}z$, which when integrated along the length gives $p(z)=\frac{16\mu }{R^3}\frac{dR}{dt}{z}^2+p(0)$. Averaging over the length of the segment yields $\overline{p}=\frac{16\mu L^2}{3R^3}\frac{dR}{dt}+p(0)$ where the first term gives the magnitude of the pressure decrement (or increment for vessel expansion) due to flow induced by the contraction of a single lymphangion. We see that the pressure increment due to flow induced by the single lymphangion also multiplies $\frac{dR}{dt}$, so it can be absorbed into the overall damping term D. For typical vessel sizes, we find that the lag due to viscosity is orders of magnitude smaller than that from chemical and mechanical lags which are on the order of one second.

NO does not produce a true outward force. However, it is conceptually equivalent to consider an effective force produced by NO that has the effect of countering ${\mathcal{F}}_{Ca}$ and the elastic effects. Mathematically, for small αC_NO, we can write this as

$$\mathcal{F}=\frac{F_{Ca}{C}_{Ca0}}{1+\alpha C_{NO}}\approx F_{Ca}{C}_{Ca0}(1-\alpha C_{NO})$$ (8)

By defining F_NO ≡ F_CaC_Ca0α, we can write

$${\mathcal{F}}_{NO}=-F_{NO}{C}_{NO}$$ (9)

And the net force from Eq 8 becomes

$$\mathcal{F}=F_{Ca}{C}_{Ca0}-F_{NO}{C}_{NO}$$ (10)

where the net contractile force is decomposed into a positive term set by the baseline Ca²⁺ levels and a negative term that represents how the Ca²⁺ levels are modulated by NO. Thus, the NO-dependent term is not a true outward force, but arises mathematically from a reduction in the Ca²⁺-dependent contractile forces.

The parameter values used in the simulations that follow are given in Table 1. The parameter values were based on experimental data where possible, but were chosen to demonstrate a wide range of mathematical behaviors for the system rather than to mimic a particular experimental data set in detail. As a representative example, we show simulations based on measurements in rats [24] which offer data relating Ca²⁺ concentrations to lymph vessel diameter and contractile tension. Our own experiments discussed later [20] were done on mice which have smaller collecting lymphatic vessels than rats.

Table 1. Baseline Parameter values.

Parameter	Symbol	Value	Units	Source
Lymphangion radius	R0	1.3x10-4	m	[15]
Mean pressure	pm	100–1000	Pa	[15]
Wall stiffening exponent	a	2.45x104	m-1	[15]
Wall stiffening coefficient	A	12.3	Pa	[15]
Offset pressure for wall stiffness	poffset	100	Pa	[15]
Wall damping coefficient	D	3x106	Pa-s/m	[15]
Baseline Ca concentration	CCa0	1
Baseline Ca release rate	SCa0	1
Ca release pulse size	SCa1	0.85		[15]
Ca force production coefficient	FCa	100	Pa	[15]
NO source from shear stress coefficient	SNO	3x10-3	m
Ca clearance rate constant	KCa	1	s-1	[15]
NO clearance rate constant	KNO	5	s-1
Contraction force suppression by NO	α	0–1
Ca clearance enhancement by NO	β	0–1
Ca source blunting by NO	γ	0–1
Ca noise standard deviation	σCa	10−3
NO noise standard deviation	σNO	10−3
Integration time step	dt	10−4	s

Parameters without units are taken to be dimensionless ratios. The concentrations are normalized relative to nominal concentrations. Force related terms are given as pressure equivalents in a circular tube.

Specific parameters governing the effects of NO are difficult to estimate, but fortunately may not be necessary here. As will be shown in the results section, we require only estimates of combinations of parameters such as S_NO and F_CaC_Ca0α, rather than values for each parameter individually. Unlike the geometrically-detailed continuum model of lymphatic NO transport in Wilson et al [25] that includes shear-induced production and clearance by diffusion, convection and reaction, our present model employs averages over a single lymphangion and combines the sensitivity to shear stress with the rate of production of NO. To that end, we employ parameter values that yield diameter changes due to NO on the order of 10% as observed in [20, 21]. Moreover, we expect the effects of NO to be rapid. NO is released by endothelial cells about 2 seconds or less after increases in shear stress as observed previously [26–29]. Lymphatic vessels can be expected to dilate faster than blood vessels [30] because their muscle cells contain more rapid-acting contractile proteins than those of blood vessels [31]. We take the clearance of NO to be similar to, but somewhat faster than, that of Ca²⁺ [32]. Parameters such as the contractility, NO production and the mechanical stiffness appear to depend on anatomical location, species and age [13, 28, 33–36], suggesting that the full range of possibilities realizable in vivo awaits further investigation.

Results

Here we first present analytical and numerical results for cases in which the stretch-Ca²⁺ dynamics are active, but with constant NO levels. We will then present results of our model for when shear-NO dynamics are active, but Ca²⁺ levels do not spike, but remain near baseline. Finally, we will present results of our model for fully coupled stretch-Ca²⁺ and shear-NO processes.

Stretch-Ca²⁺ Dynamics with Constant NO Levels

In the absence of dynamic activation, Eq 6 implies the Ca²⁺ concentration during each contraction cycle will decay as $C_{Ca}(t)=S_{Ca1}{e}^{-K_{Ca}t}$. Using this as an input to Eq 5, we find that the radius varies from its baseline value during each contraction cycle as

$$\Delta R(t)=\frac{F_{Ca}{S}_{Ca1}}{E_1{K}_{Ca}}\frac{(e^{-t/t_{Ca}}-e^{-t/t_{mech}})}{(t_{mech}-t_{Ca})}$$ (11)

where we see that the return to equilibrium depends on two characteristic times, one set by the rate of Ca²⁺ clearance t_Ca = 1/K_Ca and the other by the mechanical lag t_mech = D/E₁ which can include the lag between the concentration increase and force production. As a reference time scale we have selected t_Ca = 1/K_Ca = 1 s which is in the range observed by Shirasawa and Benoit [15]. They observed a similar lag between the rise in Ca²⁺ concentration and the peak force generation. Here we use this lag as an estimate of t_mech which we take to incorporate the visco-elastic and chemical-mechanical transduction lags.

While both time constants contribute to the overall response, the slower of the two characteristic times gives the dominant time constant t_c that determines the return to equilibrium. Experimental observations of the magnitude of radius change as a function of pressure show that it decreases with increased internal pressure [21]. This phenomenon is reproduced by our model as the vessel wall stiffens (larger E₁ in the denominator) at greater radius. The amplitude may be further modified if the myosin cross bridging is length dependent as seen in skeletal muscle [36].

The frequency of contractions at constant NO levels is set by the interplay between the characteristic time for calcium t_Ca and the magnitude of the random activation term. In addition to the steady source of Ca²⁺ that establishes the vascular tone, we include a random component ${\mathcal{A}}_{CaRand}(R,t)$ with zero mean and a standard deviation σ that can be applied to either the concentration itself or to the threshold level at which a new release of Ca²⁺ is triggered. A higher radius leads to more stretch in the LMC membrane and therefore greater sensitivity of ion channels. This can be modeled by increasing the noise level (for example let σ ∝ p_m). This will lead to a higher frequency at larger radii as found experimentally [21]. Exponential decay of Ca²⁺ near equilibrium leads to a latency period between contractions that varies as T = t_c log(C_max/σ) where C_max is the magnitude of the Ca²⁺ increment from baseline.

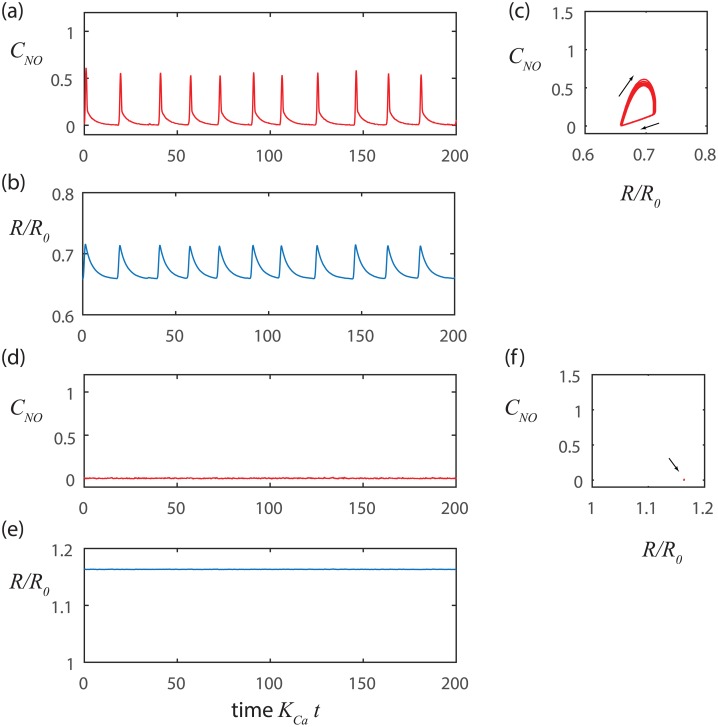
We further investigated random activation with the aid of numerical simulations implemented with the Euler-Maruyama method [37], which properly scales the computational time step with the standard deviation of the noise (Fig 2). The simulation presented in Fig 2d–2f results from a higher mean pressure than Fig 2a–2c. Thus, the baseline radius is larger in Fig 2d–2f, which in turn yields a stiffer wall (larger E₁) leading to a smaller mechanical time constant (smaller t_mech) and reduced amplitude for change in the radius.

Fig 2. Stretch-Ca dynamics at constant NO with noise triggering.

At lower pressure a-c) p_m = 100 Pa, t_Ca = 1s and t_mech = 1.22 s, and at a higher pressure d-f)p_m = 500Pa, t_Ca = 1s, and t_mech = 0.24 s. The noise level is σ = 0.01. In each case the overall time constant is given approximately by the greater of t_Ca and t_mech. The period is predicted approximately by t_c log(C_max/σ) where C_max is the amplitude of the change in Ca²⁺ concentration.

We note that our simple model of stretch-Ca²⁺ dynamics replicates important features of the contraction cycles observed in vivo [20] where contractions are generally similar to one another in magnitude and duration, but may be separated by inconsistent periods of latency. In Fig 2, we see that the simulated contractions are nearly identical to each other (that is, the trajectories nearly retrace one another in the phase portraits shown Fig 2c and 2f), but occur on inconsistent intervals. Even though the intervals between contractions are not perfectly uniform, they are well estimated by t_c log(C_max/σ). We also see that increased transmural pressure can reduce the interval between contractions by stiffening the wall (p_m ↑⇒ R₁ ↑⇒ E₁ ↑⇒ t_mech ↓⇒ t_c ↓⇒ T↓) and also by increasing the sensitivity of the Ca²⁺ channels by stretching the vessel wall (p_m ↑⇒ σ ↑⇒ T ↓) yielding higher frequency contractions (compare Fig 2b and 2e).

We also find that our model of the stretch-Ca²⁺ process readily synchronizes when we impose extrinsic rhythmic pace-making since only small variations in the Ca²⁺ concentration relative to the threshold level are needed to initiate the next contraction cycle (Fig 3). Such small variations in Ca²⁺ concentration can be readily introduced by diffusion or voltage signals from adjacent LMCs. Alternatively, the vessel may be locally stretched by lymph arriving from upstream, which can also trigger a local contraction. In this way, neighboring LMCs can synchronize contractions to coordinate flow along a series of lymphangions throughout a connected network of collecting lymphatic vessels [38, 39].

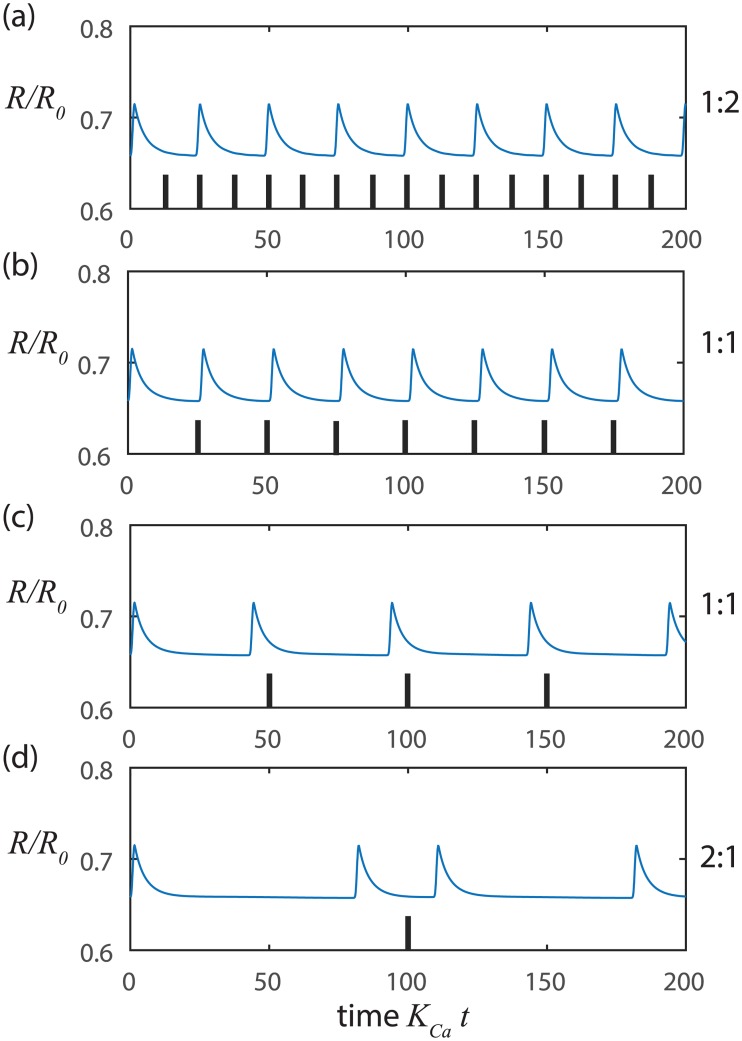
Fig 3. Synchronization of stretch-Ca dynamics with small amplitude sinusoidal inputs at constant NO.

At higher pressure p_m = 500 Pa, t_Ca = 1 s, and t_mech = 0.24 s with input amplitude of 0.01 and input frequencies of a) 0.3 Hz, b) 0.2 Hz, c) 0.1 Hz and d) 0.05 Hz. The tick marks indicate the beginnings of successive cycles of the sinusoidal input signal. The ratio of output frequency to input frequency is at the right of each panel.

Shear-NO Dynamics with Ca²⁺ Near Baseline Levels

The conditions for oscillations in radius to arise near baseline Ca²⁺ levels in the absence of sharp spikes in Ca²⁺ as considered in the previous section are available from linear stability analysis of the shear-NO process near a point R₁ which yields

$$\left[\begin{array}{c}\dot{R}\\ \stackrel{.}{C_{NO}}\end{array}\right]=\left[\begin{array}{cc}-\frac{E_1}{D}& \frac{F_{NO}}{D}\\ -\frac{S_{NO}{E}_1}{D{R}_1^2}& sgn(\dot{R})\frac{S_{NO}{F}_{NO}}{D{R}_1^2}-K_{NO}\end{array}\right]\left[\begin{array}{c}R\\ C_{NO}\end{array}\right]+[inputs]$$ (12)

where the inputs include all extrinsic disturbances from the adjacent lymphangions and surrounding tissue. We treat small variations in R parametrically so that the dynamics of the system may be characterized by the eigenvalues of the Jacobian matrix [40] which are roots of the characteristic polynomial:

$${\lambda }^2+\left(\frac{E_1}{D}+K_{NO}-sgn(\dot{R})\frac{S_{NO}{F}_{NO}}{D{R}_1^2}\right)\lambda +\frac{E_1{K}_{NO}}{D}=0$$ (13)

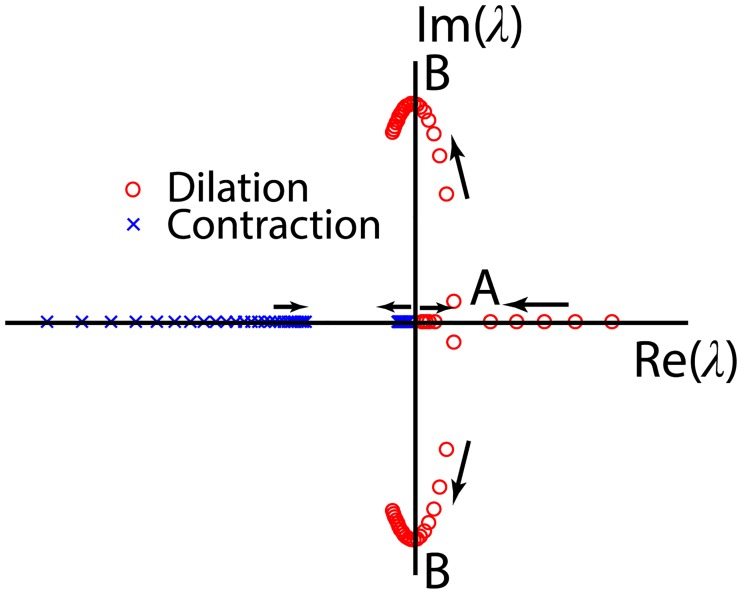
Since all of the coefficients are positive, stability requires only that the second term be positive. Thus the system is always stable during contraction ($\dot{R}<0$). However during dilation ($\dot{R}>0$) the second term can be positive or negative which allows the system to switch between stability and instability (Fig 4).

Fig 4. Location of the shear-NO eigenvalues in the complex plane as the baseline radius R₁ increases parametrically.

The arrows indicate the direction of increasing R₁. The eigenvalues during contraction always have a negative real part indicating stability. When the baseline radius is large enough to move the eigenvalues beyond point B the system is inherently stable during dilation. At point B the system is marginally stable and will oscillate at frequency f = (E₁K_NO/D)^1/2/2π. For smaller baseline radius, between points A and B, the response is unstable, but oscillatory. And when the baseline radius is smaller at point A, the dynamic component of the radius increases exponentially without oscillation until the radius is large enough to reach the range between A and B where oscillations can occur.

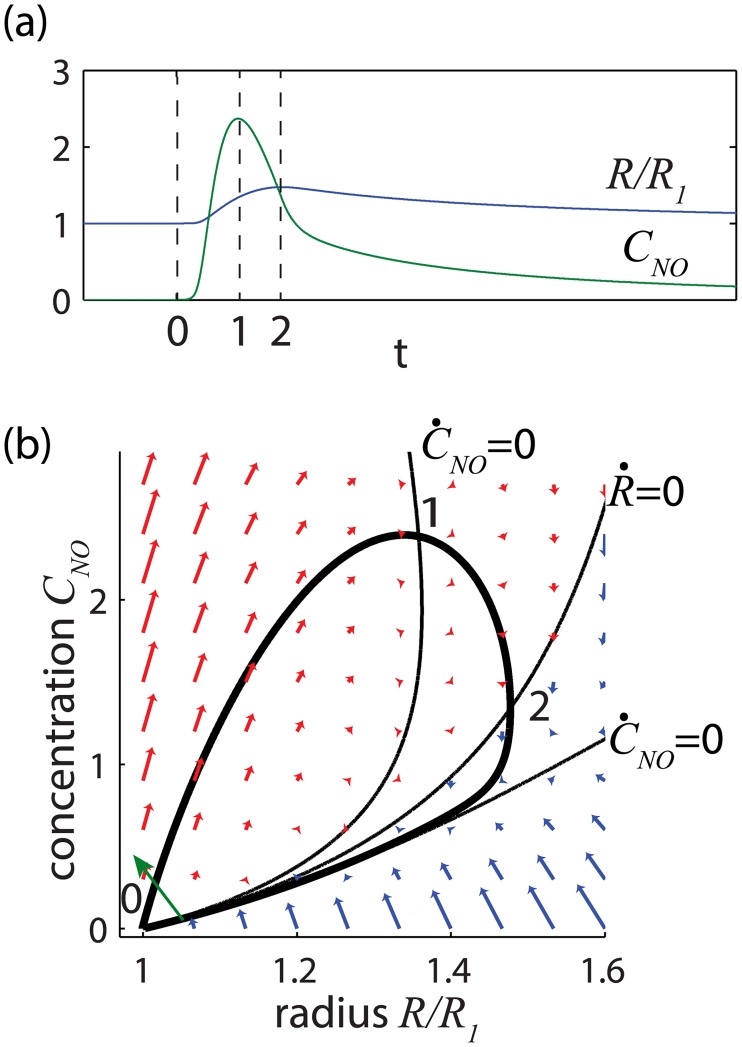
Herein is the key feature from which NO can induce spontaneous oscillations in the radius without the sharp spikes in Ca²⁺ concentration described in Eq 6. If the radius is large enough so that E₁/D + K_NO > S_NOF_NO/DR², then the fixed point is inherently stable. If instead, the radius is small enough that E₁/D + K_NO < S_NOF_NO/DR² then the radius will unstably increase when perturbed. The instability arises because a slight increase in radius (from point 0 on Fig 5) pulls fluid into the lymphangion, increasing shear and temporarily creating a runaway effect wherein more NO is released from the LEC further increasing the radius and drawing in still more fluid (upper branch from point 0 to point 2 on Fig 5b). The instability persists until the radius becomes large enough at point 2 that the shear stresses begin to drop because more cross-sectional area is available for lymph flow. Thereafter the release of NO occurs more slowly than its degradation so that the system can return stably to equilibrium along the lower branch of the trajectory from point 2 to 0. Mathematically, the unstable increase in radius persists until the sign of $\dot{R}$ changes at point 2. A change in the sign of $\dot{R}$ does not require that the eigenvalues move to the left half of the complex plane at point B on Fig 4 as required for inherent stability, but rather requires only that the radius increase sufficiently to move the eigenvalues off of the real axis beyond point A, thus permitting at least a partial cycle of oscillation that includes a time at which $\dot{R}=0$. As the vessel begins to contract, the sign of S_NOF_NO/DR² changes at the R-nullcline where $\dot{R}=0$, leading to an unconditionally stable return to the original radius. The time scale for contraction is approximated by t_c ≈ t_mech + t_NO + t_FNO where the three contributions arise from mechanical lag t_mech as before, the clearance of NO t_NO = 1/K_NO, and the rate of force modulation by NO t_FNO = S_NOF_NO/E₁K_NOR². To a similar degree of approximation, the instability of the NO-shear dynamics requires t_mech + t_NO ≤ t_FNO. In other words, the change in force elicited by shear stress must persist longer than processes that tend to dissipate its effects. Exact algebraic expressions for the eigenvalues may be employed if desired, but this approximation captures the key dependencies. See Table 2.

Fig 5. a) Generic time response and b) phase portrait of the shear-NO oscillator.

Following a small perturbation shown as a green arrow near equilibrium at point 0, by either a decrease in radius or an increase in concentration, the radius increases unstably (red arrows $\dot{R}>0$) until $\dot{R}=0$ at point 2. Thereafter, the trajectory begins a stable return (blue arrows $\dot{R}<0$) to equilibrium at point 0. NO reaches its peak concentration at point 1 before the radius reaches its maximum, but this point does not directly influence the stability of the system.

Table 2. Representative Time Constants Based on Parameters in Table 1.

	Equilibrium Radius	Linearized Stiffness	Mechanical Time Constant	Calcium Clearance Time Constant	NO Clearance Time Constant	NO-Shear Time Constant	Overall Time Constant
	R1(m)	E1(Pa/m)	tmech(s)	tCa(s)	tNO(s)	tFNO(s)	tc(s)
pm = 100 Pa α = 1 β = γ = 0	8.5x10-5	2.45x106	1.22	1	0.2	3.35	4.77
pm = 500 Pa α = 1 β = γ = 0	1.51x10-4	1.23x107	0.24	1	0.2	0.21	0.66

The NO cycle can be generalized into a controllable and synchronizable oscillator. Fig 6 shows the behavior of the NO cycle in response to small random disturbances. During the stable contraction process, the vessel remains refractory to disturbances until close enough to equilibrium for a random disturbance to trigger another cycle, much as we found with the stretch-Ca process. Here the period of the NO-induced oscillations varies as t_c log(C_max/σ) as before but t_c and C_max now refer to NO rather than Ca²⁺. As with Ca²⁺, a relatively quiet environment or reduced sensitivity to disturbance will elicit longer latency periods between cycles but will not significantly change the shape of the shear-NO cycle.

Fig 6. Shear-NO dynamics at constant Ca²⁺ with noise triggering.

At low pressure a-c) p_m = 100 Pa, t_Ca = 1 s, t_mech = 1.22 s, t_NO = 0.2 s and t_FNO = 3.35 s where the shear-NO oscillator is unstable (t_mech + t_NO < t_FNO) and at a higher pressure d-f) p_m = 500 Pa, t_Ca = 1 s, t_mech = 0.24 s, t_NO = 0.2 s and t_FNO = 0.21 s where the shear-NO oscillator is stable (t_mech + t_NO > t_FNO) yielding little change in radius. The noise level is σ = 0.01. In each case the overall time constant for return to equilibrium is given approximately by t_mech + t_NO + t_FNO. The period is predicted approximately by t_c log(C_max/σ) where C_max is the amplitude of the changes in NO concentration.

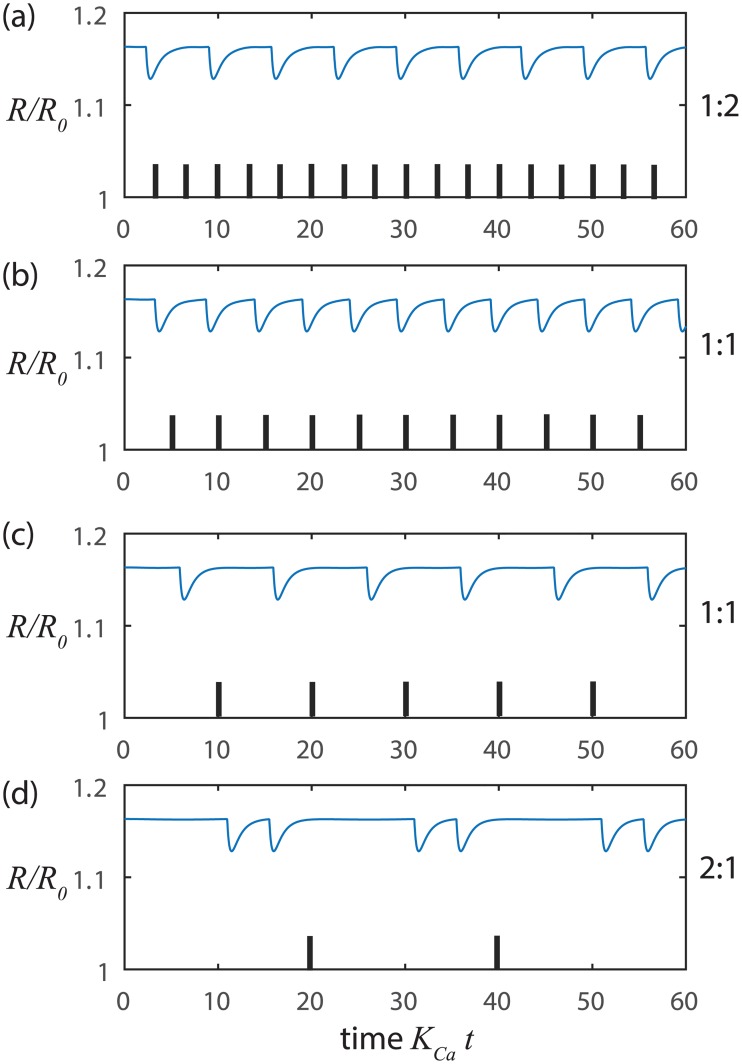
The NO dynamics can also readily synchronize with externally-imposed, small-amplitude sinusoids (Figs 7 and 8). Fig 7b and 7c show how the radius oscillates at precisely the input frequency for frequencies reasonably close to the response when noise triggered (Fig 6). However, when the input frequency is too high (Fig 7a) or too low (Fig 7d) synchronization occurs, but at half or double the input frequency, respectively. Fig 8 shows a parametric study of synchronization over a wide range of input frequencies and amplitudes where we find that synchronization can include a variety of integer ratios between input and output frequencies as explained further in the Discussion.

Fig 7. Synchronization of shear-NO dynamics with small amplitude sinusoidal inputs at constant Ca.

At lower pressure p_m = 100 Pa, t_Ca = 1 s, t_mech = 1.22 s, t_NO = 0.2 s and t_FNO = 3.35 s where the shear-NO oscillator is unstable (t_mech + t_NO < t_FNO) with input amplitude of 0.01 and input frequencies of a) 0.08 Hz, b) 0.04 Hz, c) 0.02 Hz and d) 0.01 Hz. The tick marks indicate the beginnings of successive cycles of the sinusoidal input signal. The ratio of the output frequency to the input frequency is at the right of each panel.

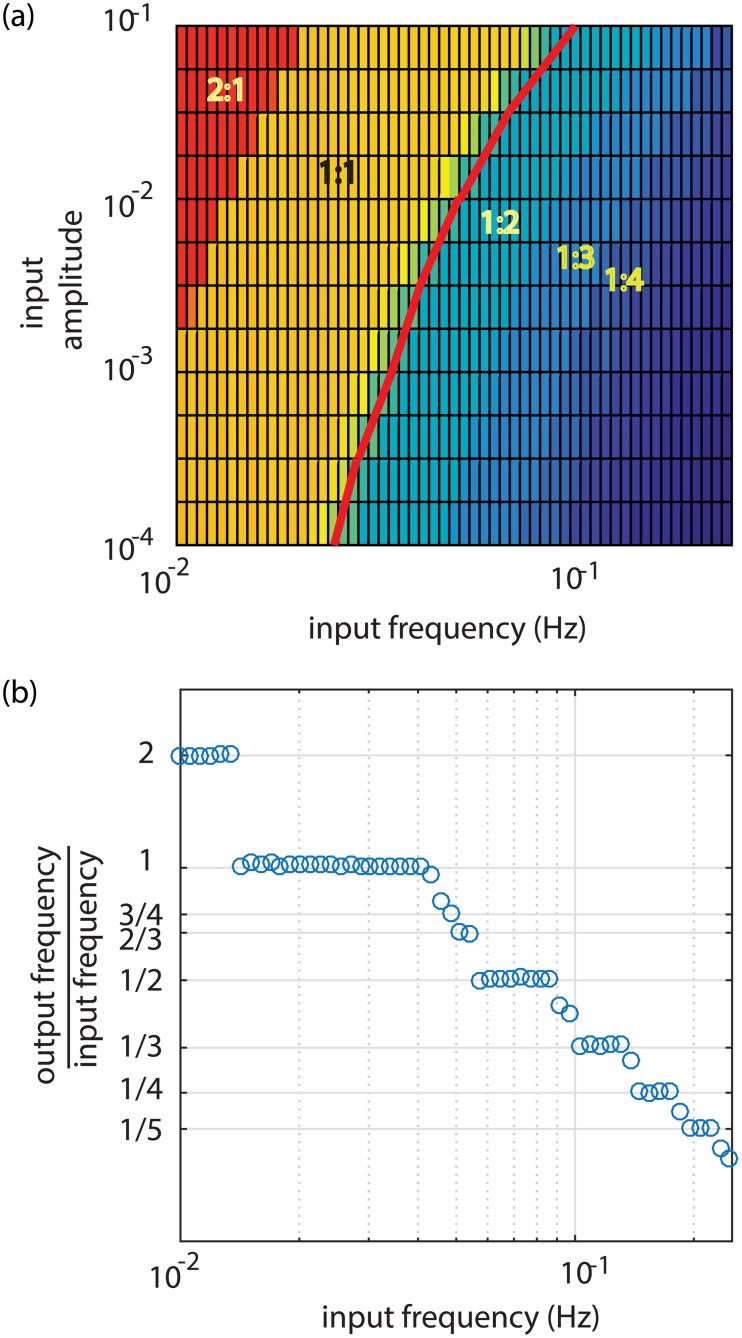
Fig 8. Synchronization of the shear-NO oscillator with a sinusoidal input.

a) Color bands indicate domains in which the output and input frequencies lock into simple, integer ratios. The red curve gives an estimate of the autonomous frequency from f = 1/(t_clog(C_NOmax/σ) where the amplitude of the noise has been replaced by the amplitude of the input sinusoid, b) Output frequencies at input amplitude of 0.01 showing a so-called Devil's staircase of discrete, rational values.

Combined Stretch-Ca²⁺ and Shear-NO Dynamics

Having explored the system dynamics when Ca²⁺ and NO are taken to be constant relative to each other we now consider their combined, dynamic effects. Our model includes three possible interactions reported in the literature: NO may i) desensitize the LMCs to Ca²⁺ as modeled by Eq 10, ii) modify the availability of Ca²⁺ by 1/(1 + γC_NO) or iii) speed clearance of Ca²⁺ by 1 + βC_NO [41, 42].

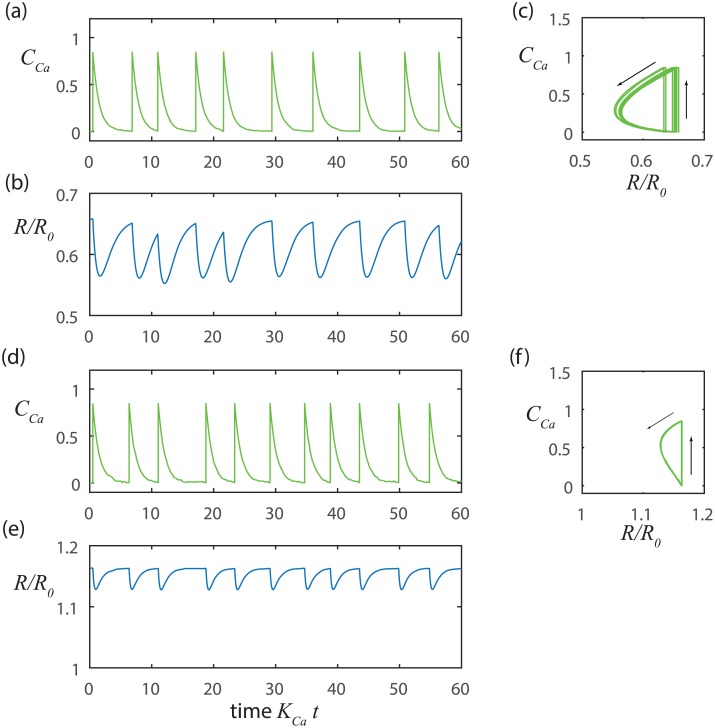
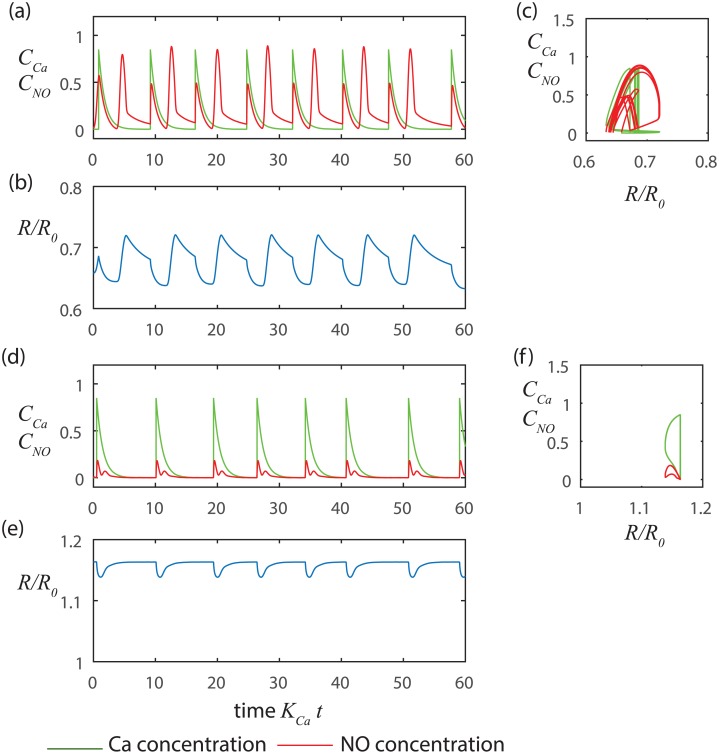
Our simulations (Fig 9) show that the dynamic effects of NO are most pronounced when the shear-NO dynamics are unstable. When the shear-NO dynamics are unstable, the radius can overshoot the nominal radius before or after a Ca²⁺-induced contraction, yielding oscillations in radius that are more symmetrical about equilibrium than when shear-NO is stable. At marginal stability (Fig 9d), the NO concentration rings at a frequency determined by the point where the eigenvalues of the shear-NO oscillator cross the imaginary axis f = (E₁K_NO/D)^1/2/2π. At larger radii, the shear-NO mechanism is inherently stable, but can still reduce the magnitude of the oscillations driven by the stretch-Ca²⁺ process. This process is important in the presence of an assisting pressure gradient because the dilation induced by the forced flow can put the vessel into the range of radii where the shear-NO mechanism can inhibit contractions that would otherwise tend to restrict free flow through the vessel.

Fig 9. Fully coupled Ca²⁺ and NO dynamics operating autonomously.

a-c) Low pressure (small radius) with overshoot of the nominal radius due to instability in the NO dynamics leading to Fig 8 trajectories in phase space (t_mech + t_NO < t_FNO) p_m = 100 Pa, t_Ca = 1 s, t_mech = 1.22 s, t_NO = 0.2 s, and t_FNO = 3.35 s, d-f) Higher pressure (large radius) without overshoot due to stable NO dynamics (t_mech + t_NO > t_FNO) p_m = 500 Pa, t_Ca = 1 s, t_mech = 0.24 s, t_NO = 0.2 s and t_FNO = 0.21 s. Note the decaying oscillations of the NO concentration in panel d. Near marginal stability (t_mech + t_NO + t_FNO) the NO concentrations oscillates at a frequency approximated by f = (E₁K_NO/D)^1/2/2π which corresponds to where the eigenvalues cross the imaginary axis at point B on Fig 4.

The overall frequency is set by a complex interplay of stretch-Ca²⁺ and shear-NO mechanisms, but will typically be dominated by the faster of the two processes. Long latency intervals between Ca²⁺-induced contractions can permit NO to produce an unstable dilation, whereas, short intervals due to Ca²⁺ can suppress the autonomous oscillations possible through the NO mechanism. Interestingly, the published clearance rates for Ca²⁺ and NO cover a wide enough range that either possibility exists in vivo [15, 32].

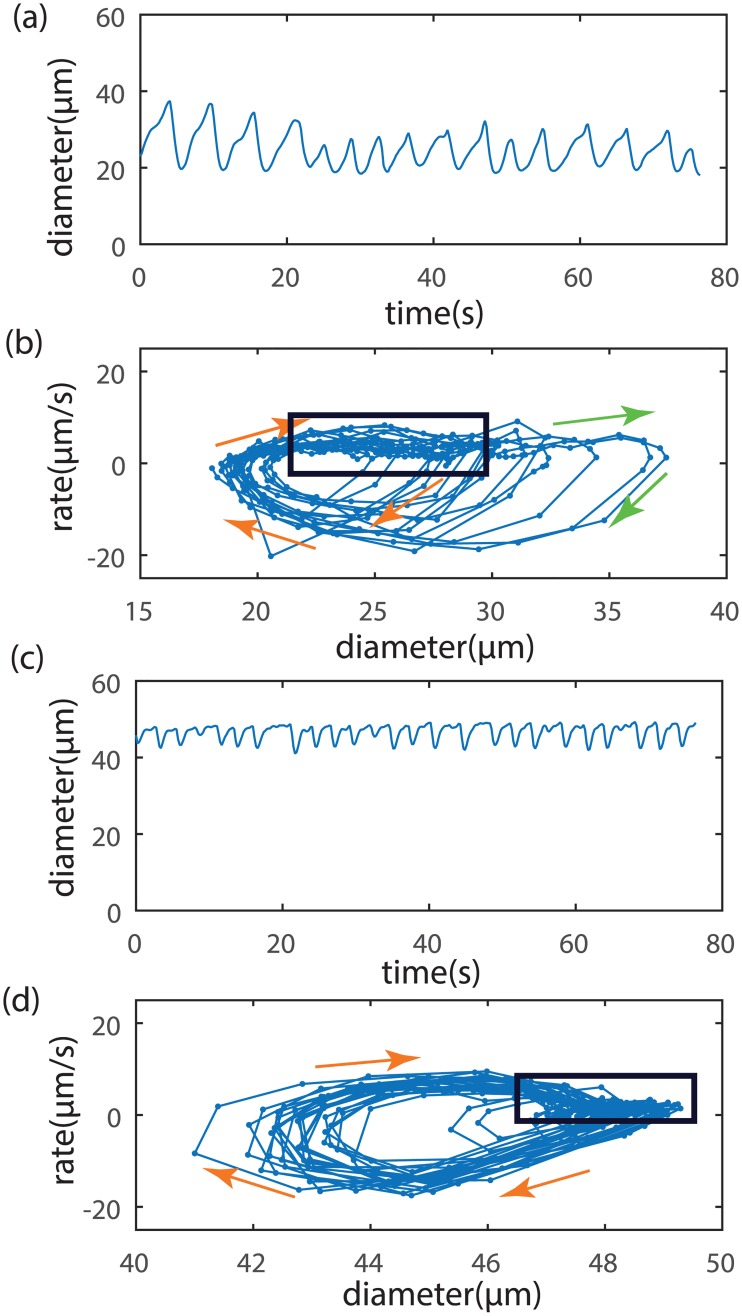
Experimental observations of diameter in vivo show cycles consistent with the model predictions (Fig 10) (data from [20]). In the absence of direct measurements of concentrations, we employ an alternative phase portrait of diameter plotted against the rate of change of diameter. Fig 10a and 10b are from a wild-type mouse in which Ca²⁺ and NO effects can operate normally. Here, we observe complex oscillations that include both rapid contractions and occasional strong dilations above the baseline diameter as expected from the shear-NO mechanism. In contrast, when the NO effects have been genetically deleted in eNOS^-/- mice in Fig 10c and 10d, we see wave forms that are nearly identical to each other but dominated by contraction with the dilatory effects of NO appearing to be substantially weakened. In all cases, we see cycles occurring on irregular intervals as we expect from noise-triggered oscillators.

Fig 10. Typical in vivo experimental measurements of lymphangion diameter (a,c) in a mouse with phase portraits of diameter vs. rate of diameter change (b,d) [20].

a,b) Wild type mice with Ca²⁺ and NO active. c,d) NO effects genetically deleted in eNOS^-/- mice. Spacing of data points indicates the rate of motion in the phase plane (sampling period 0.21 s). The box surrounds a region of closely spaced points indicative of an equilibrium condition. Orange arrows show the trajectory during a contraction, while green arrows show a dilation. Contraction and dilation dynamics are generally more erratic when the vessel is small and has active NO than when the vessel is larger and has suppressed NO activity.

Discussion

While the correspondence between the experiments and the model is encouraging, we should not expect a model of an isolated lymphangion to reproduce all features of a vessel in an intact, in vivo vascular network. For example, the effects of flow introduced from upstream or disturbances from surrounding tissue are inputs present in the animal, but are not included in the modeled dynamics. We have also not yet included effects due to nonlinear valve efficiencies or the bias of the check valves toward the open position [43]. Nonetheless, phase portraits, such as those newly employed here, promise to assist further study of the nonlinear dynamics that govern vascular oscillations.

While our results await further experimental validation and improved estimates of key parameter values, it is interesting to consider the newly identified shear-NO oscillator more generically from a nonlinear dynamics perspective. The shear-NO oscillator has some important similarities and differences from the well-known Van der Pol oscillator [44] which has the form

$$\ddot{x}-A(1-x^2)\dot{x}+x=g(t)$$ (14)

The form of the characteristic polynomial in Eq 13 implies that the shear-NO oscillator may be written as

$$\ddot{x}+A(1-sgn(\dot{x})B/x^2)\dot{x}+(x-x_1)=g(t)$$ (15)

where the generic variable x fills the role of the radius in the shear-NO model, x₁ is the nominal operating point and g(t) is a forcing function that can include steady, random or periodic components.

The stability-determining second term in both oscillators can change sign based on the magnitude of the variable with a positive second term implying stability. The Van der Pol oscillator is known to self-sustain oscillations about the origin in phase space $(x,\dot{x})=(0,0)$ when g(t) = 0, as its second term changes sign during different phases of each cycle. In contrast, the shear-NO oscillator operates near $(x,\dot{x})=(x_1,0)$, but with x > x₁. Therefore, the second term in Eq 15 can be either i) always be positive ($x_1^2>B$) regardless of the sign on $\dot{x}$ implying inherent stability or ii) can be conditionally positive depending on both the magnitude of B and the sign of $\dot{x}$. As a result, the shear-NO oscillator cannot produce self-sustained oscillations for large radius ($x_1^2>B$). Furthermore, even when the radius is sufficiently small ($x_1^2<B$), the radius will return unequivocally to equilibrium as long as $\dot{x}$<0 unless a non-zero forcing function is present to change the sign of $\dot{x}$. However, we find that when $x_1^2<B$ the magnitude of the forcing needed to start a new cycle can be arbitrarily small and in the form of either random noise or a periodic stimulus provided that enough time has passed for the system to approach its equilibrium point.

In the context of the shear-NO dynamics, the key to oscillations is the inverse dependence on radius for the NO source due to shear stress in Eq 7. As long as the exponent on R⁻² remains negative (increasing radius leading to lower shear stress and less NO production), then the NO-shear mechanism will be capable of a mathematical transition from unstable to stable as seen above in the generic oscillator in Eq 15. The physiological impact of this result then depends on the relative magnitude of the time scales identified herein, not on any single parameter value. For example, the stability of the NO-shear mechanism depends on groups of parameters such as t_FNO = S_NOF_NO/E₁K_NOR², which combines the sensitivity of the vessel to shear stress, the contractile force, the wall stiffness and the NO clearance rates.

Inputs of constant magnitude have the effect of adjusting the equilibrium point. Using the shear NO oscillator as an example, an increase in transmural pressure will dilate the vessel, as will a pressure gradient that assists flow by inducing NO production via a steady shear stress. Likewise, a steady source of NO from local inflammation will chronically dilate the vessel [20]. If the vessel becomes sufficiently large, the stability criterion found above suggests that the shear-NO process will not support self-sustaining oscillations, in part due to the direct effect of radius on the stability criterion, but also due to greater stiffness of the wall at larger radius (higher E₁). Nonlinearities in the force production and chemical source/elimination terms may also alter the stability in similar ways.

Numerical simulation and examination in the phase plane reveal that the stretch-Ca²⁺ and shear-NO processes possess numerous symmetries that offer intriguing possibilities when the processes act together (Figs 2 and 6, Table 3). Most notably, we see that the shear-NO process produces rapid and unstable dilation toward a larger radius, followed by stable contraction, while the stretch-Ca²⁺ process causes the vessel to contract rapidly and unstably toward a smaller radius and then to dilate stably. An essential feature of both the Ca²⁺ and NO mechanisms is that taken separately they do not produce traditional, self-sustaining limit cycles, but instead have a one-sided stability near equilibrium from which a new cycle begins only with a perturbation from the local environment. Interestingly, a suitable trigger for the stretch-Ca²⁺ oscillator can be an increase in radius produced by the shear-NO mechanism. And conversely, the shear-NO oscillatory can be triggered by a contraction arising from the stretch-Ca²⁺ mechanism. Balanov et al [45] reviews a variety of similar, so-called “noise-induced” oscillators in contexts outside of lymphatic physiology such as neurons and electrical monovibrators, but to our knowledge, the coupling of symmetric, noise-induced oscillators described in the present study has not been previously investigated.

Table 3. Comparison of Ca²⁺-Stretch and NO-Shear Mechanisms Acting Alone.

	Ca2+-Stretch	NO-Shear
Sequence	Contraction then dilation	Dilation then contraction
Contraction Speed	Fast	Slow
Dilation Speed	Slow	Fast
Phase Plane Trajectory	Clockwise	Counterclockwise
Contraction Stability	Unstable	Stable
Dilation Stability	Stable	Unstable for small R1
Trigger	Increasing R	Decreasing R
Time Constant During Stable Return	$t_c\approx \text{max}(\frac{1}{K_{Ca}},\frac{D}{E_1})$	$t_c\approx \frac{1}{K_{NO}}+\frac{D}{E_1}+\frac{S_{NO}{F}_{NO}}{E_1{K}_{NO}{R}_1^2}$
Effect of Noise on Period	Increasing period with smaller noise T ≈ tc log(CCamax/σ)	Increasing period with smaller noise T ≈ tc log(CNOmax/σ)
Effect of Radius on Frequency	Increasing frequency with larger R1	Increasing frequency with larger R1
Effect of Radius on Amplitude	Decreasing amplitude with larger R1	Decreasing amplitude with larger R1

Balanov et al [45] also review how nonlinear oscillators can synchronize with small-amplitude sinusoidal inputs. Here we found that synchronization of either oscillator can occur over a wide range of frequencies (shear-NO shown in Fig 8, similar behaviors for stretch-Ca²⁺ acting alone and in combination with shear-NO can be observed). The synchronization behavior seen here is similar to that for the forced Van der Pol oscillator in its ability to produce so-called Arnold tongues which are broad domains within which the input and output frequencies are locked in ratios of m:n where m and n are small integers [44, 46].

Kornuta et al [47] recently showed that lymphatic vessels studied ex vivo synchronize their contractions in a 1:1 fashion with imposed oscillatory variations in shear stress when the amplitude of the stimulus is sufficient large and the frequency of the input is relatively close to the autonomous frequency. Interestingly, they also observed that small amplitude variation in transmural pressure did not yield 1:1 frequency locking. However, our examination of their results (Fig 8 in [47]) suggests that 2:3 locking may have occurred. In the absence of imposed flow, they also found that the vessel continued to contract, but with a lower and more erratic frequency consistent with our simulated noise-triggered oscillator (Figs 2 and 3) in the absence of the shear-NO mechanism. Ohhashi et al [48] also examined sinusoidal variations in transmural pressure at frequencies well away from the spontaneous frequency. Here too, 1:1 frequency locking did not arise, but the frequency of the contractions responded strongly to the input waveform. Given the subtlety of identifying non-1:1 synchronization, further examination of the experimental record may be warranted.

In conclusion, we have presented a model of a vascular oscillator. The present analysis is sufficiently general to point toward several features that are likely found in other systems. The linear stability analysis shows: (i) complementary mechanisms for dilation and contraction of collecting lymphatic vessels, (ii) a fast, unstable process that recovers slowly and stably to a one-sided equilibrium, (iii) disturbance-based triggering that facilitates either synchronization with a cyclic pacemaker or spontaneous oscillations from random disturbances and (iv) the capability for reciprocal modulation between contractile and relaxation effects. Those features are not only limited to the presented example of Ca²⁺ and EDRFs but can be extended into other fields. The ability of the Ca²⁺ and NO based oscillators to respond to each other and external stimuli explains how lymphatic pumping can be coordinated along extended lengths of collecting lymphatic vessels without the need for higher order coordination. This new class of coupled, noise-driven oscillator can help to explain the diverse pumping behavior of lymphatic vessels.

Data Availability

The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper and its Supporting Information files.

Funding Statement

This work was funded by National Institutes of Health Grants R01-HL149285 (to LLM), R21-AI097745 and DP2-OD008780 (to TPP), and R01-HL128168 (to JWB, TPP, LLM) nih.gov. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.