Novel, full 3D scintillation dosimetry using a static plenoptic camera

Abstract

Purpose:

Patient-specific quality assurance (QA) of dynamic radiotherapy delivery would gain from being performed using a 3D dosimeter. However, 3D dosimeters, such as gels, have many disadvantages limiting to quality assurance, such as tedious read-out procedures and poor reproducibility. The purpose of this work is to develop and validate a novel type of high resolution 3D dosimeter based on the real-time light acquisition of a plastic scintillator volume using a plenoptic camera. This dosimeter would allow for the QA of dynamic radiation therapy techniques such as intensity-modulated radiation therapy (IMRT) or volumetric-modulated arc therapy (VMAT).

Methods:

A Raytrix R5 plenoptic camera was used to image a 10 × 10 × 10 cm³ EJ-260 plastic scintillator embedded inside an acrylic phantom at a rate of one acquisition per second. The scintillator volume was irradiated with both an IMRT and VMAT treatment plan on a Clinac iX linear accelerator. The 3D light distribution emitted by the scintillator volume was reconstructed at a 2 mm resolution in all dimensions by back-projecting the light collected by each pixel of the light-field camera using an iterative reconstruction algorithm. The latter was constrained by a beam's eye view projection of the incident dose acquired using the portal imager integrated with the linac and by physical consideration of the dose behavior as a function of depth in the phantom.

Results:

The absolute dose difference between the reconstructed 3D dose and the expected dose calculated using the treatment planning software Pinnacle³ was on average below 1.5% of the maximum dose for both integrated IMRT and VMAT deliveries, and below 3% for each individual IMRT incidences. Dose agreement between the reconstructed 3D dose and a radiochromic film acquisition in the same experimental phantom was on average within 2.1% and 1.2% of the maximum recorded dose for the IMRT and VMAT delivery, respectively.

Conclusions:

Using plenoptic camera technology, the authors were able to perform millimeter resolution, water-equivalent dosimetry of an IMRT and VMAT plan over a whole 3D volume. Since no moving parts are required in the dosimeter, the incident dose distribution can be acquired as a function of time, thus enabling the validation of static and dynamic radiation delivery with photons, electrons, and heavier ions.

I. INTRODUCTION

Recent advances in linac technology, on both hardware and software control, have enabled the development and widespread use of dynamic radiotherapy techniques such as intensity-modulated radiation therapy (IMRT),^1,2 volumetric-modulated arc therapy (VMAT),^3,4 and tomotherapy⁵. The complexity of these delivery techniques calls for a personalized treatment quality assurance (QA), which is usually performed using 2D dosimetry.^6,7 However, as 2D measurements only represent a partial sampling of the planned 3D dose distribution, it is recognized by the medical physics community that only 3D dosimeters offer a truly comprehensive verification of dynamic dose delivery.^7,8 Moreover, it is our hypothesis that the validation of such dynamic treatment techniques would benefit from a real-time dosimeter, i.e., a detector which would record the incident dose distribution as a function of time.

Current dosimetric systems using polyacrylamide,^9,10 Fricke,^11,12 or radiochromic^13,14 gels offer desirable levels of precision and accuracy at a spatial resolution ranging from 0.5 to 5 mm. However, these systems have several disadvantages limiting to quality assurance. Indeed, most gel dosimeters involve laborious and time consuming preparation and processing manipulations, leading to variations between gel batches, as well as delayed dose information. Moreover, gels are, fundamentally, integrating dosimeters and can only provide information on the total dose delivered and do not qualify as real-time detectors. Hence, many groups are researching on the use of scintillator volumes or liquids to perform 3D dosimetry. Many of these dosimeters make use of the concept of tomography to reconstruct a 3D scintillation volume from many different perspectives (or projections).^15–17 While these techniques have shown potential to perform accurate dosimetry on a whole 3D volume, their application to dynamic, modulated radiation delivery is not straightforward, since components of the dosimeter need to rotate during acquisition, a fact which limits their real-time capability. Some other approaches use only fixed components to image and reconstruct a scintillating volume in real-time.^18,19 However, these techniques are usually restrained to very simple fields, such as intensity-modulated proton therapy or square photon fields, as a limited number of perspectives are used to image the scintillation volume of interest.

In this work, we investigated the possibility of conducting real-time 3D dosimetry on a volume of plastic scintillator using the light acquisition from a plenoptic camera. The main advantage of plenoptic cameras over conventional ones is that the light rays integrated by each pixel of the camera sensor originate from a known and restrained angle range. Thus, with the constraint of a beam's eye view projection of the deposited dose, the light integrated by each plenoptic camera sensor pixel can be back-projected into the scintillator volume using reconstruction algorithms similar to those developed for tomodosimetry,²⁰ computed tomodensitometry (CT), or positron emission tomography (PET). This kind of methodology allows for water-equivalent, high resolution, real-time, and full 3D dosimetry using only static detectors and phantoms.

We designed a 3D tomodosimeter based on the plenoptic camera technology to reconstruct the incident dose distribution on a volume of plastic scintillator as a function of delivery time. In this study, we developed the background method of 3D light reconstruction from a plenoptic camera acquisition and evaluated experimentally the detector's performance in the measurement of IMRT and VMAT clinical plans.

II. METHODS AND MATERIALS

II.A. Plenoptic camera

A plenoptic camera, also referred to as a light-field or a single lens 3D camera, consists of a conventional camera having an array of microlenses coupled to its digital image sensor. In photography or microscopy, this additional optical component allows an adjustment of the focus or the point of view of an image after it has been recorded.^21–25

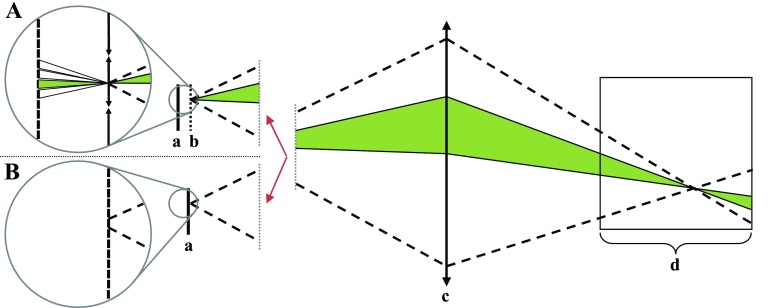
Figure 1 compares the ray tracings for a conventional and a plenoptic camera. The sensor pixels of a conventional camera solely record spatial information of incident photons: each sensor pixel is produced from the sum of all light rays striking the pixel's position. On the other hand, in a plenoptic camera, each microlens covers several sensor pixels, thus separating the light rays passing through the camera's main lens into smaller images recorded by the sensor. In this case, a sensor pixel represents a sum of light rays over a small portion of incident angles, providing spatial and directional information of incident photons. However, a point in the object side of the main lens can be imaged in more than one sensor pixel, thus reducing the spatial resolution of the system.²¹

FIG. 1.

Comparison of the ray tracings for a plenoptic (A) and a conventional camera (B). A conventional camera's sensor pixel intensity represents a sum of light rays over all incident angles (dotted lines). A plenoptic camera's sensor pixel intensity is produced by a sum of light rays from a small, known range of incident angles (shaded region). (a) Camera sensor; (b) microlens array; (c) main lens; and (d) scintillator volume.

Different types of plenoptic cameras differ mainly by the distance between the array of microlenses and their sensor. “Standard” plenoptic cameras set this distance to the focal length of one microlens, which is usually around 500 μm. This configuration has the advantage of providing maximal angular resolution of the captured light-field at the expense of a very coarse spatial resolution.²¹ In a “focused” plenoptic camera, this distance is made smaller (for a virtual main lens image) or larger (for a real main lens image) than the microlens focal length.²³ This type of configuration allows for a compromise between angular resolution and spatial resolution, maintaining the latter sufficiently fine for photography standards.

The purpose of a plenoptic camera in 3D dosimetry is based on using the angular information gathered from an imaged scintillator volume to reconstruct the 3D emitted light pattern. Using the spatial and directional information recorded by the plenoptic camera, an iterative, expectation maximization algorithm back-projects the photons received by the sensor pixels into the scintillating volume. The 3D dose distribution inside the scintillator volume can then be obtained from the 3D light pattern, as the light yield of organic scintillator is proportional to the energy deposited in its volume, independently of dose rate or energy in the therapeutic photon energy range.²⁶

II.B. Dose integral calculation

The relationship between a plenoptic camera pixel intensity and the dose deposited in each region of a scintillator volume is in essence very similar to the relationship between the light yield of a long scintillating optical fiber and the dose profile incident on the fiber.^16,20,27 Mathematically speaking one has:

$$\vec{p}=A·\vec{D},$$ (1a)

where $\vec{p}=\left\{p_j:j\in \left\{1,...,n\right\}\right\}$ is the vector of weighted dose integrals, n is the number of plenoptic camera sensor pixels used, $\vec{D}=\left\{D_i:i\in \left\{1,...,m\right\}\right\}$ is the vector of three-dimensional dose distribution, m is the number of dose voxels in the scintillator volume, and A is the n × m projection matrix. Each element A_j,i of this projection matrix corresponds to the contribution of the ith dose voxel to the jth weighted dose integral. Details on the calculation of A are provided in Sec. II C.

The weighted dose integral (p_j) for each plenoptic camera sensor pixel is computed from its collected intensity (I_j) using the formalism developed for 2D tomodosimetry:²⁰

$$p_j=\frac{I_j}{I_{j,\mathrm{ref}}}·A_{j,*}·{\vec{D}}_{\mathrm{ref}},$$ (1b)

where the indices “ref” refer to a normalization field of known 3D dose distribution, ${\vec{D}}_{\mathrm{ref}}$ represents the vector of the three-dimensional dose distribution of the normalization field and A_j,* represents the jth row of the projection matrix A of Eq. (1a). As was the case for 2D tomodosimetry, ${\vec{D}}_{\mathrm{ref}}$ should ideally be known to a good precision (e.g., using a square or near-square radiation field) since an error on ${\vec{D}}_{\mathrm{ref}}$ could bias the computation of the weighted dose integrals, and thus the results of the 3D dosimeter. Additionally, the normalization field should be wide enough as to enable the simultaneous irradiation of the whole scintillator volume.

The main difference between the weighted dose integrals calculated for a scintillating optical fiber and those calculated for a volume of scintillator is that, for the latter case, optical artifacts affect the propagation of light inside the scintillator and in the camera lens system. While most of these optical artifacts can be taken into account directly by the projection matrix A (see Sec. II C), optical scattering inside the scintillator volume is better modeled using a direct correction of the weighted dose integrals.

Two types of optical scattering were considered in this work. First order optical scattering represents the capacity of the scintillator and lens system to resolve a point light source inside the scintillator. If the magnitude of this effect is large in comparison to the system spatial resolution, its behavior can be modelled by the point-spread function (PSF) of the dosimeter system, and will affect the calculation of the weighted dose integrals as follows:

$$\vec{p}=A·\left(PSF\otimes \vec{D}\right),$$ (2a)

where the PSF is usually experimentally measured for a given scintillator and lens system.

Second order optical scattering represents the amount of light emitted from the whole scintillator volume by a point light source as a result of multiple absorption and reemission processes inside the scintillator. Moreover, due to the high refraction indices of scintillator plastic, light rays emitted inside the scintillator volume will be more likely to undergo total internal reflections, hence increasing the amount of light scattered far away from the emission point. Such behavior is modelled in this work as a homogeneous background of scattered scintillation light which is proportional to the total amount of dose deposited inside the scintillator volume. Mathematically speaking, one has

$$p_{j,c}=\frac{I_j-\beta ·{\sum }_i{A}_{j,i}{\sum }_i{D}_i}{I_{j,\mathrm{ref}}-{\beta }_{\mathrm{ref}}·{\sum }_i{A}_{j,i}{\sum }_i{D}_{i,\mathrm{ref}}}{A}_{j,*}·{\vec{D}}_{\mathrm{ref}},$$ (2b)

where p_j,c represents the corrected jth dose integral; β and β_ref are proportionality constants; and the summation on each row of the projection matrix (${\sum }_i{A}_{j,i}$) represents the geometric area of the scintillator contributing to the jth pixel. Note that since the dose inside the scintillator is usually not known during the dose integral calculation, the total amount of dose deposited inside the scintillator volume can be approximated as proportional to the total amount of light collected from the scintillator volume by all pixels of the CCD camera:

$$p_{j,c}=\frac{I_j-\alpha ·{\sum }_i{A}_{j,i}{\sum }_{j_2}{I}_{j_2}}{I_{j,\mathrm{ref}}-{\alpha }_{\mathrm{ref}}·{\sum }_i{A}_{j,i}{\sum }_{j_2}{I}_{j_2,\mathrm{ref}}}{A}_{j,*}·{\vec{D}}_{\mathrm{ref}},$$ (2c)

where α and α_ref are proportionality constants. Note that in the presence of a non-negligible first order optical scattering, ${\vec{D}}_{\mathrm{ref}}$ should also be convolved using the measured PSF of Eq. (2a).

II.C. Computation of the projection matrix

Each row of the projection matrix A represents the contribution of all dose voxels to the corresponding camera sensor pixel weighted dose projection. In this work, the computation of A was performed using paraxial ray tracing,²⁸ i.e., light rays were propagated, starting from the camera sensor pixel, through the microlenses and main lens, then finally inside the scintillator volume. The contribution of any given voxel to the weighted dose projection under analysis is then proportional to the path length of the light rays inside this voxel. More specifically, each row of the projection matrix A was calculated taking into account:

• •The size of the sensor pixel and all possible ray angles between the sensor pixel and its corresponding microlens;
• •The focal length of each of the microlenses and the main lenses, as well as the optical distance between each optical element;
• •The total internal reflection at each side of the scintillator volume;
• •The partial reflection at the back of the scintillator volume, using Fresnel equations;²⁸
• •The optical attenuation occurring inside the scintillator volume, following the exponential decay law. More specifically, the paraxial ray tracing was weighted by an exponential factor $e^{-\lambda ·x_{sc}}$, where x_sc represents the total distance travelled inside the scintillator volume by the considered ray.

The paraxial approximation was used for the ray tracing to optimize computational speed and also because the ray angles encountered were smaller than ±5° in our configuration. No visible lens aberrations (e.g., distortion, astigmatism, coma) were observed. Lens aberrations were thus deemed negligible, although their effects could also be incorporated into the calculations (e.g., by using nonparaxial ray tracing). Vignetting was also neglected in our calculation of A, since the illumination falloff for pixels far from the central optical axis was the same for the normalization field and the field under analysis, thus cancelling out when applying Eq. (1b) or (2c).

II.D. Reconstruction algorithm

Similarly to previous work on tomodosimetry, Eq. (1a) was solved using an expectation maximization (EM) algorithm.^16,20 In addition to the weighted dose projection acquired using the plenoptic camera, a relative 2D beam's eye view (BEV) projection of the incident dose distribution was measured to guide the 3D dose reconstruction process. Finally, an additional hypothesis on the relationship between the dose and the depth inside the scintillator was incorporated in the reconstruction algorithm. More specifically, it was assumed that the dose at any point in the scintillator was a smooth, decreasing function with respect to the distance to the radiation source (z_s), also taking into account the z_s⁻² geometric decrease on the dose.

Thus, based on our previously developed method of tomographic dose reconstruction,^16,20 each iteration of the reconstruction algorithm was split into three successive parts:

• (a)
  The constraints of Eq. (1a) were satisfied using the EM algorithm:

  $$\begin{array}{ccc}\hfill D_{i,EM}^{\left(k\right)}& =& D_i^{\left(k-1\right)}·\frac{1}{{\sum }_{j=1}^n{A}_{j,i}}\hfill \\ & & \times \left(\sum _{j=1}^n{A}_{j,i}\frac{p_{j,c}}{A_{j,*}·{\vec{D}}^{\left(k-1\right)}}\right),\hfill \end{array}$$ (3)

  where $D_i^{\left(k-1\right)}$ represents the value of D_i after the three parts of the previous iteration and $D_{i,EM}^{\left(k\right)}$ represents the value of D_i at the kth iteration of the algorithm after the application of the EM algorithm;
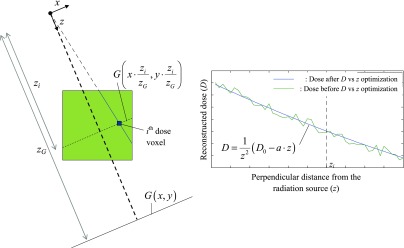
• (b)
  The reconstructed dose was constrained by the relative shape of the BEV projection. As seen in Fig. 2, the 2D BEV projection (G) is scaled at the height of each pixel of interest (z_i) and its magnitude is adjusted using ${\vec{D}}_{EM}^{\left(k\right)}$ from step (a). Mathematically speaking, one has

  $$\begin{array}{ccc}\hfill D_{i,\mathrm{BEV}}^{\left(k\right)}& =& G\left(x_i·\frac{z_i}{z_G},y_i·\frac{z_i}{z_G}\right)·\left(\frac{\int \int dx·dy}{\int \int G·dx·dy}\right)\hfill \\ & & ·\frac{{\sum }_{l=1}^m{D}_{l,EM}^{\left(k\right)}·\delta \left(z_i-z_l\right)}{{\sum }_{l=1}^m\delta \left(z_i-z_l\right)},\hfill \end{array}$$ (4)

  where δ represents the discrete Dirac delta function (which equals 1 only if its argument is zero); x_i, y_i, and z_i represent the spatial coordinate of the ith dose pixel in the radiation source frame of reference; z_G represents the perpendicular distance from the source to the BEV projection plane and $D_{i,\mathrm{BEV}}^{\left(k\right)}$ represents the value of D_i at the kth iteration of the algorithm after the application of the BEV projection constraints;
• (c)
  The reconstructed dose was constrained by the expected dose vs depth relationship inside the scintillator. This relationship hypothesizes a square law decay of the dose with respect to the radiation source perpendicular distance (z), convolved with a linear relationship between the remaining quantity (analog to the tissue-maximum ratio) and z. To realize this constraint, as seen on Fig. 2, a line passing through the radiation source and each pixel of interest is first plotted. Each value on this line is obtained from the trilinear interpolation of the $D_{i,\mathrm{BEV}}^{\left(k\right)}$ values of step (b). After applying a z⁻² factor on the obtained data to account for the square law decay of the dose, the remainder is then linearly fitted as a function of z. The obtained fit parameters are then used to evaluate the dose at the pixel of interest. Mathematically speaking, one has

  $$\begin{array}{c}\hfill D_i^{\left(k\right)}=\frac{1}{z_i^2}\left(D_{0,i}-a_i·z_i\right),\end{array}$$ (5)

  where D_0,i and a_i are the aforementioned linear fit parameters.

FIG. 2.

Schematic view of the reconstruction algorithm used in this work from the plenoptic camera point of view. After an expectation maximization step using the acquired dose projections from the camera, the dose at the plane located at a distance z from the source inside the scintillator volume (large square) is constrained using the relative dose distribution acquired using the beam's eye view projection (G) (left). Then, the dose at the ith dose voxel (small square) is optimized assuming a smooth, decreasing dose with respect to the distance to the radiation source (right).

The stopping criterion for the algorithm was based on the pixel-by-pixel absolute dose variation (ΔD):

$$\Delta D^{\left(k\right)}=\frac{\sum _i\left|D_i^k-D_i^{k-1}\right|}{V_s},$$ (6)

where V_s represents the total scintillator volume. Namely, the reconstruction process was terminated when ΔD went below a fixed threshold, set in this work at 10⁻⁹ cGy per cubic mm of reconstructed volume. It should be noted that the initial dose distribution in the algorithm (${\vec{D}}^{\left(0\right)}$), while arbitrary, should be nonzero. In this work, a homogeneous dose distribution of 0.01 cGy was chosen as ${\vec{D}}^{\left(0\right)}$.

II.E. Experimental prototype

The prototype presented in this work is composed of a 10 × 10 × 10 cm³ green plastic scintillator cube (EJ-260; density, 1.023 g/cc; Eljen technology, Sweetwater, TX) embedded in the center of a 10 cm radius by 17 cm long truncated cylindrical acrylic phantom (see Fig. 3). The scintillator was imaged with a “focused” plenoptic color camera (Raytrix R5, Raytrix GmbH, Kiel, Germany) using a f/2.9, 54 mm focal length lens (JML Optical Industries, Rochester, NY) and a 90° mirror to enable lead shielding of the camera during irradiation. The scintillator was covered on all sides except the one facing the plenoptic camera by a black cardboard and its center was placed at the isocentre of a Varian Trilogy linear accelerator (Varian Medical Systems, Palo Alto, CA). Light acquisition using the plenoptic camera was performed at a rate of one image per second, and each image recorded by the plenoptic camera was treated for transient noise coming from stray radiation.²⁹ Only the green pixels of the camera sensor were used in this work.

FIG. 3.

Experimental prototype used in this work. A 10 × 10 × 10 cm³ cube of green plastic scintillator (A) was inserted inside a cylindrical acrylic phantom (B) and imaged using a plenoptic camera (C) with the help of a 90° mirror (D) to enable radiation shielding of the camera. A beam's eye view projection of the incident radiation field was also acquired using the linac portal imager (E).

A beam's eye view projection of the incident radiation field was obtained using the raw images acquired using the linear accelerator portal imaging device. The imager was operated in the continuous acquisition mode at a rate of approximately three acquisitions per second. Each acquisition was corrected for imager sagging and was convolved using a Gaussian kernel to better model the penumbra region of each acquired field, as suggested in earlier publication on IMRT field verification using the EPID.³⁰ The 3D dose inside the scintillator volume was reconstructed at a resolution of 2 × 2 × 2 mm³ using the weighted dose projection calculated as in Sec. II B and the reconstruction algorithm described in Sec. II E. An 11 × 11 cm² square radiation field was used as the normalization field in weighted dose projection calculations performed using Eqs. (1b) and (2c). ${\vec{D}}_{\mathrm{ref}}$ was obtained for this normalization field using calculation performed by the treatment planning system (TPS) (Pinnacle³ 9.2, Philips Healthcare, Andover, MA) on a CT scan of the previously described phantom. An optical index of 1.58 and an attenuation length of λ = 1/150 cm⁻¹ was used in the calculation of the projection matrix (see Sec. II C), according to the scintillator manufacturer specifications.

The linac gantry angle, needed in the reconstruction algorithm (see Sec. II D), was determined directly from the linac interface for static gantry delivery, and calculated from the camera image acquisition in the case of dynamic gantry delivery. In the latter case, this information was determined using a maximum gradient search method on the intensity image recorded by the plenoptic camera.

II.F. Field acquisition

To evaluate the PSF of the scintillator and imaging system, an orthovoltage x-ray therapy system (Xstrahl200, Xstrahl Ltd., Camberley, UK) was used as a 180 kV photon radiation source to irradiate the cube. Two lead sheets of approximately 2 mm thickness each were used to create a scintillation edge at the center of the cube by shielding half of the top of the scintillator. The sheets were placed perpendicular to the central beam axis and the obtained edge-spread function (ESF) was then numerically differentiated to obtain a line-spread function (LSF), which was then fitted with a Gaussian curve to estimate the width of the PSF.

Parameters α and α_ref of Eq. (2c) were estimated using a 5 × 5 cm² 6 MV square photon field produced in the linear accelerator configuration of Sec. II E. Measured weighted dose projections calculated using Eq. (1b) were compared to the expected dose projections (p_j,e) calculated using the following formula:

$$p_{j,e}=A_{j,*}·{\vec{D}}_e,$$ (7)

where ${\vec{D}}_e$ represents the expected dose distribution of the 5 × 5 cm² field as calculated with the TPS on the phantom CT. Parameters α and α_ref were automatically adjusted until the difference between the weighted dose projections calculated from Eqs. (2c) and (7) was minimal.

Finally, two treatment plans from two clinical brain tumor cases were acquired using the dosimeter prototype. The first was a seven incidences step-and-shoot IMRT plan and the second was a 360° rotation SmartArc VMAT delivery, each delivered with 6MV photons. For each case, the reconstructed dose at a resolution of 2 × 2 × 2 mm³ was compared to the expected dose calculated using the Pinnacle³ TPS. Each delivery integrated dose was also compared to a radiochromic film acquisition. To do so for both treatment plans, the scintillator cube was removed from its acrylic phantom and replaced by three 11 × 10 cm² sheets of radiochromic film (Gafchromic EBT3, Ashland Inc., Covington, KY) immersed in water in a Lat/AP orientation. Each film was scanned in reflection mode using a flatbed scanner (Epson 10000XL, Epson Canada Ltd., Markham, Canada) before and 40 h after irradiation.³¹ Optical densities measured in the red channel were converted to dose with the help of a calibration curve. The latter was obtained using small squares of the same film batch irradiated inside a solid water phantom at the same linac used for irradiation.

III. RESULTS

III.A. Optical scattering characterization

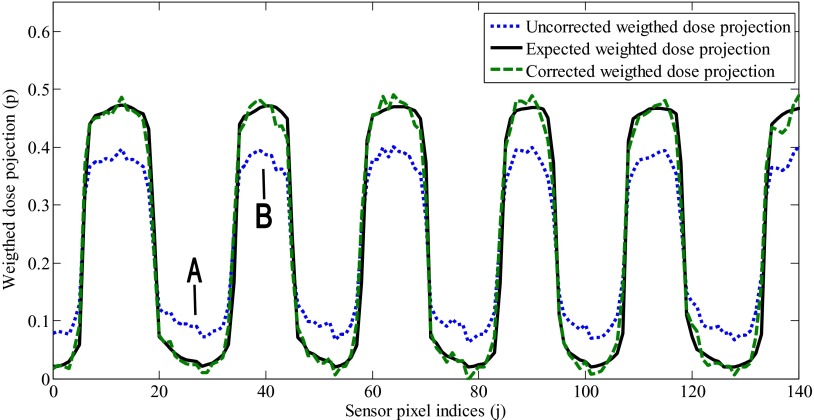
The full width half maximum (FWHM) of the measured PSF was of (0.5 ± 0.2) mm. As this width is small with respect to the length of each dose voxel (2 mm), the PSF was approximated by a Dirac delta function and Eq. (1a) was used instead of Eq. (2a) in the dose reconstruction process. The optimal value for the parameters α and α_ref of Eq. (2c) were found to be 4.0 × 10⁻⁶ and 4.2×10⁻⁶, respectively. The effect of the second order optical scattering correction on the weighted dose projections is presented in Fig. 4. Without second order optical scattering correction, the weighted dose projections are overestimated in the low-light region of the scintillator, while they are underestimated in the high-light region of the scintillator.

FIG. 4.

Second order scattering correction of the computed weighted dose projection (p) of a 5 × 5 cm² 6MV photon field. Due to scattering, the uncorrected weighted dose projections (dotted line) are overestimated in low-light regions (A) and underestimated in high-light regions of the scintillator (B). The calculated weighted dose projections were corrected using Eq. (2c) (dashed line) so that they matched the expected weighted dose projection calculated using Pinnacle³ (solid line).

III.B. 3D dose comparison with the TPS

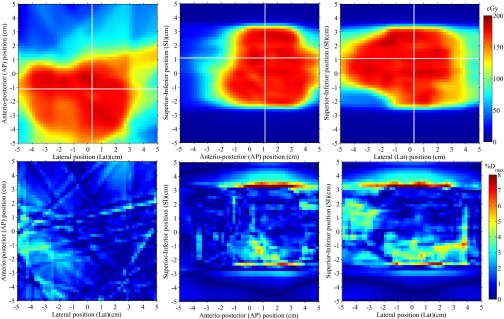
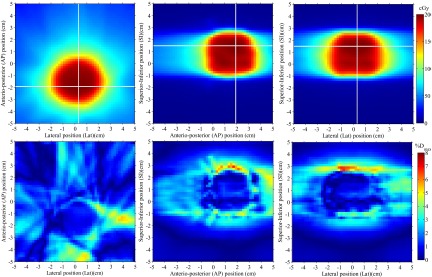
The 3D dose reconstructed inside the scintillator volume for the whole IMRT and VMAT plan are presented in Figs. 5 and 6, respectively. Three orthogonal 2D views of the reconstructed dose are presented for each plan, along with their absolute dose deviation from the expected TPS dose. Dose accuracy for the IMRT field was overall better than 4% of the maximum dose except for regions of high dose gradient. For the VMAT plan the accuracy was overall better than 3% of the maximum dose outside of high dose gradient regions.

FIG. 5.

3D dose reconstruction of a seven-field clinical step-and-shoot IMRT brain treatment. Three perpendicular dose planes are shown (top), along with their absolute dose differences with respect to the expected input dose from Pinnacle³ (bottom). Horizontal and vertical white lines on each 2D dose distribution represent the localization of the two other depicted dose planes.

FIG. 6.

3D dose reconstruction of a 360° rotation VMAT brain treatment. Three perpendicular dose planes are shown (top), along with their absolute dose differences with respect to the expected input dose from Pinnacle³ (bottom). Horizontal and vertical white lines on each 2D dose distribution represent the localization of the two other depicted dose planes.

The gamma test success rates and mean absolute dose difference for each reconstructed dose distributions are summarized in Table I. Each gamma test was performed using a linearly interpolated TPS dose distribution at a resolution of 0.1×0.1 mm² and a dose difference threshold expressed as a percentage of the maximum TPS dose. For all but two IMRT incidences, 3%/3 mm, 2%/2 mm, and 3%/1 mm gamma test success rates were greater or equal to 98.1%, 90.0%, and 93.7% for the pixels receiving over 10% of the maximum dose, respectively. Dose difference statistics were computed over the low gradient (<1% D_max/mm) region of each field. The mean absolute dose differences calculated over this region in the high dose (D > 50% D_max) and low dose (50% > D/ D_max > 10%) regions of the field were under 2% of the maximum dose for all but two incidences of the step-and-shoot IMRT plan.

TABLE I.

Gamma test success rates and mean gamma computed between the reconstructed dose planes and the predicted dose planes from the Pinnacle³ treatment planning system for a seven incidence step-and-shoot IMRT and an VMAT rotational plan.

								Mean absolute dose
		Gamma test (D > 0.10 Dmax)						difference (% Dmax)
		3%/3mm		2%/2mm		3%/1mm		High dose	Low dose
		Success	Mean	Success	Mean	Success	Mean	low gradient	low gradient
Field analyzed	Gantry angle (º)	rate (%)	gamma	rate (%)	gamma	rate (%)	gamma	regiona	regionb
Step-and-shoot IMRT fields	0	89.0	0.38	78.0	0.57	82.4	0.53	2.53	1.48
	51	99.2	0.28	92.2	0.41	93.7	0.47	1.72	1.46
	103	100	0.16	99.7	0.24	99.9	0.27	0.96	1.00
	145	98.9	0.25	94.4	0.38	95.1	0.40	1.32	1.70
	215	96.9	0.40	82.6	0.61	84.8	0.68	3.00	3.10
	257	98.1	0.26	90.0	0.39	95.6	0.41	1.98	2.20
	309	99.3	0.26	94.1	0.39	98.2	0.38	1.48	1.28
Step-and-shoot IMRT whole treatment		99.9	0.20	98.5	0.30	98.8	0.35	1.39	1.16
VMAT whole treatment		99.7	0.23	96.8	0.34	97.7	0.38	0.95	1.25

^aCalculated for each field over the region with dose higher than 50% D_max and gradient lower than 1% D_max/mm.

^bCalculated for each field over the region with dose lower than 50% D_max and gradient lower than 1% D_max/mm.

III.C. Dose comparison with radiochromic films

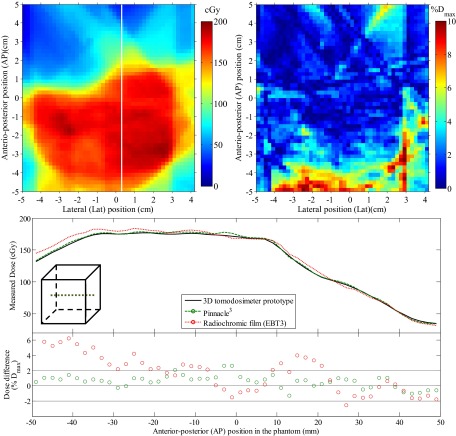
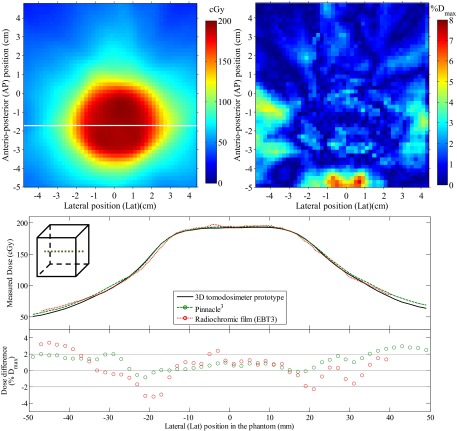
Comparison between the reconstructed dose in the scintillator volume and the dose measured using radiochromic films is presented in Figs. 7 and 8 for the whole IMRT and VMAT treatment, respectively. For the IMRT plan, dose differences were overall less than 5% outside of high dose gradient regions. A mean absolute dose difference of 2.1% was obtained in the high dose (D > 50% D_max), low gradient (<1% D_max/mm) region of the field and a mean absolute dose difference of 1.6% in the low dose (D < 50% D_max), low gradient (<1% D_max/mm) region of the field. For the VMAT plan, dose differences were overall less than 3% outside of high dose gradient regions. A mean absolute dose difference of 1.14% was obtained in the high dose (D > 50% D_max), low gradient (<1% D_max/mm) region of the field and a mean absolute dose difference of 1.15% in the low dose (D < 50% D_max), low gradient (<1% D_max/mm) region of the field.

FIG. 7.

Dose comparison between the reconstructed dose and a radiochromic film acquisition of a seven-field clinical step-and-shoot IMRT brain treatment. The dose measured by the radiochromic film is presented (top left) along with the 2D dose difference map with respect to the reconstructed 3D dose interpolated at the film position in the phantom (top right). An anterio-posterior dose profile is also presented for both the dosimeter and the reference dose from Pinnacle³ (bottom), along with the point-by-point dose difference with respect to the 3D dosimeter.

FIG. 8.

Dose comparison between the reconstructed dose and a radiochromic film acquisition of a 360° rotation VMAT brain treatment. The dose measured by the radiochromic film is presented (top left) along with the 2D dose difference map with respect to the reconstructed 3D dose interpolated at the film position in the phantom (top right). A lateral dose profile is also presented for both the dosimeter and the reference dose from Pinnacle³ (bottom), along with the point-by-point dose difference with respect to the 3D dosimeter.

IV. DISCUSSION

IV.A. Quality of the 3D dosimetry

The presented 3D dosimeter is capable of performing real-time, full 3D dosimetry of intensity-modulated plans at a resolution of 2 mm, which is, to the best of our knowledge, a first in the field of experimental dosimetry. In addition to the novelty of this approach, it also shows good accuracy for both IMRT and VMAT dose distributions. Namely, deviations between the reconstructed 3D dose distribution and the expected dose from the treatment planning system Pinnacle³ are typically within 3% of the maximum dose in the low dose gradient region of each field, as seen in Table I and Figs. 5 and 6. It should be also be noted that, although not explicitly visible in the presented results, the 3D dose distribution was obtained as a function of delivery time, a desirable feature for dynamic treatment experimental verification.

The benefit of using a plenoptic camera in this methodology comes from the fact that each pixel of the camera sensor is associated with a narrower spatial region of the 3D scintillator volume than in the case of a conventional camera, as seen in Fig. 1. As an example, while a conventional sensor pixel can integrate over a 10° range of incident light ray angles, the same sensor pixel in our plenoptic configuration covers less than a 1° range of angles. The loss in spatial resolution of the plenoptic camera image is not of particular importance, since the reduced spatial resolution remains under 0.2 × 0.2 mm² per sensor pixel at the point of focus, which is largely adequate for application in millimeter resolution dosimetry.

This level of dose accuracy could not be obtained using only the measured dose projections without some kind of orthogonal dose projection information. Indeed, similarly to what was observed with simulations in cylindrical tomodosimetry,¹⁶ the light impinging on the camera comes from a limited set of relatively small angles. This fact makes it impossible to resolve spatial details in the direction of increasing distance relative to the camera sensor. As the range of ray angles acquired using a single, fixed camera are very limited, the portal imager of the linear accelerator was used as a beam's eye view dose projection to improve the spatial resolution of the reconstructed 3D dose distribution, especially in the direction parallel to the main optical axis of the camera. The choice of the portal imager was made mainly because it is, by construction, always approximately perpendicular to the radiation field incidence, and it is also readily available on most linear accelerators. Without loss of generality and/or applicability of the proposed method, a second camera, plenoptic or conventional, could also have been used to acquire a beam's eye view projection by imaging the scintillator volume from the radiation source's point of view.

The resolution of the presented prototype, 2 mm in each spatial direction, is higher than most dosimetric gel systems¹⁰ but is still considered adequate for IMRT and VMAT QA applications. Indeed, Fourier analysis studies concluded that a dose grid resolution of 2.5 mm or lower would be sufficient to detect dose errors larger than a percent for IMRT cases.³² While this conclusion was made for 2D dose distributions, it is expected to extend to three-dimensional measurements. It should be noted that the well demonstrated properties of plastic scintillators²⁶ are also expected to apply to the 3D dosimetry using the present methodology. As such, the presented prototype is expected to show no dose or dose-rate dependence. Moreover, since most camera sensors have an adjustable acquisition time, no maximum usable dose range is foreseen. The time needed for each 3D dose reconstruction was of approximately 3 min per plenoptic camera acquisition on a 2.67 GHz CPU using a MATLAB^® implementation, but is expected to require only a few seconds per reconstruction using GPU implementation of the algorithm.³³ It should also be noted that the reconstruction time is expected to be proportional to the number of scintillator volume voxels and the number of camera sensor pixels. Stability of the response over time will mostly depend on the variation over time of the scintillator optical attenuation λ, which usually tends to increase with radiation damage in plastics. Although the optical attenuation is of minor impact in the presented methodology, any variations are expected to be accounted for using detector recalibration. Signal contamination by Cerenkov emission was evaluated to less than 0.5% of the collected scintillation light for all fields investigated, and therefore Cerenkov light filtration was deemed unnecessary.

IV.B. Comparison with radiochromic films

To account for possible errors in the TPS, a verification of the delivered dose on the scintillator was made using radiochromic films. Once again, the agreement between the 3D reconstructed dose and the radiochromic films were overall better than 5% for the IMRT delivery, and 3% for the lower gradient VMAT delivery, as seen in Figs. 7 and 8, respectively.

The higher dose differences between the radiochromic films and the 3D reconstructed dose than those of the previous comparison with the Pinnacle³ TPS are assumed to come from:

• (a)the high uncertainties of radiochromic films reading and processing, especially at low doses;³¹
• (b)the fact that the phantom was not 100% identical for the beam delivery on the scintillator volume and the radiochromic film. Indeed, in the latter case, the scintillator phantom cavity section not occupied by radiochromic films was filled with water. Although the scintillator itself is water-equivalent and a subsequent CT scan showed no important difference between the two phantom configurations, some dose inaccuracies could have been noticeable at the border of the scintillator cavity, where a small air gap was present in the scintillator configuration but not in that of the water fill-in;
• (c)some residual registration error between the scintillator and the 3D reconstructed dose, especially for the IMRT cases where higher dose gradients were observable.

IV.C. Optical scattering and other current limitations

Since the spatial magnitude of first order optical scattering (approximately 0.5 mm FWHM) is small with respect to the system's current spatial resolution (2 mm in each direction), we concluded that this effect need not to be considered significant, and thus Eq. (1a) was used instead of Eq. (2a) in the dose reconstruction process. However, as the spatial resolution of the 3D dose distribution is a free parameter in the reconstruction algorithm, this effect may be of interest in future work if the spatial resolution is to be improved.

The impact of second order optical scattering is however more important than first order scattering in the presented methodology. Indeed, without second order scattering corrections, the weighted dose projections can suffer from large relative errors, especially in regions of low light level (i.e., in the out-of-field regions), as seen in Fig. 4. However, such errors have only a small effect on the spatial resolution of the 3D reconstructed dose, as the latter is also constrained by the BEV projection. In our particular case, the BEV projection was free of second order optical scattering consideration, since the portal imager is sensitive to ionizing radiation only. Errors on the weighted dose projections caused by second order optical scattering will however largely affect the reconstructed dose output and should be corrected for optimal accuracy. The correction proposed in this work makes the assumption that the second order optical scattering magnitude is evenly distributed throughout the scintillator volume, and thus corrects each weighted dose projection of a given acquisition by the same amount [see Eq. (2c)]. A 5 × 5 cm² field was selected to determine the α and α_ref constants of Eq. (2c) mainly because it allowed the clear visualization of both low-light and high-light region in the scintillator (see region A and B in Fig. 4). It should be noted that the value of α_ref employed for the reference field correction was 5% higher than the value of α used every other acquired field correction. This difference was mainly attributable to the fact that only the reference field used in this work (11 × 11 cm²) was wide enough as to enable the irradiation of the whole scintillator cube, including its edges and external faces. It is hypothesized that imperfections at these edges and faces may have caused more second order scattering per deposited dose than for smaller radiation field. While second order optical scattering correction works well for most cases, as suggested by the results presented in Sec. III A, it may however be considered simplistic; thus, a more detailed model of second order scattering production inside the scintillator may lead to even more accurate results.

Apart from optical scattering, the main source of inaccuracy in the presented 3D dosimeter comes from the BEV projections itself. Indeed, while this projection mainly guides the 3D reconstruction by providing spatial information of the incident 3D dose pattern, it also influences the amount of out-of-field dose relative to the in-field dose recorded by the dosimeter. The choice of the portal imager to perform the BEV projection in this work was based on its availability and ease of use; however, it is not considered to be very accurate in the low dose regions without extensive correction factors such as nonuniform backscatter and flatness corrections.³⁰ An alternative to the portal dosimetry solution would be to use another high resolution 2D detector for the BEV projection, or even to image the scintillator volume from the source point of view using a mirror system or a second camera, either plenoptic or other.

Finally, the acquisition rate of the plenoptic camera is expected to influence the dose reconstruction process of dynamic arc delivery in the proposed method. Indeed, the linac gantry is considered static in the BEV and dose vs depth constraints of the presented algorithm (Eqs. (4) and (5), respectively), which is a valid approximation only if the acquisition time is small with respect to the gantry rotation speed. However, the shorter the camera acquisition time, the noisier each camera pixel data will be and the longer it will take to reconstruct the whole 3D dose for the entire treatment. The acquisition rate of one image per second was considered in this paper as a compromise between the abovementioned effects, but could be reduced in the future using, for example, a high sensitivity CCD sensor.^17,18

V. CONCLUSION

We developed a 3D dosimeter that allows the iterative reconstruction of full three-dimensional dose distributions in real-time using plenoptic camera technology. Dose reconstructions of both IMRT and VMAT fields showed promising results when compared to the planned dose calculated on the phantom geometry by the treatment planning software, and are comparable to the results obtained using radiochromic film acquisition. The presented prototype achieved water-equivalent, 2 × 2 × 2 mm³ resolution dosimetry on a 1000 cm³ volume using only a fixed plenoptic camera and the linac portal imaging device. We expect this kind of dosimeter to be very promising in dynamic treatment quality assurance, especially for rotational treatment such as VMAT and even stereotactic treatment delivery validation. The same approach could also be used for proton and heavy-ion beams as long as correction for scintillation quenching is provided.