Monitor unit calculations for external photon and electron beams: Report of the AAPM Therapy Physics Committee Task Group No. 71

Abstract

A protocol is presented for the calculation of monitor units (MU) for photon and electron beams, delivered with and without beam modifiers, for constant source-surface distance (SSD) and source-axis distance (SAD) setups. This protocol was written by Task Group 71 of the Therapy Physics Committee of the American Association of Physicists in Medicine (AAPM) and has been formally approved by the AAPM for clinical use. The protocol defines the nomenclature for the dosimetric quantities used in these calculations, along with instructions for their determination and measurement. Calculations are made using the dose per MU under normalization conditions, $D_0^{\prime }$, that is determined for each user's photon and electron beams. For electron beams, the depth of normalization is taken to be the depth of maximum dose along the central axis for the same field incident on a water phantom at the same SSD, where $D_0^{\prime }$ = 1 cGy/MU. For photon beams, this task group recommends that a normalization depth of 10 cm be selected, where an energy-dependent $D_0^{\prime }$ ≤ 1 cGy/MU is required. This recommendation differs from the more common approach of a normalization depth of d_m, with $D_0^{\prime }$ = 1 cGy/MU, although both systems are acceptable within the current protocol. For photon beams, the formalism includes the use of blocked fields, physical or dynamic wedges, and (static) multileaf collimation. No formalism is provided for intensity modulated radiation therapy calculations, although some general considerations and a review of current calculation techniques are included. For electron beams, the formalism provides for calculations at the standard and extended SSDs using either an effective SSD or an air-gap correction factor. Example tables and problems are included to illustrate the basic concepts within the presented formalism.

I. INTRODUCTION

On the basis of clinical dose-response data, the International Commission on Radiation Units and Measurement (ICRU) states that dosimetry systems must be capable of delivering dose to an accuracy of 5%.¹ Furthermore, improvements in this level of accuracy are warranted to improve the modeling and prediction of dose-volume effects in radiation therapy.² Many factors contribute to both random and systematic deviations in dose delivery, including daily patient setup, target delineation, and dose calculation. It is apparent that the errors associated with each step of the treatment process must be substantially less than the overall tolerance. Thus, as improvements are made in immobilization techniques, patient setup, and image quality, similar improvements are necessary in dose calculations to obtain greater accuracy in overall dose delivery. The accurate determination of dose per monitor unit (MU) at a single calculation point is an essential part of this process.

The calculation of MUs has evolved over the past several years as treatment planning has increased in accuracy and complexity. Historically, MUs were determined using a manual calculation process, where the calculations were based on water phantom data gathered at time of machine commissioning. Over time, manual calculations have become more accurate due to more detailed characterizations of dosimetric functions. Nevertheless, these calculations are based on machine data, which are typically gathered with a flat, homogeneous water phantom.

Additional improvements in dose-calculation accuracy within computer treatment-planning systems have been made possible with the incorporation of patient-specific anatomical information. Early computer algorithms calculated the two-dimensional scatter characteristics based on patient-specific external contour information.³ The advent of image-based treatment planning has allowed incorporation of patient-specific internal heterogeneity information into the calculation of dose. The use of this information to determine the dose through a complex two- or three-dimensional algorithm is limited to a “computer calculation,” although a subset of this information may be used to improve the accuracy of a manual calculation (e.g., the use of an effective or radiological depth).

Despite the improvements possible with current and future computer-calculated MUs, manual calculations will be still required for several reasons. First, some patients may not require a computerized treatment plan and it may be most efficient to calculate the MU for their treatments manually. This is especially common in the palliative or emergent setting. Second, although the computer calculation may incorporate additional information, there is no assurance that the computer-calculated MUs are more accurate for all conditions. There are a number of different commercial treatment-planning systems available, each of which has a different technique for determining dose. For example, with some computer algorithms, it may be difficult to model a particular clinical setup or accessory. Finally, both Task Group (TG)-40 and TG-114 of the American Association of Physicists in Medicine (AAPM) recommend^4,5 that the output of a computer calculation be independently verified with an alternative calculation method. This check becomes more important as the sophistication of the planning algorithm increases.

Many manual methods are currently being used to determine MUs. The use of many different approaches increases the probability of calculational errors, either in the misunderstanding of varying nomenclatures or in the absence or misuse of important parameters within the calculation formalism. Furthermore, using multiple approaches results in reduced clinical workflow efficiency. In addition to the time required for each clinic to develop inhouse MU calculation protocols, the retraining of personnel who move between clinics or the interpretation of clinical data from other clinics is made more difficult when different calculational approaches are used. The clinical application of the formalism presented within is the subject of another AAPM report.⁵

This task group report presents a consistent formalism for the determination of MUs for photons and electrons. For photons, the report describes MU calculations for fields with and without beam modifiers for both isocentric and source-surface distance (SSD) setups. The protocol includes the use of dynamic or virtual wedges (VW) and static multileaf collimation. Although intensity modulated radiation therapy (IMRT) calculations are beyond the scope of this report, a brief review of current algorithms is made, along with general recommendations of this task group. The current protocol is applicable for megavoltage linear accelerators or Co-60 teletherapy units. For electrons, calculations for standard or irregularly shaped fields at standard or extended SSDs are described.

The protocol's calculations are referenced to $D_0^{\prime }$, the dose per MU or dose rate of the user's beam under normalization conditions. At the time of calibration, the output of each beam is adjusted to deliver a specific $D_0^{\prime }$ that is determined by the user. Under normalization conditions, although many of the dosimetric functions within this protocol have a value of unity, $D_0^{\prime }$ is not necessarily 1 cGy/MU, and may vary between beams.

Here we differentiate normalization conditions from reference conditions, the latter of which represents the measurement conditions for the determination of absorbed dose to water within the AAPM TG-51 protocol.⁶ For example, TG-51 specifies that the reference depth, d_ref, be equal to 10 cm for photon beam calibration. In this report, the photon beam normalization depth, d₀, is distinct from but may be equal to d_ref (10 cm), or to any other depth at or beyond the maximum depth of d_m. For electron beams, the normalization depth for a given field is taken to be the depth of maximum dose along the central axis for the same field incident on a water phantom at the same SSD.^7,8

The choice of the normalization depth(s) for photon beams should be made after considering several issues. If d₀ is different from d_ref, it is necessary to convert the calibration dose per MU at d_ref to the dose per MU at d₀. This conversion introduces a potential source of error if the percentage depth dose data used for this conversion are inaccurate and/or different from the data used elsewhere in the MU calculation. Additional uncertainty arises if d₀ is set equal to d_m, where it has been noted that electron contamination within the photon beam makes the determination of dose in this region more difficult.⁹ Furthermore, other studies have shown that for higher energy beams, electron contamination penetrates much farther than d_m.^10,11 Choosing d₀ = 10 cm for photon beams eliminates the uncertainty associated with converting the calibrated output to the dose rate at other depths, particularly at d_m.

Choosing a normalization depth of 10 cm has additional advantages. Different machines of the same energy will be matched at a more clinically relevant depth, which may decrease the differences in programmed MU when moving patients from one machine to another. Some of the field-size dosimetric quantities vary less significantly at depths greater than d_m, making dosimetric measurements less susceptible to setup error. Some treatment-planning systems require measured output factors at a depth of 10 cm, thus requiring users to measure these data anyway. Choosing a normalization depth of 10 cm eliminates the duplication of effort, either at time of commissioning or during annual inspections.

Thus, this task group recommends that the normalization depth be set to 10 cm for photon beams. However, the formalism presented within this protocol is valid for any choice of d₀. If another depth is chosen for d₀, at a minimum this depth shall be greater than or equal to the maximum d_m depth, determined from percent depth dose measurements for the smallest field size and greatest SSD used clinically.

It is recognized that a 10-cm normalization depth represents a change for most clinics. To aid the clinician in the development of data tables, we have included a set of example tables which have been normalized at this depth. A set of example problems have also been included in Sec. VIII of this report.

II. CALCULATION FORMALISM

II.A. Photons

MU calculations for photon beams may be performed using either a TPR (isocentric) or PDD (nonisocentric) formalism.

II.A.1. Monitor unit equations

II.A.1.a. Photon calculations using tissue phantom ratio

For calculations using TPR, the equation for MU is given by

$$\mathrm{MU}=\frac{D}{D_0^{\prime }·S_c\left(r_c\right)·S_p\left(r_d\right)·\mathrm{TPR}(d,r_d)·\mathrm{WF}(d,r_d,x)·\mathrm{TF}·\mathrm{OAR}(d,x)·{\left(\frac{{\mathrm{SSD}}_0+d_0}{\mathrm{SPD}}\right)}^2}.$$ (1)

In the case where dose is calculated at the isocenter point, Eq. (1) reduces to

$$\mathrm{MU}=\frac{D}{D_0^{\prime }·S_c\left(r_c\right)·S_p\left(r_d\right)·\mathrm{TPR}(d,r_d)·\mathrm{WF}(d,r_d)·\mathrm{TF}·{\left(\frac{{\mathrm{SSD}}_0+d_0}{\mathrm{SAD}}\right)}^2}.$$ (2)

II.A.1.b. Photon calculations using percentage depth dose

Although Eq. (1) may be used to determine MUs for any setup, including nonisocentric cases, it may be preferable to use normalized percentage depth doses in some circumstances. In this case, the MU equation is given by

$$\mathrm{MU}=\frac{D·100\%}{D_0^{\prime }·S_c\left(r_c\right)·S_p\left(r_{d_0}\right)·{\mathrm{PDD}}_N(d,r,\mathrm{SSD})·\mathrm{WF}(d,r_d,x)·\mathrm{TF}·\mathrm{OAR}(d,x)·{\left(\frac{{\mathrm{SSD}}_0+d_0}{\mathrm{SSD}+d_0}\right)}^2}.$$ (3)

II.A.2. Field-size determination

Many of the dosimetric functions in Eqs. (1)–(3) are field-size dependent due to the variation in scattered radiation originating from the collimator head or the phantom. Dosimetric functions are usually tabulated as a function of square field size. In general, values for irregular fields may be approximated by using the equivalent field size, defined as the square field that has the same depth-dose characteristics as the irregular field.¹² In many cases, the treatment-planning system will report the equivalent square of the photon beam. In this case, users should understand the methodology by which this equivalent square is determined, including whether the effects of blocking and/or tissue heterogeneities are included. The equivalent square may also be estimated by approximating the irregular field as a rectangle, and then determining the rectangle's equivalent square either with a calculated table¹² or with the method of Sterling et al.,¹³ which sets the side of the equivalent square to four times the area divided by the perimeter of the rectangular field. This “4A/P” formula works well in most clinical circumstances but should be verified for highly elongated fields (e.g., 5 × 40 cm²) and for in-air output ratios.

This Section (II A 2) describes the determination of field size for use in Eqs. (1)–(3).

II.A.2.a. Determination of field size for S_c

The function S_c models the change in incident fluence as the collimation in the treatment head is varied. The change in incident fluence can be modeled by the collimation of a primary source at the target and a radially symmetric planar extended scattered-radiation source close to the target.^14–20 The volumes of these two sources that are not blocked by the jaws and the field shaping collimator (e.g., blocks and MLC) from the point of view of the point of calculation (point's-eye-view or PEV) determine S_c. Because this exposed region from PEV depends on both the jaw settings and the field-shaping collimator that are at different distances from the sources, an accurate formalism will involve a method to combine the effects of different collimators into an equivalent field size. There are three different methods to calculate an equivalent square field size for S_c in order of increasing accuracy: equivalent square of jaw settings, PEV model of collimating jaws, and PEV model of all collimators. Unless the treatment field is highly irregular (e.g., heavily blocked or highly elongated), the equivalent square method predicts S_c reasonably well²¹ and will be described in this section. A description of the PEV models is included in Appendix B of this report.

Additionally, backscattered radiation from the adjustable jaws to the monitor chamber will affect the collimator scatter factor. Modern accelerators either have a retractable foil between the monitor chamber and the adjustable jaws to attenuate the backscattered radiation, or the collimators are far enough from the monitor chamber so that the significance of monitor backscatter is reduced.²¹ For further details, the reader is referred to the AAPM TG 74 report.¹⁰

II.A.2.ai. Open or externally-blocked fields

The upper and lower jaws are the collimators closest to the target. Thus these collimators are the main factors determining S_c. Although these two sets of collimators are at different distances from the source, the difference in the distances is much smaller than the distance from the source to the isocenter. If one makes the approximation that the upper and lower jaws are at the same distance from the sources and they are the only collimators that are shaping the exposed region of the sources from PEV, the equivalent square for S_c can be modeled as the equivalent square of the rectangle formed by the jaws at isocenter. Using the 4A/P formula, the equivalent square used for determining S_c will be:¹³

$$r_c=4\left(\frac{r_{jU}·r_{jL}}{2r_{jU}+2r_{jL}}\right),$$ (4)

where r_jU is the upper jaw setting and r_jL is the lower jaw setting, defined at the machine isocenter.

Equation (4) is used to determine the equivalent square for open fields or those using externally mounted blocks. In the latter case, the blocks are placed farther away from the target than the collimators, so that little if any of the source is obscured from the PEV of the calculation point.

The difference in distances from the target of the upper and lower collimator jaws results in deviations from the equivalent square model. The “collimator exchange effect” describes the differences in output when the upper and lower field-size settings are reversed.¹⁰ The collimator exchange effect is not modeled using 4A/P; for example, this approximation will predict the same S_c for a 5-cm wide 40-cm long field and a 40-cm wide 5-cm long field. The error introduced by this approximation is typically small (<2%),²¹ but is dependent on the accelerator design and should be measured for evaluation. The collimator exchange effect is accounted for in the PEV models described in Appendix B.

II.A.2.aii. MLC-blocked fields

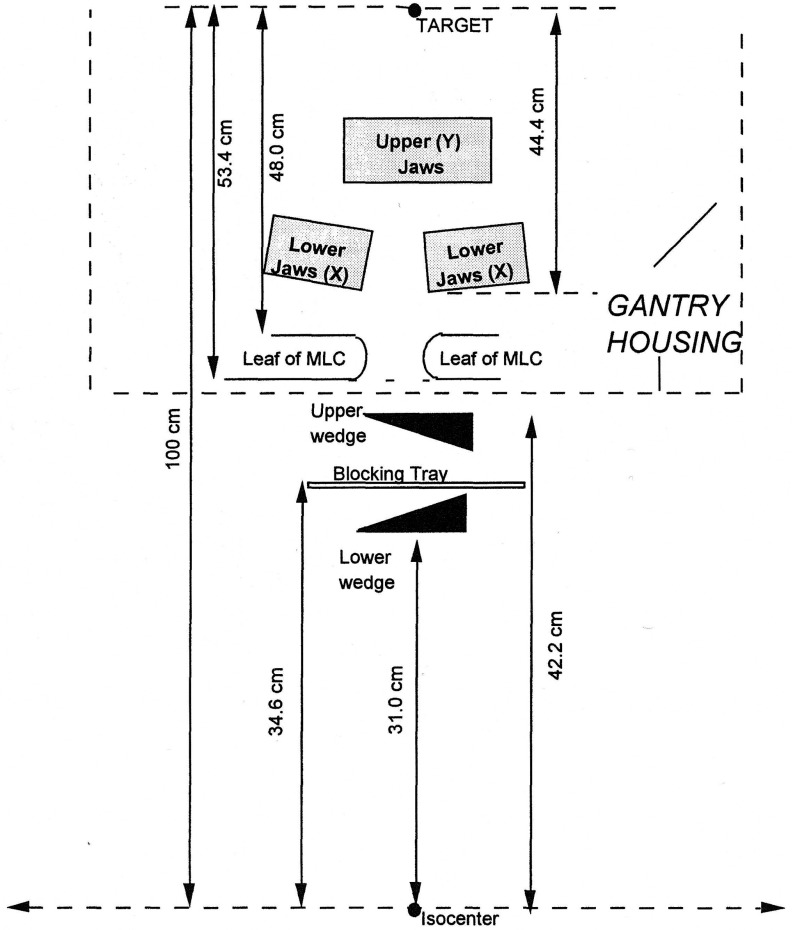
Currently, almost all linear accelerators come equipped with some form of multileaf collimator, or MLC. Figures 1–3 show examples of commercially available MLCs categorized as a total or partial replacement of the upper or lower jaws or as tertiary collimation configurations. Because of the different position of each of these configurations with respect to the target, each system will have a different amount of scattered photons reaching the point of calculation for the same incident field size.

FIG. 1.

Cross-sectional view of Elekta MLC head. The leaf banks are mounted in place of the upper collimator in order to fit in the standard head cover. Each of the 80 tungsten leaves is of 7.5 cm thickness, equivalent to approximately two tenth value layers. A leaf has a width of 1 cm and a range of movement 20 cm away from the central axis to 12.5 cm across it. The 3-cm thick Y back-up diaphragm is intended to reduce any leakage through the gaps between the leaves (Ref. 22).

FIG. 2.

Schematic diagram of the Siemens MLC head. In this design, the double-focused bank of 54 leaves is mounted in place of the lower collimator. Each of the tungsten leaves is 7.6-cm thick and projects to a 1.0-cm wide radiation field at isocenter. All leaves can be independently moved to an overtravel of 10 cm past the central axis (Ref. 24).

FIG. 3.

Cross-sectional view of Varian MLC head for a 2100C accelerator (Ref. 26). In this design, the leaf banks are mounted in carriages placed below the lower collimator, with leaf widths of 0.5- or 1.0-cm projected at SAD, depending on MLC model.

Currently, the Elekta/Philips MLC is designed as an upper-jaw replacement.²² Backup diaphragms located beneath the leaves augment the attenuation provided by the individual leaves. Figure 1 shows a cross-section of the Elekta head design. Measurements by Palta et al.,²³ have demonstrated S_c for the upper-jaw replacement system can be accurately calculated by using the equivalent square of the MLC blocked field area.

The Siemens MLC is designed as a lower-jaw replacement. The upper jaws are strategically placed at the upper and lower borders of the field. Figure 2 displays the Siemens MLC head. Das et al.,²⁴ characterize S_c for the Siemens system in the same fashion as the upper jaw replacement system by using the equivalent square of the MLC blocked field area for the argument of S_c.

The Varian MLC is an example of a tertiary collimator system. This device is positioned just below the level of the standard upper and lower adjustable jaws. The y-jaws are strategically placed at the upper and lower borders of the field. Figure 3 describes the Varian MLC head design. Boyer et al.²⁵ and Klein et al.²⁶ found that the tertiary MLC design is best treated as a block. That is, the equivalent square of the collimator field size is used.

II.A.2.b. Determination of field size for S_p

For S_p, the field size is proportional to that incident on the patient. This may be smaller than the collimator field size if the scatter volume is reduced by either tertiary blocking or patient limits or larger in the case of extended SSD.

The field-size argument r_d of S_p in Eqs. (1) and (2) is the equivalent square of the field size incident on the patient, projected to the depth of the point of calculation. Thus, unlike S_c, the argument for S_p will change with a change of source-point distance (SPD).

The field-size argument $r_{d_0}$ of S_p in Eq. (3) is the equivalent square of the field size incident on the patient, projected to the normalization depth. In some texts, the argument is written using the field size defined at the patient surface.²⁷ For a normalization depth at or near d_m, only a negligible difference is found using the equivalent field size on the surface of the patient. However, for greater d₀'s (e.g., d₀ = 10 cm), this approximation cannot be made. In this case, the projected field size is relatively larger and the field-size dependence of S_p is greater.

II.A.2.c. Determination of field size for TPR or PDD_N

As with S_p, the field size argument for these quantities is proportional to that incident on the patient, which will be affected by either tertiary blocking or patient limits.

For isocentric calculations, the field size argument for TPR is the equivalent square of the field size incident on the patient, projected to the depth of the point of calculation. For SSD calculations, the field-size argument for PDD_N is the equivalent square of the field size incident on the patient.

II.A.2.d. Determination of field size for wedge factor (WF)

II.A.2.di. Physical wedges

Physical wedges may be classified into two types, distinguished by their placement relative to the secondary collimating jaws. Internal wedges (sometimes called motorized wedges or universal wedges), located above the collimating jaws are designed using a single wedge with a large wedge angle (60°). The internal wedge is inserted into the field using a motorized drive within the accelerator. Wedged isodose distributions with smaller wedge angles are produced by combining the internal wedge field with a corresponding open field with appropriate relative weighting. In contrast, external wedges are placed below the collimating jaws. External wedges are manually inserted into the collimator assembly, and are located much closer to the patient, with source-wedge distances ranging from 40% to 70% of the SAD.

The field size dependency of physical wedges appears to originate from a wedge-induced increase in head scatter.²⁸ Investigations have determined that the WF for rectangular fields is closely approximated by the WF of the equivalent square for both external^29,30 and internal³¹ wedges, regardless of orientation. For wedged fields with blocks or MLCs, it is recommended to use the equivalent square of the irregular field for the argument of WF.³²

II.A.2.dii. Nonphysical wedges

Wedge factors for nonphysical, or filterless wedges represent the fractional change in dose per MU at the calculation depth after the treatment field is completed. This protocol will discuss two current vendor implementations of this technology.

The first step by commercial vendors to intensity modulate a beam was the application of the Varian dynamic wedge (DW).³³ Both DW and its successor, the enhanced dynamic wedge (EDW) takes advantage of a collimation jaw moving in conjunction with adjustment of the dose rate over the course of one treatment. The variation of jaw position and dose rate is driven by a segmented treatment table (STT), which is unique for each energy, wedge angle, and field size. The basis for the EDW generation is a “golden” STT (GSTT) for a 60°, 30-cm wedge, from which the treatment STTs for other wedge angles are calculated.

In contrast to physical wedges, Varian dynamic wedges have very steep field-size dependencies. Thus, it is critical that the input field size be correct for the calculation. The WF for EDW is primarily dependent on the position of the fixed Y jaw, and is virtually independent of the X collimator setting, the initial moving Y jaw position, and the MLC or blocked field size.

Siemens introduced a dynamic jaw wedging system entitled the VW. The VW operates similar to the Varian EDW, with capabilities for additional intermediate wedge angles and operation with the lower jaws, with limited range.

The most notable difference between the EDW and VW is how the energy fluence pattern is generated. As the VW attempts to deliver the same dose on central axis as the open field with the same field size, the WF is designed to be unity for a standard range of field sizes and wedge angles. The user should verify the field-size dependency (or lack thereof) for all field sizes to be used clinically.

II.A.3. Radiological depth determination

Equations (2) and (3) assume dose is to be delivered to a flat, homogeneous water phantom. To correct for internal heterogeneities within the patient, the calculated homogeneous dose per MU, D^′(Homogeneous), is multiplied by a correction factor (CF) defined as

$$\begin{array}{c}\hfill \mathrm{CF}=\frac{D^{\prime }\left(\mathrm{Heterogenous}\right)}{D^{\prime }\left(\mathrm{Homogenous}\right)}.\end{array}$$ (5)

Methods of varying levels of complexity exist in the literature for determining CF.³⁴ Many of these are impractical for application in a manual calculation. Two methods that may be employed are detailed below.

Each of these simple methods relies on attenuation data, typically measured under conditions of electronic equilibrium. Unfortunately, data in nonequilibrium conditions (e.g., d < d_m) are suspect and often not even measured. Physicists must use caution with these solutions and not, for example, try to calculation CF in locations near heterogeneity interfaces.

II.A.3.a. Method 1

This method represents the simplest technique for determining the heterogeneity correction factor. It is used in the simplest heterogeneity correction methods that examine only the path of primary radiation.³⁵ Often called the ratio of TAR method, or RTAR, the correction factor uses a water-equivalent or radiological depth, d_eff, calculated along the line from the source to the point of calculation:

$$d_{\mathrm{eff}}=\sum _{i=1}^n{d}_i·{\rho }_{e,i},$$ (6)

where d_i and ρ_e,i are the distance and relative electron density (respectively) for the ith element along the line. For calculations based on CT-based treatment planning, this scaled depth is often reported by the treatment-planning system. In this case, the correction factor is given by

$$\mathrm{CF}=\frac{\mathrm{TPR}(d_{\mathrm{eff}},r_d)}{\mathrm{TPR}(d,r_d)}.$$ (7)

II.A.3.b. Method 2

The method, known as the power law TAR or the Batho method,³⁶ determines the dose for calculation points beneath a heterogeneity. In this method, the correction factor is given by

$$\mathrm{CF}={\left(\frac{\mathrm{TPR}(d_1,r_d)}{\mathrm{TPR}(d_2,r_d)}\right)}^{{\rho }_e-1},$$ (8)

where ρ_e is the electron density of the inhomogeneity relative to water and d₁ and d₂ are the distances from the calculation point to the proximal and distal limits of the heterogeneity. This method has also been extended to cases of multiple heterogeneities.³⁷

II.B. Electrons

The AAPM Task Group 70 (TG70) (Ref. 38) defined the electron output factor, S_e, as

$$\begin{array}{ccc}\hfill S_e(r_a,\mathrm{SSD})& =& \frac{D/\mathrm{MU}(d_m\left(r_a\right),r_a,\mathrm{SSD})}{D/\mathrm{MU}(d_m\left(r_0\right),r_0,{\mathrm{SSD}}_0)}\hfill \\ & =& \frac{D^{\prime }(d_m\left(r_a\right),r_a,\mathrm{SSD})}{D_0^{\prime }},\hfill \end{array}$$ (9)

where D/MU is the dose per MU (TG70 notation, D^′ in this report), d_m(r_a) is the depth of maximum dose for the treatment field size, r_a, and d_m(r₀) is the depth of maximum dose for the reference field size, r₀. As defined above, the output factor includes applicator, insert, and treatment distance effects.

II.B.1. Monitor unit equations

II.B.1.a. Electron calculations at standard SSDs

The equation for MUs for electron beams at the nominal SSD is given by

$$\mathrm{MU}=\frac{D·100\%}{D_0^{\prime }·\mathrm{PDD}(d,r_a,{\mathrm{SSD}}_0)·S_e(r_a,{\mathrm{SSD}}_0)},$$ (10)

where the PDD is normalized to the depth of maximum dose for the treatment field size, and S_e is the dose output for a field size (combination of applicator and insert) of r_a. The percentage depth dose term is included to allow for the common practice of prescribing the dose to a point other than the depth of maximum dose along the central axis. Shiu et al.³⁹ found that the PDD is dependent on the insert size, rather than the applicator size, so we can consider it to be a function of insert size only if needed. In cases where skin collimation is used, the output is primarily determined by the applicator and insert sizes; however, the PDD is primarily determined by the skin collimation field size.⁷ Therefore, if skin collimation is used, the field size used for the PDD term in Eq. (10) should be the skin collimation field size, rather than the insert and applicator.

II.B.1.b. Electron calculations at extended SSDs

The definition of the output factor includes treatment distance effects; therefore, monitor units can be calculated using Eq. (10) replacing SSD₀ with SSD. However, a more common practice is to separate field size effects from treatment distance effects. In other words, the output factor is usually tabulated as a function of applicator and insert size, r_a, at the standard SSD. The effect of treatment distance not equal to the standard SSD can be accounted for in two ways, as described in the AAPM Task Group 25 report.⁷

II.B.1.bi. Effective SSD technique

$$\mathrm{MU}=\frac{D·100\%}{D_0^{\prime }·\mathrm{PDD}(d,r_a,\mathrm{SSD})·S_e(r_a,{\mathrm{SSD}}_0)·{(({\mathrm{SSD}}_{\mathrm{eff}}\left(r\right)+d_0)/({\mathrm{SSD}}_{\mathrm{eff}}\left(r\right)+d_0+g))}^2},$$ (11)

where g is the difference between the treatment SSD and the calibration SSD, and SSD_eff is the effective source to surface distance for the given field size.

II.B.1.bii. Air-gap technique

$$\mathrm{MU}=\frac{D·100\%}{D_0^{\prime }·\mathrm{PDD}(d,r_a,\mathrm{SSD})·S_e(r_a,{\mathrm{SSD}}_0)·{(({\mathrm{SSD}}_0+d_0)/({\mathrm{SSD}}_0+d_0+g))}^2·f_{\mathrm{air}}(r_a,\mathrm{SSD})},$$ (12)

where g is the difference between the treatment SSD and the calibration SSD, and f_air is the air-gap correction factor for the given field size and SSD.

II.B.2. Field-size determination

We follow the AAPM TG70 notation in that r_a represents the applicator and insert size for the electron beam under consideration. The vendor-stated applicator size is typically used, which may be defined at either the isocenter or at the applicator base. In this report, the insert size represents the size of the electron field incident on the patient, projected to the isocenter.

For rectangular electron fields, where the insert size is L × W, the square root (geometric mean) method of Mills et al.,⁴⁰ should be utilized

$$\begin{array}{c}\hfill S_e(r_a,L\times W)={[\left(S_e(r_a,L\times L)\right)·\left(S_e(r_a,W\times W)\right)]}^{1/2},\end{array}$$ (13)

where the same applicator size for all field sizes is implicit. Shiu et al.,³⁹ found this method to be more accurate than the equivalent square method of Meyer et al.⁴¹

It is also recommended that the square root method be used to determine PDD for rectangular fields. Shiu et al.³⁹ found that the square root method determines rectangular field PDD to within 1%. When applying this method, the depths of maximum dose may not be the same for each field size, so a final renormalization of the geometric mean calculation may be required.

There are many methods of determining the output factor for an irregularly shaped electron field. Many centers measure the output for each irregular field, especially if their use is infrequent. If the physicist keeps track of the results, then previously measured data may be used if the energy is the same and the field shape and size are similar.

A second method of determining the dose output is through the use of an analytical algorithm, such as the method described by Khan et al.,^42,43 or a Monte Carlo code. An example of the latter is given by Kapur et al.⁴⁴ These types of systems are not in widespread clinical use, but may become more prevalent in the future. Details of these approaches are also discussed in the AAPM TG 70 report.³⁸

A third method is to approximate the irregular field by a rectangle and then use Eq. (13) to calculate the output of the field. Fundamental principles for determining equivalent rectangles have been provided by Hogstrom et al.:⁴⁵

• (a)The equivalent rectangle for the dose output is determined for the field shape defined by the applicator insert, not by the skin collimator.
• (b)The maximum dose output usually occurs in the broadest region of the field, i.e., at the point surrounded by the greatest diameter circle that is enclosed by the field.
• (c)The dose output usually varies little beyond some minimum square field size. Hence, areas of the field located greater than one-half of that distance can be assumed to contribute insignificantly to the dose output. [According to Khan et al.⁴² the minimum radius for lateral scatter equilibrium is $0.88\sqrt{E_{p,0}}$. For example, at 9 MeV, areas of the field greater than 2.6 cm from the estimated location for which dose output is being estimated are insignificant].
• (d)The rectangle should be constructed to minimize the difference in area between it and the irregular field less any regions ignored. Rotations about the beam central axis should be used.
• (e)The method may not be sufficiently accurate to be used for highly irregular fields. In such cases, measurement or other means of calculation are recommended.⁴⁵

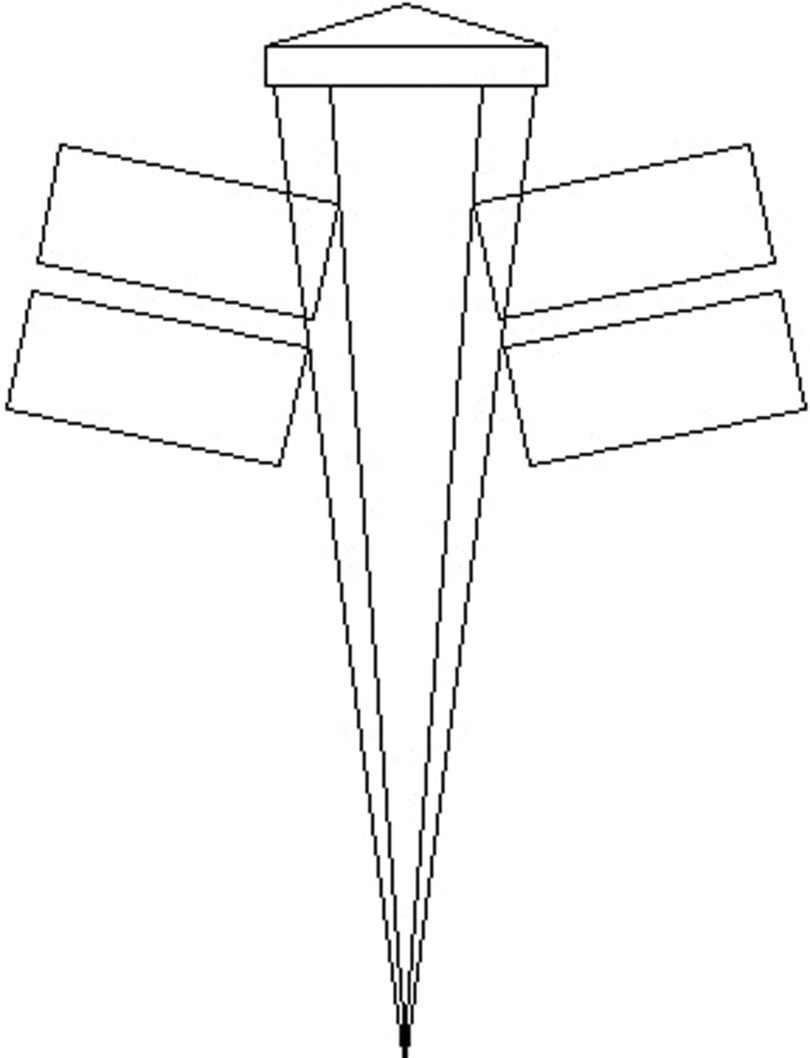
Figure 4 shows a few clinical examples that illustrate how the equivalent rectangular field is estimated.

FIG. 4.

Electron equivalent field sizes. Examples of constructing rectangular fields whose output approximates that of the irregular field for: (a) a posterior cervical strip; (b) a posterior cervical strip plus submandibular nodes; and (c) an internal mammary chain. The irregular field is delineated by the irregularly shaped curve. The beam axes are delineated by orthogonal 10 cm line segments. The constructed rectangle is delineated by the four intersecting lines, the center delineated by “x.” The arcs are a distance 3 cm from the center of the rectangle (Ref. 45).

Corrections for rectangular fields that are centered away from the central axis are rarely needed, especially if beam flatness is well controlled. In cases where such a correction is desired, a multiplicative factor (off-axis ratios; OAR) can be used to account for beam nonuniformity. A major axis scan measured at a depth near d_m for each energy-applicator combination should be sufficient to estimate OAR values under most conditions. The radial distance from the central axis should be used, because the scattering foil system is radially symmetric.

In cases where skin collimation is used, although the electron percent depth dose is determined by the skin collimation size,⁷ the output factor is primarily determined by the applicator and insert sizes.

III. DETERMINATION OF DOSIMETRIC QUANTITIES

In this section, we outline a set of measurements for generating data sufficient to perform calculations according to this protocol. The guidelines for relative dosimetry measurements made in the AAPM TG-70 (Ref. 38) and AAPM TG-106 (Ref. 46) reports should be followed as well.

III.A. Dosimetry equipment

Ionometric measurements are recommended for the majority of measurements described in this protocol. An ionometric dosimeter system for radiation therapy includes one or more ionization chamber assemblies, a measuring assembly (electrometer), one or more phantoms with waterproof sleeves, and one or more stability check devices.^47–49

III.A.1. Ionization chambers

Procedures involved in the use of ionization chambers have been described by a number of reports.^{7,47,48,50–54} At a minimum, the chambers should meet the minimum requirements described for gathering data necessary for commissioning the treatment-planning system. These characteristics include, but are not limited to low leakage (<10 pA), low stem effect (<0.5%), low angular and polarity dependence (<0.5%), and high collection efficiency. Details on chamber construction are available from their respective data sheets provided by vendors. For cylindrical chambers, the chamber cavity volume should be less than 1 cm³. The size is a compromise between the need for sufficient sensitivity and the ability to measure dose at a point. For most field sizes, cylindrical chambers with internal cavity diameter of less than 7 mm and internal cavity length of less than 25 mm meet these requirements.⁴⁸ For small field measurements (e.g., ⩽3 × 3 cm²), smaller chambers may be required. Users are referred to the upcoming Task Group 155 report on small field dosimetry.⁵⁵ During measurements the chambers should be aligned in such a way that the radiation fluence is uniform over the cross-section of the air cavity. For the scanning measurements made to determine percent depth dose and/or off-axis profiles, it is important that the chambers be as small as practicable.

Plane-parallel chambers having collection-volume heights and diameters not exceeding 2 mm and 2.0 cm, respectively, can be used for relative dose measurements in both photon and electron beams. Following the recommendation of the AAPM TG-51 protocol, the point of measurement of a cylindrical chamber is taken to lie on the central axis of the cavity at the center of the active volume of the cavity. For a plane-parallel chamber, the point of measurement is at the inner surface of the entrance window, at the center of the window, for all beam qualities and depth. The effective point of measurement for a cylindrical chamber is upstream of the chamber center (i.e., closer to the radiation source) due to the predominantly forward direction of the secondary electrons (because the primary beam enters the chamber at various distances upstream). Plane-parallel chambers may be designed so that the chamber samples the electron fluence incident through the front window, with the contribution of the electrons entering through the side walls being negligible. This design justifies taking the effective point of measurement of the chamber to be at the inner surface of the entrance window, at the center of the window.^7,48,54

III.A.2. Phantoms

It is the recommendation of this task group that water be used as the standard phantom material for the dosimetric measurements of all quantities outlined in this report. The size of the phantom must be large enough so that there is at least 5 cm of phantom material beyond each side of the radiation field employed at the depth of measurement and a margin of at least 10 cm beyond the maximum depth of measurement.

In some cases it is necessary to use solid, nonwater phantoms. For example, S_c measurements can be made using a solid mini-phantom that is thick enough (in the beam direction) to eliminate electron contamination and small enough (perpendicular to the beam) to keep the amount of phantom-scattered photons constant for all measured field sizes. Van Gasteren et al.,⁵⁶ described the use of a mini-phantom that was constructed to best meet these requirements. Ideally, the solid phantom material should be water equivalent, i.e., it should have the same electron density and effective atomic number as water.⁷ In the event these conditions are not met, it should be verified that the measured values agree with those obtained using water or water equivalent solid mini-phantoms.

III.B. Measurements of dosimetric quantities

In Secs. III B 1 and III B 2, we describe recommended techniques for determining the dependencies (e.g., field size, depth, SSD) of dosimetric parameters required by this protocol. Typically, users will generate tables of dosimetric quantities produced based on measured set of data for the users beam. A set of sample data tables are included at the end of this report.

In general, it is recommended that data be measured such that variation between any two data points is less than 2%. Linear or nearest neighbor interpolation may be used to determine data located between measured results. More advanced interpolation methods may be used as well, provided the results are bounded by the neighboring measured data. Extrapolation of data beyond that measured is not allowed. If the field parameters used for the calculation are outside those tabulated, the output should be directly measured by the user.

Additional guidelines for these measurements may be found in AAPM TG-106 (Ref. 46) and AAPM TG-70 (Ref. 38) reports.

III.B.1. Measurements of dosimetric quantities: Photon beams

In Secs. III B 1 and III B 2, we outline a set of commissioning measurements that may be used to generate the required data for this protocol.

III.B.1.a. Dose per MU under normalization conditions ($D_0^{\prime }$)

This protocol requires the knowledge of the linear accelerator's dose rate or dose per MU, $D_0^{\prime }$, under normalization conditions. The normalization conditions are not necessarily equal to the reference conditions under which the linear accelerator is calibrated. For example, although the AAPM TG-51 report⁶ specifies that the reference depth for photon calibration is 10 cm, data from the RPC indicates that currently over 90% of monitored clinics perform calculations using a normalization dose rate of 1 cGy/MU at a depth of d_m. As stated in the Introduction, this difference is acceptable within the current protocol, as long as the normalization depth d₀ is at or beyond the maximum depth of d_m.

For a given set of normalization conditions, the choice of $D_0^{\prime }$ will be limited to the output range of the linear accelerator. A linear accelerator calibrated to deliver 1 cGy/MU at d_m may require $D_0^{\prime }$ to be less than 1 cGy/MU at a normalization depth of 10 cm. For clinics that transition from a normalization depth of d_m to 10 cm, it may be preferable to select a $D_0^{\prime }$ value that has a minimal impact on their current linear accelerator output. This selection would minimize the change in calculated MUs for patients currently under treatment. Furthermore, it would allow direct comparison between the old and new MU calculation systems to verify that the new calculation methodology was implemented correctly.

As an example consider the transition from a nonisocentric system that defines $D_0^{\prime }$ to be 1 cGy/MU at 100 cm SSD and a depth of d_m, to an isocentric system that defines $D_0^{\prime }$ at 100 cm SAD (isocentric), and a depth of 10 cm. In the nonisocentric system, the dose per MU at the normalization point of the isocentric system is given by TMR(10, 10 × 10) · ((100 + d_m)/100)². This value will change depending on the energy of the photon beam. Table I shows the calculated dose per MU at d₀ = 10 cm for a number of different energy photon beams using data taken from British Journal of Radiology Supplement 25.⁵⁷ In the last column of the table, $D_0^{\prime }$ has been set to this value rounded to the nearest 0.01 cGy/MU, keeping the difference in beam output less than 1%. If users have multiple machines of the same nominal energy, $D_0^{\prime }$ could also be selected to match the average calculated dose per MU of each of these machines.

TABLE I.

Determination of $D_0^{\prime }$ for photon beams using 10-cm normalization depth. For a nonisocentric system with 1 MU defined to deliver 1 cGy at 100 cm SSD and depth = d_m, the dose/MU is calculated at the suggested normalization conditions of d = 10 cm, 100 cm SAD, using depth of d_m and TMR data taken from Ref. 57. The suggested $D_0^{\prime }$ maintains the definition 1 MU under a new, 10-cm normalization condition.

Energy	d m	TMR		Dose/MU	Suggested $D_0^{\prime }$
(MV)	(cm)	(10, 10×10)	${\left(\frac{100+d_m}{100}\right)}^2$	(cGy/MU)	(cGy/MU)
4	1	0.738	1.020	0.753	0.750
5	1.25	0.759	1.025	0.778	0.780
6	1.5	0.786	1.030	0.810	0.810
8	2	0.820	1.040	0.853	0.850
10	2.3	0.839	1.047	0.878	0.880
12	2.6	0.858	1.053	0.903	0.900
15	2.9	0.877	1.059	0.929	0.930
18	3.2	0.896	1.065	0.954	0.950
21	3.5	0.914	1.071	0.979	0.980
25	3.8	0.933	1.077	1.005	1.000

III.B.1.b. Normalized percent depth dose

The normalized percent depth dose, PDD_N, is defined as the percentage ratio of the dose rate at depth to the dose rate at the normalization depth in a water phantom. The definition of PDD_N is equivalent to the reference percent depth dose defined in the European Society for Radiotherapy and Oncology (ESTRO) report⁹ and differs from the traditional definition in that the normalization depth is not necessarily at or near d_m. PDD_N is dependent on depth, SSD, and field size on the phantom surface.

The recommendations of the AAPM TG-51 protocol should be followed for the measurement of depth dose curves for photon beams.⁶ If a cylindrical or spherical ionization chamber is used, the effective point of measurement of the chamber must be taken into account. This requires that the complete depth ionization curve be shifted to shallower depths (i.e., upstream) by a distance proportional to r_cav, where r_cav is the radius of the ionization chamber cavity. For photon beams, the shift is taken as 0.6 r_cav.⁴⁸ On the other hand, no shift in depth-ionization curves is needed if well-guarded plane-parallel ionization chambers are used for the measurement of photon- or electron-beam depth-ionization curves.

For photon beams the variation in electron spectra are small past d_m, such that the stopping-power ratio between water and air is negligible;⁵⁸ furthermore, the perturbation effects of the air cavity can be assumed to a reasonable accuracy to be independent of depth for a given beam quality and field size. The depth-ionization curve can thus be treated as depth dose curve for photon beams.

PPD_N data should be acquired for a series of field sizes ranging from the smallest to the largest field to be used clinically. If TPRs are to be calculated from PDD_N, the minimum measured field size for PDD_N must be smaller than the minimum field size tabulated for TPRs. The number of measurements should be sufficient such that PDD_N varies by less than 3% between any two measured field sizes. This will require data more closely spaced for smaller field sizes. Sample PDD_N data (d₀ = 10 cm) for a 6 MV beam are given in Table II.

TABLE II.

Normalized percent depth doses (PDD_N) (d₀ = 10 cm) for 6-MV x-rays, SSD = 100 cm.

Field size	3 × 3	4 × 4	5 × 5	6 × 6	7 × 7	8 × 8	9 × 9	10 × 10	11 × 11	12 × 12	13 × 13	14 × 14	15 × 15	16 × 16	17 × 17
Depth
1.5	164.5	161.8	158.6	155.8	154.0	152.6	151.3	150.1	149.0	148.1	147.4	146.8	146.2	145.6	145.0
2.0	162.0	159.3	156.6	153.7	151.8	150.5	149.2	148.1	146.9	145.9	145.2	144.7	144.2	143.6	143.0
2.5	157.7	155.3	152.6	150.7	148.9	147.3	146.0	144.9	143.9	143.1	142.4	141.8	141.2	140.6	140.1
3.0	153.3	151.1	148.9	146.6	145.1	143.9	142.7	141.6	140.7	139.9	139.3	138.8	138.3	137.8	137.3
3.5	148.6	147.0	145.1	143.1	141.8	140.7	139.5	138.4	137.5	136.8	136.3	135.9	135.5	135.0	134.5
4.0	144.6	142.9	141.5	139.3	138.0	137.2	136.3	135.4	134.7	134.0	133.5	133.0	132.6	132.2	131.8
4.5	140.4	139.0	137.7	135.9	134.8	134.0	133.1	132.3	131.7	131.1	130.6	130.2	129.8	129.4	129.0
5.0	136.4	135.3	134.0	132.5	131.5	130.7	130.0	129.3	128.7	128.2	127.8	127.5	127.2	126.8	126.4
5.5	132.2	131.5	130.3	129.0	128.2	127.6	126.9	126.3	125.7	125.1	124.8	124.5	124.3	124.0	123.6
6.0	128.3	127.7	126.6	125.5	124.9	124.4	123.8	123.2	122.7	122.3	122.0	121.8	121.6	121.3	121.0
6.5	124.4	124.0	123.1	122.1	121.6	121.3	120.6	120.0	119.6	119.3	119.1	118.9	118.8	118.6	118.3
7.0	120.5	120.3	119.3	118.7	118.3	118.0	117.5	117.0	116.7	116.5	116.2	116.0	115.7	115.5	115.3
7.5	116.8	116.8	115.8	115.3	114.9	114.5	114.2	113.9	113.7	113.5	113.3	113.2	113.0	112.9	112.7
8.0	113.4	113.2	112.5	112.1	111.8	111.6	111.2	110.9	110.7	110.5	110.4	110.3	110.3	110.2	110.1
8.5	109.6	110.0	109.1	108.9	108.8	108.7	108.4	108.0	107.9	107.8	107.8	107.7	107.7	107.6	107.5
9.0	106.1	106.6	106.0	105.8	105.7	105.7	105.5	105.3	105.3	105.3	105.2	105.2	105.1	105.1	105.0
9.5	102.9	103.2	102.7	102.9	102.9	102.8	102.6	102.5	102.5	102.6	102.6	102.5	102.5	102.5	102.5
10.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0
10.5	96.9	97.2	97.0	97.2	97.3	97.4	97.4	97.4	97.5	97.6	97.7	97.7	97.7	97.7	97.7
11.0	94.0	94.4	94.2	94.4	94.6	94.7	94.8	94.8	94.8	94.9	95.0	95.2	95.3	95.4	95.4
11.5	91.1	91.6	91.5	91.7	91.9	92.1	92.2	92.3	92.4	92.6	92.7	92.8	92.9	93.0	93.0
12.0	88.4	88.9	88.7	89.0	89.2	89.4	89.6	89.8	90.0	90.2	90.4	90.5	90.6	90.7	90.7
12.5	85.5	86.0	85.9	86.3	86.6	86.9	87.0	87.2	87.5	87.8	87.9	88.0	88.0	88.1	88.3
13.0	83.4	83.3	83.3	83.7	84.1	84.4	84.5	84.7	85.0	85.4	85.6	85.7	85.8	85.9	86.1
13.5	80.4	80.8	80.7	81.3	81.8	82.1	82.3	82.5	82.8	83.1	83.3	83.5	83.7	83.9	84.0
14.0	77.8	78.5	78.4	79.0	79.5	79.8	79.9	80.1	80.5	80.9	81.2	81.5	81.7	81.9	82.0
14.5	75.4	76.1	76.2	76.7	77.1	77.5	77.8	78.1	78.5	78.9	79.2	79.5	79.7	79.9	80.0
15.0	73.3	73.8	74.0	74.5	75.0	75.4	75.6	75.9	76.3	76.8	77.1	77.4	77.6	77.8	78.0
16.0	69.1	69.7	69.8	70.6	71.1	71.4	71.6	71.9	72.4	72.9	73.2	73.4	73.6	73.9	74.1
17.0	64.9	65.5	65.7	66.4	67.0	67.5	67.8	68.0	68.5	69.0	69.3	69.6	69.9	70.2	70.4
18.0	61.1	61.6	61.8	62.6	63.2	63.6	63.9	64.2	64.8	65.4	65.8	66.1	66.3	66.6	66.8
19.0	57.5	58.1	58.2	59.0	59.5	59.9	60.3	60.8	61.4	61.9	62.3	62.6	62.9	63.2	63.5
20.0	54.1	54.8	55.0	55.8	56.4	56.9	57.2	57.6	58.2	58.8	59.1	59.4	59.6	59.9	60.2
21.0	51.2	51.6	51.9	52.8	53.4	53.9	54.2	54.5	55.0	55.6	56.0	56.4	56.7	57.0	57.3
22.0	48.2	48.7	48.8	49.9	50.5	50.9	51.2	51.5	52.2	52.9	53.3	53.5	53.7	54.0	54.2
23.0	45.4	46.1	46.0	46.9	47.6	48.2	48.4	48.6	49.3	50.0	50.4	50.7	50.9	51.2	51.5
24.0	42.8	43.5	43.4	44.2	44.9	45.4	45.7	46.0	46.6	47.3	47.7	48.0	48.2	48.5	48.8
25.0	40.3	41.1	41.0	42.0	42.6	43.0	43.2	43.5	44.2	44.9	45.3	45.6	45.8	46.1	46.4
Field size	18 × 18	19 × 19	20 × 20	21 × 21	22 × 22	24 × 24	26 × 26	28 × 28	30 × 30	32 × 32	34 × 34	36 × 36	38 × 38	40 × 40
Depth
1.5	144.4	143.9	143.4	143.0	142.5	141.8	141.2	140.8	140.4	140.0	139.6	139.3	139.0	138.7
2.0	142.4	141.8	141.3	140.8	140.4	139.7	139.2	138.8	138.5	138.1	137.8	137.5	137.1	136.8
2.5	139.6	139.1	138.7	138.3	137.8	137.1	136.6	136.3	136.0	135.7	135.4	135.1	134.8	134.5
3.0	136.9	136.4	136.0	135.6	135.2	134.6	134.1	133.6	133.3	133.0	132.7	132.5	132.3	132.1
3.5	134.1	133.6	133.2	132.8	132.5	131.9	131.5	131.2	130.9	130.6	130.4	130.1	129.9	129.7
4.0	131.4	131.0	130.7	130.4	130.1	129.5	129.1	128.8	128.5	128.2	128.0	127.8	127.6	127.5
4.5	128.7	128.3	128.0	127.7	127.4	126.9	126.6	126.3	126.1	125.9	125.6	125.4	125.2	125.0
5.0	126.1	125.7	125.4	125.1	124.9	124.5	124.2	124.0	123.8	123.6	123.4	123.1	122.9	122.6
5.5	123.3	123.0	122.7	122.5	122.3	122.0	121.7	121.5	121.2	121.0	120.8	120.6	120.5	120.4
6.0	120.8	120.5	120.2	120.0	119.7	119.4	119.1	118.9	118.8	118.6	118.5	118.3	118.2	118.0
6.5	118.1	117.8	117.6	117.4	117.2	116.9	116.7	116.5	116.3	116.1	116.0	115.9	115.8	115.7
7.0	115.2	115.0	114.9	114.8	114.6	114.4	114.2	114.1	114.0	113.9	113.8	113.6	113.5	113.4
7.5	112.6	112.4	112.3	112.1	112.0	111.7	111.5	111.4	111.3	111.2	111.1	111.1	111.0	111.0
8.0	109.9	109.8	109.7	109.6	109.5	109.4	109.2	109.0	108.8	108.7	108.6	108.6	108.6	108.7
8.5	107.4	107.2	107.1	107.0	107.0	106.8	106.8	106.7	106.6	106.5	106.5	106.4	106.4	106.4
9.0	105.0	104.9	104.9	104.8	104.7	104.6	104.5	104.4	104.4	104.4	104.3	104.3	104.2	104.2
9.5	102.4	102.4	102.4	102.4	102.3	102.2	102.2	102.2	102.3	102.3	102.3	102.2	102.2	102.1
10.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0	100.0
10.5	97.7	97.7	97.7	97.7	97.7	97.7	97.7	97.8	97.8	97.8	97.9	97.9	98.0	98.0
11.0	95.5	95.5	95.5	95.5	95.5	95.5	95.5	95.6	95.7	95.8	95.8	95.8	95.8	95.8
11.5	93.1	93.1	93.2	93.3	93.3	93.5	93.5	93.5	93.5	93.5	93.6	93.6	93.7	93.8
12.0	90.7	90.8	90.8	90.9	91.0	91.2	91.3	91.3	91.3	91.3	91.4	91.4	91.5	91.6
12.5	88.4	88.5	88.7	88.8	88.9	89.1	89.2	89.3	89.3	89.3	89.4	89.5	89.5	89.6
13.0	86.2	86.3	86.4	86.5	86.6	86.8	87.0	87.1	87.2	87.3	87.4	87.5	87.5	87.6
13.5	84.1	84.3	84.4	84.6	84.7	85.0	85.1	85.2	85.2	85.3	85.4	85.5	85.6	85.7
14.0	82.2	82.3	82.4	82.5	82.6	82.8	83.0	83.2	83.3	83.4	83.6	83.7	83.8	83.9
14.5	80.2	80.3	80.4	80.5	80.7	80.9	81.1	81.2	81.3	81.4	81.6	81.7	81.8	82.0
15.0	78.2	78.3	78.5	78.7	78.8	79.1	79.3	79.5	79.6	79.7	79.9	80.0	80.1	80.2
16.0	74.3	74.6	74.8	75.0	75.2	75.6	75.8	75.9	76.0	76.1	76.3	76.4	76.6	76.8
17.0	70.7	70.9	71.1	71.3	71.6	71.9	72.2	72.3	72.4	72.5	72.7	72.8	73.0	73.2
18.0	67.0	67.3	67.5	67.8	68.0	68.4	68.7	68.9	69.0	69.2	69.3	69.5	69.7	69.9
19.0	63.7	64.0	64.2	64.5	64.7	65.1	65.4	65.6	65.8	66.0	66.2	66.4	66.6	66.8
20.0	60.5	60.8	61.1	61.4	61.6	62.1	62.4	62.7	62.9	63.1	63.3	63.5	63.7	63.8
21.0	57.5	57.8	58.0	58.3	58.6	59.2	59.5	59.8	59.9	60.1	60.3	60.5	60.7	60.9
22.0	54.5	54.8	55.1	55.4	55.8	56.3	56.7	56.9	57.0	57.2	57.4	57.6	57.8	58.1
23.0	51.7	52.0	52.3	52.6	53.0	53.5	53.9	54.1	54.2	54.4	54.6	54.9	55.1	55.4
24.0	49.1	49.4	49.7	50.0	50.4	50.9	51.3	51.5	51.6	51.8	52.0	52.2	52.4	52.7
25.0	46.7	47.0	47.3	47.7	48.0	48.6	49.0	49.1	49.2	49.4	49.6	49.8	50.1	50.4

One could calculate PDD_N at different SSDs assuming that the TPR is independent of the source to point distance.

Substituting f_i(d) ≡ (SSD_i + d)/SSD_i, the following relationship holds:

$$\begin{array}{ccc}\hfill \frac{{\mathrm{PDD}}_N(d,r,{\mathrm{SSD}}_2)}{{\mathrm{PDD}}_N(d,r,{\mathrm{SSD}}_1)}& =& F·\frac{\mathrm{TPR}(d,r·f_2\left(d\right))}{\mathrm{TPR}(d,r·f_1\left(d\right))}\hfill \\ & & ·\left[\frac{S_p(r·f_1\left(d_0\right))}{S_p(r·f_1\left(d\right))}·\frac{S_p(r·f_2\left(d\right))}{S_p(r·f_2\left(d_0\right))}\right],\hfill \end{array}$$ (14)

where F is the Mayneord F factor⁵⁹ given by

$$F={\left(\frac{{\mathrm{SSD}}_2+d_0}{{\mathrm{SSD}}_2+d}·\frac{{\mathrm{SSD}}_1+d}{{\mathrm{SSD}}_1+d_0}\right)}^2.$$ (15)

Although the magnitude of the term in the brackets in Eq. (14) increases with depth,⁶⁰ it is typically small (e.g., <0.5%) for all practical clinical setups and can usually be ignored.

III.B.1.c. Tissue phantom ratios

The TPR is defined as the ratio of the dose rate at a given point in a water phantom to the dose rate at the same point at the normalization depth. TPRs can be measured directly, but may also be calculated using the following equation:

$$\begin{array}{ccc}\hfill \mathrm{TPR}(d,r_d)& =& \left(\frac{{\mathrm{PDD}}_N(d,r,\mathrm{SSD})}{100\%}\right){\left(\frac{\mathrm{SSD}+d}{\mathrm{SSD}+d_0}\right)}^2\hfill \\ & & \times \left(\frac{S_p\left(r_{d_0}\right)}{S_p\left(r_d\right)}\right).\hfill \end{array}$$ (16)

TPR is dependent on both the depth and field size at the depth of measurement. If a reference depth is not beyond the range of electron contamination, then TPR may also vary with SSD. If Eq. (16) is used to compute TPRs, spot-check measurements should be made to confirm agreement. In regions of electronic disequilibrium, Eq. (16) is only approximate,⁶⁰ although differences between measured and calculated values are small.

Table III gives sample TPR data (d₀ = 10 cm) for a 6 MV photon beam, calculated using Eq. (16), and the data from Tables II and IV.

TABLE III.

Tissue phantom ratios (TPRs) for 6-MV photons (d₀ = 10 cm).

Field size	4 × 4	5 × 5	6 × 6	7 × 7	8 × 8	9 × 9	10 × 10	11 × 11	12 × 12	13 × 13	14 × 14	15 × 15	16 × 16	17 × 17
Depth
1.5	1.390	1.364	1.340	1.323	1.313	1.302	1.291	1.281	1.273	1.267	1.261	1.256	1.251	1.246
2.0	1.381	1.360	1.336	1.317	1.307	1.296	1.286	1.275	1.267	1.260	1.255	1.251	1.246	1.241
2.5	1.360	1.338	1.321	1.305	1.292	1.281	1.270	1.261	1.254	1.247	1.241	1.237	1.232	1.228
3.0	1.335	1.318	1.298	1.283	1.273	1.263	1.253	1.244	1.238	1.232	1.227	1.223	1.219	1.214
3.5	1.311	1.296	1.279	1.266	1.257	1.247	1.237	1.228	1.221	1.216	1.212	1.209	1.205	1.201
4.0	1.286	1.275	1.258	1.244	1.236	1.229	1.221	1.213	1.208	1.202	1.198	1.194	1.191	1.187
4.5	1.263	1.252	1.238	1.226	1.219	1.212	1.204	1.197	1.192	1.188	1.183	1.180	1.177	1.173
5.0	1.240	1.230	1.217	1.207	1.200	1.193	1.187	1.181	1.177	1.172	1.169	1.167	1.164	1.161
5.5	1.216	1.207	1.196	1.187	1.181	1.176	1.170	1.164	1.159	1.155	1.152	1.150	1.148	1.145
6.0	1.192	1.183	1.174	1.166	1.162	1.157	1.152	1.147	1.143	1.139	1.137	1.135	1.133	1.131
6.5	1.167	1.161	1.152	1.146	1.143	1.139	1.133	1.127	1.124	1.122	1.120	1.119	1.117	1.115
7.0	1.142	1.135	1.129	1.125	1.122	1.118	1.114	1.110	1.107	1.105	1.103	1.100	1.098	1.096
7.5	1.119	1.112	1.106	1.102	1.098	1.095	1.092	1.090	1.088	1.086	1.085	1.083	1.082	1.081
8.0	1.094	1.089	1.084	1.082	1.079	1.077	1.074	1.071	1.069	1.067	1.066	1.066	1.065	1.065
8.5	1.072	1.067	1.062	1.061	1.060	1.058	1.055	1.052	1.051	1.050	1.050	1.050	1.049	1.049
9.0	1.047	1.045	1.041	1.040	1.039	1.038	1.037	1.035	1.035	1.035	1.034	1.034	1.033	1.033
9.5	1.023	1.020	1.019	1.020	1.020	1.019	1.017	1.016	1.017	1.017	1.017	1.017	1.016	1.016
10.0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
10.5	0.980	0.979	0.979	0.981	0.982	0.982	0.982	0.982	0.983	0.984	0.985	0.985	0.985	0.985
11.0	0.960	0.959	0.959	0.961	0.962	0.963	0.964	0.964	0.965	0.965	0.966	0.967	0.969	0.970
11.5	0.939	0.940	0.939	0.941	0.943	0.945	0.946	0.947	0.948	0.950	0.951	0.952	0.953	0.953
12.0	0.919	0.919	0.918	0.921	0.923	0.925	0.927	0.929	0.931	0.933	0.934	0.936	0.937	0.938
12.5	0.896	0.897	0.897	0.901	0.904	0.906	0.908	0.909	0.912	0.915	0.917	0.918	0.918	0.918
13.0	0.877	0.876	0.877	0.882	0.885	0.888	0.889	0.891	0.893	0.897	0.900	0.901	0.902	0.903
13.5	0.856	0.857	0.858	0.863	0.868	0.870	0.873	0.875	0.877	0.880	0.883	0.885	0.887	0.888
14.0	0.838	0.840	0.840	0.846	0.850	0.853	0.855	0.856	0.859	0.863	0.867	0.870	0.872	0.874
14.5	0.818	0.822	0.823	0.828	0.832	0.835	0.838	0.841	0.845	0.848	0.852	0.855	0.857	0.860
15.0	0.801	0.804	0.806	0.811	0.815	0.819	0.822	0.824	0.828	0.832	0.836	0.839	0.842	0.844
16.0	0.768	0.771	0.773	0.781	0.785	0.788	0.791	0.793	0.797	0.802	0.806	0.809	0.811	0.813
17.0	0.733	0.737	0.739	0.746	0.752	0.756	0.760	0.762	0.766	0.770	0.775	0.779	0.782	0.784
18.0	0.701	0.704	0.706	0.714	0.720	0.724	0.727	0.731	0.735	0.740	0.746	0.750	0.753	0.756
19.0	0.671	0.675	0.675	0.683	0.689	0.693	0.697	0.701	0.706	0.712	0.717	0.722	0.725	0.728
20.0	0.642	0.647	0.648	0.656	0.663	0.667	0.672	0.675	0.679	0.685	0.691	0.696	0.698	0.701
21.0	0.616	0.619	0.621	0.630	0.637	0.642	0.646	0.649	0.653	0.657	0.663	0.668	0.672	0.676
22.0	0.590	0.593	0.593	0.603	0.612	0.616	0.619	0.622	0.626	0.632	0.639	0.645	0.648	0.651
23.0	0.565	0.570	0.568	0.575	0.585	0.590	0.595	0.597	0.600	0.605	0.612	0.619	0.623	0.626
24.0	0.541	0.546	0.544	0.550	0.559	0.564	0.569	0.572	0.576	0.581	0.588	0.594	0.598	0.601
25.0	0.517	0.524	0.522	0.529	0.539	0.543	0.547	0.550	0.553	0.558	0.565	0.572	0.576	0.579
Field size	18 × 18	19 × 19	20 × 20	21 × 21	22 × 22	24 × 24	26 × 26	28 × 28	30 × 30	32 × 32	34 × 34	36 × 36	38 × 38	40 × 40
Depth
1.5	1.241	1.237	1.232	1.228	1.224	1.218	1.212	1.207	1.204	1.200	1.196	1.192	1.189	1.186
2.0	1.236	1.231	1.226	1.222	1.218	1.211	1.205	1.201	1.199	1.195	1.192	1.188	1.185	1.181
2.5	1.223	1.219	1.215	1.211	1.207	1.200	1.194	1.190	1.188	1.185	1.182	1.179	1.176	1.173
3.0	1.210	1.206	1.203	1.199	1.195	1.189	1.184	1.179	1.176	1.173	1.170	1.167	1.164	1.162
3.5	1.197	1.193	1.189	1.186	1.182	1.177	1.172	1.168	1.166	1.163	1.160	1.157	1.155	1.152
4.0	1.184	1.181	1.177	1.174	1.171	1.166	1.161	1.158	1.155	1.152	1.150	1.148	1.145	1.143
4.5	1.170	1.167	1.164	1.161	1.158	1.153	1.149	1.146	1.144	1.142	1.139	1.137	1.135	1.132
5.0	1.157	1.154	1.151	1.148	1.145	1.141	1.138	1.135	1.133	1.131	1.129	1.127	1.124	1.122
5.5	1.142	1.139	1.136	1.134	1.132	1.129	1.126	1.123	1.120	1.118	1.116	1.114	1.112	1.111
6.0	1.128	1.126	1.123	1.121	1.118	1.115	1.111	1.109	1.107	1.106	1.104	1.103	1.101	1.099
6.5	1.113	1.111	1.109	1.107	1.105	1.102	1.099	1.096	1.094	1.093	1.091	1.090	1.088	1.087
7.0	1.094	1.093	1.092	1.091	1.089	1.087	1.085	1.083	1.082	1.081	1.080	1.078	1.077	1.076
7.5	1.079	1.078	1.077	1.076	1.074	1.072	1.069	1.067	1.066	1.065	1.064	1.063	1.062	1.062
8.0	1.063	1.062	1.061	1.060	1.059	1.058	1.056	1.054	1.052	1.051	1.049	1.048	1.048	1.048
8.5	1.048	1.047	1.045	1.044	1.043	1.042	1.041	1.040	1.039	1.038	1.038	1.037	1.037	1.036
9.0	1.032	1.032	1.032	1.031	1.031	1.029	1.028	1.027	1.026	1.026	1.026	1.025	1.025	1.024
9.5	1.016	1.016	1.016	1.015	1.015	1.014	1.014	1.013	1.013	1.014	1.014	1.014	1.014	1.013
10.0	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
10.5	0.986	0.986	0.986	0.986	0.985	0.985	0.985	0.986	0.986	0.986	0.987	0.987	0.988	0.988
11.0	0.970	0.971	0.971	0.971	0.972	0.972	0.972	0.972	0.973	0.973	0.974	0.975	0.975	0.975
11.5	0.954	0.955	0.955	0.956	0.956	0.957	0.959	0.960	0.960	0.960	0.960	0.960	0.961	0.961
12.0	0.938	0.938	0.939	0.939	0.940	0.941	0.943	0.945	0.945	0.945	0.945	0.946	0.946	0.947
12.5	0.920	0.921	0.922	0.924	0.925	0.927	0.929	0.931	0.932	0.932	0.933	0.933	0.934	0.935
13.0	0.904	0.905	0.906	0.908	0.909	0.911	0.913	0.915	0.916	0.917	0.918	0.920	0.921	0.922
13.5	0.890	0.891	0.892	0.894	0.895	0.898	0.901	0.903	0.904	0.905	0.905	0.906	0.907	0.908
14.0	0.876	0.877	0.879	0.880	0.881	0.883	0.885	0.887	0.889	0.891	0.892	0.894	0.895	0.897
14.5	0.861	0.863	0.864	0.866	0.867	0.869	0.872	0.874	0.876	0.877	0.878	0.880	0.881	0.883
15.0	0.846	0.848	0.849	0.851	0.853	0.856	0.859	0.862	0.864	0.865	0.867	0.868	0.870	0.871
16.0	0.815	0.818	0.820	0.822	0.825	0.829	0.833	0.837	0.839	0.840	0.842	0.843	0.845	0.846
17.0	0.787	0.789	0.792	0.794	0.796	0.801	0.805	0.809	0.812	0.814	0.815	0.816	0.818	0.820
18.0	0.758	0.761	0.763	0.765	0.768	0.773	0.777	0.782	0.786	0.787	0.789	0.791	0.793	0.795
19.0	0.730	0.733	0.736	0.739	0.741	0.746	0.751	0.756	0.760	0.762	0.764	0.766	0.769	0.771
20.0	0.703	0.706	0.709	0.712	0.715	0.721	0.727	0.732	0.736	0.739	0.742	0.744	0.747	0.749
21.0	0.679	0.682	0.685	0.687	0.690	0.695	0.701	0.707	0.713	0.716	0.718	0.720	0.722	0.725
22.0	0.653	0.655	0.658	0.661	0.664	0.670	0.677	0.683	0.689	0.692	0.694	0.696	0.698	0.700
23.0	0.628	0.631	0.634	0.636	0.639	0.645	0.652	0.659	0.665	0.668	0.670	0.672	0.674	0.676
24.0	0.603	0.606	0.609	0.612	0.615	0.622	0.629	0.636	0.642	0.646	0.648	0.650	0.651	0.654
25.0	0.582	0.584	0.587	0.591	0.594	0.600	0.607	0.615	0.621	0.626	0.628	0.629	0.630	0.633

TABLE IV.

Scatter correction factors for 6-MV x-rays (d₀ = 10 cm).

Field size		Total scatter	In-air output	Phantom scatter
Equivalent		correction factor	ratio	factor
square	A/P	S c,p	S c	S p
4.0	1.0	0.866	0.957	0.905
5.0	1.25	0.895	0.968	0.925
6.0	1.5	0.922	0.977	0.944
8.0	2.0	0.964	0.990	0.974
10.0	2.5	1.000	1.000	1.000
12.0	3.0	1.028	1.008	1.020
14.0	3.5	1.051	1.014	1.037
16.0	4.0	1.070	1.018	1.051
20.0	5.0	1.102	1.024	1.076
24.0	6.0	1.127	1.029	1.096
28.0	7.0	1.149	1.034	1.111
32.0	8.0	1.167	1.040	1.123
40.0	10.0	1.194	1.048	1.139

III.B.1.d. S_c

S_c is the ratio of in-air radiation output for a given collimator setting to that for a collimator setting of 10 × 10 cm².¹⁰ Figure 5 diagrams a typical measurement setup, for a ion chamber placed in a mini-phantom at the isocenter. S_c is measured for different square collimator settings ranging over all clinically used field sizes. It is recommended that a sufficient number of field sizes be measured such that S_c changes by less than ∼1% between consecutive measured collimator settings. The magnitude of the collimator exchange effect for large, clinically relevant aspect ratios (e.g., 5 × 40 and 40 × 5 cm²) should be determined and the accuracy of the algorithm in predicting the output for these field shapes should be verified. For these field sizes, users should account for the stem effect in the measurement results.

FIG. 5.

Diagram illustrating measurement setup for S_c. The cylindrical mini-phantom is aligned coaxially with the central axis of the beam, with the ion chamber positioned at the source-detector distance corresponding to the chosen normalization conditions. The field size is maintained large enough to ensure coverage of the mini-phantom, and other scattering materials are removed from the treatment field.

The effective thickness of buildup material along the direction of the radiation beam has been discussed in several reports.^10,61–64 The thickness of material perpendicular to the beam direction should provide enough lateral scatter⁶⁵ so that the accuracy of the measured S_c is maintained. This task group recommends a 4-cm diameter cylindrical mini-phantom⁵⁶ coaxial with the central axis of the beam with the detector at 10-cm depth for the measurement of S_c independent of the normalization depth. It is pointed out in the report of the AAPM Therapy Physics Committee TG 74 (Ref. 10) that it is more accurate for calculations beyond the range of contamination electrons to use S_c measured at 10 cm. Water-equivalent materials are recommended for the construction of the mini-phantom, given reports of some variation in results using high Z build-up materials.⁶⁵ However, for field sizes between 1 and 5 cm, a high Z mini-phantom can be used as long as the S_c is renormalized so that the S_c measured at 5 cm field size matches that measured with a water equivalent mini-phantom, as described in the TG-74 report.¹⁰

S_c should be measured with the detector at the isocenter unless the field size for the measurement does not encompass the whole phantom. Care should be taken to minimize the amount of scattered radiation from structures close to the detector, such as support stands, the floor, the wall, or the table. A Styrofoam stand can be used to support the detector away from any backscattering material. It is recommended that the measurements be made with the beam pointing at the wall instead of the floor to reduce scattered radiation. This irradiation configuration also allows the alignment of the axis of the mini-phantom with the central axis of the beam using lasers and crosshair. The detector should be checked for stem and cable effects, especially for fields with large aspect ratios.

In order to commission the calculation algorithm based on the point's-eye-view of the treatment head, the distances of the proximal surface of all collimators from the target along the direction of the central axis should be either obtained from the manufacturer or measured.

Table IV gives S_c data for a 6-MV photon beam with a normalization depth of 10 cm.

III.B.1.e. S_p

S_p is defined as the ratio of the dose rate at the normalization depth for a given field size in a water phantom to that of the reference field size for the same incident energy fluence. S_p can be computed as a function of the field size at the irradiated volume from the measured quantities S_cp and S_c,

$$S_p\left(r\right)=\left(\frac{S_{c,p}\left(r\right)}{S_c\left(r\right)}\right).$$ (17)

S_cp is measured in a water phantom at SSD₀ with the detector at d₀ for different collimator settings. For the same d₀, S_p should display little to no variation between linear accelerators with the same beam quality, so that comparisons between different machines and/or with published results⁶⁶ may be useful in verifying results of a specific machine.

Table IV displays sample S_p data for a 6 MV photon beam for a normalization depth of 10 cm. In contrast to the data for S_c, these data exhibit a much greater dependence on the depth of normalization.

III.B.1.f. Off-axis ratios

In this protocol, MU calculations to off-axis points are made using central axis dosimetric quantities (e.g., S_cp, TPR), with an open-field off-axis ratio, OAR. Although there are circumstances where off-axis calculations are preferred (e.g., when the central axis is blocked or in regions of electronic disequilibrium), this task group recommends that every attempt be made to keep this calculation on the central axis to avoid the complications associated with off-axis calculations.

Several methods have been proposed for the determination of OAR for MU calculation. Early recommendations were to equate OAR with large field central axis profile data.^67,68 However, measured profile data inherently contain changes in the relative scatter contribution within the phantom which are not accounted for in the current formalism.⁶⁹ Although good agreement is obtained for points close to the central axis,^67,70 errors greater than 5% can be obtained using profile data close to the edge of the field (e.g., x > 10 cm). Although calculations to points this far off-axis are unlikely to be seen in the clinic with any frequency, caution should be used when using these data for OAR.

Better agreement has been found equating OAR to the primary off-axis ratio, POAR. This quantity represents the ratio of doses due only to primary (unscattered) photons. POARs may be obtained either by extraction from large-field central axis profiles or by direct measurement. Unlike large-field profile data, POARs will not decrease near the field edge due to reduced scatter. Chui et al.⁷¹ proposed determining POAR by measuring profiles at extended distances, where the scatter contributions to the projected off-axis points have equilibrated. In their work, profile data were measured at various depths on the floor using film dosimetry.

Gibbons and Khan⁷⁰ measured transmitted dose profiles through different thicknesses of absorbers under “good geometry” conditions (narrow beam and large detector-to-absorber distance). In this method, the beam is collimated using asymmetric fields or MLCs to define small fields (e.g., 2 × 2 cm²) on-axis and at off-axis positions. POARs are calculated using the ratio of in-air ion chamber readings (with appropriate buildup) at large distances from the source to minimize scatter. Plastic absorbers are placed near the collimating jaws to determine the depth dependence of these ratios.

Finally, there are independent analytic formalisms that remove the scatter component from measured commissioning data.^70,72–74 Additionally, depending on the planning system it may be possible to extract the primary energy fluence transmitted through a flat water phantom to determine POAR. In either case, it is recommended that a few sample measurements be made to confirm these data. This can be easily performed by measuring the dose per MU for some simple off-axis fields.

It is the recommendation of the task group that primary off-axis profiles be used for OARs. Typically, these data do not change rapidly with off-axis distance or depth, and interpolation between a few points will provide sufficient accuracy. An example dataset is shown in Table V, which displays sample POAR data for a 6-MV photon beam. These OAR data were taken from the “primary profile” data of the Theraplan treatment-planning system, originating from measured large field profiles.⁷⁵ The radial distance from the central axis should be used, because the flattening filter is radially symmetric.

TABLE V.

Open field off-axis ratios for 6-MV x-rays. Sample data from a Varian Clinac 2100C accelerator.

OADa
(cm)	0	2	4	6	8	10	15	18
Depth (cm) 1.5	1.000	1.006	1.022	1.030	1.034	1.043	1.055	1.058
3.0	1.000	1.011	1.027	1.033	1.040	1.045	1.056	1.058
5	1.000	1.017	1.033	1.041	1.046	1.048	1.058	1.057
8	1.000	1.011	1.030	1.036	1.040	1.043	1.050	1.051
10	1.000	1.006	1.028	1.030	1.031	1.031	1.033	1.032
12	1.000	1.006	1.023	1.028	1.029	1.026	1.026	1.026
15	1.000	1.007	1.016	1.025	1.025	1.018	1.016	1.016

^aRadial off axis distances projected on a plane at 100 cm from source.

III.B.1.g. Tray factors (TF)

TF is defined as the ratio of the dose rate at the point of calculation for a given field with and without a blocking tray in place. TF is almost independent of field size, depth, and SSD, and a constant value is sufficient in most cases. The presence of the tray will affect the dose in the build-up region through the production of secondary electrons as well as the absorption of secondary electrons produced upstream of the tray. Thus, it is recommended that this factor be measured at a depth well beyond the maximum range of electron contamination. The TF may also be used to account for attenuation due to other devices, such as additional trays, beam spoilers, or special patient support devices.

III.B.1.h. Compensators

Unlike blocking trays, compensators are specifically designed to affect the dose per MU within the field and often have a more significant impact on the MU calculation. In addition, the presence of a compensator mounting tray must be included in the calculation. The calculation is most significantly affected by the thickness of the compensating filter placed directly over the point of calculation.

Ideally, compensators are designed such that no compensating material is placed directly over the point of calculation and no correction is required. Otherwise, compensators may be included within the calculation in a couple of ways. First, the compensator may be included in the TF, which represents the ratio of doses to the point of calculation with and without the compensator for a given number of monitor units. For a compensator of a given thickness, the amount of attenuation depends on a variety of parameters including beam energy, compensator-to-patient surface distance, field size, and depth.⁷⁶ These dependencies are usually slowly varying, although larger variations have been noted for regions near highly sloped surfaces or within or near the buildup region.⁷⁷ For a given geometry and beam quality, however, the compensator effect can be approximated as being dependent only on the amount of compensating material placed directly above the point of calculation. The net effect can be determined either by direct measurement, or approximated by effective (broad-beam) linear attenuation coefficients. If simple step-wedge compensators are fabricated using a combination of a number of individually positioned sheets, one may create a table of attenuation factors as a function of the number of sheets. As in the case of blocking trays, the attenuation factors should be measured at a depth beyond the range of contaminant electrons, e.g., at the normalization depth.

An alternative approach is to treat the compensator as replacing tissue deficit.²⁷ In this approach, there is no modification of the attenuation factor, and the beam attenuation is accounted for by the increased effective depth of the point of calculation. The amount of missing tissue “replaced” by the compensator is determined by scaling the tissue deficit by the ratio τ/ρ_e, where τ is a unitless factor that accounts for the resulting loss of scatter due to the compensator's placement in the collimator head, and ρ_e is the electron density (relative to water) of the compensating filter material. Details of this approach have been published in Ref. 27.

III.B.1.i. Wedge factors

The wedge factor WF is defined as the ratio of the dose rate at the point of calculation for a wedged field to that for the same field without a wedge modifier. Although the presence of the wedge will affect several other dosimetric quantities, within this protocol, all these effects are incorporated into the WF. This approach eliminates the need for separate wedge-field data tables, but may require field size and depth dependent wedge factors.

Since wedge field isodose plans are calculated using a treatment-planning system, it is important that the physicist fully understands how field weights are handled in the presence of a wedge. In some cases it is possible to mistakenly apply a “double-wedge factor.” This occurs when the treatment-planning computer assigns a beam weight that builds in the wedge transmission factor, and the physicist in turn uses this filtered weight to calculate monitor units, and then once again accounts for the wedge factor. Additional considerations are discussed in Secs. V and VII.

III.B.1.ii. Physical wedges

A number of investigators have studied the field size and depth dependence of internal and external WFs. The field size dependency appears to originate from a wedge-induced increase in collimator scatter.^28,78 Heukelom et al.⁷⁸ accurately predicted the field-size dependence of internal wedges, which demonstrate a larger variation with field size. A field-size dependence may also be necessary for external wedges, particularly for higher wedge angles.⁷⁹

The depth dependence of WF has been attributed both to beam hardening as well as “dose-gradient” effects, i.e., changes in depth dose due to the dose gradient across the field.⁸⁰ McCullough et al.⁸¹ demonstrated that for depths less than 10 cm, an error of less than 2% is made if this quantity is ignored. Nevertheless, the increased use of wedged fields for depths beyond 10 cm has necessitated the inclusion of this dependency in clinical calculations.⁷⁹

It is the recommendation of this task group that physical wedge factors be measured as a function of both field size and depth. With the chamber axis perpendicular to the gradient direction of the wedge, two sets of measurements should be made with the wedge in opposite orientations to accommodate uncertainties in the chamber position and wedge mounting. It is recommended that measurements be made with the chamber at the isocenter. An example dataset of measured physical wedge factor for a 6 MV photon beam is shown in Table VI.

TABLE VI.

Physical wedge factors for 6-MV x-rays. Sample data for a Varian Clinac 2100C accelerator.

15°						30°
Depth	Side of equivalent square (cm)					Depth	Side of equivalent square (cm)
(cm)	5	10	15	20	30	(cm)	5	10	15	20	30
1.5	0.696	0.707	0.714	0.720	0.752	1.5	0.531	0.539	0.553	0.567	0.578
5.0	0.697	0.709	0.715	0.721	0.738	5.0	0.536	0.544	0.557	0.570	0.570
10.0	0.709	0.711	0.717	0.723	0.738	10.0	0.546	0.549	0.558	0.566	0.586
15.0	0.709	0.718	0.722	0.727	0.740	15.0	0.551	0.561	0.565	0.569	0.572
20.0	0.715	0.721	0.726	0.730	0.742	20.0	0.554	0.565	0.572	0.579	0.580
25.0	0.721	0.729	0.733	0.737	0.749	25.0	0.557	0.565	0.579	0.593	0.578
45°						60°
Depth	Side of equivalent square (cm)					Depth	Side of equivalent square (cm)
(cm)	5	10	15	20	30	(cm)	5	10	15	20	30
1.5	0.479	0.480	0.486	0.495		1.5	0.392	0.396	0.402
5.0	0.483	0.485	0.489	0.497		5.0	0.397	0.400	0.404
10.0	0.491	0.492	0.494	0.500		10.0	0.405	0.406	0.412
15.0	0.500	0.500	0.500	0.505		15.0	0.411	0.414	0.417
20.0	0.505	0.505	0.506	0.511		20.0	0.416	0.421	0.425
25.0	0.512	0.514	0.515	0.519		25.0	0.424	0.429	0.431

In this report, these data are considered independent of SSD. However, for treatments at extended distances (e.g., SSD > 120 cm), it would be prudent to confirm the accuracy of the wedge factor determined at isocenter, as investigators have noted a slight dependence on SSD.^82,83 For these calculations, it is also necessary to account for the field size divergence with distance. For calculations at an off-axis point within a physically wedged field, WF will change significantly. For off-axis points along the principal axis in the gradient direction of the wedge, Khan proposed that WF may be approximated by the product of the central-axis WF and the corresponding off-axis profile value measured for the largest available wedged-field.⁸⁴ This method agreed within 3% with 6-MV measurements for a calculation points positioned in the geometric center of the asymmetric field for an external wedge. A few years later, Georg⁸⁵ proposed two alternative methods consistent with the ESTRO protocol. Each of these methods employed a primary wedge factor measured in a mini-phantom, as well as wedged-field output ratios and TPRs. Although this approach compares well with the measurement approach,⁸⁶ it is not consistent within the formalism presented in this report.

Both Smulders et al.⁸⁶ and Mihailidis et al.⁸⁷ have proposed methods for off-axis wedged calculations which use open field dosimetry parameters combined with wedged-field off-axis ratios. The method of Smulders and co-workers used a product of off-axis WFs for distances parallel to and perpendicular to the gradient direction of the wedge. Wedged OARs were taken as the ratio of measured doses in phantom for symmetric fields centered off and on the central axis. The measured OARs for both 6- and 18-MV beams on an Elekta internal wedge showed only a small field size dependence, whereas the 18-MV results demonstrated a large depth dependence. Mihailidis and co-workers equated wedged OAR_S to primary OARs measured using techniques employed for open fields.⁷⁰ Their results also demonstrated good agreement (i.e., within 2%) with measured doses for 6- and 18-MV beams with 15° and 45° external wedges.

For calculations at off-axis points along the principal axis in the nongradient direction, additional corrections may be necessary in addition to open field OARs. Chui and LoSasso,⁸⁸ first demonstrated differences between off-axis wedged and open field profiles, measured for external wedged-fields. Storchi and Woudstra⁸⁹ proposed using open field OARs in this direction, but at a depth increased by the water equivalent thickness of the wedge at that point. Myler and Szabo,⁹⁰ obtained agreement within 1% by multiplying central axis WFs with off-axis correction factors. These factors were determined by measuring the effective wedge attenuation coefficient as a function of off-axis position.

The use of wedged-field off-axis ratios is not consistent with this protocol, as the WF is defined at the change in dose rate at the calculation point. Nevertheless, the above techniques may be used to determine WF at off-axis points. In most of the above techniques, it may be necessary to remove the open-field OAR values from these results to avoid double counting the OAR in the final calculation.

To avoid complications associated with off-axis calculations; this task group recommends that every attempt be made to keep this calculation on the central axis. If this cannot be avoided, users are encouraged to verify the dose per MU at the calculation point by measurement, particularly if the field geometry is complex or outside the range of tabulated data.

III.B.1.iii. Nonphysical wedges

The same concepts that apply in calculating MUs with a physical wedge apply in calculating MUs with a nonphysical or filterless wedge. Wedge factors for both physical and nonphysical wedges depend on the selection of wedge angle and energy. The main difference is the dependence on field size and depth of calculation. The field-size dependence is highly dependent on the software that drives the filterless wedge, whereas the depth dependence is nearly eliminated due to the removal of the physical filter beam hardening.

A number of researchers have derived methods to predict the WF for Varian's EDW treatment fields. Liu et al.⁹¹ extended their method adopted for DW to EDW. In this effort, they remove the majority of the field-size dependence by defining a normalization function determined from the STT value for the final moving jaw position. They then calculate a normalized WF according to the output for the EDW and the Normalized Golden STT value for the final jaw position. It is important to point out that the normalized WF defined in this work may not be used within this protocol because it requires both an additional normalization function, as well as an in-air output ratio determined within the EDW field. In a follow-up publication, however, Liu et al.⁹² used this approach to determined WF consistent with this report.

Additional methods have been proposed to determine the WF from the MU fraction model for EDW. Papatheodorou et al.⁹³ determined the WF using an exponential model of the GSTT for the 60° EDW. Klein et al.⁹⁴ derived a more complex method according to a technique that utilizes the manufacturer's method of constructing a STT by a fitting polynomial. The algorithm for the WF depends on the fixed-jaw position and energy-dependent correction factors.

Although the MU fraction model accurately predicts WF for most clinical cases, differences of ∼4% exist between WF measured for larger field size and wedge angles.⁹⁵ A number of papers have been published to improve agreement between calculated and measured data. Using an exponential model of dose outside the field, Gibbons⁹⁵ formulated an analytic algorithm for the WF that demonstrated agreement within 2% to measured data in the center of symmetric and asymmetric fields. Prado et al.⁹⁶ used an empirical formula to determine the dose to arbitrary points within the field. Miften et al.⁹⁷ determined a scatter dose correction determined from the differences between measured and calculated WF for a 60° EDW. Finally, Yu⁹⁸ and Kuperman⁹⁹ modified the MU fraction model by shifting the calculation point in the Y-direction (i.e., along the direction of jaw motion), although the magnitude and field size dependence of this shift is controversial.¹⁰⁰

The methods above also apply for calculations to points along the principal axis in the wedge-gradient direction. In these cases, the MU fraction model equates the WF to the fraction of MUs delivered, while the off-axis calculation point is in the direct beam. These models therefore approximate the fraction of dose delivered to the off-axis point of calculation, consistent with the definition of WF within this protocol. Because the change in dose for nonphysical wedges in the nongradient direction is negligible,¹⁰¹ only the off-axis distance parallel to the wedge-gradient direction should be used as input in determining WF. However, the radial off-axis distance x (projected to 100 cm) should still be used in calculating the OAR.

The method of choice for a clinic may be somewhat dependent on the clinic's resources and capabilities. A clinic may calculate a subset of WF to be used in a look up table for either manual or computer-based applications. The one comforting aspect of using either an algorithm or fixed tables is that a WF for a given energy is independent of treatment machine. Therefore, one algorithm or one table can be used for a single energy. Klein et al.,⁹⁴ compared the measured WFs for three accelerators and found differences of less than 0.5% on average, with no difference more than 1.5% (see Fig. 6).

FIG. 6.

Measured 6-MV EDW wedge factors for three different Varian machines represented by solid, dashed, and dotted lines. The close agreement between multiple machines allows a common wedge factor table for use in MU calculations (Ref. 94).

The Siemens VW implementation uses an analytic model to determine the jaw position, rather than the tabular methods employed by EDW. For a desired wedge angle θ, the moving jaw position and dose rate are varied during treatment delivery in order to deliver a pattern of energy fluence denoted by

$$\Psi \left(x\right)=e^{c\left(E\right)\mu x\tan \theta },$$ (18)

where x is the distance from the central axis, μ is an effective linear attenuation coefficient in water, and c(E) is a energy-dependent calibration factor.

The Siemens VW also differs from the EDW in that the programmed MU is the number of MU the central axis remains within the direct beam. Thus, within the MU fraction model, the WF for the virtual wedge is unity. As is the case for the EDW wedge factors, investigators^102–104 have found that the WF is unity for most cases with the exception of the 60°, large-field VW fields.

For points of interest away from the central axis, the MU delivered across the beam can be described according to the following formula:

$$\mathrm{MU}\left(x\right)=\mathrm{MU}\left(0\right)e^{-c\left(E\right)\mu x\tan \theta },$$ (19)

where MU(x) = the MU required to deliver the desired dose to position x (see Fig. 7).

FIG. 7.

Example of a MU versus coordinate curve for the virtual wedge. Displayed are MU(x), the number of monitor units given, while a point at position x is irradiated, versus off-axis position x. The moving jaw is initially at the position of the opposing jaw (x_min), with a minimum gap width, ℓ_gap, of 1 cm projected at SAD (Ref. 103).

For both EDW and VW, it is recommended that the constancy of the WF be confirmed by measurement, especially for large wedge angle and field size combinations.

III.B.1.j. SSD₀

For calculations with photon beams within this protocol, the nominal SSD or SPDs have been used to compute the inverse-square correction. However, it has been pointed out that extra-focal radiation will contribute to small but detectable deviations from the inverse-square law for photon beams.¹⁰⁵ The effect of this on most clinical calculations is typically negligible, but should be verified by the physicist at the time of machine commissioning for the range of SSDs expected to be used in the clinic. This is particularly true for treatments at greatly extended SSDs, such as those performed for total body irradiation. The reader is referred to the AAPM Task Group 29 report for these situations.¹⁰⁶

III.B.2. Measurements of dosimetric quantities: Electron beams

III.B.2.a. Dose per MU under normalization conditions ($D_0^{\prime }$)

For electron beams within this protocol, the dose rate or dose per MU, $D_0^{\prime }$, under normalization conditions is set to be 1.0 cGy/MU.

III.B.2.b. Percent depth dose

The recommendations of the AAPM Task Group 70 report³⁸ should be followed for the measurement of depth dose curves for electron beams. If a cylindrical ionization chamber is used, the effective point of measurement of the chamber must be taken into account. This requires that the complete depth ionization curve be shifted to shallower depths (i.e., upstream) by a distance proportional to r_cav, where r_cav is the radius of the ionization chamber cavity. For electron beams, the shift is taken as 0.5 r_cav.⁷ If a well-guarded plane-parallel ionization chamber is used, no shift in depth-ionization curves is needed. Converting relative ionization to relative dose for ionization chambers requires multiplying by a stopping power ratio and a replacement factor, both as a function of depth. The expression given by Burns et al.,¹⁰⁷ which is also in the TG-70 Report, should be used for the stopping power ratio, and the replacement correction factor should be as described in the TG-25 report.⁷

III.B.2.c. Output factors

At the time of beam commissioning, the field size dependence of the output is measured as a function of field size for each energy and applicator combination at the reference SSD and d_m. If the applicator accepts inserts, then output is typically measured for a range of square insert sizes from 2 × 2 cm² to the size of the open applicator. Each of these measurements is taken at the depth of d_m, which may shift toward the surface for small inserts. Table VII illustrates these data for a 9-MeV beam for a Varian Clinac 2100C.

TABLE VII.

Electron output factors. Electron output factors versus field size for various applicators for a 9 MeV beam on a Varian Clinac 2100C (SSD = 100 cm).

Field size	Applicator size (cm2)
(cm2)	10 × 10	15 × 15	20 × 20	25 × 25
2 × 2	0.843	0.846	0.824	0.812
3 × 3	0.908	0.908	0.891	0.871
4 × 4	0.963	0.954	0.936	0.911
5 × 5	0.991	0.982	0.962	0.936
6 × 6	1.003	0.997	0.976	0.951
7 × 7	1.005	1.004	0.983	0.960
8 × 8	1.003	1.006	0.986	0.964
10 × 10	1.000	1.003	0.985	0.965
12 × 12		0.997	0.980	0.962
15 × 15		0.992	0.976	0.955
20 × 20			0.981	0.950
25 × 25				0.955

III.B.2.d. Effective SSDs

SSD_eff can be used to determine MU for electron fields at distances other than the nominal SSD. SSD_eff is dependent on electron energy and field size.

The method described by Khan¹⁰⁸ may be used to determine SSD_eff. Beam output is measured over clinically relevant ranges of SSDs (100–120 cm, for example), field sizes, and beam energies. For each field size and energy combination, a fit is made of the square root of the output ratio $\sqrt{D^{\prime }(r_a,{\mathrm{SSD}}_0)/D^{\prime }(r_a,{\mathrm{SSD}}_0+g)}$ versus the gap, g, where D^′(r_a, SSD₀ + g) is the output measurement and the gap is the distance between the treatment and nominal SSDs. A least-squares fit of the data on each plot gives a slope that relates to the SSD_eff as follows:

$${\mathrm{SSD}}_{\mathrm{eff}}=\frac{1}{\mathrm{slope}}-d_m$$ (20)

where d_m is the depth of maximum dose on central axis for the field of interest. SSD_eff for field sizes that have not been measured can be interpolated. In cases of extreme field irregularity or large gaps from SSD₀, special dosimetry is recommended.

For a given applicator, there is a strong dependence of SSD_eff on insert size.¹⁰⁹ Investigators have shown that SSD_eff is only weakly dependent on the applicator^40,110 so tables of SSD_eff versus insert size are clinically adequate. In fact, Sharma and Johnson¹¹¹ suggested that a single SSD_eff for each energy can be used for field sizes larger than 10 × 10 cm². Table VIII displays SSD_eff, categorized by insert size and energy. SSD_eff is smallest for small fields and low electron energy. For rectangular field sizes, it is recommended that the geometric mean of SSD_eff for each side be used as the SSD_eff, as this can be shown to be equivalent to the square root method of Mills et al.¹¹² The field size dependence is caused by a lack of lateral scatter equilibrium for small apertures.^40,113 Potential dose-delivering electrons near the central axis are scattered out of the field and not fully replaced by electrons originating peripheral to the central axis. The net loss of scatter to the central axis causes the fluence to decrease with SSD more rapidly than the inverse-square law predicts. The energy dependence is caused by the increased outward scattering of low energy electrons, which also decreases the fluence to the central axis.

TABLE VIII.

Electron SSD_eff table. Table of SSD_eff averaged over applicator size for a Varian Clinac 2100C. For this table, SSD_eff is a function of insert size and energy only.

Insert size	Energy (MeV)
(cm2)	6	9	12	16	20
4	46.2	61.1	72.5	76.4	76.6
6	62.2	74.7	80.2	81.8	80.6
8	77.6	83.8	83.2	83.6	82.7
10	82.9	85.9	86.8	85.5	83.8
15	90.7	90.9	90.1	90.0	89.7
20	90.0	91.8	91.4	90.9	92.0
25	90.7	91.9	91.0	92.5	93.3

III.B.2.e. Air-gap correction factors (f_air)

The air-gap correction factor f_air is defined as the ratio of the electron dose rate at the normalization depth at extended SSD to that predicted using only inverse square corrections. This quantity represents the deviation from the inverse-square law due to the loss of side scatter equilibrium¹¹⁴ and is assumed independent of applicator size. For an electron beam, f_air is dependent on the insert size and the SSD.

f_air is determined by evaluating the following equation using square field output data at the standard SSD (SSD₀) and extended SSDs,

$$\begin{array}{c}\hfill f_{\mathrm{air}}(r_a,\mathrm{SSD})=\frac{D^{\prime }(r_a,\mathrm{SSD})}{D^{\prime }(r_a,{\mathrm{SSD}}_0)}·{\left[\frac{\mathrm{SSD}+d_m\left(r_a\right)}{{\mathrm{SSD}}_0+d_m\left(r_a\right)}\right]}^2,\end{array}$$ (21)

where D^′(r_a, SSD) is the measured output for the given SSD.

For rectangular fields, f_air may be estimated using the square-root method:

$$f_{\mathrm{air}}(L\times W)={[f_{\mathrm{air}}(L\times L)\times f_{\mathrm{air}}(W\times W)]}^{\frac{1}{2}},$$ (22)

where the same applicator is again implicit in the equation. It should be noted that nominal rather than virtual SSDs are used in Eq. (21). Although this method differs from the TG-25 implementation,⁷ the corresponding difference in the inverse square term is small and this small difference is absorbed into the air-gap factor.

Table IX displays sample air-gap factors for a 9-MeV electron beam.

TABLE IX.

Electron air gap factor table. Air gap factor versus field size (defined at SSD = 100 cm) and SSD for a 9 MeV electron beam on a Varian Clinac 2100C. Values for f_air < 0.95 are italicized to indicate conditions of lateral electronic disequlibrium. Taken from Ref. 45.

Field size	SSD (cm)
(cm2)	100	105	110	115	120
2 × 2	1.000	0.882	0.743	0.611	0.505
3 × 3	1.000	0.946	0.878	0.792	0.715
4 × 4	1.000	0.942	0.902	0.862	0.815
6 × 6	1.000	0.978	0.954	0.940	0.915
10 × 10	1.000	0.984	0.972	0.961	0.955
15 × 15	1.000	0.988	0.978	0.970	0.963
20 × 20	1.000	0.987	0.975	0.971	0.963
25 × 25	1.000	0.987	0.982	0.974	0.970

IV. INTERFACE WITH TREATMENT-PLANNING SYSTEMS

Dose calculation algorithms in external beam treatment planning are often classified as correction-based and model-based. The correction-based algorithms calculate the dose in a patient by correcting the measured dose distribution in a water phantom to account for beam geometry, beam modifiers, patient contours, beam aperture opening, and tissue heterogeneities. The model-based algorithms compute the dose in a patient from “first principles” using a model of radiation transport. Computations of dose using either correction-based or model-based algorithms require measurement of beam data in a water phantom. For correction-based algorithms, the measured data are first parameterized into functions that are subsequently used to reconstitute each treatment beam used in a patient treatment plan. For model-based algorithms, the measured data are used to define the description of the beam. The fundamental difference between the two classes of algorithms is that model-based calculations do not reconstitute measured data before correcting it for the clinical situation.

Regardless of which type of algorithm is used, the treatment-planning system should be able to report the dose from each beam to any point in the dose matrix for which the user will perform the manual calculation. Users can then verify the treatment-planning systems reported MUs using calculation points located in regions of less uncertainty (i.e., away from block edges or heterogeneities). Additional information detailed below should also be provided to the user to aid in the MU calculation. Unfortunately, there are a number of different terminologies used in different vendor implementations. It is critical that treatment planning vendors specify quantities that are consistent with the nomenclature defined in this and other task group reports.

MU calculations should always be performed in conjunction with computer treatment plans to serve as an independent verification of the treatment plan determined MUs. Differences in results may be due to either deficiencies in the “manual” calculation algorithm (i.e., due to the approximations inherent flat, water-phantom based calculation), to errors in the treatment-planning systems MUs (i.e., due to errors in input parameters, input beam data, modeling, etc.), or to both. As discussed in the quality assurance (QA) section, differences exceeding reasonable limits should be investigated, for example, via direct measurement. A completely independent calculation would require that all input data be obtained outside the planning system. This is rarely practical or necessary, if it has been determined that the planning system is accurate in providing correct input data for the independent check. Furthermore, vendor provision of appropriate calculation input data (e.g., radiological depth, equivalent square) significantly aids the user's determination of the source of the discrepancy. Quality assurance measures for treatment planning systems have been addressed in the AAPM Task Group 53 report.¹¹⁵

For treatment plans performed on CT datasets, vendors should provide both the physical and radiological depth of each beam to the calculation point. These reported depths should be those measured along the path from the source to the point of calculation, for example, accounting for changes in patient anatomy at off-axis positions. Verification of the planning algorithm should be made before using depths reported for noncoplanar beams. Further caution should be taken for noncoplanar calculations, as the accuracy of depth determination will be compromised by coarse slice spacing or incomplete datasets.

Users performing manual calculations must rely on the equivalent square of the collimating jaws to determine the argument for S_c. Depending on the treatment-planning algorithm employed, more complex calculations of head scatter including primary and extra-focal components can be made, even including the effects of additional apertures such as MLCs. For each beam, planning vendors should provide the user with the equivalent square field size of a field that produces the same collimator output. For additional details, see the AAPM TG-74 report.¹⁰

For S_p and TPR (or PDD_N), users must estimate the equivalent square of each field incident onto the patient. Treatment-planning systems should provide more accurate equivalent squares, incorporating corrections for patient anatomy (external and internal) as well as more accurate corrections for irregular fields. These data can aid users in determining the cause of differences between manual and TPS-calculated MUs.

Users should take great care to ensure that the point of calculation matches that referenced in the treatment plan output.

V. MU CALCULATIONS FOR IMRT FIELDS

At the time the task group was formed, methodologies for performing independent checks of MU calculations for IMRT treatment fields were not prevalent in the clinical environment. Since that time, a number of papers have been written to address these types of calculations.^116–128 Additionally, several vendors of MU-calculation software have expanded their products to include MU calculations for IMRT fields. Given the widespread use of these products, a discussion of IMRT MU calculation methodology is warranted. This task group report will give no recommended formalism, but will discuss some general considerations. AAPM Task Group 219 is charged with investigating this area in greater detail.

V.A. Calculation methodologies

The IMRT Collaborative Working Group¹²⁹ defined a number of classes of IMRT delivery methods. Gantry-static techniques are divided into segmental-MLC (SMLC) and dynamic-MLC (DMLC) depending on whether the collimator shape varies during irradiation. Gantry-dynamic techniques include serial and helical tomotherapy, as well as volumetric modulated arc therapy (VMAT). Each of these delivery methods presents unique challenges to the determination of MU.

Several papers have been written discussing the calculation of MU for SMLC-IMRT. One of the first papers dealing with the subject of IMRT MU calculations was the work of Boyer et al.¹¹⁶ who derived an algorithm for IMRT MU calculations for the Corvus treatment-planning system. In this algorithm, the intensity-modulated field was modeled by an ensemble of beamlets whose calculated dose was scaled by an inverse square and primary off-axis ratio correction factors depending on their location within the field. The total MU was scaled by a modulation scale factor, representing the maximum number of steps (per number of levels) required to achieve the designed modulation between any two pair of opposing leaves. The algorithm was designed for a one-dimensional sliding window-type leaf-sequencing algorithm. The results agreed within 4% for the cylindrical phantom studied.

The concept of subdividing the intensity-modulated field into a number of beamlets was extended by both Xing et al.,¹¹⁹ and Kung et al.¹¹⁸ Xing et al. extended the work of Boyer to create an algorithm that was independent of the leaf-sequencing method employed by the treatment-planning system. Consider a SMLC-IMRT field of K segments that may be subdivided into M beamlets. Let f_k represent the fractional MU delivered during the kth segment (f_k = MU_k/MU). In Xing's approach, if $d_m^0$ is defined as the dose contribution from the mth beamlet (per MU) when it is open, the dose from the intensity-modulated field is given by

$$D=\mathrm{MU}\sum _m^M{C}_m{d}_m^0,$$ (23)

where

$$C_m=\sum _k^K[{\delta }_{m,A_k}+\alpha (1-{\delta }_{m,A_k})]f_k.$$ (24)

In Eq. (24), δ_m,Ak is defined as 1 if beamlet m is in the open area of segment k, and 0 otherwise, and α is the transmission through the MLC leaf. The increase in MU needed to deliver an intensity modulated field is given by the C_m factor. All that remains within this formalism is the determination of the beamlet dose, $d_m^0$. Both Xing et al. and Kung et al. used this approach to compute isocentric doses using a modified Clarkson integration method to add doses from outside beamlets or sectors. Yang et al.¹²⁰ extended this work to include calculations to arbitrary points on or off the central axis. Yang also used a three source model to calculate the head scatter for the fields. The improved algorithm demonstrated agreement to within 3% with both ion chamber measurements and doses computed with the Corvus system. More complex approaches have also been published to calculate irregular field outputs from first principles.¹³⁰

DMLC-IMRT fields represent an increased level of complexity, as the number of control points within an intensity modulated field is typically much larger than that for SMLC-IMRT. Linthout et al.¹²¹ described a technique for verification of DMLC-IMRT treatment delivery on a BrainLab Novalis system. In this work, calculations were made by summing field segments of uniform intensity, rather than individual beamlets. Calculations were made to the isocenter and the dose algorithm used was limited to homogeneous media. Chen et al.¹²² developed an algorithm for use in verifying DMLC-IMRT treatments planned using a sliding window leaf sequencing algorithm. This method was not restricted to the isocenter and included the effects of leaf-end leakage. Comparisons with 25 patients and 169 intensity modulated fields demonstrated good agreement between the proposed technique and doses calculated with the Eclipse treatment-planning system.

Less data are available for tomotherapy-type delivery techniques. Ayyangar et al.¹²³ proposed a method to verify dose calculations for the serial tomotherapy Peacock system. In their paper, calculations are made by summing the dose from open beamlets. The beamlet dose was computed using a pencil beam model that incorporated profiles from the planning system and an exponential fit to the TMR. Although this method was used to generate fully independent isodoses distributions, point dose calculations were possible as well. Tsai et al.¹³¹ also developed what they called a “quasiindependent” MU calculation that is based on the vane patterns from the MIMiC collimators. For helical tomotherapy, Gibbons et al.¹²⁴ described an approach in which the total dose was calculated as a sum of doses from each projection. The modulated projection field was approximated by a sum of equal intensity segments that were used to compute the total dose. For point-dose calculations to the center of the PTV, good agreement was found between the proposed method and the treatment-planning system for a number of phantom and patient plan calculations.

V.B. Task group recommendations

Due to the increased complexity of IMRT plans, well-designed QA tests are required to validate treatment plans for individual patients. Verification of a patient-specific IMRT treatment plan is typically accomplished through dose measurements of the plan recomputed on a clinical measurement phantom. However, as pointed out by the AAPM IMRT subcommittee's guidance document on implementation of IMRT,¹³² although such a QA procedure is valuable for testing the accuracy of the delivery system, some errors in dose calculations (e.g., failure to remove the planning CT couch, an incorrect patient CT dataset, or an incorrect CT-density table) will not be detected using a phantom plan evaluation. The inability to detect all errors is supported by the data from the Radiological Physics Center's independent audit of IMRT delivery using their anthropomorphic QA phantoms, which nearly a third of all institutions fail on their first attempt.¹³³ Hence, a comprehensive QA program should include verification of both the dose calculation and dose delivery.

This task group report recommends that a second check dose calculation be used to verify IMRT treatment deliveries. The use of a second independent check of machine time settings (minutes or MUs) for a patient treatment is standard of care in radiation therapy. Historically in medical physics, new technologies have been implemented with extreme care because failure modes are unknown. As experience grows, quality assurance methods become more focused and efficient. Consequently, we do not perform individual QA measurements for three-dimensional conformal radiation therapy or most other external beam treatments. Individual patient QA measurements are currently performed for IMRT treatments because they are still relatively new. We foresee a time in the future, when confidence in IMRT delivery and treatment planning will be high enough that clinics will desire to replace them with an independent calculation. As noted by the AAPM IMRT Subcommittee report: “This is the norm for conventional treatments and may become so for IMRT as the field evolves.”¹³²

VI. QUALITY ASSURANCE

The treatment time set to deliver the prescribed dose to a patient involves numerous steps from beam commissioning to daily QA checks. Table VII in the Task Group 40 (TG-40) report on “Comprehensive QA for Radiation Oncology” lists the factors that affect the accuracy of the MU calculation.⁴ Each one of these steps, to some degree, should be considered as part of a clinic's QA program. The MU set calculated for a patient's treatment, whether by using the treatment-planning system, inhouse developed calculation software, or manually by looking up factors in tables, should always be verified by another individual in an independent manner from the initial calculation as recommended by TG-40. It is preferred that a radiation oncology physicist be the reviewer; however when there is only one physicist available, a dosimetrist or other individual, authorized by the physicist, can be designated as the reviewer. The goal of this MU verification is to minimize the number of errors that may result in the dose delivery to a patient early in the patient's treatment. The MU verification should occur prior to the patient's first treatment; when this is not possible, then it should be performed before the third fraction is delivered or before 10% of the dose has been delivered, whichever occurs first.⁴ More details regarding the clinical application of this formalism described in this report, as well appropriate action levels are contained in a separate AAPM report.⁵

Verification of the MU calculation should include checking all of the dosimetry factors used in the calculation of the treatment time. These factors include the machine, modality, energy, SSD, or SAD, collimator setting, treatment depth, depth dose data, TFs, WFs, OARs and any other parameter necessary to calculate the monitor unit set. We recommend that the individuals who performed the initial MU calculations and the MU verification sign and date the calculations.

Prior to clinical use, the treatment-planning system from which the patient monitor unit set is calculated should undergo rigorous QA testing as outlined by the TG-53 report on “Quality Assurance for Clinical Radiotherapy Treatment Planning.”¹¹⁵ These tests include QA of the input data (i.e., Can the system reproduce the input data correctly?), algorithm verification to determine the accuracy of the dose calculation algorithm itself, and calculation verification to determine whether the results from the planning system agree with experimentally measured dose values. Verification of current beam modeling planning systems' ability to calculate dose correctly for many complex clinical situations is best accomplished by ion chamber measurements in a water phantom. Verification of heterogeneity calculations requires special phantoms, both slab and anthropomorphic.³⁴ The planning systems' dose calculation algorithm applicability and limitations should be determined and then the dose calculations for the complete range of clinical situations need to be assessed. Once the user has confidence that their planning system can calculate accurate MU sets for patients, then attention to developing an independent means of verifying the planning system's calculation of MU is needed.

The best check is one that uses a different method of calculation other than that used in the initial calculation. A different computer calculation (inhouse or commercial MU-calculation software, or other treatment-planning system) or manual calculation technique is recommended. Many of the newer treatment-planning systems calculate MU settings in a manner that is not consistent with the formalism specified in this report. It is the responsibility of the planning system manufacturer to provide the system's formalism for calculating monitor units to the physicist. The physicist should understand how the planning system calculates dose and MUs in order to be able to compare the initial MU calculation with the independent calculation. For the model-based planning systems, we recommend the physicist use the formalism outlined in this report to verify the MU set calculations. The physicist, based on the accuracy and precision of the dosimetry data used for the check, must also develop action criteria for the agreement between the initial MU calculation and redundant check. The criterion most often used in the radiation oncology community is 2%–3% agreement between the initial calculation and the redundant check. There can be exceptions to the action criteria, when the physicist understands the reason for the differences or the limitations of the algorithms used for the initial and redundant check calculations. An example of the two calculations disagreeing is the failure of the initial MU calculation or redundant check to incorporate the appropriate changes in depth dose as the beam is hardened by a large angle wedge, which may or may not be accounted for in the treatment-planning system and/or manual method. Another possible difference between the initial MU calculation and the independent check might result from not accounting for missing tissue or curvature as normally observed with tangential breast treatments.

There are two primary sources of dosimetry data that can be used with the MU calculation formalism presented in this report to perform a redundant MU check. The first and recommended source is to use your own measured data for each therapy beam. Because the newer model-based treatment-planning systems rely on less measured data, the physicist may be required to perform additional dosimetry measurements to develop a comprehensive set of dosimetry data for each beam to be used in the redundant check. The physicist should develop tables of dosimetry data ensuring the accuracy of the data within each table and that any error introduced by interpolation between two tabular points is minimized to achieve an overall 2% accuracy for each MU calculation. As a minimum, the physicist should have a full set of fixed SSD depth-dose data and/or tissue-phantom ratio data, collimator and phantom scatter factors, WFs (both field size and depth dependent), tray factors and off-center ratios for the redundant checks. The model based planning systems' ability to calculate accurately the dose to a point in phantom, which is directly related to its ability to calculate accurately MU times, should also be verified for several different clinically relevant setups using ion chamber measurements. Examples of some clinical situations that may require measurement verification include calculations off axis using asymmetric fields both under a large wedge and open field, calculations at depth for highly irregular MLC field-size settings, calculations of outputs for small field sizes (<4 × 4 cm²) and calculations of doses at depths less than d_m.

A second and less rigorous source of dosimetry data for the redundant checks can be the “standard data” for the particular make, model, modality, and energy of interest. Most of the newer linear accelerators models are similar in design and are tuned to have the same basic dosimetry parameters. However, occasionally a linear accelerator does not have the same basic dosimetry parameters as the other accelerators of the same make, model, and energy. For this reason prior to any “standard data” use in a clinic, a set of measurements must be made to ascertain whether these data in fact matches the dosimetry parameters for the specific linear accelerator. Several publications,⁶⁶ including the TG-46 report¹³⁴ have provided the basic dosimetry data needed for MU calculations. One has to realize that these standard data are typically averages of measured data and therefore have a slightly higher uncertainty (∼1%) compared to the actual measured values for a specific accelerator. The Radiological Physics Center (RPC) maintains a set of standard data for 129 different make/model/photon energy combinations. The RPC data consist of output factors, depth dose data, in-air off-axis factors, WFs and TFs, which are available to the radiation oncology community upon request. These standard data sets can provide a unique independent redundant check mechanism for most clinics.

Verification of the MU calculation technique used by a clinic can also be performed by an independent quality audit. The audit by an individual from outside of the clinic will typically use an independent method for checking the MU set calculations. Physicists from nearby clinics, consultant physicists, local AAPM chapter physicists, and the RPC physicists can provide this type of quality audit. The RPC conducts audits of clinics participating in clinical trials in two ways. First, by providing the clinic with several hypothetical patients for specific treatments (reference or benchmark cases) and recalculating the dose delivered from the clinic's MU set, although using their calculation technique. This method allows the auditor to isolate the individual parameters to discern any differences noted. Second, during on-site dosimetry-review visits by the RPC, several treatment records for different treatment sites are checked for accuracy, inclusion of all necessary information, and consistency of the dosimetry data used to calculate the MU set. The independent audit is the most costly; however, it provides the best redundant check of a clinic's MU set calculations to discover potential systematic errors that might otherwise be missed if the clinic's physicist performs the redundant check.

Finally, we note that additional quality assurance measures may be warranted for complex field shapes and/or patient geometries, where the accuracy of the MU algorithm is limited. AAPM Task Group Report 114 has established agreement criteria and presents specific action level guidelines for disagreement between independent MU calculation methods.⁵ Patient in vivo dosimetry may also be useful in verifying the results of a computer treatment plan. The reader is referred to AAPM Task Group 62 Report on diode in vivo dosimetry for more information.¹³⁵

VII. SUMMARY OF RECOMMENDATIONS

We recommend that

• 1.The formalism embodied in Eqs. (1) and (3) for photon beams, and Eq. (10) for electron beams should be used for the calculation of monitor units.
• 2.For photon beams, the task group recommends that a normalization depth of 10 cm be chosen for MU calculations. If another depth is chosen, this depth shall be greater than or equal to the maximum depth of d_m, determined from percentage depth dose measurements for the smallest field size and greatest SSD.
• 3.For electron beams, the normalization depth for a given field is taken to be the depth of maximum dose along the central axis for the same field incident on a water phantom at the same SSD.
• 4.Treatment planning software vendors should provide data necessary to verify their calculation of MU through this protocol. Vendors should specify quantities that are consistent with the nomenclature and definitions found in this and other AAPM task group reports.
• 5.MU verification of patient plans should occur prior to the patient's first treatment; when this is not possible, then it should be performed before the third fraction is delivered or before 10% of the dose has been delivered, whichever occurs first.

VIII. EXAMPLES

The following examples have been included to aid the user in the application of the protocol to clinical problems. In all cases, the tables included in the Appendix have been used to perform the calculations.

VIII.A. Photon calculations

These example calculations use a 6-MV beam (Varian Clinac 21EX), 100-cm SAD, with a 0.8 cGy/MU dose rate at the normalization point (SSD₀ = 90 cm, r_c = 10 × 10 cm², d₀ = 10 cm). The equivalent square of the collimator and effective field sizes has been determined using the A/P approximation.

• 1.Calculate the MUs required to deliver 250 cGy to the isocenter. Collimator field size of 10.0 × 15.0 cm², depth = 6 cm and no blocking.
  Answer: This example is easiest to solve using an isocentric technique. Using 4A/P, the equivalent square field size for 10 × 15 cm² is 12 × 12 cm² and is the appropriate field size for use with S_c, S_p, and TPR. From Eq. (1), the MUs are

  $$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{D}{D_0^{\prime }·S_c\left(12\right)·S_p\left(12\right)·\mathrm{TPR}(6,12)}\hfill \\ & =& \frac{250\mathrm{cGy}}{\left(0.8\mathrm{cGy}/\mathrm{MU}\right)·\left(1.008\right)·\left(1.020\right)·\left(1.143\right)}\hfill \\ & =& 266\mathrm{MU}.\hfill \end{array}$$ (25)

  The calculation may also be performed nonisocentrically. Note that three different field sizes must be used: the field size at the isocenter for S_c, the field size at the surface for PDD_N and the field size at the normalization depth (i.e., surface + 10 cm) for S_p. An inverse-square correction is also required. The equivalent square of (12 cm)² projects to (11.3 cm)² and (12.5 cm)² at the surface and depth of 10 cm, respectively. Using Eq. (3), the MUs are

  $$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{250\mathrm{cGy}}{\left(0.8\mathrm{cGy}/\mathrm{MU}\right)·{\mathrm{S}}_{\mathrm{c}}\left(12\right)·{\mathrm{S}}_{\mathrm{p}}\left(12.5\right)·\frac{{\mathrm{PDD}}_{\mathrm{N}}(6,11.3,94)}{100\%}·{\left(\frac{100}{94+10}\right)}^2}\hfill \\ & =& \frac{250}{\left(0.8\right)·\left(1.008\right)·\left(1.024\right)·\left(1.231\right)·\left(0.925\right)}\hfill \\ & =& 266\mathrm{MU},\hfill \end{array}$$ (26)

  where the PDD_N has been taken from Table II and corrected for the change in SSD using Eq. (14).
• 2.Calculate the MUs required to deliver 90 cGy to the isocenter of an AP lung field displayed in Fig. 8. The collimator field size is 18.0 × 12.0 cm², and the physical depth = 10.0 cm. The field is blocked using a tertiary MLC and a 15° physical wedge is added to the field. Repeat the calculation using a tissue heterogeneity correction using a radiological depth of 6 cm.
  Answer: In this example, the effective field size is estimated to be 14 × 8 cm² (equivalent square = 10.2 cm), which is used to determine S_p and TPR. Note that some flexibility is allowed in this estimate: identical results are obtained with an equivalent square range of 9–13 cm. Since the MLC is tertiary, the collimator field size is used for the argument S_c. The effective field size is used to determine the physical WF, although little difference is found using either field size. The calculated MUs are

  $$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{90\mathrm{cGy}}{(0.8\mathrm{cGy}/\mathrm{MU})·{\mathrm{S}}_{\mathrm{c}}\left(14.4\right)·{\mathrm{S}}_{\mathrm{p}}\left(10.2\right)·\mathrm{TPR}(10.2,10)·\mathrm{WF}(10.2,10)}\hfill \\ & =& \frac{90\mathrm{cGy}}{\left(0.8\mathrm{cGy}/\mathrm{MU}\right)·\left(1.015\right)·\left(1.002\right)·\left(1\right)·\left(0.711\right)}\hfill \\ & =& 156\mathrm{MU}.\hfill \end{array}$$ (27)

  The correction factor for the RTAR method [see Eq. (7)] is equal to TPR(10.2,6) = 1.152, giving MU = 135 for the heterogeneous calculation. Because the WF for this wedge depends only slightly with depth, the same answer is obtained using the radiological depth in Eq. (27).

• 3.Calculate the MUs to deliver 45 cGy to the isocenter (depth = 9.5 cm) of a superior–anterior oblique pituitary field. The collimator field size is asymmetric (X1 = 2.0, X2 = 3.5, Y1 = Y2 = 3.5), with blocking (see Fig. 9) using a tertiary MLC. A 45° EDW is added, in the Y1 orientation (Y2 jaw fixed). Repeat the calculation to an off-axis point at the same depth, located at (1,1) cm in the (X2,Y2) direction.

FIG. 8.

Beam's eye view DRR for photon problem #2.

FIG. 9.

Beam's eye view DRR for photon problem #3.

Answer: In this example, the equivalent square of the collimator field size (5.5 × 7 cm²) is 6.2 cm². The effective field size at the isocenter is estimated to be 4 × 5 cm². The EDW factor is determined predominately by the fixed jaw position (Y2 = 3.5 cm) and has been calculated to be 0.845 using an analytic equation.⁹⁵ The total MUs are given by

$$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{45\mathrm{cGy}}{D_0^{\prime }·S_c\left(6.2\right)·S_p\left(4.4\right)·\mathrm{TPR}(4.4,9.5)·\mathrm{WF}(Y2=3.5)}\hfill \\ & =& \frac{45\mathrm{cGy}}{\left(0.8\mathrm{cGy}/\mathrm{MU}\right)·\left(0.978\right)·\left(0.914\right)·\left(1.023\right)·\left(0.845\right)}\hfill \\ & =& 73\mathrm{MU}.\hfill \end{array}$$ (28)

For the off-axis calculation, because the calculation point is closer to the fixed jaw, it remains in the open field longer and the WF is increased. The off-axis distance used for this calculation is the distance along the gradient (or Y) direction of the wedge, which is 1 cm in this case. Again, using the same analytic formula, the WF is found to be 0.892. An open-field OAR is also required, but the radial off-axis distance of 1.4 cm is used in this function. The total MUs in this case is given by

$$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{45\mathrm{cGy}}{D_0^{\prime }·S_c\left(6.2\right)·S_p\left(4.4\right)·\mathrm{TPR}(4.4,9.5)·\mathrm{WF}(1,Y2=3.5)·\mathrm{OAR}(1.4,9.5)}\hfill \\ & =& \frac{45\mathrm{cGy}}{\left(0.8\mathrm{cGy}/\mathrm{MU}\right)·\left(0.978\right)·\left(0.914\right)·\left(1.023\right)·\left(0.892\right)·\left(1.005\right)}\hfill \\ & =& 69\mathrm{MU}.\hfill \end{array}$$ (29)

VIII.B. Electron calculations

These example calculations use a 9-MeV beam (Varian Clinac 21EX), with a 1.0-cGy/MU dose rate at the normalization point (SSD₀ = 100 cm, r_c = 10 × 10 cm², d_m = 2.1 cm).

• 1.
  Calculate the MUs required to deliver 200 cGy to a depth of d_m at 100-cm SSD for a 6 × 10-cm² insert in a 15 × 15-cm² applicator.Answer: For the standard 100-cm SSD, the MU can be obtained using Eq. (10). Using data from Table VII and the square-root rule for the output factor, the total MUs are given by

  $$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{200\mathrm{cGy}}{(1.0\mathrm{cGy}/\mathrm{MU})·\sqrt{0.997·1.003}}\hfill \\ & =& 200\mathrm{MU}.\hfill \end{array}$$ (30)
• 2.Repeat the calculation for a treatment at 110 SSD.

Answer: The problem may be solved using either the effective SSD technique or the air-gap technique. For the effective SSD technique, SSD_eff is found in Table VIII using the field size of the insert (6 × 10-cm²). For the rectangular field, the geometric mean of the corrections for each of the dimensions of the insert size is used. The MUs are found using Eq. (11),

$$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{200\mathrm{cGy}}{\left(1.0\mathrm{cGy}/\mathrm{MU}\right)·\sqrt{0.997·1.003}·\left(\frac{74.7+2.1}{74.7+2.1+10}\right)·\left(\frac{85.9+2.1}{85.9+2.1+10}\right)}\hfill \\ & =& 252\mathrm{MU}.\hfill \end{array}$$ (31)

The air-gap factor data required for this problem are found in Table IX. The square-root rule is used for both the output factor and the air-gap factor. The MUs using the air-gap technique are found using Eq. (12),

$$\begin{array}{ccc}\hfill \mathrm{MU}& =& \frac{200\mathrm{cGy}}{\left(1.0\mathrm{cGy}/\mathrm{MU}\right)·\sqrt{0.997·1.003}·{\left(\frac{100+2.1}{100+2.1+10}\right)}^2·\sqrt{0.954·0.972}}\hfill \\ & =& 250\mathrm{MU}.\hfill \end{array}$$ (32)

Note that these two techniques may not give the exact same answer.

NOTATION AND DEFINITIONS

The following defines the dosimetric quantities used for MU calculations within this protocol.

D

The absorbed dose at the point of interest from the individual field under calculation.

D^′

The dose rate or dose per monitor unit at the point of interest.

$D_0^{\prime }$

The dose rate or dose per monitor unit of the user's beam under normalization conditions.

d

Depth of the point of calculation.

d_eff

Water-equivalent depth of the point of calculation.

d₀

The normalization depth for photon and electron dosimetry. For photons, d₀ = 10 cm is recommended, but not required. For each photon beam, d₀ is independent of field size and shall be greater than or equal to the maximum d_m.

 

For electrons, d₀ is taken to be the depth of maximum dose along the central axis for the same field incident on a water phantom at the same SSD.⁸ It is field-size dependent.

d_m

The depth of maximum dose on the central axis.

E

The nominal beam energy of the user's photon or electron beam.

f_air(r,SSD)

Air-gap correction factor (Sec. 1.A.2.e). The ratio of the electron dose rate at extended SSD to that predicted using only inverse-square corrections.

OAR(d,x)

Off-axis ratio (Sec. 1.A.1.f). The ratio of the open field dose rate at an off-axis point to that for the same field (e.g., 10 × 10 cm²) shifted such that the point of calculation lies on the central axis. The Primary Off-Axis Ratio, POAR, is preferred to be used for OAR(d,x).

PDD(d,r,SSD)

Percent depth dose. The ratio, expressed as a percentage, of the dose rate at depth to the dose rate at d_m in a water phantom for a given field size and SSD.

PDD_N(d,r,SSD)

Normalized percent depth dose (Sec. 1.A.1.b). The ratio, expressed as a percentage, of the dose rate at depth to the dose rate at the normalization depth in a water phantom for a given field size and SSD.

x

Off-axis distance. Distance from central axis to a fan line through the point of calculation measured in a plane perpendicular to the central axis at the isocenter. As such, x represents the radial distance rather than the distance along either principal axis.

r_a

The applicator size for electron beams.

r_c

The side of the equivalent square for the collimator field size defined at isocenter.

r, r_d

The side of the equivalent square for the field size incident on the patient, defined at the surface and at depth d, respectively.

r₀

The side of the equivalent square for the reference field size for photon and electron dosimetry. The reference field size within this protocol is 10 × 10 cm², defined at the isocenter.

S_e(r_a,r)

Output factor for electron beams (Sec. 1.A.2.c). For electrons, the ratio of the dose rate at d_m for a given applicator, field size, and SSD to the dose rate at d_m for the reference applicator, reference field size, and reference SSD.

S_c,p(r_c,r_d)

(In-water) output ratio. The ratio of the dose per MU in phantom for a given field size to that for the reference field size. S_c,p is measured at the normalization depth in a water phantom and depends on field size and the choice of normalization depth. The increase in scatter dose with field size is due both to increased energy fluence originating from the collimator head and from scattered photons within the phantom. S_c,p is approximated to be separable into machine (collimator) and phantom-dependent components.

S_c(r_c)

In-air output ratio (Sec. 1.A.1.d). The ratio of the output (i.e., energy fluence) in air for a given field size to that for the reference field size. S_c represents that component of S_c,p excluding changes in scattered radiation from the irradiated volume in a phantom.

S_p(r_d)

Phantom scatter factor (Sec. 1.A.1.e). The ratio of the dose per MU at the normalization depth for a given field size in a water phantom to that of the reference field size for the same incident energy fluence.

SAD

Source-axis distance. Distance between the x-ray physical source position and the isocenter. For most linear accelerators, this value is nominally 100 cm.

SPD

Source-point distance. The distance from the x-ray physical source to the plane (perpendicular to the central axis) that contains the point of calculation.

SSD

Source-surface distance. The distance along the central axis from the physical source to the patient/phantom surface.

SSD₀

Standard source-surface distance. The distance along the central axis from the physical source to the patient/phantom surface under normalization conditions.

SSD_eff

Effective source-surface distance. The distance along the central axis from the effective source to the patient/phantom surface, determined by best fit of output versus the inverse of the distance squared.

TPR(d,r_d)

Tissue phantom ratio (Sec. 1.A.1.c). The ratio of the dose rate at a given depth in phantom to the dose rate at the normalization depth for a given field size.

TF

Tray factor. The ratio of the central-axis dose rate for a given field with and without a blocking tray. TF is assumed independent of depth and field size in this report. This factor may be used to account for the attenuation through additional materials (e.g., special patient support devices) as needed.

WF(d,r_d,x)

Wedge factor (Sec. 1.A.1.i). The ratio of the dose rate at the point of calculation for a wedged field to that for the same field without a wedge modifier. The wedge may be a physical filter or not (i.e., dynamic or virtual). Depending on the type and angle of the wedge modifier, WF may depend on the wedge angle, field size, depth, and off-axis distance.

APPENDIX A: DERIVATION OF MONITOR UNIT EQUATIONS

Appendix A outlines the derivation of Eqs. (1) and (3) for photon beam calculations on the central axis. For off-axis calculations, the reader is encouraged to refer to derivation contained within the AAPM Task Group 74 report.¹⁰

The generic equation to determine MUs may be written

$$\mathrm{MU}=\frac{D}{D^{\prime }},$$ (A1)

where D is the prescribed dose, and D^′ is the dose rate at the point of calculation. The dose rate, i.e., dose per monitor unit (Linac) or dose per unit time (Co-60), at an arbitrary point may be calculated in terms of the dose rate to the point of normalization, $D_0^{\prime }$. $D_0^{\prime }$ is determined under normalization conditions of depth, d₀, field size, r₀, and source-surface distance, SSD₀, or source-normalization point distance, SPD₀ (i.e., SPD₀ = SSD₀ + d₀). This calculation may be done either using isocentric or nonisocentric dosimetry functions.

I. TPR (“isocentric”) method

Consider point 1 in Fig. 10, located at depth d, source-point distance SPD, collimator field setting r_c, and effective field size at depth, r_d. Let $D_1^{\prime }$ be the dose rate at 1, $D_2^{\prime }$ be the dose rate at 2, etc. Referring to Fig. 10, the dose rate at 1 may be written in terms of the normalization dose rate, $D_0^{\prime }$, at point 8,

$$\begin{array}{ccc}& & D_1^{\prime }\left(\frac{D_1^{\prime }}{D_2^{\prime }}\right)\times \left(\frac{D_2^{\prime }}{D_3^{\prime }}\right)\times \left(\frac{D_3^{\prime }}{D_4^{\prime }}\right)\times \left(\frac{D_4^{\prime }}{D_5^{\prime }}\right)\times \left(\frac{D_5^{\prime }}{D_6^{\prime }}\right)\hfill \\ & & \times \left(\frac{D_6^{\prime }}{D_7^{\prime }}\right)\times \left(\frac{D_7^{\prime }}{D_8^{\prime }}\right)\times D_8^{\prime }\hfill \\ & & =\mathrm{WF}(d,r_d)\times \mathrm{TPR}(d,r_d)\times \mathrm{TAR}(d_{\mathrm{o}},r_d)\times {\left(\frac{{\mathrm{SPD}}_0}{\mathrm{SPD}}\right)}^2\hfill \\ & & \times \left(\frac{1}{\mathrm{TAR}\left(d_{\mathrm{o}},r_d\left(\frac{{\mathrm{SPD}}_0}{\mathrm{SPD}}\right)\right)}\right)\times \left(\frac{\mathrm{TF}\times S_p\left(r_d\left(\frac{{\mathrm{SPD}}_0}{\mathrm{SPD}}\right)\right)}{S_p\left(r_c\right)}\right)\hfill \\ & & \times \left(\frac{S_{c,p}\left(r_c\right)}{1}\right)\times D_0^{\prime }.\hfill \end{array}$$

FIG. 10.

Diagram illustrating derivation of isocentric MU equation.

At the reference depth d_o, the ratio of TARs may be written in terms of S_p,

$$\begin{array}{c}\hfill \frac{\mathrm{TAR}(d_o,r_d)}{\mathrm{TAR}\left(d_o,r_d\left(\frac{{\mathrm{SPD}}_0}{\mathrm{SPD}}\right)\right)}=\frac{S_p\left(r_d\right)}{S_p\left(r_d\left(\frac{{\mathrm{SPD}}_0}{\mathrm{SPD}}\right)\right)}.\end{array}$$

So that the equation becomes

$$\begin{array}{ccc}\hfill D_1^{\prime }& =& \mathrm{WF}(d,r_d)\times \mathrm{TPR}(d,r_d)\times {\left(\frac{{\mathrm{SPD}}_0}{\mathrm{SPD}}\right)}^2\hfill \\ & & \times \mathrm{TF}\times S_p\left(r_d\right)\times S_c\left(r_c\right)\times D_0^{\prime }.\hfill \end{array}$$ (A2)

II. PDD (“nonisocentric”) method

Consider point 1 in Fig. 11, located at depth d, off-axis distance x (projected to the isocenter), source-surface distance SSD, collimator field size r_c, and effective field size on the surface, r. Let D₁ be the dose rate at 1, D₂ be the dose rate at 2, etc. Referring to Fig. 11, the dose rate at 1 may be written in terms of the normalization dose rate, $D_0^{\prime }$, at point 8,

$$\begin{array}{ccc}\hfill D_1^{\prime }& =& \left(\frac{D_1^{\prime }}{D_2^{\prime }}\right)\times \left(\frac{D_2^{\prime }}{D_3^{\prime }}\right)\times \left(\frac{D_3^{\prime }}{D_4^{\prime }}\right)\times \left(\frac{D_4^{\prime }}{D_5^{\prime }}\right)\times \left(\frac{D_5^{\prime }}{D_6^{\prime }}\right)\hfill \\ & & \times \left(\frac{D_6^{\prime }}{D_7^{\prime }}\right)\times \left(\frac{D_7^{\prime }}{D_8^{\prime }}\right)\times D_8^{\prime }\hfill \\ & =& \mathrm{WF}(d,r_d)\times \frac{{\mathrm{PDD}}_N(d,r,\mathrm{SSD})}{100\%}\hfill \\ & & \times \mathrm{TAR}\left(d_0,r\left(\frac{\mathrm{SSD}+d_0}{\mathrm{SSD}}\right)\right)\times {\left(\frac{{\mathrm{SSD}}_0+d_0}{\mathrm{SSD}+d_0}\right)}^2\hfill \\ & & \times \left(\frac{1}{\mathrm{TAR}\left(d_o,r\left(\frac{{\mathrm{SSD}}_0+d_0}{\mathrm{SSD}}\right)\right)}\right)\hfill \\ & & \times \left(\frac{\mathrm{TF}\times S_p\left(r\left(\frac{{\mathrm{SSD}}_0+d_0}{\mathrm{SSD}}\right)\right)}{S_p\left(r_c\right)}\right)\times \left(\frac{S_{c,p}\left(r_c\right)}{1}\right)\times D_0^{\prime }.\hfill \end{array}$$

FIG. 11.

Diagram illustrating derivation of nonisocentric MU equation.

Substituting for the TARs as above, the equation becomes:

$$\begin{array}{ccc}\hfill D_1^{\prime }& =& \mathrm{WF}(d,r_d)\times \frac{{\mathrm{PDD}}_N(d,r,\mathrm{SSD})}{100\%}\times {\left(\frac{{\mathrm{SSD}}_0+d_0}{\mathrm{SSD}+d_0}\right)}^2\hfill \\ & & \times \mathrm{TF}\times S_p\left(r\left(\frac{\mathrm{SSD}+d_0}{\mathrm{SSD}}\right)\right)\times S_c\left(r_c\right)\times D_0^{\prime }\hfill \end{array}$$ (A3)

APPENDIX B: CALCULATION OF S_c USING A PEV MODEL

I. PEV of jaws

In order to take into account the difference in distance of the upper and lower jaws from the sources, the exposed region of the sources from PEV needs to be included in the model. Figure 12 is a schematic diagram of the cross-section of the treatment head, showing the relative positions of the flattening filter, monitor chamber, and upper and lower jaws. The area of the flattening filter which is “visible” from the point of calculation is displayed in the figure. It is clear from the figure that for the same setting at isocenter, the collimator closer to the source projects to a smaller opening in PEV. The upper jaw setting (r_jU) is scaled by a reduction factor F to produce the equivalent setting of the lower jaw that provides the same opening in PEV. From the PEV projection geometry,

$$F=\frac{c(a-b)}{b(a-c)},$$ (B1)

where c is the source to upper jaw distance, a is the source to calculation point distance, and b is the source to lower jaw distance. Since most calculation points are close to the isocenter except for extended SSD treatments, a can be approximated by the SAD. For treatment at extended distances, this will introduce an error typically less than 1%. The side of the equivalent square will then be¹³⁶

$$r_c=\frac{(F+1)·r_{jU}·r_{jL}}{F·r_{jU}+r_{jL}}.$$ (B2)

The factor (F + 1) in Eq. (B2) ensures that square jaw settings at isocenter will produce equivalent squares of the same size.

FIG. 12.

Points eye view of upper and lower jaws. Schematic diagram of the treatment head showing flattening filter, monitor chamber, and upper and lower jaws. The lower jaws have been rotated by 90° for clarity.

II. PEV of all collimators

For fields that have field shaping collimator (blocks or MLC) much closer to the point of calculation than the jaws, the area of the sources that is visible from the PEV may be partly determined by the field shaping collimator (Fig. 12). In order to estimate the area in the PEV, some scaling of the jaw setting is necessary. The scale factor formula of Eq. (B1) can also be used. Since it is easier to scale the straight jaw edges than the shaped field edges, the upper jaw and lower jaw settings are reduced by their corresponding scale factors to equivalent sizes of the field shaping collimator

$$\begin{array}{ccc}\hfill F_U& =& \frac{U(A-M)}{M(A-U)}\hfill \\ \hfill F_L& =& \frac{L(A-M)}{M(A-L)},\hfill \end{array}$$ (B3)

where F_U is the reduction factor for the upper jaws and F_L is the reduction factor for the lower jaws, U is the source to upper jaw distance, L is the source to lower jaw distance, M is the source to field shaping collimator distance, and A is the SAD. The scaled jaw edges are drawn on the beam's eye view plot (BEV) or simulation film with the reduced settings to generate the PEV. The side of the equivalent square s_M of the irregular area of the source that is visible in the PEV is estimated with the same method described above for the treatment field. The equivalent square s_M is then scaled by a factor f to give

$$\begin{array}{ccc}\hfill r_c& =& f·s_M,\mathrm{where}\hfill \\ \hfill f& =& \left(0.5\right)\frac{F_U+F_L}{F_U{F}_L}.\hfill \end{array}$$ (B4)

The factors F_U, F_L, and f are constants for a given treatment machine and can be tabulated. Except for the scaling of the field sizes, the above procedure is very similar to the estimation of the equivalent square in the BEV. For most clinical cases, the jaw settings reduced by F_U and F_L define a rectangle totally inside the shaped field in PEV, the equivalent square is determined only by the jaws and the method in Appendix B above gives identical result.