Abstract
Purpose:
This paper derives a ray-by-ray weighted filtered backprojection (rFBP) algorithm, based on our recently developed view-by-view weighted, filtered backprojection (vFBP) algorithm.
Methods:
The rFBP algorithm directly extends the vFBP algorithm by letting the noise weighting vary from channel to channel within each view. The projection data can be weighted in inverse proportion to their noise variances. Also, an edge-preserving bilateral filter is suggested to perform post filtering to further reduce the noise. The proposed algorithm has been implemented for the circular-orbit cone-beam geometry based on Feldkamp's algorithm.
Results:
Image reconstructions with computer simulations and clinical cadaver data are presented to illustrate the effectiveness and feasibility of the proposed algorithm. The new FBP-type algorithm is able to significantly reduce or remove the noise texture, which the conventional FBP is unable to do. The computation time of the proposed rFBP algorithm is approximately the same as the conventional FBP algorithm.
Conclusions:
A ray-based noise-weighting scheme is introduced to the FBP algorithm. This new FBP-type algorithm significantly reduces or removes the streaking artifacts in low-dose CT.
Keywords: image reconstruction, analytical reconstruction algorithm, tomography, noise modeling, CT, edge-preserving filtering
I. INTRODUCTION
The filtered backprojection (FBP) algorithm has been in use for several decades.1–5 It is the work horse in x-ray CT and nuclear medicine image reconstruction. A drawback of the FBP algorithm is that it produces very noisy images when the data are noisy. By contrast, the iterative algorithms are able to incorporate the projection noise model and produce less noisy images than the FBP algorithm.6–10 As a trend, the FBP algorithm is gradually getting replaced by iterative algorithms. However, iterative algorithms have long computation times. In order to shorten the computation times, effort has been made to transform a regular iterative algorithm into an iterative FBP algorithm.11
Recently we developed a noniterative FBP algorithm that can model the projection noise on a view-by-view basis, in which an average or a maximum noise variance is used for all projection rays in each view.12 It was an initial attempt to use the FBP algorithm to model data noise. In the view-by-view weighted FBP (vFBP) algorithm, a single weighting factor, w(view), is assigned to all projection rays in a view. This noise-weighting scheme is not as accurate as ray-by-ray noise weighting, which is now proposed in the current paper.
The regularization term in our previous vFBP algorithm was quadratic. We realize that a quadric regularization term is unable to perform edge-preserving smoothing. The current paper therefore uses an edge-preserving bilateral filter as a post filter to further reduce the noise. The ray-wise weighting FBP (rFBP) algorithm will be developed in Sec. II. A specially designed bilateral filter is also presented in Sec. II. Computer simulations and an application to low-dose clinical cone-beam CT image reconstruction are presented in Sec. III. Discussion and conclusions are given in Sec. IV.
II. METHODS
II.A. Ray-by-ray noise weighted FBP algorithm
Statistical weighting in iterative reconstruction algorithms is a well-established practice.13–15 Because the iterative algorithms use long computations times, in CT imaging, noise control is normally achieved using either prefiltering or postfiltering.16–20 In prefiltering methods, a lowpass filter or a nonlinear filter can be used, where the filtering strength or bandwidth for each measurement is determined by the model.16,19 We have previously introduced a view-by-view weighting FBP algorithm (referred to as the vFBP algorithm) by minimizing a weighted least-square objective function.12 The vFBP algorithm is almost the same as the conventional FBP algorithm, except that the ramp filter |ω| is replaced by
with ω ≠ 0,
| (1) |
where ω is the frequency variable in the projection space, k corresponds to the iteration number in an iterative algorithm, α corresponds to the step-size in an iterative algorithm, β is the contributing factor of the regularization term in the objective function, w is the weighting function varying with the view angle [i.e., w = w(view)], and R is the filter function in the regularization term. In this paper, the minimum norm regularization is assumed and R is a constant 1 in (1). The generalized ramp-filter (1) is used for projection data filtering, and the filtered data are backprojected to obtain the final image. No modification is required for the backprojector, for the vFBP or for the new rFBP algorithm.
Next, we will extend the view-by-view noise weighting to ray-by-ray noise weighting in an ad hoc manner. For the ray-based noise weighting, w is a function of the ray: w = w(ray). A popular approach to assigning the weighting factor is to let w(ray) be proportional to the reciprocal of the noise variance of the ray measurement. At each view angle, we quantize the ray-based weighting function into N + 1 values: w0, w1, …, wN, which in turn give N + 1 different filters as defined in (1). They are
with
| (2) |
for n = 0, 1, 2, …, N. Using these N + 1 filters, N + 1 sets of filtered projections are obtained. Before backprojection, one of these N + 1 projections is selected for each ray according to its proper weighting function, which will be further explained when implementation issues are discussed later in this paper. Only one backprojection is performed using the selected filtered projections.
II.B. Edge-preserving bilateral filter
One drawback of the rFBP algorithm is that its Bayesian (regularization) prior must be quadratic and it is unable to incorporate edge-preserving filtering during image reconstruction. The objective function and the Bayesian prior are not shown in this paper; the interested reader should refer to Ref. 12 for its setup. Our strategy is to apply a nonlinear, edge-preserving, bilateral filter to the result of the rFBP reconstruction.
Bilateral filters are a class of nonlinear filters that are specified by both domain (Fdomain) and range (Frange) functions.21 A general form of the input/output relationship of a bilateral filter is
| (3) |
where represents the jth pixel of the input (unfiltered) image, represents the jth pixel of the output (filtered) image, Ω(k) is a neighborhood around pixel k, Fdomain is a “domain” function, and Frange is a “range” function. In many applications, Fdomain and Frange are chosen to be Gaussian functions.
Bilateral filters can be specially designed according to the application. The edge-preserving bilateral filter in this paper is described as follows.
-
•
Specify a small neighborhood Ω(k) centered at pixel k, for example, an r x r region in a two-dimensional (2D) image. At each image pixel k, filtering is performed only in this region.
-
•
Specify a threshold value Th. This value Th represents the smallest edge jump or smallest detectable contrast. Image variation smaller than this value Th is considered noise.
-
•
At each image pixel k, the filtered image value xk is the average value of all pixels in the set {xj: j ∈ Ω(k) and |xk − xj| < Th}.
Using the notation in (3), our design is as follows:
| (4) |
and
| (5) |
and
| (6) |
Our strategy is to use the average value to replace the original image value. Not every image pixel is allowed to participate in the “average” operation. To be qualified, a pixel xj must satisfy two conditions: it must be in the close neighborhood of the pixel of interest xk, and its value xj is close enough to the value of xk. One could use a larger neighborhood Ω(k) or use a smaller neighborhood Ω(k) but apply the smaller filter multiple times.
A drawback of this bilateral filter is that if the noise influence is larger than the smallest contrast Th, the noise influence cannot be filtered out. Any edge whose contrast is smaller than Th will be smoothed out.
II.C. Implementation of the new rFBP algorithm
Let the inverse Fourier transform of Hk, α, β, w(ω) be hk, α, β, w(t), which is the spatial-domain kernel of the 1D modified ramp filter. In the rFBP algorithm, w is a function of the projection ray, therefore, w = w(t, θ). Let p(t, θ) be the projection at view θ and location t on the detector, and q(t, θ) be the filtered projection. Then q(t, θ) is defined by the following integral:
| (7) |
which is not a convolution, because the kernel hk, α, β, w(t, θ)(τ) depends on t. The final image is obtained by backprojecting q(t, θ) into the image domain, and the backprojector is the same as that in a conventional FBP algorithm. Therefore, the only thing new in implementing the rFBP algorithm is to calculate q(t, θ), which will be discussed in detail as follows.
One way to calculate q(t, θ) is to use (7) to filter the projections in the spatial domain. However, we currently do not have an analytical expression for the integration kernel hk, α, β, w(t). Our strategy is to implement (7) in the Fourier domain and to quantize the weighting function w(t, θ) into 11 values of exp(− 0.1 · n · pmax), where pmax is the maximum projection value, and n = 0, 1, 2, …,10. The efficient fast Fourier transform (FFT) is used. The implementation steps of calculating q(t, θ) are given below.
Before the projections data are ready to process, form 11 Fourier domain filter transfer functions as defined in (2) with wn = exp ( − 0.1 · n · pmax ), n = 0, 1, 2, …,10, respectively. Note that in implementation, ω is a discrete frequency index and takes the integer values of 0, 1, 2, … and so on.
Step 1: At each view angle θ, find the 1D Fourier transform of p(t, θ) with respect to t, obtaining P(ω, θ).
Step 2: Form 11 versions of Qn(ω, θ) = P(ω, θ) with n = 0, 1, …, 10.
Step 3: Take the 1D inverse Fourier transform of Qn(ω, θ) with respect to ω, obtaining qn(t,θ) with n = 0, 1, …, 10.
Step 4: Construct q(t,θ) by letting q(t,θ) = qn(t,θ) if p(t, θ) ≈ 0.1 · n · pmax.
II.D. Low-dose cadaver CT study
To illustrate the feasibility of the proposed rFBP algorithm, a cadaver torso was scanned using an x-ray CT scanner with a low-dose setting. The images were then reconstructed by a conventional FBP (the Feldkamp) algorithm23 as well as the proposed rFBP algorithm. Data were collected with a diagnostic scanner (Aquilion ONETM, Toshiba America Medical Systems, Tustin, CA, USA; raw data courtesy of Leiden University Medical Center).
The imaging geometry was cone-beam, the x-ray source trajectory was a circle of radius 600 mm. The detector had 320 rows, the row-height was 0.5 mm, each row had 896 channels, and the fan angle was 49.2°. A low-dose noisy scan was carried out. The tube voltage was 120 kV and current was 60 mA. There were 1200 views uniformly sampled over 360°.
The Feldkamp algorithm is an FBP algorithm. The data were first weighted with a cosine function, and then a 1D ramp filter was applied to each row of the cone-beam projections. Finally a cone-beam backprojection was used to generate a 3D image volume. In our implementation, the 1D ramp filter was replaced by the newly developed ramp filter (2). The parameter β was selected as 2.6 × 10−5, iteration index k was chosen as infinity, and the step-size α was not needed. The noise weighting function was defined by w(t, θ) = exp ( − p(t, θ)), in which we assumed that the transmission measurement was approximately Poisson distributed and the line-integral p(t,θ) was the logarithm of the transmission measurement.
The image volume was reconstructed in a 512 × 512 × 320 3D array, and one axial slice is used for display in this paper. The bilateral post filtering was performed slice by slice, using a 9 × 9 neighborhood and the threshold of 70 HU.
II.E. Computer simulation
The image array was 800 × 800, the pixel size was 0.575 mm × 0.575 mm, the number of views was 900 over 360°, the number of detection channels was 896, and the focal length was 600 mm. The x-ray source flux had 106 counts.
The images were reconstructed by both the conventional FBP algorithm and the proposed rFBP algorithm. In the rFBP reconstruction, the parameter k was chosen as 1 000 000 and the parameter α was 0.5. The noise weighting was chosen as w = e−0.3p, where p was the converted line-integral measurement for a ray. Noise weighting w is a double-edged sword. It can suppress some noise that is caused by anisotropic noise contribution from different projections; it can also cause some shadow artifacts if the noise weighting function w fluctuates too much. Since the standard noise weighting function w = e−p introduces some severe shadow artifacts, we replaced it by w = e−0.3p that has less dynamic change than w = e−p.
A bilateral post filter with r = 9 and Th = 50 HU was used to further reduce the noise.
III. RESULTS
III.A. The cadaver data
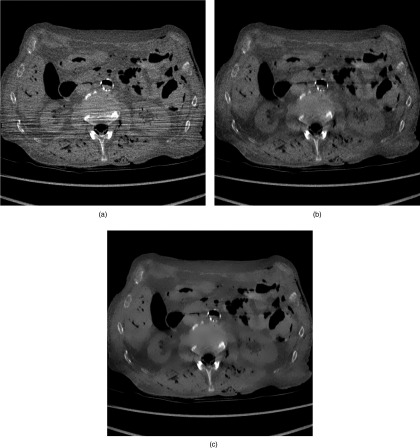
Figure 1(a) shows the conventional FBP Feldkamp's reconstruction of a transverse slice in the abdominal region of the cadaver. This study used low dose. The cadaver arms were outside the display field of view; the arms further attenuated the x-rays, creating streak artifacts in the middle of the image from left-to-right across the torso. Figure 1(b) shows the rFBP reconstruction, with β = 2.6 × 10−5, k = ∞, and w = e−p. The ray-based noise weighting in the rFBP algorithm effectively removes the streaking artifacts that appear in Fig. 1(a).
FIG. 1.
Reconstruction results for the clinical cadaver data: (a) The conventional FBP reconstruction, (b) The rFBP reconstruction, and (c) The rFBP reconstruction with bilateral post filtering. Display window is from −400 HU to 400 HU.
Figure 1(c) shows the result of the bilateral post filtering, using the rFBP result as the input. The image in Fig. 1(c) is less noisy than Fig. 1(b) while it maintains the main edges in Fig. 1(b) un-smoothed. The images are displayed from −400 HU to 400 HU.
III.B. Computer simulation data
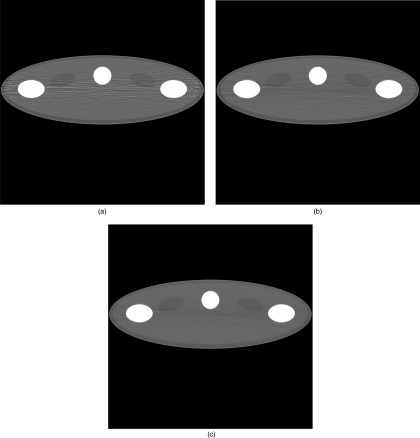
Figure 2 shows a real-size phantom study, which compares the conventional FBP reconstruction (see Fig. 2(a)) with the proposed rFBP reconstruction (see Fig. 2(b)), using β = 0, k = 1 000 000, α = 0.5, and w = e−0.3p. It is observed that streaking artifacts that appeared in the FBP reconstruction have been reduced in the rFBP reconstruction. The bilateral post filtering result is shown in Fig. 2(c); the input image for the bilateral filter is the result of the rFBP reconstruction. The images are displayed from −400 HU to 400 HU.
FIG. 2.
Reconstruction results for the computer simulation data: (a) The conventional FBP reconstruction, (b) The rFBP reconstruction, and (c) The rFBP reconstruction with bilateral post filtering. Display window is from −400 HU to 400 HU.
IV. DISCUSSION AND CONCLUSIONS
IV.A. Reduction of the number of parameters
Both parameter k and parameter β can be used for noise regularization. A smaller k or a larger β can blur the image more. It is not clear how these two parameters interact with each other.
In order to make the rFBP algorithm more user-friendly, one can set k to infinity (as in our clinical study example), which also makes α unnecessary. Only one parameter β needs to be adjusted. In the case of k being infinity, β cannot be 0 otherwise the noise weighting is not effective. It is suggested to use a very small β value, approximately 10−5. Using optimization analogy, this method gives a Bayesian optimization solution, and its associated objective function has a weighted least-squares term and a Bayesian term.12 The Bayesian term encourages a minimum norm solution.
Another way is to set β = 0 and keep k finite (as in our computer simulation example). The step-size α can be set as a fixed value as long as α satisfies |1 − α/|ω| | < 1 for all nonzero discrete frequencies ω. In the case of β being 0, k cannot be infinity; otherwise the noise weighting is not effective. We would point out that the terms “iteration number k” and “step size α” are borrowed from iterative algorithm terminology. Our rFBP algorithm is noniterative; however, the function of k and the function of α are similar to those in an iterative algorithm.12,22 Using optimization analogy, this method gives an “early stopped” solution of a weighted least-squares problem that is solved by an iterative algorithm.12
The above two methods have similar effects, and the user has the freedom to choose a preferred approach.
IV.B. Adaptive filter vs rFBP
Various adaptive filters have been in use for more than 10 years.16–18 Like the rFBP algorithm, the strategies of all these methods are the same, that is, to apply more smoothing for noisier measurements and to apply less smoothing (or no smoothing at all) for less noisy measurements.
The closest adaptive filter to the filter used in the rFBP algorithm was developed by Kachelrieß et al.18 Their adaptive filter uses a spatially varying triangular kernel. In x-ray imaging, the ray-sum p represents the total attenuation along the ray, and a larger value of p is associated with a noisier measurement.
The following explains how the adaptive filter works. A threshold T is first selected. If a ray-sum p is less than T, no prefiltering is needed. If a ray-sum p is greater than T, lowpass prefiltering is performed and the prefilter has a triangle spatial domain kernel.
The adaptive filter has the potential to have multiple threshold values and multiple triangular lowpass prefilters. In this more sophisticated case, the adaptive prefilter together with the conventional FBP algorithm is similar to our rFBP algorithm, because the generalized ramp-filter (2) can be decomposed into two parts: the conventional ramp filter |ω| and window function GrFBP(ω) (by assuming k = ∞ for simplicity):
| (8) |
which is a lowpass prefilter.
Notice that the Fourier transform of a triangular function is the square of a sinc function:
| (9) |
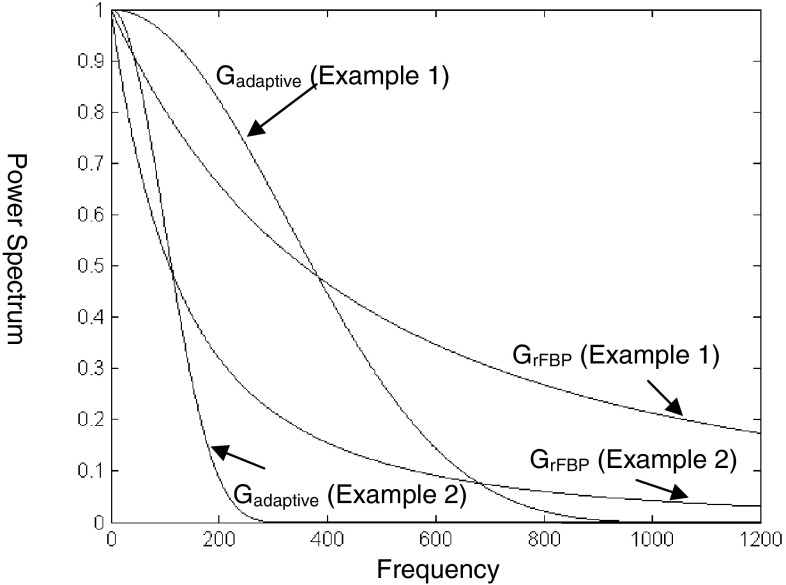
where γ is a parameter to determine the bandwidth of the lowpass adaptive prefilter. By selecting proper parameters β, wn, and γ, prefilters (8) and (9) can give the same bandwidth. Figure 3 shows a power spectrum plot for these two filters (8) and (9), and two pairs of the curves are shown. One pair has a wider half-power bandwidth than the other pair. These two types of filters behave differently; the adaptive prefilters (9) have a sharper transition band than the rFBP prefilters (8). The triangular filters also have some small ripples in the Fourier domain.
FIG. 3.
Power spectrum plots for the prefilters that are used in the rFBP algorithm and in an adaptive filtering approach. Two pairs of examples are shown. The curve shapes are different even when they have the same half-power bandwidth.
We believe that as long as one follows the principle of “applying more smoothing for noisier measurements and applying less smoothing (or no smoothing at all) for less noisy measurements” one has a freedom to design a proper filter for the applications in hand, to reach targeted performance.
IV.C. Noise weighting
A popular approach to assigning the weighting factor is to let w(ray) be proportional to the reciprocal of the noise variance of the ray-sum measurement. This approach is justified by using the likelihood function (i.e., the joint probability density function) as the objective function for an optimization problem. The philosophy is that we should trust the less noisy measurements more than noisier measurements. In x-ray imaging, noise in measured data can be approximately described by a Poisson distribution, i.e., var(I) ∼ I, where I denotes an x-ray intensity transmission measurement. After log conversion the noise variance is described by var(I) / I2 ∼ 1/I, that is, noise variance in the line-integral projection data is inversely proportional to the measured transmission measurement intensity.16 If the x-ray source flux is stable and consistent, measurement intensity I is inversely proportional to exp(−p), where p is the ray-sum or the total attenuation along the ray. Since the weighting function w(t, θ) and Cw(t, θ) (where C is an arbitrary constant) have the same effect for any weighted least-squares scheme, the x-ray source flux is not required to be included in the weighting function.
We notice that the noise-weighted (either iterative or noniterative) image reconstruction is not critically sensitive to the noise model and noise variance. We see subtle differences between the vFBP and rFBP reconstructions. In some applications, the vFBP algorithm can still be used and is sufficient to reduce the artifacts and noise.
In some cases, more accurate noise modeling does not always translate to better (e.g., less severe artifacts) reconstructions. Nonsmooth weighting functions can introduce new artifacts into the reconstruction. Our experience in iterative and noniterative image reconstruction suggests that using a less-fluctuating weighting function helps to obtain a less noisy reconstruction. This was the reason that we used w = e−0.3p instead of w = e−p in the rFBP reconstruction of computer simulated data.
IV.D. Conclusions
This paper introduces a ray-by-ray noise-weighting scheme to the FBP algorithm, to obtain an rFBP algorithm. An edge-preserving-smoothing postfilter is suggested to further reduce noise. An important application of the rFBP algorithm is in low-dose x-ray CT image reconstruction. The computation time of the proposed rFBP algorithm is almost the same as the conventional FBP algorithm. As illustrated by the cadaver x-ray CT study and computer simulation study, streaking artifacts in low-dose CT can be effectively removed or reduced by the proposed rFBP algorithm. Evaluation of more clinical data and comparison with other algorithms will be topics of our future research. This rFBP algorithm is readily applicable to any imaging geometries as long as an FBP algorithm exists.
ACKNOWLEDGMENTS
The authors thank Dr. Roy Rowley of the University of Utah for English editing. The authors also thank Raoul M. S. Joemai of Leiden University Medical Center for collecting and providing us raw data of the cadaver CT scan.
REFERENCES
- 1. Shepp L. A. and Logan B. F., “The Fourier reconstruction of a head section,” IEEE Trans. Nucl. Sci. NS-21, 218–227 (1974). 10.1109/TNS.1974.4327465 [DOI] [Google Scholar]
- 2. Radon J., “Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten,” Ber. Verh. Sächs. Akad. Wiss. Leipzig, Math.-Nat. K1 69, 262–267 (1917). [Google Scholar]
- 3. Bracewell R. N., “Strip integration in radio astronomy,” Aust. J. Phys. 9, 198–217 (1956). 10.1071/PH560198 [DOI] [Google Scholar]
- 4. Vainstein B. K., “Finding structure of objects from projections,” Kristallografiya 15, 984–902 (1970). [Google Scholar]
- 5. Zeng G. L., Medical Image Reconstruction, A Conceptual Tutorial (Springer, Beijing, 2010). [Google Scholar]
- 6. German S. and McClure D. E., “Statistical methods for tomographic image reconstruction,” Bull. Internat. Statist. Inst. LII-4, 5–21 (1987). [Google Scholar]
- 7. Dempster A., Laird N., and Rubin D., “Maximum likelihood from incomplete data via the EM algorithm,” J. R. Stat. Soc. Ser. B (Methodol) 39B, 1–38 (1977). [Google Scholar]
- 8. Shepp L. A. and Vardi Y., “Maximum likelihood reconstruction for emission tomography,” IEEE Trans. Med. Imaging 1, 113–122 (1982). 10.1109/TMI.1982.4307558 [DOI] [PubMed] [Google Scholar]
- 9. Hudson H. M. and Larkin R. S., “Accelerated image reconstruction using ordered subsets of projection data,” IEEE Trans. Med. Imaging 13, 601–609 (1994). 10.1109/42.363108 [DOI] [PubMed] [Google Scholar]
- 10. Langer K. and Carson R., “EM reconstruction algorithms for emission and transmission tomography,” J. Comput. Assist. Tomogr. 8, 302–316 (1984). [PubMed] [Google Scholar]
- 11. Delaney A. H. and Bresler Y., “A fast and accurate Fourier algorithm for iterative parallel-beam tomography,” IEEE Trans. Image Process. 5, 740–753 (1996). 10.1109/83.495957 [DOI] [PubMed] [Google Scholar]
- 12. Zeng G. L., “A filtered backprojection MAP algorithm with non-uniform sampling and noise modeling,” Med. Phys. 39, 2170–2178 (2012). 10.1118/1.3697736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Shi D., Zou Y., and Zamyatin A. A., “Weighted simultaneous algebraic reconstruction technique,” in Proceedings of the 11th International Meeting on Fully Three-Dimensional Image Reconstruction Meeting in Radiology and Nuclear Medicine, Potsdam, Germany (2011), pp. 160–162. [Google Scholar]
- 14. Thibault J., Sauer K., Bouman C., and Hsieh J., “A three-dimensional statistical approach to improved image quality for multislice helical CT,” Med. Phys. 34, 4526–4544 (2007). 10.1118/1.2789499 [DOI] [PubMed] [Google Scholar]
- 15. Kohler T., Proksa R., and Nielsen T., “SNR-weighted ART applied to transmission tomography,” IEEE Nuclear Science Symposium and Medical Imaging Conference Record (IEEE, Portland, Oregon, 2003), pp. 2739–2742. [Google Scholar]
- 16. Hsieh J., “Adaptive streak artifact reduction in computed tomography resulting from excessive x-ray photon noise,” Med. Phys. 25, 2139–2147 (1998). 10.1118/1.598410 [DOI] [PubMed] [Google Scholar]
- 17. Kachelrieß M., “Branchless vectorized median filtering,” IEEE Medical Imaging Conference Record, Workshop on High Performance Medical Imaging (IEEE, Orlando, Florida, 2009), Vol. HP3-5, pp. 4099–4105. [Google Scholar]
- 18. Kachelrieß M., Watzke O., and Kalender W. A., “Generalized multi-dimensional adaptive filtering for conventional and spiral single-slice, multi-slice, and cone-beam CT,” Med. Phys. 28, 475–490 (2001). 10.1118/1.1358303 [DOI] [PubMed] [Google Scholar]
- 19. Zamyatin A. A., Yang Z., and Akino N., “Streak artifacts and noise reduction in low dose computed tomography,” IEEE Nuclear Science Symposium and Medical Imaging Conference Record (IEEE, Valencia, Spain, 2011), pp. 4150–4151. [Google Scholar]
- 20. Yang Z., Silver M. D., and Noshi Y., “Adaptive weighted aniso-tropic diffusion for computed tomography denoising,” Proceedings of the 11th International Meeting on Fully Three-Dimensional Image Reconstruction Meeting in Radiology and Nuclear Medicine (IEEE, Potsdam, Germany, 2011), pp. 210–213. [Google Scholar]
- 21. Tomasi C. and Manduchi R., “Bilateral Filtering for Gray and Color Images,” in Proceedings of the 1998 IEEE International Conference on Computer Vision (IEEE, Bombay, India, 1998). [Google Scholar]
- 22. Zeng G. L., “A filtered backprojection algorithm with characteristics of the iterative Landweber algorithm,” Med. Phys. 39, 603–607 (2012). 10.1118/1.3673956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone beam algorithm,” J. Opt. Soc. Am. A 1, 612–619 (1984). 10.1364/JOSAA.1.000612 [DOI] [Google Scholar]