Modeling the Brownian relaxation of nanoparticle ferrofluids: Comparison with experiment

Abstract

Purpose:

The authors investigate the ability of current models for magnetic nanoparticles immersed in dilute ferrofluids and external sinusoidal magnetic fields to explain recent experiments in which the relaxation effects are dominated by viscous damping.

Methods:

The Fokker–Planck (FP) equation appropriate for the nanoparticle magnetic moment distribution corresponding to the underlying stochastic Langevin model is numerically studied and solutions compared to experimental results. The FP equation is solved using an expansion in Legendre polynomials. The polydisperse properties of the ferrofluids are incorporated into the analysis.

Results:

By using a FP approach that includes polydispersion, the authors obtain good agreement with recent experimental results using ferrofluids containing nanoparticles with average hydrodynamic diameters in the 40–120 nm range.

Conclusions:

For nanoparticles used in recent magnetic spectroscopy experiments, the FP approach can be used to accurately model experimental data in the situation where Brownian relaxation effects are dominant and the ferrofluids are dilute.

I. INTRODUCTION

There is by now a significant world of applications for magnetic nanoparticles including their roles as tracer materials, biomarkers, and biosensors, especially as components of dilute ferrofluids. Their robust interactions with external magnetic fields, and the resulting changes in their magnetization, are the key to these applications. We can readily detect these interactions even at low concentrations, and measurements that rely on the advantages of mobility and reduced organ toxicity may be made. An example of the broader interest in nanoparticle ferrofluids is magnetic particle imaging (MPI) based on the nonlinear magnetization of iron oxide tracers. MPI generates maps of tracer concentration through the use of combined oscillating and gradient magnetic fields.^1–6 Since its introduction, there has been significant progress in both scanner hardware design and imaging theory.^1,2

Magnetic particle spectroscopy (which has no spatial localization requirements, and only utilizes the oscillating magnetic field) can provide insight into the dynamical properties of the ferrofluid in general by measuring the magnetization response and the harmonic signal spectrum of the tracer materials.^3,7 For instance, utilizing third- and fifth-order harmonics, Ferguson et al.⁴ have studied the nanoparticle sizes that lead to maximum signals and Weaver et al.³ have focused on what the magnetization relaxation mechanisms typical of ferrofluids can tell us about viscosity, chemical binding, and temperature. We see the connection of the magnetization of the ferrofluid to the emf signal picked up inductively in a nearby detector coil⁸ is the key to determining nanoparticle properties and their interaction with the fluid environment. Along with the applications, and largely preceding them, there is an accumulated wealth of modeling work in the literature, both to help understand and to predict the experimental results.^6,9–14,16 A starting point is the equation of motion of the magnetic moment of the nanoparticle under the influence of thermal torques in addition to relaxation and external magnetic field effects. This is the famous Langevin stochastic differential equation with random variables describing the thermal torquing.^17,18 In general, there is a Brownian motion connection between the viscous relaxation effect and the thermal torquing due to fluid fluctuations.

The two relaxation mechanisms correspond, respectively, to the viscous resistance to any rotation of the particle (Brownian relaxation) and to the preferred internal direction of the particle magnetization (Neel relaxation). Here the focus is on the orientation of the magnetic moment of the particle and in first approximation we assume a fixed magnetic dipole moment relative to the particle body. If an internal magnetization direction is strongly preferred and the viscosity is sufficiently small, we have the magnetic moment locked into the particle body orientation and the Neel relaxation time is much larger than the Brownian relaxation time. In this paper the focus is on situations in which Brownian relaxation is dominant and Neel relaxation can be ignored.

In the present study, we consider the important class of experiments where the external magnetic external field oscillates along a fixed axis (the z-axis) with sinusoidal time dependence

$$\vec{B}\left(t\right)=B_0\cos \left(\omega t\right)\widehat{z}.$$ (1)

For sufficiently large B₀, the nonlinear magnetization of the nanoparticles generates higher order harmonics as a signal when they are driven by the single-frequency external excitation field.

In addition, the experiments pertain to a range of nanoparticle diameters running approximately from 40 to 120 nm. These nanoparticles have iron oxide (or more specifically magnetite) cores with an approximately spherical polymer layer serving, for example, as a surfactant. The outer shell of surfactants reduces agglomeration of the particles. The nanoparticles are also small enough to avoid ferromagnetic agglomeration. This outer diameter is called the hydrodynamic diameter, as it is the appropriate scale for the nanoparticle fluid dynamics.

Before examining the Langevin equation as a quantitative handle on these properties and interactions and their connection to the ferrofluid magnetization, we require the formula for the connection of the magnetization to the detector signal. As suggested above, when the oscillating external field is applied to the ferrofluid, the magnetization due to magnetic fraction of the ferrofluid is now the source of an oscillating magnetic field contribution itself. The time-dependent magnetization will induce an emf, S(t), in a pickup coil. Due to fundamental feed through from the drive field, significant filtering is usually used in the receive chain, and after taking the Fourier time transform, only the harmonics are of interest. In particular, the ratios of the harmonics are important, as the signal dependence on sample size and coil sensitivity is common for all harmonics. Thus we have

$$S\left(t\right)\propto \frac{d⟨M\left(t\right)⟩}{dt},$$ (2)

where ⟨M(t)⟩ is the average magnetization magnitude.

To model the behavior of the magnetization we begin with the Langevin equation¹⁷ of rotational motion of a single nanoparticle with a magnetic dipole moment in the presence of an external sinusoidal magnetic field, including viscous damping and random thermal fluctuations. Next, the magnetization is calculated for an ensemble of individual nanoparticles. The corresponding Fokker–Planck (FP) equation for the magnetic moment distribution (also called the Smoluchowski equation) can be derived from the Langevin equation. This distribution is a function of moment orientation angles for an ensemble of nanoparticles.^13,17 In the present paper we numerically solve the FP equation for the distribution as a function of orientation angles. The theoretical methods and the numerical approaches are described in Sec. II, the comparison of the simulations and the experimental results follow, with conclusions and comments in Sec. V.

II. METHODS: MODELS FOR NANOPARTICLE MAGNETIZATION

II.A. The Langevin equation

For magnetic nanoparticles in an external magnetic field, the microscopic equation of motion is determined by the stochastic Langevin equation. Given a spherical particle with magnetic moment $\vec{m}$ under the influence of the external magnetic field $\vec{B}$, the equation of motion can be written as¹⁷

$$\zeta \frac{d\vec{m}}{dt}=\vec{\lambda }\left(t\right)\times \vec{m}\left(t\right)+[\vec{m}\left(t\right)\times \vec{B}\left(t\right)]\times \vec{m}\left(t\right),$$ (3)

where $\vec{\lambda }$ is the white noise driving torque due to rotational Brownian motion and ζ = 8πηR³ is the friction coefficient, which comes from the viscous drag on the rotation of spherical particles within the ferrofluid. The coefficient η is the dynamic viscosity of the surrounding fluid and R is the hydrodynamic radius of the particle.

The white noise torque $\vec{\lambda }$ satisfies the statistical averages¹⁷

$$\begin{array}{ccc}\hfill ⟨{\lambda }_i\left(t\right)⟩& =& 0,\hfill \\ \hfill ⟨{\lambda }_i\left(t\right){\lambda }_j\left(t^{\prime }\right)⟩& =& 2k_{B}T\zeta {\delta }_{i,j}\delta (t-t^{\prime }),\hfill \end{array}$$ (4)

where T is the absolute temperature and k_B is Boltzmann's constant. The familiar rotational Brownian relaxation time is given by²¹

$${\tau }_B=\frac{3\eta V}{k_{B}T},$$ (5)

where $V=\frac{4}{3}\pi R^3$ is the hydrodynamic volume of the particle, which includes any nonmagnetic surface layer. Note that ζ and τ_B are related by ζ = 2k_BTτ_B.

II.B. The Fokker–Planck equation

Equation (3) is for a single particle with a dipole moment, but we must apply this to an ensemble of magnetic nanoparticles. There are two basic approaches for numerical solution of a system of nanoparticles: the numerical solution of the Langevin equation, Eq. (3), for a large number of particles; or the numerical solution of the equation describing the time evolution of the distribution function for the orientation angles of the particles, that is the corresponding Fokker–Planck equation.

The magnetic moment of an individual particle can be written as $\vec{m}=m_0\widehat{u}$, where $\widehat{u}$ is a unit vector in the direction of the magnetic dipole moment and the magnitude of the dipole moment m₀ is a constant. The probability density of the moment orientations is then written as a function $F(\widehat{u},t)$ of the unit vector $\widehat{u}$ whose time evolution is given by Eq. (3). Assuming that the magnetic field is along the z-axis, the distribution function will be cylindrically symmetric, and the Fokker–Planck equation may be written as^13,17

$$\begin{array}{ccc}& & \frac{\partial }{\partial t}F(x,t)\hfill \\ & & =D_R\frac{\partial }{\partial x}\left[(1-x^2)\left(\frac{\partial }{\partial x}F(x,t)-\alpha \left(t\right)F(x,t)\right),\right]\hfill \end{array}$$ (6)

where $x=\cos \theta =\widehat{u}·\widehat{z}$, D_R = k_BT/ζ = 1/2τ_B, and α(t) = α₀cos (ωt), where α₀ = m₀B₀/k_BT. The distribution is normalized so that ${\int }_{-1}^{1}F(x,t)dx=1$. Note that the magnetization is given by $\vec{M}\left(t\right)=n{m}_0⟨x\left(t\right)⟩\widehat{z}=n{m}_0{\int }_{-1}^{1}xF(x,t)dx\widehat{z}$, where n is the nanoparticle number density.

II.C. The FP adiabatic approximation

In the adiabatic approximation (i.e., when the magnetic field is changing slowly enough), one assumes that the system is in equilibrium at each instant of time. While it is straightforward to calculate the magnetization in the adiabatic limit, this approach will not include the relaxation effects (effects of viscosity) which are important at even low frequencies. However, it is useful in obtaining the solution in the zero-frequency limit, which is used for the plots at zero frequency.

To find the equilibrium distribution we solve the FP equation for a static magnetic field. We ignore the time dependence in Eq. (6) by setting ∂F/∂t = 0 and setting α(t) to a constant value α_eq. Properly normalized the equilibrium solution is given by

$$F_{\mathrm{eq}}\left(x\right)=\frac{{\alpha }_{\mathrm{eq}}}{2\sinh {\alpha }_{\mathrm{eq}}}{e}^{{\alpha }_{\mathrm{eq}}x}.$$ (7)

This is simply the Boltzmann distribution. From this equation one obtains ⟨x⟩_eq = L(α_eq), where

$$L\left(\xi \right)=\coth \xi -\frac{1}{\xi }$$ (8)

is the famous Langevin function.

The adiabatic approximation to the FP equation is derived by assuming the distribution density F_ad(x, t) is in equilibrium at each instant of time. The solution to the FP equation is then in the form of Eq. (7) except with α_eq replaced be α(t). The result is

$$F_{\mathrm{ad}}\left(x\right)=\frac{\alpha \left(t\right)}{2\sinh \alpha \left(t\right)}{e}^{\alpha \left(t\right)x},$$ (9)

where we recall α(t) = α₀cos (ωt). From this equation one obtains

$${⟨x\left(t\right)⟩}_{\mathrm{ad}}=L\left(\alpha \left(t\right)\right).$$ (10)

Besides its role in finding the zero-frequency limit, Eq. (7) is the form assumed in the effective-field solution described next.

II.D. Effective-field FP approximation

An improvement over the adiabatic approximation which is accurate for sufficiently low frequencies is the effective-field approximation^13–15 introduced to MPI by Rauwerdink and Weaver.¹¹ Multiplying Eq. (6) by x, and integrating the second-derivative term by parts twice and the first-derivative term by parts transforms the FP into

$$\frac{d}{dt}⟨x⟩=D_R\left[-2⟨x⟩+\alpha \left(t\right)\left(1-⟨x^2⟩\right)\right].$$ (11)

An approximate solution to this equation can be found by assuming that the distribution of moments at any instant of time has the same form as Eq. (7)

$$F_{\mathrm{eff}}(x,t)=\frac{{\alpha }_{\mathrm{eff}}}{2\sinh {\alpha }_{\mathrm{eff}}}{e}^{{\alpha }_{\mathrm{eff}}x},$$ (12)

where α_eff is a function of time, but is not necessarily equal to α(t). With this assumption, the two lowest moments of the distribution in the effective-field approximation are

$$\begin{array}{ccc}\hfill {⟨x⟩}_{\mathrm{eff}}& =& L\left({\alpha }_{\mathrm{eff}}\right),\hfill \end{array}$$ (13)

$$\begin{array}{ccc}\hfill 1-{⟨x^2⟩}_{\mathrm{eff}}& =& \frac{2}{{\alpha }_{\mathrm{eff}}}{⟨x⟩}_{\mathrm{eff}},\hfill \end{array}$$ (14)

and Eq. (11) can be written as

$$\frac{d}{dt}{⟨x⟩}_{\mathrm{eff}}=-\frac{1}{{\tau }_B}\left[1-\frac{\alpha \left(t\right)}{{\alpha }_{\mathrm{eff}}}\right]{⟨x⟩}_{\mathrm{eff}}.$$ (15)

At any time t the value of α_eff is determined implicitly from Eq. (13). However, to avoid solving the Langevin function implicitly for α_eff, a differential equation can be obtained for α_eff:

$$\frac{d{\alpha }_{\mathrm{eff}}}{dt}=-\frac{1}{{\tau }_B}\frac{L\left({\alpha }_{\mathrm{eff}}\right)}{L^{\prime }\left({\alpha }_{\mathrm{eff}}\right)}\left[1-\frac{\alpha \left(t\right)}{{\alpha }_{\mathrm{eff}}}\right],$$ (16)

where L^′(α_eff) ≡ dL(α_eff)/dα_eff and ⟨x⟩_eff is given by Eq. (13). Recall that ⟨x⟩ = ⟨m_z⟩/m₀.

II.E. Numerical approach to the Fokker–Planck equation

To solve Eq. (6), we expand F(x, t) in terms of the Legendre polynomials P_n(x), a natural basis for the cosine variable. With the expansion

$$F(x,t)=\sum _{n=0}^{\infty }{a}_n\left(t\right)P_n\left(x\right).$$ (17)

Equation (6) can be converted into a set of coupled ordinary differential equations¹³ for the Legendre coefficients a_n

$$\begin{array}{c}\hfill \frac{d{a}_n}{dt}=n(n+1)D_R\left[-a_n+\alpha \left(t\right)\left(\frac{a_{n-1}}{2n-1}-\frac{a_{n+1}}{2n+3}\right)\right],\end{array}$$ (18)

which can be solved by numerical integration. The normalization condition ${\int }_{-1}^{1}F(x,t)dx=1$ gives a₀(t) = 1/2. Also relevant is the first moment of the distribution since it is proportional to the magnetization. It is easy to show that $⟨x\left(t\right)⟩=\frac{2}{3}{a}_1\left(t\right)$.

II.F. The Fokker–Planck equation for polydisperse particles

Up to this point it has been assumed that the nanoparticles in the ferrofluid have the same size (the monodisperse case). We now generalize to a distribution in the hydrodynamic size of the particles (the polydisperse case). The distribution function for the orientation angles F(x, t; R) is now also a function of the hydrodynamic radius R appearing in the Fokker–Planck equation, Eq. (6), through the diffusion coefficient D_R = k_BT/(8πηR³). The overall distribution function G(x, t) for the orientation angles for polydisperse nanoparticles is then given by

$$G(x,t)={\int }_0^{\infty }\Phi \left(R\right)F(x,t;R)dR.$$ (19)

The coefficients a_n(t) in Eq. (18) will also be a function of R. G(x, t) can then be expanded as

$$G(x,t)=\sum _{n=0}^{\infty }{b}_n\left(t\right)P_n\left(x\right),$$ (20)

where

$$b_n\left(t\right)={\int }_0^{\infty }\Phi \left(R\right)a_n(t;R)dR.$$ (21)

If A_k(R) are the complex Fourier coefficients of a Fourier series for a₁(t; R) and B_k are the complex Fourier coefficients of a Fourier series for b₁(t), then these coefficients are related by

$$B_k={\int }_0^{\infty }\Phi \left(R\right)A_k\left(R\right)dR.$$ (22)

A convenient choice to describe the distribution in the particle radii is the gamma distribution^19,20

$$\Phi \left(R\right)=\frac{1}{R_0\Gamma (\beta +1)}{\left(\frac{R}{R_0}\right)}^{\beta }{e}^{-R/R_0},$$ (23)

where R is the hydrodynamic radius of the spherical nanoparticle. The parameters of the gamma function, R₀ and β, are related to the average hydrodynamic radius and standard deviation (or rms spread) in the hydrodynamic radius via ⟨R⟩ = R₀(β + 1) and $\sigma =R_0\sqrt{\beta +1}$. Note that the percent standard deviation in the hydrodynamic radius is given by $100\%/\sqrt{\beta +1}$.

II.G. Fokker–Planck frequency scaling law

As shown by Weaver and Kuehlert,⁷ the experimental data follow a scaling law when the nanoparticles are immersed in fluids of different viscosities. When plotted as a function of frequency, the ratios of the fifth to third harmonic lie on different curves for each of the viscosities. However, when plotted as a function of the dimensionless parameter ωτ_B the measured ratios all lie on the same curve as expected from the scaling law.

In the calculations this scaling law can be shown by defining the scaled frequency as

$$\Omega \equiv \omega {\tau }_B=\frac{4\pi \eta \omega R^3}{k_{B}T}$$ (24)

and the scaled time as t^′ ≡ t/τ_B. Then the Fokker–Planck equation may be written as

$$\begin{array}{ccc}& & \frac{\partial }{\partial t^{\prime }}F(x,t^{\prime })\hfill \\ & & =\frac{1}{2}\frac{\partial }{\partial x}\left[(1-x^2)\left(\frac{\partial }{\partial x}F(x,t^{\prime })-{\alpha }_0\cos \left(\Omega t^{\prime }\right)F(x,t^{\prime })\right)\right],\hfill \end{array}$$ (25)

which depends on only two independent parameters: α₀ and Ω. Thus, for a given value of α₀, the probability distribution function F(x, t^′) depends only on the scaled frequency Ω.

To see that the polydisperse case also satisfies this scaling law we use Eq. (24) and make a change of variables from R to Ω in Eq. (19). The distribution function for the orientation angles in the polydisperse case can then be written as

$$G(x,t^{\prime })={\int }_0^{\infty }\Psi \left(\Omega \right)F(x,t^{\prime };\Omega )d\Omega ,$$ (26)

where

$$\begin{array}{c}\hfill \Psi \left(\Omega \right)=\frac{{(\beta +1)}^{(\beta +1)}}{3\Gamma (\beta +1)⟨\Omega ⟩}{\left(\frac{\Omega }{⟨\Omega ⟩}\right)}^{(\beta -2)/3}{e}^{-(\beta +1){\left(\Omega /⟨\Omega ⟩\right)}^{1/3}}.\end{array}$$ (27)

Here the average scaled frequency ⟨Ω⟩ is defined by ⟨Ω⟩ ≡ 4πηω⟨R⟩³/k_BT, which is simply Eq. (24) with R and Ω replaced by their averaged quantities.

In the polydisperse case there are now three independent parameters: α₀, β, and ⟨Ω⟩. Thus, for given values of α₀ and β, the probability distribution function G(x, t^′) depends only on the average scaled frequency ⟨Ω⟩. The important point is that the polydisperse case follows the same scaling law as in the monodisperse case and is consistent with the scaling law observed experimentally by Weaver and Kuehlert.⁷

For calculations of the harmonic ratio it is useful to see how the complex coefficients of a Fourier transform for the polydisperse case are obtained. If A_k(Ω) are the complex Fourier coefficients of a Fourier series for a₁(t^′; Ω), where $F(x,t^{\prime };\Omega )={\sum }_{n=0}^{\infty }{a}_n(t^{\prime };\Omega )P_n\left(x\right)$; and B_k are the complex Fourier coefficients of a Fourier series for b₁(t^′), where $G(x,t^{\prime })={\sum }_{n=0}^{\infty }{b}_n\left(t^{\prime }\right)P_n\left(x\right)$, the coefficients B_k for the polydisperse problem will satisfy

$$B_k={\int }_0^{\infty }\Psi \left(\Omega \right)A_k\left(\Omega \right)d\Omega ,$$ (28)

where Ψ(Ω) is given by Eq. (27).

Referring to Eq. (22), it may appear that in order to calculate the mode ratio from the Fokker–Planck equation for the polydisperse case for a range of frequencies, it would be necessary to calculate the FP equation for a range of radii for each of those frequencies, which would be very time consuming. However, referring to Eqs. (24), (27), and (28), and noting that R (as well as η and ω) appears only in Ω, it is necessary to calculate A_k(Ω) for a range of scaled frequencies only once. Then Eq. (28) can be applied for each of those frequencies. More specifically, to calculate the polydisperse curve of the fifth to third mode ratio for a range of frequencies, the complex Fourier coefficients A_k(Ω) (or the coefficients of a sine and cosine series) of the time series a₁(t^′) for the FP monodisperse problem were first calculated for a range of scaled frequencies from Ω = 0 to about Ω = 35. For a given value of β, B_k was then calculated from Eq. (28) for values of ⟨Ω⟩ = 0 to about ⟨Ω⟩ = 25. Note that the values of Ω must extend further than the values of ⟨Ω⟩ to allow for the spread in Ω.

II.H. Numerical methods

The numerical solution to Eq. (25) was obtained by transforming Eq. (18) to the scaled variables (Ω and t^′) and then using the MATLAB^® ode15s routine to integrate the coupled ordinary differential equations. The series given by Eq. (17) converges rapidly for large n. In the numerical simulation of Eq. (18), we truncated the series at 30 terms, although 20 terms would have sufficed.

The same integration routine used for the FP equation, MATLAB^® ode15s, was also used for the numerical solution of the effective-field approximation equation, Eq. (16). Note that the numerical solution of Eq. (16), a single ordinary differential equation, is much simpler than the numerical solution of Eq. (18), which is the reason that it is sometimes used for the modeling of magnetic nanoparticles.

The numerical solution of the FP equation can be verified by averaging over the numerical solution of the stochastic Langevin equation for a large number of particles, which was done for all the FP calculations. For the numerical solution of the Langevin equation, Eq. (3), the stochastic generalization of the deterministic Heun scheme was employed.¹⁸

III. SIMULATION RESULTS

In Sec. II, we have reviewed the Fokker–Planck equation and its method of solution. In the present section we compare the calculations to experimental results—namely, the work of Weaver and Kuehlert (WK) (Ref. ⁷) on the signals from ferrofluids with different viscosities and containing nanoparticles with hydrodynamic diameters in the 40–120 nm range. We compare these data using the Fokker–Planck approach with Brownian motion by considering both monodisperse and polydisperse models.

There are two sets of data with which we will compare our calculations, where different viscosities are studied in each set. These data correspond to what the authors in Ref. 7 refer to as “$100\mathrm{nm}$” iron oxide and “$40\mathrm{nm}$” iron oxide samples. Recall that the calculation methods are: (1) the effective-field approximation to the Fokker–Planck equation, and (2) the Fokker–Planck equation for either monodisperse or polydisperse models.

The dipole moment and hydrodynamic diameter distribution are not known so we allow variation in those parameters in order to achieve a good fit with the measured data. This section focuses on the results of these fits and we defer the discussion of discrepancies to Sec. IV.

It is important to note that the experimental signal S(t) is proportional to the time derivative of the magnetization M(t). If the A_k are the complex Fourier coefficients in the expansion

$$⟨x\left(t\right)⟩=\sum _k{A}_k{e}^{ik\omega t}$$ (29)

then the time differentiation of M(t) contributes an additional factor of kω to the terms of Fourier expansion for the signal S(t). Thus the ratio of the signal harmonics is given by the ratio of the magnetization harmonics multiplied by the ratio of the harmonic numbers. In other words, the ratio of the fifth to third harmonic plotted in our figures is related to the ratio of the magnetization harmonics via 5 |A₅|/3 |A₃|.

III.A. Results for “100 nm” iron oxide particles in water

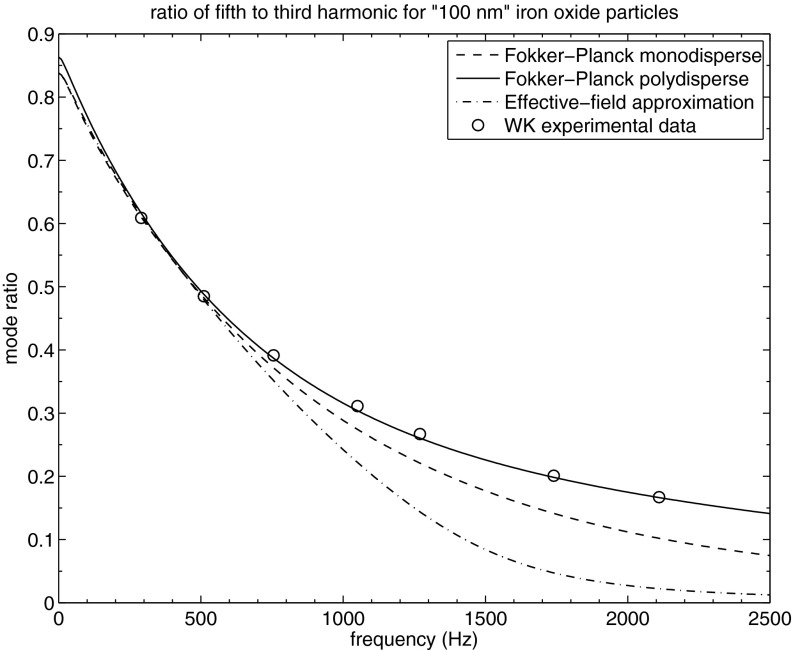
Experimental data and theoretical curves for a ferrofluid consisting of water and the “$100\mathrm{nm}$” iron oxide nanoparticles are shown in Fig. 1. The water viscosity is $\eta =1.0049\mathrm{mPa}\text{-}\mathrm{s}$, and, for all experiments, the temperature is 20 °C and the magnetic field amplitude $B_0=10\mathrm{mT}$. The measured points from Ref. 7 are indicated by circles with errors that appear to be on the order of a few percent.

FIG. 1.

Measured and calculated ratios of the fifth to third harmonics as a function of frequency for the water ferrofluid with the “$100\mathrm{nm}$” iron oxide sample. The measured values (indicated with circles) are from Weaver and Kuehlert (Ref. ⁷). The calculated curves assume $T=293\mathrm{K}$, $\eta =1.0049\mathrm{mPa}\text{-}\mathrm{s}$, $B_0=10\mathrm{mT},$ and $R=65.5\mathrm{nm}$ for the monodisperse case. For the polydisperse case R refers to the average radius. The dot-dashed line is the ratio from the effective-field approximation, the dashed line is the ratio from the FP monodisperse model, and the solid line is the ratio from the FP polydisperse model. The magnetic dipole moments and other parameters in the fits are described in the text. Excellent agreement is obtained for the polydisperse model.

In an attempt to make a monodisperse fit we assume all particles have a hydrodynamic diameter $2R=113\mathrm{nm}$ which is given as a mean value in Ref. 7. The magnetic dipole moment $m_0=7.96\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$ was chosen so that the experimental data and theoretical curve agreed at the lowest frequency data point. We solve the FP equation with the above parameters, which corresponds to α₀ = 19.67 and ${\tau }_B=0.563\mathrm{ms}$, and show the corresponding curve in Fig. 1. It is observed that while the agreement is good at the lower frequencies, the calculated curve has fallen to about half the measured value at $2110\mathrm{Hz}$. Taking this to be significantly outside the measured errors, and ignoring possible systematic errors, we expand our model to include polydispersion.

In fact, the manufacturer's technical data sheets for the “$100\mathrm{nm}$” iron oxide sample (Micromod Partikeltechnologie GmbH, Rostock-Warnemuende, Germany) indicate the nanoparticles are polydisperse with as much as a 20% standard deviation in the hydrodynamic diameter. Through a fit utilizing the gamma distribution in Eq. (23) and fixing the average diameter to $2⟨R⟩=113\mathrm{nm}$, we find $m_0=9.42\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$ and β = 80 which corresponds to a standard deviation of 11%. Excellent agreement is now achieved throughout the entire frequency range of the data.

Here and elsewhere we quote more significant digits than are justified, for numerical comparisons by other investigators. We did not formally determine an error for the fit parameters, but we estimate that they are several percent. The estimation was made by observing poor agreement between measurement and calculations when the fit parameters were varied by a few percent.

In Fig. 1, we also include a plot of the ratio of the fifth to third harmonic as calculated using the effective-field approach for the monodisperse case discussed in Sec. II D. At the lower frequencies the effective-field approximation agrees well with the data and the complete Fokker–Planck solution, but the approximation is less accurate at the higher frequencies, falling to about 10% of the measured value at $2110\mathrm{Hz}$.

III.B. Results for “100 nm” iron oxide particles in water and glycerol–water solutions

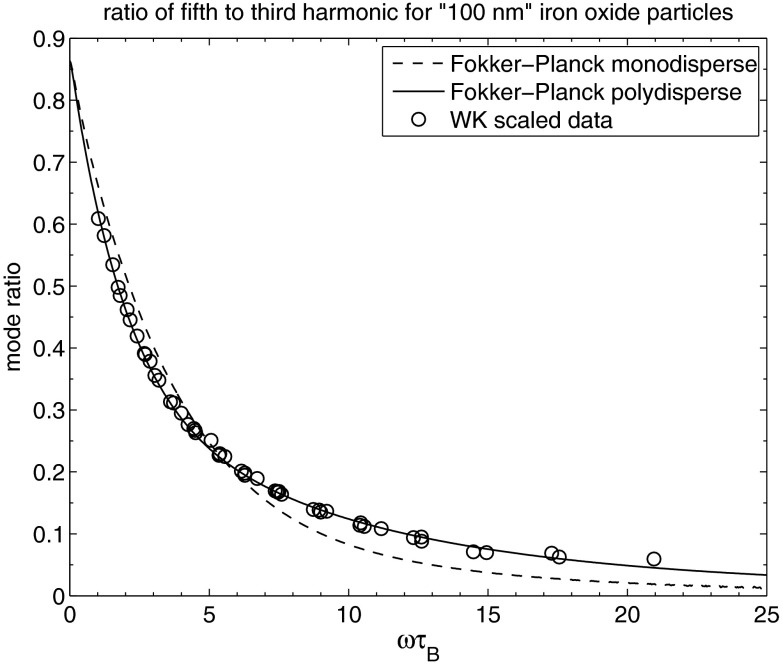
Experimental data and theoretical curves for “$100\mathrm{nm}$” iron oxide nanoparticles immersed in water and glycerol mixtures are shown in Fig. 2. The data all use the same “$100\mathrm{nm}$” iron oxide particles, but they are immersed in seven different glycerol–water solutions with viscosities in the range η = 1.00–$2.82\mathrm{mPa}\text{-}\mathrm{s}$ as described in Ref. 7. This gives rise to 7 different curves—one for each viscosity. In view of the scaling discussed in Sec. II G the data may be plotted on a single curve as a function of ωτ_B.

FIG. 2.

Measured and calculated ratios of the fifth to third harmonics as a function of the scaled frequency Ω = ωτ_B for the “$100\mathrm{nm}$” iron oxide particles in the glycerol–water ferrofluids. The measured values are for a range of viscosities and are from Weaver and Kuehlert (Ref. ⁷). They are scaled as a function of ωτ_B—a valid scaling law as demonstrated in the experiment with varying values of the viscosity η. The calculated curves assume $T=293\mathrm{K}$, $\eta =1.0049\mathrm{mPa}\text{-}\mathrm{s}$, $B_0=10\mathrm{mT}$, $R=65.5\mathrm{nm}$, and $m_0=9.42\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$. For the polydisperse case β = 80 and R refers to the average radius. The measured data from Weaver are indicated with circles, the dashed line is the harmonic ratio from the Fokker–Planck approach (monodisperse) and the solid line is the ratio from the FP approach (polydisperse).

For the polydisperse calculation plotted in Fig. 2 we use the same parameters as in the water sample calculation in Sec. III A. (The magnetic moment is set to $m_0=9.42\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$ and the distribution in the hydrodynamic radii is given by the gamma distribution in Eq. (23) with an average diameter of $2⟨R⟩=113\mathrm{nm}$ and β = 80, corresponding to an standard deviation of 11%.) There is excellent agreement throughout the entire range of ωτ_B confirming that the Fokker–Planck polydisperse model remains valid at the larger values of ωτ_B corresponding to the measurements with the higher viscosity glycerol–water solutions.

The difference between the monodisperse and polydisperse calculations of the ratio of the fifth to third harmonics is illustrated in Fig. 2. For the monodisperse Fokker–Planck calculation, all parameters are the same as the polydisperse calculation except that there is no spread in the hydrodynamic radii. With the monodisperse model, the calculated ratio is larger than the experimental data for ωτ_B < 5 and smaller than the experimental data for ωτ_B > 5. So the effect of the polydispersion is to decrease the ratio of fifth to third harmonics for smaller values of ωτ_B and increase the ratio of fifth to third harmonic for larger values of ωτ_B.

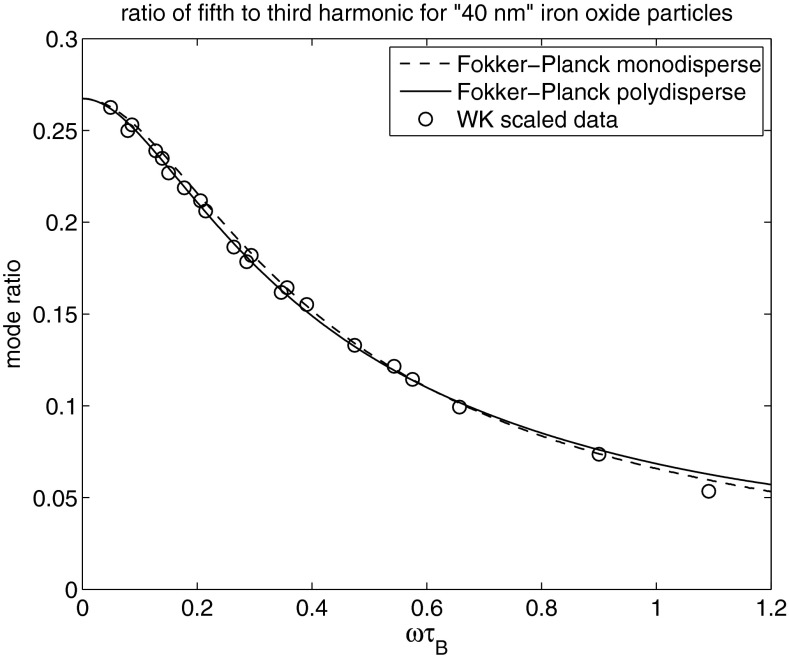
III.C. Results for “40 nm” iron oxide particles in water and glycerol–water solutions

Next we turn our attention to the data for the “$40\mathrm{nm}$” iron oxide nanoparticles immersed in both water and glycerol–water solutions. We note that, compared to the “$100\mathrm{nm}$” experiments, there are fewer measurements (21 versus 49) and the distribution of the hydrodynamic diameters is not as firmly established.²² See Sec. IV for further discussion regarding the hydrodynamic diameter.

We fit these data by adjusting the values of the magnetic moment and hydrodynamic radius in our calculations. The three different sets of data correspond to glycerol–water solutions with viscosities in the range η = 1.00–$3.08\mathrm{mPa}$. This gives rise to three different curves—one for each viscosity. In view of the scaling discussed in Sec. II G the data in Fig. 3 may be plotted on a single curve as a function of ωτ_B. We find that the monodisperse calculations (dotted line) with $m_0=1.31\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$ (which corresponds to α₀ = 3.24), and an average hydrodynamic radius of $41\mathrm{nm}$ provides very good agreement throughout the entire range of ωτ_B.

FIG. 3.

Measured and calculated ratios of the fifth to third harmonics for monosdisperse nanoparticles for the “$40\mathrm{nm}$” iron oxide case. The measured values are from Weaver and Kuehlert (Ref. ⁷) and are scaled as a function of ωτ—a valid scaling law as demonstrated in the experiments with different values of the viscosity η. The calculated curves assume $T=293\mathrm{K}$, $\eta =1.0049\mathrm{mPa}\text{-}\mathrm{s}$, $B_0=10\mathrm{mT}$, $R=20.5\mathrm{nm}$, and $m_0=1.31\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$. For the polydisperse case β = 200 and R refers to the average radius. The measured data from Weaver are indicated with circles, the dashed line is the harmonic ratio from the Fokker–Planck approach (monodisperse) and the solid line is the ratio from the FP approach (polydisperse).

Although the monodisperse calculation gives a good fit, we also compare the data to the Fokker–Planck calculation assuming polydispersion in the hydrodynamic diameter with an standard deviation of 7% (β = 200). As seen in Fig. 3, this is an improved fit for some of the lower frequency points, but does not agree as well for the two highest frequency data point.

IV. DISCUSSION

The models for magnetic nanoparticles in solution described in Sec. III have been found to lead to excellent fits for the two sets of data. The fits correspond to particular values, or distributions in these values, for the parameters representing the outside hydrodynamic diameters and the magnetic moments. How consistent are these particular values for the picture one has for the iron oxide core embedded in, for example, a starch shell? Are the hydrodynamic diameter and the effective core diameter implied by the magnetic moments sensible?

To address these questions, we first recall a single value for the magnetic moment $m_0=9.42\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$ was used in the best (polydisperse) fit for the “$100\mathrm{nm}$” data. This is to be compared to the magnetic dipole moment of the particles as gleaned from the technical data sheet of the “$100\mathrm{nm}$” sample (Micromod Partikeltechnologie GmbH, Rostock-Wamemuende, Germany). Using the iron content of the ferrofluid ($15\mathrm{mg}/\mathrm{ml}$) and the number density of particles ($1.5\times {10}^{13}\mathrm{particles}/\mathrm{ml}$) reported in the technical data sheet, along with the chemical composition (${\mathrm{Fe}}_3{\mathrm{O}}_4$) and density of magnetite ($5.2\mathrm{g}/\mathrm{ml}$), the average volume of the iron oxide core is calculated to be $2.66\times {10}^5{\mathrm{nm}}^3$. (We note that this is the same volume as an $80\mathrm{nm}$ diameter spherical particle.)

If the magnetization in all of the domains within the core were aligned, then the estimated dipole moment is simply the product of the particle volume and the saturation magnetization of magnetite ($4.74\times {10}^5\mathrm{A}/\mathrm{m}$). In the case of the “$100\mathrm{nm}$” particles, this results in a magnetic dipole moment of $1.26\times {10}^{-16}\mathrm{A}{\mathrm{m}}^2$ which is 13 times greater than the dipole moment used in the calculations.

That this is not surprising can be seen by the illustration shown in Fig. 4. The iron oxide core appears to be an irregular cluster of tens of rectangular crystals with random orientations. The multiple domains are not likely to be aligned in view of the anisotropy in their nonsymmetrical geometrical clustering. Therefore, the significant decrease in average magnetization implied by our fit does not seem unreasonable.

FIG. 4.

Figure of BNF starch particles from Micromods 2011/2012 Product Catalog. The iron oxide core appears to be an irregular cluster of rectangular crystals.

Also the theoretical fit to the “$100\mathrm{nm}$” iron oxide data clearly indicates the presence of a 11% standard deviation in the hydrodynamic nanoparticle diameter, consistent with the experimental information. (Spreads of up to 20% are indicated by the manufacturer's technical data sheets.) The fairly precise shape of the experimental curve precludes a description using only a monodisperse model.

A qualitatively similar reduction in magnetization is seen for the “$40\mathrm{nm}$” data where the magnetic moment $m_0=1.31\times {10}^{-18}\mathrm{A}{\mathrm{m}}^2$ was used in the best (monodisperse) fit. If the iron oxide core diameter, which is close to spherical, were as large as $40\mathrm{nm}$, the implied average magnetization of the core is $39.1\mathrm{kA}/\mathrm{m}$, which is about 11 times smaller than the saturation magnetization $M_s=447\mathrm{kA}/\mathrm{m}$ of magnetite. This does not seem unreasonable since the core may consist of many magnetic domains which are not aligned in the same direction.

We cannot rule out other solutions corresponding to a possible spread in magnetic moments for both data sets. We assume that manufacturing processes can control the core size and this is what has been assumed for the two data sets. This remains an open question in the present study, however. It should also be kept in mind that the “$40\mathrm{nm}$” and “$100\mathrm{nm}$ samples originated from different manufacturers.

In the comparison between the experimental data and the calculational fit, a discrepancy arises concerning the hydrodynamic diameter of the “$40\mathrm{nm}$” iron oxide particles. In Ref. 7 the mean hydrodynamic diameter of the nanoparticles is reported to be $65\mathrm{nm}$ as measured by the Malvern (Worchester, UK) ZetaSizer Nano ZS. We could not achieve a reasonable fit with our models by fixing the mean hydrodynamic diameter to this value. A good fit could be achieved if the mean hydrodynamic diameter takes on the smaller value of $41\mathrm{nm}$. Based on discussions with one of the authors (Weaver²²) of Ref. 7, we conjecture that the size discrepancy may be a result of aggregation occurring during the sufficiently long time between the harmonic measurements and the ZetaSizer measurements. This aggregation could result in a larger average diameter being measured by the ZetaSizer. It is also important to note the manufacturers, processes, and hydrodynamic shell material of the two data-set samples are all different.

V. CONCLUSIONS

We have compared theoretical calculations to recent experimental measurements of the magnetization of ferrofluids subject to external oscillating magnetic fields. The calculations are based on the Fokker–Planck approach with the Langevin equation providing the underlying dynamics in situations where Brownian relaxation is the dominant relaxation mechanism. What is measured are ratios of lower harmonic signals covering nanoparticle hydrodynamic diameters in the 40–120 nm range and field frequencies below $2200\mathrm{Hz}$.

Excellent agreement between experiment and theory is found by fitting the data with reasonable choices for the nanoparticle core magnetic moments. All particles in a given ferrofluid experiment are assumed to have the same (common) iron oxide core, a point to which we return below. Additionally, the fits, which include variations in the nanoparticle overall size distribution, are consistent with the information available about the hydrodynamic diameters.

The progress made through the WK experiments and, we hope, the comparison with our theoretical simulations highlights a number of new directions for the future. We expect that the iron oxide cores, especially for nanoparticles in the $100\mathrm{nm}$ range should have some spread in their magnetic moment magnitudes. Although we have had success in finding good fits to the data without considering this spread in moment value, a useful project for the future will be to find all solutions that give the same good fit in a two-dimensional study of spreads in both moments and hydrodynamic size. More experimental information on the core size and crystalline structure could provide tests to distinguish these solutions. And more experimental information for smaller particles and larger frequencies than those considered in this paper will bring up very interesting modeling where Neel relaxation must be considered. This is important for magnetic particle imaging, another of the exciting nanoparticle applications.