Evaluation of tumor-derived MRI-texture features for discrimination of molecular subtypes and prediction of 12-month survival status in glioblastoma

Abstract

Purpose:

Glioblastoma multiforme (GBM) is the most common and aggressive primary brain cancer. Four molecular subtypes of GBM have been described but can only be determined by an invasive brain biopsy. The goal of this study is to evaluate the utility of texture features extracted from magnetic resonance imaging (MRI) scans as a potential noninvasive method to characterize molecular subtypes of GBM and to predict 12-month overall survival status for GBM patients.

Methods:

The authors manually segmented the tumor regions from postcontrast T1 weighted and T2 fluid-attenuated inversion recovery (FLAIR) MRI scans of 82 patients with de novo GBM. For each patient, the authors extracted five sets of computer-extracted texture features, namely, 48 segmentation-based fractal texture analysis (SFTA) features, 576 histogram of oriented gradients (HOGs) features, 44 run-length matrix (RLM) features, 256 local binary patterns features, and 52 Haralick features, from the tumor slice corresponding to the maximum tumor area in axial, sagittal, and coronal planes, respectively. The authors used an ensemble classifier called random forest on each feature family to predict GBM molecular subtypes and 12-month survival status (a dichotomized version of overall survival at the 12-month time point indicating if the patient was alive or not at 12 months). The performance of the prediction was quantified and compared using receiver operating characteristic (ROC) curves.

Results:

With the appropriate combination of texture feature set, image plane (axial, coronal, or sagittal), and MRI sequence, the area under ROC curve values for predicting different molecular subtypes and 12-month survival status are 0.72 for classical (with Haralick features on T1 postcontrast axial scan), 0.70 for mesenchymal (with HOG features on T2 FLAIR axial scan), 0.75 for neural (with RLM features on T2 FLAIR axial scan), 0.82 for proneural (with SFTA features on T1 postcontrast coronal scan), and 0.69 for 12-month survival status (with SFTA features on T1 postcontrast coronal scan).

Conclusions:

The authors evaluated the performance of five types of texture features in predicting GBM molecular subtypes and 12-month survival status. The authors’ results show that texture features are predictive of molecular subtypes and survival status in GBM. These results indicate the feasibility of using tumor-derived imaging features to guide genomically informed interventions without the need for invasive biopsies.

1. INTRODUCTION

In 2013, over 23 000 patients in the United States were diagnosed with brain cancer, and over 14 000 patients with brain cancer died.¹ Generally, among all primary brain tumor cases, more than 15% of adult patients have glioblastoma (GBM), the most common and aggressive type of brain cancer.² Median overall survival (OS) for GBM patients is only 12–15 months.³ Recent studies have identified four different subtypes of GBM:⁴ classical, mesenchymal, neural, and proneural, each representing distinct molecular alterations. Due to this underlying molecular heterogeneity, each subtype requires potentially different treatment strategy. For example, intensive therapy (concurrent chemotherapy and radiation) results in better survival outcomes in classical and mesenchymal patients, but not in patients with the proneural subtype.⁴ In addition, these subtypes are also associated with distinctly different survival outcomes (for example, the proneural subtype has a better overall survival than the other molecular subtypes).⁵ Currently, the only way to determine a patient’s tumor subtype is to perform an invasive brain biopsy followed by mRNA profiling.⁶ However, a brain tumor biopsy not only is costly⁷ but also poses risks inherent to an invasive procedure.^8,9 An imaging based characterization also presents other advantages,¹⁰ such as permitting interrogation of tumor heterogeneity characteristics and an assessment of tumor pathophysiology. More recently, it has also been suggested that GBMs harbor multiple cell subpopulations;¹¹ hence, an imaging based examination can also provide an insight into the molecular programs driving the disease.

Magnetic resonance imaging (MRI) has been routinely used for noninvasive assessment of many cancers, including brain cancer,¹² pancreatic cancer,¹³ and breast cancer.¹⁴ Gutman et al.¹⁵ demonstrated that manually extracted visual features from MRI are associated with the GBM molecular profiles and survival duration. Apart from human-expert derived radiographic evaluation, computer-based evaluation techniques (image analysis and machine learning algorithms) have shown enormous potential in tackling detection and classification tasks on radiologic data.¹⁶ For example, Arbach et al.¹⁷ investigated machine learning algorithms for assessment of lesion malignancy in breast cancers based on MRI scans. These algorithms are capable of capturing additional information that could strongly complement human visual interpretations of MRI scans.¹⁸ Of the many image analysis techniques, computer derived texture features from MRI scans, a characterization of gray-level tumor heterogeneity, have been of particular interest in tissue and tumor segmentation tasks in GBM.^19,20 Other studies have indicated that MRI texture analysis can differentiate GBM from other types of brain tumors, such as low-grade gliomas or malignant glioneuronal tumors.^21,22 Also, texture features and gray-level tumor heterogeneity in MRI have been studied for survival prediction in GBM patients.^23,24 These studies all suggest that clinical aspects of GBM can be characterized quite effectively by MRI-derived tumor texture features. However, the relationship between any specific measure of gray-level tumor heterogeneity from tumor MRI scans and the underlying tumor biology (molecular status) in GBM is still unclear. Some recent studies have suggested that texture features from diagnostic (MRI) images might have predictive value for the determination of tumor molecular phenotype (subtype) status in breast tumors.^25,26 Hence, we sought to investigate the feasibility of using texture features from tumor MRI scans for discrimination of molecular subtypes and 12-month OS status in GBM. In particular, we evaluated the performance of five commonly used two-dimensional (2D) texture feature descriptors for their potential value in these classification tasks. We also aim to compare the information presented in different image planes (axial, coronal, or sagittal) and different MRI sequences [postcontrast T1 weighted or T2 fluid-attenuated inversion recovery (FLAIR)].

2. METHODS

2.A. Dataset

Eighty two patients (26 females, 56 males) with primary GBM were identified from the Cancer Genome Atlas (TCGA). These patients had routine MR imaging which includes both postcontrast T1-weighted and T2-weighted FLAIR MRI images available in their medical records (data obtained from The Cancer Image Archive). All MRI images were acquired prior to treatment. All patients received standard of care which includes surgical resection followed by concurrent chemoradiation.³ This study was IRB-exempt under TCGA data use agreement. Molecular subtype labels and survival data for these patients were obtained from the cBioPortal, a public domain repository of genomic and clinical data from TCGA patient cohort.²⁷

Of the 82 GBM patients, 21 had the classical subtype, 29 had the mesenchymal subtype, 12 had the neural subtype, and 20 had the proneural subtype. We also dichotomized the overall survival duration data into long survival (overall survival > 12 months, n = 49) and short survival (OS < 12 months, n = 33) categories.

The MRI sequences used included axial postcontrast T1-weighted (TE/TR = 2.1–20 ms/4.94–3285.62 ms; slice thickness = 1.4–5 mm; spacing between slices = 0.7–6.5 mm; $\text{matrix size}=256\times 256$ or 512 × 512; and pixel spacing = 0.47–1.02 mm) and axial T2-FLAIR (TE/TR = 14–155 ms/400–36 737.38 ms; slice thickness = 2.5–5 mm; spacing between slices = 2.5–7.5 mm; $\text{matrix size}=256\times 256$ or 512 × 512; and pixel spacing = 0.43–1.09 mm).

2.B. Image preprocessing

MRI scans were processed in three steps: nonparametric intensity nonuniformity normalization (N3-correction), tumor segmentation, and image reslicing.

N3-correction corrects the inhomogeneity in each set of MRI scans.²⁸ Such inhomogeneity, or shading artifacts, is due to intensity variations caused by inhomogeneous radio-frequency excitation or spatial variation in the reception sensitivity. N3-correction corrects this inhomogeneity by iteratively estimating the spatial variation of sensitivity and tissue intensity distribution.²⁸ N3-correction was performed using the Medical Image Processing, Analysis, and Visualization software (National Institutes of Health, Bethesda, MD).²⁹

To extract tumor image features, tumor segmentation was done using the Medical Imaging Interaction Toolkit software (Heidelberg, Germany).³⁰ The segmentation was performed on a slice-by-slice basis separately on the postcontrast T1-weighted and the T2 FLAIR sequences of each patient, yielding two three-dimensional (3D) tumor volumes per patient. For postcontrast T1-weighted sequences, the contrast enhancing tumor was segmented. For T2 FLAIR sequences, the solid tumor as well as infiltrating tumor and edema that is delineated by increased intensity was segmented. No image registration is done between the T1-postcontrast and the T2-FLAIR image sequences—thus, geometrical distortions between the two have not been considered.

In these scans, the axial plane has a higher resolution than do the coronal and sagittal plane resolution. To account for the unequal pixel resolutions across the three image planes, image reslicing was performed (using trilinear interpolation) so that the voxel dimensions in the resulting 3D image were isotropic (1 × 1 × 1 mm). The reslicing step was performed in matlab using the NIfTI toolbox (MathWorks, Natick, MA).

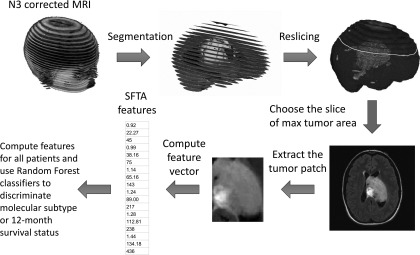
2D texture features were evaluated on the image slices with maximum tumor area from each of the image planes (axial, coronal, or sagittal) and for each MRI sequence (T1 postcontrast or T2 FLAIR). A rectangular tumor region (that encloses the segmented tumor area at that slice) was extracted, and image features were computed (Fig. 1).

FIG. 1.

A flow chart showing the preprocessing and feature extraction steps. Parts of a SFTA feature vector are shown on the bottom left for illustration purpose. A detailed description of feature extraction algorithms is in Sec. 2.C.

2.C. Feature descriptors

We extracted five sets of global image features: segmentation-based fractal texture, run-length matrix (RLM), local binary patterns (LBPs), histogram of oriented gradients (HOGs), and Haralick texture features. The detailed methods for deriving these features are described as follows, and the parameters we used for each type of features are summarized in Table S2 of the supplementary material.³¹

2.C.1. Segmentation-based fractal texture analysis (SFTA)

SFTA uses fractal dimension analysis to describe the complexity and texture features in the image.³² The binary decomposition step in SFTA captures the regions with high intensity variations. The complexity of these regions is quantified by the Hausdorff’s fractal dimension. The Hausdorff’s fractal dimension of a 2D tumor area is defined as

$${\displaystyle D_0=-\underset{\epsilon \to 0}{lim}{log}_{\epsilon }N\left(\epsilon \right)=\underset{\epsilon \to 0}{lim}\frac{logN\left(\epsilon \right)}{log{\epsilon }^{-1}},}$$

where N(ε) is the number of ε × ε squares needed to cover the 2D area.³³ For digital images, the value of D₀ can be approximated by the box-counting algorithm.³⁴

To compute SFTA features, we first find eight intensity thresholds {t,  t₂,  …,  t₈} by applying multilevel Otsu algorithm.³⁵ The multilevel Otsu algorithm determines the intensity thresholds so that the between-class variance is maximized. Then, we decomposed a grayscale tumor image into 16 binary images using the two-threshold binary decomposition algorithm. Subsequently, these thresholds are applied to the grayscale image to generate binary maps. For each binary map, we computed three values as texture feature descriptors: fractal dimension, mean gray level, and area. These steps are illustrated in Fig. 2.

FIG. 2.

SFTA feature extraction. A tumor ROI is decomposed to 16 binary images by applying the two-threshold binary decomposition algorithm. For each binary image, three features are computed: fractal dimension, area, and the average gray level of the corresponding pixels in the original image. The 48 features are combined to form the SFTA feature descriptor. “I” refers to the gray-level representation of the image. t_n and t_n+1 represent the upper and lower limits of the nth intensity bin.

2.C.2. RLM

A RLM essentially describes the distribution of gray-level runs and captures coarseness in a grayscale image.³⁶ In a RLM, the entry $\left(i,j\right)$ is the number of gray-level runs with gray-level i and run-length j. A gray-level run is defined as a set of connected and collinear pixels that are of the same gray level. The length of the run is the number of pixels in that run.

For each tumor image, we constructed four RLMs, one for each direction of the run (0°, 45°, 90°, and 135°). Figure 3 shows how a typical RLM is constructed. For the RLM in each of the four directions, we extracted 11 RLM texture features by weighting and summing different terms in the RLM.^37,38 To obtain rotational invariance, we summed the texture features from all four directions. The formulas for computing 11 RLM features are listed in the supplementary material.³¹

FIG. 3.

Computing the RLM. The original tumor ROI is reduced to a 4-bit grayscale image (16 different intensities). RLM is constructed by counting the number of runs with each gray level and run-lengths. Eleven features can be computed by weighting and summing different entries of the matrix.

2.C.3. LBPs

LBP describes the texture features of an image by comparing the intensities of neighboring pixels in small patches.^39,40 Consider the 3 × 3 patch around one pixel in a grayscale image. If the intensity of a surrounding pixel was greater than the center pixel, a 1 is recorded as the comparison result for that pixel; otherwise, a 0 is recorded. Because there are eight surrounding pixels in a 3 × 3 patch, we arranged the comparison results into an 8-bit binary number, which was then converted to a decimal ranging from 0 to 255. These steps are summarized in Fig. 4.

FIG. 4.

Computing LBP. In step 1, for each pixel in the tumor ROI, a 3 × 3 patch covering the pixel is extracted. In step 2, we compare the pixel intensity of the surrounding pixels with the center pixel. The comparison results are either 1 (the surrounding pixels are more intense) or 0 (the surrounding pixels are less intense) and are recorded in a 3 × 3 table. In step 3, the results in the table form in the indicated direction a binary string, which is then converted to a decimal number. Eventually, each pixel has a decimal number describing its binary pattern. We use the normalized histogram of these decimal numbers as the LBP texture features.

We obtained a binary pattern (a decimal) for every pixel in the tumor image. Then, we computed the histogram of these binary patterns across all the pixels in the image. The histogram had 256 bins, and the height in each bin was the frequency with which the binary pattern occurred in the image. After normalization, the histogram served as LBP texture features of the tumor image, quantifying the distribution of the 256 binary patterns within 3 × 3 patches.

2.C.4. HOGs

HOG captures the distribution of intensity gradients in small regions in an image.^41,42 Similar to other texture descriptors, HOG is a representation of the neighborhood structure of pixel intensities.

To compute HOG features, we first computed the gradient of the image. Then, we divided the gradient map into nonoverlapping square patches (called cells). In each cell, we constructed a histogram in which the bin centers are directions $\left(20°,\hspace{0.17em}40°,\hspace{0.17em}\dots ,\hspace{0.17em}180°\right)$, and the heights are a combination of frequency and gradient intensity in that direction. Next, the cells (and the histograms) were grouped together to form blocks for normalization. In general, each cell is 8 × 8 pixels. Each block consists of four cells (thus, the size of each block is 16 × 16) and the stride (block overlap) is 8 pixels. The four histograms within each block were normalized together with the L2-Hys scheme (clipping the unit length vector then renormalizing).⁴³ The concepts of cells, blocks, and histograms of gradients are illustrated in Fig. 5.

FIG. 5.

Computing HOG features. To ensure that the final HOG features had the same dimension, we resized all the original tumor ROIs to 40 × 40. Then, the gradient map is computed and divided into 25 8 × 8 cells. In each cell, we compute the histogram of the gradient intensities in each of the nine directions. The histograms are illustrated by the short white lines in each cell. In each 2 × 2 blocks (such as the one in red full lines and the one in black dotted lines), the histograms are normalized via the L2-Hys scheme.

2.C.5. Haralick texture features

Haralick texture features quantitatively describe the homogeneity, luminance, complexity, etc., of an image through 13 numerical texture features extracted from the gray-level co-occurrence matrix (GLCM).⁴⁴ The entry (i, j) in a GLCM is the total number of pixel pairs that have a gray level i and j in the image in a specific direction and distance. The 13 features are derived from the GLCM.

To obtain rotational invariance, we summed the GLCM over four directions (0°, 45°, 90°, and 135°). We repeated the GLCM calculation with different pixel distance offsets to obtain both fine and coarse features. Figure 6 shows the four GLCMs computed for a tumor region of interest (ROI).

FIG. 6.

Computing Haralick features. The tumor ROI was reduced to a 4-bit grayscale image (16 different intensities). The entry (i, j) of a GLCM can be computed by counting the total number of pixel pairs that have a gray level i and j in the image at the specific distance. For each GLCM, 13 Haralick features can be computed by weighting and summing different entries of the matrix. Finally, we found a total of 52 Haralick features for each tumor ROI (by concatenating the 13 features across different distances).

2.D. Classification algorithm

We used random forest (RF) classifiers to predict GBM molecular subtypes and to predict 12-month survival status (alive or dead at 12-month time point).⁴⁵ RF is an ensemble learning algorithm that combines the individual predictions of a collection of individual learners (decision trees) to predict a target class. Each decision tree in the RF is trained via bootstrap resampling of the data.⁴⁵ The sampling is stratified by the class composition of the original data, thus providing tradeoff of true positive and true negative rates. RF has several advantages over other classifiers: it can handle high dimensional data (e.g., 576 HOG features in our study), including situations where the number of features is much larger than the number of cases, in addition to providing intrinsic cross-validation via an “out-of-bag” (OOG) estimation of error rate.⁴⁵

For each combination of feature set, image plane and MRI sequence, we build five individual RF binary classifiers, one for each of the five prediction tasks: to discriminate each subtype vs the rest, as well as for 12-month survival status (alive or dead at 12-month time point). As the occurrence of the subtypes does not necessarily preclude the occurrence of other subtypes,^11,46 independently assessing the biology of the tumor for each molecular subtype is useful. No variable selection was done for classifier construction, rather, the classifier was trained over all variables in a feature set (e.g., all 48 SFTA features). The algorithm for building random forest models as well as out-of-bag validation procedure is summarized as follows.⁴⁷

• 1.From the 82 patients, 500 bootstrap samples (with replacement, of size twice that of the minority class) are drawn.
• 2.A binary decision tree classifier is trained on each bootstrap sample. For each node of the tree, best split is chosen from $\sqrt{p}$ randomly selected features (“p” represents the total number of features in the feature set). All the trees are grown until the terminal nodes are pure.
• 3.Each tree classifier predicts a label for data points not included in the bootstrap sample used to create that tree. These held-out data, also referred to as the OOB data, are used for estimation of classifier performance. On average, each data point (patient) is out-of-bag for one-third of the 500 trees, on which the predictions are aggregated by majority voting. The overall performance of the random forest model is evaluated based on these OOB predictions.

We used the “randomForest” package in R to build random forest models.⁴⁷

2.E. Performance evaluation

The performance of the five classifiers was evaluated with receiver operating characteristic (ROC) curves. ROC curves show how the false-positive prediction rates (FPRs) vary with the true-positive prediction rates (TPRs), i.e., sensitivity vs 1-specificity. For each of the four molecular subtype classification tasks, we define the patients of that specific subtype as positive cases and the patients of other subtypes as negative cases. For classification of 12-month survival status, we define the patients who are alive at 12-month point as positive cases and those are deceased as negative cases. For each random forest model, the FPR and TPR are computed with the following formulas:

$${\displaystyle \text{TPR}=\frac{\text{number of true positive cases}}{\text{number of actual positive cases,}}}$$

$${\displaystyle \text{FPR}=\frac{\text{number of true negative cases}}{\text{number of actual negative cases}}.}$$

The area under the ROC curve (AUC) quantifies the classification performance with a single number. The value of AUC ranges from 0 to 1; a high AUC indicates good performance. In addition to the AUC, the p-value of the AUC given by Mann–Whitney U test is also used to evaluate the classifier relative to random classification (AUC = 0.5).⁴⁸ These p-values are adjusted for multiple testing using Benjamini–Hochberg (BH) procedure to assess significance.⁴⁹

The intent of the Benjamini–Hochberg procedure is to control the false discovery rate (FDR), which in our case is the expected proportion of classification performance AUCs that are erroneously called significant. To perform Benjamini–Hochberg correction, we first fix a user-defined level α and rank the p-values in increasing order. Let M denote the total number of p-values, i denote the rank of the p-value p_i, and AUC_i denote the AUC associated with p_i. Then, AUC_i is called significant if it satisfies the following:

$${\displaystyle p_i\le p_L,L=max\left\{j:p_j<\frac{\alpha \cdot j}{M}\right\}.}$$

This correction with Benjamini–Hochberg procedure has the property FDR ≤ α.⁴⁸

3. RESULTS

For each patient, three 2D ROIs (from slices of maximum area in axial, coronal, and sagittal planes, respectively) were used for feature extraction. For each tumor ROI, we obtained 48 SFTA features, 44 RLM features, 576 HOG features, 256 LBP features, and 52 Haralick features.

As discussed above, we implemented five binary classification tasks (each subtype vs rest, as well as for 12-month survival status) with RF classifiers. The classification task was performed for each of the four molecular subtypes and for 12-month survival status using each of the five texture descriptors. Table I summarizes the AUC values of the five texture descriptors for all four subtypes and for 12-month survival status, with both postcontrast T1-weighted and T2-weighted FLAIR modalities across three different anatomic planes (axial, sagittal, and coronal). The lower and upper bounds of 95% confidence intervals (CIs) as well as the p-value of the AUC are also noted in Table I. For example, the result in the fifth entry in the first column of Table I refers to the performance of Haralick features derived from the axial slice of the postcontrast T1 weighted image to predict the classical subtype. The first number 0.72 refers to the AUC, and the numbers in the parentheses (0.59, 0.82) refer to the lower and upper limits of a 95% CI. The last number 0.00 refers to the p-value of the AUC and the asterisk marked on the p-value indicates that the AUC was statistically significant after correction for multiple testing (Benjamini and Hochberg with α < 0.05).

TABLE I.

AUC for evaluating the performance of classifiers for each of the four glioblastoma subtypes as well as 12-month survival status using five texture feature sets. In each cell, the four numbers are organized as “AUC value (95% confidence limits), p-value.” Each column corresponds to the performance of applying different texture feature sets on different scan modalities and anatomic planes. Abbreviations: T1 post, postcontrast T1-weighted image; T2 FLAIR, T2-weighted fluid-attenuated inversion recovery image; SFTA, segmentation-based fractal texture analysis; HOG, histogram of oriented gradients; RLM, run-length matrix; LBP, local binary patterns; and HARA, Haralick texture features.

	Classical	Mesenchymal	Neural	Proneural	12-month survival status
T1 post axial
SFTA	0.56 (0.43, 0.73), 0.20	0.54 (0.41, 0.67), 0.30	0.60 (0.41, 0.75), 0.14	0.67 (0.52, 0.78), 0.01	0.64 (0.51, 0.76), 0.02
HOG	0.56 (0.40, 0.68), 0.22	0.55 (0.43, 0.70), 0.21	0.61 (0.44, 0.79), 0.12	0.52 (0.36, 0.65), 0.42	0.62 (0.50, 0.78), 0.04
RLM	0.71 (0.57, 0.81), 0.00a	0.57 (0.44, 0.71), 0.14	0.65 (0.46, 0.79), 0.05	0.55 (0.40, 0.70), 0.25	0.62 (0.49, 0.74), 0.04
LBP	0.60 (0.45, 0.74), 0.08	0.58 (0.43, 0.71), 0.11	0.73 (0.56, 0.86), 0.01	0.74 (0.61, 0.84), 0.00a	0.64 (0.51, 0.77), 0.02
HARA	0.72 (0.59, 0.82), 0.00a	0.63 (0.50, 0.74), 0.03	0.67 (0.49, 0.81), 0.03	0.50 (0.31, 0.62), 0.50	0.51 (0.37, 0.63), 0.45
T1 post sagittal
SFTA	0.59 (0.43, 0.70), 0.12	0.58 (0.42, 0.68), 0.13	0.67 (0.49, 0.81), 0.03	0.78 (0.68, 0.86), 0.00a	0.57 (0.44, 0.70), 0.14
HOG	0.62 (0.48, 0.76), 0.06	0.54 (0.39, 0.66), 0.28	0.50 (0.29, 0.66), 0.50	0.65 (0.50, 0.77), 0.03	0.61 (0.48, 0.72), 0.04
RLM	0.66 (0.52, 0.79), 0.02	0.55 (0.40, 0.67), 0.24	0.74 (0.58, 0.84), 0.00a	0.62 (0.48, 0.75), 0.05	0.45 (0.34, 0.59), 0.24
LBP	0.60 (0.44, 0.72), 0.09	0.51 (0.37, 0.64), 0.45	0.50 (0.29, 0.65), 0.49	0.62 (0.47, 0.77), 0.05	0.64 (0.52, 0.75), 0.01
HARA	0.64 (0.50, 0.75), 0.03	0.52 (0.38, 0.64), 0.38	0.61 (0.43, 0.76), 0.12	0.52 (0.37, 0.67), 0.40	0.50 (0.37, 0.62), 0.49
T1 post coronal
SFTA	0.53 (0.37, 0.65), 0.32	0.49 (0.35, 0.62), 0.44	0.66 (0.47, 0.82), 0.04	0.82 (0.69, 0.90), 0.00a	0.69 (0.56, 0.79), 0.00a
HOG	0.71 (0.57, 0.83), 0.00a	0.53 (0.40, 0.66), 0.31	0.51 (0.33, 0.69), 0.46	0.54 (0.37, 0.67), 0.32	0.61 (0.48, 0.72), 0.05
RLM	0.67 (0.53, 0.77), 0.01	0.47 (0.33, 0.60), 0.32	0.65 (0.46, 0.77), 0.05	0.63 (0.47, 0.74), 0.04	0.61 (0.49, 0.74), 0.04
LBP	0.51 (0.37, 0.66), 0.44	0.51 (0.34, 0.62), 0.43	0.57 (0.41, 0.77), 0.21	0.49 (0.35, 0.64), 0.44	0.60 (0.47, 0.72), 0.06
HARA	0.61 (0.46, 0.73), 0.07	0.64 (0.51, 0.75), 0.02	0.61 (0.48, 0.73), 0.05	0.65 (0.51, 0.77), 0.01	0.50 (0.36, 0.61), 0.48
T2 FLAIR axial
SFTA	0.57 (0.44, 0.76), 0.19	0.53 (0.41, 0.69), 0.34	0.74 (0.57, 0.88), 0.00a	0.61 (0.47, 0.75), 0.07	0.55 (0.41, 0.67), 0.24
HOG	0.61 (0.47, 0.77), 0.06	0.70 (0.56, 0.80), 0.00a	0.69 (0.52, 0.80), 0.02	0.48 (0.36, 0.65), 0.42	0.53 (0.41, 0.66), 0.32
RLM	0.59 (0.43, 0.73), 0.13	0.66 (0.52, 0.77), 0.01	0.75 (0.54, 0.88), 0.00a	0.42 (0.29, 0.57), 0.13	0.47 (0.36, 0.61), 0.34
LBP	0.60 (0.46, 0.75), 0.09	0.52 (0.38, 0.65), 0.37	0.66 (0.49, 0.82), 0.04	0.48 (0.33, 0.63), 0.40	0.51 (0.40, 0.65), 0.42
HARA	0.65 (0.51, 0.79), 0.02	0.57 (0.44, 0.69), 0.15	0.72 (0.58, 0.84), 0.01	0.61 (0.46, 0.75), 0.07	0.62 (0.48, 0.73), 0.04
T2 FLAIR sagittal
SFTA	0.65 (0.50, 0.78), 0.02	0.51 (0.37, 0.64), 0.43	0.70 (0.52, 0.86), 0.02	0.58 (0.42, 0.72), 0.15	0.55 (0.43, 0.69), 0.22
HOG	0.64 (0.50, 0.77), 0.03	0.55 (0.43, 0.70), 0.21	0.61 (0.42, 0.75), 0.12	0.53 (0.36, 0.66), 0.33	0.67 (0.54, 0.76), 0.01
RLM	0.56 (0.40, 0.68), 0.22	0.62 (0.48, 0.71), 0.04	0.65 (0.49, 0.84), 0.05	0.56 (0.42, 0.71), 0.21	0.59 (0.44, 0.71), 0.09
LBP	0.50 (0.32, 0.62), 0.50	0.65 (0.52, 0.75), 0.01	0.54 (0.34, 0.69), 0.34	0.57 (0.44, 0.77), 0.17	0.58 (0.43, 0.68), 0.13
HARA	0.64 (0.49, 0.80), 0.03	0.48 (0.32, 0.58), 0.40	0.72 (0.56, 0.85), 0.01	0.64 (0.50, 0.78), 0.03	0.57 (0.44, 0.70), 0.16
T2 FLAIR coronal
SFTA	0.57 (0.43, 0.73), 0.17	0.51 (0.39, 0.66), 0.43	0.69 (0.51, 0.87), 0.02	0.60 (0.45, 0.72), 0.10	0.64 (0.51, 0.73), 0.02
HOG	0.48 (0.35, 0.64), 0.39	0.61 (0.47, 0.72), 0.06	0.62 (0.44, 0.76), 0.09	0.54 (0.38, 0.67), 0.30	0.59 (0.46, 0.72), 0.09
RLM	0.53 (0.37, 0.66), 0.33	0.58 (0.46, 0.71), 0.11	0.75 (0.56, 0.89), 0.00a	0.62 (0.47, 0.75), 0.06	0.51 (0.39, 0.66), 0.43
LBP	0.63 (0.48, 0.77), 0.04	0.48 (0.38, 0.64), 0.39	0.54 (0.37, 0.74), 0.33	0.57 (0.41, 0.70), 0.17	0.48 (0.34, 0.61), 0.40
HARA	0.49 (0.40, 0.71), 0.46	0.63 (0.50, 0.75), 0.03	0.74 (0.56, 0.81), 0.01	0.58 (0.41, 0.69), 0.14	0.58 (0.46, 0.70), 0.11

^aSignificance after BH correction with α = 0.05. The p-values for the four subtypes are corrected together.

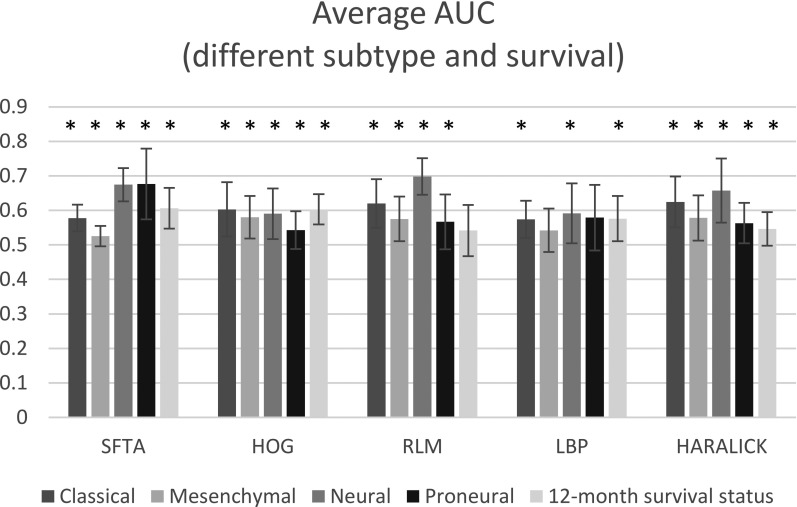
Figure 7 shows the average AUC for different subtypes as well as for 12-month survival status based on different feature sets. Each average AUC is the arithmetic mean of six AUCs (three image planes and two MRI sequences). The “*” on top of each average AUC indicates that the AUC is significant higher than 0.5 under a Mann–Whitney U test. By comparing the height of the bars of the same color, we see that the classical subtype was best predicted by Haralick features (average AUC = 0.62 ± 0.07); the mesenchymal subtype was best predicted by HOG (average AUC = 0.58 ± 0.06); the neural subtype was best predicted by RLM (average AUC = 0.70 ± 0.05); and the proneural subtype was best predicted by SFTA (average AUC = 0.68 ± 0.10).

FIG. 7.

Performance of five texture feature descriptors in classifying different subtypes of glioblastoma. The AUCs are averaged over both modalities (postcontrast T1-weighted and T2-weighted fluid-attenuated inversion recovery) and all anatomic planes (axial, sagittal, and coronal). The * sign on each bar indicates that the average AUC for that feature set is significantly higher than random classification (AUC = 0.5). Abbreviations: SFTA, segmentation-based fractal texture analysis; HOG, histogram of oriented gradients; RLM, run-length matrix; LBP, local binary patterns; and HARALICK, Haralick texture features.

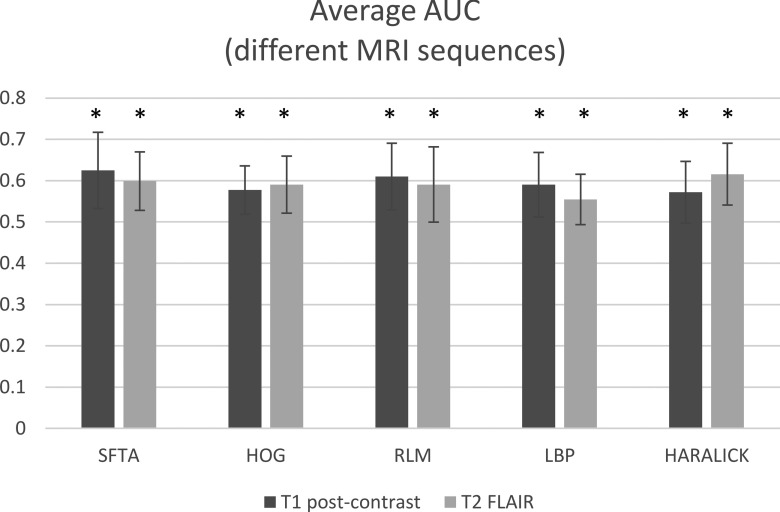
Figure 8 shows how different MRI sequences affect performance in classifying GBM subtypes. For this comparison, the average AUC is taken over three different image planes and the five different classification tasks. For classification with postcontrast T1-weighted images, SFTA features performed the best (average AUC = 0.63 ± 0.09); for classification with T2-weighted FLAIR images, Haralick features performed the best (average AUC = 0.62 ± 0.07).

FIG. 8.

Performance of classifiers for predicting glioblastoma subtypes using five feature descriptors extracted from scans of two magnetic resonance imaging modalities: postcontrast T1-weighted (T1-post-Gd) and T2-weighted FLAIR. The AUCs are averaged over all subtypes and anatomic planes (axial, sagittal, and coronal). Abbreviations: SFTA, segmentation-based fractal texture analysis; HOG, histogram of oriented gradients; RLM, run-length matrix; LBP, local binary patterns; and HARALICK, Haralick texture features. The * sign on each bar indicates that the average AUC for that feature set is significantly higher than random classification (AUC = 0.5).

Figure 9 shows the performance of classifiers predicting GBM subtypes using different features on images of different planes. The average AUC is the mean of 10 AUCs (two MRI sequences and five classification tasks). Haralick features give the best performance with axial scans (average AUC = 0.62 ± 0.08); SFTA features give best performance with sagittal (average AUC = 0.61 ± 0.08) and coronal scans (average AUC = 0.62 ± 0.09).

FIG. 9.

Performance of classifiers predicting glioblastoma subtypes using five texture feature descriptors extracted from scans of different image planes. The AUCs are averaged over all subtypes and both modalities (postcontrast T2-weighted and T1-weighted fluid-attenuated inversion recovery magnetic resonance imaging scans). The * sign on each bar indicates that the average AUC for that feature set if significantly higher than random classification (AUC = 0.5). Abbreviations: SFTA, segmentation-based fractal texture analysis; HOG, histogram of oriented gradients; RLM, run-length matrix; LBP, local binary patterns; and HARALICK, Haralick texture features.

4. DISCUSSION

Texture features are capable of characterizing gray-level heterogeneity in the images. As a first attempt to understand what specific aspects of gray-level tumor heterogeneity in MRI scans are relevant to GBM molecular subtype, we evaluated five texture feature types for their ability to discriminate molecular subtype and 12-month OS status. Our results show that tumor derived texture features were predictive of 12-month survival status and molecular subtypes. With the appropriate combination of texture feature set, image plane (axial, coronal, or sagittal) and MRI sequence, the AUC values for predicting different molecular subtypes and 12-month survival status are 0.72 for classical (with Haralick features on T1 postcontrast axial scan), 0.70 for mesenchymal (with HOG features on T2 FLAIR axial scan), 0.75 for neural (with RLM features on T2 FLAIR axial scan), 0.82 for proneural (with SFTA features on T1 postcontrast coronal scan), and 0.69 for 12-month survival status (with SFTA features on T1 postcontrast coronal scan). No single image feature type gave the universally best performance in discriminating all four molecular subtypes or for predicting 12-month survival status, suggesting that different feature characteristics are relevant to different prediction tasks. Specific investigation into the biological correlates of such predictive texture features (within contrast enhancing or nonenhancing, infiltrating regions of the tumor) could yield insights into the underlying tumor biology and is a subject of future study. Such investigation is now feasible given the availability of companion genomics and proteomics data underlying large-scale efforts such as TCGA.

4.A. Performance in predicting 12-month survival status

The last column of Table I presents the performance for predicting 12-month survival status under different combinations of image features, sequences, and image planes (axial, coronal, or sagittal). The best predictive combination was SFTA features on coronal postcontrast T1-weighted images, with an AUC of 0.69. HOG features also performed well (AUC 0.67) on sagittal T2 FLAIR images.

One of the main reasons for relatively low AUC on survival prediction task is likely that tumor volume (which is related to survival) may not be adequately described by image texture features. Thus, in the clinical context, a combination of volumetric and texture features might be better suited for prediction of survival status.

4.B. Performance in predicting molecular subtypes

Overall, SFTA gave the best performance in terms of AUC averaged across all four molecular subtypes, two imaging modalities, and three image-planes. The average AUC was 0.61. SFTA is especially good in discriminating proneural cases with postcontrast T1-weighted images in coronal and sagittal plane, with AUCs of 0.78 and 0.82, respectively.

For postcontrast T1-weighted and T2-weighted FLAIR scans of GBM, the variation in intensities within the tumor suggests different tumor subcompartments (for example, necrosis has lower intensities in postcontrast T1-weighted images and edema has higher intensities in T2-weighted FLAIR image). Thus, the binary maps generated by the thresholding step in SFTA are likely to capture the boundaries between different tumor compartments. By computing the fractal dimension, SFTA can describe the complexity of the boundaries, which may be related to subtype status.

The other texture descriptors have different advantages. HOG is the only descriptor that effectively could predict the mesenchymal subtype (on an axial T2-weighted FLAIR scan). As with most descriptors that are based on gradient, HOG emphasizes the object’s overall shape in addition to the texture features. Haralick texture features had the best performance in predicting the classical subtype, with an average AUC of 0.62. LBP was able to discriminate the neural and proneural subtypes in axial T1-weighted contrast, which makes LBP useful when only axial postcontrast T1-weighted scans are available. These results indicate that combining different texture features might have predictive value for noninvasive characterization of molecular status.

Most texture features performed well in classifying the neural subtype, with an average AUC of 0.64. However, the texture descriptors perform relatively poorly (average AUC 0.56) for discriminating the mesenchymal subtype.

Our results also suggest that image features derived from nonaxial scans (coronal and sagittal) have predictive value for molecular characterization. Figure 4 shows that when predicting subtypes, SFTA is better with sagittal scans (average AUC = 0.63) and coronal scans (average AUC = 0.61) than with axial scans (average AUC = 0.60). Though these differences are not appreciable and likely due to random variation, a deeper examination of the systematic differences in performance due to different image planes is essential to validate these findings. This variation in predictive value with image plane also suggests an investigation of 3D tumor texture features for these prediction tasks and their value relative to 2D texture features alone. The comparison of 2D vs 3D texture features is also necessary to assess and quantify the trade-off between computation efficiency and loss of information between 2D and 3D image texture characterizations.

Although SFTA features were mostly predictive regardless of the orientation of the slice (coronal, sagittal, or axial), the average AUCs of the LBP and Haralick features from the sagittal and coronal scans were substantially lower than the AUC from the axial scan. The lower AUCs from the nonaxial planes are likely an artifact of the redundancy introduced (from the interpolation procedure) during the reslicing process. The computation of Haralick and LBP features both involves a step that compares each pixel’s gray level with those of its immediate neighbors. This step can capture subtle intensity variations in the axial scan but is confounded by information loss in the sagittal and coronal planes, thereby explaining the low AUCs. These results suggest that a systematic evaluation of these feature sets in a controlled validation cohort (with isotropic pixel resolution) is required to appropriately characterize the predictive value of texture features across different image planes.

Clinical utility requires the classifiers to have strong sensitivity and specificity characteristics. Therefore, in addition to the AUCs in Table I, the sensitivity, specificity, accuracy, and precision of the classifiers are listed in the supplementary material of Table S1 (Ref. 31) as a complementary measure of the classifier performance. For consistency, all the numbers in the supplementary material of Table S1 (Ref. 31) are assessed at the point with the maximum sum of sensitivity and specificity along the ROC curve. However, the most practical sensitivity–specificity combination should be determined by the specific performance criteria. These measures demonstrate how the classifier trade-off between sensitivity and specificity, while the AUCs characterize the classifier’s overall performance.

We also note that other factors, such as MR hardware (coil pattern) and scanning parameters (TE, TR, etc.), will also have a direct impact on the image intensity histogram. A future texture analysis study controlling these factors will lead to potential ways of improving prediction performance.

Finally, some of these texture features can be computed on irregularly shaped ROIs (although these modifications may not be trivial) instead of the current rectangular ROIs. The classification performance with features from irregularly shaped ROIs needs further investigation. It also remains to be determined how the variation in inter-rater tumor segmentation affects the prediction performance of texture features. A detailed study that examines this variation across multiple human segmentations is another essential next step.

4.C. Conclusion

In this paper, we evaluated the performance of different texture features for predicting GBM molecular subtypes and 12-month survival status. The results show that several texture feature types were predictive of survival and molecular subtypes. We find that Haralick features on the T1-postcontrast axial scan are most predictive of classical subtype, HOG features on the T2-FLAIR axial scan are most predictive for mesenchymal subtype, RLM features on the T2-FLAIR axial scan are most predictive for neural subtype, and SFTA features on the T1-postcontrast coronal scan are most predictive for proneural subtype and 12-month survival status. Our results suggest that different combinations of image features, MR sequence, and image plane are predictive for different tasks. Further, we observe that nonaxial scans are potentially useful for classification of GBM molecular subtype and survival status, but this needs to be validated in a controlled cohort. This study is intended to be a baseline characterization on the limits of prediction power of 2D texture features. 3D feature extraction is an opportunity for future investigation.