Abstract
Purpose:
T2-weighted magnetic resonance imaging (MRI) is commonly used for anatomical visualization in the pelvis area, such as the prostate, with high soft-tissue contrast. MRI can also provide functional information such as diffusion-weighted imaging (DWI) which depicts the molecular diffusion processes in biological tissues. The combination of anatomical and functional imaging techniques is widely used in oncology, e.g., for prostate cancer diagnosis and staging. However, acquisition-specific distortions as well as physiological motion lead to misalignments between T2 and DWI and consequently to a reduced diagnostic value. Image registration algorithms are commonly employed to correct for such misalignment.
Methods:
The authors compare the performance of five state-of-the-art nonrigid image registration techniques for accurate image fusion of DWI with T2.
Results:
Image data of 20 prostate patients with cancerous lesions or cysts were acquired. All registration algorithms were validated using intensity-based as well as landmark-based techniques.
Conclusions:
The authors’ results show that the “fast elastic image registration” provides most accurate results with a target registration error of 1.07 ± 0.41 mm at minimum execution times of 11 ± 1 s.
Keywords: non-rigid image registration, diffusion imaging, prostate
1. INTRODUCTION
Prostate cancer is the most common tumor, and the second most common cause of cancer related death in American men.1 Magnetic resonance imaging (MRI) is currently regarded as the best, noninvasive modality for localization and staging of prostate cancer due to its superior soft-tissue contrast and high resolution.2
However, the T2-weighted imaging alone is reported to have a wide range of sensitivity and specificity of 22%–85% and 50%–99%, respectively.3,4 Consequently, additional MR techniques have been explored to improve the localization and characterization of prostate cancer. Diffusion-weighted imaging (DWI) has shown great benefits in clinical MR exams because it can visualize the molecular diffusion process of water and hence can provide additional information about the tissue structure on a cellular level.
In most clinical applications, the diffusion process can be modeled by an exponential decay over a series of images acquired at different diffusion gradient strengths/durations, so-called b-values.5 With a negligible contribution of pseudodiffusion, the exponential decay can be modeled by
| (1) |
where S0 is the signal intensity at b-value equal to zero, i.e., without diffusion gradient, Sb is the signal intensity at b-value b, D is the diffusion coefficient, f is the perfusion fraction, and K is the diffusion kurtosis. Applying the natural logarithm to both sides of Eq. (1) and assuming that b2D2K/6 < < bD (see Ref. 5 for details) results in
| (2) |
The linear Eq. (2) can be used to approximate the unknown variables f and D in the least squared sense. With the above assumption b2D2K/6 < < bD, D is called the apparent diffusion coefficient (ADC). In practice, Eq. (2) is applied to each image voxel over varying b-values to produce an ADC map where each voxel is encoded with the estimated diffusion coefficient.
Diffusion images are commonly overlaid onto or fused with a T2 anatomical reference image so that functional information from DWI can be correlated to the corresponding anatomical information derived from T2. However, accurate alignment of DWI and T2 images is hindered by the following two problems. First, physiological motion might lead to misalignments within the DWI series (inner-DWI distortions), so that the exponential fit as described in Eq. (1) is distorted. Second, physiological motion as well as B0-inhomogeneity induced image distortions caused by echo-planar image (EPI) acquisitions can lead to misalignments between DWI and T2 (DWI to T2 distortions), and accurate fusion of ADC with T2 is hindered.
Intensity-based nonrigid image registration techniques have been developed to estimate and correct for deformations and motion between scans.6–8 These deformations can be estimated using parametric approaches (e.g., spline-based approaches) or using nonparametric approaches that estimate motion on a voxel-wise basis (e.g., optical flow methods). In this paper, we correct the DWI series for inner-series distortions using a simple affine motion correction. While researchers have corrected for EPI-specific distortions resulting from B0 field variations,9 physiological motion between DWI and T2 will always remain. Here, we capture susceptibility induced deformations as well as deformations resulting from physiological motion at once by using nonrigid image registration. We investigate the performance of five different state-of-the-art algorithms (two B-spline approaches, one local affine approach, the Demons algorithm, and an elastic image registration approach) to correct for interseries deformations, i.e., between the registered DWI series and a T2 reference scan. All registration algorithms were validated on 20 diseased patients showing cancerous lesions and cysts within the prostate.
2. METHODS
In Sec. 2.A, the registration strategy to compensate for inner-DWI as well as for DWI to T2 deformation is described. The subsequent Sec. 2.B describes the five registration algorithms that are compared with each other with respect to their registration accuracy.
2.A. Registration strategy
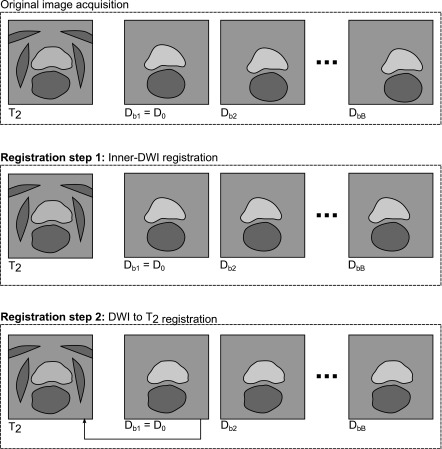
Figure 1 illustrates the registration strategy to align the DWI series with the anatomical reference T2 image. Two steps are performed. Registration step1 compensates for affine inner-series deformations within the DWI series. Registration step 2 compensates for the deformation between DWI and T2 using the nonrigid registration algorithms. Note that the comparison of the five registration techniques is only applied in Registration step 2. Sections 2.A.1 and 2.A.2 describe these two steps in further detail.
FIG. 1.
Overview plot illustrating the applied image registrations to align a DWI series (with b-values bi) with an anatomical reference T2 image. After image acquisition (top), EPI-specific distortions and physiological motion occurs within the DWI series as well as between DWI and T2. The first Registration step 1 compensates for inner-DWI motion and aligns all Db (b > 0) with the reference D0. This is illustrated by a global translation for each Db to the horizontal image center. The subsequent Registration step 2 estimates local nonrigid deformations between D0 and T2. The resulting deformation is applied to all remaining Db (b > 0). This is illustrated by local shape changes of prostate and rectum. In this last registration step, the comparison of five different state-of-the art registration algorithms is performed.
2.A.1. Registration step 1 (inner-DWI registration)
In this step, the first image from the DWI series with b-value b = 0, D0, is selected as reference image. The remaining images from the DWI series might be motion corrupted with respect to D0 by physiological motion. We observed that an affine correction showed robust results even for high b-value images. When applying nonrigid registrations with a large number of degrees of freedom to those images, the signal drop and hence the decrease in structural information leads to unreliable deformations. Consequently, we decided to choose an affine registration algorithm11 to compensate for inner-DWI deformations. All Db (b > 0) are registered to the reference DWI image D0 leading to a new set of inner-series motion compensated DWI images. In the following, this affine registration algorithm will be referred to as areg.
2.A.2. Registration step 2 (DWI to T2 registration)
In this step, D0 is registered to the reference T2 to correct for nonrigid physiological motion as well as EPI-specific distortions between DWI and T2. Since all DWI (b ≠ 0) were aligned with D0 in Registration step 1, the resulting deformation is applied to D0 and all Db (b > 0) to align the complete DWI series with T2. In this nonrigid registration step, the comparison of the five different nonrigid registration algorithms (described in Sec. 2.B) is performed.
2.B. Nonrigid registration algorithms
Image registration is based on deforming a moving or floating image so that its transformation aligns with a nonmoving or reference image , for all voxels in the overlap region of F and R. The resulting deformation field mapping from to is commonly denoted as .
In the following, we give an overview about five different nonrigid registration algorithms that were applied in Registration step 2. Three parametric approaches were considered: a B-spline algorithm with a gradient descent optimizer12 provided by the elastix toolbox,13 a B-spline algorithm with a Levenberg–Marquardt optimizer,14 and a hierarchical local affine registration approach;15 and two nonparametric approaches: the demons deformable registration algorithm16 implemented in the plastimatch toolbox, and the fast elastic image registration approach.10 These algorithms are now described in further detail.
2.B.1. B-spline registration with gradient descent optimizer (bsp)
The B-spline registration algorithm,12 or so-called free-form deformation (FFD) algorithm, estimates soft-tissue deformation on a regular grid of control points defined by the control point spacing c. Deformation between the control points is interpolated via B-splines. Compared to other spline-based approaches such as thin plate splines, B-splines are computationally attractive since each control point only affects its local surroundings, and effective implementation schemes are available.17 The final deformation of a coordinate on the complete image grid is modeled by cubic B-splines
| (3) |
where is a grid coordinate, , and (βl, βm, βn) are the cubic B-spline functions. In the following, this algorithm will be referred to as bsp.
2.B.2. B-spline registration with Levenberg–Marquardt optimizer (breg)
While common B-spline algorithms such as bsp exploit gradient-based optimizers, a Levenberg–Marquardt optimizer has been proposed to reduce the number of iterations of common gradient-based algorithms and consequently to reduce computation time.14 Similar to Eq. (3), the deformation at point is described by cubic B-splines
| (4) |
In the following, this algorithm will be referred to as breg.
2.B.3. Hierarchical local affine registration (lreg)
The hierarchical local affine registration algorithm15 attempts to estimate soft-tissue deformation by subdividing the nonrigid registration problem into multiple more simple locally affine registration problems. To allow an estimation of large and small deformation, a hierarchical subdivision strategy is employed, that successively estimates large to small affine deformations. The estimated affine deformation at a coordinate is initially described as:
| (5) |
where A is a 3 × 3 matrix describing three components for rotation, three for scaling, three for shearing, and is a vector describing three components for translation. For each hierarchical registration level, cubic B-splines are employed to produce a nonrigid deformation as a smooth combination of all affine components. In the following, this algorithm will be referred to as lreg.
2.B.4. Demons deformable registration algorithm (demons)
The demons deformable registration algorithm16 is based on Maxwell’s effectors, so-called demons, that were originally designed for thermodynamics to regulate particle transitions at semipermeable membranes. In image processing, object contours of the floating image F can be seen as such membranes. Demons are located on the object’s surface and regulate boundary attraction between the images F and R, while image intensities are treated as particles being inside or outside of an object. Similar to optical flow methods, the final displacement is modeled as
| (6) |
where is the image gradient (or force) in R that iteratively pushes image intensities of F to the inside or the outside of the corresponding object in R. In the following, this algorithm will be referred to as demons.
2.B.5. Fast elastic image registration (feir)
The elastic registration algorithm10 is based on modeling the deformation between F and R as the one of an elastic material. The algorithm attempts to find the deformation field by minimizing a similarity measure based on normalized gradient fields as well as the contribution of a Navier–Lamé regularizer which is included for motion field regularization. To obtain the final motion field , the following functional needs to be minimized
| (7) |
where μ and λ are the Lamé constants, ▽ is the Nabla operator, 〈⋅, ⋅〉 indicates the scalar product, and and are the orientation-dependent image gradients of and that are included in the similarity measure. In the following, this algorithm will be referred to as feir.
3. EXPERIMENTS
3.A. Materials
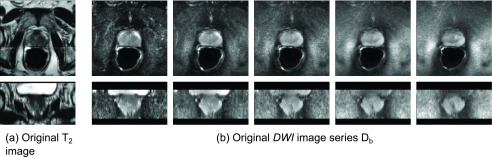
Three-dimensional (3D) image data from 20 patients were acquired on a 3T MRI Scanner (Philips Achieva, Best, The Netherlands) at the National Institutes of Health, Bethesda, MD. As anatomical reference, a T2-weighted turbo-spin echo scan was performed with the following parameters: FOV 140 × 140 × 80 mm, reconstructed voxel size 0.27 × 0.27 × 3 mm, flip angle 90°, TR/TE = 8870/120 ms. For diffusion imaging, a single-shot spin-echo EPI sequence was employed to acquire five diffusion-weighted images with the following parameters: FOV 160 × 180 × 60 mm, stack of 20 image slices with axial orientation, reconstructed voxel size 1.03 × 1.03 × 2.73 mm, flip angle 90°, TR/TE = 4584/59 ms, and the following b-values: 0, 188, 375, 563, and 750 s/mm2. Figures 2(a) and 2(b) give an example of the acquired T2 image and the acquired DWI series (in axial and coronal views) from a single patient, Pat1.
FIG. 2.
Two example 3D acquisitions from a single patient, Pat1. (a) T2-weighted anatomical reference image. (b) Diffusion-weighted image series containing 5 images Db with b-values 0 (left), 188, 375, 563, 750 s/m2 (right). All images are shown in axial (top) and coronal view (bottom).
3.B. Image registrations
Since some of the applied algorithms required an isotropic resolution, all images (all Db and T2) were resampled to an isotropic resolution of 1 mm3, before any registration was executed.
Registration step 1 was executed to correct for inner-DWI motion (using areg). A Gauss–Newton optimizer and cross correlation as similarity measure were employed.
Registration step 2 was executed to correct for motion occurring between DWI and T2. In this step, the performance of the five different registration algorithms (Sec. 2.B) was compared. For this local registration problem, none of the common similarity measures such as sum of squared differences (SSD), normalized cross correlation (NCC), or normalized mutual information (NMI) showed acceptable results due to large differences between DWI and T2 with respect to contrast and structural information. As can be seen in Fig. 2, SSD is not applicable since there is no identity relationship between DWI and T2; NCC is not applicable since there is no linear relationship either; and even NMI did not provide good results since the dark homogeneous background surrounding the prostate in DWI is mapped to multiple intensities in T2 due to large structural differences in that region. However, our experiments showed that these measures were applicable when registering the corresponding gradient images (to align tissue boundaries with each other). feir already includes a gradient-based similarity measure. For the other four nonrigid registration algorithms, the Sobel-based gradient images of D0 and T2, and , were used for registration, and the resulting motion fields were applied to the original images to align D0 with T2.
For speedup purposes, a multiresolution approach was employed using three resolution stages, from 4 × 4 × 4 mm (resolution level 2) over 2 × 2 × 2 mm (resolution level 1) to 1 × 1 × 1 mm (resolution level 0). In other words, all registration algorithms estimated the final deformation on the resampled 1 mm image resolution of resolution level 0.
All algorithms were available as CPU-based implementations (i.e., no implementations on graphic cards), and all registrations were run on a 12-core workstation, Intel(R) Xeon(R) CPUs at 2.5 GHz, 97 GB RAM memory. Since some algorithms supported multithreading executions while others did not, the single-threaded execution time as the sum of all CPU times was considered as overall execution time to allow a valid comparison.
For most optimal parameter selection, image registration experts were recruited to tune the parameters of all five algorithms. In the following, algorithm-specific parameters are given for all approaches.
3.B.1. B-spline registration with gradient descent optimizer (bsp)
For bsp, NCC was used as similarity measure. Similar to the multi-image resolution approach, a multi B-spline grid approach with three grid levels was employed. Initial deformation was estimated at grid level 2 with control point spacings of 12 mm. The following grid levels 1 and 0 with 6 and 3 mm spacing, respectively, were used to refine the estimated deformation.
3.B.2. B-spline registration with Levenberg–Marquardt optimizer (breg)
For breg, NCC was used as similarity measure. Similar to bsp, three grid levels with 12, 6, and 3 mm control point spacing were employed.
3.B.3. Hierarchical local affine registration (lreg)
For lreg, NCC was used as similarity measure. Global rigid block transformations (showing more robust results than affine transformations) and regular block splittings were employed. A minimum block size was set to 5 mm.
3.B.4. Demons deformable registration algorithm (demons)
For demons, mean squared error (MSE) was used as similarity measure. The plastimatch implementation was used, with 300 iterations for all resolution levels.
3.B.5. Fast elastic image registration (feir)
For feir, orientation-dependent normalized gradient was used as similarity measure [see Eq. (7)]. The Lamé constants λ = 0 and μ = 0.25 were empirically chosen to model the elastic properties, and an abort criterion of 0.05 mm maximum displacement update was used.
3.C. Validation
The performance analysis of our applied registrations was analyzed according to our two registration steps (Sec. 2.A). To allow accurate validation of the applied algorithms, two MR experts were recruited. These experts manually defined a set of L = 10 anatomically significant landmarks that were visible in both the T2 image and in the reference DWI image, D0. First the landmarks were identified in T2. Second, the corresponding landmarks at the same anatomical position were selected in D0. Note that landmark selection in higher b-valued image was not possible due to poor image contrast. These landmarks were located around anatomically significant points, such as
-
•
entry point of the urethra into the prostate,
-
•
entry point of the ejaculatory duct into the prostate,
-
•
interface to the neurovascular bundle,
-
•
boundary of prostate,
-
•
basal and apical cysts,
-
•
center point of small lesions,
-
•
midgland peripheral zone.
The selected landmarks were used for the validation of Registration step 1 and Registration step 2, as described in Secs. 3.C.1 and 3.C.2.
3.C.1. Validation step 1 (inner-DWI registration)
In the first validation step, we analyzed the affine registration performance of Registration step 1, i.e., how well the DWI images align with each other (Fig. 3). Note that this validation is included to assess the performance of the overall procedure for ADC map generation but is independent of our registration comparison. As a measure of registration accuracy, we used the following two methods.
FIG. 3.
Validation step 1 (inner-DWI registration). (a) As an intensity-based measure for image alignment, the normalized cross correlation between the reference D0 and the transformation of the image with the highest b-value within a ROI was considered. (b) As a quality measure of the exponential signal decay, the exponential fit error EFE(DWI) over all landmarks, i.e., the mean deviation of the image intensities of all at (indicated as filled dots) to the exponential fit function , was considered. Note that according to Sec. 1, the image D0 is excluded from the fitting process.
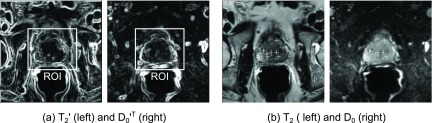
The first method [Fig. 3(a)] computes the intensity-based alignment between the first D0 and the transformed image from the last image D750 where the largest distortion is expected. NCC within a manually defined region of interest (ROI) as the bounding box around the prostate was computed,
| (8) |
where N is the number of voxels in ROI, mD0 and are the mean values, and σD0 and are the standard deviations of D0 and , respectively.
The second method [Fig. 3(b)] measures deviations of the DWI image intensities at the selected landmark positions from their exponential fit function [see Eq. (1)]. In other words, we measured how well an exponential function can be fitted to the acquired DWI images containing B images Db. We computed the exponential fit error (EFE) as follows:
| (9) |
where is a landmark coordinate from the set of L = 10 selected landmarks and is the exponential function that was fitted to the images (that align with D0 after registration) at coordinate . Note that according to Eq. (1), the fitting process is only applied to b-values greater than zero, hence the normalization to B − 1.
3.C.2. Validation step 2 (DWI to T2 registration)
In this validation step, we analyzed the output of Registration step 2, i.e., how well the DWI series (after the previous inner-DWI registration) aligns with the reference T2 image (Fig. 4) and includes the performance comparison of the five different nonrigid registration algorithms. As a measure of registration accuracy, we used the following two methods.
FIG. 4.
Validation step 2 (DWI to T2 registration). (a) As an intensity-based measure, the normalized cross correlation between the absolute gradient images and the transformation of , was computed to estimate how well the image edges of T2 align with those in . (b) As a measure of real anatomical motion, we computed the target registration error over a set of landmarks that were manually selected in T2 and in D0 and located in based on the estimated motion fields.
The first method [Fig. 4(a)] computes the intensity-based alignment between D0 and T2. Similar to the metric selection in Sec. 3.C.1, we computed the normalized cross correlation of the image gradients of DWI0 and T2 within the same ROI as used in Validation step 1. We estimated how well the edges of D0 align with the edges of T2,
| (10) |
where is the absolute Sobel-based gradient image of T2, is the transformation (i.e., the result after registration) of , and are the mean values, and and are the standard deviations of and , respectively.
While NCC has to be treated with care because its intensity-based nature only gives an indication of registration accuracy, the second method [Fig. 4(b)] measures the accuracy of real anatomical motion. Based on the landmarks defined in T2 and those defined in D0, the target registration error (TRE) was computed describing the mean distance between those points,18
| (11) |
where is a selected landmark in T2 and is the corresponding one in D0 being transformed to the image space of T2.
4. RESULTS
4.A. Image registrations
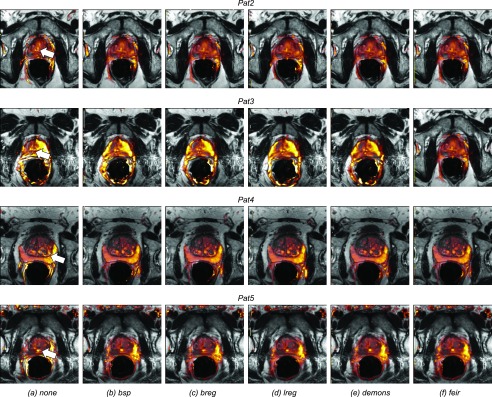
Figure 5 shows an example of image registrations applied to the images from Pat1. The reference T2 image is shown on the left again. In Fig. 5(a), the first Registration step 1 (inner-DWI registration) was applied. The DWI images Db with b-values 0 (left), 188, 375, 563, and 750 s/m2 (right) are shown after affine motion correction to the reference image D0 using areg. Figures 5(b)–5(f) show the results of Registration step 2 (nonrigid DWI to T2 registration) using the five different registration algorithms (bsp, breg, lreg, demons, feir). The resulting DWI images should now align with T2 as accurate as possible. From the motion corrected DWI series, ADC maps were computed using Eq. (1) and overlaid onto the anatomical T2 reference image. Figure 6(a) shows such ADC maps fused with T2 (before registration) from another four patients (Pat2 to Pat5). As can be observed, the generated and uncorrected ADC maps do not align with T2 accurately, e.g., for the bright cysts from Pat2 and Pat3, the boundary between central and peripheral zone from Pat4, or the urethra from Pat5 (all indicated as white arrows). For comparison, Figs. 6(b)–6(e) show the motion compensated ADC maps which were generated after applying areg and the five different registration algorithms. As can be observed, image alignment between the ADC maps and the reference T2 images is clearly improved for all registration algorithms.
FIG. 5.
Registration steps for inner-DWI and DWI to T2 registration from the same patient as in Fig. 2. (a) Registration step 1 (inner-DWI registration). (b)–(f) Registration step 2 (DWI to T2 local nonrigid motion correction). White arrows in all D0 point to deformations with respect to the original diffusion image D0 in (a).
FIG. 6.
ADC maps from another four patients, Pat2 to Pat5. (a) Zoom onto the prostate in the T2 reference image overlaid by the ADC maps before any image registration. Image alignment between ADC and T2 is not optimal, as can be observed at the bright cysts from Pat2 and Pat3, the boundary between central and peripheral zones from Pat4, or the urethra from Pat5 (all indicated as white arrows). (b)–(f) Zoom onto the T2 prostate now overlaid by the motion-compensated ADC maps using bsp, breg, lreg, demons, and feir. Visual inspection shows that feir successfully aligned all ADC maps with T2.
4.B. Validation
4.B.1. Validation step 1 (inner-DWI registration)
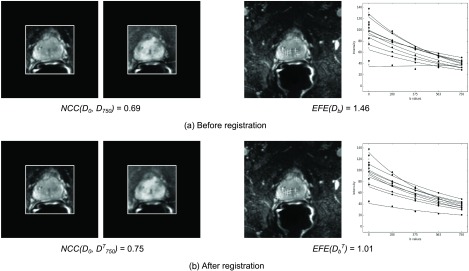
Figure 7 shows the result of the inner-DWI registration for Pat6. Figure 7(a) shows exemplary images being used for our validation method before any registration was performed, i.e., using the originally acquired image data. For this patient, a normalized cross correlation between the first and last DWI image NCC(D0, D750) = 0.69 within a region of interest around the prostate was computed [Fig. 7(a), left]. Figure 7(a), right shows the exponential fit functions that were fitted to the signal decay over the DWI series (one for each landmark). As can be seen in the example of the bottom curve, an exponential fit was not always optimal and physically not plausible, leading to a large exponential fit error EFE(Db) = 1.46 over the images Db of the DWI series. For comparison, Fig. 7(b) shows the results after applying areg. The correlation between the first image and the transformation of the last image was improved to . Similarly, the motion compensated images were more suitable to model the exponential signal decay over the DWI series [as can be observed in the bottom curve in Fig. 7(b), right], and the exponential fit error was reduced to EFE(Db) = 1.01. Considering all 20 patients, areg achieved similar improvements, from NCC(D0, D750) = 0.68 to and a reduction in the exponential fit error from EFE(D0, D750) = 1.46 to , which is an improvement of 7% and 15%, respectively.
FIG. 7.
Validation step 1 (inner-DWI registration), images from Pat6 showing representative results with respect to all patients. (a) Before inner-DWI registration, the normalized cross correlation NCC(D0, D750) = 0.69 between D0 and the last image with the highest b-value, D750, within a ROI around the prostate was computed. As second measure, the exponential fit error EFE(Db) = 1.46 at the landmark locations (projected onto the axial view and indicated as crosses) and over the complete series were computed. As can be seen on the right, an exponential fit over all Db from this patient (one curve for each landmark) was not always optimal due to motion in between the DWI images (e.g., the bottom curve). (b) After registration using areg, a NCC between D0 and the transformation of D750, was improved to . Similarly, the motion-compensated DWI images were more suitable for an exponential fit (e.g., the bottom curve again), and a reduced error of was achieved.
4.B.2. Validation step 2 (DWI to T2 registration)
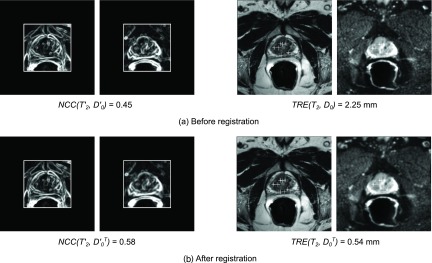
Figure 8 shows the images from another patient, Pat7, to validate our DWI to T2 registration algorithms. Figure 8(a), left shows the original gradient images and from the same patient, i.e., before applying any registration. These images were used to compute a normalized cross correlation of . Figure 8(a), right shows the selected landmarks in T2 and D0. Note that the selected landmarks are projected onto the axial view. Based on these landmarks, a registration error as the misalignment between the landmarks in T2 and those in D0 was computed: TRE(T2, D0) = 2.25 mm. For comparison, Fig. 8(b) shows the reference T2 and the transformation of D0, , using feir as registration example. The correlation after registration, i.e., between T2 and was improved to . Similarly, the target registration error between the landmarks in T2 and those in the transformed image was reduced to mm.
FIG. 8.
Validation step 2 (DWI to T2 registration), images from Pat7 showing representative results with respect to all patients. (a) Before DWI to T2 registration, we measured how well the image edges aligned with each other and computed a normalized cross correlation between the absolute gradient images and of D0 and T2 within a rectangular ROI around the prostate. Our second measure was based on the landmarks that were selected in T2 and D0 (overlaid as projections onto the axial plane), and we computed a target registration error of TRE(T2, D0) = 2.25 mm. (b) After registration (here using feir as example algorithm), image alignment between T2 and the transformation of D0, , was achieved, with a and a mm.
The results for all patients are given in Table I (mean ± standard deviation as well as the minimum/maximum range). As can be observed, the B-spline approaches show highest registration errors with and mm, respectively. Registration accuracy was improved by the local affine approach [ and mm] and by the Demons approach [ and mm]. While the fast elastic registration approach feir showed a smaller intensity-based than demons (note that NCC has to be treated with care because of its pure intensity-based nature), feir provided the most accurate results with respect to real anatomical motion, with mm. Considering the computation times, feir was clearly the fastest algorithm as well with 11 s mean execution time, while bsp was the slowest one with 216 s mean execution time.
TABLE I.
Comparing registration algorithms in Validation step 2 (DWI to T2 registration) from the results of all 20 patients. Values for mean and standard deviation are given, as well as the minimum and maximum values.
| NCC | TRE (mm) | Duration (s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Description | Algorithm | Mean ± std | Min | Max | Mean ± std | Min | Max | Mean ± std | Min | Max |
| none | 0.36 ± 0.07 | 0.22 | 0.47 | 2.21 ± 1.00 | 1.12 | 4.77 | — | — | — | |
| Nonrigid registrations | ||||||||||
| bsp | 0.12 ± 0.10 | 0.01 | 0.41 | 1.88 ± 0.73 | 0.97 | 3.97 | 216 ± 5.4 | 208 | 225 | |
| breg | 0.39 ± 0.09 | 0.22 | 0.53 | 2.05 ± 1.05 | 0.83 | 4.77 | 105 ± 13.8 | 70 | 130 | |
| lreg | 0.52 ± 0.07 | 0.41 | 0.67 | 1.47 ± 0.53 | 0.70 | 2.87 | 125 ± 17 | 92 | 165 | |
| demons | 0.64 ± 0.09 | 0.41 | 0.76 | 1.53 ± 0.97 | 0.65 | 3.86 | 36 ± 1 | 35 | 37 | |
| feir | 0.52 ± 0.08 | 0.36 | 0.67 | 1.07 ± 0.41 | 0.40 | 2.03 | 11 ± 1 | 9 | 13 | |
5. DISCUSSION
This paper compared the performance of five state-of-the-art nonrigid registration algorithms for the registration of diffusion images onto a T2 anatomical reference image from 20 patients showing cysts or cancerous prostate lesions. Before the comparison, affine motion correction was applied to the acquired DWI series to compensate for inner-series image distortions. We observed that the correlation between the first D0 and the last image D750 from the series (between which the largest deformation was expected) could be reduced by 7% (before vs after registration using areg). Similarly, the affine correction reduced deviations from the voxel-wise exponential fit over the series by 15%.
In the performance comparison of DWI to T2 registration, the applied B-spline algorithms showed the largest registration errors with a TRE of 1.88 and 2.05 mm and long execution times of 216 and 105 s, respectively. For comparison, the local affine algorithm lreg and the demons algorithm performed better in terms of registration accuracy and achieved a TRE of 1.47 and 1.53 mm, respectively. The fast elastic registration algorithm, feir, showed both the smallest execution times with 11 s, as well as the highest registration accuracy with a reduced TRE of 1.07 mm.
We observed several weaknesses for some of the algorithms. breg and bsp seem not to be applicable since B-splines might not be capable of modeling very small and localized prostate deformations in between control points and hence require very small control point spacings. However, a small control point spacing leads to large execution times due to a high number of optimization parameters. lreg was originally designed for respiratory motion correction, and its hierarchical structure allows the estimation from large to small deformations without the need of initialization. However, in our current application, only very local deformations were expected, and the motion estimation of nonpresent large deformations led to increased execution times. While lreg showed reasonable results in terms of registration accuracy, a starting affine block size could be implemented (similar to a starting control point spacing in B-spline-based algorithms) to focus on small deformations only and hence to minimize execution times. demons performed well in terms of registration accuracy as well as execution times. The available implementation did not include a stopping condition though, i.e., the number of iterations was always fixed according to the parameter selection. In very few cases, this led to large unrealistic deformations of the image and consequently to larger registration errors. An implementation of a reasonable stopping condition would be required to ensure accurate registration results in all cases. Finally, feir provides both most accurate and fastest results and was the algorithm that showed the smallest error variations and smallest maximum TRE over all patients. In another experiment, we used the modality-independent standard parameter setting of feir (same λ, μ, and maximum iteration number as before, but registration stopped at image resolution 2 × 2 × 2 mm). In other words, these parameters were not tuned to the specific application of registering MR prostate images. With these settings, the execution time was further decreased to 4 s resulting in a TRE of 1.28 ± 0.45 mm, which is still the best TRE with respect to the other four registration algorithms.
While researchers applied B0-inhomogeneity correction to compensate for EPI-specific distortions,9 such correction requires (1) additional acquisition of a B0 map (which is associated with a significant increase in scan time) and (2) zero-motion between the B0 scan and the DWI scan (otherwise B0-inhomogeneity correction would not be accurate). In our prostate application, we assumed that EPI-specific distortions can well be modeled by the selected nonrigid registration algorithms, and we chose to correct the total deformation comprising EPI-specific distortions as well as physiological motion at once. However, for the sake of completeness, we analyzed the motion fields from feir as the most accurate algorithm to estimate which motion component is dominant. We observed largest motion variations (over the complete image) between T2 and DWI along the through-plane craniocaudal direction with the lowest image resolution of 3 mm in T2 and 2.73 mm in DWI. This motion component showed a mean value of −0.32 ± 1.13 mm over all patients. The in-plane left–right/anterior–posterior motion components showed mean values of −0.14 ± 0.23 mm and −0.19 ± 0.22 mm, respectively. We would expect the largest EPI-specific distortions along the phase-encoding direction, which was left–right here. However, because the in-plane motion values were similar in each direction, the proportion of EPI-specific distortions seemed to be minor compared to patient-induced motion.
While the focus of this paper was the comparison of nonrigid registration techniques for the registration of DWI to T2, we could improve the accuracy of our inner-DWI motion correction, because we expect an improvement in diagnostic value of the resulting ADC maps. However, this assumption has to be proven, e.g., using biopsies. First, we could investigate if the affine transformation during inner-DWI registration is sufficient to correct for EPI-specific image distortions. feir as the best registration algorithm could be applied alternatively before proceeding to the registration of DWI to T2. Second, we could investigate the impact of volume-preserving registrations19,20 during inner-DWI and DWI to T2 registration. To the knowledge of the authors, none of the applied registration algorithms allow volume preservation. This might lead to inaccurate image intensities during image deformations making quantitative ADC mapping and hence image diffusion measurements unreliable. Algorithmic extensions to allow volume preservation could be investigated to increase ADC map quantification accuracy. Finally we could include dynamic contrast enhanced (DCE) image series into the registration pipeline to include DCE as additional modality leading to an increase in diagnostic value in multimodal prostate oncology.
6. CONCLUSION
In this paper, we compared five state-of-the-art nonrigid registration algorithms to compensate for EPI-specific and patient-induced deformations between a DWI series and a T2 reference scan. For the presented application of prostate imaging, we observed that the fast elastic image registration algorithm feir can reduce the DWI to T2 misalignment from 2.21 to 1.07 mm within 11 s, which is an improvement by 52%. Our evaluation showed feir appears to be the most suitable registration algorithm in prostate imaging, with most accurate results and fastest performance in terms of execution times.
ACKNOWLEDGMENTS
The authors thank the National Institutes of Health (NIH) and The Cancer Imaging Archive (TCIA, http://www.cancerimagingarchive.net) for providing us with the MR image data. They also thank Yogish Mallya and Thomas Netsch for their support in tuning the applied registration parameters for most accurate motion estimations.
REFERENCES
- 1.Jemal A., Siegel R., Ward E., Hao Y., Xu J., and Thun M. J., “Cancer Statistics,” Ca-Cancer J. Clin. 59, 225–249 (2009). 10.3322/caac.20006 [DOI] [PubMed] [Google Scholar]
- 2.Barentsz J. O., Richenberg J., Clements R., Choyke P., Verma S., Villeirs G., Rouviere O., Logager V., and Fütterer J. J., “ESUR prostate MR guidelines 2012,” Eur. Radiol. 22, 746–757 (2012). 10.1007/s00330-011-2377-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Turkbey B., Albert P. S., Kurdziel K., and Choyke P. L., “Imaging localized prostate cancer: Current approaches and new developments,” Am. J. Roentgenol. 192, 1471–1480 (2009). 10.2214/AJR.09.2527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Turkbey B., Pinto P. A., and Choyke P. L., “Imaging techniques for prostate cancer: Implications for focal therapy,” Nat. Rev. Urol. 6, 191–203 (2009). 10.1038/nrurol.2009.27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pang Y., Turkbey B., Bernardo M., Kruecker J., Kadoury S., Merino M. J., Wood B. J., Pinto P. A., and Choyke P. L., “Intravoxel incoherent motion MR imaging for prostate cancer: An evaluation of perfusion fraction and diffusion coefficient derived from different b-value combinations,” Magn. Reson. Med. 69(2), 553–562 (2012). 10.1002/mrm.24277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hill D. L. G., Batchelor P., Holden M., and Hawkes D. J., “Medical image registration,” Phys. Med. Biol. 46, R1–R45 (2001). 10.1088/0031-9155/46/3/201 [DOI] [PubMed] [Google Scholar]
- 7.Maintz J. B. A. and Viergever M. A., “A survey of medical image registration,” Med. Image Anal. 2, 1–36 (1998). 10.1016/S1361-8415(01)80026-8 [DOI] [PubMed] [Google Scholar]
- 8.Zitov B. and Flusser J., “Image registration methods: A survey,” Image Vision Comput. 21, 977–1000 (2003). 10.1016/S0262-8856(03)00137-9 [DOI] [Google Scholar]
- 9.Jezzard P. and Balaban R. S., “Correction for geometric distortion in echo planar images from B0 field variations,” Magn. Reson. Med. 34, 65–73 (1995). 10.1002/mrm.1910340111 [DOI] [PubMed] [Google Scholar]
- 10.Kabus S. and Lorenz C., “Fast elastic image registration,” Proceeding of the Medical Image Analysis for the Clinic—A Grand Challenge, MICCAI, 81–89 (2010). [Google Scholar]
- 11.Netsch T. and van Muiswinkel A., “Image registration for distortion correction in diffusion tensor imaging,” Biomedical Image Registration, Lecture Notes in Computer Science(2003), Vol. 2717, pp. 171–180. 10.1007/978-3-540-39701-4_18 [DOI] [Google Scholar]
- 12.Rueckert D., Sonoda L. I., Hayes C., Hill D. L. G., Leach M. O., and Hawkes D. J., “Nonrigid registration using free-form deformations: Application to breast MR images,” IEEE Trans. Med. Imaging 18, 712–721 (1999). 10.1109/42.796284 [DOI] [PubMed] [Google Scholar]
- 13.Klein S., Staring M., Murphy K., Viergever M. A., and Pluim J., “Elastix: A toolbox for intensity-based medical image registration,” IEEE Trans. Med. Imaging 29, 196–205 (2010). 10.1109/TMI.2009.2035616 [DOI] [PubMed] [Google Scholar]
- 14.Kabus S., Netsch T., Fischer B., and Modersitzki J., “B-spline registration of 3D images with Levenberg-Marquardt optimization,” Med. Imaging 5370, 304–313 (2004). 10.1117/12.533976 [DOI] [Google Scholar]
- 15.Buerger C., Schaeffer T., and King A. P., “Hierarchical adaptive local affine registration for fast and robust respiratory motion estimation,” Med. Image Anal. 15, 551–564 (2011). 10.1016/j.media.2011.02.009 [DOI] [PubMed] [Google Scholar]
- 16.Thirion J. P., “Image matching as a diffusion process: An analogy with Maxwell’s demons,” Med. Image Anal. 2, 243–260 (1998). 10.1016/S1361-8415(98)80022-4 [DOI] [PubMed] [Google Scholar]
- 17.Unser M., Aldroubi A., and Eden M., “B-spline signal processing. II. Efficiency design and applications,” IEEE Trans. Signal Process. 41, 834–848 (1993). 10.1109/78.193221 [DOI] [Google Scholar]
- 18.Fitzpatrick J. M., West J. B., and C. R. Maurer, Jr., “Predicting error in rigid-body point-based registration,” IEEE Trans. Med. Imaging 17, 694–702 (1998). 10.1109/42.736021 [DOI] [PubMed] [Google Scholar]
- 19.Rohlfing T., Maurer C. R., Bluemke D. A., and Jacobs M. A., “Volume-preserving nonrigid registration of MR breast images using free-form deformation with an incompressibility constraint,” IEEE Trans. Med. Imaging 22, 730–741 (2003). 10.1109/TMI.2003.814791 [DOI] [PubMed] [Google Scholar]
- 20.Haber E. and Modersitzki J., “Numerical methods for volume preserving image registration,” Inverse Probl. 20, 1621–1638 (2004). 10.1088/0266-5611/20/5/018 [DOI] [Google Scholar]