Simultaneous beam sampling and aperture shape optimization for SPORT

Abstract

Purpose:

Station parameter optimized radiation therapy (SPORT) was recently proposed to fully utilize the technical capability of emerging digital linear accelerators, in which the station parameters of a delivery system, such as aperture shape and weight, couch position/angle, gantry/collimator angle, can be optimized simultaneously. SPORT promises to deliver remarkable radiation dose distributions in an efficient manner, yet there exists no optimization algorithm for its implementation. The purpose of this work is to develop an algorithm to simultaneously optimize the beam sampling and aperture shapes.

Methods:

The authors build a mathematical model with the fundamental station point parameters as the decision variables. To solve the resulting large-scale optimization problem, the authors devise an effective algorithm by integrating three advanced optimization techniques: column generation, subgradient method, and pattern search. Column generation adds the most beneficial stations sequentially until the plan quality improvement saturates and provides a good starting point for the subsequent optimization. It also adds the new stations during the algorithm if beneficial. For each update resulted from column generation, the subgradient method improves the selected stations locally by reshaping the apertures and updating the beam angles toward a descent subgradient direction. The algorithm continues to improve the selected stations locally and globally by a pattern search algorithm to explore the part of search space not reachable by the subgradient method. By combining these three techniques together, all plausible combinations of station parameters are searched efficiently to yield the optimal solution.

Results:

A SPORT optimization framework with seamlessly integration of three complementary algorithms, column generation, subgradient method, and pattern search, was established. The proposed technique was applied to two previously treated clinical cases: a head and neck and a prostate case. It significantly improved the target conformality and at the same time critical structure sparing compared with conventional intensity modulated radiation therapy (IMRT). In the head and neck case, for example, the average PTV coverage D99% for two PTVs, cord and brainstem max doses, and right parotid gland mean dose were improved, respectively, by about 7%, 37%, 12%, and 16%.

Conclusions:

The proposed method automatically determines the number of the stations required to generate a satisfactory plan and optimizes simultaneously the involved station parameters, leading to improved quality of the resultant treatment plans as compared with the conventional IMRT plans.

1. INTRODUCTION

Station parameter optimized radiation therapy (SPORT)^1–4 has recently been introduced to utilize maximally the unique features of digital linear accelerators (LINACs) and bridge the gap between intensity modulated radiation therapy (IMRT)^5,6 and volumetric modulated arc therapy (VMAT).⁷ Clinically, IMRT often does not possess sufficient angular sampling and VMAT may under- or overmodulate the beam intensity in some or all directions. SPORT aims to optimize the interplay between the angular sampling and beam modulation and promises to deliver a highly conformal radiation dose distribution efficiently. Despite the demonstrated benefits of SPORT in preliminary studies, a mathematically rigorous treatment planning framework capable of optimizing SPORT treatment has yet to be developed. This paper presents a SPORT framework by combining three complementary optimization algorithms: column generation, subgradient method, and pattern search. The algorithms automatically determine the number of the stations required to generate a satisfactory plan and optimize other parameters characterizing involved station points, including their angles, aperture shapes, and intensities.

There are numerous studies in the literature on optimizing the aperture shapes for VMAT or IMRT. The apertures can generally be optimized in two ways. The first optimizes the beamlet intensities and then segments the optimal beam profile into apertures^8–12 (two-stage method). The second way to proceed is to optimize the apertures directly. Heuristic techniques have been popularly used to deal with the nonconvexity of the problem of direct aperture optimization. Otto¹³ suggested stochastic random-based search method. Shepard et al.¹⁴ and Earl et al.¹⁵ used simulated annealing, and Cotrutz and Xing¹⁶ used genetic algorithm to solve the problem. Column generation based methods have attracted much attention recently.^17–21 In this approach, a very large optimization problem with a variable corresponding to each possible aperture shape is solved, and the dimensionality problem is handled by solving the so-called pricing problem that searches through all the variables at each iteration and finds a variable that improves the objective function the most. Cassioli and Unkelbach²² suggested to use the trust-region-based local search approach in combination with column generation to optimize the aperture shapes. Hardemark et al.²³ proposed a local search technique on top of the two-stage method to refine the aperture shapes, and Papp and Unkelbach²⁴ employed a convex formulation of the problem by using some approximations.

The beam angle optimization for IMRT has been addressed by using a variety of methods ranging from beam angle scoring and scoring function guided beam orientation optimization,^25,26 class-solution,²⁷ metaheuristic techniques such as simulated annealing^28,29 and genetic algorithm,³⁰ exact methods such as pattern search,³¹ gradient-based local search,³² and mixed integer programming.^33,34

To the best of our knowledge, there is no published research to address the problem of optimizing the beam angles and apertures altogether for IMRT or VMAT that we can borrow and adapt for SPORT. On the other hand, the optimization technique introduced in this paper for SPORT is applicable for IMRT and VMAT. This work is aimed at developing an algorithm to simultaneously optimize the angular sampling and aperture shapes of station points by integrating three complementary optimization techniques: column generation, subgradient method, and pattern search.

1.A. Optimization model

Let N be the maximum allowed number of the stations. We seek for a set of the stations, characterized by the corresponding beam angles θ_b, aperture shapes X_b, and aperture intensities η_b(b = 1, …, N), to minimizing a predefined metric function F of dose distribution. The dose distribution Z is related to the decision variables (X_b, θ_b, η_b) as described in the following.

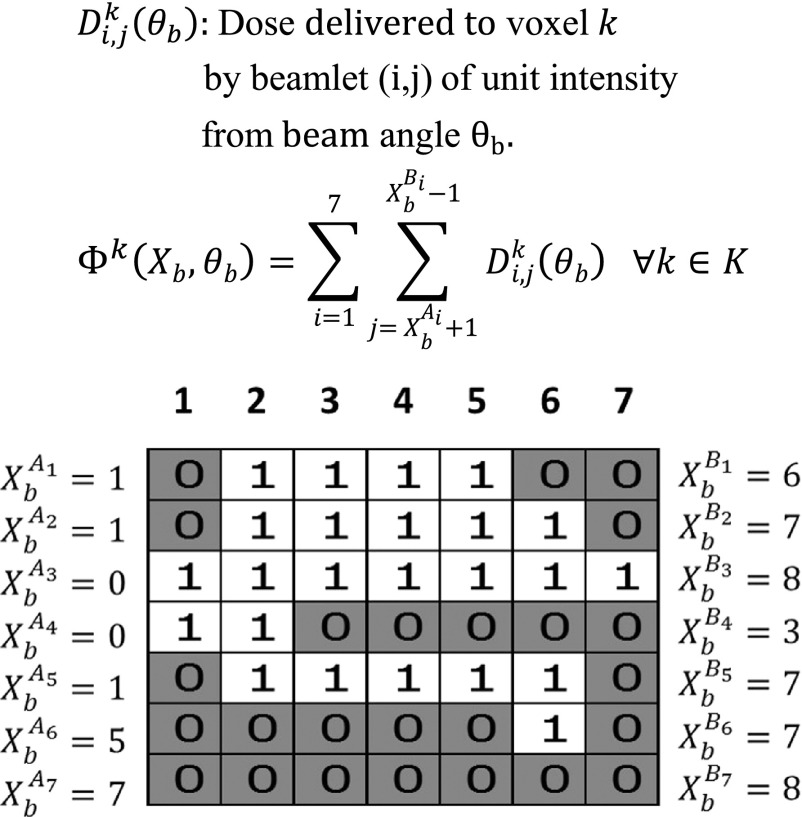
We discretize each beam into a set of beamlets with precalculated dose deposition matrices for the beamlets. Let us denote by $D_{i,j}^k\left({\theta }_b\right)$, the dose delivered to voxel k by beamlet (i, j) (beamlet in row i and column j) of unit intensity from beam angle θ_b. The dose at voxel k from the station b of unit intensity, ${\mathrm{\Phi }}^{\text{k}}\left(X_b,{\theta }_b\right)$, is then obtained by summing the contributions from all open beamlets. Figure 1 illustrates this process using a beam with 7 × 7 beamlets. Dark squares labeled with “0” show the beamlets blocked by leaves, and the remaining squares labeled with “1” represent the open beamlets. $X_b^{A_i}$ and $X_b^{B_i}$ represent the position of the left and right leaves of the ith row, respectively. The accumulated dose from all stations is obtained by multiplying ${\mathrm{\Phi }}^{\text{k}}\left(X_b,{\theta }_b\right)$ by the intensity of the station, η_b, and then summing up over all the stations.

FIG. 1.

A sketch illustrating the calculation of Φ(X_b, θ_b) as a function of the leave position and the beam angle. Given that the dose contribution of each beamlet to each voxel is precalculated by $D_{i,j}^k\left({\theta }_b\right)$, Φ^k(X_b, θ_b) can be obtained by summing up on $D_{i,j}^k\left({\theta }_b\right)$ over all open beamlets at station (X_b, θ_b). These open beamlets are labeled with “1” in this figure.

Now, we formulate our optimization problem as

$${\displaystyle \text{min}\left\{F\left(Z\right)|Z^k=\sum _{b=1:n}{\mathrm{\Phi }}^k\left(X_b,{\theta }_b\right){\eta }_b,\right.\left.{\eta }_b\ge 0,k\in V,(X_b,{\theta }_b)\in \mathrm{\Omega }\times B,n\le N\right\},}$$ (1)

where B and Ω are the set of allowed beam angles and aperture shapes, respectively, and V is the set of voxel indices. The objective function F is typically a convex function of the dose distribution Z. In the case that our clinically relevant metric is not a convex function (e.g., it is based on the dose volume histogram concept), then a surrogate convex function can be employed.^35,36

1.B. Integrated algorithm

The difficulty in Problem (1) lies in the lack of a standard implicit and explicit representation of Φ(X_b, θ_b) as a function of X_b and θ_b. On the other hand, once Φ(X_b, θ_b) is known, we can easily find the optimal intensity by solving Problem (1) with η as the only set of the variables. Therefore, we split Problem (1) into a two-layer problem where the aperture shapes and beam angles are optimized in outer-layer Problem (2) and aperture intensities are optimized in inner-layer Problem (3) which is defined as

$${\displaystyle \text{min}\left\{G\left(X,\theta \right)|\left(X,\theta \right)=\left(\left(X_1,{\theta }_1\right),\right.\right.\left.\left.\left(X_2,{\theta }_2\right),\dots ,\left(X_n,{\theta }_n\right)\right),(X_b,{\theta }_b)\in \mathrm{\Omega }\times B\forall b,n\le N\right\},}$$ (2)

$${\displaystyle G\left(X,\theta \right)=\text{min}\left\{F\left(Z\right)|Z^k=\sum _{b=1:n}{\mathrm{\Phi }}^k\left(X_b,{\theta }_b\right){\eta }_b,\right.\left.k\in V,\eta \ge 0,n\le N\right\}.}$$ (3)

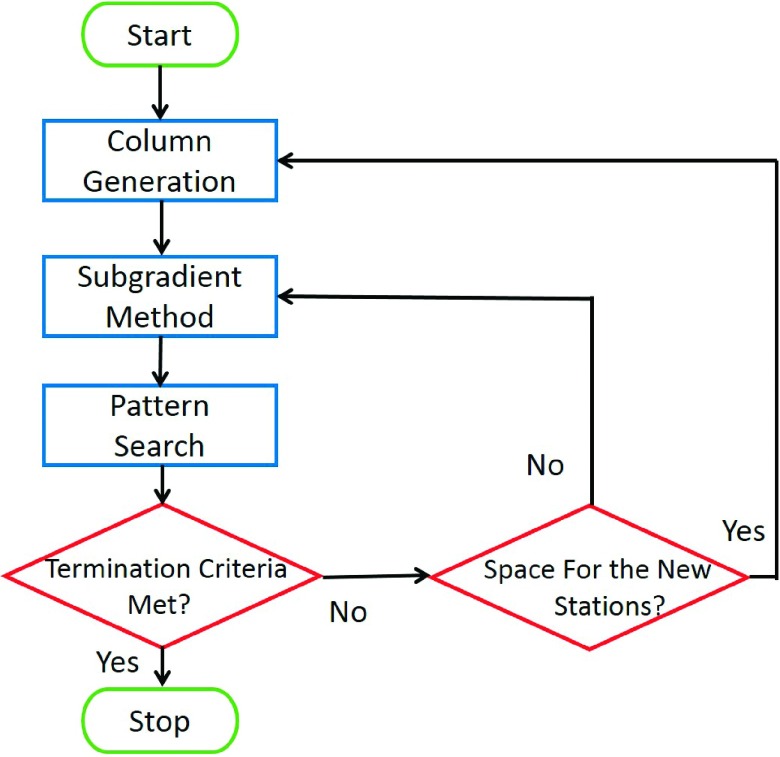
It can be readily shown that an optimal solution of Problems (2) and (3) would also be optimal for Problem (1) [$\left(\left(X_1,{\theta }_1,{\eta }_1\right),\dots ,\left(X_n,{\theta }_n,{\eta }_n\right)\right)$ is a feasible solution of Problem (1) with an objective function equal to $F\left(\sum _{b=1:n}{\mathrm{\Phi }}^k\left(X_b,{\theta }_b\right){\eta }_b\right)$ if and only if it is a feasible solution of Problems (2) and (3) with the same objective function.] While, in principle, Problem (2) can only be solved by using one of those general and computationally expensive techniques such as pattern search, we employ a column generation and the subgradient method to speedup the optimization process and to find the number of stations needed to produce a satisfactory SPORT plan. As illustrated in Fig. 2, we employ the column generation method to find an initial set of the stations for Problem (2) (see Sec. 1.B.1). New stations are added sequentially until the objective function saturates (or stops to improve sufficiently) with any further increase in the number of station points. At this stage, we apply the subgradient method (see Sec. 1.B.2) and pattern search (see Sec. 1.B.3) to improve the current solution by reshaping the apertures and changing the beam angles of the current stations. The algorithm terminates if none of the aforementioned optimization techniques improve the current solution sufficiently; otherwise, we recall column generation again to check the possibility of adding the new beneficial stations if there is space to have extra stations.

FIG. 2.

Flowchart of the proposed SPORT optimization algorithm. Column generation improves the solution continuously by sequential adding of new station points, while the station parameters are refined by the subgradient method and pattern search.

It should be noted that the subgradient method and pattern search do not generate a new station but only improve the current station configuration. However, some of the stations may be withdrawn from the pool of selected stations if their intensity becomes zero after applying the subgradient method or pattern search.

1.B.1. Column generation

Column generation is a sequential optimization technique specialized to handle problems with a large number of variables. Its objective is to find the most beneficial variable(s) at each iteration by solving an extra optimization problem, usually referred to as the “pricing” problem, and then add that variable to the pool of existing variables. This technique has been employed in IMRT and VMAT to optimize the aperture shapes.^18,20,37,38

Given a set of the apertures and beam angles $\left(X_1,{\theta }_1\right),\left(X_2,{\theta }_2\right),\dots ,\left(X_k,{\theta }_k\right)$, pricing problem searches through all plausible aperture shapes from all angles and finds (X_k+1, θ_k+1) that improves the objective function the most. The algorithm stops if either the maximum allowed number of stations is reached, or the improvement in the objective function becomes insignificant according to a predefined criterion (e.g., the relative improvement in the objective function is less than 1%). In this work, we employ the pricing problem introduced by Romeijn et al.¹⁸

The pricing problem searches for a station with the highest rate of improvement in the objective function of Problem (2) with respect to the intensity of the station. For a beamlet (i, j) at beam angle θ_b, the rate of change in the objective function with respect to the intensity of the beamlet is obtained by using the chain rule as

$${\displaystyle {\pi }_{i,j}\left({\theta }_b\right)=\sum _{k\in V}\frac{\partial F}{\partial Z_k}{D}_{i,j}^k\left({\theta }_b\right).}$$ (4)

Now, the rate of change in the objective function with respect to the intensity of a station $\left(X_b,{\theta }_b\right)$ can be obtained by adding up together Eq. (4) for all open beamlets,

$${\displaystyle \sum _{i\in R}\sum _{j=\underset{b}{\overset{A_i}{X}}+1}^{X_b^{B_i}-1}{\pi }_{i,j}\left({\theta }_b\right),}$$

where R is the set of row indices. Problem (5) represents the pricing problem,

$${\displaystyle min\left\{\sum _{i\in R}\sum _{j=\underset{b}{\overset{A_i}{X}}+1}^{X_b^{B_i}-1}{\pi }_{i,j}\left({\theta }_b\right),\left(X_b,{\theta }_b\right)\in \left(\mathrm{\Omega },B\right)\right\}.}$$ (5)

To solve Problem (5), we first find the best aperture shape for each individual angle, and then we pick the one with the highest rate of improvement. For a specific angle, it immediately follows that the objective function in Eq. (5) decomposes by beamlet row. On the other hand, we can find the optimal position of the left and right leaves for each row by looking for a consecutive set of beamlets for which the sum of their values $\left({\pi }_{i,j}\left({\theta }_b\right)\right)$ is minimal. While it can be done by simply enumerating all the possibilities in O(n²) (n is the number of beamlets in a given row), there is also an efficient algorithm to do that in O(n) (the reader is referred to Romeijn et al.¹⁸ for more details).

1.B.2. The subgradient method

Column generation finds a good initial solution that is not necessarily optimal due to the nonconvexity of the problem. So, we carry out the subgradient method and pattern search to improve the current solution. The gradient is usually considered as the best direction to improve a function locally, especially in the absence of second order information. In literature, the gradient information has been utilized to optimize the beam angles for the beamlet-based optimization problem.^29,32 Let $\left(X,\theta \right)=\left(\left(X_1,{\theta }_1\right),\left(X_2,{\theta }_2\right),\dots ,\left(X_n,{\theta }_n\right)\right)$ denote the current solution. According to the gradient descent method, we need to update this solution using the gradient of the objective function as follows:

$${\displaystyle \left(X,\theta \right)\leftarrow \left(X,\theta \right)-\lambda \left(\nabla G_X\left(X,\theta \right),\nabla G_{\theta }\left(X,\theta \right)\right),}$$ (6)

where λ is obtained using a backtracking search method to assure improvement in the objective function.^39,40 While G is defined in Eq. (3) only for discrete values, we can consider the natural extension of G by applying, for example, a linear interpolation to make the derivative well-defined. In this case, although G is not differentiable, it is left and right differentiable, making it possible to build a subgradient direction to take over the gradient in Eq. (6). Subgradient is basically a generalized version of gradient for nondifferentiable functions.⁴⁰ We define a subgradient direction g by using the fact that the objective function improves if we increase a variable with the negative right derivative, or if we decrease a variable with the positive left derivative,

$${\displaystyle g_i=\left\{\begin{array}{ll}{\partial }_i^{+}G,\hfill & {\partial }_i^{+}G<0\hfill \\ {\partial }_i^{-}G,\hfill & {\partial }_i^{-}G>0\hfill \\ 0,\hfill & \text{otherwise.}\hfill \end{array}\right.}$$

It is not difficult to show that −g is a descent direction. In order to keep the variables integer, we round the variables after moving toward the subgradient direction. Moreover, when a beam angle is changed, the corresponding MLC leaf settings may need to be adjusted to close those beamlets which do not belong to the beam-eye-view (BEV) of the new angle.

We can compute the right/left derivative for each variable by recalculating function G [by resolving Problem (3)] and using a finite difference method. However, this is computationally prohibitive and we instead approximate function G by assuming that the optimal value of the variable η does not change in the neighborhood of the current solution $\left(X,\theta \right)$ (the neighborhood includes all the points generated by moving a leaf or an angle of the current solution by one discretized step). The fact that the derivative calculation is based on the evaluation of the function in the neighborhood of the current solution justifies this approximation. This assumption yields

$${\displaystyle G\left(X,\theta \right)\cong F\left(\sum _{b=1:N}\mathrm{\Phi }\left(X_b,{\theta }_b\right){\eta }_b^{*}\right),}$$

where η^* denotes the optimal solution of Problem (3) at the current solution. Now, we can calculate the right/left derivative of G using the finite difference method or using the analytical derivative rules such as chain rule. Since the number of beam angle variables θ is relatively small (∼30–70), a more accurate finite difference method is adopted. For the leaf position variables X (∼2000–4000 variables), an analytical derivative approach is applied (see Appendix).

In general, our subgradient method does not guarantee the local optimality because of using the approximated subgradient direction and also the presence of the integer decision variables (leaf positions and beam angles, whose values are rounded after each iteration). Moreover, global search is required due to the nonconvexity of function G and to avoid being trapped in possible local optima. While a comprehensive local and global search such as pattern search is required to guarantee the optimality, the subgradient method is computationally much more efficient and hence is integrated with pattern search in our implementation. Interestingly, the derivative information obtained in the subgradient method is also used in pattern search, improving the computational efficiency of pattern search.

1.B.3. Pattern search

Pattern search (or directional direct search) is a family of derivative-free optimization techniques designed to solve optimization problems with nondifferentiable or very complex objective functions.⁴¹ Rocha et al.³¹ have employed this technique to optimize the beam angles for their beamlet-based IMRT optimization model. Pattern search seeks for an improving direction in the so-called positive basis to improve the current solution, and it concludes optimality if there is no improving direction.

Let us denote the positive basis by V = {v₁, v₂, …, v_m} where there are two directions corresponding to each leaf (moving to the right and left) as well as two directions corresponding to each angle (moving clockwise and counter clockwise). Pattern search has two search strategies known as search step and poll step. In the poll step, we aim to improve the current solution by moving toward one of the directions in V (poll directions), while in the search step, we examine a finite set of directions where each is a non-negative and integer combination of the poll directions. We use a random combination of the poll directions to construct directions for the search step. Due to the selection of positive basis, in the poll step, we aim to improve the current solution by moving an individual leaf (toward right/left) or changing a beam angle (clockwise or counter clockwise), and in the search step, we aim to make an improvement by changing multiple leaves and/or beam angles. The search step is conducted first and iterates until it fails, the poll step is then executed.

A bottleneck in efficient pattern search optimization is that it requires examining the directions one-by-one to find the right direction to make a movement. For improved performance, we reorder the poll directions and check the directions that are more likely to improve the solution first by incorporating the derivative information obtained in the subgradient method. In fact, the right and left derivatives of a variable are telling us how beneficial the increase or decrease of that variable is. So, we reorder the poll directions based on these information. Moreover, we use nonuniform random sampling for the search step by incorporating the derivative information as the weights. This is a simple technique to speedup the algorithm without impairing its convergence properties.

As pointed out before, our problem is nonconvex, and we need to provide the local and global searches to assure global optimality. We perform the local search by taking the step size equal to one in both search and poll steps (it is the smallest possible step size in our problem). As for the global search, we have the step size randomly selected between two and the maximum possible value. For each leaf, the maximum possible value is defined based on the position of its pair leaf to avoid any collision and also based on the BEV to avoid opening beamlets outside the BEV. For each angle, the maximum step size is 179 (we have 180 beam angle candidates in our implementation).

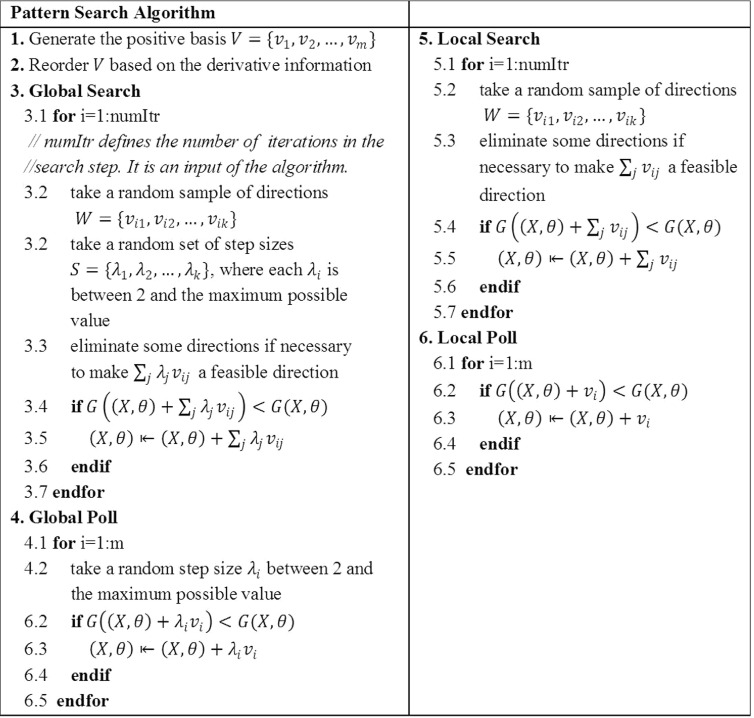
Figure 3 demonstrates the pattern search algorithm in more detail. First, we generate the positive basis directions and reorder them based on the derivative information. Each positive basis direction corresponds to moving a leaf or a beam angle within one unit. Then, we apply global search, global poll, local search, and local poll, respectively.

FIG. 3.

The pseudocode for the proposed pattern search algorithm. The algorithm runs global search, global poll, local search, and local poll, respectively. The local poll examines all the directions for possible improvement, and the local search checks some random combination of the direction. The local and global poll/search only differ in the step size, which is equal to one for the local poll/search and is randomly generated for the global poll/search.

2. RESULTS

We demonstrate the performance of the proposed algorithm by using a head and neck and a prostate case. For each case, we compare the SPORT result with (1) a plan obtained by optimizing only the aperture shapes using a uniform beam angle distribution and (2) an IMRT plan with 7 equispaced beam angles. For the IMRT plan, we use the beamlet-based optimization model that representing the best solution for the chosen beam configuration. For the objective function, we use the following piecewise quadratic objective function which has been quite popular in radiotherapy optimization:^11,14,15,23

$${\displaystyle F\left(Z\right)=\sum _{j\in V}{w}_j^{-}max{\left(0,Z_j^L-Z_j\right)}^2+w_j^{+}max{\left(0,Z_j-Z_j^U\right)}^2,}$$

where $Z_j^L$ and $Z_j^U$ are, respectively, the low dose and high dose thresholds for voxel j, and $w_j^{-}$ and $w_j^{+}$ are their corresponding weighting factors. We adjust all of these parameters manually for each patient in IMRT planning, and then, we use the same objective function and parameters for SPORT to have a fair comparison.

We set the beamlet size to 1 × 1 cm² and precalculate the dose deposition matrix for 180 equispaced beam angles using a pencil beam dose calculation algorithm [quadrant infinite beam (QIB)] that is included in CERR (Ref. 42) (A computational environment for radiotherapy research). The size of the MLC is 40 × 40 cm² and the number of voxels used in optimization is 33 893 and 30 810 for the head and neck and the prostate case, respectively. The computations are conducted using matlab R2013b on a PC with Intel Core i7 3.40 GHz CPU and 32 GB RAM.

2.A. Head and neck

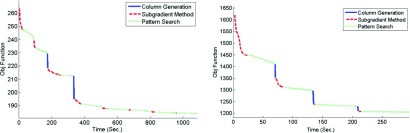
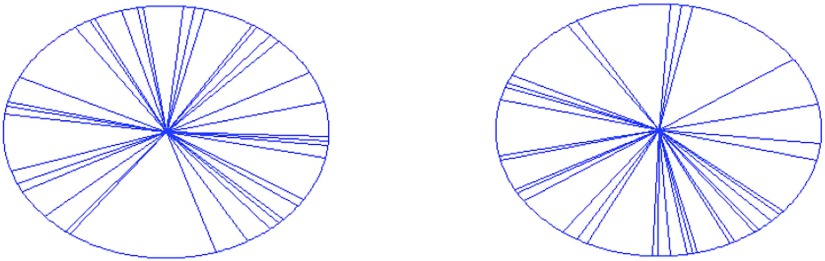
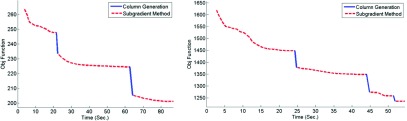
Figure 4-left demonstrates the convergence behavior of the algorithm by depicting the objective function value as a function of time. The solid, dashed, and dotted lines are used to illustrate the contributions of three optimization techniques, respectively. First, column generation runs and finds the initial solution including 24 stations with the value of objective function reaches to ∼264 (adding more apertures would improve the objective function less than 1% at this point). Then, the subgradient method and pattern search run to improve the 24 selected stations, reducing the objective function down to ∼230. Next, column generation runs again and finds additional three beneficial stations, and the algorithm continues so on. At the end of the calculation, 36 stations are allocated in ∼1070 s. As can be seen in Fig. 4-left, the column generation takes least time, whereas pattern search is the slowest process. Figure 5-left illustrates the distribution of the optimal beam angles for this case.

FIG. 4.

The convergence behavior of the algorithm for the head and neck (left) and the prostate case (right).

FIG. 5.

The optimal beam angle distribution for the head and neck (left) and the prostate case (right).

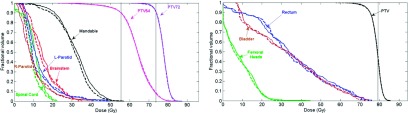
Figure 6-left reveals the importance of optimizing the beam angles by comparing the plan that is obtained by only optimizing the aperture shapes for 36 uniformly distributed angles (dashed line) against the SPORT plan that is obtained by optimizing both beam angles and aperture shapes (solid line). The two vertical lines represent the PTVs’ prescription doses. This figure demonstrates a significant improvement in critical structure sparing and a slight improvement in tumor coverage using the SPORT plan. Table I-left does the comparison based on some clinically important metrics. Since the higher value is preferred for the PTV underdose and the lower value is preferred for the PTV overdose, the better value for each criterion is shown in bold to make the visual comparison easier. According to this table, SPORT improves the cord and brainstem maximum doses, mandible and left/right parotid mean doses, respectively, by 42%, 7.1%, 4.3%, 16%, and 36.3%. SPORT also improves slightly the PTV coverage criterion D (99%) for PTV72 and PTV54 (almost 4%). In terms of the PTV dose inhomogeneity criterion D (5%), both plans are almost the same (less that 1% difference).

FIG. 6.

Comparison of the SPORT plan (solid line) with the plan obtained by optimizing only the aperture shapes and using the uniform beam angles (dashed line) for the head and neck (left) and the prostate case (right).

TABLE I.

Using some clinically important metrics to compare the head and neck SPORT plan with (left table) the plan obtained using uniform beam angles and (right table) the IMRT plan. For each criterion, the better score is bolded.

Organ	Specific interest	SPORT	Uniform angles	Relative difference (%)
PTV72	D(5%)	81.8	82	0.2
	D(99%)	69.4	66.8	3.8
PTV 54	D(5%)	75	74.9	0.1
	D(99%)	35.9	34.7	3.3
Cord	Max	21.2	32.6	42
Brainstem	Max	34.9	37.5	7.1
Mandable	Mean	31.9	33.3	4.3
Left parotid	Mean	13	15.3	16
Right parotid	Mean	9.7	14	36.3
PTV72	D(5%)	81.8	81.6	0.2
	D(99%)	69.4	66.6	4.1
PTV 54	D(5%)	75	75.9	1.2
	D(99%)	35.9	32.2	10.8
Cord	Max	21.2	30.9	37.2
Brainstem	Max	34.9	39.4	12.1
Mandable	Mean	31.9	31.7	0.6
Left parotid	Mean	13	13	0
Right parotid	Mean	9.7	11.4	16.1

Figure 7-left and Table I-right compare the SPORT plan with the IMRT plan, which represents the ideal situation for the given fixed-gantry beam configuration without any constraint on beam intensity modulation. Again, we can observe improvement in critical structure sparing as well as tumor coverage by delivering the SPORT plan. Regarding Table I-right, except for the mandible mean dose and PTV72 inhomogeneity criterion D (5%) that are deteriorated less than 1%, all other criteria are improved using SPORT; particularly, the cord and brainstem maximum doses and PTV54 coverage D(99%) are, respectively, improved by 37.2%, 12.1%, and 10.8%.

FIG. 7.

Comparison of the SPORT plan (solid line) with the ideal IMRT plan (dashed line) for the head and neck (left) and the prostate case (right).

A practical concern arises here with regard to the necessity of the pattern search, especially considering the slow convergence of pattern search in Fig. 4-left. Figure 8-left depicts the convergence behavior of the algorithm when only the column generation and subgradient method are used. While the computational speed is enhanced by about ten times, it is seen from Fig. 9-left and Table II-left that the critical structure sparing is degraded when the pattern search is excluded. Figure 9-left shows that the PTV coverage is almost the same in both plans. However, according to Table II-left, by excluding the pattern search, mandible and left/right parotid mean doses, and cord maximum dose are deteriorated by 8%, 11%, 14%, and 24% and only brainstem maximum dose is improved by 5%. This result emphasizes the important role of pattern search in SPORT optimization.

FIG. 8.

The convergence behavior of the algorithm without applying pattern search for the head and neck (left) and the prostate case (right).

FIG. 9.

Comparison of the SPORT plan generated using the hybrid algorithm including pattern search (solid line) with the plan generated using only the column generation and subgradient method (dashed line) for the head and neck (left) and the prostate case (right).

TABLE II.

Comparison of the critical structure sparing of the head and neck SPORT plan with (left table) the plan obtained using only the column generation and subgradient method and (right table) the plan obtained by relaxing the constraint of at most one aperture per angle. For each criterion, the better score is bolded.

Organ	Specific interest	SPORT	SPORT without pattern search	Relative difference (%)
Cord	Max	21.2	26.9	24
Brainstem	Max	34.9	33	5
Mandable	Mean	31.9	34.5	8
Left parotid	Mean	13	14.5	11
Right parotid	Mean	9.7	11.2	14
Cord	Max	21.2	21.4	1
Brainstem	Max	34.9	33.2	5
Mandable	Mean	31.9	30.5	4
Left parotid	Mean	13	12.2	6
Right parotid	Mean	9.7	10	3

We note that a constraint that only one aperture is permissible per angle is imposed in the above calculation. Figure 10-left and Table II-right show that a relatively insignificant improvement is found when the constraint is removed for the case studied here. In Fig. 10-left, the solid line represents the SPORT plan with 36 stations and angles, and the dashed line shows the result obtained with 36 stations distributed among 30 angles (six angles in this case are picked twice). In either case, the plan can be delivered efficiently with the state-of-the-art digital LINACs. Regarding Table II-right, by relaxing the constraint, brainstem maximum dose, and mandible and left parotid mean doses are improved by 5%, 4%, and 6%, and cord maximum dose and right parotid mean dose are deteriorated by 1% and 3%. Looking at Fig. 10-left, the PTV coverage seems to be practically the same in both plans.

FIG. 10.

Comparison of the SPORT plan with the constraint of at most one aperture per angle (solid line) with the SPORT plan without this constraint (dashed line) for the head and neck (left) and the prostate case (right).

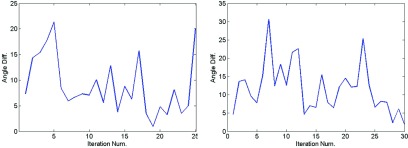
Finally, we would like to mention that even though the subgradient method uses the approximated version of the subgradient direction, this method turns out to perform well, as shown in Fig. 4. Most notably, it outperforms the pattern search in improving the current stations. A natural question that arises here is “how closely is the subgradient approximated?” Fig. 11 answers this question by depicting the angular difference between the approximate and actual subgradients. As Fig. 11-left demonstrates, the difference is less than 22° across all iterations. The small size of this difference justifies our approximation technique and the performance of the algorithm. This approximation is desirable since it takes about 50 s to calculate the actual subgradient on our PC, whereas this time is less than 1 s for the approximated version.

FIG. 11.

The angular difference between the approximate and the actual subgradients for the head and neck (left) and the prostate case (right).

2.B. Prostate

We present the summary of the results for the prostate case. Figure 4-right shows the performance of the algorithm and the contribution of each technique for this case. First of all, column generation finds 23 stations with ∼1620 objective function value. The algorithm terminates in about ∼300 s with 34 stations. Figure 5-right depicts the distribution of the optimal beam angles.

Figure 6-right compares the SPORT plan with the plan obtained by optimizing the aperture shapes for the 34 equispaced beam angles. It reveals the improvement in plan quality, in terms of tumor coverage and critical structure sparing, using the SPORT plan. Figure 7-right compares the ideal IMRT plan obtained using seven equispaced beam angles with the SPORT plan. While two plans are comparable in terms of tumor coverage and femoral heads sparing, the SPORT plan delivers less radiation to the rectum and bladder.

Figure 8-right depicts the performance of the algorithm without applying pattern search. It is seen that the computational speed is enhanced about six times. Figure 9-right demonstrates the contribution of pattern search, and Fig. 10-right reveals the improvement that can be gained by removing the constraint that only one aperture is permissible per angle. The SPORT plan in this case includes 34 stations and 27 angles (five angles are picked twice and one angle is picked three times). Figure 11-right illustrates that the approximate and the actual subgradients are close to each other.

3. DISCUSSION AND CONCLUSION

The essence of SPORT is the optimal (often nonuniform) distribution of the station points in the angular space with consideration of the interplay between all involved station parameters to best cover the target volume and spare the sensitive structures.⁴ SPORT optimizes the station point parameters instead of the beam fluences as in IMRT, which is typically a composite of a set of station parameters or optimization of a predefined set of beams as in VMAT. While SPORT allows highly conformal dose distributions by fully utilizing the capability of the new digital LINACs, its planning generally requires searching through a much enlarged and nonconvex search space of the involved machine parameters. In this paper, an effective optimization framework that combines three complementary optimization techniques is proposed to tackle the difficult problem. Column generation provides an initial solution and also finds the number of stations needed to produce a satisfactory SPORT plan. The subgradient method, which is based on the approximation, is only included for the computational efficiency, and it does not guarantee the local/global optimality. Pattern search is included to guarantee the convergence of the algorithm. We optimized the aperture shapes and beam angles using the proposed framework and demonstrated the performance of the integrated algorithm and the quality of the SPORT plans by using two case studies.

Pattern search is a computationally expensive method, which significantly slows down the algorithm; however, it is included in the hybrid algorithm to guarantee the convergence. While more experimental studies are clearly needed before drawing any conclusion about the role of pattern search in plan quality, the resource and time availability would be the practical factor to determine whether a pattern search should be included in the algorithm.

The comparison of the SPORT plans with conventional IMRT showed that SPORT is capable of generating improved treatment plans. Noteworthy, a significant improvement in plan quality was observed for the head and neck case. We would like to mention that a manual adjustment process was employed for the selection of the weighting factors in the optimization of the quadratic objective function, but this can be alleviated by incorporating the knowledge either from prior clinical experience^25,43,44 or from the data of previously treated patients.⁴⁵ In this case, all we need is an automated procedure to adjust the parameters in order to replicate prior clinical data.

In practice, SPORT can be implemented and realized in different ways depending on the clinical goal and/or predefined solution space. This work is focused on the use of coplanar station points. The delivery of this type of treatment can be realized using fixed-gantry delivery or by rotational arc SPORT, which improves current VMAT by using only a single arc rotation to produce conformal dose distribution. The dosimetric improvement of rotational SPORT arises from the differential angular distribution of the station points in accordance to the actual demand of the specific clinical case. More generally, SPORT with collimator modulation,⁴⁶ noncoplanar, and/or even nonisocentric beams can also be optimized using this framework. Clearly, more future research is needed for this type of treatment to be implemented clinically.

For generality, physical constraints of the delivery system are not fully included in the current study. While future implementation of the algorithm may have to consider the vendor specific constraints, we would like to mention that all three optimization techniques in the hybrid algorithm have the ability to incorporate the machine constraints. Peng et al.²⁰ have showed that how column generation can take care of the machine constraints. For the subgradient method and pattern search, one can do an appropriate projection after each iteration to assure that the new solution satisfies the machine constraints.

In conclusion, an integrated optimization method has been developed for simultaneous optimization of beam angles and aperture shapes. The formalism paves the way for the realization of SPORT and may find useful applications in other related modalities such as VMAT and IMRT.

APPENDIX: ANALYTICAL CALCULATION OF THE DERIVATIVES

For the sake of simplicity, we use Fig. 1 and explain how we can calculate the right and left derivatives of the function G analytically for the variable $X_b^{A1}$.

According to the chain rule and the fact that the function F approximates the function G [see Eq. (6)], we have

$${\displaystyle \frac{\partial G}{{\partial }^{+}{X}_b^{A1}}\left(X,\theta \right)\cong \frac{\partial F\left(Z\right)}{\partial Z}\times \frac{\partial \left(\sum _{b=1:N}\mathrm{\Phi }\left(X_b,{\theta }_b\right){\eta }_b^{*}\right)}{{\partial }^{+}{X}_b^{A1}}.}$$ (A1)

Figure 1 shows that increasing $X_b^{A1}$ by one unit is equivalent to closing the (1, 2) beamlet and so decreasing $\mathrm{\Phi }\left(X_b,{\theta }_b\right)$ by D_1,2(θ_b). So,

$${\displaystyle \frac{\partial \left(\sum _{b=1:N}\mathrm{\Phi }\left(X_b,{\theta }_b\right){\eta }_b^{*}\right)}{{\partial }^{+}{X}_b^{A1}}=-{\eta }_b^{*}{D}_{1,2}\left({\theta }_b\right).}$$ (A2)

Combining the above two equations, we have

$${\displaystyle \frac{\partial G}{{\partial }^{+}{X}_b^{A1}}\left(X,\theta \right)\cong -\frac{\partial F\left(Z\right)}{\partial Z}\times {\eta }_b^{*}{D}_{1,2}\left({\theta }_b\right).}$$ (A3)

We can have the same argument for the left derivative. In this case, decreasing $X_b^{A1}$ by one unit means opening the (1, 1) beamlet and increasing $\mathrm{\Phi }\left(X_b,{\theta }_b\right)$ by D_1,1(θ_b). Therefore, we have

$${\displaystyle \frac{\partial G}{{\partial }^{-}{X}_b^{A1}}\left(X,\theta \right)\cong \frac{\partial F\left(Z\right)}{\partial Z}\times {\eta }_b^{*}{D}_{1,1}\left({\theta }_b\right).}$$ (A4)