Abstract
Purpose:
The authors present a novel paddle-based rotating-shield brachytherapy (P-RSBT) method, whose radiation-attenuating shields are formed with a multileaf collimator (MLC), consisting of retractable paddles, to achieve intensity modulation in high-dose-rate brachytherapy.
Methods:
Five cervical cancer patients using an intrauterine tandem applicator were considered to assess the potential benefit of the P-RSBT method. The P-RSBT source used was a 50 kV electronic brachytherapy source (Xoft Axxent™). The paddles can be retracted independently to form multiple emission windows around the source for radiation delivery. The MLC was assumed to be rotatable. P-RSBT treatment plans were generated using the asymmetric dose–volume optimization with smoothness control method [Liu et al., Med. Phys. 41(11), 111709 (11pp.) (2014)] with a delivery time constraint, different paddle sizes, and different rotation strides. The number of treatment fractions (fx) was assumed to be five. As brachytherapy is delivered as a boost for cervical cancer, the dose distribution for each case includes the dose from external beam radiotherapy as well, which is 45 Gy in 25 fx. The high-risk clinical target volume (HR-CTV) doses were escalated until the minimum dose to the hottest 2 cm3 (D2cm3) of either the rectum, sigmoid colon, or bladder reached their tolerance doses of 75, 75, and 90 Gy3, respectively, expressed as equivalent doses in 2 Gy fractions (EQD2 with α/β = 3 Gy).
Results:
P-RSBT outperformed the two other RSBT delivery techniques, single-shield RSBT (S-RSBT) and dynamic-shield RSBT (D-RSBT), with a properly selected paddle size. If the paddle size was angled at 60°, the average D90 increases for the delivery plans by P-RSBT on the five cases, compared to S-RSBT, were 2.2, 8.3, 12.6, 11.9, and 9.1 Gy10, respectively, with delivery times of 10, 15, 20, 25, and 30 min/fx. The increases in HR-CTV D90, compared to D-RSBT, were 16.6, 12.9, 7.2, 3.7, and 1.7 Gy10, respectively. P-RSBT HR-CTV D90-values were insensitive to the paddle size for paddles angled at less than 60°. Increasing the paddle angle from 5° to 60° resulted in only a 0.6 Gy10 decrease in HR-CTV D90 on average for five cases when the delivery times were set to 15 min/fx. The HR-CTV D90 decreased to 2.5 and 11.9 Gy10 with paddle angles of 90° and 120°, respectively.
Conclusions:
P-RSBT produces treatment plans that are dosimetrically and temporally superior to those of S-RSBT and D-RSBT, although P-RSBT systems may be more mechanically challenging to develop than S-RSBT or D-RSBT. A P-RSBT implementation with 4–6 shield paddles would be sufficient to outperform S-RSBT and D-RSBT if delivery times are constrained to less than 15 min/fx.
Keywords: brachytherapy, intensity modulated brachytherapy, rotating-shield brachytherapy, cervical cancer, electronic brachytherapy
1. INTRODUCTION
Conventional high-dose-rate brachytherapy (HDR-BT) uses unshielded radiation sources that emit dose distributions that are radially symmetric about the source axis. This limits the deliverable radiation dose to cervical cancer tumors without exceeding the maximum allowable dose to the organs-at-risk (OARs) adjacent to the tumor. This is especially true in cases where the tumor is bulky (>40 cm3), laterally extended, or nonsymmetric2–5 where this can compromise treatment effectiveness if the high-risk clinical target volume (HR-CTV) is underdosed as a result.
Interstitial brachytherapy is one option to overcome this limitation and is the recommended treatment modality of the American Brachytherapy Society (ABS).6–8 Another option is the use of supplementary interstitial needles along with an intracavitary applicator (IS+ICBT).3,9,10 Tandem and ring3,9 or tandem and ovoid10 applicators with additional provision for needle placement have been introduced for IS+ICBT. These applicators enable enhanced tumor coverage under 3D image guidance, but are invasive due to the use of the interstitial needles. Even if the number of catheters, the location of catheters, and the source dwell times are computed in an optimized fashion, the resulting dose distributions are still constrained by the radially symmetric dose distribution, source emissions.
Intensity-modulated brachytherapy techniques such as rotating-shield brachytherapy (RSBT)11–13 and dynamic modulated brachytherapy (DMBT)14–16 were introduced as a means of improving intracavitary brachytherapy dose distributions for rectal and cervical cancer. When used as proposed by the authors, RSBT works by using a shield that partially occludes an electronic brachytherapy (eBT) source (Xoft Axxent™, iCAD, Inc., Nashua, NH, USA), which rotates in a manner that directs radiation away from healthy sensitive tissues and into cancerous tissue.11–13 Due to the diversity in tumor shapes seen in cervical cancer patients, multiple different shield emission angles would need to be made available to users in order to ensure the dose conformity of laterally extended tumors. Small emission angles with RSBT result in increased treatment times. A rapid emission angle selection (REAS) technique with single-shield RSBT (S-RSBT) was proposed to strike the best balance between treatment time and dose distribution quality, which is measured by tumor coverage and OAR sparing.12 Dynamic-shield RSBT (D-RSBT) allows the use of different azimuthal emission angles during the delivery via a layered shielding apparatus, with each layer independently rotatable to flexibly form different emission windows.17 With a delivery time of 20–30 min per treatment fraction (fx), D-RSBT can produce better treatment plans than S-RSBT, while S-RSBT may perform better when the delivery time is limited (<20 min/fx) since it can make use of a single large emission angle.17 The major limitation of D-RSBT lies in the limit of the maximal azimuthal emission angle that can be formed by the apparatus.
In this study, we propose a paddle-based rotating-shield brachytherapy (P-RSBT) device, a novel conformal brachytherapy treatment technique. The concept of shield paddles for IMBT was previously proposed;18 however, no subsequent study was conducted to reveal its capability or demonstrate its clinical potential. The proposed P-RSBT system is able to utilize the full angular delivery space and only one delivery source is needed. P-RSBT has the potential to improve tumor coverage without compromising OAR sparing with the same treatment time, as compared to S-RSBT and D-RSBT.
2. MATERIALS AND METHODS
2.A. System overview, dose calculation, and anchor plan generation
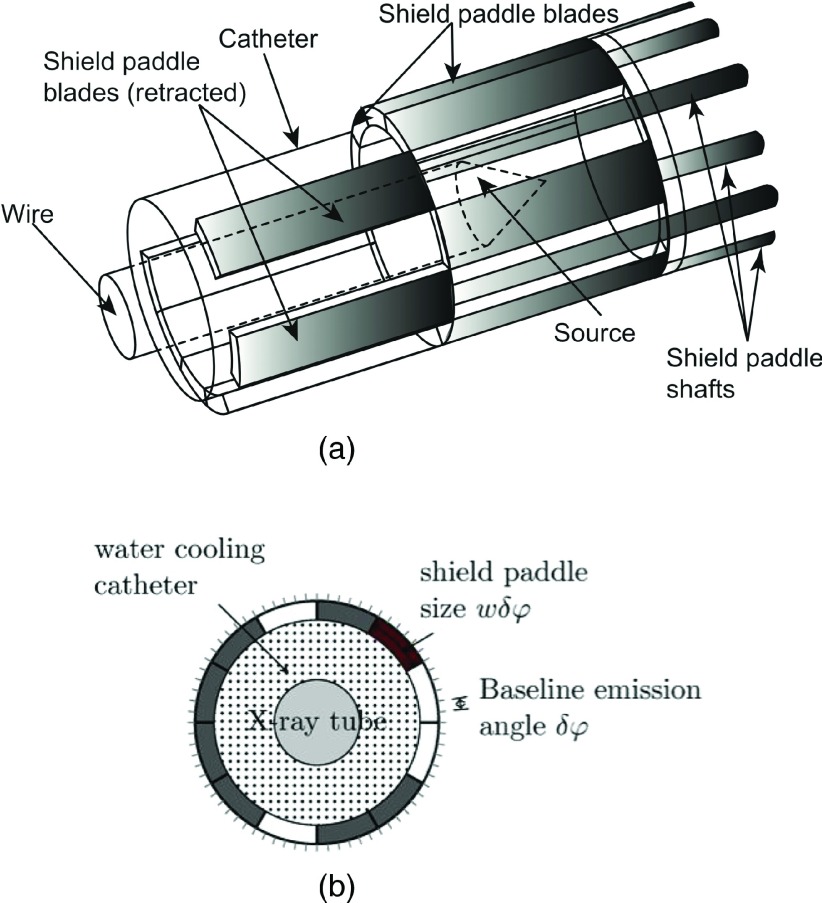
P-RSBT uses a set of independently operated shield paddles, each of which covers a sector of the radiation field, to achieve intensity modulation. The modulation is achieved by the insertion and retraction of the shield paddles (assumed to be constructed of tungsten alloy), as well as the rotation and translation of the whole applicator, shown in Fig. 1. As this is a conceptual study for assessing the P-RSBT technique, the exact diameter of the applicator is not finalized. It is expected that an applicator with a diameter of less than 10 mm could be constructed, which would necessitate appropriate anesthesia techniques for the brachytherapy procedure. As shown in Fig. 1, an integer, K, number of shield paddles, is arranged to form a cylindrical tube with each paddle shielding a sector of 360°/K angularly. The maximum number of paddles (K) achievable will depend upon the method used to drive the paddles. A candidate motor available today is the Faulhaber microdrive, of 1.9 mm diameter and 9.5 mm length. With a 5.4 mm radiation source, up to four microdrives could be used in principle to control up to four paddles. Constructing the tandem applicator so that it has two corkscrewlike tracks or keyways, on the inner wall is one method for controlling the rotation of the apparatus. The angular separation between the keyways is half that of the paddle emission angle or 45° for a 90° paddle. The P-RSBT apparatus would have a laterally protruding key that fits into a keyway, causing the paddle apparatus to rotate about the source catheter as it is inserted into the applicator. With two keyways, the apparatus only needs to rotate by an angular amount equal to half the paddle emission angle every 5 mm (45°/5 mm = 9°/mm), the keyway would have a 360° rotation for every 40 mm for P-RSBT. The set of shield paddles can move in (close) and out (open) independently to block and to expose the source, respectively. The paddle openings form a shield aperture to azimuthally modulate the radiation dose intensity. In the longitudinal direction, the zenith emission angle is fixed. The shield paddles can be constructed of 0.5 mm thick tungsten, providing an eBT source dose transmission of less than 0.1%.11 The shield is rotatable about the source in a fine angular stride, further improving dose conformity. The P-RSBT source is assumed to be a shielded 50 kV photon source (Xoft Axxent™, iCAD, Inc.) in this study.
FIG. 1.
A conceptual design of a P-RSBT applicator (a) 3D view. For the purpose of legibility, not all paddle shafts are drawn. (b) Cross-sectional view.
During the P-RSBT delivery, the shield travels together with the source through an intracavitary applicator inserted in the tumor. The source stops at multiple dwell positions along the central path with a spacing of Δλ, which is set to 5 mm in this study. At each dwell position, a number of shield apertures are formed in an optimized fashion to deliver the radiation dose sequentially. The shield may rotate when necessary during the delivery.
The paddles are indexed counterclockwise with, initially, the kth paddle (k = 0, 1, …, K − 1) shielding the sector from degrees k ⋅ δφ to (k + 1) ⋅ δφ, where δφ is the angular size of a paddle. A RSBT beamlet is defined as the dose rate at the point due to a shielded radiation source at dwell position with the kth paddle open. The total dose delivered to point i is calculated as a time-weighted sum of the beamlets over all dwell positions,
| (1) |
where τj,k is the emission time for which the source is located at dwell position j with the kth paddle open. To improve the quality of the dose plan, small emission angle beamlets are used with δφ = 5°. The asymmetric dose–volume optimization with smoothness control (ADOS) method1 was used for dose optimization to generate anchor plans for P-RSBT. The following objective function was used:
| (2) |
| (2a) |
| (2b) |
In the objective function, is the prescribed dose for each voxel in the volumes of interest (VOI’s), and and are coefficients for the overdose and underdose penalties, respectively. is a Heaviside step function. The second smoothness term in the objective function is used to ensure a smooth emission time sequence at each dwell position, which is important to improve the delivery efficiency with a limited quality loss of the delivered plan.
This optimization model aims to achieve a high quality anchor plan. However, the plan in its present design may not yet be clinically practical since (1) the use of a large number of paddles profoundly complicates the control of the shielding device, and (2) the total delivery time may still be too long for clinical use. To overcome those limitations, we propose using a rotatable shielding device with larger-sized paddles (size expressed in Sec. 2.B) and develop an optimal shield-sequencing algorithm to compute a deliverable plan to “best” approximate the anchor plan while remaining cognizant of the delivery time constraint.
2.B. Generating P-RSBT delivery plans with optimal sequencing
The use of large-sized (i.e., larger than δφ used in anchor plan generation) paddles may not be able to deliver the anchor plan exactly, thus compromising the quality of the delivered dose distribution relative to that of the anchor plan. On the other hand, it may help improve the delivery efficiency. Although the rotation capability of the paddles can better approximate the quality of the anchor plan, it also prolongs the delivery time. The goal of the optimal shield-sequencing algorithm is to compute a deliverable P-RSBT plan from the anchor plan and strike a balance between the plan quality and the delivery time.
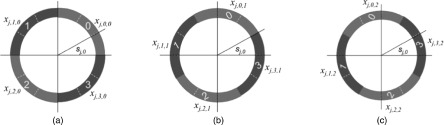
Assuming that the size of a paddle Δφ is a multiple of the beamlet size used in the anchor plan generation, that is, Δφ = w ⋅ δφ (w > 1 is an integer), the number of paddles is K/w, which is an integer. The rotation stride of the paddles can also be a multiple of δφ. In the following shield sequencing model, we consider a rotation stride to be degree δφ and rotation to be in the counterclockwise direction. The model is ready to be extended with a rotation stride of multiple δφ. In Fig. 2, the size of a beamlet is δφ = 30°, and the paddle size Δφ = 90° (that is, w = 3).
FIG. 2.
Beam coverage with rotations. The P-RSBT shield consists of four paddles each with a size of 90°. The size of a beamlet is 30°. Each beamlet bj,k covers a sector sj,k. While opening a paddle forms a beam which can cover multiple sectors. The sector sj,0 is covered by the beams formed with paddle 0 open (a) and with paddle 3 open after a rotation of degree 30° (b) and a rotation of degree 60° (c).
A P-RSBT aperture can be represented by the superposition of a set of beamlets. Let xj,m,l denote the emission time for which the source is located at dwell position j with the mth paddle open (m = 0, 1, …, K/w − 1) and after a rotation of degree l ⋅ δφ (l = 0, 1, …, w − 1). Note that it is not necessary for a paddle to rotate to a degree larger than (w − 1) ⋅ δφ. Consider the sector sj,k (k = 0, 1, …, K − 1) corresponding to the beamlet bj,k in the anchor plan. Let and , where is the floor function and % is the modulo operator. The qth paddle is immediately adjacent to the pth paddle in a clockwise rotation. Sector sj,k is irradiated by the beams with the pth paddle open and l = 0, …, k%w and by the beams with the qth paddle open and l = (k%w) + 1, …, w − 1. Thus, the irradiation time tj,k for sj,k is . For instance, in Fig. 2, the sector sj,0 is covered by paddle 0 with a rotation of 0° and by paddle 3 with rotations of 30° and 60°. If we assume that the emission time of the beamlet bj,k is τj,k in the anchor plan, then we can introduce the delivery error εj,k, with εj,k = tj,k − τj,k.
For each dwell position j and each rotation configuration l, our goal is to deliver the fluence map Mj,l = {xj,m,l|m = 0, 1, …, K/w − 1} in the minimum amount of time. Note that each entry xj,m,l of Mj,l corresponds to a paddle indexed by m. Without a loss of generality, we assume that all nonzero entries in Mj,l are different. The method is ready to be extended to the case of equal nonzero entries. We first sort Mj,l in a nondecreasing order with the sorted nonzero entries being xj,m0,l < xj,m1,l < ⋯ < xj,mκ,l (κ > 0).
The following method is then used to efficiently deliver Mj,l. At the very beginning, open all paddles corresponding to nonzero entries in Mj,l. After delivering radiation for xj,m0,l units of time, close paddle m0. At the time, the sector corresponding to paddle m0 receives the appropriate dose. Then, continue to irradiate for xj,m1,l − xj,m0,l units of time before closing paddle m1. When paddle m1 is closed, the sector corresponding to paddle m1 receives the desired dose. In general, paddle mi is open until completing irradiation in xj,mi,l − xj,mi−1,l units of time after paddle mi−1 is closed (i = 1, 2, …, κ). In this way, the minimum delivery time for Mj,l is . The total delivery time for all the fluence maps Mj,l’s is then .
The goal of the sequencing method is to compute a set of delivery plan times, xj, m,l, that best approximates the anchor plan subject to a given delivery time budget T. Here, we propose to minimize the total delivery error between the anchor plan and the delivery plan,
| (3) |
| (3a) |
| (3b) |
| (3c) |
H(x) in Eq. (3) is a Heaviside function introduced for considering the difference between overdosing and underdosing. and are the corresponding coefficients for overdosing and underdosing penalties. Equation (3) is formulated to a quadratic programming problem and solved by an in-house CPLEX-based optimizer.19
2.C. Clinical cases, treatment goals, and plan quality metrics
Five cervical cancer cases, with HR-CTVs ranging from 43.2 to 78.9 cm3, were retrospectively studied in this work. All cases were clinically treated by Fletcher-Suit-Delclos style titanium tandem and ovoids based upon conventional point A plans but using 3 T MRI guidance.6,7,20,21 The HR-CTV and the OARs, namely the rectum, sigmoid colon, and bladder, were delineated by a radiation oncologist following GEC-ESTRO recommendations.22,23 For each patient, P-RSBT simulation was delivered through a single-channel tandem applicator without a ring or ovoids. It was assumed that the HR-CTV and OARs received a dose of 45 Gy of external beam radiation therapy (EBRT) in 25 fx at 1.8 Gy/fx. It was also assumed for all patients that the same HDR-BT plan was delivered for all five treatment fractions, which is standard number of fractions at the authors’ institution. The HR-CTV doses [Gy10] and OAR doses [Gy3] were expressed as equivalent doses in 2 Gy fractions of EBRT (EQD2),15 using α/β values of 10 and 3 Gy, respectively.2
No explicit dose prescription was assumed for the HDR-BT delivery. The P-RSBT treatment goal was to escalate tumor dose while satisfying both OAR tolerance limits and the given delivery time constraint. The minimum dose received by 90% of the HR-CTV (D90) was calculated to be as close to the maximum dose constraint to the hottest 2 cm3 (D2 cm3) of the rectum, sigmoid colon, and bladder and could not exceed the tolerance doses2,13 of 75, 75, and 90 Gy3, respectively. Therefore, the HR-CTV D90 values represent overall treatment plan quality with a given RSBT technique, since they refer to maximally achievable tumor coverage without compromising any of the OAR tolerances. Hereafter, all HR-CTV D90 values represent the maximally achievable dose without compromising the OAR sparing.
2.D. Treatment planning
For each of the five clinical cases, an anchor plan was generated using the ADOS method1 with the beamlet size δφ = 5° (see Sec. 2.A). The P-RSBT optimal shield sequencing was then applied to the anchor plan with a different paddle size w ⋅ δφ for w = 1, 3, 6, 9, 12, 18, and 24. For the shield rotation stride, we considered r ⋅ δφ for r = 1, 2, …, 6 to study the sensitivity of the P-RSBT design to different rotation strides. For the purpose of comparison, S-RSBT and D-RSBT optimal sequencings were applied to the anchor plans to generate delivery plans.
For each anchor plan, a delivery efficiency curve was computed by using each of the P-RSBT, D-RSBT, and S-RSBT methods, showing the trade-off between the delivery time (x-axis) and the HR-CTV D90 (y-axis) of the delivery plan.12,13,17 For the P-RSBT method, one delivery efficiency curve was computed for each combination of the different paddle sizes and the rotation strides considered. One delivery efficiency curve (segment) can be considered to be superior to another if it is located above and/or to the left of another.
Quantitative comparisons on HR-CTV D90 were also performed for P-RSBT with different paddle sizes against S-RSBT and D-RSBT, while setting different delivery time budgets (10, 15, 20, 25, and 30 min/fx).
3. RESULTS
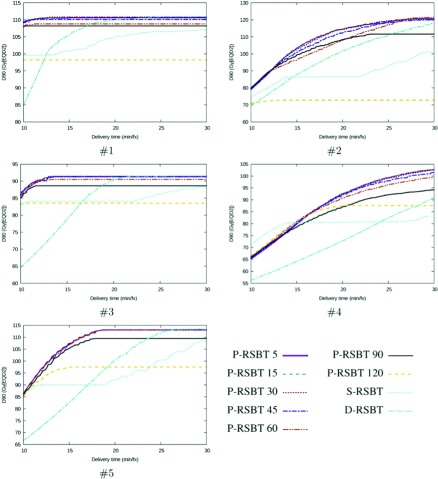
As shown by the delivery efficiency curves in Fig. 3, for all the five cases tested, the P-RSBT technique was able to achieve higher HR-CTV D90-values for the delivery plans than those achieved by S-RSBT and D-RSBT, especially when the delivery time ranged from 10 to 20 min/fx.
FIG. 3.
Delivery efficiency curve comparisons. P-RSBT with different paddle sizes was compared to S-RSBT and D-RSBT on five clinical cases. A point on a delivery efficiency curve stands for the maximal D90 (y-axis) that can be achieved with the corresponding delivery method for a given delivery time (x-axis). The rotation stride r ⋅ δφ for P-RSBT was 5°.
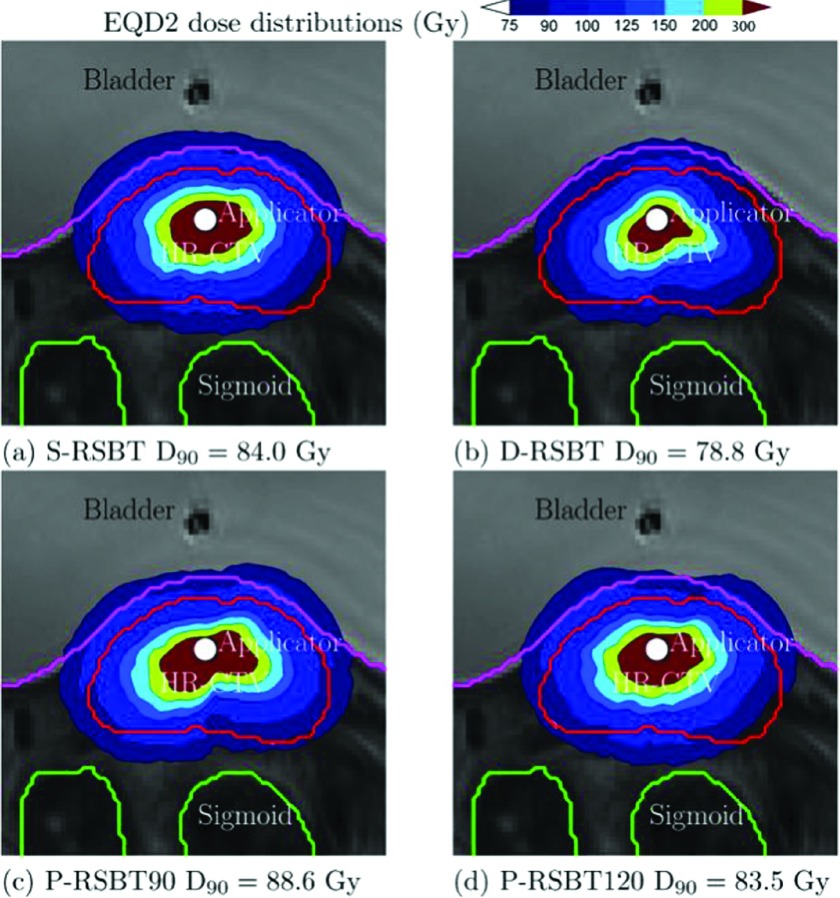
P-RSBT dose distributions are insensitive to the paddle size when it is 60° or less. For seven different paddle sizes tested in this study, the impact of the paddle size change on the plan quality was minimal. Consider the treatment time budget of 15 min/fx as an example. Although the HR-CTV D90 of the delivery plan decreased while increasing the paddle size, the average D90 decrease was very small. In fact, the average D90 achieved by P-RSBT-30 (the number stands for the shield paddle size, measured in degrees) was only 0.1 Gy10 less than that achieved by P-RSBT-5. Further increase of the paddle size to 60° resulted in 0.6 Gy10 in the HR-CTV compared to P-RSBT-5. The HR-CTV D90 decrease increased to 2.5 Gy10 with P-RSBT-90. However, if the paddle size was increased to 120°, the D90 decrease was about 12 Gy10. The detailed quantitative comparisons are shown in Table I. For all these experimental data, the rotation stride r ⋅ δφ = 5°.
TABLE I.
HR-CTV D90 (Gy10) comparisons between P-RSBTs with different paddle sizes, S-RSBT, and D-RSBT on five clinical cases under different delivery time limits. The rotation stride for P-RSBT was 5°.
| Case | Delivery time (min/fx) | P-RSBT-5 | P-RSBT-15 | P-RSBT-30 | P-RSBT-45 | P-RSBT-60 | P-RSBT-90 | P-RSBT-120 | S-RSBT | D-RSBT |
|---|---|---|---|---|---|---|---|---|---|---|
| #1 | 10 | 109.4 | 109.1 | 109.1 | 108.6 | 107.7 | 107.6 | 98.2 | 99.4 | 84.9 |
| 15 | 110.5 | 110.8 | 110.8 | 110.1 | 108.8 | 108.2 | 98.2 | 100.8 | 105.3 | |
| 20 | 110.6 | 110.8 | 110.8 | 110.1 | 108.8 | 108.2 | 98.2 | 105.1 | 109.9 | |
| 25 | 110.6 | 110.8 | 110.8 | 110.1 | 108.8 | 108.2 | 98.2 | 106.5 | 110.7 | |
| 30 | 110.6 | 110.8 | 110.8 | 110.1 | 108.8 | 108.2 | 98.2 | 107.1 | 110.9 | |
| #2 | 10 | 79.2 | 79.3 | 79.4 | 79.1 | 79.9 | 80.0 | 70.9 | 74.7 | 69.7 |
| 15 | 103.4 | 103.1 | 102.5 | 100.7 | 96.2 | 99.2 | 72.8 | 86.2 | 87.7 | |
| 20 | 114.5 | 114.4 | 114.3 | 112.2 | 107.8 | 108.3 | 72.8 | 86.2 | 101.3 | |
| 25 | 118.6 | 119.1 | 119.3 | 118.1 | 117.1 | 111.6 | 72.8 | 92.8 | 111.0 | |
| 30 | 120.6 | 120.9 | 120.2 | 119.9 | 121.3 | 111.6 | 72.8 | 100.8 | 117.8 | |
| #3 | 10 | 86.0 | 85.9 | 86.0 | 86.0 | 85.3 | 85.1 | 83.1 | 83.0 | 64.6 |
| 15 | 91.4 | 91.4 | 91.3 | 91.3 | 90.5 | 88.6 | 83.5 | 84.0 | 78.8 | |
| 20 | 91.4 | 91.4 | 91.3 | 91.3 | 90.5 | 88.6 | 83.5 | 84.0 | 90.1 | |
| 25 | 91.4 | 91.4 | 91.3 | 91.3 | 90.5 | 88.6 | 83.5 | 86.0 | 91.4 | |
| 30 | 91.4 | 91.4 | 91.3 | 91.3 | 90.5 | 88.6 | 83.5 | 88.3 | 91.5 | |
| #4 | 10 | 65.2 | 65.2 | 65.3 | 65.5 | 66.0 | 65.9 | 66.5 | 71.1 | 56.3 |
| 15 | 79.8 | 79.9 | 80.0 | 80.2 | 80.9 | 78.5 | 80.7 | 80.5 | 64.1 | |
| 20 | 92.3 | 92.3 | 92.2 | 92.0 | 90.3 | 87.1 | 87.4 | 80.5 | 72.7 | |
| 25 | 99.3 | 99.1 | 99.1 | 97.9 | 96.1 | 91.9 | 87.6 | 80.5 | 82.4 | |
| 30 | 102.7 | 102.5 | 102.6 | 101.4 | 99.6 | 94.1 | 87.6 | 83.2 | 90.8 | |
| #5 | 10 | 86.5 | 86.5 | 86.5 | 86.5 | 86.4 | 85.8 | 85.2 | 86.0 | 66.7 |
| 15 | 107.3 | 107.3 | 107.4 | 106.9 | 106.6 | 105.3 | 97.5 | 90.0 | 82.6 | |
| 20 | 113.0 | 113.1 | 113.1 | 113.1 | 113.0 | 109.5 | 97.5 | 91.8 | 100.2 | |
| 25 | 113.0 | 113.1 | 113.1 | 113.1 | 113.0 | 109.5 | 97.5 | 100.2 | 111.4 | |
| 30 | 113.0 | 113.1 | 113.1 | 113.1 | 113.0 | 109.5 | 97.5 | 108.3 | 113.5 | |
| Avg | 10 | 85.2 | 85.2 | 85.2 | 85.1 | 85.0 | 84.9 | 80.8 | 82.8 | 68.4 |
| 15 | 98.5 | 98.5 | 98.4 | 97.8 | 96.6 | 96.0 | 86.5 | 88.3 | 83.7 | |
| 20 | 104.4 | 104.4 | 104.3 | 103.7 | 102.1 | 100.4 | 87.9 | 89.5 | 94.8 | |
| 25 | 106.6 | 106.7 | 106.7 | 106.1 | 105.1 | 102.0 | 87.9 | 93.2 | 101.4 | |
| 30 | 107.7 | 107.7 | 107.6 | 107.2 | 106.6 | 102.4 | 87.9 | 97.5 | 104.9 |
Table I also demonstrates the quantitative comparisons among P-RSBT, S-RSBT, and D-RSBT. For instance, comparing P-RSBT-60 and S-RSBT, the average HR-CTV D90 increases for all five cases were 2.2, 8.3, 12.6, 11.9, and 9.1 Gy10, respectively, while setting the delivery time to 10, 15, 20, 25, and 30 min/fx; and the HR-CTV D90 increases against D-RSBT were 16.6, 12.9, 7.2, 3.7, and 1.7 Gy10, respectively.
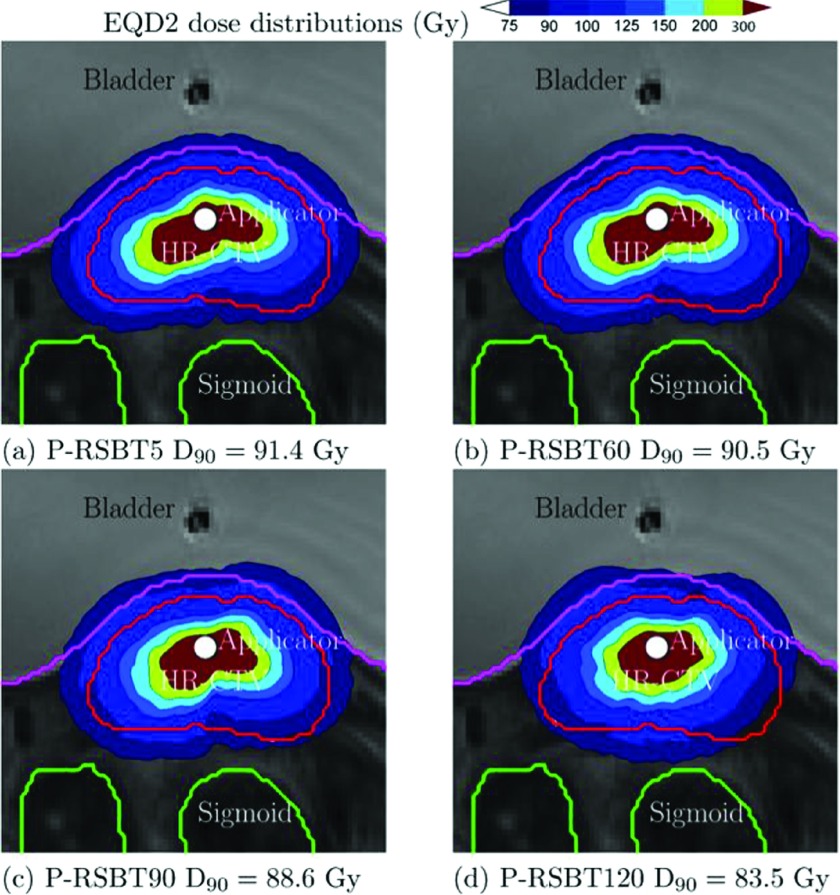
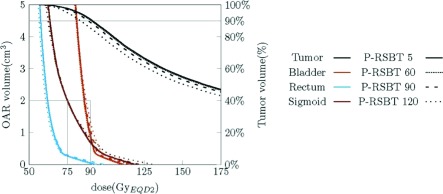
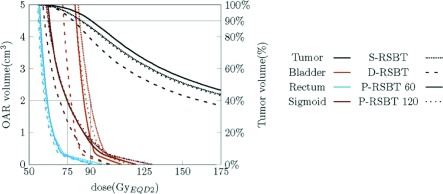
The example dose distributions are shown in Fig. 4 for case #3 using different paddle sizes of 5°, 30°, 60°, and 90° for a delivery time constraint of 15 min/fx. The corresponding dose–volume histograms (DVHs) are plotted in Fig. 5. The isodose lines in Fig. 4 were less conformal to the HR-CTV boundary as the paddle size increased, although the changes were marginal. The corresponding DVHs in Fig. 5 also present minimal differences when using less than 60° paddle sizes. The HR-CTV D90’s of those four P-RSBT delivery settings were 91.4, 91.3, 90.5, and 88.6 Gy10, respectively. Comparisons for dose distributions and DVHs between P-RSBT, S-RSBT, and D-RSBT for case #3 are shown in Figs. 6 and 7, respectively.
FIG. 4.
EQD2 dose distributions for case #3 with a delivery time of 15 min/fx using P-RSBT with different paddle sizes of 5°, 60°, 90°, and 120°, and the rotation stride r ⋅ δφ = 5°.
FIG. 5.
Dose–volume histogram plots for case #3 with a delivery time of 15 min/fx using P-RSBT with different paddle sizes of 5°, 60°, 90°, and 120°, and the rotation stride r ⋅ δφ = 5°.
FIG. 6.
EQD2 dose distributions of case #3 with a delivery time 15 min/fx using S-RSBT, D-RSBT, P-RSBT-90, and P-RSBT-120. The rotation stride r ⋅ δφ for P-RSBT was 5°.
FIG. 7.
Dose–volume histogram plots for case #3 with a delivery time of 15 min/fx by S-RSBT, D-RSBT, P-RSBT-60, and P-RSBT-120. The rotation stride r ⋅ δφ for P-RSBT was 5°.
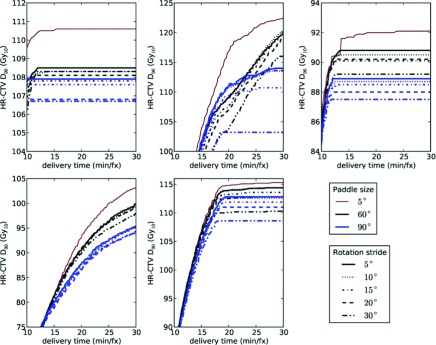
The delivery efficiency curves for P-RSBT with respect to different rotation strides are shown in Fig. 8 for P-RSBT-60 and P-RSBT-90. The detailed HR-CTV D90 comparisons for the delivery plans computed by P-RSBT with different combinations of the paddle size and the rotation stride are demonstrated in Table II. In general, the increase of the rotation stride compromised the quality of the delivery plan with respect to HR-CTV D90. However, the HR-CTV D90 decreases were marginal. In all five cases, with the rotation stride increasing from 5° to 20°, the HR-CTV D90 decreases of the delivery plans by P-RSBT were within 1.5 Gy10 while the delivery time ranged from 10 to 30 min/fx. While the rotation stride is set to 10°, the HR-CTV D90 decreased less than 0.6 Gy10.
FIG. 8.
Comparisons of delivery efficiency curves for five clinical cases by P-RSBT with different combinations of the paddle size and the rotation stride. In each figure panel, the top-most efficiency curve using P-RSBT with a paddle size of 5° (no rotations) is used as a reference, which serves as an upper bound for all the other efficiency curves.
TABLE II.
HR-CTV D90 (Gy10) comparison of the delivery plans using P-RSBT with different combinations of the paddle size and the rotation stride, the HR-CTV D90’s were calculated as the mean over five clinical cases.
| Rotation strides | |||||||
|---|---|---|---|---|---|---|---|
| Delivery time (min/fx) | 5° | 10° | 15° | 20° | 25° | 30° | |
| 10 | 85.1 | 85.1 | 85.1 | 84.9 | 84.9 | 84.6 | |
| 15 | 97.8 | 97.4 | 97.2 | 96.6 | 96.6 | 96.5 | |
| P-RSBT-45 | 20 | 103.7 | 103.2 | 103.0 | 102.0 | 102.0 | 101.6 |
| 25 | 106.1 | 105.7 | 105.4 | 104.6 | 104.4 | 103.9 | |
| 30 | 107.2 | 106.5 | 106.2 | 105.3 | 105.1 | 104.5 | |
| 10 | 85.0 | 85.0 | 84.8 | 84.7 | 84.7 | 84.5 | |
| 15 | 96.6 | 96.4 | 96.3 | 96.0 | 95.8 | 95.1 | |
| P-RSBT-60 | 20 | 102.1 | 101.8 | 101.3 | 100.9 | 100.4 | 99.5 |
| 25 | 105.1 | 104.8 | 104.2 | 103.5 | 103.2 | 101.6 | |
| 30 | 106.6 | 106.5 | 105.7 | 104.7 | 104.3 | 102.1 | |
| 10 | 84.9 | 84.9 | 84.7 | 84.7 | 84.4 | 84.4 | |
| 15 | 96.0 | 95.8 | 95.4 | 95.2 | 94.4 | 93.8 | |
| P-RSBT-90 | 20 | 100.4 | 100.0 | 99.4 | 99.1 | 98.3 | 96.8 |
| 25 | 102.0 | 101.6 | 101.0 | 100.4 | 99.8 | 97.8 | |
| 30 | 102.4 | 102.0 | 101.5 | 100.7 | 100.1 | 98.1 | |
4. DISCUSSION
P-RSBT outperforms S-RSBT in general. The P-RSBT plan can be delivered using S-RSBT by setting the azimuthal emission angle of the shield to coincide with the paddle size. However, this S-RSBT technique may prolong the delivery time compared to P-RSBT since P-RSBT can have multiple paddles open simultaneously during delivery, while S-RSBT just simulates the P-RSBT delivery with one paddle open at a time. For a given delivery time, P-RSBT is able to achieve a higher quality plan delivery than S-RSBT. It is also possible for a S-RSBT plan to be converted to a P-RSBT plan with a shorter delivery time. Our experimental data generally support this analysis, with the exception of case #4 where the delivery time was 10 or 15 min/fx. This was caused by the fact that the P-RSBT shield sequencing did not seek all possible paddle sizes. The S-RSBT plan seeks an emission angle that creates a delivery plan analogous to the anchor plan. The emission angles used in the S-RSBT delivery plans for case #4, while the delivery times were 10 and 15 min/fx, respectively, were 285° and 235°.
P-RSBT also performs better than D-RSBT simply because it is able to form beam apertures with larger coverage. The maximum beam coverage with D-RSBT is 180°, while P-RSBT can cover 360°. P-RSBT does not have a significant advantage over D-RSBT in forming beam apertures with fine-tuned beam coverage; thus, it is not prominently better than D-RSBT while given a sufficiently large delivery time (∼30 min/fx), which allows using more beams with small emission angles. With a delivery time constraint of 30 min/fx, the average HR-CTV D90 of the delivery plans achieved using P-RSBT was marginally higher than that achieved by D-RSBT, which was less than 3 Gy10.
For the three RSBT delivery techniques, S-RSBT, D-RSBT, and P-RSBT, the ability to form small beam apertures improves the dose distribution quality, while the ability to form large beam apertures reduces the treatment time. It is relatively easy to make use of large beam apertures in S-RSBT, while it is easy to make small beam apertures in D-RSBT. P-RSBT provides a way to combine those two features together, yet at the price of more complex apparatus design.
Reducing the paddle size theoretically improves the performance of P-RSBT, but may significantly complicate the design of the P-RSBT system. Fortunately, our experiments demonstrated that the HR-CTV D90 minimally decreased while increasing the paddle size from 5° to 90°. As shown in Table I, P-RSBT-60 with six paddles and P-RSBT-90 with four paddles could be considered as a good balance between system complexity and plan quality. Further reducing the number of paddles (e.g., P-RSBT-120) may result in significant loss of plan quality.
The size of rotation stride r ⋅ δφ is another important parameter to be considered in the P-RSBT system design. While a smaller rotation stride generally provides improved dose conformity, it requires more precise control and tends to be more vulnerable to motion uncertainty. Our experiments showed marginal HR-CTV D90 decreases, while the rotation stride increased from 5° to 20° regardless of the delivery times between 10 and 30 min/fx. This demonstrates the feasibility of having a P-RSBT system with a small number of paddles and a large rotation stride, which may significantly simplify the complexity of a P-RSBT system design.
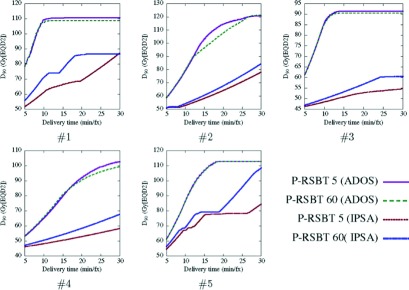
Our experiments further reveal that the smoothness of the emission times between adjacent beamlets in an anchor plan played an important role for P-RSBT to achieve high-quality plans. Figure 9 shows the delivery efficiency curves by P-RSBT-5 and P-RSBT-60 for the anchor plans computed by two different dose optimizers: one was the ADOS method1 in which emission time smoothness is enforced by the L2-norm, and the other was based on the inverse planning by simulated annealing (IPSA) technique where no smoothness was enforced. The HR-CTV D90’s of the anchor plans using ADOS and IPSA were 91.4 and 94.0 Gy10, respectively. HR-CTV D90 decreases between the delivery plans when using P-RSBT-5 and P-RSBT-60 based on the ADOS anchor plans were larger than those based on the IPSA anchor plans. Also, the delivery efficiency curves for the ADOS anchor plans were superior to those for the IPSA anchor plans. These preliminary data justify the importance of smoothness in an anchor plan for P-RSBT to adopt large-sized paddles and large rotation strides, thus decreasing the complexity of the delivery system.
FIG. 9.
Delivery efficiency curves comparison between P-RSBTs with different paddle sizes with different dose optimizers for five cases.
In this study, we did not include the comparisons of high dose levels such as HR-CTV D50 and V150 (V150 is the volume receiving at least 150% of the prescription dose). As clinical data indicating the maximum tolerable hot spots for cervical cancer brachytherapy are lacking,11–13 it is not possible to definitely claim a maximum allowable dose–volume value corresponding to hot spots in a cervical cancer tumor. Caution must be exercised, however, prior to using RSBT techniques for cervical cancer.
5. CONCLUSION
The proposed P-RSBT technique shows promise for improving tumor coverage (HR-CTV D90) without compromising rectum, bladder, and sigmoid sparing with a clinically acceptable treatment time. Compared to S-RSBT and D-RSBT, P-RSBT improved HR-CTV D90 (tumor coverage) on average by 8.3 and 12.9 Gy10, respectively, using the same 15 min delivery time constraint per fraction. A P-RSBT implementation with 4–6 shield paddles would be sufficient to outperform S-RSBT and D-RSBT if delivery times are constrained to less than 15 min/fx.
ACKNOWLEDGMENTS
The authors thank Gareth Smith, who proofread and edited this paper. This research was supported in part by the NSF Grant No. CCF-1318996 and the NIH Grant No. 1R01-EB020665.
REFERENCES
- 1.Liu Y., Flynn R. T., Kim Y., and Wu X., “Asymmetric dose-volume optimization with smoothness control for rotating-shield brachytherapy,” Med. Phys. 41(11), 111709 (11pp.) (2014). 10.1118/1.4897617 [DOI] [PubMed] [Google Scholar]
- 2.Potter R., Dimopoulos J., Georg P., Lang S., Waldhausl C., Wachter-Gerstner N., Weitmann H., Reinthaller A., Knocke T. H., Wachter S., and Kirisits C., “Clinical impact of MRI assisted dose volume adaptation and dose escalation in brachytherapy of locally advanced cervix cancer,” Radiother. Oncol. 83, 148–155 (2007). 10.1016/j.radonc.2007.04.012 [DOI] [PubMed] [Google Scholar]
- 3.Dimopoulos J. C. A., Kirisits C., Petric P., Georg P., Lang S., Berger D., and Potter R., “The Vienna applicator for combined intracavitary and interstitial brachytherapy of cervical cancer: Clinical feasibility and preliminary results,” Int. J. Radiat. Oncol., Biol., Phys. 66, 83–90 (2006). 10.1016/j.ijrobp.2006.04.041 [DOI] [PubMed] [Google Scholar]
- 4.Tanderup K., Nielsen S. K., Nyvang G. B., Pedersen E. M., Rohl L., Aagaard T., Fokdal L., and Lindegaard J. C., “From point A to the sculpted pear: MR image guidance significantly improves tumour dose and sparing of organs at risk in brachytherapy of cervical cancer,” Radiother. Oncol. 94, 173–180 (2010). 10.1016/j.radonc.2010.01.001 [DOI] [PubMed] [Google Scholar]
- 5.Anderson J. W., Xia J., Flynn R. T., Modrick J. M., Bhatia S. K., Jacobson G. M., and Kim Y., “High resolution (3 tesla) MRI-guided conformal brachytherapy for cervical cancer: Consequences of different high-risk CTV sizes,” J. Contemp. Brachytherapy 5, 101–109 (2013). 10.5114/jcb.2013.36180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Viswanathan A. N. and Thomadsen B., “American Brachytherapy Society consensus guidelines for locally advanced carcinoma of the cervix. Part I: General principles,” Brachytherapy 11, 33–46 (2012). 10.1016/j.brachy.2011.07.003 [DOI] [PubMed] [Google Scholar]
- 7.Viswanathan A. N., Beriwal S., De Los Santos J. F., Demanes D. J., Gaffney D., Hansen J., Jones E., Kirisits C., Thomadsen B., and Erickson B., “American Brachytherapy Society consensus guidelines for locally advanced carcinoma of the cervix. Part II: High-dose-rate brachytherapy,” Brachytherapy 11, 47–52 (2012). 10.1016/j.brachy.2011.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Syed A., Puthawala A. A., Abdelaziz N. N., el-Naggar M., Disaia P., Berman M., Tewari K. S., Sharma A., Londrc A., and Juwadi S., “Long-term results of low-dose-rate interstitial-intracavitary brachytherapy in the treatment of carcinoma of the cervix,” Int. J. Radiat. Oncol., Biol., Phys. 54, 67–78 (2002). 10.1016/S0360-3016(02)02900-0 [DOI] [PubMed] [Google Scholar]
- 9.Kirisits C., Lang S., Dimopoulos J., Berger D., Georg D., and Potter R., “The Vienna applicator for combined intracavitary and interstitial brachytherapy of cervical cancer: Design, application, treatment planning, and dosimetric results,” Int. J. Radiat. Oncol., Biol., Phys. 65, 624–630 (2006). 10.1016/j.ijrobp.2006.01.036 [DOI] [PubMed] [Google Scholar]
- 10.Jurgenliemk-Schulz I. M., Tersteeg R. J., Roesink J. M., Bijmolt S., Nomden C. N., Moerland M. A., and de Leeuw A. A., “MRI-guided treatment-planning optimisation in intracavitary or combined intracavitary/interstitial PDR brachytherapy using tandem ovoid applicators in locally advanced cervical cancer,” Radiother. Oncol. 93, 322–330 (2009). 10.1016/j.radonc.2009.08.014 [DOI] [PubMed] [Google Scholar]
- 11.Yang W., Kim Y., Wu X., Song Q., Liu Y., Bhatia S. K., Sun W., and Flynn R. T., “Rotating-shield brachytherapy for cervical cancer,” Phys. Med. Biol. 58, 3931–3941 (2013). 10.1088/0031-9155/58/11/3931 [DOI] [PubMed] [Google Scholar]
- 12.Liu Y., Flynn R. T., Yang W., Kim Y., Bhatia S. K., Sun W., and Wu X., “Rapid emission angle selection for rotating-shield brachytherapy,” Med. Phys. 40, 051720 (12pp.) (2013). 10.1118/1.4802750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu Y., Flynn R. T., Kim Y., Yang W., and Wu X., “Dynamic rotating-shield brachytherapy,” Med. Phys. 40, 121703 (11pp.) (2013). 10.1118/1.4828778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Webster M., Scanderbeg D., Watkins T., Stenstrom J., Lawson J., and Song W., “Dynamic modulated brachytherapy (DMBT): Concept, design, and application,” Med. Phys. 38, 3702 (2011). 10.1118/1.3612878 [DOI] [Google Scholar]
- 15.Webster M. J., Devic S., Vuong T., Yup Han D., Park J. C., Scanderbeg D., Lawson J., Song B., Watkins W. T., Pawlicki T., and Song W. Y., “Dynamic modulated brachytherapy (DMBT) for rectal cancer,” Med. Phys. 40, 011718 (12pp.) (2013). 10.1118/1.4769416 [DOI] [PubMed] [Google Scholar]
- 16.Webster M. J., Scanderbeg D. J., Watkins W. T., Stenstrom J., Lawson J. D., and Song W. Y., “Dynamic modulated brachytherapy (DMBT): Concept, design, and system development,” Brachytherapy 10, S33–S34 (2011). 10.1016/j.brachy.2011.02.046 [DOI] [Google Scholar]
- 17.Wu X. and Liu Y., “Solving circular integral block decomposition in polynomial time,” in Algorithms and Computation, Lecture Notes in Computer Science (Springer, New York, NY, 2012), pp. 342–351. [Google Scholar]
- 18.Smith P. C., Klein M., Hausen H., and Lovoi P. A., “Radiation therapy apparatus with selective shielding capability,” U.S. patent 7686755 (30 March 2010).
- 19.I. I. CPLEX, V12.1: User’s Manual for CPLEX (International Business Machines Corporation, New York, NY, 2009), Vol. 46, p. 157. [Google Scholar]
- 20.Anderson J., Huang Y., and Kim Y., “Dosimetric impact of point A definition on high-dose-rate brachytherapy for cervical cancer: Evaluations on conventional point A and MRI-guided, conformal plans,” J. Contemp. Brachytherapy 4, 241–246 (2012). 10.5114/jcb.2012.32559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sun W., Bhatia S. K., Jacobson G. M., Flynn R. T., and Kim Y., “Target volume changes through high-dose-rate brachytherapy for cervical cancer when evaluated on high resolution (3.0 Tesla) magnetic resonance imaging,” Pract. Radiat. Oncol. 2, e101–e106 (2012). 10.1016/j.prro.2012.03.012 [DOI] [PubMed] [Google Scholar]
- 22.Haie-Meder C., Potter R., Van Limbergen E., Briot E., De Brabandere M., Dimopoulos J., Dumas I., Hellebust T. P., Kirisits C., Lang S., Muschitz S., Nevinson J., Nulens A., Petrow P., and Wachter-Gerstner N., “Recommendations from Gynaecological (GYN) GEC-ESTRO Working Group (I): Concepts and terms in 3D image based 3D treatment planning in cervix cancer brachytherapy with emphasis on MRI assessment of GTV and CTV,” Radiother. Oncol. 74, 235–245 (2005). 10.1016/j.radonc.2004.12.015 [DOI] [PubMed] [Google Scholar]
- 23.Potter R., Haie-Meder C., Van Limbergen E., Barillot I., De Brabandere M., Dimopoulos J., Dumas I., Erickson B., Lang S., Nulens A., Petrow P., Rownd J., and Kirisits C., “Recommendations from Gynaecological (GYN) GEC ESTRO Working Group (II): Concepts and terms in 3D image-based treatment planning in cervix cancer brachytherapy-3D dose volume parameters and aspects of 3D image-based anatomy, radiation physics, radiobiology,” Radiother. Oncol. 78, 67–77 (2006). 10.1016/j.radonc.2005.11.014 [DOI] [PubMed] [Google Scholar]