Generation of brain pseudo-CTs using an undersampled, single-acquisition UTE-mDixon pulse sequence and unsupervised clustering

Abstract

Purpose:

MR-based pseudo-CT has an important role in MR-based radiation therapy planning and PET attenuation correction. The purpose of this study is to establish a clinically feasible approach, including image acquisition, correction, and CT formation, for pseudo-CT generation of the brain using a single-acquisition, undersampled ultrashort echo time (UTE)-mDixon pulse sequence.

Methods:

Nine patients were recruited for this study. For each patient, a 190-s, undersampled, single acquisition UTE-mDixon sequence of the brain was acquired (TE = 0.1, 1.5, and 2.8 ms). A novel method of retrospective trajectory correction of the free induction decay (FID) signal was performed based on point-spread functions of three external MR markers. Two-point Dixon images were reconstructed using the first and second echo data (TE = 1.5 and 2.8 ms). R2^∗ images (1/T2^∗) were then estimated and were used to provide bone information. Three image features, i.e., Dixon-fat, Dixon-water, and R2^∗, were used for unsupervised clustering. Five tissue clusters, i.e., air, brain, fat, fluid, and bone, were estimated using the fuzzy c-means (FCM) algorithm. A two-step, automatic tissue-assignment approach was proposed and designed according to the prior information of the given feature space. Pseudo-CTs were generated by a voxelwise linear combination of the membership functions of the FCM. A low-dose CT was acquired for each patient and was used as the gold standard for comparison.

Results:

The contrast and sharpness of the FID images were improved after trajectory correction was applied. The mean of the estimated trajectory delay was 0.774 μs (max: 1.350 μs; min: 0.180 μs). The FCM-estimated centroids of different tissue types showed a distinguishable pattern for different tissues, and significant differences were found between the centroid locations of different tissue types. Pseudo-CT can provide additional skull detail and has low bias and absolute error of estimated CT numbers of voxels (−22 ± 29 HU and 130 ± 16 HU) when compared to low-dose CT.

Conclusions:

The MR features generated by the proposed acquisition, correction, and processing methods may provide representative clustering information and could thus be used for clinical pseudo-CT generation.

1. INTRODUCTION

PET/MR is an emerging technology with exciting potential for improvements over PET/CT for staging, multiparametric therapy planning, and functional assessment of treatment response. Indeed, PET/MR has already outperformed PET/CT in patients with metastatic breast cancer, where it demonstrated fewer false-positives and improved the detection of soft-tissue lesions in the brain, liver, and lymph nodes.¹ In prostate cancer, it allows improved visualization and anatomic localization of lesions with new agents such as [¹¹C]choline and [⁶⁸Ge]PSMA.^2,3 However, current PET/MR systems lack accurate attenuation correction, which is the most significant of all of the corrections applied during PET image reconstruction. In particular, standardized uptake value (SUV) errors in brain of 20% or more have been reported relative to PET/CT (Ref. 4) and thus pose concerns regarding the use of the technology in clinical trial settings.^5–11 Similar errors and issues have been reported for body imaging, with the largest number of errors occurring within and adjacent to bone tissue.^10–15 These results are not surprising as at least four tissue types, including bone, are required in order to achieve accurate SUVs,^5,16 whereas current commercial PET/MR attenuation correction (MR-AC) solutions use a three- or four-class segmentation that neglect bone.¹³ The three-class segmentation method identifies air (external to the patient) and lungs and classifies the rest of the patient as soft tissue. The four-tissue segmentation method further delineates soft tissue into fat and water.

MR-based radiation therapy planning (MR-RTP) and integrated MRI treatment machines are another emerging technology, with the potential to improve radiation delivery, given the improved tumor visualization compared to conventional systems. Traditionally, patients undergo CT for dose calculation and diagnostic imaging for tumor delineation requiring coregistration for treatment planning. Similar to the situation with attenuation correction for PET/MR, radiation absorption in tissue depends on photon interaction with electrons, and MR does not directly measure such effects. Previously, investigators have demonstrated that manually contouring structures on MRI and assigning corresponding bulk densities have the potential for accurate dose calculations. However, this approach is labor intensive and clinically impractical.^17–19 An automatic, voxelwise method could resolve these limitations.

Therefore, there is a common need for both MR-AC and MR-RTP: a MR acquisition method that supports the ability to identify multiple tissue types, including bone as the most attenuating tissue type, so that radiation attenuation and absorption can be accurately determined. A particular challenge is that when using conventional MR pulse sequences, bone and air have similar MR signal amplitudes and cannot be differentiated despite the extremes of photon attenuation. As bone has low signal due to its very fast T2* relaxation and air has low signal due to its low proton density, ultrashort echo time (UTE) MR pulse sequences have been investigated because of their ability to distinguish bone from air, as this is of great importance in the head and neck where there is juxtaposition of air, cortical bone, trabecular bone, and soft tissue in the skull and sinuses.^{4,5,7,9,20,21} Furthermore, there is interest in using the Dixon approach to differentiate soft tissue into fat and water components.^5,22,23

Another common need for both MR-AC and MR-RTP is an analysis method to convert MR information to CT. Hsu et al. proposed a clustering-based approach to generate a pseudo-CT.²⁴ A number of MR features, i.e., T1-weighted, T2-weighted, UTE with two TEs, Dixon-fat, Dixon-water, and time-of-flight based vessel images, were obtained retrospectively in order to generate pseudo-CT using the fuzzy C-means (FCM) pattern recognition. This approach demonstrated the possibility of clustering-based pseudo-CT generation. Mixing the clusters according to the estimated membership function showed a strong potential for preserving tissue heterogeneity. However, a limitation of this method is acquiring all these MR data sets was time-consuming, i.e., requiring approximately 12 min,²⁴ and thus limiting its clinical practicality.

Even though previous methods of UTE-based MR-AC and MR-RTP have constituted an active research field during the past decade, they face unique challenges regarding their ultimate clinical adoption due to their unstable image quality, lack of flexibility for image planning, and impractically long acquisition times.^7,8,25 We have previously demonstrated that undersampling with UTE can achieve fast image acquisition, while retaining good image quality and the ability to differentiate bone from air.²¹ However, there are other factors that limit the clinical use of UTE. For example, it relies on non-Cartesian encoding schemes to sample k-space, and as this is not the conventional approach for clinical MRI, UTE images may have stability artifacts caused by hardware limitations predominately due to eddy currents. Previously published studies have reported several attempts to correct these artifacts by characterizing the gradient system and applying the corresponding measurements in the MR reconstruction of the UTE images.^26,27 However, these approaches significantly limit the clinical flexibility of UTE scans as they require a number of additional calibrations before or after MR acquisition.

Herein, we present a novel, single acquisition UTE-mDixon with 25% angular undersampling.^21,28 Also, we propose a unique retrospective, image-based, eddy-current calibration method used to ensure high-quality MR data compared to the prospective, eddy-current characterizations previously described.²⁹ The overall goal of the work is to provide a clinically practical approach which involves minimal manual intervention to the workflow and allows maximum flexibility in the scan parameter selections such as the number of spatial samplings and field-of-view (FOV) while maintaining satisfactorily distinguishable tissue-signal properties for pseudo-CT generation.

2. MATERIALS AND METHODS

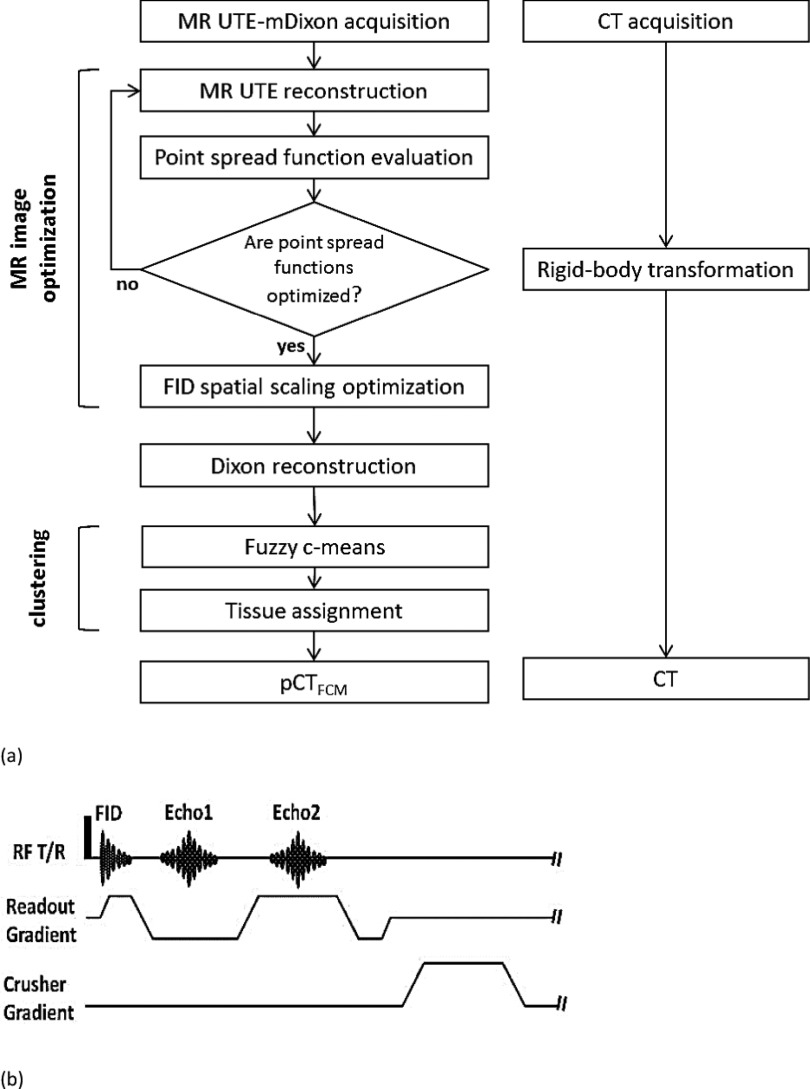
To establish a clinically practical workflow, multiple steps including acquisition, correction, and processing were developed to obtain the data with the best quality that can be achieved within a single MR acquisition. Figure 1 shows a flow chart of the proposed workflow and a pulse diagram of the UTE-mDixon MR sequence. The details of each step will subsequently be described.

FIG. 1.

A data acquisition, correction, and processing scheme (a) and a pulse diagram of the UTE-mDixon sequence (b).

2.A. Data acquisition

Nine patients were recruited for this study using a protocol that was approved by the University Hospitals Case Medical Center Institutional Review Board. The clinical PET/MR brain workflow was modified so as to incorporate the research sequence at the beginning of the scan on the Philips Ingenuity TF PET/MR scanner.^30,31 MR UTE-mDixon images were acquired using an 8-channel, SENSE head coil, which is the standard setup for Philips brain PET/MR workflow protocol. A radial-encoding, multiecho, ultrashort echo sequence with a 25% angular sampling density was performed. As detailed in our previous report,²¹ the 100% angular sampling is defined by the number of phase-encoding directions required for a Cartesian acquisition of the same volume and spatial resolution. Therefore, the 25% sampling density speeds up the overall scan fourfold. The detailed MR sequence parameters are listed in Table I. Following the initial, free induction decay (FID) signal, two subsequent echoes were collected at the minimal echo spacing determined by the hardware performance and imaging geometry. No gradient rewinding was applied between the echoes in order to minimize the overall scan duration. To allow retrospective trajectory-delay calibration, external MR markers, i.e., three water-filled NMR tubes attached orthogonally to the head coil, were placed in the FOV and imaged together at the time of the clinical scans.³² Fully calibrated and corrected k-space raw data were saved and exported for dedicated MR reconstruction.

TABLE I.

MR sequence parameters.

Scanner	Philips ingenuity TF PET/MR
Total scan duration	190 s
Sampling density	25%
Sequence type	Multi-echo UTE-mDixon
TR	5.1 ms
TE	0.1, 1.5, and 2.8 ms
Acquisition bandwidth	1050 Hz
Acquisition orientation	Axial
Field of view	320 × 320 × 320 mm3
Acquisition voxel size	1.25 × 1.25 × 1.25 mm3
Excitation type	Nonselective 3D isotropic
Flip angle	8°

Low-dose CT images with 120 kVp and 50 mAs were acquired using Philips GEMINI TF PET/CT,³³ a Philips Brilliance 64-channel CT scanner. The helical CT raw data with a collimation of 64 × 0.625 mm were collected and reconstructed using filtered back projection in the voxel size of 1.17 × 1.17 × 5.00 mm³, as recommended by the vendor in order to obtain images with high quantitative accuracy and an acceptable noise level. In this study, the measured CT images were treated as the reference approach for validating pseudo-CT generated from MR images.

2.B. MR reconstruction and trajectory delay correction

Customized, reconstruction software was designed as stand-alone executables that can be run on a research workstation. The customized, stand-alone reconstruction is capable of performing radial encoding gridding with undersampling, as described by Stehning, Börnert et al.²⁸ and Hu et al.,²¹ and in Dixon reconstruction.³⁴ To achieve retrospective image calibration and correction, a baseline FID and two echo images were first reconstructed without trajectory delay calibration using the stand-alone reconstruction software and by setting the trajectory delay to the default value (0 μs in this study). The retrospective, trajectory-delay correction³² was performed using matlab (The MathWorks, Natick, MA) software to drive the reconstruction executables. Specifically, the trajectory delay parameter value used in the reconstruction was swept through the feasible range of the MR scanner from −3 to +3 μs. A nonzero trajectory delay time is added to the readout encoding by shifting the origin of the k-space to a positive or negative encoding direction for the FID images. In our investigation, the impact of the eddy current can be modeled as a pure global delay factor for the readout gradient, which induces a linear shift on the actual trajectory, when the simple, fixed exponential eddy current decay was applied.³⁵ Images reconstructed at each value are analyzed in order to select the optimal delay as that which results in the sharpest profile defined as the fewest nonzero pixels through the three external markers. Finally, in order to correct for the gradient scaling artifacts caused by the eddy currents during the rising slope of the readout gradient for the FID image acquisition,⁵ a global resizing factor was obtained by estimating the spatial scaling factor between the FID image and the two echo images which were free from the scaling artifact because echoes are acquired on the plateau of the readout gradient and are autocentered to the origin of the k-space.

2.C. Coregistration between CT and MR

A rigid-body, affine transformation was performed for CT and MR registrations using the comkat software suite.^36,37 The measured CT data were reconstructed with a slice thickness of 5 mm to result in images with an acceptable noise level for the low-dose scanning protocol. The UTE MR images were, therefore, treated as the reference for the registration as the slice thickness with MR (isotropic 1.25 mm) was much less than that of the low-dose CT. The resulting, registered, and resampled 1.25-mm CT data set was saved for further analysis.

2.D. Clustering approach and class assignment

To transform the undersampled UTE-mDixon MR data into images that could be used for attenuation correction and therapy planning, a pseudo-CT image volume was created using an unsupervised clustering method. Specifically, the FCM algorithm was implemented^24,38 and optimized in matlab in order to perform clustering wherein the number of data points is large (see the Appendix for details). Performance of the optimized FCM program, now available within the comkat software suite (http://comkat.case.edu), was compared to that of the FCM method provided within the matlab fuzzy logic toolbox. The computational speeds were measured using a single computer having an Intel^® i7 3.4 GHz CPU, 16 GB RAM, and running Windows 7 64-bit, and given the same data and FCM parameter settings.

With the intent of identifying the brain, fluid, fat, bone, and air, FCM was used to identify five clusters. Three feature images, i.e., fat, water, and R2^∗, were used as input data for the FCM algorithm and were derived from the three primitive MR data, i.e. FID, the first echo, and the second echo. Fat and water image volumes were reconstructed from the first and second echoes using the modified, two-point Dixon method (mDixon). The difference between regular and modified Dixon approaches lies in the choice of TEs. One of the TEs for the standard Dixon must be in-phase or out-of-phase, while the modified Dixon relaxes this requirement.³⁴ Therefore, minimal echo spacing may be used for the modified Dixon approach in order to achieve the minimal TR and, therefore, further minimize the total acquisition time. The R2^∗ map, i.e., 1/T2^∗, was estimated from the primitive image series using the equation

$${\displaystyle I\left(p\right)=I_0{\text{e}}^{-R{\text{2}}^{*}\times \text{TE}\left(p\right)},}$$

where I₀ denotes the MR signal intensity when TE(p) = 0 and I(p) denotes the signal intensity acquired when the TE was equal to the pth TE of the acquisition series. Due to the fact that the fitted R2^∗ of air would be greatly affected by the noise, an air mask was generated by taking a 5% threshold of the maximum of the FID and then performing morphologic closing to remove artifactual islands of nonair followed by opening to fill in gaps at air-tissue interfaces.^5,8 R2^∗ values were set to zero in voxels identified as air and were otherwise estimated by fitting. Air voxels in other feature images were also set to zero for clustering.

The five clusters were identified using the FCM method and were assigned as air, brain, fat, fluid, and bone based on a two-step method.

• 1.R2^∗ sorting: Clusters were ordered according to the R2^∗ coordinate of the cluster centroid and were then identified as air < brain < fat < fluid < bone.
• 2.Fat-class determination: Another step was taken to classify the tissue classes which had similar R2^∗ values, i.e., fat and fluid. The class with the highest Dixon-fat value would be reassigned to the fat class if it were misclassified to the fluid class during the first step.

The pseudo-CT was created assuming that each voxel represents a mixture of different tissue types. Specifically, the value of each voxel of the pseudo-CT was calculated as a weighted sum of the Hounsfield values of different tissue types. The weights were set equal to the class membership values estimated by FCM. This is consistent with membership values being interpreted as the volume-fraction composition of the tissue types.^24,39 The Hounsfield values of pure air, fat, fluid, brain, and cortical bone were set to −1000, −98, 13, 40, and 1524 HU, respectively.⁴⁰

2.E. Resolution matching filtering

To facilitate comparison of the pseudo-CT to the low-dose CT which served as a reference, the spatial resolution of the two image volumes was made to be comparable. Noting that the spatial resolution of the MR and, therefore, that of the pseudo-CT exceeded that of the low-dose CT as acquired in the context of PET/CT for the brain, the pseudo-CT was smoothed using a 3D Gaussian kernel. This was based on the spatial resolutions of the MR and CT that were measured with physical phantoms.

2.F. Figures of merits for evaluation

The means and standard deviations (SDs) of the centroids corresponding to different tissue types estimated by the FCM in each patient were calculated and analyzed with regard to consistency and potential overlap. A discriminant function analysis was then performed using sas 9.4. The coordinates of the estimated centroids, i.e., R2^∗, Dixon-fat, and Dixon-water, were treated as the predictor and class as the outcome. In addition, the mean absolute prediction deviation (MAPD) was used to show the difference between measured and pseudo-CTs in a given range of CT numbers,^41–43

$${\displaystyle \text{MPAD}\left(b\right)=\frac{1}{N\left(b\right)}\sum _{i\in \underset{b}{S}}\left|{\text{CT}}_{\text{pseudo}}\left(i\right)-\text{CT}\left(i\right)\right|,}$$

where MPAD(b) is the MAPD of the subset of voxels S_b having a value of b ± 10 HU, in which i denotes the spatial index and N(b) denotes the number of voxels in the subset S_b. MAPD, without specifying b, was calculated using voxels of all of the HU values. To evaluate the bias, an analogous measure, i.e., the mean prediction deviation (MPD), was calculated without evaluating the absolute operation. In these calculations, voxels outside the CT field of view were excluded.

3. RESULTS

3.A. Trajectory delay correction and derived feature images

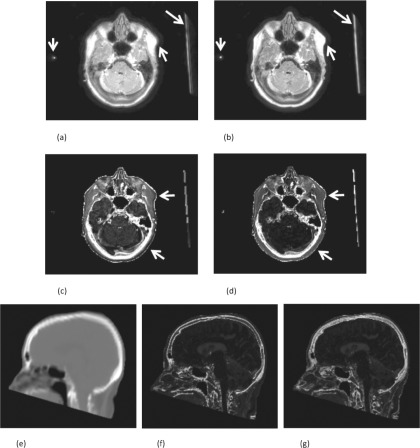
The mean estimated trajectory delay of the FIDs among the patients was 0.774 μs (min: 0.180 μs, max: 1.350 μs). Figure 2 shows the effect of the results of the trajectory correction on the images. The arrows highlight areas where the edges are sharpened and well-defined in the result with the correction. Furthermore, the correction reduces blurring of tissue edges and partial volume averaging of fine structures. Therefore, correction makes the brain appear darker even though the gray level display scaling is calibrated to have a similar brightness to that of fat.

FIG. 2.

MR trajectory delay correction. The FID images without (a) and with (b) trajectory delay correction of +1.18 μs. The (c) and (d) are the corresponding R2^∗ images estimated without (c) and with (d) the correction. Common display scales are used to display the same types of images. The arrows point to the edges and regions in which the improvement can be seen between images without and with the correction. In addition, a sagittal slice is selected to compare the bone structure of the CT (e) with the FCM estimated bone memberships without (f) and with (g) trajectory delay correction.

In addition to the trajectory delay correction, a global resizing factor is needed to account for the effects of eddy currents during the rising slope of the readout gradient. The average resizing factor is 0.979 (min: 0.973, max: 0.986). This value being less than 1.0 indicates that the brain and other anatomy shown in the uncorrected FID image appear larger than in the echo images. Accordingly, the FID images are also corrected by resampling in order to shrink them and restore their proper size.

The two corrections directly affect the quality and the accuracy of the estimated R2^∗ images. The results shown in Figs. 2(c) and 2(d) indicate that the average R2^∗ value (1/T2^∗) of brain tissue without the correction (0.11 ms⁻¹) is larger than with the correction (0.02 ms⁻¹). The R2^∗ with the correction matched the results reported in previously published studies (brain T2^∗ = 49 ms),⁴⁴ and the bone and skin details are much more distinct in the R2^∗ with the correction. Figures 2(e)–2(g) show a sagittal slice to compare the estimated bone structure without [Fig. 2(f)] and with the [Fig. 2(g)] correction. In Fig. 2(f), the edge of the estimated bone structure was incorrectly enhanced due to the mismatched tissue signal between the FID and the echo images. The skull and spine structure in Fig. 2(g) is clearer than that in Fig. 2(f), in which the data without the correction were used, and the MAPD between CT and pseudo-CT was reduced by 12.3% when the correction was applied.

3.B. Centroids of FCM clustering

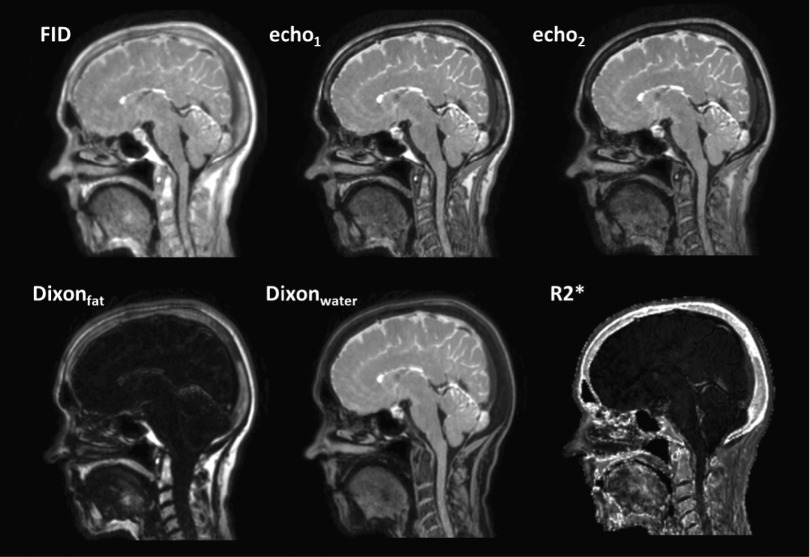
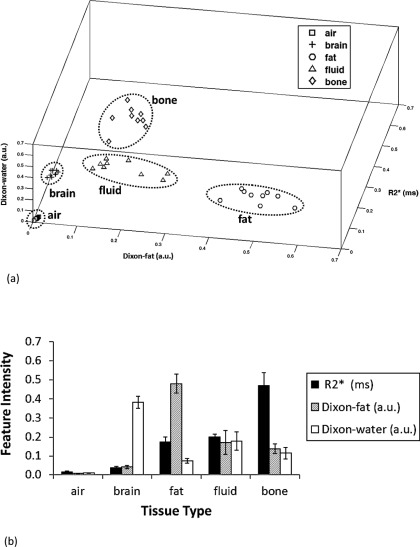
Figure 3 images show the primitive magnitude images (FID, the first echo, and the second echo) with the FID corrected for trajectory delay and global resizing, as well as the associated feature images (R2^∗, Dixon-fat, and Dixon-water) which serve as the inputs to FCM clustering. The locations of the resulting cluster centroids of the five tissue classes are shown in the feature space in Fig. 4(a). The bars in Fig. 4(b) show the means and standard deviations of each centroid coordinate for all of the patients. The results show that the mean values of the R2^∗ of the different tissues are, with the possible exception of fat and fluid, well-separated from each other so that sorting by R2^∗ can be used as the primary method for assigning clusters to tissue types. The potential ambiguity of fat and fluid can be resolved using the Dixon-fat signal as a secondary criterion. In particular, the Dixon-fat signal is highest in voxels of the fat class. Therefore, the tissue types could be robustly determined based on the proposed R2^∗ sorting and fat-determination criteria previously described. Indeed, discriminant analysis of R2^∗, Dixon-fat, and Dixon-water showed that they are all statistically significant predictors of class (p < 0.0001).

FIG. 3.

UTE-mDixon magnitude and derived images (FID, the first echo, the second echo, Dixon_fat, Dixon_water, and R2^∗).

FIG. 4.

Coordinates of the centroids of the five, cluster centroids corresponding to different tissue types. A 3D plot in the feature space of all patients’ centroids (a) and a bar chart of the means and standard deviations of the centroids shown in (b) for different tissue types. In (a), the 45 points correspond to 9 patients × 5 cluster centers each. Significant differences are found among the coordinates of the cluster centers (discriminant analysis, p < 0.0001).

3.C. Evaluation of pseudo-CTs

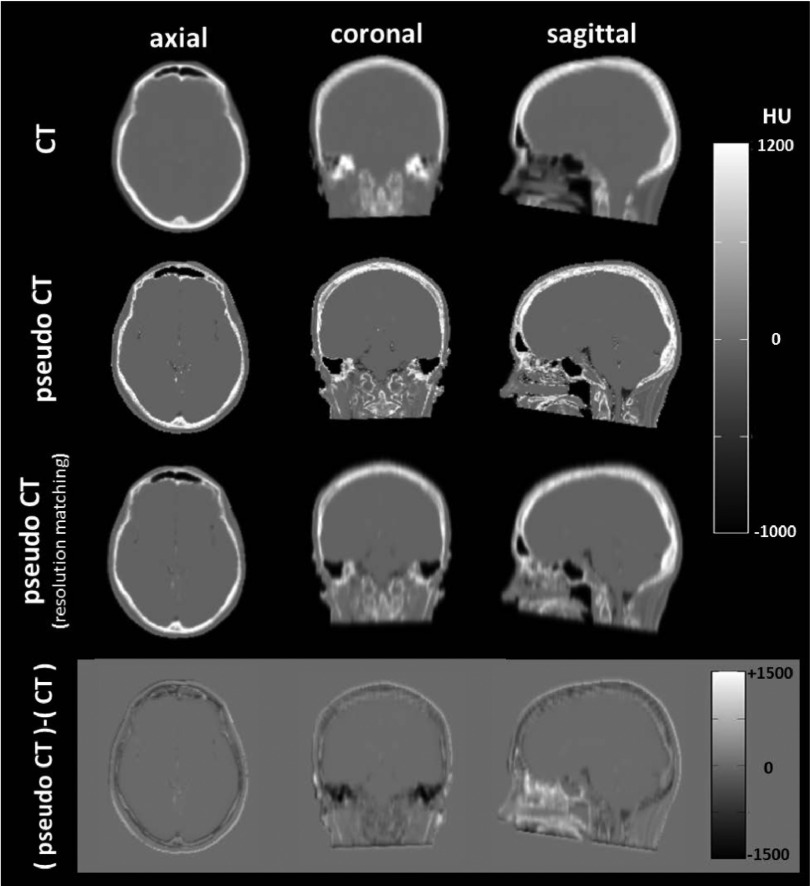
Figure 5 shows a comparison between the calculated pseudo-CT and the measured CT images. The measured CT (first row) is smoother than the pseudo-CT (second row) because the pseudo-CT is determined from the MR data, which have better spatial resolution (1.5 × 1.5 × 1.5 mm³) than the low-dose CT (1.7 × 1.7 × 6.3 mm³). Therefore, the application of resolution matching filtering makes the pseudo-CT (third row) more similar to the measured CT. The difference images (fourth row equals third row minus the first) show that the voxel values in the pseudo-CT tend to be overestimated in the nasal cavity, underestimated in the ear, and slightly underestimated in the cerebrospinal fluid (CSF) close to the brain stem and in the cortical bone of the skull.

FIG. 5.

CT versus pseudo-CT. The measured CT images (reference) are shown in the top row. The second and third rows are the pseudo-CT images and the pseudo-CT images with resolution matching filtering. The bottom images show the differences between the resolution-matched pseudo-CT and the measured CT. For comparison, the pseudo-CTs are cropped to match the FOV of the measured CT.

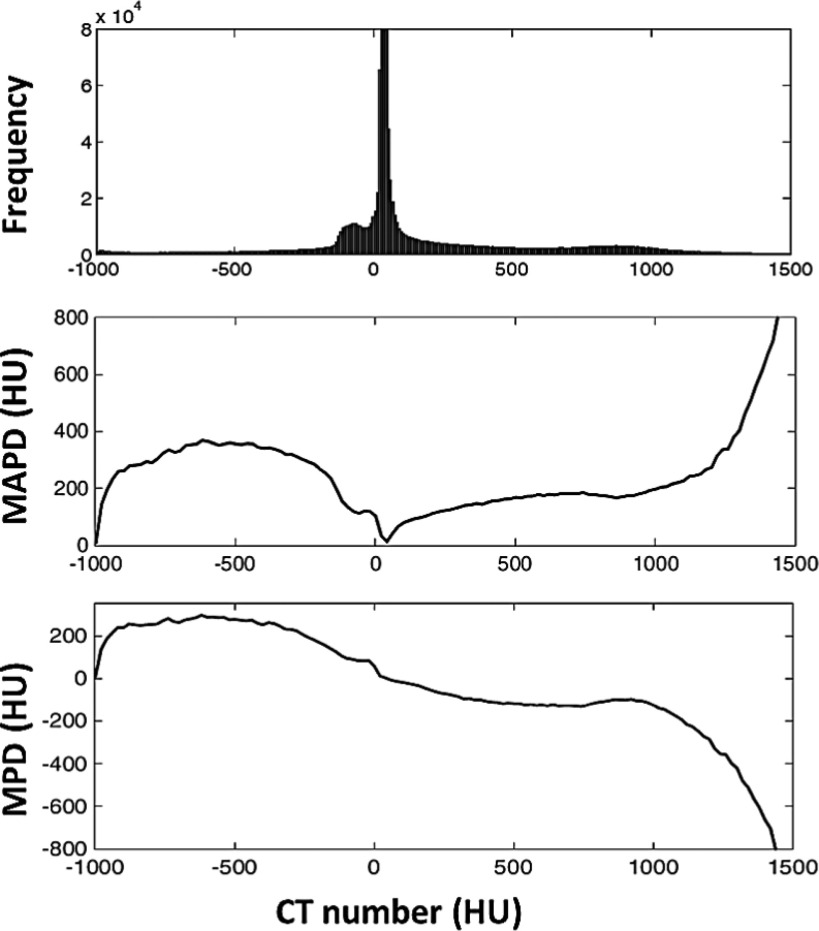
To evaluate the voxelwise accuracy of the estimated pseudo-CT, the CT histogram and MAPD curve were generated (Fig. 6). The results of the MAPD (middle) represent the average absolute HU error as a function of the measured HU value. The peak located at −600 HU with an amplitude of 360 HU indicates that some voxels are incorrectly assigned to values close to −240 HU, i.e., −600 + 360 HU, due to the positive bias shown in the MPD (lower). Upon further investigation, the voxels with values of −600 HU in the measured CT correspond to air-tissue interfaces mapped primarily to a mixture of air, fluid, and bone. Despite the relatively large magnitude of such an error, it occurred in very few voxels as the histogram (upper) indicates that very few voxels had measured HU values of −600. On the other hand, the histogram indicates that there are many voxels with measured values near 0 HU at which the MAPD (error) is quite low. In fact, the MAPD of the entire volume is 130 ± 16 HU (mean ± SD). Furthermore, the MPD is −22 ± 29 HU, thus suggesting that the overall bias of the pseudo-CT is also low.

FIG. 6.

A comparison between the voxel HU values of the pseudo-CT and those of the measured CT. The upper plot shows a frequency histogram of the pixel values in the measured CT, while the middle and lower plots show the mean absolute prediction deviation (MAPD) and mean prediction deviation (MPD). Although the MAPD has peaks at approximately −600 and 1400 HU and thus indicating high-magnitude errors, the histogram indicates that there are very few pixels, i.e., less than 0.1% and 0.01%, respectively, of the total number of voxels having these errors.

3.D. Computation cost of a three-dimensional volume using the FCM

We compared the FCM of comkat (FCM_COMKAT) and that of the fuzzy logic toolbox (FCM_toolbox). The average computing time per iteration for the FCM_comkat (0.6 s) was approximately half that with FCM_toolbox (1.2 s). Consequently, the average clustering time per patient is 67.3 s for FCM_comkat and 123.1 s for FCM_toolbox.

4. DISCUSSION

Various approaches have been developed to estimate CT-equivalent information from MR data for MR-AC and MR-RTP. Most of these approaches focused on developing different data analysis algorithms, e.g., clustering/classification,^24,45,46 supervised learning,^8,47 supervised regression,^{25,41–43,45,48} and atlas-based approaches.^49–51 However, despite the importance of a sophisticated algorithm, the signal information contained in the MR data input to the algorithm is also critical for estimating CT-equivalent information. For this reason, investigators have incorporated multiple MR sequences, e.g., T1-weighted, T2-weighted, and UTE images, which can provide separable signal information among different tissue types for CT generation. Although this strategy increases the capability of tissue discrimination, acquiring multiple MR scans is time-consuming and thus making implementation into the clinical workflow challenging.

In order to address this difficulty, we proposed a single-acquisition, undersampled UTE-mDixon protocol including scan preparation, retrospective MR image correction, and tissue clustering for pseudo-CT generation. We demonstrated that the undersampled UTE-mDixon acquisition can be completed within a clinically practical scan time of less than 200 s and with a finely sampled isotropic voxel size of 1.25 mm and which has previously been a major limitation for non-Cartesian UTE acquisition schemes. In our study, we obtained images with high image quality for anatomical localization using the water/fat separation of mDixon reconstruction. Specifically for PET/MR clinical applications, the spatial resolution of the UTE-mDixon sequences can be further reduced in order to accelerate the acquisition, as the attenuation coefficient map would be smoothed in order to match the PET image resolution before being used for reconstruction. One approach to further reduce the acquisition time is to decrease the angular sampling density. As has previously been reported,²⁸ the acquisition time can be reduced in a factor of 2 if the 12.5% angular sampling density is used. However, the signal-to-noise ratio would then decrease by approximately 30%. For this reason, the UTE-mDixon signal property among different sampling rates for the pseudo-CT generation is task-dependent and worth further study.

One of the important steps for pseudo-CT generation is to obtain MR data with the best image quality for clustering within a clinically acceptable acquisition time. The previous work of Berker et al. showed that the trajectory delay directly affects the quality of FID images.⁵ Dickson et al. also reported that their FID images showed artifactual, left-to-right asymmetry.⁴ Taken together, these factors indicate the need for careful calibrations and corrections in order to ensure good data quality. For this reason, we implemented a novel patient-customized trajectory delay correction and gradient scaling for the FID. To achieve this, we place three NMR tubes orthogonally in the FOV to measure the image blurring resulting from the trajectory delay effect. The need for a patient-specific correction is supported by our results indicating that the trajectory delays ranged from 0.180 to 1.350 μs. The use of external MR markers could also be extended to serve as an image-based positioning locator of surface coils, as it has been reported in previously published studies.^52,53 The location of the coils may be incorporated into the PET reconstruction for the purpose of correcting for coil attenuation. Differing from the proposed marker-based correction approach, it is possible to perform trajectory delay correction based on the sharpness of the edge of a patient’s skull. Therefore, the correction may be able to be performed when the markers are absent. However, the imperfection of trajectory delay correction results in tissues with multiple edges as well as image size and shape distortion. Therefore, trajectory delay correction based on the skull margin in a fully automated fashion requires further investigation.

In our study, a five-tissue model, including air, brain, fat, fluid, and bone, was used to generate pseudo-CTs. To identify those five tissues, the informative features, i.e., Dixon-fat, Dixon-water, and R2^∗ images, all of which provide distinguishable fat-, water-, and bone-signal patterns, were selected. This selected feature further emphasizes the importance of FID correction. The degradation of the FID caused by the trajectory delay and eddy current scaling is propagated to the R2^∗ feature and degrades the clustering accuracy. An imperfect FID greatly reduces the quality of bone structure estimation secondary to the blurring and distorted gradient scaling of FID images. Therefore, the R2^∗ image is not as accurate in Fig. 2(b) as it is in Fig. 3 due to the double edges and blurring artifact seen in Fig. 2(b).

Two other features used for clustering are Dixon-fat and Dixon-water. The two-point Dixon technique for water/fat separation has been shown to be a consistent and necessary clinical input for diagnostic radiology and radiation oncology when used as an anatomical reference as well as providing additional information for tissue classification.^22,54 Traditionally, two-point Dixon is limited to exactly in-phase and out-of-phase echo times which limit the choice of the acquisition parameters.³⁴ Our mDixon overcomes this limitation and allows consistent image quality for water/fat separation at flexible echo times. Therefore, the minimal echo times and spacing can be achieved based on the limitation of the MR hardware in order to minimize the acquisition time.

One important point regarding clustering and which directly affects the robustness of the tissue identification is whether the cluster centroids for different tissue types are well-separated in the selected feature space. The results of the centroids shown in Fig. 4(a) indicate that the centroids of different tissue types are clearly separated. Furthermore, the features of Fig. 4(b) show that each type of tissue has a unique pattern with well-differentiated clusters.

Although the measured CT is treated as the reference in this study, there are two potential issues, which may limit the accuracy of the estimation of the skull structure and the HU values in the measured CT. First, due to consideration of the radiation dose, a low-dose CT is usually acquired with low spatial resolution and reconstruction into thick, axial slices. Owing to the mismatched spatial resolutions of the measured and pseudo-CT, the resolution-matching filtering has an important role when we compare measured CT to pseudo-CT. Another issue regarding measured CT is that the CT Hounsfield unit of the inner table of skull bone is overestimated due to the beam-hardening effect of CT images. Consequently, as shown in Fig. 5, the details of the inner table of the calvarium may be more clearly depicted in pseudo-CT than in measured CT. Overall, MR-based pseudo-CT has a great potential to provide more anatomical detail of skull than measured CT regardless of the dose consideration.

Some clustering errors occur in pseudo-CT as a consequence of the MR acquisition. The CT numbers of the voxels in pseudo-CT are overestimated in the ethmoid sinus and underestimated in the temporal bone along the petrous ridge. In both of these anatomical areas, tissue-air interface causes a local magnetic inhomogeneity. This phenomenon results in susceptibility artifacts and a fast T2^∗ decay, i.e., a large R2^∗ value. Furthermore, some bone details in the ear cavities are removed by applying the air mask on the R2^∗ map. For this reason, some fine, osseous structures in the auditory cavities are incorrectly assigned to air. As has been reported, the estimation error of pseudo-CT in the sinus and nasal cavities would result in overestimated PET activities in the corresponding regions, while the errors of the brain activity were small.⁵⁵ For this reason, the proposed pseudo-CT generation method may not be a suitable approach for target tissue located in these regions.

Another clustering error is identified in Fig. 5 regarding the CSF voxels adjacent to the brainstem. Those voxels are represented by a linear combination of both air and fluid classes and are underestimated in pseudo-CT. This effect has been previously described and is largely due to CSF flow effects⁵⁶ and a signal loss of a long T1 tissue acquired with a short repetition time MR sequence.²⁵ An approach to reduce this clustering error is to use the RF spoiling technique in the UTE-mDixon acquisition. A typical Dixon acquisition uses RF spoiling to spoil the residual magnetization between RF excitation pulses.³⁴ Using this approach on the UTE-mDixon acquisition would enhance T1-weighted contrast and generate uniform, homogeneous suppression of CSF to allow for a feature that is consistently identified by the FCM.

As shown in Fig. 6, a negative bias was found for the bone tissue. The main reason for this is that the presumed CT number of the bone class, 1524 HU, was assigned based on the average tissue composition of the cortical bone⁴⁰ but which may not represent the CT number of the dense bone in the head region. The optimal presumed CT number of the bone class should represent the CT number of the most dense bone tissue in the entire image volume. For this reason, optimization of the presumed CT numbers can be performed to further improve the accuracy of pseudo-CT generation.

Our current work is limited by the field-of-view, i.e., brain, obtained with the 8-channel SENSE head coil. However, it may be extended to other anatomic segments such as head/neck, thorax, and pelvis with dedicated coils and can be applied for related applications, e.g., MR-based pulmonary function measurement for COPD and bronchiectasis^57,58 and radiation treatment planning for pelvis and prostate cancers.^48,59 Another limitation of this study is that the features used as inputs for clustering were selected based on the assumption that the Dixon-water, Dixon-fat, and R2^∗ properties of the target tissues are the appropriate features for identifying different tissue types. While our results shown in Fig. 4 support this supposition, a systematic evaluation or optimization could be performed to determine whether a reduced feature set would support pseudo-CT generation or whether an expanded feature set could improve the accuracy and remains to be determined in future studies. Alternative classification methods should also be considered. In particular, we used FCM, an unsupervised method, in order to directly focus on the sufficiency of the information in the acquired data. Supervised learning methods, which use training data sets and incorporate prior knowledge, e.g., a Gaussian mixture regression model,^25,41–43 probabilistic neural network,⁴⁷ and support vector regression,⁸ might achieve better accuracy and feasibility of pseudo-CT generation with the proposed, single-scan UTE-mDixon approach.

In conclusion, the proposed UTE-mDixon acquisition and correction approach can provide MR signal with correct R2^∗ and bone structure estimation with a single MR scan. Furthermore, the MR features obtained by the scan showed well-discriminated signal properties among different tissue types and which can provide sufficient tissue information for pseudo-CT generation.

APPENDIX: FUZZY C-MEANS CLUSTERING

FCM is one of the representative fuzzy clustering methods³⁸ and it can be briefly described as follows.

Given a dataset D = {x_i|x_i ∈ R^d, i = 1, …, n} with x_i presenting the data instance, and d and n denoting the data dimension and data size, respectively. Assuming that there are C (0 < C ≤ n) different clusters in this dataset, the mathematical model of FCM can then be represented as

$${\displaystyle \underset{\mathit{V,U}}{min}\left\{\sum _{i=1}^n\sum _{j=1}^C\underset{ij}{\overset{m}{\mu }}{‖{\mathit{x}}_{\mathit{i}}-{\mathit{c}}_{\mathit{j}}‖}^2\right\}\text{,}m>\text{1, s.t. 0}\le {\mu }_{ij}\le 1\text{ and }\sum _{j=1}^C{\mu }_{ij}=1,1\le i\le n,\text{1}\le j\le C,}$$ (A1)

where V ∈ R^C×d presents the cluster center matrix consisting of C cluster centers c_j ∈ R^d (j = 1, …, C), U ∈ R^C×n presents the membership matrix with each entry μ_ij denoting the membership of data instance x_i to the cluster prototype c_j, and m is any real number larger than 1. m was set to 2 in order to facilitate the performance of the FCM clustering in this study.

Using the Lagrange optimization, the update equations of the cluster centroid, c_j, and the membership, μ_ij in Eq. (A1) can be deduced as follows:

$${\displaystyle {\mathit{c}}_{\mathit{j}}=\frac{\sum _{i=1}^n{\mu }_{ij}^m{\mathit{x}}_{\mathit{i}}}{\sum _{i=1}^n{\mu }_{ij}^m},j=1,\dots ,C,}$$ (A2)

$${\displaystyle {\mu }_{ij}=\frac{1}{\sum _{l=1}^C{\left(\frac{\left|\right|{\mathit{x}}_{\mathit{i}}-{\mathit{c}}_{\mathit{j}}\left|\right|}{\left|\right|{\mathit{x}}_{\mathit{i}}-{\mathbf{c}}_l\left|\right|}\right)}^{2/\left(m-1\right)}},i=1,\dots ,n;j=1,\dots ,C.}$$ (A3)

Based on Eqs. (A2) and (A3), we can consequently describe the detailed procedure of the FCM algorithm.

Algorithm I.

Algorithm:	FCM clustering
Inputs	The dataset D, the number of cluster C, the maximum number of iterations maxiter, the termination condition of iterations ε.
Outputs	The memberships, U, and the cluster center, V.
Step 1	Set the iteration counter t = 1 and initialize the memberships U(t);
Step 2	Calculate the cluster centers V(t + 1) using Eq. (A2) and U(t);
Step 3	Calculate the memberships U(t + 1) using Eq. (A3) and V(t + 1);
Step 4	If maxij{|μij(t+1) − μij(t)|} < ε or t = maxiter go to step 5, otherwise, t = t + 1 and go to step 2;
Step 5	Output the eventual cluster centers, V, and memberships, U.