Automatic labeling of MR brain images by hierarchical learning of atlas forests

Abstract

Purpose:

Automatic brain image labeling is highly demanded in the field of medical image analysis. Multiatlas-based approaches are widely used due to their simplicity and robustness in applications. Also, random forest technique is recognized as an efficient method for labeling, although there are several existing limitations. In this paper, the authors intend to address those limitations by proposing a novel framework based on the hierarchical learning of atlas forests.

Methods:

Their proposed framework aims to train a hierarchy of forests to better correlate voxels in the MR images with their corresponding labels. There are two specific novel strategies for improving brain image labeling. First, different from the conventional ways of using a single level of random forests for brain labeling, the authors design a hierarchical structure to incorporate multiple levels of forests. In particular, each atlas forest in the bottom level is trained in accordance with each individual atlas, and then the bottom-level forests are clustered based on their capabilities in labeling. For each clustered group, the authors retrain a new representative forest in the higher level by using all atlases associated with the lower-level atlas forests in the current group, as well as the tentative label maps yielded from the lower level. This clustering and retraining procedure is conducted iteratively to yield a hierarchical structure of forests. Second, in the testing stage, the authors also present a novel atlas forest selection method to determine an optimal set of atlas forests from the constructed hierarchical structure (by disabling those nonoptimal forests) for accurately labeling the test image.

Results:

For validating their proposed framework, the authors evaluate it on the public datasets, including Alzheimer’s disease neuroimaging initiative, Internet brain segmentation repository, and LONI LPBA40. The authors compare the results with the conventional approaches. The experiments show that the use of the two novel strategies can significantly improve the labeling performance. Note that when more levels are constructed in the hierarchy, the labeling performance can be further improved, but more computational time will be also required.

Conclusions:

The authors have proposed a novel multiatlas-based framework for automatic and accurate labeling of brain anatomies, which can achieve accurate labeling results for MR brain images.

1. INTRODUCTION

Accurate brain anatomy labeling is a task of pivotal importance to region-based analysis of MR brain images. It can be further applied to the research and clinical studies, such as for facilitating diagnosis, guiding treatment, and monitoring disease progression.¹ Since it is labor-intensive and impractical to label a large set of 3D MR images manually, a number of attempts have been devoted to automatic labeling of neuroanatomical structures in the literature.^2–5

The multiatlas-based approaches, which concentrate on propagating the label information from the (training) atlas images to the test image(s), have proven to be effective for brain image labeling. Generally, there are two research directions for the related methods: (1) improving the image registration for better spatial alignment of all atlases onto the test image(s)^6,7 and (2) improving the label fusion for better integrating the labeling results from different training atlases.^8–11 Recently, Zikic et al.¹² developed an alternative multiatlas-based labeling approach based on the random forest technique. Specially, by establishing the relationship between the visual features of individual voxels and their labels, they presented a simple but efficient single-atlas encoding scheme for MR brain image labeling.

In this paper, by exploring the recent development of image labeling approaches, we propose a novel hierarchical learning framework for significantly improving the labeling performance compared to the conventional forest-based methods. The basic idea is to label the MR brain images by a collection of random forests, which are hierarchically trained from multiple atlases. Our framework is developed based on the two novel strategies:

• (1)In the training stage, a hierarchical learning procedure is proposed to generate a hierarchy of forests in which the higher-level forests are entitled with better generalization capability for labeling MR brain images.
• (2)In the testing stage, a novel atlas forest selection (AFS) strategy, which focuses on finding an optimal set of atlas forests from the constructed hierarchical structure, is introduced to improve the labeling performance for the test image under study.

This paper is organized as follows. Section 2 summarizes the related literature in the field of MR brain image labeling. Section 3 presents the details of the proposed framework including its two novel strategies. Section 4 shows the experimental results, which demonstrate the capability of the proposed framework in brain labeling and also compare its performances with the alternative methods. Finally, Sec. 5 concludes our work with extended discussions.

2. RELATED WORKS

2.A. Multiatlas-based labeling

Multiatlas-based methods are regarded as a popular way for MR brain image labeling, due to their robustness and simplicity in incorporating the prior label information from multiple atlases. First, let each atlas be the pairing of a structural MR scan and its corresponding manually labeled map. Then, the information extracted from each atlas can be propagated to the new test image for labeling. There are basically two steps in the multiatlas-based labeling approaches: (1) produce label estimation from each atlas by spatially aligning the atlas image with the test image through a certain image registration and (2) combine label estimations from all atlases by a certain label fusion strategy for final labeling. These two steps allow multiatlas-based labeling approaches to account for intersubject variability between each atlas and the test image and also produce reliable label estimation through label fusion.

There are some efforts in the literature to improve the first step of the multiatlas-based labeling approaches, i.e., spatial registration of all atlases to the test image(s). For example, Jia et al.⁶ introduced an iterative multiatlas-based multi-image segmentation (MABMIS) approach by first utilizing a sophisticated registration scheme for spatial alignment and then determining the labels of all test images simultaneously for consistent labeling. On the other hand, Wolz et al.⁷ conducted label estimation by learning an image manifold, so that the labels could be effectively propagated to the test image by using only those nearby atlases that can provide more reliable label information.

Many attempts have also been taken on improving the second step of the multiatlas-based labeling approaches, i.e., label fusion for integrating contributions from the selected set of atlases. Specially, the weighted voting strategy, which uses the similarity between each atlas image and the test image as weight, is popularly used for label fusion. Here, the atlases with higher weights have more contributions in determining the labeling results, since they are more similar to the test image and thus may contain more relevant information for better label estimation.^13–17 Note that the weight can be estimated globally,¹³ locally,¹⁵ or semilocally,¹⁷ depending on the applications.

Another attempt in label fusion was conducted by Warfield et al.⁸ based on the expectation–maximization technique in the field of image segmentation, which is called as simultaneous truth and performance level estimation (STAPLE). In addition, it was demonstrated that STAPLE could incorporate the image intensity information to the process of label estimation in a seamless way as well.^18,19

The patch-based strategy also plays an important role in the multiatlas-based labeling.^11,20–23 The basic assumption in the patch-based methods is that, if two image patches are similar, they should belong to the same anatomical area and thus should have the same anatomical label.²⁰ Various patch-based methods have been developed, including the use of sparsity²⁴ and label-specific k-NN search structure.²² Recently, Wu et al.⁹ proposed a generative probability model for labeling the test image by selecting the best representative atlas patches and further determining their respective weights according to the training atlases.

Most patch-based labeling (PBL) methods perform label fusion in a nonlocal manner. Specifically, the idea of the nonlocal approach that is widely applied for texture synthesis,²⁵ inpainting,²⁶ restoration,¹⁰ and denoising¹⁰ was borrowed in the work of Coupé et al.,¹¹ for integrating the labels from different aligned atlases. This method relaxed the demanding requirement of accurate image registration in multiatlas-based labeling approaches. Instead, after aligning all atlases with the test image just via affine registration, each voxel in the test image is then labeled by integrating the labels of the nonlocal voxels in all linearly aligned atlases by following their respective patch-based similarities to the voxel under labeling. In addition, Asman and Landman²⁷ resolved the problems in the STAPLE method by formulating this statistical fusion method within a nonlocal mean perspective.

2.B. Atlas selection

Although the nonlocal label fusion methods have high accuracy in labeling, there are two main drawbacks that limit their applications. First, the methods are computationally demanding in the labeling procedure. For example, the current typical nonlocal label fusion methods require 3–5 h per single labeling process on a dataset containing 15 subjects.^27,28 The situation could further deteriorate when the dataset becomes larger, such as the ADNI dataset with hundreds of MR images. Second, when all the training atlases are considered in label fusion, certain atlases might contribute misleading information to label the specific test image and thus undermine the labeling performance.

In order to solve the aforementioned issues, it is important to implement atlas selection during the labeling procedure. Therefore, the computational cost can be greatly reduced, by eliminating atlases that are unsuitable for labeling the test image. For example, Aljabar et al.²⁹ demonstrated that the use of atlas selection can significantly improve labeling than the case without atlas selection. Generally, the intensity-based similarity (i.e., the sum of squared differences of intensities) or normalized mutual information is used for atlas selection. More references on atlas selection can be found in the work of Rohlfing et al.¹⁶ and Wu et al.³⁰

2.C. Random forest

Random forest^31–34 has been proven as a robust and fast multiclass classifier, which has been widely applied in many applications, such as image segmentation and pose recognition.³⁵ In the medical image analysis field, random forest is also recognized as an effective technique, i.e., for MR image labeling.³⁶

The main advantage of using random forest is that it can efficiently handle the large number of images and labels, which is important for multiatlas-based image labeling. For example, Zikic et al.³⁷ intended to implement random forest for automatic labeling of high-grade gliomas using multichannel MR images. Later they proposed the atlas forest strategy,¹² where the main idea is to encode each individual atlas and its corresponding label map via random forest. Their purpose is to reduce the computational cost and improve the efficiency for experiments especially when following the leave-one-out settings. In the testing, each atlas forest produces a probabilistic labeling map for the test image, and the final labeling result can be obtained by label fusion such as simple averaging of all the probabilistic labeling maps from all atlas forests. Experimental results indicated that the performance was favorable compared to the alternatives, e.g., nonlocal method.^10,20

However, there are several drawbacks in the work of Zikic et al.¹² First, each atlas forest is trained using only a single atlas. Although such strategy has the advantage of training efficiency, it also negatively influences the labeling performance since it could lead to overfitting. Second, after obtaining the labeling result from each trained atlas forest, the tentative result is not fully utilized (e.g., by other atlas forests) for further improving the labeling performance. Third, simple averaging of labeling results from all atlas forests might not optimal for the input test image, since no atlas selection strategy was proposed and applied.

It is noted that in this paper, we introduce a novel selection strategy for resolving this issue, by optimal selection of the atlas forests. Also, this atlas forest selection strategy is significantly different from most existing atlas selection approaches, which generally focus on finding atlas images instead. Details of the atlas forest selection strategy are presented in Sec. 3.E.

3. METHODS

In this section, we present a detailed description of the novel hierarchical learning framework. Our goal in this paper is to improve the labeling performance over the current random forest approaches. Accordingly, we present two novel strategies: (1) construction of the hierarchy of the atlas forests and (2) optimal selection of the atlas forests for each test image. The two strategies are implemented in both training and testing stages, respectively.

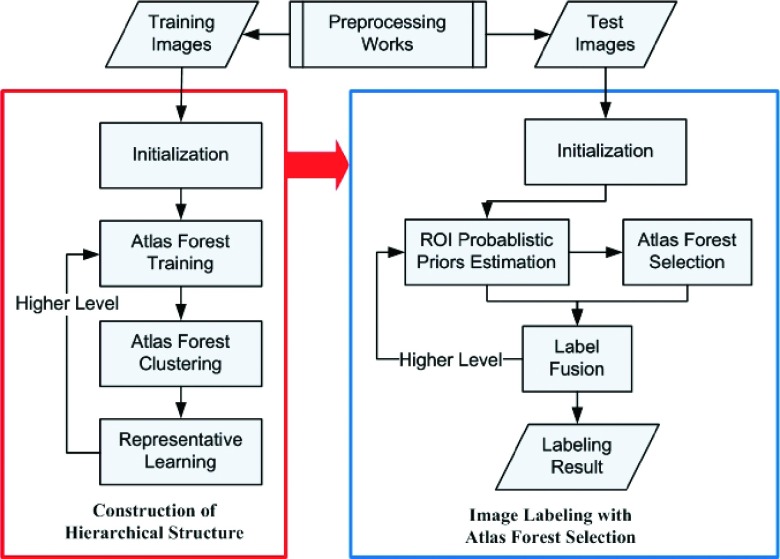
The flowchart for our proposed framework is summarized in Fig. 1. First, the main idea of the hierarchy construction and its steps is introduced in Sec. 3.A, such as atlas forest training, atlas forest clustering, and representative learning. Then, more detailed descriptions on the processes of forest training and label fusion are given in Sec. 3.B. In Sec. 3.C, we present atlas forest clustering that intends to group the trained classifiers based on their similar labeling capabilities. We also incorporate autocontext model to improve the labeling performance in the representative learning step, which is introduced in Sec. 3.D. Section 3.E describes atlas forest selection, as well as other implementation details, for labeling the testing images. Finally, we summarize our method in Sec. 3.F.

FIG. 1.

The flowchart of the proposed framework. The training and the testing steps are shown within the red and blue boxes, respectively.

3.A. Hierarchical structure of forests

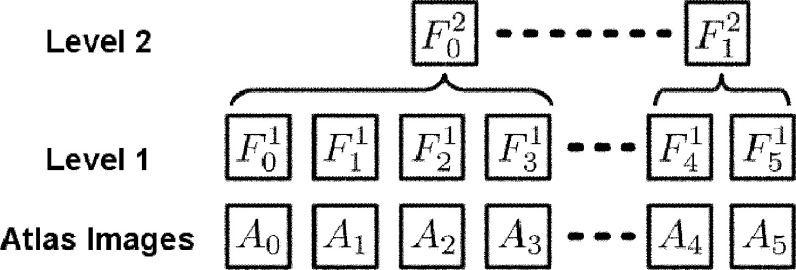
In this paper, we construct a hierarchy of forests such that each level contains a set of atlas forests in the training stage, while an optimal subset of the forests can be adaptively selected and hierarchically fused for labeling the test images. In particular, the representative forest in the higher level is not selected from the lower level; instead, it is retrained using all atlas information that contributes to the clustered forests in the lower level. The lower-level forests are clustered together according to their similar labeling capabilities. Therefore, the representative forest, which incorporates all clustered atlas information from the lower level, should have better generalization capability than the individual lower-level forest.

Figure 2 shows an example of a two-level hierarchical structure of the forests developed in the training stage. Note that, the block of $F_j^i$ represents the jth forest learned in the ith level in the figure. $A_j=\left\{I_j,L_j\right\}$ denotes the jth atlas, with I_j and L_j as the intensity image and the label map, respectively. We also have two notations $M_j^i$ and $C_j^i$, where $M_j^i$ is the set of forests that are the child nodes of $F_j^i$ in the hierarchical structure and $C_j^i$ denotes the set of atlas images utilized by the sub-hierarchy rooted at $F_j^i$. For example, for Fig. 2, we can write as $C_0^1=\left\{A_0\right\}$, $M_0^1=\varnothing$, $C_1^2=\left\{A_4,A_5\right\}$, and $M_1^2=\left\{F_4^1,F_5^1\right\}$.

FIG. 2.

An example of a two-level hierarchy of forests, built during the training process.

3.B. Random forest and atlas forest

The atlas forests, as introduced in Sec. 2, is the extension of conventional random forest techniques for effective image labeling. The forest technique utilizes the uniform bagging strategy,³¹ i.e., each tree is trained on a subset of training samples with only a subset of features that are randomly selected. Thus, the bagging strategy can inject randomness during the training process, which helps in avoiding the overfitting issue and improves the robustness of label prediction.

There are two types of nodes in the decision trees, i.e., the internal node and the leaf node.³⁴ In the training stage, the decision tree is first constructed from the root (internal) node, which has a split function to divide the training sets into its left or right child node based on one feature and one threshold. The split function is optimized to maximize the information gain of splitting training data.³¹ The tree grows by recursively optimizing the split function in each child internal node and splitting the training data into subsets with more consistent label distributions, until either the tree reaches the maximum tree depth or the number of training samples is too small to split. Then, the leaf nodes are appended to store the class label distribution of training samples falling into each leaf. In the testing stage, we calculate features of each to-be-labeled voxel. The features are pushed to each trained tree starting from the root (internal) node. Guided by the learned splitting functions, the voxel will finally reach a leaf node, where the stored label distribution can be considered as the posterior label distribution of this voxel. The final posterior label distribution is obtained by averaging results from different trees.

3.C. Clustering of atlas forests

Since it is difficult to directly compare and cluster the atlas forests, we here use their labeling capabilities to guide their clustering. Denote $S\left(F_m^i,F_n^i\right)$ as the similarity between two atlas forests $F_m^i$ and $F_n^i$ in the ith level, defined as follws:

$${\displaystyle S\left(F_m^i,F_n^i\right)=\frac{1}{2\left|C_m^i\right|}\sum _{A_j\in C_m^i}\mathrm{DSC}\left(A_j|F_n^i\right)+\frac{1}{2\left|C_n^i\right|}\sum _{A_l\in C_n^i}\mathrm{DSC}\left(A_l|F_m^i\right),}$$ (1)

where $C_m^i$ and $C_n^i$ are the sets of the atlas images utilized by $F_m^i$ and $F_n^i$, respectively, and $\text{DSC}\left(A_j|F_n^i\right)$ denotes the labeling accuracy on the atlas A_j by using $F_n^i$, measured by the Dice similarity ratio (DSC) with respect to the ground-truth. Given the similarity measure between any pair of atlas forests, we can construct an affinity/similarity matrix for clustering atlas forests.

There exist many clustering algorithms in the literature (e.g., nearest neighbor, K-means, and EM). In this paper, we choose the affinity propagation method³⁸ for clustering atlas forests as it can automatically find the number of clusters for the input affinity matrix. The affinity propagation algorithm can be briefed as follows. For each node in the affinity matrix, we commence by initializing its preference value representing its likelihood of being chosen as exemplar. Also, there are two kinds of messages that are passing between the nodes and the exemplar candidates: the “responsibility” and the “availability.” In each iteration, the two messages are updated by exchanging their values between the nodes, and the preference values are then computed from the two messages. The iteration continues until the updates in the two messages are converged. Details of the affinity propagation method can be found in the paper of Frey and Dueck.³⁸

3.D. Learning refinement by context features

As mentioned in Sec. 3.B, the higher-level forests can encode more comprehensive information than those lower-level forests. To further improve the generalization capability of the higher-level forests, we develop a novel hierarchical learning framework by incorporating the autocontext model in the work of Tu and Bai,³⁹ as it is simple and efficient to implement.

The autocontext model intends to train several levels of classifiers during the computation, which uses not only the visual features from the intensity images for training the lower-level forests but also the context features extracted from the outputs of the lower-level forests for training the higher-level forests. Therefore, the tentative labeling results are automatically updated through the increased levels of the hierarchy. The outputs from the lower-level forests can thus be refined by the higher-level forests, thus eventually generating more robust and accurate labeling results.

It is also worth noting that there is an exception for the very bottom level of the hierarchy, where no tentative labeling results exist for computing the context features. To this end, we first estimate the spatial prior of each label by averaging the initially aligned label maps of all training atlases, and then use this spatial prior to obtain the context features for encoding each atlas in the very bottom level. Note that all atlas images and the test images are affine aligned to the common space after our preprocessing, with the reference image randomly selected from the training atlases in the dataset. The spatial priors can thus largely reflect the locations of each label under consideration.

For computational efficiency and simplicity, we choose to use 3D Haarlike operators for calculating both visual features and context features.⁴⁰ Mathematically, by letting R denote a patch region centered at voxel x in the atlas image, we can first randomly sample two cubic regions (i.e., R₁ and R₂) within R. Then, the respective Haarlike features can be computed by two ways: (1) the local mean intensity of a cubic region [Fig. 3(a)] or (2) the difference of local mean intensities of two cubic regions⁴¹ [Fig. 3(b)]. The equation for computing Haarlike feature can be written as follows:

$${\displaystyle f_{\text{Harr}}\left(x,A_i\right)=\frac{1}{\left|R_1\right|}\sum _{u\in R_1}{A}_i\left(u\right)-b\frac{1}{\left|R_2\right|}\sum _{v\in R_2}{A}_i\left(v\right),R_1\in R,R_2\in R,b\in \left\{0,1\right\},}$$ (2)

where $f_{\text{Harr}}\left(x,A_i\right)$ is a Haarlike feature for voxel x in the atlas image A_i, and the parameter b is 0 or 1, determining the selection of one or two cubic regions. It should be also noted that the sizes of the cubic regions are randomly chosen from an arbitrary range, which is {1, 3, 5} in this paper. The locations of the two cubic regions are also randomly decided, only if it can fit the constraints described above. In general, we randomly sample the parameters for computing the Haarlike features. In this way, we can avoid the costly computation of the entire feature pool and then sample features from the pool.

FIG. 3.

The Haarlike features in 2D illustration.

In general, we have the estimated 3D Haarlike features computed from two sources: (1) the training atlas images and (2) the context information obtained from the outputs of the lower-level forests. Note that the outputs mentioned above are the set of estimated probability maps, with one probability map corresponding to one to-be-segmented label. In the training stage, for each to-be-trained voxel, we extract its patches from all the probability maps, along with the input intensity images. From each source, we compute its corresponding Haarlike features using Eq. (2), and then use them as the visual features and the context features, respectively. Following the strategy of the autocontext model, these two types of features are further integrated together to train the next-level classifiers. It is worth noting that the numbers of features extracted from the two sources are generally the same, indicating that these two types of features are treated equally when training the forests.

3.E. Atlas forest selection

In contrast to the conventional atlas selection approaches as mentioned in Sec. 2, we here select atlas forests in the hierarchy by actively predicting their capabilities in labeling the test image. With “atlas forest selection,” the novel strategy can better suit our needs, by selecting only the potentially suitable atlas forests, instead of using all learned atlas forests as described in the work of Zikic et al.¹² This will lead to the improvements of the labeling performance, since the negative influences from the certain “bad” atlas forests can be eliminated.

Besides, different from the traditional atlas selection approaches such as the work in Aljabar et al.,²⁹ our novel atlas forest selection method is developed based on the clustering information obtained in the training stage. Generally speaking, if a cluster of atlas forests can well handle the test image, their outputs should be also similar to the actual labeling of the test image, and thus they should be highly consistent. On the contrary, if the atlas forests in the cluster are more likely to generate incorrect labeling results with respect to the unknown actual labeling of the test image, their outputs are more inconsistent due to the unpredictable and uncontrollable error patterns in the labeling process. Therefore, when the consistency across the labeling outputs from different atlas forests in each cluster is computed, it can be used to gauge the cluster as well as its member atlas forests, which can be further utilized when selecting the set of atlas forests for labeling the current test image.

By denoting $\tilde{I}$ as a test image, we commence by applying all forests $F_k^{i-1}$ in the cluster $M_j^i$ to $\tilde{I}$ and then compare their labeling outputs with each other by using the DSC measures. The mean value of the pairwise DSC measures on all training atlas images is regarded as the absolute labeling consistency coefficient for the cluster $M_j^i$ denoted as $D\left(\tilde{I},M_j^i\right)$.

It is worth noting that the measure $D\left(\tilde{I},M_j^i\right)$ is computed only in accordance to the specific cluster $M_j^i$. Thus, the measurements from different clusters cannot be directly compared. To this end, we further divide the absolute consistency coefficient by a population-level consistency indicator of each cluster to convert it into a relative measure. The population-level consistency indicator is computed over all training atlas images. Particularly, the consistency between any pair of atlas forests in the same cluster is first calculated and averaged upon all training atlas images. Then, the population-level consistency indicator of the cluster $\overline{D}\left(M_j^i\right)$ is defined as the mean of all pairwise consistency measures within the cluster. Finally, the relative labeling consistency coefficient $W\left(\tilde{I},M_j^i\right)$ is obtained as follows:

$${\displaystyle W\left(\tilde{I},M_j^i\right)=\frac{D\left(\tilde{I},M_j^i\right)}{\overline{D}\left(M_j^i\right)}.}$$ (3)

Therefore, the relative consistency measures can now be utilized for the selection of the optimal atlas forests. Clusters with the top W scores can be selected, and their corresponding atlas forests can be used for labeling the test image. The overall labeling map in the current level is produced from those labeling estimates using the majority voting approach.¹⁴ This obtained label map is then used to compute the context features and fed into the next higher level.

3.F. Summary of the hierarchical learning framework

In this section, the algorithms for both training and testing stages are summarized as follows.

3.F.1. Training stage

After initializing the context information by following the strategy described in Sec. 3.D, the atlas forests in the bottom level are trained by following the single-atlas encoding method as introduced in the work of Zikic et al.¹² In the ith iteration, the process of training atlas forests is described below:

• (1)After obtaining the lower-level label map, the context features are extracted, in addition to the original visual features extracted from the atlas A_l. For each voxel, the abundant Haarlike operators are used for efficient feature extraction.⁴⁰
• (2)With both the new context features and the original visual features, the higher-level forest $F_j^i$ is learned to classify the labels of individual voxels.
• (3)After a new set of forests is retrained in the higher level, these forests are clustered again by following the similarity defined in Eq. (1). Afterward, the clustered forests are also used to help learn the new forests in the next higher level.
• (4)This iterative clustering and retraining procedure continues until convergence. Note that there should be at least two forests available in each level; otherwise, the atlas forest selection strategy cannot be applied.

3.F.2. Testing stage

Given a new test image $\tilde{I}$, we commence by initializing the context features, which are identical to those in the bottom level of the hierarchical structure. The population-level consistency indicator $\overline{D}\left(M_j^i\right)$ in the bottom level is also computed by following the strategy in Sec. 3.E. Afterward, the iterative process in the testing stage is performed as follows:

• (1)After computing the labeling output using all the forest in the (i − 1)-th level, all the absolute labeling consistency coefficients $D\left(\tilde{I},M_j^i\right)$ are obtained for the forests clustered in $M_j^i$.
• (2)Using Eq. (2), the coefficient $W\left(\tilde{I},M_j^i\right)$ (which is regarded as the relative labeling consistency coefficient) is obtained. Then, the clusters with the top W scores are selected, and their corresponding forests are used for labeling.
• (3)In the higher level, the labeling result in the lower level is used as the source for computing the context features, and then the higher-level forests are identified by including the selected forests in the lower level.
• (4)By iteratively performing this atlas forest selection and brain labeling in the next higher level, the labeling result of the test image can be gradually refined. This iterative process ends when reaching the top-most level of the hierarchy.

4. EXPERIMENTAL RESULTS

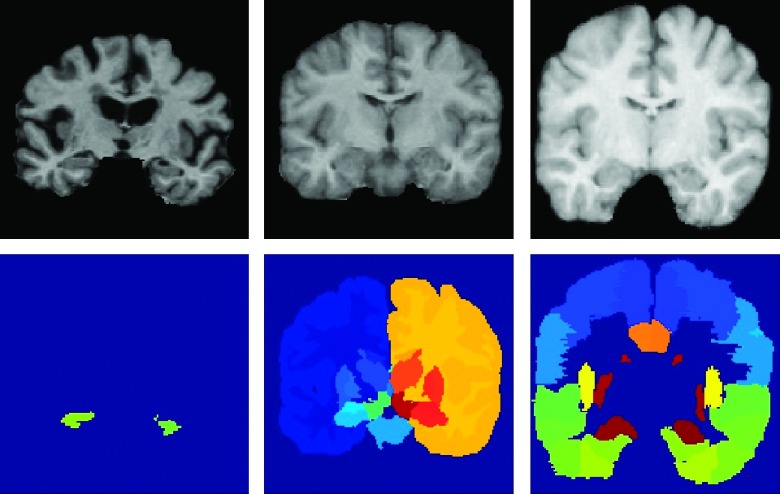
In this section, we evaluate the proposed framework for anatomical labeling of MR brain images. Here, we have employed three public datasets that have been widely used for brain labeling: the Alzheimer’s disease neuroimaging initiative (ADNI) dataset (http://adni.loni.ucla.edu),⁴² the Internet brain segmentation repository (IBSR) dataset (https://www.nitrc.org/projects/ibsr), and the LONI LPBA40 dataset (http://www.loni.usc.edu).⁴³ We select them for covering different cases in brain image labeling, i.e., the ADNI dataset provides rich brain MR images for labeling hippocampal regions, the IBSR dataset has only a limited number of atlases, and the regions of interest (ROIs) for LONI LPBA40 dataset are mostly within the cortex of the brain. Our goal in this section is to demonstrate that the proposed framework is suitable for various challenges in brain image labeling. Examples of the atlases in each of three datasets are provided in Fig. 4.

FIG. 4.

Examples of MR images in the ADNI (left), IBSR (middle), and LONI LPBA40 (right) datasets. The first row shows the intensity images, and the second row shows the manually segmented labels.

In each dataset, we perform cross-validation experiments to demonstrate the performance of the proposed framework. Note that the same settings and parameters were used in all the experiments. Specifically, there are 8 trees in each trained forest, and the maximum depth of trees is 30. Each leaf node has a minimum of eight samples. The maximal patch size is 10 × 10 × 10 mm, in which 1000 Haarlike features are calculated for training the classifier. Also, for the atlas forest selection process, we set W = 2 so that only two clusters of forests with the highest scores are selected in the fusion process.

Before the computation, we apply the same preprocessing procedures as introduced in the work of Coupé et al.¹¹ to all the datasets under study, to ensure the fairness of evaluation and comparison. For example, we applied the ITK-based histogram-matching program to the atlas images for overall intensity normalization, and then the intensities were rescaled to the interval [0 255]. Also, the flirt program in the FSL library⁴⁴ was used for affine registration, in order to bring all images into the same space.

It is also noted that, while three levels can be constructed for the ADNI dataset, only two levels can be constructed for both IBSR and LONI LPBA40. This is mainly because, when constructing the third level for IBSR or LONI dataset, there is only one forest remained, which does not satisfy the requirement listed in Sec. 3.F. For all the hierarchical structure trained in the experiments, we consider each atlas forest as an individual cluster in the bottom level. Using the proposed method, we can group the atlas forests into several larger clusters in the second and higher levels. We apply the affinity propagation method by following its recommended settings³⁸ to cluster the atlas forests according to their similarity measures defined in Sec. 3.C.

4.A. ADNI dataset

The first experiment is to apply the proposed framework to the ADNI dataset, which provides a large set of adult brain MR images acquired from 1.5 T MR scanners, along with their annotated left and right hippocampi.⁴²

We randomly selected 100 ADNI images, with 34 from Normal Control (NC) subjects, 33 from Mild Cognitive Impairment (MCI) subjects, and 33 from Alzheimer’s disease (AD) subjects. To demonstrate the validity of the proposed framework, we have performed 10-fold cross-validations. Briefly, the selected images are equally divided into 10-folds. In each fold, we select onefold (containing ten images) for testing, and the rest for training. It is worth noting that, in each fold, the numbers of the selected test images from the three subject groups (NC, MCI, and AD) are basically identical, in order to ensure the validity of the proposed framework on all three subjects groups.

Note that the baseline method under comparison, which is implemented without hierarchical learning and AFS, generally follows the same strategy with the single-atlas encoding method in the work of Zikic et al.¹² Our goal is to compare the performance between Zikic et al.¹² and our proposed framework, and then show the improvement of the performance when the two novel strategies of hierarchical learning and atlas forest selection are adopted in the proposed framework. Table I compares the labeling performance with respect to different configurations. It can be observed that the proposed framework leads to higher DSCs than the baseline method in both left and right hippocampi. The overall improvement of the DSC measure is more than 10%. When we increase the level, the performance gradually converges. As shown in Table I, the labeling performances of the third level are similar to that of the second level. This convergence property is also observed in the original autocontext model described in the work of Tu and Bai.³⁹

TABLE I.

Quantitative comparison of performances in different configurations when labeling the left and the right hippocampi.

	Bottom level		Second level		Top level
DSC	Without AFS (baseline)	With AFS	Without AFS	With AFS	Without AFS	With AFS
Left hippocampi (%)	63.55 ± 9.38	65.57 ± 8.10	73.79 ± 7.16	75.54 ± 5.27	74.75 ± 7.23	76.38 ± 5.56
Right hippocampi (%)	61.37 ± 10.49	64.25 ± 9.00	73.10 ± 8.62	75.24 ± 6.82	75.01 ± 7.39	76.68 ± 5.74
Overall (%)	62.46 ± 9.94	64.91 ± 8.55	73.45 ± 7.89	75.39 ± 6.05	74.88 ± 7.31	76.53 ± 5.65

It is also noted that the average computation time of labeling by the atlas forest method is around 10 min using a standard PC (CPU i7-3610, memory 8 GB), while it takes 27 min by the proposed method, since the test image needs to go through three levels of classifiers to obtain the result. Similarly, for both LONI and IBSR datasets, the proposed method takes about two times more than the atlas forest method, as only two levels are constructed for them.

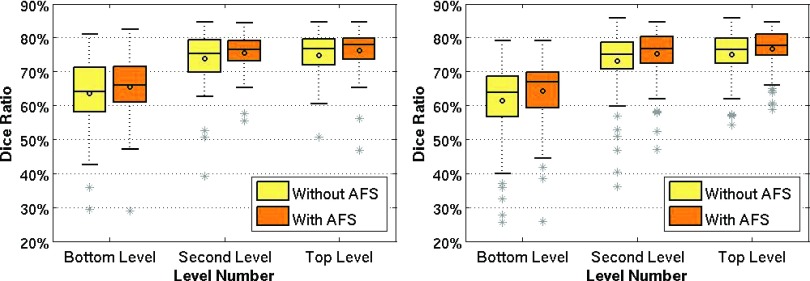
Next, we break down two proposed novel strategies for evaluation. Figure 5 shows the box plots for comparing results between the ground-truth and the estimates using the DSCs in four different configurations. The left panel in the figure presents the performance of labeling the left hippocampus, while the right panel is for the right hippocampus. From Table I and each panel of Fig. 5, we observe the following:

• (1)All results in the top level are better than the bottom level, indicating the effectiveness of the clustering and hierarchical retraining of the forests.
• (2)The labeling accuracies of the proposed framework with (optimal) AFS (2nd and 4th columns in the figures) are always better than those without AFS (1st and 3rd columns), demonstrating the effectiveness of the AFS module in the proposed framework.

FIG. 5.

The box plot for the labeling accuracies of different configurations on the left (left panel) and the right (right panel) hippocampi.

More importantly, it is also worth noting that the p-value in the two-tailed paired t-test between any two different configurations for both the left and the right hippocampi is below 0.05, which is same for the Wilcoxon rank based t-test. All these indicate the statistical significance of the two proposed strategies in improving labeling accuracy for MR brain images. We also compare the labeling performance with alternative multiatlas-based method, i.e., PBL method.^11,20 The overall performance when using these tools for labeling ADNI dataset is 66.38%. It can be thus concluded that the proposed framework outperforms the alternative methods.

4.B. IBSR dataset

In the next experiment, we applied the proposed framework to the IBSR dataset. The MR brain images in the dataset were acquired by the Center for Morphometric Analysis at Massachusetts General Hospital (MGH). There are totally 18 images, each with 32 manual labels. For this dataset, we performed sixfold cross-validations, where in each fold 15 images were selected for training and the rest 3 images were used for testing.

Table II presents the results of the DSC measures for the selected ROIs in the IBSR dataset, indicating around 3% of overall improvement when using our proposed strategies of hierarchical learning and atlas forest selection. Note that there are some extremely large labeled regions in the IBSR dataset. We discarded these large regions since all methods can produce reasonable results. Also, we discarded several other ROIs (e.g., the left and right accumbens) in that (1) the manual labeling is inconsistent across all images in the IBSR dataset or (2) their sizes are too small to provide enough sample voxels for training. It is noted that we compare the labeling performance on the IBSR dataset with PBL method, which can achieve the average DSC measure of 72.85%. This demonstrates that the proposed framework can be compared favorably with the alternative methods.

TABLE II.

Quantitative comparison of DSC values obtained by the baseline method and the proposed method for the selected ROIs in the IBSR dataset.

Label No.	Brain regions	Baseline method (%)	Proposed method (%)
1a,b	L. lateral ventricle	81.12 ± 7.39	85.27 ± 5.33
2a,b	L. thelamus	87.47 ± 2.76	88.57 ± 2.57
3a,b	L. caudate	78.85 ± 6.64	83.57 ± 4.98
4a,b	L. putamen	82.16 ± 6.95	84.01 ± 6.40
5	L. pallidum	74.47 ± 6.08	74.29 ± 7.69
6	3rd ventricle	74.86 ± 7.45	74.83 ± 10.03
7a,b	4th ventricle	70.65 ± 12.97	76.46 ± 8.63
8a,b	L. hippocampus	67.40 ± 8.79	74.15 ± 6.14
9a	L. amygdala	64.74 ± 16.08	68.51 ± 11.65
10a,b	L. ventral DC	80.86 ± 4.79	81.67 ± 4.39
11a,b	R. lateral ventricle	79.97 ± 7.80	85.16 ± 6.49
12b	R. thalamus	86.38 ± 2.92	87.72 ± 4.07
13a,b	R. caudate	77.70 ± 8.28	81.86 ± 7.85
14a,b	R. putamen	82.74 ± 4.68	84.97 ± 5.43
15	R. pallidum	75.56 ± 4.78	75.75 ± 6.34
16a,b	R. hippocampus	71.05 ± 7.67	76.08 ± 5.62
17	R. amygdala	65.18 ± 14.26	66.55 ± 11.44
18a,b	R. ventral DC	80.14 ± 4.31	81.83 ± 3.95
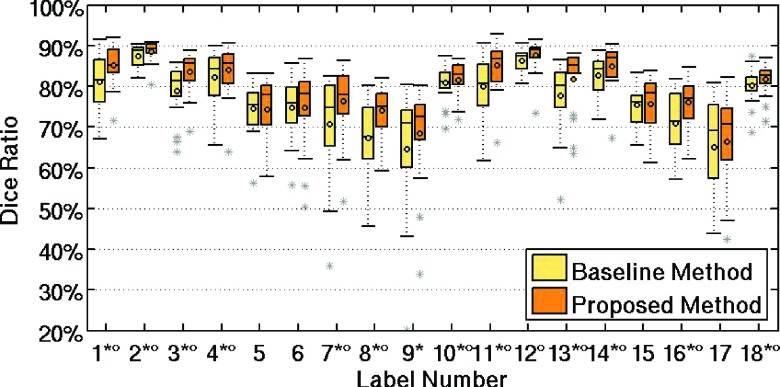
Overall		76.74 ± 7.48	79.51 ± 6.61

^aThe label index indicate the statistically significant difference between the baseline method.

^bThe label index indicate the statistically significant difference between the proposed method.

We also show the box plots to compare the detailed performances of the baseline method with the proposed method in Fig. 6. Note that the label index indicted by the symbols in the figures and tables indicates the statistically significant difference between the baseline method and the proposed method (asterisk symbol for p < 0.05 with the two-tailed paired t-test, and round symbol for p < 0.05 with the Wilcoxon rank based t-test). The results demonstrate the validity of the proposed framework when applied to the IBSR dataset.

FIG. 6.

Comparison of the DSC measures obtained by the baseline method and the proposed method in the IBSR dataset. The ROI indices can be found in Table II.

4.C. LONI LPBA40 dataset

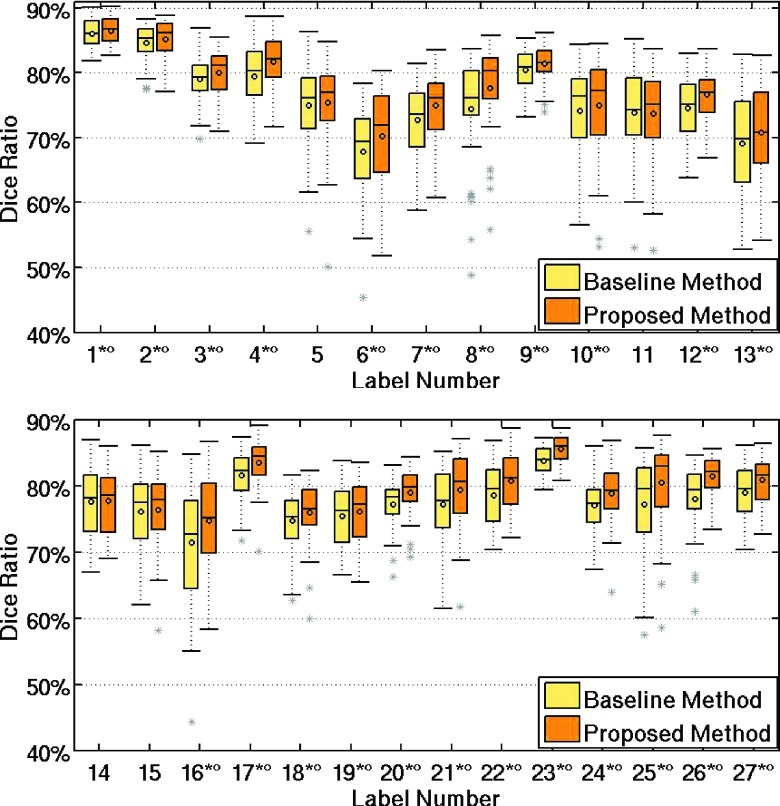
In the third experiment, we applied the proposed framework to the LONI LPBA40 dataset.⁴³ There are 40 brain images in the dataset, each containing 54 manually labeled ROIs. Similar to the previous experiments, we perform fourfold cross-validations by dividing 40 images into 4 groups. In each fold, 30 subjects are used for training, and the rest 10 subjects as the testing images. The DSC evaluations for the baseline method and the proposed framework are shown in Tables III and IV, respectively, for ROIs in the left and the right hemispheres. We observe from these two tables that, for 42 out of 54 ROIs in the LONI LPBA40 dataset, the proposed method has much higher DSC measures than the baseline method.

TABLE III.

Quantitative comparison of the DSC measures obtained by the baseline method and the proposed method for the left-hemisphere ROIs in the LONI LPBA40 dataset.

Label No.	Left brain regions	Baseline method (%)	Proposed method (%)
1	Superior frontal gyrus	85.75 ± 2.35	85.93 ± 2.48
2a	Middle frontal gyrus	84.41 ± 2.93	84.70 ± 2.99
3	Inferior frontal gyrus	78.79 ± 4.60	79.16 ± 4.59
4a,b	Precentral gyrus	78.88 ± 4.25	80.77 ± 4.20
5	Middle orbitofrontal gyrus	74.91 ± 6.32	75.48 ± 6.95
6a,b	Lateral orbitofrontal gyrus	66.38 ± 9.57	68.55 ± 9.57
7a,b	Gyrus rectus	74.37 ± 5.81	76.07 ± 5.05
8a,b	Postcentral gyrus	75.12 ± 5.59	77.21 ± 5.21
9	Superior parietal gyrus	79.96 ± 4.26	80.41 ± 4.03
10b	Supramarginal gyrus	73.51 ± 6.14	74.13 ± 6.57
11	Angular gyrus	74.80 ± 4.16	75.00 ± 4.14
12a,b	Precuneus	75.35 ± 4.72	77.07 ± 4.30
13a,b	Superior occipital gyrus	67.38 ± 7.18	69.00 ± 7.49
14	Middle occipital gyrus	76.92 ± 4.93	76.88 ± 4.77
15	Inferior occipital gyrus	74.90 ± 6.25	75.04 ± 5.57
16a,b	Cuneus	70.72 ± 7.87	74.20 ± 7.21
17a,b	Superior temporal gyrus	81.89 ± 3.15	83.77 ± 2.71
18a,b	Middle temporal gyrus	77.20 ± 3.96	78.35 ± 3.96
19a,b	Inferior temporal gyrus	77.77 ± 4.80	78.23 ± 5.14
20a,b	Parahippocampal gyrus	76.42 ± 4.01	78.61 ± 3.91
21a,b	Lingual gyrus	77.80 ± 5.53	79.58 ± 5.39
22a,b	Fusiform gyrus	79.07 ± 4.86	79.72 ± 5.06
23a,b	Insular cortex	82.15 ± 3.36	84.02 ± 2.65
24a,b	Cingulate gyrus	75.93 ± 5.44	77.39 ± 6.53
25a,b	Caudate	76.39 ± 5.55	80.70 ± 4.56
26a,b	Putamen	78.81 ± 3.97	81.83 ± 2.77
27a,b	Hippocampus	79.45 ± 3.14	81.15 ± 2.64
Overall		76.85 ± 4.99	78.26 ± 4.83

^aThe label index indicate the statistically significant difference between the baseline method.

^bThe label index indicate the statistically significant difference between the proposed method.

TABLE IV.

Quantitative comparison of the DSC measures obtained by the baseline method and the proposed method for the right-hemisphere ROIs in the LONI LPBA40 dataset.

Label No.	Right brain regions	Baseline method (%)	Proposed method (%)
1a,b	Superior frontal gyrus	86.03 ± 2.26	86.49 ± 2.08
2a,b	Middle frontal gyrus	84.64 ± 2.83	85.20 ± 3.07
3a,b	Inferior frontal gyrus	78.99 ± 3.43	79.97 ± 3.42
4a,b	Precentral gyrus	79.41 ± 4.82	81.65 ± 3.92
5	Middle orbitofrontal gyrus	75.01 ± 6.52	75.48 ± 6.80
6a,b	Lateral orbitofrontal gyrus	67.92 ± 7.41	70.27 ± 7.27
7a,b	Gyrus rectus	72.74 ± 5.20	75.02 ± 5.08
8a,b	Postcentral gyrus	74.47 ± 8.05	77.64 ± 7.07
9a,b	Superior parietal gyrus	80.41 ± 3.11	81.48 ± 2.88
10a,b	Supramarginal gyrus	74.18 ± 7.25	74.94 ± 7.28
11	Angular gyrus	73.85 ± 6.91	73.74 ± 7.03
12a,b	Precuneus	74.58 ± 4.52	76.66 ± 3.90
13a,b	Superior occipital gyrus	69.10 ± 7.99	70.86 ± 7.32
14	Middle occipital gyrus	77.57 ± 5.31	77.71 ± 5.00
15	Inferior occipital gyrus	76.04 ± 6.33	76.34 ± 5.72
16a,b	Cuneus	71.42 ± 8.70	74.79 ± 6.65
17a,b	Superior temporal gyrus	81.52 ± 3.75	83.50 ± 3.75
18a,b	Middle temporal gyrus	74.71 ± 4.56	76.00 ± 4.59
19a,b	Inferior temporal gyrus	75.39 ± 4.79	76.15 ± 4.82
20a,b	Parahippocampal gyrus	77.17 ± 3.85	79.00 ± 3.58
21a,b	Lingual gyrus	77.16 ± 6.12	79.32 ± 5.70
22a,b	Fusiform gyrus	78.57 ± 4.60	80.73 ± 4.44
23a,b	Insular cortex	83.82 ± 2.13	85.59 ± 1.95
24a,b	Cingulate gyrus	77.05 ± 3.56	78.80 ± 4.38
25a,b	Caudate	77.17 ± 6.86	80.50 ± 6.39
26a,b	Putamen	78.07 ± 5.19	81.49 ± 2.87
27a,b	Hippocampus	78.98 ± 3.96	80.90 ± 3.38
Overall		76.89 ± 5.19	78.53 ± 4.83

^aThe label index indicate the statistically significant difference between the baseline method.

^bThe label index indicate the statistically significant difference between the proposed method.

Here, we also compare the DSC results with other alternative approaches. In the work of Zikic et al.,¹² the labeling results on the LONI LPBA40 dataset reached the average DSC of 77.46% by using a leave-one-out cross-validation, while our baseline method obtains 76.87%, indicating the close performance of these two implementations of the same method although we used very restrict 4-fold cross-validation compared to the leave-one-out cross-validation used in the work of Zikic et al.¹² Referred from the tables, it can be observed that the proposed framework also achieves a more accurate estimation in terms of the average DSC, which is 78.40%. We also compare this with PBL method which has the average DSC measure of 73.01%. It can be concluded that the proposed framework can produce more accurate labeling results and can be compared favorably with the alternative methods.

Furthermore, we compare the performances between the baseline method and the proposed method by using box plots, as shown in Figs. 7 and 8. Figure 7 presents the DSC measures for ROIs in the left hemisphere of the brain, while Fig. 8 is for the right hemisphere. These two figures indicate better labeling accuracy by the proposed method, compared to the baseline method. Besides, each ROI marked with the symbols means the statistically significant difference between the proposed method and the baseline method (asterisk for p < 0.05 with the two-tailed paired t-test, and round for p < 0.05 with the paired Wilcoxon rank based t-test). These results again demonstrate the advantages of using our two proposed novel strategies of hierarchical learning and AFS.

FIG. 7.

Comparison of the DSC measures obtained by the baseline method and the proposed method in labeling the left hemisphere of the brain using LONI dataset.

FIG. 8.

Comparison of DSC values obtained by the baseline method and the proposed method in labeling the right hemisphere of the brain using LONI dataset.

5. CONCLUSION

In this paper, we have presented a novel hierarchical learning framework for brain labeling by using the state-of-the-art random forest technique. Our framework is designed to iteratively cluster atlas forests and learn next higher-level forests for constructing a hierarchical structure of forests, with the forests in the higher levels having higher capacities for labeling the MR brain images. Besides, a novel atlas forest selection strategy is also proposed to exclude the potentially negative influences from the unsuitable atlas forests, thus further improving the labeling performance. By integrating these two novel strategies of hierarchical learning and atlas forest selection, our proposed method is entitled with greater capabilities in labeling MR brain images.

In the experiments, we demonstrate the performance of our proposed framework on three public datasets, i.e., ADNI, IBSR, and LONI LPBA40. In particular, we generate an exemplar two-level hierarchical structure of the forests for brain labeling of images in IBSR and LONI LPBA40, and then compare the labeling results with the conventional methods. Experimental results on all three datasets show that, when the two novel strategies of hierarchical learning and atlas forest selection are adopted, significant improvements in terms of labeling accuracy can be achieved.

We also constructed the third level for the ADNI dataset and investigated its computational cost and labeling performance. It is found that more computational time is required when adding more levels, but the labeling performance can be improved progressively. It is also noted in Sec. 3 that, when using more training atlases available, the maximum number of levels for constructing the hierarchy can be potentially increased.

In future work, more comprehensive evaluations will be conducted by employing more datasets and also other anatomical labels. We will further explore the possibility of extending our method to labeling other nonbrain structures such as prostate and knee cartilage.