Assessment of radiation dose in nuclear cardiovascular imaging using realistic computational models

Abstract

Purpose:

Nuclear cardiology plays an important role in clinical assessment and has enormous impact on the management of a variety of cardiovascular diseases. Pediatric patients at different age groups are exposed to a spectrum of radiation dose levels and associated cancer risks different from those of adults in diagnostic nuclear medicine procedures. Therefore, comprehensive radiation dosimetry evaluations for commonly used myocardial perfusion imaging (MPI) and viability radiotracers in target population (children and adults) at different age groups are highly desired.

Methods:

Using Monte Carlo calculations and biological effects of ionizing radiation VII model, we calculate the S-values for a number of radionuclides (Tl-201, Tc-99m, I-123, C-11, N-13, O-15, F-18, and Rb-82) and estimate the absorbed dose and effective dose for 12 MPI radiotracers in computational models including the newborn, 1-, 5-, 10-, 15-yr-old, and adult male and female computational phantoms.

Results:

For most organs, ²⁰¹Tl produces the highest absorbed dose whereas ⁸²Rb and ¹⁵O-water produce the lowest absorbed dose. For the newborn baby and adult patient, the effective dose of ⁸²Rb is 48% and 77% lower than that of ^99mTc-tetrofosmin (rest), respectively.

Conclusions:

⁸²Rb results in lower effective dose in adults compared to ^99mTc-labeled tracers. However, this advantage is less apparent in children. The produced dosimetric databases for various radiotracers used in cardiovascular imaging, using new generation of computational models, can be used for risk-benefit assessment of a spectrum of patient population in clinical nuclear cardiology practice.

1. INTRODUCTION

Nuclear cardiovascular imaging plays a pivotal role in the assessment of myocardial ischemia, infarction, and damage associated with various congenital or acquired heart diseases.¹ Each year, more than 10 × 10⁶ nuclear cardiac studies are performed in the US for the assessment of myocardial perfusion and/or viability.² These procedures are performed using a variety of either single-photon-emitting (SPECT) or positron-emitting (PET) radiotracers, involving the exposure of patients to radiation ranging between 5 and 57 mSv.² The growth of nuclear cardiology studies led to substantial increase of radiation dose to patients, placing them as major contributors to global radiological burden, actually accounting for 85% of nuclear medicine exposure to the US population.³ In pediatric cardiology, myocardial perfusion imaging (MPI) is used in cardiac stress tests of children,⁴ monitoring of myocardial ischemia,⁵ evaluation of the effects of coronary arterial intervention,⁶ stratification of cardiac risks of children with Kawasaki disease,⁷ detection of congenital heart disease,⁸ identification of myocardial perfusion in children after arterial switch operation,⁹ estimation of right ventricular pressure overload,¹⁰ and determination of myocardial disease (such as hypertrophic cardiomyopathy and cardiomyopathy in Duchenne muscular dystrophy).¹¹ However, the exposure of pediatric patients to ionizing radiation during nuclear cardiology procedures is a matter of concern.^12,13 With the same absolute level of radiation dose, children may experience greater stochastic effects from ionizing radiation than adults because they have a proportionally higher percentage of replicating cells, which are more radiosensitive than other cells.¹⁴ Since children have longer postirradiation life period for the emergence of deleterious stochastic effects, they are also at higher cancer risk from ionizing radiation compared to adults.¹⁵ Therefore, the assessment of absorbed radiation dose for patient populations of various age groups resulting from nuclear cardiology imaging procedures (SPECT and PET) is of paramount importance in clinical practice.

To this end, organ absorbed doses are often estimated using computational phantoms and Monte Carlo calculations.^16–22 These phantoms and computer codes, respectively, mimic the morphology and internal anatomic structures of the human body and simulate the interaction of ionizing radiation with biological tissues, thus allowing tracking the transport of radiation in the body. Depending on their geometric features, computational models can be divided into three basic categories: stylized models which employ simple equation-based mathematical functions, voxel-based models which use matrices obtained from segmented medical images, and boundary representation (BREP) models which employ nonuniform rational B-splines (NURBS) or polygonal meshes to represent the surface contour of individual organs and the whole body.^23–26 In most studies reported in the literature, the estimation of organ absorbed dose for a spectrum of populations of different ages from radiopharmaceuticals used in nuclear cardiology was performed using mathematical phantoms,^27–29 mirdose (Ref. 30), or olinda/exm version 1.0.³¹ The new version of the latter, olinda/exm version 2.0,³² replaced the previous generation of mathematical phantoms with realistic NURBS-based anthropomorphic models, thus providing more accurate dose calculations. Significant differences were reported between dosimetric results of stylized and voxel-based models of the same subject.^33–39 For a variety of exposure conditions, the differences of effective dose between stylized adult phantom and voxel-based adult phantom of ICRP reference anatomic data have been reported to range between −50% and 60%.⁴⁰ For pediatric populations, the relative differences of the effective dose between University of Florida-National Cancer Institute (UF-NCI) phantoms and stylized phantoms may change between −24% and 33% for positron-emitting radiotracers.³⁵ Therefore, the assessment of organ absorbed dose and effective dose for commonly used nuclear cardiology radiotracers using new generation computational phantoms is desired.

In this work, we use the UF-NCI family of pediatric models and the ICRP reference adult voxel-based phantom to perform Monte Carlo-based particle transport simulation of radiation emitted by different radionuclides (Tl-201, Tc-99m, I-123, C-11, N-13, O-15, F-18, and Rb-82) to calculate S-values for the considered series of anatomical models. The obtained radiation dosimetry database is then used for the assessment of organ absorbed doses and effective dose of 12 radiotracers used in nuclear cardiac imaging. The effective dose per unit administered activity of 12 radiotracers was calculated for the newborn, 1-, 5-, 10-, 15-yr-old, and adult population based on the new ICRP tissue-weighting factors. Understanding the variability of the absorbed dose with patient’s body weight and age may advance the perception of the uncertainties involved in internal radiation dosimetry calculations and risk-benefit analyses in pediatric nuclear cardiology practice. The detailed age-specific dosimetric calculations can be used for both prospective monitoring of cumulative exposure to chronic patients requiring multiple diagnostic procedures, as well as retrospective epidemiological studies.

2. MATERIALS AND METHODS

2.A. Computational phantoms

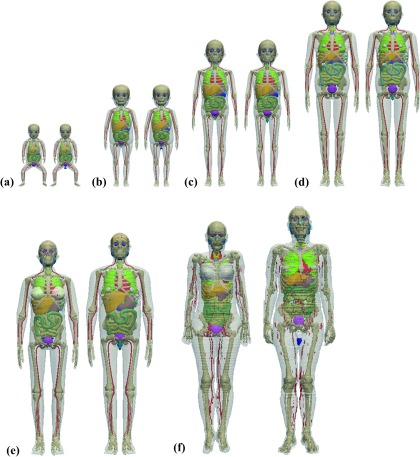
The UF-NCI hybrid pediatric phantom series were developed from patients’ CT images using 3D image segmentation software and Rhinoceros package. The modeled NURBS-based UF-NCI phantoms were voxelized using an in-house matlab code. For the alimentary tract organs of the UF-NIC phantoms, the central trace of each segment was first extracted from original patient CT images and adjusted to match corresponding ICRP reference lengths. A NURBS pipe model was then generated along the constructed central tracks until a realistic shape and curvature were obtained. The thicknesses of the alimentary tract wall were modified to match corresponding ICRP reference masses. The voxelized UF-NCI computational phantom series, including the reference newborn, 1-, 5-, 10-, and 15-yr-old male and female models, and the ICRP reference adult male and female phantoms, were used in this work to represent patient populations of various ages for Monte Carlo-based internal radiation dosimetry calculations. The organ masses and body weights of the UF-NCI phantoms and ICRP reference models are close to the recommended anatomical data reported by the ICRP for population of corresponding age groups.^41,42 A unified voxel dimension of 1.8 × 1.8 × 3 mm³ was set for all computational models (interpolated from the original resolution) to minimize the differences across different models. For the sake of convenience in terms of effective dose calculation, homogeneous organs such as the left lung and right lung, the submaxillary salivary gland and sublingual salivary gland, the cartilage, cortical bone, and spongiosa at different bone sites were merged as one identified region. A unified organ ID was set for the UF-NCI phantom series and ICRP models. Body weights and organ/tissue masses for the pediatric and adult phantoms are summarized in Table I. Figure 1 shows the front 3D views of the 12 computational phantoms used in this work.

TABLE I.

Organ masses of computational phantoms.

		Newborn		1-yr-old		5-yr-old		10-yr-old		15-yr-old		Adult
Organs∖masses (g)	ID	Female	Male	Female	Male	Female	Male	Female	Male	Female	Male	Female	Male
Adipose tissue	11	658.7	659.3	3653.0	3652.6	4642.8	4649.0	6 435.8	6 435.8	11 649.8	6 748.7	23 632.0	20 350.1
Adrenal	12	5.9	5.9	4.0	4.0	5.0	5.0	7.0	7.0	9.0	10.0	13.0	14.0
Brain	13	314.8	314.8	945.2	945.2	1241.0	1241.0	1 305.4	1 305.4	1 294.0	1 415.5	1 301.1	1 450.5
Colon wall	14	16.8	16.8	49.4	49.4	118.4	118.4	206.9	206.8	295.6	297.8	360.0	369.9
Colon content	15	43.8	43.8	50.8	50.8	89.7	89.7	93.6	93.6	158.8	243.7	320.0	300.1
GB wall	16	0.5	0.5	1.4	1.4	2.6	2.6	4.4	4.4	7.2	7.5	10.2	13.9
GB content	17	2.8	2.8	8.0	8.0	14.9	14.9	25.8	25.8	41.5	44.7	45.8	54.1
Heart wall	18	19.9	19.9	50.0	50.0	85.2	85.2	138.3	138.3	219.7	229.9	250.5	329.9
Heart content	19	6.0	6.0	47.4	47.4	133.6	133.6	228.3	228.3	317.6	425.2	370.0	510.0
Kidney cortex	20	18.3	18.3	51.0	51.0	79.4	79.4	131.3	131.3	176.2	183.2	192.5	217.0
Kidney medulla	21	6.5	6.5	18.2	18.2	28.8	28.8	46.8	46.8	62.1	65.2	68.8	77.6
Kidney pelvis	22	1.3	1.3	3.5	3.5	5.6	5.6	9.1	9.1	12.0	12.8	13.8	15.5
Liver	23	128.6	128.6	327.1	327.1	567.0	567.0	824.5	824.5	1 290.5	1 290.4	1 400.0	1 799.8
Lung	24	58.8	58.8	149.3	149.3	297.9	297.9	489.1	489.1	752.9	886.8	950.3	1 201.5
Pancreas	25	6.0	6.0	19.8	19.8	34.6	34.6	59.7	59.7	99.2	109.1	120.0	140.0
Salivary glands	26	5.9	5.9	23.7	23.7	33.6	33.6	43.9	43.9	62.7	67.0	70.0	85.0
SI wall	27	29.3	29.3	82.1	82.1	210.9	210.9	355.6	357.5	496.4	503.3	601.1	649.9
SI content	28	31.4	31.4	48.9	48.9	38.3	38.3	162.6	161.6	279.1	267.3	280.9	350.0
Spinal cord	29	6.4	6.4	24.6	24.6	31.4	31.4	68.5	68.5	68.4	42.5	18.6	36.6
Spleen	30	9.4	9.4	28.7	28.7	49.6	49.6	79.4	79.4	128.9	128.7	130.0	150.0
Stomach wall	31	6.9	6.9	19.7	19.7	49.5	49.5	83.7	83.7	118.5	117.5	140.0	150.0
Stomach content	32	25.0	25.0	66.1	66.1	82.7	82.7	116.3	116.3	199.4	199.8	230.0	250.0
Thymus	33	12.8	12.8	16.1	16.1	30.0	30.0	37.5	37.5	29.9	34.6	20.0	25.0
Thyroid	34	1.3	1.3	1.8	1.8	3.4	3.4	7.8	7.8	12.1	11.9	17.0	20.0
UB wall	35	3.9	3.9	8.8	8.9	15.7	15.6	24.3	24.8	34.3	39.4	40.0	50.0
UB content	36	9.9	9.9	9.9	10.9	60.7	60.7	97.4	97.0	132.2	151.0	199.2	200.0
Blood vessel	37	11.0	11.0	23.6	23.6	62.3	62.3	134.0	134.0	226.1	252.5	384.3	371.5
Muscle	38	1530.0	1532.8	3186.8	3155.3	7367.7	7364.3	16 285.3	16 288.4	26 141.4	34 689.0	17 500.0	28 971.7
Cortical bone	39	76.4	76.4	293.3	293.3	735.7	735.7	1 704.6	1 704.6	2 932.7	3 264.6	3 228.0	4 438.4
Spongiosa	40	171.2	171.2	572.8	572.8	1266.7	1266.7	2 668.8	2 668.8	4 047.8	4 674.5	3 919.3	5 906.0
Ovariesa/testesb	41	0.3	0.8	0.8	1.5	2.0	1.7	3.4	2.0	5.8	15.8	11.0	35.0
Uterusa/prostateb	42	3.9	0.8	1.5	1.0	3.0	1.2	4.0	1.6	29.6	4.3	80.0	17.0
Cartilage	43	126.1	126.1	37.7	37.7	55.9	55.9	128.2	128.2	150.7	138.8	651.7	145.2
Penisb/ureterc	44	—	0.6	—	3.6	—	6.5	—	6.6	—	29.2	15.0	16.0
Pituitary gland	45	0.1	0.1	0.2	0.2	0.3	0.3	0.4	0.4	0.5	0.5	0.6	0.6
Tonsil	46	0.1	0.1	0.5	0.5	2.0	2.0	2.9	2.9	2.9	2.9	3.0	3.0
Breast	47	0.1	0.1	0.4	0.4	0.9	0.9	7.6	7.6	306.7	14.7	500.1	25.0
Esophagus	48	2.0	2.0	4.9	4.9	9.9	9.9	17.8	17.8	27.9	29.4	35.0	40.0
Bronchi	49	0.4	0.4	2.0	2.0	3.0	3.0	3.6	3.5	7.3	8.0	8.7	66.3
Eye balls	50	5.9	5.9	6.8	6.8	10.8	10.8	11.7	11.7	13.0	12.9	14.6	14.6
Larynx	51	1.3	1.3	3.9	3.9	6.8	6.8	11.8	11.8	14.4	21.7	14.3	28.4
Lens	52	0.1	0.1	0.2	0.2	0.3	0.3	0.4	0.4	0.4	0.5	0.4	0.4
Nasal layer	53	0.8	0.8	2.1	2.1	8.5	8.5	9.0	9.0	9.0	11.5	4.3	11.0
Oral cavity layer	54	0.7	0.7	0.6	0.6	1.2	1.2	1.1	1.1	8.0	5.2	22.5	35.8
Pharynxd/lymphatic nodesc	55	0.3	0.3	0.8	0.8	1.9	1.9	1.9	1.9	3.1	2.9	79.4	138.1
Tongue	56	3.5	3.5	9.8	9.8	18.8	18.8	31.5	31.5	52.8	55.4	41.6	42.3
Trachea	57	0.5	0.5	1.5	1.5	2.4	2.4	4.4	4.4	5.4	7.5	8.0	10.0
Skin	58	96.5	98.2	188.0	211.8	638.2	642.8	806.4	809.7	1 690.1	1 806.7	2 749.9	3 882.0
Total bodye (kg)	100	3.5	3.5	10.0	10.0	18.2	18.2	32.9	32.9	53.6	58.6	60.1	73.0
Heighte (cm)	—	47.0	47.0	77.0	77.0	110.0	110.0	140.0	140.0	161.0	166.0	163.0	176.0

^aOrgan for female.

^bOrgan for male.

^cOrgan for pediatric phantoms.

^dOrgan for adult phantoms.

^eThe height for the 1-yr, 5-yr, and 10-yr-old phantoms and the weight of all phantoms were chosen according to the reference data provided in the ICRP publication 89, while the height for the newborn and 15-yr-old phantoms was obtained from the NHANES IV (1999–2002) survey.

FIG. 1.

3D visualization of computational phantoms of (a) newborn, (b) 1-yr-old, (c) 5-yr-old, (d) 10-yr-old, (e) 15-yr-old, and (f) adult male (right) and female (left).

2.B. Monte Carlo simulations

The Monte Carlo N-particle extended—mcnp X—code (version 2.5.c) was adopted for radiation transport simulation in the UF-NCI and ICRP reference phantoms. The decay data of the investigated radionuclides were obtained from the radiation dose assessment resource (RADAR).⁴³ Uniformly distributed radionuclide sources (Tl-201, Tc-99m, I-123, C-11, N-13, O-15, F-18, and Rb-82) were simulated in 48 source regions. The energy spectrum of photons, positrons, and electrons were determined from the decay schemes of the investigated isotopes and were manually defined in mcnpX input file. See supplementary Table A15 for decay data of the investigated radionuclides.⁶¹ The energy deposition in the target regions was recorded in unit of MeV per particle using the mcnpX tally card ∗F8. The MCPLIB02 photon cross section library and the default electron/positron transport algorithms of mcnp were adopted for radiation transport simulations. An in-house c++ code was developed to process the output of the mcnp code and calculate the S-values of radionuclides as well as the absorbed doses and effective doses for the considered radiotracers using published biokinetic data from various sources^28,29,44,45 and the tissue weight factors recommended by ICRP publication 103.⁴⁶ The density and elemental compositions of organs/tissues for each anatomical model were obtained from the reference data reported in ICRP publication 89.⁴² A total of 1.0 × 10⁷ primary particles were generated such that the statistical uncertainty in terms of coefficient of variation was less than 2% in most cases.

2.C. Cardiovascular imaging radiotracers

The radiotracers investigated in this work are ²⁰¹Tl, ^99mTc-sestamibi, ^99mTc-tetrofosmin, ^99mTc-furifosmin, ¹²³I-BMIPP, ¹¹C (realistic maximum model), ¹³N-ammonia, ¹⁵O-water, ¹⁸F-flurpiridaz, ¹⁸F-FDG, ¹⁸F-LMI1195, and ⁸²Rb. Of these tracers, ²⁰¹Tl has been extensively used as a perfusion radiotracer in cardiovascular imaging owing to its excellent myocardial first pass extraction and good relationship between blood flow and myocardial uptake at higher flow rates during stress testing.^{47 99m}Tc-sestamibi, ^99mTc-tetrofosmin, and ^99mTc-furifosmin have experienced widespread sustained clinical use in nuclear cardiology since the 1990s,^48,49 whereas ¹²³I-BMIPP proved to be a useful iodinated branch chain fatty acid for evaluation of myocardial fatty acid uptake.^{50,51 11}C-labeled radiotracers, such as ¹¹C-meta-hydroxyephedrine, are adopted for PET imaging of heart failure.^{52 13}N-ammonia, ¹⁵O-water, ⁸²Rb, and ¹⁸F-FDG are common PET tracers and are increasingly used for myocardial perfusion and viability studies because of advantages they offer in terms of improved diagnostic accuracy and functional assessments.^{53 18}F-LMI1195 is a novel ¹⁸F-labeled ligand for the norepinephrine transporter for mapping cardiac nerve terminals⁵⁴ whereas ¹⁸F-flurpiridaz is a novel PET mitochondrial complex 1 inhibitor for detection of coronary artery disease and risk stratification.⁵⁵ The biokinetic data of these radiotracers were obtained from the supplementary materials of ICRP publication 80,²⁸ ICRP publication 106 (Ref. 29), and the additional literature.^44,45

2.D. Dosimetry calculations

S-values of Tl-201, Tc-99m, I-123, C-11, N-13, O-15, F-18, and Rb-82 as well as the absorbed dose and effective dose of 12 nuclear cardiology radiotracers were calculated for the newborn, 1-, 5-, 10-, 15-yr-old, and the adult male and female computational phantoms according to the medical internal radiation dose (MIRD) schema.⁵⁶ The radiation absorbed dose $D\left(r_T,T_D\right)$ delivered to any target tissue r_T from source organ r_S is given by

$${\displaystyle D\left(r_T,T_D\right)=\sum _{\underset{S}{r}}\tilde{A}(r_S,T_D)S(r_T\leftarrow r_S),}$$ (1)

where $\tilde{A}(r_S,T_D)$ is the cumulated (time-integrated) activity of the radiopharmaceutical in the source region and S(r_T←r_S) is the S-value describing the equivalent dose rate in the target organ per unit activity in the source organ. The latter can be calculated by S(r_T←r_S) = 1/M_T∑_iE_iY_iϕ(r_T←r_S, E_i), where E_i is the individual energy of the ith radiation, Y_i is the yield of ith radiation per nuclear transformation, M_T is the mass of the target organ, ϕ(r_T←r_S, E_i) is the absorbed fraction given by ϕ(r_T←r_S, E_i) = E_d/E_i, where E_d is the recorded energy deposition in the target tissue. The uncertainty estimation of S-values for isotope R in target organ r_T is given by $S_R=1/M_T\sqrt{{\sum }_i{\left(Y_i{F}_i{\overline{x}}_i\right)}^2}$ where F_i and ${\overline{x}}_i$ are output relative errors and scored values by mcnp tallies for the ith radiation in the considered target regions, respectively.

The equivalent dose, which relates the absorbed dose to stochastic effects, is calculated by multiplying the absorbed dose of organs by the radiation-weighting factors. To reflect the combined detriment from stochastic effects of equivalent doses in all organs of the human body, the concept of effective dose was introduced by the ICRP and is calculated by the sum of the product of tissue-weighting factor (ω_T) and equivalent doses.⁴⁶ The effective dose is defined by a weighted sum of tissue equivalent doses as $\text{Effective}\text{dose}={\sum }_T{\omega }_T{H}_{r_T}={\sum }_T{\omega }_T{\sum }_R{\omega }_R{D}_R\left(r_T,T_D\right)$, where ω_T is the tissue-weighting factors for target organ r_T, ω_R is the radiation-weighting factor for radiation type R, and H_rT is the absorbed equivalent dose in the target organ from the administered radiotracer.

3. RESULTS

3.A. S-values

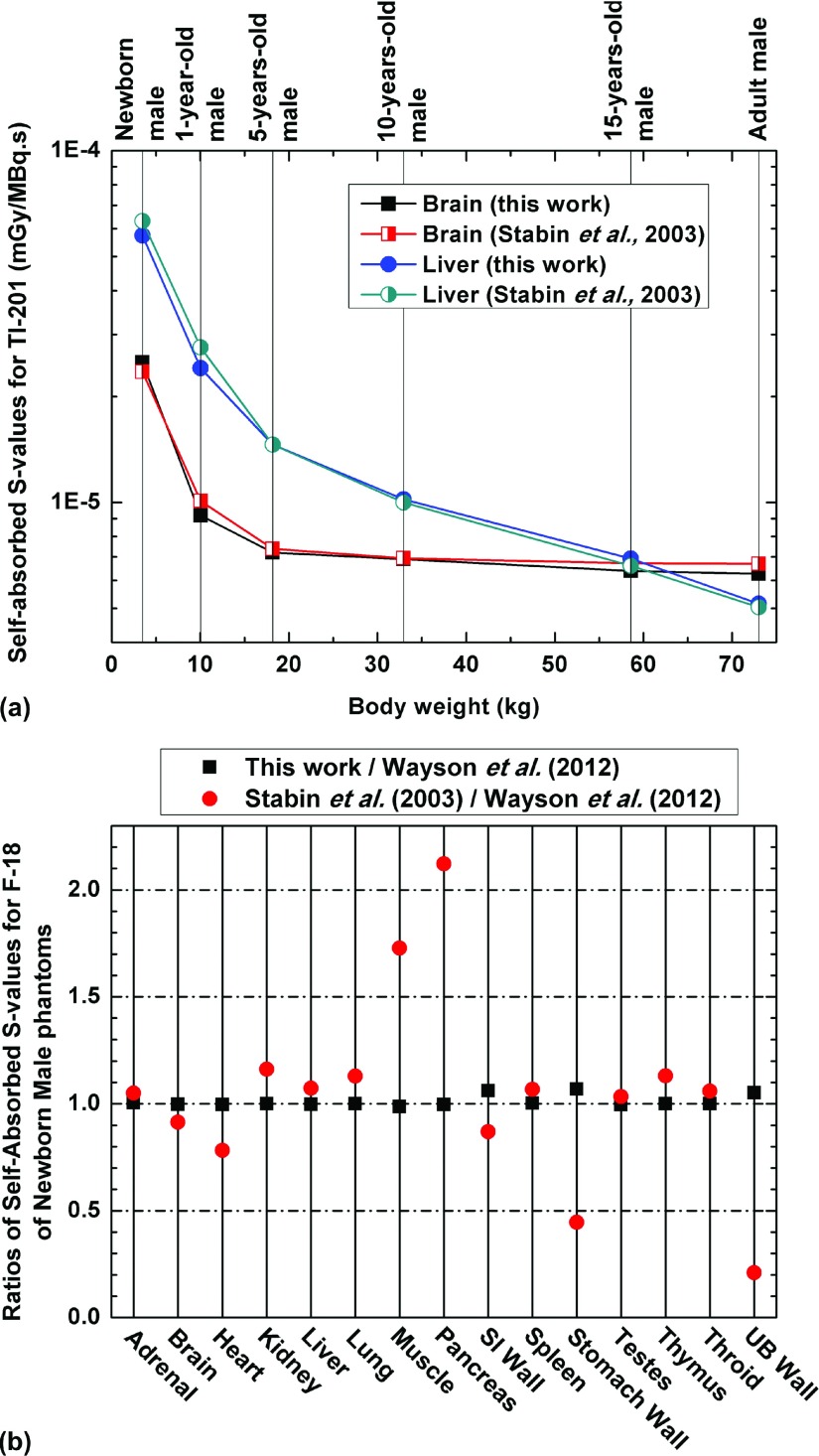
The S-values of eight investigated radionuclides for the considered source-target organ pairs were calculated in the considered computational phantoms. Figure 2 illustrates the self-absorbed S-values of Tl-201 for the brain and liver of the newborn, 1-, 5-, 10-, 15-yr-old, and adult male phantoms and the self-absorbed S-values of F-18 for representative organs of the male newborn. Comparisons between the results obtained in this work and those reported by Stabin and Siegel⁵⁷ and Wayson et al.⁵⁸ for self-absorbed S-values are shown. The same trend can be seen in Fig. 2(a) for self-absorbed S-values of Tl-201 for the brain and liver between our results and those reported in the literature for population of different age groups. For solid organs of the newborn phantom [Fig. 2(b)], there is good agreement between S-values of self-irradiation scenarios between this work and Wayson et al.⁵⁸ while for hollow organs, the self-absorbed S-values of organ walls are about 5%–7% larger than those of Wayson et al.⁵⁸ and present a higher sensitivity to changes in the voxel size (0.663 × 0.663 × 0.663 mm³ for the model used by Wayson et al.⁵⁸ and 1.8 × 1.8 × 3 mm³ for the model used in this work). The S-value differences between the results of Stabin and Siegel⁵⁷ and this work may be attributed to the differences between the geometries of the stylized and voxel-based models.

FIG. 2.

(a) Comparisons of self-absorbed absorbed S-values for ²⁰¹Tl of the brain and liver between the results of this work and Stabin and Siegel (Ref. 57) for male. (b) Comparisons of self-absorbed S-values of the newborn male phantom obtained in this work and reported by Stabin and Siegel (Ref. 57) to those reported by Wayson et al. (Ref. 58) for F-18.

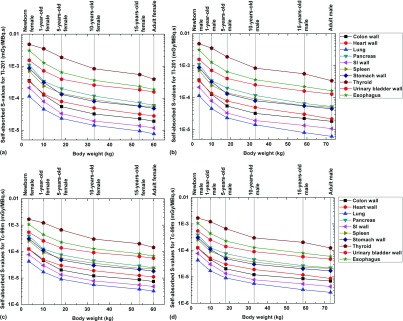
Figure 3 shows the self-absorbed S-values of Tl-201 and Tc-99m for selected internal organs. For all radionuclides, the self-absorbed S-values of organs decrease when the body weight increases and present with negative correlations with organ mass. The correlation between the cross-absorbed S-values and body weight is more complicated because the energy deposition pattern of particles in the target region from cross-irradiation is more affected by source/target distance.

FIG. 3.

Comparisons of self-absorbed S-values for selected internal organs of ²⁰¹Tl in (a) female and (b) male and ^99mTc in (c) female and (d) male.

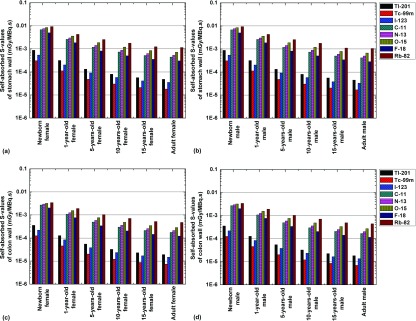
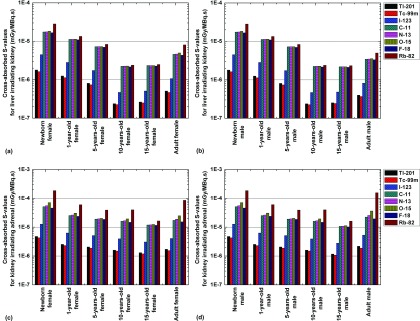
Figures 4 and 5 illustrate the self-absorbed S-values for the stomach wall and colon wall and the cross-absorbed S-values for the liver irradiating the kidney and the kidney irradiating the adrenals, respectively, for the defined computational phantoms and the eight considered radionuclides. Of these radionuclides, Rb-82 and Tc-99m produce the largest and lowest self-absorbed S-values for most organs, respectively. For SPECT radionuclides, the self-absorbed organ S-values for Tl-201 and I-123 are quite similar and about 70%–190% larger than those obtained for Tc-99m, while the cross-absorbed organ S-values for Tl-201 and Tc-99m are comparable and about 50%–60% smaller than those obtained for I-123. The cross-absorbed S-values of C-11, N-13, O-15, and F-18 are similar and about 9 times higher than those of Tl-201 and Tc-99m. A plausible explanation of these observations is that the cross-absorbed S-values are mostly contributed by photons³⁸ and the 511 keV annihilation photons emitted by positron-emitting radionuclides contribute similar energy deposition patterns and result in higher energy deposition in target regions than the low-energy photons emitted by Tl-201 and Tc-99m.

FIG. 4.

Comparisons of self-absorbed S-values of radionuclides of ²⁰¹Tl, ^99mTc, ¹²³I, ¹¹C, ¹³N, ¹⁵O, ¹⁸F, and ⁸²Rb for the stomach wall of (a) female and (b) male and colon wall of (c) female and (d) male.

FIG. 5.

Comparisons of cross-absorbed S-values of radionuclides of ²⁰¹Tl, ^99mTc, ¹²³I, ¹¹C, ¹³N, ¹⁵O, ¹⁸F, and ⁸²Rb for liver irradiating kidney of (a) female and (b) male models and kidney irradiating adrenal of (c) female and (d) male models.

3.B. Absorbed dose and effective dose

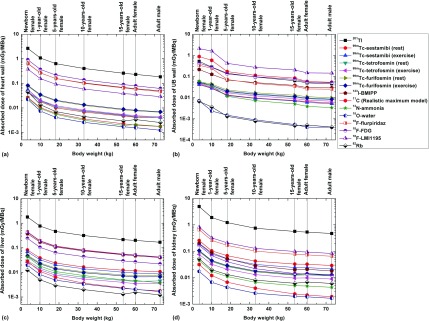
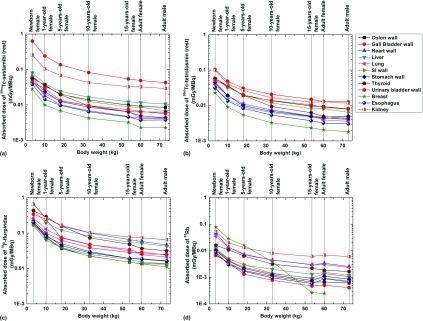
The absorbed dose to 48 target organs from the 12 investigated radiotracers was calculated in the considered computational phantoms. It was observed that the highest absorbed dose to critical organs is delivered to the testes, kidney, thyroid, and heart wall for ²⁰¹Tl; gall bladder wall, kidney, salivary glands, liver, uterus, colon wall, and urinary bladder wall for ^99mTc-sestamibi, ^99mTc-tetrofosmin, and ^99mTc-furifosmin; heart wall, liver, and urinary bladder wall for ¹²³I-BMIPP; the UB wall and uterus for ¹¹C (realistic maximum model); the liver, urinary bladder wall, and kidney for ¹³N-ammonia; the liver, spleen, thyroid, and testes for ¹⁵O-water; the kidney, heart wall, and liver for ¹⁸F-flurpiridaz; the heart wall and urinary bladder wall for ¹⁸F-FDG; the urinary bladder wall and thyroid for ¹⁸F-LMI1195; and uterus, kidney, and lung for ⁸²Rb. Figure 6 shows the absorbed dose from considered radiotracers for the heart wall, UB wall, kidney, and liver for the newborn, 1-, 5-, 10-, 15-yr-old female, and the adult male and female models. For the kidney, the absorbed dose from ²⁰¹Tl is about 300, 90, and 20 times higher than from ¹⁵O-water, ⁸²Rb, and ^99mTc-sestamibi (rest), respectively. For most radiotracers, the organ absorbed dose per unit administered activity decreases when the body weight increases. Among all considered radiotracers, ²⁰¹Tl produces the highest absorbed dose to all organs because of the long half-life of the radionuclide (73 h), in contrast to the relatively shorter half-lives of ¹⁵O-water and ⁸²Rb (2.04 and 1.27 min), respectively, which produces the lowest absorbed dose in most organs. However, for the UB wall, ¹⁸F-LMI1195 produces the highest absorbed dose because of its long residence time in the urinary bladder. Figure 7 shows the absorbed dose per unit administered activity to representative critical organs of ^99mTc-sestamibi, ^99mTc-tetrofosmin, ¹⁸F-flurpiridaz, and ⁸²Rb. For most organs, organ absorbed doses in the newborn phantom are 3.6–8.5 times higher than those of 10-yr-old phantom and 7.6–13.1 times higher than those of the adult for the considered radiotracers.

FIG. 6.

Comparisons of absorbed dose of (a) heart wall, (b) UB wall, (c) liver and, (d) kidney from investigated 14 radiotracers.

FIG. 7.

Comparisons of absorbed dose for selected internal organs from (a) ^99mTc-sestamibi (rest), (b) ^99mTc-tetrofosmin (rest), (c) ¹⁸F-flurpiridaz, and (b) ⁸²Rb.

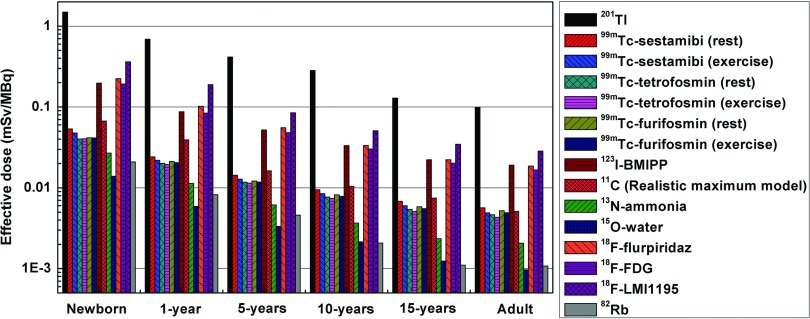
The effective dose per unit administered activity of 12 radiotracers in the newborn, 1-, 5-, 10-, 15-yr-old, and adult models calculated using tissue-weighting factors of the ICRP 103 is shown in Fig. 8. Among the considered radiotracers and population of various age groups, ²⁰¹Tl produces the highest effective dose ranging from 0.099 to 1.49 mSv/MBq, while ¹⁵O-water and ⁸²Rb produce the lowest effective dose ranging from 0.001 to 0.014 mSv/MBq and 0.001 to 0.021 mSv/MBq, respectively. Tc-99m-labeled radiotracers resulted in similar effective dose ranging from 0.004 to 0.054 mSv/MBq. The effective doses of ¹²³I-BMIPP, ¹⁸F-flurpiridaz, and ¹⁸F-FDG are comparable and about 86% lower than those of ²⁰¹Tl and 4.4 times and 14 times higher than the effective dose of Tc-99m-labeled tracers and ⁸²Rb, respectively. The effective dose of ⁸²Rb is about 80% and 50% lower than the corresponding dose of Tc-99m-labeled tracers in the adult and the newborn, respectively. ¹⁸F-LMI1195, as a novel investigational PET tracer for cardiovascular imaging, delivers a high absorbed dose to the urinary system (kidney and UB) and results in an effective dose ranging from 0.028 to 0.362 mSv/MBq to reference patients at different ages. See supplementary Tables A3–A14 for the calculated absorbed organ doses and effective doses for the considered radiotracers (the values are shown as mean value ±2 standard deviations).⁶¹ The uncertainties associated with absorbed dose and effective dose estimates are computed directly from Monte Carlo estimates.

FIG. 8.

Effective dose of 14 studied radiotracers of the newborn, 1-yr-old, 5-yr-old, 10-yr-old, 15-yr-old, and adult reference human.

4. DISCUSSION

The voxel size of the ICRP reference male and female phantoms was interpolated from 2.137 × 2.137 × 8 mm³ and 1.775 × 1.775 × 4.84 mm³ to 1.8 × 1.8 × 3 mm³ with average interpolation errors of 0.07% and 0.13%, respectively. The largest errors introduced in organ volumes for the ICRP male and female phantoms were 1.99% and 1.43%, respectively. See supplementary Table A16 at Ref. 61 for tissue-weighting factors given in ICRP publication 103,⁴⁶ which are not age- and gender-specific and were used in this work for the calculation of the effective dose of both adult and pediatric phantoms. For children at different ages, the use of the effective dose calculated from recommended tissue-weighting factors may introduce uncertainties less than 40%.⁵⁹ Variability is also introduced when effective doses are calculated using different tissue-weighting factors. The mean relative difference between effective doses calculated using ICRP 60 and ICRP 103 tissue-weighting factors was reported to be about 7.3% ± 9.1% for positron-emitting radiotracers using pediatric models.³⁵ The dose estimation in diagnostic nuclear medicine is commonly based on mean or median biokinetic data of a small group of animal or human subjects and the involved uncertainties have been reported to be within the range of 10%–30% for computational models (organs/tissues) of different sizes.⁶⁰

The development of novel nuclear cardiology imaging probes for diagnosis of cardiovascular disease is an active research field.⁵³ Accurate dose calculations for representative patient groups at different ages are needed to optimize the dose regimens of various radiotracers and to investigate the collective radiation exposure and risks associated with nuclear medicine procedures. In this work, we estimated the S-values for Tl-201, Tc-99m, I-123, C-11, N-13, O-15, F-18, and Rb-82 using a new generation of age- and sex-dependent computational phantoms including the newborn, 1-, 5-, 10-, 15-yr-old, and adult male and female and calculated organ absorbed doses and effective doses of 12 radiotracers used in nuclear cardiology based on the latest available dosimetric data.

The Monte Carlo method is a powerful and popular tool for internal radiation dosimetry calculation where accurate dose estimates are grounded on reliable computational phantoms that mimic the internal anatomic geometries and physical characteristics of the human body. The equivalent dose to patients from administered radiotracers is frequently calculated from tabulated absorbed dose rate derived from stylized phantoms.^27–31 However, significant differences between the dosimetric characteristics of stylized and voxel-based models for the same subject are often reported.^33–38 Since some biological organs/tissues in populations of different ages may have substantially different physical and biochemical characteristics and present with different radiosensitivity and radiation risks, the evaluation of age-dependent absorbed dose using realistic anatomical computational phantoms is commended.

Among the evaluated radionuclides, Tl-201, Tc-99m, and I-123 are adopted for SPECT cardiovascular imaging while C-11, N-13, O-15, F-18, and Rb-82 are commonly used for PET cardiovascular imaging. The organ absorbed dose depends on the S-value and physical half-life of the radionuclide and the biological half-life and biodistribution of the radiotracer. For most organs, Rb-82 produces the highest self-absorbed S-values which decrease with increasing age and weight and the second lowest absorbed organ dose because of its short half-life. Overall, among the considered nuclear cardiology radiotracers, Tl-201-labeled tracers produce the highest absorbed dose and effective dose in humans; I-123 and F-18-labeled tracers produce the second highest radiation dose, while Tc-99m and C-11-labeled tracers produce the third highest radiation dose. A lower effective dose in adults is observed for ⁸²Rb-labeled tracers compared to ^99mTc-labeled tracers, while this advantage is less apparent in children.

5. CONCLUSION

A systematic study was conducted to evaluate the radiation dose from nuclear cardiology (SPECT and PET) procedures to pediatric and adults populations using the latest generation computational phantoms and the up-to-date dosimetric data available. The generated database of organ absorbed dose and effective dose for radiotracers used in nuclear cardiovascular imaging can be used for radiation risk assessment for the pediatric and adult population in clinical routine.