The Segregation and Integration of Distinct Brain Networks and Their Relationship to Cognition

Abstract

A critical feature of the human brain that gives rise to complex cognition is its ability to reconfigure its network structure dynamically and adaptively in response to the environment. Existing research probing task-related reconfiguration of brain network structure has concluded that, although there are many similarities in network structure during an intrinsic, resting state and during the performance of a variety of cognitive tasks, there are meaningful differences as well. In this study, we related intrinsic, resting state network organization to reconfigured network organization during the performance of two tasks: a sequence tapping task, which is thought to probe motor execution and likely engages a single brain network, and an n-back task, which is thought to probe working memory and likely requires coordination across multiple networks. We implemented graph theoretical analyses using functional connectivity data from fMRI scans to calculate whole-brain measures of network organization in healthy young adults. We focused on quantifying measures of network segregation (modularity, system segregation, local efficiency, number of provincial hub nodes) and measures of network integration (global efficiency, number of connector hub nodes). Using these measures, we found converging evidence that local, within-network communication is critical for motor execution, whereas integrative, between-network communication is critical for working memory. These results confirm that the human brain has the remarkable ability to reconfigure its large-scale organization dynamically in response to current cognitive demands and that interpreting reconfiguration in terms of network segregation and integration may shed light on the optimal network structures underlying successful cognition.

SIGNIFICANCE STATEMENT The dynamic nature of the human brain gives rise to the wide range of behaviors and cognition of which humans are capable. We collected fMRI data from healthy young adults and measured large-scale functional connectivity patterns between regions distributed across the entire brain. We implemented graph theoretical analyses to quantify network organization during two tasks hypothesized to require different combinations of brain networks. During motor execution, segregation of distinct networks increased. Conversely, during working memory, integration across networks increased. These changes in network organization were related to better behavioral performance. These results underscore the human brain's ability to reconfigure network organization selectively and adaptively when confronted with changing cognitive demands to achieve an optimal balance between segregation and integration.

Introduction

It is proposed that a dynamic, adaptable brain network configuration in response to one's environment underlies successful cognition (Dehaene et al., 1998; McIntosh, 1999; Bressler and Kelso, 2001; Fries, 2005). Whole-brain intrinsic functional connectivity patterns as measured during a resting state have been associated with general intelligence (van den Heuvel et al., 2009; Santarnecchi et al., 2014), working memory capacity (Stevens et al., 2012; Alavash et al., 2015), and other cognitive abilities (for a review, see Vaidya and Gordon, 2013). However, to understand fully the relationship between brain networks and cognition, it is important to also investigate the patterns of functional connections when individuals are confronted with a variety of cognitive demands (Smith, 2012; Buckner et al., 2013). One promising approach is to measure whole-brain functional connectivity in an individual during the engagement of multiple cognitive tasks, allowing for the quantification of changes in network structure due to changing cognitive demands.

Several studies using this approach have found that while there are many similarities in network structure during rest and during the performance of different cognitive tasks (Cole et al., 2014; Krienen et al., 2014), there are also meaningful task-specific differences (Cole et al., 2013; Krienen et al., 2014; Davison et al., 2015). The current study aimed to expand this work by relating intrinsic network organization (as assessed during rest) to reconfigured network organization during two tasks assumed to tap different (and dissociable) brain modules or networks (Dehaene et al., 1998; Mesulam, 1998): a sequence tapping task purported to require motor execution and an n-back task purported to require working memory. While motor execution is a cognitive function thought to be subserved by a single brain network, working memory likely requires coordination across multiple brain networks supporting many cognitive processes, such as sustained attention and inhibition.

With the relatively recent application of network analysis tools to functional brain imaging data, there is an emerging interest in understanding how both the segregation and the integration of brain networks underlie successful cognition (Friston, 2009; Sporns, 2013; Deco et al., 2015). For example, research probing coactivation of regions across the entire brain during a variety of cognitive tasks points to segregated networks that are functionally specialized (Crossley et al., 2013; Bertolero et al., 2015; Yeo et al., 2015). It is additionally theorized that a highly interconnected group of regions, the “rich club,” is critical for integration across distinct networks (van den Heuvel et al., 2012). Further, patterns of integration alter based on current cognitive demands, with distinct profiles of cooperative and competitive connections underlying different aspects of cognition (Cocchi et al., 2013). Extant literature makes it clear that it is critical to understand both network segregation and network integration and how they relate to different aspects of cognition. In this study, we probed network reconfiguration when performing cognitive tasks that engage either a single specialized brain network or the coordination of multiple specialized networks. Our goal was to determine whether interpreting network structure in terms of segregation and integration could explain observed patterns of reconfiguration. By applying whole-brain graph theoretical methods to functional connectivity data acquired using fMRI, we tested the hypothesis that motor execution would be associated with an increase in local, within-network connectivity and a decrease in global integration, whereas working memory would be associated with a decrease in local, within-network connectivity and an increase in global integration. Further, we hypothesized that successful task-specific reconfiguration would be associated with better task performance.

Materials and Methods

Participants

Thirty-five healthy young adult participants were recruited for this study (mean age = 21.74 years, SD = 2.73, 17 females). All participants were native English speakers, had normal or corrected-to-normal vision, and normal hearing. Participants were excluded for any history of neurological or psychiatric disorders, use of psychotropic drugs, a history of substance abuse, or MRI contraindications. All participants provided written informed consent according to the procedures of the University of California, Berkeley (UC Berkeley) Committee for the Protection of Human Subjects.

Five participants were excluded for falling asleep during a resting scan as assessed by a camera focused on each participant's right or left eye and by observing extended eye closures despite task instructions to maintain fixation with eyes open. Therefore, 30 participants were included in the analyses (mean age = 22.07 years, SD = 2.73, 13 females). In analyses involving the sequence tapping task (see below for task description), one additional participant was excluded (age = 23 years, male) due to a computer malfunction that caused the task to terminate early.

Experimental design and procedure

Participants underwent 2 testing sessions ∼1 week apart (average duration = 7.47 d, SD = 2.47, range = 2–16). During each session, participants received relevant training and were then administered a task flanked by two resting scans in the MRI scanner. The order of sessions was counterbalanced.

Sequence tapping task.

During one of the testing sessions, participants performed a sequence tapping task in the scanner (Sun et al., 2004). Before the scan, participants were well trained on two sequences. The first sequence required a response of four button presses with fingers of the right hand followed by four button presses with fingers of the left hand, which we named “right-then-left.” When defining each key press by a letter (R = right, L = left) and a number (2 = index finger, 3 = middle finger, 4 = ring finger, 5 = pinkie finger), the sequence order was as follows: R3–R5–R2–R4–L5–L2–L3–L4. The second sequence required interleaved bimanual responses in which participants alternated right and left button presses for a total of eight presses: R3–L5–R5–L2–R2–L3–R4–L4. This sequence was named “interleaved,” and alternated the right-handed and left-handed sequences of the right-then-left condition. Each sequence was considered learned only after participants were able to execute the sequence with an accuracy of at least 80% and a mean response time to complete the eight button presses of <2500 ms. Training lasted on average 27 min, with a mean of 115 trials of the right-then-left sequence (always learned first) and 251 trials of the interleaved sequence (always learned second).

Each participant performed four runs of ∼7.5 min of the task, for a total of 48 right-then-left and 48 interleaved sequences (Fig. 1A). Each run began with a 10 s fixation (crosshair) followed by 12 right-then-left and 12 interleaved sequences randomly interspersed with the constraint that no condition occurred >3 times in a row. On each trial, a visual cue (“right-then-left” or “interleaved”) indicated to the participant which sequence to execute. Participants were instructed in advance to complete each sequence accurately over the course of ∼2 s (1 press per 250 ms). On average, participants completed each right-then-left sequence in 2336.5 ms and each interleaved sequence in 2486.8 ms. Participants received visual feedback regarding the accuracy and speed of their response immediately after the completion of each sequence or after 4500 ms if the sequence had not been completed. The feedback remained on the screen for 2000 ms. Intertrial interval length was randomly jittered so that total trial length (including cue, response, and feedback) was 16, 18, or 20 s. Each trial length occurred 8 times per run, randomly interspersed with the constraint that no one length occurred >3 times in a row. After the participant's response and the feedback, participants fixated on a crosshair in the center of the screen for the remainder of each trial.

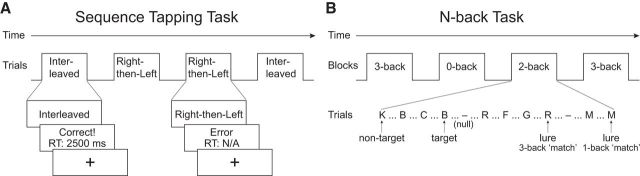
Figure 1.

A, Sequence tapping task. Participants were trained and tested on two sequences: right-then-left and interleaved. During scanning, each trial began with a visual cue instructing participants which sequence to execute. After completion of the sequence, participants received accuracy and response time feedback. B, N-back task. All blocks consisted of sequences of 20 letters presented one at a time. The 3 trial types (targets, lures, and nontargets) are illustrated here on a 2-back block.

N-back task.

During the other testing session, participants received an n-back task in the scanner (Jacobs and D'Esposito, 2011), which consisted of four runs of ∼11.5 min (Fig. 1B). Participants completed 3 loads of the task (0-, 2-, and 3-back) during which they were presented visually with a series of single consonants that appeared sequentially every 2 s. Using two buttons with the index and middle fingers of their right hand, participants indicated whether the current letter did not match (left button press) or matched (right button press) the letter seen n previously. A “target” was a letter that matched the letter seen n previously. For example, in a 3-back condition, the second “R” in the sequence R–T–K–R–D was a target. A “lure” was a letter that matched a letter seen n ± 1 times previously. For example, in a 3-back condition, the second D in the sequence D–T–K–R–D was a lure; it matched the letter seen 4 letters earlier, but not 3 as the condition specified. All other trials were categorized as “nontargets.” On 0-back blocks, participants indicated whether a target letter (“X”) appeared. The 0-back blocks consisted of targets and nontargets; lure trials were not relevant in that condition.

There were 32 n-back blocks divided evenly over the 4 runs: 10 0-back, 11 2-back, and 11 3-back ordered pseudorandomly so that each run consisted of at least 1 block of each load and no load was presented more than twice sequentially. Each block consisted of 20 trials plus 5 randomly placed null events. The null events introduced temporal jitter to allow for event-related analyses. Each trial included the stimulus (an uppercase letter) presented for 1 s, followed by a 1 s delay (blank screen); null events consisted of a blank screen for 2 s. Each block began with a 6 s instruction period and a 10 s fixation period. Each block was followed by a 20 s fixation period. There were 20% targets, 15% lures, and 65% nontargets in the 2-back and 3-back conditions, for a total of 44 targets, 33 lures, and 143 nontargets per condition. There were 20% targets and 80% nontargets in the 0-back condition, for a total of 40 targets and 160 nontargets. These proportions ensured that targets and lures were rare enough so as to not be expected, but often enough to be analyzed reliably.

Resting state.

Before and after each task, participants received a single resting state scan (10 min). Participants were instructed to stay awake with their eyes open and to fixate on a white crosshair in the center of a gray screen. Only data from the two pre-task resting scans will be analyzed here.

Although data exist indicating that functional connectivity during rest is influenced by a recent task, it has been found that by 12 min intrinsic connectivity returns to its pre-task baseline (Barnes et al., 2009; Tung et al., 2013). The average time between the termination of behavioral training on the sequence tapping task and the initiation of the resting state scan during that session for all participants was 25.72 min (SD = 7.06, range = 17–47). Comparing the pre-task resting scans of each session revealed that, whereas there was some variability across sessions, resting organization was not significantly different across the two sessions in the metrics and brain atlases examined here (all corrected p > 0.98, false discovery rate [FDR] corrected for 12 comparisons; see below for description of the metrics and brain atlases). This confirms that the pre-task resting state scans were not influenced by pre-scan training.

fMRI data acquisition

Imaging data were collected using a 12-channel head coil on a 3-tesla Siemens MAGNETOM Trio whole-body MR machine at the UC Berkeley Henry H. Wheeler Jr. Brain Imaging Center. Whole-brain functional data were acquired using a T2*-weighted echoplanar imaging (EPI) pulse sequence (37 descending axial slices parallel to the AC–PC line, slice thickness 3.5 mm, interslice distance = 0.7 mm, TR = 2000 ms, TE = 24 ms, FA = 60°, matrix 64 × 64, field of view 224 mm). A total of 300 volumes were collected for each resting state run, 224 for each run of the sequence tapping task, and 345 for each run of the n-back task. A high-resolution T1-weighted structural 3D MP-RAGE was also acquired (160 slices, slice thickness 1 mm, TR = 2300 ms, TE = 2.98 ms, FA = 9°, matrix 256 × 256, field of view 256 mm). An LCD projector back projected visual stimuli onto a screen mounted to the RF coil. PsychoPy software (http://www.psychopy.org) was used to present stimuli and record responses and latencies via a fiber-optic motor response recording device for the sequence tapping task and E-Prime software (Psychology Software Tools) was used for the n-back task.

fMRI data processing

Functional image preprocessing was performed using AFNI (Cox, 1996, RRID:SCR_005927). Images were corrected for differences in motion and slice timing acquisition, the brain was extracted from the skull, and images were coregistered into each participant's own high-resolution structural (MP-RAGE) space. The MP-RAGE was segmented using SPM8 (Wellcome Department of Cognitive Neurology, London, United Kingdom, RRID:SCR_007037) to create white matter and ventricle regions of interest (ROIs) from which average time-series were calculated as nuisance regressors. Functional images were then spatially smoothed with a 6 mm FWHM isotropic Gaussian kernel. Finally, the functional time-series were band-pass filtered (0.009–0.08 Hz) and signal from movement, white matter, and ventricles (as well as temporal derivatives) was regressed out simultaneously. This method has been shown to control effectively time-series variability related to nuisance variables, including movement (Hallquist et al., 2013). In a second set of analyses, we added nuisance regressors corresponding to stimulus events for each task to remove potential effects of stimulus presentation that were not directly relevant to the cognitive processes of interest. Because the nuisance regression was different for rest and for the tasks, we only related the differences in network organization across sequence tapping and n-back tasks for this analysis. When comparing the differences across tasks observed using both sets of nuisance regressors (with and without stimulus events), our results did not change when including the extra task-related regressors: statistical comparison of the t statistics of the two regression methods resulted in all p-values greater than 0.72 when FDR correcting for 12 comparisons. This result is not surprising because the sequence tapping and n-back tasks were designed to require sustained cognitive processes throughout task blocks, as opposed to transient processes that could have been affected by individual stimuli. Given the similarity in results across the two regression methods, we are only reporting our initial analyses without including task regressors (described in detail below).

Data from all relevant volumes were included in all analyses, given evidence that the simultaneous filtering/nuisance regression approach implemented here reduces correlations adequately between time-series fluctuations and motion (Hallquist et al., 2013). To rule out motion effects, we calculated average frame-wise displacement (FD) across each run (Power et al., 2012). We found that all participants had minimal motion (across all participants and all runs: mean = 0.14 mm; max = 0.34 mm; average percentage of volumes with > 0.3 mm motion = 4.67%). In addition, motion did not differ across tasks (F_(2,84) = 0.57, p = 0.57). There were also no significant relationships between FD and any of the brain or behavioral metrics of interest described below (all p > 0.39, FDR corrected for 50 comparisons).

Functional connectivity

To calculate functional connectivity between pairs of brain regions, we partitioned the brain into cortical ROIs using two different whole-brain atlases: the 96 cortical ROIs from the anatomical Harvard–Oxford atlas (Desikan et al., 2006) and the 264 cortical and subcortical ROIs from a commonly used functional brain atlas, the areal atlas from Power et al. (2011). Throughout, we refer to the Harvard–Oxford atlas as the anatomical atlas and the Power atlas as the functional atlas. We conducted all analyses on each atlas separately to confirm that our results were not due to the idiosyncrasies of any single atlas. For each atlas, the fully processed time-series data were averaged within each ROI and then each ROI's average time-series was correlated with the average time-series for all other ROIs, resulting in a 96 × 96 (anatomical atlas) or 264 × 264 (functional atlas) correlation matrix for each task (or rest) block of each participant. We constructed the correlation matrices identically for rest and for both tasks with the goal of relating overall functional connectivity during rest (intrinsic connectivity) to that during task performance (encompassing both task-related and background connectivity). The correlation coefficients were standardized into z-scores to allow for statistical conclusions to be made from the magnitudes of the correlations. Due to minor signal dropout in the inferior temporal and orbitofrontal cortex, data from six ROIs of the anatomical atlas and 18 ROIs of the functional atlas were not collected in all 30 included participants. Therefore, all analyses were conducted on a 90 × 90 (anatomical) or 246 × 246 (functional) Fisher-transformed connectivity matrix that included only ROIs with data from all participants.

For the resting state scans, each time-series included the entire run (600 s; 300 volumes). For the task scans, each time-series included only the relevant volumes for a given block. Each block time-series began 6 s (3 volumes) after the start of each block and ended 6 s (3 volumes) after the end of each block to account for the delay of the hemodynamic response. Although concatenating across nonadjacent volumes is typically done when probing time-series that are not contiguous in time (i.e., across task blocks within a scan or combining data across multiple scans), concatenation ignores important temporal information that may be critical when measuring low-frequency neural oscillations. For example, if signal intensity changes from the last volume of one block to the first volume of the next, spurious correlations could be induced. Therefore, we chose to analyze our data in two different ways to ensure that any results were not due to the specific data combination procedure selected. First, we calculated time-series correlations within each block individually and then averaged across all blocks to result in a single, average time-series for each condition. For this method, termed “block-wise connectivity,” each sequence tapping task time-series was 14 s (7 volumes) and each n-back task time-series was 50 s (25 volumes). Sequence tapping time-series were separated into right-then-left and interleaved conditions (48 blocks each). N-back time-series were separated into 0-back, 2-back, and 3-back conditions (10 blocks of 0-back; 11 blocks each of 2-back and 3-back). Connectivity matrices of all blocks of a given condition were averaged together to stabilize connectivity values. Although the block length was quite different across tasks, the total number of volumes used to calculate each connectivity value was similar (300 volumes for resting blocks; 336 volumes for each sequence tapping condition; 275 volumes each for n-back 2-back and 3-back conditions). Second, we standardized each block (mean = 0; SD = 1) to minimize the possibility of spurious correlations being induced due to changes in signal intensity or variability across blocks and then concatenated across blocks. This method, termed “concatenated connectivity,” resulted in a single time-series for each condition, with 336 volumes for each sequence tapping condition and 275 volumes each for n-back 2-back and 3-back conditions. As before, there was a single block of 300 volumes for the resting state, since resting state blocks were continuous and thus did not require averaging or concatenation. Results were nearly identical regardless of which method was used. Statistical comparison of the results of the two methods with paired t tests resulted in all p-values greater than 0.99 when FDR correcting for 60 comparisons (one for each statistical test conducted). Given that there were no significant differences in results when comparing the two methods, we only report results for the block-wise connectivity method.

Graph construction

To create graphs from the Fisher-transformed connectivity matrices of the anatomical and functional atlases, we used tools from the Brain Connectivity Toolbox (www.brain-connectivity-toolbox.net; Rubinov and Sporns, 2010, RRID:SCR_004841). First, we assigned each node to a network using the consensus clustering method (Lancichinetti and Fortunato, 2012). We used the Louvain community detection algorithm with weighted edges (positive only) to produce an estimate of the optimal partitioning of nodes into networks (Rubinov and Sporns, 2011). We set the resolution parameter (γ), which determines the size of each network within the whole-brain graph, to 1.25 because this value produced functional graphs with the same number of networks that were reported in the initial study describing the functional atlas (Power et al., 2011). To maintain analytical consistency across atlases, we used γ = 1.25 for both the anatomical and functional atlases. Because the Louvain community detection algorithm is stochastic, we ran this algorithm 150 times and created a consensus matrix, D, from the 150 partitions, where each cell (D_ij) indicates the proportion of partitions that particular pair of nodes (i,j) were assigned to the same network. We thresholded each cell at 0.5. In other words, the agreement of all pairs of nodes that were not assigned to the same network at least 50% of the time was set to 0. The goal of this step was to remove the influence of noisy, and potentially spurious, node agreement. Last, we created a consensus partition from the agreement matrix, D, by running the Louvain algorithm 100 times to create 100 consensus partitions. This last step was repeated until a single representative partition was obtained. This method has been shown to produce more accurate partitions than other commonly used algorithms (Lancichinetti and Fortunato, 2012).

For each atlas, we created optimal network partitions separately for each condition of each task for each participant. We then constructed undirected, unweighted graphs using the Fisher-transformed correlation matrices described above. First, we thresholded each connectivity matrix to create an adjacency matrix of 1s (above threshold) and 0s (below threshold). Each of the ROIs was a node of the graph and each of the above-threshold connections was an edge. To be able to compare graphs most directly across conditions and participants, we equated the number of edges across all graphs (van Wijk et al., 2010; Garrison et al., 2015). We did this by thresholding each graph at a set cost, or percentage of total edges. Each analysis was conducted over a range of costs (10–25% in 5% increments) to ensure that any results were not due to the chosen threshold. All graph metrics reported are the average value across all costs. The range of thresholds was chosen because it is within the range of values that produce graphs with small world characteristics (Bullmore and Bassett, 2011).

Graph theoretical metrics

To calculate all graph theoretical metrics, we used an in-house software toolbox developed at UC Berkeley that was programmed with Python (www.python.org, RRID:SCR_008394). The toolbox, Brainx (https://github.com/nipy/brainx), is based on the Networkx graph theory package (https://networkx.github.io/). First, we calculated the modularity of the graphs using the adjacency matrices and the optimal network partitions of each graph as input. Modularity relates the number of within-network connections to all connections to quantify the strength of segregation into distinct networks. Higher values indicate stronger separation of networks. Modularity (Q) is defined as follows:

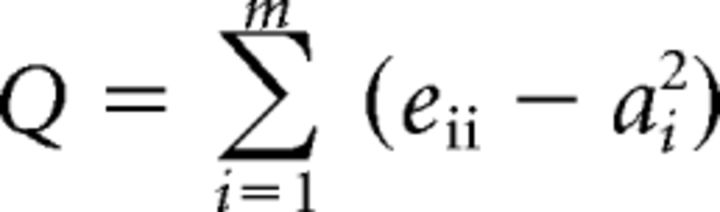where e_ii is the fraction of all edges that connect two nodes within module i, a_i is the fraction of edges that connect a node in module i to any other node, and m is the total number of modules.

Next, we calculated the strength of system segregation of our graphs (Chan et al., 2014). We used the unthresholded, Fisher-transformed connectivity matrices to calculate system segregation based on nodal assignment of the optimal partitions described above. Within-network connectivity strength was calculated as the mean connectivity strength of edges between all pairs of nodes within the same network (z̄_w). Between-network connectivity strength was calculated as the mean connectivity strength of edges between all pairs of nodes that spanned two networks (z̄_b). System segregation was calculated to describe the relative strength of within-network connectivity compared to between-network connectivity as follows:

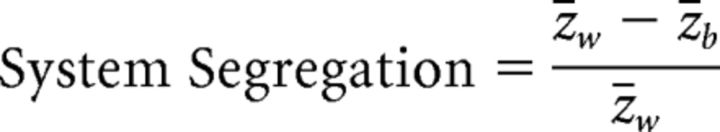In addition to network-based measures, we calculated average local efficiency and global efficiency across all nodes regardless of network membership (Latora and Marchiori, 2001; Achard and Bullmore, 2007). Both are calculated using the metric of minimum path length (L), which counts the smallest number of edges that must be crossed to get from node i to node j. The efficiency of each node, nodal efficiency (E_nodal), is calculated as the inverse of the harmonic mean of L between node i and all other nodes as follows:

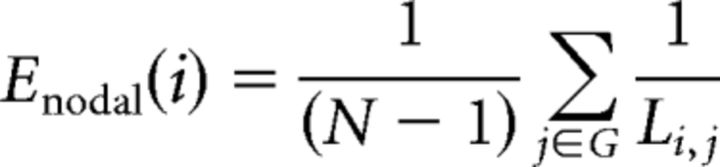where N is the number of nodes in graph G, and L_i,j is the minimum path length between nodes i and j.

Local efficiency (E_local) is a measure of the efficiency of information transfer limited to neighboring nodes (i.e., nodes with direct edges [L = 1] to the node of interest). Local efficiency is calculated as the average nodal efficiency among the neighboring nodes of node i, excluding node i itself, as follows:

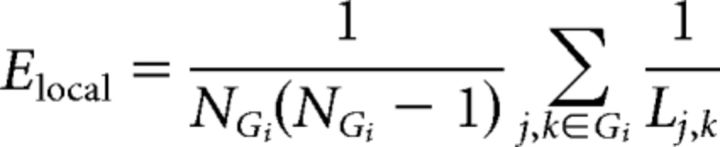where N is the number of nodes in graph G_i. G_i is the subgraph of graph G that includes all neighboring nodes of i (excluding i).

Global efficiency (E_global) is a measure of the efficiency of information transfer among all pairs of nodes in the graph, and is simply calculated as the average nodal efficiency of all nodes as follows:

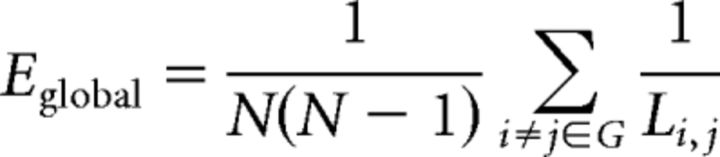Last, we quantified two properties of individual nodes: participation coefficient, an index of internetwork connections, and within-module degree, an index of intranetwork connections (Guimerà and Amaral, 2005a,2005b). Participation coefficient (PC) is defined as follows:

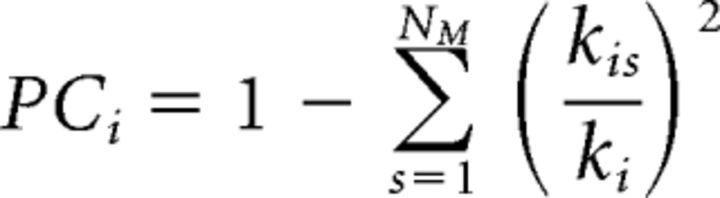where k_is is the degree (number of connections) of node i to other nodes in its own network (s), and k_i is the degree of node i regardless of network membership. By subtracting that ratio from 1, participation coefficient is a normalized measure of the connections that are not within a node's own network, or that are across networks.

Within-module degree (WD) is defined as follows:

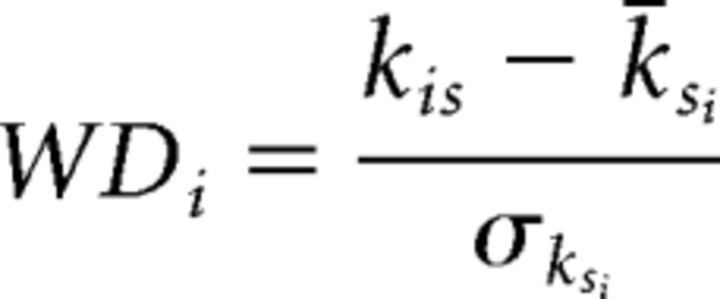where k_is is the degree of node i to other nodes in its own network (s), k̄_si is the average degree of all nodes in s (only including within-network connections), and σ_ksi is the SD of the degree of all nodes in s. Within-module degree, therefore, is a standardized (z-scored) metric of how connected a node is to all other nodes within its own network.

Participation coefficient and within-module degree can be used to define different types of nodes that are important for network communication. Here, we investigated how two of these types of nodes were related to specific cognitive demands: provincial hubs and connector hubs. We adapted the definitions of these two node types from Guimerà and Amaral (2005a, 2005b). These investigators defined provincial hubs as nodes that are important for within-network, but not between-network, communication as assessed by high WD (≥ 2.5) and low PC (≤0.3). Due to the different types of networks examined, their WD was higher than that observed in our participants; therefore, we defined provincial hubs as WD ≥ 1.5 and PC ≤ 0.3. Connector hubs were defined by Guimerà and Amaral (2005a, 2005b) as nodes that are important for between-network, but not within-network, communication (WD < 2.5, PC > 0.62). Again, we adapted their definition and defined connector hubs in our study as WD < 1.5 and PC > 0.8. The thresholds were chosen to ensure that all participants had at least one node above that threshold for at least one task. A schematic describing all metrics calculated is visualized in Figure 2.

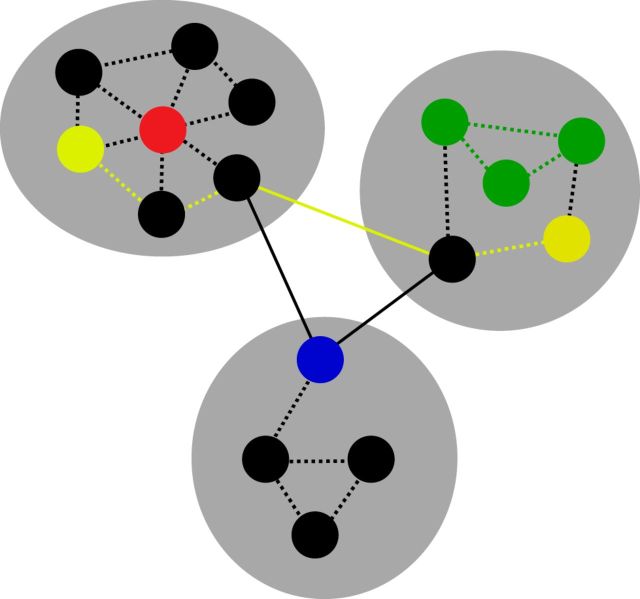
Figure 2.

Measures of network organization. Gray ovals are networks of the graph, circles are nodes, solid and dashed lines are edges. Modularity is a measure of network segregation into distinct networks, with sparse connections across networks. System segregation is a measure of the relative strength of within-network connections (dashed lines) to between-network connections (solid lines). Green nodes and edges depict a cluster of nodes with high local efficiency (the efficiency of information transfer among neighboring, or directly connected, nodes). Yellow edges depict the shortest path between the two yellow nodes; the shorter the average path length across all pairs of nodes, the higher the global efficiency (the efficiency of information transfer across the entire system). The red node depicts a provincial hub (strong within-network, but weak between-network connectivity). The blue node depicts a connector hub (strong between-network, but weak within-network connectivity). Figure adapted with permission from Rubinov and Sporns (2010).

For statistical comparisons between the resting and task scans, as well as between the two tasks, metrics for both active conditions of each task were averaged (right-then-left and interleaved conditions for the sequence tapping task and 2-back and 3-back conditions for the n-back task). We combined the two conditions of each task because the average metrics for each task condition were not significantly different from each other, with one expected exception: system segregation, which measures the relative strength of between-network and within-network connectivity, was significantly stronger during the right-then-left than during the interleaved condition of the sequence tapping task, for the functional atlas only (t₍₂₈₎ = 3.33, corrected p = 0.015). This was expected due to the increased interhemispheric integration anticipated during the interleaved condition (Sun et al., 2004; Grefkes et al., 2008). Importantly for the below analyses, investigating the two conditions separately did not change the results, so they are reported combined to remain consistent (all other p-values > 0.08, FDR corrected for 6 comparisons). Paired t tests were conducted to compare any two tasks within an individual (rest vs sequence tapping, rest vs n-back, sequence tapping vs n-back). For comparisons involving the sequence tapping task, in which one additional participant was excluded due to computer malfunction (see “Participants” section), that participant was also removed from the comparison task to limit comparisons to the same participants for both tasks. For relationships with performance, behavior and brain metrics for only the most difficult condition were correlated using Pearson's correlations because brain–behavior relationships were not identical for the two task conditions. We focused on the most difficult condition of each task to maximize the effort needed for successful performance, which we hypothesized would maximize concentration on the task and therefore brain–behavior relationships. Because we did not have specific hypotheses regarding which graph metrics would be related to behavior, we related behavioral performance on the relevant task to all six graph theoretical metrics that we calculated during the interleaved condition of the sequence tapping task and the 3-back condition of the n-back task (modularity, system segregation, local efficiency, global efficiency, number of provincial hubs, and number of connector hubs). Because of a computer malfunction, behavioral data were not collected for one participant during the n-back task, so that participant was excluded from the correlations with behavior, leaving 29 participants for those analyses.

In addition, a participant was excluded for an individual correlation analysis if that participant was an outlier for the relevant brain or behavior metric (as defined by being >3 SDs from the mean); this resulted in a single participant being excluded from 2 of the 24 analyses: functional atlas n-back task global efficiency and number of provincial hub nodes, leaving 28 participants for those two correlations with behavior. No other participants for any other analyses were outliers.

All analyses that compared rest to sequence tapping, rest to n-back, and sequence tapping to n-back using paired t tests were FDR corrected for three comparisons. The behavioral correlations were FDR corrected for six comparisons for each task separately. Corrected p-values are reported at a significance threshold of corrected p = 0.05.

Results

Graph partitions

First, we defined participant-specific and condition-specific brain networks during rest and each of the tasks using consensus clustering to define community structure. Qualitatively, we observed a greater separation of distinct brain networks during the sequence tapping task as compared to both rest and the n-back task and an increase in connections across networks during the n-back task as compared to both rest and the sequence tapping task. This pattern was observed consistently when examining network organization using both the anatomical and the functional atlases (Fig. 3). The following analyses will address the potentially increased segregation during the sequence tapping task and increased integration during the n-back task quantitatively.

Figure 3.

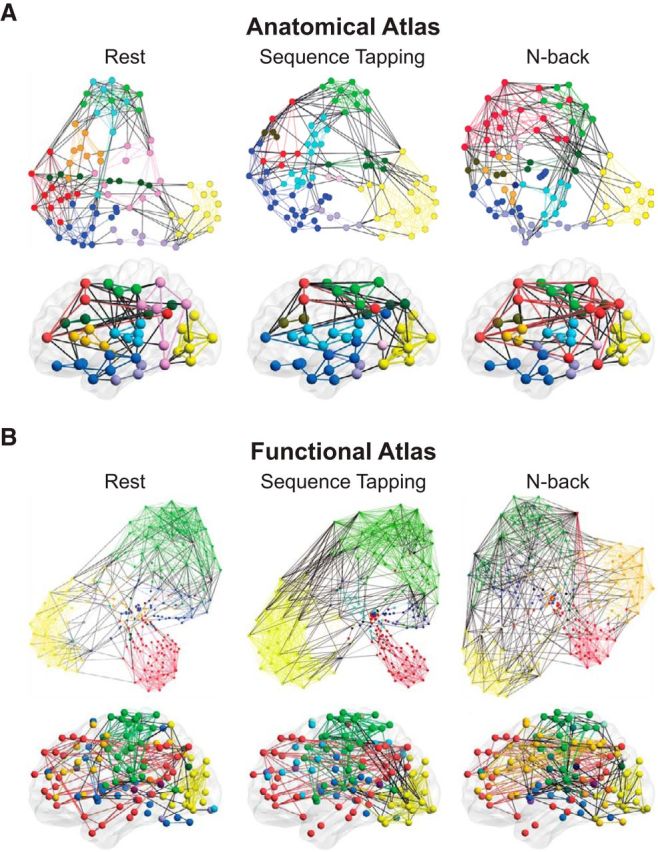
Depiction of network assignment for rest, sequence tapping, and n-back tasks optimized separately for each task for (A) the anatomical analysis and (B) the functional atlas. Each color represents a network, each colored line represents a within-network edge, and each black line represents a between-network edge. For visualization purposes, the anatomical atlas is displayed at cost = 0.1 and the functional atlas is displayed at cost = 0.04. In the top panel of each subfigure, nodes are depicted based on connections; nodes with more shared connections are closer together. In the bottom panel of each subfigure, nodes are depicted in brain space; each circle corresponds to the coordinates of the center of each ROI. Note that qualitatively, whereas the number and nodal composition of networks is similar for rest and the sequence tapping tasks, there is a greater separation of different networks during sequence tapping. Conversely, the greatest increase in between-network edges occurs during the n-back task. For example, there are more nodes from different networks with closely shared connections during the n-back task. Connection space graphs were visualized with Gephi (Bastian et al., 2009, https://gephi.org/). Brain space graphs were visualized with BrainNet Viewer (Xia et al., 2013, http://www.nitrc.org/projects/bnv/).

Modularity and system segregation

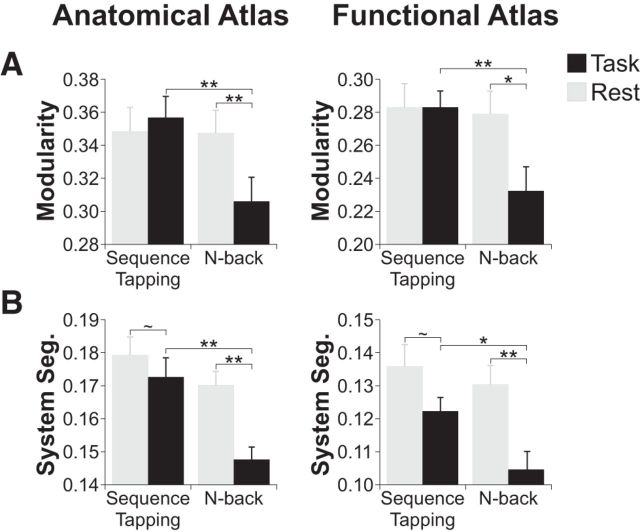
Modularity was significantly higher during the sequence tapping task than during the n-back task (anatomical atlas: t₍₂₈₎ = 3.25, corrected p = 0.005; functional atlas: t₍₂₈₎ = 3.32, corrected p = 0.008). Modularity during rest was equivalent to modularity during the sequence tapping task and higher than modularity during the n-back task (anatomical atlas: rest vs sequence tapping t₍₂₈₎ = 0.04, corrected p = 0.70, and rest vs n-back t₍₂₉₎ = 3.17, corrected p = 0.005; functional atlas: rest vs sequence tapping t₍₂₈₎ = 0.06, corrected p = 0.95, and rest vs n-back t₍₂₉₎ = 2.85, corrected p = 0.01; Fig. 4A).

Figure 4.

A, Modularity was lower during the n-back task than during the sequence tapping task and during rest. B, Whole-brain system segregation was significantly higher during rest and during the sequence tapping task than during the n-back task. **p < 0.01; *p < 0.05; ∼ p < 0.10.

We also assessed how the balance of within-network connections, which are likely responsible for local processing, and between-network connections, which are likely responsible for global, integrative processing, differed across tasks. First, we measured the connectivity strength of within-network connections and between-network connections. We used a measure of system segregation that quantifies the relative difference in strength of within- versus between-network connections (larger positive values indicating stronger within-network connectivity compared to between-network connectivity; Chan et al., 2014). We found that system segregation was consistently higher during the sequence tapping task compared to the n-back task (anatomical atlas: t₍₂₈₎ = 3.34, corrected p = 0.004; functional atlas: t₍₂₈₎ = 2.58, corrected p = 0.02). This difference in system segregation across tasks was driven by a large numerical and significant decrease in system segregation between rest and the n-back task (anatomical atlas: t₍₂₉₎ = 4.20, corrected p = 0.0007; functional atlas: t₍₂₉₎ = 3.69, corrected p = 0.003), accompanied by a smaller, numerical but nonsignificant trend toward a decrease in system segregation between rest and the sequence tapping task (anatomical atlas: t₍₂₈₎ = 1.82, corrected p = 0.08; functional atlas: t₍₂₈₎ = 1.74, corrected p = 0.09; Fig. 4B).

Local and global efficiency

In addition to measuring the strength of connections within defined networks, we measured the graph theoretical properties of local and global efficiency, which are calculated independently from network structure, to determine how these two distinct types of information transfer may contribute differentially to performance of the sequence tapping and n-back tasks.

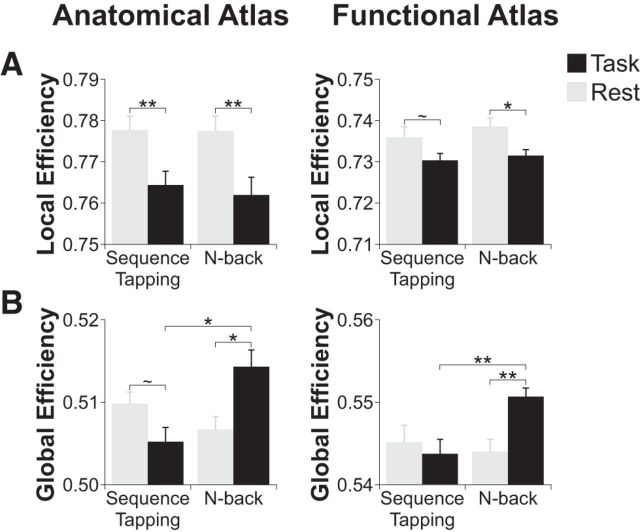
We found that local efficiency, a measure of how interconnected neighboring nodes are to each other, was consistently higher during rest compared to both the sequence tapping and n-back tasks (anatomical atlas: rest vs sequence tapping t₍₂₈₎ = 2.95, corrected p = 0.009, and rest vs n-back t₍₂₉₎ = 3.72, corrected p = 0.003; functional atlas: rest vs sequence tapping t₍₂₈₎ = 2.01, corrected p = 0.08, and rest vs n-back t₍₂₉₎ = 3.09, corrected p = 0.01). Local efficiency was not significantly different across tasks (both atlases corrected p-values > 0.48; Fig. 5A).

Figure 5.

A, Local efficiency decreased during both sequence tapping and n-back tasks compared to rest. B, Global efficiency was significantly lower during the sequence tapping task than during the n-back task. Global efficiency increased compared to rest during the n-back task and numerically but nonsignificantly decreased compared to rest during the sequence tapping task. **p < 0.01; *p < 0.05; ∼ p < 0.10.

Global efficiency, a measure of the interconnectedness of all nodes globally across the entire brain, was significantly higher during the n-back task compared to the sequence tapping task (anatomical atlas: t₍₂₈₎ = 3.10, corrected p = 0.01; functional atlas: t₍₂₈₎ = 3.15, corrected p = 0.006). Similar to the findings when measuring system segregation, this result was driven by an increase in global efficiency between rest and the n-back task (anatomical atlas: t₍₂₉₎ = 2.51, corrected p = 0.03; functional atlas: t₍₂₉₎ = 3.40, corrected p = 0.006), accompanied by a smaller, numerical (but nonsignificant) decrease in global efficiency between rest and the sequence tapping task (anatomical atlas: t₍₂₈₎ = 1.72, corrected p = 0.097; functional atlas: (t₍₂₈₎ = 0.54, corrected p = 0.59; Fig. 5B).

Nodal roles

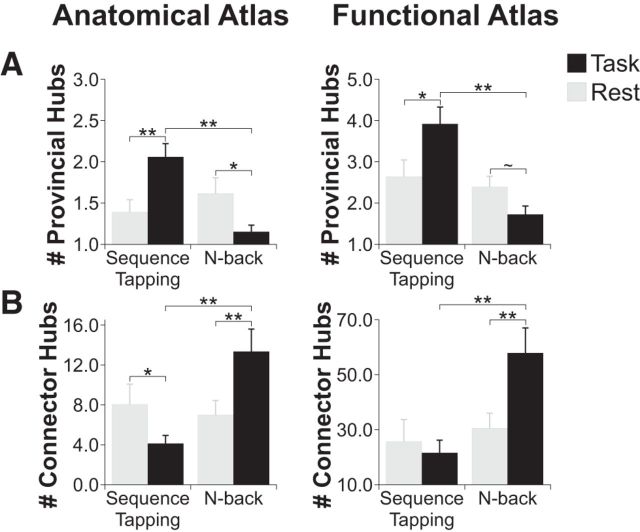
Another important characteristic of large-scale brain organization is how individual brain regions, or nodes, communicate with the rest of the brain. Two types of nodes that can be distinguished using graph theory are provincial hubs, which are important for within-network communication, and connector hubs, which are important for between-network integration (Guimerà and Amaral, 2005a,2005b). We investigated whether the number of provincial and connector hubs changed from rest during each of the tasks, as well as how they compared across the two tasks. We found that the number of provincial hubs was higher during sequence tapping than during the n-back task (anatomical atlas: t₍₂₈₎ = 4.57, corrected p = 0.0003; functional atlas: t₍₂₈₎ = 4.49, corrected p = 0.0003), indicating that there were more highly connected nodes within networks during the sequence tapping task. This finding was driven by both an increase in number of provincial hubs during sequence tapping compared to rest (anatomical atlas: t₍₂₈₎ = 3.88, corrected p = 0.0009; functional atlas: t₍₂₈₎ = 2.47, corrected p = 0.03) and a decrease in number of provincial hubs during the n-back task compared to rest (anatomical atlas: t₍₂₉₎ = 2.22, corrected p = 0.03; functional atlas strong but nonsignificant trend: t₍₂₉₎ = 1.96, corrected p = 0.06; Fig. 6A).

Figure 6.

A, The number of provincial hubs was significantly higher during the sequence tapping task compared to the n-back task and rest, and decreased between rest and the n-back task. B, The number of connector hubs was significantly lower during the sequence tapping task compared to the n-back task. The number of connector hubs increased significantly during the n-back task compared to rest, and decreased during the sequence tapping task compared to rest for the anatomical atlas only. **p < 0.01; *p < 0.05; ∼p < 0.10.

In contrast, we found that the number of connector hubs was significantly higher during the n-back task than during the sequence tapping task (anatomical atlas: t₍₂₈₎ = 3.98, corrected p = 0.001; functional atlas: t₍₂₈₎ = 3.97, corrected p = 0.001). This result was driven by a significant increase in number of connector hubs during the n-back task compared to rest (anatomical atlas: t₍₂₉₎ = 3.60, corrected p = 0.002; functional atlas: t₍₂₉₎ = 3.17, corrected p = 0.005). The number of connector hubs additionally decreased between rest and sequence tapping, although not consistently across the anatomical and functional atlases (anatomical atlas: t₍₂₈₎ = 2.33, corrected p = 0.03; functional atlas: t₍₂₈₎ = 0.72, corrected p = 0.48; Fig. 6B).

Relationships between network organization and behavioral performance

If one's underlying network organization is critical to successful cognition, then behavioral performance should be related to brain organization. Therefore, we conducted exploratory analyses relating each of the above graph metrics to behavioral performance on each of the tasks. We focused on performance and brain organization during the most difficult condition of each task (interleaved sequence tapping trials and 3-back lure trials), when cognitive effort was presumably maximized. All participants were highly trained on the sequence tapping task, so their accuracy was quite high compared to n-back task accuracy (mean interleaved condition accuracy = 88.8%; mean 3-back lure accuracy = 69.4%). Therefore, we correlated brain organization with the SD of response times during the interleaved sequence tapping trials, with lower response time variability indicating a better command of the test sequences. For the n-back task, we correlated accuracy on lure trials during the 3-back condition. We focused specifically on lure trial accuracy during the n-back task because these trials presumably required the most cognitive control. These are trials during which the current stimulus matched the stimulus seen n ± 1 previously. Therefore, they were nonmatches, but the letter was familiar in approximately the location of a match (which would have been n previous), so the prepotent inclination to respond “match” had to be suppressed on these trials.

We report correlations between functional brain network organization and behavioral performance that were statistically significant when using either one or both brain atlases. In all instances in which a significant effect was found in only one atlas, the effect was in the same direction when using the other atlas and the statistical effect did not differ between the atlases (all p-values relating brain–behavior correlation strength across atlases > 0.05).

Sequence tapping task (interleaved condition)

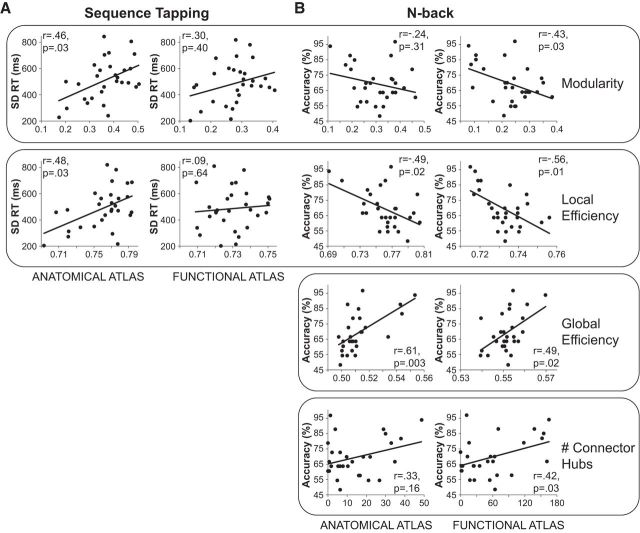
Modularity, which did not change between rest and sequence tapping, was positively correlated with response time variability (anatomical atlas: r = 0.46, corrected p = 0.03; functional atlas: r = 0.30, corrected p = 0.40), indicating that higher modularity was related to poorer—more variable—performance. Local efficiency, which was the only measure of network segregation that decreased between rest and sequence tapping, was also positively correlated with response time variability (anatomical atlas: r = 0.48, corrected p = 0.03; functional atlas: r = 0.09, corrected p = 0.64), indicating that lower local efficiency was related to improved—more stable—performance (Fig. 7A).

Figure 7.

Relationships between behavioral performance and network organization. A, For interleaved trials on the sequence tapping task, higher modularity (top row) and higher local efficiency (second row) were both related to poorer performance, as indexed by increased variability of responding. B, For 3-back blocks on the n-back task, higher modularity (top row) and higher local efficiency (second row), two measures of network segregation, were both related to poorer performance (lower accuracy on 3-back lure trials). Conversely, higher global efficiency (third row) and a greater number of connector hubs (bottom row), two measures of network integration, were both related to higher accuracy on 3-back lure trials. All reported p-values are FDR corrected for multiple comparisons.

N-back task (3-back lure condition)

Modularity, which decreased between rest and the n-back task, was negatively correlated with accuracy (anatomical atlas: r = −0.24, corrected p = 0.31; functional atlas: r = −0.43, corrected p = 0.03). Local efficiency, which decreased between rest and the n-back task, was also negatively correlated with accuracy (anatomical atlas: r = −0.49, corrected p = 0.02; functional atlas: r = −0.56, corrected p = 0.01). Conversely, global efficiency, which increased between rest and the n-back task, was positively correlated with accuracy (anatomical atlas: r = 0.61, corrected p = 0.003; functional atlas: r = 0.49, corrected p = 0.02). Finally, the number of connector hubs, which increased between rest and the n-back task, was positively correlated with accuracy (anatomical atlas: r = 0.33, corrected p = 0.16; functional atlas: r = 0.42, corrected p = 0.03; Fig. 7B).

Discussion

This study related large-scale network organization during an intrinsic, resting state to organization during a sequence tapping task, which is thought to engage a single brain network subserving motor execution, and an n-back task, which is thought to require the coordination of multiple brain networks subserving cognitive processes required by working memory. Consistent across multiple whole-brain atlases, several measures of network segregation and integration, and several data analytic methods, we found that local, within-network communication is critical for motor execution, whereas integrative, between-network communication is critical for working memory.

Extant literature emphasizes strong similarity in network organization across rest and multiple cognitive tasks: ∼60% of connections do not change between rest and multiple cognitive tasks (Cole et al., 2014; Krienen et al., 2014), whole-brain network correspondence between rest and different tasks is quite high (r > 0.69 between each task pair; Krienen et al., 2014), and connections that change do so minimally (average absolute change in r = 0.04; Cole et al., 2014). Although there is general agreement that observed network variations are related to differences in task-specific brain network engagement (or differences between rest and tasks), there is no unifying hypothesis regarding why certain connections change during the performance of certain tasks. In some studies, connections stemming from nodes within a frontoparietal network purported to underlie cognitive control are most variable (Cole et al., 2013; Krienen et al., 2014); in others, connections involving those same nodes are highly consistent (Mennes et al., 2013; Davison et al., 2015). These seemingly contradictory findings highlight the importance of developing a cohesive framework within which to interpret results of network studies. We demonstrate that a task engaging a single discrete brain network (sequence tapping) results in increased segregation of brain networks, whereas a task requiring the engagement of multiple brain networks (n-back) results in increased global integration. This emphasizes the utility of interpreting task-related differences in brain organization in terms of segregation and integration.

Despite recognition that both segregation and integration of brain networks are critical for cognitive function (Friston, 2009; Sporns, 2013; Deco et al., 2015), existing literature relating network reconfiguration across tasks rarely interprets findings within this dual segregation-integration framework (but see Bertolero et al., 2015; Crossley et al., 2013; Yeo et al., 2015). For example, complex tasks result in increased long-range connections compared to rest (Davison et al., 2015), which is consistent with our finding that n-back performance results in increased long-range connections integrating across distinct networks compared to performing sequence tapping or to rest. However, that study did not assess segregation and integration across distinct functional networks, nor were the complex tasks related to a simpler task thought to engage a single network. As another example, whole-brain connectivity patterns during a semantic n-back task are more different from connectivity patterns during rest than are connectivity patterns of simpler tasks such as passive observation or stimulus detection, which likely require fewer discrete brain networks (or a single network; Krienen et al., 2014). Although this finding is similar to ours in that n-back performance resulted in greater changes to intrinsic network structure than sequence tapping, differences across tasks were not classified in terms of within-network connections (segregation) and between-network connections (integration).

Few studies have examined whole-brain organization during motor tasks such as sequence tapping. Two recent motor learning studies focused on the contrast between stable, task-relevant core networks and flexible, peripheral networks (Bassett et al., 2013, 2015). The segregation of two task-relevant networks, a sensorimotor and a visual network, increased with training. Further, a greater reduction in the involvement of other networks, a frontocingulate network in particular, led to increased learning (Bassett et al., 2015). These results are consistent with our finding that increased network segregation occurs during sequence tapping. Increased network segregation during a well-learned (i.e., automatic) task could reflect greater autonomy of the task-related network and a less resource-intensive process, preserving resources for cognitively demanding events that may arise (Bassett et al., 2015). Importantly, a study probing a similar question during visuospatial attention found increased integration across networks during the task and that increased integration was related to higher behavioral accuracy (Spadone et al., 2015). Together, these results emphasize that the segregation/integration tradeoff is not general to all tasks, but rather is dependent upon cognitive demands.

Although most studies examining connectivity during motor-related tasks focus on within-network organization (Biswal et al., 1995; Jiang et al., 2004; Rissman et al., 2004; Sun et al., 2004, 2007; Zhuang et al., 2005; Bardouille and Boe, 2012), many studies probing working memory focus on internetwork integration. Our findings are consistent with previous studies demonstrating increased integration during tasks presumed to tap working memory with increasing load or compared to rest (Kitzbichler et al., 2011; Gordon et al., 2012; Cohen et al., 2014; Liang et al., 2016) and that increased integration is related to increased behavioral performance (Bassett et al., 2009; Cohen et al., 2014; Stanley et al., 2014; Braun et al., 2015). We extend this literature by using several measures of segregation and integration to provide convergent evidence for increased integration during working memory. Critically, we also demonstrate that increased integration is not general to all cognitively demanding tasks because integration decreased during motor execution in the same participants.

A cognitive function such as working memory, in contrast to motor execution, likely requires the engagement of multiple brain networks such as those underlying memory, sustained attention, and inhibition of irrelevant information. For example, during 3-back blocks, one must maintain the previous three stimuli in mind while suppressing the memory of stimuli before those. Network segregation, or autonomy, may be detrimental to working memory, which requires the coordination of multiple components of cognition; instead, integration across distinct networks may be necessary. This is the basis for theories that propose transient, flexible coordination across distinct brain regions and networks as necessary for complex cognition (Dehaene et al., 1998; McIntosh, 1999; Bressler and Kelso, 2001; Fries, 2005). Complex cognitive tasks may temporarily induce long-range, integrative connections that are more costly metabolically than short, local connections—perhaps too costly to remain constantly engaged.

Not every segregation and integration metric that we quantified related differentially to the sequence tapping and n-back tasks. Local efficiency decreased during both tasks compared to rest. Decreased local efficiency, which measures how interconnected a node's neighbors are to each other regardless of network membership, may indicate a pruning of task-irrelevant connections. Such pruning may occur in all cognitively demanding tasks due to limited resources.

Critically, we found significant relationships between network measures and behavior. During the interleaved condition of the sequence tapping task, lower local efficiency, which decreased on average during sequence tapping, was related to better performance (i.e., more stable response times). Modularity did not change on average during sequence tapping, but lower modularity was related to more stable response times. During the 3-back condition of the n-back task, lure trial accuracy was negatively related to measures of segregation (modularity, local efficiency) and positively related to measures of integration (global efficiency, number of connector hubs). These relationships between functional brain network organization and behavior indicate that the whole-brain organizational changes observed during each task were reflective of the ability to adjust dynamically to current task demands. In other words, participants whose brain networks flexibly reconfigured appropriately for each task performed better on that task.

We may have observed fewer and less consistent relationships between network organization and behavior during sequence tapping due to the high levels of performance on this well-trained task. An easy task could allow for successful performance despite suboptimal network organization, which could result in consistent neural effects but more variability in terms of relationships with performance. Conversely, the n-back task may have required optimization of network organization to be performed successfully. In future studies, a task with more varied performance would be better able to test whether successful network segregation is necessary for high motor execution performance.

These findings improve our understanding of brain network dynamics during cognition and how the balance between network segregation and network integration contributes to successful performance in a manner that is specific to particular cognitive demands. It has been theorized that neuronal axons (structural connectivity) provide the necessary, relatively stable infrastructure for flexible communication across brain regions and networks (Ghosh et al., 2008; Honey et al., 2009). Functional connectivity may measure a combination of direct and indirect neuronal connections that arise through neural synchronization caused by either external (i.e., task stimuli) or internal (i.e., attention) inputs (Bressler and Kelso, 2001; Fries, 2005); therefore, functional connectivity on its own does not indicate the existence of direct connections (nor can it speak to directionality of connections). Computational modeling of large-scale network dynamics has recently provided insight into the impact of external (stimuli) and internal (state of alertness) perturbations on global connectivity and the dynamics of neural segregation and integration (Deco et al., 2015). fMRI, although an invaluable tool for measuring dynamic functional connectivity, must be combined with structural imaging, functional imaging with higher temporal resolution (EEG/MEG), and computational modeling to assess such hypotheses. Further, methods such as dynamic causal modeling with fMRI or EEG/MEG data, or electrophysiological recordings in humans with epilepsy using electrocorticography or in animals, can address hypotheses about specific nodes that cause dynamic changes in the balance of segregation and integration across brain networks.

In conclusion, this study used several metrics derived from graph theory to provide convergent evidence that the brain has the ability to reconfigure flexibly into different patterns of functional network organization based on the specific brain networks engaged by individual tasks. We propose that interpreting reconfiguration in the context of balancing network segregation and integration will elucidate the optimal network structures underlying various aspects of successful cognition. Future research investigating the mechanisms underlying flexible network dynamics during cognitive tasks and how such dynamics relate to successful performance and errors will increase knowledge of how brain network organization and dynamics underlie cognition.