Bottom-up and Top-down Input Augment the Variability of Cortical Neurons

SUMMARY

Neurons in the cerebral cortex respond inconsistently to a repeated sensory stimulus, yet they underlie our stable sensory experiences. Although the nature of this variability is unknown, its ubiquity has encouraged the general view that each cell produces random spike patterns that noisily represent its response rate. In contrast, here we show that reversibly inactivating distant sources of either bottom-up or top-down input to cortical visual areas in the alert primate reduces both the spike train irregularity and the trial-to-trial variability of single neurons. A simple model in which a fraction of the pre-synaptic input is silenced can reproduce this reduction in variability, provided that there exist temporal correlations primarily within, but not between, excitatory and inhibitory input pools. A large component of the variability of cortical neurons may therefore arise from synchronous input produced by signals arriving from multiple sources.

INTRODUCTION

The seemingly erratic activity of cortical neurons is a deep mystery, since it is unclear how spike patterns resembling the random clicks of a Geiger counter can encode sensory experience reliably enough to guide behavior (Adrian, 1928). Determining the origin of this variability is therefore a key part of deciphering the neural code (Schiller et al., 1976; Reich et al., 2001).

Several lines of evidence are consistent with the idea that variability arises mainly from the high degree of cortical connectivity (Markov et al., 2014) rather than from intrinsic properties of neurons. Indeed, peripheral sensory neurons can exhibit as little variability as theoretically possible given the discrete nature of spikes (de Ruyter van Steveninck et al., 1997; Berry and Meister, 1998; Kreiman et al., 2000). Even cortical neurons, when harvested for in vitro recordings, show reduced variability (Holt et al., 1996; Nawrot et al., 2008; Stevens and Zador, 1998) and can produce virtually identical responses to repeated injections of a fluctuating current pattern (Mainen and Sejnowski, 1995). In contrast to the peripheral and in vitro studies, single cell recordings in the alert monkey tend to show high variability (Softky and Koch, 1993); see, however, (Bair and Koch, 1996).

We hypothesized that the heterogeneous and variable sources of input to a cortical neuron play a significant role in driving spike train changes across trials. To directly test this hypothesis, we analyzed the activity of single neurons in visual area MT of alert monkeys when a source of bottom-up input was temporarily inactivated (Smolyanskaya et al., 2015). Cryoloops were chronically implanted to reversibly inactivate portions of visual areas V2 and V3 (Lomber et al., 1999), which project to the middle temporal visual area (MT) in parallel with direct input from primary visual cortex (V1) (Maunsell and van Essen, 1983). The stability and reproducibility of this intervention allowed us to record from well-isolated, single MT neurons before, during and after inactivation (Figure 1A; Experimental Procedures). We demonstrate that the variability of cortical neurons is significantly reduced when a portion of the input is eliminated, and we provide a simple computational model to account for the findings.

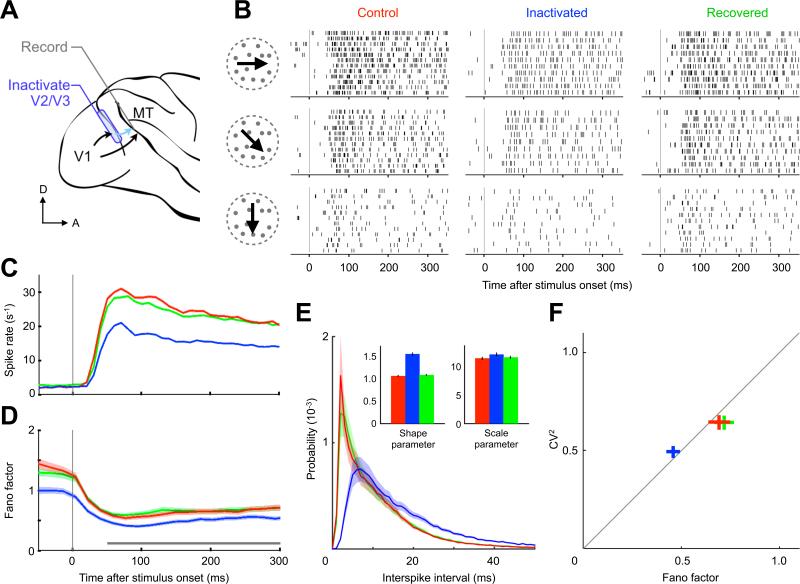
Figure 1. Bottom-up Input Inactivation Reduces Neuronal Variability.

(A) Single MT neurons in the alert macaque were recorded with bottom-up sources V2 and V3 intact (control, red), inactivated (blue) and later recovered (green). Data are presented according to this color scheme hereafter. (B) Spike raster from one neuron during a 350 ms random dot stimulus for three directions of motion. During inactivation, trial-to-trial variability and spike train irregularity decrease. (C) Spike rate and (D) Fano factor averaged over 39 neurons (shading represents SEM; gray bar indicates estimation window for next panels). The spike rate and the trial-to-trial variability decrease upon input inactivation. (E) Interspike interval histogram averaged over the population. Inset shows mean and 95% confidence interval of fitted gamma distribution parameters (excluding 2 ms refractory period). The increase in the shape parameter indicates that the intervals become more regular during inactivation due to a disproportionate reduction of short intervals. (F) Population mean ± SEM of interval CV² versus spike count Fano factor.

RESULTS

Random dot fields with varying directions of motion and different binocular disparities were used to stimulate the recorded MT cells while monkeys foveated a fixation spot. We found that V2/V3 inactivation moderately reduced visually evoked responses in MT (Figures 1B and 1C), consistent with previous findings (Ponce et al., 2008). Intriguingly, inactivation also led to a robust decrease in the variability of these responses—an effect that was also observed while monkeys performed signal detection tasks (Smolyanskaya et al., 2015, see their Figure 5). We quantified the trial-to-trial variability by computing the Fano factor, defined as the variance-to-mean ratio of the spike counts across repeated stimulus presentations (Supplemental Experimental Procedures). Inactivation led to a 34% reduction of the Fano factor from 0.70 ± 0.05 to 0.46 ± 0.03 (mean ± SEM, n = 432 neuron-conditions; t test, p < 0.001). That is, after a fraction of their bottom-up input was silenced, MT neurons became more consistent in their responses across trials. This reduction persisted throughout the entire trial and was present even before stimulus onset (Figure 1D). Concomitant with the reduction in trial-to-trial variability, we also observed an enhanced degree of regularity in the spike trains within a trial (e.g., Figure 1B and Figure S1). We found that changes in Fano factor were accompanied by concomitant changes in the squared interspike interval coefficient of variation, CV² (Figures 1E and 1F), reflecting a remarkable increase in spike pattern regularity. Finally, all changes in spike rate and variability at both short and long timescales were fully reversed upon recovery of the inactivated areas (Figure 1, green traces).

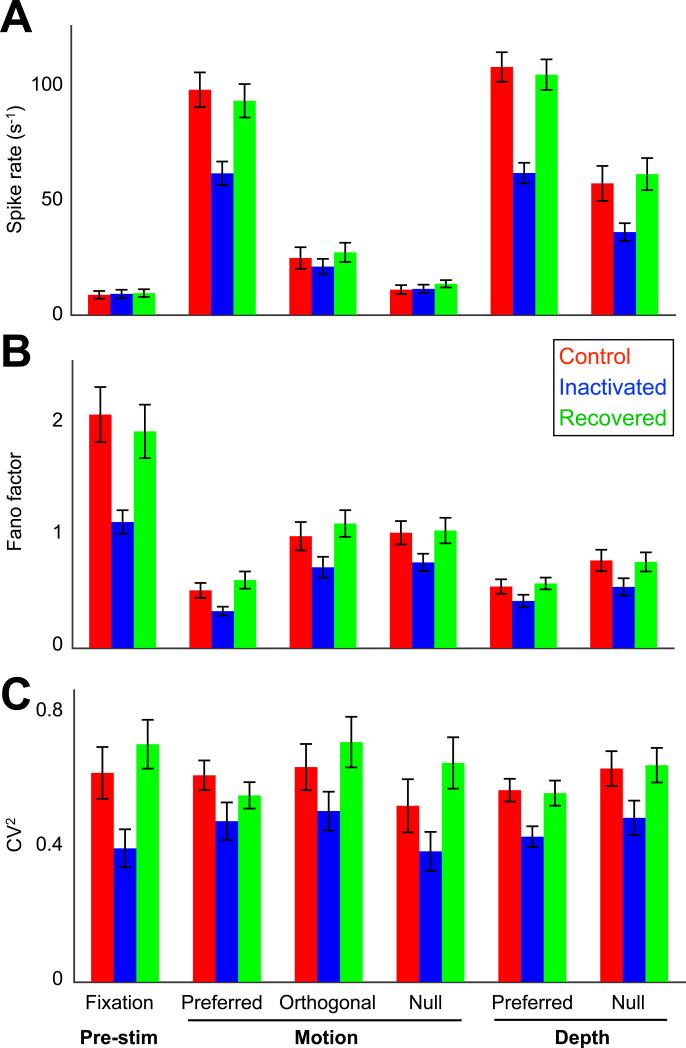
The inactivation-induced changes in neuronal variability could in principle be driven by changes in firing rate, such that a reduced rate could lead to lower variability. Several lines of evidence rule out this possibility. First, unlike the stimulation epoch, we did not observe a significant spike rate change in the pre-stimulus fixation period during inactivation (Figure 2A; control rate 8.7 ± 1.6 s⁻¹, V2/V3 inactive rate 9.0 ± 1.6 s⁻¹; mean ± SEM, n = 432 neuron-conditions, t test, p = 0.71). Nevertheless, the Fano factor as well as the CV² decreased significantly without V2/V3 input (Figure 1D; Figures 2B and 2C, left-most columns). Second, we compared inactivation effects across conditions grouped by stimulus preferences; i.e., where spike rates are systematically higher for more ‘preferred’ stimuli (Figure 2A). Again, no relationship was found between stimulus preference and the inactivation-induced changes of either Fano factor (Figure 2B; ANOVA, F_4,172 = 0.39, p = 0.82) or CV² (Figure 2C; ANOVA, F_4,163 = 0.01, p > 0.99). Furthermore, inactivation did not lead to detectable rate changes during ‘null’ motion stimulation (Figure 2A), but the corresponding variability statistics decreased nonetheless (Figures 2B and 2C). It is notable that the reduction in Fano factor was significantly larger during spontaneous activity (ΔFano factor = 0.95 ± 0.2) than during visual stimulation (all stimulus conditions, ΔFano factor = 0.25 ± 0.06; t test, p = 0.003; Figure 2B). Third, we examined how changes in variability relate to changes in rate across individual neurons. We reasoned that if the variability changes are governed by the reduction in firing rate, we would observe larger reductions in variability for those neurons that experienced larger drops in firing rate. Instead, neurons with larger changes in firing rate tended to show smaller changes in Fano factor (Figure S2A) or no change in CV (Figure S2B). Finally, we matched firing rates across inactivation conditions by randomly deleting spikes in the control condition. We found that the reduction in Fano Factor (Figure S2C) and the changes in CV (Figure S2D) were not affected by rate matching. Taken together, these analyses demonstrate that both trial-by-trial variability and spike train irregularity are largely independent of spike rate and are both significantly reduced when sources of long-range input are inactivated.

Figure 2. Inactivation-induced Variability Reduction is Ubiquitous.

(A) Spike rate of MT neurons for separate stimulus conditions with V2/V3 input intact (control; red), inactivated (blue), and recovered (green; n = 39 cells; 250 ms estimation window shown in Figure 1D). (B) Trial-to-trial variability, quantified by the Fano factor, reduced consistently for each stimulus condition during inactivation. The effect size was comparable across the five stimulus conditions (ANOVA, p = 0.82) but was significantly larger during spontaneous activity (t test, p = 0.003). (C) Same as (B) except for CV². Spike pattern irregularity appeared to decline uniformly across all stimulus conditions during inactivation, including pre-stimulus fixation (ANOVA, p > 0.99). Data represented as mean ± SEM.

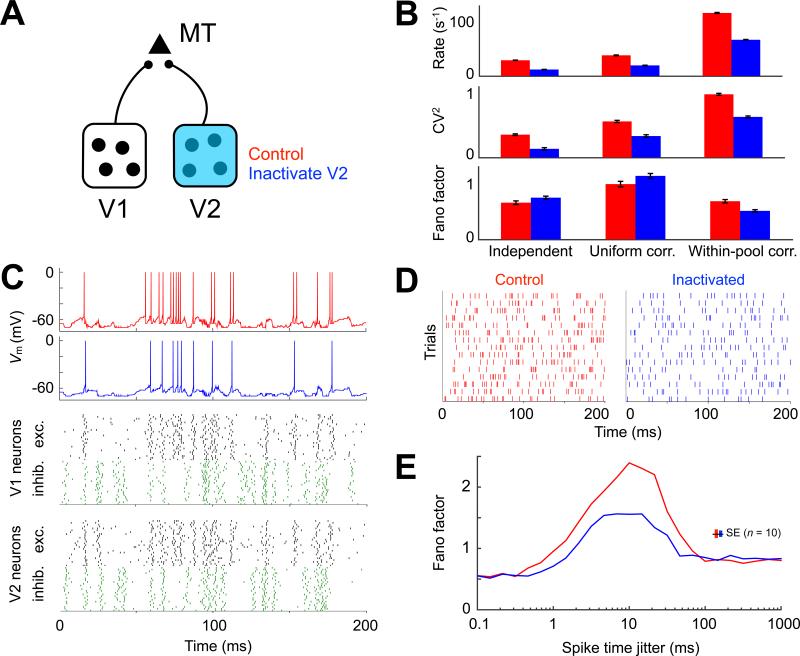
How might silencing a fraction of the bottom-up input reduce the variability of cortical neurons? We investigated this phenomenon with a standard model in which one neuron receives input from a group of other neurons and integrates balanced excitatory (E) and inhibitory (I) post-synaptic potentials towards a threshold for spiking (Shadlen et al., 1996). We simulated a “probe” MT neuron responding to a barrage of balanced input from two hypothetical sources (“V1” and “V2”) and observed how the inactivation of V2 affected its behavior (Figure 3A; Experimental Procedures). We found that the simplest case, where all input units fired independently, failed to reproduce our experimental results (Figure 3B, left): input inactivation in this model did not reproduce a decrease in Fano factor. Given the prominent role that correlated input have in regulating trial-to-trial variability (Softky and Koch, 1993; Stevens and Zador, 1998), we next considered an extension to this model that included varying degrees of synchronous firing between the input neurons. We considered two additional models: a “uniform correlation” model, where correlations existed uniformly within and between E and I pools; and a “within-pool correlation” model, possessing correlated activity within E and I pools but not between them. In both models, we also allowed correlations to exist between V1 and V2 input (see Supplemental Experimental Procedures and the next paragraph for details). We found that inactivating half of the input neurons (i.e., those from V2) reproduced the experimentally observed reduction in spike rate, CV² and Fano factor, provided that there were temporal correlations primarily within, but not between, excitatory and inhibitory pools (Figure 3B, right). The within-pool correlation structure produced a relatively quiescent membrane potential, which was rapidly depolarized toward threshold during bouts of correlated excitatory input that were unchecked by inhibition. The transition to this depolarized state enabled the rapid succession of action potentials until the barrage of correlated excitation ended or was interrupted by inhibition (Figure 3C, red trace). Inactivation of the V2 group of neurons, which was parametrically identical to the V1 group, weakened the impact of this phenomenon by reducing the number of correlated excitatory synapses that were available to sustain depolarization. During an excitatory bout under simulated inactivation, the probe neuron was therefore more likely to either fail or emit a single spike rather than reach a sustained state of rapid spiking (Figure 3C, blue trace). This phenomenon primarily reduced the occurrence of the shortest interspike intervals, thus regularizing the spike patterns (Figure 3D) as observed in our experiments (Figures 1B and 1E; Figure S1). We tested the robustness of this inactivation-induced phenomenon by systematically varying the extent of synchrony within the input ensembles. Either very high or low synchrony settings led to relatively low variability, and input inactivation of such activity did not lead to detectable changes. Inactivation-induced effects, however, were clear for spike-time synchrony between 1 and 100 ms, with the largest impact occurring around 10 ms (Figure 3E).

Figure 3. Within-pool Correlation Model Reproduces Inactivation Results.

(A) Model schematic showing probe MT neuron that responds to excitatory input counterbalanced by inhibition from sources V1 and V2. (B) Spike rate, CV² and Fano factor for control (red) and V2 inactivated (blue) conditions under three balanced E–I input regimes: independent, uniform correlation, and within-pool correlation. Only within-pool correlation model input inactivation reproduced the experimentally observed reductions in all three quantities. (C) Integrate-and-fire membrane potential (V_m) of the MT neuron during a single trial. The raster represents the within-pool correlation model input ensembles in V1 and V2. One neuron per row: excitatory cells in black; inhibitory cells in green. (D) Trial-by-trial raster of MT neuron activity. Inactivation decreased the interspike interval irregularity and spike count variability across trials. (E) Fano factor as a function of synchrony within E and I ensembles. Synchrony was controlled by jittering spike times within each ensemble using a Laplace distribution of varying width (determined by the shape parameter b ≥ 0 plotted along the abscissa). Simulations shown in previous panels had b = 1, which led to probe output that most closely resembled the experimental data. Simulations represented as mean ± SEM in (B) and (E).

The model predicts that excitatory input does not arrive steadily in time but rather arrives in clusters that are not always tracked by their inhibitory counterparts. A corollary to this is that multiple long-range sources (e.g., V1 and V2) are probably not independently generating clusters of excitation in the MT circuit, as they would effectively smooth out the total input by filling in each other's gaps. Instead, V1 and V2 input are likely to synchronize excitation in the target MT circuit. Indeed, at least some correlation was needed between the V1 and V2 input to reproduce the data. When this correlation was eliminated, V2 inactivation did not lead to a detectable change in Fano factor (Figure S3A). Subsequent simulations ruled out rate-change artefacts (Figure S3B) and demonstrated model robustness to the number of input neurons and their degree of irregularity (Figure S3C). We further considered other simple alternatives that lacked the within-pool correlation structure but displayed E–I imbalance, spike-count correlations between input, or a fluctuating rate during stimulation (Supplemental Experimental Procedures); none of these could reproduce the experimental data (Figure S4). In summary, the model proposes a parsimonious description of the reduction in variability upon input inactivation by coordination of long-range synchronized excitation in the recipient area.

Another prediction of the model is that the augmentation of trial-to-trial variability by multiple sources of long-range input is a general property of the cortex, independent of the stimulus properties and the specifics of the cortical circuitry. The stimulus independence of variability reduction was demonstrated in Figure 2. The prediction that the observations depend not on the specific nature of the cortical circuitry led us to ask whether neuronal variability might also be similarly influenced by other input, such as those projecting from higher to lower cortical visual areas. In the primate brain, such corticocortical feedback has been shown to accompany virtually all forward projections (Markov et al., 2014). Feedback is generally thought to be computationally distinct from bottom-up drive (Angelucci and Bressloff, 2006; Mumford, 1992), for instance, by modulating responses according to stimulus size but not contrast (Nassi et al., 2014). We therefore reasoned that examining V1 responses while inactivating V2/V3 would provide a challenging test for the generality of our conclusions.

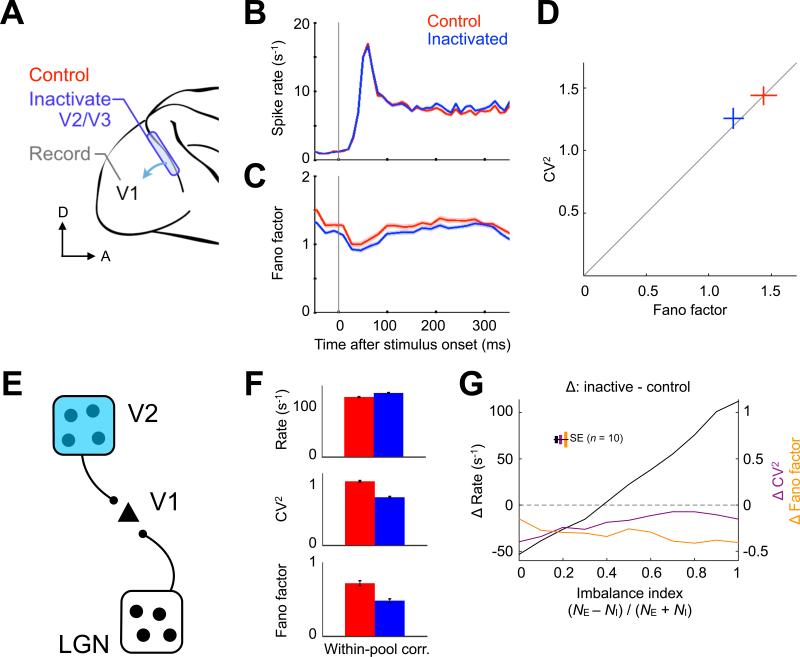
We analyzed single V1 neuron responses to stationary gratings of sinusoidal luminance before and during V2/V3 inactivation in a separate group of alert monkeys from an earlier study (Nassi et al., 2013) (Figure 4A; Experimental Procedures). In contrast to the findings in MT, most V1 neurons showed modest increases in their spike rates during V2/V3 inactivation that were most pronounced for large stimuli activating the suppressive surrounds of V1 receptive fields (Nassi et al., 2013), though this was less apparent when spike rates were averaged across the entire response period and all stimuli (Figure 4B; control rate 8.4 ± 0.2 s⁻¹, V2/V3 inactive rate 9.1 ± 0.3 s⁻¹; mean ± SEM, n = 588 neuron-conditions, t test, p = 0.09). Despite this different effect on spike rate, the Fano factor of the V1 responses decreased in the same manner described in MT, albeit to a lesser degree (17%, from 1.44 ± 0.10 to 1.20 ± 0.08; Figures 4C and 4D; mean ± SEM, n = 588 neuron-conditions, t test, p < 0.001). These results suggest that top-down input also contributes to the variability of cortical neurons. The within-pool correlation model used to describe the MT data (Figure 3) was also capable of explaining the effect of top-down input inactivation, when corticocortical feedback was made to promote more inhibition than excitation (Figure 4E). During simulated inactivation, this E–I imbalance led to a spike rate increase, even though CV² and Fano factor both declined (Figure 4F). We found that the degree of imbalance caused by input inactivation influenced spike rate changes linearly but had little impact on inactivation-induced reductions in variability (Figure 4G), demonstrating that rate and variability can, at least in principle, be independently affected by correlated input.

Figure 4. Top-down Input Inactivation Reduces Neuronal Variability.

(A) Single V1 neurons in the alert macaque were recorded with top-down sources V2 and V3 intact (control, red) and inactivated (blue). (B) Spike rate and (C) Fano factor averaged over 36 neurons. Top-down input inactivation decreased the Fano factor throughout the trial, despite an increasing trend in spike rate (shading represents SEM). (D) Population mean ± SEM of interval CV² versus spike count Fano factor. Top-down input inactivation reduces neuronal variability in the same manner as was observed for bottom-up input inactivation. (E) Within-pool correlation model responding to a bottom-up source (LGN) and a top-down source (V2). (F) Changes in spike rate, CV² and Fano factor match the experimental data when V2 inactivation produces an E > I imbalance. (G) Inactivation-induced changes in spike rate, CV² and Fano factor as a function of the imbalance index, quantifying the discrepancy in the remaining excitatory (N_E) and inhibitory (N_I) synaptic input. Imbalance primarily affected rate change and preserved the inactivation-induced variability reduction. Simulations represented as mean ± SEM in (F) and (G).

It is also possible that V2/V3 inactivation could produce indirect effects on visual areas. For instance, because some neurons in V1 project to MT (Maunsell and van Essen, 1983), the effects of eliminating V2/V3 feedback onto these V1 neurons might indirectly affect MT activity. Although the model does not implement indirect input, the simulations suggest that second order effects of inactivation—i.e., rate or variability changes of an otherwise intact input—are playing a much smaller role than the complete inactivation of a direct input source. We found that reducing spike rates without inactivation had a negligible effect on output variability (Figure S3B), and inactivation-induced changes in mean input rate alone also failed to account for the data (Figure 3B, left column). Rather, to reproduce the variability decrease observed, changes in input correlations were required and could be achieved by the inactivation of one of various correlated input sources. Even under these conditions, the precise quantity of input variability used in those simulations was not critical, since doubling input variability only slightly influenced the effect of inactivation (Figure S3C, middle column). Altogether, the neuronal variability within a given area seems to depend mostly on the correlation structure imposed by its direct input.

DISCUSSION

Deciphering the neural code is a central challenge in neuroscience, and, because of its relevance to this issue, the nature of neuronal variability has been intensely studied. We show that reversible inactivation of corticocortical input reduces the variability of neurons in the recipient area, independently of changes in spike rate. To investigate plausible mechanisms, we implemented a simple integrate-and-fire model driven by either correlated or uncorrelated input. We found that a non-trivial arrangement of excitatory and inhibitory pre-synaptic potentials was needed to account for our experimental observations. During inactivation, the model could match the experimentally measured reduction in variability only when its long-range input engendered synchrony primarily within, not between, excitatory and inhibitory ensembles in the recipient area.

The model led to multiple predictions that were evaluated on the experimental data. First, variability in the model depends on the relative degree of heterogeneous synchronous input and does not depend on the tuning properties of each neuron or the stimulus. This is confirmed by the experimental findings (Figure 2). Second, the stimulus-independence in the model suggests that the changes in variability should also be present during fixation, prior to stimulus presentation, as demonstrated in Figures 1 and 2. Third, the model predicts that inactivating any source of correlated corticocortical input should reduce variability of the neurons in its target area. This prediction led us to evaluate the effects on variability in V1 after inactivating V2/V3 (Figure 4).

The model posits that correlated input within a relatively narrow temporal interval (~10 ms) plays an important role in driving variability and that there is stronger correlation within excitatory or inhibitory pools rather than between these pools. To our knowledge, this assumption has not been tested directly; however, some experimental evidence supports it. Extracellular spike trains from nearby visual cortical neurons have revealed cross-correlogram widths between 10–100 ms (Bair et al., 2001; Reich et al., 2001), which are in the upper range of our predictions. Also consistent with our interpretation, intracellular recordings have revealed a substantial lag between excitatory and inhibitory fluctuations (Haider et al., 2010; Ozeki et al., 2009). Indeed, to reproduce the high irregularity observed in vivo, this within more than between correlation structure was crucial for our model and for an earlier study using direct current injection in cortical slices (Stevens and Zador, 1998). Moreover, the predicted membrane potential dynamics arising from input of this nature—quiescent resting periods interrupted by bouts of depolarization—have been confirmed by intracellular recordings of cortical neurons in the alert rodent (Poulet and Petersen, 2008) and the alert nonhuman primate (Tan et al., 2014).

The model also leads to several new predictions. First, the reduction in variability in MT was larger than the corresponding variability change in V1, and, therefore, the magnitude of the variability changes seems to be proportional to the strength of the inactivated input (V2/V3 provides strong input to MT and weaker modulatory input to V1). We therefore expect that the contribution of each cortical area to variability in the target area will be proportional to the strength of its correlated input, other things being equal. Second, stimulation of a cortical area would also decrease target variability, assuming that input homogeneity effectively increases when any one of multiple input sources is driven synchronously. This is consistent with earlier work examining response variability after chemical stimulation (Noudoost and Moore, 2011). Third, sensory stimulation or behavioral conditions that increase the input homogeneity to a given area should also reduce neuronal variability. This is consistent with reports demonstrating trial-to-trial variability reductions by stimulus onset (Churchland et al., 2010), spatial cueing (Cohen and Maunsell, 2009) and saccade planning (Zénon and Krauzlis, 2012). Finally, situations that, on the contrary, increase input heterogeneity should increase the variability of the target cells. One example of this has been shown in the MT neurons of amblyopic monkeys (El-Shamayleh et al., 2010). Taken together, these results impose strong constraints on theories of neuronal variability by causally linking the presence of corticocortical input to the spiking statistics of neuronal activity.

In summary, the observations reported here, combined with an integrative model that can account for observations across multiple studies, argue that a large fraction of the spiking irregularity of cortical neurons can be accounted for by the convergence of input from different sources. While a significant degree of variability still remains under the conditions examined here, it is not yet clear to what extent it reflects the numerous other sources of input that remained intact versus intrinsic neuronal noise. As newer methods allow us to manipulate the input to cortical neurons both more selectively and comprehensively, it just might turn out that neurons do not play dice after all.

EXPERIMENTAL PROCEDURES

Neuronal recordings and cortical inactivation

We report data from 75 well-isolated visual cortical neurons from 4 adult male rhesus monkeys (Macaca mulatta, 7–12 kg) while they fixated a marker centered on a computer monitor. These subjects were used in earlier studies of area MT (Smolyanskaya et al., 2015) and area V1 (Nassi et al., 2013); however, the analyses presented here are new. Using extracellular tungsten micro-electrodes, each cell was held for approximately three hours, while long range input from other visual cortical areas was acutely inactivated and subsequently recovered. Reversible inactivation of the cortex was accomplished by using three cryoloops (Lomber et al., 1998) implanted along the dorsal aspect of the lunate sulcus in the right hemisphere, which corresponds to the left perifoveal representation of areas V2 and V3 (Gattass et al., 1981; Gattass et al., 1988). The territory of cortex inactivated by the cryoloops was directly measured with hybrid electrode/thermal probes (Nassi et al., 2013), and the resulting V2/V3 scotoma was mapped by psychophysical and electrophysiological methods (Ponce et al., 2008; Smolyanskaya et al., 2015). All animal procedures complied with the National Institutes of Health Guide for Care and Use of Laboratory Animals and were approved by the Harvard Medical Area Standing Committee on Animals.

Integrate-and-fire neuron model

All simulations implemented a standard leaky integrate-and-fire membrane (Softky and Koch, 1993), driven by N_E excitatory and N_I inhibitory neurons generating presynaptic currents J^E(t) and J^I(t) for each input neuron k:

$$\tau \frac{\mathrm{dV}}{\mathrm{dt}}=\mathrm{R}\left[\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{E}}}{\mathrm{J}}_{\mathrm{k}}^{\mathrm{E}}\left(\mathrm{t}\right)+\sum _{\mathrm{k}=1}^{{\mathrm{N}}_{\mathrm{I}}}{\mathrm{J}}_{\mathrm{k}}^{\mathrm{I}}\left(\mathrm{t}\right)\right]-(\mathrm{V}\left(\mathrm{t}\right)+{\mathrm{V}}_0),$$ [4]

where J^E(t) takes the value 0 or a constant Δ depending on the spiking status of unit k and similarly J^I(t) takes the value 0 or −Δ. The resting potential V₀, membrane resistance R, time constant τ and current amplitudes were set such that the action potential threshold could be achieved in √N_E steps from rest, thus, V_th = V₀ + Δ√N_E (van Vreeswijk and Sompolinsky, 1996). We limited membrane hyperpolarization to −70 mV, set the voltage decay constant to τ = 20 ms, and imposed a 1 ms absolute refractory period. Such constraints led to reasonable values for a wide range of input ensemble sizes. We used parameters V₀ = −65 mV, V_th = −55 mV and R = 80 MΩ, which led to synaptic currents between 1 ≤ Δ ≤ 20 pA for ensemble sizes spanning two orders of magnitude (10²–10⁴). All simulated trials ran for 200 ms with 0.1 ms steps.

We explored how synchronized input affects the spiking irregularity of an integrate-and-fire neuron driven by a balanced E–I regime. Synchronization among the ensembles was implemented using the following algorithm applied:

1. Generate a template spike train μ from a gamma distribution with parameters k and θ from equation [3]. All ensemble neurons are weakly synchronized to the template μ.

2. For each ensemble neuron, generate a synchronized spike train s with spike times that deviate from each spike time μ[t] by drawing i.i.d. jitter times from a Laplace probability distribution with mean μ[t] and shape parameter b ≥ 0 corresponding to temporal jitter with standard deviation b√2.

3. For each ensemble neuron, generate an independent spike train x from the same gamma distribution as in step 1.

4. If μ has more spikes than x, then randomly delete spikes from s until it has the same number of spikes as x. Otherwise, if μ has fewer spikes than x, then randomly copy spikes from x to s until it has the same number of spikes as x. This step de-correlates trial-to-trial spike counts.

5. Ensure that the refractory period ε is not violated by adequately delaying s[t + 1] when s[t + 1] – s[t] ≤ ε.

The correlation structures for the “uniform correlation” and “within-pool correlation” models in the main text used the synchrony parameter b = 1. Correlation between V1 and V2 was implemented by embedding a fraction (0 ≤ ρ ≤ 1) of common spikes in both input (before jitter). The simulations used ρ = 0.1.