Emergence of an abstract categorical code enabling the discrimination of temporally structured tactile stimuli

Significance

What are the neural codes that allow the discrimination of two vibrotactile stimulus patterns of equal mean frequency? We recorded single-neuron activity in primary somatosensory (S1) and dorsal premotor (DPC) cortex while trained monkeys performed a challenging pattern discrimination task. We found a faithful representation of the stimuli in S1 and a heavily transformed, more abstract, and highly varied set of responses in DPC. Most notably, in addition to memory-related activity and responses encoding the monkeys’ choices, the DPC data included a large set of categorical neurons that code specific combinations of past and present stimuli and, at the same time, are strongly predictive of the monkeys’ behavior.

Abstract

The problem of neural coding in perceptual decision making revolves around two fundamental questions: (i) How are the neural representations of sensory stimuli related to perception, and (ii) what attributes of these neural responses are relevant for downstream networks, and how do they influence decision making? We studied these two questions by recording neurons in primary somatosensory (S1) and dorsal premotor (DPC) cortex while trained monkeys reported whether the temporal pattern structure of two sequential vibrotactile stimuli (of equal mean frequency) was the same or different. We found that S1 neurons coded the temporal patterns in a literal way and only during the stimulation periods and did not reflect the monkeys’ decisions. In contrast, DPC neurons coded the stimulus patterns as broader categories and signaled them during the working memory, comparison, and decision periods. These results show that the initial sensory representation is transformed into an intermediate, more abstract categorical code that combines past and present information to ultimately generate a perceptually informed choice.

From the most stereotyped behavior of invertebrates to the most elaborate behavior of primates, a central issue in neurobiology is elucidating how sensory information is represented in neural circuits and how it is used to generate actions. In principle, this process can be understood as a chain of three basic neuronal operations. The representation of the physical/chemical attributes of the environment and the execution of motor commands can be regarded as the end points of this chain of neuronal operations. In the middle of this chain is a crucial processing step in which the sensory representations are analyzed and transformed in such a manner that the nervous system is able to choose the adequate motor action.

We have investigated this chain of processes by analyzing the neuronal activity of parietal and frontal cortices in trained monkeys performing a vibrotactile frequency discrimination task (VFDT; reviewed in refs. 1–3). In this task, monkeys compared the frequencies of two vibratory stimuli applied sequentially to the skin of one fingertip and then used their free hand to push one of two response buttons to indicate whether the second stimulus frequency (f2) was lower or higher than the first stimulus frequency (f1). The VFDT, although apparently simple, is designed so that it can only be executed when a minimum number of neuronal operations or cognitive steps are performed: coding f1, holding f1 in working memory, comparing f2 with the memory trace of f1, and, finally, executing a motor response to indicate whether f2 > f1 or f2 < f1. Thus, the VFDT allowed us to investigate a wide range of essential neural processes during perceptual decision making (1–3). However, the VFDT poses a fundamental problem: What is the neural code(s) that an observer might use to decide whether f2 > f1 or f2 < f1?

The initial hypothesis was that an observer discriminated between the two stimulus frequencies by comparing the differences in the time intervals of the corresponding evoked neuronal responses (4, 5). Indeed, neurons from the primary somatosensory cortex (S1) respond to a wide range (5–40 Hz) of stimulus frequencies by phase-locking their spikes to the mechanical sinusoids (5–8). Thus, an observer could discriminate between two frequencies by directly computing the difference in the time intervals of the spikes produced in S1 (temporal code). However, the mean firing rate also varies as a function of stimulus frequency (intensive code). This happens not only for many of the S1 neurons that show phase-locked responses but also for a subset of S1 neurons (approximately a third) that lack the prominent phase-locked responses (6, 8). The simple firing rate code (intensive code) suffices for discriminating the two stimulus frequencies to the level of accuracy demonstrated behaviorally (6–8). Moreover, in areas downstream from S1 the phase-locked responses are virtually nonexistent; instead, a simple firing rate code is used to represent stimulus frequency during the stimulation, working memory, and comparison periods of the task (1–3). In addition, animals are able to discriminate the mean frequencies of aperiodic stimuli with discrimination thresholds almost identical to those obtained with periodic stimuli (6–10). Neurometric thresholds calculated from the mean firing rates evoked by periodic and aperiodic stimuli are essentially identical and are tightly correlated with psychophysical performance (6–8). The conclusion is that a simple firing rate code is sufficient for frequency discrimination across task variants and cortical areas. Thus, stimulus frequency is initially represented via a temporal code by the S1 population, but this signal is thereafter transformed into an intensive code (1–3).

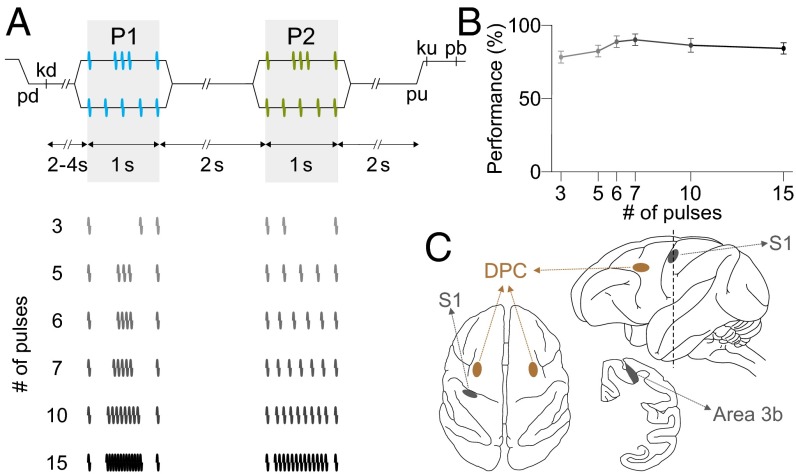
However, there are behavioral conditions in which knowledge of the temporal structure of the stimulus pattern is essential. Here, we focused on this problem. For this, we modified the VFDT (11, 12). In the new task, we sequentially delivered two vibrotactile stimuli of equal average frequency, so the discrimination could not be based on an intensive code for mean frequency. Another key modification, relative to the VFDT, is that the monkeys were asked to indicate whether the two vibrotactile patterns were the same or different. In each trial (Fig. 1), monkeys pay attention to the first stimulus pattern (P1) and hold it in working memory, then compare the second stimulus pattern (P2) against P1, and after another delay between P2 and probe up indicate whether P2 was the same (match, P2 = P1) or different (nonmatch, P2 ≠ P1) than P1 by pressing one of two push buttons. Thus, in this task, the animals discriminate the two stimulus patterns based on their temporal configurations (temporal code).

Fig. 1.

TPDT and recording sites. (A) Sequence of events in each trial. The mechanical probe is lowered (pd), indenting (500 μm) the glabrous skin of one fingertip of the right, restrained hand; the monkey places its free hand on an immovable key (kd). After a variable delay (2–4 s), the probe oscillates vertically, generating one of two possible stimulus patterns [P1, either grouped pulses (G) or extended pulses (E); individual mechanical pulses lasted 20 ms; 1 s of stimulus duration]. After a fixed delay (memory delay, 2 s), a second stimulus is delivered, again at two possible pattern configurations (P2, either G or E; 1 s of stimulus duration); after a second fixed delay (decision delay, 2 s) between the end of P2 and the probe up (pu), the monkey releases the key (ku) and presses with its free hand either the lateral or medial push button (pb) to indicate whether the P1 and P2 were the same or different. P1 and P2 always had equal mean frequency. (B) Discrimination performance for each block of trials of equal mean frequency. Each block consisted of four possible combinations of patterns, as illustrated in A. (C) Top (Left), lateral (Top Right), and coronal (Bottom Right) views of the brain locations where single neurons were recorded. Recordings were made in area 3b of S1 (contralateral to stimulated finger, gray spots) and in dorsal premotor cortex (DPC, both hemispheres, contralateral and ipsilateral to the stimulated finger, orange spots).

We hypothesized that S1 (area 3b) neurons faithfully represent the temporal pattern configurations and that their mean firing rates are similar across stimuli, so that an intensive code is out of the picture. We also hypothesized that S1 neurons code the temporal patterns during stimulation only, and not during the working-memory, comparison and delay-decision, and response periods, as in the VFDT (1–3, 13). Here, we confirmed these two hypotheses by analyzing the neuronal responses of S1 while monkeys performed the temporal pattern discrimination task (TPDT). Furthermore, if S1 serves to represent the stimulus features only but does not encode the cognitive components of the task, the question is, Where and how in the cerebral cortex are the stimulus patterns coded during the working memory, comparison, and decision periods? We chose the dorsolateral premotor cortex (DPC) because it has been previously associated with the encoding of sensory features during those periods in the VFDT (13). During the experiment, we recorded single neurons in DPC while the monkey performed the TPDT. We found groups of DPC neurons that reflected the relevant categories in which the temporal patterns fell. Neurons displayed a categorical representation of P1, both during the first stimulation period and during the delay between P1 and P2, as well as a categorical representation of the result of the comparison, which was maintained until the end of the delay between P2 and the decision motor report. Contrary to S1, the activity of DPC neurons was strongly indicative of the animal’s errors and virtually disappeared during a visual control task in which the same stimulus pairs were delivered, but the animal was cued in advance about which push button to press for reward. These results indicate that there is a dramatic transformation of the neural code: from a faithful temporal representation of the stimulus in S1 that is insensitive to task contingencies, to a binary representation of the choice in DPC, via a distinct categorical code, also in DPC, that is highly invariant to irrelevant stimulus features and strongly correlates with the animal’s decisions.

Results

Two monkeys (Macaca mulatta) were trained to report whether two patterns composed of vibrotactile flutter stimuli were the same or different (Fig. 1A and SI Materials and Methods). Over their full duration (1 s), the patterns had equal mean frequency. In each trial, monkeys paid attention to the first pattern, P1, stored a trace of it during the delay between P1 and P2, and compared that stored trace to the second pattern, P2. Then, after another delay period during which the comparison between P2 and P1 had to be remembered, the monkey pressed one of two push buttons to indicate whether P2 = P1 (match) or P2 ≠ P1 (nonmatch). For each fixed number of pulses (or fixed mean frequency) there were two distinct patterns (Fig. 1A), grouped (G) and extended (E), and thus four possible same/different stimulus pairs. Each of the four possible pattern combinations in a block of trials with fixed mean frequency is called a class, and classes were pseudorandomly interleaved with the same probability (P = 0.25). Because we used a fixed delay period between P1 and P2, monkeys could anticipate the time of delivery of P2, but not whether P2 = P1 or P2 ≠ P1, which had equal probabilities. Monkeys performed the TPDT in blocks of trials with fixed numbers of mechanical pulses (3, 5, 6, 7, 10, or 15) delivered in 1 s (Fig. 1A). Thus, for example, the patterns with five pulses had a mean frequency of 5 Hz (Fig. 1A). The success rates of the monkeys, measured as percentages of correct discriminations, were highly consistent across mean frequencies (Fig. 1B) and across stimulus patterns G or E. Given this task design, the neuronal responses (S1 and DPC) across trials can be analyzed as functions of P1, P2, P2 = P1 vs. P2 ≠ P1, or as functions of the monkeys’ two possible motor choices.

S1 Responses During the Pattern Discrimination Task.

We recorded from 169 single neurons in S1 (area 3b, Fig. 1C) while monkeys performed the TPDT. All of those neurons had small cutaneous receptive fields on the distal segment of one fingertip. Each S1 neuron was classified according to its adaptation properties (14). The majority of those neurons had quickly adapting (QA) responses (n = 161, 95.2%) and only a few showed slowly adapting (SA) properties (n = 8, 4.8%). Because they were the overwhelming majority, and their signals were more informative (8, 14), we focused the analysis on the QA population. First, we investigated their stimulus encoding properties during task performance; second, we determined their pattern discrimination capacities; and third, we examined whether they reflected in their activities the animal’s discrimination performance.

Fig. 2A shows the responses of a typical S1 neuron. The neuron was entrained by the vibrotactile stimulus patterns, but beyond that, notice that there was no sign of any firing rate modulation associated with the working memory, comparison, or postponed decision-report periods of the task. For each of the four classes of stimulus pairs (Fig. 2B) the firing patterns of the example neuron were similar to those observed in the normalized population activity [latency for P1 and P2: 23.6 ± 3.8 ms (SD) and 24.8 ± 4.4 ms, respectively]). Strong entrainment was evident for all mean frequencies (3–15 Hz; Fig. S1 A–C). Thus, in general, the S1 spike trains seemed to faithfully track the internal temporal structure of the stimulus patterns throughout the frequency range.

Fig. 2.

S1 responses during the pattern discrimination task. (A) Raster plots of one representative neuron during TPDT consisting of five pulses delivered in 1 s. Each row of ticks is one trial, and each tick is an action potential. Trials were randomly delivered but have been sorted into four pattern combinations of 20 trials each. Stimulus patterns are shown at the top of each row with the following color code: class 1 (red, G-G), class 2 (orange, G-E), class 3 (green, E-G) and class 4 (blue, E-E). Traces below the raster plots are peristimulus time histograms (constructed with time window of 50 ms displaced every 10 ms). (B) Normalized population activity from n = 161 neurons.

Fig. S1.

Related to Fig. 2. S1 responses for different stimulation frequencies. Normalized population activity for three different mean frequencies (3, 7, and 15 Hz). Hit trials (A–C) were analyzed separately from error trials (D–F). For each trial class, the difference between hits vs. errors was measured using the integral square error, which was quite small (from 0.5 to 2.0%).

To test this quantitatively, we first measured the mean firing rates evoked by the stimuli throughout the entire stimulation period (1 s) and for each mean stimulation frequency compared the results across pattern identities (G vs. E, Fig. 3). We found that the firing rates evoked by the two types of pattern were statistically identical (Fig. 3A; note that most points fall near the diagonal line: left panel, 46.4 ± 5.7° for the P1 interval and right panel, 45.1 ± 6.5° for the P2 interval; Kolmogorov–Smirnov, P > 0.05). This means that, for an ideal observer, it would be impossible to discriminate between temporal patterns, G vs. E, based on the S1 mean firing rates calculated over the entire stimulation periods.

Fig. 3.

Comparison of S1 responses across temporal patterns. (A) Firing rate elicited by pattern G (x axis) is compared against firing rate evoked by pattern E (y axis). Each dot corresponds to one neuron tested (n = 161). Diagonal line (45°) indicates equality between x and y axes. Inset histograms show angular distributions for stimulus P1 (Left) and P2 (Right). (B) Mean pattern information carried by S1 neurons, measured in bits (SI Materials and Methods), as a function of window size (50–1,000 ms in steps of 50 ms) during P1 (Left, cyan) and P2 (Right, light green). (C) Mean pattern information as a function of time (window size was 200 ms). Optimal integration time was 340 ms from stimuli onset. (D) Percentage of S1 neurons with significant pattern information during P1 (cyan) and P2 (light green) as a function of window size. Optimal integration window was 200 ms for both stimuli.

Next, we considered whether such an observer would be more successful if she/he considered the finer temporal structure of the neural responses. Thus, we calculated Shannon’s mutual information for each neuron using time windows of different lengths (from 50 ms to 1,000 ms in steps of 50 ms). We then averaged the pattern information across all neurons to obtain the mean population information for each window. This analysis further showed that the mean firing rate computed over the entire stimulation period (1,000 ms) was, in fact, the least informative (Fig. 3B). However, the mean population information reached a maximum value when the window was ∼ 200 ms wide (Fig. 3B). This raises the question of whether the 200-ms window carries the same amount of information independently of its temporal position, or whether there is a particular point at which the information is highest (e.g., beginning, middle, or end of the stimulation period). To address this, we used a deterministic window of 200 ms displaced in consecutive 10-ms steps and computed the average population information about patterns P1 (cyan) and P2 (light green) as a function of time (Fig. 3C). Notably, the variations of this metric over time were virtually identical for the two periods, P1 and P2. Information about pattern identity began to rise 240 ± 55 ms after stimulus onset (coding latency), and thereafter it varied nonmonotonically. The most informative point in time was 340 ± 75 ms after stimulus onset. These results suggest that, if an observer computed the S1 firing rate using an appropriately chosen time window, she/he would be able to determine the identity of the stimulus pattern with relatively high accuracy, albeit only during the stimulation periods.

S1 Stimulus Pattern Discrimination As a Function of Time.

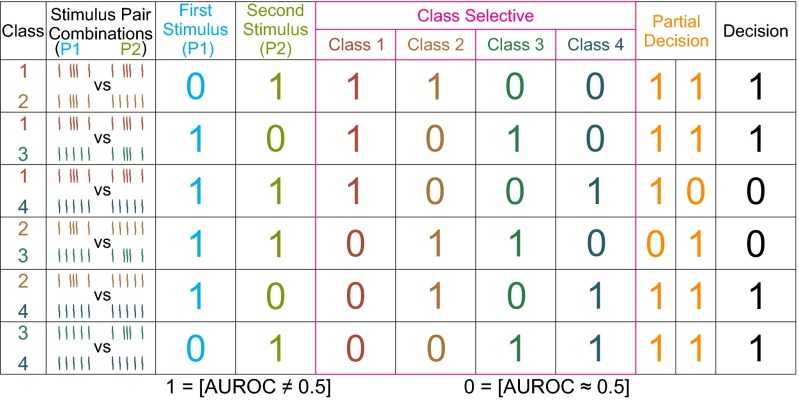
To further test this hypothesis, we measured the discrimination capacities of S1 neurons as functions of time (SI Materials and Methods). We found that firing rates are different for patterns G and E during P1 and P2 but similar for the same stimuli across time periods. The coding capacity of each S1 neuron was assessed by performing a time-dependent firing rate analysis for each trial using different sliding windows (from 50 ms to 1,000 ms stepping every 50 ms), as before (Fig. 3B). At each time bin, and using hit trials only, we constructed firing rate distributions for each stimulus class: c1, G-G; c2, G-E; c3, E-G; and c4, E-E. Then, to identify class-differential responses as functions of time, we computed the area under the receiver operating characteristics curve (AUROC; ref. 15) for the six possible class comparisons: c1-c2, c1-c3, c1-c4, c2-c3, c2-c4, and c3-c4 (Fig. 4). This analysis produced a binary code for each bin composed of six binary digits resulting from the six comparisons (SI Materials and Methods). Each time bin was tested for classification into one of four possible coding profiles during the task (P1, P2, class selective, or decision coding). For example, for P1 coding, the responses must be similar for classes c1 and c2, and for c3 and c4, which have the same P1, but must differentiate between all other class comparisons, which have different P1 patterns (binary code: 0-1-1-1-1-0).

Fig. 4.

Classification of coding responses. Coding responses were defined according to specific profiles of significant differences (1) and statistical equalities (0) between classes (ROC analysis, P < 0.05). Trial classes were labeled from 1 to 4 depending on the pattern combinations: c1 in red, G-G; c2 in orange, G-E; c3 in green, E-G; and c4 in blue, E-E, where G denotes grouped stimulus pulses and E denotes extended stimulus pulses. Each row corresponds to the comparison of two classes, or stimulus pair combinations (first and second columns). Each binary entry indicates the result of the corresponding comparison for that row, and the binary words composed of the six digits of each column represent the possible coding profiles of the cells, based on all six possible class comparisons. The coding profiles refer to coding of the first (P1) and second (P2) stimulus patterns (third and fourth columns, respectively), coding of one specific class (fifth to eighth columns), coding the decision partially (same or different but distinguishing between E-G and G-E combinations, or between E-E and G-G combinations; ninth and 10th columns), and coding the complete decision [same (P1 = P2) or different (P1 ≠ P2); 10th column].

Using this new procedure, we calculated the percentage of S1 neurons with significant P1 (cyan) or P2 (light green) coding (Fig. 3D; see also Fig. 4). Notably, we verified that the 200-ms time window was indeed the optimal one for decoding the stimulus pattern (note same peak locations in Fig. 3 B and D). By using this procedure with the optimal window length for all of the recorded S1 neurons beginning 1 s before P1 up to the end of the trial (1 s after push button press), we constructed a plot tracking how the stimulus encoding varied over time (Fig. 5 A and B). This simple procedure showed that S1 neurons discriminate between stimulus patterns exclusively during the stimulation periods. Moreover, a similar coding response was found during the light control task (Fig. 5C), in which the same stimulus pairs were delivered but the animal knew in advance which push button to press to obtain its reward (SI Materials and Methods). Thus, S1 discriminates between stimulus patterns whether or not the monkey uses that sensory information to guide its choice.

Fig. 5.

S1 population activity in relation to behavior. (A) Times at which individual neurons significantly discriminated G vs. E patterns. Each row corresponds to one cell. Colored lines indicate times with significant level for comparisons based on P1 (cyan) and P2 (light green). Responses were calculated in consecutive bins of 200 ms displaced every 50 ms (n = 161). (B) Percentage of neurons with significant pattern coding as a function of time. Note increase confined to the stimulation periods, and absence of signal during the working memory and decision periods. (C) Percentage of neurons with significant pattern coding as a function of time during a control task in which the correct response was visually cued (n = 92). (D) Mean choice probability for the same population of S1 neurons (n = 161).

S1 Responses Do Not Covary with Perceptual Judgment.

To further document the conclusion reached above, we compared the response patterns evoked during hits (Figs. S1 A–C and S2A) and error trials (Figs. S1 D–F and S2B). We found no statistical differences between the respective responses based on mean squared errors (variations of 0.5–1.5% for each stimulus class). The responses were indistinguishable from those in the light control task as well (Fig. S2C). We also quantified whether the activity of S1 neurons predicted the animal’s choice using choice probability (16) (SI Materials and Methods). The results indicated that there were no significant differences between hits and errors for any stimulus class (Fig. 5D). Thus, we conclude that S1 responses encode the stimulus patterns accurately, but only during the stimulation periods and regardless of the monkey’s performance. Therefore, there must be an area (or multiple areas) downstream from S1 that not only represents the temporal patterns throughout the task duration but also is consistent with the animal’s discrimination performance. Next, we describe neuronal codes that have those properties.

Fig. S2.

Related to Fig. 5. Comparison of S1 responses during hits, errors, and control trials. (A) Normalized population activity for hits, (B) errors, and (C) light control trials. For each trial class, differences between conditions were calculated using the integral square error and were quite small (from 0.5 to 1.5%).

Pattern and Choice Coding in DPC Neurons.

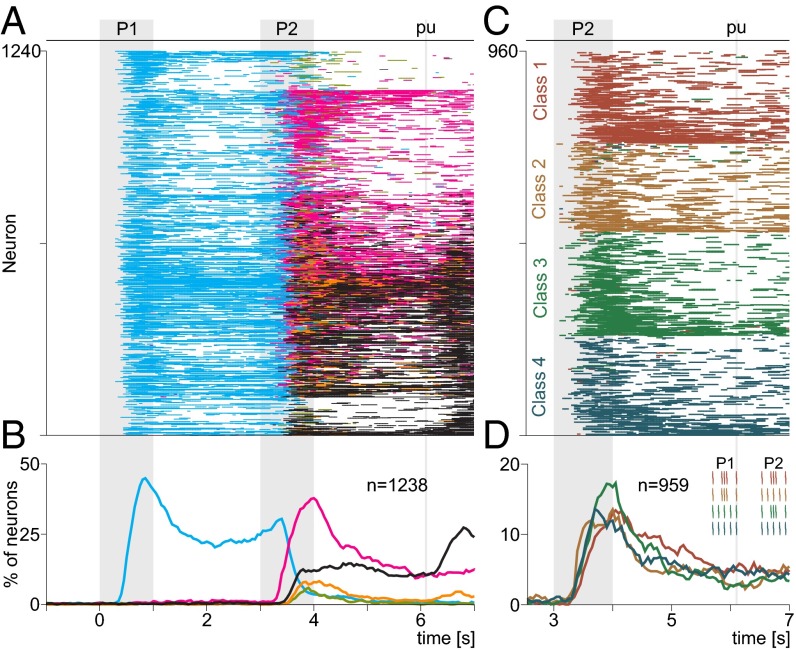
A large number of the recorded DPC neurons (1,473 of 1,574, 93.5%) significantly changed their firing rates during at least one of the relevant periods of the task compared with a control period preceding the beginning of each trial (P < 0.05, Wilcoxon rank-sum test; ref. 17). Out of the 1,473 responsive neurons, 1,238 (84%) were found, based on off-line statistical tests, to have firing rates that varied significantly with the relevant task variables (Fig. 4 and SI Materials and Methods). These 1,238 neurons were recorded in both hemispheres of the two trained monkeys (398 recording sessions; approximately three neurons per session, on average). Response coding classification was based on the same procedures used for S1 (Fig. 4 and SI Materials and Methods). The examples in Fig. 6 and Figs. S3 and S4 illustrate typical DPC activity, with horizontal lines below raster plots indicating the time periods of significant coding and line color indicating which signal was encoded (Fig. 4).

Fig. 6.

Single neuron activity in DPC during the pattern discrimination task. (A–D) Raster plots of four example neurons sorted according to the four possible combinations of G and E stimulus patterns delivered during P1 and P2. The resulting four classes are c1 (G-G, red), c2 (G-E, orange), c3 (E-G, green), and c4 (E-E, blue). Each row of ticks is one trial, and each tick is an action potential. Trials were randomly delivered and were sorted by class afterward (only 10 out of 20 trials per class are shown). Correct and incorrect trials are indicated by black and purple ticks, respectively. Horizontal colored bars below rasters indicate times at which the neurons carried a significant signal (Fig. 4) encoding the pattern presented during P1 (cyan), the pattern presented during P2 coding (light green; not shown here), the class (pink), the decision partially (light orange), or the complete decision (black).

Fig. S3.

Related to Figs. 6 and 7. (A–D) Additional single-unit DPC responses during the pattern discrimination task. Plots show activity of four single neurons in DPC in the same format as in Fig. 6.

Fig. S4.

Related to Figs. 6–8. Single-neuron responses in DPC for different stimulus frequencies. (A–C) Raster plots of three example neurons in the same format as in Fig. 6. In each panel, the three columns correspond to the activity of the same cell evoked by similar trial classes (E, G combinations) with different mean frequencies (5, 10, and 15 Hz). Note the consistency of each cell’s coding properties across frequencies.

In contrast to S1, DPC displayed a large repertoire of neuronal responses associated with one or several of the relevant task components. For example, some neurons responded selectively during P1 to pattern G (Fig. 6A and Figs. S3 A–D and S4A) or to pattern E (Fig. 6B and Fig. S3D). We refer to these responses as P1 coding (horizontal cyan line below raster plots; cyan profile in Fig. 4). In the case of the example neuron of Fig. 6A (P1 coding for pattern G in c1 and c2), the firing rate began increasing during P1 and maintained its high level during the delay period between P1 and P2 until about the middle of P2 (horizontal cyan line). The example neuron of Fig. 6B had similar properties but preferred pattern E (c3 and c4). In some of the error trials (purple raster plots in Fig. 6A and Figs. S3 A–D and S4A), the strong activation evoked by pattern G during hit trials disappeared during the delay period, and, likewise, intense activity was seen during this period when the animal erroneously judged the first stimulus pattern as E instead of G in classes c3 and c4 (purple raster plots). The neurons that coded pattern E showed a similar switch in activity (Fig. 6B and Fig. S3C). Thus, these neurons selectively coded patterns G or E between the first and second stimulation periods, and their activity correlated with the monkey’s behavior.

In total, 793 (64% of 1,238) DPC neurons showed P1 coding during a period of at least 200 ms. Horizontal cyan lines in Fig. 7A indicate significant P1 coding for each neuron, and the cyan trace in Fig. 7B shows the corresponding percentage of significant neurons as a function of time. Among them, 430 (54.2% of 793) coded pattern G, 296 (37.3% of 793) coded pattern E, and 67 of these (8.4% of 793) switched from coding one pattern to another pattern (48 switched from pattern G to pattern E, 71.6% and 19 switched from pattern E to pattern G, 28.3%), as illustrated for the example neuron in Fig. S3D. To appreciate how these numbers and their corresponding percentages changed over time, we quantified them in intervals of 1 s, beginning from P1 up to the end of the task. During P1 (0 s to 1 s), 505 neurons coded the stimulus patterns (353 for pattern G, 69.9% and 152 for pattern E, 30.1%). This means that, during this period, the population showed a preference for pattern G over pattern E—but this preference changed gradually. During the first second between P1 and P2 (1 s to 2 s), 489 neurons coded the stimulus patterns (318 for pattern G, 65% and 171 for pattern E, 35%). During the last second of the delay (2 s to 3 s), 363 neurons coded the stimulus patterns (200 for pattern G, 55.1% and 163 for pattern E, 44.9%). Finally, during P2 (3–4 s), 388 neurons coded the pattern shown during P1 (189 for pattern G, 48.7% and 199 for pattern E, 51.3%). After P2, the number and percentage of neurons coding the P1 stimulus collapsed almost to zero. This shows that the preference for pattern G wanes over the delay period, such that the numbers of neurons preferring patterns G and E become essentially identical by the end of P2. Notably, in contrast to the P1 coding, we found few neurons that coded the patterns G and E delivered during the second stimulation period, P2 (105 of 1,238, 8.5%), and none of them showed persistent activity during the delay period between the end of P2 and pu (light green lines in Fig. 7 A and B). These results in DPC contrast with those obtained in S1, where the percentages of neurons coding P1 and P2 were essentially identical (Fig. 5B).

Fig. 7.

Population coding dynamics in DPC during pattern discrimination. (A) Times at which individual DPC neurons carried a significant signal. Horizontal colored lines indicate time bins encoding (Fig. 4) the first pattern (P1 cyan), the second pattern (P2 light green), the trial class (pink), the decision partially (light orange), or the complete decision (black). Each row corresponds to a single neuron. (B) Percentage of neurons with significant encoding as a function of time. (C) Results for class-selective neurons sorted according to specific classes: class 1 (red, n = 241), class 2 (orange, n = 219), class 3 (green, n = 263), and class 4 (blue, n = 236). (D) Percentage of neurons with significant class-selective coding as a function of time.

In addition to these types of sensory representation, DPC neurons showed class-selective responses (see Fig. 4 for class types; pink traces in Fig. 7 A and B). By definition, class-selective coding refers to each P1 and P2 combination of stimulus patterns, so it occurred only during P2 and between P2 and pu. Class-selective coding was more frequent (959 of 1,238, 77.4%) than P1 coding (793 of 1,238, 64%). Class-selective neurons were almost equally distributed across the four possible classes (class 1, n = 241, 25.1%; class 2, n = 219, 22.8%; class 3, n = 263, 27%; and class 4, n = 236, 24.6%; Fig. 7D). This categorical code was also very stable (Fig. 7 C and D): The class-selective responses began during P2 with a high percentage of neurons and decreased thereafter. Furthermore, in some of the error trials (purple rasters), the class coding observed during hit trials disappeared (see also c3 in Fig. S3A, c1 in Fig. S4B, and c2 in Fig. S4C), whereas in other error trials it surfaced when the animal erroneously judged the true category as the cell’s preferred category (c4 as c3 in Fig. 6C, c1 as c3 in Fig. S4B, and c2 as c1 and c4 in Fig. S4C). Thus, the activity of class-coding neurons was often predictive of the monkey’s performance (correct vs. incorrect, discussed below). These results contrast sharply with those obtained in S1, where we did not find a single class-selective neuron.

Besides coding for specific stimuli and classes, DPC neurons also reflected the monkey’s decision, that is, whether P2 = P1 or P2 ≠ P1. This type of coding was labeled with horizontal black and light orange lines below rasters (see also black and light orange entries in Fig. 4). Example neurons showing this type of coding are in Fig. 6 A, B, and D and Figs. S3 B–D and S4A. As for the class-selective coding, the responses encoding the decision began during P2 or during the delay period following P2. We identified 701 (56.6% of the 1,238) neurons with decision coding (horizontal black and light orange lines and traces in Fig. 7 A and B). Decision-coding neurons could be of three types: those that coded the decision fully, consistently selecting either P2 = P1 or P2 ≠ P1 without any further distinction (n = 513, 73.2%); those that coded it partially, selecting P2 = P1 or P2 ≠ P1 but preferring one class combination over another (n = 139, 19.8%); and a minority that coded it in both ways at different times (n = 49, 7%). Thus, the complete-decision responses were more common than the partial ones. Fig. S3C shows an example neuron with partial decision coding (light orange line below rasters). It fired weakly for P2 ≠ P1 (without distinguishing c2 vs. c3) and much more intensely for P2 = P1, but it distinguished statistically between c1 and c4 within the P2 = P1 condition. We will show below that the partial and complete decision codes have the same properties in regard to hit vs. error trials. Combining both types of neurons (n = 701), we found that 323 (46.1%) coded P2 = P1, 340 (48.5%) coded P2 ≠ P1, and 38 (5.4%) switched between P2 = P1 and P2 ≠ P1 (Fig. 7 A and B). In terms of their temporal distribution, note that the number of complete-decision responses increased during the motor report period (black trace in Fig. 7B). As for the P1 and class-selective codes, the complete and partial decision codes faltered during error trials when the animals made the nonpreferred decision instead of the preferred one (Fig. 6 B and D, P2 = P1 preferred response drops during c1 and c4 errors; Fig. 6A and Fig. S3B, P2 ≠ P1 preferred response drops during c2 and c3 errors). Conversely, for the same neurons, the responses changed in the opposite direction during error trials in which the monkeys reported the preferred decision instead of the nonpreferred one (c2 and c3 in Fig. 6 B and D; c1 and c4 in Fig. 6A and Fig. S3B).

The results described above were obtained with the stimulus patterns of 5 Hz mean frequency. A key question is whether the dynamics described above are affected by stimulus frequency (Fig. 1B). To answer this, many of the neurons were also tested with other stimulus frequencies (3 Hz, n = 204; 6 Hz, n = 265; 7 Hz, n = 207; 10 Hz, n = 145; and 15 Hz, n = 206). Fig. S4 shows example neurons whose coding profiles remained almost identical when probed with the different stimulus frequencies (note colored bars below rasters). We found that 72% of the neurons tested with more than one frequency maintained their coding profiles. Furthermore, when considering the coding dynamics of the whole population (Fig. 7B, 5 Hz), we found that large variations in mean frequency had a minimal effect on the coding profiles over time (Fig. 8 F–J, mean stimulus frequencies of 3–15 Hz). It is also worth noting that the monkeys were not retrained for these additional experimental runs. They were able to perform the task with the additional frequencies from the very first sessions. These results indicate that the representation of stimulus patterns found in DPC is rather abstract.

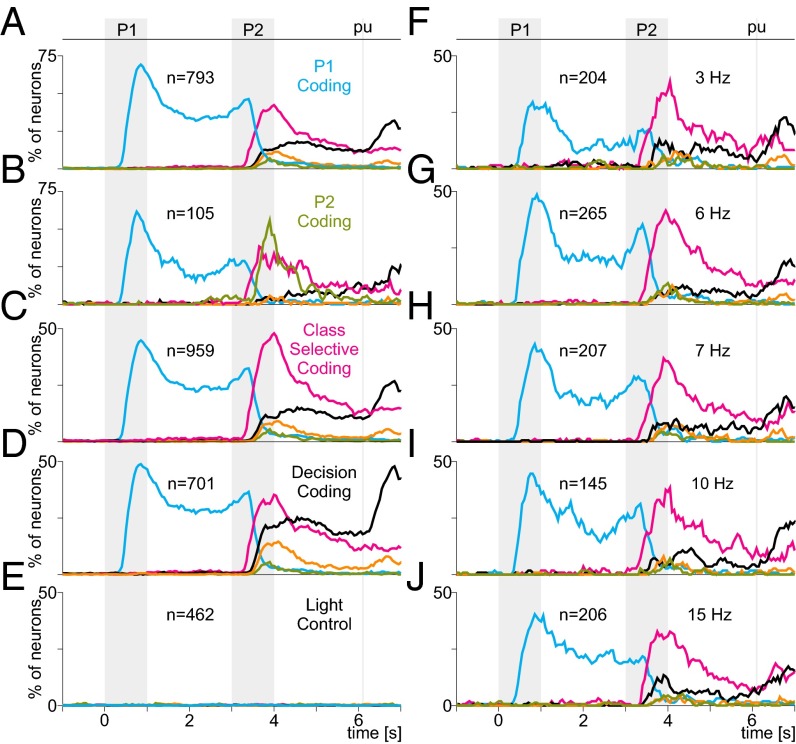
Fig. 8.

Selectivity of DPC coding profiles. (A–D) Percentage of neurons with a significant signal as a function of time (mean frequency of 5 Hz). Different panels include different subsets of neurons selected according to their selectivity. (A) Neurons significantly encoding the first pattern (cyan; n = 793). A large percentage of these neurons were also selective for class (pink), but very few encoded the second pattern (light green). Orange and black traces indicate partial and complete coding of the decision, respectively. (B) Neurons significantly encoding the second pattern (light green; n = 105). A large percentage of these neurons were also selective for the first pattern (cyan) and for class (pink), but few encoded the decision (orange, black). (C) Neurons significantly encoding trial class (pink; n = 959). Many of these neurons also encoded the first pattern (cyan), almost none encoded the second (light green), and only a few encoded the decision (orange, black). (D) Neurons carrying a complete, significant decision signal (black; n = 701). Many of these neurons also encoded the first pattern (cyan) and the trial class (pink), and virtually none encoded the second pattern (light green). (E) Selectivity during the light control task. None of the neurons tested in this task (n = 462) showed significant selectivity to any of the components of the TPDT. (F–J) Percentages of neurons with significant encoding during blocks of trials with different mean frequencies. Numbers of cells and mean frequencies are indicated. Note similar selectivity profiles across frequencies.

Response and Coding Latencies in DPC.

We calculated the response latencies for DPC neurons (using data collected with 5 Hz) during the task, that is, the times at which their activities increased significantly above baseline (SI Materials and Methods). During the P1 period, we focused on the neuronal population with P1 coding (Fig. 7B). We found that the mean response latencies for the populations that coded pattern G (251 ± 148 ms) and pattern E (248 ± 137 ms) were indistinguishable, indicating that they did not depend on pattern identity. Thus, for P1, the response latency in DPC was much higher and more variable than in S1 (23.6 ± 3.8 ms). We also considered the latencies of the earliest DPC responses during P1 (approximately the fastest 10%) and again did not find significant differences between the populations that coded patterns G (103 ± 32 ms) and E (105 ± 35 ms).

These measures quantify how quickly the DPC neurons begin to respond, but not when they start to code the stimulus patterns. We found that, for the same neural population, the mean latency to P1 coding was much higher (616 ± 113 ms). Even for the fastest neurons, the coding latency was higher (386 ± 46 ms) than the response latency described above for the entire population. In comparison, for the S1 neurons (Fig. 3C) the minimum time necessary to discriminate pattern G vs. pattern E was ∼ 240 ms. This means that the DPC neurons with the shortest coding latencies needed ∼146 ms more than the minimal possible time to discriminate between patterns. One potential concern here is that the coding latency could vary depending on the mean stimulus frequency used during the task. However, the latencies were statistically indistinguishable across stimulus frequencies (603 ± 124 ms for 3 Hz, n = 53; 616 ± 113 ms for 5 Hz, n = 592; 610 ± 121 ms for 6 Hz, n = 130; 608 ± 126 ms for 7 Hz, n = 85; 598 ± 120 ms for 10 Hz, n = 64; and 611 ± 121 ms for 15 Hz, n = 89).

Focusing on the P2 period, we estimated the extinction latency of P1 coding (see cyan trace in Fig. 7B). For each neuron, this latency was defined as the latest time bin with P1 coding. For the neurons that had significant P1 coding during P2, the mean extinction latency was 520 ± 128 ms, calculated from the beginning of P2. Finally, we also calculated the latencies for other coding types during P2. For class-selective coding (pink trace in Fig. 7B), on average it was 601 ± 132 ms (the values were similar for each of the four classes in Fig. 7D: c1, 614 ± 113 ms, n = 173; c2, 593 ± 123 ms, n = 157; c3, 608 ± 118 ms, n = 188; and c4, 605 ± 124 ms, n = 166) and for the fastest 10% of the neurons it was 374 ± 48 ms. The mean latency for P2 coding (light green trace in Fig. 7B) was 654 ± 128 ms, and for decision coding (black and light orange trace in Fig. 7B) it was 693 ± 140 ms (for the fastest 10% of the neurons it was 513 ± 49 ms). In summary, the coding latencies during P2 began with the extinction of the P1 signal (working memory), followed by the appearance of class-selective coding, then by P2 coding, and finally by coding of the decision itself.

DPC Coding Dynamics.

Fig. 7B shows the coding profile of the entire population as a function of time. However, this graph obscures the combinatorial quality of the DPC responses, whereby neurons convey different types of information at different points in time. Fig. 8 A–D shows the coding dynamics in a similar format but for selected groups of neurons that carried a given signal for at least 200 ms. For instance, the neurons with significant P1 coding (n = 793, Fig. 8A) displayed P2, class, and decision coding during and after P2 and did so in proportions that were similar to those seen for the entire population (Fig. 7B). Similar results were obtained for profiles based on neurons with significant P2 coding (n = 105, Fig. 8B), class-selective coding (n = 959, Fig. 8C), and decision coding (n = 701, Fig. 8D). Thus, there were no groups of DPC neurons uniquely dedicated to coding single, specific components of the task; each cell seemed to have been assigned multiple relevant variables (pattern, class, and decision) at random.

DPC Responses During the Light Control Task.

The DPC neurons carry information that qualifies as sensory (i.e., about individual stimuli), categorical (i.e., about combinations of stimuli or classes), and decision-related (i.e., about the monkey’s perceptual evaluation). To what extent are those neuronal signals dependent on the animal’s active evaluation? Do they occur only during task execution, or are they to some degree insensitive to the animal’s state? To answer these questions, in addition to the standard test, many of the neurons (n = 462) with P1, class-selective, and decision coding were also tested in a variant of the task in which identical stimuli were delivered but the correct answer was provided by a visual cue (SI Materials and Methods). Under those conditions, DPC neurons no longer coded information about the stimulus patterns or their combinations (Fig. 8E and Fig. S5 show that the four example neurons of Fig. 6 no longer code the relevant task components during the control test). Furthermore, note that the decision signal (Fig. 7B, after pu) was no longer present either, even though the animals executed the same movements in the two task conditions. Thus, contrary to S1, DPC activity is strongly dependent on behavioral context and on the cognitive processing of the discriminated stimuli. In particular, the decision signal is not a simple, obligatory representation of the monkeys’ movements or their underlying kinematic parameters.

Fig. S5.

Related to Figs. 6 and 8. DPC activity in the control condition. (A–D) Raster plots of the same four example neurons shown in Fig. 6 but recorded during the light control task, in which identical tactile stimuli were delivered but the correct choice was visually cued. There were no incorrect trials. No significant coding (Fig. 4) was found in any of the four neurons in this condition.

DPC Pattern and Class Coding During Hit and Error Trials.

To determine the degree to which the activity in DPC predicted the monkey’s choice, we investigated whether, for each stimulus pair, the evoked activity was somehow different between correct (hit) vs. incorrect (error) trials. For this, we used the normalized activity (z-score) at all time bins from the 1,238 neurons with significant coding (SI Materials and Methods). For each type of coding, we divided the normalized responses into hit and error trials and quantified the neurometric discriminability of the relevant coded variable by contrasting the normalized responses across stimuli within each group. For instance, for the neurons with P1 coding, we found that the responses associated with patterns G and E were very different, and thus highly discriminable, during hit trials (Fig. 9A, Left; P < 0.01, ROC test). However, in error trials (Fig. 9A, Right), the two response distributions corresponding to patterns G and E (same color traces as for Fig. 9A, Left) were statistically indistinguishable (P > 0.1). These results were consistent across time (Fig. S6A). Thus, when the monkey made a mistake, the distinction that the DPC neurons were expected to make became much more blurry.

Fig. 9.

DPC coding in hit vs. error trials. Z-score distributions [P(z|class)] for hit (Left) and error trials (Right) for different subsets of neurons. Z-scores indicate normalized differences between responses to different classes, accumulated across cells and time bins. (A) Z-scores based on the responses of P1 coding neurons. Trace colors correspond to the classes illustrated at the top. The strong selectivity observed during hit trials (Left, P < 0.01, ROC test) disappeared in error trials (Right, P > 0.1). (B–E) Z-scores based on the responses of class-selective. In hit trials (Left), all z-score distributions from the preferred class were statistically different from the rest (P < 0.01), and no statistical differences were found between the distributions of nonpreferred classes (P > 0.1). In error trials (Right), the distributions were statistically different (P < 0.05) for classes with different decision outcome as the preferred class (P2 ≠ P1 in c1 and c4 coding neurons; P2 = P1 in c2 and c3 coding neurons) but were the same for classes with the same decision outcome as the preferred class (P > 0.1). (F) Z-scores based on the responses of decision-selective neurons. Z-score distributions are significantly different (P < 0.01) between P2 = P1 vs. P2 ≠ P1 classes during both hit (Left) and error trials (Right). The response distributions show a switch in the sign of the z-score as a result of a switch (correct–incorrect) in the decision outcome.

Fig. S6.

Related to Fig. 9. Population encoding during hits vs. errors as a function of time. (A) Mean z-scored activity from neurons and time bins with significant P1 coding. Trials were sorted according to the type of temporal pattern delivered during the first stimulus (P1): grouped (G, red) or extended (E, blue), in correct (dark colors) or incorrect (light colors) trials. Resulting P(z|P1) distributions were statistically different between hit trials (P < 0.01, AUROC = 0.79) but not between error trials (P > 0.1, AUROC = 0.52). (B) Mean z-scored activity from neurons and time bins with P2 coding. Same color code as in A. Z-score distributions were significantly different between hit trials (P < 0.01, AUROC = 0.78) but not between error trials (P > 0.1, AUROC = 0.53). (C) Mean z-scored activity from neurons and time bins with significant class-selective coding. In this case, activity was sorted into two groups of trials: those of the preferred class (red) and those of the three remaining nonpreferred classes (green). During hit trials (dark traces), the z-score distributions were statistically different for the preferred vs. nonpreferred groups (P < 0.01, AUROC = 0.76). During error trials (light traces) a small statistical difference was found (P < 0.05, AUROC = 0.57). (D and E) Z-scores for complete (D) and patial (E) decision-coding responses. In this case, trials were sorted according to decision outcome: P2 = P1 (green traces) or P2 ≠ P1 (orange traces). Both trial types, hits (dark traces) and errors (light traces), showed significant differences between z-score distributions (hits: P < 0.01, AUROC = 0.78; errors: P < 0.01, AUROC = 0.76). Consistent with encoding of the motor choice, however, in this case there was a switch in the sign of the z-score, whereby P2 = P1 correct trials exhibited similar activity as P2 ≠ P1 incorrect responses, and vice versa.

To evaluate the error effect in P2 coding neurons, we combined the data from the two classes that shared the same pattern (c1 and c3 for pattern G and c2 and c4 for pattern E) because there were too few error trials to analyze each individual class separately. However, the results were qualitatively the same as for P1 coding (Fig. S6B): The responses associated with different patterns were highly discriminable in correct trials (P < 0.01), but this signal was lost during error trials (P > 0.1).

In the case of class-selective coding, we found that during hit trials (Fig. 9 B–E, Left) the z-score distribution for the preferred class was always statistically different from the distributions for the nonpreferred ones (P < 0.01, ROC test), and there was no statistical difference between the three distributions associated with the nonpreferred classes (P > 0.1, ROC test). In contrast, during error trials (Fig. 9 B–E, Right), we found that the class selectivity disappeared, but did so in a particular way. In trials in which class c was presented and was erroneously judged, the cells that preferred class c fired significantly less than usual (P < 0.01; Fig. 9 B–E, Right; note bumps on the left side, z < 0, for responses to each preferred class). Conversely, during those error trials in which the outcome was the opposite of the one normally associated with c, the neurons with preferred classes consistent with that opposite outcome fired more than usual (P < 0.05; Fig. 9 B–E, Right; note bumps on the right side, z > 0, for responses to classes with opposite outcomes). For example, the neurons selective for class c1, which is consistent with P2 = P1, responded weakly (negative z) during errors in which c1 was presented (Fig. 9B, Right, red trace); however, the same cells responded strongly (positive z) during errors in which classes c2 and c3, which are consistent with P2 ≠ P1, were presented (Fig. 9B, Right, green and orange traces).

This type of response inversion is seen in the examples displayed in Fig. 6C and Fig. S4 B and C. A similar effect was reported for false alarms during a somatosensory detection task (18). To further quantify this phenomenon, we constructed a response template (18) for each class-selective type, based on hits only and time bins in which each participating neuron coded the preferred class for at least 400 ms (eight time bins of 200 ms displaced every 50 ms, n = 282; ref. 18). The resulting template represents the typical response profile seen over time during correct discriminations. Once obtained, we then calculated its frequency of occurrence in error trials. The response template was found in only 9% of the error trials of the preferred class and in 7% of the error trials of the class with the same decision outcome as the preferred one. However, remarkably, we found a much higher percentage of template occurrences in error trials in which the complementary classes (i.e., those with opposite outcomes) were presented (c2 and c3 for the example neuron of Fig. 6C). In error trials in which the pattern P2 was confounded (c3 in Fig. 6C), the template frequency was 43%, whereas in trials in which the P1 pattern was confounded (c2 in Fig. 6C) the number was 47%. Thus, the class-selective neurons often confounded the temporal patterns held in working memory in a way that mimicked the monkey’s mistakes.

DPC Decision Coding During Hit and Error Trials.

In the case of decision coding, we found that the z-score distributions showed significant differences (P < 0.01) between match (P2 = P1, c1 and c4) vs. nonmatch (P2 ≠ P1, c2 and c3) classes during both hit (Fig. 9F, Left) and error trials (Fig. 9F, Right). However, the response distributions switched their z-score signs as a result of the change in decision outcome (correct vs. incorrect, or left vs. right choices). In this case we computed a population choice probability index (CPI) to compare the distributions for hit vs. error trials in each class and found that the CPI values were similarly high for all classes (c1: 0.76,; c2: 0.79, c3: 0.77, and c4: 0.79; P < 0.01, ROC test). In Fig. S6D we combined the z-score values for pairs of classes associated with the same decision outcome (c1–c4 for P2 = P1and c2–c3 for P2 ≠ P1) and found significant CPIs of 0.76 when P2 = P1 (P < 0.01) and 0.77 when P2 ≠ P1 (P < 0.01). Thus, the two decisions were represented with equal fidelity. Interestingly, the same effects were found for partial decision neurons (Fig. S6E), for which the CPIs were 0.71 when P2 = P1 and 0.70 when P2 ≠ P1. The coding dynamics in hit and error trials were similar whether the neurons coded the decision fully or partially.

To determine how the decision signal unfolded over time, we analyzed decision coding neurons (n = 314) with at least 1 s of significant activity (20 time bins of 200 ms displaced every 50 ms) during hit and error trials. This decision signal was evident during the delay between P2 and pu (Fig. S7 A and B). Hit and error z-scores became significantly separated (Fig. S7 A and B, dashed line, P < 0.05; ROC test) from each other 400 ms after the beginning of P2 for P2 = P1 and P2 ≠ P1 classes. In terms of choice probability, the CPI became significant right after those points (CPI = 0.67, P < 0.05, ROC test; Fig. S7 B and D) and remained so thereafter (CPI = 0.82, P < 0.01; Fig. S7E). This suggests that the neuronal correlate of the choice in DPC emerged during the middle of P2 and continued until the end of the trial.

Fig. S7.

Related to Results. Time course of DPC decision coding. (A) Mean z-scored activity as a function of time for neurons (n = 314) with at least 20 time bins (1 s) with significant decision coding. Responses were divided according to P2 = P1 (green traces) and P2 ≠ P1 (orange traces) preferences, and further split into hit (dark traces) and error trials (light traces). (B) Mean choice probability for the same population of DPC neurons (n = 314). (C–E) Z-score distributions during three different time periods. Before the second stimulus appeared (P2), it was impossible to determine the choice, or whether it was correct or not (C). From t = 3.42 s (dashed line in A and B) until the end of the second stimulus, the distributions showed a significant difference between choices in both hit and error trials (D; P < 0.05, AUROC = 0.65). Those differences increased thereafter (E; P < 0.01, ROC = 0.81).

SI Materials and Methods

TPDT.

Two monkeys (Macaca mulatta) were trained to discriminate whether the temporal structure of two vibrotactile stimuli of equal mean frequency was the same (P2 = P1) or different (P2 ≠ P1; Fig. 1A). Monkeys performed the task in blocks of trials in which the two patterns had a fixed mean frequency of 3, 5, 6, 7, 10, or 15 Hz (Fig. 1A). Monkeys were rewarded with a drop of liquid for correct discriminations. Because the two stimulus patterns had equal mean frequency over their full duration (1 s), discrimination had to be based on comparison of their temporal structure over a time scale shorter than 1 s.

The monkey sat on a primate chair with its head fixed. The right hand was restrained through a half-cast and kept in a palm-up position. The left hand operated an immovable key (elbow at ∼90°) and two push buttons in front of the animal, 25 cm away from the shoulder and at eye level. The centers of the push buttons were located 7 and 10.5 cm to the left of the midsagittal plane. In all trials, the monkey first placed the left hand on the key and later projected to one of the two push buttons. Stimuli were delivered to the skin of one digit from the distal segment of the right, restrained hand, via a computer controlled stimulator (2-mm round tip; BME Systems). The initial indentation was 500 µm (pd in Fig. 1A). Vibrotactile stimuli consisted of trains of short mechanical pulses. Each of those pulses consisted of a single-cycle sinusoid lasting 20 ms. During trials, two vibrotactile stimulus patterns (P1 and P2) were delivered consecutively to the glabrous skin of one fingertip, separated by a fixed interstimulus delay period of 2 s. The monkeys were asked to report whether P2 = P1 (match) or P2 ≠ P1 (nonmatch) after a fixed delay period of 2 s between the end of P2 and a go signal that triggered the beginning of the motor response (pu in Fig. 1A). Discrimination was indicated by pressing one of two push buttons with the left hand (lateral push button for P2 = P1, medial push button for P2 ≠ P1). The animal was rewarded for correct decisions with a drop of liquid. Performance was quantified through psychometric techniques (Fig. 1B). Monkeys were handled according to the institutional standards of the National Institutes of Health and Society for Neuroscience. All protocols were approved by the Institutional Animal Care and Use Committee of the Instituto de Fisiología Celular of the National Autonomous University of Mexico.

Because we were interested in finding cortical activity related to the sensory events, particularly in DPC, it was crucial to minimize or eliminate modulatory effects arising from the well-known dependence of arm movement direction (13) or on parameters that covary with it. The setup was thus arranged to filter out directionally tuned responses. The distance between the push buttons was 3.5 cm, and these were 18 cm away from the immovable key. Directional neurons fire at frequencies that range between ∼5 and 25 spikes per s (13), corresponding to their antipreferred and preferred directions, respectively. Therefore, on average, directional neurons modulate their firing rates by ∼25 spikes per s when movement direction changes by 180°. The expected effect on an 11° change in direction is thus on the order of one spike per s. Under these conditions some activity related to arm motion may be expected but should be practically identical for the two arm movements.

Light Control Task.

During the control task, events proceeded exactly as described above and in Fig. 1A, except that when the probe touched the skin one of the two push buttons was illuminated, indicating the correct choice. The same stimulus sets used in the discrimination task (Fig. 1B) were delivered to the fingertip while recording cortical neurons from S1 or DPC. The light was turned off when the probe was lifted off the skin (pu in Fig. 1A), triggering the hand/arm movement. The monkey was rewarded for pressing the previously illuminated push button. Thus, stimuli and arm movements were identical to those in the original task but were cued by visual stimuli.

Recordings.

Neuronal recordings were obtained with an array of seven independent movable microelectrodes (2–3 MΩ; ref. 29) inserted into each cortical area, contralateral (left hemisphere) or ipsilateral (right hemisphere) to the stimulated hand, except in S1, in which recordings were always contralateral to the stimulated hand. We collected data using the stimulus set of Fig. 1A, usually 20 trials per stimulus pair (Fig. 2A). We used well-established electrophysiological and anatomical criteria to distinguish between cortical areas (Fig. 1C; ref. 13). In S1 (area 3b), we recorded single neurons with cutaneous receptive fields confined to the distal segments of the glabrous skin of one fingertip of digits two, three, or four and that had QA properties (95.2%; 4.8% with SA properties). All recordings in DPC were made in the arm region of F2 (5). This region is in front of M1 (F1), lateral to the central dimple, posterior to F7 and the genu of the arcuate sulcus (26). Recordings sites changed from session to session and the locations of the penetrations were used to construct surface maps of all of the penetrations in each cortical area. This was done by marking the edges of the small chamber (7 mm in diameter) placed above each cortical area.

Data Selection.

We considered a neuron’s response as task-related if during any of the relevant periods [P1, delay between P1 and P2, P2, delay between P2 and pu, reaction time (RT), or movement time (MT)] its mean firing rate was significantly different from a control period of equal duration (500 ms) but preceding the initial probe indentation at the beginning of each trial (Wilcoxon test, P < 0.01; ref. 17). By definition, P1 and P2 correspond to the first and second stimulus periods, respectively. The first delay period was divided into consecutive intervals of 500 ms beginning at the end of P1 and up to the beginning of P2. Similar intervals were used for the second delay between the end of P2 and pu. The RT was the period between the end of pu to the beginning of key up (ku, Fig. 1A). The MT was the period between the end of ku to the beginning of the push button press (pb, Fig. 1A).

Coding of Trial Class As a Function of Time.

This analysis was designed to quantify whether the activity of each neuron from S1 and DPC was modulated by each of the four stimulus pattern combinations used in the task (Fig. 1A): class 1 (c1, patterns G-G), class 2 (c2, patterns E-G), class 3 (c3, patterns E-G), and class 4 (c4, patterns E-E), where G corresponds to the stimulus pattern with grouped pulses (for example, P1 with 5 pulses in upper trace of Fig. 1A) and E corresponds to the stimulus pattern with extended pulses (for example, P1 with five pulses in lower trace of Fig. 1A). The four possible combinations of E and G patterns (i.e., classes) were used at each fixed mean frequency (Fig. 1 A and B).

For each neuron, we calculated a time-dependent firing rate per trial using a 200-ms sliding window displaced every 50 ms, beginning 1 s before pattern P1 until the end of the trial (1 s after the push button). Using hit trials only, we constructed a firing rate distribution for each class. At each time bin we used the ROC (15) to identify class-differential responses. Using these class firing rate distributions we computed the area under the ROC curve (AUROC value) for the six possible class comparisons: c1 vs. c2, c1 vs. c3, c1 vs. c4, c2 vs. c3, c2 vs. c4, and c3 vs. c4. In this analysis, AUROC values range from 0 to 1. A value of 0.5 means that the two class-specific response distributions are indistinguishable from each other (overlapped distributions). Values higher or lower than 0.5 indicate that, on average, one class evoked a higher or lower response than the other (partially overlapped distributions). To compare AUROC values across neurons, values lower than 0.5 were rectified to their corresponding values in the range between 0.5 and 1 (e.g., an AUROC value of 0.2 was changed to 0.8). To determine significant AUROC values, we performed a permutation test by shuffling the class labels across trials and recomputing the AUROC values with the shuffled trials. This procedure was repeated 1,000 times at each time bin and for each of the six class comparisons for each neuron. If the unshuffled AUROC value (≠0.5) reached or exceeded the 95% of the distribution obtained from the 1,000 shuffled surrogates (P < 0.05), the two compared classes were labeled statistically different; otherwise, the two classes were labeled as equal. We should emphasize that statistical equality means that there is not enough neuronal response information to differentiate the two distributions, which is what we were looking for; we do not imply that both distributions are exactly the same.

This analysis produced a binary code for each bin composed of six binary digits resulting from the six comparisons. In this method, the 0’s are as important as the 1’s for the coding schemes. Because of that, the criterion to assign both was very strict: To avoid random assignments at each time window, we only assigned a binary label of statistical equality (0) or inequality (1) if the same digit was kept for at least four consecutive bins (200 ms); otherwise, no label could be obtained and that time bin was excluded from the classification. This part of the method was designed to correct for multiple comparisons.

It is important to note that for each time bin this procedure generates a unique code for each neural response. However, besides the nine distinct codes mentioned in Fig. 4, the rest of the possible 64 binary words represent mixed, ambiguous codes.

Neuronal Coding Types.

Using the binary words (difference profile) computed from the six AUROC values as described above, each time bin was tested for classification into one of four possible coding profiles during the task (Fig. 4).

P1 coding.

This profile applied to responses that tracked the identity of the P1 pattern (cyan traces). In this case, the responses must be similar for classes c1 (G-G) and c2 (G-E), and for c3 (E-G) and c4 (E-E), which have the same P1, but must differentiate between all other class comparisons, which have different P1 patterns. This coding profile corresponds to the following binary code: 0-1-1-1-1-0 (third column in Fig. 4).

P2 coding.

P2 coding was done as described above, but for responses that tracked the identity of P2 (light green traces). Responses must be similar for c1 and c3, and for c2 and c4, which have identical P2; they must be different for all other class combinations, which have different P2 patterns. This profile corresponds to the following binary code: 1-0-1-1-0-1 (fourth column in Fig. 4).

Class-selective coding.

This profile corresponds to neurons that responded preferentially to one of the four trial classes (pink traces, columns 5–8 of Fig. 4). Time bins were labeled according to the class that selectively evoked a response (Fig. 9). Four binary words were associated with this profile, but all followed the same rule: The preferred class evoked a different response than the three remaining classes, and the three nonpreferred classes were indistinguishable between each other.

Decision coding.

This label was applied to two similar coding profiles, one that tracked the choice without any ambiguity (dark traces, 11th column in Fig. 4) and another that tracked the choice with a relatively minor ambiguity (light orange traces, ninth and 10th columns in Fig. 4). These are referred to as complete and partial decision profiles, respectively. The former tracked the comparison between the two patterns (same vs. different). In this case the responses must be similar for classes c1 (G-G) and c4 (E-E), and c2 (G-E) and c3 (E-G), which have the same outcomes (either P1 = P2 or P1 ≠ P2) and different for all other class comparisons, for which the outcomes are different. The complete coding profile corresponds to the binary word 1-1-0-0-1-1. The partial coding profile was applied to time bins encoding the same/different decision, as above, but which, in addition, also differentiated between classes with identical outcomes. This could happen in two ways, with different responses for G-G vs. E-E (binary word: 1-1-1-0-1-1), or with different responses for G-E vs. E-G (binary word: 1-1-0-1-1-1).

Any time bin in which none of the six comparisons fit any of the binary words just described (Fig. 4) was considered as a noncoding time bin. Moreover, to consider that a neuron had significant coding, its profile had to be constant for at least five consecutive bins (250 ms). Using this procedure for all of the recorded neurons, it was possible to depict the neurons’ encoded signals as functions of time. For S1 neurons, we used this same procedure (with different time windows) to estimate the percentage of neurons with binary encoding of P1 and P2 (Fig. 3D). Optimal decoding was produced with 200-ms windows (Fig. 3D).

Two main motivations for this coding scheme were (i) being able to quantitatively assess and describe all of the possible neural codes during all task epochs and across areas and (ii) generating coding types that would not overlap in their meaning. Take P1 coding as an example. Our scheme allowed us to identify this code even during P2 (look at Fig. 7B and neurons S3C–D). During P2, the coding scheme also allowed us to differentiate between P2 coding and class coding. For example, for neuron S3A, if we had just compared c1 + c3 (both with P2 = G) vs. c2 + c4 (P2 = E), the differences would have been statistically significant, indicating a signal related to pattern identity—even though, upon visual inspection, we appreciate a clear class-selective coding during P2. In light of this, the interpretation that we try to convey when we write that P1 or P2 coding are “tracking the identity” is that the code specifically indicates the stimulus patterns (E or G) when they are present during the first stimulus (P1 coding) or the second stimulus (P2).

Regarding decision coding, we faced essentially the same problem. If we had used a simpler code, we would have confounded decision coding with class-selective coding. Neuron S3A is again a good example: If we had compared c1 + c4 (both corresponding to “same”) vs. c2 + c3 (“different”), the differences would have been statistically significant, even though, upon visual inspection, we can appreciate a clear class-selective coding during P2. The requirements of a useful classification scheme (completeness and lack of overlap) are crucial constraints that are not easily satisfied by simpler, intuitive comparisons that do not consider class selectivity. In other words, to establish the type of coding (if any) that a neuron is implementing in any given time bin, the comparison between responses to different classes is crucial.

Also of note, a multifactor regression model (18) would have been of limited usefulness for disentangling the different coding types, given their variety. This is related to the issues discussed in the previous two paragraphs. The results of linear regression are conditioned on the coordinate base used to represent the dependencies: If we had used P1 and P2 as a base, for instance, we would not have identified the class selective responses (e.g., neuron S3A). Similar problems arise with other coordinates, P1 and Decision, for example. A more complex, but still intuitive, coordinate base that could explain the full variability observed in the recorded data is a base with each of the four classes as elements. However, in this base interpreting the combinations of projections of the neural responses would be at least as complicated as interpreting the results from an ROC analysis. A nonparametric analysis is more appropriate, and other nonparametric statistical methods for comparing two distributions would have yielded similar results (e.g., mutual information).

Population Responses.

To describe the neuronal population responses of each cortical area (S1 and DPC), we normalized the firing rates for each time bin (50-ms window displaced every 10 ms) using the z-score transform. The z-score was computed by subtracting from each trial (hit, error, and control trials) the mean firing rate and dividing the result by the SD at each time window. The mean and SD for each neuron were calculated using the recorded firing rate activity in hit trials from all time bins in the interval from −1 to 7 s of the task. We calculated a mean z-score value for hit, error, and control (light control task) trials for each class to obtain an average population response as a function of time. We transformed back the mean population z-scores to show responses in terms of firing rates instead of z-scores (Fig. 2 and Fig. S2). Back-transformation was computed using the average values of mean firing rates and SDs from all recorded neurons and for each cortical area.

To combine all of the responses from different neurons for the same class, first we defined a sign for each type of coding: P1 and P2 codes were labeled as positive if the G pattern evoked the higher firing rate and were otherwise labeled as negative. Class-selective codes had a positive sign if the preferred class produced an increase in firing rate and were negative if the preferred class exhibited a decreased selective response. Decision codes were marked as positive if the P2 = P1 condition produced a higher firing rate than the P2 ≠ P1 condition and were otherwise marked as negative. Neurons with an identified coding profile in at least 10 time bins were considered for further analysis. Then, to average across neurons, the sign of the z-score was reversed for those cells with negative tuning. It is well-established methodology to invert the sign in negative tuning to join positive and negative distributions (see figure 4 in ref. 28). Afterward, at each time bin the normalized activity was averaged according to class (c1 to c4) and sorted according to the four types of coding, separating hit from error trials. Additionally, we also constructed time-averaged probability distributions from the z-score values for each class [P(z|class)]. This was done separately for each type of coding profile (distributions in Fig. 9).

To improve the quality of the distributions of error trials, we averaged the responses from those classes that did not show significant differences according to the “profile-differences” criteria (Figs. S6 and S7): P1 encoding allowed us to average classes c1 and c2 and classes c3 and c4. For P2 encoding, we averaged classes c1 and c3 and classes c2 and c4. For class-selective coding, two groups of mean normalized responses were defined. The first one included the preferred response class and the second one included the three remaining classes (nonpreferred). For decision encoding, we computed distributions for the two match classes (c1 and c4) and, separately, for two nonmatch classes (c2 and c3). We stress that we searched for decision tuning bins throughout the whole trial, for each neuron, and across the two areas. We found that DPC neurons coded the decision from the second stimulation period onward (Fig. 7) and did not find decision tuning in 3b neurons (Fig. 5). Finally, to obtain the temporal evolution showed in Fig. S7, we identified all of the neurons with more than 1 s of decision encoding (n = 314) and plotted their mean z-score value as a function of time. Using this approach, we investigated and determined the time at which the decision signals arose.

Information Estimates in S1 Neurons.

Using the firing rate values, we measured their association with P1 and P2 in terms of Shannon’s mutual information (8) for each time window, using the following equation:

$$I={\displaystyle \sum _{r,s}P\left(s\right)P\left(r|s\right){\log }_2\left(\frac{P\left(r|s\right)}{P\left(r\right)}\right)}.$$ [S1]

Here, the information (I), measured in bits, quantifies the accuracy with which the neural response (the firing rate r) can be used to determine the identity of the stimulus pattern (s). The expression P(r) corresponds to the probability of observing a response (r) regardless of the value of the stimulus pattern. It was estimated using the firing rate probability distribution from all hit trials during the same time window. P(s) represents the probability that the stimulus pattern takes a value s (G or E), taking into account hit trials only. P(r|s) is the conditional probability of observing a response r given a specific stimulus pattern s.

We considered different sliding window durations (from 50 to 1,000 ms), moving in 50-ms steps, and for each window quantified the information conveyed by each neuron about pattern identity (G or E) during P1 or P2. Averaging across time points, for each neuron, we computed the mean information values for P1 and P2 as functions of window duration. Finally, we averaged the pattern information values from all S1 neurons to obtain the mean population information for each window.

Thereafter, using a deterministic integration window of 200 ms, we calculated the average population information for P1 or P2 as a function of time and found the optimal time point, which maximized the mean information that S1 conveys about pattern identity.

Choice Probability.

The CPI was calculated using methods from signal detection theory (15). In this case, the ROC measures the overlap between hit and error responses for each stimulus pair (P1, P2). A value of 0.5 indicates full overlap, whereas 1 and 0 indicate completely separate distributions. Thus, the CPI quantifies the selectivity for one or the other decision outcome during the discrimination process. To compute the CPI as function of time, we used a window of 200-ms duration moving in steps of 50 ms, beginning 1,000 ms before P1 and ending 1,000 ms after the animal reported the comparison between P2 and P1. To combine the responses from all neurons at each time bin, the CPI values were averaged across all S1 neurons (Fig. 5D).

It is important to note that Fig. 9 and Figs. S6 and S7 compared error and hit distributions for each type of coding in DPC neurons. This analysis is much more detailed and specific than a CPI. For each type of tuning, it quantifies the differences between hit and error trials. Quickly adapting (QA) neurons from area 3b are homogenous and it is not necessary to divide their responses into different types.

Response Latencies.

We calculated two different latencies, a response latency, which corresponds to the time at which the stimulus-driven neural activity (during P1) becomes significant, and a coding latency, which corresponds to the time at which the encoded signal becomes significant (during P1).

Response latency.

Firing rate distributions were generated at each time point using a time window of 200 ms sliding steps of 1 ms during P1 and were compared against the rates obtained in a control period (200 ms before P1 onset) using the ROC method (13, 15). The first time window at which the AUROC was significantly different from 0.5 (permutation test, P < 0.05) was considered as the response latency to P1. This latency was computed separately for stimulus patterns G and E.

Coding latency.

This latency varied depending on the coding profile of the cells. The P1 coding latency was estimated for each neuron by identifying the first of three consecutive bins significantly coding patterns G or E. We examined two measures of population latency. The first was to compute the mean latency from all of the neurons with P1 coding within the stimulation period (0–1 s). The second was to measure the mean latency for the fastest 10% of neurons with P1 coding. The analysis was analogous for P2, class-selective, and decision-coding signals. In addition, during the P2 period, we evaluated the extinction latency of the working memory, defined as the last time bin at which a neuron demonstrated significant P1 coding during the second stimulus period.

Template Matching for Class-Selective Neurons During Error Trials.

We identified all DPC neurons with at least 400 ms of class-selective coding (n = 282). For these, we computed the mean firing rate for hit trials of the preferred class (template; ref. 18) for all of the time bins where the neurons showed consecutive class coding (200-ms sliding window displaced every 50 ms). Computing the mean square error (MSE) between this template and each hit trial, we constructed a confidence interval. The confidence interval was considered proportional to the variance of the MSE distribution (1.5 SD, two-sided). Then, for each neuron, we calculated the MSE between the template and the responses in single error trials to determine the class preference associated with each error trial. A significant match was identified in a trial if the MSE was within the corresponding confidence interval. The template duration was not fixed across neurons because it depended on the number of bins with significant class coding.

Discussion

The experiments described above were designed to address the following question: What are the neural codes that allow the discrimination of temporally structured vibrotactile patterns of equal mean frequency? To answer it, we recorded neuronal activity in S1 and DPC while trained monkeys performed the TPDT. Note that we do not mean to imply that the neuronal activity from these two cortical areas is sufficient for discrimination; rather, the idea is simply that the neuronal activity studied could serve to identify the codes associated with diverse cognitive components of the task and understand how information about temporal patterns is represented and transformed as it flows from S1 to DPC. The task design allowed us to relate neuronal activity to perceptual discrimination performance and to investigate how neural circuits generalize, because although the two stimulus patterns to be compared always had equal mean frequency, a wide range of frequencies was used across trials. Indeed, we found a subset of DPC neurons that were selective for specific combinations of stimulus patterns, in effect implementing a categorical code from which the perceptual judgment (“same” or “different”) can be easily read out. These cells were abundant, their responses were abstract in that they were highly invariant to mean stimulus frequency, their activity was strongly task-dependent, and their response fluctuations across trials were highly predictive of behavior. Crucially, unlike the decision-related neurons in DPC, which encoded the monkey’s choice in essentially a binary way, the categorical neurons were highly informative about both the stimulus patterns presented in each trial and the monkey’s decision—and from a computational point of view, although their existence seems logical, it was by no means guaranteed, nor absolutely necessary. In fact, we identified these cells by exploring a wide variety of code formats for representing the different elements of the TPDT. We discuss this below, first for S1 and then for DPC.

For an observer, the overall activity evoked in S1 by each stimulus pattern (1 s) was useless for discrimination, because the mean firing rate was essentially identical for P1 and P2, and for E and G patterns. Instead, the observer trying to infer the identity of a stimulus pattern had to consider the firing rate at shorter periods of time. We found that this strategy was most effective for identifying pattern G vs. pattern E when using a time window of ∼200 ms. Here, the temporal code is not defined in terms of the precision of the neuronal spike interval sequences, but on a critical, short time window that captured in the firing rate fluctuations, the higher amount of information of the temporal stimulus pattern. This window maximized both the amount of information conveyed about pattern identity and the percentage of S1 neurons with significant information and represents a plausible time period for neuronal integration (7). Also, from a methodological point of view, it allowed us to use identical methods and tests for analyzing the data from S1 and DPC, so the results could be directly comparable. Regarding this point, it becomes important to discuss the role that a temporal code could play in the context of this task.

A temporal neural code refers to situations in which precise spike timing or very fast firing rate fluctuations carry information (19, 20). Studies in subcortical areas and sensory cortices have reported that spike timing may add significant information to that carried by spike counts alone (21, 22). Although temporal codes have the inherent capacity to convey more information than spikes integrated over long intervals, and some studies suggest that neural synchrony could play a role in perceptual experiences (23, 24), firing rate codes have proved to be significantly correlated with animals’ psychophysical performance in multiple tasks (17). In the case of vibrotactile stimuli, it was initially thought that frequency discrimination would rely on a neural mechanism capable of reading out periodic interspike intervals (5), because periodic stimuli evoke strongly periodic spike trains in S1 (5–8). However, no relationship was found between variations in periodicity in S1 and psychophysical performance in single trials (6, 8). Furthermore, in S1 itself, periodicity diminishes appreciably from area 3b to area 1 and essentially vanishes in the secondary somatosensory cortex (S2; ref. 8) and further downstream (1–3, 13). In contrast, during VFDT, the firing rate of S1 neurons computed over intervals of several hundred milliseconds already encodes stimulus frequency and is directly associated with the animal’s psychophysical performance (6, 8).

In the TPDT used here, we removed the most extreme version of the firing rate code by presenting pairs of stimuli with equal mean frequency. In this case, the optimal time window for discriminating the stimulus patterns with a single scalar quantity was much shorter than the full stimulation window (1 s), but still much longer than the typical time scale of a temporal code.

Consistent with previous results (6, 8, 13), when the same stimuli were delivered but the animal knew in advance which button to press for a reward (light control task), the S1 responses were no different from during active discrimination. Also, S1 responses were present only during the stimulation periods, and we did not find any differences in stimulus coding between correct and error trials. Thus, S1 seems mainly associated with faithfully coding the stimulus patterns, but not other, more cognitive components of the task, such as information stored in working memory or the animals’ decisions. However, evidence indicates that the S1 output is necessary for igniting or gating the activity of downstream circuits where, by successive transformations, the subject’s choices are eventually generated (2, 6, 8, 13).

In contrast, the DPC neurons coded all of the relevant task components of the TPDT: the stimuli, the P1 information that had to be remembered, and the decision. In addition, however, they prominently represented specific combinations of stimuli, thus generating an intermediate, more abstract categorical code. Importantly, though, most DPC neurons coded more than one variable (mixed selectivity; ref. 25). The DPC responses began during P1 with a coding latency largely delayed relative to that of S1. This suggests that a large number of circuits between S1 and DPC are involved in this task. In fact, S1 (area 3b) does not project directly to DPC. Information from S1 (area 3b) could be routed via successive relays in the somatosensory pathway (areas 1 and 2), going through the more central somatosensory circuits (S2 and areas 5a and 7b of the posterior parietal cortex), which then connect with DPC and other frontal lobe circuits (26). A similar hierarchical scheme was proposed for the vibrotactile detection and discrimination tasks (13, 27). However, the coding latencies for the amplitude and VFDT were shorter than for the TPDT (13, 27). This could be not only because of differences in the stimuli themselves, but also because the different tasks may effectively require different time windows for temporal integration (7).

A notable feature of the activity recorded in DPC is that P1 coding was maintained during the working memory period between P1 and P2, ending by the middle of P2, just before the emergence of class and decision coding. Recordings in DPC and other frontal lobe circuits have demonstrated similar memory-related activity coding for stimulus frequency during a VFDT with a similar structure, in which two stimuli are presented sequentially (1–3, 13, 28, 29). Neural correlates of working memory have also been reported with match-to-sample tasks in related cortical circuits (30, 31). This suggests that, in general, these circuits have the capacity to maintain sensory-related activity during working memory, but it is unclear how such a general computational process, applicable to a wide range of stimuli, takes place in DPC, or how the stored information is routed to DPC. Clearly, the memory-related activity arises only when it is necessary, because the responses coding for P1 disappeared during the light control task, when the same stimulus patterns were delivered but the animal knew the correct answer in advance. Furthermore, for most DPC neurons, the memory-related response was independent of mean stimulus frequency, so it coded the identity of the stimulus pattern in a frequency-invariant, and thus somewhat abstract, format. Interestingly, although initially there was a strong overrepresentation of pattern G during P1, this bias gradually diminished over the course of the delay between P1 and P2, with nearly equal numbers of neurons coding patterns E and G at the end. Such equalization may be useful for subtracting common noise and increasing coding efficiency (32, 33). In any case, this shows, together with the frequency invariance mentioned above, that the sustained, memory-related activity is not just a literal copy of the activity evoked in S1 but rather a more heavily processed signal that may be transformed via divisive normalization or other circuit operations. These properties provide important constraints for future computational models of delay period activity.

A large proportion of the DPC neurons were class-selective, that is, they responded to one combination of P1 and P2 patterns but not to the others. This is interesting given that the core of the task is precisely the comparison of the current stimulus pattern P2 against the stored trace of the past pattern P1. That the class-selective neurons evenly coded the four relevant classes seems logical but was by no means a foregone conclusion. Other combinations were possible, such as neurons with graded selectivities across the four classes, or neurons with one nonpreferred class and three preferred ones, and so on. Also, P2 coding itself was negligible. The class selectivity could have been present only for specific mean frequencies, or over narrow frequency ranges, or it could have been biased toward particular classes (say, those corresponding to the “same” outcome), but this was not the case either; the class-selective neurons preferred the four possible classes equally, without bias, and were largely insensitive to mean stimulus frequency. The circuit seems to have arrived at a particularly elegant solution for performing the TPDT. Furthermore, we found that, in error trials, two complementary things happened: First, the neurons selective for the true, presented class fired less than usual, and second, the neurons selective for the two competing classes, that is, those leading to the opposite outcome, fired more than usual. Not only that, during errors those “competing” neurons showed a high probability of responding with the same temporal profile of activity (template) identified in hit trials. Thus, the activity of class-selective neurons not only predicted the occurrence of an incorrect behavioral response, but also provided important insight as to how such misjudgment might have been generated—namely, by the conjunction of two effects, too little activity in support of the correct pattern combination and too much activity in support of the erroneous combinations. This demonstrates that the perceptual evaluation depends on more than two identified neuronal types, four in our case, that jointly contribute to error trials. This type of coding represents an intermediate step linking stimulus selectivity and perceptual decision; it has elements of both the sensory input (which is nontrivial, given that the selectivity is for two patterns presented sequentially) and the binary motor report. As for P1 coding neurons, during the light control task the class-selective activity disappeared, so it is generated in the appropriate cognitive context only. Whether class coding arises locally in DPC or is imported from another area is unknown. In the case of the VFDT, the relevant decision signal is likely to emerge initially in the secondary somatosensory cortex, with different strengths and latencies across cells (13). This might also be the case for the TPDT. It is also possible that analogous categorical activity arises in DPC with similar tasks based on other modalities, but this is difficult to assess given the lack of comparable studies in the literature.

During the postponed decision period, the percentages of class- and decision-coding neurons were very similar. The presence of sensory information during the postdiscrimination period might be important in case the motor report of the decision needs to be updated (7). These results fit well with the idea that the preparatory activity observed in areas of the frontal lobe during delay periods represents not only the planning of motor actions (34, 35) but also the information on which those motor plans are based (36, 37). The decision neurons in DPC encoded the monkey’s choice with essentially equal strength during correct and error trials. However, their differential activation not only was associated with minimal variations in arm movements (SI Materials and Methods) but also vanished the during the light control task. Therefore, their activity during the TPDT is not trivially related to a motor action; either it reflects the final result of the comparison between patterns or it represents a motor plan that is fully gated by the behavioral context of the task. Previous studies have shown similar results (2, 3).

Notably, we also found that a considerable percentage of neurons continued coding the stimulus class or the decision (“same” or “different”) after the monkey had emitted its motor response. Again, this activity did not occur during the light control task. This suggests that the DPC also maintains information that may be necessary to evaluate the consequences or the value of the decision report (38). It is possible that the DPC plays a role in evaluating choice outcomes, which can serve to learn, in general, and to adapt future decisions according to behavioral context and environmental demands.

In summary, the neuronal activity studied served to identify multiple neural codes that participate in a perceptual evaluation process, including an intermediate categorical one that is partially sensory and partially choice-related. It also served to determine how information about temporal patterns is represented and transformed in S1 vs. DPC. Whether the S1 representation is gradually or abruptly transformed in its transit to DPC, and which representations are held in working memory, are open questions (13, 27) for future experiments and computational analyses.

Materials and Methods

Monkeys were trained to report whether the temporal structure of two vibrotactile stimuli of equal frequency was the same or different (SI Materials and Methods). Neuronal recordings were obtained in S1 and DPC while the monkeys performed the task (SI Materials and Methods). Coding of trials class as function of time was calculated from S1 and DPC neurons (SI Materials and Methods). Information and response latencies for each neuron are described in SI Materials and Methods. All protocols were approved by the Institutional Animal Care and Use Committee of the Instituto de Fisiología Celular, Universidad Nacional Autónoma de México. Monkeys were handled according to the institutional standards of the National Institutes of Health and Society for Neuroscience.