Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Nov 14;59(23):10788–10793. doi: 10.1021/acs.jmedchem.6b01110

Measurement of Ligand–Target Residence Times by 1H Relaxation Dispersion NMR Spectroscopy

Thomas Moschen 1, Sarina Grutsch 1, Michael A Juen 1, Christoph H Wunderlich 1, Christoph Kreutz 1,*, Martin Tollinger 1,*
PMCID: PMC5150660  PMID: 27933946

Abstract

graphic file with name jm-2016-01110h_0005.jpg

A ligand-observed 1H NMR relaxation experiment is introduced for measuring the binding kinetics of low-molecular-weight compounds to their biomolecular targets. We show that this approach, which does not require any isotope labeling, is applicable to ligand–target systems involving proteins and nucleic acids of variable molecular size. The experiment is particularly useful for the systematic investigation of low affinity molecules with residence times in the micro- to millisecond time regime.

Introduction

According to the residence time model of drug action, the lifetime of a drug–target complex, rather than its affinity, is the key determinant of pharmacological activity in vivo.1−3 On the basis of this proposition, residence-time-driven lead optimization has been suggested,4,5 and significant amounts of data supporting this model have been accumulated.6−11 In fragment-based drug design, residence-time-driven lead optimization relies on the initial identification of weakly interacting core structures (fragments) from compound libraries. These compounds are subsequently subject to optimization by chemical modification, using the residence time as optimization criterion, searching for compounds that dissociate slowly from their biomolecular targets. Typically, lead compounds identified by fragment screening are of low molecular weight, with affinities in the micromolar to millimolar range.12 While optical biosensors are routinely used to measure the binding kinetics of high-affinity ligands with residence times exceeding ∼1 s,13,14 measurements of more rapidly dissociating fragments with lower affinities are, in many cases, outside the range of this technique.15

Here, we describe a one-dimensional NMR experimental scheme to measure ligand dissociation rate constants, koff, of complexes with residence times (τ = 1/koff) in the micro- to millisecond time regime. Our approach is based on the Carr–Purcell–Meiboom–Gill (CPMG)16,17 relaxation dispersion (RD) technique using protons (1H) in the ligand molecule as sensors for binding and unbinding kinetics and does not require any isotope labeling.

Results

Ligand-observed CPMG experiments are commonly used in early stage NMR based assays for fragment screening. Exploiting the full quantitative potential of the CPMG technique, relaxation dispersion experiments are available to monitor the binding process of ligand molecules to proteins18−26 or nucleic acids27 in a protein18−20 or ligand-observed manner.21−27 Ligand detection has the distinctive benefit of enabling measurements with the sensitivity of low molecular weight compounds, reducing the experimental time that is required for data acquisition considerably. So far, ligand-observed CPMG-RD measurements of binding kinetics have been performed for peptides interacting with proteins using 15N- or 13C-CPMG-RD experiments,21−23 as well as chemically synthesized (15N or 19F labeled) low-molecular weight compounds interacting with RNA or proteins.24−27 However, for routine analysis of ligand binding kinetics it is desirable to obtain data rapidly and at natural abundance, i.e., without requiring isotope labeling. Ligand-observed 1H-CPMG-RD experiments clearly are the method of choice.

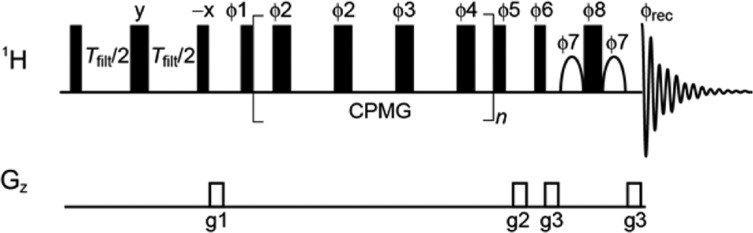
Figure 1 shows the one-dimensional NMR pulse scheme that we propose for this purpose. In this experiment, resonances from low-molecular weight compounds are selected by a transverse relaxation filter, followed by a 1H-CPMG pulse train and a water suppression scheme.29 In the 1H-CPMG block the timing between the 1H refocusing pulses is varied, leading to a modulation of the refocusing efficiencies so long as the chemical shifts of a particular ligand resonance in free and bound states are different, and exchange between these states occurs on the micro- to millisecond time scale. As a consequence, the kinetic transition between complexed and free ligand molecules results in a measurable contribution to relaxation dispersion profiles. To reduce cumulative errors in the 1H-CPMG block, we employ the [0013] phase alternation scheme.28 This scheme provides accurate measurements of RD profiles covering a wider range of resonance frequencies than CPMG schemes without phase alternation30 and is more tolerant to pulse miscalibration.31

Figure 1.

Figure 1

Open in a new tab

NMR pulse scheme for measuring ligand-observed 1H-CPMG relaxation dispersion profiles. During the CPMG element, pulses [ϕ2, ϕ2, ϕ3, ϕ4] are phase-cycled according to the [0013] alternation scheme.28 See the Supporting Information for details.

Figure 2 shows experimental ligand-observed 1H-CPMG-RD data, recorded at 25 °C, for four different ligand–receptor systems using low-molecular weight (<500 Da) compounds binding to biomolecules with molecular masses ranging from 10 kDa (RNA aptamers) to 66 kDa (BSA). In our study we chose to vary the saturation of ligand with protein or nucleic acid in six steps between 0% and 5% (proflavin-trypsin), 7.5% (preQ1-Fsu and TTe aptamers) or 10% (indoxyl sulfate-BSA, isoquercitrin-Bet v 1a), respectively, with low-molecular-weight compound concentrations of 1–5 mM and protein or RNA concentrations below 0.2 mM in all cases. The length of the transverse relaxation filter, Ttfilt was set to values between 40 and 80 ms. Because large scalar couplings can interfere with echo formation during CPMG trains,32 we analyzed the 1H relaxation dispersion data only of protons with homonuclear JHH scalar couplings of <1.5 Hz (as measured in one-dimensional 1H experiments). The 3JHH scalar couplings of 1H-2 in indoxyl sulfate and 1H-8 in preQ1 to the imidazole 1HN were eliminated by recording RD experiments in 100% 2H2O buffer.

Figure 2.

Figure 2

Open in a new tab

Ligand-observed 1H-CPMG relaxation dispersion data for (A) indoxyl sulfate binding to bovine serum albumin BSA (66 kDa), (B, C) proflavin binding to bovine trypsin (24 kDa), (D) isoquercitrin (R = β-d-glucoside) binding to the birch pollen allergen Bet v 1a (Bet v 1.0101, 17 kDa), (E, F) preQ1 binding to its class I aptamer from Fusobacterium nucleatum (Fsu, 10 kDa) and Thermoanaerobacter tengcongensis (TTe, 10 kDa), respectively. Data are shown for the protons indicated in red in the ligand structures (indoxyl sulfate, 1H-2; proflavin, 1H-4/5, 1H-9; isoquercitrin, 1H-6; preQ1, 1H-8). Exchange contributions to the relaxation dispersion profiles, Rex, are displayed in all cases. The solid lines are fits to the data, yielding koff values for the five ligand–receptor systems. All data were recorded on a 600 MHz Bruker Avance II+ NMR spectrometer equipped with a prodigy cryogenic probe. Experiments were repeated on an Agilent DirectDrive2 500 MHz spectrometer, Figure S1 and Table S1.

In all cases perfectly flat 1H-CPMG-RD profiles were obtained for the low-molecular-weight compounds in the absence of biomolecules, indicating that any residual (<1.5 Hz) scalar couplings do not significantly interfere with the experiment. Moreover, it is evident that addition of biomolecular targets induces a sizable contribution to the relaxation dispersion data. The RD profiles display a clear dependence on the ligand–target concentration ratio; higher saturation of ligand with target generally produces larger relaxation dispersion profiles, as characterized by increased values of Rex, i.e., the difference in effective relaxation rates (R2,eff) at low and high CPMG refocusing frequencies.

The experimental 1H-CPMG-RD data were analyzed by fitting a two-site kinetic model (allowing for transitions between free and target-bound ligand) to the six RD profiles in each case.33 By this approach, the rate constants for ligand dissociation, koff, were determined, yielding values between 1000 and 5400 s–1 for the five different ligand–receptor systems, corresponding to residence times, τ, between approximately 1.0 and 0.2 ms (Table 1). Of note, the residence time for the preQ1-Fsu aptamer complex obtained by 1H-CPMG-RD, τ = 0.63 ± 0.08 ms, agrees well with τ = 0.67 ± 0.03 ms, as extracted from ligand-observed CPMG-RD experiments of 15N labeled preQ1,27 demonstrating the robustness of the approach. Furthermore, very similar off-rates were obtained from 1H-CPMG-RD experiments on a 500 MHz spectrometer and by fitting data from 500 and 600 MHz spectrometers simultaneously (Table S1 and Figure S2). While experimental times for recording 1H-CPMG and 15N-CPMG RD data (∼5 h for 6 RD profiles each) and material consumption are similar, 1H-CPMG-RD provides the advantage of not requiring additional time and resources for the chemical synthesis of isotope labeled ligand.

Table 1. Ligand–Target Residence Times τ Obtained by Ligand-Observed 1H-CPMG-RD Experiments, 600 MHz, 25 °C, and Relevant Complex Dissociation Constants (Kd).

ligand resonance target τ [ms] Kd [μM]
indoxyl sulfate 1H-2 BSA 0.67 ± 0.09 3034
proflavin 1H-4/5 trypsin 0.19 ± 0.02 14035
proflavin 1H-9 trypsin 0.20 ± 0.03 14035
isoquercitrin 1H-6 Bet v 1a 1.0 ± 0.1 n/a
preQ1 1H-8 Fsu apt. 0.63 ± 0.08 0.2836
preQ1 1H-8 TTe apt. 0.23 ± 0.03 0.00237
Open in a new tab

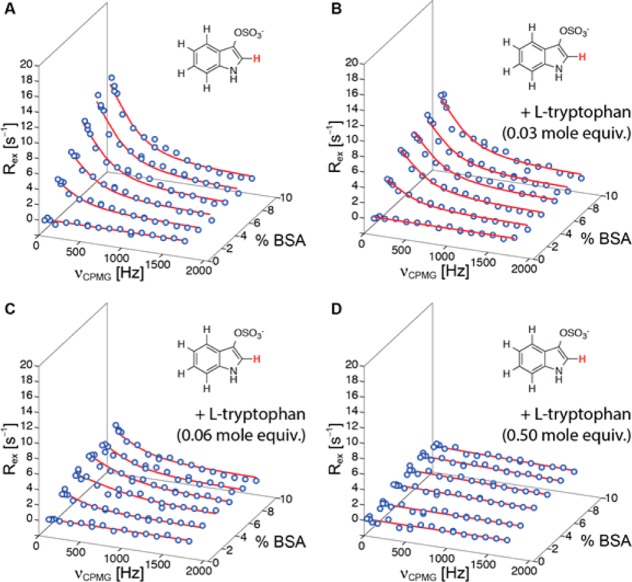
To illustrate further applications and to validate our approach, we performed competitive 1H-CPMG-RD experiments using indoxyl sulfate as a ligand for bovine serum albumin and adding l-tryptophan to the sample (Figure 3). Tryptophan and indoxyl sulfate bind serum albumins at Sudlow site II.38 It is evident from the 1H-CPMG-RD data in Figure 3 that addition of l-tryptophan induces a significant reduction of the magnitude of the indoxyl sulfate RD profiles, indicating that l-tryptophan perturbs the interaction between indoxyl sulfate and BSA. Interestingly, quantitative analysis of the 1H-CPMG-RD data shows that koff for indoxyl sulfate is not affected by l-tryptophan. Values of koff were determined as 1700 ± 100, 1700 ± 200, and 1600 ± 400 s–1 for samples containing 0, 0.03, and 0.06 mol equiv (with respect to indoxyl sulfate) of l-tryptophan, respectively. The reduction of the magnitude of the RD profiles can thus be attributed to a lower population of ligand-bound indoxyl sulfate in samples where l-tryptophan is present, indicating that both ligands indeed compete for the same binding site. Of note, addition of 0.50 mol equiv of l-tryptophan produces flat RD profiles for indoxyl sulfate, which is consistent with l-tryptophan having a higher affinity for serum albumins than indoxyl sulfate.39,40 This is further supported by our observation that l-tryptophan binding kinetics to BSA cannot be studied by 1H-CPMG-RD experiments (Figure S3), presumably because koff is outside (below) the range of time scales that can be measured by this technique.

Figure 3.

Figure 3

Open in a new tab

500 MHz ligand-observed 1H-CPMG relaxation dispersion data for 2.0 mM indoxyl sulfate (1H-2) interacting with BSA (up to 10% saturation) before (A) and after addition of (B) 0.06 mM (0.03 mol equiv with respect to indoxyl sulfate), (C) 0.12 mM (0.06 mol equivalents), and (D) 1.0 mM (0.50 mol equiv) of l-tryptophan.

As a negative control experiment (Figure 4), we show that indoxyl sulfate does not bind to bovine trypsin and also does not interfere with the binding of proflavin, a generic serine protease inhibitor, to trypsin.41

Figure 4.

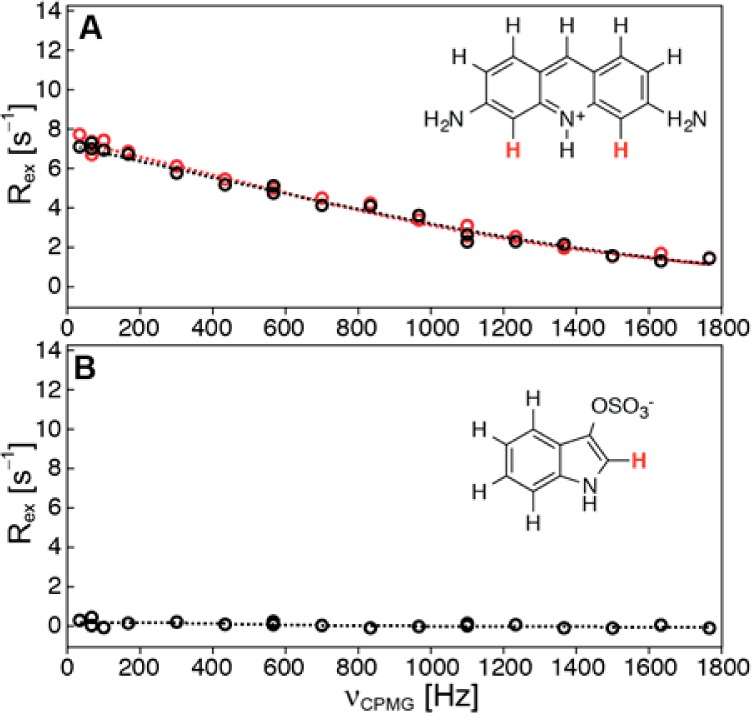
Figure 4

Open in a new tab

500 MHz ligand-observed 1H-CPMG relaxation dispersion data for (A) proflavin (1H-4/5) interacting with bovine trypsin (3% saturation) before (red) and after (black) addition of equimolar amounts of indoxyl sulfate and (B) data for indoxyl sulfate (1H-2) in the presence of trypsin (3% saturation).

Discussion and Conclusions

Ligand-observed 1H-CPMG-RD experiments combine a number of advantages. Measurement at high sensitivity in one-dimensional NMR spectra (approximately 30–120 min per sample on a 600 MHz NMR spectrometer equipped with a cryogenic probe, and approximately 60–240 min on a room temperature probe 500 MHz spectrometer) is possible without requiring isotope labeling. Addition of only low mole fractions of biomolecular targets (<10%, concentration typically up to 100–200 μM) ensures that ligand can be observed at high sensitivity even when high-molecular-weight proteins or nucleic acids are studied. Due to the high magnetogyric ratio of 1H, even relatively small chemical shift differences between free and bound states (∼0.1 ppm) can produce large enough relaxation dispersion profiles for recording 1H-CPMG-RD data. Moreover, sample heating in 1H-based CPMG experiments is significantly lower than for heteronuclear (15N or 13C) CPMG experiments,42 which enables the use of higher pulse repetition rates to sample RD profiles over a wider range and hence the measurement of processes as fast as ∼104 s–1 and above. In addition, 1H-CPMG refocusing pulses are typically shorter than those of 15N or 13C nuclei, reducing systematic errors arising from off-resonance effects.43

In practice, ligand-observed 1H-CPMG-RD measurements are viable for low-molecular weight compounds that bind to proteins or nucleic acids with ligand on–off rates in the micro- to millisecond time regime, corresponding to affinities in the micromolar to millimolar range for diffusion limited complex formation. It is important to be aware of the boundary conditions for ligand-observed 1H-CPMG-RD measurements that are imposed by potential systematic sources of error. As mentioned above, only ligand 1H resonances with scalar JHH couplings not exceeding ∼1.5 Hz were used for analysis. Larger homo- or heteronuclear couplings can result in contributions to relaxation dispersion profiles that are related to the interchange of magnetization within the scalar coupling network during the CPMG element.32 We estimate that ∼40–50% of all molecules in commercial small fragment libraries contain one or more protons that fulfill these criteria and can be used for ligand-observed 1H-CPMG-RD measurements.

Another potential source of error is dipolar 1H cross relaxation between nearby protons during 1H-CPMG pulse trains,44 which can cause spurious oscillations in RD profiles.32 In addition, intrinsic micro- to millisecond conformational exchange in small ligand molecules can result in nonflat relaxation dispersions even in the absence of a biomolecular target.45 Because these effects can seriously compromise the extraction of kinetic data, it is critical to assess the quality of the data before initiating a ligand binding study by recording a RD profile of unbound ligand. In our case, only resonances with deviations of <1 s–1 from flat dispersion profiles in the absence of biomolecule were used for analysis. Adding only a low mole fraction of protein or nucleic acids maintains the high sensitivity of the small ligand molecule for detection that would otherwise be compromised, in particular for ligands binding to large targets, and keeps dipolar cross relaxation effects between ligand and biomolecule at a low level. Of note, these effects can, in principle, be efficiently reduced or abolished by (partial) deuteration of the biomolecular target.

Taken together, we have shown here that ligand-observed 1H-CPMG-RD represents a simple and reliable tool for the determination of residence times of low molecular weight compounds. Since this approach does not require isotope labeling, it is applicable to a wide range of ligand-binding systems and may well serve as standard technique for residence-time-driven lead optimization in drug development. This experiment has similar sample and affinity requirements as STD and WaterLOGSY and can be used at the same stage of the optimization process. 1H-CPMG-RD experiments have the potential to routinely measure residence times of chemically modified low-molecular-weight compounds and to systematically probe the structural determinants of ligand–target binding kinetics.46 Such structure–kinetic relationships represent a critical and essential tool for rationally modifying drug–target residence times during lead optimization.

Experimental Section

Sample Preparation and NMR Experiments

Targets: Bet v 1a (Bet v 1.0101) protein, Fsu, and TTe RNA aptamers were prepared by bacterial overexpression and solid-phase synthesis, respectively, and purified chromatographically as described.47,48 Purities were determined by electrospray ionization mass spectrometry (purity ≥95% for all targets). Bovine serum albumin (BSA) and bovine trypsin were purchased from Sigma-Aldrich (100% pure, as determined by agarose electrophoresis and UV spectroscopy, respectively; see Supporing Information). Ligands: Indoxyl sulfate, 3,6-diaminoacridine (proflavin), quercetin 3-β-d-glucoside (isoquercetin), preQ1, and l-tryptophan were purchased from Sigma-Aldrich (with purities of 100%, 96.3% 92.1%, 98%, and 100%, respectively, as determined by TLC and HPLC, see Supporing Information). The purity of these ligands was verified by 1H NMR spectroscopy.

Concentrations and buffers in NMR experiments. Indoxyl sulfate binding to BSA: 50 mM potassium phosphate buffer (pH 5.8), 25 mM NaCl, 1 mM NaN3, 100% D2O, indoxyl sulfate 2.0 mM, BSA [0, 40, 80, 120, 160, 200 μM]. Isoquercetin binding to Bet v 1.0101: 5 mM sodium phosphate buffer (pH 8.0), 10% D2O, isoquercetin 2.0 mM, Bet v 1a [0, 40, 80, 120, 160, 200 μM]. Proflavin binding to trypsin: 20 mM Tris·HCl buffer (pH 7.5), 5 mM CaCl2, 4% dimethyl sulfoxide, 10% D2O, proflavin 2.0 mM, trypsin [0, 20, 40, 60, 80, 100 μM]. PreQ1 binding to Fsu and Tte aptamers: 10 mM sodium cacodylate buffer (pH 6.4), 2 mm MgCl2, 100% D2O, PreQ1 [2.0, 5.3, 2.7, 1.8, 1.3, 1.1 mM], RNA [0, 80, 80, 80, 80, 80 μM]. All NMR experiments were performed at 25 °C.

RD profiles were recorded as follows. The length of the CPMG element, Trelax, was set to 60 ms (indoxyl sulfate, isoquercetin, proflavin) and 30 ms (preQ1) (Figure S4). The number of basic [0013] elements, n, each containing four 1H refocusing pulses, was set to [1, 2, 3, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49, 53] (indoxyl sulfate, isoquercetin, proflavin) and [1, 2, 3, 5, 6, 9, 12, 15, 17, 19, 21, 23, 25, 27, 29, 30] (preQ1), resulting in νCPMG values of [33, 67, 100, 167, 300, 433, 567, 700, 833, 967, 1100, 1233, 1367, 1500, 1633 1767] Hz and [66, 133, 200, 333, 400, 600, 800, 1000, 1267, 1400, 1533, 1667, 1800, 1933, 2000] Hz, respectively. In addition, repeat experiments were recorded at νCPMG values of [67, 567, 1100] Hz for indoxyl sulfate, isoquercetin, and proflavin experiments and [133, 333, 600] Hz for preQ1 experiments. The length of the transverse relaxation filter, Ttfilt, was set to 40 ms for indoxyl sulfate/BSA, 80 ms for isoquercetin/Bet v 1a, 60 ms for proflavin/trypsin, and 60 ms for preQ1/Fsu/Tte (see Figure S2). Number of transients: between 48 (for uncomplexed ligand) and 512 (for the highest level of receptor saturation) per one-dimensional experiment.

NMR Data Analysis

RD data were processed and analyzed with the nmrPipe/nmrDraw suite of programs.49 Resonance intensities, ICPMG, were measured by adding the intensities in ±3 grids centered on the peak maximum (covering ∼20% of the peak width) and converted to effective relaxation rates, R2,eff, as R2,eff = (−1/Trelax)ln(ICPMG/I0), where I0 is the resonance intensity in the reference experiment. The data were subsequently analyzed by fitting a two-site kinetic model allowing for transitions between free and receptor-bound ligand (L + T ↔ LT) where L is the low-molecular-weight ligand, T is the biomolecular target, LT is the ligand–target complex, and kon and koff are the second order association rate constant and the dissociation rate constants of the ligand–target complex, respectively. The fractional populations of target-bound (LT) and unbound (L) ligand molecules are given by pLT and pL, with pLT + pL = 1. The chemical shift difference for a particular ligand resonance between the target-bound and the free from is Δω.

Because significantly different rotational correlation times of free and target-bound ligand molecules are to be expected, different values for the intrinsic relaxation rates of ligand in its free form (R0,L) and in the ligand–target complex (R0,LT) have to be taken into account. R0,L is known from the RD data in the absence of target and can be constrained in the fitting procedure. Moreover, because in (moderately) fast exchange processes fractional populations and chemical shift differences are correlated and associated with a single shared parameter Φex = pLT(1 – pLT)Δω2, these values cannot be determined separately, while the exchange rate constant, kex, is accessible from the data. The exchange rate constant is related to kon and koff as kex = kon[L] + koff. Because at equilibrium koff = f·kon[L], with f = (1 – pLT)/pLT, at ligand/biomolecule saturation levels below the binding midpoint, i.e., pLT < 0.5, f > 1 and koff is greater than kon[L]. In our experimental setup with saturation levels below 10%, koff thus exceeds kon[L] significantly and kex is dominated by koff, irrespective of the on-rate kon. Therefore, at low saturation levels, koff is accessible from RD data under (moderately) fast exchange conditions.

Exchange parameters were obtained by simultaneously fitting all six RD profiles for each titration experiment to the above two-site kinetic model, employing the equation given by Baldwin.33 We extracted a single (global) value for koff, along with values of Φex for each titration step and a single (global) value of RLT,0. In Figures 2–4, S1, and S3 the exchange contributions to RD profiles, Rex = R2,eff – R2,eff(νCPMG = ∞), are shown. Uncertainties in koff were estimated via a Monte Carlo approach using 500 synthetic data sets generated on the basis of the experimental uncertainties (as determined from the repeat experiments) and propagated to residence times τ by error propagation; standard deviations are reported.

Acknowledgments

Funding was provided by the Austrian Science Fund FWF (Grant P26550 to C.K. and Grant P26849 to M.T.).

Glossary

Abbreviations Used

CPMG

Carr–Purcell–Meiboom–Gill

RD

relaxation dispersion

BSA

bovine serum albumin

TTe

thermoanaerobacter tengcongensis

Fsu

Fusobacterium nucleatum

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jmedchem.6b01110.

  • Details of the NMR pulse scheme, Figures S1–S4, Table S1, and provider supplied proofs of purity for all purchased compounds (PDF)

The authors declare no competing financial interest.

Supplementary Material

jm6b01110_si_001.pdf (1.7MB, pdf)

References

  1. Copeland R. A.; Pompliano D. L.; Meek T. D. Drug-target residence time and its implications for lead optimization. Nat. Rev. Drug Discovery 2006, 5, 730–739. 10.1038/nrd2082. [DOI] [PubMed] [Google Scholar]
  2. Tummino P. J.; Copeland R. A. Residence time of receptor-ligand complexes and its effect on biological function. Biochemistry 2008, 47, 5481–5492. 10.1021/bi8002023. [DOI] [PubMed] [Google Scholar]
  3. Copeland R. A. The drug-target residence time model: a 10-year retrospective. Nat. Rev. Drug Discovery 2016, 15, 87–95. 10.1038/nrd.2015.18. [DOI] [PubMed] [Google Scholar]
  4. Swinney D. C. The role of binding kinetics in therapeutically useful drug action. Curr. Opin. Drug Discovery Dev. 2009, 12, 31–39. [PubMed] [Google Scholar]
  5. Lu H.; Tonge P. J. Drug-target residence time: critical information for lead optimization. Curr. Opin. Chem. Biol. 2010, 14, 467–474. 10.1016/j.cbpa.2010.06.176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Vilums M.; Zweemer A. J.; Yu Z.; de Vries H.; Hillger J. M.; Wapenaar H.; Bollen I. A.; Barmare F.; Gross R.; Clemens J.; Krenitsky P.; Brussee J.; Stamos D.; Saunders J.; Heitman L. H.; Ijzerman A. P. Structure-kinetic relationships--an overlooked parameter in hit-to-lead optimization: a case of cyclopentylamines as chemokine receptor 2 antagonists. J. Med. Chem. 2013, 56, 7706–7714. 10.1021/jm4011737. [DOI] [PubMed] [Google Scholar]
  7. Louvel J.; Guo D.; Agliardi M.; Mocking T. A.; Kars R.; Pham T. P.; Xia L.; de Vries H.; Brussee J.; Heitman L. H.; Ijzerman A. P. Agonists for the adenosine A1 receptor with tunable residence time. A case for nonribose 4-amino-6-aryl-5-cyano-2-thiopyrimidines. J. Med. Chem. 2014, 57, 3213–3222. 10.1021/jm401643m. [DOI] [PubMed] [Google Scholar]
  8. Bradshaw J. M.; McFarland J. M.; Paavilainen V. O.; Bisconte A.; Tam D.; Phan V. T.; Romanov S.; Finkle D.; Shu J.; Patel V.; Ton T.; Li X.; Loughhead D. G.; Nunn P. A.; Karr D. E.; Gerritsen M. E.; Funk J. O.; Owens T. D.; Verner E.; Brameld K. A.; Hill R. J.; Goldstein D. M.; Taunton J. Prolonged and tunable residence time using reversible covalent kinase inhibitors. Nat. Chem. Biol. 2015, 11, 525–531. 10.1038/nchembio.1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Tiwary P.; Limongelli V.; Salvalaglio M.; Parrinello M. Kinetics of protein-ligand unbinding: predicting pathways, rates, and rate-limiting steps. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, E386–E391. 10.1073/pnas.1424461112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Guo D.; Heitman L. H.; Ijzerman A. P. The role of target binding kinetics in drug discovery. ChemMedChem 2015, 10, 1793–1796. 10.1002/cmdc.201500310. [DOI] [PubMed] [Google Scholar]
  11. Mollica L.; Theret I.; Antoine M.; Perron-Sierra F.; Charton Y.; Fourquez J. M.; Wierzbicki M.; Boutin J. A.; Ferry G.; Decherchi S.; Bottegoni G.; Ducrot P.; Cavalli A. Molecular dynamics simulations and kinetic measurements to estimate and predict protein-ligand residence times. J. Med. Chem. 2016, 59, 7167–7176. 10.1021/acs.jmedchem.6b00632. [DOI] [PubMed] [Google Scholar]
  12. Hajduk P. J.; Greer J. A decade of fragment-based drug design: strategic advances and lessons learned. Nat. Rev. Drug Discovery 2007, 6, 211–219. 10.1038/nrd2220. [DOI] [PubMed] [Google Scholar]
  13. Cooper M. A. Optical biosensors in drug discovery. Nat. Rev. Drug Discovery 2002, 1, 515–528. 10.1038/nrd838. [DOI] [PubMed] [Google Scholar]
  14. Nunez S.; Venhorst J.; Kruse C. G. Target-drug interactions: first principles and their application to drug discovery. Drug Discovery Today 2012, 17, 10–22. 10.1016/j.drudis.2011.06.013. [DOI] [PubMed] [Google Scholar]
  15. Shepherd C. A.; Hopkins A. L.; Navratilova I. Fragment screening by SPR and advanced application to GPCRs. Prog. Biophys. Mol. Biol. 2014, 116, 113–123. 10.1016/j.pbiomolbio.2014.09.008. [DOI] [PubMed] [Google Scholar]
  16. Carr H. Y.; Purcell E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954, 94, 630–638. 10.1103/PhysRev.94.630. [DOI] [Google Scholar]
  17. Meiboom S.; Gill D. Modified spin echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. 10.1063/1.1716296. [DOI] [Google Scholar]
  18. Meneses E.; Mittermaier A. Electrostatic interactions in the binding pathway of a transient protein complex studied by NMR and isothermal titration calorimetry. J. Biol. Chem. 2014, 289, 27911–27923. 10.1074/jbc.M114.553354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mittermaier A.; Meneses E. Analyzing protein-ligand interactions by dynamic NMR spectroscopy. Methods Mol. Biol. 2013, 1008, 243–266. 10.1007/978-1-62703-398-5_9. [DOI] [PubMed] [Google Scholar]
  20. Vallurupalli P.; Hansen D. F.; Stollar E.; Meirovitch E.; Kay L. E. Measurement of bond vector orientations in invisible excited states of proteins. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 18473–18477. 10.1073/pnas.0708296104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Zintsmaster J. S.; Wilson B. D.; Peng J. W. Dynamics of ligand binding from 13C NMR relaxation dispersion at natural abundance. J. Am. Chem. Soc. 2008, 130, 14060–14061. 10.1021/ja805839y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Tolkatchev D.; Xu P.; Ni F. Probing the kinetic landscape of transient peptide-protein interactions by use of peptide 15N NMR relaxation dispersion spectroscopy: binding of an antithrombin peptide to human prothrombin. J. Am. Chem. Soc. 2003, 125, 12432–12442. 10.1021/ja021238l. [DOI] [PubMed] [Google Scholar]
  23. Sugase K.; Dyson H. J.; Wright P. E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 2007, 447, 1021–1025. 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
  24. Lin P. C. Assessment of chemical exchange in tryptophan-albumin solution through 19F multicomponent transverse relaxation dispersion analysis. J. Biomol. NMR 2015, 62, 121–127. 10.1007/s10858-015-9929-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Dalvit C. Ligand- and substrate-based 19F NMR screening: principles and applications to drug discovery. Prog. Nucl. Magn. Reson. Spectrosc. 2007, 51, 243–271. 10.1016/j.pnmrs.2007.07.002. [DOI] [Google Scholar]
  26. Dubois B. W.; Evers A. S. 19F-NMR spin-spin relaxation (T2) method for characterizing volatile anesthetic binding to proteins. Analysis of isoflurane binding to serum albumin. Biochemistry 1992, 31, 7069–7076. 10.1021/bi00146a007. [DOI] [PubMed] [Google Scholar]
  27. Moschen T.; Wunderlich C. H.; Spitzer R.; Levic J.; Micura R.; Tollinger M.; Kreutz C. Ligand-detected relaxation dispersion NMR spectroscopy: dynamics of preQ1-RNA binding. Angew. Chem., Int. Ed. 2015, 54, 560–563. 10.1002/anie.201409779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Yip G. N.; Zuiderweg E. R. A phase cycle scheme that significantly suppresses offset-dependent artifacts in the R2-CPMG 15N relaxation experiment. J. Magn. Reson. 2004, 171, 25–36. 10.1016/j.jmr.2004.06.021. [DOI] [PubMed] [Google Scholar]
  29. Piotto M.; Saudek V.; Sklenar V. Gradient-tailored excitation for single-quantum NMR spectroscopy of aqueous solutions. J. Biomol. NMR 1992, 2, 661–665. 10.1007/BF02192855. [DOI] [PubMed] [Google Scholar]
  30. Bain A. D.; Anand C. K.; Nie Z. Exact solution to the Bloch equations and application to the Hahn echo. J. Magn. Reson. 2010, 206, 227–240. 10.1016/j.jmr.2010.07.012. [DOI] [PubMed] [Google Scholar]
  31. Myint W.; Ishima R. Chemical exchange effects during refocusing pulses in constant-time CPMG relaxation dispersion experiments. J. Biomol. NMR 2009, 45, 207–216. 10.1007/s10858-009-9344-9. [DOI] [PubMed] [Google Scholar]
  32. Ishima R.; Torchia D. A. Extending the range of amide proton relaxation dispersion experiments in proteins using a constant-time relaxation-compensated CPMG approach. J. Biomol. NMR 2003, 25, 243–248. 10.1023/A:1022851228405. [DOI] [PubMed] [Google Scholar]
  33. Baldwin A. J. An exact solution for R2,eff in CPMG experiments in the case of two site chemical exchange. J. Magn. Reson. 2014, 244, 114–124. 10.1016/j.jmr.2014.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Davilas A.; Koupparis M.; Macheras P.; Valsami G. In-vitro study on the competitive binding of diflunisal and uraemic toxins to serum albumin and human plasma using a potentiometric ion-probe technique. J. Pharm. Pharmacol. 2006, 58, 1467–1474. 10.1211/jpp.58.11.0007. [DOI] [PubMed] [Google Scholar]
  35. Hedstrom L.; Farr-Jones S.; Kettner C. A.; Rutter W. J. Converting trypsin to chymotrypsin: ground-state binding does not determine substrate specificity. Biochemistry 1994, 33, 8764–8769. 10.1021/bi00195a018. [DOI] [PubMed] [Google Scholar]
  36. Rieder U.; Kreutz C.; Micura R. Folding of a transcriptionally acting preQ1 riboswitch. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 10804–10809. 10.1073/pnas.0914925107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Jenkins J. L.; Krucinska J.; McCarty R. M.; Bandarian V.; Wedekind J. E. Comparison of a preQ1 riboswitch aptamer in metabolite-bound and free states with implications for gene regulation. J. Biol. Chem. 2011, 286, 24626–24637. 10.1074/jbc.M111.230375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ghuman J.; Zunszain P. A.; Petitpas I.; Bhattacharya A. A.; Otagiri M.; Curry S. Structural basis of the drug-binding specificity of human serum albumin. J. Mol. Biol. 2005, 353, 38–52. 10.1016/j.jmb.2005.07.075. [DOI] [PubMed] [Google Scholar]
  39. Fielding L.; Rutherford S.; Fletcher D. Determination of protein-ligand binding affinity by NMR: observations from serum albumin model systems. Magn. Reson. Chem. 2005, 43, 463–470. 10.1002/mrc.1574. [DOI] [PubMed] [Google Scholar]
  40. Berge-Lefranc D.; Chaspoul F.; Cerini C.; Brunet P.; Gallice P. Thermodynamic study of indoxylsulfate interaction with human serum albumin and competitive binding with p-cresylsulfate. J. Therm. Anal. Calorim. 2014, 115, 2021–2026. 10.1007/s10973-013-3067-6. [DOI] [Google Scholar]
  41. Conti E.; Rivetti C.; Wonacott A.; Brick P. X-ray and spectrophotometric studies of the binding of proflavin to the S1 specificity pocket of human alpha-thrombin. FEBS Lett. 1998, 425, 229–233. 10.1016/S0014-5793(98)00235-X. [DOI] [PubMed] [Google Scholar]
  42. Wang A. C.; Bax A. Minimizing the effects of radio-frequency heating in multidimensional NMR experiments. J. Biomol. NMR 1993, 3, 715–720. 10.1007/BF00198374. [DOI] [PubMed] [Google Scholar]
  43. Czisch M.; King G. C.; Ross A. Removal of systematic errors associated with off-resonance oscillations in T2 measurements. J. Magn. Reson. 1997, 126, 154–157. 10.1006/jmre.1997.1168. [DOI] [PubMed] [Google Scholar]
  44. Ishima R.; Louis J. M.; Torchia D. A. Transverse 1H cross relaxation in 1H-15N correlated 1H CPMG experiments. J. Magn. Reson. 1999, 137, 289–292. 10.1006/jmre.1998.1672. [DOI] [PubMed] [Google Scholar]
  45. Ge X.; Sem D. S. NMR structure and dynamics of the NADH nicotinamide ring bound to dihydrodipicolinate reductase. FASEB J. 2008, 22, 1058.2. [Google Scholar]
  46. Pan A. C.; Borhani D. W.; Dror R. O.; Shaw D. E. Molecular determinants of drug-receptor binding kinetics. Drug Discovery Today 2013, 18, 667–673. 10.1016/j.drudis.2013.02.007. [DOI] [PubMed] [Google Scholar]
  47. Grutsch S.; Fuchs J. E.; Freier R.; Kofler S.; Bibi M.; Asam C.; Wallner M.; Ferreira F.; Brandstetter H.; Liedl K. R.; Tollinger M. Ligand binding modulates structural dynamics and compactness of the major birch pollen allergen. Biophys. J. 2014, 107, 2972–2981. 10.1016/j.bpj.2014.10.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Micura R. Small interfering RNAs and their chemical synthesis. Angew. Chem., Int. Ed. 2002, 41, 2265–2269. . [DOI] [PubMed] [Google Scholar]
  49. Delaglio F.; Grzesiek S.; Vuister G. W.; Zhu G.; Pfeifer J.; Bax A. NMRPipe: A multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR 1995, 6, 277–293. 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jm6b01110_si_001.pdf (1.7MB, pdf)

Articles from Journal of Medicinal Chemistry are provided here courtesy of American Chemical Society

RESOURCES