Subjective and Objective Assessments of Flow–Volume Curve Configuration in Children and Young Adults

Abstract

Rationale: Analysis of maximal expiratory flow–volume curves (MEFVCs) allows for determination of airway obstruction, but quantitative methods to describe these curves are not commonly used.

Objectives: We sought to determine the variability in MEFVC concavity assessment by pulmonary physicians, whether objective indices of concavity can be substituted for subjective expert impression, and whether MEFVC concavity correlates with clinical outcomes.

Methods: A survey of 37 MEFVCs (plus 3 duplicates) was sent to pulmonologists for quantitative assessment of MEFVC concavity. Objective indices (β-angle, ratio forced expiratory flow at 50% of total lung volume to peak expiratory flow rate [FEF₅₀/PEFR], ratio of maximum mid-expiratory flow to FVC [MMEF/FVC], k_max, and averaged flow–volume second derivatives) were calculated for each MEFVC and were correlated with the mean expert score. Both the mean expert scores and the best-performing index were then correlated with hospitalizations.

Measurements and Main Results: Ninety-two respondents provided usable data. There was substantial variability in concavity scores between subjects, but strong intrasubject reliability. Mean expert score did not differ by physician years of experience. Several indices (β-angle, FEF₅₀/PEFR, FEV₁/FVC, MMEF/FVC, FEF₅₀, and forced expiratory flow between 25 and 75% of total lung volume) correlated strongly with mean expert scores. A new variable (β-MMEF) was constructed using coefficients from stepwise linear regression and accurately predicted the mean expert score (R² = 0.96). Mean expert score and β-MMEF showed similar odds ratios for hospitalization (2.13 and 2.32, respectively) with identical positive (∼71%) and negative (87%) predictive values. The β-MMEF was also associated with hospitalizations in two independent cohorts of children with asthma and cystic fibrosis.

Conclusions: The β-MMEF is an objective measure of maximal expiratory flow–volume curve concavity and highly correlates with expert impression. Both the mean expert score for expiratory curve concavity and the β-MMEF were associated with increased risk of subsequent hospitalization. The β-MMEF may be a useful biomarker for disease severity in asthma and cystic fibrosis.

Maximal expiratory airflow can be influenced by a variety of factors, including intraluminal obstruction due to mucus plugging, extraluminal smooth muscle contraction, increased airway compliance, and decreased lung elastic recoil. Spirometry allows for measurement of airflows that are reflective of airway caliber (1) and is the most commonly used test to assess lung function. The main indication for the use of spirometry is to document the presence and severity of airway obstruction, which is commonly seen in asthma, cystic fibrosis (CF), chronic obstructive pulmonary disease (COPD), and a variety of other conditions.

According to American Thoracic Society (ATS) criteria, airway obstruction is defined by a reduced ratio of FEV₁ to FVC (FEV₁/FVC) (2). Obstruction is also inferred from the configuration of the maximum expiratory flow–volume curve (MEFVC), with concavity toward the volume axis (“concave up” in calculus terminology) suggestive of lower airway obstruction.

The assessment of MEFVC concavity is performed visually by pulmonary physicians or other providers when evaluating spirometry results. Objective, quantitative analysis of the MEFVC has been a subject of interest to pulmonary physiologists for more than 30 years. Mead described a “slope ratio” to quantify curvilinearity (3) and used an instantaneous slope at a variety of volumes, comparing it with the slope of a chord from each volume point to FVC.

Calculus provides an additional way of describing curve configuration. The second derivative of a function can describe its convexity or concavity. If the second derivative of a function is positive, the curve is described as “concave upward”; if it is negative, the curve is described as “concave downward.” As the second derivative of higher order polynomials is a function, it varies across the domain (reflecting changes in configuration at different points along the function); in this case it describes the variation of the MEFVC slope over the vital capacity. The average value of the second derivative over a portion of the curve can describe the concavity of that portion of the MEFVC.

Although many commercial spirometry algorithms can describe the abnormality attributable to standard parameters (e.g., FEV₁ or FVC), none currently attempt to describe the MEFVC configuration. In this study we aim to describe the variability in MEFVC concavity assessment by pulmonary physicians, to determine whether objective indices of concavity could be substituted for this subjective expert impression, and whether MEFVC concavity correlates with clinical outcomes.

Methods

Subjects

Fifty patients were randomly chosen from the pulmonary function test (PFT) laboratory database (ComPAS; Morgan Scientific, Haverhill, MA) at the Children’s Hospital of Pittsburgh (Pittsburgh, PA). Their MEFVCs and associated lung function variables such as FEV₁, FVC, forced expiratory flow at 50% of total lung volume (FEF₅₀), forced expiratory flow between 25 and 75% of total lung volume (FEF_25–75%, also known as maximum mid-expiratory flow [MMEF]), peak expiratory flow rate (PEFR), and others were extracted from each of the selected spirometry charts.

Two pulmonologists independently reviewed the 50 curves (blinded to the patients’ clinical characteristics), and 37 curves that met ATS criteria for acceptability were selected (with 3 curves to be duplicated) to ensure a broad concavity range in the curves for study. The number of curves selected was based on a desired survey duration of no more than 20 minutes.

Survey

The 37 selected curves were used to construct a secure, Web-based survey (Qualtrics, Provo, UT) whereby respondents were asked to assess MEFVC concavity, using a 10-point scale. Each survey question presented the expiratory curve at the top and a slider scale at the bottom with instructions to rate the concavity of the curve on a scale of 0.0–10.0 (0, no concavity; 10, most severe concavity). Three curves were presented in duplicate to assess intrasubject reliability. All 40 curves (including the duplicates) were presented in random order to each respondent.

The survey was sent by e-mail to pulmonologists identified from the ATS online membership roster and via a pediatric pulmonology list-server. Pulmonologists were asked to report their experience (as a categorical response for years since completion of training), and no other identifying information. This study was approved by the University of Pittsburgh Institutional Review Board (PRO15030238).

Curvature Indices

Five objective curvature indices were calculated according to previously published methods: the β-angle z score (4), the ratios FEF₅₀/PEFR and MMEF/FVC, k_max (5), and the second derivatives of flow with respect to volume averaged over a portion of the exhaled volume. The β-angle is calculated as β = 180 − tan^–1[(PEFR − MEF₅₀)/(0.5 × FVC)] + tan^–1[MEF₅₀/(0.5 × FVC)] (see Figure 3A); reference ranges were used to calculate z scores (zβ-angle) for patients less than 25 years of age (6), as z = [(β-angle/μ)^L − 1]/(L × σ), where μ = 186.4 + [270.8/(age²)], σ = e^{–2.245 − 0.429 × height (m)}, and L = –2.216.

Figure 3.

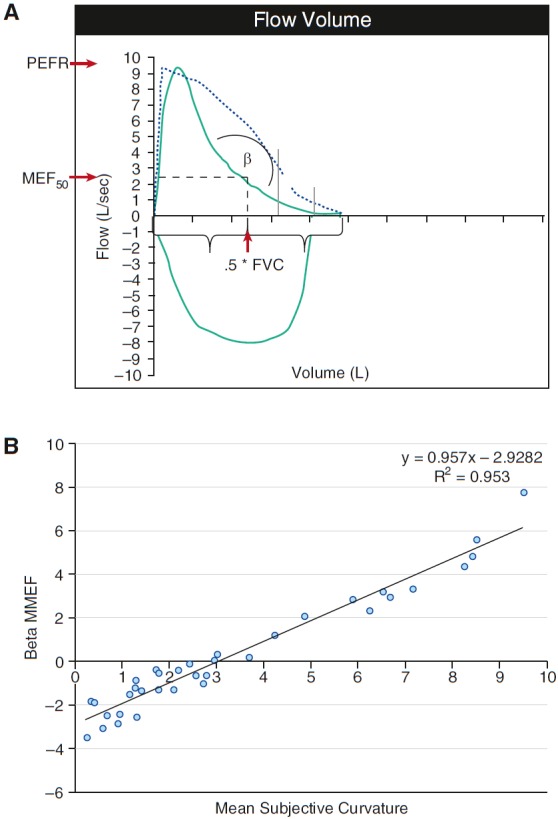
(A) Graphical depiction of the β-angle. The β-angle is calculated as β = 180 − tan^–1[(PEFR − MEF₅₀)/(0.5 × FVC)] + tan^–1[MEF₅₀/(0.5 × FVC)]. Values of β > 180° correspond to a configuration in which the curve is convex, whereas values of β < 180° correspond to a curve that is concave. The vertical dashed line represents the volume corresponding to 0.5 × FVC, and the intersecting horizontal line depicts the flow at this point (MEF₅₀). (B) Association between β-MMEF and mean expert score (MES).

To calculate the second derivative (f′′) of flow (V′) with respect to volume (V), raw flow and volume data (at 200 Hz) were exported from the ComPAS database, using software provided by the manufacturer. The extracted data were restricted to two boundary ranges: (b1) from the volume corresponding to peak flow to 75% of the vital capacity, and (b2) from 30 to 70% of FVC. A sixth-degree polynomial function was fit to the flow data as a function of volume over these two ranges, and the second derivative of this polynomial was calculated, using standard calculus techniques. The average value for the derivative across the specified volume range was then calculated with the two boundaries: ${\overline{f}}_{\text{b}1}^{\text{″}}$ calculated as

$$\frac{1}{0.75\text{FVC}-\text{VolPEFR}}\underset{0.75\text{FVC}}{\overset{\text{VolPEFR}}{{\displaystyle \int }}}{f}^{″}\left(V^{\prime }\right)dV$$

and ${\overline{f}}_{\text{b}2}^{\text{″}}$ calculated as

$$\frac{1}{0.70\text{FVC}-0.30\text{FVC}}\underset{0.30\text{FVC}}{\overset{0.70\text{FVC}}{{\displaystyle \int }}}{f}^{″}\left(V^{\prime }\right)dV$$

Disease Severity

The electronic medical records of the patients whose curves were selected for the study were abstracted for the 12-month period following the index spirometry, and the number of hospitalizations during that period was recorded as a measure of disease severity.

Validation Populations

Children (age, 7–18 yr) with asthma were identified in a separate data set from an unrelated pulmonary function study (n = 120). Values were extracted from these spirometries and used to calculate the curvature indices, and hospitalizations were abstracted from the medical records. In addition, clinical data were abstracted from the Cystic Fibrosis Patient Registry for patients (age, 6–21 yr) seen at our center in the prior year (n = 224); the last available spirometry from 2014 was used to calculate curvature indices, and hospitalizations in 2015 were used as the outcome.

Statistical Analysis

For each curve, the “mean expert score” (MES) was created by averaging the subjective scores for all survey respondents. Variability of the MES was graphically examined using box–whisker plots, and intrasubject reliability for the three duplicated curves was analyzed by modified Bland–Altman analysis (7). The effect of respondent experience (i.e., years in practice) on MES was analyzed by pairwise t tests.

Correlations between the MES and the objective indices were assessed; stepwise logistic regression including all significantly correlated indices and adjusted for patient age and sex was then used to determine which index/indices best approximated the MES. Both adjusted regression and receiver operating characteristic (ROC) analyses were used to examine the association between MES or curvature indices and hospitalizations (8).

Results

Of 107 survey responses, 15 were excluded because 12 or fewer questions were answered (median of 1 question answered) and/or time spent on the survey was less than 120 seconds (median, 50 s). The remaining 92 respondents spent a median 8 minutes (interquartile range, 5.8–10.4) taking the survey, and answered a mean (±SD) of 33.3 ± 6.6 out of 40 possible questions. Eighteen (19.5%) respondents had less than 5 years of experience, 21 (22.8%) had 5–10 years of experience, and 51 (55.4%) had 10 or more years of experience. None of the excluded respondents reported their experience level.

The characteristics of subjects from whom flow–volume curves were obtained are described in Table 1.

Table 1.

Characteristics of study subjects

	Asthma	CF	Other	All
	(n = 11)	(n = 18)	(n = 8)	(N = 37)
Age, yr	16.4 (7.7)	19.9 (10.3)	19.5 (14.3)	18.8 (10.4)
Male sex, %	45	50	50	49
BMI, kg/m2	25.3 (7.1)	22.5 (4.7)	23.9 (4.7)	23.6 (5.5)
FEV1, L	2.9 (0.7)	2.3 (1.0)	2.8 (1.3)	2.6 (1.0)
FVC, L	3.5 (0.9)	3.5 (1.3)	3.6 (1.3)	3.5 (1.2)
FEV1/FVC, %	81.5 (5.5)	67.1 (15.9)	77.4 (16.9)	73.6 (15.1)
FEF25–75%, L/s	2.8 (0.9)	1.8 (1.6)	2.9 (1.8)	2.3 (1.5)
Any hospitalization, %	9.1	33.3	25	24.3

Definition of abbreviations: BMI = body mass index; CF = cystic fibrosis; FEF_25–75% = forced expiratory flow between 25 and 75% of total lung volume.

Shown are the characteristics of patients whose flow–volume curves were used in the study. Shown are percentages for binary variables (sex, hospitalization), and means (standard deviation) for continuous variables.

There was substantial variability in respondent scores for the majority of curves, with wider variability in the middle range and tighter scores in the near-normal and very severe extremes (Figure 1). However, MESs from respondents with different experience levels were very highly correlated with each other (see Table E1 in the online supplement). In addition, Bland–Altman analysis was performed for the respondents who provided a concavity score for the three duplicated pairs of curves (n = 85, n = 89, and n = 68 survey takers responded to both curves for the three pairs).

Figure 1.

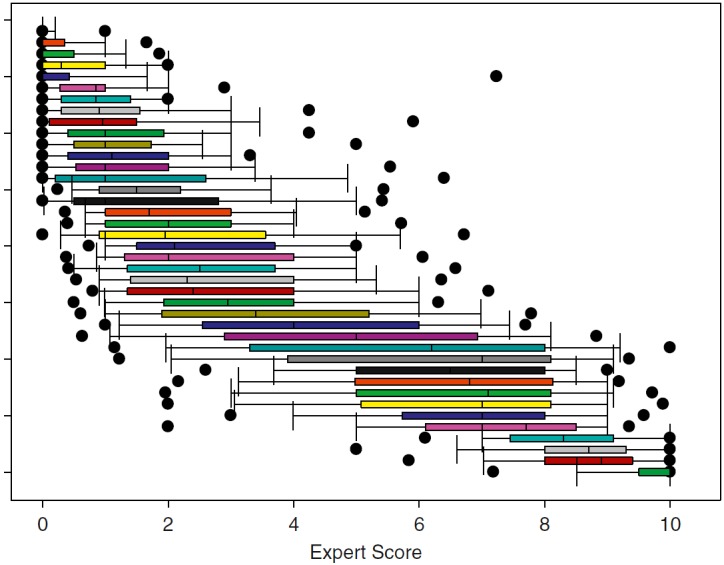
Distribution of expert scores for survey curves. Shown is a box-and-whisker plot of expert scores for the 40 curves presented to survey respondents. Each vertical bar represents the median (50th percentile), the bar edges represent the interquartile range (25th and 75th percentiles), and the whiskers represent 5th and 95th percentiles. Solid dots represent extreme values for responses. Questions were presented in random order; bars are sorted according to mean of the expert responses.

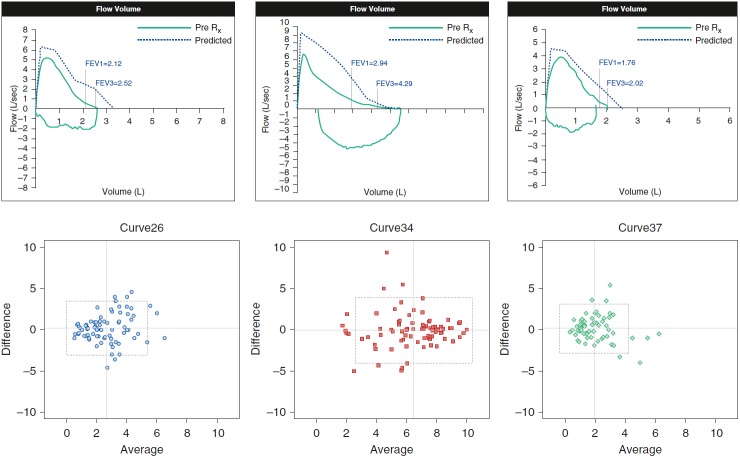
There was good intrasubject agreement in the group of respondents as a whole (Figure 2) and when stratified by experience level (Figure E1). Bias and variance analysis for these curves, using all respondents within an experience level group as replicates, showed no significant differences by experience level (Table 2).

Figure 2.

Duplicated curves and intrarater reliability. Modified Bland–Altman plots show difference versus average of scores for the duplicated loops. Cross-hairs represent means for each measure. Boxes represent means ± 1.96 SD for the difference (horizontal dashed lines) and the average (vertical dashed lines). R_x = prescription.

Table 2.

Intrasubject reliability for maximal expiratory flow–volume curve concavity scores

Curve Set	All Respondents	Experience
		<5 yr	5–10 yr	>10 yr
A	−0.1868 (–0.5508, 0.1773)	−0.2944 (–0.4334, 1.0223)	0.0905 (–0.4842, 0.6651)	−0.1592 (–0.8377, 0.5194)
B	0.0494 (–0.3788, 0.4777)	−0.1333 (–0.753, 1.020)	0.1688 (–0.2227, 0.5602)	−0.4250 (–0.9795, 0.1295)
C	−0.2353 (–0.5941, 0.1236)	−0.333 (–1.203, 0.5367)	−0.4143 (–1.0942, 0.2657)	−0.1286 (–0.6411, 0.384)

Numbers shown represent intrasubject test–retest bias (and 95% confidence interval) for each of three duplicated curve sets, for all respondents and stratified by experience level. Bias was nonsignificant (confidence intervals include 0) for all curves and subgroups.

Despite wide intersubject variability, the MES correlated strongly with the zβ-angle, FEF₅₀/PEFR, FEV₁/FVC, MMEF/FVC, FEF₅₀, and FEF_25–75% and more weakly with k_max, ${\overline{f}}_{\text{b}1}^{\text{′′}}$, and ${\overline{f}}_{\text{b}2}^{\text{′′}}$ (Table 3). FVC and PEFR did not correlate with MES.

Table 3.

Correlations between mean expert score and objective indices

	MES	FEV1	FVC	FEV1/FVC	FEF25–75%	FEF50	kmax	PEFR	zβ Angle	FEF50/PEFR	MMEF/FVC	${\overline{f}}_{\text{b}1}^{\text{′′}}$
FEV1	−0.554	1
FVC		0.818	1
FEV1/FVC	−0.931	0.468		1
FEF25–75%	−0.816	0.817	0.383	0.796	1
FEF50	−0.824	0.826	0.391	0.807	0.994	1
kmax	0.757	−0.668		−0.604	−0.764	−0.778	1
PEFR		0.874	0.769		0.664	0.674		1
zβ Angle	−0.959	0.470		0.923	0.728	0.750	−0.724		1
FEF50/PEFR	−0.938	0.420		0.911	0.765	0.776	−0.692		0.944	1
MMEF/FVC	−0.887	0.413		0.944	0.825	0.821	−0.572		0.856	0.928	1
${\overline{f}}_{\text{b}1}^{\text{′′}}$	0.594	−0.541	−0.399	−0.522	−0.462	−0.481	0.787	−0.313	−0.676	−0.549	−0.429	1
${\overline{f}}_{\text{b}2}^{\text{′′}}$	0.580	−0.332		−0.530	−0.546	−0.536	0.438		−0.573	−0.667	−0.658	0.416

Definition of abbreviations: FEF_25–75% = forced expiratory flow between 25 and 75% of total lung volume; FEF₅₀ =  forced expiratory flow at 50% of total lung volume; MES = mean expert score; MMEF = maximum mid-expiratory flow; PEFR = peak expiratory flow rate; for other abbreviations, see text.

Shown are Pearson correlation coefficients (r) for significant (P < 0.05) correlations. Correlations range from r = 1.0 to r = –1.0.

Stepwise regression analysis adjusted for patient age and sex yielded a model that included zβ-angle, FEF₅₀, and FEF_25–75% (adjusted R² = 0.97). A simplified model that included only zβ-angle and FEF_25–75% performed similarly (adjusted R² = 0.95) and accurately predicted the mean expert score (β-coefficient = 0.9999, 95% confidence interval [CI] = 0.92–1.08, P < 0.001, adjusted R² = 0.96). On the basis of the regression model coefficients, a composite variable “β-MMEF” was constructed: β-MMEF = –0.5497 × (zβ-angle) − 0.4957 × (FEF_25–75%); regression analysis confirmed that β-MMEF tightly approximated the MES (see Figure 3B).

Logistic regression was then used to explore the association between the MES or β-MMEF and the risk of hospitalization in the year subsequent to the spirometry (Table 4). Each one-point increase in MES was associated with a 2.13-fold increase in the odds of hospitalization (95% CI = 1.25–3.60, P = 0.005). Similarly, each one-point increase in β-MMEF was associated with a 2.32-fold increase in the odds of hospitalization (95% CI = 1.27–4.23, P = 0.006). For the MES, the area under the curve (AUC) was 0.91, the positive predictive value (PPV) was 71.4%, the negative predictive value (NPV) was 86.7%, and 83.8% of subjects were correctly classified as hospitalized versus not; almost identical results were obtained for β-MMEF (Table 4). ROC curves for MES and β-MMEF versus hospitalizations are shown in the online supplement (Figure E2).

Table 4.

Association between mean expert score, β-MMEF, and hospitalizations

	MES	β-MMEF
Odds ratio for hospitalization (95% CI)	2.13 (1.26–3.60)	2.32 (1.28–4.23)
P value	0.005	0.006
Pseudo R2	0.42	0.44
Log likelihood	−11.8	−11.5
Bayesian information criterion	38.1	37.4
Area under curve	0.91	0.90
Sensitivity	55.6%	55.6%
Specificity	92.9%	92.9%
Positive predictive value	71.4%	71.4%
Negative predictive value	86.7%	86.7%
Correctly classified	83.8%	83.8%

Definition of abbreviations: CI = confidence interval; MES = mean expert score; for other abbreviations, see text.

Shown are receiver operator curve analysis and regression analysis (adjusted for age and sex) of the relationship between the MES or β-MMEF and hospitalizations.

Using ROC analysis and predicted probabilities, we estimated cutoff points for β-MMEF (<0.4 vs. ≥0.4). Only 8% of patients with low β-MMEF were hospitalized, compared with 54% of those with high β-MMEF; the AUC was 0.87, and the PPV, NPV, and classification rates were identical to the MES and the continuous β-MMEF.

Finally, the association between β-MMEF and clinical outcomes was analyzed after separating the population of curves based on diagnoses. For CF (n = 18), there was an odds ratio for hospitalization of 1.9 (P = 0.07); asthma (n = 11) had an odds ratio of 1.8 (P = 0.66); and all others (n = 8) had an odds ratio of 2.6 (P = 0.47). However, the original survey was not designed with sufficient sample size for this analysis; thus we sought independent populations for external validation and assessment of specific diagnoses (asthma and CF).

In the secondary asthma data set (n = 120), the odds ratios (for each one-point increase in β-MMEF) were 2.74 for hospitalizations (95% CI = 1.34–5.59, P = 0.006), 2.04 for emergency department visits (95% CI = 1.24–3.37, P = 0.005), and 1.55 for prednisone use (95% CI = 1.04–2.31, P = 0.031). In the secondary cystic fibrosis data set (n = 224), the odds ratio for hospitalizations was 1.21 (95% CI = 1.03–1.43, P = 0.025).

Discussion

Our study has three main findings. First, despite wide variability in intersubject assessment, there is good intrasubject reproducibility in expert assessment of MEFVC configuration, regardless of years of experience. Second, the mean expert score from 92 pulmonologists was significantly associated with risk of subsequent hospitalization, as a measure of disease severity. Third, we present an objective index, β-MMEF, that can be automatically calculated, accurately matched the mean expert score, and was also significantly associated with the risk of hospitalization; as such, this index may be useful in future clinical trials or for patient management.

This is the first study to obtain MEFVC concavity assessment by a large number of pulmonary specialists (our sample size was approximately 7.5% of the total number of board-certified pediatric pulmonologists [9]). Although there was substantial variability in scores for a given loop, there were no significant differences by experience level, and there was good intrasubject reliability. Some of the intersubject variability may be due to inconsistent use of flow–volume curve data by the pulmonologists; that is, evaluating the whole curve from PEFR, or only sections after an inflection point. Similarly, the calculation of ${\overline{f}}^{\text{'}\text{'}}$ to determine average concavity of the MEFVC is clearly impacted by the boundaries for integration. In addition, the other indices may reflect curvature at different portions of the curve, as some include PEFR (reflecting the configuration at higher lung volume) whereas others include MMEF (which may instead reflect the middle portion of the curve). This may explain some of the discrepancy between the different measurements and the expert assessments.

More importantly, our study demonstrates a significant relationship between the MES and the risk of hospitalization in the population as a whole in the year following the spirometry. Although a decrease in lung function often justifies hospitalization for patients with CF (10), it would be an uncommon reason for hospitalization of patients with asthma (11). However, MEFVC concavity represents airway obstruction (12), which serves as a proxy for asthma disease severity or lack of control and may thus identify patients at risk for severe exacerbations (13). When the population was analyzed after stratification by diagnosis, the results were not statistically significant; this issue is attributable to the fact that the data set was not constructed with consideration regarding distribution of diagnoses, leading to low numbers of subjects in each individual diagnostic group. However, β-MMEF was associated with increased risk of hospitalization in two larger, independent populations of children with asthma and with cystic fibrosis; this serves as external validation of the β-MMEF index, as well as verification that it works well independent of underlying diagnosis.

Previous studies have attempted to quantify the degree of MEFVC concavity. In an analysis of flow–volume curves from 5,140 participants (50% pediatric) selected from three communities (4), Kapp and colleagues defined the β-angle by joining the residual volume point of the MEFVC to the flow point at mid-volume, and then joining the flow point at mid-volume to peak flow. A β-angle less than 180° indicates a concave curve. The β-angle decreased with age, had lower day-to-day variability than other indices, and was lower in men, cigarette smokers, and patients with lung disease including asthma and chronic bronchitis. Nève and colleagues analyzed the β-angle in 132 healthy preschool children and 171 preschoolers with wheezing from northern France (14). In this population, too, children with wheezing had reduced β-angle and MEF₅₀/PEFR.

Other curvilinearity indices include k_max, which uses a hyperbolic function of flow, volume, and flow × volume, with coefficients determined from the descending phase of the curve (5). Zheng and colleagues (5) determined k_max for 67 adult patients with a broad range of lung function, but they did not describe an association between k_max and symptoms. In our sample, however, k_max did not correlate well with MES. Wildhaber and colleagues (15) recruited 48 pediatric patients with asthma to perform spirometry, and their MEFVCs were semiquantitatively assessed by three pediatric pulmonologists for concavity without access to the spirometric indices. The investigators also computed an average curvature index, using a quadratic function fit to the MEFVC, and applied this to determine the first and second derivatives of flow. As in our study, subjective impressions among the three pulmonologists varied broadly. The average curvature index correlated better with symptom scores than with FEV₁ and FEF_25–75%, although correlation was still only low to moderate (r = 0.53).

Using stepwise regression on all indices that strongly correlated with the mean expert score, we were able to calculate a composite index based on the zβ-angle and FEF_25–75%. This calculated variable, β-MMEF, closely approximated the mean expert score for all respondents, had high PPV and NPV, and correctly classified patients into hospitalization (or not) a majority of the time. Moreover, after selecting a cutoff point, only 8% of patients with “low β-MMEF” were hospitalized, compared with 54% of those with “high β-MMEF.” This variable could be easily incorporated into spirometric software, and be used for future studies or for patient management, particularly in settings where it may be difficult to obtain an official interpretation by a pulmonary specialist.

Limitations

There are several limitations to our study. The selected curves lacked confounding influences (cough, glottis closure, circuit noise, etc.) that negatively impact the quality of spirometry. How the calculated indices will perform on curves that do not meet ATS criteria remains to be elucidated in future studies.

The respondents could see only one curve at a time, and therefore may not have anticipated the spectrum of concavity that would be presented. As such, their use of the concavity scale may have changed as they evaluated various curves during the survey; however, by design the survey presented all curves in random order to each participant, and thus should have prevented differential bias in the group as a whole. In addition, survey curves were selected without regard for the underlying diagnosis of the patient; it seems logical that MEFVC concavity would represent airway obstruction regardless of the disease process.

Given our original sample size we were unable to adequately analyze clinical outcomes specific to each disease; nonetheless, we propose that hospitalization is a severe outcome regardless of diagnosis. Validation analyses using independent data sets of children with asthma or cystic fibrosis appear to confirm our findings from the original cohort. We could evaluate only hospitalizations that were documented in the patients’ medical records at our institution. The average of all expert scores was associated with the clinical outcome, but there was marked variation in the individual scores assigned by each respondent; the β-MMEF approximates the “consensus” score and likely mitigates this variability, but prospective studies should attempt validation in independent cohorts and different settings. As Mead noted nearly 40 years ago (with respect to slope ratios), “a final answer to this question will require better measurements on better selected patients”; additional studies with larger populations and a wider range of curve configurations (including those that do not meet ATS criteria) will be required before recommending clinical adoption of the β-MMEF.

Conclusions

Indices such as the β-MMEF are straightforward to compute and correlate with the average expert impression of flow–volume curve configuration. In addition, there was a relationship between the average expert impression of MEFVC configuration and some clinical markers of disease severity, and the β-MMEF performed almost identically to the expert impression. This index could potentially be used by pulmonary function software to assist in the automated interpretation of spirometry. As such, it deserves further exploration as a potential biomarker for disease severity and morbidity in asthma and cystic fibrosis.