A TWO-PART MIXED EFFECTS MODEL FOR CIGARETTE PURCHASE TASK DATA

Abstract

The Cigarette Purchase Task is a behavioral economic assessment tool designed to measure the relative reinforcing efficacy of cigarette smoking across different prices. An exponential demand equation has become a standard model for analyzing purchase task data, but its utility is compromised by its inability to accommodate values of zero consumption. We propose a two-part mixed effects model that keeps the same exponential demand equation for modeling nonzero consumption values, while providing a logistic regression for the binary outcome of zero versus nonzero consumption. Therefore, the proposed model can accommodate zero consumption values and retain the features of the exponential demand equation at the same time. As a byproduct, the logistic regression component of the proposed model provides a new demand index, the “derived breakpoint”, for the price above which a subject is more likely to be abstinent than to be smoking. We apply the proposed model to data collected at baseline from college students (N = 1,217) enrolled in a randomized clinical trial utilizing financial incentives to motivate tobacco cessation. Monte Carlo simulations showed that the proposed model provides better fits than an existing model. We note that the proposed methodology is applicable to other purchase task data, for example, drugs of abuse.

Relative reinforcing efficacy is a central concept in behavioral economic research. The Cigarette Purchase Task is a self-report survey used to measure hypothetical cigarette consumption at escalating prices and has been proven to be a useful tool for quantifying the relative reinforcing efficacy of smoking (Jacobs & Bickel, 1999). The indices of relative reinforcing efficacy estimated from the cigarette purchase task data have been shown to relate to smoking behavior and be predictive of outcomes of smoking cessation interventions (MacKillop et al., 2016; MacKillop et al., 2008; Murphy, MacKillop, Tidey, Brazil, & Colby, 2011; Secades-Villa, Pericot-Valverde, & Weidberg, 2016).

A brief introduction of the cigarette purchase task data and the associated reinforcing efficacy indices is as follows. Based on Jacobs and Bickel’s original model (1999), survey completers are asked to give their hypothetical daily cigarette consumption under 19 different unit prices: 0¢, 1¢, 5¢, 13¢, 25¢, 50¢, $1, $2, $3, $4, $5, $6, $11, $35, $70, $140, $280, $560, and $1,120 (“How many cigarettes would you smoke per day if they were 0¢, 1¢, …, per cigarette?”). Data from the cigarette purchase task can be used to create a demand curve and five indices of relative reinforcing efficacy can be determined: (a) breakpoint (i.e., the first price at which consumption is zero); (b) intensity (i.e., consumption at the zero price); (c) Omax (i.e., maximum expenditure); (d) Pmax (i.e., price at which maximum expenditure is reached); and (e) elasticity of demand (i.e., sensitivity of consumption to increased price). Elasticity of demand is defined as the partial derivative of the log-demand with respect to log-price (i.e., elasticity (p) = ∂ log Q/ ∂ log p, where Q denotes the amount of consumption under unit price p). Note that all the above demand indices except for elasticity can be empirically estimated from the cigarette purchase task data without any assumptions on the form of the demand curve. However, we should note that a survey conducted at a different price grid (e.g., a fine vs. a coarse grid) could result in the empirical estimates of breakpoint, Omax, and Pmax with different precision. Moreover, these demand indices can be nonestimable if they are not achieved at the highest price given in the survey, in which case we refer to these estimates as “right-censored”.

In behavioral economics, a demand equation (Hursh, 1980; Hursh, Raslear, Shurtleff, Bauman, & Simmons, 1988; Hursh & Silberberg, 2008) refers to the mathematical expression of the relationship between the amount of commodities demanded (i.e., consumption) and the factors affecting the ability and willingness of a consumer to buy the commodity (e.g., price). Hursh and Silberberg (2008) introduced an exponential demand curve model that has been frequently used for cigarette purchase task data (e.g., Murphy et al., 2011) and other purchase task data (e.g., Aston, Metrik, & MacKillop, 2015). The exponential demand curve takes the form:

$$\text{log }Q=\text{log }{Q}_0+k({\mathrm{e}}^{-\alpha p}-1),$$ (1)

where Q₀ is the model-based or derived intensity, k is the range of consumption in the log scale, and α and k jointly determine the elasticity of demand at price p by elasticity (p) = − k α p e^−αp. Hence, the derived Pmax can be obtained by solving the equation, k α p e^−αp − 1 = 0, and the derived Omax can be obtained by Omax = Pmax · Q₀ · exp{k (e^{−α Pmax} − 1)}.

In application, researchers who analyze purchase task data fit either an individual regression model for each subject (e.g., MacKillop et al., 2008) or a mixed effects model for the aggregated data of all subjects (e.g., Collins, Vincent, Yu, Liu, & Epstein, 2014; Yu, Liu, Collins, Vincent, & Epstein, 2014). In the individual regression approach, each subject has one fitted curve and one set of estimated parameters, giving rise to an overparameterized model. In the mixed-model approach only one curve and one set of parameters (i.e., population-average parameters) are estimated for the whole population, and each subject’s parameters (i.e., subject-specific parameters) are assumed to deviate from the population-average parameters by a random error which can be estimated by the empirical Bayes method (Laird and Ware, 1982). However, when the exponential demand curve is assumed, zero consumption values cannot be directly used in the regression because the log of zero is negative infinity.

A simple and frequently used strategy is to impute an arbitrary, small positive value, such as 0.001, for zero consumption (e.g., Murphy et al., 2011). There have been debates on whether (1) all zero consumption values should be imputed and used in the regression, or (2) only the first zero consumption should be imputed with all subsequent zeros being excluded from the regression, or (3) a small positive value should be added to all consumption values. All these ad hoc approaches present problems for the analysis and interpretation of data (e.g., Liao et al., 2013; Yu et al., 2014).

Recently, Liao et al. (2013) proposed a left-censored mixed effects model to avoid arbitrarily imputing values for zero responses. This model assumes that the true demand associated with a zero response is a positive value subject to a detection limit below which the true demand cannot be observed. This model introduces no additional parameters than those already in the demand curve except for an assumed known detection limit.

While the left-censored model by Liao et al. (2013) provides a convenient way to apply the exponential demand curve to cigarette purchase task data with zero responses, this method and the aforementioned ad hoc imputation methods overlook the fact that cigarette purchase task data may reflect respondents’ two distinct tobacco use statuses under different prices, the smoking status (consumption > 0) and the abstinence status (consumption = 0). In statistical literature, we refer to such data as “semicontinuous” data, meaning that the data follow a continuous distribution for the positive values and have a discrete probability mass for zero. In semicontinuous data, the zero values represent true responses rather than the censored responses in left-censored data. With semicontinuous cigarette purchase task data, positive responses and zero responses can be modeled separately.

When semicontinuous data are independent (e.g., each subject provides only one response), various statistical methods have been proposed (see review in Min & Agresti, 2002). For repeated measures of semicontinuous data, such as the cigarette purchase task data in which each respondent estimates the demand at multiple prices, Olsen and Schafer (2001) proposed a two-part mixed effects model. The first part of this model utilizes logistic regression with random effects to model the binary outcome of zero versus positive values and the second part utilizes linear mixed regression to model the positive values only. The two parts are then linked by imposing a correlation structure on the random effects.

We propose a new two-part mixed effects model that incorporates the nonlinear form of the exponential demand curve for positive consumption values while providing a logistic regression model to estimate the probability of abstinence. As a byproduct of the logistic regression, a new demand index, the so-called “derived breakpoint”, is proposed for the price level above which a subject is more likely to be abstinent than smoking. We apply the proposed two-part mixed effects model to the analysis of cigarette purchase task data collected at baseline from college students enrolled in a randomized clinical trial utilizing financial incentives to motivate tobacco cessation. Monte Carlo simulations are conducted to demonstrate the performance of the proposed model.

Method

Study Population and Procedures

The cigarette purchase task data were collected at baseline from subjects enrolled in a randomized trial evaluating the impact of financial incentives on tobacco abstinence outcomes. The “Enhanced Quit and Win Contests to Improve Smoking Cessation among College Students” (hereafter abbreviated as “Enhanced Quit & Win”) study compared multiple versus single contests and counseling versus no counseling on tobacco abstinence. A total 1,217 college smokers were recruited from 19 two- or four-year universities and colleges in the midwest between 2010 and 2013 using three annual waves of recruitment. The details of the study population and procedures have been reported elsewhere (Thomas et al., 2016).

In the trial, the cigarette purchase task survey was designed using the original form by Jacobs and Bickel (1999), but was delivered electronically. Only one question was prompted on the screen at a time and questions were presented in the order of increasing prices. Respondents were presented with continued questions until they gave a zero response. Therefore, based on our survey administration strategy, each respondent’s data could have more or fewer responses depending on where the first zero response occurred. Following Liao et al. (2013), we restrict our analysis to data at prices less than or equal to $11 as there is evidence showing that higher prices are associated with the lower reliability (Murphy, MacKillop, Skidmore, & Pederson, 2009).

Statistical Methods

We propose a two-part mixed effects model for modeling the probability of cessation and the number of cigarettes hypothetically smoked under different prices simultaneously. First we define some notations. Let Q_ij denote the demand of respondent i at price p_j, let δ_ij denote the binary outcome of having a zero response or not (= 1 if Q_ij = 0; and = 0 if Q_ij > 0), and let π_ij = Pr(δ_ij = 1) denote the probability of abstinence. The two-part mixed effects model assumes:

• Part I Model: The binary outcome of having a zero response (i.e., cessation) follows a mixed-effects logistic regression model,

  $$\text{logit }({\pi }_{ij})={\beta }_0+{\beta }_{1}f(p_j)+a_i,$$

  where f (․) is a proper function of price such as the shifted log transformation, log (p_j + 0.001), and a_i is the random intercept;
• Part II Model: The positive response (Q_ij > 0) follows a nonlinear mixed effects model,

  $$\text{log }{Q}_{ij}={\mu }_{ij}\text{+}{\epsilon }_{ij}=(\text{log}{Q}_{\mathit{0}}+b_i)+k({\mathrm{e}}^{-(\alpha +ci)p_j}-1)+{\epsilon }_{ij},$$

  where μ_ij is the expected log-demand, b_i is the random intercept, c_i is the random slope for the price variable, ε_ij is the error term following a normal distribution with mean 0 and variance σ_e². We assume that the three random effects, (a_i, b_i, c_i) follow a multivariate normal distribution with zero means and an unstructured variance-covariance matrix $\left[\begin{array}{lll}{\sigma }_a^2\hfill & {\sigma }_{ab}\hfill & {\sigma }_{ac}\hfill \\ {\sigma }_{ab}\hfill & {\sigma }_b^2\hfill & {\sigma }_{bc}\hfill \\ {\sigma }_{ac}\hfill & {\sigma }_{bc}\hfill & {\sigma }_c^2\hfill \end{array}\right]$. The fixed-effect parameters, log Q₀ and α, are similar to those in the individual exponential demand curve in Equation (1) but have a population-average effect interpretation here. Their corresponding subject-specific effects are (log Q₀ + b_i) and (α + c_i), which are referred to as subject-specific log-intensity and subject-specific α, respectively. The range parameter k is fixed for all subjects.

As a byproduct of the logistic regression component, we can derive the price, above which a subject is more likely to be abstinent than smoking (i.e., the price associated with π_ij = 0.5):

$${p_{ij}|}_{(\pi ij=0.5)}=f^{-1}\{-({\beta }_0+a_i)/{\beta }_1\},$$

where f⁻¹(·) is the inverse function of f (·). When f (p_ij) = log (p_ij + 0.001), we have p_ij|_{(πij = 0.5)} = exp{− (β₀ + a_i)/β₁} − 0.001. The population-average derived breakpoint is p|_{(π = 0.5)} = f⁻¹(−β₀/β₁).

The likelihood function for the two-part mixed effects model and detailed estimation procedure can be found in Appendix A. The maximization of the likelihood was carried out with the NLMIXED procedure in SAS 9.4 (SAS Institute Inc., Cary, NC). The SAS code for analyzing the data is provided in Appendix B. Because there is no existing method for testing the functional form of a covariate in a mixed-effects logistic regression setting, we used the generalized estimating equations (GEE)-based model diagnosis method proposed by Lin, Wei, and Ying (2002) to determine the functional form for price in the logistic regression by using the SAS GENMOD procedure with the ASSESS statement. A p-value > .05 from this diagnostic test was considered as an adequate model fit. Furthermore, we note that the proposed model includes three random effect terms (a_i, b_i, and c_i) to account for heterogeneity in respondents. A simplified model with two random effects (a_i and b_i) was carried out and the likelihood ratio test (Pinheiro & Bates, 2000) was performed to assess whether adding a random slope c_i to the two-part model would significantly improve the model fit to our data.

To validate the parameter estimates from the proposed model, we calculated the association of the derived demand indices with their empirical counterparts. We also investigated their association with smoking-related variables such as cigarettes smoked per day (CPD) and the first item of the Fagerström Test for Nicotine Dependence (FTND), which was dichotomized to a high nicotine dependence group (smoke first cigarette within 30 min of waking) and a low nicotine dependence group (30 + min after waking; Heatherton, Kozlowski, Frecker, & Fagerström, 1991). Correlations involving one or two right-censored continuous variables (Omax, Pmax, and empirical breakpoint) were estimated based on general Kendall’s τ (Newson, 2006) using STATA 13 (StataCorp., 2013). Pearson’s correlations were calculated for noncensored continuous variables (intensity, α, derived breakpoint, and CPD). The associations of nicotine dependence with noncensored and censored demand indices were based on t-tests and log-rank tests, respectively.

We also investigated whether the derived demand indices from the proposed model predicted urine-verified abstinence and/or reduction in cigarettes smoked per day among those who failed to quit at 6 months postrandomization. Smoking reduction was defined as the percent change in CPD on smoking days relative to the baseline level. Analyses of the abstinence outcome followed the intent-to-treat principle that retained all randomized participants and assumed any participants with missing self-report abstinence status or missing urine samples were nonabstinent (see Thomas et al., 2016). Each demand index was fitted in a separate regression (logistic or linear) model, adjusting for the two intervention conditions (multiple vs. single contests and counseling vs. no counseling).

Simulations

A series of Monte Carlo simulation studies were performed in SAS to assess the performance of the proposed model. One thousand datasets were simulated with N = 1,000 subjects in each dataset from the two-part mixed effects model. Specifically, in the logistic regression component, price was transformed by log (p + 0.001) and a random intercept (a_i) was assumed. In the nonlinear mixed effects regression component, a random intercept (b_i) was assumed. The variance of the two random effects was a 2×2 matrix indexed by σ_a², σ_b², and σ_ab. For each respondent daily cigarette consumption was simulated with increasing unit price until a zero response was generated or the highest unit price ($11) was reached, whichever occurred first. Relative bias (i.e., the difference between the estimated value and the true value divided by the true value) and standard error (SE) were calculated for each parameter and simulated dataset. Average bias and average SE over 1,000 datasets were calculated and presented together with the coverage rate (i.e., the percentage of the one thousand 95% confidence intervals [CI] covering the true parameter value) and the Monte Carlo standard deviation (SD). The true parameter values chosen for the simulation studies were close to those estimated from the Enhanced Quit & Win study. The proposed model and the left-censored model (Liao et al., 2013) were compared using the simulated data.

Results

Enhanced Quit & Win Study Participants

Overall, 1,217 biochemically verified smokers were enrolled into the randomized clinical trial. Three participants were excluded from our analysis; one participant did not have any baseline cigarette purchase task data and two participants responded zero when cigarettes were free (i.e., intensity = 0), which was considered an invalid response. Other unexpected patterns of the data, such as fluctuations in consumption with increasing price, were allowed and considered as measurement errors. A descriptive summary of the remaining 1,214 subjects is presented in Table 1.

Table 1.

Baseline demographic and tobacco-related variables for participants in the Enhanced Quit & Win Study

Variable	Total
N	1214
Age (years, mean ± SD)	26.2 ± 7.7
Sex (n, % female)	666 (54.9%)
Ethnicity (n, % White)	1093 (90.0%)
2- or 4- year school (n, %)
2-year school	392 (32.3%)
4-year school	822 (67.7%)
Year in school (n, %)
Nondegree seeking	20 (1.6%)
Undergraduate year 1	210 (17.3%)
Undergraduate year 2	275 (22.6%)
Undergraduate year 3	296 (24.4%)
Undergraduate year 4+	263 (21.7%)
Graduate/professional degree program	150 (12.4%)
Working status (n, % full time)	211 (17.4%)
Days smoked last 30 days (mean ± SD)	28.5 ± 3.8
CPD on smoking days (mean ± SD)	11.5 ± 8.1
≥10 CPD	687 (56.6%)
<10 CPD	527 (43.4%)
How soon after waking smoke first cigarette (n, %)
0–5 min	135 (11.1%)
6–30 min	462 (38.1%)
31–60 min	293 (24.1%)
61+ min	324 (26.7%)
CPT empirical demand indices
Intensity (mean ± SD)	14.9±9.0
aBreakpoint ($, median [IQR])	4.0 [2.0, 6.0]
aOmax ($, median [IQR])	6.0 [3.5,10.0]
aPmax ($, median [IQR])	1.0 [0.5, 3.0]

Note: SD: standard deviation; CPD: cigarettes per day; CPT: cigarette purchase task; IQR: interquartile range (25^th, 75^th percentile).

^aRight-censored

Analysis of the Enhanced Quit & Win Data

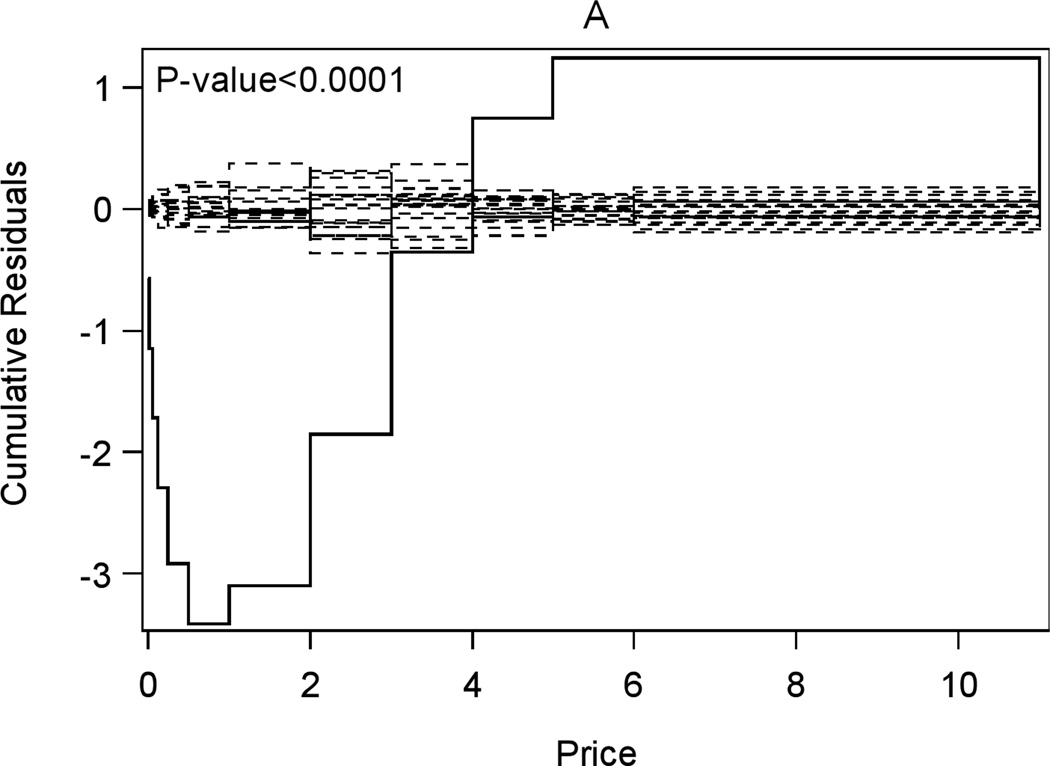
Before applying the proposed two-part mixed effects model, we first attempted a logistic regression on the dichotomous data with the raw/untransformed price variable (i.e., f (p) = p). The model diagnostic test was highly significant (p-value < .001) indicating that the model with untransformed price did not provide an adequate fit to the data. We compared the shape of the cumulative residual plot in Figure 1A with the theoretical residual plot when the true data followed a model with the covariate log (x) but were fitted with a misspecified model with the covariate x (Lin et al., 2002, Fig. 2a). The resemblance of the two residual plots suggested that a log transformation would be a sensible choice for the price variable in the logistic regression.

Fig. 1.

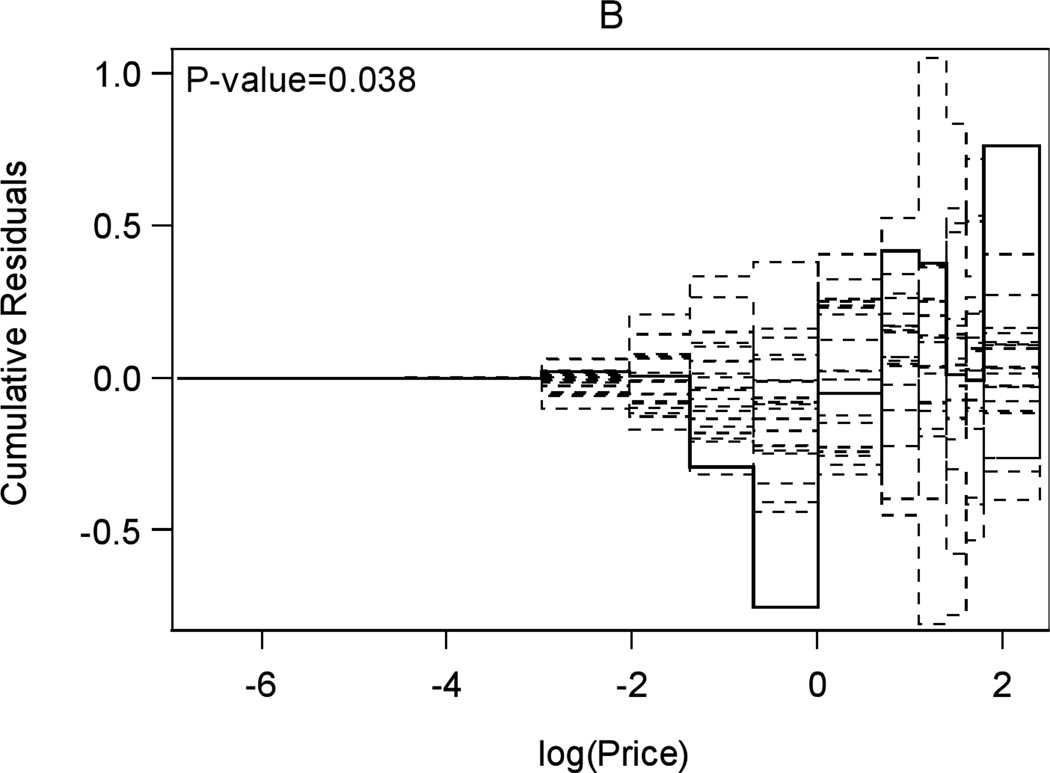
Checking functional form of the price variable in the logistic regression component of the two-part mixed effects model for the Enhanced Quit & Win data. Panel A: cumulative residuals of the model fitted with untransformed price, p (solid line is for the observed data, dashed lines are 20 random samples of 10,000 simulated datasets based on the tested functional form); Panel B: cumulative residuals of the model fitted with transformed price, log (p + 0.001).

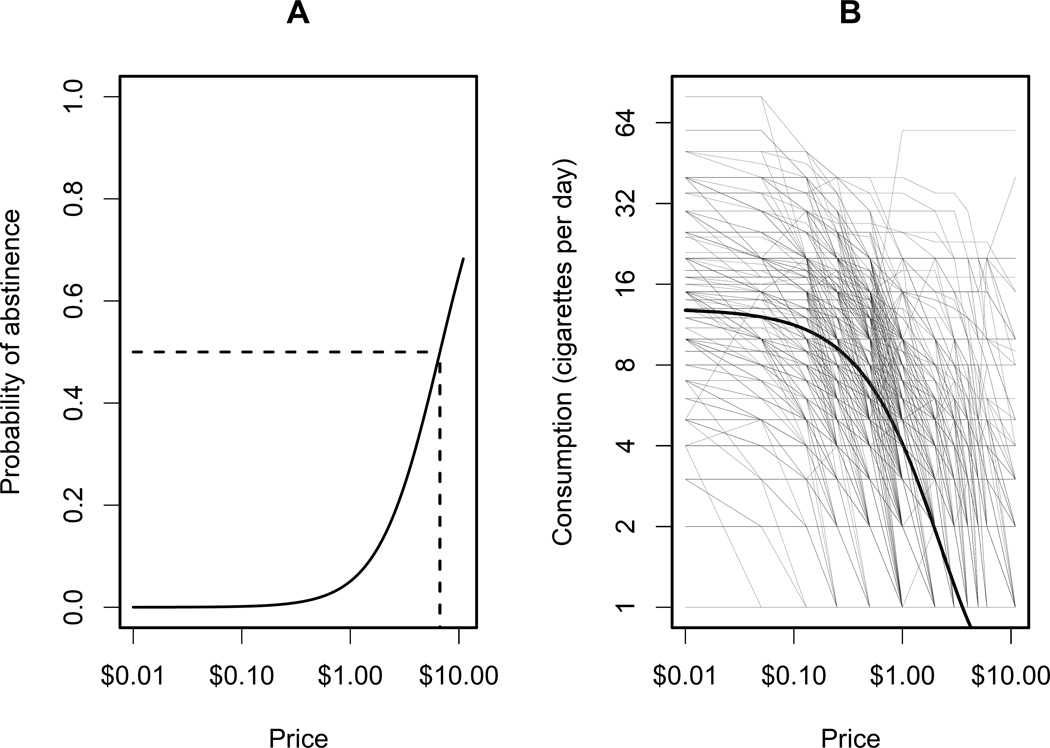
Fig. 2.

Illustration of the two-part mixed effects model using the population-average parameters estimated from the Enhanced Quit & Win data. Panel A: the probability of abstinence curve (π) based on the logistic regression of the two-part model, where the intersection of the dashed line and the curve indicates the derived breakpoint; Panel B: the consumption curve (Q) based on the nonlinear regression of the two-part model, where the gray lines represent the raw individual demand data.

We then attempted a shifted log transformation on price, f (p) = log (p + 0.001), which yielded an improved model fit with a larger p-value (=.038, shown in Fig. 1B). Although the p-value was still below the selected cut-off, .05, we suspected that the small p-value was caused by the large sample size. Hence, we randomly selected smaller samples (N = 200, 400, 600, 800, or 1,000) from the original 1,214 subjects and performed the model diagnosis test based on these smaller samples repeatedly for 5,000 times. The average test p-values were .335, .249, .168, .108, .065, and .040, respectively, for the sample sizes ranging from 200 to 1,000, which confirmed that the significance of the model diagnosis test was caused by the large sample size and the shifted log transformation in the logistic regression provided an adequate fit to the data.

We attempted a two-part mixed effects models with three random effects (a_i, b_i, and c_i) versus two random effects (a_i and b_i). The likelihood ratio test was highly significant (p-value < .001 based on both χ₂² test and χ₃² test), suggesting that the model with three random effects had a better model fit. Hence, the two-part mixed effects model with three random effects was chosen as the final model.

The estimated population-average effects are presented in Table 2. An illustration of the two-part mixed effects model using the estimated population-average parameters is presented in Figure 2. The estimated average derived intensity for the population was 13.0 cigarettes per day (Q₀ = e^2.563, 95% CI: 12.5, 13.4), which was close to the mean empirical intensity (= 14.9). The estimated population-average derived breakpoint was $6.69 (p|_{(π = 0.5)} = e^2.929/1.541 − 0.001), which was illustrated in the left panel of Figure 2. As shown in the right panel of Figure 2, the estimated population-average demand curve well represented the raw individual demand data of the population. These results indicate that the proposed model fitted the data reasonably well.

Table 2.

Parameter estimation results based on the two-part mixed effects model for the Enhanced Quit & Win data

Parameter	Estimates	SE	p-value
Part I model parameters
β0	−2.929	0.079	<.0001
β1	1.541	0.062	<.0001
Part II model parameters
logQ0	2.563	0.018	<.0001
k	3.210	0.020	<.0001
α	0.448	0.011	<.0001
Variance parameters
σa2	1.459	0.175	<.0001
σb2	0.381	0.016	<.0001
σc2	0.094	0.005	<.0001
σab	−0.234	0.034	<.0001
σac	0.308	0.023	<.0001
σbc	0.047	0.006	<.0001
σe2	0.058	0.001	<.0001

Note. SE: standard error.

The top panel of Table 3 illustrates the correlations among the empirical and derived demand indices based on the proposed two-part mixed effects model, and their association with number of cigarettes smoked per day. The bottom panel of Table 3 shows the test statistics when comparing the two nicotine dependence groups (high vs. low) in terms of different demand indices. All derived indices from the proposed model were significantly correlated with their empirical counterparts (all p-values < .001). The new demand index or “derived breakpoint” was significantly correlated with all other derived and empirical indices (all p-values < .001) with the strongest correlation being observed with Omax (correlation = 0.74 and 0.82 with the empirical and derived Omax values, respectively).

Table 3.

Associations among empirical demand indices, derived demand indices based on the two-part mixed effects model, and smoking variables.

	Correlations
Demand indices	Intensity		Omax		Pmax		Breakpoint		α	CPD
	Empirical	Derived	Empirical	Derived	Empirical	Derived	Empirical	Derived
Empirical intensity	—	0.92***	0.31***	0.30***	−0.03	−0.12***	0.09***	0.33***	0.24***	0.61***
Derived intensity		—	0.30***	0.30***	−0.07***	−0.13***	0.06**	0.34***	0.24***	0.62***
Empirical Omax			—	0.82***	0.48***	0.37***	0.51***	0.74***	−0.49***	0.35***
Derived Omax				—	0.41***	0.41***	0.44***	0.82***	−0.53***	0.38***
Empirical Pmax					—	0.41***	0.59***	0.44***	−0.52***	0.01
Derived Pmax						—	0.30***	0.53***	−0.80***	0.02
Breakpoint (empirical)							—	0.45***	−0.40***	0.10***
Breakpoint (derived)								—	−0.71***	0.40***
α (derived)									—	−0.03
CPD										—
	Comparing two nicotine dependence groups (high vs. low) in terms of demand indices
	Intensity		Omax		Pmax		Breakpoint		α
	Empirical	Derived	Empirical	Derived	Empirical	Derived	Empirical	Derived
aT-test or log- rank test statistics	15.1***	16.4***	90.2***	90.8***	8.1**	2.8	30.3***	10.8***	0.7

Note: CPD = cigarettes per day.

^*p < .05,

^**p < .01,

^***p < .001

^aT-test was used for intensity and derived breakpoint, and log-rank test was used for Omax, Pmax, and empirical breakpoint.

Compared with the empirical indices, the derived indices from the proposed model showed consistently stronger correlations with CPD and nicotine dependence, except that the association of nicotine dependence with the derived Pmax was lower than that with the empirical Pmax. These findings suggest that using derived indices might improve the power of detecting the association between demand indices with other smoking-related variables.

Regression analyses investigating whether the demand indices derived from the proposed two-part mixed effects model predicted abstinence (top panel of Table 4) were not statistically significant (odds ratios ranged from 1.00 to 1.17, p-values ranged from .36 to .64). Among participants who failed to quit at 6 months, two demand indices significantly predicted reduction in CPD (bottom panel of Table 4): lower intensity and lower breakpoint (both p-values < .0001).

Table 4.

Abstinence and smoking reduction as predicted by demand indices derived from the two-part mixed effects model.

Abstinence at 6 months
Demand indices	Odds ratio	95% CI	Type III test statistics	p-value
Intensity	1.01	(0.99, 1.03)	0.84	.36
Omax	1.00	(0.99, 1.01)	0.27	.60
Pmax	1.02	(0.95, 1.10)	0.37	.54
α	1.17	(0.64, 2.15)	0.26	.61
Breakpoint	1.01	(0.98, 1.04)	0.64	.64
Percent reduction in cigarettes per day among smokers at 6 months
Demand indices	β	95% CI	Type III test statistics	p-value
Intensity	−4.4%	(−5.4%, −3.3%)	71.40	<.0001
Omax	−0.2%	(−0.4%, 0.0%)	2.83	.09
Pmax	0.0%	(−3.7%, 3.9%)	0.00	.96
α	−2.5%	(−34%, 29%)	0.02	.88
Breakpoint	−4.1%	(−5.6%, −2.6%)	29.17	<.0001

Note. For abstinence, odds ratio and Wald chi-square test statistics from logistic regression were reported; for smoking reduction, regression coefficient β and F test statistics, F(1, 718) from linear regression were reported.

Simulation Results

The true parameter values for simulating the data and the summary of the simulation results for the proposed two-part mixed effect model are shown in the top panel of Table 5. The mean relative biases for all parameter estimates were within ± 2%, indicating satisfactory point estimations. The mean coverage rates of the 95% CIs were all close to their nominal level (= 0.95) and the Monte Carlo SDs were all close to model-based standard errors, indicating satisfactory variance estimations.

Table 5.

Simulation results for two-part mixed effects model and left-censored mixed effects model.

Parameter	True value	Relative bias	Coverage rate	Monte Carlo SD	Model-based SE
Two-part mixed effects model
β0	−4.00	0.003	0.936	0.368	0.384
β1	3.00	0.001	0.936	0.383	0.399
logQ0	2.50	−0.000	0.955	0.018	0.019
k	4.00	−0.000	0.954	0.005	0.005
α	0.35	0.000	0.947	0.001	0.001
σa2	4.00	0.017	0.919	1.362	1.481
σb2	0.36	0.001	0.953	0.016	0.016
ρab	0.50	0.013	0.956	0.040	0.041
σe2	0.0025	−0.001	0.958	0.000	0.000
Left-censored mixed effects model
logQ0	2.50	0.012	0.583	0.019	0.017
k	4.00	0.035	0.000	0.018	0.025
α	0.35	0.175	0.000	0.005	0.005
σb2	0.36	−0.250	0.000	0.012	0.013
σe2	0.0025	1.422	0.000	0.007	0.002

Note. SD: standard deviation; SE: standard error; Relative bias = (estimate – true)/true ×100%; The correlation coefficient parameter ρ_ab is defined as ρ_ab = σ_ab/(σ_a·σ_b).

The results of fitting the left-censored model to the simulated data are presented in the bottom panel of Table 5. The parameters from the left-censored model had greater biases than those from the two-part model. The coverage rates of the left-censored model parameters departed from 0.95. These simulation results suggest that it would not be appropriate to apply the left-censored model on the cigarette purchase task data when zero responses are due to quitting.

Discussion

The exponential demand curve (Hursh & Silberberg, 2008) has become a standard model for analyzing cigarette purchase task and other purchase task data. However, data at the breakpoint (i.e., zero consumption values) cannot be naturally included in the model. Our proposed two-part mixed effects model can incorporate breakpoint data without arbitrarily imputing small values for zeros or assuming a left-censoring detection limit. In the proposed two-part mixed effects method, we model the zero consumption (vs. nonzero consumption) values in a logistic regression jointly with a nonlinear regression model for nonzero consumption data. The random effects from the two parts of the proposed model are assumed to be correlated to account for the correlated structure of the purchase task data.

The difference between the two-part mixed-effects model presented here and the left-censored mixed-effects model by Liao et al. (2003) is two-fold. Statistically, the left-censored model allows the same underlying distribution to determine two stochastic processes: (1) whether the observed response is zero or positive, and (2) the magnitude of the positive value. The two-part model allows flexibility in determining the two different (but related) processes in separate models. The left-censored model assumes that the zero responses indicate cigarette demand falling below a certain threshold that respondents would not bother to report. In comparison, the two-part model recognizes that zero responses may reflect the true abstinence of the respondents and uses separate models with different parameters to determine abstinence status and the number of cigarettes smoked.

We also propose a new demand index, the “derived breakpoint,” as a byproduct of the logistic regression component of the two-part model. Based on the Enhanced Quit & Win data, we found that the “derived breakpoint” was significantly correlated with all other demand indices, with the strongest correlation with Omax. However, it is counterintuitive that the strongest correlation was not observed between the “derived breakpoint” and its empirical counterpart. A similar phenomenon was observed for the derived and empirical Pmaxes. Thus, further investigation into the relationship of this proposed demand index with other demand indices using other data samples is warranted.

As compared with their empirical counterparts directly estimated from the data, we found that the derived demand indices were more strongly correlated with cigarettes smoked per day and nicotine dependence in our study. Hence, using derived indices instead of empirical indices could improve the statistical power in detecting the association between demand indices and smoking variables. We also found that the derived breakpoint had similar predictive power as the derived intensity in predicting smoking reduction among people who failed to quit at 6 months. However, none of the derived demand indices were able to predict 6-month abstinence. Because studies prospectively examining the predictive validity of the cigarette purchase task instrument on abstinence outcomes are generally sparse (e.g., MacKillop et al., 2016), it is warranted to examine the predictive power of demand indices in future studies using different settings or interventions, especially when the interventions include financial incentives.

Finally, although we focused on fitting the exponential demand curve to cigarette purchase task data, the statistical methodology identified is also applicable to other purchase task data (e.g., marijuana purchase task). Other demand curve models such as the linear-elasticity demand model (Hursh et al., 1988) can also be augmented to a two-part mixed effects model with a logistic regression component dedicated to the binary outcome of zero versus nonzero consumption. Investigation of the two-part mixed effects model based on other demand curve models is certainly warranted.

Appendix A

Estimation for Two-Part Mixed Effects Model

Let N denote the total number of subject and n_i the number of observations before (including) the breakpoint for subject i, that is Q_i1 > 0, …, Q_i,ni−1 > 0, and Q_i,ni = 0. The likelihood function of the two-part mixed effects model based on the observed data (i.e., j = 1, 2, …, n_i for subject i) is:

$$\prod _{i=1}^N\{\int (\prod _{j=1}^{n_i}{\left({\pi }_{ij}\right)}^{{\delta }_{ij}}{\left[\right(1-{\pi }_{ij}\left){\sigma }_e^{-1}\phi \right\{(\text{log }{Q}_{ij}-{\mu }_{ij})/{\sigma }_e\left\}\right]}^{1-{\delta }_{ij}}\left)\phi \right({\gamma }_i\left)d{\gamma }_i\right\},$$

where γ_i = (a_i, b_i, c_i)^T denotes the vector of random effects and φ (․) is the probability density function of γ_i. Since the mechanism of the missing data (i.e., Q_ij when j > n_i) is independent of the missing data given the observed data (called “missing at random” or MAR), the inference based on the observed data likelihood above is the same as the inference based on the full likelihood (Little & Robin, 2002). Maximization of the likelihood function was carried out using the NLMIXED procedure in SAS 9.2 (SAS Institute Inc., Cary, North Carolina).

Appendix B

SAS Program for Analyzing the Enhanced Quit & Win Data with the Two-Part Mixed Effects Model

proc NLMIXED data=cleandata tech=NRRIDG ITDETAILS optcheck maxiter=200;
       parms
               beta0=−2.5527
               beta1=0.9973
               logQ0=2.5729
               k=1.8229
               alpha=0.8281
               logsigma_a=0.6
               logsigma_b=−0.5
               logsigma_c=−1.8
               logsigma_e=−0.3436
               rho_ab=−0.5
               rho_ac=0.2
               rho_bc=0.2;
       bounds −1< rho_ab < 1, −1< rho_ac < 1,−1< rho_bc < 1;
       eta=beta0+beta1*log(price+0.001)+ai;
       exp_eta=exp(eta);
       pi_ij=exp_eta/(1+exp_eta);
       mu_ij=(logQ0+bi)+k*(exp(0−(alpha+ci)*price)−1);
       * Conditional log-likelihood;
       if delta=1 then logL=log(pi_ij);
       else logL=log(1−pi_ij)−log(exp(logsigma_e))−0.5*log(8*atan(1))−0.5*(((logQ−
mu_ij)/exp(logsigma_e))**2);
       * Variance parameters;
       var_a = exp(2*logsigma_a);
       var_b = exp(2*logsigma_b);
       var_c = exp(2*logsigma_c);
       cov_ab = sqrt(var_a*var_b)*rho_ab;
       cov_ac = sqrt(var_a*var_c)*rho_ac;
       cov_bc = sqrt(var_b*var_c)*rho_bc;
       var_e = exp(2*logsigma_e);
       * Subject-sepecific parameters;
       intensity_i=exp(logQ0+bi);
       alpha_i=alpha+ci;
       breakpoint_i=exp(0−(beta0+ai)/beta1)−0.001;
       * Model;
       model D~general(logL);
       random ai bi ci ~ normal([0,0,0],[var_a,cov_ab,var_b,cov_ac,cov_bc,var_c])
subject=STUDYID;
       * Estimate model parameters;
       estimate 'var[a]' var_a;
       estimate 'var[b]' var_b;
       estimate 'var[c]' var_c;
       estimate 'covariance[a,b]' cov_ab;
       estimate 'covariance[a,c]' cov_ac;
       estimate 'covariance[b,c]' cov_bc;
       estimate 'var[e]' var_e;
       * Predict subject-specific parameters;
       predict ai out=ai;
       predict intensity_i out=intensity_i;
       predict alpha_i out=alpha_i;
       predict breakpoint_i out= breakpoint_i;
run;