Controlling for Informed Presence Bias Due to the Number of Health Encounters in an Electronic Health Record

Abstract

Electronic health records (EHRs) are an increasingly utilized resource for clinical research. While their size allows for many analytical opportunities, as with most observational data there is also the potential for bias. One of the key sources of bias in EHRs is what we term informed presence—the notion that inclusion in an EHR is not random but rather indicates that the subject is ill, making people in EHRs systematically different from those not in EHRs. In this article, we use simulated and empirical data to illustrate the conditions under which such bias can arise and how conditioning on the number of health-care encounters can be one way to remove this bias. In doing so, we also show when such an approach can impart M bias, or bias from conditioning on a collider. Finally, we explore the conditions under which number of medical encounters can serve as a proxy for general health. We apply these methods to an EHR data set from a university medical center covering the years 2007–2013.

Electronic health records (EHRs) are becoming an increasingly common resource for clinical research. They present the opportunity to analyze hundreds of thousands, if not millions, of patients across a variety of health conditions. This affords tremendous analytical flexibility that is typically not possible with even large epidemiologic cohorts. While these high-dimensional data present many opportunities, one of the primary challenges of EHR data is that they are fundamentally observational. While the analytical biases in observational studies have been well noted (1), there are unique challenges that arise in the analysis of EHR data (2, 3). The primary concern, one that we address here, is the possibility of “informed presence.”

We define informed presence as the notion that inclusion in an EHR is not random but rather indicates that the subject is ill, making people in EHRs systematically different from those not in EHRs. As other authors have noted, persons contained within an EHR data set tend to be sicker than the population to whom results are meant to be generalized (4). Since people within the EHRs are observed not randomly but only when they have a medical encounter, there is the potential for bias in the collected data. One way this can manifest is that patients with more medical encounters have more opportunity to be diagnosed with various conditions. We consider this to be analogous to Berkson's bias (5), a form of ascertainment bias in hospital-based studies that is particular to EHRs and administrative data. As has been illustrated with Berkson's bias, this can lead to spurious associations between different diagnoses (6). Our goal in this paper is to illustrate the conditions under which this problem manifests in the analysis of EHR data and how it can be controlled.

Motivating example

In our motivating analysis, we wanted to use data from the EHRs of our university medical center (described below) to understand the co-occurrence of 2 chronic diseases: diabetes mellitus and depression (7). To assess the relationship, we extracted data from the EHRs and performed a simple logistic regression analysis, regressing the presence of depression onto diabetes. If we minimally adjusted for age, sex, and race/ethnicity, people with diabetes had 2.15 (95% confidence interval (CI): 2.05, 2.24) times higher odds of being diagnosed with depression than persons without diabetes. However, as described above, we considered that people who were more frequent visitors to the medical center would have a greater opportunity to be diagnosed with each condition. Therefore, we conducted a second analysis adjusting for number of health-care encounters. This time we estimated an odds ratio of 1.36 (95% CI: 1.29, 1.42)—a meaningfully different effect estimate. We further considered that perhaps people who are diabetic and/or depressed are just sicker in general and have other comorbidity that may be confounding the relationship. Therefore, we adjusted for a range of comorbid conditions and estimated an odds ratio of 1.29 (95% CI: 1.23, 1.35). Finally, we assessed what would happen if we adjusted for both the number of medical encounters and comorbidity, and we obtained an estimate of 1.11 (95% CI: 1.06, 1.17).

Partially due to other analytical concerns, we ultimately decided that the model adjusting for only the number of encounters was best (7). However, we wanted to further understand the role of confounding in this situation. Below we describe the theoretical basis for confounding in EHR studies, as well as the opportunity for additional biases if we inappropriately adjust for the number of encounters. Next we describe a simulation study created to explore this issue and present the results. We then return to our EHR data, illustrating these issues using real data. We finish with some concluding thoughts.

The opportunity for confounding and M bias

We first consider the opportunity for bias due to confounding. Consider that a person with diabetes regularly frequents a medical center. That person may be visiting the medical center to receive treatment for diabetes, in which case diabetes will likely be noted in the patient's medical record. This may be in the form of a billing code, laboratory test, or medication prescription. However, it is possible that the patient is seeing a physician not for diabetes but for another reason (related or unrelated to diabetes) for which diabetes is less likely to be noted. It is also possible that the person decides to seek treatment at another facility, so the diagnosis of diabetes is less likely to be noted during abstraction of the current EHR—this would be of particular concern in the analysis of an acute event such as a surgical procedure.

When analyzing EHR data, an important step is implementing an algorithm to define the presence of the clinical phenotype of interest, such as diabetes. To do so, one looks across an array of data fields (e.g., diagnosis codes, laboratory tests, medications) to derive a diabetes phenotype (8). Depending on the criterion, definitions of diabetes mellitus (DM) will vary in their sensitivity and specificity. We can imagine that each medical encounter has some probability, Pr(DM), of being related to diabetes management and therefore noted in the medical record. Across a set of medical encounters, the conditional probability of observing diabetes given that the person has diabetes, Pr(DM_obs|DM), is referred to as the sensitivity of the phenotyping algorithm. Quan et al. (9) assessed sensitivities based on International Classification of Diseases, Ninth Revision, codes across 32 common conditions. They found that sensitivities for prevalence of a condition ranged from 9.3% (weight loss) to 83.1% (metastatic cancer). Diabetes with complications, for example, has a sensitivity of 63.6%. Therefore, the more medical encounters someone has, the more likely that the presence of diabetes will be detected. However, another challenge can arise. Since phenotype algorithms are generally designed to detect the prevalence of a condition via ever/never algorithms (you either have the condition or you don't), the more health-care encounters someone has the higher the probability of a false-positive diagnosis. Such false-positive diagnoses, expressed through specificity, may occur through a “rule-out” diagnosis, an aberrant laboratory test, or miscoding. In the same study (9), the comparable specificity was higher, but there still existed an approximately 1% false-positive rate (99% specificity) across various conditions.

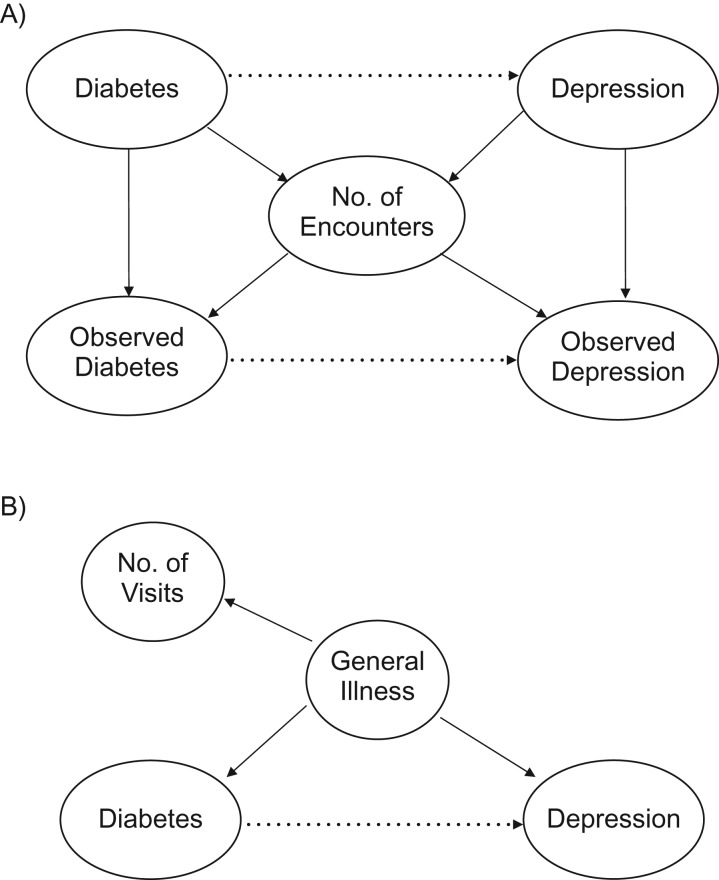
A typical clinical question of interest may be whether 2 chronic conditions are related; for example, do persons with diabetes have an increased risk of depression (sensitivity = 56.6%)? To answer such a question, one would typically regress the presence of depression onto the presence of diabetes (and other factors) in the form of a logistic regression, as we did in our motivating example. As the above scenario suggests, diabetics with more health-care encounters are more likely to have diabetes noted in the medical record. Similarly, depressed persons with more encounters are more likely to have depression noted. We can picture this in a causal diagram (Figure 1A). In this sense, we can consider the number of medical encounters to be a confounder of the proposed observed diabetes-depression relationship, as people with more encounters are more likely to have their clinical condition noted in the EHR. To resolve this confounding, it is clear that conditioning on the number of inpatient encounters removes this bias.

Figure 1.

Causal diagram illustrating number of health-care encounters as a confounder of the observed relationship between diabetes and depression. A) Basic causal model, where number of health-care encounters can serve as a confounder of the proposed (dotted line) diabetes-depression relationship. B) Causal model in which number of encounters may serve as a proxy for general illness.

While the opportunity for confounding is clear from Figure 1A, what is less evident is the potential for M bias (10)—bias from conditioning on a collider. In the causal literature, a collider is a variable that is an outcome of 2 other variables (11). Here, the number of health-care encounters is a result of one's underlying disease state. Therefore, while number of encounters is a confounder of the observed diabetes-depression relationship, it is also a collider of the actual diabetes-depression relationship. Moreover, as Greenland suggests theoretically (10) and others have shown in simulation (12), as the strength of the actual-observed relationship increases (i.e., Pr(DM_obs|DM) → 1), the greater the potential for M bias.

Finally, as the motivating example illustrates, there is another potential source of confounding: general illness (Figure 1B). It is possible that other disease states are driving both the presence of diabetes and depression. These states may or may not be fully captured or known. In the absence of such precise measurements, the number of encounters may be able to serve as a proxy for general illness, since sicker people are more likely to use the medical system. Therefore, even if we have a perfect phenotyping algorithm, there still may be utility to conditioning on the number of medical encounters.

METHODS

Simulation study

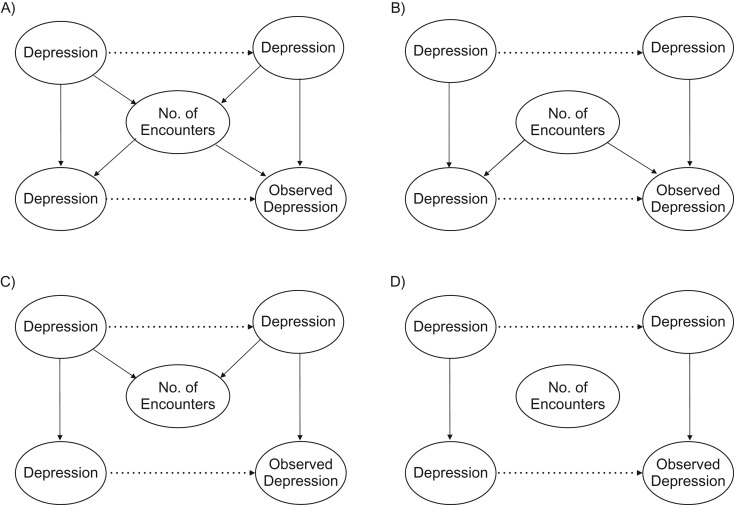
To explore the potential for bias and the effect of adjustment, we first performed a simulation study under 4 basic conditions. Described further below is a fifth simulation that assesses the use of number of encounters as a proxy for general health. Figure 2 illustrates the causal diagrams for these conditions. The first scenario (Figure 2A) is the basic confounding scenario described above, where people with a chronic disease have more medical encounters and the number of encounters increases the probability of observing the condition. Here we would expect controlling for number of encounters to improve estimation. However, as Pr(DM_obs|DM) approaches 1, we would expect M bias to occur. Scenario 2 (Figure 2B) is the no-collider scenario when Pr(DM_obs|DM) < 1. However, people with the chronic condition do not go to the doctor any more than others. In this case, we would expect controlling for the confounder to be beneficial, and we would not expect there to be any M bias, since the number of encounters is not a collider. Scenario 3 (Figure 2C) is the no-confounding scenario. Here Pr(DM_obs|DM) = 1, so the number of encounters has no effect on whether one observes the condition. This would be the case with a high-sensitivity phenotyping algorithm, where the condition is likely to be captured. In this case, we do not expect there to be any bias from not adjusting for number of encounters, but there is the greatest potential for M bias. Finally, scenario 4 (Figure 2D) is the null case, where there is no impact of the number of medical visits. Here we would expect there to be no effect of adjusting.

Figure 2.

Four simulation strategies for relating number of health-care encounters to observed data. A) People who have the disease have more health-care encounters, making number of encounters a collider of the actual relationship. Having more encounters increases the likelihood of observing the condition, making it a confounder of the observed relationship. B) The number of health-care encounters is only a confounder. C) The phenotyping algorithm is perfect, so the number of encounters is only a collider. D) The number of encounters is not related to actual or observed disease.

Each scenario had the same simulation structure:

1. We simulated an equal number of people with and without “diabetes” (n = 2,000).

2. We simulated the presence of “depression.” We repeated each simulation twice, once under a null association and once where diabetics had 25% increased odds of depression.

3. We simulated a number of health-care visits. To correspond with observed data, we had the number of visits follow a lognormal (skewed) distribution. In scenarios 1 and 3, people with diabetes and/or depression had more visits. In scenarios 2 and 4, all people had the same number of expected visits.

4. For scenarios 1 and 2, we varied the probability that an individual visit would yield either a diabetes (DM) or depression (DEP) diagnosis. These probabilities were 10%, 25%, 50%, 75%, 90%, and 100%. Therefore, scenarios 1 and 2 had 36 cases each. We note that when Pr(DM_obs|DM) = Pr(DEP_obs|DEP) = 1, scenarios 1 and 2 correspond to scenarios 3 and 4, respectively.

5. We next conducted 2 regression analyses:

   1. Depression regressed on diabetes.
   2. Depression regressed on diabetes, controlling for the number of medical encounters.

6. We repeated this 500 times.

In the fifth simulation, we simulated a causal scenario similar to Figure 1B. Here the goal was to assess the conditions under which number of visits could serve as a proxy for a true confounder, such as general health. To do so, we varied the strength of the relationship between number of visits and general health.

1. We generated a random variable indicating “overall health.”

2. Using a logistic model, we simulated the presence of both “diabetes” and “depression” as a function of “overall health.”

3. We simulated the number of visits with varying degrees of correlation (r = 0, 0.1, 0.25, 0.50, 0.75, 0.90, or 1) with “overall health.”

4. We performed 4 regression analyses:

   1. Depression regressed on diabetes.
   2. Depression regressed on diabetes, controlling for general health.
   3. Depression regressed on diabetes, controlling for number of medical encounters.
   4. Depression regressed on diabetes, controlling for both general health and number of encounters.

Our primary interest was in assessing the conditions under which controlling for number of medical encounters could serve as a proxy for general health. Therefore, for simplicity, in these simulations Pr(DM_obs|DM) = Pr(DEP_obs|DEP) = 1, removing the C-D and C-E pathways from Figure 1B. For each scenario, across the 500 simulations, we calculated the average bias and a 95% confidence interval. Simulation code is provided in the Web Appendix (available at http://aje.oxfordjournals.org/).

Data illustration

We next illustrate these points with real data. We abstracted data from EHRs in the Duke University Health System (DUHS). The DUHS consists of a network of community outpatient clinics, as well as 3 hospitals. Approximately 80% of Durham County, North Carolina, residents receive their regular medical care from the DUHS (13). Using data from 2007–2013, we extracted information on all patients living in Durham County. Since the DUHS is a referral system, by limiting the data to Durham County residents we increased the likelihood that we were observing local patients who received their regular health care through the medical system.

For each person in the medical records, we abstracted his/her age, sex, and number of encounters. Next we identified which individuals had a range of comorbid conditions. Since theory suggests that the effect of adjusting for number of encounters should be greatest when the sensitivity of the algorithm defining the comorbid condition is lowest, we chose comorbidities that had both high and low sensitivity, respectively. We used the study by Quan et al. (9) for these purposes. In our low-sensitivity case, we regressed the probability of observing depression (sensitivity (Sn) = 56.6%) onto the probability of observing weight loss (Sn = 9.3%). For our high-sensitivity case, we regressed the probability of a myocardial infarction (Sn = 72.4%) onto the probability of hypertension (Sn = 78.6%).

For each association analysis, we performed 4 regressions. We first regressed the outcome onto the exposure, adjusting only for age and sex. Secondly, we adjusted for number of medical encounters. To assess whether controlling for number of encounters was simply the same as controlling for general illness, we calculated the Charlson Comorbidity Index (CCI) (14), a single summary measure of 19 comorbid conditions, and adjusted for the score. Finally we adjusted for both the number of encounters and the Charlson score. We computed the estimated odds ratio for the exposure in each regression and calculated the change in the log odds ratio from the baseline (minimally adjusted) case. To illustrate the potential for confounding, we also computed the median number of encounters for people who had neither the outcome nor exposure, either the outcome or exposure, and both the outcome and exposure. Note that the regression estimates do not reflect actual expected associations, since other confounders were not considered.

We defined the comorbid conditions using the algorithms presented by Quan et al. (15). All analyses were performed in R 3.1.2 (R Foundation for Statistical Computing, Vienna, Austria) (16).

RESULTS

Simulation results

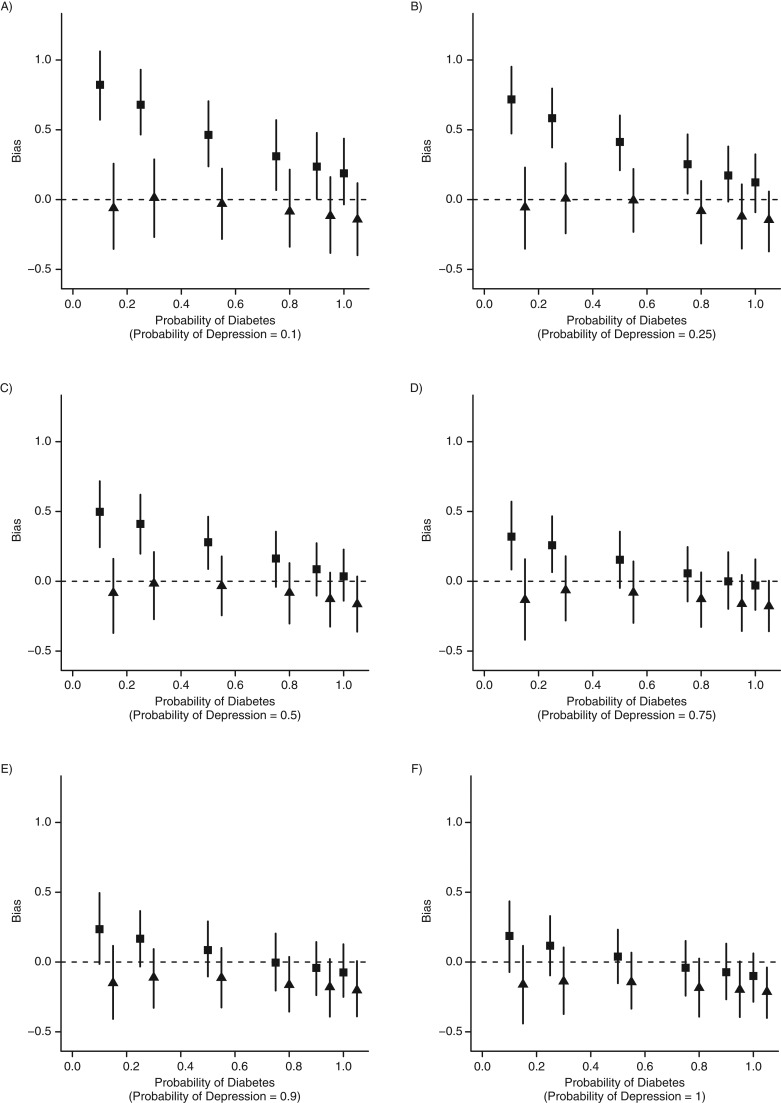
Figures 3 and 4 show the simulation results derived from the various scenarios. Results were very similar under the alternative hypothesis (association between diabetes and depression) and the null hypothesis, so we present only the results obtained under the alternative hypothesis. In scenario 1, confounding bias is greatest when Pr(DM_obs|DM) or Pr(DEP_obs|DEP) is relatively low. Adjusting for the number of encounters removes this bias. However, as Pr(DM_obs|DM) and Pr(DEP_obs|DEP) both increase, confounding bias attenuates, and M bias increases. M bias is larger than confounding bias when Pr(DM_obs|DM) ≥ Pr(DEP_obs|DEP) ≥ 0.9, having its strongest effect when Pr(DM_obs|DM) = Pr(DEP_obs|DEP) = 1 (scenario 3). However, even in this case the estimate is only slightly biased (bias = −0.21, 95% CI: −0.400, −0.039).

Figure 3.

Simulation results from different phenotyping algorithm sensitivities (scenarios 1 and 3). The figure shows the estimated bias when people with disease are more likely to have more health-care encounters. As the quality of the phenotyping algorithm increases (moving from part A to part F and from left to right within the figure), we expect less bias due to confounding (▪, unadjusted). Adjusting for the number of health-care encounters removes this bias (▴, adjusted). As the quality of the phenotyping algorithm increases, the potential for M bias increases (part F).

Figure 4.

Simulation results from different phenotyping algorithm sensitivities (for scenarios 2 and 4). The figure shows the estimated bias when people with disease are no more likely to have more health-care encounters than people without disease. As the quality of the phenotyping algorithm increases (moving from part A to part F and from left to right within the figure), we expect less bias due to confounding (▪, unadjusted). Adjusting for the number of health-care encounters removes this bias (▴, adjusted). However, since the number of encounters is no longer a collider, the potential for M bias is removed (part F).

In the second set of simulations, we removed the pathways between the disease and the number of encounters (Figure 2B). In this case, we would expect confounding but no M bias. Our simulations support this (Figure 4), since we see evidence of confounding but no M bias, as the adjusted estimates are essentially unbiased. The overall confounding bias in scenario 2 is less than that in scenario 1. As Pr(DM_obs|DM) → Pr(DEP_obs|DEP) → 1 (scenario 4), we notice that there is no difference between the adjusted and unadjusted estimates.

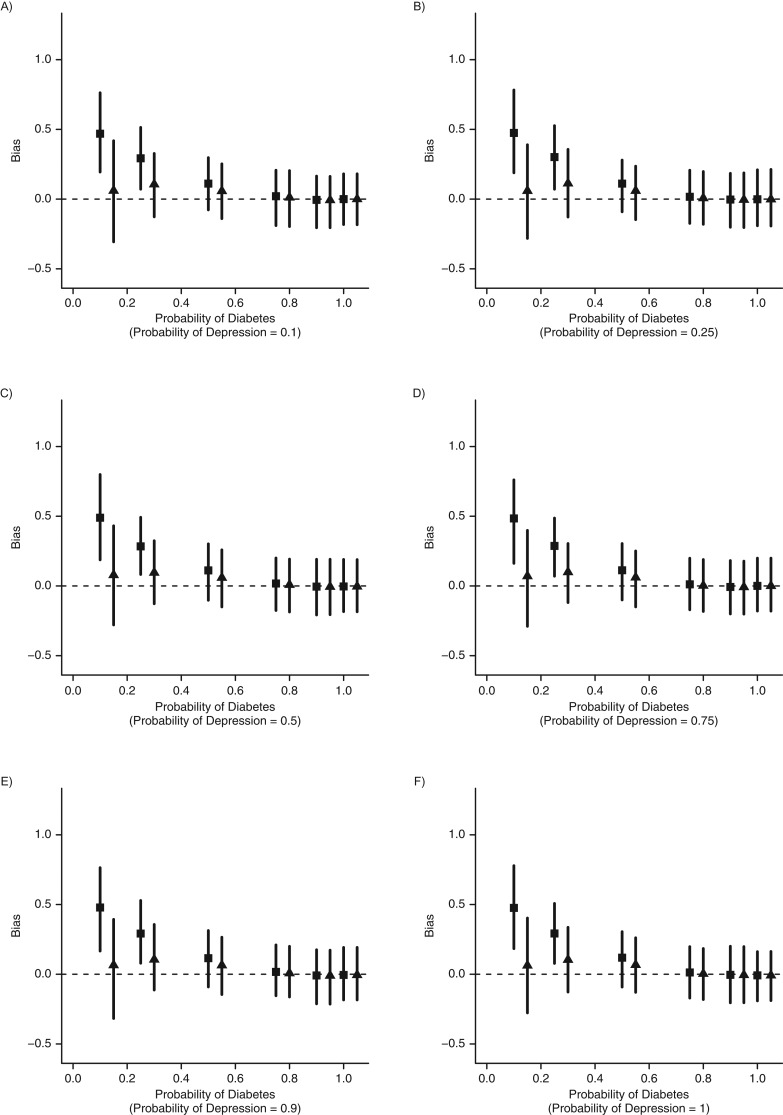
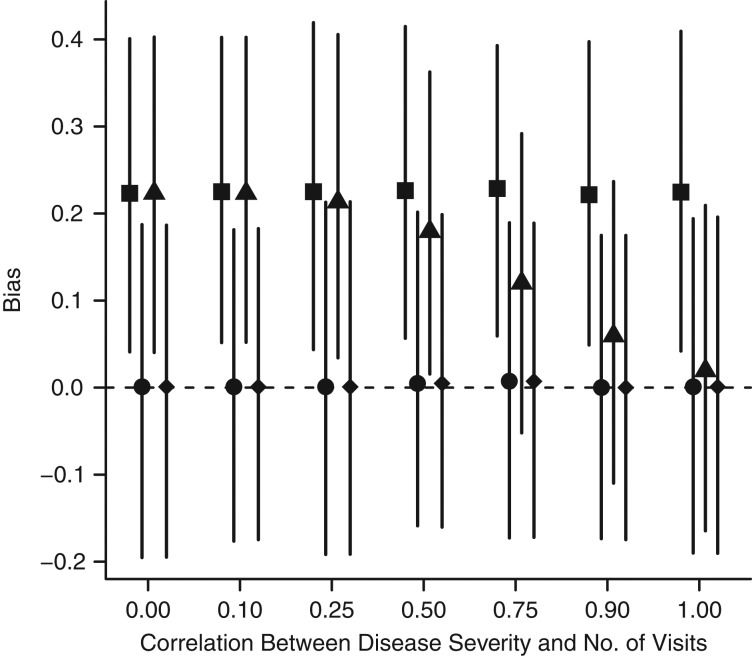
In the final set of simulations, we explored the conditions under which number of encounters could serve as a proxy for general health. Figure 5 shows the results obtained under varying correlations between number of encounters and general health. As expected, the effect estimate is biased under no adjustment and unbiased after adjustment for general health (the true model). When only information on number of encounters is used in the model, the correlation between general health and number of encounters needs to be relatively strong (r > 0.75), to serve as a reasonable proxy. There was no observed bias from adjusting for both encounters and general health.

Figure 5.

Estimated bias from a simulation allowing number of health-care encounters to serve as a proxy for disease severity. There needs to be a relatively strong correlation (r > 0.75) in order for number of medical encounters to serve as a proxy for general health. ▪, unadjusted; ●, adjusted for general health; ▴, adjusted for number of visits; ♦, adjusted for both general health and number of visits.

Data results

We assessed how adjustment performs in a real data set while evaluating associations between comorbid conditions that should be captured with low and high sensitivity, respectively. We first note that whether someone had both conditions, 1 condition, or neither condition was meaningfully related to the number of medical encounters, highlighting the potential for confounding (Table 1). After adjustment for number of encounters (Table 2) in our low-sensitivity-condition scenario, depression–weight loss, the association decreased by 0.52 units on the log odds scale (we reemphasize that these are not causal associations but illustrative). This attenuation was greater than that obtained by adjusting for the CCI (0.35 log odds units). Moreover, adding the Charlson score to the number of encounters had a minimal impact. In our high-sensitivity scenario, myocardial infarction–hypertension, we saw a much smaller attenuation in the log odds ratio after adjustment (0.16 log odds units). Notably, the CCI produced much larger attenuation (0.39 log odds units), which was not amplified by the addition of number of encounters. Finally, the coefficient for correlation (r) between the CCI and the number of encounters was 0.47, suggesting that number of medical encounters would serve as a moderate proxy for general health.

Table 1.

Median Number of Health-Care Encounters According to Disease State in Electronic Health Records From the Duke University Health System, Durham County, North Carolina, 2007–2013

	Sensitivity, %	Median No. of Medical Encounters
		Without Condition	With Condition
Low sensitivity
Depression	56.6	6	38
Weight loss	9.3	7	45
High sensitivity
Myocardial infarction	72.4	7	41
Hypertension	78.6	5	31

Table 2.

Change in Estimated Associations Between Depression and Weight Loss and Between Myocardial Infarction and Hypertension After Adjustment for Number of Health-Care Encounters, Durham County, North Carolina, 2007–2013

Model	Depression–Weight Loss (Low Sensitivity)				Myocardial Infarction–Hypertension (High Sensitivity)
	OR	95% CI	Change in Log Odds	Change in OR	OR	95% CI	Change in Log Odds	Change in OR
Minimal adjustmenta	3.98	3.81, 4.17			12.93	11.75, 14.25
+ No. of medical encounters	2.37	2.26, 2.50	−0.52	−1.61	11.02	9.99, 12.15	−0.16	−1.91
+ CCI	2.82	2.69, 2.96	−0.35	−1.16	8.78	7.94, 9.71	−0.39	−4.15
+ No. of encounters and CCI	2.30	2.18, 2.42	−0.55	−1.68	8.66	7.82, 9.58	−0.4	−4.27

Abbreviations: CCI, Charlson Comorbidity Index; CI, confidence interval; OR, odds ratio.

^a Results were adjusted for age and sex.

DISCUSSION

In this simulation study, we illustrate the potential for bias in the analysis of EHR and administrative data. If the presence of a medical condition is not captured with high probability (i.e., high sensitivity), there is the potential for inflation of the effect estimate for association with another such condition. This potential for bias is exacerbated when the medical condition also leads to more patient encounters—something our data example illustrates and other authors have suggested (4).

Theory suggests, and our simulations confirm, that conditioning on the number of health-care encounters can remove this bias. The impact of conditioning is greatest for diagnoses captured with low sensitivity. While we did not explore the role of specificity explicitly, one may expect that this would also be the case for diagnoses captured with low specificity. However, as the work validating phenotyping algorithms has shown, specificity is usually quite high (approximately 99%) while sensitivity can be more variable (9), suggesting that the low-specificity case is of lesser concern.

While conditioning on the number of encounters seems to be a simple solution, analysis of causal diagrams suggests that there is the potential for M bias, or bias from conditioning on a collider. We would expect M bias to be largest when sensitivity (and specificity) was highest. This was, in fact, observed to be the case. As Pr(Outcome_obs|Outcome) = Pr(Predictor_obs|Predictor) approached 1, the degree of bias associated with conditioning increased. Moreover, this is the same scenario where confounding bias is least noticeable. This suggests that researchers ought to be aware of the sensitivity and specificity of their phenotyping algorithms. However, as theory suggests (10) and others have illustrated (12), M bias is usually smaller than confounding bias. This was confirmed in our analysis, where even the most extreme case, Pr(Outcome_obs|Outcome) = Pr(Predictor_obs|Predictor) = 1, still provided nominal 95% coverage of the true parameter value. Therefore, if one is not certain of the sensitivity and specificity of the phenotyping algorithm, it seems prudent to consider conditioning on the number of encounters.

We also considered the situations in which the number of medical encounters could serve as a proxy for general health—something challenging to ascertain from claims-based data. The simulation study suggests that there needs to be a relatively high correlation between the two measures (r > 0.75) in order to do so. We observed only moderate correlation (r > 0.47) in our data analysis using the CCI to define general health. Our empirical evaluation suggests that controlling for general health is distinct from controlling for number of encounters. Where informed presence is expected (the low-sensitivity condition), controlling for number of encounters provides greater attenuation than does the Charlson score. However, when informed presence is not expected (the high-sensitivity condition), the Charlson score provides more attenuation. Interestingly, the presence of both metrics seems to have a minimal effect on overall attenuation, suggesting that while the mechanisms may be different, they are capturing overlapping information. This is a point worthy of further consideration.

We have couched the possibility of confounding and M bias through the sensitivity of a phenotyping algorithm. However, it is important to note that this is only one means through which informed presence may occur. An algorithm may have perfect sensitivity but still have Pr(DM_obs|DM) < 1. For example, if someone seeks care at multiple facilities or moves to a different facility and his/her medical records are not forwarded to the new system, there would be similar capture issues. As other authors have noted, Berkson's bias can be construed as a missing data problem (6, 17), which is also the case here. We have chosen to focus on the sensitivity component, because this is particularly unique to EHRs. It is likely that other approaches may be needed to address these other sources of bias, and this is worthy of further research.

While we have introduced the notion of informed presence as a form of Berkson's bias, we emphasize that this is only one way in which informed presence can manifest. The fact that people who interact with a medical center are usually sicker than the general population can lead to different biases, each likely requiring different solutions. Moreover, it is important to note that all EHR analyses are inherently conditional on people having at least 1 health encounter. While we assessed bias by comparing our estimates with the true population-level parameter value, future work ought to more fully assess how EHR-based inference pertains to the general population.

This study had several strengths and weaknesses. Encouragingly, our simulation results correspond well with both the findings of previous simulation studies (12) and epidemiologic theory (10). Moreover, we were able to empirically illustrate the effect of conditioning with anticipated results. Overall, the proposed solution is intuitive and easy to implement. The primary weakness of this study was the simplicity of the simulation study and analysis. Disease relationships are obviously much more complex than illustrated in our causal diagrams and corresponding analyses. It is possible that a more complex, and realistic, analysis would inherently control for such capture biases—perhaps by controlling for factors like disease severity. Moreover, as more complex EHR data become more accessible, phenotyping algorithms are becoming more complex (8) and ultimately more precise, making such solutions less necessary. Even so, it is important to be wary of such biases and how they may affect analyses and inference. Finally, the results suggest that it is important to be aware of the sensitivity of one's phenotyping algorithm. However, unless researchers perform a validation study within their own EHR system, it is challenging to know exactly which conditions are not well captured. Studies like those of Quan et al. (15) can serve as a guide, but it is hard to know how well the results will transfer to different systems.

Overall, we illustrate a potential bias inherent in the analysis of EHRs and administrative data and propose a simple solution. While there is the potential for residual M bias, the conditions under which this may occur are (potentially) predictable and can be avoided. As EHR data become more of a standard for clinical analyses, identification of such problems with corresponding solutions will become more salient.