Noninvasive Electromagnetic Source Imaging and Granger Causality Analysis: An Electrophysiological Connectome (eConnectome) Approach

Abstract

Objective

Combined source imaging techniques and directional connectivity analysis can provide useful information about the underlying brain networks in a non-invasive fashion. Source imaging techniques have been used successfully to either determine the source of activity or to extract source time-courses for Granger causality analysis, previously. In this work, we utilize source imaging algorithms to both find the network nodes (regions of interest) and then extract the activation time series for further Granger causality analysis. The aim of this work is to find network nodes objectively from noninvasive electromagnetic signals, extract activation time-courses and apply Granger analysis on the extracted series to study brain networks under realistic conditions.

Methods

Source imaging methods are used to identify network nodes and extract time-courses and then Granger causality analysis is applied to delineate the directional functional connectivity of underlying brain networks. Computer simulations studies where the underlying network (nodes and connectivity pattern) is known were performed; additionally, this approach has been evaluated in partial epilepsy patients to study epilepsy networks from inter-ictal and ictal signals recorded by EEG and/or MEG.

Results

Localization errors of network nodes are less than 5 mm and normalized connectivity errors of ~20% in estimating underlying brain networks in simulation studies. Additionally, two focal epilepsy patients were studied and the identified nodes driving the epileptic network were concordant with clinical findings from intracranial recordings or surgical resection.

Conclusion

Our study indicates that combined source imaging algorithms with Granger causality analysis can identify underlying networks precisely (both in terms of network nodes location and internodal connectivity).

Significance

The combined source imaging and Granger analysis technique is an effective tool for studying normal or pathological brain conditions.

I. Introduction

The brain is organized as an interconnection of many networks and neural circuits which interact with each other constantly [1]–[3]. In order to understand the functional connections among different brain regions and networks, it is important to detect and analyze the nature of such connections. Conventional methods such as coherence [4], [5], measure the functional connectivity or the existence of such connections, trying to answer the question of which regions are demonstrating highly correlated activity [6]. While finding functional connectivity has been a major focus in neuroscience research, the more interesting problem, however, is to study the effective connectivity of underlying neural networks. A crucial step towards this end, is to study the direction of connections among regions of interest in the brain, to investigate for example if regions A and B are correlated (functional connectivity), is A driving B or is B driving A or neither is influencing the other directly (directional connectivity). In the previous example, it might turn out that A and B are being driven by another region C, thus resulting in the determination of the effective connectivity [7], [8]. Thus, directional connectivity analysis is a crucial step in further understanding and interacting with the brain, either to study brain functions or dysfunctions or to intervene in case of pathophysiological processes [3], [9].

Granger causality analysis [10]–[12] provides such a framework, with the idea that if a time series Y is causally driving a time series X, then the previous samples of Y should improve the predictions of future values of X compared to the case where only previous samples of X are used to predict future values of X. This idea can be generalized for application to multivariate time series (as opposed to the bivariate example with X and Y) which makes it suitable for studying brain signals [13], [14].

Modeling the activity of brain regions using multivariate autoregressive (MVAR) models, directional connectivity can be inferred from activation of different brain regions. Based on the coefficients estimated from the MVAR model, Kaminski and Blinowska proposed a spectral measure called directed transfer function (DTF) which provides a spectral measure for directed connections among the modeled time series by the MVAR [13], [14]. DTF on intra-cranial recordings has proven useful in objectively determining underlying connections, specifically in pathological cases such as epilepsy [13], [15]–[20]. Other measures such as partial directed coherence (PDC) and direct DTF (dDTF) have also been proposed based on the MVAR model coefficients or DTF coefficients [21], [22]. PDC and dDTF are claimed to deal better with indirect causal links compared to DTF. Astolfi et al., however, showed that all three methods function well in determining underlying brain networks under realistic settings [23].

While applying directional connectivity to intracranial and electrocorticography (ECoG) recordings is useful, DTF analysis was tested on noninvasive recordings such as EEG and MEG, early on. Initially, the Granger analysis was performed in the sensor space and on recorded EEG time series [13], [14]. While this provided insight about the nature of underlying brain processes, two major disadvantages were evident. Firstly, the analyzed connectivity on sensor space was not directly related to source space and brain regions, thus if for example, an electrode located in the frontal area was determined as a driving node, it is vague as to where exactly in the brain does this activity pertain to. Secondly, due to volume conduction and mixing, the time series recorded on the surface EEG could potentially be highly correlated which can potentially obscure the connectivity estimation. Due to these issues, more effort and emphasis has been put in place to estimate directional connectivity from source signals in the brain by combining source imaging techniques and connectivity analysis [24].

Electromagnetic source imaging (ESI) techniques basically estimate the neuronal electrical activity of the brain from electromagnetic surface recordings such as EEG and MEG [25]–[27]. Using high-density measurements, ESI techniques can provide quite robust estimates of the cortical activation [28], [29]. Combining ESI techniques with connectivity analysis not only helps with reducing volume conduction effects but could also be used to objectively determine the brain regions involved, rather than resorting to pre-defined cortical segmentation [30]–[32].

The underlying assumption of the MVAR analysis is that the underlying signal is stationary and the inter-relation of the time series does not change over the window of study. As brain signals could change rather fast, an adaptive DTF analysis (ADTF) has been proposed [16], [33], which looks at data at windows that are short enough to ensure quasi-stationarity and at the same time, long enough to determine the MVAR model parameters [34], [35].

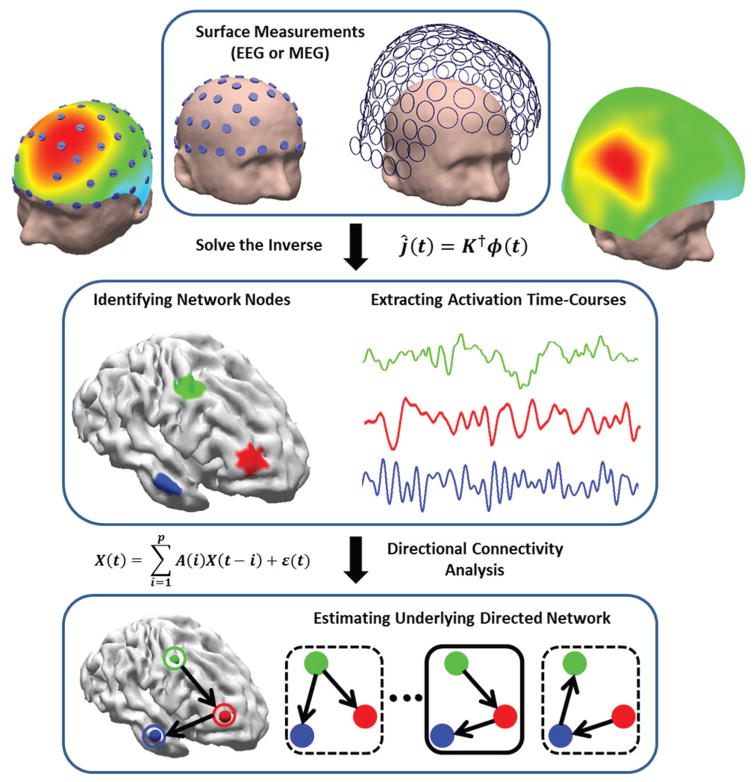
This study aims to implement the combined ESI and A/DTF analysis to investigate the efficacy of this method in determining brain networks. In order to estimate underlying networks the nodes or regions of interest (ROI) will first be determined using ESI and then the activation time-course of each ROI will be extracted. Finally the directional connections will be analyzed using DTF analysis. The overall strategy of combined ESI and directional functional connectivity analysis is schematically depicted in Fig. 1. This study differs from previous studies in the sense that no pre-defined ROIs will be assumed and basically the whole process from identifying network nodes, extracting time series for each node and applying ADTF analysis will be completely data driven under the combined ESI and A/DTF framework.

Fig. 1. Mapping and imaging the electrophysiological connectome (eConnectome).

The combined ESI and directional functional connectivity analysis identifies nodes and inter-nodal connections of the network under study. ESI can objectively determine the network nodes and extract activation time-courses and feed them to a directional functional-connectivity analysis, such as Granger causality analysis, to determine the directional connectivity patterns.

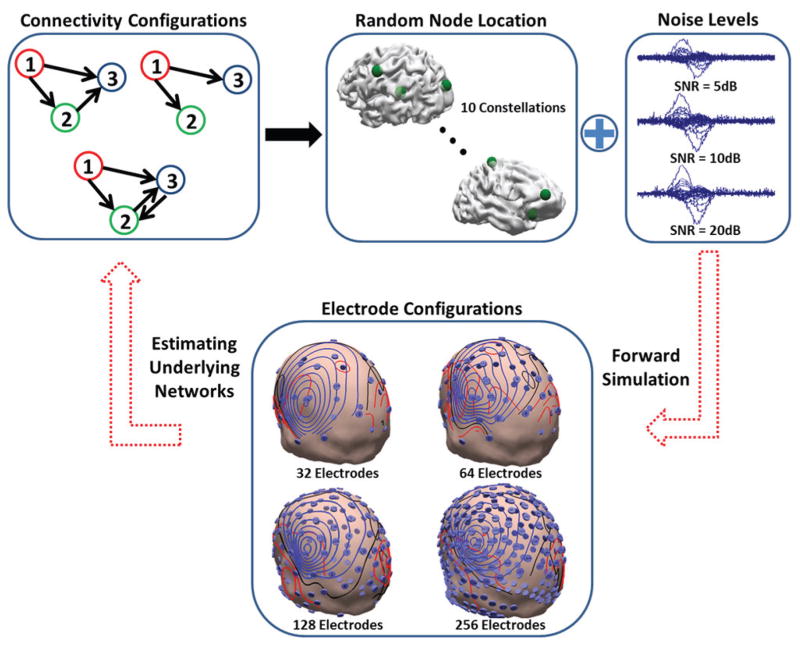
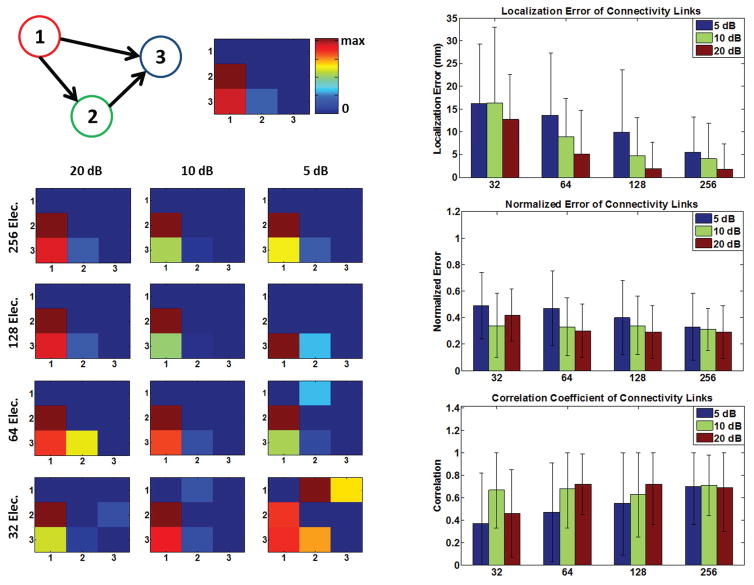
A series of computer simulations based on this idea is conducted first, to assess the feasibility and performance of this approach in practical settings and under realistic conditions, when the “ground truth” is available (ground truth is the simulated/target network in simulation studies and clinical findings in clinical data analysis). The errors computed for these simulations will comprise of localization and connectivity errors to determine how well the underlying networks can be determined. Various electrode configurations (256, 128, 64 and 32 electrodes) and noise levels have been tested in these simulation studies (Fig. 2). The present approach was then validated in two epilepsy patients using intracranial recordings and surgical resection. These simulation and clinical studies provide a carefully designed study to assess the effective connectivity from noninvasive EEG or EEG/MEG.

Fig. 2. Simulation protocol.

The different connectivity configurations in this simulation study are presented in this figure (upper left). Network nodes are randomly chosen and different noise levels are added to the simulated scalp maps (upper row right). Four different electrode configurations are used in this study (lower). The goal is to estimate the underlying networks, node location and nodal interconnections, from scalp measurements.

II. Methods

A. Electromagnetic Source Imaging

ESI algorithms try to solve the bio-electromagnetic inverse problem which is the process of estimating underlying neuronal activity from limited scalp measurements such as EEG and MEG. This can be formulated as follows

$$\mathrm{\varphi }(\mathrm{t})=\mathrm{K}(\mathrm{R},\mathrm{Q})\mathrm{j}(\mathrm{t})+\mathrm{n}(\mathrm{t})$$ (1)

Where ϕ(t) is the electrical potential (magnetic field in case of MEG) recorded on the scalp by EEG at every time point t, K(R,Q) is the lead field matrix for a current dipole at location R with orientation Q, j(t) is the source activation profile in time (current density) and n(t) is the measurement noise. The goal is to estimate j(t) given ϕ(t). The lead field matrix is calculated using a three layer boundary element method (BEM) model constructed from subjects’ MRI images [36], [37]. The BEM model is composed of skin, skull and brain with the conductivity of 0.33 S/m, 0.0165 S/m and 0.33 S/m, respectively [38], [39], where the three layers were obtained from subject’s MRI (in clinical data analysis). In this paper we confined the source space to the cortical layer, using the cortical current density model [40].

In this paper two inverse algorithms were used, the minimum norm (MN) estimate [41] and the standardized low resolution electromagnetic tomography (sLORETA) [42] to obtain the underlying neuronal activity. The MN is a linear inverse estimate of the form,

$$\begin{array}{l}\widehat{\mathrm{j}}(\mathrm{t})=\mathrm{T}\mathrm{\varphi }(\mathrm{t})=\text{TKj}(\mathrm{t})+\text{Tn}(\mathrm{t})\\ \mathrm{T}={\mathrm{K}}^{\mathrm{T}}{({\text{KK}}^{\mathrm{T}}+\mathrm{\lambda }\mathrm{I})}^{†}\end{array}$$ (2)

Where † is a symbol for Moore-Penrose pseudo-inverse and λ is a hyper-parameter related to scalp measurement noise. For the simulation study, sLORETA was utilized to solve the inverse as sLORETA estimates seem to be more accurate than MN solutions. The algorithm, sLORETA, is based on MN estimates, but further divides the MN solution by the estimated source covariance at each dipole location to accommodate for the distortion caused by the inverse kernel T (which in turn is also related to the lead field matrix, K) and noise variation [42],

$$\begin{array}{l}{\mathrm{j}}_{\mathrm{r}}^{\text{sLORETA}}={\widehat{\mathrm{j}}}_{\mathrm{r}}^{\mathrm{T}}{\{[{\mathrm{S}}_{\widehat{\mathrm{j}}}]\}}^{-1}{\widehat{\mathrm{j}}}_{\mathrm{r}}\\ {\mathrm{S}}_{\widehat{\mathrm{j}}}={\mathrm{K}}^{\mathrm{T}}{({\text{KK}}^{\mathrm{T}}+\mathrm{\lambda }\mathrm{I})}^{†}\mathrm{K}\end{array}$$ (3)

Where ĵ_r is the MN solution from (2) for dipole located at location r. In effect, sLORETA solutions from (3), have the form of a pseudo “F” statistics [42]. Due to this correction, sLORETA solutions are more robust against noise and are less biased towards superficial sources.

B. Functional Connectivity Analysis

DTF, ADTF and PDC analysis were used to derive directional connectivity in this study. DTF and PDC analysis were used for the computer simulation study [13], where the underlying connectivity was kept constant and ADTF was used for clinical data analysis [16], [33]. The MVAR model was first fit to the time series under study,

$$\mathrm{X}(\mathrm{t})={\sum }_{\mathrm{i}=1}^{\mathrm{p}}\mathrm{A}(\mathrm{i})\mathrm{X}(\mathrm{t}-\mathrm{i})+\mathrm{\epsilon }(\mathrm{t})$$ (4)

Where X(t) is the multi-dimensional time series under study, A(i) are coefficient matrices of the MVAR model to be estimated and ε(t) is the vector of white noise, driving the MVAR model. The order of this MVAR model is p, as the model leans upon the effect of p previous values of the time series to predict the future values. The model order can be determined using the Schwarz Bayesian criterion (SBC) or the Akaike information criterion (AIC) [43], [44]. The transfer function of the system can be derived by taking the Fourier transform of (4) and inverting the coefficient matrix as follows,

$$\mathrm{A}(\mathrm{f})\mathrm{X}(\mathrm{f})=\mathrm{E}(\mathrm{f})\to \mathrm{X}(\mathrm{f})=\mathrm{A}{(\mathrm{f})}^{-1}\mathrm{E}(\mathrm{f})=\mathrm{H}(\mathrm{f})\mathrm{E}(\mathrm{f})$$ (5)

Where H(f) is the transfer matrix of the system. The DTF value γ_ij (f) represents the signal flow from time series of node j to node i, which can be obtained as follows,

$${\mathrm{\gamma }}_{\text{ij}}(\mathrm{f})=\frac{{\mid {\mathrm{H}}_{\text{ij}}(\mathrm{f})\mid }^2}{{\sum }_{\mathrm{m}=1}^{\mathrm{n}}{\mid {\mathrm{H}}_{\text{im}}(\mathrm{f})\mid }^2}$$ (6)

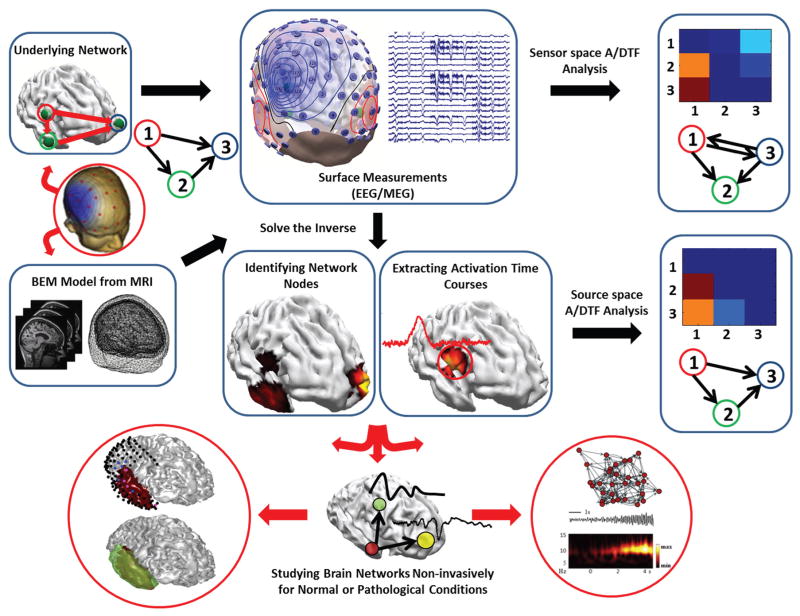
As the relation between the A/DTF and the time series are highly nonlinear, a nonparametric statistical testing was employed to reject spurious connections due to random noise [45], [46]. The surrogate data were generated by keeping the amplitude of the time series spectrum the same as the original data but permuting the phases. This shuffling procedure was performed for 1000 times and if the A/DTF value computed passed the significance level (p < 0.05), they were kept, otherwise replaced by zero [31]–[33]. This shuffling process has been performed for all A/DTF analysis presented in this paper. The DTF analysis was performed using eConnectome [47] which is an open source software freely available at (http://econnectome.umn.edu). The combined ESI and A/DTF analysis adopted in this study is summarized graphically in Fig. 3.

Fig. 3. Combined ESI and A/DTF analysis applied in this study.

The strategy pursued in this work to study brain networks is schematically depicted. ESI algorithms not only provide information about the activation of source nodes but can also be used to objectively determine the network nodes. A/DTF analysis provides vital information about directional information flow in the brain. This approach is powerful in studying brain networks in normal conditions and/or pathological networks such as epilepsy.

PDC was also tested in the simulation studies to compare its performance with DTF analysis. PDC is claimed to be more accurate in determining the direct connectivity compared to DTF (for more details on the definition of PDC and its properties please refer to [21], [48]), which captures direct and indirect connectivity effects. The PDC algorithm was implemented using the AsymPDC package which is an open source software for calculating PDC and DTF, freely available from (http://www.lcs.poli.usp.br/~baccala/pdc/) [49], [50].

C. Dynamic Seizure Imaging

The Dynamic seizure imaging (DSI) algorithm [51], decomposes the scalp potential into independent components using the independent component analysis (ICA) and then identifies the components that are due to ictal activity. The selected components will be inverted and transformed into the source space, only to be recombined using the activation time-courses of each component (derived from the ICA) to estimate and monitor the generation and propagation of ictal activity. EEG signal can be decomposed into independent components (IC) as follows [52],

$$\mathrm{\varphi }=\text{WMT}={\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{c}}}{\mathrm{w}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}{\mathrm{T}}_{\mathrm{i}}$$ (7)

Where ϕ is the potential recorded by scalp EEG, N_c is the number of ICs, w_i are the weights of each IC, M_i is the weighting of the ICs for each recorded EEG channel which is interpreted as topographical scalp maps and T_i is the activation time-course associated with each IC.

Components contaminated by artifacts such as movement artifact and eye blink or movement, were removed by visual inspection. Within the remaining ICs the correlation between the spectrogram of the IC components and the ictal EEG was computed. ICs showing significantly high correlation with the ictal time-course (p < 0.05) were selected (N_s) as ictally relevant ICs [51]. As outlined previously, the inverse problem was solved by inverting each IC and recombining in source space as follows,

$$\widehat{\mathrm{j}}(\mathrm{t})={\mathrm{K}}^{†}\mathrm{\varphi }(\mathrm{t})={\mathrm{K}}^{†}{\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\mathrm{w}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{i}}{\mathrm{T}}_{\mathrm{i}}={\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\mathrm{w}}_{\mathrm{i}}({\mathrm{K}}^{†}{\mathrm{M}}_{\mathrm{i}}){\mathrm{T}}_{\mathrm{i}}={\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{s}}}{\mathrm{w}}_{\mathrm{i}}({\widehat{\mathrm{S}}}_{\mathrm{i}}){\mathrm{T}}_{\mathrm{i}}$$ (8)

Where K^† is the operation of cancelling the volume conduction due to the mixing of the lead field and Ŝ_i is the estimated source from the topographical scalp map of each selected IC. DSI has been tested in epileptic patients and has proven to be quite effective in determining the SOZ [51], [53], [54].

D. Simulation Protocols

A series of computer simulations were performed in this study to investigate the efficacy of the combined ESI and DTF analysis (graphically depicted in Fig. 3). Three different network configurations (in terms of connectivity) were modeled (refer to Fig. 2). The networks consisted of three nodes. The three nodes of the network were randomly placed on a realistic cortex (very deep nodes near the thalamus or in the inter-hemisphere region were excluded) segmented from a human MRI. The time activity of the three nodes was simulated based on the MVAR model of (4) to create the desired configurations depicted in Fig. 2. For more details on implementation please refer to the supplementary materials.

The forward problem was solved and white noise with different strength was added to the simulated scalp maps (in addition to the internal noise driving the MVAR model of the underlying source activities) to obtain average signal-to-noise ratios (SNR) of 5, 10 and 20dB. Additionally the whole process was repeated for various electrode configurations of 32, 64, 128 and 256 electrodes.

After the forward problem was solved and EEG signals simulated, the inverse problem was solved using sLORETA for each case (connectivity type, node location, SNR, electrode number) and the nodes of the network were determined by observing the hot-spots of the source space to find dipole locations which demonstrated a strong and frequent dipole activity. This process was achieved by taking the singular value decomposition (SVD) of the estimated source currents and looking at the dominant components (components corresponding to large singular values which were distinct from noisy and background components once the singular values were plotted), which spatially corresponded to simulated nodes of the network. Once nodes of the networks were determined the activation of the dipole located at the estimated node was extracted and used for the subsequent DTF analysis. Additionally, we used another method to extract the activation time-courses of the underlying sources. After the location of the network nodes were estimated, the lead field matrix columns corresponding to those locations were selected and the scalp potential was projected to these columns to estimate the source activation of each estimated node location,

$$\widehat{{\mathrm{j}}_{\mathrm{s}}}(\mathrm{t})={({{\mathrm{K}}_{\mathrm{s}}}^{\mathrm{T}}{\mathrm{K}}_{\mathrm{s}})}^{-1}{{\mathrm{K}}_{\mathrm{s}}}^{\mathrm{T}}\mathrm{\varphi }(\mathrm{t})$$ (9)

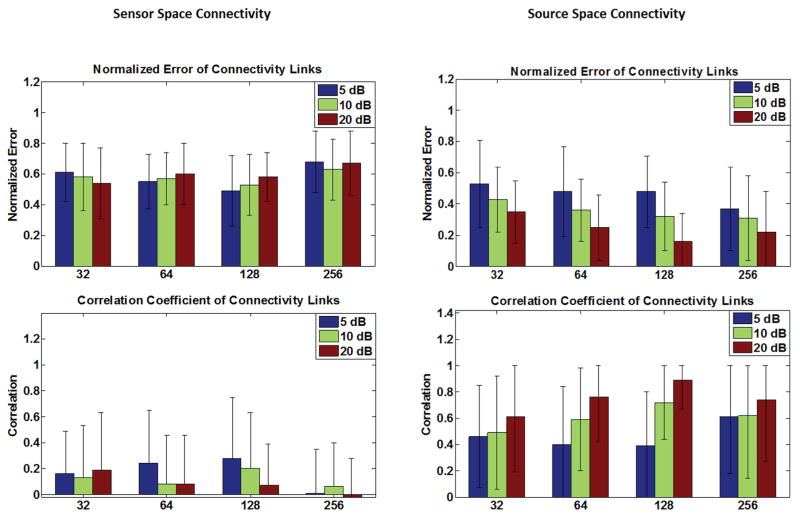
Where K_s is the reduced lead field matrix where only the columns corresponding to the estimated nodes are selected; thus K_s is a tall matrix and K_s ^TK_s is full rank. The connectivity results for time-courses extracted using the method formulated in (9) are analyzed and presented separately (Fig. 4) from the results pertaining to the case where time courses were extracted from sLORETA solutions. The results of connectivity analysis when activation time-courses are extracted directly from sLORETA solution are presented with the localization error (of network nodes) in Fig. 5. To compare the connectivity results two measures are used: correlation and normalized error. The true DTF/PDC matrix is derived from simulated time-courses, first. The DTF/PDC are N×N×F matrices where N is the number of network nodes or time series and F is the number of frequency bins at which the DTF/PDC is calculated. These three-dimensional matrices are averaged over frequency to obtain two-dimensional matrices (N×N) which bear average information regarding the connectivity among nodes over the span of the spectrum. These average DTF/PDC matrices are computed for the original and estimated time-courses, as mentioned before. To compare these two matrices which show the pattern of connectivity among nodes, a simple metric would be to look at the correlation coefficient between the DTF/PDC matrices of the simulated and estimated time-courses. Basically, the estimated DTF/PDC is computed and correlated with the true DTF/PDC to see how close the two matrices are (higher values indicate a better match).

Fig. 4. Simulation results (I).

The connectivity performance of the sensor-space connectivity (left column) and the source-space connectivity (right column) are presented in this figure. The source-space connectivity is for the case where the nodes’ locations are estimated from sLORETA but the time series are estimated from projecting the scalp potentials to the known lead field columns. Error bars depict standard deviation. Refer to Eq. (9) in the Methods section for more details.

Fig. 5. Simulation results (II).

The connectivity results for a simulated network (a particular configuration: left upper panel) is presented (left column) for different electrode configurations and SNR levels, as an example. The “ground truth” network connectivity map, i.e. simulated network, is depicted in the upper middle panel. The localization error (of network nodes), and connectivity metrics are also depicted for the case where the activation time-courses are extracted from sLORETA solutions (right column). Error bars depict standard deviation. Refer to the Methods section for more details.

Additionally the estimated and true DTF are normalized by the total outflow (sum of the elements in each column of the DTF matrix) of the network nodes (to better deal with potential scaling) and the norm of the difference is calculated (smaller values indicate a better match). This metric basically seeks the norm of the difference between the original and estimated DTF/PDC matrices (the norm of the matrix obtained by subtracting the DTF/PDC matrix derived from original and estimated time-courses). Thus, it can be concluded that the correlation matrix measures the similarity of the estimated DTF/PDC matrices with the ground truth while the normalized error measures the deviation of the two. The simulation results are summarized in Fig. 4 and 5. Sensitivity and specificity were also calculated to determine the performance of the simulations results. Please refer to the supplementary materials to review these results and for more details.

Additionally the DTF values were computed on the sensors. To avoid applying the analysis on all electrodes (due to the large number of electrodes), three electrodes were selected for further Granger causality analysis. The scalp maps (for each network configuration and noise level) were searched to find electrodes that demonstrated strong and frequent activity (over the simulation time course) compared to their neighboring electrodes; basically being a local maxima in the scalp topography. Among all such electrodes, the three electrodes demonstrating the strongest activity (over the scalp map) were chosen as the three nodes of the network reflecting the underlying three brain network nodes. Although, knowing the number of nodes a priori is not usually an option in practice, this approach was pursued to provide a fair framework to compare sensor space connectivity and source space connectivity. The results of sensor and source space connectivity are presented side by side, in Fig. 4, for better comparison.

E. The Effect of Correlated Noise

In order to more realistically model the problem, a new set of simulation studies were conducted in which correlated noise (in sensor space) was also included (in addition to the white noise added in sensor level modeling the measurement noise). White Gaussian noise was added in all source locations to model background activity of the brain [55], thus source level and sensor level noise were included in this new simulation study to better model various possible noise sources. The results of these simulations are presented in the supplementary section (Fig. S1). The results (in terms of localization error of network nodes and connectivity measures) do not change drastically.

F. Clinical Studies and Data Acquisition

Two epilepsy patients suffering from medically intractable focal seizures were included in this study. The study was performed based on a protocol approved by the institutional review boards (IRB) of the University of Minnesota, Mayo Clinic and Allina Hospitals and Clinics. The patients had undergone surgery and were seizure-free after the surgery. The first patient was a parietal-lobe epilepsy case which was seizure-free for a period of one year post-operation and the second patient was a temporal-lobe epilepsy patient who became seizure-free during a follow-up of 6 months post-operation.

The first patient had pre-operational scalp EEG recordings with multiple ictal recordings and also underwent intra-cranial EEG recordings before the surgery. A total of 76 EEG channels sampled at 500 Hz were recorded in this patient (Mayo Clinic). The EEG was later filtered between 1 and 50 Hz for DSI analysis. Three seizures in this patient were analyzed. ECoG electrodes marked as SOZ (by the physician) was available in this patient. The surgical resection surface was also extracted from post-operational MRI. Such clinical findings were used to validate the DSI results (sLORETA was used to invert each IC). After the seizure was imaged and ictal components were derived, the time-course of the location pertaining to the maximum dipole strength for each IC map, were extracted and input into ADTF analysis to determine, which component drove the brain into ictal activity.

Pre-operational structural MRI (voxel size: 0.937×0.937×1.2 mm3, 196 slices) obtained from a 3 Tesla GE Signa scanner (General Electric Medical Systems, Milwaukee, WI) were used to create the BEM model, as detailed above. The BEM model was reconstructed using Curry software (Compumedics, Charlotte, NC).

The second patient suffered from temporal lobe epilepsy. Simultaneous 64-channel EEG and 148-channel MEG were recorded inter-ictally with a 1KHz sampling rate (Allina Hospitals and Clinics). The EEG and MEG were filtered between 1 and 50 Hz for later analysis. Intra-cranial recordings were not available in this patient but post-operational MRI was used to extract the surgically resected surface. The EEG and MEG recordings were monitored for inter-ictal spikes (IIS) and averaged IIS were input into the MN inverse algorithm [41] to estimate underlying epileptic networks to determine the epileptogenic zone. Utilizing the theory of Granger Causality and computing ADTF, directional connectivity among the ROIs (determined by source imaging) was estimated from the activity time-course (estimated from source imaging results). The shuffling procedure destroying the phase information of the original signals was repeated 1000 times and the DTF values with the significance level (p < 0.05) were considered as true connections based on which the primary region responsible for seizure generation was determined.

III. Results

A. Computer Simulation

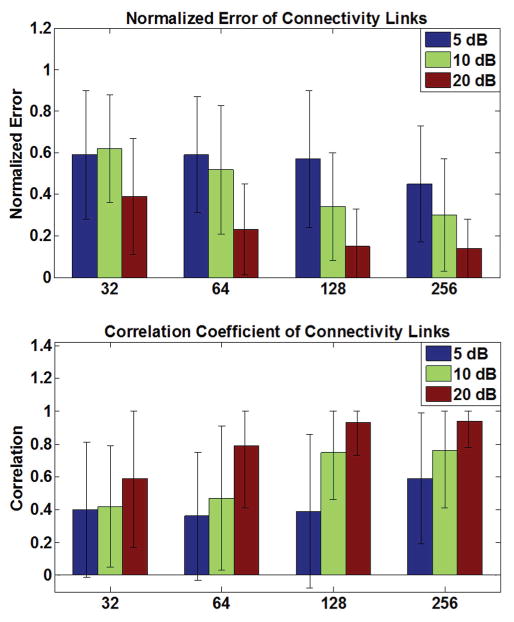
The simulation results are presented in Fig. 4–6. Comparing the results in Fig. 4 and Fig 5, it is observed that connectivity results in sensor space show more spurious activity than source space results (smaller correlation values and higher normalized error values). This is expected due to the volume conduction effect and mixing, as previously reported for Granger causality analyses [56], [57]. Comparing Fig. 4 and Fig. 5, it is also interesting to note that connectivity results are slightly better when the time-course of source activation is estimated (Fig. 4, right column) using (9) compared to the case where the time-courses are extracted from sLORETA solution (Fig. 5, right column). Comparing the results of PDC analysis in Fig. 6 with DTF analysis results in Fig. 4 and 5, it can be observed that PDC analysis seems to perform slightly better. While DTF and PDC both measure directed connectivity, DTF analysis measures the non-direct and direct effects while PDC is claimed to measure the direct effects [21]. Given that the metrics used to quantify the performance of our simulation studies (correlation and normalized error), measure direct links and penalize non-direct links, the obtained results were expected. It is worthy to note that, in practice both direct and non-direct connections are important; for instance, when trying to determine the source of seizure in an epileptic patient. Philosophically, one could also argue that non-direct links are causally related as well. For example, if node A is driving node B and node B is driving node C, it could be argued that node A is driving node C (as long as we believe that causality is a transitive property).

Fig. 6. Simulation results (III).

The connectivity results using PDC as the connectivity measure, is presented for different electrode configurations and SNR levels. Comparing with DTF analysis results, some improvement is observed. Error bars depict standard deviation.

The localization error presented in Fig. 5 (right column), shows that in general, node locations can be extracted relatively precisely even under noisy conditions. The localization error calculated pertains to the localization error of network nodes for all the conditions. Another interesting phenomenon observed, is that not only the localization error decreases once more EEG channels are recorded, but the improvement rate decreases, as well. Effectively, a “plateauing effect” can be observed [58]. It also seems that in lower SNRs the improvement due to using more electrodes is more prominent. Similar patterns can be observed for connectivity results, where including more electrodes improves the results to a certain point. Note that the correlation metric shows also a saturating effect towards higher values (higher connectivity values in configurations which have more electrodes).

B. DSI Analysis in Parietal Lobe Epilepsy Patient

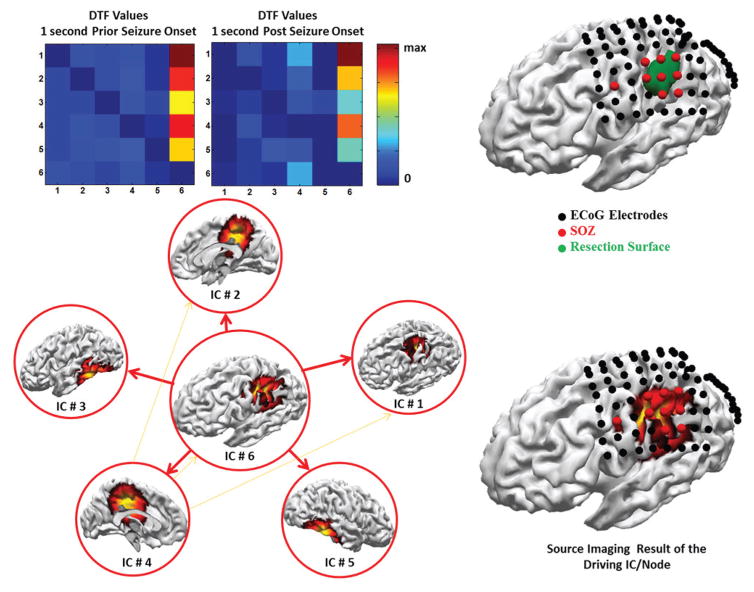
The combined DSI and ADTF analysis for patient 1 is presented in Fig. 7. In this figure the ICs related to the ictal activity are presented (in source space). The location corresponding to the strongest dipole for each inverted IC map, was selected as network nodes. In the following when we refer to IC we are really referring to the inverted IC map as we are interested in the location and spatial distribution of each component to determine where in the brain it is arising from. After the time-course from different ICs were recombined in the source space, the total activation time-course for each of those nodes were extracted for further ADTF analysis. The ADTF values were averaged for a period of 1 second prior to seizure onset and post-ictally in the 1 to 20 Hz frequency band (where most of the seizure spectrum power is concentrated) and are presented in Fig. 7 (denoted as DTF values as averaged over time).

Fig. 7. Identifying epileptic networks from ictal signals in patient I.

Dynamic seizure imaging is applied to the seizures recorded in the EEG of this patient prior to surgery to identify the nodes of the ictal network. ADTF analysis was then applied to combined source space signals to determine the driving IC (left). The identified IC is in good accord with clinical findings, i.e. SOZ electrodes and surgical resection (right).

As it can be seen from the ADTF analysis (Fig. 7) the component which is driving the ictal network is IC #6. This is reflected in the DTF values presented; by looking at the DTF-value matrix it can be observed that the 6^th column of this matrix demonstrates high DTF values (hot colors). This means that the 6^th node of the network is driving the other nodes while no reciprocal back-activations are observed in the network (look at the almost zero values of other elements of the connectivity matrix). It can be concluded that the 6^th node corresponding to IC #6 is the driving node of the epileptic network. The location of this node is in the ipsilateral side of the resection hemisphere and furthermore corresponds with SOZ electrodes pretty well (red electrodes in Fig. 7). The aforementioned IC corresponds well with the resection, as well. Another interesting observation is that post-ictally the seizure starts to propagate, and another component (IC #4) also begins to drive other nodes of the ictal network (look at the increasing DTF values of the 4^th column of the DTF-value matrix which is still much weaker compared to IC #6). Seizure propagation is one important reason, why directional connectivity analysis such as Granger causality is crucial in studying epilepsy networks and identifying the seizure onset zone.

C. Inter-ictal Activity Analysis for E/MEG Recordings in a Temporal Lobe Epilepsy Patient

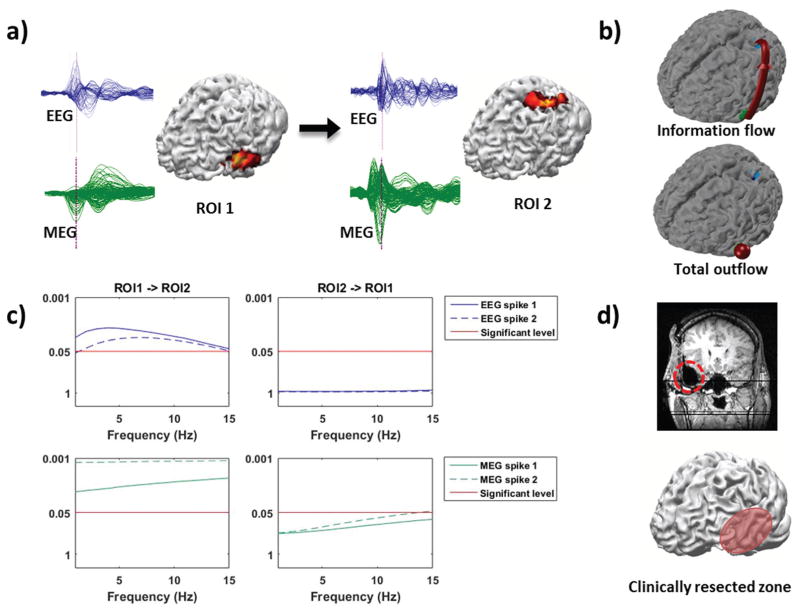
The source imaging and connectivity analysis results of patient 2 are shown in Fig. 8. Two types of spikes (both observed in EEG and MEG) were observed. One type of the extracted spikes, localized to the temporal region (21 spikes in EEG and 23 spikes in MEG), and the other type to the left parietal-occipital region (8 spikes in EEG and 8 spikes in MEG), when the inverse problem was solved for the peak of the averaged spike. The spikes were averaged and the MN solution was obtained to find regions of interest (ROIs). ROIs found using both EEG spikes and MEG spikes overlap well with each other (ROI centers are within 10 mm). In Fig. 8(a), the source locations and extent are displayed with the cortex model constructed from the pre-operative MRI of the patient. The averaged spikes are also displayed next to the sources in Fig. 8(a). Spikes in the left column of a) (spike 1) were used to find ROI 1 and spikes in the right column of a) (spike 2) were used to find ROI 2.

Fig. 8. Identifying epileptic networks from IIS in patient II.

(a) Spikes (blue from EEG, green from MEG), estimated sources, and directional causality of two regions of interest. (b) Information flow direction and comparison of total outflow volumes between the two ROIs depicted on cortex model. (c) Statistical testing results of DTF values between the two ROIs. DTF values above the red line are significant with a corresponding p-value < 0.05. (d) Surgical resection marked by red dotted line on post-operative MR image and red oval on the cortex model. This patient suffered from left temporal lobe epilepsy, and is seizure-free after the resection.

The arrow between the two panels of Fig. 8(a) indicates the information flow derived from connectivity analysis, directing from the primary source to the secondary source where the epileptic activity propagates after being generated by the primary source. This can also be seen from the information flow direction and comparison of total outflow volume (between the two nodes) in Fig. 8(b). The significance level of DTF information flow between ROI 1 and ROI 2 is depicted in Fig. 8(c) as a function of frequency. What these curves reflect are the significance of the calculated DTF value as compared to the surrogate DTF values for every frequency in the 1–15 Hz frequency band where signal energy is most concentrated in; thus only DTF values that are statistically significant and are above the red line indicate meaningful connections. DTF results above the red line pass the significance level (p < 0.05) of the information flow and are thus significant (refer to the Methods section for more detail on the shuffling process). In this patient, ROI 1 shows significant information flow to ROI 2 while no such significance can be observed from ROI 2 to ROI 1. Both spike 1 and spike 2 were used to calculate the DTF values and the connectivity results presented in Fig. 8(c) indicates that the flow from ROI 1 to ROI 2 passes the significance level (left column) while the flow from ROI 2 to ROI 1 does not pass the significance level (right column). Thus, ROI 1 which is located in the left temporal lobe was identified as the primary source. Fig. 8(d) shows the post-operative MR image with the red line marking out the surgically resected area. The resection is also approximately marked with the red oval on the cortex. The results indicate that source imaging results and connectivity analysis results from E/MEG coincide well with the clinical findings and analyzing IIS network sheds light on the underlying epileptic network.

IV. Discussion

This study along with previous studies has shown the usefulness and strength of combining source imaging with directional functional connectivity analyses, in particular Granger-Geweke Causality analysis [23], [24], [30]–[32], [47], [59]. Furthermore, we have shown in this study that ESI algorithms can be used to identify network nodes in an objective matter in addition to activation time-course extraction, under realistic conditions and in data recorded in clinical settings.

Granger causality analysis is basically a data-driven technique where no prior assumptions about the type, direction and strength of interactions among the network nodes are assumed. As opposed to data-driven techniques, model-driven techniques assume prior models about the underlying network interactions and update the model parameters or compare between different viable models to choose the model that best explains the data. Structural equation modeling (SEM) and dynamic causal modeling (DCM) are two noteworthy algorithms belonging to the model-based category [60], [61]. The number of citations for both DCM and Granger causality analysis has been increasing over the past years [62]. In order for DCM to work efficiently, the experiment has to be designed in such a manner that brain responses can be measured and a good prior model to explain the observations and hidden states of the model should exist; additionally many alternative models need to be assumed as well to ensure unbiased results [63]. This means that DCM computations can be time-consuming and that there must be enough prior knowledge about the network under study to be able to construct alternative models and hypothesis, whereas in Granger causality analysis such issues are not met. However, this enables DCM to deal with nonlinearity and non-stationarity. It should be noted though, that nonlinear and adaptive Granger causality analysis techniques have been proposed which could potentially circumvent the difficulties caused by non-stationarity and nonlinearity [16], [33], [64]. All in all, Granger causality analysis and DCM might have more in common (although based on different premises) and ultimately converge in many ways [65].

Granger causality methods have been criticized for being susceptible to noise [66], [67]. Haufe et al. [67] have shown in a simulation study (sensor space) that conventional Granger causality analysis and surrogate testing by phase shuffling, might not be as effective as measures such as phase-slope index (PSI) [68], [69]. Haufe et al. have also proposed an time-reversed scheme for Granger causality analyses and have shown that this improves the results and makes it as good as PSI performance [67], [70]. A later study by Vinck et al. demonstrated that correlated and uncorrelated noise might have different effects on the causality analysis results [57]. They also demonstrated that the time-reversed scheme applied to Granger causality analysis produces much less false positives compared to PSI or conventional Granger analysis results in case of correlated noise [57]. Nalatore et al., have also applied a combination of kalman filtering and expectation maximization denoising algorithm to alleviate this problem [71]. This can be thought of as another opportunity for ESI algorithms to remove the effect of correlated and uncorrelated noise through the process of solving the inverse problem, provided that noise covariance matrix is estimated and dealt with properly [72]. This can also be observed in our simulations where uncorrelated noise in the sensor space and correlated noise in the source space were used in simulations, yet the network nodes and inter-connections were detected (refer to Supplementary section). Our simulation results and specifically the comparison between sensor and source space connectivity results attest to the fact that solving the inverse problem helps in removing spurious connections otherwise occurring in sensor space connectivity analyses. It must be stated though, that due to the difficulty of removing volume conduction effects, some errors and spurious connection might be detected [73], [74]. Thus the choice of the inverse algorithm, noise level, electrode configuration and connectivity analysis used can all affect the results, as comprehensively demonstrated in this work. Additionally, selecting a handful of electrodes to perform the sensor space connectivity could potentially induce some erroneous results when studying the connectivity. This issue seems very difficult to circumvent for practical and theoretical reasons. Firstly, due to the high number of electrodes used in this study (which also seems to be a general trend), performing connectivity analysis on all electrodes is very time consuming [75], [76]. Additionally, since we simulated a network with finite number of nodes, in order to compare the results we needed to match the number of nodes in the estimated and simulated network, thus selecting a somewhat optimal set of electrodes was unavoidable. Secondly, the sensor and source spaces are very distinct spaces and it is very difficult to meaningfully relate the connectivity results derived in the sensor space to anatomical regions in the brain. While solving the inverse problem might add some difficulties, our simulations results demonstrate that once applied with tact and care, much can be gained.

Recently, sparse connectivity networks have been proposed as well [77]–[79], which might prove to be more robust against spurious connections and links. Information theoretic measures might also prove useful in determining underlying connectivity of brain networks effectively [80].

Volume conduction and mixing in the source space could potentially cause Granger analysis results to detect more spurious links [81]. Although, solving the inverse problem could potentially neutralize the effect of volume conduction, but it cannot remove the effects completely. Our simulations results also showed the detrimental effect of volume conduction on estimating connectivity. It was observed that sensor space connectivity results show much more spurious connections than source space connectivity results. Hui et al. performed a simulation study, starting from ECoG recordings and solving the forward problem to obtain corresponding EEG signals [56]. Then by solving the inverse problem and going back to the cortex, calculated the connectivity on the ECoG nodes (a priori known locations) and compared their results to the connectivity derived from directly feeding the ECoG activity into the Granger causality analysis. They have shown that MN-type solutions might detect erroneous links, due to the ineffective removal of volume conduction and proposed to use a nulling beamformer technique to alleviate this problem and have shown improvements [56]. While nulling beamformer can be very effective, it only works well if the number of ROIs are less than number of measurements (electrodes) and the location of the nodes need to be specified prior to applying the method, which could limit its application in practice. On a similar note, Cheung et al. proposed a combined algorithm where estimating the MVAR model of the source activity and solving the inverse problem is combined into one step rather than two steps [82] and show that their method is less susceptible to detection of erroneous connections. However, this method also needs the prior knowledge of network nodes on the cortex, which is generally unknown in practice.

Another work by Gómez-Herrero et al. attempts to estimate the MVAR model for the underlying sources from the MVAR model of EEG signals, essentially performing an inverse by cancelling the volume conduction effects [83]. The volume cancellation was achieved through a process of removing instantaneous connectivity of the sources (which is due to volume conduction and not neurophysiological processes as neurological connections happen with delays due to synaptic delays) applying ICA [83]. This approach of solving the inverse problem may lead to spurious results depending on the type of noise present, and is quite different from the approach adopted in our work.

The combined ESI and A/DTF analysis presented in this paper seems a viable path to objectively estimate network nodes and interactions. It has been tested in previous studied specifically in estimating epilepsy network nodes [31], [32], [84], [85]. Other networks like the pain network have also been studied using combined ESI and ADTF analysis [86]. However, for inverse solutions to be accurate enough, the number of measurements needs to be large enough. Placing electrodes on the scalp can be thought of as a spatial sampling process [87], [88], thus using too few electrodes can result in undersampling and aliasing happens. The effect of electrode numbers on source localization has been studied previously [28], [32], [58], [89], [90]. As it has been shown in these studies, source localization accuracy is improved when more electrodes are used but the rate of improvement decreases with the increasing electrode number. This plateauing effect has been observed in localization error (network nodes) and connectivity performance in the results presented in this paper, as well. This is an interesting observation for connectivity measures and our results are the first to quantify the effect of electrode number on the accuracy of estimated networks, to the best of our knowledge. Our results indicate that high density electrode configuration (64 electrodes and above) is needed for more accurate localization of network nodes, as well as the underlying connectivity. The simulations results provided in this paper quantify this effect to some extent.

In this study we estimated the nodes’ locations by finding the dipole location with the maximum amplitude within the distributed current density estimation (which is consistent with our simulations). This might not be the case when studying brain networks, thus being able to estimate the extent of underlying brain networks seems crucial and has to be assessed further in the future. We have proposed a source imaging algorithm that can potentially achieve this goal by objectively estimating the source extent [91], and would be useful once implemented in the framework of combined ESI and A/DTF analysis.

In this paper we looked at the application of Granger causality analysis in identifying epilepsy networks, as in such clinical cases independent information about the underlying sources and connectivity would be available through intracranial recordings or validated by surgical resection. Inter-ictal recordings from EEG and MEG [30], [35], [84], [92], [93], as well as ictal signals have been analyzed to delineate underlying brain networks’ connectivity [31], [32], [94], [95]. Investigating network connectivity in resting state has also been adopted recently, and seems encouraging [96]–[98]. These functional connectivity studies add to our knowledge about localization and imaging of epileptogenic networks using various source imaging techniques alone [28], [51], [91], [99]–[101].

Combining the A/DTF connectivity analysis with the DSI algorithm to identify driving nodes of the ictal network is another novel feature of this work. Previously, Yang e al. [51] used the initial segment of the ictal recordings (after seizure onset) to localize ictal sources and showed good concordance with clinical findings, but did not perform A/DTF analysis on the results to identify the ictal network and its causal links. We believe that the example presented in this paper, could potentially be applied to ictal recordings and lead to a better understanding of ictal networks, as more information about the underlying connectivity can be provided. This is of importance in studying ictal networks as such networks could evolve in a fast pace and propagate from the initiation site pretty fast, making it difficult to identify the SOZ. The proposed DSI and A/DTF integrated analysis might provide a better framework for studying ictal networks.

Another novel aspect of this work is the application of the combined approach to study epileptogenic networks using inter-ictal spikes recorded from simultaneous EEG and MEG. While Dai et al. [30] used inter-ictal spikes from MEG to study the epileptic networks and reported results which were in agreement with clinical findings, no study to date has applied the combined ESI and ADTF analysis in simultaneous EEG and MEG recordings to study epileptic networks, to the best of our knowledge. This approach could potentially provide more insight into the nature of epileptic networks as EEG and MEG have different sensitivity to source location and orientation and thus could potentially provide slightly complementary information about underlying epileptic sources [102], [103]. The presented example in this paper showed EEG and MEG results to be consistent and in agreement with each other, but this approach could potentially lead to more comprehensive findings in the future. All in all, we have demonstrated in this paper that both ictal and inter-ictal signals can reveal valuable and relevant information about the underlying epilepsy networks by means of the combined ESI and A/DTF analysis framework.

Functional brain connectivity mapping could potentially help address the grand challenges of studying the brain [9], [25]. A number of studies have looked into various metrics of connectivity among multiple brain regions from EEG/MEG [47], [104]–[112] and from fMRI [113]–[120]. In addition to Granger causality and DCM approaches, graph theoretic methods have also been used to study brain functional connectivity from ECoG [121] and EEG [122], [123].

V. Conclusion

This work demonstrated the possibility of using the combined ESI and A/DTF analysis approach to identify the network nodes, extract activation time-courses and ultimately estimate the directional inter-nodal connections in an objective manner, in computer simulations and clinical data analysis. We presented two new approaches in epileptic network analysis which can potentially further our understanding of underlying mechanisms of focal epilepsy.

In conclusion, this work along with the existing literature has demonstrated the efficacy and usefulness of combined ESI and A/DTF analysis in non-invasively studying underlying brain networks from surface measurements (EEG and MEG). ESI algorithms can help identify the nodes of the network and source activation time-courses and in combination with A/DTF analysis the directional inter-nodal connections and causal links can be estimated. The present simulation and clinical evaluation results are promising and provide a quantitative assessment of directional connectivity estimated from noninvasive EEG/MEG measurements.