Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2004 Sep;14(9):1786–1796. doi: 10.1101/gr.2395204

De Novo Repeat Classification and Fragment Assembly

Paul A Pevzner 1, Haixu Tang 1, Glenn Tesler 2,3
PMCID: PMC515325  PMID: 15342561

Abstract

Repetitive sequences make up a significant fraction of almost any genome, and an important and still open question in bioinformatics is how to represent all repeats in DNA sequences. We propose a new approach to repeat classification that represents all repeats in a genome as a mosaic of sub-repeats. Our key algorithmic idea also leads to new approaches to multiple alignment and fragment assembly. In particular, we show that our FragmentGluer assembler improves on Phrap and ARACHNE in assembly of BACs and bacterial genomes.

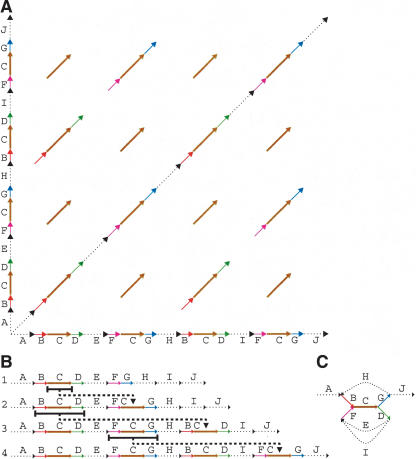
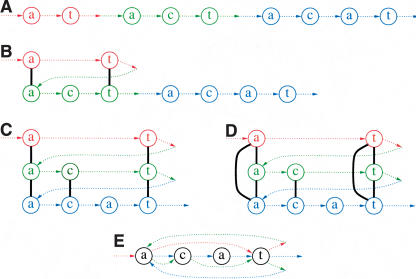
A fundamental and still open question in bioinformatics is how to represent all repeats in a genomic sequence. In a pioneering paper, Bao and Eddy (2002) wrote, “The problem of automated repeat sequence family classification is inherently messy and ill-defined and does not appear to be amenable to a clean algorithmic attack.” One of the difficulties in repeat classification is that many repeats represent mosaics of sub-repeats (Bailey et al. 2002). Different combinations of sub-repeats form different repeat copies (Fig. 1A), making it difficult to delineate the boundaries of sub-repeats (repeat boundary problem) and to represent the overall repeat structure.

Figure 1.

Figure 1

Open in a new tab

(A) Genomic dot-plot of an imaginary sequence with repeats containing sub-repeats. How many repeats are really present? The coloring shows the repeats from which it was constructed. In a real sequence, we would not know the sub-repeat structure and thus we would not be able to color the dot-plot. Also, because the repeats would not be perfect, there would be gaps, substitutions, and indels distorting each diagonal. In certain applications, there would be reverse diagonals, corresponding to alignments with opposite strands. (B) An imaginary evolutionary process leading from a repeat-free genome to the genome in A with four repeat copies. Each step duplicates a region and inserts it elsewhere. (C) Gluing repeated regions leads to the repeat graph of the final genome. Deleting the multiplicity 1 edges (shown dotted) in this graph leaves a single component, called a tangle or repeat. It consists of five edges B, C, D, F, G (shown solid) called sub-repeats. Every new duplication in B creates a more and more complicated tangle describing an evolving repeat structure. The graph structure of this tangle documents the evolutionary history of duplications.

Figure 1A shows a genomic sequence with repeats already decomposed into sub-repeats as well as a “genomic dot-plot” representing all local alignments within this sequence. However, constructing such a decomposition is a nontrivial problem (Bailey et al. 2002) that is often a prerequisite to further repeat classification and analysis. In this paper, we address the problem of deriving the mosaic repeat structure from a set of pairwise similarities. Although this problem is easy to solve for the toy example in Figure 1A, gaps, poorly defined alignment endpoints, and inconsistencies in local alignments make it rather difficult for real genomic sequences.

The mosaic structure of repeats is best revealed by the de Bruijn graph (de Bruijn 1946), and in this paper we advocate use of these graphs for repeat representation. However, the de Bruijn graph represents repeat families as mosaics of “perfect” (error-free) sub-repeats, whereas repeat families in DNA sequences are mosaics of sub-repeats that typically include mismatches and gaps. Unfortunately, the de Bruijn graph is not defined for such approximate similarities, and therefore repeat representation in DNA sequences remains, indeed, messy and ill defined. In this paper, we generalize the notion of the de Bruijn graph for imperfect repeats and provide a well-defined algorithmic solution for the repeat representation problem. For an arbitrary set of pairwise alignments 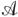Inline graphic , we introduce a new graph (called the A-Bruijn graph) that generalizes the de Bruijn graph. The applications of A-Bruijn graphs in bioinformatics extend well beyond repeat classification and include multiple alignments and fragment assembly.

Repeat classification is a multifaceted problem that covers many biological tasks, ranging from characterization of mobile elements to analysis of mosaic structure of segmental duplications. The solution of all these problems often starts from defining the boundaries of “elementary repeats”4 (the repeat representation problem), which is the focus of this paper. Many other aspects of repeat classification (like characterization of repeat sub-families or further analysis of sub-repeats with the goal to identify the transposable elements) remain outside the scope of this paper. The repeat representation problem is not limited to repeat analysis; in fact, fragment assemblers implicitly face a similar problem while assembling repetitive regions. However, in the past there was little overlap between fragment assembly and repeat classification research despite the fact that these two problems are computationally very similar. In this paper, we establish the connection between fragment assembly and repeat classification and show that they both can be viewed as special cases of our A-Bruijn graph approach.

The best known programs for repeat annotation are Repeat-Masker (A.F.A. Smit and P. Green, unpubl.) and MaskerAid (Bedell et al. 2000), which use precompiled repeat libraries to find copies of known repeat families represented in RepBase. However, the repeat libraries have to be manually compiled for any new genome because they are genome-specific. De novo compilation of the RepeatMasker libraries remains a challenging bioinformatics problem.

A very useful approach to repeat analysis is to simply list all pairs of repeated regions. RepeatMatch (Delcher et al. 1999) and REPuter (Kurtz et al. 2000, 2001) are efficient computational tools that can find repeats even in very long genomic sequences. However, their approach (based on pairwise alignments) does not provide a compact overview or summary of the repeat families in the genome. On the other hand, construction of multiple (rather than pairwise) alignments of repeats is a difficult and still unsolved problem. Moreover, even if this problem were solved, repeat family classification would remain an open problem: Different copies of a repeat often have different lengths and have mosaics of sub-repeats not adequately represented in a multiple alignment (Volfovsky et al. 2001; Bao and Eddy 2002; Lee et al. 2002).

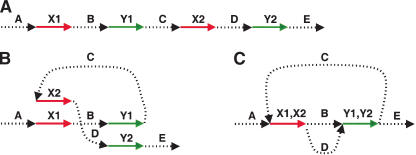
Figure 2 illustrates the idea of our approach. By gluing points together, repeats in a DNA sequence transform a genomic sequence into the A-Bruijn graph described below.

Figure 2.

Figure 2

Open in a new tab

(A) A hypothetical DNA sequence with unique regions A, B, C, D, E and repeats X (appearing twice as X1 and X2) and Y (appearing twice as Y1 and Y2). (B) Same sequence, drawn differently to prepare for gluing of repeats. (C) Glue together repeats.

Repeats are caused by an evolutionary process, and an important goal of repeat classification is to reveal the evolutionary relationships between different copies of repeats. Figure 1B shows an imaginary evolutionary process leading to a “genome” with four repeat copies. The duplication process creates an intricate structure of sub-repeats in this genome (shown by several colors), and the question arises how to represent this structure. The multiple alignment approach would represent all four repeats by sub-repeat C—the only one that is present in all four copies. Therefore, the consensus repeat representation erases important evolutionary relationships between different repeat copies. A more general approach would be to represent each repeat as a mosaic (tangle) of sub-repeats (Fig. 1C), but it is not clear how to define and efficiently construct this representation.

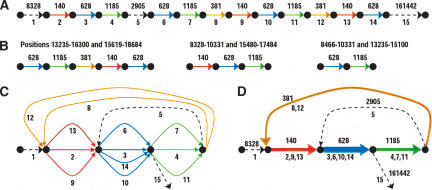
Figure 3A is an illustration of this mosaic repeat organization for a BAC from human Chromosome Y (GenBank ID: AC006983) with a relatively simple repeat structure. This BAC has several repeats formed by four sub-repeats: a red one of (consensus) length 140 with multiplicity 3, a blue one of length 628 with multiplicity 4, a green one of length 1185 with multiplicity 3, and a brown one of length 381 with multiplicity 2. These lengths are the consensus lengths; each individual segment's length may vary slightly. We emphasize that the partition of repeats into sub-repeats shown in Figure 3A is not immediately apparent, and the goal of repeat classification tools is to reveal this partition. REPuter outputs three repeat “pairs” (Fig. 3B), whereas RepeatFinder and RECON each outputs a single repeat family represented by three repeat copies (note that the Repeat-Finder classification differs from the RECON classification). All these programs fail to reveal the mosaic structure formed by red, blue, green, and brown sub-repeats and to correctly identify the maximum multiplicity in this case (4, as defined by the multiplicity of the blue sub-repeat).5 RepeatGluer uses a graph representation (Fig. 3C,D) that reveals the mosaic structure of sub-repeats and correctly identifies all multiplicities. One can visualize the graph in Figure 3D as the result of “gluing” of all sub-repeats of the same color. This “gluing” is easy to do when the sub-repeat structure is known in advance. We describe an algorithm for generating such graphs (and thus revealing the mosaic structure of repeats) without knowing the mosaic structure of repeats in advance.

Figure 3.

Figure 3

Open in a new tab

Mosaic repeat organization of BAC from human Chromosome Y. For purposes of illustration, only sufficiently long and very conservative repeats are shown. (A) Partitioning of BAC into 15 segments (numbers shown underneath) with approximate lengths of the segments shown on top. Each dashed black line represents a unique region. Each color represents a different repeat region, and occurs multiple times. (B) Repeat pairs constructed by REPuter are just the numeric ranges shown on the first line. These correspond to our division into sub-repeats, shown as colored segments on the second line, but REPuter does not identify the four sub-repeats. (C) Repeat multigraph. The edges with labels 1, 2,..., 15 form a path through this graph corresponding to the sequence in A. (D) Repeat graph, with repeated regions collapsed together. The repeat graph reveals the presence of four sub-repeats in this BAC as edges with multiplicity >1.

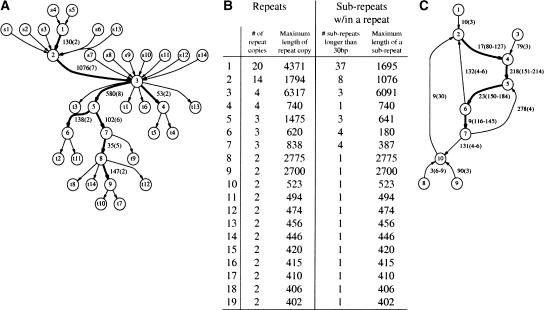
Figure 4A illustrates how the process in Figure 1B materializes in larger genomes. It represents the structure of a 14-copy transposase IS30 repeat family in the Neisseria meningitidis genome formed by eight sub-repeats of various lengths (every repeat copy may include one to four sub-repeats). Figure 4A illustrates a complicated evolutionary history of duplications with widely varying (rather than fixed) duplication endpoints. Each duplication may produce a longer or shorter version of a repeat and eventually gives rise to new sub-repeats.

Figure 4.

Figure 4

Open in a new tab

RepeatGluer representation of a 14-copy transposase IS30 repeat family in the N. meningitidis genome as a mosaic of eight sub-repeats >30 bp (shown by bold edges). The similarity matrix A is constructed based on a 90% similarity threshold and minimum repeat length 400. (A) Transposase IS30 family tangle (with adjacent edges) in the repeat graph. Every repeat copy corresponds to a path from a source sI to a sink tI. Edge label 130(2) indicates the length of the sub-repeat (130 nt) and its multiplicity (2). (B) Summary of all 19 repeat families (>400 bp with 90% similarity threshold) produced by RepeatGluer in the N. meningitidis genome. (C) Simplified tangle corresponding to the most common Alu repeat family in the first 1 Mb of human Chromosome X. Because the real tangle (even for 1 Mb sequence, let alone the entire genome) is too complicated, we removed all edges with multiplicities smaller than 3. This Alu repeat is broken into four sub-repeats with multiplicities ranging from 116 to 214. The multiplicities of every sub-repeat vary along the length of sub-repeat because many Alu repeats are incomplete versions of the canonical Alu (e.g., the multiplicity of the sub-repeat of length 218 varies from 151 to 214).

Figure 4B shows a summary of all 19 long repeats in the N. meningitidis genome. The most complicated 20-copy repeat in the N. meningitidis genome consists of 37 sub-repeats. In many bacterial genomes, a series of duplication events has created a rather complex mosaic of sub-repeats, and decoding the evolutionary history of duplications remains an open problem. Repeats in eukaryotic genomes are a few orders of magnitude more complicated, and their classification is a challenging problem with important applications in evolutionary studies. In particular, we are unaware of another algorithm that would automatically generate a summary of all sub-repeats in a bacterial genome similar to the one presented in Figure 4 or the mosaic representation of segmental duplications in the human genome (Bailey et al. 2002).

The early single linkage clustering approaches to repeat classification (Agarwal and States 1994; Kurtz et al. 2000) start from finding pairwise similarities and use clustering to group similar sequences together. Although finding pairwise similarities can be done efficiently, clustering of these similarities presents a serious problem because local sequence alignments do not typically correspond to the biological boundaries of a repeat (Bao and Eddy 2002). Volfovsky et al. (2001) and Bao and Eddy (2002) recently developed new heuristic algorithms for de novo repeat classification that perform well in practice (RepeatFinder and RECON). However, these approaches lack the generality of the de Bruijn approach, and our goal is to develop an efficient repeat classification tool that would match the power of the de Bruijn approach.

The use of the de Bruijn graphs in computational molecular biology goes back to the late 1980s (Pevzner 1989). Idury and Waterman (1995), Pevzner et al. (2001), Shamir and Tsur (2001), Heber et al. (2002), Peer et al. (2002), Li and Waterman (2003), Zhang and Waterman (2003), and Bocker (2003) further applied de Bruijn graphs to fragment assembly, resequencing with DNA arrays, EST analysis, and computational mass spectrometry. The de Bruijn graph represents every l-mer in a genomic sequence as a vertex and connects two vertices by a directed edge if they correspond to a pair of consecutive (overlapping) l-mers in the genome (see the books Gusfield 1997 or Pevzner 2000 for more details). The multiplicity of this edge is the number of such l-mer pairs. The genomic sequence corresponds to an Eulerian path in the resulting multigraph. “Tangles” in this graph (Pevzner et al. 2001) describe the mosaic structure of sub-repeats.

Although de Bruijn graphs were very successful in many applications outside bioinformatics (including coding theory, network design, optimal routing, the NASA Galileo project, etc.), all these applications refer to the representation of “perfect” repeats, and it is not clear how to adjust the powerful de Bruijn approach (or suffix tree approach) to the case of approximate repeats. As a result, until recently, de Bruijn graphs were of little use in the analysis of real repeat families with many mismatches and gaps.6 Below, we generalize the notion of the de Bruijn graph to work with imperfect repeats and introduce the concept of the A-Bruijn graph, defined for an arbitrary collection of alignments 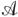Inline graphic . The A-Bruijn graphs are equivalent to the de Bruijn graphs in the special case that 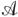Inline graphic is the collection of all perfect similarities of length l (l-mers).

Based on the notion of A-Bruijn graphs, we developed the RepeatGluer algorithm (available from http://nbcr.sdsc.edu/euler/) to find all sub-repeats in a genomic sequence. For every sub-repeat, RepeatGluer identifies the consensus sequence as well as the number of copies. Using this classification, it forms a new sequence (called the consensus of S) that is a copy of the genomic sequence S with each sub-repeat substituted by its consensus sequence. Such a consensus sequence can be viewed as a repeat masking tool that allows one to mask all sub-repeats with multiplicity larger than a predefined threshold.7 In addition, Repeat-Gluer outputs “tangle graphs” that describe repeats as mosaics of sub-repeats. Below we introduce the A-Bruijn graphs and describe their applications for repeat analysis and fragment assembly. Our extensive benchmarking (http://nbcr.sdsc.edu/euler/benchmarking) on BACs and bacterial genomes implies that a new fragment assembler based on the A-Bruijn graph approach outperforms Phrap and ARACHNE, which are currently perceived as among the best fragment assembly tools.

METHODS

A-Bruijn Graphs

Let S be a genomic sequence of length n and A = (aij) be a binary n × n “similarity matrix” representing the set 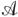Inline graphic of all significant local pairwise alignments between regions from S. The matrix A is defined as aij = 1 if and only if the positions i and j are aligned in at least one of the pairwise alignments and aij = 0 otherwise (note that insertions and deletions are not recorded in A). Matrix A represents an “adjacency matrix” of a graph (called the A-graph) on n vertices 1,..., n (vertices i and j are connected iff aij = 1). Let V be the set of connected components of this graph and let vi ∈ V be the connected component containing vertex i (1 ≤ i ≤ n). The A-Bruijn graph G(V, E) is defined as the multi-graph on the vertex set V with (n-1) directed edges (vi, vi+ 1) for 1 ≤ i < n. One can view the A-Bruijn graph as the Eulerian path obtained from the path (1,..., n) after contracting each connected component into a single vertex (Figs. 5 and 6). Vertices v1 and vn are called the source and sink.

Figure 5.

Figure 5

Open in a new tab

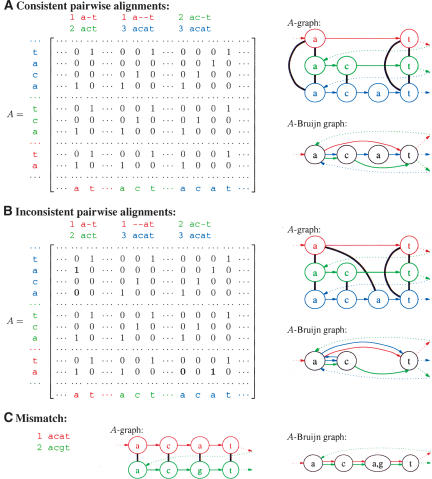
(A) Construction of the A-graph from the sequence...at...act...acat by applying three pairwise alignments (B) a-t versus act, (C) act versus acat, and (D) a-t versus acat. (D) The A-graph consists of the eight nodes plus the seven thick, black edges created from the alignments; the colored edges are shown to indicate the relation of the nodes to the sequence, but they are not part of the A-graph. (E) Each of these alignments serves as “gluing instructions” that transform the sequence into the A-Bruijn graph on four vertices; the colored edges are in the A-Bruijn graph, although the coloring itself is not.

Figure 6.

Figure 6

Open in a new tab

Construction of A-Bruijn graphs from (A) consistent pairwise alignments and (B) inconsistent pairwise alignments, for the genomic sequence...at...act...acat... with a repeat represented by three copies: at, act, acat. In the A-graphs, the thick, black edges connect vertices according to the adjacency matrix A. In the A-Bruijn graph, the colored edges show how the sequence threads through the vertices; they are also shown in the A-graph but technically are not part of it. Gaps in pairwise alignments create bulges in the A-Bruijn graph; for example, the third alignment in example A creates a bulge on vertices c, a, and t consisting of three edges (c, a), (a, t), and (c, t). Inconsistencies in pairwise alignments create whirls; for example, a blue whirl a → c → a in B. (C) A-graph and A-Bruijn graphs of a mismatch in the genomic sequence...acat...acgt....

When the matrix A corresponds to all starting positions of perfect (error-free) alignments of length l within a genome, the A-Bruijn graph corresponds to the classical de Bruijn graph (with minor technical modifications). However, the A-Bruijn graph is well defined for any collection of alignments 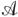Inline graphic. This generalization, although very powerful, comes with a trade-off—A-Bruijn graphs may become very complicated and difficult to analyze because of numerous short cycles caused by gaps and inconsistencies in pairwise alignments (Fig. 7).

Figure 7.

Figure 7

Open in a new tab

A repeat region in an A-Bruijn graph in which alignment inconsistencies have caused a whirl and a network of bulges.

The A-Bruijn graphs can be viewed as weighted graphs with the weight (multiplicity) of an edge between two vertices equal to the number of edges connecting these vertices. For example, in Figure 6A, there are two edges from the first a to c, which could be viewed as a single edge of weight 2. A cycle in a graph is called short if it has less than girth edges, where girth is a parameter. There are two types of short cycles in the A-Bruijn graphs: whirls and bulges. Whirls are short, oriented cycles (i.e., all edges of the whirl are oriented the same way), whereas bulges are short cycles that contain both forward and reverse edges. A gap of length g in a pairwise alignment typically creates a bulge of length g + 2 in the A-Bruijn graph (Fig. 6A). Whirls are caused by inconsistencies (see Morgenstern et al. 1996) in pairwise alignments (Fig. 6B). Bulges and whirls may further aggregate into networks of bulges/whirls that complicate the analysis of the A-Bruijn graph (as compared with the de Bruijn graph) and hide the underlying repeat structure. The de Bruijn graphs often can be simplified by collapsing every simple path (a maximal directed path in the graph satisfying the condition that all its internal vertices have one incoming and one outgoing edge) into a single edge. Such collapsing does not help much in the case of A-Bruijn graphs with numerous bulges and whirls (Fig. 7). To produce a sensible repeat classification, one has to remove whirls and bulges. Such removal may sacrifice the fine details of some repeats in favor of revealing the mosaic structure shared by different repeat copies.

Cleaning Up Whirls and Bulges

Figure 6B presents a set of inconsistent pairwise alignments that cannot be combined into a three-way multiple alignment (see Morgenstern et al. 1996 for more details on inconsistent pairwise alignments). Inconsistent pairwise alignments often can be transformed into consistent ones by either changing the positions of gaps or removing some matches from the alignments.8

Inconsistencies in pairwise alignments result in whirls in A-Bruijn graphs and present a major challenge in repeat analysis. A straightforward whirl removal may alter the consensus repeat sequence because some whirls may represent well-conserved parts of a repeat. We now describe an approach that eliminates inconsistencies from the alignments 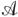Inline graphic rather than removing entire whirls.

For a vertex v, let P(v) be the set of positions in the connected component of the A-graph that was merged into v in the process of the A-Bruijn graph construction. A vertex v is called composite if P(v) contains two closely located (within distance girth) genomic positions.

Whirls may correspond either to inconsistencies in alignments or to very short tandem repeats. For the sake of simplicity, we assume that such short tandem repeats are not included in the alignments 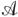Inline graphic .9 In this case, every composite vertex v indicates a potential inconsistency within the alignments 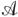Inline graphic and implies that some edges within the connected component on the set of positions P(v) have to be removed to make 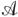Inline graphic consistent [i.e., aij should be changed from 1 to 0 for some positions i and j from P(v)]. However, deciding which edges have to be removed to produce a consistent set of pairwise alignments is a nontrivial problem. The simplest solution is to delete all edges within connected components of A-graphs corresponding to composite vertices. However, this solution may cause the RepeatGluer algorithm to deviate from the consensus repeat sequence in favor of a randomly chosen (and not necessarily representative) copy of a repeat. Below we describe a better approach based on splitting composite vertices (Fig. 8A,B).

Figure 8.

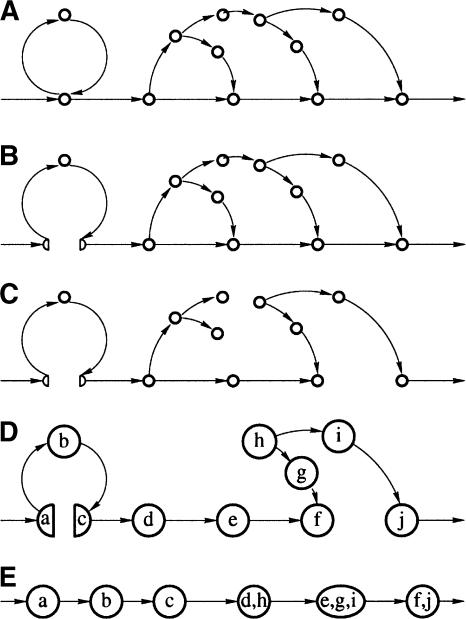
Figure 8

Open in a new tab

(A) Initial A-Bruijn graph (weighted graph representation instead of multigraph). (B) Whirl elimination. (C) Bulge removal. (D) Erosion. (E) Zigzag path straightening.

Define a “split edge” as an edge of maximal multiplicity m among all edges connecting composite and noncomposite vertices in the A-Bruijn graph. Let v be the composite vertex incident to this edge and P(v) be the set of positions corresponding to v. A split edge of multiplicity m corresponds to m pairs of consecutive genomic positions; let M be the set of m positions within P(v) defined by this edge (note m <|P(v)|). The splitting procedure removes all edges connecting the positions from M with the positions from P(v)\M within connected component v, thus splitting v into at least two vertices. The matrix A is changed accordingly by setting aij = 0 for every i ∈ M and j ∈ P(v)\M. This ensures that at least one of the newly created vertices is noncomposite. The iterative splitting procedure converges to a graph without composite vertices.

A bulge may be destroyed by removing any of its edges. We argue that the best way to destroy a bulge is to remove one of its low-multiplicity edges because high-multiplicity edges typically connect the most conserved positions in the repeat. In reality, the situation is significantly more complicated, because bulges are not isolated but form complex networks of bulges. This motivates the Maximum Subgraph with Large Girth (MSLG) Problem.

The MSLG Problem aims to remove bulges from the graph and amounts to finding a maximum weight sub-graph in the graph (i.e., a collection of edges of maximum total weight) that does not contain short cycles (cycles of length less than a parameter girth). The MSLG Problem with parameter girth = ∞ is the well-known and easy to solve Maximum Spanning Tree Problem (Cormen et al. 1989). However, for an arbitrary girth, the MSLG Problem is far from easy (S. Skiena, unpubl.); below we propose an approximation algorithm that produces good results (Fig. 8C). The bulge removal algorithm uses an optimal solution of the Maximum Spanning Tree Problem to arrive at an approximate solution of the MSLG Problem.

The algorithm finds a maximum spanning tree T in the A-Bruijn graph and analyzes the remaining edges in the graph in order of decreasing multiplicities. An edge is added to the graph if and only if it does not form a short cycle with already present edges; otherwise, it is deleted from the graph. Because bulge removal solves the shortest cycle problem at every iteration, it may appear to be rather time-consuming (A-Bruijn graphs contain millions of vertices even for bacterial genomes). However, for a typical genome, only a tiny fraction of edges is added to the graph while most edges are deleted efficiently because they form bulges with the tree T.

RepeatGluer Algorithm

The input of the RepeatGluer algorithm is the genomic sequence S of length n, the n × n similarity matrix A, and the parameter girth. The output is the classification of repeats (as described by tangles in repeat graphs) and the consensus sequence of S. In addition to whirl elimination and bulge removal, the algorithm includes other important steps (erosion, zigzag path straightening, and threading) that are discussed below. After performing these steps, every simple path in the resulting graph can be further collapsed into a single edge, resulting in the “repeat graph.” The multiplicity of an edge in the repeat graph is defined as the multiplicity of the corresponding simple path. Every nonrepetitive region in the genome corresponds to an edge of multiplicity 1 (a “nonrepetitive edge”) in the repeat graph, whereas repetitive regions correspond to edges of multiplicity >1 (sub-repeats in the genome). Repeat graphs provide a solution of the “repeat boundary problem” posed by Bao and Eddy (2002; Fig. 4A). If one deletes the nonrepetitive edges from the repeat graph, it gets broken into connected components called tangles (Pevzner et al. 2001). Tangles provide a concise representation of all repeats in a genome and specify the mosaic of sub-repeats forming a given repeat. Every edge within a tangle represents a sub-repeat, and every valid path in the tangle represents a sequence of sub-repeats forming a given repeat.10

RepeatGluer Algorithm

  1. Construct the A-Bruijn graph from matrix A.

  2. Eliminate whirls in the A-Bruijn graph by splitting the composed vertices (i.e., vertices that contain close positions) and modifying A accordingly.

  3. Remove bulges from the A-Bruijn graph by constructing a maximum spanning tree and adding edges of the A-Bruijn graph (in decreasing order of multiplicity) that do not form “short” cycles with already present edges.

  4. Perform girth iterations of the erosion procedure in the graph by removing all leaves (except source and sink) in every iteration.

  5. Straighten zigzag paths in the graph.

  6. Thread the genomic sequence S through the graph, and form the consensus sequence of S.

  7. Form the repeat graph by collapsing simple paths in the resulting graph. The multiplicity and the consensus sequence for an edge in the repeat graph are defined as the multiplicity and consensus sequence of the corresponding simple path.

  8. Output repeat families as tangles in the repeat graph. Every tangle is a collection of edges (sub-repeats) with corresponding consensus sequences.

Erosion

Although the graph obtained after bulge removal does not contain short cycles, it still may contain many small tree-like subgraphs (remains of the bulges) that complicate further analysis of this graph (Fig. 8D). To delete the remains of the bulges, we apply the erosion procedure, which removes all leaves (vertices of total degree 1) from the graph except the source and the sink. The erosion procedure is repeated several times (the number is determined by the maximal gap allowed in the alignments 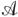Inline graphic ) to remove the remains of all bulges from the graph.

Zigzag Paths and Consensus Sequences of Sub-Repeats

The graph generated after the erosion procedure typically consists of a small number of long simple paths. The question is how to define the consensus nucleotide for every vertex in the resulting graph. Every vertex v in the A-Bruijn graph is associated with its set of genomic positions P(v). We define a “consensus” nucleotide of v as the most frequent nucleotide at these positions (the nucleotides at these different positions may differ because of mismatches within different copies of repeats). The hope is that the sequence of consensus nucleotides along a simple path in the resulting graph spells out the consensus sequence of the sub-repeat corresponding to this path.

However, the graph generated after the erosion procedure is a directed graph, and some of the simple paths in this graph may include both forward and reverse edges (zigzag paths). Although such paths are rare for highly conserved repeat families, less conserved repeat families may create complex networks of bulges in the A-Bruijn graph and lead to zigzag paths. We straighten every zigzag path from the start vertex s to the terminal vertex t by first computing index(v) for every intermediate vertex v on this path as the difference between the number of forward and reverse edges in the sub-path from the start vertex s to v. The straightened path (Fig. 8E) is defined as the path on the set of indices ranging from 0 to index(t). The set of genomic positions assigned to the vertex i on the straightened path is defined as the union of P(v) over all vertices v with index(v) = i. The consensus nucleotide of vertex i on the straightened path is defined as the most frequent nucleotide at these positions.

Threading the Genomic Sequence Through the Graph

The genomic sequence corresponds to an Eulerian path in the A-Bruijn graph. Some vertices of the A-Bruijn graph survive the bulge removal and erosion procedures whereas others are deleted, thus breaking the Eulerian path into segments. We attempt to “thread” this broken path through the resulting graph by repairing gaps between consecutive surviving segments.

Let v1,..., vk be an arbitrary sequence of vertices in a directed graph G. Path(G, v1,..., vk) is defined as a path in G composed from the (k-1) shortest directed paths between every pair of consecutive vertices vi and vi+ 1 for 1 ≤ i < k. Path(G, v1,..., vk) is not uniquely defined in case there are multiple shortest paths for some pairs of vertices vi and vi+ 1. However, in our applications, this path is usually uniquely defined because the distances between consecutive vertices vi and vi+ 1 are typically short and G does not have bulges.

Because every vertex v of the A-Bruijn graph G is associated with a set of genomic positions P(v), one can label positions in the genomic sequence S by vertices of the graph G [a position i is labeled by vertex v iff i ∈ P(v)]. Some positions in S may remain unlabeled because the erosion procedure deleted some vertices from the original A-Bruijn graph. However, the labels of positions along the sequence S define an (ordered) sequence of vertices v1,..., vk. The path Path(G, v1,..., vk) is called the threading of genomic sequence S through the graph G. We define the “maximum threading span” as the maximum length of shortest paths between vi and vi+ 1 (1 ≤ i < k) and remark that the maximum threading span for real genomes is typically small.

Threading defines a “consensus path” in G that spells out the consensus of genomic sequence S with all sub-repeats in S substituted by their consensus sequences. Threading also defines the multiplicity of every simple path p in G as the number of times the consensus path traverses p.

Timing

RepeatGluer is a polynomial-time algorithm that is very fast in practice: Under the assumption that girth and the maximum threading span are bounded, it runs in linear time (assuming the size of the input is defined by the number of 1s in the matrix A). RepeatGluer typically takes <10 min to generate a summary of repeats in a bacterial genome similar to that in Figure 4B (not counting the step that generates the similarity matrix A).11 In fact, the most time-consuming part of any approach to repeat classification is hidden in the “pairwise similarities” step that precedes the RepeatGluer algorithm.

To illustrate the complexity of the problem, Figure 4C shows the greatly simplified tangle of the most common repeat in the first 1 Mb of human Chromosome X, representing (not surprisingly) Alu elements and their interactions with other repeats. Figure 4C shows several sub-repeats with length ranging from 3 to 278 bp and with multiplicities ranging from 3 to 30 (the complex structure of some Alu elements was also discussed in Perl et al. 2000 and Bao and Eddy 2002). These sub-repeats either represent common extensions of canonical Alu repeats or other repeats that are often found in conjunction with Alu repeats. Although these sub-repeats are not as frequent as the major Alu sub-repeats, a simple extrapolation implies that each of them may be present in at least 1% of all Alu repeats, resulting in tens of thousands of occurrences in the whole human genome. Therefore, careful analysis of these sub-repeats is important for studies of repeat evolution.12

Multiple Alignments

Given t sequences S1,..., St of total length n and t(t - 1)/2 pairwise alignments between these sequences, one can concatenate S1,..., St into a single sequence S of length n and compose the n × n similarity matrix A from t(t - 1)/2 pairwise alignments. The only difference between the A-Bruijn graph of multiple sequences S1,..., St and the A-Bruijn graph of a single sequence S is that edge (vi, vi+ 1) is removed from the A-Bruijn graph of multiple sequences if positions i and (i + 1) in S correspond to the last and the first positions in the consecutive sequences Sk and Sk+ 1. Therefore, the A-Bruijn graph may have up to t sources and t sinks.

Our approach to multiple alignment13 follows the spirit of the recent pioneering work by Lee et al. (2002), who were the first to ask the provocative question, “Should multiple alignment be linear?” Most multiple alignment algorithms are based on progressive application of pairwise alignments; CLUSTALW (Thompson et al. 1994) is an example of very efficient software based on this approach. However, Thompson et al. (1994) highlighted some problems with progressive multiple alignments, most importantly, dependence on the order of pairwise alignments. Lee et al. (2002) highlighted an even more troublesome aspect of the classical notion of multiple alignment: It assumes that all regions of all sequences are homologous over the entire length. The problems with this assumption are well known; in fact, experienced CLUSTALW users clip the sequences before alignment to remove nonhomologous parts.

Lee et al. (2002) addressed this problem by introducing the notion of partial order graphs of multiple alignments and designing a new Partial Order Alignment (POA) multiple alignment algorithm. POA outputs graphs that are similar to the tangles produced by our approach. However, POA suffers from the same order dependency as CLUSTALW, whereas our A-Bruijn graph approach is order-independent. In addition, the approach in Lee et al. (2002) is not suitable for proteins with shuffled domain structure (no cycles in the partial order graphs), whereas our approach handles this case as well.

Constructing A-Bruijn Graphs Without the Similarity Matrix

The construction of the A-Bruijn graph assumes that the genomic sequence S and the matrix A are given. A surprising and useful property of the A-Bruijn graph is that it often can be constructed from alignments of substrings of S without knowledge of the entire sequence S and matrix A. The key idea here is that if reads “cover” the entire genome, then “gluing” of reads produces the same A-Bruijn graph as “gluing” of genomic sequences. The order in which the reads are subjected to such gluing (multiple alignment of reads) does not affect the resulting A-Bruijn graph.

A set of substrings {S1,..., St} of a genomic sequence S is called a “covering” set if for every pair of consecutive positions in S there exists a substring Si (1 ≤ i ≤ t) containing these positions. Let S be an (unknown) genomic sequence of an (unknown) length with an (unknown) alignment matrix A (we assume that aii = 1 for all 1 ≤ i ≤ n). Let S1,..., St be a covering set of strings for S, and 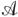Inline graphic be the collection of t(t - 1)/2 sub-matrices of A for every pair of substrings Si and Sj. Every such|Si| ×|Sj| sub-matrix is a snapshot of a “small” area of matrix A (|Si| is the length of the string Si). The question is whether one can reconstruct the A-Bruijn graph from these snapshots rather than from the entire matrix A.

We emphasize that neither coordinates of the strings S1,..., St, nor their ordering in the sequence S is known. However, one can prove that the A-Bruijn graph of sequence S and the A′-Bruijn graph of sequence S′ coincide, where S′ is a concatenation of S1,..., St (in any order) and A′ is the corresponding block matrix, comprised of the matrices in 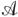Inline graphic . Indeed, the condition aii = 1 ensures that all replicas of node i in different substrings are glued together in A′. The covering condition ensures that all nodes and edges produced by S occur at least once in S′ and that all additional gluings specified by A are also specified in A′. Therefore, the A-Bruijn graph of sequence S and the A′-Bruijn of any collection of its covering substrings concatenated in an arbitrary order are the same. An important implication of this fact is that RepeatGluer leads to a new and efficient fragment assembly algorithm.14

To assemble reads S1,..., St into a genomic sequence, one concatenates them (in any order) to form a sequence S′ of length n′, composes the set of all pairwise alignments between reads into an n′' × n′ similarity matrix A′, and constructs the A′-Bruijn graph of reads S1,..., St. Below we describe a modification of the RepeatGluer algorithm for fragment assembly.

Fragment Assembly

After Myers et al. (2000) proved that large genomes can be assembled in the WGS approach, there was an explosion of new fragment assemblers (Pevzner et al. 2001; Aparicio et al. 2002; Batzoglou et al. 2002; Wang et al. 2002; Mullikin and Ning 2003). Surprisingly enough, although these assemblers were successful in assembling large genomes, Phrap (Green 1994) remains the dominant BAC assembly tool.

BAC sequencing becomes particularly important when the genomic projects move into the finishing stage. “Extreme fragment assembly” (like assembly of the highly repetitive Y-chromosome) is an open problem: Many BACs and bacterial genomes remain unassembled or assembled with likely errors. The accuracy of the recently released WGS assemblers as compared with Phrap remains unclear when it comes to assembly of BACs or bacterial genomes. Moreover, there are some problems with recent assemblies of mammalian genomes, and revealing comparative strengths and weaknesses of WGS assemblers may lead to better quality assembly of mammalian genomes.

Many difficult-to-assemble BACs are comparable in complexity to bacterial genomes and require significant finishing efforts. Although Phrap makes assembly errors for long and repetitive genomes, it is an excellent tool for assembling low-coverage nonrepetitive regions and using low-quality reads (Yang 2002).15 In contrast, the genome-scale assemblers outperform Phrap in assembling highly repetitive regions but discard low-quality reads and read ends to ensure that the assembly is error-free. For example, the Celera assembler (Myers et al. 2000) carefully trims reads to ensure that the remaining portions are at least 98% accurate. Such trimming significantly reduces the coverage and leads to an increased number of contigs as compared with Phrap, which carefully analyzes Phred quality values and meticulously works with untrimmed read ends. This observation implies that the best WGS assemblers are not necessarily the best BAC assemblers.

We recently developed the EULER assembler (available at http://nbcr.sdsc.edu/euler), which has proved to be very accurate in handling high-quality reads in highly repetitive regions (Pevzner et al. 2001). However, as with other recently developed assemblers, EULER produced more contigs than Phrap when assembling low-coverage regions and low-quality reads. Our goal is therefore to build an accurate assembler that combines EULER's accuracy in analyzing repeats with Phrap's ability to handle low-coverage regions, low-quality reads, and read ends.16 Fragment-Gluer does not remove low-quality reads and does not trim low-quality read ends, yet still maintains high accuracy of assemblies. It also uses less memory than the original EULER (by eliminating the huge hash tables), thus overcoming a major bottleneck in applying EULER to larger genomes.

The input of FragmentGluer is a set of reads {S1,..., St}, a set of pairwise alignments between some of the t(t - 1)/2 pairs of reads, a parameter girth, and a set of “mate-pairs” (pairs of reads) with corresponding “mate-pair distances.” FragmentGluer assembles the reads into a set of contigs and classifies repeats in the process of fragment assembly.

FragmentGluer Algorithm

  • 0a. Identify and remove chimeric reads from {S1,..., St}.

  • 0b. Concatenate the remaining reads and their reverse complements into a sequence of length n and compose the n × n similarity matrix A from the pairwise alignments of reads.

  • 1. Construct the A-Bruijn graph of sequences S1,..., St from the matrix A.

  • 2. Eliminate whirls in the A-Bruijn graph by splitting the composed vertices, and modify the matrix A accordingly.

  • 3. Remove bulges from the A-Bruijn graph by constructing a maximum spanning forest and adding edges of the A-Bruijn graph (in decreasing order of multiplicities) that do not form “short” cycles with already present edges.

  • 4. Perform girth iterations of the erosion procedure in the graph by removing all leaves in every iteration.

  • 4a. Recover sources and sinks by adding, for every leaf, a longest path of removed vertices attached to the leaf.

  • 5. Straighten zigzag paths in the graph.

  • 6. Thread each read through the graph and define the coverage of a vertex in the graph as the number of reads that are threaded through this vertex. Define coverage of simple paths as the average coverage of their vertices.

  • 7. Form the repeat graph by collapsing simple paths in the graph. The consensus sequence of an edge in the repeat graph is defined as the consensus sequence of the corresponding simple path. The multiplicity of an edge in the repeat graph is defined by the EULER Copy Number algorithm (Pevzner and Tang 2001).

  • 8. Output repeat families as tangles in the repeat graph. Every tangle is a collection of edges (sub-repeats) with corresponding consensus sequences.

  • 9. Transform mate-pairs into mate-paths in the graph obtained after step 6, and perform equivalent transformations on the resulting set of mate-paths (Pevzner and Tang 2001).

  • 10. Define contigs as consensus sequences of simple paths in the resulting graph. Assemble the resulting contigs into scaffolds by the EULER Scaffolding algorithm (Pevzner and Tang 2001).

The FragmentGluer algorithm addresses the following complications of the assembly problem:

Identification of Chimeric Reads (Step 0a)

Huang (1992, 1996) and Green (1994) were the first to develop efficient algorithms for chimeric read identification. Our new approach is influenced by these ideas and is based on a modification of the first four steps of the RepeatGluer algorithm (to be described elsewhere).

Analyzing Reads From Both DNA Strands (Step 0b)

We double the set of reads by adding the reverse complement of every read to the pool of all reads. Thus, for every vertex in the A-Bruijn graph, there is a complementary vertex (inverted repeats may merge some of these pairs of vertices into a single vertex). At every step of further analysis, to preserve strand symmetry, we analyze both vertices of such pairs at the same time.

Protecting Sources and Sinks From Erosion (Step 4a)

The set of reads typically does not cover the genomic sequence, thus creating gaps in the coverage and generating many gap-induced sources and sinks in A-Bruijn graphs. These gap-induced sources and sinks have to be protected against the erosion procedure.

Finding Multiplicities of Repeats (Step 7)

Although high coverage usually correlates with high repeat multiplicity, the attempts to accurately derive multiplicities from coverage alone failed at the genomic scale. To address this complication, we use the EULER Copy Number algorithm (Pevzner and Tang 2001) to derive multiplicities of edges in the repeat graphs.

Analyzing Mate-Pairs and Spurious Similarities in Matrix A (Steps 9, 10)

To assemble reads from low-coverage regions, one has to take into account short alignments between read ends. Such short overlaps may either indicate connections in low-coverage regions or spurious similarities that further tangle the A-Bruijn graph. Equivalent transformations with mate-pair data untangle the A-Bruijn graph and allow one to distinguish between these two situations (see Pevzner and Tang 2001 for details).

RESULTS AND DISCUSSION

Benchmarking

How accurate are the (finished) sequence of the human genome and the (unfinished) sequence of the mouse genome? How many highly repetitive BACs (e.g., BACs from the Y-chromosome) or bacterial genomes deposited in GenBank have assembly errors? To answer these questions, one should first answer this question: “What is the accuracy of the assemblers used in these projects?” Unfortunately, this question remains unanswered because only limited benchmarking of these assembly tools has been published so far (Pevzner et al. 2001; Pop et al. 2002, 2004; Yang 2002). Few biologists realize that the mouse and rat genomic WGS assemblies are likely to have thousands of assembly errors resulting in “misjoint” segments and collapsed repeats. Mouse and rat genomic sequences reveal a surprisingly large number of microrearrangements (as compared with human) for species that diverged just 14 million years ago, an indication that these genomes may be assembled with some errors. Moreover, the rate of microrearrangements in the rat lineage is three times higher than in the mouse lineage, thus pointing to potential misassemblies in the rat genome (Bourque et al. 2004). Such misassemblies may disrupt genes, disconnect genes and regulatory regions, and lead to other serious annotation problems.

The recent assemblies of the mouse and rat genomes are triumphs of the WGS approach. However, there is no doubt that these genomes have many assembly errors, and it remains unclear how to correct these errors in the future. It is now clear that finishing procedures are much more expensive than generating the shotgun reads even for bacterial, let alone mammalian, genomes. Because no mammalian WGS project has been finished yet, we can only speculate that the cost of such efforts may be prohibitive. The question then arises whether there is any way to improve the accuracy of the WGS assemblies in silico.

The surprising thing is that both the old (CAP, Phrap, and TIGR), and the new (ARACHNE, Celera, and Phusion) assemblers had rather limited benchmarking in a rigorous academic setting. We argue that benchmarking on accurately finished BACs and bacterial genomes may reveal the comparative strengths of different assemblers. If an assembler has weaknesses in assembling bacterial genomes and BACs, there is no reason to believe that these weaknesses do not propagate to longer genomes. We therefore chose Phrap and Arachne (which are the most widely used assemblers today) for a rigorous benchmarking study of BAC and bacterial assemblies. We developed a benchmarking software suite (that, in particular includes all BACs from human Chromosome 20) and conducted the largest comparative test of fragment assemblers so far.

Our benchmarking results for three publicly available benchmarking samples are available at the Web site http://nbcr.sdsc.edu/euler/benchmarking. The WUSTL sample was designed by S.P. Yang to ensure that BACs are free from misassembly artifacts. The Sanger Center sample consists of all reads in human Chromosome 20 (organized in a BAC-by-BAC fashion), prepared by Jim Mullikin. The TIGR sample of bacterial genomes was designed by Mihai Pop (Pop et al. 2004).

The Sanger Center sample describes benchmarking of 518 BACs from human Chromosome 20. For this sample, Phrap misassembled 37 contigs, ARACHNE misassembled 17, and EULER+ misassembled 7. EULER+ also had the least number of missing repeat copies (four), ahead of Phrap (five) and Arachne (nine). The average number of contigs per clone was the least for EULER+ (6.2) and Phrap (6.8), with ARACHNE producing significantly more contigs (13.8), thus making it difficult to use ARACHNE in high-volume BAC sequencing. Coverage produced by all three programs was comparable (Phrap produced slightly higher coverage than EULER+ and ARACHNE).

The analysis of the TIGR sample indicates that as soon as the number of repeats increases, Phrap becomes unacceptable, producing a large number of “difficult-to-fix” assembly errors. In contrast, both ARACHNE and EULER+ withstand this increase in repeats (no assembly errors), with EULER+ still producing a significantly smaller number of contigs than ARACHNE.

EULER+ represents a significant improvement as compared with our previous EULER as seen from benchmarking of EULER in Yang (2002) and benchmarking of EULER+ at http://nbcr.sdsc.edu/euler/benchmarking on the same sample. We observed that the repeat graphs are less fragmented in EULER+ as compared with EULER, because local alignments (used in EULER+) better glue the repeat graph than l-mers (used in EULER). For BACs and bacterial genomes, the core structure of the repeat tangles remains roughly the same, but is somewhat simplified in EULER+; slight differences between repeat copies cause less branching within a tangle in EULER+ than in EULER. Generating the repeat graphs for larger, highly repetitive genomes remains a challenging algorithmic problem.

Acknowledgments

We are indebted to Derrek Kisman, Ming Li, and Bin Ma, who kindly modified their PatternHunter software for our purposes, and to Shiaw-Pyng Yang for providing a sample of “difficult-to-assemble” BACs. We are grateful to Concordia Chen and Vagisha Sharma for benchmarking ARACHNE and to David Jaffe for help with installing it. We are grateful to Vineet Bafna, Fan Chung Graham, Ron Graham, Alkes Price, and Steven Skiena for helpful discussions, and to the anonymous referees for many more helpful suggestions. This work was supported by NHGRI grant 1 R01 HG02366.

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.

Footnotes

[The following individuals kindly provided reagents, samples, or unpublished information as indicated in the paper: D. Kisman, M. Li, B. Ma, and to S.-P. Yang.]

Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.2395204.

4

The concept of an “elementary repeat,” although important, was never rigorously defined in the recent papers on repeat analysis (Volfovsky et al. 2001; Bailey et al. 2002; Bao and Eddy 2002). Although it is well defined for perfectly conserved repeats (e.g., as maximal simple paths of multiplicity >1 in the de Bruijn graph), the imperfectly conserved repeats defy simple definitions. “Elementary repeats” are defined in this paper as maximal simple paths of multiplicity >1 in the A-Bruijn graph. This definition is not perfect either, but we believe that it fits the spirit of Bailey et al. (2002). However, in many biological applications, this concept needs to be adjusted (e.g., by introducing appropriate thresholds that remove low-multiplicity edges from A-Bruijn graphs) to account for high-multiplicity mobile elements, fractured repeats, and other biological complications.

5

We are not criticizing other repeat classification programs here: They were designed with the primary goal of characterization of high-multiplicity mobile elements rather than the explicit representation of mosaic structure of sub-repeats. The goal of this example is to illustrate that the problem of mosaic repeat representation raised by Bailey et al. (2002) is not adequately addressed by the existing software tools. We also remark that our approach reveals mobile elements as well (as high-multiplicity edges/paths in A-Bruijn graphs).

6

Pevzner et al. (2001) introduced an error-correction procedure that mimics de Bruijn graphs for nearly identical repeats (repeats that are 98%-99% similar), a small step toward a generalization of the original de Bruijn approach. However, extending this approach beyond nearly identical repeats remains an open problem. Our construction of repeat graphs (below) is very different and more general.

7

Although the A-Bruijn graphs may be very complicated for highly repetitive genomes, they are often broken into simple paths if one removes all low-multiplicity edges. These paths (formed by high-multiplicity edges) typically correspond to mobile elements studied in Bao and Eddy (2002).

8

For example, inconsistent pairwise alignments in Figure 6B can be made consistent by moving the gap in the alignment of at and acat from positions 1-2 to positions 2-3.

9

Short tandem repeats deleted during whirl elimination can be easily added to the repeat graphs.

10

RepeatGluer classifies repeat families in a single DNA strand. To account for both strands and for inverted repeats, one has to concatenate both DNA strands into a single sequence S.

11

We emphasize that highly repetitive sequences correspond to a similarity matrix with a large number of 1s, which may be quadratic in the length of the sequence. Although it does not present a problem for genomes under study, it may present a problem for longer genomes. A possible approach to reducing the running time in this case is to limit the number of 1s for each column/row. Such filtering of 1s in the similarity matrix has to be done with caution to ensure that all copies of a mobile element are “glued together” with high probability (e.g., all copies of a perfect m-copy repeat can be glued with m-1 1s instead of m2 1s). Also, blocks of adjacent 1s are represented as position and length. Another approach (that is equivalent to the “repeat masking” procedure used in many WGS assemblers) is to simply glue together all predefined high-multiplicity repeats at the preprocessing stage.

12

If one removes low-multiplicity edges from the graph in Figure 4C, the resulting path on four bold edges will correspond to the consensus Alu repeat. Other transposable elements can be extracted from the A-Bruijn graphs by applying different thresholds depending on the multiplicity of the transposable element (applications of RepeatGluer for finding transposable elements will be described elsewhere).

13

Multiple alignment is not a focus of this paper, and the goal of this section is simply to introduce the construction that is used in the follow-up fragment assembly section (we view fragment assembly as multiple alignment of reads). The applications of RepeatGluer for multiple alignment of proteins with shuffled domains will be described elsewhere.

14

The informed reader may notice parallels between our A-Bruijn graph approach to fragment assembly and two earlier approaches pioneered by Idury and Waterman (1995) and Myers (1995). Although the earlier algorithms look very different, both implicitly tried to develop the idea of the repeat graph. Myers tried doing this by collapsing the overlap graph at the level of read (∼500 bp) resolution, whereas Idury and Waterman tried simplifying the de Bruijn graph at the level of l-mer resolution. Our key contribution is the A-Bruijn graph construction that deals with fragment assembly at the level of single-nucleotide resolution. This increased granularity alleviates challenging algorithmic problems that we faced trying to design an efficient assembler for low-coverage regions and low-quality reads/read ends.

15

Low-quality reads can be defined as reads with fewer than 100 positions with Phred quality values above 15.

16

It may sound like a simple integration problem, but it turned out to be a very difficult task that required development of a new idea for fragment assembly (our FragmentGluer algorithm, implemented in EULER+). The difficulty is that it is unclear how the algorithmic ideas used in the recent WGS assemblers can be adjusted for working with low-coverage and low-quality sequencing data (like read ends).

References

  1. Agarwal, P. and States, D. 1994. The Repeat Pattern Toolkit (RPT): Analyzing the structure and evolution of the C. elegans genome. Proc. Int. Conf. Intel. Syst. Mol. Biol. 2: 1-9. [PubMed] [Google Scholar]
  2. Aparicio, S., Chapman, J., Stupka, E., Putnam, N., Chia, J., Dehal, P., Christoffels, A., Rash, S., Hoon, S., Smit, A., et al. 2002. Whole-genome shotgun assembly and analysis of the genome of Fugu rubripes. Science 297: 1301-1310. [DOI] [PubMed] [Google Scholar]
  3. Bailey, J., Yavor, A., Viggiano, L., Misceo, D., Horvath, J., Archidiacono, N., Schwartz, A., Rocchi, M., and Eichler, E. 2002. Human-specific duplication and mosaic transcripts: The recent paralogous structure of chromosome 22. Am. J. Hum. Genet. 70: 83-100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bao, Z. and Eddy, S. 2002. Automated de novo identification of repeat sequence families in sequenced genomes. Genome Res. 8: 1269-1276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Batzoglou, S., Jaffe, D., Stanley, K., Butler, J., Gnerre, S., Mauceli, E., Berger, B., Mesirov, J., and Lander, E. 2002. Arachne: A whole-genome shotgun assembler. Genome Res. 12: 177-189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bedell, J., Korf, I., and Gish, W. 2000. MaskerAid: A performance enhancement to RepeatMasker. Bioinformatics 16: 1040-1041. [DOI] [PubMed] [Google Scholar]
  7. Bocker, S. 2003. Sequencing from compomers: Using mass spectrometry for DNA de-novo sequencing of 200+ nt. In 3rd Workshop on Algorithms in Bioinformatics, Budapest, Hungary, September 2003. Lecture Notes in Computer Science, 2812: 476-497. Springer-Verlag, Berlin. [Google Scholar]
  8. Bourque, G., Pevzner, P., and Tesler, G. 2004. Reconstructing the genomic architecture of ancestral mammals: Lessons from human, mouse, and rat genomes. Genome Res. 14: 507-516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cormen, T., Leiserson, C., and Rivest, R. 1989. Introduction to algorithms. The MIT Press, Cambridge, MA.
  10. de Bruijn, N. 1946. A combinatorial problem. Koninklije Nedderlandse Academie van Wetenshappen Proc. A49: 758-764. [Google Scholar]
  11. Delcher, A., Kasif, S., Fleischmann, R., Peterson, J., White, O., and Salzberg, S. 1999. Alignment of whole genomes. Nucleic Acids Res. 27: 2369-2376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Green, P. 1994. Documentation for PHRAP. http://www.genome.washington.edu/UWGC/analysistools/phrap.htm.
  13. Gusfield, D. 1997. Algorithms on strings, trees, and sequences. Computer science and computational biology. Cambridge University Press.
  14. Heber, S., Alekseyev, M., Sze, S., Tang, H., and Pevzner, P. 2002. Splicing graphs and EST assembly problem. Bioinformatics 18 Suppl. 1: S181-S188. [DOI] [PubMed] [Google Scholar]
  15. Huang, X. 1992. A contig assembly program based on sensitive detection of fragment overlaps. Genomics 14: 18-25. [DOI] [PubMed] [Google Scholar]
  16. ____. 1996. An improved sequence assembly program. Genomics 33: 21-31. [DOI] [PubMed] [Google Scholar]
  17. Idury, R. and Waterman, M. 1995. A new algorithm for DNA sequence assembly. J. Comput. Biol. 2: 291-306. [DOI] [PubMed] [Google Scholar]
  18. Kurtz, S., Ohlebusch, F., Schleiermacher, C., Stoye, J., and Giegerich, R. 2000. Computation and visualization of degenerate repeats in complete genomes. Proc. Int. Conf. Intel. Syst. Mol. Biol. 8: 228-238. [PubMed] [Google Scholar]
  19. Kurtz, S., Choudhuri, J., Ohlebusch, E., Schleiermacher, C., Stoye, J., and Giegerich, R. 2001. REPuter: The manifold applications of repeat analysis on a genomic scale. Nucleic Acids Res. 29: 4633-4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lee, C., Grasso, C., and Sharlow, M. 2002. Multiple sequence alignment using partial order graphs. Bioinformatics 18: 452-464. [DOI] [PubMed] [Google Scholar]
  21. Li, X. and Waterman, M.S. 2003. Estimating the repeat structure and length of DNA sequences using L-tuples. Genome Res. 13: 1916-1922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Morgenstern, B., Dress, A., and Werner, T. 1996. Multiple DNA and protein sequence alignment based on segment-to-segment comparison. Proc. Natl. Acad. Sci. 93: 12098-12103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mullikin, J. and Ning, Z. 2003. The Phusion assembler. Genome Res. 13: 81-90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Myers, E.W. 1995. Toward simplifying and accurately formulating fragment assembly. J. Comput. Biol. 2: 275-290. [DOI] [PubMed] [Google Scholar]
  25. Myers, E.W., Sutton, G.G., Delcher, A.L., Dew, I.M., Fasulo, D.P., Flanigan, M.J., Kravitz, S.A., Mobarry, C.M., Reinert, K.H., Remington, K.A., et al. 2000. A whole-genome assembly of Drosophila. Science 287: 2196-2204. [DOI] [PubMed] [Google Scholar]
  26. Peer, I., Arbili, N., and Shamir, R. 2002. A computational method for resequencing long DNA targets by universal oligonucleotide arrays. Proc. Natl. Acad. Sci. 99: 15492-15496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Perl, A., Colombo, E., Samoilova, E., Butler, M., and Banki, K. 2000. Human transaldolase-associated repetitive elements are transcribed by RNA polymerase III. J. Biol. Chem. 275: 7261-7272. [DOI] [PubMed] [Google Scholar]
  28. Pevzner, P. 1989. l-tuple DNA sequencing: Computer analysis. J. Biomolecular Struct. Dyn. 7: 63-73. [DOI] [PubMed] [Google Scholar]
  29. ____. 2000. Computational molecular biology: An algorithmic approach. The MIT Press, Cambridge, MA.
  30. Pevzner, P. and Tang, H. 2001. Fragment assembly with double-barreled data. Bioinformatics 17: S225-S233. [DOI] [PubMed] [Google Scholar]
  31. Pevzner, P., Tang, H., and Waterman, M. 2001. An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. 98: 9748-9753. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pop, M., Salzberg, S., and Shumway, M. 2002. Genome sequence assembly: Algorithms and issues. IEEE Computer 35: 47-54. [Google Scholar]
  33. Pop, M., Kosack, D., and Salzberg, S. 2004. Hierarchical scaffolding with Bambus. Genome Res. 14: 149-159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Shamir, R. and Tsur, D. 2001. Large scale sequencing by hybridization. In Proceedings of the Fifth Annual International Conference on Computational Molecular Biology (RECOMB-01), Montreal, Canada, April 2001 (eds. T. Lengauer et al.), pp. 267-279. ACM Press, New York.
  35. Thompson, J., Higgins, D., and Gibson, T. 1994. CLUSTAL W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22: 4673-4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Volfovsky, N., Haas, B., and Salzberg, S. 2001. A clustering method for repeat analysis in DNA sequences. Genome Biol. 2: RESEARCH0027. Epub 2001 Aug 01. [DOI] [PMC free article] [PubMed]
  37. Wang, J., Wong, G., Ni, P., Han, Y., Huang, X., Zhang, J., Ye, C., Zhang, Y., Hu, J., Zhang, K., et al. 2002. RePS: A sequence assembler that masks exact repeats identified from the shotgun data. Genome Res. 12: 824-831. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yang, S. 2002. Comparison of genomic assemblers. Advances in Genome Biology and Technology, February 2002, Marco Island, Florida. GCorp Inc., Waltham, MA.
  39. Zhang, Y. and Waterman, M.S. 2003. An Eulerian path approach to global multiple alignment for DNA sequences. J. Comput. Biol. 10: 803-819. [DOI] [PubMed] [Google Scholar]

WEB SITE REFERENCES

  1. http//nbcr.sdsc.edu/euler; EULER Web site.
  2. http//nbcr.sdsc.edu/euler/benchmarking; Comparison of Phrap, Arachne, and EULER assemblers.

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES