Comparing algorithms for automated vessel segmentation in computed tomography scans of the lung: the VESSEL12 study

Abstract

The VESSEL12 (VESsel SEgmentation in the Lung) challenge objectively compares the performance of different algorithms to identify vessels in thoracic computed tomography (CT) scans. Vessel segmentation is fundamental in computer aided processing of data generated by 3D imaging modalities. As manual vessel segmentation is prohibitively time consuming, any real world application requires some form of automation. Several approaches exist for automated vessel segmentation, but judging their relative merits is difficult due to a lack of standardized evaluation. We present an annotated reference dataset containing 20 CT scans and propose nine categories to perform a comprehensive evaluation of vessel segmentation algorithms from both academia and industry. Twenty algorithms participated in the VESSEL12 challenge, held at International Symposium on Biomedical Imaging (ISBI) 2012. All results have been published at the VESSEL12 website http://vessel12.grand-challenge.org. The challenge remains ongoing and open to new participants. Our three contributions are: (1) an annotated reference dataset available online for evaluation of new algorithms; (2) a quantitative scoring system for objective comparison of algorithms; and (3) performance analysis of the strengths and weaknesses of the various vessel segmentation methods in the presence of various lung diseases.

1. Introduction

The vasculature is involved in many diseases including the most lethal ones, such as cardiovascular and cerebrovascular disease. Vascular trees are ubiquitous, found nearly in every organ, complex and highly intertwined; and vessel segmentation is both a common and a challenging task. Reliable quantitative medical image analysis requires automatic vessel segmentation, whenever possible, to discriminate vessels from organs of interest. It is thus not surprising that vessel segmentation has received a large amount of interest.

1.1. Overview of existing methods

To date, no single method can successfully segment vessels from every imaging modality and every organ. The complexity of vessel segmentation in different organs and for different purposes has given rise to multiple segmentation methods.

Many methods rely on combination of vascular models, image features, and extraction schemes; most models rely on some prior knowledge about the features of vessels such as intensity, curvature, tubularity, centerline and smoothness. Applying Hessian-based scale-space enhancement filters (Frangi et al., 1998; Sato et al., 1998; Krissian et al., 2000) results in disconnection because filter response is low along bifurcations. Enhancement filters have been combined with tracking (Aylward and Bullitt, 2002), bifurcation enhancement and suppression of non-vessel structures (Zhou et al., 2006). Seed-point based algorithms have also been used, in both region growing techniques (Lavi et al., 2004; Metz et al., 2007) and fast marching techniques (Bülow et al., 2005). Other recent methods include fuzzy shape representation (Agam et al., 2005), and fuzzy-connectedness (Kaftan et al., 2008). These are but few of the most recent methods in vessel segmentation. A more exhaustive review can be found in Lesage et al. (2009), which classified various vessel lumen segmentation methods in contrast-enhanced imaging modalities (such as magnetic resonance angiography and computed tomography angiography), analyzing the different models, features and extraction schemes. A slightly older, extensive vessel segmentation review (Kirbas and Quek, 2004) classified the various methods according to which approach they belong to: pattern recognition, model-based, tracking, artificial intelligence-based, or machine learning.

In analysis of data generated by 3D imaging modalities such as thoracic computed tomography (CT) scans, vessel segmentation is often required before proceeding to diagnose higher order disease patterns. It has been used to aid segmentation of nearby anatomical structures such as pulmonary lobes (Kuhnigk et al., 2005; Ukil and Reinhardt, 2009; Lassen et al., 2012) and lung airways (Lo et al., 2010; Bülow et al., 2005). In computer-aided nodule detection, having vessel segmentation reduces ambiguities and improves nodule detection performance (Agam et al., 2005). Excluding vessel volume is also important where accurate quantification is essential, such as follow-up studies of tumor volumetry (Reeves et al., 2006), lung perfusion study (Risse et al., 2009), as well as parenchymal (Korfiatis et al., 2011) and interstitial lung diseases (Marten et al., 2009; Kumar et al., 2012). Vessel segmentation is fundamental in automated detection of lung-related conditions such as pulmonary emboli that occur in pulmonary arteries (Masutani et al., 2002; Zhou et al., 2005; Peters et al., 2007). Pulmonary vessel tree dimensions also help to characterize pulmonary hypertension (Linguraru et al., 2010; Matsuoka et al., 2010), and using these dimensions, to calculate bronchoarterial ratio to characterize risk of cardiovascular diseases.

Segmenting vessels in the lungs has been addressed by various groups (Agam et al., 2005; Shikata et al., 2004; Fetita et al., 2009a; Kaftan et al., 2008; Xiao et al., 2011) using variants of the techniques described in the overview of existing methods. In lung images, there is a natural contrast due to the high density difference between the vessels and the background, lung parenchyma. Although it is relatively straightforward to use the difference in intensity to segment vessels, there are other structures besides vessels having similar intensities (e.g. tumor nodules, dense lesion), and vessel trees are highly complex and highly intertwined. There is a still more complicated task of distinguishing arteries from veins, which only few have begun to explore (Lei et al., 2001; van Bemmel et al., 2003; Yonekura et al., 2007; Gao et al., 2012).

1.2. Necessity of fair performance comparison

Producing a complete vessel tree segmentation for a single scan manually is a daunting task. For multiple scans this requires a prohibitive amount of time and resources. As a result, many vessel segmentations – as shown in the previously cited reviews (Kirbas and Quek, 2004; Lesage et al., 2009) – are evaluated on a set of data particular to their respective studies, and there is a lack of standardized reference data and validation criteria to objectively compare various segmentation algorithms. The BrainWeb (Aubert-Broche et al., 2006) project for vessels in brain magnetic resonance images provides a valuable, although synthetic, reference.

Distinct from publicly available databases, collaborative efforts to solve complex problems gave rise to various challenge frameworks. Challenge frameworks provide a fair comparison and ability to analyze in depth the strengths and weaknesses of each method. Direct comparison between algorithms becomes possible when standardized evaluation is performed using standardized data. From most of these challenges emerged publicly available databases for future comparison. Several past and ongoing challenge frameworks are listed on sites such as http://www.grand-challenge.org. The first one was the liver segmentation challenge SLIVER07 (Heimann et al., 2009). Several of these frameworks focus on vessels, e.g. coronary artery centerline extraction CORONARY (Schaap et al., 2009), and carotid artery lumen segmentation CAROTID (Hameeteman et al., 2011). Several more challenges focusing on the lungs, include nodule detection ANODE09 (van Ginneken et al., 2010), airway detection EXACT09 (Lo et al., 2012), lung registration evaluation EMPIRE10 (Murphy et al., 2011), lung lobe analysis LOLA11 (http://www.lola11.com) and nodule volume change analysis VOLCANO’09 (http://www.via.cornell.edu/challenge).

1.3. Objectives

The aim of VESSEL12 Challenge, organized in conjunction with the International Symposium on Biomedical Imaging 2012 (ISBI’12), is to provide a public platform to compare the performance of different segmentation algorithms to identify lung vessels in thoracic computed tomography (CT) data. An additional goal is to characterize what kind of anatomical neighborhood may complicate vessel segmentation, for example the presence of nodules, dense consolidation and parenchymal or bronchial abnormalities.

1.4. Contributions

The first contribution of this paper is an annotated reference data set. Constructing such a data set is an extremely labor-intensive task. Secondly, we propose a quantitative scoring system for objective comparison of algorithms. Thirdly, we present an evaluation of the strengths and weakness of the various vessel segmentation methods in the presence of various lung diseases.

1.5. Structure

In Section 2 of this paper, we describe the images that make up the reference data, the method to select points for evaluation and the data annotation process. In Section 3, we describe the evaluation categories, the evaluation process for each submission, and the scoring system used. In Section 4, we describe the challenge setup and challenge participation, both before and after the ISBI’12 Challenge Workshop. In Section 5, we describe the results. In Section 6, we discuss the challenge evaluation, the influence of lung pathologies, and the performance of each segmentation method, with a conclusion in Section 7.

2. Material and methods

2.1. Data collection

The scans for this challenge were collected from the anonymized image repositories of three hospitals: University Medical Center Utrecht (Utrecht, The Netherlands), the University Clinic of Navarra (Pamplona, Spain), and Radboud University Nijmegen Medical Centre (Nijmegen, The Netherlands). The data included both clinical exams taken for a variety of indications, and scans from two lung cancer screening trials: NELSON, the Dutch-Belgian randomized controlled lung cancer CT screening trial (van Klaveren, 2011) and I-ELCAP, the International Early Lung Cancer Action program (de Torres et al., 2007). In the institutes where approval of the institutional ethics committee is required, a written consent for retrospective studies had been previously obtained from each participant.

The variety of sources ensures that a wide range of clinical images typically used in diagnostic settings is present in the data-set: high and low resolution, standard or low-dose chest CT, and Angio-CT – CT with intravenous contrast; each with their own scanning parameters and reconstruction kernels. Scanners from three major manufacturers were included: Philips, Siemens, and Toshiba. We selected CT scan images taken from individual patients diagnosed with a spectrum of lung pathologies, including diffuse interstitial disease, pulmonary thromboembolism, pulmonary hypertension, alveolar inflammation, lung nodules, and emphysema. To ensure that the images were as isotropic as possible, we selected only thin slice images having slice spacing between 0.59 mm and 0.89 mm, averaging at 0.74 mm. Accurate vessel segmentation requires thin slice data, as vessels are often blurred out in CTs with thicker slices. From this cohort of images, we finally selected 20 scans, described in Table 1. This heterogeneous data closely reflects the diversity of CT scans encountered in clinical practice.

Table 1.

Description of the twenty CT scans that make up the VESSEL12 challenge dataset. Angio-CT: CT with contrast agent, LD: low-dose, HR: high resolution, ILD: (diffuse) interstitial lung disease

Scan	Image type	Pathology	Scanner and kernel	Spacing (mm)	Z-spacing (mm)	# Of slices	kV/mAs
01	Angio-CT	Alveolar inflammation	Siemens SOMATOM Sensation 64, B60f	0.76	1	355	120/40
02	Chest CT	Alveolar inflammation	Philips Mx8000 IDT 16, B Kernel	0.71	0.7	415	140/74
03	Chest CT	ILD	Philips Mx8000 IDT 16, B Kernel	0.62	0.7	534	120/77
04	LD Chest CT	ILD	Toshiba Acquilion ONE, FC55	0.86	1	426	100/44a
05	Chest CT	ILD	Philips Mx8000 IDT 16, B Kernel	0.72	0.7	424	140/73
06	Angio-CT	ILD	Siemens SOMATOM Sensation 64, B30f	0.63	1	375	120/81
07	LD Chest CT	ILD	Toshiba Acquilion ONE, FC55	0.69	1	461	100/23a
08	Chest CT	ILD	Philips Mx8000 IDT 16, B Kernel	0.78	0.7	442	140/64
09	Angio-CT	ILD	Siemens SOMATOM Sensation 64, B25f	0.68	1	543	100/150
10	Angio-CT	ILD	Toshiba Acquilion ONE, FC83	0.88	1	426	120/68a
11	Angio-CT	ILD and emphysema	Toshiba Acquilion ONE, FC83	0.77	1	421	100/120
12	Angio-CT	Secondary pulmonary arterial hypertension	Toshiba Acquilion ONE, FC83	0.8	1	446	100/92a
13	Angio-CT	Pulmonary thromboembolism	Toshiba Acquilion ONE, FC83	0.89	1	471	120/ 117a
14	LD Chest CT	Pulmonary thromboembolism and emphysema	Toshiba Acquilion ONE, FC83	0.71	1	386	100/33a
15	Angio-CT	Pulmonary thromboembolism	Siemens SOMATOM Sensation 64, B25f	0.65	1	378	100/150
16	LD Chest CT	Small nodules	Toshiba Acquilion ONE, FC83	0.75	1	451	100/38a
17	Angio-CT	Nodules and diffuse abnormalities	Siemens SOMATOM Sensation 64, B25f	0.59	1	429	100/135
18	Chest CT	Normal	Philips Brilliance 16P, B Kernel	0.78	0.7	408	140/73
19	HR Chest CT	Small nodules	Toshiba Acquilion ONE, FC83	0.69	1	396	120/68a
20	LD Chest CT	Emphysema	Toshiba Acquilion ONE, FC55	0.75	1	406	100/32a

^aToshiba Acquilion ONE modulates the dosage during acquisition. Average dose over all slices is given.

All 20 scans were then anonymized and made available for download to registered VESSEL12 challenge participants in Meta (MHD/raw) format. To facilitate vessel segmentation only within the lung areas, the lung masks for each image were also provided. The lung masks were generated using the method described in van Rikxoort et al. (2009) and were slightly edited manually in a few cases where necessary.

2.2. Reference data annotation

In this challenge we use real world data. Therefore, human annotation is the only method of obtaining a reliable reference. Since it is not feasible to perform manual segmentation of the entire vessel tree for all twenty scans, manual annotation was performed only on specific pre-generated points of interest (POIs). In addition, for evaluation of specific vessel-like structures and abnormalities within the lung, points were freely chosen by the annotators.

Using fully human annotation has its limitations. Due to the partial volume effect, human performance at assessing whether a voxel on the border of a vessel is truly part of a vessel (i.e. consists of more than 50% of vessel), is at best erratic. Taking this into consideration, the POIs were generated to avoid most of the vessel border points, following an approach previously proposed by van Dongen and van Ginneken (2010).

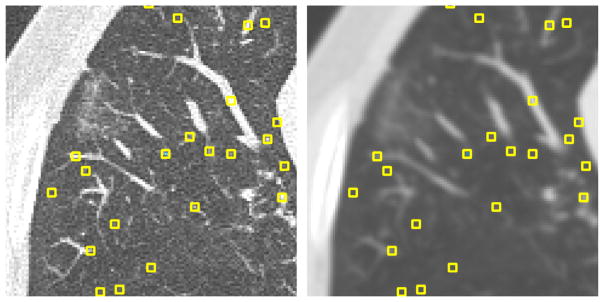
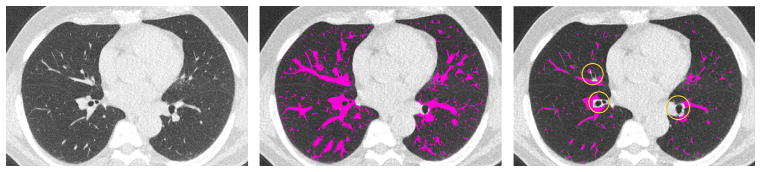
To automatically generate POIs, we first computed the 3D local maxima on a blurred version of each scan. Blurring was done on each axial slice using a Gaussian kernel with a scale of 1.0 mm (see Fig. 1). To prevent points from being too close to each other, the list of initial points was pruned. First, the points were sorted by density in descending order. Starting from the top of the list, moving downwards, all points within distance of five voxels to a point higher on the list were removed. As the majority of points selected in this way turn out to be vessels, an equal number of randomly generated points at least five voxels from any other point were then added to the list of POIs. For each scan, four axial sections along the z-axis direction were filled with POIs in this way. In each scan, we have selected sections which are approximately evenly distributed in the z-axis and which contain a large proportion of lung tissue. Fig. 2 illustrates the location of the four sections in which POIs have been generated from two scans.

Fig. 1.

(Left) Original axial section from scan 01; (Right) same slice after blurring, overlaid with automatically generated POIs. The POIs are local maxima, sorted by intensity and pruned to be further than five voxels apart. Squares in the figure have been magnified for illustration purpose.

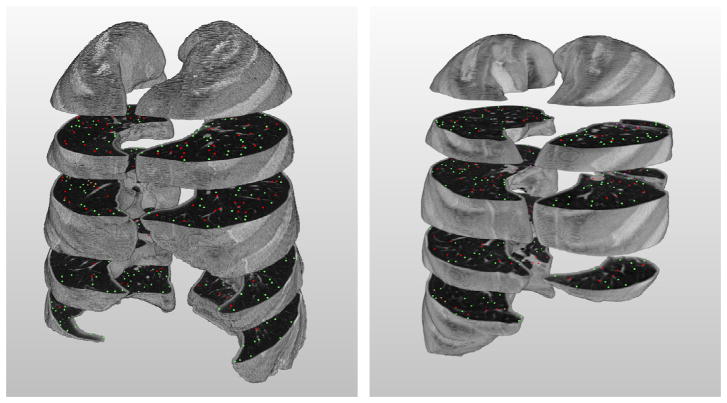
Fig. 2.

Illustration of the slices and annotated POIs in scan 01 (left) and 06 (right) after labeling process; red points indicate those which are marked as vessels, green non-vessels. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

For each POI to be annotated, the graphical interface (developed using MevisLab (Ritter et al., 2011)) displays the corresponding slice centered at the point to be evaluated. The point to be classified is also shown in three orthogonal sideviews: axial, coronal and sagittal. For both main and sideview displays, 4 mm Average Intensity Projection reformatting was used to better discriminate noise from small vessels. Having orthogonal views is important for the annotators to be able to distinguish vessels from structures which may look vessel-like when viewed only from a single plane. In addition, annotators could zoom in or scroll through the scan in the z-direction. Each point to be annotated was shown sequentially.

The annotation of the POIs was performed by three trained medical students. Training was done in three stages: (1) two hours of initial familiarization with the graphical interface, (2) 8.5 h of free testing annotation, followed by (3) a revision with radiologists, before the actual annotation of all images was performed. During the familiarization and free testing sessions, all annotators were trained to distinguish the appearance of vessels as seen through all three orthogonal views. Each annotator worked individually to mark POIs and labeled it with one out of four possible labels: vessel, lung parenchyma, airway wall, or lesion. Only POIs for which all three annotators agreed on the label have been included in the analysis.

Specific types of lesions that only occur occasionally – rare among the POIs – such as atelectasis, fibrosis, adhesive straining, consolidation and mucus filled bronchi, were interactively added by a radiologist going through all scans. Similarly, the number of automatically generated POIs labeled as airway wall points is too low for reliable statistics, therefore the annotators were asked to specifically label additional airway wall points in each scan. Furthermore, extra POIs labeled as lung nodules were generated by a nodule-detecting CAD system (Murphy et al., 2009), which were then manually reviewed by the annotators. Only points on structures that were visually confirmed to represent pulmonary nodules were then included.

2.3. Training data

We did not initially provide any training data for this challenge. Upon request of several participants, reference data was published for three example CT scans outside the original set of 20 scans. This reference data has been constructed using the same procedure as the original dataset. The three scans and their annotations are intended as an illustration of the annotation process rather than a machine learning dataset.

3. Evaluation

3.1. Evaluation categories

Performance of vessel segmentation algorithms cannot be adequately captured in a single parameter. We therefore defined several metrics which express segmentation performance in specific contexts. We looked at sensitivity of methods in segmenting larger and smaller vessels, and specifically focused on the effect of the presence of disease-induced confounding structures. Diseases such as interstitial lung disease, cystic fibrosis, asthma and chronic obstructive pulmonary disease (COPD) can cause lung tissue to deform into structures which might be mistaken for vessels. In addition, such diseases can be accompanied by mucus production, filling the bronchi, giving rise to images in which a bronchus suddenly looks like a vessel.

For nodule detection, the most widely studied CAD task in chest CT, good vessel segmentation helps to eliminate false positives on vessels, and yet it is crucial that nodules do not get classified as vessels. Similarly, there are also vessels within consolidations, which may take up significant volume that is not strictly part of the lesion.

To evaluate different performance aspects of vessel segmentation algorithms, we present nine evaluation categories, as summarized in Table 2.

Table 2.

Categories used for the evaluation. Note that only unanimously labeled automatic points have been included. AW: airway wall, DL: dense lesion, MB: mucus-filled bronchi.

Category		Source	Positive class	Negative class	Number of points
					Total	Positive	Negative
1	Principal (ALL)	Automatic	All vessel points	All non-vessel points	7352	2238	5114
2	Large vessel	Automatic	All largea vessel points	All non-vessel points	5891	777	5114
3	Medium vessel	Automatic	All mediumb vessel points	All non-vessel points	5860	746	5114
4	Small vessel	Automatic	All smallc vessel points	All non-vessel points	5818	704	5114
5	Vessel/Airway walls	Automatic + Interactive	All vessel points	All automatic + interactively added AW points	8101	2238	5863
6	Vessel/Dense lesion	Automatic + Interactive	All vessel points	All automatic + interactively added DL points	2702	2238	464
7	Vessel/Mucus-filled bronchi	Automatic + Interactive	All vessel points	Interactively added MB points	2336	2238	98
8	Vessel-in-lesion/Lesion	Automatic + Interactive	All vessels points within consolidation	All automatic + interactively added DL points	401	146	255
9	Vessel/Nodules	CAD	All vessel points	All CAD-detected nodule points manually verified	3227	2238	989

^aLarge: greater than –615 HU after blurring.

^bMedium: between –765 and –615 HU after blurring.

^cSmall: less than –765 HU after blurring.

• Principal (1st)

  The Principal category evaluates how well the algorithm distinguishes vessels from non-vessels. All the points given the same label by three annotators independently make up the principal dataset that is used for this category. A total of 9419 points across all 20 scans were annotated. Of these, the annotators unanimously agreed upon the labels of 7352 points (78%). This is the general evaluation category used for overall ranking.

• Small vessel (2nd), Medium vessel (3rd), and Large vessel (4th) These categories evaluate to what extent the vessel sizes affect segmentation performance. Vessel points from the Principal category are subdivided into three subsets: large, medium and small. As proxy for vessel size, we used the intensity of a point after 1 mm Gaussian blurring, assuming lower intensity points belong to smaller vessels. In the set of all vessel points from the Principal category, we used the 33rd and the 66th percentile intensity values as dividing points between large medium and small vessels. We divided the data into large (intensity higher than 3615 HU), medium (intensity between 3765 and 3615 HU) and small (intensity lower than 3765 HU) vessels. The threshold values were used on both contrast and non-contrast images, as separating these two image types does not yield significant difference in the values calculated. To these three groups of vessel points, all the non-vessel points were added to make up the Large vessel, Medium vessel, and Small vessel categories, respectively. See Fig. 3(a)–(c) for examples.

• Vessel/Airway walls (5th)

  The Vessel/Airway walls category was designed to evaluate the ability of segmentation methods to distinguish vessels from airway walls (see Fig. 3(d)). Airway walls have tissue density values similar to vessels, and are therefore easily confounded with vessels. Part of the airway wall points in this category are points labeled as airway walls in the principal dataset. Because these are relatively few in number, airway wall points were interactively added. These airway wall points were then combined with an equal number of vessel points from the Principal category.

• Vessel/Dense lesions (6th), Vessel/Mucus-filled bronchi (7th), and Vessel-in-Lesion/Dense lesions (8th)

  The three categories Vessel/Dense lesions, Vessel/Mucus-filled bronchi, and Vessel-in-lesion/Dense lesions, are designed to evaluate the ability of segmentation methods to distinguish several types of dense abnormalities from vessels. The datasets for these categories contain lesions that can be divided roughly into three classes: (1) dense lesions, which include atelectasis, fibrosis, adhesive straining, and other dense lesions, (2) mucus-filled bronchi, which are airways that instead of being clear, are filled with liquid such as mucus, which might lead them to be identified as high-intensity tubular structures, and (3) consolidations, which may also contain vessels, visible only in contrast scans. Fig. 4 shows examples of dense abnormalities present.

  In contrast-enhanced images, some vessels are visible even within the dense lesions, as shown in Fig. 5. In the Vessel-in-Lesion/Dense lesions category, only vessel points from the principal dataset and points within dense lesions, added by a radiologist, were included.

• Vessel/Nodules (9th)

  The last category evaluated the ability of segmentation methods to distinguish vessels from nodules. Fig. 4(d) shows an example of a nodule.

Fig. 3.

A slice from scan 05 showing (a) small (–818 HU), (b) medium (–727 HU) and (c) large (–382 HU) vessel points. The post-blurring CT values of each vessel point is within the range of CT values corresponding to each vessel size classification. (d) Point showing airway wall.

Fig. 4.

Examples of lesions which might be confounded with vessels: (a) mucus-filled bronchus (scan 12) is shown here as a bright tubular structure with an air bubble, (b) dense lesions (scan 01), (c) fibrosis (scan 02), and (d) nodule (scan 01).

Fig. 5.

Examples of vessels found within dense lesion (from contrast scan 05) shown in three orthogonal views: (a) axial, (b) sagittal, and (c) coronal. Window level has been modified to preferentially increase contrast for this illustration purpose only.

3.2. Submission format requirement

To ensure that all results provided by the participants of the VESSEL12 Challenge could be fairly evaluated, the submission requirement was standardized. For each scan, the participant was asked to submit an image of 8-bit unsigned char, with each voxel value representing the probability (between 0 and 255) of that voxel being a vessel. Binary submissions were also accepted. Each submission was then evaluated for all the categories described in the earlier section.

3.3. Evaluation methods of submitted data

For each scan in the VESSEL12 dataset, each submission contains a full vessel tree segmentation. Our evaluation data consists of hundreds of labeled points in each scan (see Section 3.1 for an exact numerical breakdown). Evaluating a submission then consists of iterating over each point and checking whether the submissions label corresponds to the label given by the panel of annotators.

An important question arises here: should anything which is probably a vessel be labeled as such, or should only vessels which are absolutely certain be labeled? Different medical applications have different requirements: an application scanning for lung emboli will require a high sensitivity, while preprocessing for nodule detection will emphasize specificity. To evaluate algorithm performance without confining ourselves to any specific application, we use Receiving Operator Characteristic (ROC) curve analysis.

An ROC curve yields information about an algorithms’ performance at different levels of sensitivity. This type of analysis requires a probabilistic segmentation, in which each voxel is assigned a probability of being a vessel. A probabilistic segmentation can yield many binary segmentations—including only those with probabilities higher than the given threshold value. An ROC curve is created by plotting the sensitivity against 1-specificity. High thresholds will typically yield a segmentation with low sensitivity but good specificity, and lower threshold typically increases sensitivity but loses specificity. We refer readers unfamiliar with ROC to Fawcett (2006) for further treatment of ROC analysis.

The principal metric for VESSEL12 evaluation is the area under the ROC curve (Az). A purely random classifier would give a point along the diagonal line of no-discrimination, giving an Az score of 0.5. The ideal curve, correctly classifying all positive voxels while making no mistakes, would go through the point (0,1) in the upper left corner, yielding an Az score of one.

When the submission is in binary format, only a single operating point will be obtained in the ROC curve. To compare performance to probabilistic submissions, a signed distance transform was computed on each binary submission. In this way the binary segmentation is transformed into an approximation of a probabilistic segmentation.

Additionally, ROC curve analysis also yields an optimal specificity/sensitivity point, which we define as the point on the ROC curve closest to point (1,0). For binary submissions, the original submission (distance transform thresholded at zero) is taken as the optimal specificity/sensitivity point.

The evaluation method is summarized in Fig. 6.

Fig. 6.

Overview of processes in the evaluation method.

3.4. Scoring

ROC curve analysis was performed on all the nine categories described in Table 2. In the ISBI’12 VESSEL12 challenge, methods were ranked according to their score on the Principal category. This category was chosen as the most unbiased overall measure of vessel segmentation performance. To evaluate various aspects of segmentation performance in detail, scores on the other eight categories are published for each method in addition to the principal score.

4. Challenge setup

4.1. Challenge format

Teams from both academia and industry were invited to participate in the challenge. We sent out notifications to various medical imaging mailing lists and individual invitations to authors as well as research groups that have previously published on the topic of vessel segmentation.

We opened online registration on November 15th, 2011, and made the data available for download on January 6th, 2012. Between the latter date and the day of the ISBI’12 Challenge, May 2nd, 2012, we worked to develop the annotation interface, annotate the reference data, define the evaluation categories and automate the online evaluation process.

4.2. Challenge participants

Out of 113 registered teams, more than half downloaded the data, and a total of 14 teams submitted their segmentations in time for the challenge day – resulting in 20 methods – with several teams submitting results from multiple methods. After the challenge day, three more teams uploaded their algorithm results, and one previously signed up team uploaded two new submissions. The labels A–W will henceforth be used to refer to each submission. Teams which did not upload algorithm descriptions or who explicitly asked to remain anonymous were excluded from the analysis (n = 2, methods A and R). To set up a baseline performance evaluation, we have included two reference methods: density method and vesselness filter method.

4.3. Brief description of each submission

Only teams which submitted their algorithm descriptions have been included in this section, described below and summarized in Table 3.

Table 3.

Challenge participants and submission types.

Team	Algorithm type	Multi-scale	Postprocessing
Probabilistic
B	Thresholding	N/A	Airway wall and nodules removal
C	Hessian-based	No	Large low-vesselness structure removal
D	Hessian-based	Yes	No
E	Hessian-based	Yes	No
G	Hessian-based	Yes	Airway walls removal
H	Hessian-based	Yes	No
I	Hessian- and region growing-based	No	Airway walls removal
K	Hessian-based	Yes	Histogram equalization
L	Hessian-based	Yes	Histogram equalization
M	Hessian-based	Yes	Histogram equalization
N	Hessian-based	Yes	Histogram equalization
Q	Hessian-based	Yes	Histogram equalization
Binary
F	Hessian- and region growing-based	Yes	No
J	Machine-learning	N/A	Large nodule removal
O	Region growing-based	N/A	Airway walls removal
P	Hessian-based	Yes	Airway walls and lobe fissure removal
Reference
R1	Thresholding	N/A	No
R2	Hessian-based	Yes	No
Post-challenge submissions
S	Machine-learning	Yes	No
T	Hessian-based	Yes	No
U	Hessian-based	Yes	No
V	Hessian- and region growing-based	Yes	(Preprocessing) Airway walls removal
W	Hessian- and region growing-based	Yes	Yes

The various submissions used techniques that can be classified as: (1) variants or direct use of Hessian-based “vesselness” filters, (2) variants of region growing methods, or (3) thresholding-based methods, or (4) machine-learning based methods.

Method B (Telecom SudParis, France) applied hysteresis thresholding within the segmented lung parenchyma region, coupled with a 3D connectivity criterion between vessels and mediastinal region (Fetita et al., 2009a). The airway wall areas were previously removed from the lung parenchyma exploiting airway lumen segmentation (Fetita et al., 2009b) and lumen caliber-related wall thickness information (Fetita et al., 2010). Finally, a shape filter based on medial axis and vessel caliber analysis (Fetita et al., 2010) was applied to remove juxtavascular nodules or fibrosis tissue. To obtain probabilities, Euclidian distance transform was then applied to the binary response.

Method C (Arizona State University, USA) used Hessian-based vesselness (Zhou et al., 2007), followed by vesselness-oriented level set (Zhu et al., 2009) and removal of large structures with low vesselness response. The probabilities were generated by applying a Gaussian kernel (size = 6, σ = 1.5) to the vessel segmentation.

Method D (Bahcesehir University, Turkey) employed Hessian-based vesselness on images denoised by 3D median filtering. The scale of the filter was selected empirically as two to achieve robustness of the algorithm. The probabilistic values were trained with the help of the training dataset. Log transformation was then performed to discriminate whenever possible – from the difference in variance – false positives from true positives. Finally, after postprocessing the vessel regions were highlighted in the probability map. Details can be found in Oksuz et al. (2013).

Method E (Brigham and Women’s Hospital, USA) first deconvolved the images, then pre-blurred them with a bank of discrete Gaussian kernels with ten scales, uniformly distributed in the range [0,6] pixels. Scale-space particle sampling was then performed to find strongest Hessian matrix-based response (Estepar et al., 2012). The particle scale was used to estimate vessel radius. Log transformation was then applied to transform binary response to probability.

Method F (CREATIS, Universite de Lyon, France & Universidad de los Andes, Colombia) is based on a variational region growing (VRG) approach introduced in Rose et al. (2009), which performs energy minimization using a region-descriptor function. Similar to Pacureanu et al. (2010), this function enforces an appropriate range of gray-levels and a tubular shape of the segmented structures by combining an intensity term and a vesselness term calculated with the Hessian-based Sato’s filter (Sato et al., 1997). These two terms were normalized by the respective maximum values found within the volume of interest (lung mask). The vesselness was calculated at scales between 0.2 and 6.0. The seeds for VRG were selected using the Hessian-based criteria proposed by Lo et al. (2010).

Method G (Radboud University Nijmegen Medical Center, the Netherlands) used normalized multiscale Frangi’s vesselness (Frangi et al., 1998) filter (scales = 7, σ = 1.0–4.5 mm), followed by optimal local thresholding. Airway wall exclusion was then performed to reduce false positives, and distance transform was applied to the final segmentation (van Dongen and van Ginneken, 2010).

Method H (Fraunhofer MEVIS, Germany) is very basic, using multiscale Frangi’s vesselness method (Frangi et al., 1998) (scales = 4, σ = 0.9, 1.6, 2.3 and 3 mm) without preprocessing.

Method I (Fraunhofer MEVIS, Germany) generated seeds for region growing using Frangi’s vesselness filter with 1 mm scale resulting in vesselness image V(x⃗). Seedpoint precursors were then defined as any voxel above the 97th percentile of intensity values. Final seedpoints s⃗_i were obtained after spatial filtering: a shrunk (eroded) lung mask was used to exclude all seedpoints less than 15 mm away from the outer lung boundary. In addition, a simple bronchi segmentation was used to remove seedpoints within bronchi. Region growing was then performed on V(x⃗), starting from S⃗_i in direction of descending vesselness values. For the “probabilistic segmentation mask”, P(x⃗) we output masks for different threshold values of the Region Growing:

$$P(\overrightarrow{x})=max(g·R_{\theta (g)}(\overrightarrow{x}))$$

where R_θ(x⃗) is a binary result mask (0 for background, 1 for vessel voxels) resulting from Region Growing in direction of descending vesselness values, stopping at the vesselness threshold θ. Every possible gray value g ∈ [1 . . . 255] is linearly mapped to a threshold $\theta (g)={\theta }_{max}·\frac{g}{255}$ (θ_max was set to 100 for the submission).

In method J (Universitat Politècnica de València, Spain), images were first normalized to 8 bits (0–255). Area opening filter was applied to reduce noise and local bright objects that have an area lower than λ (8 pixels), followed by close-hole operator to enhance vessel structures. Classification was then performed using K-means clustering (k = 3), followed by 3D filtering to remove spurious elements – such as tumors – with size lower than certain threshold (4000 voxels).

Method K (LUMC, the Netherlands & Hunan University, China) performed Frangi’s vesselness (σ = 1, 2, and 3 mm) filter. The free parameters were chosen as α = β = 0.5 as recommended in Frangi et al. (1998) and c = 500 (related to the intensity range in lung CT data). All output images were first rescaled to a range [0, 10⁶] and rounded to the nearest integer. Subsequently, histogram equalization was employed in order to have an equal distribution of the responses at a certain threshold. Finally, the result was rescaled to the range [0,255].

Method L (LUMC, the Netherlands & Hunan University, China) was similar to submission K. The vesselness enhancement filter that was used, however, was a central adaptive medialness function, inspired by the work of Krissian et al. (2000). It is defined as −λ₂/λ₃ (λ₂ + λ₃) when the sum of all eigenvalues is less than zero, and zero otherwise. It uses no free parameters.

Like method L, the processing in method M (LUMC, the Netherlands & Hunan University, China), is similar to submission K. The vesselness enhancement filter used was the same as L, except that the underlying Gaussian kernel to compute the eigenvalues was replaced by a bi-Gaussian kernel (Xiao et al., 2013). The traditional Gaussian operator has infinite support and its response is therefore influenced by structures adjacent to a vessel. The bi-Gaussian kernel, however, allows independent selection of foreground and background scales. By taking a narrower local neighborhood for contrast computation, closely located adjacent structures can be separated better, while keeping the intra-vessel noise suppressing ability of the conventional Gaussian scale space.

Similar to what was described in method K, method N (LUMC, the Netherlands & Hunan University, China) also performed postprocessing. The vesselness enhancement filter however was based on a strain energy tensor decomposition, measuring intensity contrast, structure strength and shape. These measures were combined with an intensity continuity term along the vessel and a step edge suppression mechanism. Details can be found in Xiao et al. (2011).

Method O (Technical University of Lodz, Poland) first normalized input data to the range of [0,1]. Assuming bimodal histogram distribution, region growing was then performed using 26-connectivity from seed areas – defined as regions of more than 50 pixels above the value at the object histogram peak. The intensity threshold was individually determined by averaging the peak values of the bimodal histogram for each normalized CT scan. Airway segmentation was performed to explicitly exclude airway walls.

Method P (Norwegian University of Science and Technology, Norway) used a multiscale tubular detection filter that fits a spline instead of circle, adapted from Krissian et al. (2000). Response was calculated as the average dot product of the inward normal of the spline and the direction of the underlying gradient vector. Region growing was performed to connect voxels with high tubularity response. A conservative segmentation of airway, followed by dilation to obtain airway walls, and lung lobe fissure segmentation were then performed to remove these known structures.

Method Q (Shahed University, Iran) employed a modified Frangi filter, followed by multiscale medialness. Radius was estimated by graph analysis, and finally vessel was grown from medial axis using estimated radius.

Reference method R1 (density method) is based on the assumption that vessels have higher density than the surrounding lung tissue and airways. Simply rescaling the values of all voxels between −1024 and 200 HU, to the range of 0–255, gives a segmentation in which any structure with higher intensity are given higher probability of being vessels. The density method should then find most vessels, but also mistake other structures for vessels.

Reference method R2 (vesselness filter method) used a vesselness filter implemented as a module (MLModule “Vesselness”) by MevisLab was employed with seven scales, evenly distributed from 1 to 4.5 mm.

4.4. Post-ISBI’12 submissions

Three more teams uploaded their submissions post-ISBI’12 Challenge Day. Methods S (University of Alberta), T (Universidad Politécnica de Madrid), and U (Graz University of Technology), enjoy the advantage of being able to study the performance of the methods submitted pre-challenge. Methods V and W were submitted by a pre-ISBI’12 participant, CREATIS.

Method S (University of Alberta, Canada) used stacked multi-scale feature learning. The features are learned from sample patches, randomly extracted at multiple scales from a 6-level Gaussian pyramid expansion of the data. Filter banks are learned using spherical k-means (Coates and Ng, 2012). A two-layer stacked representation was obtained by performing the learning on the outputs of the first layer. Each layer had 32 features. While learning is from randomly sampled patches, usage is by conventional convolution with the image data to obtain the filter response vector for each voxel. The three example scans were used for training a L₂-regularized logistic regression classifier using the learned voxel features as inputs. The parameters were selected using 10-fold cross validation. Final probability was then obtained by linearly scaling the predicted probabilities to [0,255].

Method T (Universidad Politécnica de Madrid, Spain) used a modified multiscale Frangi’s vesselness enhancement filter, by incorporating airway wall information to penalize the probability of a voxel being a vessel (Jimenez-Carretero et al., 2013). Airways enhancement was first performed applying eigenvalue analysis of the Hessian to give a higher response in dark tubes. Voxels where the plane perpendicular to the airway direction eigenvector intersects a hollow sphere of radius σ, with wall thickness w (estimated from the maximum scale), following Montaudon et al. (2007), were then marked as airway walls. The probability of being a vessel of each voxel was then subtracted by its probability of being airway wall.

Method U (Graz University of Technology) used a multiscale vessel enhancement filter adapted from the tube detection filter by Bauer et al. (2010), followed by centerline extraction. Vessel enhancement consisted of an analysis of the Hessian eigenvectors and computation of an offset vesselness function containing the gradient information sampled at circles of different radii perpendicular to the tube direction (eigenvector with smallest eigenvalue), a local symmetry measure, and an adaptive vesselness threshold. Centerline fragments from non-maxima suppression were then connected using a shortest path algorithm, and the vessel radius was estimated using a spherical ray-cast approach, which was finally refined by minimizing a geodesic active contour energy, as proposed by Reinbacher et al. (2010). The final probability was obtained by weighting the segmentation based on the original vesselness response, which was rescaled to [0,255]. The method was presented in more detail in Helmberger et al. (2013).

Method V used the same variational region growing (VRG) approach and same initialization as method F. However, the vesselness term was calculated using the Frangi’s filter (Frangi et al., 1998) at scales ranging from 0.2 to 3.5, and the lung mask was modified as follows. The volume of interest was eroded to reduce false positives near the pleural surface. The bronchi and their walls were masked. To do so, first the bronchial tree was segmented by region growing with leakage detection (Mori et al., 2000), which iteratively increases a threshold value until the number of voxels aggregated in one iteration becomes too large. Then the branches of the segmented tree were dilated proportionally to the branch thickness. The tree was successively pruned by morphological opening with a bank of increasing-size structuring elements, thus generating several trees, each one only keeping the branches thicker than the structuring element. Each of these trees was then dilated with a structuring element half as large as the one used for opening. The final bronchial-tree mask was obtained as union of all the dilated trees.

Method W is a probabilistic version of method V. It uses the binary segmentation result and the vesselness map calculated by method V. The latter were scaled to fit the dynamics required from the submissions. Each voxel belonging to the segmented vascular tree was assigned the value of the corresponding voxel from the vesselness map, while the voxels beyond the vessel tree were assigned zeros. The method was presented in more detail in Orkisz et al. (2014).

5. Results

On the principal dataset, the Az value was calculated for each individual image, as well as combining all points. For each submission, the optimal threshold – threshold at which the optimal specificity/sensitivity was obtained – was calculated with the principal dataset and was used as the optimal threshold across the other datasets. Each submission received a table containing the Az score and the specificity and sensitivity point at the optimal threshold, across all nine datasets as well as for each of the twenty scans.

For the Principal category, the majority of methods do a good job segmenting vessels, with the median performer having Az score of 0.932, and thirteen submissions scoring more than 0.9 (see Tables 4 and 5 for exact scores breakdown). Individually, the top five methods have very similar optimal specificity-sensitivity points (above 0.93/0.93), as shown in Fig. 7 (right).

Table 4.

Scores for all submissions across all categories. Principal Rank is derived from the Az score on the Principal category. For each method, Average Rank indicates the average of its rank across all categories. (Categories 1: Principal, 2: Small Vessels, 3: Medium Vessels, 4: Large Vessels, 5: Vessel/Airway Wall, 6: Vessel/Dense Lesion, 7: Vessel/Mucus-filled bronchi, 8: Vessel-in-lesion/Lesion, 9: Vessel/Nodules).

	Principal score		Az score for each category							As of ISBI’12		Post-ISBI’12
	1	2	3	4	5	6	7	8	9	Average rank	Principal	Average rank	Principal
Probabilistic
B	0.837	0.665	0.885	0.947	0.819	0.709	0.660	0.627	0.735	9.9	13	13.2	18
C	0.812	0.583	0.862	0.972	0.658	0.479	0.355	0.712	0.355	13.6	14	17.8	19
D	0.980	0.976	0.979	0.985	0.934	0.635	0.607	0.757	0.358	6.2	5	7.9	6
E	0.852	0.645	0.918	0.974	0.766	0.655	0.597	0.699	0.557	10.0	12	13.2	17
G	0.932	0.885	0.954	0.955	0.912	0.625	0.404	0.649	0.461	10.7	10	13.1	12
H	0.984	0.972	0.986	0.993	0.908	0.555	0.397	0.654	0.330	8.1	1	10.1	2
I	0.981	0.975	0.985	0.983	0.943	0.706	0.617	0.750	0.617	4.0	3	5.2	4
K	0.975	0.952	0.975	0.995	0.738	0.565	0.462	0.750	0.336	8.3	6	10.8	7
L	0.984	0.979	0.982	0.991	0.940	0.624	0.513	0.734	0.300	6.7	1	8.2	2
M	0.981	0.978	0.983	0.981	0.941	0.679	0.619	0.752	0.397	5.1	3	6.4	4
N	0.956	0.964	0.955	0.949	0.953	0.726	0.661	0.652	0.466	7.1	8	8.9	10
Q	0.561	0.479	0.485	0.709	0.492	0.528	0.450	0.651	0.571	14.7	18	18.9	23
Binary
F	0.739	0.444	0.766	0.981	0.544	0.510	0.276	0.790	0.385	12.9	15	16.7	20
J	0.652	0.448	0.566	0.920	0.376	0.419	0.184	0.829	0.544	14.4	17	18.4	22
O	0.737	0.500	0.742	0.947	0.556	0.554	0.236	0.779	0.580	12.7	16	16.6	21
P	0.902	0.821	0.921	0.955	0.865	0.683	0.462	0.645	0.507	10.3	11	13.1	13
Reference
R1	0.970	0.929	0.984	0.995	0.775	0.471	0.416	0.745	0.248	9.6	7	12.4	9
R2	0.946	0.933	0.946	0.957	0.948	0.792	0.707	0.730	0.788	5.9	9	7.4	11
Post-ISBI’12 submissions
S	0.986	0.977	0.986	0.994	0.944	0.667	0.595	0.654	0.439	-	-	6.2	1
T	0.972	0.943	0.983	0.987	0.900	0.58	0.509	0.763	0.287	-	-	9.9	8
U	0.863	0.781	0.848	0.951	0.851	0.712	0.677	0.646	0.659	-	-	12.0	16
V	0.874	0.673	0.950	0.982	0.794	0.480	0.364	0.696	0.281	-	-	16.0	15
W	0.879	0.693	0.953	0.976	0.845	0.583	0.495	0.766	0.367	-	-	12.2	14

Table 5.

Optimal Specificity/Sensitivity points across all categories. For probabilistic methods, the optimal operating point is calculated across all the points within the category. For binary methods, the optimal operating point is the original binary submission. (Categories 1: Principal, 2: Small Vessels, 3: Medium Vessels, 4: Large Vessels, 5: Vessel/Airway Wall, 6: Vessel/Dense Lesion, 7: Vessel/Mucus-filled bronchi, 8: Vessel-in-lesion/Lesion, 9: Vessel/Nodules).

	Specificity/Sensitivity score for each category
	1	2	3	4	5	6	7	8	9
Probabilistic
B	0.99/0.68	1.00/0.34	0.99/0.78	0.99/0.90	0.94/0.68	0.56/0.68	0.44/0.68	0.55/0.62	0.56/0.68
C	0.98/0.64	0.98/0.19	0.98/0.74	0.98/0.95	0.66/0.64	0.44/0.64	0.25/0.64	0.66/0.82	0.32/0.64
D	0.95/0.95	0.94/0.94	0.98/0.95	0.98/0.97	0.82/0.95	0.37/0.95	0.29/0.95	0.50/0.83	0.06/0.95
E	0.92/0.74	0.98/0.36	0.95/0.85	0.95/0.95	0.52/0.74	0.33/0.74	0.21/0.74	0.53/0.84	0.16/0.74
G	0.94/0.90	0.92/0.84	0.96/0.93	0.95/0.93	0.83/0.90	0.35/0.90	0.18/0.90	0.50/0.82	0.15/0.90
H	0.94/0.95	0.91/0.94	0.96/0.95	0.99/0.98	0.70/0.95	0.26/0.95	0.11/0.95	0.08/0.97	0.03/0.95
I	0.95/0.94	0.92/0.93	0.96/0.96	0.97/0.96	0.85/0.94	0.39/0.94	0.26/0.94	0.56/0.78	0.16/0.94
K	0.91/0.96	0.89/0.95	0.93/0.97	0.98/0.98	0.38/0.96	0.20/0.96	0.06/0.96	0.44/0.86	0.03/0.96
L	0.96/0.95	0.94/0.96	0.96/0.96	0.98/0.98	0.83/0.95	0.37/0.95	0.20/0.95	0.49/0.84	0.07/0.95
M	0.95/0.95	0.93/0.95	0.95/0.96	0.98/0.94	0.83/0.95	0.43/0.95	0.29/0.95	0.58/0.77	0.16/0.95
N	0.94/0.92	0.93/0.95	0.96/0.91	0.98/0.90	0.95/0.92	0.57/0.92	0.43/0.92	0.60/0.59	0.17/0.92
Q	0.95/0.17	0.95/0.01	0.95/0.02	0.95/0.45	0.79/0.17	0.88/0.17	0.70/0.17	0.93/0.36	0.98/0.17
Binary
F	0.83/0.56	0.33/0.65	0.78/0.61	0.98/0.97	0.28/0.56	0.42/0.56	0.14/0.56	0.57/0.91	0.29/0.56
J	0.56/0.60	0.41/0.59	0.51/0.58	0.94/0.84	0.08/0.60	0.31/0.60	0.00/0.60	0.34/0.96	0.53/0.60
O	0.75/0.59	0.43/0.59	0.76/0.59	0.98/0.89	0.26/0.59	0.42/0.59	0.02/0.59	0.63/0.79	0.59/0.59
P	0.95/0.84	0.94/0.71	0.96/0.88	0.96/0.92	0.74/0.84	0.48/0.84	0.16/0.84	0.60/0.64	0.35/0.84
Reference
R1	0.92/0.91	0.85/0.91	0.96/0.97	0.98/0.99	0.50/0.91	0.21/0.91	0.12/0.91	0.44/0.86	0.02/0.91
R2	0.88/0.89	0.85/0.89	0.89/0.88	0.90/0.89	0.89/0.89	0.57/0.89	0.38/0.89	0.69/0.70	0.53/0.89
Post-ISBI’12 submissions
S	0.94/0.95	0.93/0.93	0.95/0.95	0.96/0.96	0.75/0.95	0.29/0.95	0.13/0.95	0.48/0.80	0.07/0.95
T	0.96/0.89	0.87/0.96	0.96/0.95	0.99/0.96	0.78/0.89	0.32/0.89	0.22/0.89	0.49/0.84	0.02/0.89
U	0.97/0.74	0.97/0.59	0.97/0.72	0.97/0.91	0.93/0.74	0.57/0.74	0.44/0.74	0.66/0.58	0.46/0.74
V	0.94/0.77	0.73/0.54	0.94/0.92	0.94/0.96	0.77/0.77	0.25/0.77	0.09/0.77	0.56/0.82	0.11/0.77
W	0.97/0.77	0.96/0.42	0.97/0.92	0.98/0.95	0.85/0.77	0.34/0.77	0.13/0.77	0.56/0.81	0.12/0.77

Fig. 7.

(Left) Individual submissions’ ROC curves for Principal Category, shown for 19 probabilistic methods (solid line) and 4 binary methods (dotted line). Letter indicates the position of optimal specificity/sensitivity point, data for methods below (0.5,0.5) in sensitivity and specificity are not shown. (Right) Zoomed in ROC curves for top five performing methods.

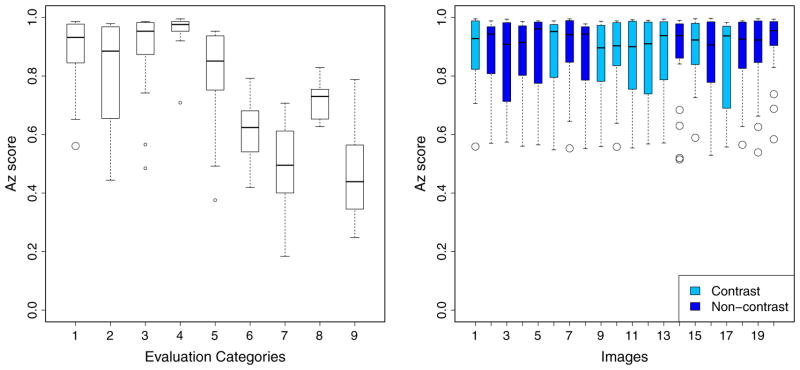
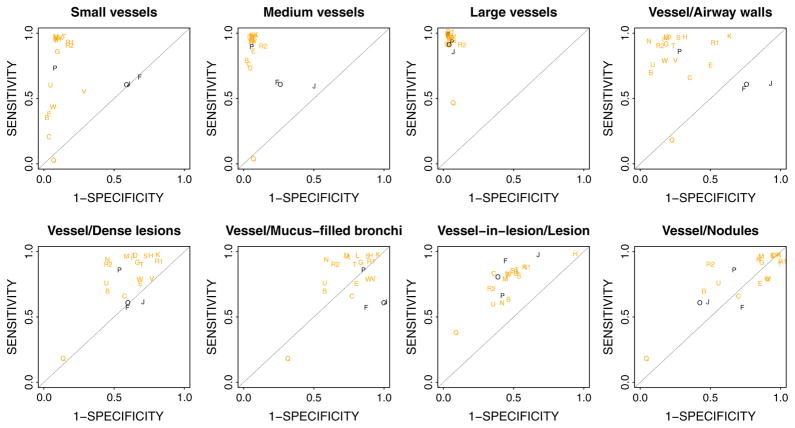
Analyzing the different categories, however, shows a wide spread (see Fig. 8 (left)) in the performance for every category except for Large Vessels (4th), where all submissions generally perform very well – as expected, gradually worsening in Medium Vessels (3rd) and Small Vessels (2nd). This reveals that small vessels segmentation is still generally difficult. Airway walls (5th category) are also source of false positives for many submissions. Several categories are more difficult – such as Vessel/Dense Lesions (median Az score: 0.625), Vessel/Mucus-filled Bronchi (median Az score: 0.509) and Vessel/Nodules (median Az score: 0.461).

Fig. 8.

(Left): Performance by Evaluation Categories, showing Az score distribution across all methods. (Right) Performance of all methods on the Principal category, analyzed by individual images. Notice there is no single pathology or image type that presents particular difficulty in vessel segmentation. A slightly smaller spread could be observed for images 14 and 20, although the median performances for these images remain comparable with the rest. (Categories 1: Principal, 2: Small Vessels, 3: Medium Vessels, 4: Large Vessels, 5: Vessel/Airway Wall, 6: Vessel/Dense Lesion, 7: Vessel/Mucus-filled bronchi, 8: Vessel-in-lesion/Lesion, 9: Vessel/Nodules).

Overall, we found no significant difference between the performance across all 20 scans (see Fig. 8 (right)). There is no single pathology that confounds the vessel segmentation significantly. Rather, it is the presence of very specific structures caused by underlying lung diseases (i.e. mucus-filled bronchi, nodules and dense lesions), which is the primary confounding factor among the submitted methods. We note, however, that in low-dose CT scans of lungs affected by emphysema (images 14 and 20), performance spread is smaller, although the median Az scores are comparable to the rest. This could be due to increased contrast observed in emphysematous lungs, characterized by destruction of lung tissues, leaving larger airspaces. We also found no statistical difference between segmentation performance for contrast and non-contrast images.

6. Discussion

In this section, we analyze the reference annotation process, the performance analysis by ROC curves and trends, strengths and weaknesses of participating algorithms.

6.1. Reference annotation and evaluation

The points whose labels the annotators did not unanimously agree made up about 22% of the total number of generated POIs. The majority of these points lie on the border of the lungs. Revisiting the rest of these contested points reveals that label discrepancy did not arise due to confounding structures which might look like vessels, but rather because many of them are located on the edge of a vessel structure. The points which lie on the vessel borders become interesting when we are addressing vessel sizes while, in the VESSEL12 Challenge, we focus on vessel detection and not in exact demarcation of vessel borders. To avoid confusion about whether a POI is just on the border or just off the border of a vessel, we included only the unanimously agreed POIs.

The manual annotation process is highly time consuming. It took an average of 14 h for each evaluator to finish annotating all the automatically generated POIs in the Principal category. A natural consequence of the evaluation process we adopted is that the annotation process did not produce complete vessel trees, which may be useful for quick visual evaluation. In addition, using only four sections from each image might seem to suggest that we are evaluating over a minuscule proportion of the CT image. To ascertain that our evaluation framework gives a stable result – that is, that we have evaluated on a sufficiently large number of points –we compared the performance of the submissions using the POIs generated for two sections only. As shown in Fig. 10, we found no significant difference between using only two slices and four slices (R = 0.9995), suggesting that with four slices we have sampled the points for the Principal category sufficiently.

Fig. 10.

Plotting the Az score for the Principal category using points from two slices against points from four slices per scan shows consistent performance across the methods submitted. The red line indicates the identity line. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

When deciding on a procedure for evaluation, one faces a number of choices. We opted for ROC analysis because it is a well-established, widely used paradigm. To allow methods that produce a binary segmentation to participate, and to be able to directly compare these methods with probabilistic methods, we decided to convert binary results into probabilistic results via a distance transform. A binary result has numerous possible corresponding probabilistic distributions. The distance transform gives but one possibility. There is a simple intuition behind this: the further away a voxel is from a confirmed vessel, the lower the probability is for it to be a vessel. Upon hindsight, it is hard to say if this procedure could really represent the actual probabilistic distribution of these methods.

We observe a marked difference in performance between the probabilistic and binary submissions (see Fig. 8 and Table 4), though not all binary submissions performed poorly, as seen from Fig. 8 – where Method P is a binary submission in the top 10 ranking for the Principal category. Generally, probabilistic submissions seem to have higher sensitivity than the binary methods in the Principal category (see Fig. 9).

Fig. 9.

Operating point for each method calculated at principal optimal threshold is here shown for all non-principal evaluation categories. Note the probabilistic methods (orange) generally have higher sensitivity than binary methods (black). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

6.2. Strengths and weaknesses of the methods

Across all submissions, none used anatomic knowledge apart from density and structure tubularity. To our knowledge, none used information about noise level associated with different reconstruction kernels, nor average vessel density in contrast vs. non-contrast scans, nor the average vessel tree volume that corresponds to different lung pathologies.

To their merit, several groups reported that their algorithms were adapted from vessel segmentation in other organs or other modalities (e.g. liver from abdominal CT, brain MRI), highlighting the relatively low barrier to develop algorithms for segmenting lung vessels.

For the challenge, each team was required to provide an estimate of the running time of each method. However, running times are as reported by individual teams and each algorithm has been run on different hardware specifications. As such, they were not exactly comparable and we have decided not to include them in the analysis.

When we performed the optimal threshold calculation, the value tends towards a low value (average: 90.3, min: 1, max: 204). There are two possible reasons: either many submissions tend to favor higher sensitivity as opposed to specificity, as seen from the optimal threshold value calculated, or they used a suboptimal conversion from other numeric types to unsigned char required to represent the probability. A method which returns a larger range of probability values that is not uniformly distributed would need to ensure that the conversion to the required range of 0–255, properly captures the method’s optimal performance range.

The performance of each method is not uniform across all categories. Most methods that performed well in the Principal category also did well in the others – the exceptions include several top-performing methods which did not take into account that there are other structures in the lungs with similar attributes –intensity or Hessian eigenvalues – such as nodules and mucus-filled bronchi. Method H, for instance, scores 18th and 19th position in the Mucus-filled bronchi (7th) and Nodules (9th) categories, while scoring 1st in the Principal category (as of ISBI’12).

We find that most Hessian-based methods generally obtain the highest Az scores on the Principal category. However, these methods still suffer in the evaluation categories containing structures with Hessian eigenvalues similar to those of vessels (e.g. airway walls, mucus-filled bronchi), since accurate determination of the structures depends highly on the scale used. Using a large number of scales—seven—, the Hessian-based method R2 was able to perform fairly in categories containing nodules, mucus-filled bronchi and dense lesions. Although structures such as nodules typically have eigenvalue scale signatures distinct from vessels, when the number and range of scales used is inadequate, many Hessian-based vesselness filters return a false significant response. See Fig. 11(e) for examples.

Fig. 11.

Top to bottom: axial, sagittal, and coronal views. (a) Original scan of a nodule from scan 01. (b–d) Same slice overlaid with vessel segmentations by top three teams (methods S, L and M). (e) Same nodule overlaid with segmentation by method R2. As the size of the nodules are larger than the scales used for vessel enhancement filter, pixels at the nodule borders return high response for vesselness. (f) Same nodule overlaid with segmentation from method J, which used explicit nodule removal.

Overall, the most difficult categories turn out to be Mucus-filled bronchi (7th) and Nodules (9th). Several methods filtered the images to remove known non-vessel structures such as fissures, airway walls, and nodules. Methods which explicitly exclude nodules have less false positives on nodules, as can be seen in Fig. 11(f). Similarly, airway wall exclusion also reduces false positives, as shown in Fig. 12. The Vessel-in-Consolidation/Consolidation (8th) category is another difficult category; none of the methods was very successful in this task.

Fig. 12.

Effect of explicit exclusion of airway walls on vessel segmentation of scan 04 (left to right): original, with no airway wall removal (method K), and airway wall excluded (method O) where the bright circles indicate airway walls which were removed explicitly. Middle image shows oversegmentation, not severely penalized because our choice of evaluation method. Refer to text of Section 6.2 for details.

Most intensity threshold-based methods include high-density structures in the lung which are not vessels. For this reason, many submissions include postprocessing steps, which explicitly excludes known structures such as airway walls, nodules, and lobar fissures. However, the postprocessing steps do not always ensure better performance. In many cases postprocessing does not catch all false positives and could be improved.

One surprising observation could be made with regards to the baseline method R1 that simply uses density as a predictor of vesselness. While multiscale vesselness filter methods perform well in all categories, the much simpler density method performs admirably in nearly all categories. This method completely fails, however, where confounding structures with similar density as vessels are present: R1 is one of the worst performers in the categories Vessel/Mucus filled bronchi (ranked 16th) and Vessel/Nodule (23rd among all participants).

6.3. Limitations of the methodology

Even though we included a large number of categories on which to assess the participating methods, the evaluation procedure adopted for the VESSEL12 Challenge has its limitations. First, the performance of the methods in determining vessel diameter cannot be evaluated. Using our method to select POIs, negative points tend to be located in the lung parenchyma – typically at several pixels from the real vessel border, thus not penalizing oversegmentation close to vessel borders (see middle plot of Fig. 12 for example of oversegmentation), nor segmentation which includes voxels where vessels are obviously not to be found (e.g., noisy area). For specifically measuring vessel size, manual precise annotations of vessel would have to be painstakingly constructed by human experts, or a scan of a physical phantom with tubes of known diameters could be used, but this would expand the scope of the challenge substantially.

The prohibitive amount of time it took to manually segment the images made it impractical to produce complete reference – which may be useful for comparing reconstructed vasculature tree and evaluating the connectivity of the submissions. In the next section, we address ways to improve a future version of the challenge without invalidating the existing results.

6.4. Future of the VESSEL12 challenge

Following the example of previous challenges, VESSEL12 will remain open to receive new submissions and evaluate these in the same manner as all already submitted results, thus providing a fair comparison. As identified in the previous Section, there is a number of limitations with respect to the evaluation procedure. Even though nine different categories are reported, several aspects of the quality of vessels segmentations are not covered by these nine metrics. However, the results of the submitted methods make it clear that methods perform very differently on these nine categories (see Fig. 9).

One of the ways to improve the challenge is to invite the research community to contribute and extend the existing evaluation procedures. This can be done in two ways. The first method is to upload new sets of labeled reference points. These could include new categories of negative points not included in the current metrics, such as fissure points and vessel junctions. Another category could be points deemed just inside and just outside vessel cross-sections, to evaluate the accuracy of diameter measurements submitted by the various methods – not captured by the current metrics. Users can then decide which combination of negative and positive points should be evaluated, similar to the selection of sets of points given in Table 2. The second method is to upload entirely new evaluation code in the form of standard C++ or Python executables. This could be used to evaluate connectivity of extracted vessels trees, for example. It could also pave the way to provide proper training and testing data sets for the evaluation of future methods.

We believe that the possibility to add new evaluation metrics to an existing challenge framework is a new step in its evolution that may stimulate further research in the area of thoracic vessel segmentation in CT.

7. Conclusions

We have presented the VESSEL12 Challenge framework that allows for direct comparison of vessel segmentation algorithms for thoracic CT data. Results show that there exist substantial performance differences between methods.

Most methods that employ techniques that detect tubular structure (vesselness-based approaches) do an admirable job in distinguishing vessels from lung parenchyma, with more than half the submissions scoring more than 0.9 in the Principal category, and the top five methods scoring more than 0.97 in the more difficult category of small vessels. Not all methods perform as well, highlighting the difficulty of the task. The other evaluation categories, however, demonstrate that none of submitted methods are capable of distinguishing vessels from other dense structures in the lungs – parenchymal and bronchial abnormalities. Some methods specifically remove well-known structures such as airway walls, but other commonly present abnormalities pose a problem. We conclude therefore that highly accurate vessel segmentation in the lungs is still very much an open problem.

We hope the contribution of the VESSEL12 Challenge will help future researchers in this area. The manually annotated reference dataset for vessels in the lungs is available online for testing of future algorithms. The categories proposed could also help those who are designing lesion-specific algorithms to focus on certain aspects of lung vessel segmentation. The evaluation of the various vessel segmentation methods in the presence of structures caused by lung diseases could help those who are working on improving techniques, to better understand the nature of the problem and address specific shortfalls of existing methods.