Abstract
Structural magnetic resonance imaging (MRI) is a very popular and effective technique used to diagnose Alzheimer’s disease (AD). The success of computer-aided diagnosis methods using structural MRI data is largely dependent on the two time-consuming steps: 1) nonlinear registration across subjects, and 2) brain tissue segmentation. To overcome this limitation, we propose a landmark-based feature extraction method that does not require nonlinear registration and tissue segmentation. In the training stage, in order to distinguish AD subjects from healthy controls (HCs), group comparisons, based on local morphological features, are first performed to identify brain regions that have significant group differences. In general, the centers of the identified regions become landmark locations (or AD landmarks for short) capable of differentiating AD subjects from HCs. In the testing stage, using the learned AD landmarks, the corresponding landmarks are detected in a testing image using an efficient technique based on a shape-constrained regression-forest algorithm. To improve detection accuracy, an additional set of salient and consistent landmarks are also identified to guide the AD landmark detection. Based on the identified AD landmarks, morphological features are extracted to train a support vector machine (SVM) classifier that is capable of predicting the AD condition. In the experiments, our method is evaluated on landmark detection and AD classification sequentially. Specifically, the landmark detection error (manually annotated versus automatically detected) of the proposed landmark detector is 2.41mm, and our landmark-based AD classification accuracy is 83.7%. Lastly, the AD classification performance of our method is comparable to, or even better than, that achieved by existing region-based and voxel-based methods, while the proposed method is approximately 50 times faster.
Index Terms: Alzheimer’s disease (AD), regression forest, landmark detection, magnetic resonance imaging (MRI)
I. Introduction
Alzheimer’s disease (AD) is one of the most common neurodegenerative disorders, with its financial and social burdens being compounded by the increase in the average lifespan [1], [2]. Early detection of AD is of great importance because treatments are most effective if performed during the earliest stages [3]. Currently, clinical diagnosis of AD depends largely on clinical history and clinical assessments that show neuropsychological evidence of cognitive impairment [4], [5]. Neurological experts, with years of experience, are able to identify the disorder and then make the correct diagnosis. However, the diagnosis procedure is time-consuming and requires extensive clinical training and experience, which makes it difficult for new or less experienced neurologists. Therefore, an efficient automatic computer-aided diagnosis system could help guide them throughout the diagnosis process.
The non-invasive structural magnetic resonance imaging (MRI) modality provides good soft tissue contrast and high spatial resolution, which is important for AD diagnosis [6]. For example, the volume of the hippocampus was found to be smaller in AD subjects, and the volume of the ventricle was found to be larger in AD subjects. When compared to the age-matched healthy controls (HCs), these abnormal sizes may come from cell dysfunction, cell death, or both. Therefore, structural abnormalities in the brain of AD subjects are important diagnosis criteria when neuroimaging studies are performed [7], [8]. It is important to point out that, in most structural imaging studies, the accuracy of the computer-aided diagnosis system largely depends on the accuracy of tissue or structural segmentation, e.g., white matter (WM) or gray matter (GM) tissue segmentations, as well as the structural segmentations of cortical and subcortical limbic shape structures. For example, Zhang et al. [9] segmented the MR images into 93 regions-of-interest (ROIs), and then extracted GM concentrations based on these ROIs for AD diagnosis. Gerardin et al. [10] extracted hippocampal shape features based on a parametric boundary description. Aguilar et al. [11] applied a multivariate analysis technique on 57 MRI measures (e.g., regional volume and cortical thickness) that were used to train an AD classifier. Traditionally, volume/density measures have been used for AD diagnosis, but recently, cortical thickness [12] appears to be a more stable measure. In particular, cortical thickness is a better measure of GM atrophy due to the cytoarchitectural feature of the GM [13], [14], [15], [16], [17]. Although those methods have been proven to be effective in AD classification, the tissue and shape structure segmentation steps typically rely on nonlinear registration, which is a very time-consuming process. Moreover, manually-defined measurements (e.g., hippocampal volume, ventricular volume, whole brain volume, and cortical thickness) are usually unable to capture all morphological abnormalities that are related to AD.
Several studies [18], [19], [20] have also focused on automatically identifying anatomical differences between AD subjects and age-matched HCs using group comparisons. For example, voxel-based morphometry (VBM) [21] was designed to identify group differences in local compositions in different brain tissues. To identify these differences, a common step is to warp individual MRI images to the same stereotactic space (or template image) using a nonlinear image registration technique. Once mapped to the template image, brain regions that show statistically significant between-group differences in brain tissue morphometry (e.g., gray matter density) are identified using a group comparison technique. Beside VBM, other methods, such as deformation-based morphometry (DB-M) and tensor-based morphometry (TBM) that focus on brain shapes estimated using a nonlinear deformation field, have also been proven to be useful [22]. In these methods, nonlinear image registration is an inevitable process. In addition to the group-comparison-based method as mentioned above, Rueda et al. [23] introduced a fusion strategy that used salient tissue/shape features by combining both bottom-up and top-down information flows to reveal complex brain patterns. Although this method is novel, the calculation of saliency maps and kernel matrices requires extensive computations.
To avoid these computationally expensive and time-consuming steps introduced by nonlinear image registration methods, here we develop a more efficient landmark-based AD diagnosis system. Importantly, nonlinear image registration and/or segmentation is not required for AD diagnosis in the proposed method. To achieve this, we first define a large set of discriminative landmarks whose local morphologies show statistically significant between-group differences. Then, we can extract morphological features according to the local regions around those discriminative landmarks for AD diagnosis. Now the problem becomes two-fold: 1) Landmark definition. That is, how to identify significant landmarks among millions of voxels in an image? And 2) fast landmark localization. How to efficiently identify landmarks in new testing images?
To address these issues, a novel landmark-based framework is proposed that only includes a nonlinear image registration step in the training stage in order to identify corresponding voxels across the training population. Specifically, in the training stage, group comparisons based on local morphological features are performed first to identify brain regions that have significant group differences. In general, the centers of the identified regions become landmark locations (or AD landmarks for short) capable of differentiating AD subjects from HCs. In the testing stage, for a new image (not included in the training data set), the identification of its AD landmarks becomes an automatic landmark detection problem. To solve this problem, a fast regression-forest-based landmark detection method that includes a shape constraint is developed. Since AD landmarks are found in local regions with significant group differences, accurate landmark detection is very difficult. To improve detection accuracy, additional landmarks with salient and consistent features, called active landmarks, are also identified to guide the AD landmark detection. Finally, a support vector machine (SVM) classifier (with a linear kernel) is trained using morphological features around the detected AD landmarks that can be used for AD diagnosis.
In summary, our major contribution is two-fold: First, neither nonlinear image registration nor brain tissue segmentation is needed to apply the proposed method because of our landmark-based diagnosis framework. Therefore, our method is computationally more efficient, and accuracy is comparable, or better than, other frameworks that require nonlinear image registration. Second, a two-layer shape constraint regression forest model is developed, which provides a more efficient and accurate approach to detect AD landmarks. Here, a parametric shape constraint is added to the regression forest model to construct a robust model, and active landmarks that are salient and consistent, are defined to extract contextual features for guiding the AD landmark detection.
II. Method
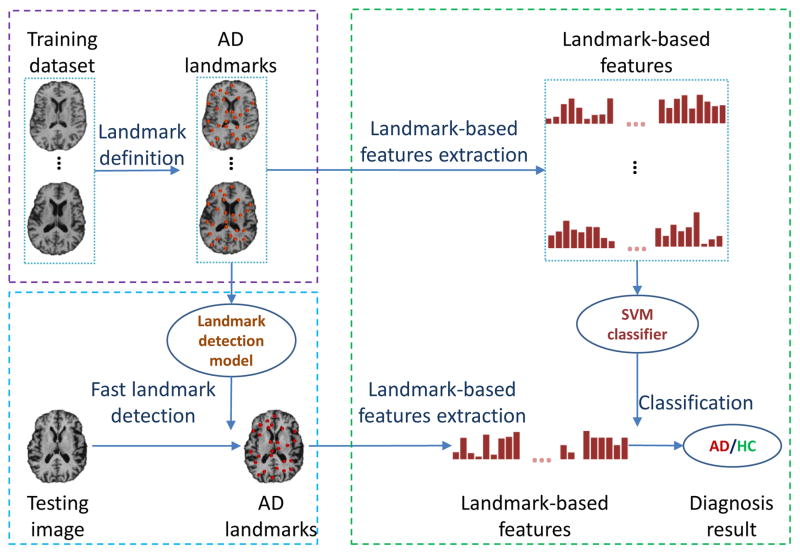
Figure 1 illustrates the general framework of the proposed method. In particular, the framework defines three sequential steps: landmark definition, landmark detection, and AD/HC classification. In the landmark definition step, AD landmarks that have statistically significant differences between AD and HC in the training images are identified. In the landmark detection step, a pre-trained landmark detection model is used to automatically and efficiently detect AD landmarks in each testing image. In the classification step, a linear SVM classifier that is trained with landmark-based morphological features from the training images is applied to classify a testing image as HC or AD.
Fig. 1.
Diagram illustrating the steps in the proposed landmark detection and AD classification framework. In general, the proposed framework defines three sequential steps: 1) landmark definition, 2) landmark detection, and 3) AD/HC classification.
A. AD landmark definition
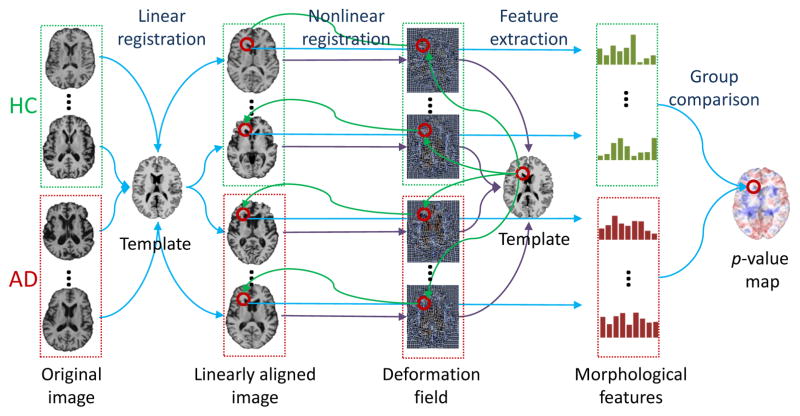
In order to discover the landmarks that differentiate AD from HC, a group comparison between AD and HC is performed on the training images. Specifically, a nonlinear registration is used to locate the corresponding voxels across all training images. Then, a statistical method, Hotelling’s T2 statistic [24], is adopted for voxel-wise group comparison. Finally, a p-value map is obtained after group comparison to identify the AD landmarks. The pipeline for defining AD landmarks is shown in Fig. 2.
Fig. 2.
AD landmark definition pipeline.
1) Voxel correspondence generation
Since the linearly-aligned images are not voxel-wisely comparable, nonlinear registration is used for spatial normalization [21]. After spatial normalization, the warped images lie in the same stereotactic space, compared with the common template image. In particular, the Colin27 template is used, which refers to the average of 27 registered scans for a single subject [25]. In general, image registration includes a linear and a nonlinear registration step. The linear registration step simply removes global translation, scale, and rotation differences, and also resamples the images to have the same spatial resolution (1 × 1 × 1 mm3) as the template image. The nonlinear registration step creates a deformation field that estimates highly nonlinear deformations that are local to specific regions in the brain.
2) Group comparison
In order to identify local morphological patterns that have statistically significant between-group differences, local morphological features are extracted. Here, we extract morphological features based on the statistics of low-level features from a cubic patch. Specifically, the oriented energies [26], which are invariant to local inhomogeneity, are extracted as low-level features. Instead of using N-ary coding [26] for vector quantization (VQ), we adopt a bag-of-words strategy [27] for VQ to obtain the final histogram features with relatively low feature dimensionality.
However, it is not appropriate to extract morphological features from the warped images because the morphological differences we are interested in may not be significant after nonlinear registration, i.e., the warped images are very similar to each other. On the other hand, linear registration only normalizes global shapes and scales of all brain images, thus, internal local differences are still kept and local distinct structures are reserved. In this way, it is reasonable to extract morphological features from linearly-aligned images.
By using the deformation field from nonlinear registration, we can build the correspondence between voxels in the template and each linearly-aligned image. For instance, for each voxel (x, y, z) in the template image, we can find its corresponding voxel (x + dx, y + dy, z + dz) in each linearly-aligned image, where (dx, dy, dz) is the displacement from the template image to the linearly-aligned image defined by the deformation field. In order to reduce the impact of potential registration errors and also expand the number of samples for statistical analysis, a number of supplemental voxels are further sampled in a Gaussian probability w.r.t. the distance to the corresponding voxel, within a limited spherical region. Therefore, for each voxel in the template, we can extract two groups of morphological features from its corresponding voxels and supplemental voxels in all training images that include both AD subjects and HCs. Finally, the Hotelling’s T2 statistic [24] is adopted for group comparison. Accordingly, each voxel in the template is assigned with a p-value, thus obtaining a p-value map w.r.t. every voxel in the template.
3) AD landmarks
Based on our obtained p-value map, discriminative AD landmarks can be identified among all voxels in the template. In particular, any voxels in the template, whose p-values are smaller than 0.01, are regarded as showing statistically significant between-group differences. To avoid large redundancy, only local minima (whose p-values are also smaller than 0.01) in the p-value map are defined as AD landmarks in the template image. Lastly, the landmarks for each training image can be easily identified by mapping these landmarks in the template using the deformation field estimated by nonlinear registration. Finally, the morphological features can be extracted according to the mapped landmarks and further used for AD/HC classification.
B. Active landmark definition
Since AD landmarks are associated with regions of statistically significant between-group differences, it is often very challenging to accurately identify them. To improve AD landmark detection accuracy, we define another type of active landmarks, which are salient and consistent, to guide the AD landmark detection. In the following paragraphs, both saliency and inconsistency, based on local patches, are defined and formulated.
1) Saliency
Similar to [28], [29], the term saliency is estimated by an entropy function that measures the complexity of the image intensities in a brain region. Because the goal is to identify informative regions in the entire brain, a saliency map is computed using the template image only. Specifically, the entropy at a voxel x in the template is defined as
| (1) |
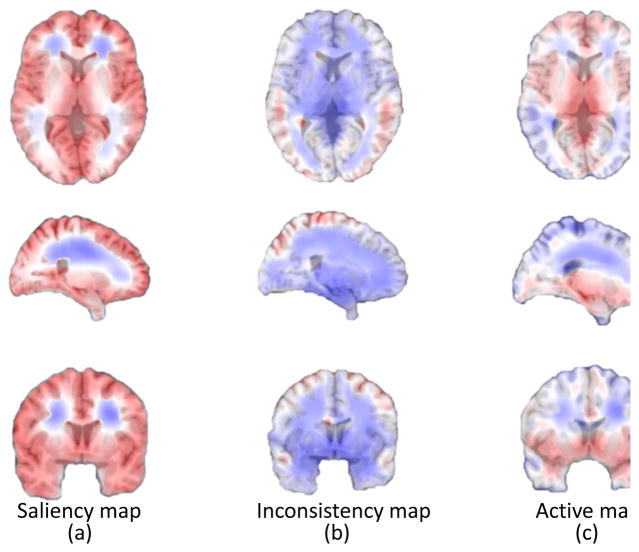
where i is a possible intensity value, and pi(s, x) is the probability distribution of intensity i defined in a spherical region Ω(s, x) centered at x with radius s. Here, different region sizes are used to calculate the entropies for each voxel in the template image, and hence, each voxel is assigned with several entropy values. We select the maximum value as the entropy for that voxel, and then obtain an entropy map corresponding to the template. An example of the saliency map is shown in Fig. 3 (a), where a large value implies that the region is very complex (i.e., rich with information).
Fig. 3.
Saliency, inconsistency and active maps. Each map is linearly stretched to [0,1] for clear visualization. (a) Saliency map, where regions with larger values are more salient than those with smaller ones. (b) Inconsistency map, where regions with larger values are more inconsistent than those with smaller ones. (c) Combined active map, where regions with larger values are more active than those with smaller ones.
2) Inconsistency
The term inconsistency is defined to describe the inconsistent degree in local structures across subjects. We adopt the variance of voxel’s local appearances across all training images as a measurement of the inconsistency. Similar to the definition of AD landmarks, we have the corresponding voxels from all training images (linearly-aligned) for each voxel in the template. For the corresponding voxel in a training image, we extract a local region Ω(s, x), which is a spherical region centered at the corresponding voxel x with a radius of s. Therefore, for a voxel in the template image, we can extract a local region from each training image and then calculate the mean intensity variance Var(s, x) across all images as
| (2) |
where N is the number of all training images and In(x) is the image intensity at x from the n-th training image. In order to measure inconsistency from both coarse and fine scales, we use the mean variance of different sizes of regions to measure the inconsistency of each voxel. The inconsistency map is shown in Fig. 3 (b), where a large value implies that the region is inconsistent across subjects.
3) Active landmarks
An active map is estimated using the saliency and inconsistency equations in Eq. (1) and Eq. (2), respectively. In particular, for each voxel x in the template image, an active value Act(x) is defined as
| (3) |
where M is the number of scales, and α is a tuning coefficient to balance the two components of saliency and consistency. Each voxel x in the template is assigned an active value Act(x). Thus, we obtain an active map corresponding to the template. Here, we select the local maxima as active landmarks. Note that the active landmarks for each training image (before nonlinear registration) can be mapped back from the active landmarks in the template, using its estimated corresponding deformation field.
C. Regression-forest-based landmark detection
Here, we automatically detect landmarks in a new testing image using existing landmark information in the training images. Similar to the generation of landmarks in training images, a straightforward method for landmark detection can be conducted using a registration approach. However, it is time-consuming and does not satisfy the purpose of our work.
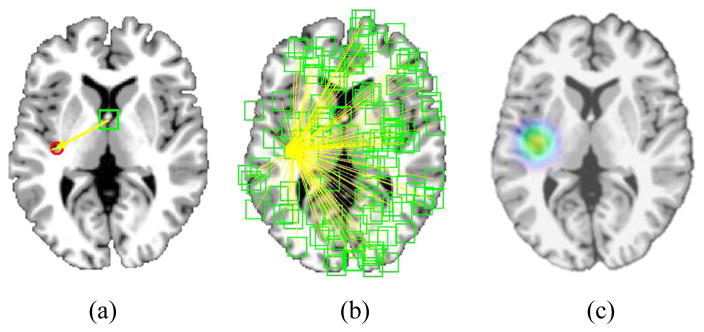
Regression-forest-based methods have demonstrated their efficacy in anatomical detection of different organs and structures [30], [31], [32], [33]. Unlike classification-based methods [34], [35], [36], which determine each landmark location based only on the local patch appearance surrounding the landmark, regression-forest-based methods utilize the contextual appearance to help localize each landmark. Specifically, in the training stage, a regression forest is used to learn a non-linear mapping between the area surrounding the voxel, e.g., patch, and its 3D displacement to the target landmark (see Fig. 4 (a)). Since a multi-variate regression forest is used, the mean variance of the targets become the splitting criteria. Generally, morphological features, such as Haar-like features [37], scale invariant feature transform (SIFT) features [38], histogram of oriented gradient (HOG) features [39], and local binary pattern (LBP) features [40], can be used to describe a voxel’s local appearance. In this study, we employ the same morphological features as those used for AD landmark definition.
Fig. 4.
Framework of regression-forest-based landmark detection. (a) Definition of displacement from a voxel to a target landmark. (b) Regression voting. (c) Voting map.
In the testing stage, the learned regression forest can be used to estimate a 3D displacement from every voxel in the testing image to the potential landmark position, based on the local morphological features extracted from the neighborhood of this voxel. There are several trees for a regression forest, so we use the mean prediction value from all trees as the output of regression forest. Therefore, by using the estimated 3D displacement, each voxel can cast one vote to the potential landmark position. Through aggregating all votes from all voxels (see Fig. 4 (b)), a voting map can finally be obtained (see Fig. 4 (c)), from which the landmark position can be easily identified as the location with the maximum vote.
Generally, the landmarks can be jointly detected using a joint trained regression forest, whose targets are the displacements to multiple landmarks. Therefore, multiple landmarks can be jointly predicted, instead of individual detection. However, there are two problems for the joint regression-forest-based landmark detection method in our application. 1) The dimensionality of targets for the regression forest is so high, making it too time-consuming to build a regression model. 2) The joint model may create an overly-strong spatial constraint to the targets, since landmarks in the whole brain may have large shape variations. To address these two problems, we propose a shape-constrained regression forest model.
D. Shape-constrained landmark detection
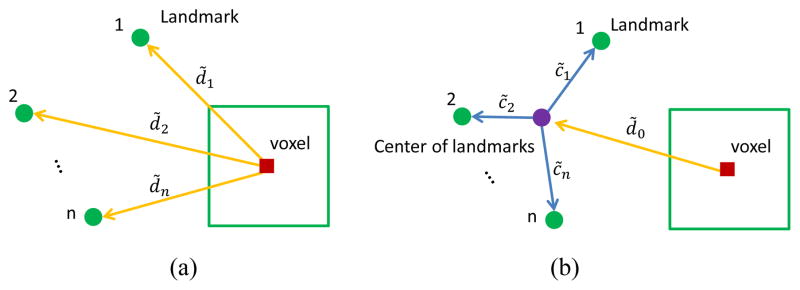
Instead of using multiple displacements as targets, a shape constraint is added to the targets in order to decrease dimensionality. As shown in Fig. 5 (a), traditional targets are [d̃1, … , d̃i, … , d̃n] for n landmarks, where d̃i is a 3D displacement from the voxel to the ith landmark. On the other hand, the relationship from a voxel to all landmarks can also be described by the displacement from the voxel to the landmark center and a star-like shape constraint from all landmarks to the landmark center, as shown in Fig. 5 (b). The targets can then be represented as [d̃0, c̃1, … , c̃i, … , c̃n], since d̃i = d̃0 + c̃i, where c̃i is the offset from the landmark center to the ith landmark. Motivated by statistical shape model [41], [42], we perform principal component analysis (PCA) [43] for the shape constraint part (i.e., [c̃1, … , c̃i, … , c̃n]) on the whole training dataset, and the shape constraint is represented by the top m principal components [λ1, … , λi, … , λm]. As a result, [d̃0, λ1, … , λi, … , λm] are used as new targets to train the regression forest model.
Fig. 5.
Targets for regression forest. (a) Targets using traditional displacements to multiple landmarks. (b) Targets using a shape constraint.
In the testing stage, a voxel’s targets can be predicted as [ ], and we can reverse them back to [ ] using the PCA coefficients. Then, the original displacements to multiple landmarks [ ] can be calculated. Finally, the voting process is performed to localize the final landmark positions, which is the same as the traditional voting strategy.
To address the second problem about the overly-strong shape constraint, the landmarks are clustered into different groups, and then each group is detected separately. To achieve this, we adopt a spectral clustering method named normalized cuts [44]. Landmark clustering is based on a dissimilarity matrix, where each entry is the variance of pair-wise landmark distances across subjects. In doing so, the shape constraint for each group is considered relatively stable, thus the regression forest model could be accurately constructed.
One major contribution of our landmark detection method is that we integrate a parametric shape constraint to the regression forest model. In the past, several studies have used shape constraints to increase landmark detection accuracy. For example, Cootes et al. [30] adopted regression forest to calculate a cost map, where a statistical shape model is applied for landmark matching. They proved that the regression forest can be used to generate high quality response maps quickly. Chu et al. [33] adopted regression forest to obtain the initial landmark positions and used sparse shape composition to correct the initial landmark positions. However, the shape constraints for these two methods are used after the regression based voting, which are different from our method that uses the constraint within the regression forest model. On the other hand, Cao et al. [45] and Chen et al. [46] also integrated shape constraints to their models and successfully detected landmarks robustly and accurately. Cao et al. [45] proposed a two-level boosted regression-based approach without using any parametric shape models. Chen et al. [46] proposed a landmark detection and shape segmentation framework by jointly estimating the image displacements in a data-driven way. Without any parametric shape models, the geometric constraints were added to the testing image in a linear way. Since both above methods used nonparametric constraints, they are different from our parametric shape constraint.
E. Active-landmark guided AD landmark detection
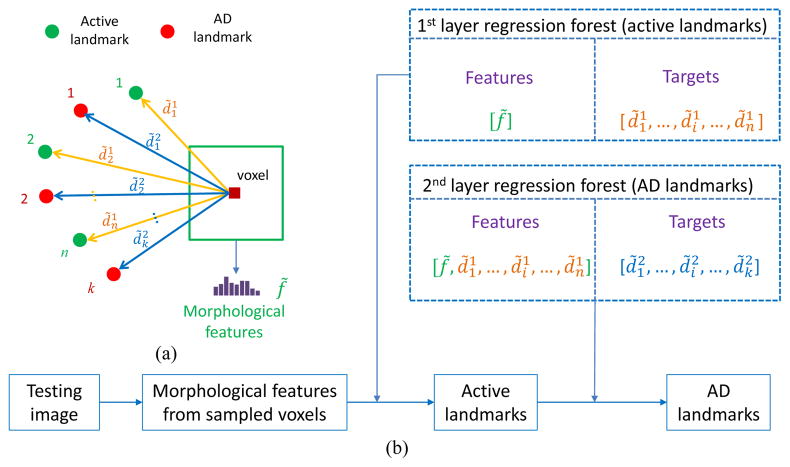
All active landmarks and AD landmarks are aggregated together and clustered into several groups. Then, the active landmarks for each group are separately detected using the proposed shape-constrained regression-forest-based method, and finally the AD landmarks are detected with the guidance of the detected active landmarks in the same group. In this study, we use active landmarks as priors for the AD landmark detection by adding auxiliary features based on active landmarks used to train the regression forest model, instead of solely using morphological features.
Specifically, not only morphological features, but also auxiliary features, such as the displacements from the voxel to the active landmarks, are extracted for each voxel, as shown in Fig. 6. The detection framework can also be viewed as a two-layer regression forest. In particular, the first layer is to obtain accurate active landmarks, and the output of the first layer is used as the input to the second layer regression forest for detecting AD landmarks. In doing so, the spatial constraints between AD landmarks and active landmarks are automatically added to the two-layer model. This is similar to the auto-context idea [47] that uses feedback of the first layer model to guide the second layer model. Note that the targets for regression forest in Fig. 6 is the 3D displacements from a voxel to multiple landmarks (not the parametrical coefficients from PCA). We show the original 3D displacements in Fig. 6 for understanding the two-layer model more easily. But, in our method, we use the shape-constrained targets as introduced in the above section.
Fig. 6.
Active-landmark guided AD landmark detection. (a) Definition of displacements to the active landmarks and AD landmarks. (b) Framework of two-layer regression-forest-based landmark detection.
F. SVM-based classification
Using the afore-mentioned landmark-based morphological features, we further perform classification to identify AD subjects from HCs, by adopting the linear SVM as the classifier. As shown in many existing AD diagnosis studies [4], [23], [48], SVM has good generalization capability across different training data, due to its max-margin classification characteristic. For more details about using linear SVM to classify AD subjects from HCs, please refer to the study in [4]. Specifically, we first normalize the landmark-based morphological features using the conventional z-score normalization method [49]. Then, the normalized features are fed into a linear SVM classifier for AD diagnosis.
III. Experiments
Subjects used in this study are from the ADNI database1. In this paper, we employ all screen MR images from ADNI-1, including 199 AD subjects and 229 age-matched HCs. We then randomly split the data into two sets, named as D1 (100 AD and 115 HC) and D2 (99 AD and 114 HC), and we perform a two-fold cross validation.
In our experiments, the size of each image is 256×256×256 with a voxel resolution of 1 × 1 × 1 mm3. For generating an active map, we fix α = 0.5 to combine the saliency map and the inconsistency map, and the multiple radii are used in this study (i.e., s = [10, 20, 30]). The dimensionality of the morphological features is 50, which is defined by the number of clustering groups when applying the bag-of-words method. For landmark detection, we use 40 principal components for shape constraint regression forest, to preserve more than 97% information. Besides, we use 10 trees, and the depth of each tree is 25. For the linear SVM, we fix the margin parameter C as 1 for both our method and those competing methods.
In the following experiments, we first illustrate the group comparison results and then evaluate the landmark detection performance. Finally, AD/HC classification results are also provided.
A. Group comparison
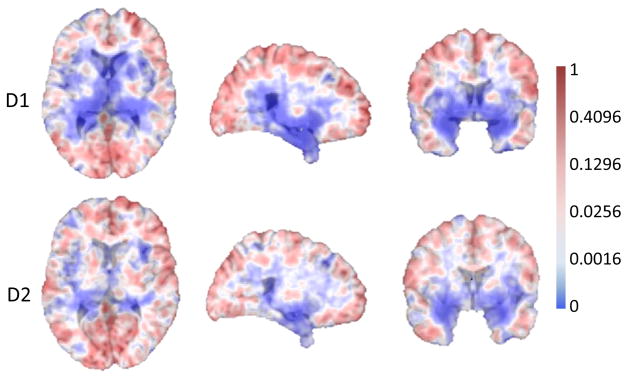
Figure 7 illustrates 2D slices of the p-value map after a group comparison is performed. It clearly indicates significant group differences in the ventricles in both D1 and D2. It is well known that the ventricular volume in AD subjects is significantly different from that in the age-matched HCs [50], [51], [52]. Because brain ventricles are surrounded by gray and white matter structures typically different than that in AD subjects, any volume or shape changes that occur in these structures will affect the volumes and shapes of the ventricles. Because of the data-driven property of our method, the p-value map for each fold is slightly different from each other (see Fig. 7). This leads to different numbers of landmarks for the two folds. In our experiment, 1741 and 1761 AD landmarks are automatically selected for D1 and D2, respectively. Meanwhile, 451 and 488 active landmarks are automatically selected for D1 and D2, respectively.
Fig. 7.
Group comparison results for two datasets, D1 and D2. Regions with very small p-values (i.e., having statistically significant difference) are shown in blue.
B. Landmark detection evaluation
Unlike traditional landmark detection problems, we do not have the benchmark (i.e., ground-truth) landmarks to evaluate the detection accuracy of our method. The reason is that both active landmarks and AD landmarks are automatically learned, and they cannot be manually annotated. As a result, it is impossible to directly evaluate the landmark detection accuracy, compared with manually annotated benchmark landmarks. To overcome this limitation, 1) we conduct an experiment based on manually annotated landmarks to evaluate the detection performance of our landmark detection method, and 2) we create “benchmark” landmarks to evaluate the landmark detection performance of AD landmarks.
1) Landmark detection based on manually annotated landmarks
We manually annotate 20 landmarks for all images based on two criteria. First, landmarks are placed at locations that can generally be identified on every individual in the study. Second, the landmarks are scattered throughout the entire brain in different tissues (the locations of landmarks are shown in the online Supplementary Materials). In our experiment, we use two-fold cross validation to evaluate the detection performance. We compare our landmark detection method with two other landmark detection methods based on (a) simple affine registration, and (b) classification forest. The implementations of these two methods are provided in the online Supplementary Materials. For our method, these landmarks are clustered into 5 landmark groups. The detection results are shown in Table I. As shown, the result of affine registration-based method has a relatively large mean detection error and a large standard deviation, since no local information is further considered. The classification forest based method improves detection performance significantly, but both the detection error and standard deviation are still larger than that obtained for the proposed method.
TABLE I.
Comparison with other landmark detection methods for manually annotated landmarks.
| Method | Affine registration | Classification forest | Proposed method |
|---|---|---|---|
| Mean error (mm) | 3.98 ± 3.37 | 2.65 ± 1.82 | 2.41 ± 1.42 |
2) Detection results of the active landmarks and the AD landmarks
Similar to the process of identifying landmarks in the training images, landmarks in the testing images are mapped from template using the deformation fields obtained by nonlinear registration. Then, these landmarks are used as the “benchmarks”, when calculating the detection error in our landmark detection method. In the online Supplementary Materials, we provide extensive experimental results based on a series of synthetic experiments to evaluate the landmark detection performance using the created “benchmark” landmarks.
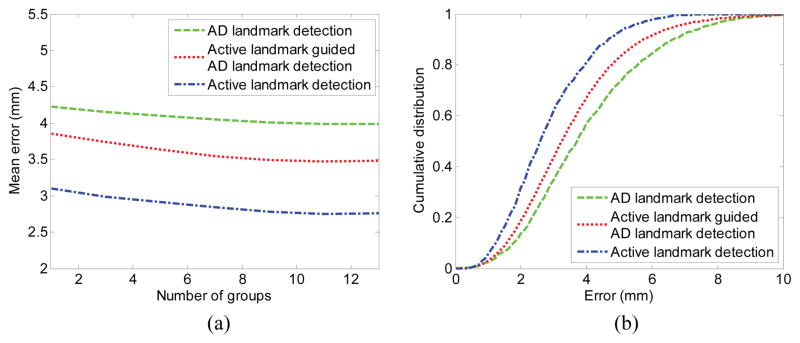
Figure 8 shows the detection results of both active landmarks and AD landmarks compared with the created “benchmark” landmarks. The mean detection errors with different numbers of partition groups (i.e., landmark clusters) are presented in Fig. 8 (a). From Fig. 8 (a), we can observe that the active landmarks can be accurately detected, primarily because the active landmarks are all located on the salient and consistent regions. On the other hand, the AD landmarks have much larger errors, but errors decrease after using the active landmarks as guidance. Moreover, the detection error decreases, along with increases in the number of groups within appropriate ranges. In our experiments, 10 groups are enough to avoid the over-strong shape constraint. In addition, the cumulative density functions (CDFs) of the error are shown in percentage in Fig. 8 (b), demonstrating that most of the landmarks are located within reasonable errors.
Fig. 8.
Detection errors for active landmarks and AD landmarks. (a) Detection errors with different numbers of partition groups. (b) Cumulative distribution with different error intervals where 10 groups are clustered.
C. AD/HC classification
After automatic AD landmark detection, we extract morphological features for each landmark from its local patch. The features for all landmarks are concatenated together to represent the subject. The AD classification is performed using SVM, where two-fold cross validation is conducted using D1 and D2 as the training and the testing alternately. In our experiment, four classification performance measures are used, namely 1) accuracy (Acc): the number of correctly classified samples divided by the total number of samples; 2) sensitivity (Sen): the number of correctly classified positive samples (AD) divided by the total number of positive samples; 3) specificity (Spe): the number of correctly classified negative samples (HC) divided by the total number of negative samples; and 4) balanced accuracy (BAC): the mean value of sensitivity and specificity.
Additionally, we compare our method with two GM-based feature extraction methods: using 1) ROI-based GM and 2) voxel-based GM. Implementations of these two methods are based on a single-atlas-based registration, with details provided in the online Supplementary Materials. In order to give more reliable classification evaluation, we repeat our two-fold cross validation 20 times by randomly splitting the dataset. As shown in Table II, our method achieves a very competitive classification accuracy of 83.7 ± 2.6%, which is slightly higher than the baseline methods using ROI-based GM (81.8 ± 2.7%) and voxel-based GM (82.0 ± 2.9%). Note that the evaluation here is about the feature extraction, not the design of classifiers, so the results may be lower than some reported classification methods [53], [54], [55]. Some feature selection methods or existing AD/HC classification methods can be potentially applied to our extracted features. Moreover, our framework does not require any nonlinear registration or segmentation to classify a new testing image.
TABLE II.
Classification results with two-fold cross validation on ADNI-1 dataset. The results shown are averaged over 20 repeats, and that plus-minus gives the standard deviation.
| Method | Acc | Sen | Spe | BAC |
|---|---|---|---|---|
| ROI-based GM | 81.8±2.7% | 75.2±3.8% | 87.9±3.1% | 81.5±2.8% |
| Voxel-based GM | 82.0±2.9% | 76.0±3.8% | 87.6±3.2% | 81.8±2.9% |
| Our method | 83.7±2.6% | 80.9±3.5% | 86.7±2.2% | 83.8±2.5% |
In order to evaluate the generalization ability of our method, we conduct an additional experiment on an independent dataset, i.e., ADNI-2. To ensure the independence of samples, subjects that appear in the ADNI-1 dataset are removed from the ADNI-2 dataset. A total of 159 AD subjects and 201 HCs from ADNI-2 are obtained. Specifically, we first train the landmark detection model and AD/HC classification model using all the data from ADNI-1 dataset, and then test the performance on the ADNI-2 dataset. The experimental results are given in Table III. As shown, classification performance of all three methods is slightly decreased. It is worth noting that our method achieves a classification accuracy of 83.1% which is still better than the two baseline methods.
TABLE III.
Classification results of AD vs. HC on ADNI-2 dataset.
| Method | Acc | Sen | Spe | BAC |
|---|---|---|---|---|
| ROI-based GM | 79.7% | 73.6% | 84.6% | 79.1% |
| Voxel-based GM | 80.6% | 76.1% | 84.1% | 80.1% |
| Our method | 83.1% | 80.5% | 85.1% | 82.8% |
Moreover, we also conduct an additional experiment of classifying MCI from HC. Similarly, we still use the data from ADNI-1 as training, while the data from ADNI-2 is used as independent testing. Thus, we have a total of 346 MCI subjects from ADNI-1 and 485 MCI subjects from ADNI-2. The experimental results are shown in Table IV. Our method achieves superior classification performance, indicating its potential capability of diagnosing MCI.
TABLE IV.
Classification results of MCI vs. HC on ADNI-2 dataset.
| Method | Acc | Sen | Spe | BAC |
|---|---|---|---|---|
| ROI-based GM | 69.1% | 70.1% | 66.7% | 68.4% |
| Voxel-based GM | 70.7% | 73.0% | 65.2% | 69.1% |
| Our method | 73.6% | 75.3% | 69.7% | 72.5% |
D. Computational cost
Since all training steps are off-line operations, we only analyze the on-line computational cost. In our implementation, we first linearly align all images to the same template with landmark-based registration. The detailed description is provided in the online Supplementary Materials.
Second, we extract morphological features of the brain images, and then sample parts of features to predict active landmarks and AD landmarks sequentially. After obtaining the AD landmarks, the morphological features for those AD landmarks can be pinpointed from previously extracted morphological features, making it an efficient procedure. As a comparison, we also calculate the computational time for ROI-based method (Since we use same registration and segmentation strategies for voxel-based method, its computational time is similar to that of ROI-based method). In our experiment, we use nonlinear registration method to map segmentations of GM and the 90 ROIs from template image to all images. The computational costs are summarized in Table V using a computer with the processor of Intel(R) Core(TM)2 i7-4700HQ 2.40GHz. The total computational cost for the ROI-based method is about half an hour, which is about 50 times slower than our method (36.05 s). For precise segmentations of some specific ROIs, e.g., hippocampus, the ROI-based methods require even greater computational costs.
TABLE V.
Computational costs.
| Method | Procedure | Implementation | Individual time | Total time |
|---|---|---|---|---|
| Our Method | Linear alignment | C++ | 5 s | 36.05 s |
| Morphological features | Matlab | 9 s | ||
| Active landmarks | C++ | 10 s | ||
| Auxiliary features | Matlab | 1 s | ||
| AD landmarks | C++ | 11 s | ||
| Landmark-based features | Matlab | Almost 0 | ||
| SVM prediction | Matlab | 0.05 s | ||
|
| ||||
| ROI-based Method | Linear alignment | C++ | 5 s | 32 mins |
| GM segmentation | HAMMER [56] | 32 mins | ||
| 90 ROIs segmentation | ||||
| Feature generation | Matlab | 3 s | ||
| SVM prediction | Matlab | 0.02 s | ||
E. Parameter analysis
We conduct experiments to evaluate the sensitivity of important parameters, when performing AD/HC classification. The indirect parameters for selecting active landmarks and AD landmarks are analyzed in the online Supplementary Materials.
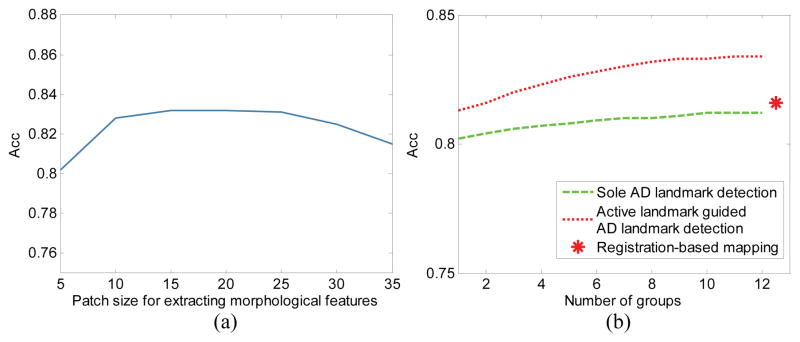
One important parameter in our method is patch size for extracting morphological features. Figure 9 (a) shows the classification results achieved by our method using different patch sizes. The figure shows that our method is not very sensitive to the patch size, so the parameter can be selected within a relatively wide range.
Fig. 9.
AD/HC classification accuracy on ADNI-1. (a) Classification accuracy with respect to different patch sizes, where the horizontal axis means the side length of the cubic patch. (b) Classification accuracy with respect to different landmark detection strategies and group numbers, where the red star is the result of registration-based landmark mapping.
In addition, Fig. 9 (b) shows the classification results achieved by our method using different number of landmark groups, as well as the result of using registration-based landmark mapping. Generally, 10 groups achieve good classification accuracy, which is better than the result of using registration-based landmark mapping. This result also illustrates the effectiveness of our landmark detection method and the landmark-based feature extraction. The underlying reason could be that the landmarks detected by our method are more accurate than those in the registration-based landmark mapping method.
IV. Discussions
A. Feasibility of landmark-based feature extraction
In Tables II and III, competitive classification accuracies are achieved by comparing our method with the conventional methods that use ROI-based GM or voxel-based GM. The primary reason for such performance may be due to local variations in morphological patterns that are more pronounced in AD subjects than in HCs. Since the proposed method takes advantage of these group differences, it is able to discover and detect local morphological differences. In Table V, the computation efficiency of the proposed landmark-based morphological feature extraction method is about 50 times higher than the conventional ROI-based method. It is worth noting that the proposed morphological feature extraction method requires more training time. However, once training is finished, our approach is extremely efficient during the testing stage.
B. Shape constraint for regression forest
In general, the primary purpose of the shape-constrained regression forest is to decrease the dimensionality of targets. This approach increases the efficiency to jointly train hundreds or thousands of landmarks in one regression model. In addition, unlike traditional methods that adjust the locations of landmarks after obtaining the initial positions, our method adds shape constraint into the regression forest model during training. The experimental results demonstrate that the proposed landmark detection method is very accurate, i.e., with small detection errors as shown in Fig. 8, and computationally efficient, only requiring approximately 36 seconds to complete.
C. Active landmarks for AD landmarks detection
Because active landmarks are located near the salient (or the most notable) and consistent regions, they can be quickly detected, and as a result, the proposed method has small detection errors. Using displacement measures as auxiliary features, the spatial relationship between active landmarks and AD landmarks are also exploited in the training stage. Although AD landmarks are located in the regions with statistically significant between-group differences, the spatial relationship to the most related active landmarks is more predictable. This spatial relationship (i.e., AD landmarks to active landmarks) increases consistency, which in turn improves overall performance of the proposed method.
D. Limitations and future directions
In this paper, a novel landmark-based feature extraction method is proposed by introducing 1) a two-layer shape-constrained regression forest for landmark detection, 2) active landmarks for guiding AD landmark detection, and 3) landmark-based morphological features for automatic AD classification. Various experiments are conducted, and the performance of the proposed method is then compared with a state-of-the-art ROI-based and voxel-based methods. Results show that the proposed method has similar or better AD/HC classification accuracy and is roughly 50 times faster than the ROI-based method. But there are also several limitations in our method. 1) Noting the data-driven property, our method relies much on the scale of training dataset. Less training subjects will adversely affect accuracy of identifying landmarks so that the learned landmarks may not significant enough for a new subject. 2) In the current study, we also simply concatenate features obtained from all landmarks. One possible solution for further improving the classification performance is to design an advanced classification model to fully take advantage of features from different landmarks. For example, we may be able to design certain hierarchical classifiers to achieve better performance. In particular, each landmark or each small group of landmarks can be designed with its individual classifier for initial AD classification, and then their obtained classification scores can be aggregated gradually for obtaining the final AD classification result. 3) Moreover, we do not consider the combination of the clusters for constructing an overall shape when detecting landmarks. It would be beneficial to construct a “sensible” overall shape. 4) Furthermore, instead of using a single template, the group-wise or multi-atlas registration can be also used to reduce registration error in the training stage. Thus, more accurate training landmarks would be identified. 5) A potential application of our method is that it can be utilized for large-scale subject indexing or retrieval. For example, for a given patient, several similar cases can be efficiently found in the large-scale database, and the treatment plan of the subject can be established by the lights of the previous successful therapeutic strategies. All these will be our future work.
Acknowledgments
This work was supported by NIH grants (EB006733, EB008374, EB009634, MH100217, AG041721, AG049371, AG042599).
Footnotes
This paper has supplementary downloadable material available at http://ieeexplore.ieee.org, provided by the authors.
Contributor Information
Jun Zhang, Email: junzhang@med.unc.edu, Department of Radiology and BRIC, University of North Carolina, Chapel Hill, NC, USA.
Yue Gao, Department of Radiology and BRIC, University of North Carolina, Chapel Hill, NC, USA.
Yaozong Gao, Department of Radiology and BRIC, University of North Carolina, Chapel Hill, NC, USA. Department of Computer Science, University of North Carolina, Chapel Hill, NC, USA.
Brent C. Munsell, Department of Computer Science, College of Charleston, Charleston, SC, USA
Dinggang Shen, Email: dgshen@med.unc.edu, Department of Radiology and BRIC, University of North Carolina, Chapel Hill, NC, USA. Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, Republic of Korea.
References
- 1.Rice DP, Fox PJ, Max W, Webber PA, Lindeman DA, Hauck WW, Segura E. The economic burden of Alzheimer’s disease care. Health Affairs. 1993;12(2):164–176. doi: 10.1377/hlthaff.12.2.164. [DOI] [PubMed] [Google Scholar]
- 2.Maresova P, Mohelska H, Dolejs J, Kuca K. Socio-economic aspects of Alzheimer’s disease. Current Alzheimer Research. 2015;12(9):903–911. doi: 10.2174/156720501209151019111448. [DOI] [PubMed] [Google Scholar]
- 3.Sperling RA, Aisen PS, Beckett LA, Bennett DA, Craft S, Fagan AM, Iwatsubo T, Jack CR, Kaye J, Montine TJ, et al. Toward defining the preclinical stages of Alzheimer’s disease: Recommendations from the national institute on aging-Alzheimer’s association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimer’s & Dementia. 2011;7(3):280–292. doi: 10.1016/j.jalz.2011.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Klöppel S, Stonnington CM, Chu C, Draganski B, Scahill RI, Rohrer JD, Fox NC, Jack CR, Ashburner J, Frackowiak RS. Automatic classification of MR scans in Alzheimer’s disease. Brain. 2008;131(3):681–689. doi: 10.1093/brain/awm319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Blennow K, de Leon MJ, Zetterberg H. Alzheimer’s disease. Lancet. 2006;368(9533):387–403. doi: 10.1016/S0140-6736(06)69113-7. [DOI] [PubMed] [Google Scholar]
- 6.Frisoni GB, Fox NC, Jack CR, Scheltens P, Thompson PM. The clinical use of structural MRI in Alzheimer disease. Nature Reviews Neurology. 2010;6(2):67–77. doi: 10.1038/nrneurol.2009.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Thompson PM, MacDonald D, Mega MS, Holmes CJ, Evans AC, Toga AW. Detection and mapping of abnormal brain structure with a probabilistic atlas of cortical surfaces. Journal of Computer Assisted Tomography. 1997;21(4):567–581. doi: 10.1097/00004728-199707000-00008. [DOI] [PubMed] [Google Scholar]
- 8.Buchanan R, Vladar K, Barta P, Pearlson G. Structural evaluation of the prefrontal cortex in schizophrenia. The American Journal of Psychiatry. 1998;155(8):1049–1055. doi: 10.1176/ajp.155.8.1049. [DOI] [PubMed] [Google Scholar]
- 9.Zhang D, Shen D, Initiative ADN, et al. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer’s disease. NeuroImage. 2012;59(2):895–907. doi: 10.1016/j.neuroimage.2011.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gerardin E, Chételat G, Chupin M, Cuingnet R, Desgranges B, Kim HS, Niethammer M, Dubois B, Lehéricy S, Garnero L, et al. Multidimensional classification of hippocampal shape features discriminates Alzheimer’s disease and mild cognitive impairment from normal aging. NeuroImage. 2009;47(4):1476–1486. doi: 10.1016/j.neuroimage.2009.05.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Aguilar C, Westman E, Muehlboeck JS, Mecocci P, Vellas B, Tsolaki M, Kloszewska I, Soininen H, Lovestone S, Spenger C, et al. Different multivariate techniques for automated classification of MRI data in Alzheimer’s disease and mild cognitive impairment. Psychiatry Research: Neuroimaging. 2013;212(2):89–98. doi: 10.1016/j.pscychresns.2012.11.005. [DOI] [PubMed] [Google Scholar]
- 12.Chetelat G, Landeau B, Eustache F, Mezenge F, Viader F, de La Sayette V, Desgranges B, Baron JC. Using voxel-based morphometry to map the structural changes associated with rapid conversion in MCI: a longitudinal MRI study. NeuroImage. 2005;27(4):934–946. doi: 10.1016/j.neuroimage.2005.05.015. [DOI] [PubMed] [Google Scholar]
- 13.Singh V, Chertkow H, Lerch JP, Evans AC, Dorr AE, Kabani NJ. Spatial patterns of cortical thinning in mild cognitive impairment and Alzheimer’s disease. Brain. 2006;129(11):2885–2893. doi: 10.1093/brain/awl256. [DOI] [PubMed] [Google Scholar]
- 14.Du AT, Schuff N, Kramer JH, Rosen HJ, Gorno-Tempini ML, Rankin K, Miller BL, Weiner MW. Different regional patterns of cortical thinning in Alzheimer’s disease and frontotemporal dementia. Brain. 2007;130(4):1159–1166. doi: 10.1093/brain/awm016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dickerson BC, Feczko E, Augustinack JC, Pacheco J, Morris JC, Fischl B, Buckner RL. Differential effects of aging and Alzheimer’s disease on medial temporal lobe cortical thickness and surface area. Neurobiology of Aging. 2009;30(3):432–440. doi: 10.1016/j.neurobiolaging.2007.07.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hutton C, De Vita E, Ashburner J, Deichmann R, Turner R. Voxel-based cortical thickness measurements in MRI. NeuroImage. 2008;40(4):1701–1710. doi: 10.1016/j.neuroimage.2008.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li Y, Wang Y, Wu G, Shi F, Zhou L, Lin W, Shen D, Initiative ADN, et al. Discriminant analysis of longitudinal cortical thickness changes in Alzheimer’s disease using dynamic and network features. Neurobiology of Aging. 2012;33(2):427–e15. doi: 10.1016/j.neurobiolaging.2010.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hinrichs C, Singh V, Mukherjee L, Xu G, Chung MK, Johnson SC Alzheimer’s Disease Neuroimaging Initiative et al. Spatially augmented lpboosting for AD classification with evaluations on the ADNI dataset. NeuroImage. 2009;48(1):138–149. doi: 10.1016/j.neuroimage.2009.05.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cuingnet R, Gerardin E, Tessieras J, Auzias G, Lehéricy S, Habert MO, Chupin M, Benali H, Colliot O, Initiative ADN, et al. Automatic classification of patients with Alzheimer’s disease from structural MRI: a comparison of ten methods using the ADNI database. NeuroImage. 2011;56(2):766–781. doi: 10.1016/j.neuroimage.2010.06.013. [DOI] [PubMed] [Google Scholar]
- 20.Liu M, Zhang D, Shen D. Relationship induced multi-template learning for diagnosis of alzheimers disease and mild cognitive impairment. Medical Imaging, IEEE Transactions on. 2016;35(6):1463–1474. doi: 10.1109/TMI.2016.2515021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ashburner J, Friston KJ. Why voxel-based morphometry should be used. NeuroImage. 2001;14(6):1238–1243. doi: 10.1006/nimg.2001.0961. [DOI] [PubMed] [Google Scholar]
- 22.Ashburner J, Friston KJ. Voxel-based morphometrythe methods. NeuroImage. 2000;11(6):805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- 23.Rueda A, González F, Romero E. Extracting salient brain patterns for imaging-based classification of neurodegenerative diseases. Medical Imaging, IEEE Transactions on. 2014;33(6):1262–1274. doi: 10.1109/TMI.2014.2308999. [DOI] [PubMed] [Google Scholar]
- 24.Mardia K. Assessment of multinormality and the robustness of hotelling’s t 2 test. Applied Statistics. 1975:163–171.
- 25.Holmes CJ, Hoge R, Collins L, Woods R, Toga AW, Evans AC. Enhancement of MR images using registration for signal averaging. Journal of Computer Assisted Tomography. 1998;22(2):324–333. doi: 10.1097/00004728-199803000-00032. [DOI] [PubMed] [Google Scholar]
- 26.Zhang J, Liang J, Zhao H. Local energy pattern for texture classification using self-adaptive quantization thresholds. Image Processing, IEEE Transactions on. 2013;22(1):31–42. doi: 10.1109/TIP.2012.2214045. [DOI] [PubMed] [Google Scholar]
- 27.Leung T, Malik J. Representing and recognizing the visual appearance of materials using three-dimensional textons. International Journal of Computer Vision. 2001;43(1):29–44. [Google Scholar]
- 28.Kadir T, Brady M. Saliency, scale and image description. International Journal of Computer Vision. 2001;45(2):83–105. [Google Scholar]
- 29.Wu G, Qi F, Shen D. Learning-based deformable registration of MR brain images. Medical Imaging, IEEE Transactions on. 2006;25(9):1145–1157. doi: 10.1109/tmi.2006.879320. [DOI] [PubMed] [Google Scholar]
- 30.Cootes TF, Ionita MC, Lindner C, Sauer P. Robust and accurate shape model fitting using random forest regression voting. ECCV 2012. 2012:278–291. doi: 10.1109/TPAMI.2014.2382106. [DOI] [PubMed] [Google Scholar]
- 31.Criminisi A, Robertson D, Konukoglu E, Shotton J, Pathak S, White S, Siddiqui K. Regression forests for efficient anatomy detection and localization in computed tomography scans. Medical Image Analysis. 2013;17(8):1293–1303. doi: 10.1016/j.media.2013.01.001. [DOI] [PubMed] [Google Scholar]
- 32.Lindner C, Thiagarajah S, Wilkinson JM, Wallis G, Cootes T Consortium T. Fully automatic segmentation of the proximal femur using random forest regression voting. Medical Imaging, IEEE Transactions on. 2013;32(8):1462–1472. doi: 10.1109/TMI.2013.2258030. [DOI] [PubMed] [Google Scholar]
- 33.Chu C, Chen C, Wang C-W, Huang C-T, Li C-H, Nolte L-P, Zheng G. Fully automatic cephalometric x-ray landmark detection using random forest regression and sparse shape composition. submitted to Automatic Cephalometric X-ray Landmark Detection Challenge. 2014 [Google Scholar]
- 34.Zhan Y, Zhou XS, Peng Z, Krishnan A. Active scheduling of organ detection and segmentation in whole-body medical images. MICCAI. 2008:313–321. doi: 10.1007/978-3-540-85988-8_38. [DOI] [PubMed] [Google Scholar]
- 35.Criminisi A, Shotton J, Bucciarelli S. Decision forests with long-range spatial context for organ localization in CT volumes. MICCAI. 2009:69–80. [Google Scholar]
- 36.Zhan Y, Dewan M, Harder M, Krishnan A, Zhou XS. Robust automatic knee MR slice positioning through redundant and hierarchical anatomy detection. Medical Imaging, IEEE Transactions on. 2011;30(12):2087–2100. doi: 10.1109/TMI.2011.2162634. [DOI] [PubMed] [Google Scholar]
- 37.Lienhart R, Maydt J. An extended set of haar-like features for rapid object detection. Image Processing. 2002. Proceedings. 2002 International Conference on; IEEE; 2002. pp. I–900. [Google Scholar]
- 38.Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision. 2004;60(2):91–110. [Google Scholar]
- 39.Dalal N, Triggs B. CVPR. Vol. 1. IEEE; 2005. Histograms of oriented gradients for human detection; pp. 886–893. [Google Scholar]
- 40.Ojala T, Pietikäinen M, Mäenpää T. Multiresolution gray-scale and rotation invariant texture analysis with local binary patterns. Pattern Analysis and Machine Intelligence, IEEE Transactions on, vol. 2002;24(7):971–987. [Google Scholar]
- 41.Cootes TF, Taylor CJ, Cooper DH, Graham J. Active shape models-their training and application. Computer Vision and Image Understanding. 1995;61(1):38–59. [Google Scholar]
- 42.Leventon ME, Grimson WEL, Faugeras O. Statistical shape influence in geodesic active contours. Computer Vision and Pattern Recognition, 2000. Proceedings. IEEE Conference on; IEEE; 2000. pp. 316–323. [Google Scholar]
- 43.Jolliffe I. Principal component analysis. Wiley Online Library; 2002. [Google Scholar]
- 44.Shi J, Malik J. Normalized cuts and image segmentation. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2000;22(8):888–905. [Google Scholar]
- 45.Cao X, Wei Y, Wen F, Sun J. Face alignment by explicit shape regression. International Journal of Computer Vision. 2014;107(2):177–190. [Google Scholar]
- 46.Chen C, Xie W, Franke J, Grutzner P, Nolte LP, Zheng G. Automatic X-ray landmark detection and shape segmentation via data-driven joint estimation of image displacements. Medical Image Analysis. 2014;18(3):487–499. doi: 10.1016/j.media.2014.01.002. [DOI] [PubMed] [Google Scholar]
- 47.Tu Z, Bai X. Auto-context and its application to high-level vision tasks and 3D brain image segmentation. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2010;32(10):1744–1757. doi: 10.1109/TPAMI.2009.186. [DOI] [PubMed] [Google Scholar]
- 48.Liu M, Zhang D, Shen D. View-centralized multi-atlas classification for Alzheimer’s disease diagnosis. Human Brain Mapping. 2015;36(5):1847–1865. doi: 10.1002/hbm.22741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jain A, Nandakumar K, Ross A. Score normalization in multimodal biometric systems. Pattern Recognition. 2005;38(12):2270–2285. [Google Scholar]
- 50.Ferrarini L, Palm WM, Olofsen H, van Buchem MA, Reiber JH, Admiraal-Behloul F. Shape differences of the brain ventricles in Alzheimer’s disease. NeuroImage. 2006;32(3):1060–1069. doi: 10.1016/j.neuroimage.2006.05.048. [DOI] [PubMed] [Google Scholar]
- 51.Nestor SM, Rupsingh R, Borrie M, Smith M, Accomazzi V, Wells JL, Fogarty J, Bartha R Alzheimer’s Disease Neuroimaging Initiative et al. Ventricular enlargement as a possible measure of Alzheimer’s disease progression validated using the Alzheimer’s disease neuroimaging initiative database. Brain. 2008;131(9):2443–2454. doi: 10.1093/brain/awn146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Apostolova LG, Green AE, Babakchanian S, Hwang KS, Chou YY, Toga AW, Thompson PM. Hippocampal atrophy and ventricular enlargement in normal aging, mild cognitive impairment and Alzheimer’s disease. Alzheimer Disease and Associated Disorders. 2012;26(1):17. doi: 10.1097/WAD.0b013e3182163b62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liu M, Zhang D, Shen D, Initiative ADN, et al. Ensemble sparse classification of Alzheimer’s disease. NeuroImage. 2012;60(2):1106–1116. doi: 10.1016/j.neuroimage.2012.01.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tong T, Wolz R, Gao Q, Guerrero R, Hajnal JV, Rueckert D, Initiative ADN, et al. Multiple instance learning for classification of dementia in brain MRI. Medical Image Analysis. 2014;18(5):808–818. doi: 10.1016/j.media.2014.04.006. [DOI] [PubMed] [Google Scholar]
- 55.Wolz R, Julkunen V, Koikkalainen J, Niskanen E, Zhang DP, Rueckert D, Soininen H, Lötjönen J, Initiative ADN, et al. Multi-method analysis of MRI images in early diagnostics of Alzheimer’s disease. PloS One. 2011;6(10):e25446. doi: 10.1371/journal.pone.0025446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Shen D, Davatzikos C. Hammer: hierarchical attribute matching mechanism for elastic registration. Medical Imaging, IEEE Transactions on. 2002;21(11):1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]