Abstract
Ventricular myocytes are excitable cells whose voltage threshold for action potential (AP) excitation is ∼−60 mV at which INa is activated to give rise to a fast upstroke. Therefore, for a short stimulus pulse to elicit an AP, a stronger stimulus is needed if the resting potential lies further away from the INa threshold, such as in hypokalemia. However, for an AP elicited by a long duration stimulus or a diastolic spontaneous calcium release, we observed that the stimulus needed was lower in hypokalemia than in normokalemia in both computer simulations and experiments of rabbit ventricular myocytes. This observation provides insight into why hypokalemia promotes calcium-mediated triggered activity, despite the resting potential lying further away from the INa threshold. To understand the underlying mechanisms, we performed bifurcation analyses and demonstrated that there is a dynamical threshold, resulting from a saddle-node bifurcation mainly determined by IK1 and INCX. This threshold is close to the voltage at which IK1 is maximum, and lower than the INa threshold. After exceeding this dynamical threshold, the membrane voltage will automatically depolarize above the INa threshold due to the large negative slope of the IK1-V curve. This dynamical threshold becomes much lower in hypokalemia, especially with respect to calcium, as predicted by our theory. Because of the saddle-node bifurcation, the system can automatically depolarize even in the absence of INa to voltages higher than the ICa,L threshold, allowing for triggered APs in single myocytes with complete INa block. However, because INa is important for AP propagation in tissue, blocking INa can still suppress premature ventricular excitations in cardiac tissue caused by calcium-mediated triggered activity. This suppression is more effective in normokalemia than in hypokalemia due to the difference in dynamical thresholds.
Introduction
Under normal conditions, ventricular myocytes have a diastolic resting potential at ∼−80 mV, stabilized by the inward rectifier K+ current (IK1). An action potential (AP) can be elicited by a brief current pulse, overcoming the stabilizing effect of IK1 and bringing the voltage to the threshold (∼−60 mV) for Na+ current (INa) activation. In other words, the voltage threshold for eliciting an AP using a brief stimulus pulse is near the INa threshold at ∼−60 mV for a ventricular myocyte. Therefore, when the resting potential is hyperpolarized (e.g., under hypokalemic conditions), a larger stimulus current for a brief pulse is needed to depolarize the membrane voltage to the INa threshold to elicit an AP. Similarly, the conduction velocity in cardiac tissue is slower for a hyperpolarized resting potential (1, 2, 3). The resting potential of a ventricular myocyte can also be destabilized by reduction of IK1 to result in pacemaking activity (4, 5) or delayed afterdepolarization (DAD)-mediated triggered activity (TA) (6, 7, 8). In both cases, a lowered IK1 allows the Na+-Ca2+ exchange current (INCX) to overcome the repolarizing effect of IK1, depolarizing the cell to the INa threshold for AP generation.
A DAD is a voltage depolarization caused by spontaneous calcium (Ca2+) release (SCR) during the diastolic phase after a previous AP (9, 10, 11, 12, 13). If the depolarization is large enough to reach the INa threshold, the DAD can trigger an AP causing TA. This phenomenon is potentiated by various diseased conditions including heart failure (7, 14) and hypokalemia (15). In heart failure, ryanodine receptors become leaky, which promotes SCRs resulting in DADs. In addition, IK1 is reduced and INCX is increased, which decreases the diastolic Ca2+-to-voltage gain to promote TA.
In hypokalemia, multiple factors come into play. Na+-K+ pump activity is reduced, which results in an elevated intracellular Na+ concentration (16, 17). This inhibits forward Na+-Ca2+ exchange, which increases intracellular Ca2+ concentration and promotes SCR. Hypokalemia also causes a reduced IK1 conductance, which tends to destabilize the resting potential and potentiates DAD-mediated TA. However, hypokalemia also causes a hyperpolarized resting potential through the left shift of reversal potential EK. This acts to move the membrane voltage further away from the INa threshold, which would seem to counter the TA-promoting effect of reduced IK1.
A recent theoretical study by Greene and Shiferaw (18) showed that the voltage threshold for DAD-mediated TA is actually lower than the INa threshold, and is determined by the voltage at which IK1 is maximal. These findings indicate that the traditional understanding of the voltage threshold for DAD-mediated TA as the voltage threshold for INa activation needs to be revisited. In this study, we seek to dissect the determinants of the threshold for DAD-mediated TA in normokalemic and hypokalemic conditions, using patch-clamp experiments, computer simulations, and nonlinear dynamics. We show that there exists a dynamical threshold for TA, which is a saddle-node bifurcation point, mainly determined by IK1 and INCX. This threshold becomes lower in hypokalemia, potentiating DAD-mediated TA in hypokalemia.
Materials and Methods
Myocyte experiments
Ventricular myocyte isolation
Young adult (3–4 months of age) New Zealand white male rabbits (1.7–2.0 kg) were euthanized by intravenous injection of heparin sulfate (1000 U) and sodium pentobarbital (100 mg/kg). Hearts were quickly excised by thoracotomy and retrogradely perfused at 37°C in Langendorff fashion with Ca2+-free Tyrode’s solution for 5–7 min followed by enzyme digestion perfusion with Tyrode’s solution containing 0.05 mg/mL Liberase TH (Roche, South San Francisco, CA) for 20–30 min at 25 mL/min. The Tyrode’s solution contained the following: 136 mmol/L NaCl, 5.4 mmol/L KCl, 0.33 mmol/L NaH2PO4, 1.0 mmol/L MgCl2, 10 mmol/L HEPES, and 10 mmol/L glucose (pH 7.4 with KOH). All chemicals were purchased from Sigma-Aldrich (St. Louis, MO) unless indicated otherwise. Myocytes were separated from digested ventricles by gentle mechanical dissociation in 0.2 mM Ca2+ Tyrode’s solution. Ca2+ concentration was gradually increased to 1.8 mmol/L over 30 min. Myocytes were used within 6–8 h. All procedures complied with UCLA Animal Research Committee policies.
Patch-clamp experiments in myocytes
Standard whole-cell patch-clamp methods were used to measure voltage in the current-clamp mode. Borosilicate glass electrodes (tip resistance 1.4–2.2 MΩ) were filled with internal solution containing 110 mmol/L K-Aspartate, 30 mmol/L KCl, 5 mmol/L NaCl, 10 mmol/L HEPES, 5 mmol/L MgATP, 5 mmol/L creatine phosphate, 1 mmol/L KH2PO4, and 0 mmol/L EGTA (pH 7.2 with KOH). All chemicals were purchased from Sigma-Aldrich unless indicated otherwise. Data were acquired with an Axopatch 200A patch-clamp amplifier and Digidata 1200 acquisition board driven by pCLAMP 9.0 software (Axon Instruments, Union City, CA). Corrections were made for liquid junction potentials. Signals were filtered at 1 kHz. All experiments were carried out in Tyrode’s solution maintained at 37°C. Constant current square pulses (2 or 200 ms duration) were applied stepwise in 0.1 nA increments from −0.2 nA up to 3.0 nA to determine AP thresholds under normokalemic ([K+]o = 5.4 mM) or hypokalemic ( = 2.7 mM) conditions. For experiments involving Na+ channel blockade, patch-clamped myocytes were rapidly superfused with either normal Tyrode’s solution or Tyrode’s solution containing 20 μmol/L tetrodotoxin (TTX) (Tocris Bioscience, Bristol, UK) using a rapid solution exchange device (19) positioned near the myocyte under the control of Axopatch software (Axon Instruments).
Computer simulations
Computer simulations were performed in a single cell and one-dimensional (1D) cables using the AP model previously described by Mahajan et al. (20). In the single-cell simulations, the cell model was first prepaced to its steady state. Spontaneous Ca2+ releases were simulated by clamping the myocyte submembrane Ca2+ level to a Gaussian-like shape during the diastolic phase after a stimulated AP, i.e., , where t0 is the peak time of (t was set to zero at the time of the stimulation; see Fig. 1), σ determines the width of the Ca2+ transient, and Capeak is the peak value. σ = 150 ms and t0 = 850 ms were used for all simulations unless otherwise specified. Submembrane Ca2+ was used to determine Ca2+ thresholds to produce a DAD of sufficient amplitude to cause TA, because the INCX dependence on Ca2+ is specifically formulated in terms of submembrane Ca2+. Normokalemia and hypokalemia were simulated by changing the value of from 5.4 to 2.7 mM. Intracellular sodium was clamped to 10 mM.
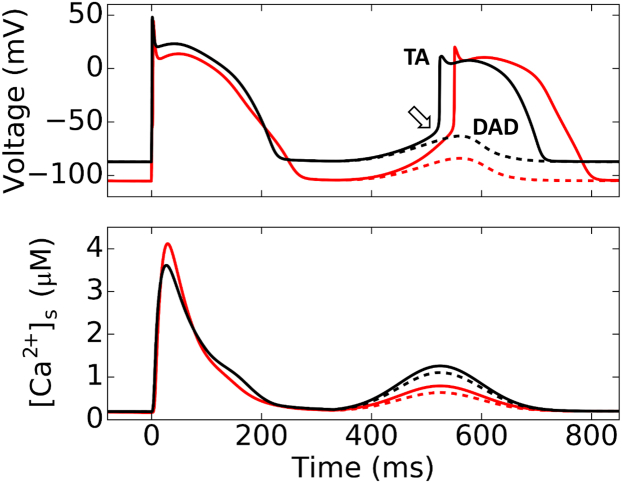
Figure 1.
Simulated DAD and TA using the AP model. Membrane voltage (upper traces) and submembrane Ca2+ concentration ([Ca2+]s, lower traces) during a normal stimulated AP followed by a DAD due to spontaneous Ca2+ release which is just above (solid lines) or below (dashed lines) the threshold to trigger an AP. (Black traces) Normokalemia ([K+]o = 5.4 mM); (red traces) hypokalemia ([K+]o = 2.7 mM). (Open arrow) INa threshold. The parameters for Gaussian-like function of the clamped spontaneous Ca2+ release (see Materials and Methods) were t0 = 525 ms and σ = 70 ms for all four traces. For normokalemia, Capeak = 1.258 μM (black solid) and 1.102 μM (black dashed), respectively. For hypokalemia, Capeak = 0.79 μM (red solid) and 0.634 μM (red dashed). To see this figure in color, go online.
One-dimensional cable simulations were carried out using the following equation for voltage:
| (1) |
where V is the membrane voltage, Cm = 1 μF/cm2 is the membrane capacitance, and D is the diffusion constant set to 0.0005 cm2/ms. The prepaced single-cell steady state was used as initial condition for each cell in the cable. DADs were simulated by a time-dependent commanded spontaneous release of the SR Ca2+ with random latencies drawn from a Gaussian distribution with a certain standard deviation as described in Xie et al. (21) and Liu et al. (22). Briefly, a SR release conductance was added with a certain strength and duration to release Ca2+ from the SR. The onset of this release was determined by a random latency drawn from the Gaussian distribution. A time adaptive algorithm was used with a time step (Δt) varying between 0.01 ms and 0.1 ms. In the single-cell simulations, DAD-mediated triggered activity was considered to have occurred if the voltage exceeded 0 mV. In the cable simulations, if a propagating wave was detected at either end of the cable after the sinus beat, a propagating premature ventricular contraction (PVC) was considered to have occurred.
Results
Hypokalemia results in a lower threshold for DAD-mediated TA in a ventricular myocyte model
We carried out simulations to examine the threshold for TA in the rabbit ventricular myocyte model by Mahajan et al. (20). The spontaneous Ca2+ release that causes a DAD or TA was simulated by a clamped Ca2+ transient (see Materials and Methods). Fig. 1 shows the voltage and [Ca2+]s for a stimulated beat followed by a spontaneous Ca2+ release just below (dashed) and above (solid) the threshold for TA. Hypokalemia hyperpolarized the resting membrane potential to <−100 mV. Despite the resting potential being 20 mV more negative, the Ca2+ amplitude threshold for DAD-mediated TA is much lower during hypokalemia than normokalemia, indicating that hypokalemia substantially lowers the threshold for TA. This is consistent with well-known experimental observations that hypokalemia potentiates DAD-mediated TA despite hyperpolarizing the resting membrane potential (15). The voltage still needs to eventually depolarize past the INa threshold to result in a fast upstroke under both normokalemia and hypokalemia. However, in the case of hypokalemia, a much smaller Ca2+ transient and thus a much smaller INCX was sufficient to depolarize the voltage to the same INa threshold. To gain a more complete understanding of the mechanisms underlying this phenomenon, we combined nonlinear dynamics analysis with computer simulations and patch-clamp experiments as described in the sections below.
Short and long current pulse thresholds for eliciting an AP
Because the duration of a DAD is much longer than that of a typical electrical stimulus, we first studied the role that the duration of a pulse stimulus plays in eliciting an AP. Fig. 2 compares excitation thresholds for a short (2 ms) versus a long (200 ms) current pulse to elicit an AP in a patch-clamped rabbit ventricular myocyte (current clamp mode) under both normokalemic ([K]o = 5.4 mM) and hypokalemic conditions ([K]o = 2.7 mM). Hypokalemia shifted the resting potential from −87 to −110 mV.
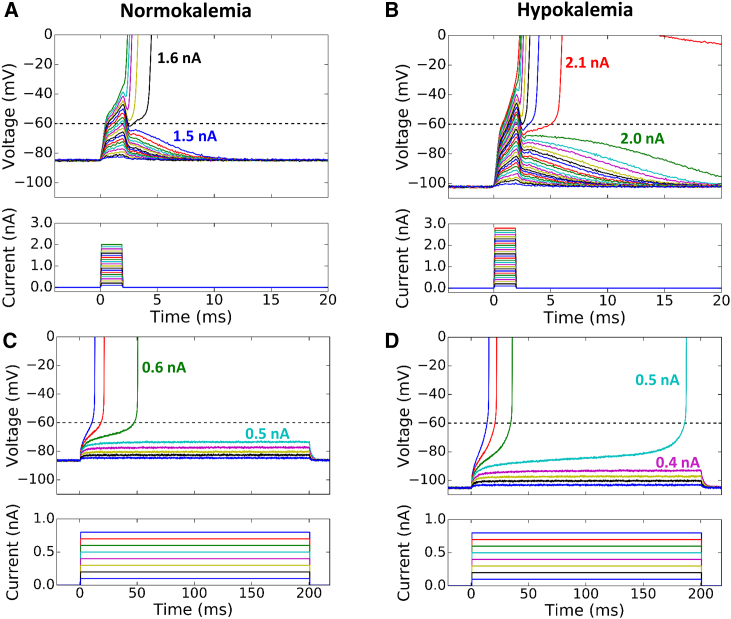
Figure 2.
Current thresholds for triggering an AP by short and long stimuli in normokalemic ([K+]o = 5.4 mM) and hypokalemic ([K+]o = 2.7 mM) rabbit ventricular myocytes. (A) Superimposed voltage (upper) and current (lower) traces during 2 ms current pulses of increasing amplitude in a normokalemic patch-clamped rabbit ventricular myocyte. The minimum current needed to elicit an AP was 1.6 nA. (B) Same as (A), but during hypokalemia. With a hyperpolarized resting potential, the minimum current needed to elicit an AP increased to 2.1 nA. (C and D) Corresponding traces for 200 ms current pulses. The minimum current needed to elicit an AP was 0.6 nA, which decreased to 0.5 nA during hypokalemia. Note how the take-off potential is lower than the INa activation threshold at −60 mV, and is further lowered in hypokalemia. To see this figure in color, go online.
For the 2 ms current pulse (Fig. 2, A and B), the minimum current required to elicit an AP increased from 1.6 nA under normokalemic conditions to 2.1 nA under hypokalemic conditions, as expected due to the more hyperpolarized resting membrane potential during hypokalemia. In both cases, the smallest current amplitude eliciting an AP depolarized the membrane very close to the INa threshold of −60 mV, followed by the AP upstroke within 5 ms. For the 200 ms current pulse (Fig. 2, C and D), however, the results were reversed, with the minimum current eliciting an AP decreasing from 0.6 nA during normokalemia to 0.5 nA during hypokalemia. Moreover, the smallest current amplitude eliciting an AP initially depolarized the membrane voltage to only −74 mV for normokalemia and −94 mV for hypokalemia. The membrane voltage then rose very slowly before finally reaching the INa activation threshold at ∼−60 mV to generate the AP upstroke. Thus, consistent with the predictions from Greene and Shiferaw (18), the threshold for a long current pulse to elicit an AP was considerably more negative than −60 mV, especially during hypokalemia.
To analyze the dynamics underlying these behaviors, we considered a system composed only of IK1 and the stimulus current (Isti), described by the following differential equation:
| (2) |
where Isti is a square pulse with a duration (τ) and height (I0), i.e.,
| (3) |
The resting potential of Eq. 2 is simply the reversal potential (EK) of IK1. The voltage at the end of the stimulus current pulse is given by
| (4) |
To facilitate analytical solutions of Eqs. 2 or 4, we approximated IK1 by a piecewise linear function as follows (Fig. 3 A):
| (5) |
where and . IK1,max is the peak IK1 at Vmax. Vmax and V0 are defined as in Fig. 3 A.
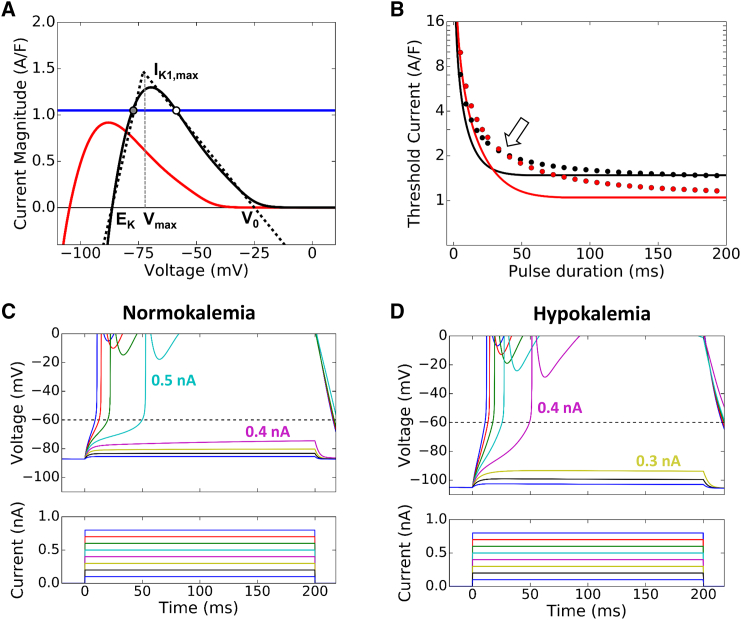
Figure 3.
Theoretical analysis of the current threshold for triggering an AP by a pulse stimulus. (A) The IK1-V curves for normokalemia ([K+]o = 5.4 mM, black) and hypokalemia ([K+]o = 2.7 mM, red). The IK1 curve is mainly determined by four parameters: EK, IK1,max, Vmax, and V0. To most closely match the actual IK1 curves, for normokalemia we used EK = −86.5 mV, IK1,max = 1.47 A/F, Vmax = −73 mV, and V0 = −25 mV. For hypokalemia, we used EK = −104.5 mV, IK1,max = 1.04 A/F, Vmax = −92 mV, and V0 = −43 mV in the linear piecewise approximation for IK1 (dotted line) used for the analytical treatment. (Blue horizontal line) Example of constant inward current that is subthreshold in normokalemia but suprathreshold in hypokalemia. (Circles) Points at which the net current is zero, i.e., the equilibrium points. (Solid circle) Stable equilibrium point; (open circle) unstable equilibrium point in normokalemia. In hypokalemia, this example has no equilibrium point. (B) The threshold current (I0,th) versus pulse duration (τ) from the theoretical prediction (lines), and from the simulations (dots) using the AP model with a constant stimulus pulse of varying duration in normokalemia (black) and hypokalemia (red). (Open arrow) Where the current threshold reverses between normokalemia and hypokalemia. (C and D) Voltage (upper) and current (lower) traces corresponding to 200 ms current pulses of increasing amplitude during normokalemia and hypokalemia, from the simulations using the AP model. The minimum current needed to elicit an AP was 0.5 nA, which decreased to 0.4 nA in simulated hypokalemia. Note again how the takeoff potential is lower than the INa activation threshold, and is further lowered in hypokalemia. To see this figure in color, go online.
When , Eq. 4 can be explicitly solved, which leads to
| (6) |
For an infinitely long pulse, the voltage reaches a steady state, which is given by
| (7) |
When , the solution of Eq. 2 can be expressed with three time regions as follows:
-
1)
For ,
| (8) |
with t′ as the time at which , obtained from Eq. 8 as
| (9) |
-
2)
For ,
| (10) |
with t″ as the time at which , obtained from Eq. 10 as
| (11) |
-
3)
For ,
| (12) |
Because the INa threshold (Vth,Na) is near −60 mV, which is higher than Vmax but lower than V0 (see Fig. 3 A), then only the cases where needs to be considered. Assume that at , the voltage reaches the INa threshold, i.e., . Equation 10 then becomes
| (13) |
which leads to
| (14) |
By inserting t′ from Eq. 9 to Eq. 14, one obtains
| (15) |
By setting in Eq. 15 (this can only be satisfied if the second logarithmic term goes to infinity), the minimum stimulus strength can be calculated as
| (16) |
Therefore, when , the voltage can never reach Vth,Na but rather asymptotically approaches the steady state (Eq. 7), which is always lower than Vmax. However, when , there always exists a finite τ during which the voltage can grow to reach Vth,Na.
Hypokalemia has three main effects on IK1: a left shift of EK; a left shift of Vmax; and a reduced IK1,max, as shown in Fig. 3 A.
In Fig. 3 B, we plot the threshold current I0,th versus the pulse duration τ using Eq. 15 for both normokalemia and hypokalemia, showing that I0,th is smaller for normokalemia than for hypokalemia when τ < 29 ms, which is reversed when τ > 29 ms. We also plot in Fig. 3 B the corresponding results (circles) from the computer simulation using the rabbit ventricular myocyte model, which agrees well with the theoretical prediction. Fig. 3, C and D, shows two examples of incremental current amplitudes with a 200 ms pulse duration to illustrate the threshold current in normokalemia ([K+]o = 5.4 mM) and hypokalemia ([K+]o = 2.7 mM).
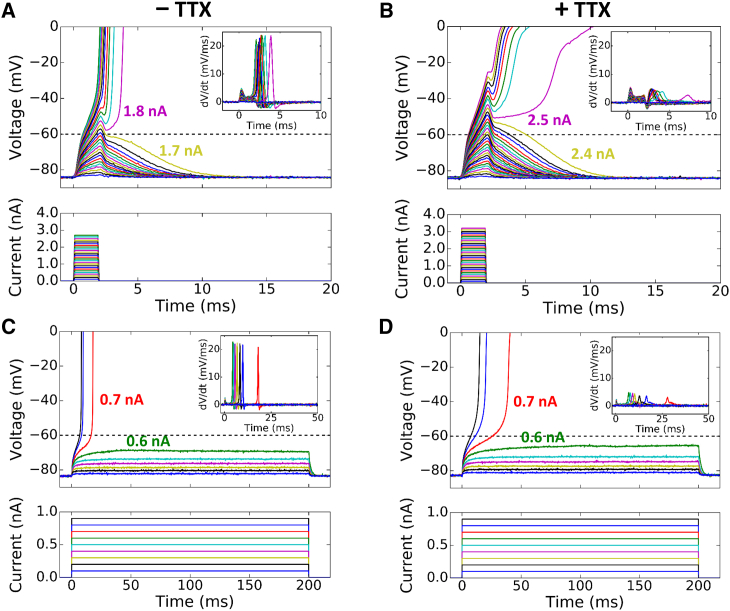
Based on Eqs. 15 and 16, the threshold current I0,th to elicit an AP depends on the voltage threshold of the Na+ channel (Vth,Na) for a short stimulus pulse but not for a long pulse. This indicates that in the absence of Na+ current (INa), a larger I0,th is required to elicit an AP for a short pulse because the voltage threshold (Vth,Ca) for L-type Ca2+ channel is higher (∼−40 mV). For a long pulse, I0,th will remain unchanged because Eq.16 is independent of either Vth,Na or Vth,Ca. To demonstrate this experimentally, we performed patch-clamp experiments as in Fig. 2 by blocking the Na+ channel using TTX (Fig. 4). For a 2 ms stimulation pulse, the addition of TTX increased the current threshold from 1.8 to 2.5 nA (Fig. 4, A and B). However, for a 200 ms stimulation pulse, the addition of TTX did not change the current threshold, which remained at 0.7 nA before and after TTX addition (Fig. 4, C and D), agreeing with the theoretical prediction. Note that after TTX application, the turning points for steep upstroke occurred at higher voltages and the maximum upstroke slopes were reduced under both short and long pulses (see corresponding dV/dt plots in the insets). This indicates that TTX was effective in blocking the Na+ channel and the AP upstroke after TTX was mediated by the L-type Ca2+ current (ICa,L). Based on our theory, this same observation should hold true for hypokalemia. However, the TTX effect of blocking the Na+ channel is voltage dependent, which becomes less effective for lower preholding voltages (23, 24, 25). Because of this voltage-dependent behavior, we were not able to convincingly repeat this experimental protocol in hypokalemia.
Figure 4.
Current thresholds for triggering an AP by short and long stimuli with and without TTX. (A) Superimposed voltage (upper) and current (lower) traces during 2 ms current pulses of increasing amplitude in a normokalemic patch-clamped rabbit ventricular myocyte (repeat of the protocol in Fig. 2A in a different cell). The minimum current needed to elicit an AP was 1.8 nA. (Inset) Rate of change of the voltage traces (dV/dt). (B) Same as (A) but in the presence of 20 μM TTX. With the addition of TTX, the minimum current needed to elicit an AP increased to 2.5 nA. (Inset) Fourfold reduction in maximum dV/dt due to TTX. (C and D) Corresponding traces for 200 ms current pulses without and with TTX, respectively. The minimum current needed to elicit an AP was 0.7 nA in both cases, demonstrating no change in the current threshold by TTX. Again, the addition of TTX reduced the dV/dt. To see this figure in color, go online.
Nonlinear dynamics caused by the interaction of IK1 and INCX
In contrast to constant current pulses, the depolarizing current INCX during a DAD is not constant, but a function of Na+, Ca2+, and voltage. Therefore, the analysis for constant current pulses above provides important qualitative insights, but it is not sufficient for a detailed understanding of the mechanisms of DAD-mediated TA. Here we further analyze the nonlinear dynamical interactions between IK1 and INCX using the following equation:
| (17) |
For simplicity, we first assume Na+ and Ca2+ to be constant parameters instead of changing variables, and thus Eq. 17 is a nonlinear equation with respect to voltage only. At equilibrium, , which leads to
| (18) |
i.e., when the magnitudes of the two currents are equal, the system is at an equilibrium point.
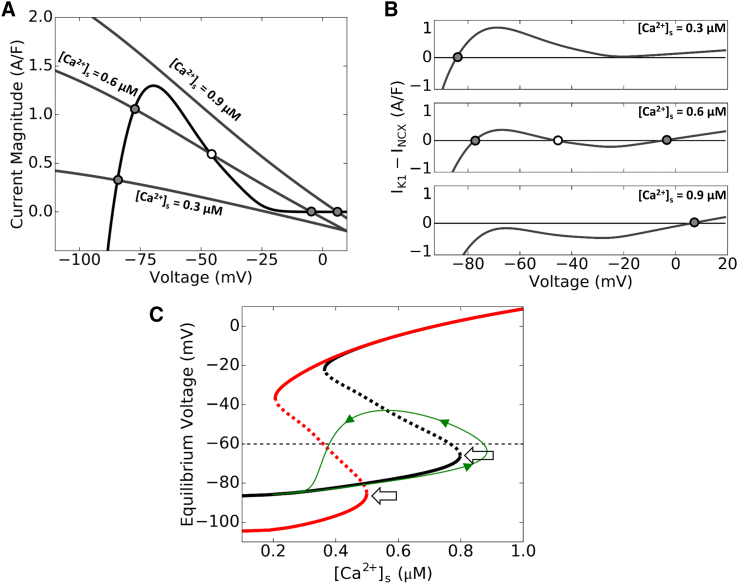
Because the currents involved are nonlinear functions of voltage, multiple equilibria can exist. Fig. 5 A plots the I-V curves for IK1 and inverted INCX (−INCX), in which the intersections of the two curves are the equilibrium points. When Ca2+ is low, INCX is small and there is only one intersection close to the reverse potential of IK1 (EK). The net current is inward when voltage is more negative than the equilibrium point and outward when voltage is more positive (top panel in Fig. 5 B). Therefore, if the voltage is displaced away from the equilibrium voltage, it is automatically driven back toward the equilibrium point, and thus the equilibrium point is stable. As Ca2+ rises, the −INCX curve increases and shifts to the right, resulting in three equilibrium points. The total net current changes from inward to outward, then to inward, and to outward again as voltage increases (middle panel in Fig. 5 B). Thus the lower and upper equilibrium points are stable while the middle is unstable. As Ca2+ rises above a critical level, the lower equilibria points converge then vanish, leaving only the single stable high voltage equilibrium point remaining. This behavior is summarized in Fig. 5 C by plotting the equilibrium voltages of this two-current system versus Ca2+ concentration, with the stable equilibrium points plotted as a solid line and unstable points as a dashed line. Therefore, when Ca2+ exceeds a critical value (arrows in Fig. 5 C), the membrane voltage will automatically depolarize toward the remaining single equilibrium point at high voltage. This occurs because of the steep negative slope of the IK1-V curve in this region causing IK1 to decrease faster than −INCX as voltage increases, making the net current always inward, thereby depolarizing the membrane voltage further. The voltage at the critical point, which occurs where the −INCX curve lies exactly tangent to IK1 slightly above Vmax, is lower than the INa threshold. Therefore, once the voltage reaches this critical value, it will continue to rise. We call this critical voltage a dynamical threshold because it is determined by the nonlinear dynamics of the interaction between IK1 and INCX. The dynamical threshold is a bifurcation point called a saddle-node bifurcation point (26). Hypokalemia results in a lower voltage threshold (red line in Fig. 5 C) due to the left shift of the IK1-V curve and reduction of maximum IK1 conductance.
Figure 5.
A dynamical threshold determined by IK1 and INCX for a constant Ca2+ condition. (A) I-V plot of IK1 and −INCX at [K]o = 5.4 mM (normokalemia), corresponding to low (0.3 μM), medium (0.6 μM), and high (0.9 μM) submembrane Ca2+ concentration levels. (Solid circles) Stable equilibrium points; (open circle) unstable equilibrium point. Note how with low Ca2+ there is only one (stable) equilibrium point at low voltage, with medium Ca2+ there are three (stable-unstable-stable) equilibrium points, and with high Ca2+ there is only one (stable) equilibrium point at high voltage. (B) Net current versus voltage for the corresponding three cases in (A), using the same symbols for the equilibrium points. (C) Equilibrium voltage versus steady-state Ca2+ during normokalemia (black) and hypokalemia (red). (Solid lines) Stable equilibrium points; (dashed lines) unstable equilibrium points for the particular Ca2+ concentration. (Arrows) Respective dynamical thresholds, which determine the voltage and Ca2+ needed to cross the saddle-node and elicit an AP. (Green trace) Example of a simulated trajectory using the simple two-current system consisting of IK1 and INCX, with a Ca2+ transient simulated by a Gaussian-shaped function similar to the function described in Fig. 1. Note that voltage continues to increase for a period of time even after the Ca2+ concentration has started to decrease, due to crossing the dynamical threshold. To see this figure in color, go online.
Influence of the intracellular Ca2+ waveform during spontaneous Ca2+ release on AP activation
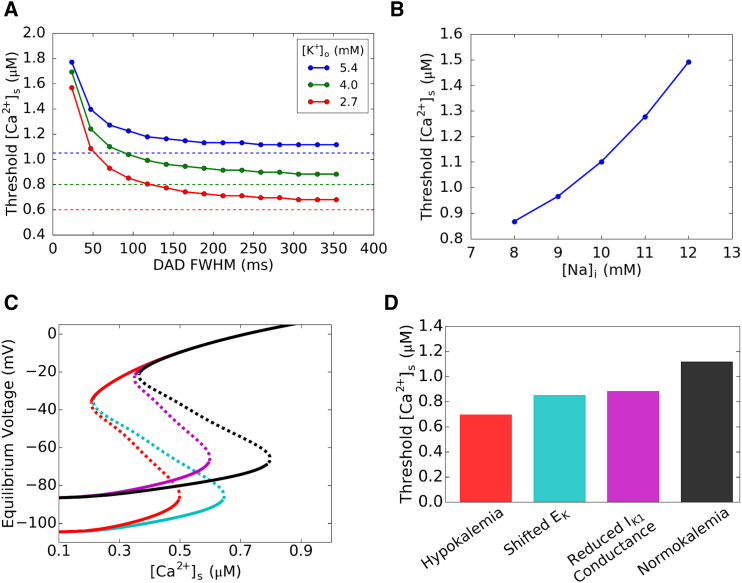
The nonlinear dynamics shown in Fig. 5 is valid when Ca2+ is constant, but during a DAD, cytosolic Ca2+ concentration rises and then falls. As Ca2+ increases from the diastolic Ca2+ concentration, the system first follows the lower branch of equilibrium voltage. When Ca2+ increases past the critical value (arrows in Fig. 5 C), voltage will continue to increase even when Ca2+ is declining (green trajectory in Fig. 5 C). Therefore, whether a cell reaches the INa threshold to trigger an AP depends not only on crossing the dynamical threshold, but also on the rate of decay of Ca2+ influencing the INCX curve. To investigate the effects of Ca2+ decay on the TA threshold, we varied the duration of a clamped Ca2+ transient with a Gaussian-like shape by changing the width of full width at half-maximum (FWHM). Fig. 6 A shows the Ca2+ transient amplitude threshold for TA (i.e., the peak amplitude of the Ca2+ transient required to trigger an AP) versus the width of the Ca2+ transient for different values of [K+]o. The Ca2+ transient amplitude threshold for TA decreased with lower [K+]o or a wider Ca2+ transient that decays more slowly. The dependence of the Ca2+ threshold on Ca2+ transient width gradually saturates when the Ca2+ transient FWHM is >∼200 ms. This indicates that when the Ca2+ transient duration is 200 ms or longer, the system has reached the steady-state solution, closely agreeing with the prediction of the bifurcation analysis, when including INaK, which contributes ∼20% to the effective IK1 peak (dashed lines in Fig. 6 A). The FWHM was observed in rabbit ventricular myocytes to be 180–300 ms (27), which easily satisfies this condition and therefore are always in the regime of the dynamical threshold.
Figure 6.
Submembrane Ca2+ transient thresholds for TA. (A) Ca2+ amplitude threshold for TA versus the FWHM of the Ca2+ transient and DAD for three different [K]o (5.4 mM blue, 4.0 mM green, and 2.7 mM red). (Dashed lines) Theoretical thresholds predicted using a three-current (IK1, INCX, and INaK) system, with INaK adding a small quantitative increase in the outward current. Because the Ca2+ transient is a Gaussian function instead of a constant value, the Ca2+ threshold at steady state is slightly above the theoretically predicted values. (B) Ca2+ amplitude threshold for TA versus the intracellular Na+ concentration [Na+]i. Lower [Na+]i values result in a lower Ca2+ threshold. (C) Equilibrium voltage versus steady-state Ca2+ concentration under different conditions: control (black); reduced IK1 only (magenta); left-shifted EK only (cyan); and hypokalemia (red). Note how the dynamical threshold shifts with each condition. (D) Ca2+ threshold results from simulations using the AP model under the same conditions in (C). Both the left shift of EK as well as the reduced IK1 peak conductance lower the Ca2+ threshold to elicit an AP. This can be predicted by the different dynamical thresholds in each condition as seen in (C). To see this figure in color, go online.
As INCX and INaK both depend on the intracellular Na+ concentration of the myocyte, we investigated the effect of [Na+]i on the TA threshold. Fig. 6 B shows that lower [Na+]i lowers the TA threshold, while higher [Na+]i increases the threshold. This can be explained by the two diastolic currents that [Na+]i affects: INaK and INCX. At higher [Na+]i, INaK contributes to a slightly higher effective IK1 peak through the INaK contribution, while INCX is reduced. Both of these factors would serve to make TA more difficult, requiring a higher Ca2+ transient amplitude. With lower [Na+]i the opposite occurs, with INaK resulting in a slightly lower effective IK1 peak with increased INCX, allowing TA to occur more easily at a lower Ca2+ transient amplitude. Note that these simulations only studied the effect of changing [Na+]i with a given Ca2+ transient, and did not take into account any Ca2+ loading effects caused by the changes in [Na+]i.
Finally, to sort out the effects of lowered resting potential and reduced IK1 conductance caused by hypokalemia, we carried out simulations under four conditions: 1) control (normokalemia); 2) reduced IK1 conductance only; 3) left shift of IK1 through EK only; and 4) both reduced IK1 conductance and left shift of EK (hypokalemia). Fig. 6 C shows the steady-state equilibrium voltage versus Ca2+ obtained using the simple system described by only IK1 and INCX (Eq. 17), which shows that the reduction of IK1 conductance and the left shift of EK alone both resulted in similar lowered Ca2+ and voltage dynamical thresholds to elicit an AP. These predictions agreed with our simulation results (Fig. 6 D) using the AP model.
TA and PVC suppression by blocking INa
The theoretical analyses above and experiments shown in Fig. 4 suggest that even in the absence of INa, the voltage will depolarize automatically beyond the ICa,L threshold near −40 mV to elicit an AP as long as the Ca2+ amplitude and duration exceed the dynamical threshold. This implies that blocking INa may not be effective in suppressing TA. To demonstrate this effect, we carried out simulations in a single isolated myocyte by reducing the maximum conductance of INa from 12 mS/μF (the control value) to zero and determined the corresponding Ca2+ transient amplitude threshold for TA (Fig. 7 A). For normokalemia, the Ca2+ threshold increased slightly as gNa was reduced from 12 to 6 mS/μF (the Ca2+ threshold was increased from 1.1 to 1.25 μM), then exhibited a faster increase as gNa was reduced from 6 to 3 mS/μF (the Ca2+ threshold was increased from 1.25 to 1.6 μM), and then saturated as gNa was finally reduced from 3 to 0 mS/μF. For hypokalemia ([K+]o = 2.7 mM), the Ca2+ threshold remained almost the same until gNa was reduced to 4 mS/μF from which the Ca2+ threshold was increased abruptly from 0.7 to 1.8 μM and then saturated. In both cases, the rapid increase in Ca2+ threshold as INa conductance decreases indicates the transition from an INa-mediated upstroke to a slower ICa,L-mediated upstroke, because it takes more time to reach the ICa,L threshold. Fig. 7 B shows AP and Ca2+ traces when INa = 0.
Figure 7.

Effects of INa blockade on TA in a single isolated myocyte. (A) Submembrane Ca2+ transient threshold for TA versus gNa in normokalemia (black) and hypokalemia (red). For most gNa values, the Ca2+ threshold for TA is lower in hypokalemia than in normokalemia. (B) Voltage and Ca2+ traces for Ca2+ transients just above threshold with gNa = 0, under normokalemic (black) and hypokalemic conditions (red). Due to the dynamical threshold automatically driving the voltage to the ICa,L threshold, we still can elicit a slow upstroke AP with complete INa block. To see this figure in color, go online.
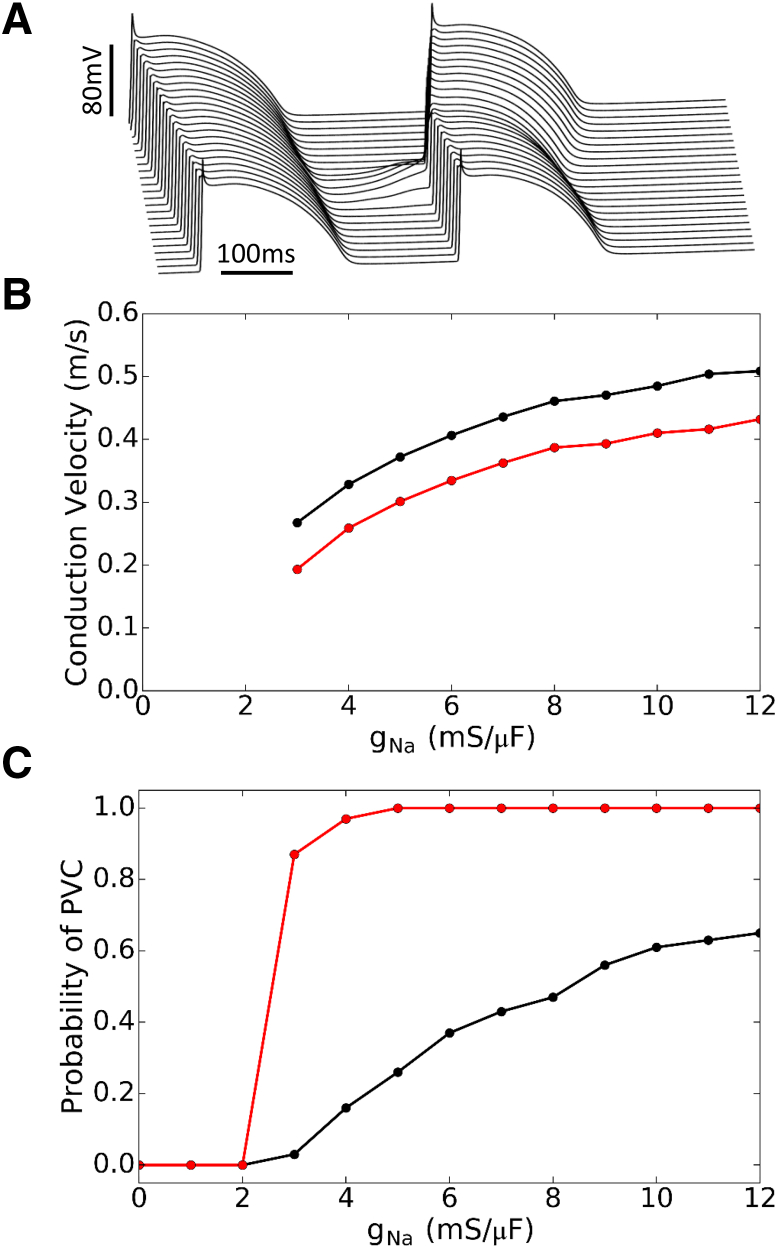
Although these results demonstrated that INa is not necessary for TA in single myocytes, whether this is also true for TA-mediated PVCs in tissue was still unclear. To investigate the effect of INa block in cardiac tissue, we simulated a cable of 500 coupled myocytes with a central region of 40 cells exhibiting DADs of the same Ca2+ release strength but with different random latencies drawn from a Gaussian distribution (see Liu et al. (22) for more details of the method), as in Fig. 8 A. For the control gNa value (12 mS/μF), the conduction velocity for AP conduction is ∼0.05 cm/ms for normokalemia and 0.042 cm/ms for hypokalemia, which decreases as gNa is lowered until gNa = 3 mS/μF, after which conduction completely fails (Fig. 8 B). As expected, hypokalemia reduces excitability and thus slows conduction.
Figure 8.
Suppression of PVCs in tissue by INa blockade. (A) Representative voltage traces for a 1D cable of 200 cells with a region of 40 cells in the center exhibiting DADs with a release strength gspon = 0.250 ms−1 whose random latencies were drawn from a Gaussian distribution with time to onset t0,onset = 300 ms and standard deviation σlatency = 50 ms. See Liu et al. (22) for details. Note also that in Liu et al. (22), t0 corresponds to the Ca2+ release onset (t0,onset), not the Ca2+ transient peak as in this article. This particular example shows a paced beat propagating through the entire cable, followed by the central region exhibiting suprathreshold DADs that trigger a propagating PVC. (B) Conduction velocity versus gNa for normokalemia (black) and hypokalemia (red). Conduction failure occurs for gNa < 3 mS/μF. (C) The probability of PVC occurring in the cable (100 random simulations per data point) versus gNa for normokalemia (black) and hypokalemia (red). For a fixed strength of spontaneous Ca2+ release in the DAD region, the probability of PVCs gradually decreased with lowered gNa in normokalemia, but remained high in hypokalemia until conduction failure occurred. To see this figure in color, go online.
We then calculated the probability of a PVC occurring in the cable at different levels of gNa in normokalemia and hypokalemia (Fig. 8 C). For control gNa with this distribution of Ca2+ release strengths, the probability of PVC is ∼65% in normokalemia but almost 100% in hypokalemia. In normokalemia, the probability of PVC decreased as INa decreased, which drops to near zero at gNa = 3 mS/μF. In hypokalemia, however, the probability of PVC exhibited almost no change until gNa was reduced to 3 mS/μF and then dropped rapidly to zero at gNa = 2 mS/μF. In both cases, the probability of PVC became zero only when INa is too small (gNa = 2 mS/μF) to support conduction at all in the cable (Fig. 8 B). Note that we used the same Ca2+ release strength for both hypokalemia and normokalemia, and because the Ca2+ threshold in hypokalemia is much lower than in normokalemia, the peak Ca2+ values were already much higher than the TA threshold in hypokalemia. Because of this, the Ca2+ transient in hypokalemia is strong enough to depolarize the voltage in the DAD region above the threshold for TA no matter how much INa is available, as long as there is enough INa strength for successful conduction (gNa > 2 mS/μF). If one used a lower Ca2+ release strength distribution, the probability of PVC would have a stronger dependence on INa, as shown in the normokalemia case. Therefore, at the tissue-scale, blocking INa can still suppress Ca2+-mediated PVCs as long as the Ca2+ transient is not much higher than the Ca2+ threshold for TA.
Discussion
In this study, we investigated the voltage threshold for eliciting an AP by current pulses and DADs in ventricular myocytes. We show that a short current pulse must provide enough charge movement to directly depolarize the membrane potential to the INa threshold near −60 mV to elicit a rapid AP upstroke. Therefore, when the resting potential is hyperpolarized and lies further away from the INa threshold, such as during hypokalemia, a stronger stimulus is required to elicit an AP, i.e., the excitability of a myocyte is reduced and conduction velocity in tissue is slower (1, 2, 3). However, during a long current pulse or a DAD, the threshold for triggering an AP is different. While the membrane voltage must eventually reach the INa threshold to trigger a rapid AP upstroke, the true threshold for TA is a dynamical threshold. In the case of a DAD, this dynamical threshold is mainly determined by IK1 and INCX (with INaK adding a small quantitative contribution, ∼20% of the effective peak IK1) manifesting as a saddle-node bifurcation in which the dynamical threshold is the bifurcation point. The dynamical threshold occurs at a lower voltage than the INa threshold during both normokalemia and hypokalemia. Once intracellular Ca2+ rises and activates sufficient INCX to depolarize the myocyte past the dynamical threshold, the voltage continues to automatically depolarize to above the INa threshold due to a steep negative slope of the IK1-V curve. Thus, despite decreased excitability in response to short current pulses, DAD-mediated TA is facilitated by hypokalemia due to the lower dynamical threshold. The nonlinear dynamical analysis shows that the lower dynamical threshold results from a reduced IK1 conductance, a well-known factor that promotes (DAD)-mediated TA (6, 7, 8), and from a left shift of EK, such that a smaller Ca2+ transient is able to induce TA. Thus, the lower dynamical threshold interacts synergistically with another key effect of hypokalemia, Na+-K+ pump inhibition causing intracellular Ca2+ overload (16, 17) and spontaneous diastolic Ca2+ release, to promote DAD-mediated TA. Because the voltage can automatically depolarize above the INa threshold to reach ICa,L threshold after passing the saddle-node bifurcation point (or the dynamical threshold), triggered APs can occur in single myocytes in the absence of INa, suggesting that blocking INa may not be effective at suppressing TA. However, because INa is important for AP propagation in tissue, blocking INa can still suppress PVCs in cardiac tissue caused by Ca2+-mediated TA.
Our findings expand on the previous work of Greene and Shiferaw (18), who demonstrated analytically that the threshold for AP excitation caused by a steady-state constant current pulse is lower than the INa threshold near the voltage at which IK1 is maximum. In addition to experimentally validating this prediction in isolated myocytes and extending the findings to hypokalemia, we performed a detailed analysis of the nonlinear dynamics for DAD-mediated TA by considering a simple system incorporating the two currents most important in determining diastolic voltage, i.e., the IK1-INCX system. We showed that the two-current system can exhibit bistability and undergoes a saddle-node bifurcation that determines the dynamical threshold. Besides the existence of a dynamical threshold, the nonlinear dynamics also predicts the following:
-
1)
Once the voltage is above the dynamical threshold, the Ca2+ concentration does not necessarily need to increase further to depolarize the voltage to the INa threshold. The voltage can still automatically depolarize further even if Ca2+ decreases during this phase (Fig. 5 C), as long as the rate of decrease in INCX is not faster than the decrease in IK1 as voltage rises to the INa threshold.
-
2)
The position of the upper equilibrium point is an important factor governing the automatic phase of depolarization beyond the dynamical threshold, affecting the efficiency at which the myocyte reaches the INa or ICa,L threshold. Note that in the constant stimulus current case as analyzed in this study and by Greene and Shiferaw (18), the upper equilibrium point does not exist. The upper equilibrium is mainly determined by INCX. It is obvious that the higher the upper equilibrium, the easier for the system to depolarize to the INa or ICa,L threshold. For example, increasing the magnitude of INCX (by simply increasing the INCX amplitude) has little effect on elevating the upper equilibrium point (although it can have an effect on lowering the dynamical threshold) because this only tilts the INCX curve more steeply to affect the saddle-node bifurcation point. In contrast, increasing Ca2+ concentration can have a large effect on both the dynamical threshold and the upper equilibrium point, because in addition to tilting INCX, a larger Ca2+ also shifts the INCX curve to the right, increasing the margin between the INCX and IK1 curves. This steep tilt and right shift of INCX effectively makes it easier to depolarize the voltage above the INa or ICa,L threshold. Similarly, reducing IK1 conductance can also lower the dynamical threshold but will have little effect on the upper equilibrium point.
In conclusion, using nonlinear dynamics and patch-clamp experiments, we have demonstrated the existence of a dynamical threshold for DAD-mediated TA, which is lower than the INa threshold. The dynamical threshold is further lowered by hypokalemia, facilitating DAD-mediated TA by hypokalemia. Our dynamical analysis and computer simulation have demonstrated distinct roles of Ca2+, IK1, INCX, and INa in potentiating DAD-mediated TA, which not only provide important insights into the mechanism of DAD-mediated TA but also useful information for future development of antiarrhythmic therapies.
Author Contributions
M.B.L., Z.S., J.N.W., and Z.Q. conceived the study; M.B.L. and Z.Q. developed the theory, designed the simulations, and wrote the article; M.B.L. performed the simulations; C.Y.K. and J.N.W. designed and performed the experiments; and all authors analyzed the data and commented on the article.
Acknowledgments
Supported by National Heart, Lung and Blood Institute grant No. P01 HL078931; UCLA MCIP institutional training grants No. T32 GM065823 (to M.B.L.) and No. T32 HL07895 (to C.Y.K.); American Heart Association predoctoral fellowship No. 16PRE27610040 (to M.B.L.); and the Laubisch and Kawata endowments.
Editor: Godfrey Smith.
Footnotes
Michael B. Liu and Christopher Y. Ko contributed equally to this article.
References
- 1.Kagiyama Y., Hill J.L., Gettes L.S. Interaction of acidosis and increased extracellular potassium on action potential characteristics and conduction in guinea pig ventricular muscle. Circ. Res. 1982;51:614–623. doi: 10.1161/01.res.51.5.614. [DOI] [PubMed] [Google Scholar]
- 2.Shaw R.M., Rudy Y. Electrophysiologic effects of acute myocardial ischemia. A mechanistic investigation of action potential conduction and conduction failure. Circ. Res. 1997;80:124–138. doi: 10.1161/01.res.80.1.124. [DOI] [PubMed] [Google Scholar]
- 3.Xie Y., Garfinkel A., Qu Z. Effects of fibroblast-myocyte coupling on cardiac conduction and vulnerability to reentry: a computational study. Heart Rhythm. 2009;6:1641–1649. doi: 10.1016/j.hrthm.2009.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Miake J., Marbán E., Nuss H.B. Biological pacemaker created by gene transfer. Nature. 2002;419:132–133. doi: 10.1038/419132b. [DOI] [PubMed] [Google Scholar]
- 5.Silva J., Rudy Y. Mechanism of pacemaking in IK1-downregulated myocytes. Circ. Res. 2003;92:261–263. doi: 10.1161/01.RES.0000057996.20414.C6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schlotthauer K., Bers D.M. Sarcoplasmic reticulum Ca2+ release causes myocyte depolarization. Underlying mechanism and threshold for triggered action potentials. Circ. Res. 2000;87:774–780. doi: 10.1161/01.res.87.9.774. [DOI] [PubMed] [Google Scholar]
- 7.Pogwizd S.M., Schlotthauer K., Bers D.M. Arrhythmogenesis and contractile dysfunction in heart failure: roles of sodium-calcium exchange, inward rectifier potassium current, and residual β-adrenergic responsiveness. Circ. Res. 2001;88:1159–1167. doi: 10.1161/hh1101.091193. [DOI] [PubMed] [Google Scholar]
- 8.Maruyama M., Joung B., Chen P.S. Diastolic intracellular calcium-membrane voltage coupling gain and postshock arrhythmias: role of Purkinje fibers and triggered activity. Circ. Res. 2010;106:399–408. doi: 10.1161/CIRCRESAHA.109.211292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rosen M.R., Moak J.P., Damiano B. The clinical relevance of afterdepolarizations. Ann. N. Y. Acad. Sci. 1984;427:84–93. doi: 10.1111/j.1749-6632.1984.tb20776.x. [DOI] [PubMed] [Google Scholar]
- 10.January C.T., Fozzard H.A. Delayed afterdepolarizations in heart muscle: mechanisms and relevance. Pharmacol. Rev. 1988;40:219–227. [PubMed] [Google Scholar]
- 11.Marban E., Robinson S.W., Wier W.G. Mechanisms of arrhythmogenic delayed and early afterdepolarizations in ferret ventricular muscle. J. Clin. Invest. 1986;78:1185–1192. doi: 10.1172/JCI112701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ter Keurs H.E.D.J., Boyden P.A. Calcium and arrhythmogenesis. Physiol. Rev. 2007;87:457–506. doi: 10.1152/physrev.00011.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Katra R.P., Laurita K.R. Cellular mechanism of calcium-mediated triggered activity in the heart. Circ. Res. 2005;96:535–542. doi: 10.1161/01.RES.0000159387.00749.3c. [DOI] [PubMed] [Google Scholar]
- 14.Yeh Y.H., Wakili R., Nattel S. Calcium-handling abnormalities underlying atrial arrhythmogenesis and contractile dysfunction in dogs with congestive heart failure. Circ. Arrhythm. Electrophysiol. 2008;1:93–102. doi: 10.1161/CIRCEP.107.754788. [DOI] [PubMed] [Google Scholar]
- 15.Morita H., Zipes D.P., Wu J. Mechanism of U wave and polymorphic ventricular tachycardia in a canine tissue model of Andersen-Tawil syndrome. Cardiovasc. Res. 2007;75:510–518. doi: 10.1016/j.cardiores.2007.04.028. [DOI] [PubMed] [Google Scholar]
- 16.Pezhouman A., Singh N., Weiss J.N. Molecular basis of hypokalemia-induced ventricular fibrillation. Circulation. 2015;132:1528–1537. doi: 10.1161/CIRCULATIONAHA.115.016217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aronsen J.M., Skogestad J., Sjaastad I. Hypokalaemia induces Ca2+ overload and Ca2+ waves in ventricular myocytes by reducing Na+,K+-ATPase α2 activity. J. Physiol. 2015;593:1509–1521. doi: 10.1113/jphysiol.2014.279893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Greene D., Shiferaw Y. Approximate analytical solutions for excitation and propagation in cardiac tissue. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2015;91:042719. doi: 10.1103/PhysRevE.91.042719. [DOI] [PubMed] [Google Scholar]
- 19.Scaringi J.A., Rosa A.O., Cleemann L. A new method to detect rapid oxygen changes around cells: how quickly do calcium channels sense oxygen in cardiomyocytes? J. Appl. Physiol. 2013;115:1855–1861. doi: 10.1152/japplphysiol.00770.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mahajan A., Shiferaw Y., Weiss J.N. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys. J. 2008;94:392–410. doi: 10.1529/biophysj.106.98160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xie Y., Sato D., Weiss J.N. So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys. J. 2010;99:1408–1415. doi: 10.1016/j.bpj.2010.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu M.B., de Lange E., Qu Z. Delayed afterdepolarizations generate both triggers and a vulnerable substrate promoting reentry in cardiac tissue. Heart Rhythm. 2015;12:2115–2124. doi: 10.1016/j.hrthm.2015.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Baer M., Best P.M., Reuter H. Voltage-dependent action of tetrodotoxin in mammalian cardiac muscle. Nature. 1976;263:344–345. doi: 10.1038/263344a0. [DOI] [PubMed] [Google Scholar]
- 24.Cohen C.J., Bean B.P., Tsien R.W. Tetrodotoxin block of sodium channels in rabbit Purkinje fibers. Interactions between toxin binding and channel gating. J. Gen. Physiol. 1981;78:383–411. doi: 10.1085/jgp.78.4.383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Carmeliet E. Voltage-dependent block by tetrodotoxin of the sodium channel in rabbit cardiac Purkinje fibers. Biophys. J. 1987;51:109–114. doi: 10.1016/S0006-3495(87)83315-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Strogatz S.H. Westview Press; Cambridge, UK: 2000. Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. [Google Scholar]
- 27.Ko C.Y., Song Z., Weiss J.N. Multiscale consequences of spontaneous calcium release on cardiac delayed afterdepolarizations. Biophys. J. 2015;108:264a. doi: 10.1016/j.bpj.2015.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]