Abstract
Electromotility of outer hair cells (OHCs) has been extensively studied with in vitro experiments because of its physiological significance to the cochlear amplifier, which provides the exquisite sensitivity and frequency selectivity of the mammalian ear. However, these studies have been performed largely under load-free conditions or with static load, while these cells function in vivo in a dynamic environment, receiving electrical energy to enhance mechanical oscillation in the inner ear. This gap leaves uncertainties in addressing a key issue, how much mechanical energy an OHC provides. This study is an attempt of bridging the gap by introducing a simple one-dimensional model for electromotility of OHC in a dynamic environment. This model incorporates a feedback loop involving the receptor potential and the mechanical load on OHC, and leads to an analytical expression for the membrane capacitance, which explicitly describes the dependence on the elastic load, viscous drag, and the mass. The derived equation of motion was examined in a mass-less model system with realistic parameter values for OHC. It was found that viscous drag is more effective than elastic load in enhancing the receptor potential that drives the cell. For this reason, it is expected that OHCs are more effective in counteracting viscous drag than providing elastic energy to the system.
Introduction
In recent years, considerable progress has been made in understanding the mechanism of prestin-based somatic motility, or “electromotility,” of outer hair cells (OHCs) in the cochlea on both the cellular (1, 2, 3) and molecular levels (4, 5, 6), clarifying its physical basis, which is electromechanical coupling (7, 8, 9). For example, experiments on isolated OHCs have determined load-free displacement (1, 2) and isometric force production (10, 11). These experimental observations can be described by static models (9, 12). Nonetheless, these are the conditions under which those cells do not provide energy. Some theoretical works have addressed energy production by OHCs (13, 14) by extrapolating from these in vitro conditions. However, these analyses do not provide an equation of motion or the dependence of nonlinear capacitance on external mechanical load, the essential features to describe the production of mechanical energy for amplifying acoustic signal.
There are a number of issues to be addressed for describing OHCs in a dynamic environment. One such issue is the frequency dependence of the motile response. The amplitude of displacement in response to voltage changes rolls off at ∼15 kHz under load-free condition, whereas force production near isometric condition remains flat up to 60 kHz (15). This difference likely indicates that the frequency response depends on the mechanical load, more specifically viscoelastic drag.
Another issue is attenuation of the receptor potential by the membrane capacitance at operating frequencies (16, 17, 18). The membrane capacitance consists of two main components. One is structural and is proportional to the membrane area. Another is a nonlinear component associated with the mobile charge of prestin, which flips in the electric field on conformational changes. Nonlinear capacitance has been described under load-free conditions, at which it is expected to be the largest. Since constraint on the membrane area almost eliminates the nonlinear component (19), it could be expected that external load reduces this component and thus reduces capacitive current, which attenuates the receptor potential at higher frequencies. This feedback would improve the performance of OHCs, particularly at high frequencies. This effect still needs to be described quantitatively. Previous treatments used either load-free capacitance (16, 20, 21, 22) or the linear capacitance alone (17, 18).
This study presents a model for describing the motion of a single OHC under mechanical loads. In the following, the basic equations are derived. That is followed by derivations of the quantities that characterize the motile element. These quantities are determined using experimental values for OHC that operates at 4 kHz. Then the balance of energy input and output is examined for those cells under mass-free condition. The implications are discussed on those cells that operate at higher frequencies.
The model
Here we consider a simple system, which consists of an OHC, elastic load, drag, and a mass (Fig. 1). This is not to approximate the organ of Corti, but to describe an OHC, which is subjected to mechanical load. This system with a single degree of freedom is described by writing down the equations for the motile mechanism, the receptor potential, and the equation of motion. These equations are interrelated and constitute a set of simultaneous equations, which are examined in the subsequent sections.
Figure 1.
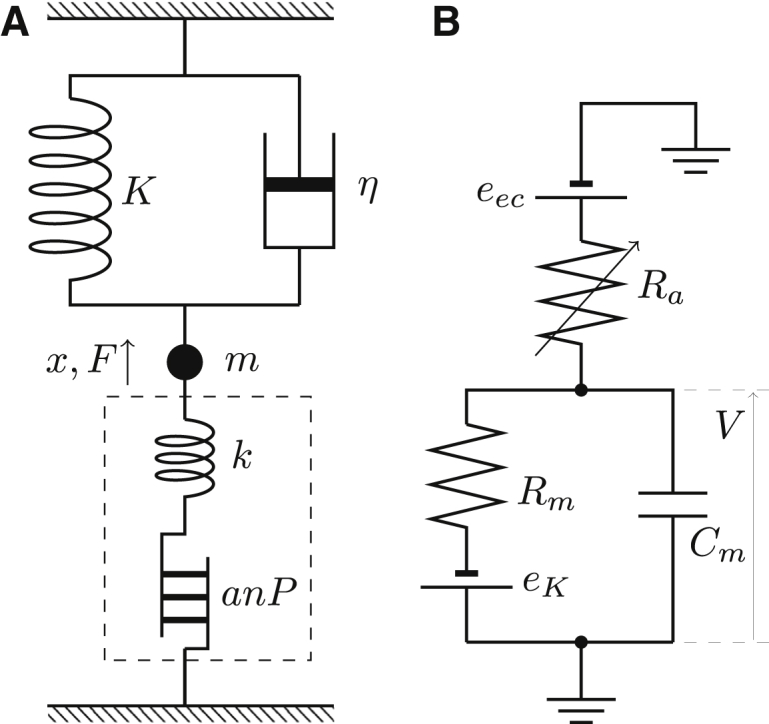
Mechanical connectivity and the equivalent electric circuit of the system examined. The system is driven by changes in hair bundle conductance Ra. Unlike in vivo condition, movement of the cell body does not affect Ra. In the mechanical schematics (A), K is stiffness of the external mechanical load, m is the mass, and positive force F and positive displacement x of the cell are upward. The drag coefficient is η. The contribution of the motile element to cell length is anP, where P, a, and n respectively represent the fraction of the motile elements in the elongated state, unitary length change, and the number of such units, the unitary change of charge of which is q. The stiffness of the cell due to the material property alone is k. The broken line indicates the border of the OHC. In the equivalent circuit (B) of the hair cell, the membrane potential is V, the hair bundle resistance is Ra, the basolateral resistance is Rm, and the total membrane capacitance of the basolateral membrane is Cm, consisting of the structural capacitance C0 and the contribution of charge movements in the motile element, which depends on the load (described in the section on nonlinear capacitance). The endocochlear potential is eec and the potential eK is due to K+ permeability of the basolateral membrane. The apical capacitance is ignored in this model.
The motile mechanism
The OHCs have a motile mechanism driven by the membrane potential based on mechanoelectric coupling. Here, a one-dimensional model is used instead of a membrane model (9) for simplicity. We assume that the cell has n motile elements, which has two discrete states (compact and extended), and, during a transition from the compact state to the extended state, the cell length increases by a and the electric charge q flips across the plasma membrane. Let P be the fraction of the motile units in the extended state. Its equilibrium value P∞ follows the following Boltzmann distribution:
| (1) |
with , where kB is Boltzmann’s constant, T is the temperature, and
| (2) |
represents the difference in the free energy in the two states, referenced to the compact state. Here F is the force applied in the direction of extending the cell and V is the membrane potential. The quantity is a constant that determines the operating point. Here both q and a are positive because rising membrane potential and decreasing extensive force increases ΔG, and thus reduces the fraction P∞ of the extended state.
Now consider a case, in which the motile mechanism is connected to an external elastic element (Fig. 1, without the mass or the dashpot). The force F applied to the cell depends on the elastic elements as well as the conformational change of the motile element elicited to the voltage change. The elastic elements include the material stiffness k of the cell as well as an external elastic load K. Assume that at the membrane potential V changed from its resting value V0. The resulting displacement x of the cell produces force F on the external spring. The same force is applied to the cell reciprocally, producing a displacement . Thus the displacement x is determined from , where the fraction P of the extended state, is changed from its resting value P0. This change is expressed by
| (3) |
| (4) |
with effective spring constant . Notice that an increase in P, which increases x, generates force in the contracting direction and that the maximal value of is k. This force F is applied to the motile element in the cell. This leads to the following expression for the difference ΔG in the free energy of the two states:
| (5) |
Notice here that an increase in P increases the energy , making a further increase less favorable. If the system is in equilibrium, P = P∞ and the equilibrium value of P∞ is determined by combining Eq. 1 with Eq. 5, in which P is substituted with P∞. Under this condition, all forces are balanced and no movement takes place.
Here we notice that ΔG, and therefore P∞, can be determined for any set of V and P by combining Eqs. 1 and 5. Since P − P∞ = 0 in equilibrium, the difference P − P∞ quantifies the deviation from equilibrium that drives the cell.
For this reason, it is useful to redefine the quantity P∞ as the target value for the fraction P of the extended state for a given set of values for P and V. In a special case in which P∞, as given by Eq. 1 with Eq. 5, happens to be identical to P, the system is in equilibrium and no changes take place. Otherwise the system continuously undergoes changes to achieve P = P∞. That process is governed by an equation of motion as described in the next section.
Equation of motion
Now we examine how to describe the movement of the cell, which has mechanical loads (Fig. 1). The system has a single degree of freedom and is described by using length displacement x of the cell as the variable. What is the force that drives the cell?
Let the displacement be fixed at x and the state of the motile element be P∞ in the beginning. Suppose the membrane potential suddenly changes at a certain moment. The cell generates force that moves the cell. The force that drive the cell is if the stiffness of the cell is k and if P∞ − P is small enough so that the linear term is dominant. Even though the motile element contributes to reduce the stiffness from the intrinsic stiffness k, we confirm below that this is indeed a good approximation for a set of parameter values that we use. Then, the equation of motion should be
| (6) |
where η is the drag coefficient, and m is the mass.
For a given displacement x, P can be given by Eq. 3. Since P0 is a time-independent constant, its time derivatives does not contribute. The equation of motion can then be expressed,
| (7) |
Notice that a factor k × na drops out from the equation because it is shared by all terms. In the special case of m = 0, Eq. 7 turns into a relaxation equation with a time constant , which is intuitive.
Receptor potential
The motile response of the cell is driven by the receptor potential, generated by the receptor current, which is, in turn, elicited by changes in the hair bundle resistance by mechanical stimulation. This current is driven by the sum of two electromotive forces. One is eK, which is primarily determined by the K+ conductance of the basolateral membrane of the cell. The other is the endocochlear potential eec, which is generated by the stria vascularis, a tissue that lines a part of the scala media (Fig. 1 B).
The magnitude of the receptor potential is determined not only by changes in the hair bundle conductance but also by the basolateral conductance because the electric current through the apical membrane must be equal to the current through the basolateral membrane. Changes in the membrane potential elicit not only ionic currents but also a capacitive current proportional to the regular capacitance in the basolateral membrane. In addition, they flip the charge of the motile units, produces an additional current, similar to the capacitive current. Thus, Kirchhoff’s law leads to
| (8) |
Here Ra is the apical membrane resistance, which is dominated by mechanotransducer channels in the hair bundle. The basolateral membrane has the resistance Rm and the linear capacitance C0, which is determined by the membrane area and the specific membrane capacitance of ∼10−2 F/m2 for biological membranes (23, 24). The apical membrane capacitance is ignored for simplicity.
The last term on the right-hand side of Eq. 8 is an additional displacement current due to the charge movement in the motile elements. It has the negative sign because a voltage increase results in a decrease in P as mentioned above. As we will see below, nonlinear capacitance appears from this term.
Results
Characterization of motile element
In the following, experimentally observable quantities are derived from the model so that values for the cellular parameters can be determined from experimental data.
Load-free displacement
Length changes of OHCs have been quantified by changing the membrane potential gradually or stepwise while measuring cell length without load. That corresponds to describing P∞ as a function of V under the condition of K = 0. Thus, Eq. 1 is accompanied by instead of Eq. 5. This equation has the same form as the one that has been used for fit experimental data (1).
Isometric force generation
Isometric force generation per voltage changes can be obtained by evaluating from the equation with Eq. 1 and for a given displacement x. This leads to
| (9) |
with . The dependence on length displacement x enters through the value of P∞. The maximum value is at .
Axial stiffness
The effective compliance of the cell can be determined by dx/dF for a given voltage V. If we introduce the effective stiffness , this leads to
| (10) |
Thus, the minimal value of the effective stiffness is at .
Nonlinear capacitance
Another characteristic quantity that described the motile element is a contribution of the motile element to the membrane capacitance, which is often referred to as nonlinear capacitance. We consider small periodic changes with amplitude v in the membrane potential on top of a constant value
| (11) |
Then the fraction P of the extended state and its target value P∞ can be described by
| (12) |
| (13) |
where the variables expressed in lower case letters are small and those marked with bars on top are time independent. Under time-independent conditions, and are expressed by Eq. 1 with ΔG, in which P is replaced by .
If the amplitude v is small, we can ignore second-order terms, Eqs. 1 and 7, respectively, which leads to
| (14) |
| (15) |
These equations then lead to
| (16) |
with constants ωη, ωr, and γ, which respectively characterize viscoelasticity, resonance, and the operating point:
The capacitive current due to voltage changes is , which also should be expressed as using a component Cnl of the membrane capacitance. Hence, because conformational change p of each motile element carries charge q and the cell has n such elements. The membrane capacitance Cm is the sum of Cnl and the structural capacitance C0 due primarily to lipid bilayer of the plasma membrane.
In the following, the contribution to the capacitance is examined. The order is from the most restricted case, where this quantity is better studied, to more general cases.
Mass-free and drag-free condition: m = 0, η = 0
Let us start with the simplest case, where m → 0 and η → 0. This leads to the total membrane capacitance Cm, expressed by
| (17) |
Letting or a → 0, we recover the familiar expression for the membrane capacitance of outer hair cells Cm = C0 + γnq2 under load-free condition (2, 25). In addition, this expression shows that nonlinear capacitance decreases with increasing elastic load. That is consistent with intuition that constraints on the cell length reduce nonlinear capacitance. In an extreme limit in which a rigid load does not allow transitions of the motor elements, the nonlinear component diminishes. This expectation is consistent with greatly diminished nonlinear capacitance observed in rounded OHCs with a constrained membrane area (19).
Mass-free condition: m = 0
We now proceed to a more general case in which the viscous term does not disappear. The total membrane capacitance Cm is expressed as
| (18) |
As expected, in the limit of low frequency, this expression turns into Eq. 17. In the limit of a → 0, it leads to the expression of the frequency dependence of nonlinear capacitance that was previously derived based on an assumption that transition rates between the states are intrinsic (26). This functional dependence supports the interpretation that the experimentally observed frequency roll-off (27, 28) of the membrane capacitance is indeed the result of viscoelastic relaxation (25, 28). It should be noted that the imaginary part of p contributes to the conductance. However, it diminishes in both low frequency limit and high frequency limit.
Mechanical resonance
A similar evaluation of nonlinear capacitance can be performed for a system with nonzero mass, which has mechanical resonance. The quantity p is expressed by
| (19) |
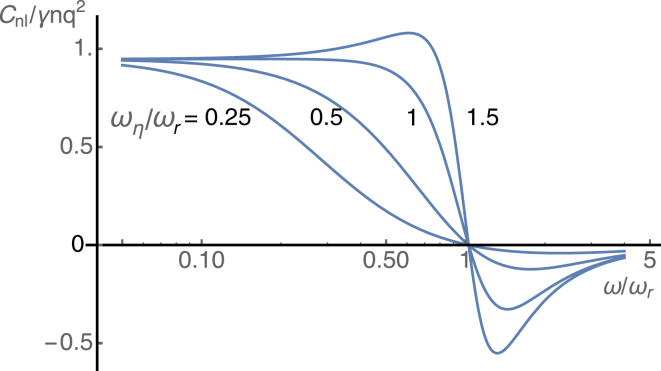
Under the condition ωr ≫ ω, Eq. 18 can be obtained. It should be noted that nonlinear capacitance disappears and Cm = C0 at . In addition, the capacitance becomes quite singular near this resonance frequency as the characteristic frequency ωη of viscoelasticity exceeds the resonance frequency ωr (Fig. 2). A reduction in the capacitance Cm near resonance leads to an increase in the receptor potential because it reduces the attenuation due to the resistance-capacitance (RC) circuit in the cell. That is analogous to piezoelectric resonance.
Figure 2.
Contribution Cnl to the membrane capacitance in the presence of mechanical resonance. The capacitance normalized to its maximum value γnq2 is plotted against the ratio of the frequency ω to the resonance frequency ωr. The plots correspond, respectively, to = 0.25, 0.5, 1, and 1.5 by changing either the drag coefficient η or the mass m, while keeping the elastic load K constant. The value for is assumed to be 0.05. To see this figure in color, go online.
Parameter values
Now we determine the parameters using experimental data. Those quantities important for determining the parameters are the amplitude an of the load-free mechanical displacement, which is between 4% and 5% of the cell length: the steepness of load-free mechanical displacement and nonlinear capacitance, both of which are characterized by q, and the number n of the motile elements in the cell, which is obtained by dividing the total charge movement Q divided by q. In addition, experimental values are available for the maximal value of nonlinear capacitance , the axial stiffness of the cell , and isometric force production dF/dV. The parameter values are listed in Table 1.
Table 1.
A Set of Parameter Values for Outer Hair Cells with 12 pF Linear Capacitance C0
| Parameter | Experimental | Used (Unit) | Remarks |
|---|---|---|---|
| eec | ∼90 | 90 (mV) | a |
| eK | −90 | −90 (mV) | a |
| C0 | 12 | 12 (pF) | (38) |
| Rm | 10 | 10 (MΩ) | (17) |
| Ra | ∼40 | 42 (MΩ) | (17) |
| Q | ∼0.8 | 0.8 (e) | b |
| n | ∼15 × 106 | 15 × 106 | b |
| An | 1.2 ± 0.1 | 0.96 (μm) | c |
| a | 6.4 × 10−5 (nm) | ||
| k | 0.016 (N/m) | ||
| Predicted | |||
| df/dV | 0.1 ± 0.04 | 0.11 (nN/V) | d |
| 0.017 ± 0.005 | 0.015 (N/m) | d | |
These values corresponds to OHCs from the region with best frequency of 4 kHz for rats and gerbils (17). The quantities in the five upper rows are electric circuit properties and those in the rest characterize the motile element. The values for resistances are from rats and values of motility-related parameters are from guinea pigs.
The sum of the endocochlear potential (eec ∼ 90 mV) (39) and the reversal potential (eK) of the basolateral membrane (∼−90 mV).
The unit mobile charge q (in the electronic charge e), and its number n have been determined by nonlinear component of the membrane capacitance.
The amplitude of load free displacement an is between 4% and 5% of the total length.
Both force generation and the elastic modulus do not show length dependence (11). The stiffness value corresponds the elastic modulus of 0.51 μN per unit strain for a 30 μm-long cell.
For numerical examination, we assume that the cell length of the OHC is 30 μm and that the motor is 40% in the elongated state in the natural length and the receptor potential is generated by 10% change in the resting hair bundle resistance Ra, which corresponds to the condition where 30% of the mechanotransducer channels are open.
Here we now examine the consistency with an assumption, which we made for deriving the equation of motion (Eq. 7). Recall that the minimal value of the stiffness of the motile element is at (Eq. 10). For this set of the parameter values, the value for this stiffness is 0.27 N/m, larger than 0.016 N/m for the intrinsic stiffness k. Thus this set of parameter values is consistent with the assumption made above.
The consistency of the one-dimensional model is tested by comparing its predicted values and experimental values for force generation dF/dV and the stiffness . The predicted values are within experimental errors (Table 1).
Response to small periodic stimulation
Here we assume small periodic changes with an angular frequency from a resting resistance of the following hair bundle resistance:
leads to the receptor potential . Eq. 8 leads to
| (20) |
with . The amplitude v of the potential leads to motile responses as described by p and p∞ in Eqs. 12–15.
The receptor potential with amplitude v, which is elicited by small periodic changes in the hair bundle resistance, induces changes in the amplitude p of changes in the fraction of the extended state of the motile element, resulting in displacements and force generation of the cell. Because of mechanoelectric coupling, the load on the motile element reciprocally affects p, which, in turn, attenuates the receptor potential v.
Examination of energy output
From here on, energy balance is examined for small periodic stimulation at the hair bundle in a mass-free system (m = 0) using the parameter values in Table 1, which corresponds to a best frequency of 4 kHz. The independent variables of the equations are r, the amplitude, and ω, the frequency of small periodic changes in the hair bundle resistance Ra. However, the receptor potential and energy output will be examined for a fixed small amplitude r because the focus of this study is the effect of mechanical load.
Nonzero mass introduces an additional time constant, requiring examining a larger number of cases. In addition, the mass may depends on the frequency because it may include fluid mass (29), and hair cell mass may not constitute a major part of the mass in vivo.
Dependence on elastic load
Before evaluating energy, it is useful to examine the membrane capacitance, which is the attenuating factor of the receptor potential. An external elastic load K affects the membrane capacitance through (see Eqs. 17 and 18). Since for K → ∞, the maximum value of this factor is at . For our set of parameter values, the maximum value of this factor is 0.11, indicating that this factor is rather small even though it is not negligible at low frequencies (ω ≪ ωη). For ω ≫ ωη, nonlinear capacitance diminishes and so does the effect of an elastic load on the membrane capacitance.
In the range where ω is comparable with the viscoelastic characteristic frequency ωη, however, the effect of the elastic load K appears mainly through the characteristic viscoelastic frequency . For a given frequency ω, an increase in the elastic load K increases ωη through and thus increases the capacitance Cm.
Energy output
In the following, energy output from OHC is examined assuming that the hair bundle is stimulated at a level at which hair bundle conductance undergoes changes with an amplitude 10% of the resting value, where the mechanochannels are assumed to be 30% open. Thus, the change is 3% of its maximal value. Parameter values are given in Table 1. This amplitude allows linearized approximation, Eqs. 14, 15, and 20. In this regime, energy output increases with the second power of the receptor potential.
The system has two characteristic frequencies, the frequency ωη of viscoelastic roll-off and the roll-off frequency of the RC circuit. Here the effect of the elastic load K is examined. The stiffness k of the cell has been determined by experiments (Table 1). Two characteristic frequencies of the system leads to two cases, which are examined here: ωη ≫ ωRC and ωη ∼ ωRC. It should be noticed, whereas ωRC is independent of K, ωη goes up as K increases. The energy Ee conveyed to the external elastic load K per half cycle can be obtained by evaluating and the work Ed against viscous drag per half cycle is .
Small viscous drag (ω ≪ ωη)
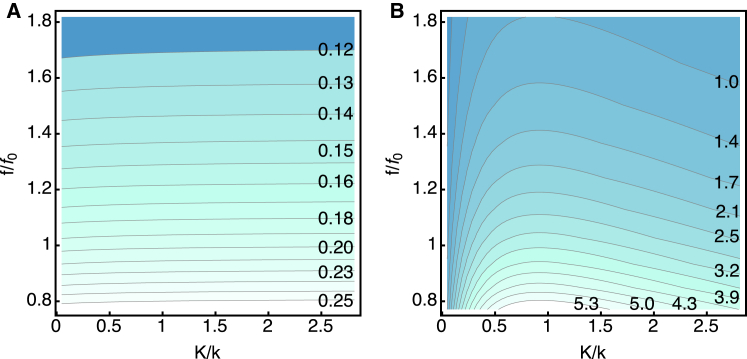
Here we examine a case in which the drag coefficient η is extremely small and viscous loss is negligible. Let η = 10−10 kg/s. This value satisfies the condition ωη ≫ ωRC except for diminishing K. This condition is satisfied even with increasing external elastic load K to ∼10k. At a given frequency, an increase in the amplitude of the receptor potential with increasing external elastic load K is too small to notice in the plot (Fig. 3 A). With a given elastic load, the amplitude of the receptor potential monotonically decreases with increasing frequency (Fig. 3 A).
Figure 3.
The effect of elastic load for small viscous drag (ωη ≫ ωRC). The dependences on the elastic load (the horizontal axis) and the frequency (the vertical axis) are shown as color-coded contour plots. Darker colors indicate lower values. Elastic load is described by the ratio K/k, where k is the intrinsic stiffness of the cell. Frequency is represented by the ratio f/f0, with f0 = 4 kHz, which corresponds to the parameter values of the cell given in Table 1. (A) The amplitude of the receptor potential. The values (in mV) are given in the plot. (B) The work against elastic load during a half cycle. The values (in zJ = 10–21 J) are given in the plot. η = 10–10 kg/s. To see this figure in color, go online.
The work against the elastic load is evaluated for a half cycle. For a given frequency, elastic energy output per half cycle has a maximum with respect to the external elastic load K at the load ratio K/k ≈ 1 (Fig. 3 B). The optimal ratio is not significantly affected by the frequency. Work output monotonically decreases with the frequency (Fig. 3 B). The plot also shows that decrease of energy with frequency is less steep at larger load. Asymmetry increases with increasing frequency, while the peak ratio K/k remains virtually unchanged.
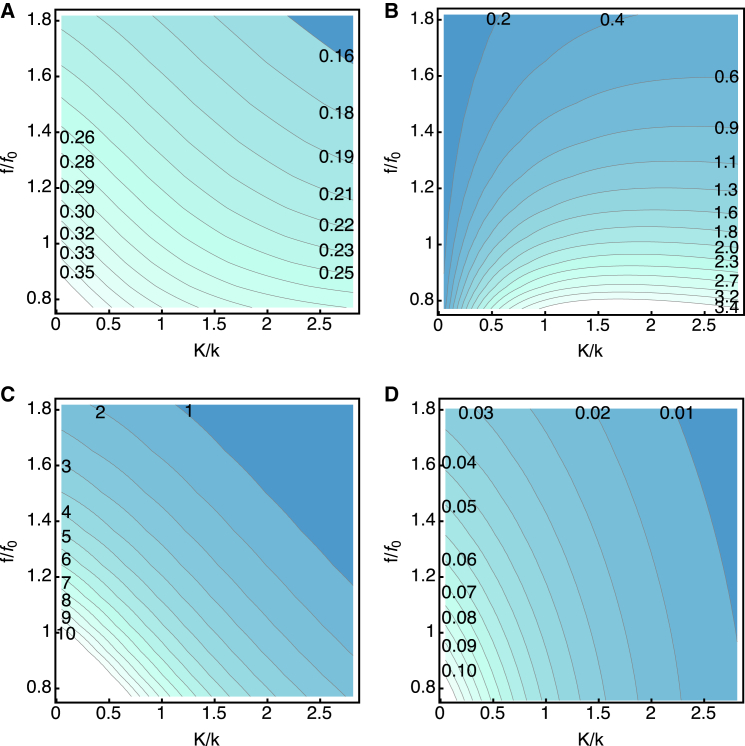
Larger viscous drag: ω ∼ ωη
If the viscous drag is larger, the receptor potential decreases with increasing stiffness ratio K/k for a given frequency (Fig. 4 A). This result may appear counterintuitive because it is the opposite of an increase, be it rather small, under the condition of small drag. This reversal is due to a change in the time constant. The membrane capacitance increases with increasing elastic load, owing to decreasing in Eq. 18. An increase in the membrane capacitance increases RC attenuation, resulting in a reduction of the receptor potential. The frequency dependence of the receptor potential is monotonic. However, smallest elastic load makes the slope steeper at higher frequencies (Fig. 4 A).
Figure 4.
The effect of elastic load for a larger drag (ωη ∼ ωRC). The dependences on the elastic load (the horizontal axis) and the frequency (the vertical axis) are shown as color-coded contour plots. Darker colors indicate lower values. Elastic load is described by the ratio K/k, where k is the intrinsic stiffness of the cell. Frequency is represented by the ratio f/f0, with f0 = 4 kHz, which corresponds to the parameter values of the cell given in Table 1. (A) Amplitude (in mV) of the receptor potential. (B) The work against the elastic load during a half cycle. The values are given in zJ (= 10–21 J). (C) The work (in zJ) against the viscous load during a half cycle. (D) Power output in fW (= 10–15 W) working against the viscous load. η = 2 × 10−6 kg/s.kg/s. To see this figure in color, go online.
The value of 2 × 10−6 g/s for the drag coefficient used in the plots is chosen to examine a condition, which nearly maximizes the work against viscous drag, as shown below. For each given frequency, the work against the elastic load has a maximum with respect to the stiffness ratio (Fig. 4 B). The load ratio K/k that maximizes the work is close to two for low frequencies, unlike with lower viscous drag. In addition, for higher frequencies the ratio that maximizes energy output increases significantly (Fig. 4 B). The maximal value at the frequency f0 (= 4 kHz) is ∼2 zJ (= 2 × 10−21 J) at K/k = 1.5.
The work against viscous drag per half cycle decreases with increasing frequency (Fig. 4 C). It also decreases monotonically with increasing stiffness ratio K/k unlike the work against the elastic load. For this reason, the comparison of magnitude with elastic work heavily depends on the ratio K/k. The work against viscous drag is much larger than the work against elastic load if the elastic load is small. At K/k = 1.5, the value at the frequency f0 is 6 zJ, still larger than the value 2 zJ for the elastic work.
Power output can be obtained by multiplying the work against drag per half cycle by twice the frequency 2f. It is less frequency dependent, even though it still decreases with increasing frequency (Fig. 4 D).
Dependence on viscous load
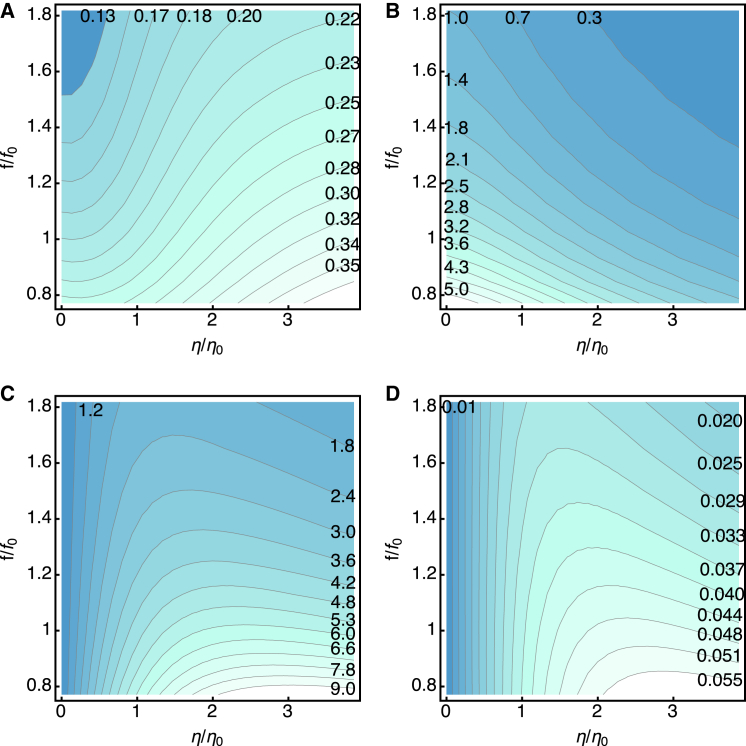
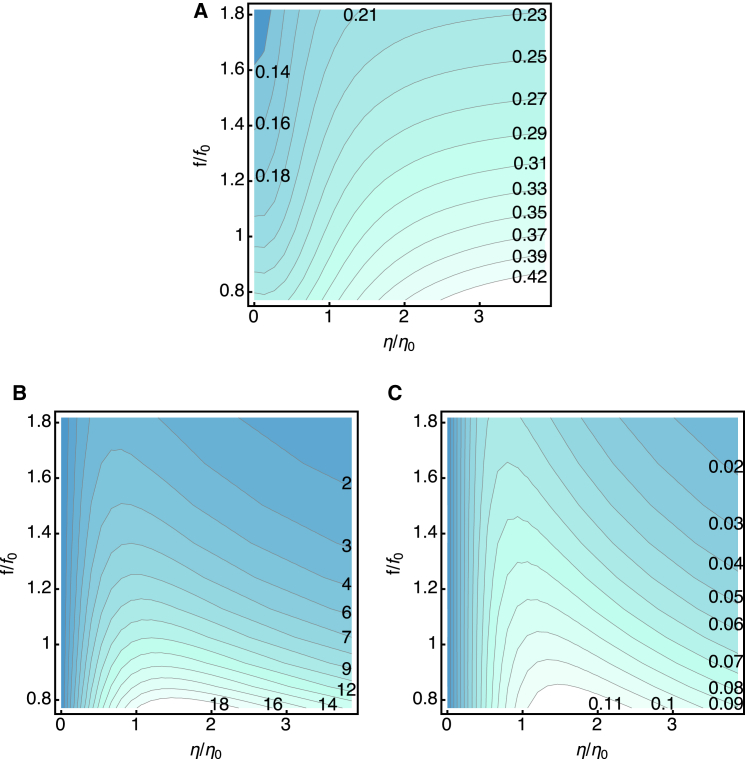
Here we examine the effect of the viscous load for fixed values of the elastic load. Two values of the external load would be of interest: one of them is the case in which the stiffness of the external elastic load is similar to the internal stiffness of the cell. The other is the case without an external elastic load. The former condition is presumably close to the physiological condition and the output in the form of elastic energy would be appreciable. The latter case is also of interest because it provides the maximal work against the viscous drag. Here we use η0 = 10−6 kg/s as the unit of drag coefficient.
With elastic load: K = k
The receptor potential significantly increases with increasing viscous drag (Fig. 5 A). A higher drag coefficient leads to less steep decline of the membrane potential with increasing frequency in the middle range of the plot (Fig. 5 A).
Figure 5.
The effect of drag in the presence of elastic load K (= k). The dependences on drag (the horizontal axis) and the frequency (the vertical axis) are shown as color-coded contour plots. Darker colors indicate lower values. Drag is described by the ratio , where η0 = 1.0 × 10−6 kg/s. Frequency is represented by the ratio f/f0, with f0 = 4 kHz, which corresponds to the parameter values of the cell given in Table 1. (A) The amplitude (in mV) of the receptor potential. (B) The work (in zJ = 10−21 J) against the elastic load during a half cycle. (C) The work (in zJ) against the viscous drag during a half cycle. (D) Power output (in fW = 10−15 W) working against the viscous drag. To see this figure in color, go online.
The work against the elastic load per half cycle decreases with increasing drag as well as frequency (Fig. 5 B), as intuitively expected. At frequency f0, it is up to ∼3.4 zJ for low drag. At η = 2η0, the value is ∼1.8 zJ.
The work against the viscous drag per half cycle monotonically decreases with the frequency. However, it has a maximum with respect to viscosity at a given frequency (Fig. 5 C). At f0, the maximal value is ∼6 zJ at η = 2η0.
Power output due to the work against viscous drag (obtained by multiplying the dissipative energy output per half cycle by 2f, twice the frequency) has a less steep frequency dependence (Fig. 5 D). The maximal output at the frequency f0 is 0.05 fW.
Without elastic load
At a given frequency, work against viscous drag is maximal at K = 0, i.e., in the absence of an external elastic load (Fig. 4). For this reason it is interesting to examine the system without external elastic load to evaluate the limit even though such a condition may not be physiological.
The receptor potential increases with increasing viscous load and decreases with increasing frequency (Fig. 6 A). At a given frequency, the work against the viscous drag per half cycle has a maximum (Fig. 6 B). The peak position shifts to at smaller drag with increasing frequency. The maximal work per half cycle is ∼12 zJ for f0(= 4 kHz). The power output shows dependence on the drag and frequency similar to the work per half cycle does, even though the frequency dependence is less steep (Fig. 6 C). The maximal power output is ∼0.1 fW.
Figure 6.
The effect of drag in the absence of elastic load. The dependences on drag (the horizontal axis) and the frequency (the vertical axis) are shown as color-coded contour plots. Darker colors indicate lower values. Drag is described by the ratio , where η0 = 1.0 × 10−6 kg/s. Frequency is represented by the ratio f/f0, with f0 = 4 kHz, which corresponds to the parameter values of the cell given in Table 1. (A) The amplitude (in mV) of the receptor potential. (B) The work (in zJ = 10−21 J) against viscous drag during a half cycle. (C) Power output (in fW = 10−15 W) working against the viscous drag. To see this figure in color, go online.
Discussion
Here we discuss energy balance in an OHC that operates at 4 kHz in the absence of mechanical resonance by examining the elastic load and viscous drag, to which the cell is likely subjected. This is followed by discussion on cells that operate at higher frequencies.
Internal drag
Of the internal mechanical load, there is no need to discuss the stiffness of the OHC because it has been determined experimentally. Some discussion would be needed regarding the internal drag of an OHC. For that purpose, the cell body is approximated by a cylinder. The velocity of the fluid is null in the middle of the cell and linearly increases toward the two ends, exactly the same as the plasma membrane. For this reason, Poiseuille’s law, for example, does not apply and viscous drag must be very small.
The magnitude of the drag on the outer surface could be estimated by Stokes’ law for a sphere, 6πμRv, where R is the radius. The resulting drag coefficient is 6.6 × 10−8 kg/s, assuming R = 5μm and 0.7 × 10−3 kg/(m s) of water for the viscosity μ. Since this value is smaller than the value ∼10−6 that maximizes dissipative energy output, the assumed drag coefficient η in Fig. 4 and η0 in Figs. 5 and 6, are dominated by the external viscous load and are not intrinsic to the cell.
Receptor potential
The numerical examination shows that the receptor potential is affected by an increase of elastic load and that of drag quite differently. Whereas an increase in drag always increases the receptor potential (Fig. 5 A), an increase in the elastic load increases the receptor potential only slightly if drag is small (Fig. 3 A) but it decreases the receptor potential if drag is larger (Fig. 4 A). These observations suggest that drag is more effective than elastic load in enhancing the receptor potential that powers the cell’s motility.
Amplifier gain
The functional significance of OHCs as the cochlear amplifier depends on the balance between energy input and output. Energy output from the cell body has been evaluated in sections above. Energy input required for stimulating the hair bundle to generate the receptor potential consists of two components. One is elastic and the other is dissipative. The elastic component is recovered in the next cycle of stimulation during sustained oscillation. The work against viscous drag cannot be recovered. Therefore the balance of the latter energy has been considered critical for the sensitivity and sharp tuning of the ear (30).
This model allows an evaluation of OHC’s output, which compensates for the dissipated energy for hair bundle stimulation. Examination of force or energy balance in the cochlea, however, cannot be made without a certain set of assumptions including the mode of motion in the cochlea (14, 20).
In the following, energy balance of a single OHC is examined. For this comparison, output values obtained under the condition K ≈ k and η ≈ 2η0 are used so that the two kinds of outputs can be realized at the same time.
Amplifier gain: dissipative energy
The hair bundle drag, which gives rise to the dissipative energy required for input has been evaluated for bull frog saccular hair bundles (31, 32. It consists of external friction between the hair bundle and the bulk fluid and internal friction due to relative motion between the stereocilia. The former is dominant when a hair bundle is stimulated by force applied to the kinocilium: the drag coefficient of a whole hair bundle is only ∼5 times as large as a single stereocilia (31). If we consider a sphere with a diameter of 8.5 μm, which is the hair bundle height, Stokes’ law gives the drag coefficient of 80 nNs/m, about the same as the drag coefficient calculated for the bundle in the frequency range higher than 2 kHz, where stereocilia moves in synchrony in response to force applied to the kinocilium (31, 32). This value can be even larger if the thickness of boundary layer is added to the diameter. Therefore, the internal drag must be smaller than the total drag at least by an order of magnitude. Here we set 1/10 of the total friction coefficient as an upper bound of the contribution of internal friction.
In the physiological conditions for OHCs, unlike a frog hair bundle stimulated by holding kinocilium, the hair bundle is in the subtectorial space between the tectorial membrane and the reticular lamina and hair bundles are stimulated by the shear in the gap. Under this condition, the external drag disappears because there is no relative motion between the bulk fluid and the hair bundle. The energy loss in that system is due to the shear between the two places and the internal drag of the hair bundle is negligible. This analysis is indeed consistent with earlier reports (20, 33, 34).
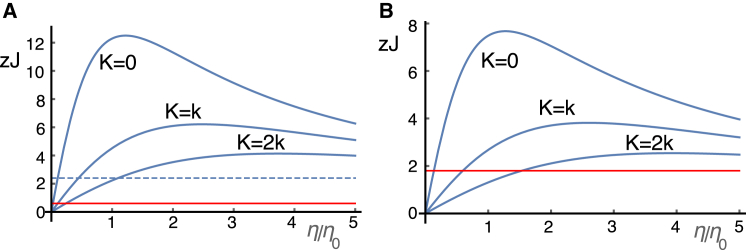
Assuming that the internal drag is less than 1/10 of the total, experimental data on frog saccular hair bundles (32) can be used to estimate an upper bound of energy dissipation. Full gating of frog hair bundle stimulated at 100 μm/s with amplitude ∼100 nm generates viscous force ∼20 pN (32). This value is about twice as large as 80 nNs/m for frequencies higher than 2 kHz (31). Energy dissipation based on this observed force is 10−19 J/half cycle for f = 500 Hz for full gating. Thus 3% gating corresponds to 3 × 10−21 J/half cycle. If we extrapolate for higher frequencies, 2.4 × 10−20 J/half cycle for frequency of 4 kHz. Since the drag coefficient at 4 kHz is less than that at 500 Hz (31), this value is an overestimate. A 10-fold reduction of this value leads to 2.4 zJ, which is given as an upper bound of energy dissipation due to internal friction of a frog hair bundle. This value is smaller than 6 zJ (= 6 × 10−21 J) with elastic load K = k (Figs. 5 C and 7 A), and 12 zJ without elastic load (Figs. 6 B and 7 A).
Figure 7.
Energy balance of an OHC (A) predicted at 4 kHz with the parameter values in Table 1; and (B) extrapolated to 12 kHz by reducing the linear capacitance C0 in half and increasing the internal stiffness k twice to account for shorter cell length of basal OHCs, without accounting for the larger hair bundle conductance, which increases the efficiency. Production of dissipative energy in zJ (= 10−21 J) per half cycle for 3% of full opening of its MET channels is plotted against drag coefficient η. The traces correspond, respectively, to K/k = 0, 1, 2 from the top. The red full lines indicate upper bounds of energy loss due to internal drag of the hair bundle. The dashed line indicates energy loss of hair bundle with external viscous drag equivalent to a sphere of 4 μm diameter. η0 = 1.0 × 10−6 kg/s. To see this figure in color, go online.
The internal friction coefficient of a OHC hair bundle is likely much smaller than that of the frog hair bundle, given the difference in their geometries. If we assume that internal friction is due to the shear between the stereocilia, the internal friction of an OHC is ∼1/4 of that of a frog hair bundle (see Supporting Material). Thus an upper bound of energy loss is ∼0.6 zJ, less than 1/10 of the energy output of an OHC. Even if we assume that the OHC is isolated and subjected to an external drag equivalent to Stokes drag for a sphere with the diameter of 4 μm, the maximal height of a hair bundle that operates at 4 kHz (35) in vivo, the comparison indicates that energy output exceeds energy loss by hair bundle drag (Fig. 7 A).
Amplifier gain: elastic energy
The observed stiffness of the hair bundle of OHCs is between 1 and 3 mN/m (36). The hair bundle displacement required for a 3% change in the bundle conductance (or resistance) is ∼0.03 nm (36). Thus the energy required for changing the conductance by 3% is 1.5 aJ in the most efficient condition based on 1 mN/m bundle stiffness. The elastic energy output obtained from the model is ∼2 zJ at 4 kHz (Fig. 4 B). It is 3.6 zJ, even for small viscous drag (Fig. 3 B). This indicates that output energy is a fraction of input energy.
Outer hair cells have, therefore, a minor effect in the elastic energy involved in the oscillation of the system. Since elastic energy is conserved it is unnecessary for the output of an amplifier to match the input.
Energy balance in more basal cells
The analysis described above shows that energy output exceeds energy input for an OHC that operates at 4 kHz even without mechanical resonance. More basal cells that operate at higher frequencies are more labile and it is difficult to obtain reliable experimental data from them. However, the energy balance in more basal cells, which operate at higher frequencies, is of great interest because it is harder to achieve a favorable energy balance at higher frequencies; therefore, it is important for understanding the effectiveness of OHC electromotility as the basis of the cochlear amplifier (14, 16, 18, 20, 21, 22, 37).
If we stimulate the same cell, for example, at 12 kHz, a frequency three times higher, the energy output is significantly less. However, the OHCs that operate at higher frequencies are shorter, with a lower linear membrane capacitance C0 and larger axial stiffness k. In addition, the hair bundle conductance is more sensitive to the strain (17). If C0 is halved and k is doubled, the energy balance is still favorable (Fig. 7 B), even without considering the higher sensitivity of the hair bundle transducer.
Notice that these comparisons are made without considering mechanical resonance. The reason for excluding resonance in this study is the sharp sensitivity of the membrane capacitance on the resonance frequency ωr as well as the characteristic viscoelastic frequency ωη (Fig. 2). Because OHCs in the cochlea work close to mechanical resonance frequencies, it is possible that the membrane capacitance in the operating condition is much smaller, enabling more efficient use of electrical energy (37). This issue, however, cannot be addressed quantitatively without precise information, such as the values for ωr and ωη as well as the sensitivity of the hair bundle.
Conclusions
This article proposes a simple model for the electromotility of OHCs to describe its behavior in a dynamic environment. The model is consistent with the experimental data obtained from isolated OHCs so far. The model also extends the expression for the membrane capacitance, incorporating the effects of frequency, drag, elastic load, and an associated mass. Monitoring the membrane capacitance could be the easiest means of testing the predictions. The effect of mass will be described in more detail elsewhere.
This model enables the description of the receptor potential and energy production of an OHC while its hair bundle is mechanically stimulated by a sinusoidal waveform. It was found that the receptor potential was more significantly affected by viscous drag than elastic load. The model predicts that the output of elastic energy is less than the input at the hair bundle. However, the output of dissipative energy is greater than the input. Because negative drag is a usual amplifying mechanism, these results are consistent with the biological role of OHCs as an amplifier.
Acknowledgments
I acknowledge Drs. Charles Steele, Anthony Ricci, Thomas Heimburg, and Frank Jülicher for their interest and comments. I also thank Drs. Jong-Hoon Nam of Syracuse University for discussion regarding hair bundle drag and Richard Chadwick, Thomas Friedman of the NIH, and three anonymous reviewers for useful comments.
Discussion with Dr. Charles Steele and Yanli Wang motivated to start the present work at Stanford, partially supported by NIH 5R01DC00791008 to Stanford University. A part of the work was done during my stay at Niels Bohr Institute, Copenhagen, and Max Planck Institute for Physics of Complex Systems, Dresden. It was also supported in part by the Intramural Research Program of the NIH National Institute on Deafness and Other Communication Disorders.
Editor: Brian Salzberg
Footnotes
Supporting Material and one figure are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30948-1.
Supporting Material
References
- 1.Ashmore J.F. A fast motile response in guinea-pig outer hair cells: the cellular basis of the cochlear amplifier. J. Physiol. 1987;388:323–347. doi: 10.1113/jphysiol.1987.sp016617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Santos-Sacchi J. Reversible inhibition of voltage-dependent outer hair cell motility and capacitance. J. Neurosci. 1991;11:3096–3110. doi: 10.1523/JNEUROSCI.11-10-03096.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dong W., Olson E.S. Detection of cochlear amplification and its activation. Biophys. J. 2013;105:1067–1078. doi: 10.1016/j.bpj.2013.06.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zheng J., Shen W., Dallos P. Prestin is the motor protein of cochlear outer hair cells. Nature. 2000;405:149–155. doi: 10.1038/35012009. [DOI] [PubMed] [Google Scholar]
- 5.Oliver D., He D.Z., Fakler B. Intracellular anions as the voltage sensor of prestin, the outer hair cell motor protein. Science. 2001;292:2340–2343. doi: 10.1126/science.1060939. [DOI] [PubMed] [Google Scholar]
- 6.Song L., Santos-Sacchi J. Disparities in voltage-sensor charge and electromotility imply slow chloride-driven state transitions in the solute carrier SLC26a5. Proc. Natl. Acad. Sci. USA. 2013;110:3883–3888. doi: 10.1073/pnas.1218341110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Iwasa K.H. Effect of stress on the membrane capacitance of the auditory outer hair cell. Biophys. J. 1993;65:492–498. doi: 10.1016/S0006-3495(93)81053-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tolomeo J.A., Steele C.R. Orthotropic piezoelectric properties of the cochlear outer hair cell wall. J. Acoust. Soc. Am. 1995;97:3006–3011. doi: 10.1121/1.411865. [DOI] [PubMed] [Google Scholar]
- 9.Iwasa K.H. A two-state piezoelectric model for outer hair cell motility. Biophys. J. 2001;81:2495–2506. doi: 10.1016/S0006-3495(01)75895-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hallworth R. Passive compliance and active force generation in the guinea pig outer hair cell. J. Neurophysiol. 1995;74:2319–2328. doi: 10.1152/jn.1995.74.6.2319. [DOI] [PubMed] [Google Scholar]
- 11.Iwasa K.H., Adachi M. Force generation in the outer hair cell of the cochlea. Biophys. J. 1997;73:546–555. doi: 10.1016/S0006-3495(97)78092-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dallos P., Hallworth R., Evans B.N. Theory of electrically driven shape changes of cochlear outer hair cells. J. Neurophysiol. 1993;70:299–323. doi: 10.1152/jn.1993.70.1.299. [DOI] [PubMed] [Google Scholar]
- 13.Rabbitt R.D., Clifford S., Brownell W.E. Power efficiency of outer hair cell somatic electromotility. PLOS Comput. Biol. 2009;5:e1000444. doi: 10.1371/journal.pcbi.1000444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ramamoorthy S., Nuttall A.L. Outer hair cell somatic electromotility in vivo and power transfer to the organ of Corti. Biophys. J. 2012;102:388–398. doi: 10.1016/j.bpj.2011.12.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Frank G., Hemmert W., Gummer A.W. Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proc. Natl. Acad. Sci. USA. 1999;96:4420–4425. doi: 10.1073/pnas.96.8.4420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Housley G.D., Ashmore J.F. Ionic currents of outer hair cells isolated from the guinea-pig cochlea. J. Physiol. 1992;448:73–98. doi: 10.1113/jphysiol.1992.sp019030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Johnson S.L., Beurg M., Fettiplace R. Prestin-driven cochlear amplification is not limited by the outer hair cell membrane time constant. Neuron. 2011;70:1143–1154. doi: 10.1016/j.neuron.2011.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ospeck M., Iwasa K.H. How close should the outer hair cell RC roll-off frequency be to the characteristic frequency? Biophys. J. 2012;102:1767–1774. doi: 10.1016/j.bpj.2012.02.049. (Correction: 103:846–847) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Adachi M., Iwasa K.H. Electrically driven motor in the outer hair cell: effect of a mechanical constraint. Proc. Natl. Acad. Sci. USA. 1999;96:7244–7249. doi: 10.1073/pnas.96.13.7244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ospeck M., Dong X.-X., Iwasa K.H. Limiting frequency of the cochlear amplifier based on electromotility of outer hair cells. Biophys. J. 2003;84:739–749. doi: 10.1016/S0006-3495(03)74893-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mistrík P., Mullaley C., Ashmore J. Three-dimensional current flow in a large-scale model of the cochlea and the mechanism of amplification of sound. J. R. Soc. Interface. 2009;6:279–291. doi: 10.1098/rsif.2008.0201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ó Maoiléidigh D., Hudspeth A.J. Effects of cochlear loading on the motility of active outer hair cells. Proc. Natl. Acad. Sci. USA. 2013;110:5474–5479. doi: 10.1073/pnas.1302911110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cole K.S. University of California Press; Berkeley, CA: 1968. Membranes, Ions, and Impulses. [Google Scholar]
- 24.Sokabe M., Sachs F., Jing Z.Q. Quantitative video microscopy of patch clamped membranes stress, strain, capacitance, and stretch channel activation. Biophys. J. 1991;59:722–728. doi: 10.1016/S0006-3495(91)82285-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Iwasa K.H. Electromotility of outer hair cells. In: Fuchs P.A., editor. The Oxford Handbook of Auditory Science. Vol. 1. Oxford University Press; Oxford, UK: 2010. pp. 179–212. [Google Scholar]
- 26.Iwasa K.H. Current noise spectrum and capacitance due to the membrane motor of the outer hair cell: theory. Biophys. J. 1997;73:2965–2971. doi: 10.1016/S0006-3495(97)78325-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gale J.E., Ashmore J.F. An intrinsic frequency limit to the cochlear amplifier. Nature. 1997;389:63–66. doi: 10.1038/37968. [DOI] [PubMed] [Google Scholar]
- 28.Dong X., Ehrenstein D., Iwasa K.H. Fluctuation of motor charge in the lateral membrane of the cochlear outer hair cell. Biophys. J. 2000;79:1876–1882. doi: 10.1016/s0006-3495(00)76437-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Freeman D.M., Weiss T.F. The role of fluid inertia in mechanical stimulation of hair cells. Hear. Res. 1988;35:201–207. doi: 10.1016/0378-5955(88)90118-9. [DOI] [PubMed] [Google Scholar]
- 30.Gold T. Hearing. II. The physical basis of the action of the cochlea. Proc. R. Soc. Lond. B Biol. Sci. 1948;135:492–498. [Google Scholar]
- 31.Kozlov A.S., Baumgart J., Hudspeth A.J. Forces between clustered stereocilia minimize friction in the ear on a subnanometre scale. Nature. 2011;474:376–379. doi: 10.1038/nature10073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bormuth V., Barral J., Martin P. Transduction channels’ gating can control friction on vibrating hair-cell bundles in the ear. Proc. Natl. Acad. Sci. USA. 2014;111:7185–7190. doi: 10.1073/pnas.1402556111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nam J.-H., Fettiplace R. Theoretical conditions for high-frequency hair bundle oscillations in auditory hair cells. Biophys. J. 2008;95:4948–4962. doi: 10.1529/biophysj.108.138560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Prodanovic S., Gracewski S., Nam J.-H. Power dissipation in the subtectorial space of the mammalian cochlea is modulated by inner hair cell stereocilia. Biophys. J. 2015;108:479–488. doi: 10.1016/j.bpj.2014.12.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Furness D.N., Mahendrasingam S., Hackney C.M. The dimensions and composition of stereociliary rootlets in mammalian cochlear hair cells: comparison between high- and low-frequency cells and evidence for a connection to the lateral membrane. J. Neurosci. 2008;28:6342–6353. doi: 10.1523/JNEUROSCI.1154-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kennedy H.J., Crawford A.C., Fettiplace R. Force generation by mammalian hair bundles supports a role in cochlear amplification. Nature. 2005;433:880–883. doi: 10.1038/nature03367. [DOI] [PubMed] [Google Scholar]
- 37.Mountain D.C., Hubbard A.E. A piezoelectric model of outer hair cell function. J. Acoust. Soc. Am. 1994;95:350–354. doi: 10.1121/1.408273. [DOI] [PubMed] [Google Scholar]
- 38.Santos-Sacchi J., Kakehata S., Takasaka T. Density of motility-related charge in the outer hair cell of the guinea pig is inversely related to best frequency. Neurosci. Lett. 1998;256:155–158. doi: 10.1016/s0304-3940(98)00788-5. [DOI] [PubMed] [Google Scholar]
- 39.Salt A.N., Inamura N., Vora A. Calcium gradients in inner ear endolymph. Am. J. Otolaryngol. 1989;10:371–375. doi: 10.1016/0196-0709(89)90030-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.