Abstract
Any cellular fission process is completed when the neck connecting almost-separate membrane compartments is severed. This crucial step is somehow accomplished by proteins from the dynamin family, which polymerize into helical spirals around such necks. Much research has been devoted to elucidating the specifics of that somehow, but despite no shortage of ideas, the question is not settled. Pictorially obvious notions of strangling or pushing are difficult to render in mechanically precise terms. Moreover, because dynamin is a GTPase, it is tempting to speculate that it has a motor activity that assists the necessary severing action, but again the underlying mechanics is not obvious. We believe the difficulty to be the mechanically nontrivial nature of confining elastic filaments onto curved surfaces, for which efficient methods to conceptualize the associated forces and torques have only recently appeared. Here we investigate the implications of a conceptually simple yet mechanically challenging model: consider an elastic helical filament confined to a surface mimicking the neck between two membrane compartments, which we assume to take the shape of a catenoid. What can we say about the expected length of such adsorbed filaments, their shapes, and the forces they exert, as a function of the key parameters in the model? While real dynamin is surely more complex, we consider such a minimal model to be the indispensable baseline. Without knowing what such a model can and cannot explain, it is difficult to justify more complex mechanisms, or understand the constraints under which this machinery evolved in the first place.
Introduction
The dynamin family of proteins mediates fission in many distinct cellular processes, including cytokinesis, endocytosis, and vacuolar as well as mitochondrial fission (1, 2, 3, 4, 5, 6, 7, 8). It has also been shown that some members of the dynamin family are able to form tubules from flat membranes (9, 10, 11). Proteins of this family appear in most phylogenetic branches, including plants, animals, yeast, and even prokaryotes (12, 13, 14, 15).
Common features in the dynamin family include GTPase domains and pleckstrin homology domains used for membrane binding. These proteins polymerize into helices that wind around their fission target (15). These features suggest a process by which these proteins mediate fission: after forming a helical scaffold around its target membrane, dynamin hydrolyzes GTP, and uses the associated energy to deform the target to its breaking point. However, this description glosses over certain subtleties. How exactly does dynamin deform the membrane (7)? How is dynamin recruited to the neck, or as van der Bliek put it, “what keeps dynamin from turning all membranes into vesicles?” (15). What assistance does it need from other proteins (16)?
In this article, we attempt to build a minimal model of a dynamin family protein’s elastic interactions with its target. This will help us to understand both how real dynamin works and the restrictions under which evolution created this fission machine. We omit GTP hydrolysis, although it is an essential step in the fission process. Our justification for this approach is that we seek to understand the passive aspects of fission before considering the active ones. What are the forces that elastic filaments can exert on surfaces on which they can polymerize, but whose curvature might not match their own? Even understanding this mechanical interaction turns out to be surprisingly informative.
Our analysis will illustrate some of the connections among elasticity, geometry, and chemistry in the design of a polymerizing fission machine. For example, we find that the pitch of the helix is closely related to the range of neck radii onto which dynamin binds. We also show fundamental limitations on how much such a polymer can deform its target, and hence offer an explanation of why dynamin-mediated fission is an active process.
In the past few years, many theoretical approaches for modeling dynamin have been developed. Each of these imagines a different idealized form for the protein and is able to capture different aspects of the fission process. For instance, considering dynamin as a mean-field density functional on the membrane surface illustrated the role of dynamical instabilities in the fission process (17). A fluid dynamical analysis showed the limitations imposed by friction during constriction (18). A model representing dynamin simply as a rigid sheath was able to show that dynamin’s recruitment can be connected to local membrane geometry (9). Other theories imagined dynamin as a closed chain (19) or as a system of insertions that agglomerate via membrane-mediated interactions (20).
However, we feel that a more detailed discussion of the elastic interaction between the dynamin polymer and the membrane is needed. This is important because, as we will show, mismatch between the preferred geometries of the protein and its target produces the force on the membrane and inhibits polymerization. A full reckoning of this interaction would require one to consider simultaneously the flexibility of the surface and the protein. At the level of continuum theory, using traditional models of curvature elastic rods and surfaces, this would entail solving a pair of coupled fourth-order nonlinear differential equations.
We will first make a small step in this direction by considering only the flexibility of the filament, with the shape of the surface fixed so that it only responds to applied forces with a global change in size. Until recently, studying elastic filaments confined to curved surfaces required unwieldy variational calculus (21). Our considerably simpler framework was first developed and deployed by two of the present authors to study closed Euler-elastic rods of fixed length confined to the surface of a sphere (22). It was later also applied to closed Euler-elastic rods on the cylinder (23). Lastly, it was extended to more general energy functionals and surface geometries (24).
To create a realistic model of dynamin in this framework we must make a few important adjustments to our previous work (23). Real dynamin polymers do not close back on themselves. Dynamin is also present at such high concentrations in cells that there is essentially a limitless supply for any given target, so it is more appropriate to treat the length of the filament as a dynamical variable, and fix a polymerization force or chemical potential that controls the length. Lastly, real dynamin polymers are helical, so we must consider polymers with preferred curvature and twist.
We therefore analyze open-ended, helical elastic filaments of variable length. The key object of study is the polymer’s lowest energy state, subject to the constraint of being in contact with the surface. First we will apply this to cylindrical substrates, as they are the most commonly studied in vitro (16, 25, 26, 27). It turns out that the symmetries of the cylinder make this calculation analytically tractable, so it will also serve as a simple introduction to some of the concepts used later, as well as highlighting the importance of symmetries. Then, we will consider a more biologically relevant surface geometry, the catenoid, which represents the neck between two splitting membranes or organelles. This neck shape must be constructed by other agents acting on the membrane, for instance clathrin in endocytosis or the endoplasmic reticulum in mitochondrial fission. Interestingly, this can be performed by local constriction of the neck or dilation of the membrane at remote locations (28). We will find that our model provides insight into the desirable features of a fission machine, which will lead us to important restrictions on the parameters of dynamin and suggest physical explanations for recruitment and constriction.
Theoretical framework
As dynamin polymerizes on a surface, it is generally prevented from relaxing to its rest shape because it must conform to the geometry of the surface. This induces stress in the polymer, causing it to exert force on the surface. Because the origin of this force is the geometrical mismatch between the two objects, this geometry will be our focus.
To do this, we consider the polymer as a continuous elastic filament, and the membrane as a fixed curved substrate. This dimensional reduction is justified because the systems we study are large enough that their transverse dimensions become irrelevant. The continuum model is justified because the polymer and membrane comprise many monomers and lipids, respectively: dynamin helices have ∼50 monomers and cover an area of ∼103 lipids (29). As a special case, we will also consider the limit of very short filaments, in which case a continuum approximation is somewhat questionable. However, the behavior we find in this limit is commensurate with what we would expect for monomers. The interesting features of the limit also hold for small finite-size polymers, for which a continuum approximation is more appropriate.
Our model begins with an energy functional that expresses the total energy of the filament as an integral over its length. Minimizing it gives us the equilibrium configurations of the filament. For a given configuration, we can calculate the filament’s total energy and the force density confining it to the surface.
Classical models of elastic filaments use an energy functional that is quadratic in the filament’s material curvatures. These are briefly explained in Appendix A in the Supporting Material. The curvatures κ1 and κ2 describe how the filament bends in each material direction perpendicular to its tangent. The twist κt describes how its cross section rotates about the tangent vector as we move along the filament.
Notice that the orientation of the cross section is not determined by the filament’s centerline; it is linked to the local material frame. However, in the case of dynamin, the orientation of the polymer relative to the surface is fixed: the protein must keep its pleckstrin homology domains in contact with the membrane to bind. This requires the polymer to twist in a way prescribed by the surface (see Fig. 1). This allows us to replace the material curvatures with the geodesic curvature κg, describing curvature tangent to the surface, and the normal curvature κn, describing curvature perpendicular to the surface (see Appendix A in the Supporting Material). The collection is referred to as the set of “Darboux” curvatures of the curve on the surface.
Figure 1.
The centerlines of the gray filaments trace the same curve on the surface, but the orientation of the filament’s cross section in the top frame is fixed with respect to the surface, while in the bottom frame it is not. To see this figure in color, go online.
The most general energy functional quadratic in the Darboux curvatures would be (24)
| (1) |
where i and j serve as indices to refer to the normal and geodesic curvatures, and are implicitly summed over. The symmetric tensor Iij is called the “inertia” tensor and describes the filament’s resistance to bending in different directions. The components of the tensor and the twist modulus γ are determined by the material parameters of the filament and the geometry of its cross section (30). The spontaneous curvatures cg and cn describe the filament’s bending when unstressed, and the spontaneous twist ct describes its twist. As shown in recent structural studies, dynamin’s cross section is approximately symmetric under reflections through the plane defined by the filament’s tangent and the local surface normal vector, implying that cg ≃ 0 (31, 32). We will therefore make the simplifying assumption that the cross section is isotropic, in which case Iij = αδij, where α is the bending rigidity. This holds automatically if the cross section is symmetric with respect to rotations about its center. While the cross section is not quite circular, the width and height are comparable (both are ∼10 nm), which also suggests that the two eigenvalues of Iij are similar. As we will see, the model will indeed be able to describe many features of dynamin’s behavior.
We can estimate the other spontaneous curvatures cn and ct from the shape of dynamin filaments formed in the absence of any binding substrate. For example, classical dynamin forms helices of radius r ≈ 15 nm and pitch 2πh ≈ 10 nm in low-salt, low pH solution (“classical dynamin” refers to the prototypical dynamin molecule, dynamin 1) (5). The curvatures and twist of a helix in terms of these parameters are
| (2a) |
| (2b) |
Assuming that this is the rest configuration of the filament, we therefore estimate that classical dynamin has , . We will use as a reference length scale, so other lengths are measured in terms of . The dimensionless ratio is an especially important parameter in our analysis. We note here that it is small for classical dynamin, although it could vary throughout the dynamin family.
The twist modulus γ is related to the bending modulus by , where ν is Poisson’s ratio (30). For ordinary materials, so that . Test cases we analyzed suggest that changing γ in this range does not qualitatively affect the behavior of the filament, so we take γ = α. This symmetry also has the advantage of offering a level of analytical tractability.
The bending rigidity α can be estimated from the persistence length of the helix, or by assuming the Young modulus of dynamin is comparable to that of similar proteins, such as actin. For classical dynamin, α ≈ 105 kBT nm (5, 18). This is large enough that thermal fluctuations are unlikely to significantly perturb the shape of the filament, justifying their omission. We will use α throughout this article to set the energy scale.
Including our simplifications, the energy functional of the filament reduces to
| (3) |
We will focus on the configuration with the lowest energy, which we will call the “ground state”. We write its energy as E(L,R), which depends on the length of the polymer L, and a parameter R characterizing the size of the surface (e.g., the radius of the cylinder). We also introduce the Legendre transform of the energy,
| (4) |
where μ represents a combination of polymerization energy, adhesion energy, and the entropy lost by confining a monomer to a two-dimensional surface. This quantity has been called the “polymerization force”, and is estimated to be for classical dynamin at concentrations of 10–15 μM (5). This is a larger concentration than what is expected in vivo, which is <1 μM. Because the polymerization force depends logarithmically on concentration, we believe this is a good order-of-magnitude estimate. We point out that this value corresponds to in terms of our energy scale α and length scale cn, a relation that will be useful later on.
Equilibrium is achieved when
| (5) |
This equation can be understood as prescribing an equilibrium length for a given value of μ, or as giving the appropriate μ for a given value of L. However, as we will see, the relationship between μ and L is not always one-to-one; often, multiple different length polymers share the same μ. In this case, we must check whether each state is stable, and compare their free energies E − μL to determine the ground state. The stability is determined by the second derivative of E: if
| (6) |
then L will correspond to an energetic minimum, and hence a stable equilibrium. Stable states that are not the ground state are called “metastable”.
Energy-minimizing configurations satisfy a system of nonlinear first-order differential equations called the shape equations, which we solve by multiple techniques. For the derivation of these equations and their boundary conditions, see Appendix B in the Supporting Material.
Confinement to the surface induces stress in the polymer. Corresponding to this stress, there is a local force density λ(s). The component of λ perpendicular to the surface is the force binding the polymer to the surface. By Newton’s third law, −λN must be the force applied to the surface. Although λ can in principle have components tangential to the surface, they are not transmitted to the surface (24).
We are especially interested in finding the value of the surface size R in equilibrium. The total radial force,
| (7) |
will vanish at some equilibrium radius R0. On the cylinder, fr is equivalent to , but this is not true in general. On other surfaces, includes contributions from components of the force that are not transmitted to the surface.
Although we use the symbol fr and the term “force”, we should emphasize that fr is not necessarily an actual force that is applied anywhere. Instead, it serves to keep track of how the energy changes with respect to the scale parameter R, and so we interpret it as a generalized force. Even with our knowledge of the local force density on the surface, λN, we do not attempt to model the surface’s full response to it. This would require solving an additional coupled fourth-order partial differential equation. As a first approximation, we allow the surface to answer with a global change in size, maintaining its (cylindrical or catenoidal) shape.
Actually, classical dynamin is much stiffer than the substrate, although it is not obvious that this holds for all proteins in the dynamin family. One might argue it would be more appropriate to allow the surface, rather than the filament, to bend. The bending moduli of the membrane and the filament can be compared (despite having different dimensions) using the membrane’s intrinsic length scale, which is defined in terms of its bending rigidity κ and tension σ as . In equilibrium, the membrane forms cylinders of radius rc. Taking rc = 15 nm, κ = 20 kBT, we see that , indicating that the filament is quite stiff. However, it is somewhat curious that classical dynamin should be so stiff. By studying a more flexible filament, we can consider hypothetical designs for dynamin, and possibly other members of the dynamin family. Furthermore, this model will serve as a stepping stone to one that includes the elasticity of both objects. We expect this model will correctly account for many qualitative properties, such as the approximate shape of the filament and binding phase diagrams determined by geometry and polymerization force.
Results and Discussion
Application to specific geometries
Cylindrical substrate
In many in vitro experiments, dynamin is bound to cylindrical membrane tubules (16, 25). The advantage of using cylindrical tubules is that the cylinder’s radius is determined by the membrane tension, and is thus easy to tune. We will now use this case to illustrate the concepts of our model without immediately getting bogged down in mathematics.
We begin by solving the shape equation for the filament. We can then calculate the total energy of the ground state as a function of L and cylinder radius R. This will allow us to determine whether the filament will bind at a given value of μ. Supposing that it does, we can then calculate the total radial force fr exerted on the surface.
On a cylinder, the Darboux curvatures are given by
| (8a) |
| (8b) |
| (8c) |
where θ is the angle between the filament’s tangent vector T and the local horizontal (see Fig. 2). In Appendix B in the Supporting Material, we show that the ground state of the filament is a helix, for which θ(s) is constant along the filament. The angle at which the helix lies is determined by the dimensionless variables Rcn and Rct,
| (9) |
Because each point along the helix is identical, θ0 completely characterizes the shape of the filament.
Figure 2.
The equilibrium configuration of filaments confined to the surface of a cylinder is helical, with pitch angle θ. To see this figure in color, go online.
Inserting θ(s) = θ0 into the energy functional, we find the total energy of the ground state
| (10) |
Note that E is a linear function of L, and hence that E − μL is as well. If E − μL is increasing as a function of L (i.e., ), the lowest energy state is realized at L = 0, so there is no polymerization at all. If E − μL is decreasing (i.e., ), there is no minimum, and polymerization continues without bound. The equilibrium length is never finite! In experiments, it is possible to find finite polymers on cylinders. Our model hence suggests that these are not in equilibrium. Indeed, in Roux et al. (9) it was found that, given enough time, cylindrical tubules will become completely coated with dynamin.
In Fig. 3, the energy density is shown as a function of R for a few values of . There is a minimum at , corresponding to the radius the helix would have in the absence of a cylinder. Because E is exactly linear in L, the energy density is equal to the binding threshold of μ. Fig. 3 can thus also be interpreted as a phase diagram with R on the horizontal axis and μ on the vertical axis. Each energy density curve is then interpreted as a phase boundary for filaments with that ratio of . If , infinite binding occurs, while no binding occurs if .
Figure 3.
Energy E per unit length on the cylinder as a function of cylinder radius. Because E is linear in L, this has a second interpretation as a phase diagram. To see this figure in color, go online.
This concept is perhaps easier to understand by imagining a system at fixed μ, with many tubules of different radius. By solving the inequality for R, we can find upon which radii the dynamin binds:
| (11) |
This inequality shows directly how μ relates to recruitment. At small μ, the range is very narrow, so dynamin only binds on tubules with geometry similar to its own. The range of permissible radii widens as μ increases. At (for classical dynamin ), the upper bound on R diverges. This prediction should be testable in a lab environment, because for this polymerization force, dynamin would even bind on a flat surface. Although the transition μ is too large to be accessible experimentally for classical dynamin, it would be much smaller for dynamin variants that have larger radii or softer bending rigidities.
When the polymerization force is more realistic, dynamin automatically polymerizes on tubules with radii close to R0. If tubules do not form spontaneously within the limits set by Eq. 11, other proteins have to partially constrict the membrane before dynamin can begin to bind and polymerize. Indeed, this role is played by clathrin in vesicle fission and the endoplasmic reticulum in mitochondrial fission.
The total radial force fr is plotted in Fig. 4. The force vanishes on cylinders of radius , as mentioned above. Intuitively, the filament pushes (or pulls) the surface toward this radius, so that the surface conforms to the polymer’s preferred size.
Figure 4.
Force per unit length on the cylinder as a function of cylinder radius. Negative forces correspond to constricting the substrate. (Solid lines) Where binding would occur given a realistic polymerization force of 5 kBT nm. To see this figure in color, go online.
Of course, whether any force is applied to the surface is contingent on the polymer binding at all. For a given value of μ, there is no force at all on tubules that do not satisfy Eq. 11. In Fig. 4, solid lines indicate the radii at which binding would occur (and hence force would be applied) given , while dashed lines indicate where it would not. For this value of μ, the equilibrium radius R0 is only ∼15% smaller than the maximum radius allowed by Eq. 11.
Note that R0 decreases for increasing ct. Thus the inner radius of the helix can be decreased by twisting as well as bending, suggesting an explanation for why dynamin twists during its conformational change (16).
Catenoidal substrate
We use a catenoid to represent the neck between two compartments undergoing fission. The catenoid is ideal for this because it has zero mean curvature, and therefore minimizes the energy of a curvature elastic membrane. Indeed, it has been shown that as the neck between two vesicles becomes much smaller than the vesicle radius, it approaches this shape (33).
On the catenoid, the translational symmetry along the z axis is broken. As a result, the shape equation (discussed and derived in Appendix B in the Supporting Material) is higher order than in the cylindrical case. The dependence of the ground state energy on L becomes nontrivial. We emphasize this distinction because it allows the possibility of finite length polymers in equilibrium. Theory and experiment both suggest that these shorter polymers are better suited to mediating fission than very long ones (18, 29, 34).
Unsurprisingly, the higher-order shape equation is also much harder to solve. We therefore seek numerical solutions guided by perturbation theory about geodesics, i.e., curves with κg = 0. Because we must impose boundary conditions at both ends of the filament, our numerical investigation uses a relaxation algorithm, discussed in more detail in Appendix B in the Supporting Material.
The parameter R now represents the radius of the neck. For surface coordinates, we use the azimuthal angle ϕ and the height z above the catenoid’s central plane.
Because they are accessible analytically, we will first discuss the L ≪ R and L ≫ R limits. Then, we will move on to our numerical studies of intermediate length regime.
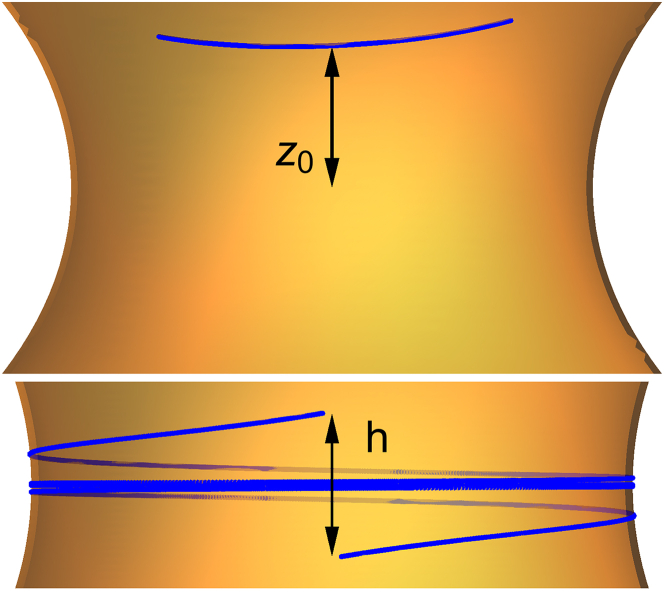
We begin our investigation of short polymers with whether, and (crucially) where, they bind. Because they prefer to bind at the part of the catenoid that most closely matches their own geometry, they may bind a finite distance z0 away from the center of the neck, spontaneously breaking the up-down symmetry of the catenoid. We can calculate z0 for very short filaments with L ≪ R. Again, we admit that in this case our continuum model does not really hold. However, we think this calculation paints an appropriate qualitative picture of dimer or oligomer binding. Let us assume that the filament approximately traces a geodesic on the surface. Then, the energy depends only on z(s) and θ(s). In the L → 0 limit, we can take z and θ to be constant, so that only rigid motions of the dimer are included. In this approximation, the dimer is a directed pointlike object. Minimizing with respect to these, we find that short filaments should have
| (12a) |
| (12b) |
where the critical radius is defined as
| (13) |
Equation 12a can be understood as follows. On necks with R < Rc, there are sites where the geometry of the surface and the polymer match exactly: the polymer can choose z and θ, so that κn and κt take their preferred values, cn and ct. However, on larger necks, the polymer prefers to be more strongly curved than any point on the catenoid, and so binds at the most curved site available, which is the center of the neck.
We can insert these results on the ground state of short filaments from Eqs. 12a and 12b into the energy functional in Eq. 3 to find the elastic energy of short filaments. This is important because the competition between this and the binding energy determines whether binding occurs at all. Differentiating the total energy with respect to L, we find
| (14) |
Binding occurs for any μ if R ≤ Rc, again because if R < Rc, there are sites on the surface matching the preferred geometry of the polymer exactly. The nonzero binding threshold for R > Rc reflects the fact that it costs energy for polymers to form on large necks. At a given value of μ, this threshold also implies an upper bound on R. Solving Eq. 14 for R, we see that binding will only occur on necks with
| (15) |
When , the upper bound diverges, and binding occurs on necks of any size. Interestingly, this is the same value at which binding occurs on cylinders of any size.
In the opposite case of large L, we have observed two types of behavior, distinguished by the curvature of the filament relative to that of the neck. If the filament is strongly curved, the polymer prefers to go toward the most curved parts of the catenoid, i.e., the center; in the weak curvature case, it instead prefers the flat parts above and below the neck. As the polymer grows, material is added to the preferred region, and the shape away from that region is left unchanged. The energetic cost of growing the polymer then becomes independent of L, so that the energy E(L,R) asymptotically grows linearly in L. It is therefore useful to define . When μ > μ∞, the ground state becomes infinitely long.
To determine μ∞, we will find the energetic cost of adding material either at the neck’s center or in the flat regions of the catenoid. Far away from the center of the neck, all curvatures are approximately zero. We calculate the energetic cost of adding material to this region by inserting κg = κn = κt = 0 into Eq. 3, and see that the energy density is
| (16) |
On the other hand, strongly curved polymers add material at the center of the neck as they grow. At that point, κg ≈ κt = 0 and . Inserting these values into the energy density gives
| (17) |
Comparing Eqs. 16 and 17 allows us to make the distinction between strong and weak curvature more precise. If , the filament’s energy is lower in the flat regions of the catenoid than at the neck. While the actual ground state in the weak curvature regime may not be a perfectly straight rod, even such a configuration is lower in energy than binding at the neck. Obviously, the ground state is not centered at the neck. This makes the regime quite unrealistic for dynamin, and so we will ignore it from now on.
We have perturbatively observed that, in the strong curvature case, for large L the amount the filament winds around the neck is asymptotically linear in L, while the height of the filament h(L) (see Fig. 5) approaches a finite value h∞. These perturbative results agree well with numerical solutions. Though we have a closed form expression for h∞, it is lengthy and not particularly illuminating. Instead of reproducing it in full, we point out that at , h∞ is approximately , reflecting that the ratio controls the aspect ratio of the helix.
Figure 5.
If R < Rc, short filaments bind away from the center (top), while on large catenoids they wind symmetrically about the neck’s center (bottom). To see this figure in color, go online.
Because strongly curved polymers are confined within the h < h∞ region, the density of polymer in this region becomes large as they grow longer. This buildup is not realistic because physical polymers have finite thickness and cannot overlap. This limits the applicability of our model in certain cases, which we discuss in the Conclusions.
The regime where L ∼ R is much more difficult analytically, and so in this case we rely on numerics. In this regime, a small increase in L can lead to global changes in the filament’s shape. As a result, is a nontrivial function of L and for certain values of μ, there are finite values of L that satisfy Eq. 5. Our numerical solutions to the shape equation show that the energy of the filament increases monotonically with L. However, its derivative is nonmonotonic in L for R < Rc, leading to multiple equilibrium states at the same μ and complex binding phase behavior.
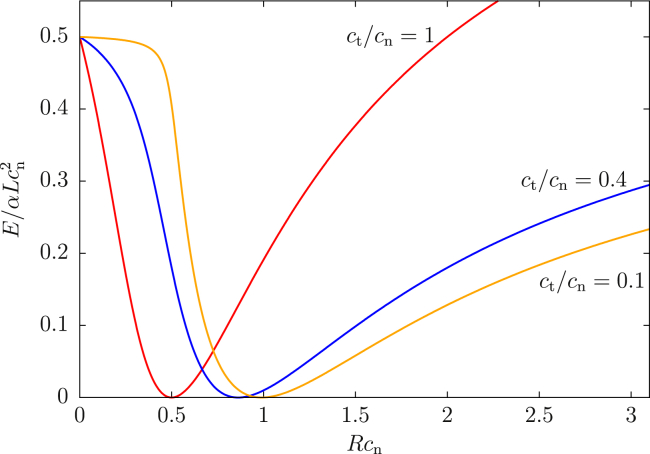
Let us define a few useful values of μ to help decipher the phase diagram in Fig. 7. In Fig. 6, we have plotted the free energy E − μL at these special values of μ at Rcn = 0.6 (note this is still the strong curvature regime, because ) with and . For small μ, the equilibrium state is a short filament centered away from the neck. Increasing μ slightly, L increases and the filament moves toward the center of the catenoid. At μ = μs1, called the “first spinodal”, there is an additional state satisfying . The higher L state is not a local minimum of E − μL, but only a saddle point. Interestingly, this state is symmetric under . Increasing μ past μs1, the symmetric state splits into two stationary states: one local minimum and one local maximum, both of which are symmetric. Eventually, μ is large enough that the stable symmetric state and the asymmetric state have the same free energy. This is called the “binodal”, and this value of μ is denoted μb. The unstable symmetric state creates an energetic barrier between the two stable states. For μ > μb, the symmetric state is the global minimum. However, the asymmetric state is still metastable until μ reaches the second spinodal point, μ = μs2. Finally, for μ > μs2 there is only one local minimum, and the ground state is symmetric. This state may or may not have infinite length, depending on whether μs2 > μ∞. Indeed, μs2 does exceed μ∞ for small , as shown in Fig. 7. In that case, the possibility arises that μb = μ∞, so that the onset of symmetric binding is simultaneous with that of infinite binding (shown in the left panel of Fig. 6).
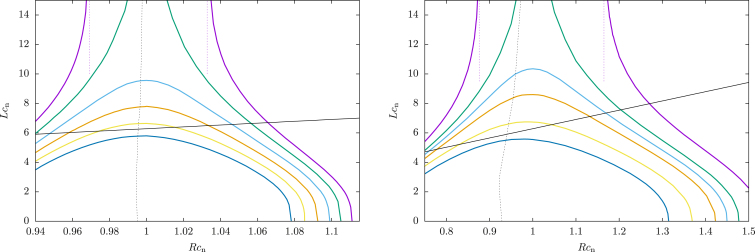
Figure 7.
Phase diagrams for binding on a catenoid with (left), and (right). Infinite binding occurs in the yellow region, asymmetric binding in the red region, and symmetric binding in the green region. The binding threshold μ0 is shown in red, the binodal μb in solid blue, the spinodals in dotted blue, and the asymptotic polymerization force μ∞ in black. The case is less realistic for classical dynamin, but better illustrates the difference between the binodal line and the two spinodal lines. (Inset in the left graph) Zoom-in on the boxed region. To see this figure in color, go online.
Figure 6.
Total free energy as a function of L for special values of μ explained in the text, with (left) and (right). In the case, the only transition is from asymmetric binding to infinite (symmetric) binding. (Inset) Zoomed-out version. To see this figure in color, go online.
Fig. 7 illustrates how these values of μ depend on R. The inset in the left panel shows the very narrow finite binding region when . We can quantify this narrowness by noting that the infinite binding threshold has a minimum at given by . For classical dynamin, this corresponds to . The fact that this is very near the estimated actual value is intriguing, especially in light of studies showing that long polymers are ill suited for fission. In Eq. 15, we found the largest neck on which polymers form at a given μ. Assuming that no infinite binding occurs, we can find an inequality that depends only on geometric features of the filament by requiring ; one finds
| (18) |
In Fig. 8, we show how the equilibrium length of the filament at fixed μ depends on the radius of the neck, again with on the left and on the right. The symmetric-asymmetric binding transition has been omitted from the figure; it would manifest as a discontinuous drop in L at lower values of R. The violet curves illustrate what happens when : if R lies within a certain finite interval (delimited by the dotted violet lines), the length diverges. The green curves have , and hence diverge at Rcn = 1. At lower values of μ, the length is always finite.
Figure 8.
Equilibrium filament length as a function of R at fixed μ with (left), and (right). (Solid black line) L = 2πR, which of course indicates the threshold for winding once around the neck. (Dotted black line) Where the energy is minimized with respect to R. On the left-hand side, the curves are going from top to bottom. On the right, they are . To see this figure in color, go online.
The dotted black line shows the radius for which the energy is minimal (which, in this case, depends on L). At a given μ, this plot thus also illustrates the energetic gradient flow. One imagines a preexisting vesicle neck, for instance as created by clathrin. If this neck is small enough, dynamin binds, and in doing so, exerts forces constricting the neck. Energy minimization causes the system to flow along a fixed-μ curve toward R0, i.e., the dotted line. As the radius decreases, the length of the polymer grows at first, reaching a maximum around Rcn ≈ 1, when, surprisingly, the polymer actually shrinks again. Ultimately, equilibrium is reached at R = R0. The filament cannot wrap entirely around the neck unless the length L is at least 2πR. The solid black line in the figure shows this minimum length. If L is below this line at the equilibrium radius, adjacent rungs of the filament are unable to interact. Because such interactions are hypothesized to be essential for fission, this threshold could be very important (29).
Although we do not have an analytical expression for E(L,R), we can determine R0 via perturbation theory when L ≪ R and L ≫ R. For very short filaments, E ≈ μ0L: minimizing the right-hand side of Eq. 14 with respect to R, one finds R0 = Rc. On the other hand, for long filaments, E ≈ μ∞L: minimization gives . Interestingly, R0 is not monotonic in L, and does not depend on ct if L is large. This suggests two advantages of shorter polymers: they have smaller equilibrium radii, and they enable the twisting motion of dynamin’s conformational change to reduce the equilibrium radius further.
With knowledge of R0 and the maximum binding radius Rmax given by Eq. 15, we can estimate how much strain dynamin imposes on a neck without GTP hydrolysis. We define the maximum strain as
| (19) |
where we have ignored the slight decrease in R0 that occurs for low L. As one sees on the left-hand side of Fig. 8, for realistic values of ct and μ the radius of the neck only decreases by ∼10–15%. It has been estimated that to induce fission, a much more dramatic decrease from 15 to 3 nm would be necessary (35).
As in the cylindrical case, the fact that the neck must be of similar size to the filament’s rest state for polymerization to occur inhibits passive constriction of the neck.
Conclusions
We have analyzed the binding of a curved polymer with constant finite polymerization force to cylindrical and catenoidal substrates with the aim of constructing a minimal model of dynamin and similar proteins. This model is a substantial jump in realism from our previous analysis of cylindrical confinement of semiflexible polymers. Here, we include helical rest configurations and a more realistic surface geometry. We also allow the length of the polymer to vary, and remove the constraint that the polymer closes back on itself.
On the cylinder, the energy of the filament is linear in L, hence it is minimized at either L = 0 or L = ∞, eliminating a finite binding phase. This suggests a limitation of experiments using only cylindrical substrates: membrane-bound dynamin polymers will tend to be very long, but shorter polymers may be more efficient fission machines (29). Experiments on cylindrically bound dynamin can be useful for studying intermediate stages in the fission process or dynamin’s conformational change (for example), but are not likely to accurately reflect the dynamics of in vivo fission.
It is possible there is a finite binding phase on cylinders that we overlooked by omitting membrane deformations from our analysis. However, no such phase was found in Roux et al. (9), which studied dynamin binding onto cylindrical tubules at many different concentrations. If such a phase does exist, it seems to occur over a very narrow range in μ.
On the catenoid, however, E depends nontrivially on L, creating the possibility for equilibrium finite-length polymers. In fact, all polymers have finite length if . Intriguingly, experimental estimates of μ are very close to this bound, suggesting that dynamin may indeed have evolved to avoid this transition. The significant difference between the binding phase diagram on the cylinder and the catenoid suggests that dynamin’s behavior depends strongly on the shape of the substrate, a fact that to our knowledge has not been explored experimentally.
We must point out, though, that the infinite polymerization presented in our model is incomplete, because we allow the polymer to wind infinitely densely around the center of the neck. It is clear that, in reality, as more dynamin binds, more of the surface is occupied. The actual behavior of very long filaments depends on how the polymer rigidity α compares to the membrane bending rigidity, usually called κ. If κ is sufficiently small, dynamin could begin to tubulate the membrane before infinite binding becomes relevant.
The equilibrium cylinder radius R0 decreases as a function of ct. This reflects the fact that twisting of the polymer can lead to constriction. For catenoidally bound polymers, R0 depends additionally on the polymer’s length. For large L, is independent of ct. If L is small, R0 ≈ Rc. The twisting motion of dynamin’s conformational change is therefore put to best use by short polymers. However, if the polymers are too short, they may just detach from the membrane when stressed, rather than induce any geometric change. Detachment is more difficult if they are long enough to wind completely around the neck. Furthermore, longer polymers are able to exert larger forces on the membrane. Understanding the balance between these considerations would require a model of the dynamin-membrane interaction far from equilibrium.
The adhesion energy or polymerization force μ limits the range of surfaces on which filaments will bind, and hence the extent to which the filament can deform the surface. Because we do not allow the surface to deform locally, we expect that in reality this range is wider than our model predicts. On cylindrical membranes, dynamin only binds if the radius is near the equilibrium radius R0. In the catenoidal case, dynamin is only drawn to the central neck if the latter is larger than the critical radius Rc. This competition of binding energy and elastic deformation leads to a physical explanation for recruitment: polymerization only occurs if the substrate is already geometrically similar to the polymer. This resolves the question, “what prevents dynamin from turning all membrane into vesicles?” (15). However, mismatch in the geometries of the filament and the substrate induces stress in the filament, and therefore force on the substrate. Thus the easier it is for dynamin to bind, the less useful it is for constricting, presenting something of a catch-22. This is perhaps why dynamin-mediated fission relies on a conformational change in the protein (16, 25, 27): without such a reconfiguration, very little constriction is possible.
We conclude that elasticity alone probably does not account for dynamin’s fission capacity. According to our model, fission requires an equilibrium-breaking active process. However, we have only examined the region of parameter space we believe to be most relevant, and we cannot totally rule out the possibility of a passive fission mechanism.
Author Contributions
Z.A.M. performed the numerical and perturbative calculations, and wrote this article; M.D. and J.G. designed and conceived this project; and P.V.-M. contributed to the theoretical framework of this article.
Acknowledgments
M.D. and Z.A.M. were partially supported via the National Science Foundation (NSF) through grant No. CHE-1464926, and J.G. acknowledges financial support from the Consejo Nacional de Ciencia y Tecnología (CONACyT) grant No. 180901.
Editor: Ana-Suncana Smith.
Footnotes
Supporting Materials and Methods are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30932-8.
Supporting Material
References
- 1.Kojima H., Ishijima A., Yanagida T. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA. 1994;91:12962–12966. doi: 10.1073/pnas.91.26.12962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jain R., Shrimal S., Bhattacharya A. Identification and partial characterization of a dynamin-like protein, EhDLP1, from the protist parasite Entamoeba histolytica. Eukaryot. Cell. 2010;9:215–223. doi: 10.1128/EC.00214-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lenz M., Morlot S., Roux A. Mechanical requirements for membrane fission: common facts from various examples. FEBS Lett. 2009;583:3839–3846. doi: 10.1016/j.febslet.2009.11.012. [DOI] [PubMed] [Google Scholar]
- 4.Morgan G.W., Goulding D., Field M.C. The single dynamin-like protein of Trypanosoma brucei regulates mitochondrial division and is not required for endocytosis. J. Biol. Chem. 2004;279:10692–10701. doi: 10.1074/jbc.M312178200. [DOI] [PubMed] [Google Scholar]
- 5.Morlot S., Roux A. Mechanics of dynamin-mediated membrane fission. Annu. Rev. Biophys. 2013;42:629–649. doi: 10.1146/annurev-biophys-050511-102247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schmid S.L., Frolov V.A. Dynamin: functional design of a membrane fission catalyst. Annu. Rev. Cell Dev. Biol. 2011;27:79–105. doi: 10.1146/annurev-cellbio-100109-104016. [DOI] [PubMed] [Google Scholar]
- 7.Sever S., Damke H., Schmid S.L. Garrotes, springs, ratchets, and whips: putting dynamin models to the test. Traffic. 2000;1:385–392. doi: 10.1034/j.1600-0854.2000.010503.x. [DOI] [PubMed] [Google Scholar]
- 8.Williams M., Kim K. From membranes to organelles: emerging roles for dynamin-like proteins in diverse cellular processes. Eur. J. Cell Biol. 2014;93:267–277. doi: 10.1016/j.ejcb.2014.05.002. [DOI] [PubMed] [Google Scholar]
- 9.Roux A., Gerbrand K., Bassereau P. Membrane curvature controls dynamin polymerization. Proc. Natl. Acad. Sci. USA. 2010;107:4141–4146. doi: 10.1073/pnas.0913734107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Praefcke G.J.K., McMahon H.T. The dynamin superfamily: universal membrane tubulation and fission molecules? Nat. Rev. Mol. Cell Biol. 2004;5:133–147. doi: 10.1038/nrm1313. [DOI] [PubMed] [Google Scholar]
- 11.Yoon Y., Pitts K.R., McNiven M.A. Mammalian dynamin-like protein DLP1 tubulates membranes. Mol. Biol. Cell. 2001;12:2894–2905. doi: 10.1091/mbc.12.9.2894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Arimura S., Tsutsumi N. A dynamin-like protein (ADL2b), rather than FtsZ, is involved in Arabidopsis mitochondrial division. Proc. Natl. Acad. Sci. USA. 2002;99:5727–5731. doi: 10.1073/pnas.082663299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ferguson S.M., De Camilli P. Dynamin, a membrane-remodelling GTPase. Nat. Rev. Mol. Cell Biol. 2012;13:75–88. doi: 10.1038/nrm3266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Leipe D.D., Wolf Y.I., Aravind L. Classification and evolution of P-loop GTPases and related ATPases. J. Mol. Biol. 2002;317:41–72. doi: 10.1006/jmbi.2001.5378. [DOI] [PubMed] [Google Scholar]
- 15.van der Bliek A.M. Functional diversity in the dynamin family. Trends Cell Biol. 1999;9:96–102. doi: 10.1016/s0962-8924(98)01490-1. [DOI] [PubMed] [Google Scholar]
- 16.Roux A., Uyhazi K., De Camilli P. GTP-dependent twisting of dynamin implicates constriction and tension in membrane fission. Nature. 2006;441:528–531. doi: 10.1038/nature04718. [DOI] [PubMed] [Google Scholar]
- 17.Shlomovitz R., Gov N.S., Roux A. Membrane mediated interactions and the dynamics of dynamin oligomers on membrane tubes. New J. Phys. 2011;13:065008. [Google Scholar]
- 18.Lenz M., Prost J., Joanny J.F. Mechanochemical action of the dynamin protein. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:011911. doi: 10.1103/PhysRevE.78.011911. [DOI] [PubMed] [Google Scholar]
- 19.Fierling J., Müller M.M., Kulić I.M. Crunching biofilament rings. Europhys. Lett. 2014;107:68002. [Google Scholar]
- 20.Fournier J.B., Dommersnes P.G., Galatola P. Dynamin recruitment by clathrin coats: a physical step? C. R. Biol. 2003;326:467–476. doi: 10.1016/s1631-0691(03)00096-9. [DOI] [PubMed] [Google Scholar]
- 21.Nickerson H.K., Manning S.G. Intrinsic equations for a relaxed elastic line on an oriented surface. Geom. Dedicata. 1988;27:127–136. [Google Scholar]
- 22.Guven J., Vázquez-Montejo P. Confinement of semiflexible polymers. Phys. Rev. E. 2012;85:026603. doi: 10.1103/PhysRevE.85.026603. [DOI] [PubMed] [Google Scholar]
- 23.Vázquez-Montejo P., McDargh Z., Guven J. Cylindrical confinement of semiflexible polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2015;91:063203. doi: 10.1103/PhysRevE.91.063203. [DOI] [PubMed] [Google Scholar]
- 24.Guven J., Valencia D.M., Vázquez-Montejo P. Environmental bias and elastic curves on surfaces. J. Phys. A. 2014;47:355201. [Google Scholar]
- 25.Bashkirov P.V., Akimov S.A., Frolov V.A. GTPase cycle of dynamin is coupled to membrane squeeze and release, leading to spontaneous fission. Cell. 2008;135:1276–1286. doi: 10.1016/j.cell.2008.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Danino D., Moon K.H., Hinshaw J.E. Rapid constriction of lipid bilayers by the mechanochemical enzyme dynamin. J. Struct. Biol. 2004;147:259–267. doi: 10.1016/j.jsb.2004.04.005. [DOI] [PubMed] [Google Scholar]
- 27.Pucadyil T.J., Schmid S.L. Real-time visualization of dynamin-catalyzed membrane fission and vesicle release. Cell. 2008;135:1263–1275. doi: 10.1016/j.cell.2008.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Božič B., Guven J., Svetina S. Direct and remote constriction of membrane necks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014;89:052701. doi: 10.1103/PhysRevE.89.052701. [DOI] [PubMed] [Google Scholar]
- 29.Shnyrova A.V., Bashkirov P.V., Frolov V.A. Geometric catalysis of membrane fission driven by flexible dynamin rings. Science. 2013;339:1433–1436. doi: 10.1126/science.1233920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Landau L., Lifshitz E. Pergamon Press; Oxford, UK: 1959. Theory of Elasticity. [Google Scholar]
- 31.Faelber K., Posor Y., Daumke O. Crystal structure of nucleotide-free dynamin. Nature. 2011;477 doi: 10.1038/nature10369. 566–560. [DOI] [PubMed] [Google Scholar]
- 32.Ford M.G.J., Jenni S., Nunnari J. The crystal structure of dynamin. Nature. 2011;477:561–566. doi: 10.1038/nature10441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fourcade B., Miao L., Zia R.K. Scaling analysis of narrow necks in curvature models of fluid lipid-bilayer vesicles. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1994;49:5276–5286. doi: 10.1103/physreve.49.5276. [DOI] [PubMed] [Google Scholar]
- 34.Morlot S., Lenz M., Roux A. Deformation of dynamin helices damped by membrane friction. Biophys. J. 2010;99:3580–3588. doi: 10.1016/j.bpj.2010.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kozlovsky Y., Kozlov M.M. Membrane fission: model for intermediate structures. Biophys. J. 2003;85:85–96. doi: 10.1016/S0006-3495(03)74457-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.