Abstract
Collagen is the fundamental structural component of a wide range of connective tissues and of the extracellular matrix. It undergoes self-assembly from individual triple-helical proteins into well-ordered fibrils, a process that is key to tissue development and homeostasis, and to processes such as wound healing. Nucleation of this assembly is known to be slowed considerably by pepsin removal of short nonhelical regions that flank collagen’s triple helix, known as telopeptides. Using optical tweezers to perform microrheology measurements, we explored the changes in viscoelasticity of solutions of collagen with and without intact telopeptides. Our experiments reveal that intact telopeptides contribute a significant frequency-dependent enhancement of the complex shear modulus. An analytical model of polymers associating to establish chemical equilibrium among higher-order species shows trends in G′ and G″ consistent with our experimental observations, including a concentration-dependent crossover in G″/c around 300 Hz. This work suggests that telopeptides facilitate transient intermolecular interactions between collagen proteins, even in the acidic conditions used here.
Introduction
Collagen is the predominant structural protein in vertebrates, where it represents more than one-quarter of the protein in our bodies. Collagen’s supramolecular structure as ordered fibrils provides connective tissues their ability to withstand stress and confers mechanical properties to the extracellular matrix that play a role in influencing cellular development (1, 2, 3). Given its preponderance and easy extraction from tissues, it is not surprising that collagen has found use in a wide variety of materials applications (4). The majority of these physiological and materials functions rely on the ability of collagen to form hierarchically-structured assemblies.
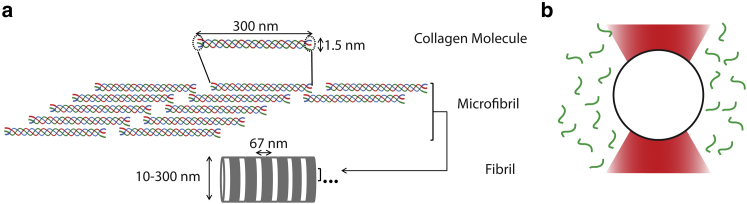
From isolated triple-helical collagen proteins, collagen forms highly ordered fibrils, whose striking degree of ordering is seen in its so-called “D-banding,” a striped pattern that reflects the differential molecular density that repeats along the fibril axis (Fig. 1 a) (5). Self-assembly of collagen can be replicated in vitro, and leads to fibrils exhibiting the same D-banding as observed in tissue-extracted fibrils. For this reason, in vitro manipulations are widely used to study collagen self-assembly.
Figure 1.
(a) Hierarchical organization pathway of fibrillar collagen. A collagen protein consists of an extended triple helix, flanked at both ends by short nonhelical domains called telopeptides that are indicated within the dashed circles. Collagens associate laterally to form well-ordered fibrils exhibiting a characteristic D-banding pattern, associated with overlap and gap regions of higher and lower collagen density along the fibril, and indicated by the white/dark striped pattern in the bottom schematic. (b) Schematic of a bead trapped via optical tweezers in a solution of collagen molecules (not to scale). Short-range thermal fluctuations of the bead are used to determine the viscoelastic properties of the surrounding collagen solution. To see this figure in color, go online.
Fibril assembly occurs in three phases: nucleation, in which a critical number of collagen molecules form a core association; growth, representing the lateral and longitudinal assembly into fibrils; and saturation, in which the solution is depleted of free collagen proteins and fibril growth terminates. Kinetics of this assembly process are affected by many different parameters, including solution conditions such as pH, ionic strength, identity of ions, and temperature (5, 6, 7, 8, 9). They are also influenced by collagen’s molecular composition. Most strikingly, the removal of collagen’s ends, called telopeptides, drastically slows fibril assembly (10, 11, 12). Telopeptides contribute less than 5% of the overall molecular weight and length to the 300 kDa, 300-nm-long collagen protein, and unlike the rest of collagen, are not triple helical. Because they are not bound in a triple helix, they can be proteolytically cleaved by noncollagenolytic proteases, a process that is performed using pepsin during high-yield extraction of collagen from tissue.
Although telopeptides influence the kinetics of fibril formation, they do not strongly affect fibrillar structure: the information required for assembly is encoded within the sequence and structure of the triple helix itself (10, 13). In vivo, telopeptides serve a vital role by forming intermolecular cross-links that stabilize fibrillar organization and contribute to tensile strength (14, 15). X-ray studies have revealed that the C-terminal telopeptides of one collagen in a fibril lie directly adjacent to the key matrix metalloprotease (MMP) cleavage site of a neighboring collagen, suggesting that their presence may play a role in regulating collagen fibril degradation (16). Supporting the physiological role of telopeptides, telopeptide fragments have been used as markers for disease progression, for example, in osteoporosis, arthritis, and cancer (17, 18, 19, 20). Despite their specific locations within fibrils, the presence or absence of telopeptides does not influence the lateral forces between collagens within a fibril, and telopeptides have been ascribed predominantly a catalytic, rather than structural, role in fibril formation (13).
The question remains as to how telopeptides facilitate more rapid assembly of collagen into fibrils. Specific, transient interactions between C-telopeptides and the MMP binding region of collagen have been posited to facilitate assembly, since blocking these interactions inhibits fibril formation (21). To date, to our knowledge, there has been no direct evidence supporting the proposed transient nature of this interaction, which is critical in promoting rapid fibril assembly.
In this study, we use the technique of microrheology to assess the interactions between collagens in solution. The high bandwidth of this technique permits the interpretation of our findings in terms of timescales of polymer dynamics. We compare the complex shear moduli of collagens with intact versus pepsin-removed telopeptides to determine how telopeptides contribute to interprotein interactions. Examination of the frequency and concentration dependence of these moduli provides insight into the mechanism underlying these telopeptide-enhanced interactions. We develop a chemical equilibrium model of Rouse polymers establishing concentration-dependent associations, which predicts qualitatively similar concentration- and frequency-dependent shear moduli as observed in experiment. By comparison of our results with predictions of this and other models invoking transient interactions, we find evidence of telopeptide-enhanced transient interactions between collagens in solution.
Materials and Methods
Materials and sample preparation
Collagen
Type I collagen from rat tail tendon (Cultrex; Trevigen, Gaithersburg, MD) was obtained in two different forms: acid-soluble (including telopeptides; “telo-collagen”) and pepsin-solubilized (telopeptides proteolytically digested by pepsin; “atelo-collagen”). Serial dilutions from the stock concentration of 5 mg/ml in 20 mM acetic acid were prepared into 20 mM acetic acid (pH 3.2).
Pepsin digestion
To control for any possible differences between commercially obtained telo- and atelo-collagen, we prepared atelo-collagen from telo-collagen by pepsin digestion. Reactions were performed by mixing collagen and pepsin (Sigma-Aldrich, Oakville, Canada) at concentrations of 4 and 0.4 mg/ml, respectively, and incubating for 3 days at 4°C (pH 3.2). A control sample was prepared by diluting telo-collagen to the same final concentration and incubating under similar conditions. To verify removal of telopeptides and assess sample purity, SDS-PAGE analysis was performed (Supporting Information and Fig. S2).
For real-time monitoring of telopeptide removal in microrheology measurements at room temperature, a lower concentration of pepsin was used such that the final concentrations of collagen and pepsin were 2 mg/ml and 0.5 μg/ml respectively; these measurements were performed at pH 2.2.
Microrheology sample preparation
For microrheology experiments, carboxylate-functionalized polystyrene microspheres with diameter ∼2.10 μm (Spherotech, Lake Forest, IL) were added to collagen solutions at a final concentration of ∼5 × 10−4% w/v. All measurements were performed at room temperature and, except for the real-time cleavage measurements, at pH 3.2. Samples (∼20 μl) were pipetted into optical tweezers sample chambers (22).
Collagen characterization
ELISA assays
Concentrations of collagen samples were quantitatively verified by ELISA (23). Wells in a 96-well plate were coated with collagen (concentration range: 0–10 μg/ml, solvent: 1X PBS) by overnight incubation at 4°C. (The use of a trapping antibody was found empirically not to be necessary.) Collagen molecules were detected with a biotinylated mouse monoclonal antirat type I collagen antibody (Chondrex, Redmond, WA) that was probed using HRP-conjugated streptavidin (Jackson ImmunoResearch, West Grove, PA).
Dynamic light scattering
Dynamic light scattering (DLS) experiments were performed to characterize collagen size, using an ALV DLS/SLS 5000 spectrometer/goniometer (ALV-Laser, Langen, Germany) with a laser power of 23 mW at a wavelength of λ0 = 632.8 nm. For these experiments, atelo-collagen (either directly from the stock solution or after ultracentrifugation) was tested at 45°. For the noncentrifuged or ultracentrifuged samples, data were respectively collected for 1 h or 10 min. The normalized autocorrelation function of the intensity of the scattered light was then calculated.
Fibril formation
Fibril formation was induced by adding 10X PBS buffer with excess phosphates to collagen stock solutions to attain the desired final concentration of collagen, and salt concentrations of 273 mM NaCl, 5 mM KCl, 42 mM Na2HPO4, and 9 mM KH2PO4, pH = 6.9.
Turbidity
The kinetics of fibril formation by telo- and atelo-collagen were monitored by changes in solution turbidity, by recording the increasing optical density at 347 nm (BioTek Synergy plate reader; BioTek, Winooski, VT) as a function of time as fibrils assemble. Optical densities are presented normalized by plateau value (13). Fibrils were formed as described in the Fibril formation section, at 30°C and at collagen concentrations of 1.5 mg/ml.
Atomic force microscopy
For structural characterization, telo- and atelo-collagen fibrils were imaged using an atomic force microscope (AFM). For these fibril experiments, atelo-collagen was prepared as described above. Fibrils were formed as described above, at room temperature (∼21°C) and at collagen concentrations of 1 mg/ml. The telo- and atelo-collagen fibrils were deposited on freshly cleaved mica sheets (Ted Pella, Redding, CA) adhered on glass slides using a double-sided tape and left to dry overnight at room temperature. To remove salt precipitates, the slides were washed with copious amounts of ddH2O and air dried before imaging. The collagen fibrils were imaged with a Bruker Catalyst AFM in peak-force tapping mode using a ScanAsyst-Air probe (Bruker, Santa Barbara, CA; stiffness κ = 0.4 N/m). A 3 × 3 μm area was scanned at 0.5 Hz. The z-range was set to 2 μm.
Passive microrheology using optical tweezers
Our microrheology experiments are shown schematically in Fig. 1 b, and a detailed description can be found in (22). An optical tweezers instrument was used for microrheology assays (22, 24, 25). Thermally induced short-range position fluctuations of optically trapped probe particles (polystyrene microspheres) were detected using a quadrant photodiode at a bandwidth of 100 kHz. Traces exhibiting large deviations in mean position, for example, due to rare interactions with contaminants, were excluded from further analysis.
The complex response function of the solution can be obtained from the power spectrum P(f) of particle fluctuations inside the trap (26). To do this, the complex response function (A∗(f) = A′(f) + iA″(f)) is obtained using the fluctuation-dissipation theorem (Eq. 1) followed by a Kramers-Kronig relation (Eq. 2):
| (1) |
| (2) |
where kB is the Boltzmann constant, and T is the temperature in Kelvin.
Viscoelastic properties of the medium in the form of the frequency-dependent complex shear modulus (G∗(f) = G′(f) + iG″f)) were determined from the complex response function using the following generalized Stokes-Einstein relation:
| (3) |
where R is the bead radius. The real part of the complex shear modulus represents the elastic (storage) modulus and the imaginary part the viscous (loss) modulus of the system.
At high frequencies, the extracted G′(f) is underestimated due to finite sampling and the infinite integration range of the Kramers-Kronig relation (Eq. 2) (26); for this reason, the values of G′(f) presented in this work extend only up to 4 kHz. Furthermore, in our system the elastic modulus (G′) contains information on elasticity of both the trap and the medium, and was corrected by removing the trap’s contribution (determined from the lowest-frequency measured value of G′ independently for each bead; G′trap ≈ 4 Pa) to give G′sample(f) = G′measured(f) − G′trap (22, 26). This correction method is supported by the apparent low-frequency plateau in G′measured (≈G′trap) even at the highest concentrations of collagen and has been validated by comparison with other rheological techniques (22). Different trap subtraction methods provide slightly different results for the lowest-frequency G′sample (f) values (Fig. S3), so G′ values are presented only for f > 10 Hz, where results are independent of correction method. The viscous modulus does not suffer from either of these effects over the presented frequency range of 1–20 kHz. The reduced viscous modulus is obtained by subtraction of solvent contribution: G″R(f) = G″measured(f) – 2πηsf, where ηs represents solvent viscosity. For ease of presentation and analysis, values of G∗(f) were averaged into logarithmically spaced frequency bins.
Model of transiently interacting collagen molecules
In our chemical equilibrium model, solutions of transiently interacting collagen molecules assume a concentration-dependent equilibrium mixture of unimers, dimers, trimers, etc. We assume that multimers grow and decrease in size only via addition and subtraction of one unimer at a time and that the binding and unbinding rates, kon and koff, respectively, are the same for all chains, that is,
and so forth. This leads to the following set of equations for the ratios of concentration of these species at equilibrium:
| (4) |
where Keq = kon/koff is the equilibrium constant. Concentrations are constrained by the total collagen concentration in solution, C, as
| (5) |
Equations 4 and 5 can be solved to give
| (6) |
This provides the unimer concentration for any given Keq and C. The concentrations of multimers follow from Eq. 4.
We used a transversely constrained Rouse model to describe the viscoelastic behavior of the above-mentioned system (27). In this model, entangled chains provide constraints on how the Rouse chains relax: segments longer than the distance between entanglements can relax only in the longitudinal direction, whereas shorter segments relax in longitudinal and transverse directions. This leads to the following time-dependent shear-stress relaxation modulus:
| (7) |
where
| (8) |
In these equations, n = 1, 2, 3, …, N represent unimer, dimer, trimer, …, N-mer, respectively, with the N-mer being the longest chain included in the calculation; each of these chains has a (number) concentration cn and a contour length Ln = nL, where L is the contour length of an individual collagen chain (300 nm). Although chains may associate to form branched structures, our model assumes linear growth for ease of calculation. p indexes the relaxation modes of the respective Rouse chain, which contains Nn (= nL/b) Kuhn segments, each with Kuhn length b. The fundamental Rouse relaxation time of the chain τR also depends on ζ, the segmental drag coefficient per Kuhn segment. Zn defines the lowest mode where entanglements do not constrain the transverse motion of the polymer, and is given by
| (9) |
where a is the characteristic distance between entanglements. We assume a to depend on the total number density of collagen molecules d as , where a0 is a dimensionless parameter.
The frequency-dependent storage and loss moduli, respectively, are then calculated as follows:
| (10a) |
| (10b) |
Parameter values can be found in the Supporting Material (Table S1).
Results and Discussion
Effects of telopeptides on fibril formation
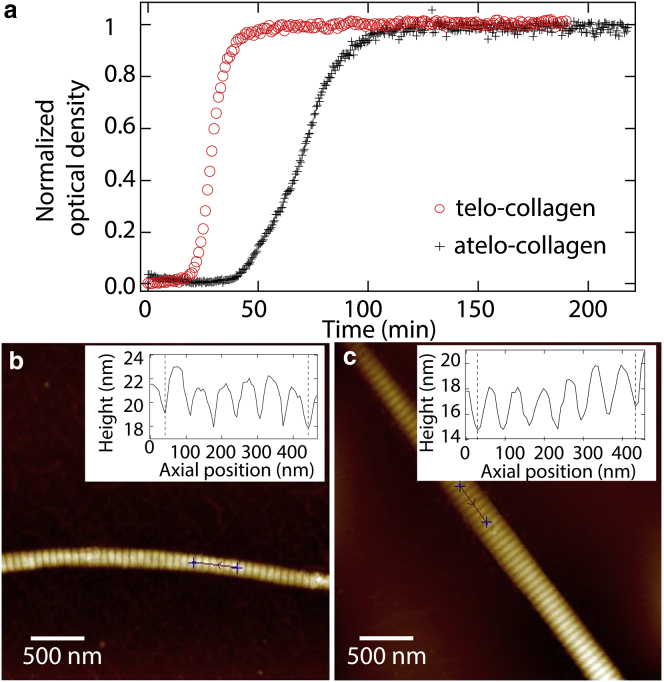
The kinetics of collagen assembly have long been known to depend on the presence of intact telopeptides (10). To verify this for our samples, the kinetics of fibril formation were monitored via the time-dependent optical density of collagen undergoing self-assembly into fibrils (6). Fig. 2 a compares the time dependence of fibril formation when telopeptides are intact with when they have been cleaved by pepsin. Throughout this article, we refer to these samples as “telo-collagen” and “atelo-collagen,” respectively, though emphasize that short stubs of telopeptides are expected to remain following pepsin treatment (28, 29). These turbidity curves display the three characteristic regimes of assembly: a lag phase before the onset of increase in optical density during which fibrils nucleate, a growth phase during which they increase in size, and a plateau phase in which saturation has occurred (5, 6, 7). As found previously (10, 11, 12), fibril nucleation kinetics are significantly slowed following pepsin digestion of telopeptides.
Figure 2.
Kinetics of collagen fibril assembly and structural characterization of fibrils. (a) The effect of telopeptide removal on the kinetics of collagen fibril formation is shown. Open red circles (telo-collagen) and black crosses (atelo-collagen) represent means from three replicate measurements of optical density during self-assembly into fibrils. (b and c) Representative AFM images of self-assembled telo- and atelo-collagen fibrils, respectively, are shown. Insets show the variations in the height of collagen fibrils along their fibrillar axes, which exhibit D-banding periodicities of ∼67 nm, as seen in native collagen type I fibrils. To see this figure in color, go online.
Collagen fibrils were imaged by AFM. Fig. 2, b and c, show representative AFM images of telo- and atelo-collagen fibrils, respectively, reconstituted in vitro. These images verified that both telo- and atelo-collagen form well-ordered fibrils with similar D-banding periodicities, as shown in the corresponding insets.
Effects of telopeptides on viscoelastic properties
Microrheology experiments were performed to measure how telopeptides affect the complex shear modulus of collagen solutions. Via determination of the system’s frequency-dependent complex shear modulus, microrheology has previously been used to show evidence of transient protein-protein interactions, for example, between filamentous actin and its cross-linking protein α-actinin (30). We sought similar signatures of interaction arising from telopeptide-associated transient cross-linking between collagen molecules in solution. Using optical-tweezers-based microrheology, we determined the local viscoelastic properties of collagen samples via their complex shear moduli: G∗(f) = G′(f) + iG″(f). Because we wished to study interactions associated with initial stages of collagen association, we performed our measurements in acidic conditions that do not promote assembly into fibrils (22). The relevance of these measurements to the mechanism of fibril assembly is discussed below.
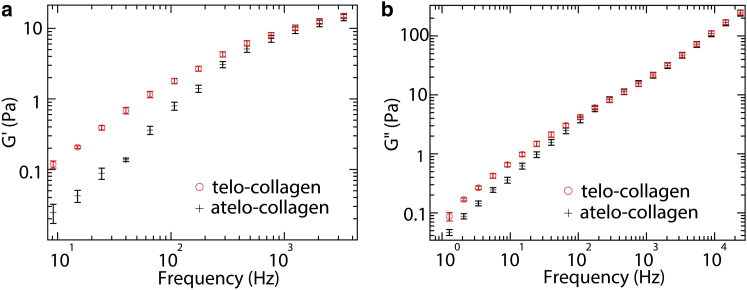
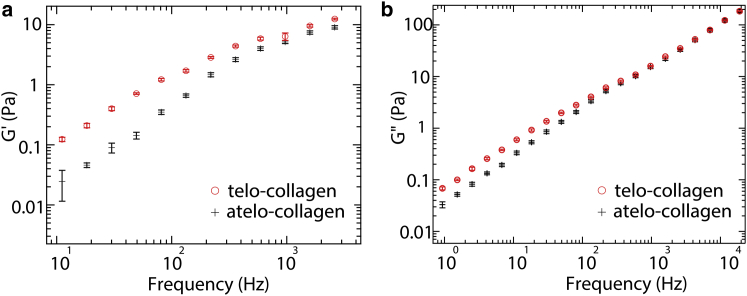
Fig. 3 shows measured elastic and viscous moduli, G′(f) and G″(f), determined for commercially obtained telo- and atelo-collagen molecules in acidic solution at nominal concentrations of 2 mg/ml. This concentration lies above the estimated overlap concentration of c∗ ≈ 1 mg/ml (22, 31). A clear feature is the significantly higher elastic moduli of the telo-collagen solution below 300 Hz. This suggests that intact telopeptides contribute increased elasticity to the solutions, for example, by enhancing interactions between collagen molecules.
Figure 3.
Contribution of telopeptides to the viscoelastic properties of commercially obtained collagen: (a) elastic and (b) viscous moduli for 2 mg/ml collagen with intact telopeptides (open red circles) and collagen with pepsin-removed telopeptides (black crosses). Presented values are averages from 10 measurements of different probe particles, and error bars represent the standard errors of the means. To see this figure in color, go online.
It is possible that these observed differences between telo- and atelo-collagen arise not from the presence or absence of telopeptides but instead simply from differences between commercial collagen samples, e.g., age-dependent chemical composition. To determine whether changes in viscoelasticity of collagen can result from pepsin digestion, we performed microrheology experiments designed to observe directly the impact of proteolytic removal of telopeptides. Incubation of telo-collagen with a low concentration of pepsin results in gradual removal of telopeptides; if this affects the interactions between collagens in solution, a commensurate reduction in the complex shear modulus of collagen solutions should result. Indeed, the data in Fig. 4 show that a gradual reduction in elasticity and viscosity was observed as telopeptides were cleaved by pepsin. In control experiments, the addition of pepsin to an atelo-collagen sample had no effect on solution viscoelasticity (Fig. S4). This indicates that it is pepsin’s activity (and availability of substrate) rather than its presence that alters the complex shear modulus. These digestion experiments establish that reductions in collagen solution viscoelasticity correlate with removal of telopeptides, and furthermore demonstrate the ability to read out, in real time, the remodeling of viscoelastic response by enzymatic activity.
Figure 4.
Gradual time-dependent reduction of (a) elastic and (b) viscous moduli of 2 mg/ml collagen as telopeptides are cleaved by 0.5 μg/ml pepsin. Symbols represent means of moduli from five independent measurements in each stated time interval, and error bars represent the standard errors of the mean. To see this figure in color, go online.
To examine more carefully the differences between telo- and atelo-collagen, we moved from commercial samples and gradual removal of telopeptides to a comparison of telo- and atelo-collagens of identical origin. To do so, we prepared atelo-collagen by pretreating telo-collagen with a sufficiently high concentration of pepsin to drive the reaction to completion. SDS-PAGE analysis verified the expected removal of telopeptides under these conditions (Fig. S2). Fig. 5 shows the complex shear moduli obtained for telo- and atelo-collagen solutions, which exhibit differences in response consistent with results shown in Figs. 3 and 4. (To ensure identical concentrations for telo- and atelo-collagen, pepsin and its cleavage products were not filtered out of these samples.) The results of the commercial and the prepared atelo-collagen differ slightly in value, which could be a result of differences in concentration, treatment protocols during extraction from tissue, and/or condition of the tissue from which the collagen was harvested. These quantitative differences are in any case minor. The collagen studies of Fig. 5 demonstrate that elastic and viscous moduli are substantially reduced over a range of frequencies (<300 Hz for G′ and <100 Hz for G″) following pepsin treatment to remove telopeptides, supporting the observations with commercially available samples (Fig. 3). The significant reduction in G′ is also consistent with findings from lower-frequency bulk rheology (31).
Figure 5.
A reduction in complex shear moduli of collagen solutions results from pepsin treatment to remove telopeptides: (a) elastic and (b) viscous moduli for telo-collagen (open red circles) and atelo-collagen (black crosses) solutions at concentrations of 2 mg/ml. Symbols indicate mean moduli, measured here from five different probe particles, and error bars represent standard errors of the mean values. To see this figure in color, go online.
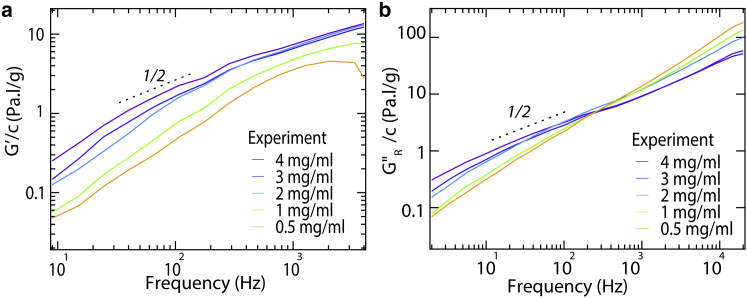
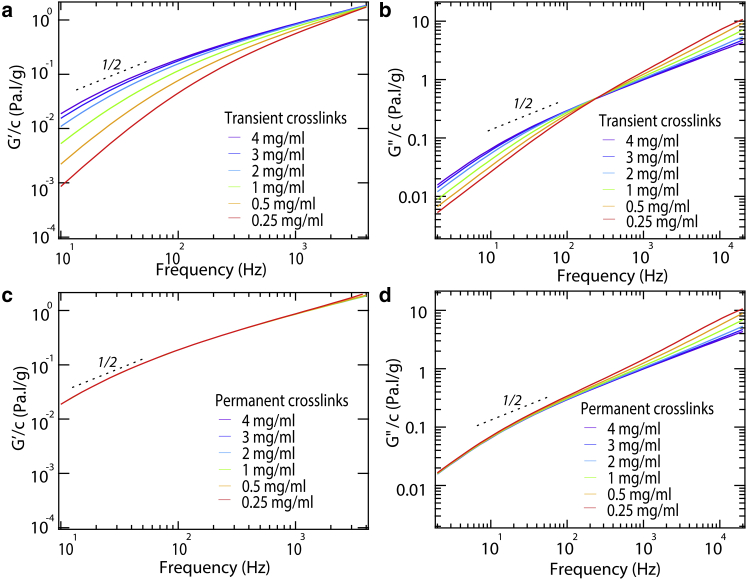
Taken together, our results clearly demonstrate an enhanced viscoelasticity of solutions of collagen containing intact telopeptides, compared with collagen whose telopeptides have been digested by pepsin. Treatment with pepsin leads to a significant reduction in both elastic and viscous moduli at intermediate frequencies, a trend that continues to the lowest frequencies investigated. Below, we outline the reasons that this difference is attributed to telopeptides and present a proposed mechanism involving telopeptide-associated transient interactions between collagens. In discussing possible molecular mechanisms that could be responsible for the enhanced moduli found in our studies, we focus on two key features: 1) the theoretical correlation of lower-frequency viscoelastic response with longer-range relaxation modes; and 2) the concentration-dependent change in the frequency scaling of moduli, with a particular focus on G″(f). Interestingly, both telo- and atelo-collagen exhibit a crossover frequency in G″R/c, in which higher concentrations of collagen contribute proportionally more response at lower frequencies and less at higher frequencies (Figs. 6 and S7). As shown below, this crossover behavior can be explained by the proposed model.
Figure 6.
Neither the elastic nor viscous moduli of telo-collagen depend linearly on concentration, as seen by the lack of convergence of (a) G′/c and (b) GR″/c over a wide range of collagen concentrations c. Dotted curves indicate a logarithmic slope of ½. To see this figure in color, go online.
Considering the longer-range modes that give rise to enhanced viscoelastic response, telopeptide-containing collagens appear to form longer-range structures than samples with telopeptides removed. The slight decrease in contour length following pepsin treatment (<5%) is not predicted to affect significantly the relaxation times of isolated chains in solution (27), and therefore cannot explain the significant (∼eightfold) decrease in elasticity at intermediate frequencies resulting from the removal of telopeptides. Instead, we examine the source of telopeptide-associated larger-scale structures in solution. Are these simply an artifact of preexisting permanently cross-linked collagens in these tissue-derived samples? Or do they arise from transient associations (21) between collagens? Here we discuss how the microrheology results can distinguish between these competing models.
Presence of permanently cross-linked collagens?
Due to the involvement of telopeptides in intermolecular cross-links within a mature collagen fibril, long-range relaxation modes in telopeptide-intact, tissue-derived collagen could arise from permanently cross-linked structures. We excluded the possibility that large-scale aggregates in telo-collagen are responsible for the enhanced shear modulus. Although our samples do contain sparse large aggregates, as seen by DLS (Fig. S5) and consistent with previous findings (32), removal of these via ultracentrifugation did not significantly alter the complex shear modulus of our collagen samples (Fig. S6). This may be because our analysis routines exclude infrequent time traces exhibiting large amplitude deviations that could arise from interaction of large aggregates with a trapped particle. Given these findings, we conclude that large aggregates are very sparse in solution and do not contribute to the observed differences in viscoelastic properties between telo- and atelo-collagen.
Although ultracentrifugation segregates large aggregates, there remains the possibility that smaller-scale telopeptide-cross-linked species, such as permanent dimers and trimers of triple helical collagen, remain in our sample. Gel electrophoresis results do not show appreciable intensity for such intermolecularly cross-linked multimers (Fig. S2), so if present, these represent an estimated <5% fraction of total collagen content. In the dilute limit, solution moduli of noninteracting chains are expected to scale linearly with total collagen concentration. This does not occur for collagen (Fig. 6 and (22)). In the high-concentration limit of a highly entangled network, 5% permanently cross-linked multimers are not predicted to increase the elastic modulus by as much as the eightfold observed here (Fig. 5) (33, 34). Below, we also show how a polymer dynamics model comprising permanently cross-linked multimers of collagens fails to agree with our concentration-dependent observations. Thus, it is unlikely that permanently cross-linked multimers are responsible for the significant differences in viscoelastic response between telo- and atelo-collagen samples.
Transiently associating collagen chains?
Transient interactions between collagen chains facilitated by intact telopeptides would produce longer-range structures. As guidance for signatures of transient interactions, we first looked to other microrheology studies of transient cross-linking between protein filaments. The complex shear modulus of filamentous actin networks increases as transient-cross-linking proteins are added (30, 35), similar to the telopeptide-dependent shear modulus of collagen solutions (Fig. 4). A peak in G″(f) at the off-rate of α-actinin dissociation from actin provided a clear signature of the well-defined, transient cross-link involved in network mechanics (30), a signature that is not exhibited here. Telopeptide dissociation might not produce a clear peak in G″(f) for a number of reasons: an interaction lifetime longer than our measurement time (36); a range of interaction times arising from the distinct sequences of N- and C-terminal telopeptides (and chemically distinct α1 and α2 sequences within type I collagen) (11, 21); and an inherently low density of “cross-linker”-“target” interaction sites (limited to a maximum of one set of telopeptides per 300 nm triple helix).
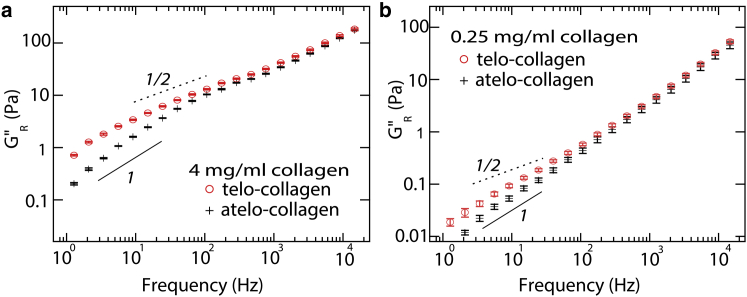
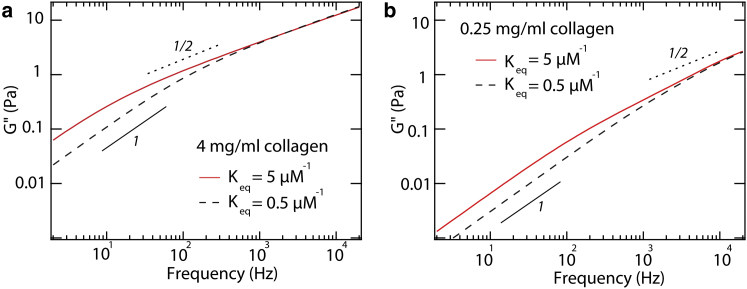
The transient nature of cross-linking in the α-actinin system was also seen in the frequency-scaling of G∗(f). At low frequencies, G′ and G″ increased as f1/2 (30). Broedersz et al. explained this power-law scaling using a network model, where unbinding of cross-linkers in a highly connected network gives rise to a scaling of G∗ f 1/2 below this unbinding rate (30). Our experiments show the reduced viscous modulus (corrected to remove contributions from solvent) to scale as GR″ f α with α ∼ ½ at intermediate frequencies (Fig. 7). This is particularly noticeable for telo-collagen and at high concentrations. An exponent of α ∼ ½ is consistent with a broad spectrum of relaxation times resulting from detachment of 1, 2, 3, … transient cross-links in a network; however, distinct from the predictions of the network model, our data demonstrate a turnover in frequency scaling toward α ∼1 at lower frequencies (Fig. 7). This implies that, if our system exhibits network-like structure facilitated by transient cross-links, it is only on a small scale and does not have the same broad range of connectivity as for actin.
Figure 7.
Comparison of reduced viscous moduli of telo- and atelo-collagen solutions at two concentrations: (a) 4 mg/ml and (b) 0.25 mg/ml. Lines with logarithmic slopes of 1 (solid line) and 0.5 (dashed line) are plotted for comparison. Symbols represent means of 10 independent measurements, with error bars indicating the standard errors of the mean. To see this figure in color, go online.
Alternatively, a scaling of α = ½ is exhibited at intermediate frequencies in the complex shear modulus of Rouse chains (37). If we consider collagen molecules as Rouse chains, what mechanism could produce differences between the moduli of telo- and atelo-collagen solutions? In the following model, we assume that collagens associate to establish concentration-dependent chemical equilibrium among Rouse chains of different lengths, each of which has a characteristic relaxation spectrum. Complex shear moduli predicted by this model exhibit similar concentration- and telopeptide-dependent behavior as observed experimentally.
Collagen modeled as multimeric polymer assemblies in chemical equilibrium
We model collagen molecules as Rouse chains that associate to form multimeric assemblies. Although telopeptide-based interactions leading to fibril formation are likely to result in dimers, trimers, etc., of branched structure (see Fig. 10 a) (21), for simplicity our model assumes that collagen molecules associate end-to-end. Telopeptide-associated interactions therefore are modeled to result in linear multimers whose lengths are integer multiples of a single collagen’s contour length (L = 300 nm). A solution of transiently interacting collagen molecules can be regarded as a mixture of unimers, dimers, trimers, etc., in chemical equilibrium. Importantly, if the lifetime of transient interactions is longer than the measurement time (1 s here), then the relaxation dynamics are determined by this steady-state mixture and detachment kinetics can be ignored (38). This is an assumption of our treatment. The fraction of total collagen existing in each of these forms depends on the total collagen concentration and the equilibrium constant Keq (Fig. S1). As the total collagen concentration increases, the solution changes from one predominantly occupied by unimers to a solution possessing an increasing fraction of dimers, trimers, and higher-order multimers. This shift in the composition of the solution to longer chains introduces to the system new relaxation modes with longer timescales.
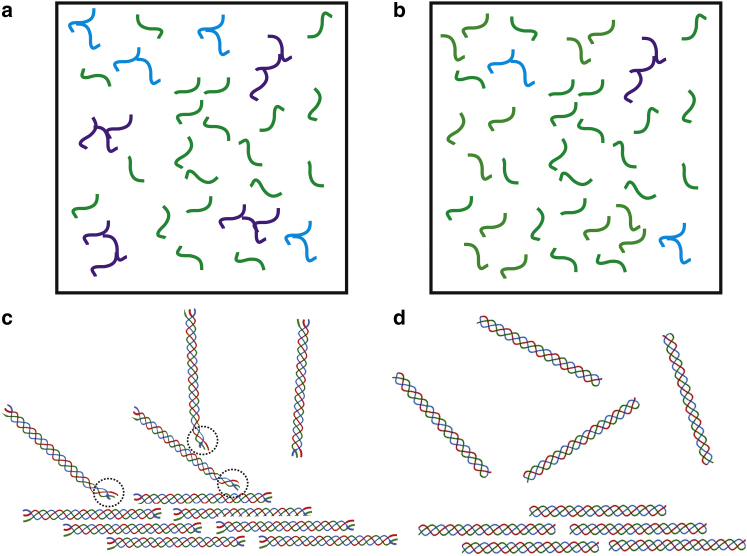
Figure 10.
Schematic illustrating how telopeptides are proposed to contribute to collagen interactions. (Top panels) Transient telopeptide-facilitated intermolecular interactions between collagen molecules in acidic solution form a greater proportion of dimers, trimers, and higher-order multimers than in collagen with pepsin-digested telopeptides. Multimeric species are colored differently for ease of viewing. Diagram is not to scale. (a) Telo-collagen and (b) atelo-collagen. (Bottom panels) Fibrils can nucleate in salt solutions at neutral pH from either telo- or atelo-collagen. (c) Telopeptides facilitate fibril formation via “toe-hold” formation on a specific docking site of a neighboring triple helix (circled), restricting the diffusional search for chain alignment. (d) Pepsin-treated collagen lacks extensive telopeptides and therefore aligns in register following a longer, less constrained three-dimensional search in solution. To see this figure in color, go online.
Each of these polymer species (unimer, dimer, etc.) is modeled as a Rouse chain, with intramolecular relaxation timescales as given in (27). At higher concentrations where the solution is no longer in the dilute limit (c∗ for collagen in acidic conditions has been estimated at 1 mg/ml (22, 31)), transverse relaxation of slower, longer-range modes is constrained. From the spectrum of (partially constrained) Rouse modes for each species, a stress-relaxation modulus is calculated; the contribution of the modulus of each species to the overall relaxation modulus of the system is then weighted by its number concentration in solution (Eq. 7). Transformation provides the predicted frequency-dependent complex shear modulus (Eq. 10).
We model the differences between telo- and atelo-collagen with two different values of Keq, differing by an order of magnitude and similar to that suggested in binding assays (see Supporting Material for a discussion of all model parameters) (21); Keq,telo = 5 μM−1 and Keq,atelo = 0.5 μM−1, respectively. We choose a nonzero Keq for the atelo-collagen because the intact short telopeptide stubs (28, 29) following pepsin digestion may contribute to weak binding interactions, as may specific interactions between other parts of the chains.
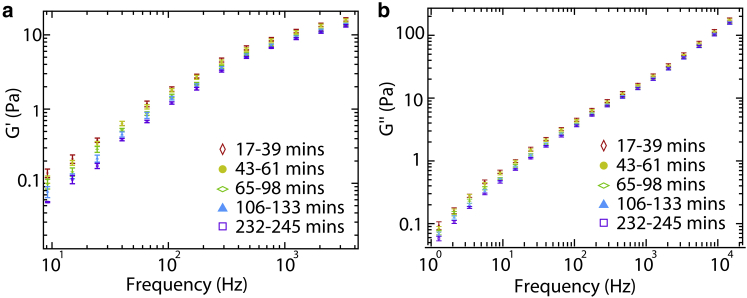
Fig. 8 shows the model predictions of G″ for telo- and atelo-collagen at high and at low total collagen concentration. The model mirrors the experimental findings of Fig. 7 in showing enhanced low-frequency G″ for telo-collagen solutions with respect to atelo-collagen, an enhancement that grows with increasing collagen concentration. This concentration dependence is expected from model assumptions: at low collagen concentrations both telo- and atelo-collagen are predominantly found as unimers, while as concentration increases, telo-collagen more strongly populates higher-order multimers (Fig. S1).
Figure 8.
Model predictions of the viscous moduli of telo- and atelo-collagen solutions at two concentrations: (a) 4 mg/ml and (b) 0.25 mg/ml. Lines with logarithmic slopes of 1 (solid line) and 0.5 (dashed line) are plotted for comparison. To see this figure in color, go online.
As seen in Fig. 9 b, our model also captures the observed higher-frequency decrease in GR″/c with concentration (Fig. 6), unexplained behavior observed previously for collagen solutions (22). This effect is exemplified by the crossover response exhibited in experimental GR″/c curves at different collagen concentrations, a response recapitulated by our model. Below the crossover frequency, GR″/c increases with increasing concentration. This is expected because increased collagen concentration shifts the equilibrium toward longer chains leading to enhanced contribution from low frequency (longer-range) relaxation modes. On the other hand, GR″/c decreases with increasing concentration above the crossover frequency. This observation may seem peculiar: How could a molecule in a concentrated solution contribute less to GR″ than one in a dilute solution? The transversely constrained Rouse model provides a plausible answer to this question. In this model, segments of a molecule longer than the distance between entanglements are constrained to relax only via longitudinal modes. The inability of these modes to undergo transverse relaxation explains why GR″/c decreases with increasing concentration in this frequency regime. As collagen concentration increases, the distance between entanglements becomes shorter, causing more modes to exhibit restricted relaxation dynamics. Similar behavior was exhibited by atelo-collagen samples (Fig. S7).
Figure 9.
Transiently versus permanently cross-linked collagen models predict distinct frequency-dependent behavior of G′/c (left) and GR″/c (right) for telo-collagen over a wide range of collagen concentrations c. Model predictions assuming transient cross-links with Keq,telo = 5 μM−1 are presented in (a) and (b), whereas predicted behavior arising from permanent cross-links is shown in (c) and (d). In (c), all curves superimpose. Dotted curves indicate logarithmic slopes of ½. To see this figure in color, go online.
By adapting the parameters in our model, we showed that permanent cross-links do not produce a crossover response. To examine the concentration-dependent response resulting from hypothetically permanent crosslinks, we assumed that all concentrations of collagen contained the same fractional composition of unimer:dimer:trimer:…; these were fixed at the levels predicted for 4 mg/ml telo-collagen (Fig. S1). This gross overestimate of the amount of higher-order species (see above and Fig. S2) was chosen to emphasize the contributions of permanently cross-linked species. Fig. 9 contrasts the predictions of our model for permanent and transient association, for both elastic and viscous moduli. The disagreement between experiment and the permanently cross-linked model is starkest for G′/c: the permanently cross-linked model predicts the superposition of all curves in the experimentally accessible frequency range, in contrast both with the experimentally observed enhancement in G′/c with increasing collagen concentration (Fig. 6 a) and with the predictions from the transient association model (Fig. 9 a). The low-frequency (<80 Hz) concentration scaling of GR″/c also exhibits a marked difference between the permanently cross-linked and the transiently interacting collagen scenarios, the latter of which shows better qualitative agreement with the experimental data.
This model of collagen as transiently interacting Rouse chains, exhibiting concentration-dependent entanglement, makes predictions of the frequency- and concentration-dependent behavior of the complex shear modulus that are in qualitative agreement with our results on collagen solutions. It supports the idea of transient associations between chains whose strength depends on the extent of telopeptides remaining at the ends of collagens. The model does not show quantitative agreement with our results, in particular underestimating the magnitude of the moduli by at least an order of magnitude. Quantitative disagreement between the model and experimental values may result from many factors. These include neglecting hydrodynamic interactions; the assumption of linear rather than branched association between chains; the assumption that the distance between entanglements depends only on collagen concentration and not its association into higher-order structures; and the omission of reptation dynamics at higher collagen concentrations. The participation of additional dynamics beyond those assumed in our model is suggested by the lower-frequency inflection in the experimental data not captured by the model (Figs. 7 and 8). Furthermore, our model treats collagen as a Rouse chain, a flexible polymer with a persistence length of 15 nm. Although this value is at the low end of literature values for persistence length (22), model predictions are qualitatively preserved upon a doubling of persistence length (data not shown). These values for lp are consistent with recent measurements of collagen’s flexibility in these acidic solvent conditions (unpublished, N. Rezaei and N. R. Forde). It is also important to note that this model ignores dissociation dynamics, implicitly assuming them to occur with rates slower than considered here (koff < 1 s−1) (38).
Telopeptide-mediated collagen-collagen interactions
Within D-banded fibrillar collagen, the C-telopeptides of one collagen adjoin the MMP site 3/4 of the length along a neighboring triple helix (39). Transient associations between telopeptides and this target site have been proposed to explain telopeptide “catalysis” of fibril assembly (21). The acidic pH of our experiments differs from the neutral conditions promoting this fibril assembly and could alter electrostatic interactions responsible for specific docking during collagen fibril formation (10). For interactions of the C-telopeptide, however, Prockop and Fertala showed that hydrophobic rather than charged residues are important for the specificity of telopeptide interactions (21). As a result, the interactions probed via microrheology may bear relevance to the telopeptide-facilitated nucleation stages of native fibril assembly. Intriguingly, the complex shear moduli of collagen solutions differ little between acidic conditions and during the nucleation phase of fibril formation (22). This observation suggests that any changes in collagen flexibility and/or interactions induced by modulation of solution pH and ionic strength do not significantly affect shear moduli at prefibrillar stages of self-assembly.
In acidic conditions, an alternative supramolecular structure known as segment long-spacing (SLS) collagen can form, in which collagen chains are laterally in register (40). The generally compact nature of these crystalline structures (41) suggests that their precursors would not contribute long-range (low-frequency) viscoelastic response to collagen solutions. Furthermore, our experiments lack a required cofactor (such as ATP) for SLS aggregate formation.
Fig. 10 summarizes in schematic form how telopeptides may influence associations between collagens. Qualitatively, our results and discussions point to the formation of longer-range, transient rather than permanent associations between collagens that are reduced by pepsin cleavage of telopeptides. Fig. 10, a and b, illustrate the differences in populations of higher-order species resulting from telopeptide-based association in acidic conditions. Here, we depict telopeptides transiently docking on neighboring collagens as proposed for assembly into fibrils (21), though association in this sequence-specific manner is not a requirement for the proposed mechanism. For example, our chemical equilibrium Rouse model assumes transient interactions via an end-to-end mechanism. The specificity of the interactions observed in acidic conditions could be compared with those proposed to promote fibril formation by, for example, cross-linking transiently interacting collagen in acidic conditions prior to inducing fibril formation, or by testing the ability of telopeptides added in trans to block these transient interactions (21). Figs. 10, c and d, illustrate the differences in fibril assembly resulting from pepsin digestion of telopeptides. This model is based on the work of Prockop and Fertala, who inhibited fibril assembly by blocking C-telopeptide-triple-helix association (21). We describe the mechanism of telopeptide-catalyzed fibril nucleation as facilitated docking: with a telopeptide-based “toe-hold” on the appropriate site of an adjacent helix, the diffusional search for specific lateral packing of two triple helices is significantly restricted (Fig. 10 c), compared with aligning two independent chains free in solution (Fig. 10 d).
In this study, we have compared the complex shear moduli of collagen with intact and digested telopeptides. Pepsin treatment is well established as a tool for investigating the influence of telopeptides on collagen properties. As noted above, pepsin is not able to cleave the telopeptides entirely. Thus, in these studies a portion of the telopeptides remains. We have captured this in our model by incorporating a weaker, but nonzero, association constant between atelo-collagens. Complete removal of telopeptides can be achieved by other proteases such as pronase, though care must be taken that digestion does not also proceed into the triple helix (13). In this case, effects on fibril formation are profound (13). If telopeptides are the sole source of specific associations between collagen proteins in acidic solutions, then for pronase-digested collagen our model would simplify to a prediction of unimer response only (Keq = 0). G′ and G″ for this fully removed telopeptide sample (unimers with no interactions) are predicted to be lower than their corresponding atelo values (Fig. S8). Moreover, G′ for this solution of unimers is predicted to scale linearly with concentration in the experimentally relevant frequency range, while G″ is predicted to increase sublinearly with concentration (Fig. S9). These predictions could be tested in future experiments.
Conclusions
This study has demonstrated that telopeptides significantly increase the complex shear modulus of collagen solutions in a frequency- and concentration-dependent manner. This effect is seen both in commercially prepared samples and in collagens digested in-house to remove telopeptides. We have interpreted these findings using a polymer model that assumes telopeptide-specific transient association, and provides frequency- and concentration-dependent moduli for telo- and atelo-collagen samples. This model complements the transient network model (30) by considering a lifetime for transient cross-links longer than measurement times. Our measurements and model-based interpretation provide physical evidence supporting a previously proposed telopeptide-dependent transient association mechanism, key to promoting nucleation and further growth of collagen into fibrils (13, 21).
Our experiments also used microrheology to read out, in real time, the evolution of complex shear modulus arising from the proteolytic removal of collagen’s telopeptides. This result demonstrates the potential of microrheology to serve as both diagnostic and synthetic tool for in situ control of viscoelastic properties: measurement of these properties in real time would enable a quench of the system via enzymatic inhibition at a desired viscoelastic end point.
Here, we have utilized the technique of optical tweezers microrheology to examine protein-protein interactions and, via modification of the protein sequences, have probed the sequence-dependence of these interactions. Importantly a key observation that motivated our model, the crossover response in G″R/c, occurs at a frequency higher than accessed by conventional bulk rheology, providing an example of how the higher frequencies accessible by optical tweezers microrheology can provide insight into interacting biopolymer systems. Although it would be tempting to ascribe to this crossover behavior a key timescale of telopeptide-mediated collagen interactions, the same behavior is exhibited in our chemical equilibrium model of associating polymers that lacks explicit association and dissociation kinetics. Our study extends previous applications of microrheology, which examined interactions of cross-linking proteins with filamentous actin substrates, by focusing on interactions intrinsic to the self-assembling proteins themselves. Extensions of this work could examine how collagen associations may be altered in disease, using recombinantly expressed proteins to test sequence-function hypotheses (42), and could explore sequence-dependent protein-protein interactions important for nucleating higher-order structure formation in other self-assembling and/or pathogenic aggregating protein systems.
Author Contributions
M.S., T.A., and N.R.F. designed research; M.S., T.A., and E.K. performed experiments and analyzed results; T.A. led development of the polymer model; and M.S. and N.R.F. led the writing of the manuscript, to which all authors contributed.
Acknowledgments
We gratefully acknowledge Barbara Frisken for use of the dynamic light scattering instrument and assistance with data analysis and interpretation. We thank Martin Zuckermann and members of the Forde lab for useful comments on this work.
This research was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC).
Editor: Keir Neuman
Footnotes
Marjan Shayegan and Tuba Altindal contributed equally to this work.
Marjan Shayegan’s present address is Department of Physics, McGill University, Montreal, Canada.
Evan Kiefl’s present address is Biophysical Sciences Graduate Program, University of Chicago, Chicago, Illinois.
Supporting Material and Methods, nine figures, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30998-5.
Supporting Citations
References (43, 44, 45, 46, 47, 48, 49, 50) appear in the Supporting Material.
Supporting Material
References
- 1.Janmey P.A., Weitz D.A. Dealing with mechanics: mechanisms of force transduction in cells. Trends Biochem. Sci. 2004;29:364–370. doi: 10.1016/j.tibs.2004.05.003. [DOI] [PubMed] [Google Scholar]
- 2.Wells R.G. The role of matrix stiffness in regulating cell behavior. Hepatology. 2008;47:1394–1400. doi: 10.1002/hep.22193. [DOI] [PubMed] [Google Scholar]
- 3.Hoffman B.D., Grashoff C., Schwartz M.A. Dynamic molecular processes mediate cellular mechanotransduction. Nature. 2011;475:316–323. doi: 10.1038/nature10316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lee C.H., Singla A., Lee Y. Biomedical applications of collagen. Int. J. Pharm. 2001;221:1–22. doi: 10.1016/s0378-5173(01)00691-3. [DOI] [PubMed] [Google Scholar]
- 5.Williams B.R., Gelman R.A., Piez K.A. Collagen fibril formation. Optimal in vitro conditions and preliminary kinetic results. J. Biol. Chem. 1978;253:6578–6585. [PubMed] [Google Scholar]
- 6.Wood G.C., Keech M.K. The formation of fibrils from collagen solutions. 1. The effect of experimental conditions: kinetic and electron-microscope studies. Biochem. J. 1960;75:588–598. doi: 10.1042/bj0750588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yang Y.L., Kaufman L.J. Rheology and confocal reflectance microscopy as probes of mechanical properties and structure during collagen and collagen/hyaluronan self-assembly. Biophys. J. 2009;96:1566–1585. doi: 10.1016/j.bpj.2008.10.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li Y., Asadi A., Douglas E.P. pH effects on collagen fibrillogenesis in vitro: electrostatic interactions and phosphate binding. Mater. Sci. Eng. C. 2009;29:1643–1649. [Google Scholar]
- 9.Fertala A., Sieron A.L., Prockop D.J. Self-assembly into fibrils of collagen II by enzymic cleavage of recombinant procollagen II. Lag period, critical concentration, and morphology of fibrils differ from collagen I. J. Biol. Chem. 1994;269:11584–11589. [PubMed] [Google Scholar]
- 10.Comper W.D., Veis A. The mechanism of nucleation for in vitro collagen fibril formation. Biopolymers. 1977;16:2113–2131. doi: 10.1002/bip.1977.360161004. [DOI] [PubMed] [Google Scholar]
- 11.Helseth D.L., Jr., Veis A. Collagen self-assembly in vitro. Differentiating specific telopeptide-dependent interactions using selective enzyme modification and the addition of free amino telopeptide. J. Biol. Chem. 1981;256:7118–7128. [PubMed] [Google Scholar]
- 12.Brennan M., Davison P.F. Influence of the telopeptides on type I collagen fibrillogenesis. Biopolymers. 1981;20:2195–2202. doi: 10.1002/bip.1981.360201012. [DOI] [PubMed] [Google Scholar]
- 13.Kuznetsova N., Leikin S. Does the triple helical domain of type I collagen encode molecular recognition and fiber assembly while telopeptides serve as catalytic domains? Effect of proteolytic cleavage on fibrillogenesis and on collagen-collagen interaction in fibers. J. Biol. Chem. 1999;274:36083–36088. doi: 10.1074/jbc.274.51.36083. [DOI] [PubMed] [Google Scholar]
- 14.Wolf K., Te Lindert M., Friedl P. Physical limits of cell migration: control by ECM space and nuclear deformation and tuning by proteolysis and traction force. J. Cell Biol. 2013;201:1069–1084. doi: 10.1083/jcb.201210152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Demou Z.N., Awad M., Boucher Y. Lack of telopeptides in fibrillar collagen I promotes the invasion of a metastatic breast tumor cell line. Cancer Res. 2005;65:5674–5682. doi: 10.1158/0008-5472.CAN-04-1682. [DOI] [PubMed] [Google Scholar]
- 16.Perumal S., Antipova O., Orgel J.P.R.O. Collagen fibril architecture, domain organization, and triple-helical conformation govern its proteolysis. Proc. Natl. Acad. Sci. USA. 2008;105:2824–2829. doi: 10.1073/pnas.0710588105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Simojoki M., Santala M., Kauppila A. Carboxyterminal telopeptide of type I collagen (ICTP) in predicting prognosis in epithelial ovarian cancer. Gynecol. Oncol. 2001;82:110–115. doi: 10.1006/gyno.2001.6212. [DOI] [PubMed] [Google Scholar]
- 18.Lohmander L.S., Atley L.M., Eyre D.R. The release of crosslinked peptides from type II collagen into human synovial fluid is increased soon after joint injury and in osteoarthritis. Arthritis Rheum. 2003;48:3130–3139. doi: 10.1002/art.11326. [DOI] [PubMed] [Google Scholar]
- 19.Vasikaran S., Eastell R., Kanis J.A. Markers of bone turnover for the prediction of fracture risk and monitoring of osteoporosis treatment: a need for international reference standards. Osteoporos. Int. 2011;22:391–420. doi: 10.1007/s00198-010-1501-1. [DOI] [PubMed] [Google Scholar]
- 20.Garnero P., Ferreras M., Delaissé J.M. The type I collagen fragments ICTP and CTX reveal distinct enzymatic pathways of bone collagen degradation. J. Bone Miner. Res. 2003;18:859–867. doi: 10.1359/jbmr.2003.18.5.859. [DOI] [PubMed] [Google Scholar]
- 21.Prockop D.J., Fertala A. Inhibition of the self-assembly of collagen I into fibrils with synthetic peptides. Demonstration that assembly is driven by specific binding sites on the monomers. J. Biol. Chem. 1998;273:15598–15604. doi: 10.1074/jbc.273.25.15598. [DOI] [PubMed] [Google Scholar]
- 22.Shayegan M., Forde N.R. Microrheological characterization of collagen systems: from molecular solutions to fibrillar gels. PLoS One. 2013;8:e70590. doi: 10.1371/journal.pone.0070590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Engvall E., Perlmann P. Enzyme-linked immunosorbent assay, Elisa. 3. Quantitation of specific antibodies by enzyme-labeled anti-immunoglobulin in antigen-coated tubes. J. Immunol. 1972;109:129–135. [PubMed] [Google Scholar]
- 24.Shayegan M., Forde N.R. Probing the viscoelasticity of collagen solutions via optical-tweezers-based microrheology. MRS Proc. 2012;1465 mrss12-1465-ss06-08. [Google Scholar]
- 25.van der Horst A., Forde N.R. Calibration of dynamic holographic optical tweezers for force measurements on biomaterials. Opt. Express. 2008;16:20987–21003. doi: 10.1364/oe.16.020987. [DOI] [PubMed] [Google Scholar]
- 26.Addas K.M., Schmidt C.F., Tang J.X. Microrheology of solutions of semiflexible biopolymer filaments using laser tweezers interferometry. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:021503. doi: 10.1103/PhysRevE.70.021503. [DOI] [PubMed] [Google Scholar]
- 27.Doi M., Edwards S.F. Oxford University Press; New York: 1988. The Theory of Polymer Dynamics; pp. 218–283. [Google Scholar]
- 28.Hulmes D.J. Springer; Boston: 2008. Collagen. [Google Scholar]
- 29.Drake M.P., Davison P.F., Schmitt F.O. Action of proteolytic enzymes on tropocollagen and insoluble collagen. Biochemistry. 1966;5:301–312. doi: 10.1021/bi00865a039. [DOI] [PubMed] [Google Scholar]
- 30.Broedersz C.P., Depken M., MacKintosh F.C. Cross-link-governed dynamics of biopolymer networks. Phys. Rev. Lett. 2010;105:238101. doi: 10.1103/PhysRevLett.105.238101. [DOI] [PubMed] [Google Scholar]
- 31.Oechsle A.M., Wittmann X., Weiss J. Collagen entanglement influenced by the addition of acids. Eur. Polym. J. 2014;58:144–156. [Google Scholar]
- 32.Claire K., Pecora R. Translational and rotational dynamics of collagen in dilute solution. J. Phys. Chem. B. 1997;101:746–753. [Google Scholar]
- 33.Rennar N., Oppermann W. Swelling behavior and mechanical properties of endlinked poly (dimethylsiloxane) networks and randomly crosslinked polyisoprene networks. Colloid Polym. Sci. 1992;270:527–536. [Google Scholar]
- 34.Saldivar-Guerra E., Vivaldo-Lima E. Wiley; New York: 2013. Handbook of Polymer Synthesis, Characterization, and Processing. [Google Scholar]
- 35.Lieleg O., Claessens M.M.A.E., Bausch A.R. Mechanics of bundled semiflexible polymer networks. Phys. Rev. Lett. 2007;99:088102. doi: 10.1103/PhysRevLett.99.088102. [DOI] [PubMed] [Google Scholar]
- 36.Müller K.W., Bruinsma R.F., Levine A.J. Rheology of semiflexible bundle networks with transient linkers. Phys. Rev. Lett. 2014;112:238102. doi: 10.1103/PhysRevLett.112.238102. [DOI] [PubMed] [Google Scholar]
- 37.Ferry J.D. Wiley; New York: 1980. Viscoelastic Properties of Polymers. [Google Scholar]
- 38.Watanabe H., Matsumiya Y., Masubuchi Y. Viscoelastic relaxation of Rouse chains undergoing head-to-head association and dissociation: motional coupling through chemical equilibrium. Macromolecules. 2015;48:3014–3030. [Google Scholar]
- 39.Orgel J.P.R.O., Irving T.C., Wess T.J. Microfibrillar structure of type I collagen in situ. Proc. Natl. Acad. Sci. USA. 2006;103:9001–9005. doi: 10.1073/pnas.0502718103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chapman J.A., Hulmes D.J.S. Electron microscopy of the collagen fibril. In: Ruggeri A., Motta P.M., editors. Ultrastructure of the Connective Tissue Matrix. Springer; Boston: 1984. pp. 1–33. [Google Scholar]
- 41.Loo R.W., Goh J.B., Goh M.C. In vitro synthesis of native, fibrous long spacing and segmental long spacing collagen. J. Vis. Exp. 2012;67:e4417. doi: 10.3791/4417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wieczorek A., Rezaei N., Forde N.R. Development and characterization of a eukaryotic expression system for human type II procollagen. BMC Biotechnol. 2015;15:112. doi: 10.1186/s12896-015-0228-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bhatnagar R.S., Qian J.J., Gough C.A. The role in cell binding of a beta-bend within the triple helical region in collagen alpha 1 (I) chain: structural and biological evidence for conformational tautomerism on fiber surface. J. Biomol. Struct. Dyn. 1997;14:547–560. doi: 10.1080/07391102.1997.10508155. [DOI] [PubMed] [Google Scholar]
- 44.Sun Y.-L., Luo Z.-P., An K.-N. Direct quantification of the flexibility of type I collagen monomer. Biochem. Biophys. Res. Commun. 2002;295:382–386. doi: 10.1016/s0006-291x(02)00685-x. [DOI] [PubMed] [Google Scholar]
- 45.Lovelady H.H., Shashidhara S., Matthews W.G. Solvent specific persistence length of molecular type I collagen. Biopolymers. 2014;101:329–335. doi: 10.1002/bip.22365. [DOI] [PubMed] [Google Scholar]
- 46.Varma S., Orgel J.P., Schieber J.D. Nanomechanics of Type I collagen. Biophys. J. 2016;111:50–56. doi: 10.1016/j.bpj.2016.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Teraoka I. Wiley; New York: 2002. Polymer Solutions: An Introduction to Physical Properties. [Google Scholar]
- 48.Shayegan, M. 2014. Determining local viscoelastic properties of collagen systems using optical tweezers. PhD dissertation. Simon Fraser University, Burnaby, Canada.
- 49.Han S., McBride D.J., Leikin S. Segregation of type I collagen homo- and heterotrimers in fibrils. J. Mol. Biol. 2008;383:122–132. doi: 10.1016/j.jmb.2008.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cannon-Carlson S., Tang J. Modification of the Laemmli sodium dodecyl sulfate-polyacrylamide gel electrophoresis procedure to eliminate artifacts on reducing and nonreducing gels. Anal. Biochem. 1997;246:146–148. doi: 10.1006/abio.1997.2002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.